Atomic modeling of cryo-electron microscopy reconstructions – Joint refinement of model and imaging parameters

Abstract

When refining the fit of component atomic structures into electron microscopic reconstructions, use of a resolution-dependent atomic density function makes it possible to jointly optimize the atomic model and imaging parameters of the microscope. Atomic density is calculated by one-dimensional Fourier transform of atomic form factors convoluted with a microscope envelope correction and a low-pass filter, allowing refinement of imaging parameters such as resolution, by optimizing the agreement of calculated and experimental maps. A similar approach allows refinement of atomic displacement parameters, providing indications of molecular flexibility even at low resolution. A modest improvement in atomic coordinates is possible following optimization of these additional parameters. Methods have been implemented in a Python program that can be used in stand-alone mode for rigid-group refinement, or embedded in other optimizers for flexible refinement with stereochemical restraints. The approach is demonstrated with refinements of virus and chaperonin structures at resolutions of 9 through 4.5 Å, representing regimes where rigid-group and fully flexible parameterizations are appropriate. Through comparisons to known crystal structures, flexible fitting by RSRef is shown to be an improvement relative to other methods and to generate models with all-atom rms accuracies of 1.5–2.5 Å at resolutions of 4.5–6 Å.

1. Introduction

In structure-function studies of large biomolecular assemblies and their interactions, hybrid analyses are increasingly the foundation (Alber et al., 2008). Most commonly, details of interactions are obtained through the computational fitting of higher resolution component structures, obtained by X-ray crystallography, NMR spectroscopy and/or homology modeling, into images of the entire assembly obtained at lower resolution, often by cryo-Electron Microscopy (EM) (Fabiola and Chapman, 2005; Goddard et al., 2007; Lasker et al., 2010; Rossmann and Arnold, 2001; Topf et al., 2008). Computational approaches have differed mostly in terms of the parameterization of the model and the method of optimization, balancing flexible adaptation of the atomic model with constraints that reduce the potential for over-fitting at low resolution. Thus, approaches have included rigid-fragment fitting (Fabiola and Chapman, 2005; Roseman, 2000), low-parameter deformations (Schröder et al., 2010; Tama et al., 2004; Wriggers, 2010) and fully flexible, all-atom gradient-descent and molecular dynamics optimizers (Topf et al., 2008; Trabuco et al., 2008). In spite of growing popularity, tests suggest that rigid-fragment refinement might typically be more accurate than flexible fitting at resolutions worse than 5 Å (Volkmann, 2009). The emergence of EM reconstructions beyond 5 Å in the last few years (Baker et al., 2010; Grigorieff and Harrison, 2011; Zhou, 2008; Zhu et al., 2010), defines a new need for flexible fitting at near-atomic resolution, and the likelihood that both flexible and rigid-group approaches will continue to be needed to service the varying resolution regimes available for different molecular systems.

Common to all approaches is a need to assess the quality of fit for an atomic model with the experimental data, and, in most cases, to predict the changes to the atomic model that will improve the fit. Many methods maximize a correlation coefficient between experimental and predicted density, or near-equivalently minimize the least-squares scaled residual difference (Chapman, 1995; Roseman, 2000; Vasishtan and Topf, 2011; Volkmann and Hanein, 1999). For computational expediency a number of approximations have been introduced. For example, fitting can be recast as a maximization of the number of atoms inside a map envelope, or a maximization of the density at atomic centers (Rossmann et al., 2001; Vasishtan and Topf, 2011). Alternatively, one of several approximations to a correlation coefficient can be employed. Particularly in crystallo-graphic applications, it is common to assume that density from neighboring atoms is non-overlapping. The correlation of density at atomic centers is then very quick to calculate, because shape of an atom’s density need not be considered (Adams et al., 2010; Emsley et al., 2010; Grosse-Kunstleve et al., 2009; Ioerger and Sacchettini, 2003; Trabuco et al., 2008; Yang et al., 2012). Such approximations may be needed for fast calculations in global searches, interactive graphics or molecular dynamics optimization. However, evaluation of a number of scoring functions shows that the approximations can come with a loss of accuracy (Vasishtan and Topf, 2011), and here it is shown that full comparison of predicted and experimental density is tractable for many EM-based refinements.

An unresolved issue in calculating the predicted density from an atomic model has been the blurring required to account for the attenuation of high resolution signal. Following the precedent set in crystallography, it is usual to represent the density of each atom as a spherical Gaussian function of width related to the resolution (Diamond, 1971; Jones and Liljas, 1984). Parametric equations were derived by Diamond to approximate the effect of truncation at crystallographic resolutions. However, in EM resolution regimes, parameterization is entirely ad hoc, even though it can affect the accuracy of the scoring function (Vasishtan and Topf, 2011). Three remedies have been proposed. Firstly, the refinement can be performed completely in reciprocal space (Navaza et al., 2002) though at some increased risk of over-fitting (Chen et al., 1999). Secondly, the calculated map can be Fourier transformed and inverted with a resolution limit prior to real-space fitting (Jacobson et al., 1996): partial derivatives for structure optimization cannot be calculated directly, so are approximated. Thirdly, the calculated map can be assembled from the densities of individual atoms, each calculated by a resolution-limited Fourier transform of the atomic scattering factor (Chapman, 1995).

The third approach was developed for crystallographic real-space refinement, but its potential in EM was demonstrated with ribosome and acto-myosin structures (Chen et al., 2001; Gao et al., 2003; Mitra et al., 2006). It was not initially widely adopted, because the crystallographic software was inefficient when applied to EM. However, it is the approach adopted in DireX (Schröder et al., 2010; Wang and Schröder, 2012), with an ad hoc modification to smooth the gradients. Smoothing would be needed, because, in addition to the hard resolution limit applicable in crystallography, EM reconstructions are blurred by the effects of a gradual, but significant instrumental signal attenuation at high resolution.

The current work was motivated by the need for an implementation that would account for resolution-dependent signal attenuation without ad hoc assumptions. This is accomplished with an extension to the previously developed theory (Chapman, 1995) and new software that inherits the RSRef name, but has been completely re-written to accommodate the needs of EM-based model refinement. We describe the algorithms and performance of software that can be used either as a stand-alone program for rigid-fragment refinement, or embedded in packages adding stereo-chemical restraints and sophisticated optimizers, including torsion angle simulated annealing (Brünger et al., 1998).

2. Materials and methods

2.1. Calculation of model electron or coulombic potential density

The new methodology embodies a series of extensions on the earlier crystallographic theory (Chapman, 1995). Assuming that atoms are isotropic (spherically symmetric), the calculated density ρ_c of each atom i, as a function of distance, r, from the center, is given by the definite Fourier integral between the resolution limits, d_min, d_max, of the atomic form factor, f_i, which describes the scattering of an atom as a function of the reciprocal space distance, h.

$${\rho }_{c,i}(r)={\int }_{h=1/d_{\text{max}}}^{h=1/d_{\text{min}}}C(h)f_i(h)\sqrt{\frac{\pi /2}{{(2\pi rh)}^3}}.J_{3/2}(2\pi rh)dh$$ (1)

As noted by Don Caspar (pers. Commun.), this form, using a ½-order Bessel function, is equivalent to a sine form derived earlier (Chapman, 1995, Eq. 11). Hard (truncation) limits on resolution are imposed through the integration limits. More gradual signal attenuation can be captured in C(h). In the new implementation, C(h) is expanded for electron microscopy to be the product of: (1) a Gaussian envelope transfer function, H_E, that approximates signal attenuation from spatial and temporal incoherence and other instrumental effects (Saad et al., 2001); (2) a Gaussian B-factor, H_B, accounting for thermal displacement/disorder in the atomic model (Stout and Jensen, 1989); and (3) a low-pass filter transfer function, H_F, to account for other loss of signal at high resolution, as seen in a Fourier shell correlation curve. A Butterworth function (5th order) (Butterworth, 1930) was chosen to represent H_F, because of its near-uniform value at low resolution, rapid but smooth fall-off, and minimal truncation ripple, features that have led to its prior use in EM processing packages (Shaikh et al., 2008). Through refinement of the parameters of these functions, the blurring of each atom’s density is adjusted to maximize agreement between calculated and experimental maps. The sharp fall-off of the Butterworth filter allows calculated density to be fit to reconstructions that have been sharpened using a (Gaussian) inverse envelope function to reveal greater detail, but in which the high resolution signal will fall precipitously at some point (Fernandez et al., 2008).

For computation, the integral is replaced by a discrete one dimensional transform with 15 shells in h. The error of discretization is not limiting: maximal deviations from FFT-calculated maps (Ten Eyck, 1973) are less than 1% over all resolutions between 1 and 15 Å. Calculation is truncated at low density levels, at a distance from atoms that is (by default) 2.5 × the nominal resolution limit. Other efficiencies made the approach tractable for large EM complexes: grid-point densities are interpolated from tables of density versus distance that are calculated when needed then cached for re-use by atoms of the same type and B-factor. Distance calculations, density interpolation and the summation of density from neighboring atoms are vectorized through use of the NumPy libraries (Oliphant, 2006).

2.2. Partial derivatives

The fit is improved by minimizing an objective function that is the least-squares difference between the reconstruction and the map calculated from the atomic model. Efficient optimizers, whether least-squares gradient descent or molecular dynamics, require the partial derivatives of the objective function with respect to each model parameter. These are calculated from the derivatives of Eq. (1) by application of the chain rule as described earlier for atomic positions, B-factors and occupancy (Chapman, 1995). New to the current implementation is rigid-group parameterization and refinement of the magnification, resolution and envelope correction, collectively termed imaging parameters, for which partial derivatives are also needed.

A Gaussian envelope correction has the same functional form as an atomic displacement “B” factor. Thus, the partial derivative of H_E can be calculated from the sum of ∂H_E/∂B (given in Chapman (1995)) over all atoms, scaling to account for different unit conventions. The transfer function for an n^th-order Butterworth low-pass filter can be differentiated with respect to the “cut-off” resolution. We use the conventional definition of cut-off as the d₀ of half-power transfer where H²(d₀)/H²(∞) = ½. (We also report d_0.5 for H(d_0.5)/H(∞) = ½ that is more consistent with FSC_0.5 and other definitions of resolution in structural biology).

$$H_F(h)=1/\sqrt{{(d_{0}h)}^{2n};}\text{where}{H}_F(d_0)/H_F(\infty )=1/\sqrt{2}$$ (2)

$$\text{then}\partial H_F/\partial d_0=-H_F^{-3/2}nh{(d_{0}h)}^{2n-1}$$ (3)

Rigid group rotations are parameterized as rotation vectors along the axis of rotation with length equal to the magnitude of rotation. Rotation-translation operators, R, are calculated as 4-by-4 augmented matrices, as are their six partial derivatives with respect to each component of the rotation and translation vectors (combined in the 6-dimensional vector, v⃗ below). Then the partial derivative of the fit function, Γ, can be calculated from the current operator, R, the starting coordinates, p⃗₀), and the partials with respect to atomic positions, ∂Γ/∂p⃗, that are calculated as described in Chapman (1995)):

$$\partial \Gamma /\partial \overrightarrow{v}=\partial \Gamma /\partial \overrightarrow{p}·\partial \overrightarrow{p}/\partial \overrightarrow{v}=\partial \Gamma /\partial \overrightarrow{p}·\partial (R{\overrightarrow{p}}_0)/\partial \overrightarrow{v}=\partial \Gamma /\partial \overrightarrow{p}·\partial R/\partial \overrightarrow{v}·{\overrightarrow{p}}_0$$ (4)

Expressed this way, the contributions of all atoms to the group partials can be calculated simultaneously as a concatenation of matrix operators using vectorized NumPy routines (Oliphant, 2006).

2.3. Symmetry and neighboring atoms

In real-space refinement, a fragment of the entire structure can be refined, as long as the overlapping density of neighboring atoms is accounted for. The new implementation can work with a unique asymmetric unit of atoms, refining all or a selected subset. The density of neighboring atoms is generated following expansion of both local molecular symmetry and space group lattice symmetry, as applicable. Computation is reduced by prior identification of potential neighbors, allowing for maximal likely shifts during refinement. With a list of neighbors, and the symmetry operators that generate them, changes to neighbors can be continually propagated from refining atoms. This implementation is therefore imposing symmetry as an exact constraint. Should deviations from exact symmetry be appropriate, multiple equivalents could be refined, but restraints on similarity would have to come from an embedding program.

2.4. Implementation

The methods are coded in ~13,000 lines of Python 2.7 (Martelli, 2006). Through extensive use of standard NumPy and SciPy libraries (Jones et al., 2001; Oliphant, 2006), implicit use is made of highly optimized compiled C and Fortran source, but there are no explicit C-extensions in RSRef, except in optional modules described below. Thus, basic functionality is supported on the wide variety of computing platforms on which Python is available.

Support for multiple common map formats is provided through a wrapper for parts of the B Soft library (Heymann and Belnap, 2007). Supported formats include MRC, Spider and CCP4. Natively, RSRef supports the X-Plor format when BSoft is not available.

A wrapper for RSRef, written in C, allows it to be embedded in external (compiled) programs through calls to a shared object library. Functionality includes map-reading, calculation of model density, evaluation of the fit, and calculation of partial derivatives. The wrapper provides a generic interface for in-memory sharing of coordinates and derivatives. A minimalist interface written in Fortran or C, is then compiled with the calling program to handle the program-specifics of data representation. The goals are to minimize changes needed in the calling program to support real-space refinement and to facilitate support of new releases. For CNS (v1.3) (Brünger et al., 1998), 12 text substitutions in four files are patched with a Python script.

In stand-alone mode, optimizations are performed with the limited memory L-BFGS constrained minimizer (Byrd et al., 1995; Zhu et al., 1997) as implemented in SciPy (Jones et al., 2001). Convergence is improved by separating optimization of imaging parameters and of atomic parameters into different batches, and applying bounds on acceptable imaging parameter values to limit fluctuations in early cycles. Parameters of different types and units can be refined together (atom positions, group rotation, B-factors etc.). However, as optimization is not scale-invariant, parameter values and partial derivatives must be normalized to a set of internal units. Default unit scaling constants have been set empirically for approximately even optimization of different parameter types in test cases. Refinement is robust if unit scaling constants are of the correct order of magnitude. As optimal values can depend on the size of molecule, resolution and stage of refinement, the scale constants are accessible for user adjustment.

2.5. Refinement modes and atom selection

Parameters that can be refined include atomic positions (‘xyz’), occupancy, displacement parameters (‘B’), EM magnification, resolution and envelope correction. Atomic parameters can be optimized in several modes/parameterizations: overall, group and individual. With stereochemical restraints available only from a calling program, stand-alone usage will usually be rigid body, either for the entire structure (‘overall’) or for one or more fragments (‘group’). In rigid body modes, positions are refined as a rotation about an axis through the center of mass, followed by a translation; displacement parameters are refined as an additional B-factor applied throughout the group; and occupancy is refined as a multiplicative factor of the starting occupancy. Mixed refinement can be specified with a syntax exemplified below:

select domains-constant: S (((‘chain == L’) and (‘residue_number >= 108’)) | ((‘cha == H’) & (‘resnum >= 121’)))

select domains-variable: (S(‘chain == L’) & S(‘residue num <= 107’)) | (S(‘chain == H’) and S(‘residue num <= 120’))

refine xyz={‘group’: domains} B={‘group’: domains[‘constant’]}, max_cycles = 5, min_improvement = 1.e–4, min_grad = 1000., analyze

In this example, an FAb is split into variable and constant domains, each containing fragments of two chains, H and L. Atomic positions are refined as rigid groups for each of the domains, while an additional B-factor is refined simultaneously, but only for the constant domain. Atom selections, “S()” above, are implemented as a sub-class of a Boolean NumPy array with an attribute that references the atomic coordinates to which it is attached. Methods set True/False values based on comparisons of any of an atoms input attributes, such as chain, residue type, atom type etc. Selections can be combined using any of the Python unary logical operators.

2.6. Stereochemical restraints and flexible fitting

Geometric restraints will come from a calling program such as CNS (Brünger et al., 1998) and are not provided by RSRef in stand-alone mode. For rigid-group refinement, it may be sufficient to include only terms for inter-subunit van der Waal’s repulsion. Should it be desirable to restrain covalent geometry between fragments of the same chain, rigid group refinement can be used with a full force field potential. Thus, rigid group refinement can be performed using RSRef either in stand-alone or embedded modes according to the need for restraints.

For flexible atomic refinement, stereochemical restraints will be needed, so the embedded mode of usage will be required. Optimizers of the calling program can extend the stand-alone capabilities of RSRef. In addition to gradient-descent minimization, CNS supports molecular dynamics optimization. It also supports parameterization of the model in both Cartesian space, and also in torsion angle space (Brünger et al., 1998). Torsion angle parameterization is of particular interest for EM resolutions, because it has fewer degrees of freedom than Cartesian-space parameterization. It is therefore less underdetermined and presumably less susceptible to over-fitting.

2.7. Distribution and documentation

Optional compilation of extensions and embedding in CNS is performed by a Python distutils setup script. HTML documentation is compiled from source-code docstrings using EpyDoc.

3. Results

The methods have been applied in two recent structure determinations that illustrate their application in two resolution regimes. The first involves the docking of an FAb’ fragment of a neutralizing antibody onto its binding site on the surface of ade-no-associated virus-2 (AAV-2) using data at ~8.5 Å resolution. The second involves the structure determination of a chimeric AAV variant, AAV-DJ using data at ~4.5 Å resolution, an example where flexible fitting was required to refine the tertiary structure. At an intermediate resolution, the methodology has also been bench-marked for both rigid-group and flexible fitting with the Methanococcus marapaludis chaperonin (Mm-cpn) EM structure (Zhang et al., 2010), for which a crystal structure is now available (Pereira et al., 2010).

3.1. Complex of FAb’ A20 with AAV-2

AAV is a small icosahedral non-enveloped virus consisting of 25 nm diameter protein shell surrounding a single-stranded DNA genome (Xie et al., 2002). The main interest in this non-pathogenic virus is in its development as a recombinant rAAV vector for human gene therapy (Carter et al., 2008; Muzyczka and Berns, 2001). One of its limitations, in vivo, is the generation of neutralizing antibodies that reduce transduction efficiency (Manno et al., 2006; Wang et al., 2011). The best characterized neutralizing monoclonal is the anti-AAV-2 antibody A20 (Wobus et al., 2000). Until recently, it remained refractory to structural studies, but the complex of an FAb’ fragment with the virus was recently determined by cryo-EM (McCraw et al., 2012).

As previously reported, EM images were collected using the Leginon system (Suloway et al., 2005) at 37,000× magnification and 120 keV on a FEI Titan Krios equipped with a Gatan Ultrascan 4 k × 4 k CCD camera with a pixel size was 2.225 Å (McCraw et al., 2012). Initial processing by Appion (Lander et al., 2009) included CTF estimation with ACE (Mallick et al., 2005). Subsequent refinement and reconstruction was with EMAN (Tang et al., 2007), eventually resulting in a reconstruction based on 11,898 particles with resolution estimates of 6.7 Å (FSC_0.143) or 8.5 Å (FSC_0.5). The map was sharpened with an inverse envelope correction applied using EMB-factor with default parameters (Fernandez et al., 2008).

The 3-D structure of antibody A20 was unknown. Using sequences for the variable regions, a homology model of the FAb’ was built using Modeller (Eswar et al., 2006) and cross-checked against a database of CDR conformation (North et al., 2011). Five of six CDRs had RMS C_α deviations of 0.4 Å, one (H3) was at 1.5 Å. With more conserved β-barrels, the overall backbone error is likely <0.7 Å.

Difference maps revealed no evidence of conformational changes, so the 3.0 Å virus structure (PDB id 1LP3) (Xie et al., 2002) was docked into the map by superposition of the icosahedral symmetry elements without further refinement. The task was to refine the 432-residue antibody fragment into the reconstruction of the complex, starting from a “manual” fitting performed with Coot (Emsley et al., 2010), that, in retrospect, appears to have accuracy of ~4 Å.

Refinement was split into four batches throughout which icosahedral symmetry was imposed (Table 1). First, the FAb’ was refined as a single rigid group using a hard 6.7 Å resolution limit corresponding to the FSC_0.143. The rotation of 9.5° and translation of 1.7 Å in this first step accounts for ¾ of the total improvement. With this partially refined atomic model, imaging parameters were optimized, yielding a 10% improvement in correlation with an envelope correction of 34 Ų and a “soft” resolution limit on the filter of d₀ = 9.6 Å, corresponding to d_0.5 = 8.6 Å, agreeing with FSC_0.5 = 8.5 Å. A magnification change of only 0.1% was indicated, but a correction of 7.5% had already been refined and applied prior to the manual fitting. Similar results in image refinement were obtained using analytical derivatives, but the convergence of was smoother using finite difference derivatives. Next, the occupancy of the FAb’ was refined to check the stoichiometry of the complex, before refining the position and atomic displacement factor of the FAb’ as a single group. With the refined imaging parameters, the FAb’ rotated 3° and translated 0.7 Å. For the final batch, the FAb’ was split into two domains which had rotations/translations of 5°/0.8 Å and 3°/0.6 Å respectively, as a large difference emerged in the displacement parameters of variable and constant domains. Further changes were small, indicating that refinement had now converged. Domain movements were <0.2°/0.03 Å, while a drop in envelope correction to 17 Ų was balanced by a small change in resolution to 9.9 Å (d_0.5 = 8.8 Å). The final correlation coefficient is 0.84. (If computed with default parameters in Chimera (Yang et al., 2012), the corresponding “correlation about mean” is a more flattering 0.93, because of the more restricted volume and thresholds used by Chimera.) The starting and refined models are compared in Fig. 1.

Table 1.

Rigid-group refinement of antibody fragment FAb’ A20 into the cryo-EM reconstruction of a complex with adeno-associated virus-2 at 9 Å resolution.

#	Description	<|Rotation|>/ <|Translation|>	RMS vs. start/RMS vs. end	Map correlation coefficient
				FAb’	FAb’ and virus
0	FAb’ homology model fit manually as a single group		0.0 Å/3.7 Å	0.630	0.678
1	FAb’ coordinates refined as a single group	9.5°/1.7 Å	3.2 Å/1.7 Å	0.695	0.711
2	Magnification, envelope correction and resolution refined for virus + Fab’			0.806	0.784
3	FAb’ coordinates/B-factor and virus B-factor refined as single groups	2.9°/0.7 Å	3.4 Å/1.3 Å	0.821	0.791
4	FAb’ coordinates and B-factors refined as two domains (variable and constant)	4.2°/0.7 Å	3.7 Å/0.0 Å	0.835	0.796

Fig. 1.

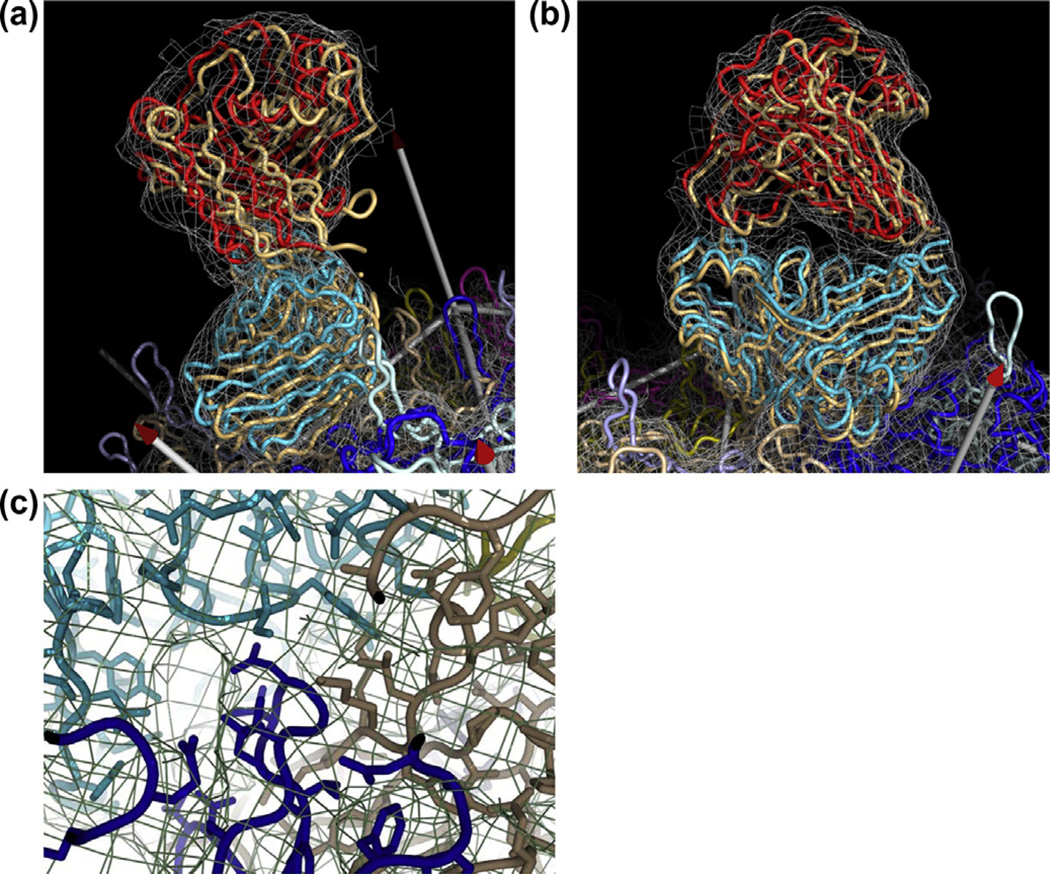
Rigid group refinement of Fab’ A20 into the 8.5 Å resolution cryo-EM reconstruction of its complex with AAV-2. Panels (a) and (b) show views of the Fab’ rotated ~60° about a vertical axis. The unrefined model that was fitted manually is shown in brown. The backbone of the refined model is colored according to B-factor, from blue (low) to red (high) as refined in domain-groups. Symmetry-equivalent viral proteins are shown in different colors. Arrows mark the locations of symmetry axes. In both cases the view is towards a 5-fold axis. Shown is the two-domain refinement without stereochemical restraints. Panel (c) shows detail of the paratope-epitope interface. In the absence of stereochemical restraints, rigid domain fitting leaves a few conflicts, such as the one seen between an Fab’ Trp (cyan) and a virus Lys (brown) - likely a change of rotamer is needed, but the resolution is not sufficient for such detailed modeling. Overall however, the complementarity of the surfaces is excellent, as is the fit within the map. The central dark blue loop is known to be antigenic, and it is easy to see how mutations could disturb the surface complementarity, leading to neutralization escape (Lochrie et al., 2006). In all panels, the map is contoured at 2σ.

Unrestrained refinements with RSRef were compared to those performed in Chimera (Yang et al., 2012). The structures differ by only 0.6 Å, cross-validating the two approaches. High consistency is expected, because refinement of two rigid groups is massively over-determined at 9 Å resolution. The RSRef structure has a higher correlation coefficient (0.84 vs. 0.78). Correlation of the Chimera-refined model improves to 0.82 with addition of RSRefs imaging parameters, the remaining difference showing the impact of imaging parameters on improving the atomic coordinates.

The two-group model was subject to additional refinement with van der Waals repulsive restraints using RSRef embedded within CNS. With weighting chosen to resolve overlap, the map correlation changed little (from 0.835 to 0.837). The two domains of the FAb’ move apart by ~1 Å, lessening overlap between FAb’ variable domain L107 and a constant domain side chain, a conflict that had become worse during unrestrained refinement. A second clash, between FAb’ E166 and AAV W92, is not improved. Both conflicts were the product of rigid-group modeling, 9 Å resolution being insufficient to define local hinge conformation and side chain rotamers. For the FAb’ complex, imposition of atomic level van der Waals restraints does not help. The most complementary fit at the epitope-paratope surface comes from refinement without explicit anti-bumping restraints (Fig. 1). RSRef accounts for the shape of the density/potential surrounding each atom, leading to mismatch with the experimental map if molecules approach too closely. This provides a softer restraint that may be more appropriate at low resolution than a conventional stereochemical term that depends on details of the atomic model.

As the scattering of each atom and the shape of the calculated map depends on displacement parameters, it is possible to refine group B-factors. Overall B-factors are co-linear with an envelope correction, so at least one B-factor must be fixed during refinement. The virus B-factors were fixed at their crystallographic values for refinement of group B-factors for the FAb’ variable and constant domains. These corresponded to rms atomic displacements of 1.1 and 1.9 Å for the variable and constant domains that are respectively proximal and distal to the viral surface. The displacement factors represent a convolution of several effects including disorder and uncertainty in the homology modeling, particularly of FAb’ side chains. Nevertheless, a simple rationalization is plausible. The variable domain, which is non-covalently bound, would be expected to have B-factors higher than the virus, and the constant domain, linked by a flexible hinge, even higher. Indeed, relative diffuseness in the outer domain density had been noted in the original publication (McCraw et al., 2012). Refinement of the B-factors is possible only by optimization of the parameters that affect the calculated shape of the map around each atom. At 9 Å resolution, the B-factors provide a domain-level estimate of uncertainty in the atomic model, the first such estimate, to our knowledge, for EM-based structures.

3.2. Benchmarking with Mm-cpn

During development, extensive testing was performed using simulated data, but the effects of real errors in starting models and experimental maps are difficult to gage. The Cryo-EM modeling challenge (Ludtke et al., 2012) made available the reconstruction and atomic model for the group II chaperonin, Mm-cpn (Zhang et al., 2010). The model had been built prior to, and was therefore unbiased by the subsequent 3.2 Å crystal structure (Pereira et al., 2010) which then provided an independent yardstick for refinement. We used the closed state reconstruction, at a nominal resolution of 4.3 Å (FSC_0.5), in which 70% of the side chains were reported visible. It is a system that has already been used to test other methods (Table 2), not only because the resolution is representative of a new generation of EM structures and the availability of a “correct solution”, but Mm-cpn embodies flexibility and conformational changes representative of the challenging regimes in which EM refinements are expected to perform.

Table 2.

Benchmarking with the 4.3 Å Mm-cpn structure.

Starting structure			Published EM (3LOS)				Homology				+MD perturbation
RMSD (Å) vs. X-ray			5.0	5.0	5.0	5.0	2.6	2.6	2.6	2.6	4.0	4.0	4.0
Refinement method			–	MDFF	DireX	RSRef	–	MultiFit	RSRef
(rigid domain; atomic gradient descent; or Simulated Anne aling)						dom/grad			dom	SA	dom	grad	SA
Local CC			.55	.56	.51	.54	.42	.52	.48	.58	.45	.40	.67
RMSD (Å) vs. crystal structure (3KFB)	All-subunit	Cα	4.1	4.2	4.8	3.7	2.1	2.8	1.7	2.0	2.2	3.4	2.4
		All	5.0	5.0	5.3	4.6	2.6	3.2	2.2	2.5	2.5	3.7	3.0
	In-register*	Cα	2.4	2.6	4.7	1.8	1.7	2.1	1.3	1.6	1.6	2.9	1.9
		All	3.0	3.0	5.2	2.5	2.1	2.6	1.8	2.1	2.0	3.2	2.4
Post facto scaled	In-register*	Cα	1.6	1.8	4.1	1.7	1.5	1.9	n/a	n/a
		All	2.4	2.5	4.8	2.4	1.9	2.4	n/a	n/a

^*The published structure (3LOS) contained local errors in loops that resulted in sequence frame-shift errors affecting 60% of the structure. The in-register statistics were calculated with the 201 residues in regions that were unaffected, where RMSD provides a better indication of progress. The out-of register errors pertain only to 3LOS, but statistics for refinements of the other models are also sub-divided for direct comparison.

Tests were performed using three starting models: (1) the published EM structure (PDB id 3LOS) (Zhang et al., 2010): this had been adapted from the structure of the thermosome homolog, KS-1, using crystallographic modeling tools (Emsley et al., 2010) and had previously served as the test model for other methods; (2) a homology model built with Modeller (Eswar et al., 2006) using two templates averaging 65% sequence identity (PDB ids 1Q3S and 1A6D), but using neither the Mm-cpn crystal structure nor the EM map; (3) the same homology model perturbed by molecular dynamics simulations using NAMD (Phillips et al., 2005) while retaining excellent stereochemistry. Problems in the 3LOS model have previously been noted (Chan et al., 2011), and consisted of mis-traced loops resulting in the sequence being out of correct register for large parts of the structure. None of the refinement methods were able to correct such errors: it would require escaping a local optimum in which the map is modeled by incorrect amino acids. However, the structure can be partitioned so that assessments can be made using parts without register errors where improvement should be reflected in decreased RMSD.

Using the 3LOS starting model, RSRef was compared to two leading flexible fitting methods: MDFF (Trabuco et al., 2008) which performs a molecular dynamics simulation in the presence of a steering potential based on agreement of the model with the EM reconstruction; and DireX which adds elastically deformable distance restraints from homolog structures (Schröder et al., 2010). The comparisons in Table 2 use refinements performed by the original authors (Chan et al., 2012; Wang and Schröder, 2012) with statistics re-calculated on a consistent basis. RMSDs were calculated following alignment of the D₈ point group symmetry of the biological complex of the crystal structure (3KFB) (Pereira et al., 2010) on the symmetry of the map, i.e. without any degrees of freedom. Local correlation coefficients between map and model were calculated using all grid points within 4.4 Å of any atom and without any density threshold.

Two more issues contributing to poor RMSDs became apparent on refinement of a homology model (see below). Firstly, RSRef’s refinement revealed a 3% error in the reported magnification of the map. This could be confirmed independently by searching for a coordinate scaling factor that minimized the RMSDs of others’ refinements with respect to the crystal structure. Thus, Table 2 also reports statistics following a post facto scaling, approximating the results expected if magnification refinement were available for the other methods. Secondly, the reported FSC_0.5 = 4.3 Å (Zhang et al., 2010) overstates the effective resolution. RSRef supports refinement of the resolution at which scattering from the atomic model should be equivalently attenuated by 0.5 for best agreement with the reconstruction. The refined 6 Å estimate is consistent with the presence of breaks in the backbone, unlike the 4.5 Å map of AAV-DJ (below), and less well defined side chains. The discrepancy between the FSC and model-based estimates is likely due to long-documented potential biases in FSC (Grigorieff, 2000), and the potential for molecular flexibility to degrade a map. The new estimate of resolution allows us to recalibrate our expectations for all of the flexible fitting methods.

With the relatively poor 3LOS starting model (RMSD 5.0 Å), all flexible fitting methods struggle. RSRef, alone, is able to improve the structure, reducing the RMSD of correctly modeled (in-register) residues by 20%. Without image refinement, the improvement would have been small. The fit of the starting model into the density had already been optimized, so the error in magnification is embodied in a strain between map correlation and stereochemistry, which is released only slowly in alternating batches of image and stereochemically-restrained model refinement. Table 2 shows the results of the 4th round in which the estimated magnification had been converging: 1.0, 1.009, 1.018, 1.021, 1.024… towards the 1.0295 refined later using the homology model. While unrestrained rigid-domain refinement speeds convergence, it alone is insufficient. Release of strain during stereochemically-restrained atomic refinement is needed to progress beyond the 1st correction of 1.009.

The right side of Table 2 shows that at an intermediate 6 Å resolution, a homology model is likely a better starting point. With a modest improvement in correlation coefficient (from 0.42 to 0.46) the magnification and model can be refined in a single round, and the RMSD reduced by about 20%. The starting model is already of high quality (2.1 Å C_α) relative to 6 Å resolution. Thus, the model improvement (to 1.7 Å RMSD) is modest. MultiFit offers a similar joint optimization of fit and stereochemical energy (Lasker et al., 2009), but without magnification refinement, the starting model is distorted to fit the unscaled map. MultiFit uses a simplified description of the model density, which is perhaps why the model improvement is smaller than RSRef’s even after the magnification is factored out. In refinement of the homology model, most of the change involves rotation about well-defined inter-domain hinges: rigid-group optimization and restrained least-squares refinements perform better than simulated annealing, which has greater propensity for over-fitting. The value of RSRef is more apparent with a perturbed starting model. At 6 Å resolution, it converges to nearly the same point as the prior refinement, eliminating 40% of the initial 4 Å RMSD error. Rigid domain refinement performs best in this case. However, with this more distant starting point, the wider convergence radius of simulated annealing over gradient descent is apparent. Relative to rigid group, simulated annealing refinement allows more over-fitting, but it might be the best approach in cases where domains are not so easily defined.

Comparison to an X-ray structure may be a safe assessment, but might underestimate the accuracy if there are real differences between flexible molecules in the crystalline and solution states. At 6 Å resolution, the most pertinent differences would be in the orientation of domains known to differ between the open and closed states. If, in calculating the RMSDs, domains are aligned separately, the C_α RMSD drops from 1.7 to 1.4 Å. A yardstick-independent assessment has been used before, comparing subunits that have been refined without symmetry restraints (Chan et al., 2012). It gives RMSDs of 1.3 Å for MDFF and 1.1 Å for simulated annealing RSRef. These statistics might reflect the limiting precision at 6 Å resolution, but ignore systematic errors that lessen accuracy. No method of assessment is unalloyed, but the aggregate indicates that C_α accuracies in the range of 1.1–1.7 Å are possible at 6 Å resolution when starting with a good homology model.

Timing of RSRef is intermediate between the fast unrestrained rigid body refinements of Chimera (Yang et al., 2012) and the computationally demanding MDFF. On a dual-core PC, a batch of image and rigid-group refinement takes 5 min for Mm-cpn, and simulated annealing takes 80 min. Times are linearly dependent on the number of atoms in the asymmetric unit. Current code does not take advantage of multi-core computers, but this is not a critical issue, because computation for Mm-cpn is three orders of magnitude less than MDFF (Chan et al., 2012). Other efficiencies come through the application of symmetry as a constraint (vs. restraint) and the use of annealing and reduced torsion angle parameterizations to improve convergence.

3.3. High resolution structure of AAV-DJ

Returning to AAV, another limitation on its use as a gene therapy vector is transducing efficiency that depends both on serotype and cell type (Shen et al., 2007). Directed evolution is being used to overcome this limitation, introducing genetic variation by random DNA shuffling between different AAVs, then selecting and cloning variants with the desired properties (Koerber et al., 2008; Maheshri et al., 2006). AAV-DJ was an early success, a chimeric recombinant of AAV-2, −8 and −9 with improved liver transduction efficiency (Grimm et al., 2008). Its structure was determined for insights into the mechanism by which transducing specificity was being modulated (Lerch et al., 2012). Cryo-EM provided higher resolution than X-ray diffraction from available crystals.

As detailed earlier (Lerch et al., 2012), the EM reconstruction was obtained with FREALIGN (Grigorieff, 2007) using 27,312 particles from 4773 images. Estimates of resolution ranged from 4.5 Å (FSC_0.143) through 5.3 Å (FSC_0.5). The reconstruction was first compared to the crystal structure of AAV-2 (Xie et al., 2002), the parental strain from which most of the AAV-DJ sequence is drawn (Grimm et al., 2008). Preliminary refinement improved the correlation by 10% with a 1.1% correction to the magnification which was applied before the refinement described below.

The initial AAV-DJ atomic model was built in Coot (Emsley et al., 2010) using substantial, but incomplete structural homology to parental strains AAV-2 and AAV-8 determined at 3.0 and 2.6 Å resolutions respectively (Nam et al., 2007; Xie et al., 2002). In retrospect, we see that AAV-DJ differs from the higher resolution homolog, AAV-8, which has 90% sequence identity, by 0.9 Å C_α RMSD, mostly in the sequencevariable loops. The 2.8 Å structure of the third parental strain, AAV-9, was published later (Dimattia et al., 2012) and used only in a retrospective analysis of the refinement (see below).

The AAV-DJ structure was refined in five batches (Table 3) using an all-atom flexible model and full stereochemical restraints. The propensity for over-fitting such a model at ~4.5 Å was soon apparent, and it was necessary to add a restraint to maintain allowable φ, ψ backbone dihedral combinations. This was done with a flat-bottom harmonic potential that allowed full flexibility within each preferred region of the Ramachandran plot. Most of the model improvement was achieved during the initial gradient descent optimization in which a 1.2 Å RMS change was accompanied by an 11% improvement in the correlation coefficient.

Table 3.

Flexible fitting of AAV-DJ into a 4.5 Å cryo-EM reconstruction.

#	Description	RMS vs. start/RMS vs.end	Correlation coefficient
0	Manually built model	0/1.23 Å	0.744
1	Gradient descent Cartesian structure optimization.	1.15/0.41 Å	0.857
2	Magnification, envelope correction and resolution refined	1.15/0.41 Å	0.861
3	Torsion angle simulated annealing optimization of structure	1.21/0.07 Å	0.862
4	B-factor refinement	1.21/0.07 Å	0.869
5	Gradient descent Cartesian structure optimization	1.23/0 Å	0.871

Refinement of imaging parameters provided a very modest improvement in correlation coefficient (0.4%). The magnification was unchanged beyond the 1.1% magnification correction refined earlier. A refined envelope correction of −5.7 applied to the model, indicated that earlier processing with EMBfactor (Fernandez et al., 2008) was close to optimal, but had slightly over-sharpened the map. The refined soft limit of 4.46 Å on the Butterworth low-pass filter was similar to the FSC_0.143 of 4.5 Å.

At crystallographic resolutions of ~2 or 3 Å, simulated annealing refinement in torsion angle space has proved to be a powerful means of automatically exploring altered backbone conformation and alternative side chain rotamers, mitigating over-fitting through the reduced-parameter coordinate system (Rice and Brün-ger, 1994). In real-space, even larger changes can be explored with annealing temperatures of up to 20,000 K, because the locally-based objective function eliminates the covariance of distant atoms associated with over-fitting in reciprocal space refinement (Chen et al., 1999). However, this had to be approached carefully, because, with EM data, there is not a means of cross-validated assessment of over-fitting corresponding to R^free (Brünger, 1992), and at low resolution there is generally greater potential for over-fitting. Slow-cooling protocols starting at 5000, 10,000 or 15,000K with the aforementioned added φ, ψ restraints, all improved map correlation coefficients modestly (1–2%) with refined coordinates that differed by 0.4–0.7 Å (all atom RMS). The biggest differences were involved side-chain rotamers where the density was weak. No single temperature gave the best fit for all side chains, likely a reflection of the stochastic nature of molecular dynamics (Rice and Brünger, 1994). It is possible that this could be exploited in the future by an algorithm that would splice together best-fitting fragments from multiple annealing runs. Subjective inspection indicated that the more conservative run at 5000 K had overall yielded the best fitting set of rotamers.

3.4. Atomic displacement parameters (B-factors)

The explicit incorporation of atomic displacement parameters (ADP) in the density calculation provides an opportunity for their refinement as a measure of local flexibility and disorder. Once again, strong restraints would be needed to mitigate over-fitting. At medium crystallographic resolutions, this is usually achieved by a restraint on the variation between the B-factors of bonded neighbors. At crystallographic resolutions worse than 3 Å, restraints are usually replaced by constrained refinement with residue-group B-factors. At the lower resolution of this EM study, it might be appropriate to additionally restrain or constrain B-factors to be similar to those of homologs refined crystallographically at higher resolution. However, we are at a disadvantage, without cross-validation to assess over-fitting. Different parameterizations and weightings could be assessed in terms of their ability to generate in dependently B-factors similar to those of a high resolution homolog, as long as the homolog was not used as a starting point or restraint. In this way, a number of strategies were assessed (Table 4).

Table 4.

Strategies for AAV-DJ B-factor refinement.

Parameterization	Initial B-factors	RMSD Ba/weight	Correlation coefficients
			Calculated vs. experimental map (start)	AAV-DJ vs. AAV-8 B-factors
Individual atomic B-factors	Uniform	1.4 Å2 (0.28)	0.869 (0.859)	0.82
	AAV-8	1.4 Å2 (0.22)	0.869 (0.862)	0.92
B-factors for each residue adjusted uniformly	Uniform	1.4 Å2 (0.15)	0.866 (0.859)	0.82
	Uniform	2.5 Å2 (0.05)	0.868 (0.859)	0.80
	AAV-8	1.5 Å2 (0.35)	0.866 (0.864b)	0.76
	AAV-8	6.8 Å2 (0.00)	0.872 (0.864b)	0.92

^aRestrained root mean square difference between B-factors of bonded neighbors; applies between residues in group refinement.

^bB-factors for 177 individual atoms were first refined (correlation increasing from 0.862 to 0.864). These atoms had been inserted with fixed B = 20.0 Ų when the sequence was changed in manual modeling.

The approach for group B-factor refinement was extended in two ways beyond that available in crystallographic programs. Firstly, group B-factors were applied in addition to underlying atomic B-factors, so that the intra-group variation in the parent homolog, such as between main-chain and side-chain atoms, could be maintained. Secondly, restraints on the similarity of B-factors between bonded neighbors of adjacent groups were added.

Group B-factor refinement, starting with the AAV-8 B-factors, but unrestrained, yielded the best correlation coefficient (Table 4, bottom row), but there were indications of over-fitting. Firstly, it was surprising that the correlation of B-factors with AAV-8, was no better than a refinement that was completely free to move away from AAV-8 (row 2). Secondly, the increase in B-factor variation from 2.6 to 6.8 Ų corresponds to >14 Ų variation between the N and C atoms of adjacent groups, the intra-group variation being constrained to be zero. Finally, when starting from uniform B-factors (rows 3 and 4), loosened restraints between adjacent groups results in improved fit, but worsening agreement with the independently determined AAV-8 crystallographic B-factors (Nam et al., 2007). When tight restraints were applied, it was better to start from uniform B-factors (row 3) than those of the homolog (row 5).

Without cross-validation, there was no internal way to determine the appropriate weight on the B-factor similarity restraint. Thus, it was adjusted to reproduce the 1.4 Ų RMSD of the AAV-2 and AAV-8 crystal structures (Nam et al., 2007; Xie et al., 2002). When starting from uniform B-factors, refinement as individual atoms yields a slightly better fit than as residue-groups, but the correlation of AAV-DJ B-factors with AAV-8 is identical. Starting with AAV-8 B-factors, refinement yields a structure with similar map correlation, and B-factors that are closer to AAV-8. With little to distinguish between the best of the B-factor refinement strategies, we proceeded with individual B-factors that had been refined from AAV-8 values with tight restraints.

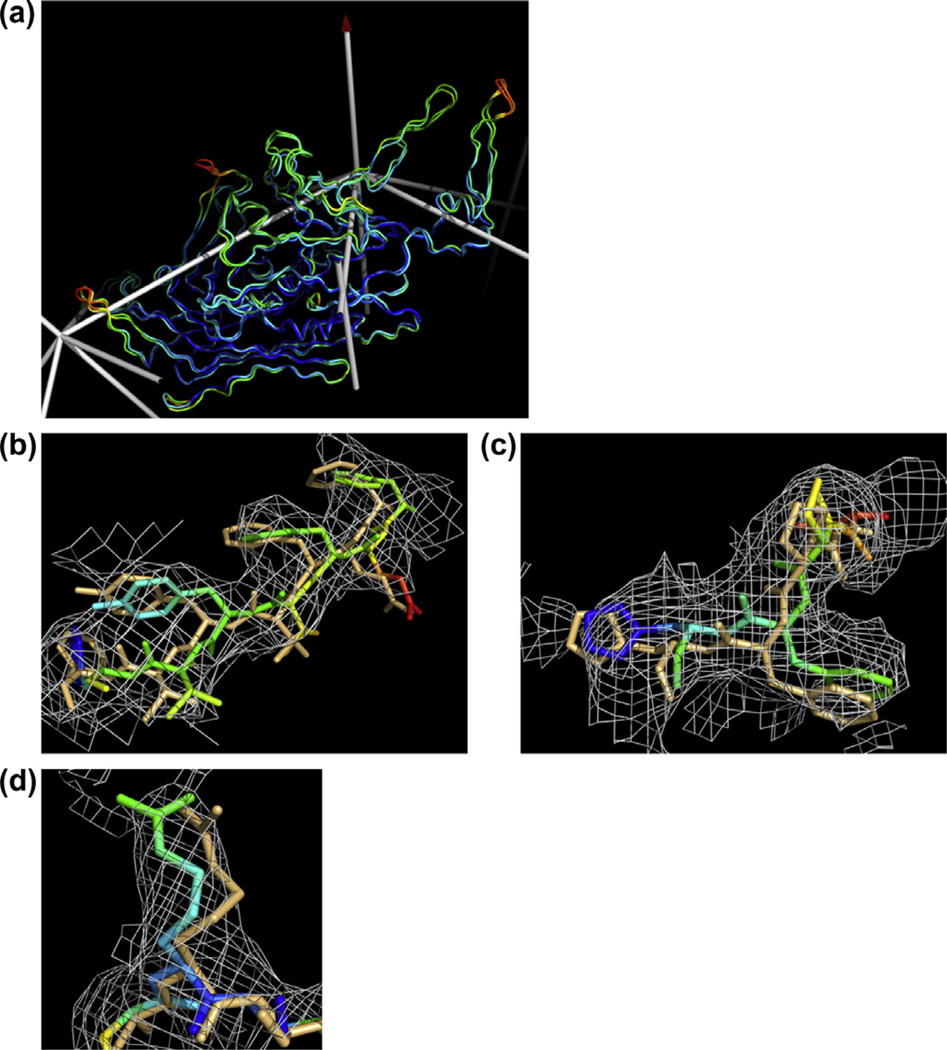
Notwithstanding discussion of which parameterization and weighting provides the optimal B-factor refinement, there is strong evidence that they are all providing meaningful information about local mobility and disorder. When C_α are colored by B-factor, independent refinements from uniform B-values show spatial distributions of atomic displacements that are highly correlated with the high resolution AAV-2 and AAV-8 crystal structures (Fig. 2). Regions of high displacement include loops on the outer surface of the virus as well as the termini of the subunit. By contrast, the core b-barrel is more ordered. Our refinement demonstrates the feasibility of distinguishing ordered and less ordered regions within a protein using EM data at only ~4.5 Å resolution.

Fig. 2.

Refinement of the AAV-DJ structure at 4.5 Å resolution. (a) One of the 60-symmetry related subunits is overlaid on the 2.8 Å resolution crystal structure of one of its ancestors, AAV-8 (Nam et al., 2007). Backbone differences are subtle and occur mostly in the outer surface loops. The structures are colored according to C_α B-factor, which, for AAV-DJ, were set to a uniform value and then refined without any knowledge of crystallographically refined B-factors. Clearly there is a high level of spatial consistency, even when refined at 4.5 Å resolution. Panels b, c and d show three examples of local improvement through the course of refinement. The starting model is colored light blue, while the refined structure is colored according to the refined B-factors (blue is low; red is high). Strong restraint on variation between the B-factors of bonded pairs of atoms was needed to avoid over-fitting, so the B-factors of individual atoms are not particularly accurate. However, local trends can be seen: groups of atoms in weak density tend to have higher B-factors. Panels (b) and (d) are contoured at 1.0σ, while panel (c) is contoured at 1.25σ. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.5. Final Steps

With relaxation of the atomic B-factors and optimization of the imaging parameters, a small improvement was possible with continued gradient descent optimization of the coordinates. However, the changes were small and refinement quickly converged at a correlation coefficient of 0.871. As previously discussed, other programs report more flattering statistics: with default parameters Chimera (Yang et al., 2012) calculates a “correlation about mean” of 0.94 for this atomic model.

The final model was used to evaluate the effective model resolution. Refinements of the filter resolution and envelope corrections are somewhat inter-dependent as the parameters have similar impact on the calculated map. This interdependence can be mitigated by choosing a hard resolution limit significantly beyond the filter resolution. The filter resolution refined to d_0.5 = 4.7Å with the refined envelope correction of −5.4 Ų or to d_0.5 = 4.5 Å if it is assumed that no envelope correction should be needed after EMB-factor (Fernandez et al., 2008). For comparison, FSC_0.143 = 4.5 Å. Exact agreement should not be expected: d_0.5 is the resolution at which the atomic model needs to be attenuated by ½ for best agreement with the map, and thereby reflects errors in both experimental data and model, as well as possible model over-fitting. FSC embodies different biases: from alignment of noise during reconstruction (Yang et al., 2003) and from use of signal-reduced half data sets. Close correspondence gives confidence in both estimates, and indicates that little more can be done to improve the atomic model with this data.

3.6. Retrospective evaluation of AAV-DJ refinements

With publication of the structure of AAV-9 (Dimattia et al., 2012), it was encouraging to see that a loop known as variable region 1, which differed from AAV-2 and AAV-8 by 4 and 6 Å RMS respectively, was now closely matched by the new crystal structure. With crystal structures of the three parent viruses now known, one could splice together a prediction of the AAV-DJ chimeric construct. Close agreement between the EM structure and this crude yardstick (RMSD 1.0 Å C_α, 1.5 Å all atom) speaks to the accuracy of the EM refinement. These statistics could be biased by memory of the AAV-8 structure (Nam et al., 2007) that guided the manual modeling of AAV-DJ into the EM reconstruction, although the simulated annealing of refinement should have removed such bias. Thus, tests were added using starting models of a different lineage. A homology model was built with Modeller (Eswar et al., 2006) using AAV-4 and AAV-5 templates (Govindasamy et al., 2006; Walters et al., 2004), structures that have <60% sequence identity to AAV-DJ’s parental strains. Four loops deviated excessively from the AAV-DJ structure where the sequence was not correctly aligned and/or loops were incorrectly folded, leading to 5–10 Å C_α errors. To bring these regions within the convergence radius of refinement, 58 residues (11%) of the manually fit AAV-DJ model were spliced in. This resulting model was then perturbed to varying degrees by simulated annealing torsion angle dynamics (in the context of icosahedral symmetry) to generate the three starting models shown in Table 5.

Table 5.

Convergence of virus structure refinement at 4.5 Å resolution.

	Weight	Temperature (K)		Cα/all-atom (Å)	Cα/all-atom (Å)	Cα/all-atom (Å)
Starting model			RMSD	3.1/3.5	4.8/5.2	5.9/6.3
			CC	0.32	0.21	0.15
Atomic gradient descent	0.5		RMSD	1.7/2.4	3.3/4.0	4.2/5.0
			CC	0.83	0.77	0.74
Simulated annealing	0.175	5000	RMSD	1.7/2.4	2.8/3.6	3.9/4.6
			CC	0.81	0.75	0.72
Simulated annealing	0.5	10,000	RMSD	1.7/2.3	2.9/3.7	4.0/4.7
			CC	0.84	0.79	0.77

The models were refined into the EM reconstruction using a single batch of stereochemcally-restrained gradient descent and then simulated annealing with either conservative or aggressive weighting/schedules. Our comparison for RMSD error calculation is the spliced yardstick described above that differed from our refined structure by 1.0 Å C_α, 1.5 Å all-atom. A single batch of least-squares refinement nearly halves a 3 Å starting error (Table 5). With starting errors of 5 or 6 Å, additional progress is seen with simulated annealing. Improvement in the models is significant, but some manual remodeling would be required for continued convergence, not unexpected for 5–6 Å RMS starting errors. More aggressive annealing does not help, leading to modest over-fitting although the propensity for over-fitting is less than with Mm-cpn, presumably due to the higher resolution and map quality. Overall, the tests show not just improved fit to the map, but significant real improvements to the structure, for starting models that should encompass the range likely to be encountered in practice.

4. Conclusions

There are several advantages of resolution-dependent density calculation in the refinement of EM-based atomic models. Firstly, it eliminates ad hoc smearing parameters that affect the course of refinement (Vasishtan and Topf, 2011). Secondly, it provides a means of refining the effective resolution during model optimization, so that model refinement does not depend on an accurate initial estimate. Thirdly, it supports the refinement of (grouped) atomic displacement parameters that introduces, for the first time to EM, a measure of molecular flexibility. Through rigorous accounting of the attenuation of signal with resolution, one is changing the predicted shape of the map surrounding atoms, and accounting for different levels of blurriness in regions with different flexibility. By reducing the residual difference between predicted and experimental density, modest improvements can be made to the atomic positions beyond those achieved without refinable imaging parameters.

In EM structure refinement, several aspects remain under active development, including model parameterization and optimization method. In terms of atomic coordinates, the improvements to be expected from the approach presented here will depend on the resolution regime. Thus, precise density calculation has not been the highest priority in all regimes, and simpler approximations have sufficed for a number of applications. That said, with improvements in computer speed and in the algorithms developed here, we are not aware of any circumstances where more rigorous accounting of the shape of density would be a disadvantage in maximizing the accuracy of atomic models. Thus, our goal has been to develop a software module that would provide the needed density and derivative calculations in a variety of contexts, so that future emphasis, here and elsewhere, can be on exploring diverse possibilities in parameterization and optimization algorithms.

Care should be taken not to infer too much from the limited comparisons of methods performed to date. However, RSRef represents at least a modest improvement upon representatives of the other approaches in use. Much of this comes from the refinement of EM magnification and other imaging parameters. However, there are other differences. The improvement relative to the MultiFit (Lasker et al., 2009) refinement of Mm-cpn is likely due to the different map-fitting functions. Improvements over MDFF and DireX (Chan et al., 2012; Wang and Schröder, 2012) appear to result from reduced over-fitting when imaging parameters are refined and when reduced-parameter atomic models are used. This experience suggests that at some resolutions, a reduction in model degrees of freedom might be more productive than addition of supplementary restraints.

There is clearly room for further methodological progress. However, this work demonstrates that real improvements to models are possible over a wide range of resolutions. Particularly exciting, beyond the ~5 Å resolution that is increasingly attainable, the AAV example shows that in favorable cases, structures with all-atom RMS errors of 1.5–2.5 Å are possible.

Abbreviations:

AAV

adeno associated virus

CDR

complementarity determiniming region

CTF

contrast transfer function

EM

electron microscopy

mAb

monoclonal antibody

Mm-cpn

Methanococcus marapaludis chaperonin

NCS

non crystallographic symmetry

RMS(D)

root mean square (deviation)

VP

viral protein