Abstract
Distinguishing the somatic mutations responsible for cancer (driver mutations) from random, passenger mutations is a key challenge in cancer genomics. Driver mutations generally target cellular signaling and regulatory pathways consisting of multiple genes. This heterogeneity complicates the identification of driver mutations by their recurrence across samples, as different combinations of mutations in driver pathways are observed in different samples. We introduce the Multi-Dendrix algorithm for the simultaneous identification of multiple driver pathways de novo in somatic mutation data from a cohort of cancer samples. The algorithm relies on two combinatorial properties of mutations in a driver pathway: high coverage and mutual exclusivity. We derive an integer linear program that finds set of mutations exhibiting these properties. We apply Multi-Dendrix to somatic mutations from glioblastoma, breast cancer, and lung cancer samples. Multi-Dendrix identifies sets of mutations in genes that overlap with known pathways – including Rb, p53, PI(3)K, and cell cycle pathways – and also novel sets of mutually exclusive mutations, including mutations in several transcription factors or other genes involved in transcriptional regulation. These sets are discovered directly from mutation data with no prior knowledge of pathways or gene interactions. We show that Multi-Dendrix outperforms other algorithms for identifying combinations of mutations and is also orders of magnitude faster on genome-scale data. Software available at: http://compbio.cs.brown.edu/software.
Author Summary
Cancer is a disease driven largely by the accumulation of somatic mutations during the lifetime of an individual. The declining costs of genome sequencing now permit the measurement of somatic mutations in hundreds of cancer genomes. A key challenge is to distinguish driver mutations responsible for cancer from random passenger mutations. This challenge is compounded by the observation that different combinations of driver mutations are observed in different patients with the same cancer type. One reason for this heterogeneity is that driver mutations target signaling and regulatory pathways which have multiple points of failure. We introduce an algorithm, Multi-Dendrix, to find these pathways solely from patterns of mutual exclusivity between mutations across a cohort of patients. Unlike earlier approaches, we simultaneously find multiple pathways, an essential feature for analyzing cancer genomes where multiple pathways are typically perturbed. We apply our algorithm to mutation data from hundreds of glioblastoma, breast cancer, and lung adenocarcinoma patients. We identify sets of interacting genes that overlap known pathways, and gene sets containing subtype-specific mutations. These results show that multiple cancer pathways can be identified directly from patterns in mutation data, and provide an approach to analyze the ever-growing cancer mutation datasets.
Introduction
Cancer is a disease driven in part by somatic mutations that accumulate during the lifetime of an individual. The declining costs of genome sequencing now permit the measurement of these somatic mutations in large numbers of cancer genomes. Projects such as The Cancer Genome Atlas (TCGA) and International Cancer Genome Consortium (ICGC) are now undertaking this task in hundreds of samples from dozens of cancer types. A key challenge in interpreting these data is to distinguish the functional driver mutations important for cancer development from random passenger mutations that have no consequence for cancer. The ultimate determinant of whether a mutation is a driver or a passenger is to test its biological function. However, because the ability to detect somatic mutations currently far exceeds the ability to validate experimentally their function, computational approaches that predict driver mutations are an urgent priority. One approach is to directly predict the functional impact of somatic mutations using additional biological knowledge from evolutionary conservation, protein structure, etc. and a number of methods implementing this approach have been introduced (see [1]–[4]). These methods are successful in predicting the impact of some mutations, but generally do not integrate information across different types of mutations (single nucleotide, indels, larger copy number aberrations, etc.); moreover, these methods are less successful for less conserved/studied proteins.
Given the declining costs of DNA sequencing, a standard approach to distinguish driver from passenger mutations is to identify recurrent mutations, whose observed frequency in a large cohort of cancer patients is much higher than expected [5], [6]. Nearly all cancer genome sequencing papers, including those from TCGA [7]–[10] and other projects [5], [11], [12], report a list of significantly mutated genes. However, driver mutations vary greatly between cancer patients – even those with the same (sub)type of cancer – and this heterogeneity significantly reduces the statistical power to detect driver mutations by tests of recurrence. One of the main biological explanations for this mutational heterogeneity is that driver mutations target not only individual genomic loci (e.g. nucleotides or genes), but also target groups of genes in cellular signaling and regulatory pathways. Consequently, different cancer patients may harbor mutations in different members of a pathway important for cancer development. Thus, in addition to testing individual loci, or genes, for recurrent mutation in a cohort of patients, researchers also test whether groups of genes are recurrently mutated. Since exhaustive testing of all groups of genes is not possible without prohibitively large sample sizes (due to the necessary multiple hypothesis testing correction), current approaches focus on groups of genes defined by prior biological knowledge, such as known pathways (e.g. from KEGG [13]) or functional groups (e.g. from GO [14]), and methods have been introduced to look for enrichment in such pre-defined groups of genes (e.g. [15]–[17]). More recently, methods that identify recurrently mutated subnetworks in protein-protein interaction networks have also been developed, such as NetBox [18], MeMO [19], HotNet [20], and EnrichNet [21].
Knowledge of gene and protein interactions in humans remain incomplete, and most existing pathway databases and interaction networks do not precisely represent the pathways and interactions that occur in a particular cancer cell. Thus, restricting attention to only those combinations of mutations recorded in these data sources may limit the possibility for novel biological discoveries. Thus algorithms that do not make this restriction – but also avoid the multiple hypothesis testing problems associated with exhaustive enumeration – are desirable. Recently, the RME [22] and De novo Driver Exclusivity (Dendrix) [23] algorithms were introduced to discover driver pathways using combinatorial constraints derived from biological knowledge of how driver mutations appear in pathways [24], [25]. In particular, each cancer patient contains a relatively small number of driver mutations, and these mutations perturb multiple cellular pathways. Thus, each driver pathway will contain approximately one driver mutation per patient. This leads to a pattern of mutual exclusivity between mutations in different genes in the pathway. In addition, an important driver pathway should be mutated in many patients, or have high coverage by mutations. Thus, driver pathways correspond to sets of genes that are mutated in many patients, but whose mutations are mutually exclusive, or approximately so. We emphasize that the driver pathways exhibiting patterns of mutually exclusivity and high coverage are generally smaller and more focused than most pathways annotated in the literature and pathway databases. The latter typically contain many genes and perform multiple different functions; e.g. the “cell cycle” pathway in KEGG contains 143 genes. It is well known that co-occurring (i.e., not exclusive) mutations are observed in these larger, multifunctional biological pathways [25]. The RME and Dendrix algorithms use different approaches to find sets of genes with high coverage and mutual exclusivity: RME builds sets of genes from pairwise scores of exclusivity, while Dendrix computes a single score for the mutual exclusivity of a set of genes, and finds the highest scoring set. The aforementioned MeMO algorithm [19] also considers mutual exclusivity between mutations, but only for pairs of genes that have recorded interactions in a protein-protein interaction network. Thus, MeMO does not attempt to identify driver pathways de novo and can only define subnetworks in existing interaction networks. While many of the strongest signals of mutual exclusivity are between genes with known interactions, below we show examples in cancer data of mutual exclusive mutations between genes with no known direct iterations.
The two existing de novo algorithms, RME and Dendrix, consider the detection of only a single driver pathway from the pattern of mutual exclusivity between mutations. However, it is well known that mutations in several pathways are generally required for cancer [26]. There is little reason to assume that mutations in different pathways will be mutually exclusive, and in contrast may exhibit significant patterns of co-occurrence across patients. Multiple pathways may be discovered using these algorithms by running the algorithm iteratively, removing the genes found in each previous iteration, and such an approach was employed for Dendrix [23]. However, such an iterative approach is not guaranteed to yield the optimal set of pathways.
Here we extend the Dendrix algorithm in three ways. First, we formulate the problem of finding exclusive, or approximately exclusive, sets of genes with high coverage as an integer linear program (ILP). This formulation allows us to find optimal driver pathways of various sizes directly – in contrast to the greedy approximation and Markov Chain Monte Carlo algorithms employed in Dendrix. Second, we generalize the ILP to simultaneously find multiple driver pathways. Third, we augment the core algorithm with additional analyses including: examining gene sets for subtype-specific mutations, summarizing stability of results across different number and size of pathways, and imposing greater exclusivity of gene sets.
We apply the new algorithm, called Multi-Dendrix, to four somatic mutation datasets: whole-exome and copy number array data in 261 glioblastoma (GBM) patients from The Cancer Genome Atlas (TCGA) [7], whole-exome and copy number array data in 507 breast cancer (BRCA) patients from TCGA [8], 601 sequenced genes in 84 patients with glioblastoma multiforme (GBM) from TCGA [7] and 623 sequenced genes in 188 patients with lung Adenocarcinoma [27]. In each dataset Multi-Dendrix finds biologically interesting groups of genes that are highly exclusive, and where each group is mutated in many patients. In all datasets these include groups of genes that are members of known pathways critical to cancer development including: Rb, p53, and RTK/RAS/PI(3)K signaling pathways in GBM and p53 and PI(3)K/AKT signaling in breast cancer. Multi-Dendrix successfully recovers these pathways solely from the pattern of mutual exclusivity and without any prior information about the interactions between these genes. Moreover, Multi-Dendrix also identifies mutations that are mutually exclusive with these well-known pathways, and potentially represent novel interactions or crosstalk between pathways. Notable examples include mutual exclusivity between: mutations in PI(3)K signaling pathway and amplification of PRDM2 (and PDPN) in glioblastoma; mutations in p53, GATA3 and cadherin genes in breast cancer.
Finally, we compare Multi-Dendrix to an alternative approach of iteratively applying Dendrix [23] or RME [22], two other algorithms that search for mutually exclusive sets. We show that these iterative approaches typically fail to find an optimal set of pathways on simulated data, while Multi-Dendrix finds the correct pathways even in the presence of a large number of false positive mutations. On real cancer sequencing data, the groups of genes found by Multi-Dendrix include more genes with known biological interactions. Moreover, Multi-Dendrix is orders of magnitude faster than these other algorithms, allowing Multi-Dendrix to scale to the latest whole-exome datasets on hundreds of samples, which are largely beyond the capabilities of Dendrix and RME. Multi-Dendrix is a novel and practical approach to finding multiple groups of mutually exclusive mutations, and complements other approaches that predict combinations of driver mutations using biological knowledge of pathways, interaction networks, protein structure, or protein sequence conservation.
Results
Multi-Dendrix algorithm
The Multi-Dendrix algorithm takes somatic mutation data from  cancer patients as input, and identifies multiple sets of mutations, where each set satisfies two properties: (1) the set has high coverage with many patients having a mutation in the set; (2) the set exhibits a pattern of mutual exclusivity where most patients have exactly one mutation in the set. We briefly describe the Multi-Dendrix algorithm here. Further details are provided in the Methods section below.
cancer patients as input, and identifies multiple sets of mutations, where each set satisfies two properties: (1) the set has high coverage with many patients having a mutation in the set; (2) the set exhibits a pattern of mutual exclusivity where most patients have exactly one mutation in the set. We briefly describe the Multi-Dendrix algorithm here. Further details are provided in the Methods section below.
We assume that somatic mutations have been measured in  cancer patients and that these mutations are divided into
cancer patients and that these mutations are divided into  different mutation classes. A mutation class is a grouping of different mutation types at a specific genomic locus. In the simplest case, a mutation class corresponds to a grouping of all types of mutations (single nucleotide variants, copy number aberrations, etc.) in a single gene. We represent the somatic mutation data as an
different mutation classes. A mutation class is a grouping of different mutation types at a specific genomic locus. In the simplest case, a mutation class corresponds to a grouping of all types of mutations (single nucleotide variants, copy number aberrations, etc.) in a single gene. We represent the somatic mutation data as an 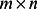 binary mutation matrix
binary mutation matrix
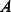 , where the entry
, where the entry 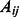 is defined as follows:
is defined as follows:
| (1) |
More generally, a mutation class may be defined for an arbitrary genomic locus, and not just a gene, and may distinguish different types of mutations. For example, one may define a mutation class as single-nucleotide mutations in an individual residue in a protein sequence or in a protein domain. Or alternatively, one may separate different types of mutations in a gene (e.g. single-nucleotide mutations, deletions, or amplifications) by creating separate mutation classes for each mutation type in each gene. We will use this later definition of mutation classes in the results below. For ease of exposition we will assume for the remainder of this section that each mutation class is a gene.
Vandin et al. [23] formulate the problem of finding a set of genes with high coverage and high exclusivity as the Maximum Weight Submatrix Problem. Here the weight 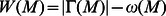 of a set
of a set 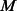 of genes is the difference between the coverage
of genes is the difference between the coverage  , the number of patients with a mutation in one of the genes in
, the number of patients with a mutation in one of the genes in 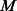 , and the coverage overlap
, and the coverage overlap 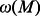 , the number of patients having a mutation in more than one gene in
, the number of patients having a mutation in more than one gene in 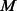 . Vandin et al. [23] introduce the De novo Driver Exclusivity (Dendrix) algorithm [23] that finds a set
. Vandin et al. [23] introduce the De novo Driver Exclusivity (Dendrix) algorithm [23] that finds a set 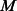 of
of 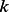 genes with maximum weight
genes with maximum weight 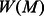 .
.
While finding single driver pathways is important, most cancer patients are expected to have driver mutations in multiple pathways. Dendrix used a greedy iterative approach to find multiple gene sets (described below), that is not guaranteed to find optimal gene sets. Identification of multiple driver pathways requires a criterion to evaluate possible collections of gene sets. Appealing to the same biological motivation as above, we expect that each pathway contains approximately one driver mutation. Moreover, since each driver pathway is important for cancer development, we also expect that most individuals contain a driver mutation in most driver pathways. Thus, we expect high exclusivity within the genes of each pathway and high coverage of each pathway on its own. One measure that satisfies these criteria is to find a collection
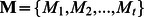 of gene sets whose sum of weights is maximized.
of gene sets whose sum of weights is maximized.
We define the Multiple Maximum Weight Submatrices problem as the problem of finding such a maximum weight collection. We solve the Multiple Maximum Weight Submatrix problem using an integer linear program (ILP), and refer to the resulting algorithm as Multi-Dendrix (see Methods). In addition, the ILP formulation used in Multi-Dendrix uses a modified weight function 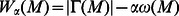 , where
, where 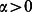 is a parameter that adjusts the tradeoff between finding sets with higher coverage
is a parameter that adjusts the tradeoff between finding sets with higher coverage 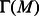 (more patients with a mutation) versus higher coverage overlap
(more patients with a mutation) versus higher coverage overlap 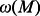 (greater non-exclusivity between mutations). We use this parameter in the breast cancer dataset below. In contrast, Dendrix was limited to
(greater non-exclusivity between mutations). We use this parameter in the breast cancer dataset below. In contrast, Dendrix was limited to 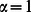 .
.
Simulated data
We compare Multi-Dendrix to iterative versions of Dendrix [23] and RME [22] on simulated mutation data with both driver mutations implanted in pathways in a mutually exclusive manner and random passenger mutations. The goal of these simulations is to compare Multi-Dendrix to other algorithms that identify mutually exclusive genes on straightforward datasets that contain multiple mutually exclusive sets. We generate mutation data for 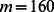 patients and
patients and 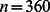 genes as follows. We select a set of four pathways
genes as follows. We select a set of four pathways 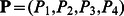 with each
with each 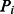 containing four genes. We select the coverage
containing four genes. We select the coverage 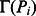 uniformly from the following intervals:
uniformly from the following intervals: 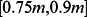 ,
, 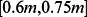 ,
, 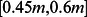 ,
, 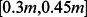 , respectively. The size of this dataset and the varying coverages of the pathways model what is observed in real data (see § Somatic Mutation data) and is consistent with models of mutation progression where driver mutations accumulate in pathways [28]. For each pathway
, respectively. The size of this dataset and the varying coverages of the pathways model what is observed in real data (see § Somatic Mutation data) and is consistent with models of mutation progression where driver mutations accumulate in pathways [28]. For each pathway 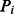 , we select
, we select 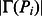 patients at random and add a driver mutation to exactly one gene from the set
patients at random and add a driver mutation to exactly one gene from the set 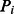 . Thus, the driver mutations in each pathway are mutually exclusive. We then add passenger mutations by randomly mutating genes in each patient with probability,
. Thus, the driver mutations in each pathway are mutually exclusive. We then add passenger mutations by randomly mutating genes in each patient with probability, 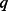 , the passenger mutation probability.We used values of
, the passenger mutation probability.We used values of 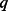 similar to our estimates for
similar to our estimates for 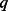 on the TCGA GBM and Lung cancer data sets (in § Somatic Mutation data below), which were
on the TCGA GBM and Lung cancer data sets (in § Somatic Mutation data below), which were 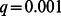 and
and 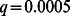 , respectively. We emphasize that these simulations do not model all of the complexities of somatic mutations in cancer e.g. gene-specific and patient-specific mutation rates, genes present in multiple pathways, etc.
, respectively. We emphasize that these simulations do not model all of the complexities of somatic mutations in cancer e.g. gene-specific and patient-specific mutation rates, genes present in multiple pathways, etc.
Since the Dendrix and RME algorithms are designed to find single pathways, we compared Multi-Dendrix to iterative versions of these methods that return multiple gene sets. For Dendrix we used the iterative approach described in [23]: apply Dendrix to find a highest scoring gene set, remove those genes from the dataset, and apply Dendrix to the reduced dataset, repeating these steps until a desired number  of gene sets are found. We will refer to this algorithm as Iter-Dendrix. Thus, Iter-Dendrix returns a collection
of gene sets are found. We will refer to this algorithm as Iter-Dendrix. Thus, Iter-Dendrix returns a collection 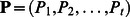 of
of  gene sets such that
gene sets such that 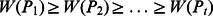 . We implemented the analogous iterative version of RME, and will refer to this algorithm as Iter-RME. We compared the collection
. We implemented the analogous iterative version of RME, and will refer to this algorithm as Iter-RME. We compared the collection 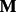 of gene sets found by each algorithm to the planted pathways
of gene sets found by each algorithm to the planted pathways  , computing the symmetric difference
, computing the symmetric difference 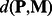 between
between 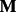 and
and  as described in Methods.
as described in Methods.
Table 1 shows a comparison of Multi-Dendrix, Iter-Dendrix, and Iter-RME on simulated mutation data for different values of 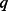 . Note that we do not show comparisons to Iter-RME for
. Note that we do not show comparisons to Iter-RME for 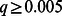 as Iter-RME did not complete after 24 hours of runtime for any of the 1000 simulated mutation data sets. While the RME publication [22] analyzed mutation matrices with thousands of genes and hundreds of patients, this analysis (and the released RME software) required that mutations were presented in at least 10% of the samples, greatly reducing the number of genes/samples input to the algorithm. In fact, a threshold of 10% will remove nearly all genes in current whole-exome studies (see § Comparison of Multi-Dendrix and RME).
as Iter-RME did not complete after 24 hours of runtime for any of the 1000 simulated mutation data sets. While the RME publication [22] analyzed mutation matrices with thousands of genes and hundreds of patients, this analysis (and the released RME software) required that mutations were presented in at least 10% of the samples, greatly reducing the number of genes/samples input to the algorithm. In fact, a threshold of 10% will remove nearly all genes in current whole-exome studies (see § Comparison of Multi-Dendrix and RME).
Table 1. A comparison of the algorithms on simulated mutation data with varying passenger mutation probability 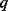 .
.
Avg. distance 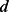 from planted pathways from planted pathways |
|||
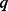
|
Multi-Dendrix | Iter-RME | Iter-Dendrix |
| 0.0 |
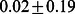
|
0.01
 0.12
0.12
|
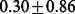
|
| 0.0001 |
0.02
 0.18
0.18
|
0.01
 0.16
0.16
|
0.30
 0.86
0.86
|
| 0.0005 |
0.04
 0.23
0.23
|
0.10 0.40 0.40 |
0.35 0.89 0.89 |
| 0.001 |
0.10
 0.35
0.35
|
0.32
 0.60
0.60
|
0.44
 1.01
1.01
|
| 0.005 |
0.44
 0.71
0.71
|
– | 0.75 1.07 1.07 |
| 0.01 |
1.03
 1.00
1.00
|
– | 1.20 1.15 1.15 |
| 0.015 |
1.68
 1.16
1.16
|
– | 1.78 1.26 1.26 |
| 0.02 |
2.17
 1.24
1.24
|
– | 2.21 1.29 1.29 |
Italicized rows correspond to values of 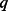 approximated from real cancer datasets. Each entry is mean (
approximated from real cancer datasets. Each entry is mean (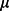 ) and standard deviation (
) and standard deviation ( ) (across 1000 simulations) of the distance
) (across 1000 simulations) of the distance 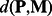 between the planted set of pathways
between the planted set of pathways  and the collections
and the collections 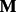 found by each algorithm. The minimum distance
found by each algorithm. The minimum distance 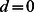 indicates an algorithm found the planted pathways exactly, while the maximum distance
indicates an algorithm found the planted pathways exactly, while the maximum distance 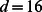 indicates that an algorithm did not find any of the genes in the planted pathways. Bold text indicates the top performing algorithm for each value of
indicates that an algorithm did not find any of the genes in the planted pathways. Bold text indicates the top performing algorithm for each value of 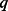 . Multi-Dendrix is the top performer for all values of
. Multi-Dendrix is the top performer for all values of 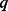 except the smallest
except the smallest 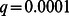 . The differences between Multi-Dendrix and both Iter-Dendrix and Iter-RME are statistically significant (
. The differences between Multi-Dendrix and both Iter-Dendrix and Iter-RME are statistically significant (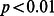 ) for
) for 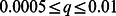 . For
. For 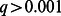 , Iter-RME did not complete after 24 hours of runtime.
, Iter-RME did not complete after 24 hours of runtime.
For 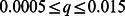 , Multi-Dendrix identifies collections of gene sets that were significantly closer (
, Multi-Dendrix identifies collections of gene sets that were significantly closer (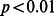 ) to the planted pathways
) to the planted pathways  than the collections found by either Iter-Dendrix and Iter-RME. These results demonstrate that Multi-Dendrix outperforms other methods, even when the passenger mutation probability
than the collections found by either Iter-Dendrix and Iter-RME. These results demonstrate that Multi-Dendrix outperforms other methods, even when the passenger mutation probability 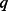 is more than 15 times greater than the value estimated from real somatic mutation data. For
is more than 15 times greater than the value estimated from real somatic mutation data. For 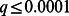 , the differences between Multi-Dendrix and Iter-RME were not significant.
, the differences between Multi-Dendrix and Iter-RME were not significant.
We also compared the runtimes of each algorithm on the simulated datasets. Multi-Dendrix was several orders of magnitude faster than Iter-Dendrix and Iter-RME on all datasets (Table 2). Note that as the passenger mutation probability 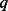 increases, the number of recurrently mutated passenger genes increases. Multi-Dendrix scales much better than Iter-RME and maintains a significant advantage over Iter-Dendrix, completing all simulated datasets in less than 5 seconds.
increases, the number of recurrently mutated passenger genes increases. Multi-Dendrix scales much better than Iter-RME and maintains a significant advantage over Iter-Dendrix, completing all simulated datasets in less than 5 seconds.
Table 2. A comparison of the runtimes of Multi-Dendrix, Iter-RME, and Iter-Dendrix on simulated mutation data with varying passenger mutation probability 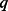 .
.
| Avg. runtime (secs) | |||
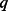
|
Multi-Dendrix | Iter-RME | Iter-Dendrix |
| 0.0001 | 0.28 | 19.22 | 609.79 |
| 0.0005 | 0.28 | 17.36 | 621.22 |
| 0.001 | 0.50 | 123.16 | 610.21 |
| 0.005 | 1.46 |
 86, 400 86, 400 |
672.43 |
| 0.01 | 2.60 |
 86, 400 86, 400 |
711.55 |
| 0.015 | 4.06 |
 86, 400 86, 400 |
730.85 |
| 0.02 | 4.93 |
 86, 400 86, 400 |
727.82 |
Runtimes for each algorithm are reported as the mean runtime of 10 runs for each value of 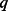 . Note that Multi-Dendrix has runtimes under 5 seconds for all datasets, and is orders of magnitude faster than the other methods for each
. Note that Multi-Dendrix has runtimes under 5 seconds for all datasets, and is orders of magnitude faster than the other methods for each 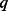 . For Iter-RME, we report a runtime of
. For Iter-RME, we report a runtime of  86,400 seconds for
86,400 seconds for 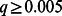 as Iter-RME did not complete within one day. Simulations were performed on machines running 64-bit Debian Linux with Xeon 2.8 GHz processors and a maximum of 8 GB of available memory.
as Iter-RME did not complete within one day. Simulations were performed on machines running 64-bit Debian Linux with Xeon 2.8 GHz processors and a maximum of 8 GB of available memory.
We evaluated how the runtime of Multi-Dendrix scales to larger datasets. Using the same passenger mutation probabilities 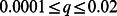 listed above, we calculated the average runtime in seconds of Multi-Dendrix for ten simulated mutation matrices with
listed above, we calculated the average runtime in seconds of Multi-Dendrix for ten simulated mutation matrices with 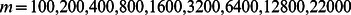 genes and
genes and 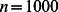 patients, more than the number of patients to be measured in any cancer study from TCGA. In each case, we run Multi-Dendrix only on the subset of genes that are mutated in more than the expected number
patients, more than the number of patients to be measured in any cancer study from TCGA. In each case, we run Multi-Dendrix only on the subset of genes that are mutated in more than the expected number 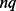 of samples. For the largest dataset with
of samples. For the largest dataset with 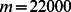 genes, the average number of genes input to Multi-Dendrix for the highest and lowest passenger mutation probabilities are
genes, the average number of genes input to Multi-Dendrix for the highest and lowest passenger mutation probabilities are 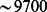 and
and 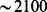 , respectively. (Table S1 shows the average number of input genes for varying
, respectively. (Table S1 shows the average number of input genes for varying  and
and  .) The average runtime for this largest dataset is under one hour (average of 54.4 minutes). Figure S1 shows the runtimes for varying
.) The average runtime for this largest dataset is under one hour (average of 54.4 minutes). Figure S1 shows the runtimes for varying  and
and  .
.
The Multi-Dendrix Computational Pipeline
We incorporate the Multi-Dendrix algorithm into a larger pipeline (Figure 1) that includes several additional pre- and post-processing tasks including: (1) Building mutation matrices for input into Multi-Dendrix; (2) Summarizing Multi-Dendrix results over multiple values for the parameters  , the number of gene sets,
, the number of gene sets, 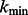 the minimum size of a gene set, and
the minimum size of a gene set, and 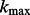 the maximum size of a gene set; (3) Evaluating the statistical significance of results; (4) Examining Multi-Dendrix results for mutually exclusive sets resulting from subtype-specific mutations. We describe these steps briefly below, with further details in the Methods and Supporting Information.
the maximum size of a gene set; (3) Evaluating the statistical significance of results; (4) Examining Multi-Dendrix results for mutually exclusive sets resulting from subtype-specific mutations. We describe these steps briefly below, with further details in the Methods and Supporting Information.
Figure 1. The Multi-Dendrix pipeline.
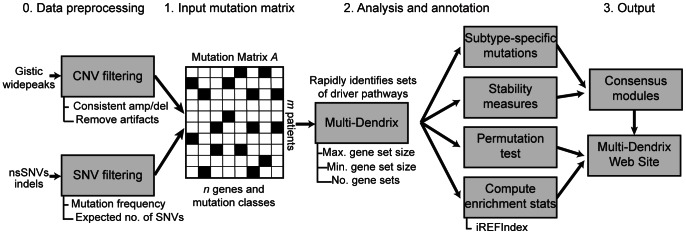
Multi-Dendrix analyzes integrated mutation data from a variety of sources including single-nucleotide mutations and copy number aberrations. Multiple gene set are identified using a combinatorial optimization approaches. The output is analyzed for subtype-specific mutations and summarized across multiple values of the parameters:  , number of gene sets, and
, number of gene sets, and 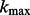 , maximum size per gene set.
, maximum size per gene set.
First, we build mutation matrices 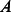 from somatic mutation data. We use several steps to process single-nucleotide variant (SNV) data, copy number variant (CNV) data, and to combine both types of data. Second, in contrast to simulated data, on real data we do not know the correct values of the parameters
from somatic mutation data. We use several steps to process single-nucleotide variant (SNV) data, copy number variant (CNV) data, and to combine both types of data. Second, in contrast to simulated data, on real data we do not know the correct values of the parameters  ,
, 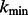 , and
, and 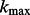 . Thus, we consider a reasonable range of values for these parameters and summarize the results over these parameters into modules. We build a graph, where the nodes are individual genes (or mutation classes) and edges connect genes (respectively mutation classes) that appear in the same gene set for more than one value of the parameters. We weight each edge with the fraction of parameter values for which the pair of genes appear in the same gene set. The resulting edge-weighted graphs provide a measure of the stability of the resulting gene sets over different parameter values. By choosing a minimum edge weight, we partition the graph into connected components, or modules. One may choose to use these modules as the output of Multi-Dendrix.
. Thus, we consider a reasonable range of values for these parameters and summarize the results over these parameters into modules. We build a graph, where the nodes are individual genes (or mutation classes) and edges connect genes (respectively mutation classes) that appear in the same gene set for more than one value of the parameters. We weight each edge with the fraction of parameter values for which the pair of genes appear in the same gene set. The resulting edge-weighted graphs provide a measure of the stability of the resulting gene sets over different parameter values. By choosing a minimum edge weight, we partition the graph into connected components, or modules. One may choose to use these modules as the output of Multi-Dendrix.
Third, we evaluate the statistical significance of our results using two measures. Since the collection 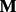 with high weight
with high weight 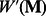 may not be surprising in a large mutation matrix
may not be surprising in a large mutation matrix 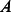 , the first measure evaluates the significance of the score
, the first measure evaluates the significance of the score 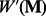 maximized by Multi-Dendrix. We evaluate whether the weight
maximized by Multi-Dendrix. We evaluate whether the weight 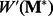 of the maximum weight collection
of the maximum weight collection 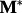 output by Multi-Dendrix is significantly large compared to an empirical distribution of the maximum weight sets from randomly permuted mutation data. We generate random mutation data using the permutation test described in [19]. This test permutes the mutations among the genes in each patient, preserving both the number of mutated genes in each patient and the number of patients with a mutation in each gene while perturbing any patterns of exclusivity between mutated genes. Note that this permutation test requires running Multi-Dendrix many times to determine statistical significance for a single parameter setting. Thus, the runtime advantages of Multi-Dendrix compared to Iter-Dendrix and Iter-RME are very important in practice on real datasets.
output by Multi-Dendrix is significantly large compared to an empirical distribution of the maximum weight sets from randomly permuted mutation data. We generate random mutation data using the permutation test described in [19]. This test permutes the mutations among the genes in each patient, preserving both the number of mutated genes in each patient and the number of patients with a mutation in each gene while perturbing any patterns of exclusivity between mutated genes. Note that this permutation test requires running Multi-Dendrix many times to determine statistical significance for a single parameter setting. Thus, the runtime advantages of Multi-Dendrix compared to Iter-Dendrix and Iter-RME are very important in practice on real datasets.
Next, we evaluate whether the collection 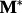 output by Multi-Dendrix contains more protein-protein interactions than expected by chance by applying our direct interactions test on a PPI network constructed from the union of the KEGG and iRefIndex PPI networks. The direct interactions test computes a statistic
output by Multi-Dendrix contains more protein-protein interactions than expected by chance by applying our direct interactions test on a PPI network constructed from the union of the KEGG and iRefIndex PPI networks. The direct interactions test computes a statistic  of the difference in the number of interactions within and between gene sets in
of the difference in the number of interactions within and between gene sets in 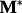 , and compares the observed value of
, and compares the observed value of  to an empirical distribution on 1000 permuted PPI networks (full details of the test are in
to an empirical distribution on 1000 permuted PPI networks (full details of the test are in  Evaluating known interactions). These permuted networks account for the observation that many genes that are frequently mutated in cancer also have large degree in the interaction network – either due to biological reasons or ascertainment bias. We use an interaction network to assess biological function rather than known pathways (e.g. KEGG pathways or GSEA sets) because most of these pathways are relatively large, while the gene sets found by Multi-Dendrix that exhibit exclusivity tend to be much smaller, each containing only a few genes.
Evaluating known interactions). These permuted networks account for the observation that many genes that are frequently mutated in cancer also have large degree in the interaction network – either due to biological reasons or ascertainment bias. We use an interaction network to assess biological function rather than known pathways (e.g. KEGG pathways or GSEA sets) because most of these pathways are relatively large, while the gene sets found by Multi-Dendrix that exhibit exclusivity tend to be much smaller, each containing only a few genes.
Finally, we examine possible correlations between the mutually exclusive sets reported by Multi-Dendrix and particular subsets of samples. A number of cancers are divided into subtypes according to pathology, cytogenetics, gene expression, or other features. Since mutations that are specific to particular subtypes will be mutually exclusive, disease heterogeneity is an alternative explanation to pathways for observed mutually exclusive sets. For example, [29] report four subtypes of GBM based on gene expression clusters, and show that several mutations – including IDH1, PDGFRA, EGFR, and NF1 – have strong association with individual subtypes. Unfortunately, if the subtypes are unknown there is no information for Multi-Dendrix, Dendrix, RME, or other algorithms that analyze mutual exclusivity to distinguish between mutual exclusivity resulting from subtypes and mutual exclusivity resulting from pathways or other causes. If subtypes are known, two possible solutions are to analyze subtypes separately, or to examine whether patterns of mutual exclusivity are associated to these subytpes. We annotate results by known subtypes as a post-processing step in Multi-Dendrix.
Somatic mutation data
We applied Multi-Dendrix and Iter-Dendrix to four somatic mutation matrices: (1) copy number variants (CNVs), small indels, and non-synonymous single nucleotide variants (SNVs) measured in 601 genes in 84 glioblastoma multiformae (GBM) patients [7]; (2) indels and non-synonymous single nucleotide variants in 623 sequenced genes in 188 Lung Adenocarcinoma patients [27]; (3) CNVs, small indels, and non-synonomous SNVs measured using whole-exome sequencing and copy number arrays in 261 GBM patients [7]; and (4) CNVs, small indels, and non-synonymous SNVs measured in 507 BRCA patients. We will refer to these datasets as GBM(2008), Lung, GBM, and BRCA below. We removed extremely low frequency mutations and known outliers from these datasets as described in Methods. After this processing, the GBM(2008) dataset contained mutation and CNV data for 46 genes in 84 patients; the Lung dataset contained somatic mutation for 190 genes in 163 patients; the GBM dataset contained mutation and CNV data for 398 genes in 261 patients; and the BRCA dataset contained mutation and CNV data for 375 genes in 507 patients. We focus here on presenting results from the latter two datasets because they are the latest whole-genome/exome datasets and most representative of the datasets that are now being produced and will be analyzed now and in the coming years. Results with the first two older and smaller datasets from targeted sequencing are described in the Supporting Information.
We compute 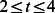 gene sets, each of minimum size
gene sets, each of minimum size 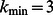 and maximum size ranging from
and maximum size ranging from 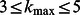 . We summarize the results over these 9 different parameter values into modules using the procedure described above.
. We summarize the results over these 9 different parameter values into modules using the procedure described above.
Mutually exclusive sets in Glioblastoma (GBM)
We applied Multi-Dendrix and Iter-Dendrix to the GBM dataset, considering EGFR amplification as a separate event (see Methods). The algorithms report the same results over all values of the parameters except 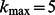 , where Iter-Dendrix includes the IRF5 gene in a gene set with RB1, CDK4(A), and CDKN2A/CDKN2B(D), and MSL3. However, Multi-Dendrix is significantly faster running in 142 seconds compared to 37,786 seconds (over 10 hours) for Iter-Dendrix.
, where Iter-Dendrix includes the IRF5 gene in a gene set with RB1, CDK4(A), and CDKN2A/CDKN2B(D), and MSL3. However, Multi-Dendrix is significantly faster running in 142 seconds compared to 37,786 seconds (over 10 hours) for Iter-Dendrix.
We summarize the results of these different parameter choices by connecting genes that appear in the same gene set at least twice, resulting in four modules (Figure 2). These four modules include all the genes (except ERBB2) that are: (1) members of the three signaling pathways highlighted in the TCGA GBM study [7], and (2) are mutated in 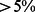 of the samples. The weight
of the samples. The weight 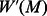 of all collections found by Multi-Dendrix on the GBM dataset are significant
of all collections found by Multi-Dendrix on the GBM dataset are significant 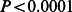 ) and the direct interactions statistic
) and the direct interactions statistic  of these four modules is also significant (
of these four modules is also significant (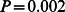 ). Three of the four modules also contain a significant number of interactions (
). Three of the four modules also contain a significant number of interactions (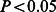 ). In addition to these four modules, two additional mutation classes, CNTNAP2 and deletion of 10q26.3, each appear in one choice of parameters for Multi-Dendrix. Since these are not part of a larger module, they are not analyzed further. Figure S2 shows a combined mutation matrix with all four modules.
). In addition to these four modules, two additional mutation classes, CNTNAP2 and deletion of 10q26.3, each appear in one choice of parameters for Multi-Dendrix. Since these are not part of a larger module, they are not analyzed further. Figure S2 shows a combined mutation matrix with all four modules.
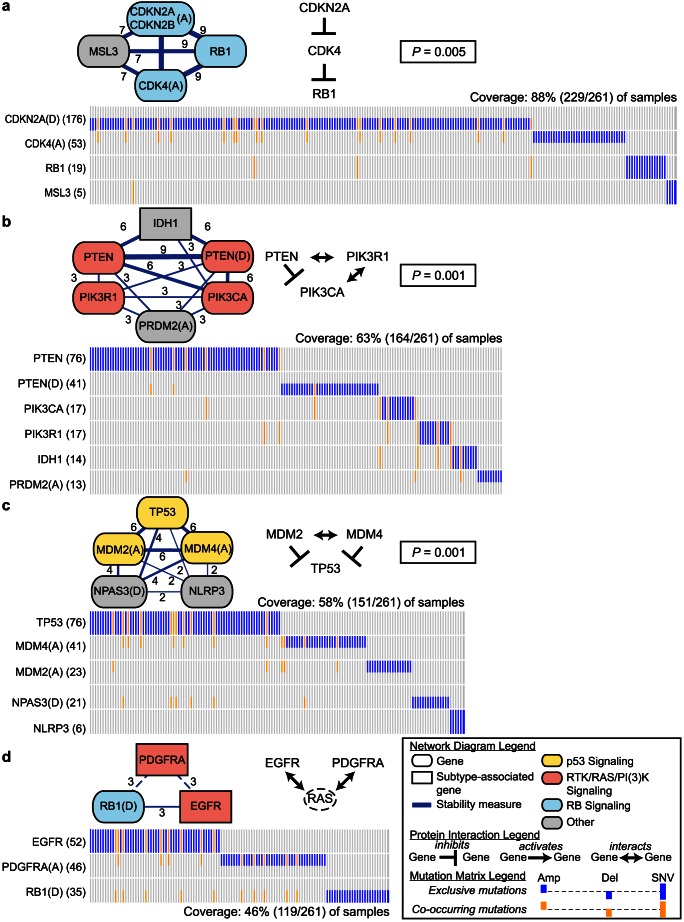
Figure 2. Multi-Dendrix results on the GBM dataset.
(Left) Nodes represent genes in four modules found by Multi-Dendrix using 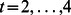 gene sets of minimize size
gene sets of minimize size 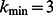 and maximum size
and maximum size 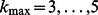 . Genes with “(A)” appended are amplification events, genes with “(D)” appended are deletion events, and genes with no annotation are SNVs. Edges connect genes that appear in the same gene set for more than one value of the parameters, with labels indicating the fraction of parameter values for which the pair of genes appear in the same gene set. Color of nodes indicates membership in three signaling pathways noted in [7] as important for GBM: RB, p53, and RTK/RAS/PI(3)K signaling. Shape of nodes indicates genes whose mutations are associated with specific GBM subtypes, and dashed edges connect genes associated with different subtypes. The direct interactions statistic
. Genes with “(A)” appended are amplification events, genes with “(D)” appended are deletion events, and genes with no annotation are SNVs. Edges connect genes that appear in the same gene set for more than one value of the parameters, with labels indicating the fraction of parameter values for which the pair of genes appear in the same gene set. Color of nodes indicates membership in three signaling pathways noted in [7] as important for GBM: RB, p53, and RTK/RAS/PI(3)K signaling. Shape of nodes indicates genes whose mutations are associated with specific GBM subtypes, and dashed edges connect genes associated with different subtypes. The direct interactions statistic  of this collection of gene sets is significant (
of this collection of gene sets is significant (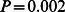 ). (Middle) Known interactions between proteins in each set and
). (Middle) Known interactions between proteins in each set and 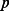 -value for observed number of interactions. (Right) Mutation matrix for each of four modules with mutual exclusive (blue) and co-occurring mutations (orange).
-value for observed number of interactions. (Right) Mutation matrix for each of four modules with mutual exclusive (blue) and co-occurring mutations (orange).
The first module includes the amplification of CDK4, mutation of RB1, and a deletion that includes both CDKN2A and CDKN2B. This module is mutated in 87.7% (229/261) of the samples, and are discovered for all parameter choices. These four genes are members of the RB signaling pathway (as annotated in [7]) involved in G1/S progression (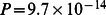 by Bonferonni-corrected hypergeometric test): CDKN2A and CDKN2B inhibits CDK4, which in turn inhibits RB1. In addition for 7/9 parameter choices, this module includes mutations in MSL3. MSL3 is a member of the MSL (male-specific lethal) complex that has a major role in dosage compensation in Drosophila. While this complex is conserved in mammals, the specific function of human MSL3 is unknown. However, the MSL complex also includes the histone acetyltransferase MOF which is involved in cell cycle regulation of p53 and may play a role in cancer [30]. Thus, the mutual exclusivity of mutations in MSL3 and the other well-known members of the RB signaling pathway is intriguing and deserves further study. This module contains two interactions (
by Bonferonni-corrected hypergeometric test): CDKN2A and CDKN2B inhibits CDK4, which in turn inhibits RB1. In addition for 7/9 parameter choices, this module includes mutations in MSL3. MSL3 is a member of the MSL (male-specific lethal) complex that has a major role in dosage compensation in Drosophila. While this complex is conserved in mammals, the specific function of human MSL3 is unknown. However, the MSL complex also includes the histone acetyltransferase MOF which is involved in cell cycle regulation of p53 and may play a role in cancer [30]. Thus, the mutual exclusivity of mutations in MSL3 and the other well-known members of the RB signaling pathway is intriguing and deserves further study. This module contains two interactions (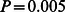 ).
).
The second module includes mutations and deletion of PTEN, mutations in PIK3CA, mutations in PIK3R1, mutations in IDH1, and an amplification that includes PDPN and PRDM2. The module is mutated in 62.8% (164/261) of the samples. PTEN, PIK3CA, and PIK3R1 are all members of the RTK/RAS/PI(3)K signaling pathway (as annotated in [7]) involved in cellular proliferation (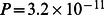 ). IDH1 is not a known member of this pathway; moreover, IDH1 is preferentially mutated in the proneural subtype of GBM [29]. Deletions in PTEN are also associated with the proneural subtype of GBM, although they are not considered a defining feature of this subtype (as IDH1 mutations are) and do not result in a gene expression signature [29]. However, there are no reports that PTEN, PIK3CA, or PIK3R1 mutations are subtype specific, and thus the mutual exclusivity of IDH1 and the remaining genes in this set is not simply explained by subtypes. PRDM2 is not known to be part of the RTK/RAS/PI(3)K signaling pathway. PRDM2 is a member of the histone methyltransferase superfamily, interacts with the RB protein [31], and is proposed as a tumor suppressor in colorectal cancer [32]. PDPN is used as a molecular marker for glioma, due to its association with clinical outcomes [33]. Our results suggest that PDPN and PRDM2 may have an undiscovered role in GBM as well. This module contains three interactions (
). IDH1 is not a known member of this pathway; moreover, IDH1 is preferentially mutated in the proneural subtype of GBM [29]. Deletions in PTEN are also associated with the proneural subtype of GBM, although they are not considered a defining feature of this subtype (as IDH1 mutations are) and do not result in a gene expression signature [29]. However, there are no reports that PTEN, PIK3CA, or PIK3R1 mutations are subtype specific, and thus the mutual exclusivity of IDH1 and the remaining genes in this set is not simply explained by subtypes. PRDM2 is not known to be part of the RTK/RAS/PI(3)K signaling pathway. PRDM2 is a member of the histone methyltransferase superfamily, interacts with the RB protein [31], and is proposed as a tumor suppressor in colorectal cancer [32]. PDPN is used as a molecular marker for glioma, due to its association with clinical outcomes [33]. Our results suggest that PDPN and PRDM2 may have an undiscovered role in GBM as well. This module contains three interactions (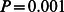 ).
).
The third module includes mutations in TP53, the amplification of MDM2, the amplification of MDM4, mutations in NLRP3, and the deletion involving AKAP6 and NPAS3. This module is mutated in 57.8% (151/261) of the samples, and appears for every parameter choice for 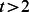 . TP53, MDM2, and MDM4 are members of the p53 signaling pathway (
. TP53, MDM2, and MDM4 are members of the p53 signaling pathway (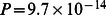 ), a critical and frequently altered pathway in GBM involved in senescence and apoptosis. NPAS3 is a transcription factor expressed in the brain and implicated in psychiatric disorders including schizophrenia [34], [35]. In addition, NPAS3 was recently shown to act as a tumor suppressor in astrocytomas, with a possible role in glioblastoma progression and proliferation [36]. This module contains three interactions (
), a critical and frequently altered pathway in GBM involved in senescence and apoptosis. NPAS3 is a transcription factor expressed in the brain and implicated in psychiatric disorders including schizophrenia [34], [35]. In addition, NPAS3 was recently shown to act as a tumor suppressor in astrocytomas, with a possible role in glioblastoma progression and proliferation [36]. This module contains three interactions (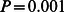 ).
).
The fourth module includes mutations in EGFR, the amplification of PDGFRA , and the deletion of RB1. This module is mutated in 45.6% (119/261) of samples, and appears for 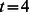 . EGFR and PDGFRA are members of the RTK/RAS/PI(3)K signaling pathway (
. EGFR and PDGFRA are members of the RTK/RAS/PI(3)K signaling pathway (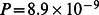 ), and RB1 is a member of the RB signaling pathway. While EGFR and PDGFRA both interact with RAS, there are no reported direct interactions between these three proteins. In addition, mutations in these three genes are significantly associated with two of the expression subtypes reported in [29]: mutations in EGFR and the deletion of RB1 are associated with the Classical GBM subtype, and the amplification of PDGFRA is significantly associated with the Proneural subtype. Thus, it appears that the mutual exclusivity discovered by Multi-Dendrix is a result of subtype-specific mutations, despite PDGFRA and EGFR being a member of the same biological pathway.
), and RB1 is a member of the RB signaling pathway. While EGFR and PDGFRA both interact with RAS, there are no reported direct interactions between these three proteins. In addition, mutations in these three genes are significantly associated with two of the expression subtypes reported in [29]: mutations in EGFR and the deletion of RB1 are associated with the Classical GBM subtype, and the amplification of PDGFRA is significantly associated with the Proneural subtype. Thus, it appears that the mutual exclusivity discovered by Multi-Dendrix is a result of subtype-specific mutations, despite PDGFRA and EGFR being a member of the same biological pathway.
In summary, we see that subtype-specific mutations provide an alternative explanation for observed mutual exclusivity and confound the identification of driver pathways. However, on the GBM data subtype-specific mutations are a minor feature in the data, and Multi-Dendrix successfully identifies de novo portions of three critical signaling pathways in GBM.
Mutually exclusive sets in Breast Cancer (BRCA)
We applied Multi-Dendrix and Iter-Dendrix to the BRCA dataset. We found that for most values of the parameters  and
and 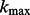 , the results combined the most frequently mutated genes into a single gene set despite the fact that these genes had high coverage overlap (Figures S4 and S5). That is, for a gene set
, the results combined the most frequently mutated genes into a single gene set despite the fact that these genes had high coverage overlap (Figures S4 and S5). That is, for a gene set 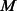 , high coverage
, high coverage 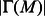 was outweighing a high coverage overlap
was outweighing a high coverage overlap 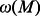 in the weight function
in the weight function 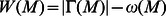 optimized by Multi-Dendrix. To enforce greater mutual exclusivity, we increased the coverage overlap penalty to
optimized by Multi-Dendrix. To enforce greater mutual exclusivity, we increased the coverage overlap penalty to 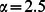 from its default value of
from its default value of 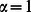 .
.
Using 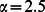 , Multi-Dendrix identifies four distinct modules (Figure 3). These four modules overlap with three pathways known to be important in BRCA: p53 signaling, PI(3)K/AKT signaling, and cell cycle checkpoints. In addition, they include genes recently identified by [8] as important BRCA genes. These modules cover a smaller proportion of samples than our results on the GBM dataset even though they include the same number of genes, suggesting greater mutational heterogeneity or disease heterogeneity (i.e. subtypes) in the breast cancer dataset. Indeed, breast cancers are commonly divided into four major subtypes: Luminal A/B, Basal, and HER2 type. We annotate the subtype-specific mutations below, and Table S6 lists the significant associations between mutations and subtypes. The weight
, Multi-Dendrix identifies four distinct modules (Figure 3). These four modules overlap with three pathways known to be important in BRCA: p53 signaling, PI(3)K/AKT signaling, and cell cycle checkpoints. In addition, they include genes recently identified by [8] as important BRCA genes. These modules cover a smaller proportion of samples than our results on the GBM dataset even though they include the same number of genes, suggesting greater mutational heterogeneity or disease heterogeneity (i.e. subtypes) in the breast cancer dataset. Indeed, breast cancers are commonly divided into four major subtypes: Luminal A/B, Basal, and HER2 type. We annotate the subtype-specific mutations below, and Table S6 lists the significant associations between mutations and subtypes. The weight 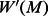 of all collections found by Multi-Dendrix on the BRCA dataset are significant (
of all collections found by Multi-Dendrix on the BRCA dataset are significant (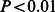 ), and the direct interactions statistic
), and the direct interactions statistic  of these four modules is also significant (
of these four modules is also significant (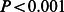 ). In addition, one module is significantly enriched for interactions (
). In addition, one module is significantly enriched for interactions (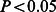 ). In addition to these four modules, five additional genes (SF3B1, CCDC150, COL23A1, C20orf26, PCDHA5) each appear in one choice of parameters for Multi-Dendrix. Since these are not part of a larger module, they were not further analyzed. Figure S3 shows a combined mutation matrix with all four modules.
). In addition to these four modules, five additional genes (SF3B1, CCDC150, COL23A1, C20orf26, PCDHA5) each appear in one choice of parameters for Multi-Dendrix. Since these are not part of a larger module, they were not further analyzed. Figure S3 shows a combined mutation matrix with all four modules.
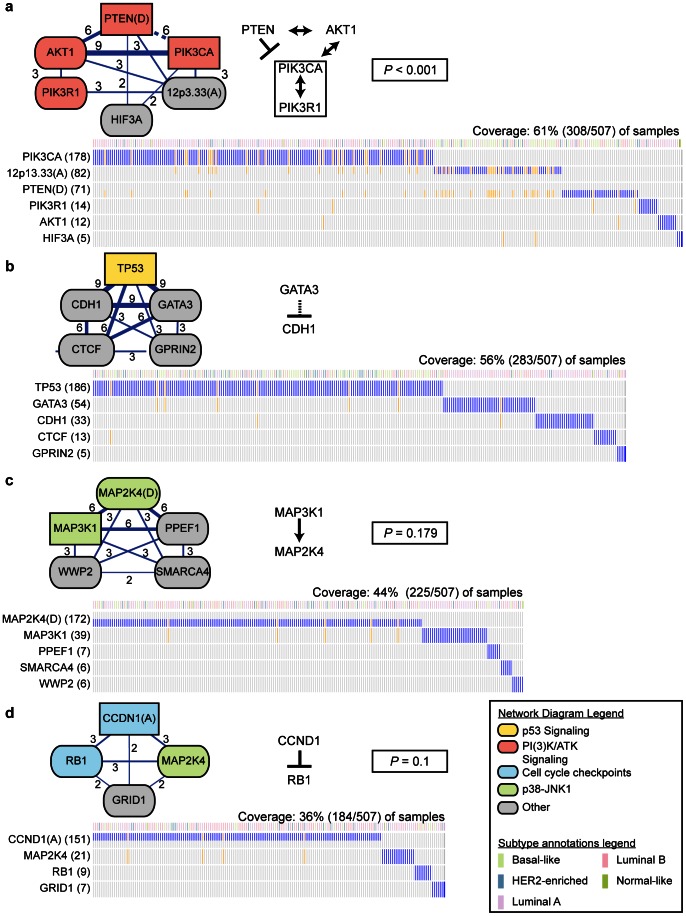
Figure 3. Multi-Dendrix results on the BRCA dataset.
Graphical elements are as described in Figure 2 caption, except for the following. Color of nodes indicates membership in four signaling pathways noted in [8] as important for BRCA: p53 signaling, PI(3)K/AKT signaling, cell cycle checkpoints, and p38-JNK1. The top row of each mutation matrix annotates the subtype of each patient. The regulatory interaction between GATA3 and CDH1 is shown as a dashed line. The direct interactions statistic  of this collection of gene sets is significant (
of this collection of gene sets is significant (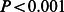 ).
).
The first module includes the deletion of PTEN, mutations in PIK3CA, PIK3R1, AKT1, HIF3A, and the amplification of genomic region 12p13.33. These six mutation classes are mutated in 61% (308/507) of the samples, and this module is discovered for all values of the parameters. PTEN, PIK3CA, PIK3R1, and AKT1 form the core of the PI(3)K/AKT signaling pathway, as annotated in [8] (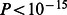 ): AKT1 is known to interact with PTEN, PIK3R1, and PIK3CA, while PTEN inhibits PIK3CA and PIK3R1. These genes constitute five of the eight genes mutated in the PI(3)K/AKT signaling pathway, as reported by [8]. One of the other mutation classes in this module is the amplification of 12p in 82 samples. This amplification event has been reported before in BRCA, although the likely target of this amplification is unknown [37]. This module contains six interactions (
): AKT1 is known to interact with PTEN, PIK3R1, and PIK3CA, while PTEN inhibits PIK3CA and PIK3R1. These genes constitute five of the eight genes mutated in the PI(3)K/AKT signaling pathway, as reported by [8]. One of the other mutation classes in this module is the amplification of 12p in 82 samples. This amplification event has been reported before in BRCA, although the likely target of this amplification is unknown [37]. This module contains six interactions (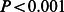 ).
).
The second module includes mutations in the genes TP53, CDH1, GATA3, CTCF, and GPRIN2. These five genes are mutated in 56% (283/507) of the samples, and are discovered for each parameter choice. TP53 is a member of the p53 signaling pathway, while GATA3, CDH1, and CTCF are well-known for their role in breast cancer and are involved in metastasis and proliferation. The loss or downregulation of CDH1, the E-cadherin gene located on 16q22.1, is implicated in breast cancer invasion and proliferation (reviewed in [38]). CTCF, also located on 16q22.1, has been found to act as a tumor suppressor in breast cancer through mechanisms similar to CDH1 [39]. GATA3 is a transcription factor that regulates immune cells, and has long been known to be involved in breast cancer tumorigenesis [40]. Recently, a novel role for GATA3 was discovered, whereby GATA3 suppresses breast cancer metastasis through inhibition of E-cadherin promoters [41]. This module contains zero known interactions.
The third module includes the deletion of MAP2K4 and mutations in MAP3K1, PPEF1, SMARCA4, and WWP2. These five mutations occur in 44.4% (225/507) of the samples, and this module is identified when the number  of gene sets is at least 3. MAP3K1 and MAP2K4 are both members of the p38-JNK1 stress kinase pathway as reported in [8], and are involved in the regulation of apoptosis. Both MAP3K1 and MAP2K4 are serine/threonine kinases, while PPEF1 is a serine/threonine phosphatase. The targets of PPEF1 are unknown, although there are reports that PPEF2, another member of the gene family, does interact with the p38-JNK pathway through the gene ASK1 [42]. SMARCA4 is also a known cancer gene, and has been shown to have a role as a tumor suppressor in lung cancer [43]. This module contains one interaction (
of gene sets is at least 3. MAP3K1 and MAP2K4 are both members of the p38-JNK1 stress kinase pathway as reported in [8], and are involved in the regulation of apoptosis. Both MAP3K1 and MAP2K4 are serine/threonine kinases, while PPEF1 is a serine/threonine phosphatase. The targets of PPEF1 are unknown, although there are reports that PPEF2, another member of the gene family, does interact with the p38-JNK pathway through the gene ASK1 [42]. SMARCA4 is also a known cancer gene, and has been shown to have a role as a tumor suppressor in lung cancer [43]. This module contains one interaction (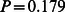 ).
).
The fourth module includes the amplification of CCND1 and mutations in MAP2K4, RB1, and GRID1. These four mutations occur in 36.3% (184/507) of the samples, and this module is discovered when the number  of gene sets is 4. CCND1 and RB1 encode interacting proteins that play a role cell cycle progression. CCND1 encodes the cyclin-D1 protein that inhibits the retinoblastoma protein encoded by RB1 via hyperphosphorylation. The hyperphosphorylation of RB inactivates its role as a tumor suppressor, and thus mutations that target either CCND1 or RB1 are thus important for proliferation in cancer [44]. Mutations in MAP2K4, as discussed above for the third module, target the p38-JNK1 pathway, and MAP2K4 is not known to have any interactions with CCND1 or RB1. This module contains one interaction (
of gene sets is 4. CCND1 and RB1 encode interacting proteins that play a role cell cycle progression. CCND1 encodes the cyclin-D1 protein that inhibits the retinoblastoma protein encoded by RB1 via hyperphosphorylation. The hyperphosphorylation of RB inactivates its role as a tumor suppressor, and thus mutations that target either CCND1 or RB1 are thus important for proliferation in cancer [44]. Mutations in MAP2K4, as discussed above for the third module, target the p38-JNK1 pathway, and MAP2K4 is not known to have any interactions with CCND1 or RB1. This module contains one interaction (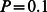 ).
).
We separately ran Multi-Dendrix on mutation data restricted to the 224 Luminal A patients, the 124 Luminal B patients, the 93 Basal-like patients, and the 58 HER2-enriched patients (as annotated in [8]) using different values of  for the different sized datasets (see Supporting Information
for the different sized datasets (see Supporting Information  BRCA subtypes for details). The gene pair {TP53, GATA3} from the Multi-Dendrix modules is also identified by Multi-Dendrix when restricting to basal-like or luminal B samples. The same is true for the gene pair {AKT1, PIK3CA} in HER2-enriched and luminal A subtypes. Thus, the mutual exclusivity between mutations in these pairs of genes is not a result of subtype-specific mutations. On the other hand, the mutual exclusivity between 12p13.33 amplification and PIK3CA mutation appears to be an effect of subtypes, as these aberrations are associated with basal-like and luminal A subtypes, respectively (Table S6), and these two aberrations are not grouped into the same module on any Multi-Dendrix run of individual subtypes. These results show that mutual exclusivity can result from mutational heterogeneity within pathways, disease heterogeneity with subtype-specific mutations, or both.
BRCA subtypes for details). The gene pair {TP53, GATA3} from the Multi-Dendrix modules is also identified by Multi-Dendrix when restricting to basal-like or luminal B samples. The same is true for the gene pair {AKT1, PIK3CA} in HER2-enriched and luminal A subtypes. Thus, the mutual exclusivity between mutations in these pairs of genes is not a result of subtype-specific mutations. On the other hand, the mutual exclusivity between 12p13.33 amplification and PIK3CA mutation appears to be an effect of subtypes, as these aberrations are associated with basal-like and luminal A subtypes, respectively (Table S6), and these two aberrations are not grouped into the same module on any Multi-Dendrix run of individual subtypes. These results show that mutual exclusivity can result from mutational heterogeneity within pathways, disease heterogeneity with subtype-specific mutations, or both.
Discussion
We introduce an algorithm Multi-Dendrix that simultaneously finds multiple cancer driver pathways using somatic mutation data from a collection of patients. Multi-Dendrix finds combinations of somatic mutations solely from the combinatorial pattern of their mutations with no prior knowledge of pathways or interactions between genes. On simulated data, Multi-Dendrix outperforms iterative versions of Dendrix and RME, two previous algorithms for identifying single driver pathways. Multi-Dendrix finds optimal groups of mutually exclusive mutations even in the presence of significant noise where the passenger mutation rate is 15 times greater than observed in real data. Multi-Dendrix is orders of magnitude faster than iterative versions of Dendrix and RME and scales to the analysis of mutations in thousands of genes from hundreds of cancer patients. Finally, Multi-Dendrix finds optimal solutions over a range of sizes for the individual gene sets, while Dendrix examines only a fixed size gene set for each run.
We apply Multi-Dendrix to multiple cancer datasets, including glioblastoma and breast cancer data from The Cancer Genome Atlas, two of the most comprehensive somatic mutation datasets from high-throughput sequencing data. Multi-Dendrix finds multiple driver pathways of interacting genes/proteins including portions of the p53, RTK/RAS/PI(3)K, PI(3)K/AKT, and Rb signaling pathways. At the same time, we identify additional genes whose mutations are mutually exclusive with mutations in these pathways. Intriguingly, these additional genes are transcription factors or other nuclear proteins involved in regulation of transcription ( SMARCA4, NPAS3, PRDM2, and MSL3). In general, gene transcription is the downstream “output” of signaling pathways, suggesting that mutations in these downstream targets may be substituting for mutations in the upstream (and presumably more general) signaling pathways.
Our results demonstrate the advantages of simultaneously finding sets of mutually exclusive genes. However, there can be multiple explanations for observed mutual exclusivity in a set of genes including both pathways (i.e., interactions between genes) as well as disease heterogeneity (i.e., cancer subtypes). Interpretation of Multi-Dendrix results should consider these various explanations. To facilitate these analyses, we include additional steps in the Multi-Dendrix pipeline to compare the results sets of mutations to known gene interactions and/or known subtypes in the samples.
Our Multi-Dendrix analysis shows an interesting feature of mutual exclusivity between SNVs and deletions in tumor suppressor genes. In the glioblastoma data, we find that SNVs in PTEN and the deletion of PTEN are mutually exclusive. It is not clear whether this is a genuine biological feature of the mutational process, where either SNVs or deletions (but not both) are present in different samples, or merely an artifact of the mutation calling. Regarding the latter, it is possible that SNVs are more challenging to detect in hemizygous samples, where the other allele has been deleted.
There are several extensions that might further improve the Multi-Dendrix algorithm. First, the ILP used in Multi-Dendrix finds optimal solutions effectively, but is not guaranteed to rigorously examine suboptimal solutions. This is in contrast to the Markov Chain Monte Carlo (MCMC) approach used by Dendrix that samples suboptimal solutions in proportion to their weight. Extending the MCMC approach to simultaneous discovery of multiple pathways, or perhaps using the ILP to initialize a sampling procedure are interesting directions for future research. Second, the weight function used by the Multi-Dendrix algorithm does not explicitly incorporate co-occurrence of mutations between genes in different gene sets. Instead, the weight function is highest for gene sets with high coverage and approximate exclusivity, which may co-occur in many patients simply due to high coverage (a trivial example is when all gene sets have full coverage, and thus all mutations co-occur across gene sets). As noted in [25], co-occurrence of mutations is known to be important in large biological pathways, and thus algorithms that explicitly optimize for collections of gene sets where mutations between gene sets co-occur a surprising amount may have an advantage in identifying key components of these larger biological pathways.
We anticipate that Multi-Dendrix will be useful for analyzing somatic mutation data from different types of cancer and with larger cohorts of patients, such as those now being generated by The Cancer Genome Atlas (TCGA) and other large-scale cancer sequencing projects. However, mutual exclusivity and high coverage are not the only criteria for selecting driver mutations, and thus the model optimized by Multi-Dendrix has some limitations. As noted above, it is well-known that each patient has multiple driver mutations and there are many examples of co-occurring mutations. Some of these co-occurring mutations are clearly in different pathways, although this depends on one's definition of a pathway. Large, multi-functional “pathways” such as the cell-cycle pathway do indeed exhibit co-occurring mutations; on the other hand, co-occurring mutations appear to be less common in directly interacting genes/proteins. In addition, the coverage, or frequency, of important driver mutations may vary considerably, according to the stage at which patients are sequenced, or extensive disease heterogeneity. Private mutations that are unique to a single individual in a study might be driver mutations, but will not exhibit a strong signal of mutual exclusivity. Multiple approaches are required to prioritize somatic mutations for further experimental study. Multi-Dendrix is a useful complement for analysis of significantly mutated genes [6], [45], [46], functional impact [1]–[4], pathway/network analysis [18]–[22], and other approaches.
Methods
Weight function for gene sets
Given a mutation matrix 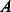 , and a set
, and a set 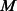 of genes (or equivalent mutation classes), Vandin et al. [23] define the weight function
of genes (or equivalent mutation classes), Vandin et al. [23] define the weight function 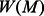 as follows. For a gene
as follows. For a gene 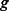 , the coverage
, the coverage
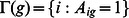 is the set of patients in which gene
is the set of patients in which gene 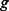 is mutated. Similarly, for a set
is mutated. Similarly, for a set 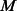 of genes, the coverage is
of genes, the coverage is 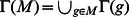 .
. 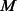 is mutually exclusive if
is mutually exclusive if 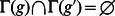 , for all
, for all 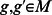 ,
, 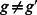 . A gene set in
. A gene set in 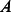 is a column submatrix of
is a column submatrix of 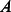 with high coverage and approximate exclusivity. Since increasing coverage may be achieved at the expense of decreasing exclusivity, [23] define a weight
with high coverage and approximate exclusivity. Since increasing coverage may be achieved at the expense of decreasing exclusivity, [23] define a weight 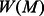 on set
on set 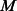 of columns of
of columns of 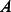 that quantifies both coverage and exclusivity of
that quantifies both coverage and exclusivity of 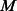 . In particular, they define the coverage overlap of
. In particular, they define the coverage overlap of 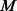 as
as 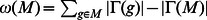 . Note that
. Note that 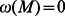 when
when 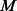 is mutually exclusive. Then
is mutually exclusive. Then 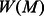 is the difference between the coverage and coverage overlap of
is the difference between the coverage and coverage overlap of 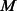 :
:
| (2) |
Note that for a mutually exclusive submatrix 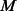 ,
, 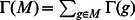 and therefore
and therefore 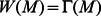 .
.
Vandin et al. [23] introduce the Maximum Weight Submatrix Problem defined for an integer 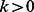 as the problem of finding the
as the problem of finding the 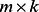 submatrix
submatrix 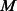 of
of 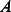 that maximizes a weight
that maximizes a weight 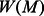 , show that this problem is NP-hard and derive the De novo Driver Exclusivity (Dendrix) algorithm to solve it. Dendrix is a Markov Chain Monte Carlo (MCMC) algorithm that samples sets of
, show that this problem is NP-hard and derive the De novo Driver Exclusivity (Dendrix) algorithm to solve it. Dendrix is a Markov Chain Monte Carlo (MCMC) algorithm that samples sets of 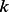 genes in proportion to their weight
genes in proportion to their weight 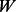 . While the MCMC algorithm is not guaranteed to find a gene set of optimal
. While the MCMC algorithm is not guaranteed to find a gene set of optimal 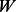 , the authors showed that applying the method to real somatic mutation data produces gene sets with high coverage and approximate exclusivity, and that the Markov chain rapidly converges to a stationary distribution.
, the authors showed that applying the method to real somatic mutation data produces gene sets with high coverage and approximate exclusivity, and that the Markov chain rapidly converges to a stationary distribution.
An ILP for the Maximum Weight Submatrix Problem
We formulate the Maximum Weight Submatrix Problem as an integer linear program, which we refer to as 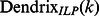 . Given a mutation matrix
. Given a mutation matrix 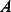 and gene set size
and gene set size 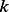 ,
, 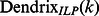 finds a gene set
finds a gene set 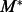 with largest weight
with largest weight 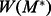 . A gene set
. A gene set 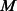 is determined by a set of indicator variables, one for each gene
is determined by a set of indicator variables, one for each gene 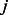 ,
,
| (3) |
To compute the weight function 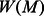 in (2), it is necessary to compute the coverage
in (2), it is necessary to compute the coverage 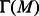 . To do this, we define an indicator variable for each patient
. To do this, we define an indicator variable for each patient  ,
,
| (4) |
Then,  is defined as follows:
is defined as follows:
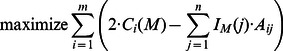 |
(5a) |
| (5b) |
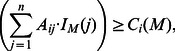 |
(5c) |
Note that the last constraint (5c) only forces  when all genes in
when all genes in 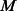 are not mutated (i.e.
are not mutated (i.e. 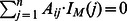 ), but does not force
), but does not force 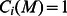 when at least one gene in
when at least one gene in 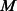 is mutated as required by (4). However, in the latter case the objective function will be maximized when
is mutated as required by (4). However, in the latter case the objective function will be maximized when 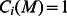 and thus (4) is satisfied.
and thus (4) is satisfied.
Note that removing equation (5b) from 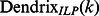 above produces a gene set with optimal
above produces a gene set with optimal 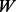 for any value of
for any value of 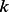 , i.e. a gene set
, i.e. a gene set 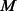 with maximum
with maximum 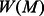 of any size. We will refer to this variant of the ILP as
of any size. We will refer to this variant of the ILP as 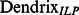 . In addition, we can set bounds on the size of the gene set
. In addition, we can set bounds on the size of the gene set 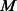 ,
, 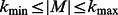 , by replacing equation (5b) with
, by replacing equation (5b) with
| (6) |
We will refer to this variant as 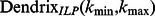 .
.
Multiple Maximum Weight Submatrices Problem
We define the following problem.
Multiple Maximum Weight Submatrices Problem
Given an
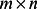 mutation matrix
mutation matrix
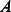 and an integer
and an integer
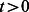 , find a collection
, find a collection
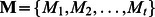 of
of
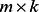 column submatrices that maximizes
column submatrices that maximizes
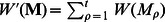 .
.
Note that this problem is NP-hard, as stated above for the case 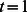 . Further note that while the weight
. Further note that while the weight 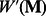 is increased by greater mutual exclusivity between mutations within a gene set, there is no restriction on the mutations between gene sets. Moreover, collections with large weight
is increased by greater mutual exclusivity between mutations within a gene set, there is no restriction on the mutations between gene sets. Moreover, collections with large weight 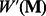 will also tend to have larger coverage
will also tend to have larger coverage 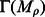 of each individual gene set
of each individual gene set 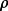 . Thus, optimal solutions will tend to produce a collection with the property that many patients have a mutation in more than one gene set; or alternatively, there may be pairs or larger sets of co-occurring mutations, a phenomenon that has been observed in cancer [25].
. Thus, optimal solutions will tend to produce a collection with the property that many patients have a mutation in more than one gene set; or alternatively, there may be pairs or larger sets of co-occurring mutations, a phenomenon that has been observed in cancer [25].
We solve the Multiple Maximum Weight Submatrix problem using an integer linear program (ILP). We define an ILP, called Multi-Dendrix, using the same definitions of 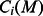 and
and 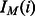 as above:
as above:
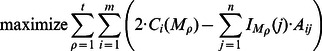 |
(7a) |
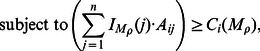 |
(7b) |
| (7c) |
We solve this ILP using CPLEX v12.3 using default parameters. It is obvious that for a mutation matrix 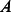 , the collections
, the collections 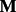 and
and 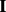 of gene sets produced by Multi-Dendrix and Iter-Dendrix, respectively satisfy
of gene sets produced by Multi-Dendrix and Iter-Dendrix, respectively satisfy 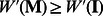 . Multi-Dendrix can also produce sets
. Multi-Dendrix can also produce sets 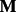 with strictly larger weight than the sets
with strictly larger weight than the sets 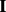 produced by Iter-Dendrix. There are a number of ways this might occur. First, there may be multiple gene sets
produced by Iter-Dendrix. There are a number of ways this might occur. First, there may be multiple gene sets 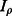 with maximum weight on iteration
with maximum weight on iteration 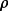 , and only one of these is extended by the iterative algorithm. Second, the maximum weight gene set
, and only one of these is extended by the iterative algorithm. Second, the maximum weight gene set 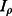 selected by Iter-Dendrix in the
selected by Iter-Dendrix in the 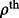 iteration may not be a member of the optimal
iteration may not be a member of the optimal 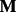 ; i.e.
; i.e. 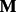 may contain gene sets that are suboptimal when considered in isolation. Third, when
may contain gene sets that are suboptimal when considered in isolation. Third, when 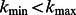 Multi-Dendrix may select gene sets with fewer than
Multi-Dendrix may select gene sets with fewer than 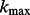 genes if this maximizes the weight
genes if this maximizes the weight 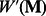 of the whole collection. We find that all of these cases occur on real somatic mutation data.
of the whole collection. We find that all of these cases occur on real somatic mutation data.
Multi-Dendrix can be extended to allow genes to be members of more than one gene set. Such genes may be involved in multiple biological processes. We define the parameter 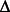 to be the maximum number of gene sets a gene can be a member of, and the parameter
to be the maximum number of gene sets a gene can be a member of, and the parameter  to be the number of overlaps allowed per gene set. Then we replace Eq. 7c with
to be the number of overlaps allowed per gene set. Then we replace Eq. 7c with 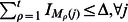 and add the constraint
and add the constraint 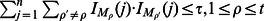 . Note that the product in the second group of constraints must be encoded using additional indicator variables and thus the number of additional constraints grows rapidly as more overlaps between gene sets are allowed. While this extension is implemented in the Multi-Dendrix package, we did not use it for the results presented herein.
. Note that the product in the second group of constraints must be encoded using additional indicator variables and thus the number of additional constraints grows rapidly as more overlaps between gene sets are allowed. While this extension is implemented in the Multi-Dendrix package, we did not use it for the results presented herein.
Simulations
We ran Dendrix with default parameters using 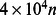 iterations for the MCMC method, where
iterations for the MCMC method, where  is the number of genes. We also used the default parameters for RME. We ran each algorithm with the true values
is the number of genes. We also used the default parameters for RME. We ran each algorithm with the true values 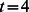 and
and 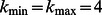 . We compared the collection
. We compared the collection  of gene sets found by each algorithm to the planted pathways
of gene sets found by each algorithm to the planted pathways  , computing the difference between
, computing the difference between  and
and  as follows:
as follows:
where  is a permutation of
is a permutation of 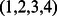 and
and  is the symmetric difference between sets.
is the symmetric difference between sets.
Construction of mutation matrices
We have two pipelines for building mutation matrices from somatic mutation data: one for the whole-exome datasets and the second for the targeted gene sequencing datasets, GBM(2008) and lung adenocarcinoma. Here we describe the pipeline for the whole-exome datasets. See Supporting Information for further details on the targeted gene sequencing data processing.
Whole-exome and copy number aberration data preparation
For the whole-exome datasets, we extracted non-silent somatic mutations from MAF files and copy number aberrations from GISTIC 2.0 [47] downloaded from the TCGA portal:
-
GBM: http://gdac.broadinstitute.org/runs/analyses__2012_09_13/data/GBM/20120913/.
MAF file: gdac.broadinstitute.org_GBM.Mutation_Assessor.Level_4.2012091300.0.0./GBM.maf.annotated.
GISTIC wide peaks: gdac.broadinstitute.org_GBM.CopyNumber_Gistic2.Level_4.2012091300.0.0.tar.gz.
-
BRCA: https://tcga-data.nci.nih.gov/docs/publications/brca_2012/.
MAF file: “Somatic MAF archive [tar.gz] (public access)”.
Segment data: “Merged segment file”.
GISTIC wide peaks: “Genes in focal peaks [xslx]”.
We applied the following filters to remove genes from the analysis:
10,443 genes in the GBM dataset and 11,428 genes in the BRCA dataset mutated in fewer than 5 samples.
209 genes in the GBM dataset and 474 genes in the BRCA dataset whose coding regions are longer than 6 Kb and had fewer mutations than expected using a binomial test with an estimate of
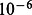 for the background mutation rate.
for the background mutation rate.94 genes from both datasets that are observed to have unusually high rates of somatic mutation in exome-sequencing data, but are likely artifacts resulting from replication timing, active transcription, and other factors (as reported by M. Lawrence here: http://1.usa.gov/RBtuz7). These include olfactory receptors, “cub and sushi” proteins, and TTN.
10 additional genes (KRTAP5-5, HEATR7B2, EML2, CC2D1A, DUS3L, GABRA6, FLG, HYDIN, SUSD3, CROCCL1) that also appear to be artifacts as they were observed to have higher than average mutation rates, but with no known role in cancer.
For copy number data, we used the “wide peaks” in the GISTIC output as the copy number aberrations in each sample, with copy number ratio thresholds of 0.1 and −0.1 for determining if a segment is amplified or deleted, respectively. We performed the following additional filtering of the copy number data.
We combine copy number aberrations that co-occur in the same sample
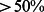 of the time and are within 10 Mb of one another into a single larger “meta” gene.
of the time and are within 10 Mb of one another into a single larger “meta” gene.We restricted analysis to 249 CNVs in the GBM data and 204 CNVs in the BRCA data that appeared in wide peaks with 20 or fewer genes or were given a peak label by GISTIC.
For BRCA, we removed segments longer than 10 Mb.
Remove wide peaks containing known fragile sites at PARK2 [48], WWOX [49], RPL5, and FAM19A5.
Note that in many cases, the wide peaks include multiple genes which we combine into a single “meta” gene for Multi-Dendrix analysis. We manually selected the target gene for the following metagenes:
For GBM, we selected CDK4, CDKN2A and CDKN2B, PTEN, PDGFRA, MDM2, MDM4, PIK3R1, and RB1 as the targets of their respective aberrations.
For BRCA, we used the GISTIC peak labels as the target for each aberration.
In the GBM dataset, we treated EGFR as a separate event and did not include it in the Multi-Dendrix analysis. EGFR amplification is the most common amplification, and second most common mutation (after CDKN2A/B deletion). There is a significant co-occurrence between EGFR amplifications and SNVs (
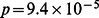 by Fisher's exact test), although EGFR amplification occurs in 74 more samples than EGFR SNV.
by Fisher's exact test), although EGFR amplification occurs in 74 more samples than EGFR SNV.
After this filtering, we analyze a total of 398 mutation classes in GBM and 375 mutation classes in BRCA (i.e. separating SNVs and CNVs in individual genes or metagenes).
Evaluating known interactions
We assess whether the mutually exclusive gene sets found by Multi-Dendrix are enriched for interacting genes using the following direct interactions test. We use two analogous tests: one test for collections, and one test for for individual gene sets.
For a collection  , let
, let  be the fraction of possible interactions between pairs of genes within each gene set
be the fraction of possible interactions between pairs of genes within each gene set  that are observed and
that are observed and 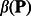 be the fraction of possible interactions between pairs of genes in different pairs of gene sets
be the fraction of possible interactions between pairs of genes in different pairs of gene sets  ,
,  that are observed. We define
that are observed. We define 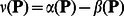 . Thus, a large value
. Thus, a large value 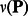 indicates a collection with many interactions between genes in the same gene set and few interactions between genes in different gene sets. This measure models our assumptions that mutual exclusivity should be strongest between genes that directly interact. Moreover, we also expect few interactions between genes in different gene sets reported by Multi-Dendrix. Thus, the measure
indicates a collection with many interactions between genes in the same gene set and few interactions between genes in different gene sets. This measure models our assumptions that mutual exclusivity should be strongest between genes that directly interact. Moreover, we also expect few interactions between genes in different gene sets reported by Multi-Dendrix. Thus, the measure  is a more strict measure of the topology of interactions than merely counting the total number of observed interactions. Similarly, we assess an individual gene set by counting the number of interactions among genes in that gene set. Let
is a more strict measure of the topology of interactions than merely counting the total number of observed interactions. Similarly, we assess an individual gene set by counting the number of interactions among genes in that gene set. Let 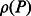 be the number of interactions among genes in
be the number of interactions among genes in 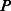 .
.
We assess the statistical significance of  and
and 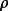 by comparing the observed value to the empirical distribution of
by comparing the observed value to the empirical distribution of  and
and 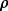 on an ensemble of permuted networks with the same degree distribution. We permute the network by swapping edges between pairs of genes, so as to preserve the distribution of edges within the network. We perform
on an ensemble of permuted networks with the same degree distribution. We permute the network by swapping edges between pairs of genes, so as to preserve the distribution of edges within the network. We perform 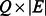 edge swaps, where
edge swaps, where  is the edges in the network and
is the edges in the network and  is some constant (we use
is some constant (we use 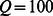 as recommended for permuting graphs with fixed degree distribution in [50]). This network permutation corrects for the observation that many genes that are frequency mutated in cancer also have many interactions in human PPI networks. Since frequently mutated genes typically appear in Multi-Dendrix results, the number of interactions between genes in Multi-Dendrix results might be higher than a random set of genes of the same size. When performing the direct interactions test, we use a protein-protein interaction (PPI) network constructed from the union of interactions reported in KEGG [13] and iRefIndex 9.0 [51] containing 236,060 interactions among 15,257 proteins. We calculate
as recommended for permuting graphs with fixed degree distribution in [50]). This network permutation corrects for the observation that many genes that are frequency mutated in cancer also have many interactions in human PPI networks. Since frequently mutated genes typically appear in Multi-Dendrix results, the number of interactions between genes in Multi-Dendrix results might be higher than a random set of genes of the same size. When performing the direct interactions test, we use a protein-protein interaction (PPI) network constructed from the union of interactions reported in KEGG [13] and iRefIndex 9.0 [51] containing 236,060 interactions among 15,257 proteins. We calculate 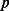 -values from 1000 permuted versions of this combined network.
-values from 1000 permuted versions of this combined network.
By examining only direct interactions between genes in our sets, we might miss cases where genes do not directly interact, but have a common interacting partner (e.g. EGFR, PDGFRA, and NF1 all share RAS as an interacting partner in the fourth module of the GBM results). Average pairwise distance is another commonly used metric for assessing whether groups of genes are clustered on an interaction network, and this metric might identify such cases. However, the tradeoff is that the diameter (average pairwise distance) of most biological interaction networks is small, and thus many genes are close on the network. We found that average pairwise distance was not a strict enough measure for examining mutually exclusive gene sets (data not shown). Finally, note that counting the number of interactions between genes in a PPI network is only an approximate measure of biological function. Current interaction networks have large number of false positive interactions – particularly when interactions from high-throughput experiments are included – as well as an unknown number of false negatives. In addition, there is a problem of ascertainment bias as cancer genes are some of the most studied human genes and many of their interactions have been assessed.
Supporting Information
Multi-Dendrix runtimes on simulated datasets. Average runtime (secs) of Multi-Dendrix on simulated data with 1000 patients and varying passenger mutation probabilities 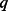 and number of genes. For each set of parameters, average runtime across 10 simulations is reported. The average runtime of Multi-Dendrix is under 3500 seconds for each dataset.
and number of genes. For each set of parameters, average runtime across 10 simulations is reported. The average runtime of Multi-Dendrix is under 3500 seconds for each dataset.
(EPS)
Multi-Dendrix results on GBM dataset as one mutation matrix. The four modules are shown in alternating gray backgrounds. For each module, patients are sorted first by those with mutations in only the module (dark blue), then by patients that have just one mutation in the module (light blue), and finally by patients that have co-occurring mutations in that module (orange). Upticks indicate amplification, downticks indicate deletions, and full ticks indicate SNVs. The four modules found by Multi-Dendrix on the GBM dataset cover 98.8% (258/261) of the patients in the GBM mutation data.
(EPS)
Multi-Dendrix results on BRCA dataset as one mutation matrix. Representation is as in Figure 5. The four modules found by Multi-Dendrix cover 91.9% (466/507) of the patients in the BRCA mutation data.
(EPS)
Multi-Dendrix results on the BRCA dataset with 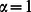 . Four genes (genes with degree zero) are output for only one choice of parameter values. The remaining genes form two connected components indicating that the collections are variable across different values of the parameters. In comparison Multi-Dendrix with
. Four genes (genes with degree zero) are output for only one choice of parameter values. The remaining genes form two connected components indicating that the collections are variable across different values of the parameters. In comparison Multi-Dendrix with 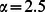 (Figure 3) finds more stable results on this dataset.
(Figure 3) finds more stable results on this dataset.
(EPS)
Iter-Dendrix results on the BRCA dataset. The modules identified by Iter-Dendrix group the most frequently mutated genes together (e.g. TP53 and PIK3CA) and thus there is a large number of samples with co-occurring mutations in each module. In comparison Multi-Dendrix with 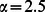 (Figure 3) finds more stable with less co-occurrence of mutations within modules on this dataset.
(Figure 3) finds more stable with less co-occurrence of mutations within modules on this dataset.
(EPS)
Multi-Dendrix results on the GBM(2008) dataset.
(EPS)
Multi-Dendrix results on the Lung dataset.
(EPS)
Multi-Dendrix results on the BRCA dataset restricted to Basal-like patients.
(EPS)
Multi-Dendrix results on the BRCA dataset restricted to Luminal A patients.
(EPS)
Multi-Dendrix results on the BRCA dataset restricted to Luminal B patients.
(EPS)
Multi-Dendrix results on the BRCA dataset restricted to HER2-enriched patients.
(EPS)
Multi-Dendrix results on the unfiltered GBM mutation data.
(EPS)
Multi-Dendrix results on the unfiltered BRCA mutation data.
(EPS)
Average number of genes input to Multi-Dendrix across 100 simulated datasets. We use a minimum threshold of 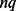 , the expected number of
, the expected number of  total samples with a mutation. We report the values for different number
total samples with a mutation. We report the values for different number  of genes and the lowest and (
of genes and the lowest and (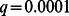 ) highest (
) highest (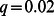 ) passenger mutation probabilities. On all simulated datasets, Multi-Dendrix 's average runtime is
) passenger mutation probabilities. On all simulated datasets, Multi-Dendrix 's average runtime is 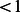 hour.
hour.
(PDF)
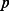 -values for the number of observed protein-protein interactions in Multi-Dendrix results (direct interactions test) for different values of parameters
-values for the number of observed protein-protein interactions in Multi-Dendrix results (direct interactions test) for different values of parameters  , the number of gene sets, and
, the number of gene sets, and 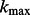 , the maximum gene set size. The minimum gene set size,
, the maximum gene set size. The minimum gene set size, 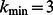 for all runs. The
for all runs. The 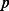 -values were calculated from 1000 permuted networks constructed from the union of the KEGG and iRefIndex PPI networks.
-values were calculated from 1000 permuted networks constructed from the union of the KEGG and iRefIndex PPI networks.
(PDF)
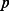 -values for the number of observed protein-protein interactions in Iter-Dendrix results (direction interactions test) for different values of parameters
-values for the number of observed protein-protein interactions in Iter-Dendrix results (direction interactions test) for different values of parameters  , the number of gene set, and
, the number of gene set, and 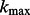 , the maximum gene set size. The minimum gene set size,
, the maximum gene set size. The minimum gene set size, 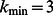 for all runs. The
for all runs. The 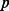 -values were calculated from 1000 permuted networks constructed from the union of the KEGG and iRefIndex PPI networks.
-values were calculated from 1000 permuted networks constructed from the union of the KEGG and iRefIndex PPI networks.
(PDF)
Significant associations (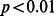 ) between mutations in genes (SNVs, amplifications “(A)”, or deletions “(D)”) and three subtypes from GBM consensus clusters.
) between mutations in genes (SNVs, amplifications “(A)”, or deletions “(D)”) and three subtypes from GBM consensus clusters. 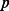 -values were calculated using Fisher's exact test with a Bonferroni correction for multiple hypotheses.
-values were calculated using Fisher's exact test with a Bonferroni correction for multiple hypotheses.
(PDF)
Significant associations (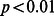 ) between mutations (SNVs, amplifications “(A)”, or deletions “(D)”) in the four BRCA subtypes.
) between mutations (SNVs, amplifications “(A)”, or deletions “(D)”) in the four BRCA subtypes. 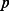 -values were calculated using Fisher's exact test with a Bonferroni correction for multiple hypotheses.
-values were calculated using Fisher's exact test with a Bonferroni correction for multiple hypotheses.
(PDF)
Gene sets found by Iter-RME in the GBM(2008), GBM, and BRCA datasets (after removing genes with mutation frequency 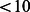 %) for maximum gene set size
%) for maximum gene set size 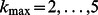 and and number
and and number  of gene sets
of gene sets 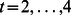 . For all values of
. For all values of 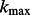 , Iter-RME returned only gene sets of size 2. “Iteration” column denotes the index of each gene set
, Iter-RME returned only gene sets of size 2. “Iteration” column denotes the index of each gene set 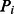 returned in each iteration of RME. Only 4/12 gene sets contain an interacting pair of genes according to the union of the KEGG and iRefIndex protein-protein interaction network.
returned in each iteration of RME. Only 4/12 gene sets contain an interacting pair of genes according to the union of the KEGG and iRefIndex protein-protein interaction network.
(PDF)
Gene sets found by Iter-RME in the GBM(2008), GBM, and BRCA datasets (after removing genes with mutation frequency <10%) for maximum gene set size kmax = 2,…,5 and and number t of gene sets t = 2,…,4. For all values of kmax, Iter-RME returned only gene sets of size 2. “Iteration” column denotes the index of each gene set Pi returned in each iteration of RME. Only 4/12 gene sets contain an interacting pair of genes according to the union of the KEGG and iRefIndex protein-protein interaction network.
(PDF)
Further analyses of the mutation data and comparisons of Multi-Dendrix, Iter-Dendrix, and RME.
(PDF)
Acknowledgments
The authors thank Hsin-Ta Wu for his assistance in visualizing mutation matrices, and the anonymous reviewers for their helpful suggestions.
Funding Statement
This work is supported by NSF grant IIS-1016648. BJR is supported by a Career Award at the Scientific Interface from the Burroughs Wellcome Fund, an Alfred P. Sloan Research Fellowship, and an NSF CAREER Award (CCF-1053753). RS was supported by a research grant from the Israel Science Foundation (grant no. 241/11). MDML was supported by NSF GRFP DGE 0228243. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Gonzalez-Perez A, Lopez-Bigas N (2012) Functional impact bias reveals cancer drivers. Nucleic acids research 40: 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Adzhubei IA, Scmidt S, Peshkin L, Ramensky VE, Gerasimoa A, et al. (2010) A method and server for predicting damaging missense mutations. Nature methods 7: 248–249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Reva B, Antipin Y, Sander C (2011) Predicting the functional impact of protein mutations: application to cancer genomics. Nucleic acids research 39: e118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Kumar P, Henikoff S, Ng PC (2009) Predicting the effects of coding non-synonymous variants on protein function using the SIFT algorithm. Nature protocols 4: 1073–81. [DOI] [PubMed] [Google Scholar]
- 5. Sjöblom T, Jones S, Wood LD, Parsons DW, Lin J, et al. (2006) The consensus coding sequences of human breast and colorectal cancers. Science 314: 268–274. [DOI] [PubMed] [Google Scholar]
- 6. Getz G, Hofling H, Mesirov J, Golub T, Meyerson M, et al. (2007) Comment on “The consensus coding sequences of human breast and colorectal cancers”. Science 317: 1500. [DOI] [PubMed] [Google Scholar]
- 7. The Cancer Genome Atlas Research Network (2012) Comprehensive molecular portraits of human breast tumours. Nature 490: 61–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. The Cancer Genome Atlas Research Network (2008) Comprehensive genomic characterization defines human glioblastoma genes and core pathways. Nature 455: 1061–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. The Cancer Genome Atlas Research Network (2012) Comprehensive molecular characterization of human colon and rectal cancer. Nature 487: 330–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. The Cancer Genome Atlas Research Network (2011) Integrated genomic analyses of ovarian carcinoma. Nature 474: 609–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Puente XS, Pinyol M, Quesada V, Conde L, Ordóñez GR, et al. (2011) Whole-genome sequencing identifies recurrent mutations in chronic lymphocytic leukaemia. Nature 475: 101–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Stephens PJ, Tarpey PS, Davies H, Van Loo P, Greenman C, et al. (2012) The landscape of cancer genes and mutational processes in breast cancer. Nature 486: 400–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Kanehisa M, Goto S, Sato Y, Furumichi M, Tanabe M (2012) KEGG for integration and interpretation of large-scale molecular data sets. Nucleic Acids Res 40: D109–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Ashburner M, Ball C, Blake J, Botstein D, Butler H, et al. (2000) Gene ontology: tool for the unification of biology. Nature Genetics 25: 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Wendl MC, Wallis JW, Lin L, Kandoth C, Mardis ER, et al. (2011) PathScan: a tool for discerning mutational significance in groups of putative cancer genes. Bioinformatics (Oxford, England) 27: 1595–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Lin J, Gan CM, Zhang X, Jones S, Sjöblom T, et al. (2007) A multidimensional analysis of genes mutated in breast and colorectal cancers. Genome research 17: 1304–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Boca SM, Kinzler KW, Velculescu VE, Vogelstein B, Parmigiani G (2010) Patient-oriented gene set analysis for cancer mutation data. Genome biology 11: R112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Cerami E, Demir E, Schultz N, Taylor BS, Sander C (2010) Automated network analysis identifies core pathways in glioblastoma. PLoS ONE 5: e8918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Ciriello G, Cerami E, Sander C, Schultz N (2012) Mutual exclusivity analysis identifies oncogenic network modules. Genome Res 22: 398–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Vandin F, Upfal E, Raphael B (2011) Algorithms for detecting significantly mutated pathways in cancer. Journal of Computational Biology 18: 507–22. [DOI] [PubMed] [Google Scholar]
- 21. Glaab E, Baudot A, Krasnogor N, Schneider R, Valencia A (2012) EnrichNet: network-based gene set enrichment analysis. Bioinformatics (Oxford, England) 28: i451–i457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Miller C, Settle S, Sulman E, Aldape K, Milosavljevic A (2011) Discovering functional modules by identifying recurrent and mutually exclusive mutational patterns in tumors. BMC medical genomics 4: 34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Vandin F, Upfal E, Raphael B (2012) De novo discovery of mutated driver pathways in cancer. Genome Res 22: 375–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Vogelstein B, Kinzler KW (2004) Cancer genes and the pathways they control. Nat Med 10: 789–799. [DOI] [PubMed] [Google Scholar]
- 25. Yeang C, McCormick F, Levine A (2008) Combinatorial patterns of somatic gene mutations in cancer. The FASEB Journal 22: 2605–22. [DOI] [PubMed] [Google Scholar]
- 26. Hanahan D, Weinberg R (2011) Hallmarks of cancer: the next generation. Cell 144: 646–74. [DOI] [PubMed] [Google Scholar]
- 27. Ding L, Getz G, Wheeler DA, Mardis ER, McLellan MD, et al. (2008) Somatic mutations affect key pathways in lung adenocarcinoma. Nature 455: 1069–1075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Gerstung M, Eriksson N, Lin J, Vogelstein B, Beerenwinkel N (2011) The temporal order of genetic and pathway alterations in tumorigenesis. PLoS ONE 6: e27136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Verhaak RGW, Hoadley Ka, Purdom E, Wang V, Qi Y, et al. (2010) Integrated genomic analysis identifies clinically relevant subtypes of glioblastoma characterized by abnormalities in PDGFRA, IDH1, EGFR, and NF1. Cancer cell 17: 98–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Rea S, Xouri G, Akhtar A (2007) Males absent on the first (MOF): from flies to humans. Oncogene 26: 5385–94. [DOI] [PubMed] [Google Scholar]
- 31. Buyse IM, Shao G, Huang S (1995) The retinoblastoma protein binds to RIZ, a zinc-finger protein that shares an epitope with the adenovirus E1A protein. Proceedings of the National Academy of Sciences of the United States of America 92: 4467–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Chadwick RB, Jiang GL, Bennington Ga, Yuan B, Johnson CK, et al. (2000) Candidate tumor suppressor RIZ is frequently involved in colorectal carcinogenesis. Proceedings of the National Academy of Sciences of the United States of America 97: 2662–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Ernst A, Hofmann S, Ahmadi R, Becker N, Korshunov A, et al. (2009) Genomic and expression profiling of glioblastoma stem cell-like spheroid cultures identifies novel tumor-relevant genes associated with survival. Clinical cancer research 15: 6541–50. [DOI] [PubMed] [Google Scholar]
- 34. Erbel-Sieler C, Dudley C, Zhou Y, Wu X, Estill SJ, et al. (2004) Behavioral and regulatory abnormalities in mice deficient in the NPAS1 and NPAS3 transcription factors. Proceedings of the National Academy of Sciences of the United States of America 101: 13648–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Huang J, Perlis RH, Lee PH, Rush AJ, Fava M, et al. (2010) Cross-Disorder Genomewide Analysis of Schizophrenia, Bipolar Disorder, and Depression. American Journal of Psychiatry 167: 1254–1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Moreira F, Kiehl TR, So K, Ajeawung NF, Honculada C, et al. (2011) NPAS3 demonstrates features of a tumor suppressive role in driving the progression of Astrocytomas. The American journal of pathology 179: 462–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. van der Groep P, van der Wall E, van Diest PJ (2011) Pathology of hereditary breast cancer. Cellular oncology (Dordrecht) 34: 71–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Cowin P, Rowlands TM, Hatsell SJ (2005) Cadherins and catenins in breast cancer. Current opinion in cell biology 17: 499–508. [DOI] [PubMed] [Google Scholar]
- 39. Green AR, Krivinskas S, Young P, Rakha Ea, Paish EC, et al. (2009) Loss of expression of chromosome 16q genes DPEP1 and CTCF in lobular carcinoma in situ of the breast. Breast cancer research and treatment 113: 59–66. [DOI] [PubMed] [Google Scholar]
- 40. Usary J, Llaca V, Karaca G, Presswala S, Karaca M, et al. (2004) Mutation of GATA3 in human breast tumors. Oncogene 23: 7669–78. [DOI] [PubMed] [Google Scholar]
- 41. Yan W, Cao QJ, Arenas RB, Bentley B, Shao R (2010) GATA3 inhibits breast cancer metastasis through the reversal of epithelial-mesenchymal transition. The Journal of biological chemistry 285: 14042–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Kutuzov Ma, Bennett N, Andreeva AV (2010) Protein phosphatase with EF-hand domains 2 (PPEF2) is a potent negative regulator of apoptosis signal regulating kinase-1 (ASK1). The international journal of biochemistry & cell biology 42: 1816–22. [DOI] [PubMed] [Google Scholar]
- 43. Medina PP, Romero Oa, Kohno T, Montuenga LM, Pio R, et al. (2008) Frequent BRG1/SMARCA4- inactivating mutations in human lung cancer cell lines. Human mutation 29: 617–22. [DOI] [PubMed] [Google Scholar]
- 44. Kaye FJ (2002) RB and cyclin dependent kinase pathways: defining a distinction between RB and p16 loss in lung cancer. Oncogene 21: 6908–14. [DOI] [PubMed] [Google Scholar]
- 45. Dees ND, Zhang Q, Kandoth C, Wendl MC, Schierding W, et al. (2012) MuSiC: identifying mutational significance in cancer genomes. Genome research 22: 1589–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Greenman C, Wooster R, Futreal PA, Stratton MR, Easton DF (2006) Statistical analysis of pathogenicity of somatic mutations in cancer. Genetics 173: 2187–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Mermel C, Schumacher S, Hill B, Meyerson M, Beroukhim R, et al. (2011) GISTIC2.0 facilitates sensitive and confident localization of the targets of focal somatic copy-number alteration in human cancers. Genome Biology 12: R41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Mitsui J, Takahashi Y, Goto J, Tomiyama H, Ishikawa S, et al. (2010) Mechanisms of genomic instabilities underlying two common fragile-site-associated loci, PARK2 and DMD, in germ cell and cancer cell lines. American journal of human genetics 87: 75–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Bednarek AK, Laflin KJ, Daniel RL, Liao Q, Hawkins KA, et al. (2000) WWOX, a Novel WW Domain-containing Protein Mapping to Affected in Breast Cancer Advances in Brief. Cancer research 60: 2140–2145. [PubMed] [Google Scholar]
- 50.Milo R, Kashtan N, Itzkovitz S, Newman MEJ, Alon U (2003) On the uniform generation of random graphs with prescribed degree sequences. eprint arXiv:cond-mat/0312028.
- 51. Razick S, Magklaras G, Donaldson I (2008) iRefIndex: a consolidated protein interaction database with provenance. BMC Bioinformatics 9: 405. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Multi-Dendrix runtimes on simulated datasets. Average runtime (secs) of Multi-Dendrix on simulated data with 1000 patients and varying passenger mutation probabilities 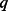 and number of genes. For each set of parameters, average runtime across 10 simulations is reported. The average runtime of Multi-Dendrix is under 3500 seconds for each dataset.
and number of genes. For each set of parameters, average runtime across 10 simulations is reported. The average runtime of Multi-Dendrix is under 3500 seconds for each dataset.
(EPS)
Multi-Dendrix results on GBM dataset as one mutation matrix. The four modules are shown in alternating gray backgrounds. For each module, patients are sorted first by those with mutations in only the module (dark blue), then by patients that have just one mutation in the module (light blue), and finally by patients that have co-occurring mutations in that module (orange). Upticks indicate amplification, downticks indicate deletions, and full ticks indicate SNVs. The four modules found by Multi-Dendrix on the GBM dataset cover 98.8% (258/261) of the patients in the GBM mutation data.
(EPS)
Multi-Dendrix results on BRCA dataset as one mutation matrix. Representation is as in Figure 5. The four modules found by Multi-Dendrix cover 91.9% (466/507) of the patients in the BRCA mutation data.
(EPS)
Multi-Dendrix results on the BRCA dataset with 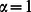 . Four genes (genes with degree zero) are output for only one choice of parameter values. The remaining genes form two connected components indicating that the collections are variable across different values of the parameters. In comparison Multi-Dendrix with
. Four genes (genes with degree zero) are output for only one choice of parameter values. The remaining genes form two connected components indicating that the collections are variable across different values of the parameters. In comparison Multi-Dendrix with 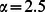 (Figure 3) finds more stable results on this dataset.
(Figure 3) finds more stable results on this dataset.
(EPS)
Iter-Dendrix results on the BRCA dataset. The modules identified by Iter-Dendrix group the most frequently mutated genes together (e.g. TP53 and PIK3CA) and thus there is a large number of samples with co-occurring mutations in each module. In comparison Multi-Dendrix with 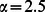 (Figure 3) finds more stable with less co-occurrence of mutations within modules on this dataset.
(Figure 3) finds more stable with less co-occurrence of mutations within modules on this dataset.
(EPS)
Multi-Dendrix results on the GBM(2008) dataset.
(EPS)
Multi-Dendrix results on the Lung dataset.
(EPS)
Multi-Dendrix results on the BRCA dataset restricted to Basal-like patients.
(EPS)
Multi-Dendrix results on the BRCA dataset restricted to Luminal A patients.
(EPS)
Multi-Dendrix results on the BRCA dataset restricted to Luminal B patients.
(EPS)
Multi-Dendrix results on the BRCA dataset restricted to HER2-enriched patients.
(EPS)
Multi-Dendrix results on the unfiltered GBM mutation data.
(EPS)
Multi-Dendrix results on the unfiltered BRCA mutation data.
(EPS)
Average number of genes input to Multi-Dendrix across 100 simulated datasets. We use a minimum threshold of  , the expected number of
, the expected number of  total samples with a mutation. We report the values for different number
total samples with a mutation. We report the values for different number  of genes and the lowest and (
of genes and the lowest and (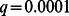 ) highest (
) highest (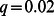 ) passenger mutation probabilities. On all simulated datasets, Multi-Dendrix 's average runtime is
) passenger mutation probabilities. On all simulated datasets, Multi-Dendrix 's average runtime is 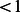 hour.
hour.
(PDF)
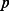 -values for the number of observed protein-protein interactions in Multi-Dendrix results (direct interactions test) for different values of parameters
-values for the number of observed protein-protein interactions in Multi-Dendrix results (direct interactions test) for different values of parameters  , the number of gene sets, and
, the number of gene sets, and 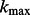 , the maximum gene set size. The minimum gene set size,
, the maximum gene set size. The minimum gene set size, 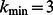 for all runs. The
for all runs. The 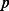 -values were calculated from 1000 permuted networks constructed from the union of the KEGG and iRefIndex PPI networks.
-values were calculated from 1000 permuted networks constructed from the union of the KEGG and iRefIndex PPI networks.
(PDF)
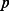 -values for the number of observed protein-protein interactions in Iter-Dendrix results (direction interactions test) for different values of parameters
-values for the number of observed protein-protein interactions in Iter-Dendrix results (direction interactions test) for different values of parameters  , the number of gene set, and
, the number of gene set, and 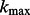 , the maximum gene set size. The minimum gene set size,
, the maximum gene set size. The minimum gene set size, 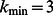 for all runs. The
for all runs. The 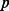 -values were calculated from 1000 permuted networks constructed from the union of the KEGG and iRefIndex PPI networks.
-values were calculated from 1000 permuted networks constructed from the union of the KEGG and iRefIndex PPI networks.
(PDF)
Significant associations (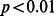 ) between mutations in genes (SNVs, amplifications “(A)”, or deletions “(D)”) and three subtypes from GBM consensus clusters.
) between mutations in genes (SNVs, amplifications “(A)”, or deletions “(D)”) and three subtypes from GBM consensus clusters. 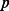 -values were calculated using Fisher's exact test with a Bonferroni correction for multiple hypotheses.
-values were calculated using Fisher's exact test with a Bonferroni correction for multiple hypotheses.
(PDF)
Significant associations (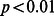 ) between mutations (SNVs, amplifications “(A)”, or deletions “(D)”) in the four BRCA subtypes.
) between mutations (SNVs, amplifications “(A)”, or deletions “(D)”) in the four BRCA subtypes. 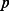 -values were calculated using Fisher's exact test with a Bonferroni correction for multiple hypotheses.
-values were calculated using Fisher's exact test with a Bonferroni correction for multiple hypotheses.
(PDF)
Gene sets found by Iter-RME in the GBM(2008), GBM, and BRCA datasets (after removing genes with mutation frequency 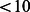 %) for maximum gene set size
%) for maximum gene set size 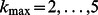 and and number
and and number  of gene sets
of gene sets 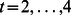 . For all values of
. For all values of 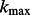 , Iter-RME returned only gene sets of size 2. “Iteration” column denotes the index of each gene set
, Iter-RME returned only gene sets of size 2. “Iteration” column denotes the index of each gene set 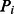 returned in each iteration of RME. Only 4/12 gene sets contain an interacting pair of genes according to the union of the KEGG and iRefIndex protein-protein interaction network.
returned in each iteration of RME. Only 4/12 gene sets contain an interacting pair of genes according to the union of the KEGG and iRefIndex protein-protein interaction network.
(PDF)
Gene sets found by Iter-RME in the GBM(2008), GBM, and BRCA datasets (after removing genes with mutation frequency <10%) for maximum gene set size kmax = 2,…,5 and and number t of gene sets t = 2,…,4. For all values of kmax, Iter-RME returned only gene sets of size 2. “Iteration” column denotes the index of each gene set Pi returned in each iteration of RME. Only 4/12 gene sets contain an interacting pair of genes according to the union of the KEGG and iRefIndex protein-protein interaction network.
(PDF)
Further analyses of the mutation data and comparisons of Multi-Dendrix, Iter-Dendrix, and RME.
(PDF)