Abstract
Kinetic and thermodynamic studies of the mechanochemical cycle of myosin motors are essential for understanding the mechanism of energy conversion. Here, we report our investigation of temperature and free Mg2+-ion dependencies of sliding velocities of a high duty ratio class-5 myosin motor, myosin-5b from D. discoideum using in vitro motility assays. Previous studies have shown that the sliding velocity of class-5 myosins obeys modulation by free Mg2+-ions. Free Mg2+-ions affect ADP release kinetics and the dwell time of actin-attached states. The latter determines the maximal velocity of actin translocation in the sliding filament assay. We measured the temperature dependence of sliding velocity in the range from 5 to 55°C at two limiting free Mg2+-ion concentrations. Arrhenius plots demonstrated non-linear behavior. Based on this observation we propose a kinetic model, which explains both sensitivity towards free Mg2+-ions and non-linearity of the temperature dependence of sliding velocity. According to this model, velocity is represented as a simple analytical function of temperature and free Mg2+-ion concentrations. This function has been applied to global non-linear fit analysis of three data sets including temperature and magnesium (at 20°C) dependence of sliding velocity. As a result we obtain thermodynamic parameters (ΔHMg and ΔSMg) of a fast equilibrium between magnesium free (AM·D) and magnesium bound acto-myosin-ADP (AM· Mg2+D) states and the corresponding enthalpic barriers associated with ADP release (ΔH1 ‡ and ΔH2 ‡). The herein presented integrative approach of data analysis based on global fitting can be applied to the remaining steps of the acto-myosin ATPase cycle facilitating the determination of energetic parameters and thermodynamics of acto-myosin interactions.
Introduction
An intrinsic property of myosins is the ability to convert chemical energy from ATP hydrolysis into mechanical force and movement through the cyclic interaction with actin filaments. Despite the high degree of structural conservation of the myosin motor domains [1] and a well defined biochemical ATPase cycle shared by all types of myosins investigated so far [2], the motors display a large variety of mechanochemical activities that range from the generation of force and tension in contractile processes e.g. muscle contraction, cellular movement, or cytokinesis [3] to strain sensing and intracellular transport functions of proteins and organelles [4]. Kinetic studies have revealed that variations in (i) the maximal actin-activated ATPase activities, (ii) the rate constants and equilibria of their interactions with actin and nucleotides, (iii) number and degree of population of the individual states of the ATPase cycle, and (iv) the fraction of the total cycle time the motors spent in each state, contribute to their different modes of mechanical activities [5]. External strain, load, and cooperative effects are additional factors that influence the motor properties of myosins [6], [7], [8], [9].
One important parameter that varies between the myosins is the fraction of time the motors spend in the strongly actin attached states during the ATPase cycle [10]. This parameter termed duty ratio classifies the myosins in high and low duty ratio motors [11]. Fast myosins such as muscle myosin-2 have a low duty ratio, while processive class-5 myosins display a high duty ratio. Biochemical studies correlate changes of the duty ratio with the rates of transition and isomerization states associated with the release of the hydrolysis products, including the dissociation of Mg2+ from the nucleotide binding pocket [12], [13]. In myosin-2, the actin-accelerated rate-limiting release of Pi precedes the fast dissociation of Mg2+ADP [14]; whereas in myosin-5 the dwell time of attached state is determined by the rate of ADP release [15]. In addition kinetic investigations revealed an equilibrium between magnesium free (AM·D) and magnesium bound acto-myosin-ADP (AM·Mg2+D) states [16], [17], [18]. Therefore, the fraction of time the myosin remains attached to actin can be affected by this equilibrium with consequences for processivity and motile activity [19], [20], [21]. While the kinetic properties and the mechanism of myosin-5 movement are well established [22], [23], [24], only little information regarding the energetics of the individual steps in the ATPase cycle of the motor is available [25]. An ultimate goal for a complete and detailed description of the myosin-5 mechanism of energy transduction should thus include the determination of the energetics of the individual steps in the acto-myosin ATPase cycle. Following the changes of rates and equilibria at different thermodynamic conditions e.g. by varying the temperature, important information on enthalpies and entropies of the intermediates that emerge during the enzymatic cycle of the acto-myosin interaction can be obtained.
Previous thermodynamic investigations have addressed temperature dependences of individual myosins in terms of their ATPases, motile activities, or ADP-release and nucleotide induced acto-myosin dissociation kinetics [25], [26], [27]. In the current study we extended the analysis of the myosin-5 ATPase cycle to thermodynamic experiments using in vitro motility assays over an extended temperature range with a high duty ratio class-5 myosin from Dictyostelium. Myosin-5b is a processive motor like myosin-5a and possesses motor properties that can be modulated by changes in the concentration of free Mg2+-ions [20]. Global fit analysis of the temperature and magnesium dependent velocities using a simple two-state kinetic model allowed us to describe the thermodynamics of two essential Mg2+-sensitive ADP release steps in the ATPase cycle of myosin-5b. Our results provide important insights on the critical role of the 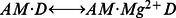 equilibrium for the high duty ratio of myosin-5 motors.
equilibrium for the high duty ratio of myosin-5 motors.
Materials and Methods
Reagents and proteins
Standard chemicals, anti-His antibodies, trichloromethyl-silane (TCMS), and tetramethyl rhodamine isothiocyanate (TRITC)-phalloidin were purchased from Sigma; rabbit skeletal muscle actin was purified from acetone powder and labeled with TRITC-phalloidin. A titrated 3.9 M stock solution of MgCl2 purchased from Sigma was used for the adjustment of free Mg2+-ion concentrations in the experimental buffers. D. discoideum myosin-5b motor domain fused to an artificial lever arm consisting of two α-actinin repeats (2R) and C-terminal octa-His tag was purified according to the previously described procedures [20].
In vitro motility assays
All experiments were performed in assay buffer (AB) containing 25 mM imidazole pH 7.4, 25 mM KCl, 1 mM EGTA, 10 mM DTT. Preparation of actin and labelling with TRITC phalloidin was done according to [28]. The concentration of ATP was 4 mM and the concentration of MgCl2 was adjusted accordingly to provide the desirable free Mg2+-ion concentration using the Maxchelator software (http://maxchelator.stanford.edu). Free Mg2+-ion concentrations are assigned as [Mg2+]. The affinity of Mg2+ for ATP is temperature dependent in aqueous solution and changes in the studied temperature range from approximately 140 µM (5°C) to 50 µM (55°C). We ignored this temperature effect for the calculation of free Mg2+-ions concentrations in the assay buffer, since we used excess ATP concentrations making the error of free Mg2+-ions concentrations negligibly small in the temperature range studied. Saturating concentrations of myosin molecules were used to obtain maximum sliding velocities. The myosin molecules were immobilized via anti-penta-His antibodies (concentration 0.025 mg/ml) on silanated glass surfaces of a flow-cell. TCMS coated cover slips were prepared according to [29]. Actin sliding motility was recorded at temperatures ranging from 5°C to 55°C using an Olympus IX81 inverted fluorescence microscope (Olympus, Hamburg, Germany) as described previously [20]. For temperature control, a spectroscopic flow-through cuvette (Type 137-QS, Hellma Analytics GmbH) was attached to the upper surface of the cover slip using silicon grease. The temperature was changed and adjusted with a water-thermostat connected to the flow-through cuvette. For temperatures above 20°C the microscope was additionally heated using objective and stage heaters. A thermal-couple digital thermometer (Center 301, Center Technology Corp., Taiwan) was directly attached to the contact between cuvette and cover slip providing reliable control of the sample temperature. The movement of more than 200 TRITC-phalloidin labeled actin filaments was recorded for each temperature point. Three independent measurements have been used for data analysis.
Data analysis
Actin filament tracking was performed with DiaTrack 3.01 (Semasopht, Switzerland). Data analysis and graphical representation of results were done with Origin 7.0 (OriginLab Corporation, U.S.A.). The non-linear least square fitter of Origin 7.0 was used for global data analysis. Equation 1 was implemented as user defined function to the fit. Global fit included three experimental data sets, each sharing the same six parameters (v 1, v 2, ΔH1 ‡, ΔH2 ‡, ΔHMg, ΔSMg), which are assumed to be temperature independent. The function was written in the script form of the software to allow conditional reassignment of the independent variables, either as reciprocal temperature or concentration of free Mg2+-ions. Additionally, errors of experimental data were included to the fit as statistical weighting parameters. The global fit analysis was performed several times with different initial guesses of parameters to avoid solutions which could correspond to local minima of fit.
Results and Discussion
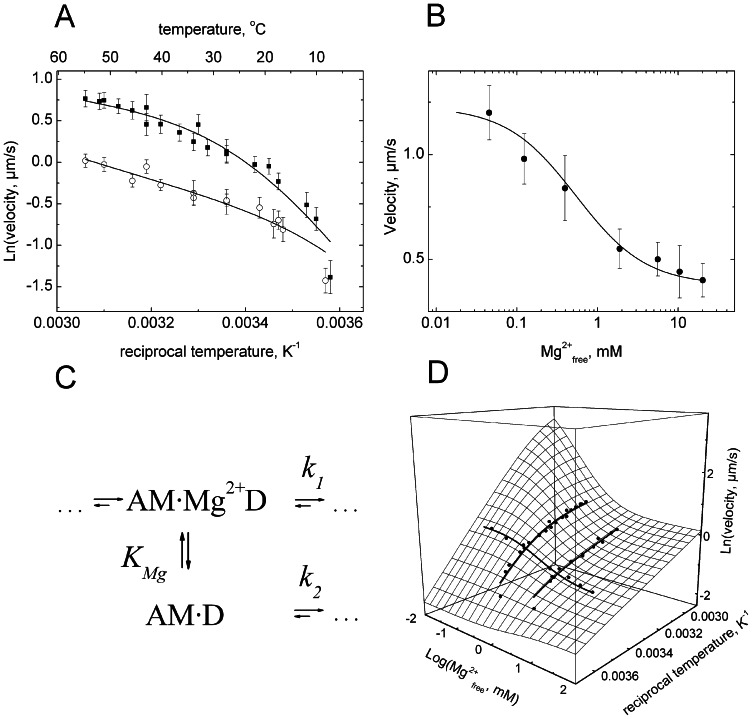
The motile activity of myosin-5b was studied at two defined free Mg2+-ion concentrations [Mg2+] over a temperature range of 50°C using in vitro motility assays. Figure 1A shows the temperature dependence of the sliding velocity in Arrhenius coordinates and figure 1B depicts the [Mg2+] dependence of the sliding velocity at 20°C. The latter data have been reported earlier in the context of the kinetic characterization of the myosin-5b [20]. [Mg2+] inhibited actin filament sliding velocity 2.5-fold with an apparent dissociation constant (K Mg) of 0.4 mM. Thus, saturating free Mg2+-ion concentrations do not fully inhibit the motile activity of myosin-5b. Previous kinetic investigations with myosin-5a propose a sequential model of product dissociation in which Mg2+ is released prior to ADP [17]. In fact the model is consistent with the observation that [Mg2+] inhibit the sliding velocity of the motor [20], but it does not explain why saturating [Mg2+] do not completely inhibit sliding velocity. In order to address this problem, we performed temperature-dependent motility assays at two limiting [Mg2+] of 0.05 mM and 4.5 mM representative for the high and low limits in sliding velocity at 20°C. Over the entire temperature range velocities at low 0.05 mM [Mg2+] (upper trace) were higher than at 4.5 mM [Mg2+] (lower trace). For both experiments a non-linear Arrhenius dependence was observed. This indicates that the underlying kinetics, which determine sliding velocity cannot be considered as a single elementary step in the reaction pathway. A similar observation was reported for the sliding velocity driven by muscle myosin-2 [30], [31]. Moreover, such convex non-Arrhenius behavior has been described as characteristic feature of the kinetics for other proteins [32], [33]. Several theoretical approaches have been made to describe this behavior of enzyme catalyzed reactions providing some explanations of non-linearity [34]. Our experimental results imply that the simplest kinetic reaction pathway explaining both non-linear Arrhenius dependence and free Mg2+ inhibition should include a fast and temperature sensitive equilibrium between Mg2+-bound and Mg2+-unbound acto-myosin-ADP (AM·D)-states that precede the subsequent and rate limiting steps of the myosin-5b ATPase cycle (Figure 1C). According to this model an alternative pathway in the acto-myosin cycle can be formulated, which includes the simultaneous release of Mg2+ and ADP in a single step [16]. Assuming a fast equilibrium between Mg2+-bound and Mg2+-unbound AM·D states, the analytical solution of the proposed kinetic model depicted in Figure 1C can be greatly simplified, where KMg represents the binding affinity of free Mg2+ to AM·D and k1 and k2 correspond to the two rate limiting steps, which determine the dwell times of myosin attached to actin. Presumably, these steps are accompanied by the release of ADP and detachment of myosin from actin. These steps are assumed to be essentially irreversible. The dwell time of the actin attached states of myosin determines the maximum sliding velocity [10]. The analytical solution of the underlying kinetic model gives a rate limiting constant as follows:
This apparent rate constant determines the overall dwell time of myosin bound to actin. Therefore, the experimentally observed sliding velocity can described as a function of temperature and free Mg2+-ion concentrations in the following form:
 |
(1) |
| (1′) |
where R is the universal gas constant, T is the temperature in Kelvin, ΔH1 ‡ and ΔH2 ‡ are the enthalpies of activation of the two alternative ADP release pathways from acto-myosin, [Mg2+] is the concentration of free magnesium ions, ν 1 and ν 2 are pre-exponential factors, which include terms of activation entropy for the corresponding transitions and factors for the conversion of rate-limiting rate constants to the sliding velocity. K Mg is the dissociation constant of Mg2+ from the AM·Mg2+ADP-complex. Equation 1′ represents K Mg as a function of standard enthalpy and entropy differences (ΔHMg and ΔSMg) between Mg2+-bound and Mg2+-unbound AM·D states.
Figure 1. Dependence of myosin-5b sliding velocity on reciprocal Kelvin temperature (A) and free Mg2+ ion concentration (B).
The data in panel A show sliding velocities at two limiting Mg2+ ion concentrations of 4.5 mM (open circles) and 0.05 mM (solid squares) over a range of 50°C. Error bars represent the mean value of half bandwidths of Gaussian distributions of sliding velocities obtained from statistical analysis of motility time lapse images averaged over 3 to 5 independent experiments for each temperature point. Panel B shows sliding velocities obtained at 20°C as a function of free Mg2+-ion concentration. All three data sets were simultaneously fitted using equation 1. Solid lines are the results of the global fit. Thermodynamic parameters of the fits are given in table 1. (C) Kinetic model of the two alternative ADP dissociation steps in the acto-myosin-5b cycle. A is F-actin, M is Dictyostelium myosin-5b, Mg2+ is the divalent magnesium cation, D is ADP. The top pathway represents the simultaneous dissociation of Mg2+ADP and the bottom pathway ADP dissociation from acto-myosin. The two states AM·Mg2+D and AMD are in fast equilibrium defined by the dissociation constant K Mg, which is temperature dependent. (D) Three dimensional surface plot of myosin-5b sliding velocity dependence on temperature and free Mg2+-ions calculated from equation 1 using parameters shown in table 1. Experimental points from A and B are included as filled circles.
We applied our three data sets (two T-dependences and one free Mg2+-concentration dependence) to a global non-linear least square fitting analysis using function 1. Results of the fit are shown as solid lines in Figures 1A,B and as a three-dimensional plot of the observed dependences and the fitting function (Figure 1D). The 3D plot exceeds the range of physiological temperature and concentration of free Mg2+-ions occurring in biological systems [35], but illustrates the extent of velocity variation and the highly non-linear character predetermined by the thermodynamic parameters obtained from the fit. These parameters are shown in Table 1. The non-linear Arrhenius behavior can be explained from a temperature-induced shift in the equilibrium between Mg2+-unbound and Mg2+-bound AM·D states. At low temperatures the Mg2+-unbound state AM·D dominates. The corresponding activation enthalpy ΔH2
‡ of the ADP release is 64 kJ/mol and can be seen from the steepness of the Arrhenius plot in the low temperature range (Figure 1A). At higher temperatures the Mg2+-bound AM·Mg2+ADP states determines the sliding velocity. This implies that the rate of Mg2+-ADP release is slower than the dissociation of ADP alone. On the other hand the activation enthalpy barrier of this pathway ΔH1
‡ is only 18 kJ/mol. This indicates that the entropic part of free energy barrier should be negative and higher in comparison to the entropic part of activation barrier for ADP release without bound Mg2+. The activation enthalpy ΔH1
‡ makes the slope in the Arrhenius plot less steep in the high temperature range. The high sensitivity of the Mg2+-associated equilibrium (K
Mg) towards the temperature gives a plausible explanation for the convex non-linear behavior of myosin-5b motility in the Arrhenius plots. The pronounced difference in activation enthalpies can be explained as a result of neutralization of the electrostatic charge of ADP by Mg2+ and therefore weakening of binding energy to the protein. The 3-fold reduction of activation enthalpy upon binding of Mg2+ is in line with an increase in the enthalpy (ΔHMg) of the Mg2+-bound state of the equilibrium. The equilibrium shift towards the AM·Mg2+D at higher temperatures implies that this state is entropically favored (ΔSMg = +234 J/molK). Moreover, since the AM·D state has a lower entropy than the AM·Mg2+D state, we can assume that the height of the entropic barrier for the release of Mg2+-ADP is dictated by the entropy of the AM·Mg2+D state. As a consequence, the rate constant for Mg2+-ADP release becomes slower. From the v
1 and v
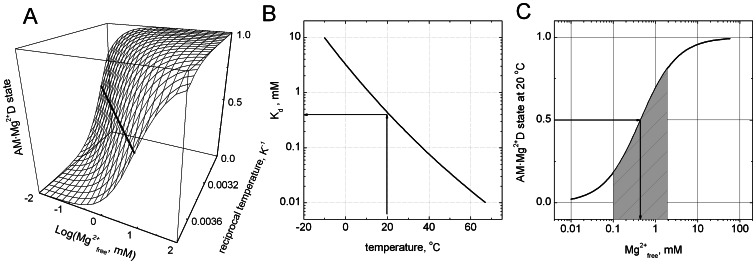
2 pre-exponential factors we can estimate the difference of entropic activation barriers between the two pathways: 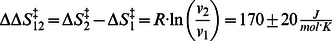 . The uncertainty of the obtained value was propagated from the errors of ν1 and ν2 (see Table 1). This estimation clearly indicates that the contribution of ΔSMg to the difference in activation entropies is significant. To show the range by which [Mg2+] and temperature influence the equilibrium we plotted the corresponding fraction of the AM·Mg2+D state
. The uncertainty of the obtained value was propagated from the errors of ν1 and ν2 (see Table 1). This estimation clearly indicates that the contribution of ΔSMg to the difference in activation entropies is significant. To show the range by which [Mg2+] and temperature influence the equilibrium we plotted the corresponding fraction of the AM·Mg2+D state 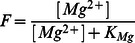 in a 3D graph shown in figure 2A. The solid line in the surface plot matches the value F = 0.5, which defines K
Mg. Figure 2B depicts this line as a function of the temperature. According to this plot, K
Mg decreases 90-fold from 1.8 to 0.02 mM in the experimental temperature range (5 to 55°C). The high enthalpy difference ΔHMg of 66.5 kJ/mol accounts for the large change in K
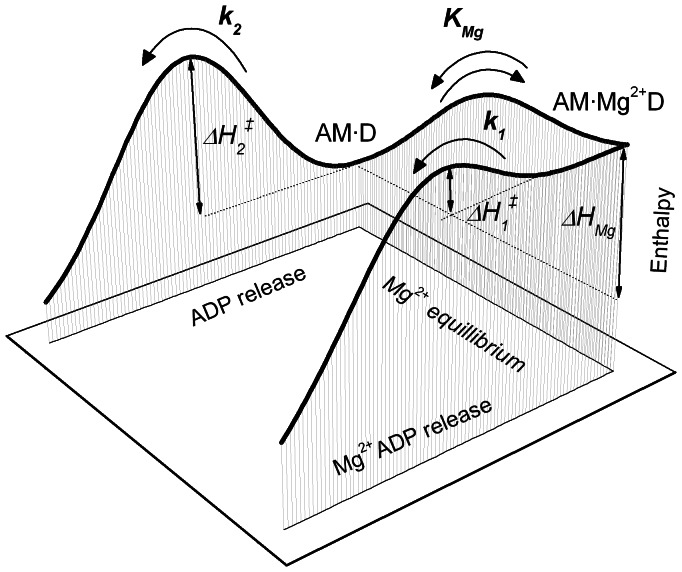
Mg. Note, in aqueous solution (pH 7.0) the increase in enthalpy for Mg2+ binding to ADP is approximately 10.5 kJ/mol, as calculated from the temperature dependence of the dissociation constant of the Mg2+-ADP complex according to NIST database parameters of the Maxchelator program. This calculation indicates that the process of Mg2+-ion coordination in the nucleotide binding site of myosin-5 is accompanied by a significant change in the energy of interactions by the protein surrounding. On the other hand the entropy driven mechanism of binding does not principally change (according to NIST database the Mg2+-ADP complex at pH 7.0 in aqueous solution has a 95 J/molK higher standard entropy than the dissociated form). The fraction of the AM·Mg2+D state depends on the concentration of free Mg2+-ions. This is shown exemplary for 20°C in figure 2C. Most pronounced variation of the equilibrium occurs around the inflection point of the sigmoidal curve, which covers the range of free Mg2+-ion concentration from approximately 0.1 to 2 mM. Interestingly, this concentration range matches the physiological range of free Mg2+-ions found in cells [36]. Therefore, the observed changes in the spatial and temporal distribution of free Mg2+-ions might be of importance for regulation of myosin motor function in vivo. Figure 3 shows the energetic landscape of the Mg2+-regulated part of the enzymatic relaxational pathway obtained from our data analysis. The diagram illustrates the temperature independent enthalpic difference of the Mg2+-equilibrium and two enthalpic barriers of the rate limiting steps of the reaction. Obviously, the actual rates of transitions and population of states within the equilibrium are defined by the Gibbs free energy values (
in a 3D graph shown in figure 2A. The solid line in the surface plot matches the value F = 0.5, which defines K
Mg. Figure 2B depicts this line as a function of the temperature. According to this plot, K
Mg decreases 90-fold from 1.8 to 0.02 mM in the experimental temperature range (5 to 55°C). The high enthalpy difference ΔHMg of 66.5 kJ/mol accounts for the large change in K
Mg. Note, in aqueous solution (pH 7.0) the increase in enthalpy for Mg2+ binding to ADP is approximately 10.5 kJ/mol, as calculated from the temperature dependence of the dissociation constant of the Mg2+-ADP complex according to NIST database parameters of the Maxchelator program. This calculation indicates that the process of Mg2+-ion coordination in the nucleotide binding site of myosin-5 is accompanied by a significant change in the energy of interactions by the protein surrounding. On the other hand the entropy driven mechanism of binding does not principally change (according to NIST database the Mg2+-ADP complex at pH 7.0 in aqueous solution has a 95 J/molK higher standard entropy than the dissociated form). The fraction of the AM·Mg2+D state depends on the concentration of free Mg2+-ions. This is shown exemplary for 20°C in figure 2C. Most pronounced variation of the equilibrium occurs around the inflection point of the sigmoidal curve, which covers the range of free Mg2+-ion concentration from approximately 0.1 to 2 mM. Interestingly, this concentration range matches the physiological range of free Mg2+-ions found in cells [36]. Therefore, the observed changes in the spatial and temporal distribution of free Mg2+-ions might be of importance for regulation of myosin motor function in vivo. Figure 3 shows the energetic landscape of the Mg2+-regulated part of the enzymatic relaxational pathway obtained from our data analysis. The diagram illustrates the temperature independent enthalpic difference of the Mg2+-equilibrium and two enthalpic barriers of the rate limiting steps of the reaction. Obviously, the actual rates of transitions and population of states within the equilibrium are defined by the Gibbs free energy values (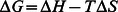 ) and therefore temperature dependent. A parameter not defined in this scheme is the activation enthalpy barrier of the equilibrium between the AM·Mg2+D and AM·D states. This barrier is drawn low enough to be consistent with the model assumption of a fast equilibrium.
) and therefore temperature dependent. A parameter not defined in this scheme is the activation enthalpy barrier of the equilibrium between the AM·Mg2+D and AM·D states. This barrier is drawn low enough to be consistent with the model assumption of a fast equilibrium.
Table 1. Thermodynamic parameters of the two alternative ADP-release pathways in acto-myosin-5b.
| Parameter |
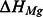 (kJ mol−1) (kJ mol−1) |
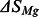 (J mol−1 K)a (J mol−1 K)a
|
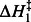 (kJ mol−1) (kJ mol−1) |
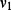 (µm s−1) (µm s−1) |
 (kJ mol−1) (kJ mol−1) |
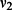 (µm s−1) (µm s−1) |
| Value ± error | 66.5±7.2 | 234±25 | 18±3 | 590±600 | 64±7 | 4×1011±1×1012 |
Note: ΔSMg is by the value of 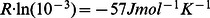 smaller than the standard entropy difference (ΔSMg
0) because Mg2+-ion concentrations have been used in mM units for data analysis.
smaller than the standard entropy difference (ΔSMg
0) because Mg2+-ion concentrations have been used in mM units for data analysis.
Figure 2. Population of the AM·Mg2+D state in the myosin-5b ATPase cycle.
Three dimensional surface plot of the fraction of populated AM·Mg2+D state 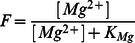 as a function of temperature and free Mg2+-ion concentrations using parameters from table 1. The solid line in the middle of panel A matches K
Mg of the equilibrium in Figure 1C. The same line as a function of the temperature is shown in panel B. Panel C shows the dependence of F on the concentration of free Mg2+ at 20°C. Shadowed area underlines the range of free Mg2+-ion concentration where the population of the AM·Mg2+D state changes from 0.2 to 0.8.
as a function of temperature and free Mg2+-ion concentrations using parameters from table 1. The solid line in the middle of panel A matches K
Mg of the equilibrium in Figure 1C. The same line as a function of the temperature is shown in panel B. Panel C shows the dependence of F on the concentration of free Mg2+ at 20°C. Shadowed area underlines the range of free Mg2+-ion concentration where the population of the AM·Mg2+D state changes from 0.2 to 0.8.
Figure 3. Energy landscape of the Mg2+-sensitive states of myosin-5b.
Illustrated are the relative changes in enthalpy (ΔH1 ‡, ΔH2 ‡, ΔHMg) of the reaction according to the proposed kinetic model. The enthalpic barriers ΔH1 ‡ and ΔH2 ‡ correspond to the two alternative Mg2+-ADP and ADP dissociation pathways, respectively. The enthalpy difference of the Mg2+-equilibrium ΔHMg explains the high temperature dependence of the AMD - AM·Mg2+D equilibrium and underlines the non-linear behavior of sliding velocity in the Arrhenius plots.
Our kinetic and thermodynamic analysis of myosin-5b allowed us to describe the Mg2+-dependence of motile activity and regulation of this motor by a simple two-state kinetic model. The herein reported methodological approach of data analysis by global fitting can be useful to interpret kinetic and thermodynamic data of other experimentally accessible reaction steps in the acto-myosin ATPase cycle, thus providing a consistent description of the energetics and equilibria of acto-myosin interactions. Moreover, our results underline the significant contribution of entropic terms to the free energies for acto-myosin interactions. At least four additional myosins including Dictyostelium myosin-1D and -1E, human nonmuscle myosin-2c, and human myosin-7a show similar variations in their kinetics as reported for myosin-5a and myosin-5b, with the ADP release step being the rate limiting and Mg2+-ion sensitive step in their ATPase cycle [37], [38], [39]. The examination of the equilibria states of these myosins can provide further validation of our model assumption.
Acknowledgments
We thank C. Waßmann for excellent technical assistant. D.J. Manstein for continuous support and discussions.
Funding Statement
The work was supported by grants from the Deutsche Forschungsgemeinschaft to Georgios Tsiavaliaris (Grant number TS 169/3-1,2) (http://www.dfg.de/). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Sweeney HL, Houdusse A (2010) Structural and functional insights into the Myosin motor mechanism. Annu Rev Biophys 39: 539–557. [DOI] [PubMed] [Google Scholar]
- 2. Geeves MA, Fedorov R, Manstein DJ (2005) Molecular mechanism of actomyosin-based motility. Cell Mol Life Sci 62: 1462–1477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Heissler SM, Manstein DJ (2013) Nonmuscle myosin-2: mix and match. Cell Mol Life Sci 70: 1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Preller M, Manstein DJ (2013). Myosin Motors: Structural Aspects and Functionality. In: Egelman EH, Goldman YE, Ostap EM, editors. Comprehensive Biophysics. Academic Press. pp. 118–150.
- 5. Bloemink MJ, Geeves MA (2011) Shaking the myosin family tree: biochemical kinetics defines four types of myosin motor. Semin Cell Dev Biol 22: 961–967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Conibear PB, Geeves MA (1998) Cooperativity between the two heads of rabbit skeletal muscle heavy meromyosin in binding to actin. Biophys J 75: 926–937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Mansson A (2010) Actomyosin-ADP states, interhead cooperativity, and the force-velocity relation of skeletal muscle. Biophys J 98: 1237–1246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Greenberg MJ, Lin T, Goldman YE, Shuman H, Ostap EM (2012) Myosin IC generates power over a range of loads via a new tension-sensing mechanism. Proc Natl Acad Sci U S A 109: E2433–2440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Laakso JM, Lewis JH, Shuman H, Ostap EM (2008) Myosin I can act as a molecular force sensor. Science 321: 133–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Uyeda TQ, Warrick HM, Kron SJ, Spudich JA (1991) Quantized velocities at low myosin densities in an in vitro motility assay. Nature 352: 307–311. [DOI] [PubMed] [Google Scholar]
- 11. De La Cruz EM, Ostap EM (2004) Relating biochemistry and function in the myosin superfamily. Curr Opin Cell Biol 16: 61–67. [DOI] [PubMed] [Google Scholar]
- 12. Harris DE, Warshaw DM (1993) Smooth and skeletal muscle myosin both exhibit low duty cycles at zero load in vitro. J Biol Chem 268: 14764–14768. [PubMed] [Google Scholar]
- 13. Moore JR, Krementsova EB, Trybus KM, Warshaw DM (2001) Myosin V exhibits a high duty cycle and large unitary displacement. J Cell Biol 155: 625–635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Takagi Y, Shuman H, Goldman YE (2004) Coupling between phosphate release and force generation in muscle actomyosin. Philos Trans R Soc Lond B Biol Sci 359: 1913–1920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. De La Cruz EM, Sweeney HL, Ostap EM (2000) ADP inhibition of myosin V ATPase activity. Biophys J 79: 1524–1529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Hannemann DE, Cao W, Olivares AO, Robblee JP, De La Cruz EM (2005) Magnesium, ADP, and actin binding linkage of myosin V: evidence for multiple myosin V-ADP and actomyosin V-ADP states. Biochemistry 44: 8826–8840. [DOI] [PubMed] [Google Scholar]
- 17. Rosenfeld SS, Houdusse A, Sweeney HL (2005) Magnesium regulates ADP dissociation from myosin V. J Biol Chem 280: 6072–6079. [DOI] [PubMed] [Google Scholar]
- 18. Jacobs DJ, Trivedi D, David C, Yengo CM (2012) Kinetics and thermodynamics of the rate-limiting conformational change in the actomyosin V mechanochemical cycle. J Mol Biol 407: 716–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Amrute-Nayak M, Diensthuber RP, Steffen W, Kathmann D, Hartmann FK, et al. (2010) Targeted optimization of a protein nanomachine for operation in biohybrid devices. Angew Chem Int Ed Engl 49: 312–316. [DOI] [PubMed] [Google Scholar]
- 20. Taft MH, Hartmann FK, Rump A, Keller H, Chizhov I, et al. (2008) Dictyostelium myosin-5b is a conditional processive motor. J Biol Chem 283: 26902–26910. [DOI] [PubMed] [Google Scholar]
- 21. Nagy NT, Sakamoto T, Takacs B, Gyimesi M, Hazai E, et al. (2010) Functional adaptation of the switch-2 nucleotide sensor enables rapid processive translocation by myosin-5. FASEB J 24: 4480–4490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Sweeney HL, Houdusse A (2004) The motor mechanism of myosin V: insights for muscle contraction. Philos Trans R Soc Lond B Biol Sci 359: 1829–1841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Bierbaum V, Lipowsky R (2011) Chemomechanical coupling and motor cycles of myosin V. Biophys J 100: 1747–1755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Rosenfeld SS, Sweeney HL (2004) A model of myosin V processivity. J Biol Chem 279: 40100–40111. [DOI] [PubMed] [Google Scholar]
- 25. Trivedi DV, David C, Jacobs DJ, Yengo CM (2012) Switch II mutants reveal coupling between the nucleotide- and actin-binding regions in myosin V. Biophys J 102: 2545–2555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Yengo CM, Takagi Y, Sellers JR (2012) Temperature dependent measurements reveal similarities between muscle and non-muscle myosin motility. J Muscle Res Cell Motil 33: 385–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Geeves MA, Jeffries TE, Millar NC (1986) ATP-induced dissociation of rabbit skeletal actomyosin subfragment 1. Characterization of an isomerization of the ternary acto-S1-ATP complex. Biochemistry 25: 8454–8458. [DOI] [PubMed] [Google Scholar]
- 28. Kron SJ, Spudich JA (1986) Fluorescent actin filaments move on myosin fixed to a glass surface. Proc Natl Acad Sci U S A 83: 6272–6276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Sundberg M, Rosengren JP, Bunk R, Lindahl J, Nicholls IA, et al. (2003) Silanized surfaces for in vitro studies of actomyosin function and nanotechnology applications. Anal Biochem 323: 127–138.30. [DOI] [PubMed] [Google Scholar]
- 30. Anson M (1992) Temperature dependence and Arrhenius activation energy of F-actin velocity generated in vitro by skeletal myosin. J Mol Biol 224: 1029–1038. [DOI] [PubMed] [Google Scholar]
- 31. Sheetz MP, Chasan R, Spudich JA (1984) ATP-dependent movement of myosin in vitro: characterization of a quantitative assay. J Cell Biol 99: 1867–1871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Chizhov I, Chernavskii DS, Engelhard M, Mueller KH, Zubov BV, et al. (1996) Spectrally silent transitions in the bacteriorhodopsin photocycle. Biophys J 71: 2329–2345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Van Brederode ME, Hoff WD, Van Stokkum IH, Groot ML, Hellingwerf KJ (1996) Protein folding thermodynamics applied to the photocycle of the photoactive yellow protein. Biophys J 71: 365–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Truhlar D, Kohen A (2001) Convex Arrhenius plots and their interpretation. Proc Natl Acad Sci U S A 98: 848–851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Sweeney HL, Kushmerick MJ (1985) Myosin phosphorylation in permeabilized rabbit psoas fibers. Am J Physiol 249: C362–365. [DOI] [PubMed] [Google Scholar]
- 36. Farruggia G, Iotti S, Prodi L, Montalti M, Zaccheroni N, et al. (2006) 8-hydroxyquinoline derivatives as fluorescent sensors for magnesium in living cells. J Am Chem Soc 128: 344–350. [DOI] [PubMed] [Google Scholar]
- 37. De La Cruz EM, Wells AL, Rosenfeld SS, Ostap EM, Sweeney HL (1999) The kinetic mechanism of myosin V. Proc Natl Acad Sci U S A 96: 13726–13731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Yengo CM, De la Cruz EM, Safer D, Ostap EM, Sweeney HL (2002) Kinetic characterization of the weak binding states of myosin V. Biochemistry 41: 8508–8517. [DOI] [PubMed] [Google Scholar]
- 39. Xie P, Dou SX, Wang PY (2006) Model for kinetics of myosin-V molecular motors. Biophys Chem 120: 225–236. [DOI] [PubMed] [Google Scholar]