Nonparametric Bayes local partition models for random effects

Summary

This paper focuses on the problem of choosing a prior for an unknown random effects distribution within a Bayesian hierarchical model. The goal is to obtain a sparse representation by allowing a combination of global and local borrowing of information. A local partition process prior is proposed, which induces dependent local clustering. Subjects can be clustered together for a subset of their parameters, and one learns about similarities between subjects increasingly as parameters are added. Some basic properties are described, including simple two-parameter expressions for marginal and conditional clustering probabilities. A slice sampler is developed which bypasses the need to approximate the countably infinite random measure in performing posterior computation. The methods are illustrated using simulation examples, and an application to hormone trajectory data.

1. Introduction

Random effects models are commonly used in the analysis of longitudinal and functional data. Suppose that data on subject i (i = 1, …, n) consist of n_i measurements, y_i = (y_i1, …, y_ini)^T, collected at times t_i = (t_i1,…, t_ini)^T, and let

$$\begin{array}{cccc}\hfill y_{\mathit{is}}& =& {\eta }_i(t_{\mathit{is}})+{\epsilon }_{\mathit{is}},\hfill & {\epsilon }_{\mathit{is}}~N(0,{\sigma }^2),\hfill \\ \hfill {\eta }_i(t)& =& \sum _{j=1}^p{\theta }_{\mathit{ij}}{b}_j(t),\hfill & {\theta }_i~P,\hfill \end{array}$$ (1)

where η_i is a function for subject i, $b={\left\{b_j\right\}}_{j=1}^p$ are basis functions, σ² is the measurement error variance, θ_i = (θ_i1,…, θ_ip)^T are basis coefficients for subject i and heterogeneity in the curves is characterized through the random effects distribution P. A potential concern is sensitivity to the choice of random effects distribution. As described by Heard et al. (2006), one strategy is to use a latent class model with $P={\sum }_{h=1}^k{\pi }_h{\delta }_{{\mathrm{\Theta }}_h}$, where δ_Θ denotes a degenerate distribution with all its mass on Θ, π_h is the probability that θ_i = Θ_h and k is the number of functional clusters. Dirichlet process priors (Ferguson, 1973, 1974) allow k = ∞ and increasing numbers of clusters with sample size, and have been widely used for random effects distributions (Bush & MacEachern, 1996; Müller & Rosner, 1997).

Although much of the recent literature on mixture models has focused on clustering as a primary goal, such models are useful even if there is no interest in clustering. For example, in the analysis of longitudinal data, one may be interested in inferences on the average trajectory over time, in estimating variability in the trajectories across subjects, or in inferences on fixed effects coefficients, with the random effects considered a nuisance. In each of these cases, it is desirable to allow the random effects distribution, P, to be unknown. In many applications, p is moderate to large, so that it is necessary to obtain a sparse approach for characterizing the unknown P due to the curse of dimensionality.

Sparsity can be formalized through favouring a small number of components. This can be accomplished through a Dirichlet process prior, P ~ DP(α P₀), where α is a concentration parameter and P₀ is a base measure. The number of unique values of ${\left\{{\theta }_i\right\}}_{i=1}^n$ increases at a rate proportional to α log n, so that the number of occupied components tends to be small relative to n. However, a drawback of the Dirichlet process is the assumption of global partitioning. In particular, θ_ij = Θ_hj implies that θ_ij′ = Θ_hj′ for all j′ ǂ j. Hence, two subjects in the same cluster for any of their random effects are forced to be in the same cluster for all of their random effects. In functional data analysis, it is common for two subjects to have similar trajectories across certain regions while having local deviations. Under the Dirichlet process, either such subjects will be inappropriately clustered together, obscuring local differences, or they will be allocated to separate clusters.

This paper proposes a class of local partition process priors for parsimonious modelling of unknown random effects distributions. The general structure can be characterized as follows:

$${\theta }_{\mathit{ij}}={\mathrm{\Theta }}_{{\psi }_{\mathit{ij}}j},{\mathrm{\Theta }}_h~P_0,{\psi }_i={({\psi }_{i1},\dots ,{\psi }_{\mathit{ip}})}^{\mathrm{T}}~Q,$$ (2)

where ψ_ij ∈ {1, …, ∞} denotes the cluster index for the jth random effect from subject i, θ_i = Θ_ψi = (Θ_ψi11, …, Θ_ψipp)^T, the elements of $\mathrm{\Theta }={\left\{{\mathrm{\Theta }}_h\right\}}_{h=1}^{\infty }$ are independent and identically distributed, and Q is a probability distribution over {1, 2, …, ∞}^p.

In specifying Q, it is convenient to let Θ = Θ₀ ∪ Θ₁, with ${\mathrm{\Theta }}_0={\left\{{\mathrm{\Theta }}_{0h}\right\}}_{h=1}^{\infty }$ global coefficient vectors and ${\mathrm{\Theta }}_1={\left\{{\mathrm{\Theta }}_{1h}\right\}}_{h=1}^{\infty }$ local coefficient vectors. As a convention, let Θ₀ denote the odd-numbered elements of Θ, with Θ₁ the even-numbered elements. To induce ψ_i ~ Q, let

$${\psi }_{\mathit{ij}}=z_{\mathit{ij}}(2{\varphi }_{i0}-1)+(1-z_{\mathit{ij}})2{\varphi }_{\mathit{ij}},z_i~G,{\varphi }_i={({\varphi }_{i0},{\varphi }_{i1},\dots ,{\varphi }_{\mathit{ip}})}^{\mathrm{T}}~H,$$ (3)

where z_ij = 1 denotes allocation of θ_ij to a global component, z_ij = 0 denotes allocation to a local component, ϕ_i0 ∈ {1, 2, …, ∞} is a global cluster index for subject i and ϕ_ij ∈ {1, 2, …, ∞} is a local cluster index for subject i and element j. From (2)-(3), the ith subject’s random effects vector is equivalent to Θ_0ϕi0 for those elements having z_ij = 1, while the remaining elements are selected from a variety of local coefficient vectors. This specification allows a combination of global and local borrowing of information. Proofs are included in an Appendix.

2. Dependent local partition process

2·1. Formulation 1

To choose G and H in (3), let

$$\begin{array}{l}{z}_{\mathit{ij}}~\mathrm{Ber}({\nu }_j),{\nu }_j~\mathrm{Be}(1,\beta )(j=1,\dots ,p),\\ {\varphi }_{\mathit{ij}}~\sum _{h=1}^{\infty }{\pi }_{\mathit{jh}}{\delta }_h,{\pi }_{\mathit{jh}}={\pi }_{\mathit{jh}}^{\ast }\prod _{l<h}(1-{\pi }_{\mathit{jl}}^{\ast }),{\pi }_{\mathit{jh}}^{\ast }~\mathrm{Be}(1,\alpha )(j=0,1,\dots ,p),\end{array}$$ (4)

where ν_j is the probability of allocation to the global component for the jth random effect, β is a hyperparameter controlling the overall weight on the local components and the elements of ϕ_i are assigned independent stick-breaking priors, with the hyperparameter α controlling how rapidly the weights π_jh decrease towards zero as the index h increases. The stick-breaking priors are chosen following the Sethuraman (1994) representation of the Dirichlet process for simplicity, though extensions to more general stick-breaking priors (Ishwaran & James, 2001) are straightforward. Let P ~ LPP₁(α, β, P₀) denote the prior on the unknown random effects distribution induced through (2)-(4).

The prior P ~ LPP₁(α, β, P₀) induces borrowing of information across subjects through both global and local clustering. In particular, if subjects i and i′ are assigned to the same global cluster, then ϕ_i0 = ϕ_i′0, and it becomes more likely that these subjects will have identical values for multiple elements of their random effects vectors, particularly if β is not large. For small β and high-dimensional random effects vectors, subjects in the same global clusters will have identical values for most of their basis coefficients, while having occasional local deviations. This structure addresses the limitations of Dirichlet process priors mentioned in § 1. In a recent application using Dirichlet process priors for the distribution of a high-dimensional latent factor vector underlying gene expression measurements, we noticed a tendency of the Dirichlet process to induce a large number of clusters, as even individuals that were quite similar overall had important local differences. In contrast, the local partition process induced a small number of global and local clusters, leading to substantial gains in efficiency.

One of the appealing characteristics of the Dirichlet process prior is the availability of simple expressions for the prior probability of clustering marginalizing out P. In particular, θ_i ~ P with P ~ DP(α P₀) implies that pr(θ_i = θ_i′) = 1/(1 + α). This illustrates the role of the precision parameter α in controlling the tendency of individuals to be clustered together. As described in Proposition 1, a similarly simple expression is obtained for the marginal prior probability of pr(θ_ij = θ_{i′ j}) under P ~ LPP₁(α, β, P₀).

Proposition 1

Assuming θ_i ~ P with P ~ LPP₁(α, β, P₀),

$$\mathrm{pr}({\theta }_{\mathit{ij}}={\theta }_{i^{\prime }j})=\left(\frac{1}{1+\alpha }\right)\left(\frac{1}{2+\beta }\right)\left(\beta +\frac{2}{1+\beta }\right)=\rho .$$

Hence, α and β are key hyperparameters controlling the clustering probability ρ with ρ monotone decreasing in α and β. In the limit as α, β → 0, ρ = 1 and all individuals are automatically grouped into a single cluster with θ_i = θ for all i. To allow the data to provide information about appropriate values for α, β, let α ~ Ga(a_α, b_α) and β ~ Ga(a_β, b_β).

If subjects i and i′ are in the same cluster for the j′th random effect, so that θ_ij′ = θ_{i′ j′}, one has information that these subjects are similar. Ideally, such information would be propagated to other random effects, increasing the probability of θ_ij = θ_{i′ j} for j ǂ j′. Proposition 2 demonstrates that the prior P ~ LPP₁(α, β, P₀) automatically induces the desired dependence in local clustering. In addition, the dependence structure has a simple form, which provides insight into the flexibility of the approach and role of the hyperparameters.

Proposition 2

Assuming θ_i ~ P with P ~ LPP₁(α, β, P₀),

$$\mathrm{pr}({\theta }_{\mathit{ij}}={\theta }_{i^{\prime }j},{\theta }_{i{j}^{\prime }}={\theta }_{i^{\prime }{j}^{\prime }})={\left(\frac{1}{1+\alpha }\right)}^2{\left(\frac{1}{2+\beta }\right)}^2\left\{{\left(\beta +\frac{2}{1+\beta }\right)}^2+\frac{4\alpha }{{(1+\beta )}^2}\right\}.$$

The joint probability in Proposition 2 is strictly larger than the product of the marginal probabilities from Proposition 1, which implies that pr(θ_ij = θ_{i′ j}) increases given knowledge that θ_ij′ = θ_{i′ j′}. The degree of positive dependence in local clustering is monotonely increasing with α and decreasing with β, being controlled by the size of 4α/(1 + β)².

As P ~ LPP₁(α, β, P₀) provides a prior for the unknown random effects distribution P, it is important to assess basic properties, such as the mean and variance. Following common convention, the notation P is used to denote both a random probability measure and the corresponding distribution. It is assumed that P₀ is a probability measure over a measurable Polish space (Ω, B), with Ω the sample space and B the corresponding Borel σ-algebra. Let θ_ij ~ P_j, with P_j the jth marginal from the joint prior, P ~ LPP₁(α, β, P₀). Then, P_j is a probability measure over (Ω_j, B_j), where Ω_j is the sample space for the jth component of θ_i, and B_j is the corresponding Borel σ-algebra. For any B ∈ B_j, P_j(B) is a random variable, with $P_j(B)\stackrel{D}{=}W{X}_1+(1-W)X_2$, where W ~ Be(1, β) and X_l ~ Be[α P_0j(B), α{1 − P_0j(B)}], for l = 1, 2, are independent random variables. Although the density of P_j(B) does not have a simple form, the expectation and variance can be derived as

$$\mathrm{E}\{P_j(B)\}=P_{0j}(B),\mathrm{V}\{P_j(B)\}=P_{0j}(B)\{1-P_{0j}(B)\}\left(\frac{1}{1+\alpha }\right)\left(\frac{1}{2+\beta }\right)\left(\beta +\frac{2}{1+\beta }\right),$$

so that the prior is centred on the base probability measure P_0j and the variance is P_0j(B){1 − P_0j(B)}ρ, with ρ the probability of clustering shown in Proposition 1.

Nonparametric Bayes procedures allow uncertainty in parametric specifications through priors with large support. The proposed prior, P ~ LPP₁(α, β, P₀), has weak support on the space of probability measures over (Ω, B). In addition, as formalized in Theorem 1, the proposed process induces a highly flexible prior on the joint distribution of the local cluster indices, ψ_i = (ψ_i1, …, ψ_ip)^T ~ Q, with Q a probability measure on {1, 2, …, ∞}^p.

Theorem 1

Let θ_i ~ P with P ~ LPP₁(α, β, P₀), with hyperpriors chosen for α and β having support on ℜ⁺. Then, the following properties are satisfied:

• Property 1. pr{Q(ψ) > ε} > δ for all ψ ∈ {1, 2, …, ∞}^p and some ε, δ > 0;

• Property 2. pr{Q(ψ_ij = ψ_{i′ j}) ∈ A} > ε for all Borel subsets A ⊂ [0, 1], ψ_l ~ Q, l = i, i′, and some ε > 0;

• Property 3. $\mathrm{pr}\{\frac{Q({\psi }_{\mathit{ij}}={\psi }_{i^{\prime }j},{\psi }_{i{j}^{\prime }}={\psi }_{i^{\prime }{j}^{\prime }})}{Q({\psi }_{i{j}^{\prime }}={\psi }_{i^{\prime }{j}^{\prime }})}⩾Q({\psi }_{\mathit{ij}}={\psi }_{i^{\prime }j})\}=1$, for all j, j′ ∈ {1, …, p}, j′ ǂ j; and

  Property 4. $\mathrm{pr}\{\frac{Q({\psi }_{\mathit{ij}}={\psi }_{i^{\prime }j},{\psi }_{i{j}^{\prime }}={\psi }_{i^{\prime }{j}^{\prime }})}{Q({\psi }_{i{j}^{\prime }}={\psi }_{i^{\prime }{j}^{\prime }})}\in A\}>\epsilon$, for all Borel subsets A ⊂ [Q(ψ_ij = ψ_{i′ j}), 1], j, j′ ∈ {1, …, p}, j′ ǂ j and for some ε > 0.

2·2. Formulation 2

In applications involving large p, it is appealing for computational reasons to consider sparse alternatives to P ~ LPP₁(α, β, P₀) that avoid the incorporation of a separate stick-breaking process for each component. As a simplification of (4), replace the second line with

$${\varphi }_{\mathit{ij}}~\sum _{h=1}^{\infty }{\pi }_h{\delta }_h,{\pi }_h={\pi }_h^{\ast }\prod _{l<h}(1-{\pi }_l^{\ast }),{\pi }_h^{\ast }~\mathrm{Be}(1,\alpha )(j=0,1,\dots ,p).$$

This modified case is denoted as P ~ LPP₂(α, β, P₀). This specification assumes a common prior distribution for each of the elements of ϕ_i, resulting in a more parsimonious model. Under P ~ LPP₂(α, β, P₀), the local clustering probability pr(θ_ij = θ_{i′ j}) is identical to the expression shown in Proposition 1, so the hyperparameters α and β have a similar role under both specifications. The main question is whether one maintains sufficient flexibility in characterizing dependence in local partitioning, which can be addressed through modifying Proposition 2 as follows.

Proposition 3

Assuming θ_i ~ P with P ~ LPP₂(α, β, P₀), then

$$\mathrm{pr}({\theta }_{\mathit{ij}}={\theta }_{i^{\prime }j},{\theta }_{i{j}^{\prime }}={\theta }_{i^{\prime }{j}^{\prime }})=\left(\frac{1}{1+\alpha }\right){\left(\frac{1}{2+\beta }\right)}^2\left(\beta +\frac{2}{1+\beta }\right)\left\{\frac{(6+\alpha )\beta }{(2+\alpha )(3+\alpha )}+\frac{2}{1+\beta }\right\}.$$

As in Proposition 2, the joint probability is strictly larger than the product of the marginal clustering probabilities, implying positive dependence in local clustering. To investigate the flexibility in the degree of positive dependence, one can vary the values of α and β widely. Ideally, as α and β are varied, any degree of positive dependence could be obtained, ranging between independence of θ_ij = θ_{i′ j} and θ_ij′ = θ_{i′ j′} to perfect dependence, with θ_ij′ = θ_{i′ j′} implying θ_ij = θ_{i′ j}. Under Property 4 in Theorem 1, the prior P ~ LPP₁(α, β, P₀) allows any degree of positive dependence. In contrast, it follows from Proposition 3 that the prior P ~ LPP₂(α, β, P₀) induces a value for pr(θ_ij = θ_{i′ j} ∣ θ_ij′ = θ_{i′ j′}) that is constrained to fall in a subset of the interval [pr(θ_ij = θ_{i′ j}), 1], so that Property 4 is not satisfied. Because this subset comprises almost the entire interval, with only values very close to the left boundary excluded, this constraint is not important from a practical perspective.

2·3. Special cases and connections

A variety of priors that have been proposed previously arise as special cases of the local partition process formulation in (2) and (3). Considering the case in which G = δ₁, so that z_ij = 1 for all i, j, one obtains ψ_ij = ψ_i, with ψ_i ~ H*, where H* is induced from H. By choosing H* to have a stick-breaking form, one can obtain any prior in the class proposed by Ishwaran & James (2001), which includes the Dirichlet process and two-parameter Poisson Dirichlet process (Pitman & Yor, 1997) as special cases. For the priors P ~ LPP₁(α, β, P₀) and P ~ LPP₂(α, β, P₀), G = δ₁ corresponds to the limiting case β → 0 in which we obtain P ~ DP(α P₀).

Another important special case corresponds to G = δ₀, so that z_ij = 0 for all i, j, which occurs in the limit as β → ∞ for the priors P ~ LPP₁(α, β, P₀) and P ~ LPP₂(α, β, P₀). In the P ~ LPP₁(α, ∞, P₀) case, one obtains θ_ij ~ P_j, with P_j ~ DP(α P_0j) independently for j = 1, …, p, with P_0j the jth marginal of P₀. Potentially, dependence can be incorporated through the base measure P₀, as in Cifarelli & Regazzini (1978), though this is a restrictive type of dependence. In the P ~ LPP₂(α, ∞, P₀) case, instead of independent Dirichlet process priors for P_j (j = 1, …, p), one obtains the following dependent Dirichlet process (MacEachern, 1999),

$$P_j=\sum _{h=1}^{\infty }{\pi }_h{\delta }_{{\mathrm{\Theta }}_{\mathit{hj}}}(j=1,\dots ,p),{\mathrm{\Theta }}_h={\left\{{\mathrm{\Theta }}_{\mathit{hj}}\right\}}_{j=1}^p~P_0,$$ (5)

with P_j ~ DP(α P_0j) marginally. Expression (5) corresponds to the fixed-π formulation of the dependent Dirichlet process (De Iorio et al., 2004).

Previous nonparametric Bayes methods for discrete random probability measures consider a single cluster index ψ_i, while local partition processes provide a methodology for multivariate ψ_i = (ψ_i1, …, ψ_ip)^T. A competing formulation relies on a matrix stick-breaking process (Dunson et al., 2008), which induces dependent local clustering through including stick-breaking random variables for every subject and predictor. This leads to substantial computational difficulties for large n or p, while requiring pr(θ_ij = θ_{i′ j} ∣ θ_ij′ = θ_{i′ j′}) > 0·5.

3. Posterior computation

Assume that y_i ~ g(θ_i, τ), where y_i is an n_i × 1 vector of measurements for subject i, θ_i ~ P is a vector of parameters specific to subject i, and τ is a vector of population parameters. Initially letting P ~ LPP₁(α, β, P₀), we propose to use an adaptation of the slice sampling approach of Walker (2007) to implement posterior computation. This slice sampler avoids the need for a finite approximation, and is simpler to implement than the retrospective sampler of Papaspiliopoulos & Roberts (2008).

In addition to the latent variables defined in (4), we introduce latent variables $u_i={\{u_{\mathit{ij}}\}}_{j=0}^p$ (i = 1, …, n), where the complete data joint likelihood of y, u and z is

$$\prod _{i=1}^n\left\{g(y_i;{\mathrm{\Theta }}_{{\psi }_i},\tau )1(u_{i0}<{\pi }_{0{\varphi }_{i0}})\prod _{j=1}^{p}1(u_{\mathit{ij}}<{\pi }_{j{\varphi }_{\mathit{ij}}}){\nu }_j^{z_{\mathit{ij}}}{(1-{\nu }_j)}^{1-z_{\mathit{ij}}}\right\},$$ (6)

where the u_ijs are constrained to fall in (0, 1). The sampler proceeds as follows.

• Step 1. For the latent u_ij, the conditional is Unif(0, π_jϕij) (j = 0, 1, …, p).

• Step 2. For the latent z_ij, the conditional distribution is Ber(p_ij), with

  $$p_{\mathit{ij}}=\frac{{\nu }_{j}g(y_i;{\theta }_{i(z_{\mathit{ij}}=1)},\tau )}{{\nu }_{j}g(y_i;{\theta }_{i(z_{\mathit{ij}}=1)},\tau )+(1-{\nu }_j)g(y_i;{\theta }_{i(z_{\mathit{ij}}=0)},\tau )},$$

  where θ_i(zij=l) denotes the current value of θ_i with the jth element set equal to Θ_0ϕi0j for l = 1 and Θ_1ϕijj for l = 0.
• Step 3. For the stick-breaking variable ${\pi }_{\mathit{jh}}^{\ast }$, the conditional density is proportional to

  $${(1-{\pi }_{\mathit{jh}}^{\ast })}^{\alpha -1}\prod _{i=1}^{n}1\left\{{\pi }_{j{\varphi }_{\mathit{ij}}}^{\ast }\prod _{l<{\varphi }_{\mathit{ij}}}(1-{\pi }_{\mathit{jl}}^{\ast })>u_{\mathit{ij}}\right\}.$$
  Letting ${\varphi }_j^{\ast }=\max \left\{{\varphi }_{\mathit{ij}},i=1,\dots ,n\right\}$, the conditional distribution of ${\pi }_{\mathit{jh}}^{\ast }$ corresponds to the Be(1, α) prior for $h>{\varphi }_j^{\ast }$, while for $h\le {\varphi }_j^{\ast }$ the posterior is a Be(1, α) distribution truncated to fall in the (a_jh, b_jh) interval with

  $$\begin{array}{lll}{a}_{\mathit{jh}}& =& \max \left\{\frac{u_{\mathit{ij}}}{{\prod }_{l<h}(1-{\pi }_{\mathit{jl}}^{\ast })},i:{\varphi }_{\mathit{ij}}=h\right\},\\ b_{\mathit{jh}}& =& 1-\max \left\{\frac{u_{\mathit{ij}}}{{\pi }_{j{\varphi }_{\mathit{ij}}}^{\ast }{\prod }_{l<{\varphi }_{\mathit{ij}},lǂh}(1-{\pi }_{\mathit{jl}}^{\ast })},i:{\varphi }_{\mathit{ij}}>h\right\}.\end{array}$$

  For all h such that ${\sum }_{i=1}^{n}1({\varphi }_{\mathit{ij}}=h)=0$, we have a_jh = 0. In addition, b_jh = 1 for $h={\varphi }_j^{\ast }$.

• Step 4. The conditional probability of ϕ_ij = h is proportional to 1(h ∈ A_ij)g(y_i; θ_i(ϕij=h), τ), where A_ij = {h : π_jh > u_ij} is a finite subset of {1, 2, …, ∞} obtained by first sampling ${\pi }_{\mathit{jh}}^{\ast }$, for h = 1, …, ϕ̃_j, with ϕ̃_j the smallest value satisfying

  $$\sum _{h=1}^{{\stackrel{\sim }{\varphi }}_j}{\pi }_{\mathit{jh}}^{\ast }\prod _{l<h}(1-{\pi }_{\mathit{jl}}^{\ast })⩾1-u_j^{\ast },$$

  where $u_j^{\ast }=\min \{u_{\mathit{ij}},i=1,\dots ,n\}$.
• Step 5. The conditional distribution of Θ_lh is proportional to

  $$g_0({\mathrm{\Theta }}_{\mathit{lh}})\prod _{i=1}^{n}g(y_i;{\theta }_i,\tau ),$$

  assuming the probability measure P₀ has density g₀ with respect to Lesbesgue measure.

• Step 6. For the probability ν_j, the conditional density is Be{1 + Σ_i z_ij, β + Σ_i (1 − z_ij)}.

• Step 7. For the parameters τ, the conditional distribution is proportional to $f(\tau ){\prod }_{i=1}^{n}g(y_i;{\theta }_i,\tau )$.

• Step 8. For the hyperparameter β, the conditional distribution is

  $$\mathrm{Ga}\left\{a_{\beta }+p,b_{\beta }-\sum _{j=1}^p\log (1-{\nu }_j)\right\}.$$
• Step 9. For the hyperparameter α, the conditional distribution is

  $$\mathrm{Ga}\left\{a_{\alpha }+\sum _{j=0}^p{\varphi }_j^{\ast },b_{\alpha }-\sum _{j=0}^p\sum _{h=1}^{{\varphi }_j^{\ast }}\log (1-{\pi }_{\mathit{jh}}^{\ast })\right\}.$$

Each of these steps is simple to implement, and good rates of mixing and convergence have been observed in several applications. Steps 5 and 7 simplify when conjugate priors are chosen. For example, when g(y_i; θ_i, τ) is the likelihood for a Gaussian linear model and P₀ is chosen to obey a Gaussian law, the conditional distribution in Step 5 is Gaussian.

To modify the algorithm for formulation 2, drop the first subscript on each of the πs in (6) and in Steps 1 and 2. In Step 3, the conditional density for ${\pi }_h^{\ast }$ is proportional to

$${(1-{\pi }_h^{\ast })}^{\alpha -1}\prod _{i=1}^n\prod _{j=0}^{p}1\left\{{\pi }_{{\varphi }_{\mathit{ij}}}^{\ast }\prod _{l<{\varphi }_{\mathit{ij}}}(1-{\pi }_l^{\ast })>u_{\mathit{ij}}\right\}.$$

Letting ϕ* = max{ϕ_ij, i = 1, …, n, j = 0, 1, …, p}, the conditional distribution of ${\pi }_h^{\ast }$ is Be(1, α) for h > ϕ*, while for h ≤ ϕ* the posterior is Be(1, α) truncated to (a_h, b_h) with

$$\begin{array}{lll}{a}_h& =& \max \left\{\frac{u_{\mathit{ij}}}{{\prod }_{l<h}(1-{\pi }_l^{\ast })},i,j:{\varphi }_{\mathit{ij}}=h,i=1,\dots ,n,j=0,1,\dots ,p\right\},\\ b_h& =& 1-\max \left\{\frac{u_{\mathit{ij}}}{{\pi }_{{\varphi }_{\mathit{ij}}}^{\ast }{\prod }_{l<{\varphi }_{\mathit{ij}},lǂh}(1-{\pi }_l^{\ast })},i,j:{\varphi }_{\mathit{ij}}>h,i=1,\dots ,n,j=0,1,\dots ,p\right\}.\end{array}$$

Step 4 is modified to let A_ij = {h : π_h > u_ij}, where ${\pi }_h^{\ast }$ is sampled for h = 1, …, ϕ̃, with ϕ̃ the smallest value satisfying ${\sum }_{h=1}^{\stackrel{\sim }{\varphi }}{\pi }_h^{\ast }{\prod }_{l<h}(1-{\pi }_l^{\ast })⩾1-\min \{u_{\mathit{ij}},i=1,\dots ,n,j=0,1,\dots ,p\}$. Steps 5–8 are unchanged, and in Step 9 the conditional distribution of α is

$$\mathrm{Ga}\left\{a_{\alpha }+{\varphi }^{\ast },b_{\alpha }-\sum _{h=1}^{{\varphi }^{\ast }}\log (1-{\pi }_h)\right\}.$$

The major computational advantage relative to formulation 1 occurs in Step 3.

4. Simulation example

To illustrate the approach, a simulation example was considered following (1)-(4), with t_is ∈ [0, 1] and basis functions b₁(s) = 1, b_j+1(s) = exp(−ψ∥s − ξ_j∥²) (j = 1, …, p − 1), with ξ₁, …, ξ_p−1 equally spaced kernel locations, ψ = 25 and p = 20. To generate n = 16 curves, let θ_ij = z_ijΘ_0j + (1 − z_ij)Θ_1j for i = 1, …, 16 and j = 1, …, 20, with z_ij ~ Ber(0·5) and the elements of Θ₀ and Θ₁ sampled independently from a mixture of a point mass at zero, having probability 0·5, and a standard normal density. The point mass allowed exclusion of basis functions. There were 40 equally spaced observations along each curve with σ² = 0·2.

The data were analyzed using P ~ LPP₁(α, β, P₀), P ~ LPP₂(α, β, P₀) and P ~ DP(αP₀), with Ga(1, 1) hyperpriors for α and β, a Ga(0·1, 0·1) hyperprior for σ⁻², and P₀ chosen to correspond to the multivariate Gaussian distribution with zero-mean and identity covariance. The slice sampler was run for 25 000 iterations, with the first 5 000 samples discarded as a burn-in and every twentieth sample collected to thin the chain. In each case, the sampler appeared to converge rapidly and to mix efficiently based on examination of trace plots of α, β, σ² and function values at a variety of locations and for a variety of individuals. Due to label switching, it is not reliable to monitor the elements of Θ_h in assessing convergence and mixing.

Figure 1 shows the data, true curves and estimates under P ~ LPP₁(α, β, P₀). The estimates are close to the truth, with average absolute bias = 0·192, mean square error = 0·060, maximum absolute bias = 0·506 and an average 99% pointwise credible interval width of 1·01. The estimated posterior mean of σ² was 0·21, with a 95% credible interval of [0·18, 0·26]. The estimate for α was 0·17, with 95% credible interval [0·10, 0·29]. The small value of α suggests the individuals are assigned to few local and global clusters. For component j (j = 0, 1, …, p), all subjects are allocated to the first ${\varphi }_j^{\ast }=\max \{{\varphi }_{\mathit{ij}},i=1,\dots ,n\}$ clusters. The posterior means of ${\varphi }_j^{\ast }$ are less than 2 for j = 0, 1, …, p, with ${\widehat{\varphi }}_0^{\ast }=1·62$ and ${\widehat{\varphi }}_j^{\ast }\in [0·99,1·30]$, for j = 1, …, p. The probability of allocation to the local component for a random element of a subject’s random effects vector is 1/(1 + β). Hence, β provides a measure of the relative importance of the local and global components, with both components receiving equal weight for β = 1 and the global component dominant for β < 1. For the simulation, we obtained β̂ = 1·23, with a 95% credible interval of [0·51, 2·42], so that the two components receive close to equal weight.

Fig. 1.

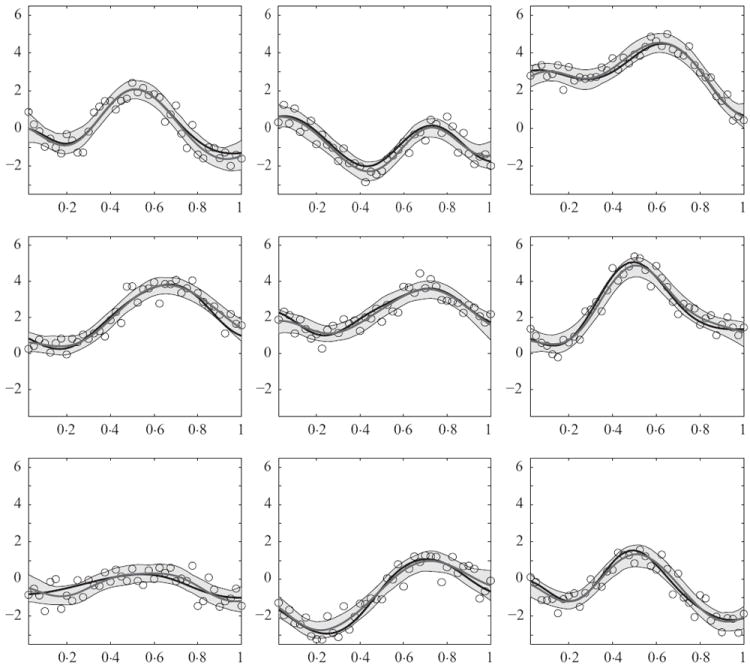
Data and results for 9 of the 16 subjects in the simulation example. Each panel corresponds to one subject in the study, the true functions are represented with black lines, the posterior means with grey lines and 99% pointwise credible intervals are shaded.

For the analysis under P ~ LPP₂(α, β, P₀), there was a substantial reduction in computational time and the results were improved, with average absolute bias = 0·168, mean square error = 0·046, maximum absolute bias = 0·520 and an average 99% credible interval width of 0·793. The estimated posterior mean of β was 1·56, with a 95% credible interval of [0·64, 3·25]· In addition, σ̂² = 0·20, with a 95% credible interval of [0·18, 0·23]. It does not appear that the more concentrated posterior distributions reflected a lack of proper account for uncertainty in that the true functions were all entirely enclosed in the 99% pointwise intervals. Hence, the narrower intervals more likely reflect an improvement in efficiency due to the incorporation of fewer parameters in the second formulation.

For the Dirichlet process, there was minimal borrowing of information across the different functions, with posterior probability of allocating the 16 functions to 13 clusters greater than 0·99. The resulting function estimates were still reasonable, but the performance was not nearly as good as for the local partition process. The average absolute bias was increased by 26%, the mean square error by 60% and the maximum absolute bias by 57% relative to the first formulation. The average credible interval widths were similar, but the true functions fell well outside the 99% intervals in two out of 16 of the cases. In addition, the estimated residual variance was σ̂² = 0·27, with 99% credible interval [0·23, 0·31] not including the true value of 0·20. This overestimation of the residual variance suggests a poor job at recovering the signal. This was the first simulation scenario considered, but there was general improvement for the local partition process over the Dirichlet process in a broad variety of scenarios, with the gain very substantial in many cases. Gains are most notable when data for each function are sparse.

5. Hormone curve application

5·1. Background and motivation

The approach is applied to post-ovulatory progesterone data collected in early pregnancy for n = 165 women (Wilcox et al., 1988). The progesterone metabolite, PdG, was measured in urine. Letting y_is denote the sth measurement of log(PdG) for woman i occurring t_is days after the estimated day of ovulation, we assume y_is ~ t_κ {η_i (t_is), σ²}, where η_i is a smooth trajectory in log(PdG) for woman i and t_κ (μ, σ²) denotes the t-density, with mean μ, degrees of freedom κ and scale σ². Expression (1) is generalized to allow t-distributed measurement errors. The data contain between n_i = 4 and n_i = 40 observations per woman, with an average of n̄ = 23·1. In general, the data are collected daily in the morning, but there are gaps, with most of these gaps corresponding to censoring in which the woman stopped collecting urine prior to day 40. Censoring occurred if menses resumed following an early pregnancy loss or the six-month collection period ended. Given the plausible missingness mechanisms, it is reasonable to assume that missingess is conditionally independent of the missing PdG values given the observed PdG values, implying data are missing at random.

The goal is to obtain a flexible, yet parsimonious representation of the progesterone trajectories. Bigelow & Dunson (2009) analyzed these data using a Dirichlet process prior for the distribution of the woman-specific basis coefficients in a spline model assuming normally distributed measurement errors. They estimated 31 PdG trajectory clusters, with 18 of these being singletons containing just one woman. Given that many of their reported trajectory clusters have similar shapes with only local deviations, it is our expectation that replacing the Dirichlet process prior on the basis coefficients with a local partition process prior can produce a more parsimonious representation.

In analyzing the data, we used the approach applied in § 4 for the simulated data after standardizing time to the [0, 1] interval and adapting the approach to accommodate t-distributed measurement errors. This adaptation was straightforward by expressing the t-distribution as a scale mixture of normals by letting $y_{\mathit{it}}~N\{{\eta }_i(s_{\mathit{it}}),{\xi }_i^{-1}{\sigma }^2\}$, with ξ_i ~ Ga(κ/2, κ/2) and with the degrees of freedom κ assigned a Ga(1, 1) hyperprior to favour very heavy tails to correspond with our prior knowledge. Under this structure, the full conditional posterior distribution for ξ_i is gamma, while κ is updated using Metropolis–Hastings steps.

5·2. Analysis and results

We focus initially on the first formulation of the local partition process. Using multiple chains with widely distributed starting points, the slice sampler was observed to exhibit good rates of convergence and mixing. Figure 2 shows the results under P ~ DP(αP₀) and P ~ LPP₁(α, β, P₀) for five women. It is clear from this plot, and from examination of plots for the other women in the study, that the local partition process method produces a good fit. The estimated value of the hyperparameter α was α̂ = 0·41, with a 95% credible interval of [0·25, 0·63]. This value suggests that few global and local clusters are needed, so that a sparse representation of the data is obtained. Indeed, the posterior probability of ${\varphi }_0^{\ast }=3$ was 0·97, suggesting that subjects were allocated to three global clusters. The number of local clusters also tended to be small, having an estimated average value of 2·91.

Fig. 2.

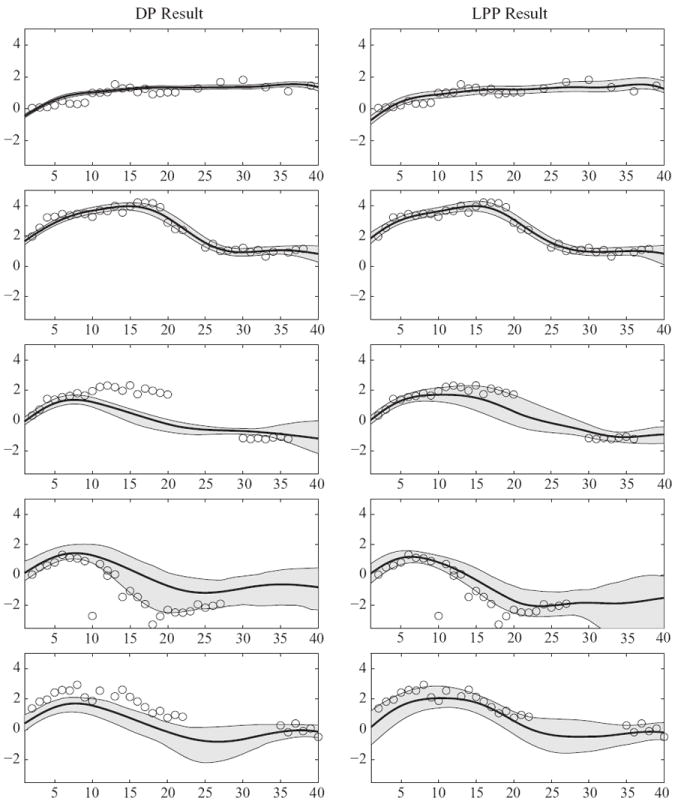
Log PdG function estimates for selected women in the Early Pregnancy Study. The posterior means are solid lines and 95% pointwise credible intervals are shown in grey. The x-axis scale is time in days starting at the estimated day of ovulation.

The estimated value of the hyperparameter β was 1·05, with a 95% credible interval of [0·63, 1·59]. Recall that values of β close to zero provide support for a joint Dirichlet process prior on the distribution of the basis coefficients, while large values provide support for independent Dirichlet process priors for the different coefficients. A value close to one instead provides evidence for a local partition process balanced between the two extremes, with a 50–50 chance of a randomly selected basis coefficient being drawn from a global versus local component. Hence, there is clear evidence in the data favouring our proposed approach over the Dirichlet process.

The estimated degrees of freedom in the t-distribution was 2·05, with a 95% credible interval of [2·01, 2·11], suggesting very heavy tails. This is as expected, since most of the values are tightly distributed about a smooth trajectory, but there are extreme outlying values in the dataset. Commenting further on the estimated hormone curves, many of the trajectories increase rapidly after ovulation and then flatten out within a week or two, while other trajectories increase initially and then decrease. It is likely that the increasing trajectories correspond to healthy pregnancies, while the trajectories that peak a week or more after ovulation and then decline correspond to early pregnancy losses.

Repeating the analysis for P ~ DP(αP₀), the posterior mean of α was 3·60, with a 95% credible interval of [1·84, 6·32]. The α parameter was slow-mixing in the Markov chain Monte Carlo implementation, with high autocorrelation. However, because traceplots of the subject-specific basis coefficients and function estimates were well behaved, the mixing problems with α did not appear to impact our inferences. The posterior mean number of clusters was 21·4, with a 95% interval of [15,37], reflecting large posterior uncertainty in clustering and a substantially larger number of clusters than in the local partition process analysis. In most cases, the estimates are similar to those obtained for P ~ LPP₁(α, β, P₀). However, as illustrated in Fig. 2, there are multiple exceptions in which the Dirichlet process approach produced an estimate inconsistent with the data. We noted particularly poor performance for women having relatively few observations. This likely reflects a tendency of the Dirichlet process to overly favour clustering together of subjects unless there are abundant data available to suggest that this clustering is not supported. Hence, in sparse data situations, one anticipates dramatic gains for the local partition process.

Finally, we implemented the sparse variant of the local partition process. The estimate of α was 0·38 with a 95% interval of [0·10, 0·95], and the estimate of β was 1·87 with a 95% interval of [1·10, 2·92]. The larger estimate of β suggests that P ~ LPP₂(α, β, P₀) places more weight on the local component than P ~ LPP₁(α, β, P₀). This is likely due to the fact that there is less of a penalty to be paid for introducing additional local clusters under P ~ LPP₂(α, β, P₀) due to the incorporation of common stick-breaking weights. The estimates for the overall number of clusters and the log(PdG) curves were very similar to those for the LPP₁(α, β, P₀). However, there was a substantial decrease in the time required per iteration of the slice sampler. The first formulation took 112 seconds per 100 iterations in Matlab on a MacBook Pro laptop, while the Dirichlet process implementation took 30 seconds and the sparse local partition process took 69 seconds. We repeated each of the analyses for a variety of hyperparameter values, with the variance multiplied by 2 and divided by 2 for α, β, P₀ and κ. There were no noticeable differences in the results.

6. Discussion

This paper proposes a generalization of the Dirichlet process, which allows dependent local clustering and borrowing of information. The emphasis is on functional data analysis applications in which each function is characterized as a linear combination of basis functions, and the goal is to flexibly borrow information to more efficiently estimate the individual functions. In order to favour more borrowing of information across the individual functions and obtain a more parsimonious representation of the data, one can allow the basis coefficients for an individual to be locally selected from a small number of vectors of unique basis coefficients. The vectors of unique basis coefficients can be viewed as representing underlying commonalities across the different functions, resulting in a discrete nonparametric analogue of functional principal components. This type of idea seems very promising as a tool for generating sparse characterizations of complex multivariate and functional data in a variety of settings. The proposed local partition process provides a simple, yet flexible approach for characterizing the local selection process. The slice sampling implementation is quite simple and efficient to implement, while allowing posterior computation for the infinite-dimensional nonparametric process instead of a finite approximation.

Appendix

Proof of Proposition 1

In order to derive the marginal probability of local clustering, pr(θ_ij = θ_{i′ j}), let

$$\begin{array}{lll}\mathrm{pr}({\theta }_{\mathit{ij}}={\theta }_{i^{\prime }j})& =& \mathit{\int }\sum _{l=0}^1\sum _{m=0}^1\mathrm{pr}({\theta }_{\mathit{ij}}={\theta }_{i^{\prime }j}\mid z_{\mathit{ij}}=l,z_{i^{\prime }j}=m)\mathrm{pr}(z_{\mathit{ij}}=l,z_{i^{\prime }j}=m\mid {\nu }_j)\mathit{d\; f}({\nu }_j)\\ & =& \mathit{\int }\frac{1}{1+\alpha }\{{\nu }_j^2+{(1-{\nu }_j)}^2\}\frac{1}{B(1,\beta )}{(1-{\nu }_j)}^{\beta -1}d{\nu }_j\\ & =& \frac{1}{1+\alpha }\left\{\left(\frac{1}{1+\beta }\right)\left(\frac{2}{2+\beta }\right)+\frac{\beta }{2+\beta }\right\},\end{array}$$

with Proposition 1 following directly, where f(π_j) denotes the Be(1, β) prior distribution for π_j and B(a, b) denotes the beta(a, b) function.

Proof of Proposition 2

The joint probability of local clustering follows along similar lines:

$$\begin{array}{lll}\mathrm{pr}({\theta }_{\mathit{ij}}& =& {\theta }_{i^{\prime }j},{\theta }_{i{j}^{\prime }}={\theta }_{i^{\prime }{j}^{\prime }})\\ & =& \mathit{\int }\frac{1}{1+\alpha }\left[\frac{1}{1+\alpha }\left\{{\nu }_j^2{(1-{\nu }_{j^{\prime }})}^2+{(1-{\nu }_j)}^2{\nu }_{j^{\prime }}^2+{(1-{\nu }_j)}^2{(1-{\nu }_{j^{\prime }})}^2\right\}+{\nu }_j^2{\nu }_{j^{\prime }}^2\right]\\ & & \times \frac{1}{B{(1,\beta )}^2}{(1-{\nu }_j)}^{\beta -1}{(1-{\nu }_{j^{\prime }})}^{\beta -1}d{\nu }_{j}d{\nu }_{j^{\prime }}\\ & =& {\left(\frac{1}{1+\alpha }\right)}^2\left\{\frac{4\beta }{(1+\beta ){(2+\beta )}^2}+{\left(\frac{\beta }{2+\beta }\right)}^2\right\}+\left(\frac{1}{1+\alpha }\right){\left(\frac{1}{1+\beta }\right)}^2{\left(\frac{2}{2+\beta }\right)}^2\\ & =& {\left(\frac{1}{1+\alpha }\right)}^2{\left(\frac{1}{2+\beta }\right)}^2\left\{{\left(\beta +\frac{2}{1+\beta }\right)}^2+\frac{4\alpha }{{(1+\beta )}^2}\right\}.\end{array}$$

Proof of Proposition 3

Express the joint probability of local clustering as

$$\begin{array}{lll}\mathrm{pr}({\theta }_{\mathit{ij}}& =& {\theta }_{i^{\prime }j},{\theta }_{i{j}^{\prime }}={\theta }_{i^{\prime }{j}^{\prime }})=\mathit{\int }\sum _{l_1=0}^1\sum _{l_2=0}^1\mathrm{pr}({\theta }_{\mathit{ij}}={\theta }_{i^{\prime }j}\mid z_{\mathit{ij}}=l_1,z_{i^{\prime }j}=l_2)\mathrm{pr}(z_{\mathit{ij}}=l_1,z_{i^{\prime }j}=l_2\mid {\pi }_j)\mathit{df}({\pi }_j)\\ & & \times \mathit{\int }\sum _{l_3=0}^1\sum _{l_4=0}^1\mathrm{pr}({\theta }_{i{j}^{\prime }}={\theta }_{i^{\prime }{j}^{\prime }}\mid {\theta }_{\mathit{ij}}={\theta }_{i^{\prime }j},z_{i{j}^{\prime }}=l_3,z_{i^{\prime }{j}^{\prime }}=l_4)\mathrm{pr}(z_{i{j}^{\prime }}=l_3,z_{i^{\prime }{j}^{\prime }}=l_4\mid {\nu }_{j^{\prime }})\mathit{df}({\nu }_{j^{\prime }})\\ & =& \left[\frac{1}{1+\alpha }\mathit{\int }\left\{{\nu }_j^2+{(1-{\nu }_j)}^2\right\}\mathit{df}({\nu }_j)\right]\left[\frac{6+\alpha }{(2+\alpha )(3+\alpha )}\mathit{\int }{(1-{\nu }_{j^{\prime }})}^2\mathit{df}({\nu }_{j^{\prime }})+\mathit{\int }{\nu }_{j^{\prime }}\mathit{df}({\nu }_{j^{\prime }})\right]\\ & =& \left(\frac{1}{1+\alpha }\right){\left(\frac{1}{2+\beta }\right)}^2\left(\beta +\frac{2}{1+\beta }\right)\left\{\frac{(6+\alpha )\beta }{(2+\alpha )(3+\alpha )}+\frac{2}{1+\beta }\right\}.\end{array}$$

Proof of Theorem 1

To demonstrate property 1, first let

$$Q(\psi )=\left\{\prod _{j:{\psi }_j\in I_o}{\nu }_j{\pi }_{0{\psi }_j}^{\ast }\prod _{l<{\psi }_j}(1-{\pi }_{0l}^{\ast })\right\}\left\{\prod _{j:{\psi }_j\in I_e}(1-{\nu }_j){\pi }_{j{\psi }_j}^{\ast }\prod _{l<{\psi }_j}(1-{\pi }_{jl}^{\ast })\right\},$$

where ψ ∈ {1, 2, …, ∞}^p, I_o = {1, 3, 5, …} and I_e = {2, 4, 6, …}. Let Q̄(ψ) denote the median of the distribution of Q(ψ) for fixed ψ. Note that Q̄(ψ) is expressed as a product of finitely many random variables in (0, 1), so that pr{Q(ψ) > 0} = 1. It follows that Q̄(ψ) > 0 and hence pr{Q(ψ) > ε_ψ} = 0·5, with ε_ψ = Q̄(ψ) > 0. Letting ε = min[ε_ψ, ψ ∈ {1, 2, …, ∞}^p], we have pr{Q(ψ) > ε} ⩾ 0·5.

To demonstrate Property 2, first let

$$\mathrm{pr}\left\{Q({\theta }_{\mathit{ij}}={\theta }_{i^{\prime }j})\in A\right\}=\mathit{\int }1\{\rho (\alpha ,\beta )\in A\}f(\alpha ,\beta )\mathit{d\alpha \; d\beta },$$

where ρ(α, β) is defined in Proposition 1, with the dependence on α and β now explicit, and f(α, β) is the prior density for α, β on (0, ∞) × (0, ∞). For any point a ∈ A, there exists a corresponding region d(a) ⊂ (0, ∞) × (0, ∞) such that ρ(α, β) = a for all (α, β) ∈ d(a). Letting d(A) = ∪_a∈A d(a), pr{Q(θ_ij = θ_{i′ j}) ∈ A} = ∫_d(A) f(α, β)dα dβ. For all Borel subsets A ⊂ (0, 1), the area of d(A) is greater than 0, so pr{Q(θ_ij = θ_{i′ j}) = A} > 0 as long as f(α, β) > 0 for all (α, β) ∈ (0, ∞) × (0, ∞), which holds for independent gamma priors on α and β.

Property 3 follows from Propositions 1 and 2. To demonstrate Property 4, first let

$$\mathrm{pr}\left\{\frac{Q({\theta }_{\mathit{ij}}={\theta }_{i^{\prime }j},{\theta }_{i{j}^{\prime }}={\theta }_{i^{\prime }{j}^{\prime }})}{Q({\theta }_{i{j}^{\prime }}={\theta }_{i^{\prime }{j}^{\prime }})}\in A\right\}=\mathit{\int }1\{{\rho }_2(\alpha ,\beta )\in A\}f(\alpha ,\beta )\mathit{d\alpha \; d\beta },$$

where ρ₂(α, β) = pr(θ_ij = θ_{i′ j} ∣ θ_{i j′} = θ_{i′ j′}, α, β). Hence, given that f(α, β) > 0 for all (α, β) ∈ (0, ∞) × (0, ∞), it suffices to show that there exists a region d₂(a) ⊂ (0, ∞) × (0, ∞) of (α, β) values that result in ρ₂(α, β) = a, with d₂(a) ǂ 0̸ for all a ∈ (0, 1). This condition follows directly if there exists an (α, β) solution to the equations ρ(α, β) = a, ρ₂(α, β) = b, for every point (a, b) in 0 < a < b < 1, which is easily verified.