Abstract
This article reviews various procedures used in the analysis of circadian rhythms at the populational, organismal, cellular and molecular levels. The procedures range from visual inspection of time plots and actograms to several mathematical methods of time series analysis. Computational steps are described in some detail, and additional bibliographic resources and computer programs are listed.
Keywords: Biostatistics, circadian rhythm, chronobiology, chronomics, time series analysis
Introduction
Circadian rhythms are partly-endogenous cycles in biological processes that recur in approximately 24-h intervals (Aschoff 1979; Halberg 1969; Pittendrigh 1993; Rietveld 1996). Although circadian oscillation is only one of many cyclic processes in organisms (Cornélissen et al. 1999; Gillette & Sejnowski 2005), it is often analyzed as an independent process. Treating circadian oscillations as independent processes is only justified under particular conditions, notably in the case of limited short time series, and is subject to several caveats to be discussed here. In particular, interactions between circadian and other oscillatory processes may invalidate the results of analyses conducted with exclusive focus on circadian rhythmicity. Empirical research has documented interactions of circadian rhythmicity with tidal rhythmicity (Akiyama 2004; Barnwell 1968; de la Iglesia et al. 1994; Palmer 1967; Stillman & Barnwell 2004; Wikelski & Hau 1995), reproductive rhythmicity (Häster & Erkert 1993; Houdelier et al. 2002; Kadono et al. 1981; Rauth-Widmann et al. 1996; Zivkovic et al. 1999), weekly rhythmicity (Cornélissen et al. 1986; Fálcon et al. 1996; Halberg et al. 1985; Sanchez de la Peña et al. 1983; Schweiger et al. 1986), and annual rhythmicity (Bertolucci et al. 2002; Honma et al. 1992; Lee & Zucker 1995; Menaker 1961; Mrosovsky et al. 1976; Wollnik & Schmidt 1995), among others.
The study of circadian rhythms is a fast-growing field of biomedical research. As of January 2006, PubMed (the US National Library of Medicine’s biomedical database) contained 50,000 abstracts of journal articles that could be retrieved by the keyword “circadian” —three times as many as those catalogued 20 years earlier. The medical importance of research on circadian rhythms is exemplified by applications in the treatment of hypertension (Cornélissen et al. 1991; Hermida et al. 2003, 2004), cancer (Halberg et al. 2003a; Hrushesky 1985; Lévi et al. 1997), rheumatoid arthritis (Günther et al. 1980), asthma (Pincus et al. 1995), the malaise associated with shift work (Boivin & James 2002; Crowley et al. 2003), sleep disorders (Czeisler et al. 1981), and numerous other conditions. As a specific example, Figure 1 shows the doubling of survival rate of cancer patients treated at the time of peak tumor temperature as compared to other circadian times (Halberg et al. 2003a). The importance of analysis of circadian rhythms for diagnosis is particularly clear in the use of the circadian amplitude and phase to diagnose separate vascular variability disorders, a public health problem par excellence, with other aspects reviewed elsewhere by Zeger et al. (2006). Thus, a circadian blood pressure overswing (or circadian hyper-amplitude-tension, CHAT, defined as a 24-hour amplitude of blood pressure above the upper 95% prediction limit derived on the basis of data from clinically healthy peers) carries a curable risk greater than hypertension, even when values are within an acceptable range and the condition is silent to both care recipient and caregiver (Cornélissen et al. 2004; Halberg et al. 2002). An odd circadian timing of blood pressure is associated with autonomic disorders, e.g. in diabetes (Halberg et al. 2002). The two conditions are confounded in many papers relying on diagnoses based on simple day – night ratios, which yield classifications of dippers, non-dippers, excessive dippers, or reverse dippers, and that fail to separate outcomes when rhythm characteristics do so (Bingham et al. 2005; Cornélissen et al. 2000, 2006).
Figure 1.
Treatment of perioral cancer timed at peak tumor temperature leads to more than doubling of the 24-month survival rate, as compared to reference groups treated 4 or 8 hours before or after the tumor temperature peak. The dashed line indicates the outcome for treatment conducted without regard for circadian time. Data from Halberg et al. (2003a), as documented by a peak test (Savage et al. 1962).
Procedures for the analysis of circadian rhythms are part of the broader set of procedures involved in time series analysis in general. This analysis of data that have been collected at different points in time is extensively used by economists, meteorologists, engineers, public health researchers, and many other professionals whose main concern is not biological rhythms (Brockwell & Davis 2002; Chatfield 2004; Diggle et al. 2002; Percival & Walden 2000; Shumway & Stoffer 2000). While this paper focuses particularly on circadian rhythmicity, the methods presented herein remain applicable to the detection and characterization of very many other components that are documented in biology and many other sciences. Figure 2 is a flowchart of some of the methods available for analysis in chronobiology. Some of the methods in the flowchart are not included in this paper (such as multivariate and discriminant analysis, cross-correlation, cross-spectral analysis and coherence, convolution and deconvolution, complex demodulation, chronodesms, cluster analysis, jackknife, and bootstrap) but are at least here mentioned for those interested in the broader context of chronobiometry. Other methods considered in the paper (Rayleigh test, Enright and Lomb – Scargle periodograms) are not included in this flowchart but are discussed in detail. Some methods referred to in the flowchart are general ones: for instance, moving spectral windows are one kind of pergressive spectral analysis, while chronobiologic serial sections are another kind. Some techniques such as time-varying phase synchronization are not covered in the paper and are not included in the flowchart either. The method(s) to be used are best considered before decisions on a sampling design.
Figure 2.
Flowchart of some of the methods available for analysis in chronobiology and for chronomics, with emphasis on extended cosinor rhythmometry. Note on the top of the chart that one can start with a time-specified datum as well as with a time series. This is because the methods of rhythmometry also serve for the preparation of reference intervals. Such time-specified reference intervals, or chronodesms, and their variants are currently a raison d’être of clinical chronobiology, as this discipline resolves the normal range of variation. Use of the procedures outlined in this flowchart has to be based on cost-effectiveness that determines the sampling requirements which in research will be much more demanding for exploring new periodicities even in the circadian spectral region than for dealing with already-mapped rhythms. As biology and medicine involve longer and longer series, it will become essential to resolve more than single components in a given spectral region, including the circadian one. As more and more variables can be studied concomitantly for long spans, procedures that analyze relations among time series will become indispensable. Adapted from Halberg et al. (1987).
Sampling
While the design of studies and the associated problems of sampling and data editing, notably with respect to outliers, are mentioned only briefly in this paper focusing on analyses, a few guidelines are provided herewith.
There are essentially three types of sampling of time series: longitudinal, transverse (cross-sectional), and hybrid sampling. Longitudinal sampling is sampling conducted continuously over many cycles, preferably at regular intervals. This sampling is especially useful to assess the time structure representing an individual. The longer the time series, the easier it is to estimate components with longer and longer periods, the easier it is to discriminate between separate components with close periods, and the better one can differentiate a rhythm spectrum from trends.
Transverse or cross-sectional sampling is sampling of many individuals, once per individual. This approach is necessary when experimental conditions do not allow longitudinal sampling, as in the case of assessment of toxicity of a drug by the endpoint lethality. In order to assess rhythmic behavior based on purely transverse sampling, each individual sample needs to be collected at a different time (or rhythm stage), an approach that presumes external synchronization. The larger the number of individuals, the better the overall population will be represented, provided individual samples are random.
The main limitation of a purely transverse design stems from the often present inter-individual differences in mean value. For this reason, hybrid (linked-cross-sectional) designs are usually preferred in chronobiological studies. Hybrid designs are a combination of longitudinal and transverse sampling. Expressing the data as a percentage of each series mean, whereby inter-individual differences are eliminated, then facilitates the analysis. Specifically, several individuals provide repeated samples at intervals to cover at least one cycle of the anticipated rhythm to be assessed. Rhythm characteristics can thus be determined for each individual assessed longitudinally. Parameter estimates thus obtained are considered as imputations and summarized across all sampled individuals to obtain an assessment of the rhythmic behavior generalizable to the population, as long as the sampled individuals constitute a random sample of the population.
Often there are constraints that limit either the duration of an experiment (upper limit for a longitudinal assessment) or the number of individuals included in an investigation. Hybrid sampling was actually conceived in the context of a biosatellite project on eight rats for 21 days, where each additional day or rat had a price tag of one million dollars (not adjusted for inflation!) and thus a design was developed wherein the rats were studied transversely in a 12-h alternation of light and darkness first and for free-running under continuous light next, in order to seek answers to major questions within the limitations of sampling within the constraints of available days and individuals (Halberg et al. 1971).
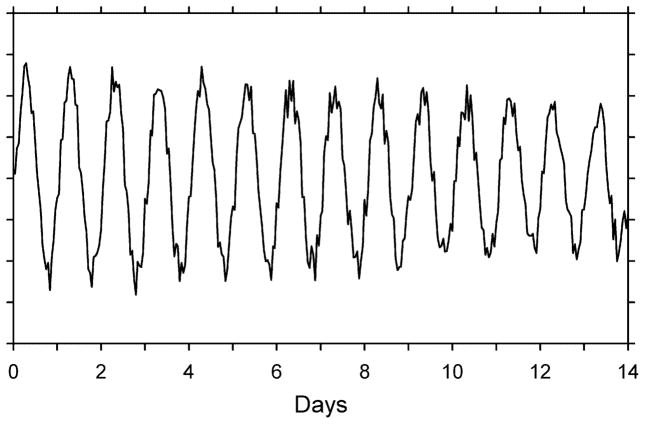
Circadian and broader maps obtained under routine synchronized conditions are highly desirable for consultation before one decides on the sampling rate, if blunders are to be avoided. Figure 3 illustrates a problem encountered when the sampling rate is insufficient. It also illustrates the danger of sampling at a fixed time of day (a common but not invariably applicable practice) when the circadian rhythm is not 24-h synchronized. The variable being studied in this case is characterized by a period of 27.43 h, desynchronized from 24 h. It is assumed to follow a sinusoidal course with no noise. Sampling once a day at a fixed clock hour is shown by the dots. Analysis of the sampled data detects a component with a period of eight days instead of 27.43 h. This phenomenon is called aliasing because one component (27.43-h) is spuriously mistaken as an eight-day (aliased) component. Sampling once a day at a fixed clock hour has also been shown to yield contradictory results when not just the MESOR but also the circadian amplitude (or acrophase) is modulated by another component. This is the case for blood pressure which tends to have a more prominent circadian variation in winter than in summer. As a consequence, daytime measurements will tend to assume higher values during the winter whereas night-time and early morning measurements will tend to assume higher values during the summer. By fixing the time of day of measurement to “control” for the circadian rhythm thus yields controversial circannual results depending on when during the day the fixed measurement is taken (Watanabe et al. 2003).
Figure 3.

Diagram illustrating aliasing (that is, identification of a spurious “rhythm” [alias] because of poor [insufficiently dense] sampling of an actual rhythmic process). The actual rhythmic component in this graph is sinusoidal with a period of 27.43 h. Sampling once a day at a fixed clock hour is shown by the dots. Analysis of the sampled data detects a component with a period of 8 days instead of 27.43 h. More generally, aliasing refers to all artifacts resulting from insufficiently dense sampling that fails to detect rhythm characteristics, such as the amplitude, acrophase or waveform (as well as the period illustrated on this graph). Adapted from Halberg et al. (1977).
Visual inspection
The first step in the analysis of any time series consists of visual inspection of a time plot. The viewing of the data guides the selection of procedures for numerical analysis. Inspection of time plots in Cartesian coordinates (sometimes called “chronograms”) has been conducted by researchers of circadian rhythms since the late 1800s and early 1900s (Benedict 1904; Ogle 1866; Simpson & Galbraith 1906) and remains essential today. Figure 4 shows the record of body temperature of a gerbil (Pachyuromys duprasi) collected by radio-telemetry every six minutes for eight consecutive days (A). For comparison, the figure also shows a data set containing temperature values sampled in the same range but temporally randomized (B). An approximately 24-h pattern of oscillation is evident in A but not in B. Because data points randomly drawn from a uniform distribution rarely create an ascending or descending sequence of more than about five consecutive points, a formal statistical test may not be necessary for the inference that the temporal pattern in A cannot be explained by chance alone. Statistical testing is needed, however, to draw any conclusion regarding the temporal pattern in B. It is good practice to invariably proceed with statistical testing, irrespective of the appearance of the chronogram. Moreover, even if hypothesis testing can be omitted in some cases, parameter estimation requires mathematical procedures.
Figure 4.
Time plots of the records of body temperature of a gerbil collected by radio-telemetry every 6 minutes for 8 consecutive days (A) and of a simulated data set containing temperature values sampled in the same temperature range but temporally randomized (B). An approximately 24-h pattern of oscillation is evident in A but not in B. Data from Refinetti (1998).
A different, but very common form of display of time series used by investigators of circadian rhythms is the actogram (DeCoursey 2004; Refinetti 1992b). Introduced in 1926 by Maynard Johnson, the actogram can be derived from a chronogram by “cutting out” the data segment for each day, “stretching” it to the full width of a page, and “pasting” it below the data of the preceding day. The resulting graph shows data for one day per line, with successive days appearing on successive lines (Figure 5). The vertical alignment of the data provides instant information about the duration of the circadian cycle (that is, its period): drifts to the left indicate that the cycle is shorter than 24 h, whereas drifts to the right indicate that the cycle is longer than 24 h. The actogram in Figure 5 shows the running-wheel activity rhythm of a Nile grass rat (Arvicanthis niloticus) recorded at 6-min intervals for 35 consecutive days. During the first 22 days, the animal was maintained under a 24-h light – dark cycle that synchronized its locomotor activity rhythm. During the following 13 days, the lights were off, which allowed the grass rat to free-run with its presumed endogenous period shorter than 24 h (as indicated by the drift to the left).
Figure 5.
Actogram of the running-wheel activity rhythm of a Nile grass rat recorded with 6-min resolution for 35 consecutive days. As indicated by the horizontal bars at the top, a light – dark cycle was in effect for the first 22 days (LD), whereas darkness prevailed for the following 13 days (DD). The rhythm free-ran in constant darkness with a period shorter than 24.0 h. Data from Refinetti (2004a).
Often, researchers are unable to perform longitudinal sampling because of methodological limitations, because the phenomenon itself has an intractable temporal structure, or because they wish to avoid a putative effect of repeated sampling on the same individual (Halberg 1953). Figure 6(A) shows the accumulated temporal distribution of train suicides in the Netherlands. Of course, any single individual can only commit suicide once; consequently, a true time series of suicides cannot be obtained at the individual level. As shown in the figure, however, an “educed” daily rhythm of suicides can be produced when populational data are accumulated over many years. This can be accomplished by stacking the data over an idealized cycle with an assumed period. The distribution of the data points (A) is quite different from the distribution of values sampled in the same range but temporally randomized (B).
Figure 6.
Temporal distributions of suicides. (A) Accumulated temporal distribution of train suicides in the Netherlands from 1980 to 1994 (data from Houwelingen & Beersma 2001). (B) Distribution of values sampled in the same range as in A but temporally randomized. (C) Longitudinal data on suicides in Minnesota from 1968 to 2002 shown as monthly means (data from Halberg et al. 2005). (D) Subset of the Minnesota data set showing the number of daily suicides during the first two months of 2001. (E) Spectrum of cosinor amplitudes for the full time series (1968 – 2002).
If the time series allows examination without stacking, such as is the case for the time series of daily suicides in Minnesota (Figure 6C, D), data analysis can be extended to longer rhythmic components (E). Thus, even though the use of educed data sets has merits, notably when the number of “events” is small, it should be realized that, once the data have been stacked, an estimate of the given period’s uncertainty in length and, more importantly, point-and-interval estimates of the length of other periods that characterize the data (as they do in the case of suicides in Minnesota) can no longer be obtained. Stacking, invaluable to visualize the waveform of a given spectral component, is only a complementary approach to curve fitting and can be particularly restrictive whenever the data series exceeds in length the period used for stacking.
Data sets obtained in biomedical or other research and practice are often not as clearly rhythmic as some of those shown above. Even when they are clearly rhythmic to the eye, the investigator must conduct numerical analysis to secure an objective index of rhythmicity. Therefore, numerical procedures must be employed. Table I lists the procedures that will be discussed and indicates literature sources for the computational details as well as sources for computer software.
Table I.
Numerical procedures for detection of circadian rhythmicity.
| Procedure | Literature | Software |
|---|---|---|
| ANOVA | Hurlburt (2003), Moore (2004), Sprinthall (2003), Weiss (2005) | SAS (SAS Institute Inc., Cary, NC), SPSS (SPSS Inc., Chicago, IL), Statistica (StatSoft Inc., Tulsa, OK), Systat (Systat Software Inc., Richmond, CA) |
| Cosinor | Bingham et al. (1982), Nelson et al. (1979) | Cosifit (Circesoft, Waltham, MA), Time Series Analysis Serial Cosinor (Expert Soft Technology, Esvres, France) |
| Extended cosinor | Cornélissen and Halberg, 2005; Halberg, 1969 | http://www.msi.umn.edu/*halberg/ |
| Enright | Dörrscheidt and Beck (1975), Refinetti (1993), Sokolove and Bushell (1978) | Chronobiology Kit Analysis (Stanford Software Systems, Santa Cruz, CA), ClockLab Analysis (Actimetrics Software, Wilmette, IL), Actiview Actogram Software (Mini-Mitter Company, Bend, OR), CD-ROM in Refinetti (2006a) |
| Fourier | Bloomfield (2000), Körner (1988), Walker (1988), Walker (1996) | SAS (SAS Institute Inc., Cary, NC), SPSS (SPSS Inc., Chicago, IL), Statistica (StatSoft Inc., Tulsa, OK), Systat (Systat Software Inc., Richmond, CA), Chronobiology Kit Analysis (Stanford Software Systems, Santa Cruz, CA), ClockLab Analysis (Actimetrics Software, Wilmette, IL), Actiview Actogram Software (Mini-Mitter Company, Bend, OR), CD-ROM in Refinetti (2006a) |
| Kolmogorov-Smirnov | Kanji (1993), Siegel (1956) | SAS (SAS Institute Inc., Cary, NC), SPSS (SPSS Inc., Chicago, IL), Statistica (StatSoft Inc., Tulsa, OK), Systat (Systat Software Inc., Richmond, CA), CD-ROM in Refinetti (2006a) |
| Lomb – Scargle | Lomb (1976), Ruf (1999), Van Dongen et al. (1999a) | AutoSignal (Systat Software Inc., Richmond, CA), CD-ROM in Refinetti (2006a) |
| Rayleigh | Batschelet (1981), Brazier (1994), Mardia (1972) | Oriana (Exeter Software, Setauket, NY), SigmaStat (Systat Software Inc., Richmond, CA), CD-ROM in Refinetti (2006a) |
| Simulated annealing | Czaplicki et al., 2006 | GOSA (www.bio-log.biz) |
Product or corporate names may be trademarks or registered trademarks and are only used for identification purposes, without intent to infringe. Although reasonable efforts have been made to provide reliable information about the products listed here, the authors and the publisher cannot assume responsibility for the performance of the products or the safety of their use.
Detection of rhythmicity
Analysis of variance (ANOVA)
Although the analysis of variance (ANOVA) can only test for equality of class means and does not in itself tell anything about periodicity, this method has often been used to distinguish noisy rhythms from random oscillation when the period is known, at least approximately, a priori. The ANOVA, a well known procedure of statistical inference developed by Ronald Fisher in the early 1900s (Fisher 1925), is explained with adequate detail in all introductory statistics textbooks of today (e.g. Hurlburt 2003; Moore 2004; Sprinthall 2003; Weiss 2005). The test is based on the F statistic, which is a quotient of two indices of variability (sums of squares divided by their numbers of degrees of freedom): the variability computed between groups (time bins) and the variability computed within groups (or an adjusted error term, if the measurements conducted on successive time bins are not independent). Under the assumption of the null hypothesis (that is, that all class means are equal and, therefore, that there is no rhythmicity in the data), the two indices of variability are expected to be the same, which results in an F of 1. If there is rhythmicity, however, the variability among time bins will be larger than the variability within time bins, and F will be larger than 1. The probability density curve of the F distribution provides the basis for the decision of whether the empirical F value is significantly larger than 1.
Consider the data in Figure 7. The concentration of cholesterol in the blood of a goat (Capra hircus) was sampled every 3 h for 10 consecutive days. The figure shows the means (and standard errors) of the 10 measurements taken at each of the eight daily collection times (A). A repeated-measures ANOVA of these data indicates that the differences among the various means are unlikely to be explained by chance alone (F7,63 = 76.378, p <0.0001). Thus, we can infer that the concentration of cholesterol is not uniform throughout the day. The result of the ANOVA constitutes suggestive evidence that the goat exhibits daily rhythmicity in blood cholesterol concentration. Unfortunately, a major drawback in the use of ANOVA for the analysis of circadian rhythmicity is that, by design, the ANOVA evaluates only whether one or more means differ significantly from the others. It does not evaluate the existence of a rhythmic pattern. As a matter of fact, ANOVA indicates that the second data set in Figure 7(B) is just as rhythmic as the first one (A). Yet, there is clearly not 24-h rhythmicity in B.
Figure 7.
Mean concentration of cholesterol in the serum of a goat sampled every 3 h for 10 consecutive days (A) and simulated data set with randomized time bins (B). Each vertical bar indicates the mean (+SE) of the 10 measurements conducted at each of the eight daily collection times. The horizontal bar at the top indicates the duration of the light and dark phases of the prevailing light-dark cycle. Analysis by ANOVA rejects the hypothesis of uniformity in both cases, but only A exhibits 24-h rhythmicity. Data from Piccione et al. (2003).
In short, although the ANOVA can satisfactorily guide the inference about the absence of circadian rhythmicity if the null hypothesis is retained, it cannot demonstrate the existence of any particular rhythmicity when the null hypothesis is rejected. The ANOVA can ascertain lack of uniformity, but lack of uniformity does not imply circadian rhythmicity. Of course, the same limitation applies to the non-parametric equivalents of the ANOVA — the Kruskal –Wallis and Friedman tests (Kanji 1993; Krauth 1988; Siegel 1956). Likewise, a test of peak values for educed time series developed in the early 1960s (Savage et al. 1962) can confirm the presence of an anticipated significant peak but cannot document rhythmicity without prior information. Another problem relates to the choice of the number of classes and of a reference time, notably when this approach is applied to a longitudinal record of non-equidistant data (Hillman et al. 1990).
Fourier analysis
A full century before Fisher developed the ANOVA, Joseph Fourier developed a powerful tool for time series analysis that is still widely used today (Beau & Vibert 2006; Bloomfield 2000; Körner 1988; Walker 1988). Fourier analysis (also called “spectral analysis”) is based on Fourier’s revolutionary insight that any time series, regardless of its shape or regularity, can be described by a series of sine and cosine waves of various frequencies (Fourier 1822). Thus, if spectral analysis of a time series identifies a major spectral component in the circadian range, then the investigator can infer that the process under study exhibits circadian rhythmicity. Arthur Schuster used Fourier analysis to evaluate periodicity in meteorological phenomena and introduced the term “periodogram” (Schuster 1898). The procedure was first applied to the analysis of circadian rhythms in the early 1950s to quantify free-running rhythms of mice after blinding (Halberg & Visscher 1954; Koehler et al. 1956).
In Fourier analysis, the spectral energy ( ) of each frequency j/N [for j = 1 to (N − 1)/2] can be calculated as:
| (1) |
| (2) |
| (3) |
In these equations, N is the number of data points in the time series, xi denotes the value of the variable at time ti, and all angular values are in radians. By computing for all j from 1 to (N − 1)/2, a periodogram can be constructed. The periodogram shows the spectral energy associated with each frequency (or its reciprocal, period). Faster computation can be conducted by Fast Fourier Transforms (Walker 1996).
Figure 8 shows records of locomotor activity of a horse (Equus caballus) monitored by actigraphy at 1-min intervals for 10 consecutive days (top) and the periodogram generated by Fourier analysis of the time series (bottom). Visual inspection of the raw data suggests the existence of 24-h rhythmicity, and the Fourier periodogram confirms it by showing a principal peak at 24.0 h. Other, smaller peaks can also be seen (arrows), and they correspond to other spectral components. The spectral components in harmonic relation with the fundamental 24-h component help characterize the complex waveform of the activity rhythm. Although Fourier did not derive a test of significance to allow quantitative distinction between noisy rhythms and random oscillation, tests of significance were developed by others (Schuster 1898; Fisher 1929; Siegel 1980). The dashed line in Figure 8 (bottom) indicates the 0.05 level of significance for the periodogram according to Fisher’s procedure. Notice that only the 24.0-h component has a peak above the significance line. The significance level of the periodogram, p(R2), can be calculated as follows:
| (4) |
where N is the number of data points in the time series and g is the quotient of the largest and the sum of all in the periodogram.
Figure 8.
Records of locomotor activity of a horse monitored by actigraphy at 1-min intervals for 10 consecutive days (top) and the periodogram generated by Fourier analysis of the time series (bottom). The dashed line in the periodogram indicates the 0.05 level of significance. Visual inspection of the raw data suggests the existence of 24-h rhythmicity, and the Fourier periodogram confirms it by showing a large peak at 24.0 h. Other, smaller peaks can also be seen (arrows). Data from Piccione et al. (2005).
Cosinor and cosine fit
The cosinor method was developed by Franz Halberg and colleagues in the early 1960s, used with chronobiological serial sections by 1965 (Halberg et al. 1965), and formally presented in 1967 (Halberg et al. 1967). Further extensions followed, including serial sections of several orders, combined gliding and global spectral windows, parameter testing, and linear – nonlinear rhythmometry (Arbogast et al. 1983; Bingham et al. 1982; Cornélissen & Halberg 2005; Halberg 1980; Nelson et al. 1979; Nintcheu-Fata et al. 2003; Rummel et al. 1974). It is appropriate not only for non-equidistant data but also for serially-independent data (that is, educed rhythms). The method is based on the reasoning that, since circadian rhythms can be thought of as smooth rhythms with added noise, a model consisting of cosine curves with known periods (24 h alone or with added harmonic terms) can be fitted by least squares to the data as an estimate of the pattern of the smooth rhythm. In the special case of a single cosinusoidal curve, the value of each point (xi) is a function of the average value of the variable under investigation, estimated as the MESOR (M, Midline Estimating Statistic Of Rhythm, a rhythm-adjusted mean that differs from the arithmetic mean when the data are not equidistant and/or do not cover an integer number of cycles), the amplitude of the oscillation (A), and the phase of the maximum in relation to a fixed reference time (φ, known as the acrophase). Since the period (P) is assumed known (or approximately known), the fit can be obtained by linear regression — the trigonometric angles (θi) corresponding to the sampling times ti (at which the data points xi were collected) being computed as θi =(2π ti)/P. The model can be written according to the equation:
| (5) |
where ei is an error term assumed to be independent and normally distributed with mean zero and fixed unknown variance σ2.
If this equation is incorporated into a model of linear regression by the method of least squares, a system of three equations with three unknowns can be derived and solved in algebraic form to provide the parameters of the cosine wave that best fits the time series (Bingham et al. 1982; Halberg et al. 1967; Nelson et al. 1979). If the fitted wave has amplitude statistically greater than zero, then the time series can be inferred to exhibit 24-h rhythmicity.
The cosinor computations are greatly simplified if the data points are equidistant and cover an integer number of cycles. In this case, the MESOR (M) is simply the arithmetic mean of all data points [M = (Σxi)/N, for i =1 to N] and A and φ are computed as:
| (6) |
| (7) |
where
| (8) |
| (9) |
The probability that the amplitude (A) is significantly different from zero can be calculated by the F distribution with 2 and N – 3 degrees of freedom because
| (10) |
where S2 is the residual variance computed as:
| (11) |
Figure 9 shows the educed rhythm of systolic blood pressure of a woman along with a cosine wave fitted by the least squares method. In agreement with the impression obtained from visual inspection, statistical testing reveals that the amplitude of the fitted wave is significantly greater than zero (as indicated by the fact that the 95% confidence interval of the amplitude, shown at the peak, does not overlap the MESOR). This demonstrates that the data conform to about a 24-h rhythmic pattern. Notice that this data set constitutes an educed rhythm with non-equidistant observations, which could not be easily assessed by Fourier analysis.
Figure 9.

Educed rhythm of systolic blood pressure of a healthy woman collected at irregular intervals over nine days (points) and cosine wave fitted by the method of the least squares (curve). The small rectangle denotes the width of the 95% confidence interval of curve fitting. Data from Cornélissen and Halberg (2005).
The cosinor procedure can also be particularly suitable for the detection of rhythmicity in cross-sectional studies, which are very common in the investigation of molecular mechanisms of circadian rhythms. In these studies, small groups of animals are killed at intervals of several hours for collection of tissue, so that only educed rhythms can be analyzed. Figure 10 shows the results of a typical study in which groups of three mice (Mus musculus) were killed at 4-h intervals for the measurement of transcriptional activity of the per1 gene in the liver and testis. The cosinor procedure provides quantitative support for the conclusion that the per1 gene is expressed rhythmically in the liver, whereas a similar conclusion cannot be reached in the case of the testis.
Figure 10.
Expression of the per1 gene in liver and testis of mice. Each data point corresponds to the mean (+SE) of three mice. The dashed lines indicate the overall means for the whole data sets. The rectangles denote the width of the 95% confidence intervals of curve fitting. The confidence interval overlaps the mean in the testis but not in the liver. Data from Yamamoto et al. (2004).
Unless a step function is used instead of cosine curves, data whose measurement scale is not numerical (i.e. not in interval or ratio scales) are best analyzed as tallies over a given interval chosen judiciously to avoid problems related to quantization, as illustrated for the suicide data in Figure 6(A). Alternatively, the frequency distribution of nominal data could be tested for uniformity by standard non-parametric statistical tests such as the Kolmogorov –Smirnov test (Kanji 1993; Siegel 1956). Similarly to the ANOVA, however, the Kolmogorov – Smirnov test can satisfactorily accept the absence of a prominent circadian rhythm if the null hypothesis is retained, but it cannot demonstrate the existence of any particular rhythmicity when the null hypothesis is rejected. Another problem related to this kind of data is that endpoints derived from most approaches are likely to be real rather than integer numbers, rendering some interpretation of the results problematic. Conversion of incidence data to rates of occurrence may avoid this difficulty.
The increase in computer availability in the last 20 years has made it possible to bypass the least-squares regression procedure and to perform curve fitting by iteration, an approach not recommended when the same progress in computer power makes it easily feasible to fit periodic regressions exactly. When focus is limited to a single component, computer programs can derive the empirical mean and amplitude of the time series, generate multiple cosine curves for all possible phase angles, and identify the curve that approximately best fits the data as the one that produces the smallest sum of squares of the deviations between iterated cosine functions and the raw data (e.g. Ceriani et al. 2002; Piccione et al. 2005). The quotient between the sums of squares (or mean squares) of the best- and worst-fitting curves can then be used as an index of strength of rhythmicity whose sampling distribution has been empirically determined (Refinetti 2006a). This procedure has been used much less often than the standard cosinor procedure and is a less desirable option reserved for investigators who wish to avoid the least-squares regression procedure. Its main disadvantages are its lack of mathematical formalism, its approximate nature, notably for non-equidistant data, and its lack of straightforward generalization to multiple components.
The single cosinor approach, which consists of fitting by least squares one or several cosine curves with or without polynomial terms to an individual time series (whether the data are serially-dependent or serially-independent as to individuals and/or as to the environment), has been complemented by the population-mean cosinor method that provides a summary of results from three or more individuals (Bingham et al. 1982; Halberg et al. 1967). This procedure tests for similarity of individual results. The underlying statistics are those of multivariate averaging, making it possible to derive inferences generalizable to the population, provided the individual series represent a random sample of that population.
In Minnesota, the cosinor has been extended further to a chronobiological serial section (Halberg et al. 1965). Halberg (1969) illustrates the use of a serial section based on the single and population-mean cosinor procedures to quantify, with their uncertainties, phase drifts and phase shifts in mice and humans, respectively. Further extensions were to a serial section on a serial section (Arbogast et al. 1983), to an estimate of the uncertainty for the period (Bingham et al. 1984), and to a gliding spectrum (Nintcheu-Fata et al. 2003), all used in combination with linear-nonlinear rhythmometry (Rummel et al. 1974).
Rayleigh test
In some research situations, the only data that can be collected are the times at which certain events occur. In the absence of an estimate of amplitude, the Rayleigh test can be very helpful. The test was developed by John William Strutt (Lord Rayleigh) in the early 1900s (Strutt 1919) and is described in various circular-statistics books (Batschelet 1981; Mardia 1972). Its purpose is to determine whether there is directionality of distribution within a circle (i.e. from 0 to 2π, or 0 to 360°). Because a clock can be considered as a circle (with 24 h corresponding to 2π), the Rayleigh test can be used to test the distribution of times at which events occur. The test corresponds to the population-mean cosinor in which all individual amplitudes are set equal to 1.
For a series of trigonometric angles θi (for i =1 to N), which correspond to the observed times ti, the Rayleigh statistic (nR2) can be computed as:
| (12) |
Statistical significance can be determined by reference to the χ2 distribution because 2 × nR2 is distributed as χ2 with two degrees of freedom.
As an illustration of the application of the Rayleigh test, consider Figure 11. Female Siberian hamsters (Phodopus sungorus) were maintained in constant darkness from the beginning of pregnancy. Shortly after weaning, the pups were given access to running wheels, so that the phases of their circadian clocks could be determined. The small dark circles indicate the times of the onsets of activity of the pups (20 pups from five litters). An equal distribution of onsets illustrated in the abstract by a uniform distribution (as if they occurred “by chance”) is shown in A; the actual distribution is shown in B. The estimated time of the activity onset of the dams (time 12 of the LD cycle preceding constant darkness) is indicated by the arrowhead. The distribution of onsets of the pups (B) seems to be different from a uniform distribution (A), which suggests previous entrainment of the pups’ rhythms by the dams. Application of the Rayleigh test confirms the inference (nR2 =8.841, p =0.0001). The added computation of a 95% confidence interval for the average phase of the pups could further determine whether this activity was synchronized in phase as well as in period with that of the dams. If the activity data had been analyzed quantitatively to also obtain an estimate of circadian amplitude, a summary by population-mean cosinor could have been prepared.
Figure 11.

Temporal distribution of activity onsets of Siberian hamster pups a few days after weaning. Each dot denotes one pup. (A) uniform distribution; (B) actual distribution. The estimated time of the activity onset of the dams (time 12 of the LD cycle preceding constant darkness) is indicated by the arrowhead. Data from Duffield and Ebling (1998).
Enright periodogram
Another procedure for the determination of circadian rhythmicity, the Enright periodogram, can be applied when serially-dependent time series with equidistant measurements are available. Continuous equidistant measurements are very common in controlled laboratory studies, even though they are rather uncommon in human studies under ordinary conditions, where self-measurement-based time series are interrupted during sleep, such as those obtained by autorhythmometry as a feature of self-help in health care.
Proposed by James Enright in the 1960s (Enright 1965), the Enright periodogram procedure can be thought of as a one-way ANOVA adapted to the test of rhythmicity. The procedure repeatedly “folds” the long stream of data into segments of different periods and calculates an index of variability for each one of them. As in the ANOVA, the test of significance for each putative period in the Enright periodogram could use the F statistic to compare the between-class and within-class variabilities, thereby testing the null hypothesis of equality of class means. The implementation developed by Dörrscheidt and Beck (1975) does use the F statistic. The more popular implementation developed by Sokolove and Bushell (1978) uses the χ2 distribution instead. (The F distribution approximates the χ2 distribution when the degrees of freedom of the denominator are much greater than the degrees of freedom of the numerator.) The Sokolove and Bushell implementation is, therefore, known as the “chi square periodogram”.
For a data set with N values (i.e. xi for i =1 to N), which can be folded into K blocks of period P, the QP statistic used in the chi square periodogram procedure is computed as:
| (13) |
where Mh is the mean of K values under each time unit of the period length [Mh =(Σxi)/K, for i =1 to (N − K) in P increments], and M is the mean of all N values [M =(Σxi)/N, for i =1 to N].
Periodograms are constructed by the calculation of QP values for various periods within a desired range of periods (say, between 20.0 and 28.0 h for the test of daily rhythmicity). Unless the time series contains more than one rhythmic component, the highest peak in the periodogram corresponds to the estimated true period of the time series. Whether the highest peak is “high enough” can be determined by reference to the χ2 distribution because QP has a probability distribution of χ2 with P–1 degrees of freedom. It should be pointed out, however, that QP is distributed as χ2 only if K ≥ 10 — that is, if the time series contains 10 or more days of data (Refinetti 1992a, 2004b; Sokolove & Bushell 1978). This does not mean that the computed periods are incorrect if fewer than 10 days are used, but it does mean that the statistical significance cannot be reliably determined in these cases.
Figure 12 shows a 10-day segment of the records of running-wheel activity of a mouse maintained under a 24-h light – dark cycle as well as three periodograms generated by analysis of these data. Visual inspection of the time plot suggests the presence of strong rhythmicity with a period of 24.0 h. The three periodograms support this interpretation. As discussed later on, the chi square periodogram has been widely used for the determination of rhythmicity under free-running conditions (when the period of the putative rhythm cannot be assumed to be 24.0 h). For those researchers who have not yet used the cosinor procedure to construct periodograms for the determination of circadian period, the procedure can be easily adapted for this purpose. As a matter of fact, a cosinor periodogram may be more sensitive than the chi square periodogram in the detection of circadian rhythmicity. Figure 13 shows the results of tests conducted on sinusoidal data sets (10 days in 6-min intervals) contaminated with different amounts of noise (random oscillation within the range of the data set). The data sets were constructed with periods of 24.0 h and were analyzed by Fourier analysis, by the cosinor procedure, by the Enright periodogram, and by the Lomb – Scargle periodogram. As expected, the significance level of the rhythmicity statistics of the four procedures varied with the signal-to-noise ratio of the data sets, but the cosinor procedure was able to identify significant rhythmicity in noisier data sets than the other procedures. The statistical power of the cosinor was also shown theoretically to be superior to the analysis of variance (Bingham et al. 1993).
Figure 12.
Ten-day segment of the records of running-wheel activity of a mouse maintained under a 24-h light-dark cycle and three periodograms generated by analysis of these data. The dashed lines in the periodograms indicate the 0.01 level of significance. Visual inspection of the time plot suggests the presence of strong rhythmicity with a period of 24.0 h. The three periodograms support this interpretation. Data from Refinetti (2004a).
Figure 13.
Probability under the null hypothesis (Ho) as a function of the signal-to-noise ratio of the data sets for tests of 24.0-h rhythmicity conducted by Fourier analysis, by the cosinor procedure, by the Enright periodogram, and by the Lomb – Scargle periodogram. The horizontal line indicates p =0.05. The cosinor procedure detected significant rhythmicity in data sets with signal-to-noise ratios as low as 0.01 (1% signal and 99% noise).
Lomb – Scargle periodogram
The Lomb – Scargle periodogram is similar to the Enright periodogram in some aspects but has the advantage of allowing the analysis of data that were collected at irregular intervals rather than under a protocol with measurements conducted at fixed intervals, say, every 6 min or every hour. It also allows the analysis of data sets that were intended to have equally-spaced observations but that are missing one or more values because of equipment failure or other problems. The procedure is based on N. R. Lomb’s modification of Fourier analysis to accommodate unequally-spaced time series (Lomb 1976). It generally assumes, but does not require, that the rhythmicity conform to a sinusoidal pattern (Bretthorst 2001). The Lomb – Scargle periodogram has been shown to match or surpass Sokolove and Bushell’s implementation of the Enright periodogram in the analysis of circadian rhythms (Ruf 1999), although it has not yet been widely adopted by researchers of circadian rhythms.
For a data set with N values (i.e. xi for i =1 to N) collected at time points ti, the PN statistic used in the Lomb – Scargle periodogram procedure is computed as:
| (14) |
where M is the mean of all N values (M =(Σxi)/N), σ2 is the variance of all N values (σ2 =[Σ(xi−M)2]/N), P is the period being tested, and δ is a term used to adjust the times of unequally spaced data that can be computed as:
| (15) |
The significance level of the periodogram, p(PN), can be calculated as follows:
| (16) |
where PNmax is the largest PN in the periodogram. An example of a Lomb – Scargle periodogram was shown in Figure 12.
Parameter estimation
How one chooses which test of rhythmicity to use is a complex process that will be addressed in the conclusion, after additional elements have been discussed. Regardless of the test used, once an investigator has determined that a data set exhibits circadian rhythmicity, he or she should determine the characteristics of the rhythm. Several data-analysis procedures will compute rhythmic parameters at the same time as they evaluate the existence of rhythmicity, but the two tasks may be thought of separately for didactical purposes.
Ideal rhythmic processes, such as those commonly analyzed by engineers, are fully characterized by four parameters: MESOR (or mean level), period, amplitude, and phase (Figure 14). The mean level (herewith referred to as mesor in a general sense and as MESOR in the context of the cosinor procedure) is the central value around which the oscillation occurs. The period is the duration of a full cycle (that is, the time distance between one peak and the next). The amplitude is half the range of excursion of the cycle with the given period; in a symmetrical oscillation, the amplitude corresponds to the distance between the mesor and the peak (or trough) of the wave. In the case of a non-sinusoidal signal, one can estimate the amplitude of the fundamental component and that of each harmonic term added in the model to account for the shape of the signal. The excursion of the composite signal (from trough to peak) has been called the magnitude. The phase (or “phase angle”) is the relative angular displacement between the oscillation and a reference angle; in the study of circadian rhythms, the phase of a rhythm is often determined in reference to the environmental light –dark cycle. The phase of the maximal value assumed by the curve is called the acrophase. In the case of a composite model, the phase of the maximum is known as the orthophase (Tong et al. 1977).
Figure 14.
Diagram of an oscillatory process identifying four parameters of the oscillation: mesor, period, amplitude, and phase.
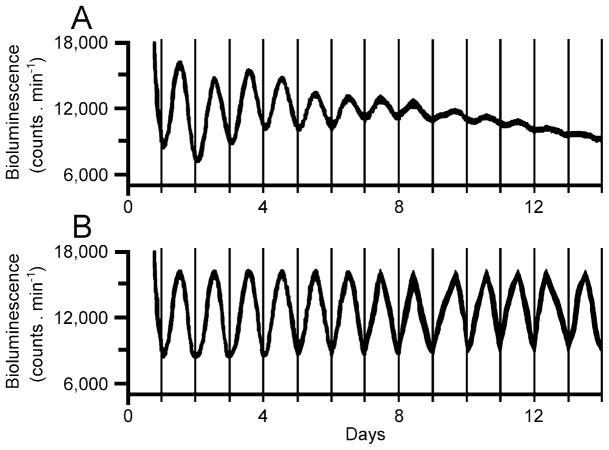
The full characterization of biological time series requires two additional elements that generally have not been incorporated into mathematical models used by researchers of biological rhythms: waveform and prominence. Waveform refers simply to the shape of the wave. As diagrammed in Figure 15, biological rhythms (including circadian rhythms) need not have a sinusoidal waveform (A). Instead, they may approximate a square wave (B), a sawtooth wave (C), or a more complex wave. The prominence of a rhythm refers to its strength and endurance. It corresponds to the proportion of the overall variance accounted for by the signal. It is thus a measure of the signal-to-noise ratio. In the absence of noise, prominence is a measure of the stationarity of a rhythm (Refinetti 2004b). A stationary oscillation is an oscillation whose parameters remain constant over time (that is, the oscillatory pattern is the same regardless of whether we examine the first wave, the second wave, or the millionth wave). Figure 15 exemplifies three cases of non-stationarity: irregular period (D), irregular waveform (E), and linear trend (mesor drift, F). Exact mathematical analysis of rhythmic parameters presupposes that the time series is stationary. Because biological rhythms are not strictly stationary (Refinetti 2004b), they can be analyzed only in an approximate manner. Investigators must be continually alert to possible intermodulations in a broad multi-frequency spectrum of rhythms and yet other interactions with other components of time structures.
Figure 15.
Diagram depicting oscillations with different waveforms (A-C), unstable period (D), unstable waveform (E), and linear trend (F).
Period
The period of a rhythm is the duration of a full cycle (that is, the reciprocal of its frequency). Different authors use slightly different notations for period. Here we use P as a generic abbreviation of period (mainly in computational formulae), τ as the period of an organism, and T as the period of an environmental synchronizer.
Particularly in the pre-computer era (but still to some extent today), inspection of actograms was a widely used method for computation of the period of circadian rhythms in laboratory studies. An example of an actogram is shown in Figure 5. During the first 22 days, the animal was maintained under a 24-h light – dark cycle, and the period of the activity rhythm matched the period of the light – dark cycle, as indicated by the vertical alignment of the daily onsets of activity. During the following 13 days, the lights were constantly off, which allowed the animal to free-run with its endogenous period shorter than 24 h (as indicated by the drift to the left). How much shorter than 24 h the period is can be determined by linear regression of the onsets against time. Notice that the onsets advance approximately 7 h in 13 days (from 08:30 on day 23 to 01:30 on day 35). This means that, on average, there is an advance of 0.54 h each day. Therefore, the period must be: 24–0.54 =23.46 h (23 h 28 min). With the popularization of computers, a purely graphic method of period determination became feasible. The method of “modulo adjustment” takes advantage of computers to force the actogram to display the data in more convenient ways. In this method, the period of a time series is determined by adjustment of the timescale used to construct the actogram. One will start with the standard 24-h scale and then shorten or lengthen the scale (i.e. reduce or increase the modulus) until the onsets are vertically aligned. The modulus of the timescale that aligns the onsets corresponds to the period of the rhythm. This method relies on visual inspection of the actograms and can, therefore, be affected by human subjectivity. When prominent circadian rhythms are present, however, the method is precise because of the high spatial resolution of the human visual system. The threshold for detection of deviation in the orientation of a test stimulus from vertical is approximately 0.6° (Heeley & Buchanan-Smith 1990), which is less than 1 pixel in a standard computer monitor.
Determination of circadian period by inspection of actograms is of limited use not only because of the subjectivity involved in the procedure but also because it does not provide a quantifiable measure of variability associated with the estimated parameter. Relying on a coefficient of linear regression and its confidence interval to obtain a measure of uncertainty for the period is feasible, but it does not account for the fact that there may also be subjectivity in deciding what is activity onset in some records. In addition, the procedure is based solely on onset times, and, therefore, ignores most of the data in the time series. As alternatives, numerous numerical procedures for the determination of circadian period have been developed or adapted from general time series tools, including serial autocorrelation (Eijzenbach et al. 1986; Halberg 1960; Hassnaoui et al. 2000; Lumineau et al. 1998; Mormont et al. 2000), inter-onset averaging (Albers et al. 1981; Diambra et al. 2002; Rao & Sharma 2002), iterative harmonics (Klemfuss & Clopton 1993), acrophase counting (Refinetti 1991), singular value decomposition (Kanjilal et al. 1999), and nonlinear multiple components analysis (Alonso & Fernández 2001; Cornélissen & Halberg 2005; Halberg 1980; Rummel et al. 1974), culminating in linear-nonlinear rhythmometry (Halberg 1980). In the case of a single component, a confidence interval for the period estimate obtained by the three periodogram procedures discussed above (the Fourier periodogram, the Enright period-ogram, and the Lomb – Scargle periodogram) can be determined by the intersection of the chosen level of significance with the envelope of the periodogram around the peak, as outlined in Bingham et al. (1984) for the cosinor. The basic cosinor procedure with one component can also be used for linear regression of phase or for the construction of a periodogram based on cosinors of a series of pre-selected periods, although this possibility has not been generally recognized (Klemfuss & Clopton 1993). The extended cosinor procedure indeed has been widely used in the analysis of broad-spectrum rhythmicity as assessed by a linear-nonlinear approach (Halberg 1980; Halberg et al. 1965; Rummel et al. 1974).
Historically, a comparison of six methods of circadian period determination (not including the multiple-components cosinor) found that the Enright (chi square) periodogram presented the best combination of accuracy, tolerance to waveform irregularity, and tolerance to noise (Refinetti 1993). A later comparison of the Lomb – Scargle periodogram with the Enright periodogram found that the two methods were equivalent, with a slight advantage for the Lomb – Scargle periodogram (Ruf 1999). Yet, both the Enright periodogram (Dörrscheidt & Beck 1975; Refinetti 1993) and the Lomb – Scargle periodogram (Schimmel 2001; Van Dongen et al. 1999b) are susceptible to artifacts. The most common and perhaps most serious problem is the detection of harmonics that do not actually exist in the data (consider Figure 16). Artificial data sets of square waves with periods of 12, 24, and 48 h were constructed and then analyzed by the chi square periodogram (QP) and the Lomb – Scargle periodogram (PN). Periods were evaluated in a broad circadian range of 14 – 34 h. Notice that the chi square periodogram identified a large 24 h component in the data set that contained only a 12-h square wave. Both methods correctly identified the 24-h component of the 24-h wave, although the Lomb – Scargle periodogram underestimated the strength of the 24-h component and erroneously identified other smaller components (arrows). When analyzing circadian rhythms, one must verify that the data set does not contain harmonic oscillations that might be responsible for the appearance of a peak in the circadian range (such as the false alarm of the chi square periodogram for the 12-h wave in Figure 16). This precaution may not be necessary when circadian rhythmicity is much stronger than ultradian and infradian components. If an ultradian peak is smaller than the circadian peak, one can safely interpret both peaks as being legitimate. Nonetheless, caution should always be exerted, and examination of the entire spectrum is recommended in the initial stages of data analysis. As pointed out in the Introduction, circadian oscillation is only one of many oscillatory processes in organisms.
Figure 16.
Artificial data sets of square waves with periods of 12, 24, and 48 h (left column) and their analyses by the chi square periodogram (QP) and the Lomb – Scargle periodogram (PN). The dashed lines in the periodograms indicate the 0.001 level of significance. The chi square periodogram identified a large 24 h component in the data set that contained only a 12-h square wave. Both methods correctly identified the 24-h component of the 24-h wave, although the Lomb – Scargle periodogram erroneously identified other smaller components (arrows). The chi square periodogram correctly failed to identify circadian rhythmicity in the 48-h wave, whereas the Lomb – Scargle periodogram identified a small 16-h component (arrow), which corresponds to the third harmonic of the 48-h component.
The issue of resolution in the determination of circadian period must be addressed in some detail. Looking back at Figure 12, one may have the impression that the Fourier periodogram has lower resolution in the circadian segment of the spectrum than do the Enright and Lomb – Scargle periodograms, as it contains only four data points in the range 20 – 28 h. This apparent lack of resolution was a major argument for the introduction of the Enright periodogram (Enright 1981). As exemplified in Figure 17(A, B), however, the region of uncertainty of the Enright periodogram is just as wide as that of the Fourier periodogram. The resolution of a periodogram is dependent on the length of the time series, not on the particular procedure used for analysis. Figure 17(C) shows that the resolution of a periodogram is not even dependent on the density of the data, although the power of the statistical test of significance is greater when the density of the data is greater.
Figure 17.
Periodograms describing sinusoidal time series with periods of 24 h. Fourier analysis (A) and chi square periodogram (B) were used to analyze segments of a time series generated with temporal resolution of 6 minutes. Notice that greater resolution of analysis is attained for longer segments of the time series. Lomb – Scargle periodogram (C) was used to analyze 10-day segments of times series generated with different temporal resolutions. Notice that statistical power (as indicated by the fraction of the curve above the significance line), but not resolution of analysis, is greater when the resolution of the data is greater. Notice also that the level of the line indicating statistical significance changes as a function of the number of degrees of freedom, which increases with the number of data available as the sampling interval gets shorter.
The argument about low resolution of Fourier analysis is in actuality an argument about visualization of the periodogram peaks. As exemplified in Figure 18(A), it is easier to visualize the resolution of two relatively close components of a time series in the Enright and Lomb –Scargle periodograms than in the Fourier periodogram. If desired, visualization of peaks in the Fourier periodogram can be enhanced by repeated analyses using shorter and longer segments of the data set. Another way to proceed is to multiply the data by a complex function to estimate the envelope in (sin x)/x related to the rectangular window corresponding to the observation span, a technique that is known as “harmonic interpolation” (De Prins et al. 1981) and is equivalent to the estimation of parameters (amplitude and phase) not only at integer but also at fractionated spectral lines (Cornélissen & De Prins 1973). Of course, visualization cannot be enhanced beyond the resolution of analysis. Figure 18(B) shows that all three methods of periodogram analysis fail to identify separate components of 23.5 h and 24.5 h in a 10-day long time series; instead, all three exhibit a single peak at 24.0 h.
Figure 18.

Periodograms describing time series containing two sinusoidal components: 21.0 and 25.0 h (A) or 23.5 and 24.5 h (B). In A, but not in B, the Enright (chi square) and Lomb – Scargle periodograms provide better visualization of the two components than does the Fourier periodogram.
The data set depicted in Figure 19 provides material for a more detailed discussion of the issue of resolution in the determination of circadian period. The data set was constructed by the addition of a 24.0-h sinusoidal signal, a 24.8-h sinusoidal signal with one-fifth the amplitude of the 24.0-h signal, and some noise. Casual inspection of the figure reveals the presence of only the 24.0-h component — and, indeed, only the 24.0-h component is identified by Fourier analysis, by the Lomb – Scargle periodogram, or by the Enright periodogram, as seen in Table II. Closer inspection, however, allows visual identification of a second component because of the reduction in amplitude in the apparently single 24.0-h component. In order to numerically identify the two distinct components, a recursive procedure with selective filtering of shorter and longer periodicities would be needed (Table II). Alternatively, a combined linear – nonlinear procedure based on the cosinor method has been proposed for the resolution of neighboring components in physiological data and has been shown to successfully resolve components of 24.0 h and 24.8 h (Halberg 1980; Rummel et al. 1974), as noted in Table II. The procedure of simulated annealing, originally developed for the solution of optimization problems in complex nonlinear systems (Cerny 1985; Kirkpatrick et al. 1983), can also resolve the two components (Czaplicki et al. 2006). Likewise, maximum entropy spectral analysis (MESA) has been shown to resolve 24.0-h and 24.8-h components in an artificial data set with 80% added random noise (Dowse & Ringo 1991), as it was with the extended linear-nonlinear cosinor (Halberg 1980; Rummel et al. 1974). The example in Figure 19 has value other than purely didactic, as the influence of both circadian and tidal components can be observed in the locomotor activity of fiddler crabs, 24.8 h corresponding roughly to twice the tidal period (Barnwell 1968).
Figure 19.
An artificial data set lasting 14 days with hourly observations. The data set, which contains a large 24.0-h component and a smaller 24.8-h component, was constructed according to Yi =100 + 10 cos (2πti/24−π) + 2 cos (2πti/ 24.8−π) + 5 R, where i =1, . . . , 336 (Δt =1 h) and R is uniformly distributed with zero mean and range =1 (±0.5).
Table II.
Comparison of methods applied to a noisy test series with two components with close periods (24.0 and 24.8 h).a
| Method | Components detected | Period (h) | p | |
|---|---|---|---|---|
| 1 | Fourier analysis | 1 | 23.93 | <0.001 |
| 2 | Lomb – Scargle periodogram | 1 | 24.00 | <0.001 |
| 3 | Enright periodogram | 1 | 24.00 | <0.001 |
| 4 | Linear cosinor | 1 | 24.00 | <0.001 |
| 5 | ARIMA.MLE in SPLUSb | 1 | 24.00 | <0.001 |
| 6 | Recursive Lomb – Scargle periodogramc | 2 | 24.0, 24.8 | <0.05 |
| 7 | Nonlinear cosinor | 2 | 23.97 (23.83, 24.10) | <0.05 |
| 24.63 (24.04, 25.21) | <0.05 | |||
| 8 | Simulated annealing | 2 | 23.96 (23.89, 24.03) | <0.05 |
| 24.6 (24.3, 24.9) | <0.05 |
The test series is shown in Figure 19.
Structure of residuals found to be correlated and modeled with an ARMA (1,1) model, with AR coefficient =0.78 (0.49, 0.89) and MA coefficient =0.54 (0.23, 0.75).
Analysis was first conducted on the raw data set and identified a major peak at 24.0 h. The data were then subjected to a 24.0-h moving-average filter and analyzed again. The second analysis identified a small peak at 24.8 h.
Resolution within the circadian range may not be a major issue when the time series contains only one circadian component. It can become an issue, however, when more than one component is present – because the components cannot be resolved if the resolution of the analytical procedure is inadequate. The simultaneous presence of two circadian components (that is, two oscillatory processes with different periods) has been described in various experimental situations, including that of humans subjected to an activity routine with period distinct from the endogenous period (Simpson et al. 1970), that of laboratory animals subjected to conflicting environmental synchronizers (Jilge & Stähle 1993), and that of animals with surgically-created “chimeric” brains (Vogelbaum & Menaker 1992). Depending on the length of the data set and on the difference in period between the components, resolution of the individual components in these cases may require one of the high-resolution methods mentioned above (recursive periodogram, linear-nonlinear cosinor, simulated annealing, or MESA). Whenever possible, entire time structures (chronomes) should be assessed.
MESOR and amplitude
The mean of a time series, as the mean of any set of data, is a measure of the “central tendency” of the data — that is, a measure of the point of balance of the distribution of values. Three traditional indices of central tendency are the mode, the median, and the mean. The three endpoints are based on different properties of the distribution and are numerically distinct unless the distribution is symmetrical. The mean — more specifically, the arithmetic mean [μ =(Σxi)/N] — is by far the most commonly used measure of central tendency in statistics, as well as in the analysis of circadian rhythms. When the data points are not equidistant in time (Δti ≠ k) and/or when they do not cover an integer number of cycles, however, the arithmetic mean differs from the average value that would be obtained in the balanced case and may, therefore, not be a good measure of central tendency. In this case, a rhythm-adjusted mean (such as the MESOR in the cosinor method) is usually more appropriate unless the data are insufficiently sampled, bringing about gross over-fitting. The MESOR is usually more accurate and more precise than the mean when the data points are unequidistant, as illustrated in Figure 20, unless there is excessive over-fitting.
Figure 20.

Advantages of the MESOR over the arithmetic mean in the estimation of central tendency of a time series. (A) the MESOR has smaller bias in the presence of unequidistant data. (B) the standard error (SE) of the MESOR reflects the variability of the data after the variability accounted for by the rhythmic pattern has been removed. It differs from the global SE reflecting the total variability of the data (most of which can be ascribed to the rhythmic time structure). From Cornélissen et al. (1999). © Halberg. Reproduced with permission.
Trigonometrically, amplitude is defined as “one-half the distance between the greatest and least values of a periodic function” (Morris 1992). Terminology used in relation to the cosinor method follows the trigonometric definition of amplitude of a rhythm in terms of the parameters of the fitted curve. The amplitude of a circadian rhythm has been defined by some scholars as half the range of excursion [A =(xmax−xmin)/2]. These investigators of circadian rhythms compute the amplitude simply as half the difference between maximum and minimum. When the maximum and minimum are computed as class means rather than as the two most extreme values in the data set, the spurious influence of unusual values (outliers) may be reduced, although the extent of reduction remains subjective, depending on the chosen class size. Naturally, empirical determinations of amplitude lack the uniformity of determinations based on fitted curves. The amplitude determined from a fitted curve is usually numerically smaller than the amplitude computed from the absolute difference between xmax and xmin. Regardless of how the amplitude is calculated, some investigators prefer to use the range of excursion (and sometimes even refer to it, erroneously, as the amplitude of the rhythm). The “double amplitude” of a fitted curve is more reliable than the range of excursion because it tells what the likely reproducible boundaries of the oscillation are (the double amplitude and magnitude represent the extent of predictable change within a cycle). The double amplitude of the fitted curve is of great utility in recognizing an elevated vascular disease risk (Cornélissen et al. 2000, 2004; Halberg et al. 2002).
Phase
Although the concept of phase, like amplitude, is well defined trigonometrically, some circadian physiologists have misused it in a variety of ways. A rather crude determination of the phase of a rhythm can be carried out by simply comparing the mean value of the variable during the light phase of the light – dark cycle with the mean value during the dark phase. In many species, this provides the basis for a dichotomous classification of diurnal (higher value during the light phase) or nocturnal (higher value during the dark phase). For precise data analysis, specialized methods are needed. Two methods have been traditionally used for computation of the phase of a rhythm. The traditional “macroscopic” method in laboratory studies with animals is a very simple method based on the actogram. As previously pointed out in connection with Figure 5, inspection of actograms provides an immediate subjective determination of the phase of the rhythm. Most often, the daily onsets of activity are used as phase markers (Daan & Pittendrigh 1976; Grosse et al. 1995; Nelson & Takahashi 1991), although the “offsets” can be used as well (Elliott & Tarmarkin 1994; Meijer & De Vries 1995; Vansteensel et al. 2003). The onset of activity is designated circadian time zero (or CT 0) in diurnal animals and circadian time twelve (CT 12) in nocturnal animals. After computers became standard research laboratory equipment, it became possible to use automated computational algorithms to determine the onset times (Herzog et al. 2004; Klemfuss & Clopton 1993; Scarbrough & Turek 1996). Different authors have used different algorithms, but the general principle involves the detection of the beginning of a more or less consolidated interval of activity following an interval of rest within each circadian or 24-h cycle.
An objective method that yields an endpoint amenable to comparison by parameter tests is the cosinor, based on the fitting of a cosine curve to the data by least squares regression (Bingham et al. 1982). The phase of the peak of the fitted curve is called the acrophase (φ) and serves as a convenient phase marker of the rhythm. The phases of the peak and trough of a composite model including harmonic terms are called the orthophase and bathyphase, respectively. In the single-component model described by Equation 5, θi and φ can be expressed in radians (or degrees) as well as in clock hours, although it is preferable to express phases in degrees or radians at first, since expressing angles in hours can be quite confusing for non-24-h components. When using clock hours, θi is entered as (2π ti)/P, where P is the pre-selected period of the rhythm (usually 24 h, unless the subject is free-running or synchronized to a non-24-h environmental cycle) and ti is the time of each observation (in clock hours). The computed acrophase (φ) can be converted back from radians to hours (φ′) by the operation φ′ =(−P/2π)φ. Cosine fits by iteration produce similar but most likely not identical values of φ as the cosinor method.
Figure 21 exemplifies the use of a moving cosinor in the analysis of phase-shifting of circadian rhythms in oral temperature following transmeridian flights in two directions. The shaded 95% confidence intervals serve to remove some of the subjectivity in looking for details of adjustment. Thus, after a first flight from east to west, involving a social/ environmental synchronizer delay, the adjustment is faster than that following a flight from west to east involving synchronizer advance. Note that the addition of 95% confidence limits allows an objective definition of the start of shift in each direction. Thus, the 95% confidence interval overlaps the target phase within one day after a flight from west to east, whereas it takes six days after the return flight for the 95% confidence interval to overlap the original phase, as shown in black in the horizontal bars. By the same token, as shown in gray, the completion of the shift also differs depending on the direction of the flight. The provision of uncertainties during a shift also allows detection of the direction of shift by an estimation of confidence limits that for quite a while, in the case of a phase advance, overlap neither the target nor the original phase. The opportunity of removing some subjectivity from assessing adjustment has broad implications in shift-work as well as after any adjustment following changes in schedule, transmeridian, transequatorial or other.
Figure 21.
Analysis by a moving cosinor of phase-shifting of circadian rhythms in oral temperature of five healthy adult white males following transmeridian flights in two directions. Adapted from Halberg (1969).
Whether the onsets of activity or the peaks of a fitted function are used as phase markers, the occurrence of day-to-day variability in the waveform of circadian rhythms ordinarily requires that estimates of phase not be made on the basis of individual data points. Estimates of phase can be attained by linear regression of daily onsets over several days or, more accurately, by the acrophase (or orthophase) of fitted curves. A valuable feature of the cosinor procedure is that it yields at once all rhythm parameters — MESOR, amplitude(s), and acrophase(s) — along with confidence intervals, routinely obtained independently of the number of components included in the model. When a composite model with k cosine curves is fitted to the data, all 2 (k + 1) parameters are estimated concomitantly, each with a 95% confidence interval.
The acrophase and amplitude of the single-component cosinor model are often reported in a polar representation of the results, which allows the simultaneous presentation of phase and amplitude, as illustrated in Figure 22. The triangles around the perimeter indicate time in degrees of arc (360° =2π), whereas the outermost ring indicates time in clock hours or in other pertinent units of time, depending on the circadian period and the problem at hand. The next ring indicates the partition of the light – dark (or wake – sleep) cycle, and a third ring is provided for the depiction of an additional synchronizing agent, if needed. The acrophase (φ) is indicated by the angle of a vector whose length corresponds to the amplitude (A). The ellipse denotes the 95% confidence region for the joint estimation of φ and A. The advantage of polar displays is that the extent of rhythm detection is readily conveyed, as is the timing of overall values in relation to one or several environmental synchronizers. When polar displays are used to report results from more than one subject or more than one variable, they also readily convey the relative prominence and any phase difference or extent of agreement among the results.
Figure 22.
Polar representation of the amplitude and acrophase of a rhythm, as computed by the cosinor method. The acrophase (φ) is indicated by the angle of a vector whose length corresponds to the amplitude (A). The ellipse denotes the 95% confidence region for the joint estimation of A and φ. Conservative estimates of 95% confidence intervals for A and φ alone can be obtained by drawing concentric circles tangent to the error ellipse for A, determining their intersection with the vector’s length (A), or by drawing tangents to the ellipse for φ.
When phase is expressed in hours, special denominations are often used to emphasize the relationship with the prevailing environmental synchronizer. In laboratory studies involving light – dark cycles as synchronizers, the expression “hours after light onset” (HALO) is often used. Equivalent, but also applicable to nonphotic synchronizers, is “zeitgeber time” (ZT). By definition, ZT 0 and 0 HALO correspond to the time of lights on, so that, for instance, ZT 15.5 or 15.5 HALO refer to the time point temporally located 15.5 h after the lights are turned on. Although the expression zeitgeber (from the German Zeit [time] and geber [giver]) is equivalent to “synchronizer”, some authors prefer the HALO designation to prevent a potential misinterpretation of “time giver” as “time generator” (that is, synchronizers are clock-time or calendar-time givers but not physiological-time givers).
The HALO and ZT denominations are particularly helpful when the period of the light –dark cycle is different from 24 h. Under these conditions, the HALO and ZT denominations allow for easy correction of the duration of each hour. Thus, under a 28-h light – dark cycle, ZT 15.5 or 15.5 HALO still refer to 15.5 synchronizer hours after light onset, even though this point in time corresponds to 18.1 clock hours after light onset. When 24-h light – dark cycles are used, the HALO and ZT denominations are very useful if the light – dark cycle is not synchronized with local time or if local time is not relevant to the study. In field studies, the use of local time is quite appropriate (e.g. “tests were conducted at 1530 hours [3:30 pm]”), although it is essential to give the calendar date of each study so that any environmental disturbance, such as an extreme magnetic storm or quiet, can be looked up from routinely recorded physical databases, preferably from the nearest geomagnetic station since there can be geographic differences in environmental effects (Halberg et al. 2006).
Waveform
An important characteristic of circadian rhythms is the waveform. Waves A and B in Figure 15 have the same mesor, same magnitude, same phase (on average), and same period. Yet, they are clearly different from each other. Their waveforms are different: A is sinusoidal and B is square. Scholars of circadian clocks have given very little attention to the issue of characterizing the waveform of rhythms. In principle, one could obtain a quantitative description of waveforms of circadian rhythms by comparing the various rhythmic components revealed by spectral analysis, in such a way that the spectral profiles would serve as tools for “rhythm finger-printing”. This has rarely been attempted in the field of time-macroscopic clocks, even if waveform is routinely taken into consideration in extended cosinor analysis in inferential statistical chronobiology. One issue that has received some attention is how the complexity of waveforms affects the computation of phase.
Within the framework of the single cosinor method, the waveform is defined by the harmonic content, that is, by the amplitude – acrophase pairs of all harmonic terms included in the model to account for the non-sinusoidality of the signal. In the cosinor method as well as in other methods, each added harmonic improves the fit (Albert & Hunsberger 2005; Almirall 1997; Alonso & Fernández 2001; Bingham et al. 1982; Cornélissen & Halberg 2005; Ruf 1996), and the decision about which harmonic term to include in the model can be based on the zero-amplitude test applied to each term as well as to the overall test of significance for the model as a whole. In the cosinor method, the use of multiple harmonics illustrates how the addition of each harmonic term modifies the estimation of the phase of maximum (acrophase and orthophase) as well as the estimation of the extent of predictable change within a cycle (double amplitude and magnitude) (Tong et al. 1977).
Composite models are necessary to provide a better description of a non-sinusoidal signal. This does not mean, however, that the multiple components identified by the model correspond to separate physiological processes. Some researchers have argued that the addition of harmonics is often arbitrary (Wang et al. 2003), which it must not be if the addition is made systematically stepwise, with the use of a harmonic term retained only when it reduces the residual variance with statistical significance. Even when the harmonic terms lack physiological meaning (Refinetti 2006a), they may serve to mathematically define a waveform, such as that of a circadian rhythm and its alteration in disease (Otsuka et al. 1997). The zero-amplitude test can be used to determine objectively whether a given harmonic term should be included in the model, that is, whether it contributes with statistical significance to the characterization of the waveform. The use of terms such as “circasemidian” to specifically refer to the 12-h component should not be viewed as meaning that it is necessarily an independent physiological entity not tied to the circadian waveform. It merely helps quantify changes in waveform such as those seen as a function of age in the case of blood pressure, for instance, where the relative prominence of the 12-h over the 24-h component of the circadian signal is seen in the elderly (Cornélissen et al. 1992), likely a feature of the aging process itself. A change in relative prominence between the 24-h and 12-h component of the circadian variation in the correlation dimension of (electrocardiographic) R – R intervals has also been observed as a feature of pathology, the 12-h component being more pronounced in patients with coronary artery disease than in clinically healthy subjects (Otsuka et al. 1997). Additional terms have been coined, such as “circaseptan”, “circasemiseptan”, “circatrigin-tan”, “circasemiannual”, and many others, for physiologically important components that all can be assessed in longitudinal series (Halberg 1969, 1995; Halberg et al. 2001; Hildebrandt & Bandt-Reges 1992; Hildebrandt et al. 1998). The chronome, as a time structure consisting of trends, rhythms and chaos, is best always considered as a whole, even when the data are limited to 24 h in the case of a circadian rhythm but are dense enough to assess endpoints of chaos such as the correlation dimension (Otsuka et al. 1997). In a clinical situation, an approach to a broad time structure (chronome), assessed first by focus on chaos by computation of the correlation dimension, can reveal that a primarily 24-hour circadian variation in clinical health assumes an altered circadian waveform characterized in addition by a statistically significant 12-h harmonic in patients with coronary artery disease (Otsuka et al. 1997).
Normally, even when a composite model is used to assess a non-sinusoidal waveform, the phase of the fundamental component remains a good operational phase marker. Thus, if the waveform is non-sinusoidal but only a single component is used, the acrophase of the single component can provide an operational phase marker.
Prominence
A sixth feature that characterizes circadian rhythms is their prominence. Prominence refers to what is known in common English as robustness: a prominent or robust process is a process that is strong and enduring (Kellerman 1986). The term robustness was occasionally used by circadian researchers in the past to denote the strength of a rhythm (Cheng et al. 2001; Gonze et al. 2002; Refinetti et al. 1994; Weinert et al. 2001). In traditional statistical usage, however, a robust procedure is a procedure that is relatively insensitive to violations of the assumptions on which it is based (Morris 1992). Thus, we prefer the term prominence to refer to the strength and endurance of a rhythm, as a measure of the signal-to-noise ratio, as discussed above.
Because circadian rhythms are not strictly stationary (Refinetti 2004b), and because the use of most methods of time series analysis implies the assumption that the oscillatory process under study is stationary, one might argue that no time series analysis of circadian rhythms is reliable. From the viewpoint of mathematics, the argument would probably be correct. From a physiological perspective, the inaccuracy of the procedures may not be greater than that resulting from usual “biological noise”. An alternative procedure for handling the non-stationarity of circadian rhythms is the wavelet transform, which was developed specifically to handle non-stationary time series (e.g. Percival & Walden 2000). Wavelet methods have been applied to the study of circadian rhythms (Wulff et al. 2003). Their usefulness in this area awaits comparisons with other methods.
In order to quantify rhythm prominence, Halberg introduced the concept of “percent rhythm” — the percentage of the variance accounted for by the fitted cosine model, which corresponds to the coefficient of determination R2 in regression analysis (Halberg et al. 1973). Currently, gliding spectra of the percentage rhythm serve to examine the time course of the relative prominence of various components in a spectral window (Halberg et al. 2006). Other authors have used the QP statistic of the chi square periodogram to quantify rhythm prominence (Eastman & Rechtschaffen 1983; Refinetti et al. 1994; Weinert et al. 2001). As an index of prominence, the QP value is sensitive to noise in the data set. It can be improved by the filtering out of noise prior to analysis (Refinetti 2004b). Of course, one could always question whether biological noise is true noise (i.e. stochastic variation) or rather a component of deterministic chaos (Casdagli 1991; Stark & Hardy 2003; Gonze et al. 2004). A resolution of this issue is desirable since it has proved already to be of clinical (Otsuka et al. 1997) and physiological (Burioka et al. 2001) interest and will become more readily feasible once dense data become routinely available.
The issue of noise-filtering requires further elaboration. High frequency oscillations (such as the spikes in the activity records in Figures 8 and 12) can be removed, if necessary, by the simple method of moving averages (Refinetti 1992b). More elaborate methods of noise-filtering (smoothing) may be used when needed (e.g. Haerdle & Schimek 1996). In procedures such as the cosinor, high frequency oscillations are generally inconsequential because they are eliminated by the curve-fitting procedure itself. Of course, elimination of high frequency oscillations is acceptable only if the investigator deems them to be unimportant. Programs have been specifically developed to deal with spikes corresponding, for instance, to the episodic bursts of hormonal secretion (Veldhuis & Johnson 1994). Whereas similar results in the ultradian domain have been obtained with these programs and with a cosinor-based approach in the case of children’s nocturnal melatonin (Salti et al. 2000), it would be interesting to further compare the relative merits of the two approaches.
Sometimes, malfunction of the recording equipment may generate spurious data points. If the spurious data points are few, and the errors are of small magnitude, their influence will usually be negligible in most approaches considered here. One option, not always advisable, is to filter them out by the moving average procedure. If the errors are large (say, a body temperature reading of 100°C when all other readings are in the 35 to 39°C range), the single spurious value may skew all rhythm parameters. In this case, it may be necessary to reject the spurious value. When the number of data points is large, leaving the rejected point as a missing value will introduce the least amount of bias. For methods requiring equidistant data, the spurious value may be replaced by linear or other (e.g. spline) interpolation. This approach is often acceptable provided that there are only isolated outliers and there is enough evidence that the outlying values are indeed invalid data. If the data set contains too many spurious points, the best approach is to discard the whole data set and redo the experiment. This cannot be done invariably in a clinical setting where an urgent decision for therapy may be needed. It may be more efficient to use more than a single method, with all the indispensable precautions that apply to all methods. Data conditioning may be employed (Levine et al. 2002). Caution should always be taken to verify that outlying and/or missing values are not valid data and that they are randomly distributed. If this is not the case and there is an underlying pattern associated with outliers and/or missing values, interpolation may actually “create” periodicities. The huge and multifaceted problem of outlier detection and handling has its own literature. In the case of temperature telemetry, it was examined by one of us (Cornélissen 1984).
Figure 15(D – F) showed theoretical examples of non-stationary rhythms. Under stable conditions, cycle-to-cycle variation in circadian period (D) is usually not a problem along the timescale of days. For instance, studies of intra-individual variability of the free-running period of activity in laboratory animals have generally found the variability to be of the order of only 0.1 h (DeCoursey 1960; Eskin 1971; Pohl 1983; Sharma 1996). In a study that examined also differences among individuals, inter-individual variability of parameters of circadian rhythms was found to be generally larger than intra-individual variability (Refinetti & Piccione 2005), which suggests that data from different individuals should be analyzed separately as well as part of a group, notably if the research requires characterization of the given subject’s rhythm parameters. Inter-individual variability can sometimes be so great that some researchers will consider excluding “abnormal” experimental subjects from a study. Exclusion of “rogues” has been justified by some scholars in cases where interest is focused on the properties of a specific mechanism (which are believed to be expressed more clearly in the retained subjects) than on the diversity of physiological responses. In laboratory research, some experimenters choose a “model system” in order to investigate a complex process in a simpler, more manageable entity (e.g. Dunlap & Loros 2005; Williams & Sehgal 2001). This approach is, however, quite different from that characterizing ecological research or clinical practice. In particular, a rogue may provide a clue that contributes more than the retained majority to the understanding of the complexity of chronomes. From this perspective, selection bias has no place in the pursuit of science.
At the cellular level, cycle-to-cycle variation in period may be substantial (Herzog et al. 2004) and may be further complicated by differences in technique used on the same materials, as can be seen for expression patterns of the per1 gene in two papers on the same animals (Ptitsyn et al. 2006; Zvonic et al. 2006; see also Ando et al. 2005). The fractionated (increment equal interval) and/or pergressive (increment smaller than interval) chronobiological serial section (Halberg et al. 1965) and/or gliding spectra (Nintcheu-Fata et al. 2003) could provide local estimates and an estimate of changes in rhythm characteristics as a function of time and/or techniques.
Irrespective of large changes in waveform (Figure 15E), small day-to-day variability is almost always present (see Figures 4, 8, and 12). This variability in waveform has important consequences for the computation of phase. In view of the often large variability in the raw data, the phase is best estimated on the basis of processed data, such as the fitted model in the single cosinor. Small changes in waveform may lead to relatively large changes in phase when the signal assumes similar values during a large fraction of the circadian cycle. In such cases, day to day (or session to session) changes in waveform may not be meaningful. A phase marker independent of the waveform (such as the acrophase of the fundamental component computed by the cosinor method) is preferable. But if the changes in waveform are substantial and may be related to some intervention such as the institution of treatment, reliance on the orthophase may convey important information. In the case of the single cosinor, tests of lack of fit help determine the need to include additional terms in the model, and parameter tests are available to test the equality of acrophases between two (or more) data series (Bingham et al. 1982), thereby helping the differentiation between random effects, a real shift in timing only, or changes in more than one parameter.
Trends (Figure 15F), uncommon in some circadian rhythms recorded under controlled conditions in the laboratory (Refinetti 2004b), should be expected when measurements are conducted over long intervals of months or years, as the parameters of circadian rhythms will most likely be affected by partly endogenous reproductive, seasonal, and other cycles or by exogenous variations in photoperiod, food availability, etc. Biological trends observed in naturalistic settings include a gradual elevation of blood pressure and heart rate in human neonates (Cornélissen et al. 1992) and a weekly and monthly elevation in testosterone secretion of men that results in part from the modulation of male sexual activity by the menstrual cycle of their female partners (Halberg et al. 1965; Hirschenhauser et al. 2002). Particularly in the study of economic and meteorological time series, trends have long been recognized as a violation of the assumption of stationarity. The autoregressive integrated moving average procedure (ARIMA) is a popular procedure used to decompose a time series into various components and to isolate the non-stationary component associated with trends (Box & Jenkins 1970; Granger & Newbold 1986). Often, the time series is decomposed into three components: a trend component, a seasonal component, and a residual component. In the study of circadian rhythms, a circadian component can be used instead of the seasonal component (e.g. Firinguetti et al. 1990).
Trends are observed in laboratory studies conducted at the cellular and molecular level, often because of suboptimal conditions of tissue preservation. An example is shown in Figure 23. The activity of neurons in the suprachiasmatic nucleus of mice was recorded in vitro by optical imaging of bioluminescence. The mouse brain is not naturally bioluminescent; modern techniques of genetic engineering, however, allowed the construction of transgenic animals in which a luciferase gene (responsible for bioluminescence in fireflies) was linked to the promoter region of a circadian clock gene (per2) in the mouse. Notice that the rhythm of luminescence gradually showed a reduction in amplitude and mesor (A). Linear changes in mesor can be easily filtered out by the gradual addition of an offset value computed by linear regression. Correction for changes in amplitude requires additional steps, such as normalization of the values on a cycle-by-cycle basis. The results of this double filter preserve the phase angle of the original data (B), although the procedure necessarily restricts focus to the 24-h component and prevents the assessment of any additional superimposed or modulating components. The procedure also prevents analysis of mesor and amplitude. An alternative procedure is to perform analyses of short segments of the time series and repeat them in an interval that is gradually displaced throughout the series (Arbogast et al. 1983; Halberg et al. 1965).
Figure 23.
Two-week segments of the records of bioluminescence of cells in the suprachiasmatic nucleus of a mouse culture in vitro. Because of suboptimal culturing conditions, the rhythm of bioluminescence showed a reduction in amplitude and mesor during the recording interval. (A) original data; (B) filtered data. Data from Yoo et al. (2004).
Multiple comparisons
Once the parameters of a rhythm have been computed, the investigator may wish to compare parameters in one subject with parameters in another subject, or perhaps parameters in one subject with parameters in the same subject measured on different days and/or in different variables. These comparisons can be conducted by standard procedures of inferential statistics. If an investigator wishes to compare the mesors, amplitudes and phases (singly or jointly), periods, waveforms, or prominence of two or more groups of observations, he or she can use standard statistical tests such as Student’s t tests and ANOVA or their non-parametric equivalents (Hays 1994; Wackerly et al. 2002). Of course, comparisons of phase are complicated by the fact that phase is a circular variable (that is, for instance, 01:00 is 22 h earlier than 23:00 but it is also only 2 h later than 23:00). If one assesses rhythm characteristics separately or jointly, special parameter tests have been developed for these purposes on endpoints of the cosinor method (Bingham et al. 1982) and for phases (Batschelet 1981; Mardia, 1972).
Depending on the number of comparisons to be performed, attention must be paid to the level of significance (α) that is chosen. The computation of probabilities in statistical tests is conducted under the assumption that only one test will be performed. If multiple tests are performed, there will be an unintended inflation of α (Hays 1994; Kirk 1995). A simple solution is to apply a Bonferroni correction to the level of significance. If we wish to keep the “familywise” probability of a Type I error at a level λ as we perform n tests, and if the comparisons are statistically independent, then we must set α at a lower level, so that: λ =1−(1−α)n. If the comparisons are not independent, then α should be set at λ/n. The overall comparison of means in the ANOVA constitutes a single test that can be performed at the desired α, but separate comparisons of pairs of means by Student’s t tests (or multiple ANOVAs on the same data) must consider the familywise probability. Many specialized tests have been developed to help control the inflation of α without the loss of power that accompanies Bonferroni corrections (Hays 1994; Kirk 1995).
Let us examine the issue of inflation of the level of statistical significance in the detection of rhythmicity by periodograms. A periodogram typically evaluates 20 or more periods at the same time (say, from 23.0 h to 25.0 h in steps of 0.1 h). Assuming that the test of each period is independent from the others, the Bonferroni correction described above would require an α of 0.002 in order to maintain λ below 0.05. One consideration is whether the tests are truly independent. Using a step of 0.1 h around a period of 24 h corresponds roughly to independent tests when the series covers 240 days or more. For shorter time series, the tests are not independent. Another consideration is that the computation of probability assumes that the time series contains only one major rhythmic component. If one is seeking only one peak in the periodogram (which is usually the case when one is attempting to determine the presence of circadian rhythmicity), correction for multiple testing may be considered unnecessary. If, however, one is seeking any rhythmicity in a long time series, one must make corrections for multiple testing. After all, when one sets α at 0.05, one is expecting that one out of 20 tests will turn out positive even if the data are randomly distributed.
Nowhere in the study of circadian rhythms is the issue of multiple comparisons more pressing than in molecular research involving the DNA (or protein) microarray methodology. The great asset of microarrays — namely, their ability to track thousands of genes (or proteins) simultaneously — is also a major statistical liability. When one wishes to test for the presence of daily rhythmicity in 10,000 genes or more in a single study, it is virtually impossible to set a reasonable level of significance for the test of each gene. If one used the Bonferroni correction, one would need to set α at about 0.000005 in order to keep λ at 0.05, which is impractical.
Figure 24 shows a sub-sample of 1,104 genes (out of a total of 14,010 genes) from a microarray study conducted on fruit flies (Drosophila melanogaster). Samples of RNA were collected at 4 h intervals from flies maintained on a light – dark cycle. Different levels of gene expression (normalized for each gene) are denoted by different shades of gray. Notice that many genes exhibited variation in expression along the day. The question is, of course, how many of the variations were statistically significant. Using their methods of data analysis, the authors found that 447 of the 14,010 genes exhibited circadian rhythmicity (Lin et al. 2002). When they calculated how many genes could show rhythmic expression by chance alone, they found the figure to be 298. Thus, the detection of rhythmicity would likely have been an artifact in more than half (66%) of the genes initially believed to exhibit rhythmicity. Evidently, something had to be done about it. The authors of the cited study chose a more stringent criterion and ended up with 22 “legitimately” rhythmic genes. They themselves acknowledged, however, that their final count was most likely an underestimate of the real number of rhythmic genes (Lin et al. 2002). By increasing the stringency of the test (that is, by lowering α), one causes a reduction in statistical power. The solution, if there is one, is to develop a global test to precede individual comparisons, just like an ANOVA precedes the test of differences between particular groups of means. The design of “planned orthogonal contrasts” should help maintain statistical power without requiring a large reduction in the level of significance (Kirk 1995; Maxwell & Delaney 2004).
Figure 24.
Graphic display of temporal pattern of gene expression of a sub-sample of 1,104 genes (out of a total of 14,010 genes) from a DNA microarray study conducted on fruit flies. Samples of RNA were collected at 4 h intervals from flies maintained under a light – dark cycle. Different levels of gene expression (normalized for each gene) are denoted by different shades of grey. Many genes exhibit variation in expression along the day. Data from Lin et al. (2002).
A novel approach to multiple comparisons was introduced a few years ago by Benjamini and Hochberg (1995). The so-called False Discovery Rate (FDR) approach consists essentially of taking into consideration only those comparisons that correctly reject the null hypothesis (and, thus, reducing the number of comparisons that require Bonferroni correction by ignoring all the comparisons that fail to reject the null hypothesis). Of course, one never knows which null hypotheses are actually true, but Benjamini and Hochberg (1995) demonstrated that the false discovery rate can be controlled and that the following procedure provides the necessary control:
Perform m comparisons and obtain the corresponding p-values;
Rank the p-values from smallest to largest (p1, p2, . . . pm);
Let k be the rank of the largest p-value for which pi ≤ (i/m) α;
All pi from i =1 to k can be considered significant.
As an example, suppose that 10 comparisons were conducted (m =10) and that the p-values were: 0.0002, 0.0008, 0.0058, 0.0097, 0.0350, 0.0671, 0.095, 0.1232, 0.4576, and 0.8659. If we adopt α =0.05, and make no corrections for multiple testing, then five of the 10 comparisons are significant. With Bonferroni correction, λ =(n α) =0.5, which means that α must be 0.005 to maintain λ at 0.05 and, consequently, only two of the comparisons are significant. Using the FDR approach, we find that 0.0097 <(4 / 10) 0.05 =0.02, so that four of the comparisons can be considered significant.
The FDR can be very useful for multiple comparisons in a variety of studies of circadian rhythms. Its application specifically to the analysis of microarray data has been suggested by statisticians (Reiner et al. 2003; Storey & Tibshirani 2003; Taylor et al. 2005), and at least one circadian microarray study has utilized it (Ptitsyn et al. 2006). Interestingly, the authors of this study did not find the FDR to be particularly useful. As a matter of fact, their results suggested that the majority of genes are rhythmic and that statistical tests should focus on identifying the relatively few genes that are not rhythmic (Ptitsyn et al. 2006). The last word on analytical procedures for microarray data has yet to be spoken.
Conclusion
This review discussed various procedures that are used to detect circadian rhythmicity, to characterize the parameters if rhythmicity is present, and to conduct comparisons among the parameters of different data sets. Many procedures are available for the detection of circadian rhythmicity. While the use of multiple procedures for the analysis of any time series is encouraged, Figure 25 provides a guide for those who have certain software packages available, but not others, with a view of the characteristics of the time series appropriate for the application of the various procedures. All methods for obtaining estimates of uncertainties of each parameter, including the period, are superior to those that do not provide, as a minimum, the four uncertainties for period, amplitude, phase, and MESOR, and preferably also those of the waveform, as assessed by the (A,φ) pairs of harmonics. Accordingly, the reader is referred to the flowchart in Figure 2 and also to Table II.
Figure 25.
Diagram to guide the selection of procedures for the detection of circadian rhythmicity.
The Enright periodogram is applicable to long time series with equally-spaced data points, as long as multiple close components need not be resolved, and may be tried, preferably after the extended cosinor as an extended plexogram (see flowchart in Figure 2). The Lomb –Scargle periodogram is applicable to unequally-spaced data points but also requires data to be collected over several cycles and, like the Enright periodogram, among others, fails to resolve two close components. The Rayleigh test is useful for a test of directionality when information on phase only is available. Equating the amplitude to 1 in the population-mean cosinor yields the same result. The single cosinor method, originally developed for application on short and sparse data series, handles non-equidistant data as well. Extension to the population-mean cosinor allows generalization to the population. Extension to linear – nonlinear rhythmometry provides an estimate of the period with a measure of uncertainty. Extension to the chronobiological serial section and to gliding spectra allows the assessment of non-stationary time series. It should be noted that reliability of the computation of the period of a rhythmic process increases when data are collected over several cycles. The estimate of the period also becomes less dependent on the particular waveform the more cycles are covered by the record.
The cosinor procedure is a reliable and convenient tool for the computation of the MESOR, amplitude, and phase angle (acrophase) of circadian rhythms. These endpoints can easily be objectively estimated by curve fitting even in situations where emphasis has been placed solely on the phase (such as in laboratory studies involving running-wheel activity, where the daily onsets of activity have been used as convenient phase markers of the rhythm). Whereas day-to-day variations in waveform may be filtered out through techniques of data conditioning, they are best assessed by curve-fitting procedures such as the cosinor method. Serial sections of the fundamental and harmonic components not only detect but also quantify small or large changes in waveform as a function of time, as well as any trends, including any change in period length. Circadian rhythms are not technically stationary, but the variability associated with non-stationarity is generally lower than that associated with usual biological noise.
Special care must be taken to prevent an inflation of the significance level when numerous comparisons are performed serially. For a relatively small number of multiple comparisons, the FDR approach provides a suitable alternative to simple Bonferroni corrections. The comparison of multiple rhythmic parameters obtained by time series analysis can be conducted by traditional procedures of inferential statistics, but special parameter tests are preferred since they allow the comparison of parameters considered either separately or jointly.
All methods here reviewed are applicable to many time series and all of them represent a step beyond the invaluable, yet insufficient visual inspection of a time plot. From study design to parameter estimation, the assessment of circadian rhythmicity provides the necessary control to avoid blunders stemming from the comparison of two (or more) groups characterized by rhythms that may differ not only in terms of the mesor but also in terms of the amplitude, acrophase and/or even period. This is illustrated in the abstract Figure 26 and the actual data-based Figure 27 that led one of us to the formulation of the concepts of both circadian rhythms and chronobiology (Halberg 1969).
Figure 26.
Blunders from time-unspecified comparisons of groups characterized by a difference in amplitude, acrophase or period but not in MESOR are best avoided by including the assessment of rhythms in the design of studies and by assessing all rhythm characteristics. Measurements conducted at arbitrary time points in ignorance of rhythmicity can lead to opposite conclusions about the characteristics of processes A and B.
Figure 27.
Confusing results, that could wrongly be interpreted as “stress” or “allergy”, are accounted for by the action of food (offered mornings) and light as competing synchronizers of circadian rhythms in counts of circulating eosinophils in C3H mice with high breast cancer incidence that can be drastically reduced by calorie restriction. Apart from constituting the beginning of Minnesotan chronobiology, and beyond the demonstration that time-unspecified spotchecks must not underlie frequently made inferences of “up-” and “down-regulation”, these studies convey the need to rely on circadian rhythms (and even broader time structures, chronomes) as the indispensable control information for any rhythmic variable, and hence the need to complement the mapping of genomes with the mapping of chronomes. From Halberg et al. (2003b). © Halberg. Reproduced with permission.
Acknowledgments
Work for this review was partially funded by grants from the National Institute of Mental Health (MH-066826) and the National Science Foundation (IBN-0343917) to RR and by a grant from the National Institute of General Medical Sciences (GM-013981) to FH. The authors thank Professors Jim Waterhouse and Wop Rietveld for comments on a previous version of the article.
References
- Akiyama T. Entrainment of the circatidal swimming activity rhythm in the cumacean Dimorphostylis asiatica (Crustacea) to 12.5-hour hydrostatic pressure cycles. Zool Sci. 2004;21:29–38. doi: 10.2108/0289-0003(2004)21[29:EOTCSA]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- Albers HE, Gerall AA, Axelson JF. Effect of reproductive state on circadian periodicity in the rat. Physiol Behav. 1981;26:21–25. doi: 10.1016/0031-9384(81)90073-1. [DOI] [PubMed] [Google Scholar]
- Albert PS. On analyzing circadian rhythms data using nonlinear mixed models with harmonic terms. Biometrics. 2005;61:1115–1120. doi: 10.1111/j.0006-341X.2005.464_1.x. [DOI] [PubMed] [Google Scholar]
- Almirall H. Modeling the body temperature throughout the day with a two-term function. Behav Res Methods Instrum Comput. 1997;29:595–599. [Google Scholar]
- Alonso I, Fernández JR. Nonlinear estimation and statistical testing of periods in nonsinusoidal longitudinal time series with unequidistant observations. Chronobiol Int. 2001;18:285–308. doi: 10.1081/cbi-100103192. [DOI] [PubMed] [Google Scholar]
- Ando H, Yanagihara H, Hayashi Y, Obi Y, Tsuruoka S, Takamura T, Kaneko S, Fujimura A. Rhythmic messenger ribonucleic acid expression of clock genes and adipocytokines in mouse visceral adipose tissue. Endocrinology. 2005;146:5631–5636. doi: 10.1210/en.2005-0771. [DOI] [PubMed] [Google Scholar]
- Arbogast B, Lubanovic W, Halberg F, Cornélissen G, Bingham C. Chronobiologic serial sections of several orders. Chronobiologia. 1983;10:59–68. [PubMed] [Google Scholar]
- Aschoff J. Circadian rhythms: influences of internal and external factors on the period measured in constant conditions. Z Tierpsychol. 1979;49:225–249. doi: 10.1111/j.1439-0310.1979.tb00290.x. [DOI] [PubMed] [Google Scholar]
- Barnwell FH. The role of rhythmic systems in the adaptation of fiddler crabs to the interdidal zone. Am Zool. 1968;8:569–583. [Google Scholar]
- Batschelet E. Circular Statistics in Biology. New York: Academic Press; 1981. [Google Scholar]
- Beau J, Vibert JF. L’analyse spectrale mais c’est tres simple! Rythmes. 2006;37:15–23. [Google Scholar]
- Benedict FG. Studies in body temperature. I. Influence of the inversion of the daily routine; the temperature of night-workers. Am J Physiol. 1904;11:145–169. [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc B. 1995;57:289–300. [Google Scholar]
- Bertolucci C, Foà A, Van’t Hof TJ. Seasonal variations in circadian rhythms of plasma melatonin in ruin lizards. Horm Behav. 2002;41:414–419. doi: 10.1006/hbeh.2002.1781. [DOI] [PubMed] [Google Scholar]
- Bingham C, Arbogast B, Guillaume GC, Lee JK, Halberg F. Inferential statistical methods for estimating and comparing cosinor parameters. Chronobiologia. 1982;9:397–439. [PubMed] [Google Scholar]
- Bingham C, Cornélissen G, Chen CH, Halberg F. Chronobiology works when day-night ratios fail in assessing cardiovascular disease risk from blood pressure profiles. III International Conference on Civilization Diseases in the Spirit of V.I. Vernadsky (People’s Friendship University of Russia; Moscow. Oct. 10–12, 2005; 2005. pp. 111–113. [Google Scholar]
- Bingham C, Cornélissen G, Halberg E, Halberg F. Testing period for single cosinor: extent of human 24-h cardiovascular “synchronization” on ordinary routine. Chronobiologia. 1984;11:263–274. [PubMed] [Google Scholar]
- Bingham C, Cornélissen G, Halberg F. Power of “Phase 0” chronobiologic trials at different signal-to-noise ratios and sample sizes. Chronobiologia. 1993;20:179–190. [PubMed] [Google Scholar]
- Bloomfield P. Fourier Analysis of Time Series: An Introduction. 2. New York: Wiley; 2000. [Google Scholar]
- Boivin DB, James FO. Circadian adaptation to night-shift work by judicious light and darkness exposure. J Biol Rhythms. 2002;17:556–567. doi: 10.1177/0748730402238238. [DOI] [PubMed] [Google Scholar]
- Box GEP, Jenkins GM. Time-Series Analysis, Forecasting and Control. San Francisco: Holden-Day; 1970. [Google Scholar]
- Brazier KTS. Confidence intervals from the Rayleigh test. Mon Not R Astron Soc. 1994;268:709–712. [Google Scholar]
- Bretthorst GL. Generalizing the Lomb-Scargle periodogram: the nonsinusoidal case. Am Inst Phys Conf Proc. 2001;568:246–251. [Google Scholar]
- Brockwell PJ, Davis RA. Introduction to Time Series and Forecasting. 2. New York: Springer; 2002. [Google Scholar]
- Burioka N, Cornélissen G, Halberg F, Kaplan DT. Relationship between correlation dimension and indices of linear analysis in both respiratory movement and electroencephalogram. Clin Neurophysiol. 2001;112:1147–1153. doi: 10.1016/s1388-2457(01)00566-1. [DOI] [PubMed] [Google Scholar]
- Casdagli M. Chaos and deterministic versus stochastic non-linear modelling. J R Stat Soc B. 1991;54:303–328. [Google Scholar]
- Ceriani MF, Hogenesch JB, Yanovsky M, Panda S, Straume M, Kay SA. Genome-wide expression analysis in Drosophila reveals genes controlling circadian behavior. J Neurosci. 2002;22:9305–9319. doi: 10.1523/JNEUROSCI.22-21-09305.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cerny V. A thermodynamical approach to the travelling salesman problem: an efficient simulation algorithm. J Optim Theory Appl. 1985;45:41–51. [Google Scholar]
- Chatfield C. The Analysis of Time Series: An Introduction. Boca Raton, FL: Chapman and Hall; 2004. [Google Scholar]
- Cheng P, Yang Y, Liu Y. Interlocked feedback loops contribute to the robustness of the Neurospora circadian clock. Proc Nat Acad Sci USA. 2001;98:7408–7413. doi: 10.1073/pnas.121170298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornélissen G. Automatic detection of multiple outliers in physiologic time series: notably temperature. In: Reinberg A, Smolensky M, Labrecque G, editors. Annual Review of Chronopharmacology. Oxford, UK: Pergamon; 1984. pp. 157–160. [Google Scholar]
- Cornélissen G, Broda H, Halberg F. Does Gonyaulax polyedra measure a week? Cell Biophysics. 1986;8:69–85. doi: 10.1007/BF02788461. [DOI] [PubMed] [Google Scholar]
- Cornélissen G, Chen CH, Halberg F. Predictive value of blood pressure variability: merits of circadian parameters versus dipping patterns. N Engl J Med. 2006 in press. [Google Scholar]
- Cornélissen G, De Prins J. Cycle detection. J Interdiscipl Cycle Res. 1973;4:159–177. [Google Scholar]
- Cornélissen G, Halberg F. Chronomedicine. In: Armitage P, Colton T, editors. Encyclopedia of Biostatistics. 2. Vol. 2. New York: Wiley; 2005. pp. 796–812. [Google Scholar]
- Cornélissen G, Halberg F, Prikryl P, Dankova E, Siegelova J, Dusek J. Prophylactic aspirin treatment: the merits of timing. J Am Med Assoc. 1991;266:3128–3129. [PubMed] [Google Scholar]
- Cornélissen G, Halberg F, Schwartzkopff O, Delmore P, Katinas G, Hunter D, Tarquini B, Tarquini R, Perfetto F, Watanabe Y, Otsuka K. Chronomes, time structures, for chronobioengineering for “a full life”. Biomed Instrum Technol. 1999;33:152–187. [PubMed] [Google Scholar]
- Cornélissen G, Haus E, Halberg F. Chronobiologic blood pressure assessment from womb to tomb. In: Touitou Y, Haus E, editors. Biological Rhythms in Clinical and Laboratory Medicine. Berlin: Springer-Verlag; 1992. pp. 428–452. [Google Scholar]
- Cornélissen G, Otsuka K, Chen CH, Kumagai Y, Watanabe Y, Halberg F, Siegelova J, Dusek J. Nonlinear relation of the circadian blood pressure amplitude to cardiovascular disease risk. Scripta Medica (Brno) 2000;73:85–94. [Google Scholar]
- Cornélissen G, Halberg F, Bakken EE, Singh RB, Otsuka K, Tomlinson B, Delcourt A, Toussaint G, Bathina S, Schwartzkopff O, Wang ZR, Tarquini R, Perfetto F, Pantaleoni GC, Jozsa R, Delmore PA, Nolley E. 100 or 30 years after Janeway or Bartter, Healthwatch helps avoid “flying blind”. Biomed Pharmacother. 2004;58(Suppl 1):S69–S86. doi: 10.1016/s0753-3322(04)80012-x. [DOI] [PubMed] [Google Scholar]
- Crowley SJ, Lee C, Tseng CY, Fogg LF, Eastman CI. Combinations of bright light, scheduled dark, sunglasses, and melatonin to facilitate circadian entrainment to night shift work. J Biol Rhythms. 2003;18:513–523. doi: 10.1177/0748730403258422. [DOI] [PubMed] [Google Scholar]
- Czaplicki J, Cornélissen G, Halberg F. GOSA, a simulated annealing-based program for global optimization of nonlinear problems, also reveals transyears. J Appl Biomed. 2006;4:87–94. [PMC free article] [PubMed] [Google Scholar]
- Czeisler CA, Richardson G, Coleman R, Zimmerman J, Moore-Ede M, Dement W, Weitzman E. Chronotherapy: resetting the circadian clocks of patients with delayed sleep phase insomnia. Sleep. 1981;4:1–21. doi: 10.1093/sleep/4.1.1. [DOI] [PubMed] [Google Scholar]
- Daan S, Pittendrigh CS. A functional analysis of circadian pacemakers in nocturnal rodents. II. The variability of phase response curves. J Comp Physiol. 1976;106:253–266. [Google Scholar]
- DeCoursey P. Phase control of activity in a rodent. Cold Spring Harb Symp Quant Biol. 1960;25:49–55. doi: 10.1101/sqb.1960.025.01.006. [DOI] [PubMed] [Google Scholar]
- DeCoursey PJ. Overview of biological timing from unicells to humans. In: Dunlap JC, Loros JJ, DeCoursey PJ, editors. Chronobiology: Biological Timekeeping. Sunderland, MA: Sinauer; 2004. pp. 3–24. [Google Scholar]
- de la Iglesia HO, Rodríguez EM, Dezi RE. Burrow plugging in the crab Uca uruguayensis and its synchronization with photoperiod and tides. Physiol Behav. 1994;55:913–919. doi: 10.1016/0031-9384(94)90079-5. [DOI] [PubMed] [Google Scholar]
- De Prins J, Cornélissen G, Hillman D, Halberg F, Van Dijck C. In: Halberg F, Scheving LE, Powell EW, Hayes DK, editors. Harmonic interpolation yields paraphases and orthophases for biologic rhythms; Chronobiology: Proceedings of the XIII International Conference of the International Society for Chronobiology; Il Ponte: Milan; 1981. pp. 333–334. [Google Scholar]
- Diambra L, Lopes JR, Menna-Barreto L, Rigolino R. Ciclograma: a tool for detection of rhythmicities in sleep/ wake cycles. Chronobiol Int. 2002;19:793–803. doi: 10.1081/cbi-120005393. [DOI] [PubMed] [Google Scholar]
- Diggle PJ, Heagerty P, Liang KY, Zeger SL. Analysis of Longitudinal Data. 2. Oxford, UK: Oxford University Press; 2002. [Google Scholar]
- Dörrscheidt GL, Beck L. Advanced methods for evaluating characteristic parameters of circadian rhythms. J Mathem Biol. 1975;2:107–121. [Google Scholar]
- Dowse HB, Ringo JM. Comparisons between “periodograms” and spectral analysis: apples are apples after all. J Theor Biol. 1991;148:139–144. doi: 10.1016/s0022-5193(05)80468-0. [DOI] [PubMed] [Google Scholar]
- Duffield GE, Ebling FJP. Maternal entrainment of the developing circadian system in the Siberian hamster (Phodopus sungorus) J Biol Rhythms. 1998;13:315–329. doi: 10.1177/074873049801300406. [DOI] [PubMed] [Google Scholar]
- Dunlap JC, Loros JJ. Analysis of circadian rhythms in Neurospora: overview of assays and genetic and molecular biological manipulations. Methods Enzymol. 2005;393:3–22. doi: 10.1016/S0076-6879(05)93001-2. [DOI] [PubMed] [Google Scholar]
- Eastman C, Rechtschaffen A. Circadian temperature and wake rhythms of rats exposed to prolonged continuous illumination. Physiol Behav. 1983;31:417–427. doi: 10.1016/0031-9384(83)90061-6. [DOI] [PubMed] [Google Scholar]
- Eijzenbach V, Sneek JH, Borst C. Arterial pressure and heart period in the conscious rabbit: diurnal rhythm and influence of activity. Clin Exp Pharmacol Physiol. 1986;13:585–592. doi: 10.1111/j.1440-1681.1986.tb00943.x. [DOI] [PubMed] [Google Scholar]
- Elliott JA, Tarmarkin L. Complex circadian regulation of pineal melatonin and wheel-running in Syrian hamsters. J Comp Physiol A. 1994;174:469–484. doi: 10.1007/BF00191713. [DOI] [PubMed] [Google Scholar]
- Enright JT. The search for rhythmicity in biological time-series. J Theor Biol. 1965;8:426–468. doi: 10.1016/0022-5193(65)90021-4. [DOI] [PubMed] [Google Scholar]
- Enright JT. Data analysis. In: Aschoff J, editor. Biological Rhythms (Handbook of Behavioral Neurobiology) Vol. 4. New York: Plenum; 1981. pp. 21–39. [Google Scholar]
- Eskin A. Some properties of the system controlling the circadian activity rhythm of sparrows. In: Menaker M, editor. Biochronometry. Washington, DC: National Academy of Sciences; 1971. pp. 55–80. [Google Scholar]
- Falcón J, Ravault JP, Cornélissen G, Halberg F. Circaseptan-modulated circadian rhythmic melatonin release from isolated pike pineal in alternating light and darkness. 4° Convegno Nazionale della Società Italiana di Cronobiologia. 1996:39–40. [Google Scholar]
- Firinguetti L, Sciolla A, Lolas F, Risco L, Larraguibel M. ARIMA modelling of chronospsychometric self-evaluation of drive and mood. Arch Biol Med Exp. 1990;23:307–314. [PubMed] [Google Scholar]
- Fisher RA. Statistical Methods for Research Workers. Edinburgh, UK: Oliver and Boyd; 1925. [Google Scholar]
- Fisher RA. Tests of significance in harmonic analysis. Proc R Soc London A. 1929;125:54–59. [Google Scholar]
- Fourier J. Théorie Analytique de la Chaleur. Paris: F. Didot; 1822. [Google Scholar]
- Gillette MU, Sejnowski TJ. Biological clocks coordinately keep life on time. Science. 2005;309:1196–1198. doi: 10.1126/science.1111420. [DOI] [PubMed] [Google Scholar]
- Gonze D, Halloy J, Goldbeter A. Robustness of circadian rhythms with respect to molecular noise. Proc Nat Acad Sci USA. 2002;99:673–678. doi: 10.1073/pnas.022628299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonze D, Halloy J, Goldbeter A. Stochastic models for circadian oscillations: emergence of a biological rhythm. Int J Quantum Chem. 2004;98:228–238. [Google Scholar]
- Granger CWJ, Newbold P. Forecasting Economic Time Series. 2. New York: Academic Press; 1986. [Google Scholar]
- Grosse J, Loudon ASI, Hastings MH. Behavioural and cellular responses to light of the circadian system of tau mutant and wild-type Syrian hamsters. Neuroscience. 1995;65:587–597. doi: 10.1016/0306-4522(94)00403-r. [DOI] [PubMed] [Google Scholar]
- Günther R, Herold M, Halberg E, Halberg F. Circadian placebo and ACTH effects on urinary cortisol in arthritics. Peptides. 1980;1:387–390. doi: 10.1016/0196-9781(80)90019-4. [DOI] [PubMed] [Google Scholar]
- Haerdle W, Schimek MG, editors. Statistical Theory and Computational Aspects of Smoothing. New York: Springer; 1996. [Google Scholar]
- Halberg F. Some physiological and clinical aspects of 24-hour periodicity. Lancet. 1953;73:20–32. [PubMed] [Google Scholar]
- Halberg F. Temporal coordination of physiologic function. Cold Spring Harb Symp Quant Biol. 1960;25:289–310. doi: 10.1101/sqb.1960.025.01.031. [DOI] [PubMed] [Google Scholar]
- Halberg F. Chronobiology. Ann Rev Physiol. 1969;31:675–725. doi: 10.1146/annurev.ph.31.030169.003331. [DOI] [PubMed] [Google Scholar]
- Halberg F. Chronobiology: methodological problems. Acta Med Rom. 1980;18:399–440. [Google Scholar]
- Halberg F. The week in phylogeny and ontogeny: opportunities for oncology. In vivo. 1995;9:269–278. [PubMed] [Google Scholar]
- Halberg F, Carandente F, Cornélissen G, Katinas GS. Glossary of chronobiology. Chronobiologia. 1977;4 (Suppl 1):1–189. [PubMed] [Google Scholar]
- Halberg F, Cornélissen G, Katinas G, Hillman D, Schwartzkopff O. Season’s Appreciations 2000: Chronomics complement, among many other fields, genomics and proteomics. Neuroendocrinol Lett. 2001;22:53–73. [PubMed] [Google Scholar]
- Halberg F, Cornélissen G, Katinas G, Syutkina EV, Sothern RB, Zaslavskaya R, Halberg F, Watanabe Y, Schwartzkopff O, Otsuka K, Tarquini R, Frederico P, Siggelova J. Transdisciplinary unifying implications of circadian findings in the 1950s. J Circadian Rhythms. 2003b;1:art. 2. doi: 10.1186/1740-3391-1-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halberg F, Cornélissen G, Katinas G, Tvildiani L, Gigolashvili M, Janashia J, Toba T, Revilla M, Regal P, Sothern RB, Wendt HW, Wang Z, Zeman M, Jozsa R, Singh RB, Mitsutake G, Chibisov SM, Lee J, Holley D, Holte JE, Sonkowsky RP, Schwartzkopff O, Delmore P, Otsuka K, Bakken EE, Czaplicki J. Chronobiology’s progress: season’s appreciations 2004–2005. Time, frequency, phase, variable, individual, age and site-specific chronomics. J Appl Biomed. 2006;4:1–38. [Google Scholar]
- Halberg F, Cornélissen G, Panksepp J, Otsuka K, Johnson D. Chronomics of autism and suicide. Biomed Pharmacother. 2005;59 (Suppl 1):S100–S108. doi: 10.1016/s0753-3322(05)80017-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halberg F, Cornélissen G, Wall D, Otsuka K, Halberg J, Katinas G, Watanabe Y, Halhuber M, Müller-Bohn T, Delmore P, Siegelova J, Homolka P, Fiser B, Dusek J, Sanchez de la Peña S, Maggioni C, Delyukov A, Gorgo Y, Gubin D, Carandente F, Schaffer E, Rhodus N, Borer K, Sonkowsky RP, Schwartzkopff O. Engineering and governmental challenge: 7-day/24-hour chronobiologic blood pressure and heart rate screening. Biomed Instrum Technol. 2002;36:89–122. 183–197. doi: 10.2345/0899-8205(2002)36[89:EAGCHC]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- Halberg F, Cornélissen G, Wang ZR, Wan C, Ulmer W, Katinas G, Singh R, Singh RK, Singh R, Gupta BD, Singh RB, Kumar A, Kanabrocki E, Sothern RB, Rao G, Bhatt MLBD, Srivastava M, Rai G, Singh S, Pati AK, Nath P, Halberg F, Halberg J, Schwartzkopff O, Bakken E, Shastri VK. Chronomics: circadian and circas-eptan timing of radiotherapy, drugs, calories, perhaps nutriceuticals and beyond. J Exp Ther Oncol. 2003a;3:223–260. doi: 10.1111/j.1533-869x.2003.01097.x. [DOI] [PubMed] [Google Scholar]
- Halberg F, Engeli M, Hamburger C, Hillman D. Spectral resolution of low-frequency, small-amplitude rhythms in excreted 17- ketosteroid: probable androgen induced circaseptan desychronization. Acta Endocrinol. 1965;103 (Suppl):5–54. doi: 10.1530/acta.0.050s0005. [DOI] [PubMed] [Google Scholar]
- Halberg F, Hastings W, Cornélissen G, Broda H. Gonyaulax polyedra “talks” both “circadian” and “circaseptan”. Chronobiologia. 1985;12:185. [Google Scholar]
- Halberg F, Katinas GS, Chiba Y, Garcia Sainz M, Kovats TG, Künkel H, Montalbetti N, Reinberg A, Scharf R, Simpson H. Chronobiologic glossary of the International Society for the Study of Biologic Rhythms. Int J Chronobiol. 1973;1:31–63. [PubMed] [Google Scholar]
- Halberg F, Nelson W, Runge WJ, Schmitt OH, Pitts GC, Tremor J, Reynolds OE. Plans for orbital study of rat biorhythms: results of interest beyond the Biosatellite program. Space Life Sci. 1971;2:437–471. [Google Scholar]
- Halberg F, Hastings W, Cornélissen G, Broda H. Gonyaulax polyedra “talks” both “circadian” and “circaseptan”. Chronobiologia. 1985;12:185. [Google Scholar]
- Halberg F, Shankaraiah K, Giese AC, Halberg F. The chronobiology of marine invertebrates: methods of analysis. In: Giese AC, Pearse JS, Pearse VB, editors. Reproduction of Marine Invertebrates. IX. General Aspects: Seeking Unity in Diversity. Palo Alto, CA: Blackwell Scientific Publications; Pacific Grove, CA: Boxwood Press; 1987. pp. 331–384. [Google Scholar]
- Halberg F, Tong YL, Johnson EA. Circadian system phase, an aspect of temporal morphology: procedures and illustrative examples. In: von Mayersbach H., editor. The Cellular Aspects of Biorhythms. Berlin: Springer; 1967. pp. 20–48. [Google Scholar]
- Halberg F, Visscher MB. Some physiologic effects of lighting. In: Tenobergen JE, editor. Proceedings of the First International Photobiological Congress. Wageningen: Veenman and Zonen; 1954. pp. 396–398. [Google Scholar]
- Hassnaoui M, Pupier R, Rehailia M. A concordance method for analyzing categorical time series: an application for the search of periodicities. Biol Rhythm Res. 2000;31:177–201. [Google Scholar]
- Häster L, Erkert HG. Alteration of circadian period length does not influence the ovarian cycle length in common marmosets Callithrix j. jacchus (Primates) Chronobiol Int. 1993;10:165–175. doi: 10.3109/07420529309073885. [DOI] [PubMed] [Google Scholar]
- Hays WL. Statistics. 5. Fort Worth; Harcourt College: 1994. [Google Scholar]
- Heeley DW, Buchanan-Smith HM. Recognition of stimulus orientation. Vision Res. 1990;30:1429–1437. doi: 10.1016/0042-6989(90)90024-f. [DOI] [PubMed] [Google Scholar]
- Hermida RC, Ayala DE, Iglesias M. Administration time-dependent influence of aspirin on blood pressure in pregnant women. Hypertension. 2003;41:651–656. doi: 10.1161/01.HYP.0000047876.63997.EE. [DOI] [PubMed] [Google Scholar]
- Hermida RC, Calvo C, Ayala DE, Domínguez MJ, Covelo M, Fernández JR, Fontao MJ, López JE. Administration-time-dependent effects of doxazosin GITS on ambulatory blood pressure of hypertensive subjects. Chronobiol Int. 2004;21:277–296. doi: 10.1081/cbi-120037772. [DOI] [PubMed] [Google Scholar]
- Herzog ED, Aton SJ, Numano R, Sakaki Y, Tei H. Temporal precision in the mammalian circadian system: a reliable clock from less reliable neurons. J Biol Rhythms. 2004;19:35–46. doi: 10.1177/0748730403260776. [DOI] [PubMed] [Google Scholar]
- Hildebrandt G, Bandt-Reges I. Chronobiologie in der Naturheilkunde: Grundlagen der Circaseptanperiodik. Heidelberg: Haug; 1992. [Google Scholar]
- Hildebrandt G, Moser M, Lehofer M. Chronobiologie und Chronomedizin: biologische Rhythmen/ medizinische Konsequenzen. Stuttgart: Hippokrates; 1998. [Google Scholar]
- Hillman D, Fernandez JR, Cornélissen G, Berry DA, Halberg J, Halberg F. Bounded limits and statistical inference in chronobiometry. Prog Clin Biol Res. 1990;341B:417–428. [PubMed] [Google Scholar]
- Hirschenhauser K, Frigerio D, Grammer K, Magnusson MS. Monthly patterns of testosterone and behavior in prospective fathers. Horm Behav. 2002;42:172–181. doi: 10.1006/hbeh.2002.1815. [DOI] [PubMed] [Google Scholar]
- Honma K, Honma S, Kohsaka M, Fukuda N. Seasonal variation in the human circadian rhythm: dissociation between sleep and temperature rhythm. Am J Physiol. 1992;262:R885–R891. doi: 10.1152/ajpregu.1992.262.5.R885. [DOI] [PubMed] [Google Scholar]
- Houdelier C, Guyomarc’h C, Lumineau S, Richard JP. Circadian rhythms of oviposition and feeding activity in Japanese quail: effects of cyclic administration of melatonin. Chronobiol Int. 2002;19:1107–1119. doi: 10.1081/cbi-120015967. [DOI] [PubMed] [Google Scholar]
- Houwelingen CAJ, van Beersma DGM. Seasonal changes in 24-h patterns of suicide rates: a study on train suicides in The Netherlands. J Affect Disord. 2001;66:215–223. doi: 10.1016/s0165-0327(00)00308-6. [DOI] [PubMed] [Google Scholar]
- Hrushesky WJ. Circadian timing of cancer chemotherapy. Science. 1985;228:73–75. doi: 10.1126/science.3883493. [DOI] [PubMed] [Google Scholar]
- Hurlburt RT. Comprehending Behavioral Statistics. 3. Belmont, CA: Wadsworth; 2003. [Google Scholar]
- Jilge B, Stähle H. Restricted food access and light-dark: impact of conflicting zeitgebers on circadian rhythms of the rabbit. Am J Physiol. 1993;264:R708–R715. doi: 10.1152/ajpregu.1993.264.4.R708. [DOI] [PubMed] [Google Scholar]
- Johnson MS. Activity and distribution of certain wild mice in relation to biotic communities. J Mammal. 1926;7:245–277. [Google Scholar]
- Kadono H, Besch EL, Usami E. Body temperature, oviposition, and food intake in the hen during continuous light. J Appl Physiol. 1981;51:1145–1149. doi: 10.1152/jappl.1981.51.5.1145. [DOI] [PubMed] [Google Scholar]
- Kanji GK. 100 Statistical Tests. London: Sage; 1993. [Google Scholar]
- Kanjilal PP, Bhattacharya J, Saha G. Robust method for periodicity detection and characterization of irregular cyclical series in terms of embedded periodic components. Phys Rev E. 1999;59:4013–4025. [Google Scholar]
- Kellerman DF, editor. New Webster’s Dictionary of the English Language. New York: Delair; 1986. [Google Scholar]
- Kirk RE. Experimental Design: Procedures for the Behavioral Sciences. 3. Pacific Grove, CA: Brooks/Cole; 1995. [Google Scholar]
- Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- Klemfuss H, Clopton PL. Seeking tau: a comparison of six methods. J Interdiscipl Cycle Res. 1993;24:1–16. [Google Scholar]
- Koehler F, Okano FK, Elveback LR, Halberg F, Bittner JJ. Periodograms for the study of physiologic daily periodicity in mice and man. Environ Med Surg. 1956;14:5–30. [PubMed] [Google Scholar]
- Körner TW. Fourier Analysis. New York: Cambridge University Press; 1988. [Google Scholar]
- Krauth J. Distribution-Free Statistics: An Application-Oriented Approach. New York: Elsevier; 1988. [Google Scholar]
- Lee TM, Zucker I. Seasonal variations in circadian rhythms persist in gonadectomized golden-mantled ground squirrels. J Biol Rhythms. 1995;10:188–195. doi: 10.1177/074873049501000302. [DOI] [PubMed] [Google Scholar]
- Lévi F, Zidani R, Misset JL. Randomised multicentre trial of chronotherapy with oxaliplatin, fluorouracil, and folinic acid in metastatic colorectal cancer. Lancet. 1997;350:681–686. doi: 10.1016/s0140-6736(97)03358-8. [DOI] [PubMed] [Google Scholar]
- Levine JD, Funes P, Dowse HB, Hall JC. Signal analysis of behavioral and molecular cycles. BMC Neurosci. 2002;3:art. 1. doi: 10.1186/1471-2202-3-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Y, Han M, Shimada B, Wang L, Gibler TM, Amarakone A, Awad TA, Stormo GD, van Gelder RN, Taghert PH. Influence of the period-dependent circadian clock on diurnal, circadian, and aperiodic gene expression in Drosophila melanogaster. Proc Nat Acad Sci USA. 2002;99:9562–9567. doi: 10.1073/pnas.132269699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lomb N. Least-squares frequency analysis of unequally spaced data. Astrophys Space Sci. 1976;39:447–462. [Google Scholar]
- Lumineau S, Guyomarc’h C, Boswell T, Richard JP, Leray D. Induction of circadian rhythm of feeding activity by testosterone implantations in arrhythmic Japanese quail males. J Biol Rhythms. 1998;13:278–287. doi: 10.1177/074873098129000110. [DOI] [PubMed] [Google Scholar]
- Mardia KV. Statistics of Directional Data. New York: Academic Press; 1972. [Google Scholar]
- Maxwell SE, Delaney HD. Designing Experiments and Analyzing Data. 2. Mahwah, NJ: Lawrence Erlbaum Associates; 2004. [Google Scholar]
- Meijer JH, De Vries MJ. Light-induced phase shifts in onset and offset of running-wheel activity in the Syrian hamster. J Biol Rhythms. 1995;10:4–16. doi: 10.1177/074873049501000101. [DOI] [PubMed] [Google Scholar]
- Menaker M. The free running period of the bat clock: seasonal variations at low body temperature. J Cell Comp Physiol. 1961;57:81–86. doi: 10.1002/jcp.1030570204. [DOI] [PubMed] [Google Scholar]
- Moore DS. The Basic Practice of Statistics. 3. New York: Freeman; 2004. [Google Scholar]
- Mormont MC, Waterhouse J, Bleuzen P, Giacchetti S, Jami A, Bogdan A, Lellouch J, Misset JL, Touitou Y, Lévi F. Marked 24-h rest/activity rhythms are associated with better quality of life, better response, and longer survival in patients with metastatic colorectal cancer and good performance status. Clin Cancer Res. 2000;6:3038–3045. [PubMed] [Google Scholar]
- Morris C, editor. Academic Press Dictionary of Science and Technology. San Diego: Academic Press; 1992. [Google Scholar]
- Mrosovsky N, Boshes M, Hallonquist JD, Lang K. Circannual cycle of circadian cycles in a golden-mantled ground squirrel. Naturwissenschaften. 1976;63:298–299. doi: 10.1007/BF00624025. [DOI] [PubMed] [Google Scholar]
- Nelson DE, Takahashi JS. Sensitivity and integration in a visual pathway for circadian entrainment in the hamster (Mesocricetus auratus) J Physiol Lond. 1991;439:115–145. doi: 10.1113/jphysiol.1991.sp018660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson W, Tong YL, Lee JK, Halberg F. Methods for cosinor rhythmometry. Chronobiologia. 1979;6:305–323. [PubMed] [Google Scholar]
- Nintcheu-Fata S, Katinas G, Halberg F, Cornélissen G, Tolstykh V, Michael HN, Otsuka K, Schwartzkopff O, Bakken E. Chronomics of tree rings for chronoastrobiology and beyond. Biomed Pharmacother. 2003;57 (Suppl 1):24–30. doi: 10.1016/j.biopha.2003.08.003. [DOI] [PubMed] [Google Scholar]
- Ogle W. On the diurnal variations in the temperature of the human body in health. St George’s Hosp Rep. 1866;1:221–245. [Google Scholar]
- Otsuka K, Cornélissen G, Halberg F. Circadian rhythmic fractal scaling of heart rate variability in health and coronary artery disease. Clin Cardiol. 1997;20:631–638. doi: 10.1002/clc.4960200710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer JD. Daily and tidal components in the persistent rhythmic activity of the crab, Sesarma. Nature. 1967;215:64–66. doi: 10.1038/215064a0. [DOI] [PubMed] [Google Scholar]
- Percival DB, Walden AT. Wavelet Methods for Time Series Analysis. New York: Cambridge University Press; 2000. [Google Scholar]
- Piccione G, Caola G, Refinetti R. Circadian rhythms of body temperature and liver function in fed and food-deprived goats. Comp Biochem Physiol A. 2003;134:563–572. doi: 10.1016/s1095-6433(02)00362-8. [DOI] [PubMed] [Google Scholar]
- Piccione G, Caola G, Refinetti R. Temporal relationships of 21 physiological variables in horse and sheep. Comp Biochem Physiol A. 2005;142:389–396. doi: 10.1016/j.cbpa.2005.07.019. [DOI] [PubMed] [Google Scholar]
- Pincus DJ, Beam WR, Martin RJ. Chronobiology and chronotherapy of asthma. Clin Chest Med. 1995;16:699–713. [PubMed] [Google Scholar]
- Pittendrigh CS. Temporal organization: reflections of a Darwinian clock-watcher. Ann Rev Physiol. 1993;55:17–54. doi: 10.1146/annurev.ph.55.030193.000313. [DOI] [PubMed] [Google Scholar]
- Pohl H. Light pulses entrain the circadian activity rhythm of a diurnal rodent (Ammospermophilus leucurus) Comp Biochem Physiol B. 1983;76:723–729. doi: 10.1016/0305-0491(83)90384-x. [DOI] [PubMed] [Google Scholar]
- Ptitsyn AA, Zvonic S, Conrad SA, Scott LK, Mynatt RL, Gimble JM. Circadian clocks are resounding in peripheral tissues. PLoS Comput Biol. 2006;2(3):e16. doi: 10.1371/journal.pcbi.0020016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao AV, Sharma VK. A simple approach for the computation of multiple periodicities in biological time series. Biol Rhythm Res. 2002;33:487–502. [Google Scholar]
- Rauth-Widmann B, Fuchs E, Erkert HG. Infradian alteration of circadian rhythms in owl monkeys (Aotus lemurinus griseimembra): an effect of estrous? Physiol Behav. 1996;59:11–18. doi: 10.1016/0031-9384(95)02009-8. [DOI] [PubMed] [Google Scholar]
- Refinetti R. An extremely simple procedure for the analysis of circadian and estrous periodicity. Physiol Behav. 1991;50:655–659. doi: 10.1016/0031-9384(91)90563-4. [DOI] [PubMed] [Google Scholar]
- Refinetti R. Analysis of the circadian rhythm of body temperature. Behav Res Methods Instrum Comput. 1992a;24:28–36. [Google Scholar]
- Refinetti R. Non-parametric procedures for the determination of phase markers of circadian rhythms. Int J Biomed Comput. 1992b;30:49–56. doi: 10.1016/0020-7101(92)90061-v. [DOI] [PubMed] [Google Scholar]
- Refinetti R. Comparison of six methods for the determination of the period of circadian rhythms. Physiol Behav. 1993;54:869–875. doi: 10.1016/0031-9384(93)90294-p. [DOI] [PubMed] [Google Scholar]
- Refinetti R. Homeostatic and circadian control of body temperature in the fat-tailed gerbil. Comp Biochem Physiol A. 1998;119:295–300. doi: 10.1016/s1095-6433(97)00436-4. [DOI] [PubMed] [Google Scholar]
- Refinetti R. Daily activity patterns of a nocturnal and a diurnal rodent in a seminatural environment. Physiol Behav. 2004a;82:285–294. doi: 10.1016/j.physbeh.2004.03.015. [DOI] [PubMed] [Google Scholar]
- Refinetti R. Non-stationary time series and the robustness of circadian rhythms. J Theor Biol. 2004b;227:571–581. doi: 10.1016/j.jtbi.2003.11.032. [DOI] [PubMed] [Google Scholar]
- Refinetti R. Circadian Physiology. 2. Boca Raton, FL: CRC Press; 2006a. [Google Scholar]
- Refinetti R. Variability of diurnality in laboratory rodents. J Comp Physiol A. 2006b;192:701–714. doi: 10.1007/s00359-006-0093-x. [DOI] [PubMed] [Google Scholar]
- Refinetti R, Kaufman CM, Menaker M. Complete suprachiasmatic lesions eliminate circadian rhythmicity of body temperature and locomotor activity in golden hamsters. J Comp Physiol A. 1994;175:223–232. doi: 10.1007/BF00215118. [DOI] [PubMed] [Google Scholar]
- Refinetti R, Piccione G. Intra- and inter-individual variability in the circadian rhythm of body temperature of rats, squirrels, dogs, and horses. J Therm Biol. 2005;30:139–146. [Google Scholar]
- Reiner A, Yekutieli D, Benjamini Y. Identifying differentially expressed genes using false discovery rate controlling procedures. Bioinformatics. 2003;19:368–375. doi: 10.1093/bioinformatics/btf877. [DOI] [PubMed] [Google Scholar]
- Rietveld WJ. General introduction to chronobiology. Brazilian J Med Biol Res. 1996;29:63–70. [PubMed] [Google Scholar]
- Ruf T. The baseline cosinus function: a periodic regression model for biological rhythms. Biol Rhythm Res. 1996;27:153–165. [Google Scholar]
- Ruf T. The Lomb-Scargle periodogram in biological rhythm research: analysis of incomplete and unequally spaced time-series. Biol Rhythm Res. 1999;30:178–201. [Google Scholar]
- Rummel J, Lee JK, Halberg F. Combined linear-nonlinear chronobiologic windows by least squares resolve neighboring components in a physiologic rhythm spectrum. In: Ferin M, Halberg F, Richart R, Wiele RV, editors. Biorhythms and Human Reproduction. New York: Wiley; 1974. pp. 53–82. [Google Scholar]
- Salti R, Galluzzi F, Bindi G, Perfetto F, Tarquini R, Halberg F, Cornélissen G. Nocturnal melatonin patterns in children. J Clin Endocr Metab. 2000;85:2137–2144. doi: 10.1210/jcem.85.6.6656. [DOI] [PubMed] [Google Scholar]
- Sanchez de la Peña S, Halberg F, Schweiger HG, Eaton J, Sheppard JR. Circadian and circaseptan rhythmic aspects of murine mortality from Plasmodium berghei inoculation. Chronobiologia. 1983;10:154–155. [Google Scholar]
- Savage IR, Rao MM, Halberg F. Test of peak values in physiopathologic time series. Exp Med Surg. 1962;20:309–317. [PubMed] [Google Scholar]
- Scarbrough K, Turek FW. Quantitative differences in the circadian rhythm of locomotor activity and vasopressin and vasoactive intestinal peptide gene expression in the suprachiasmatic nucleus of tau mutant compared to wildtype hamsters. Brain Res. 1996;736:251–259. doi: 10.1016/0006-8993(96)00709-3. [DOI] [PubMed] [Google Scholar]
- Schimmel M. Emphasizing difficulties in the detection of rhythms with Lomb-Scargle periodograms. Biol Rhythm Res. 2001;32:341–345. doi: 10.1076/brhm.32.3.341.1340. [DOI] [PubMed] [Google Scholar]
- Schuster A. On the investigation of hidden periodicities with application to a supposed 26 day period of metereological phenomena. Terrestr Magnet. 1898;3:13–41. [Google Scholar]
- Schweiger HG, Berger S, Kretschmer H, Morler H, Halberg E, Sothern RB, Halberg F. Evidence for a circaseptan and a circasemiseptan growth response to light/dark cycle shifts in nucleated and enucleated Acetabularia cells, respectively. Proc Nat Acad Sci USA. 1986;83:8619–8623. doi: 10.1073/pnas.83.22.8619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma VK. Light-induced phase response curves of the circadian activity rhythm in individual field mice, Mus booduga. Chronobiol Int. 1996;13:401–409. doi: 10.3109/07420529609020911. [DOI] [PubMed] [Google Scholar]
- Shumway RH, Stoffer DS. Time Series Analysis and Its Implications. New York: Springer; 2000. [Google Scholar]
- Siegel AF. Testing for periodicity in a time series. J Am Stat Assoc. 1980;75:345–348. [Google Scholar]
- Siegel S. Nonparametric Statistics for the Behavioral Sciences. New York: McGraw-Hill; 1956. [Google Scholar]
- Simpson HW, Lobban MC, Halberg F. Urinary near-24-hour rhythms in subjects living on a 21-hour routine in the Arctic. Arctic Anthropol. 1970;7:144–164. [Google Scholar]
- Simpson S, Galbraith JJ. Observations on the normal temperature of the monkey and its diurnal variation, and on the effect of changes in the daily routine on this variation. Trans R Soc Edinb. 1906;45:65–104. [Google Scholar]
- Sokolove PG, Bushell WN. The chi square periodogram: its utility for analysis of circadian rhythms. J Theor Biol. 1978;72:131–160. doi: 10.1016/0022-5193(78)90022-x. [DOI] [PubMed] [Google Scholar]
- Sprinthall RC. Basic Statistical Analysis. 7. Boston, MA: Allyn and Bacon; 2003. [Google Scholar]
- Stark J, Hardy K. Chaos: useful at last? Science. 2003;301:1192–1193. doi: 10.1126/science.1087822. [DOI] [PubMed] [Google Scholar]
- Stillman JH, Barnwell FH. Relationship of daily and circatidal activity rhythms of the fiddler crab, Uca princeps, to the harmonic structure of semidiurnal and mixed tides. Marine Biol. 2004;144:473–482. [Google Scholar]
- Storey JD, Tibshirani R. Statistical significance for genomewide studies. Proc Nat Acad Sci USA. 2003;100:9440–9445. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strutt JW. On the problem of random vibrations and of random flights in one, two or three dimensions. Phil Mag 6th Series. 1919;37:321–347. [Google Scholar]
- Taylor J, Tibshirani R, Efron B. The ‘miss rate’ for the analysis of gene expression data. Biostatistics. 2005;6:111–117. doi: 10.1093/biostatistics/kxh021. [DOI] [PubMed] [Google Scholar]
- Tong YL, Nelson WL, Sothern RB, Halberg F. Estimation of the orthophase (timing of high values) on a non-sinusoidal rhythm, illustrated by the best timing for experimental cancer chronotherapy. Proceedings of the XII International Conference of the International Society for Chronobiology; Washington, D.C., Il Ponte: Milan; 1977. pp. 765–769. [Google Scholar]
- Van Dongen HPA, Olofsen E, Van Hartevelt JH, Kruyt EW. A procedure of multiple period searching in unequally spaced time series with the Lomb-Scargle method. Biol Rhythm Res. 1999a;30:149–177. doi: 10.1076/brhm.30.2.149.1424. [DOI] [PubMed] [Google Scholar]
- Van Dongen HPA, Olofsen E, Van Hartevelt JH, Kruyt EW. Searching for biological rhythms: peak detection in the periodogram of unequally spaced data. J Biol Rhythms. 1999b;14:617–620. doi: 10.1177/074873099129000984. [DOI] [PubMed] [Google Scholar]
- Vansteensel MJ, Deboer T, Dahan A, Meijer JH. Differential responses of circadian activity onset and offset following GABA-ergic and opioid receptor activation. J Biol Rhythms. 2003;18:297–306. doi: 10.1177/0748730403254283. [DOI] [PubMed] [Google Scholar]
- Veldhuis JD, Johnson ML. Analytical methods for evaluating episodic secretory activity within the neuroendocrine axes. Neurosci Biobehav Rev. 1994;18:605–612. doi: 10.1016/0149-7634(94)90019-1. [DOI] [PubMed] [Google Scholar]
- Vogelbaum MA, Menaker M. Temporal chimeras produced by hypothalamic transplants. J Neurosci. 1992;12:3619–3627. doi: 10.1523/JNEUROSCI.12-09-03619.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wackerly DD, Mendenhall W, Scheaffer RL. Mathematical Statistics with Applications. 6. Pacific Grove, CA: Duxbury; 2002. [Google Scholar]
- Walker JS. Fourier Analysis. New York: Oxford University Press; 1988. [Google Scholar]
- Walker JS. Fast Fourier Transforms. 2. Boca Raton, FL: CRC Press; 1996. [Google Scholar]
- Wang Y, Ke C, Brown MB. Shape-invariant modeling of circadian rhythms with random effects and smoothing spline ANOVA decompositions. Biometrics. 2003;59:804–812. doi: 10.1111/j.0006-341x.2003.00094.x. [DOI] [PubMed] [Google Scholar]
- Watanabe Y, Cornélissen G, Halberg F. Thousands of blood pressure and heart rate measurements at fixed clock hours may mislead. Neuroendocrinol Lett. 2003;24:339–340. [PubMed] [Google Scholar]
- Weinert D, Fritzche P, Gattermann R. Activity rhythms of wild and laboratory golden hamsters (Mesocricetus auratus) under entrained and free-running conditions. Chronobiol Int. 2001;18:921–932. doi: 10.1081/cbi-100107968. [DOI] [PubMed] [Google Scholar]
- Weiss NA. Elementary Statistics. 6. Reading, MA: Addison-Wesley; 2005. [Google Scholar]
- Williams JA, Sehgal A. Molecular components of the circadian system in Drosophila. Ann Rev Physiol. 2001;63:729–755. doi: 10.1146/annurev.physiol.63.1.729. [DOI] [PubMed] [Google Scholar]
- Wikelski M, Hau M. Is there an endogenous tidal foraging rhythm in marine iguanas? J Biol Rhythms. 1995;10:335–350. doi: 10.1177/074873049501000407. [DOI] [PubMed] [Google Scholar]
- Wollnik F, Schmidt B. Seasonal and daily rhythms of body temperature in the European hamster (Cricetus cricetus) under semi-natural conditions. J Comp Physiol B. 1995;165:171–182. doi: 10.1007/BF00260808. [DOI] [PubMed] [Google Scholar]
- Wulff K, Wulff W, Siegmund R. Circadian patterns of rest and activity in infants and their mothers analyzed by SOPRAN, a wavelet application for actigraphic data. Neuroendocrinol Lett. 2003;24 (Suppl 1):236–237. [Google Scholar]
- Yamamoto T, Nakahata Y, Soma H, Akashi M, Mamine T, Takumi T. Transcriptional oscillation of canonical clock genes in mouse peripheral tissues. BMC Mol Biol. 2004;5:art. 18. doi: 10.1186/1471-2199-5-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoo SH, Yamazaki S, Lowrey PL, Shimomura K, Ko CH, Buhr ED, Siepka SM, Hong HK, Oh WJ, Yoo OJ, Menaker M, Takahashi JS. PERIOD2::LUCIFERASE real-time reporting of circadian dynamics reveals persistent circadian oscillations in mouse peripheral tissues. Proc Nat Acad Sci USA. 2004;101:5339–5346. doi: 10.1073/pnas.0308709101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeger SL, Irizarry R, Peng RD. On time series analysis of public health and biomedical data. Ann Rev Publ Health. 2006;27:57–79. doi: 10.1146/annurev.publhealth.26.021304.144517. [DOI] [PubMed] [Google Scholar]
- Zivkovic BD, Underwood H, Steele CT, Edmonds K. Formal properties of the circadian and photoperiodic systems of Japanese quail: phase response curve and effects of T-cycles. J Biol Rhythms. 1999;14:378–390. doi: 10.1177/074873099129000786. [DOI] [PubMed] [Google Scholar]
- Zvonic S, Ptitsyn AA, Conrad SA, Scott LK, Floyd ZE, Kilroy G, Wu XY, Goh BC, Mynatt RL, Gimble JM. Characterization of peripheral circadian clocks in adipose tissues. Diabetes. 2006;55:962–970. doi: 10.2337/diabetes.55.04.06.db05-0873. [DOI] [PubMed] [Google Scholar]