Abstract
Zinc nitride (Zn3N2) nanowires (NWs) with diameters of 50 to 100 nm and a cubic crystal structure have been grown on 1 nm Au/Al2O3 via the reaction of Zn with NH3 including H2 between 500°C and 600°C. These exhibited an optical band gap of ≈ 3.2 eV, estimated from steady state absorption-transmission spectroscopy. We compared this with the case of ZnO NWs and discussed the surface oxidation of Zn3N2 NWs which is important and is expected to lead to the formation of a Zn3N2/ZnO core-shell NW, the energy band diagram of which was calculated via the self-consistent solution of the Poisson-Schrödinger equations within the effective mass approximation by taking into account a fundamental energy band gap of 1.2 eV. In contrast, only highly oriented Zn3N2 layers with a cubic crystal structure and an optical band gap of ≈ 2.9 eV were obtained on Au/Si(001) using the same growth conditions.
Keywords: Zinc nitride, Nanowires, Optical properties, Electronic structure
Background
III-V compound semiconductor nanowires (NWs) such as InN [1] and GaN [2,3] NWs are currently being investigated in view of their potential application as nanoscale optoelectronic devices for solid state lighting and solar energy conversion. However, their distinct disadvantage is their high cost. Low cost, viable alternatives are therefore desirable and interesting from a technological and fundamental point of view.
To date, there are very few investigations on II-V or IV-V nitrides such as Zn3N2 and Sn3N4 NWs, in contrast to the extensive research that has been carried out on their metal-oxide (MO) counterparts, i.e. ZnO [4] and SnO2 NWs [5]. More specifically, Sn3N4 NWs [6,7] with diameters of 100 nm and lengths of 1 to 2 μm were only obtained recently by halide chemical vapour deposition. On the other hand Zn3N2 NWs have been grown by Zong et al. [8] via the direct reaction of Zn with 250 sccms of NH3 at 600°C. The Zn3N2 NWs had diameters ≈100 nm, lengths between 10 and 20 μm, and were dispersed in Zn. Irregular, Zn3N2 hollow-like spheres with diameters of ≈3 μm were also obtained under identical growth conditions [9]. Similarly Zn3N2 nanoneedles have been prepared by Khan et al. [10] and by Khan and Cao [11] who found an indirect energy band gap of 2.81 eV. In contrast, Zn3N2 layers [12] have been studied in more detail, while p-type ZnO layers have been prepared by thermal oxidation of Zn3N2[13] which is important since ZnO is usually n-type due to oxygen defects. It should be noted, however, that p-type ZnO layers have also been obtained by nitrogen doping of ZnO using small flows of NH3[14,15], which is a topic of active interest since nitrogen is considered to be a shallow-like, p-type impurity in ZnO. In this case, no changes occur in the crystal structure of ZnO. Recently, we carried out a systematic investigation of the post-growth nitridation of ZnO NWs and the changes that occurred in the crystal structure using moderate flows of NH3 and temperatures ≤600°C. These favour the formation of ZnO/Zn3N2 core-shell NWs since we were able to observe not only the suppression of the XRD peaks related to ZnO but also the emergence of new ones corresponding to the cubic crystal structure of Zn3N2[16]. Higher temperatures, flows of NH3 or the inclusion of H2 did not lead to the complete conversion of ZnO into Zn3N2 NWs, instead led to the complete elimination of the ZnO NWs.
Here, we have undertaken an investigation of the synthesis of Zn3N2 NWs on Si(001) and Al2O3 via the direct reaction of Zn with NH3, thereby complementing our previous study on the post-growth nitridation and conversion of ZnO into Zn3N2 NWs.
Zn3N2 NWs with diameters between 50 and 100 nm, lengths of many tens of micrometres, and a cubic crystal structure have been grown on ≈1 nm Au/Al2O3 between 500°C and 600°C. These exhibited an optical energy band gap of EG = 3.2 eV, estimated from steady state absorption-transmission measurements. In contrast, only Zn3N2 layers were obtained on 1 nm Au/Si(001) using similar growth conditions, which showed photoluminescence (PL) at 2.9 and 2.0 eV with relative strengths depending on their distance from Zn. We compared this with the case of ZnO NWs and discussed the sensitivity of Zn3N2 to ambient conditions, which is expected to lead to the formation of Zn3N2/ZnO core-shell NWs, the energy band diagram of which has been determined via the self-consistent solution of the Poisson-Schrödinger equations within the effective mass approximation by taking into account a fundamental energy band gap of 1.2 eV [17].
Methods
Zn3N2 was grown using an atmospheric pressure chemical vapour deposition reactor consisting of four mass flow controllers and a horizontal quartz tube (QT) furnace capable of reaching 1,100°C. For the growth of Zn3N2, Zn pellets (2 to 14 Mesh, 99.9%; Aldrich Company, Wyoming, IL, USA) were cut into small fragments that were weighed individually with an accuracy of ±1 mg. Square pieces of p+Si(001) ≈7 mm × 7 mm were cleaned sequentially in trichloroethylene, methanol, acetone, and isopropanol; rinsed with de-ionised water; dried with N2 and coated with Au, ≈0.5 to 20 nm by sputtering using Ar at 1 × 10−2 mBar after removing the native SiO2 in HF. Square samples of Al2O3 were coated with a thin layer of 0.5 to 1.0 nm of Au after cleaning with the same organic solvents.
After carefully loading 0.2 to 1.0 g of Zn fragments and Au/p+Si(001) or Au/Al2O3 substrates into a boat and recording their positions and relative distances, the boat was inserted into the QT, which was subsequently purged with 450 sccm Ar and 50 sccms H2 for 10 min. Then, the temperature was ramped to the desired growth temperature (TG) using a ramp rate of 10°C/min and flows of 250 to 450 sccms NH3, see Table 1. A smaller flow of 50 sccms H2 was added in order to eliminate the background O2.
Table 1.
Temperatures and gas flows used for the growth of Zn3N2 on 1.8 nm Au/Si(001)
| TG (°C) | NH3 (sccm) | H2 (sccm) | |
|---|---|---|---|
| CVD1066 |
700 |
250 |
- |
| CVD1065 |
600 |
250 |
- |
| CVD1070 |
500 |
450 |
50 |
| CVD1069 |
500 |
450 |
- |
| CVD1072 |
500 |
250 |
- |
| CVD1068 | 500 | 50 | - |
The temperature ramp was 10°C/min, and 0.9 g of Zn was used in all cases. Upon reaching TG = 500°C to 700°C, the same flow of NH3 and H2 was maintained for a further 60 min; after which, the reactor was allowed to cool down slowly for at least 30 min without changing the gas flows.
The sample was always removed when the temperature was lower than 100°C, and the weight of the remaining Zn was measured to find the amount transferred into the gas stream. The QT was changed regularly in order to maintain a clean, high temperature zone for the growth of the Zn3N2 NWs.
The morphology of the Zn3N2 NWs was examined with a scanning electron microscope (SEM; TESCAN, Brno, Czech Republic), while their crystal structure and phase purity were determined using a XRD-6000 X-ray diffractometer (Shimadzu Corporation, Tokyo, Japan) with Cu-Kα source, by performing a scan of θ to 2θ in the range between 10° to 80°. Finally, PL was measured at 300 K using excitation at λ = 267 nm, and the absorption-transmission spectra were taken with a Lambda 950 UV-vis spectrophotometer (Perkin-Elmer Inc., MA, USA).
Results and discussion
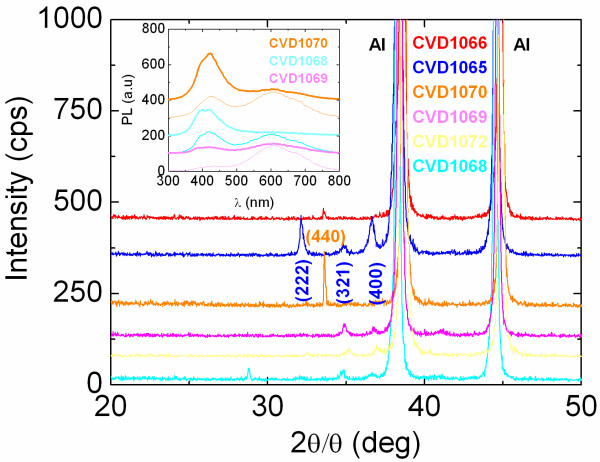
We will begin by describing the growth of Zn3N2 on Au/p+Si(001) under different growth conditions listed in Table 1. The reaction of Zn with NH3 over Au/p+Si(001) between 500°C and 700°C gave very uniform layers with a characteristic yellow or light blue colour. These layers exhibited clear peaks in the XRD, as shown in Figure 1, corresponding to the cubic crystal structure of Zn3N2. For TG = 500°C, we find that small to large flows of 50 to 450 sccms of NH3, see Table 1 (CVD1068, CVD1072 and CVD1069), give a set of peaks that are very similar to those of the Zn3N2 layers prepared by Futsuhara et al. [12], Zn3N2 NWs of Zong et al. [8,9] and the Zn3N2 powders of Partin et al. [18]. However, the addition of 50 sccms of H2 at the same temperature (CVD1070) led to the complete suppression of all these peaks and the emergence of a single, strong peak at θ = 33.3° corresponding to the (440) direction of Zn3N2. Similar (440) oriented Zn3N2 layers were obtained at higher temperatures, e.g. 700°C, using moderate flows of 250 sccms of NH3 (CVD1066).
Figure 1.
XRD spectra of the Zn3N2 layers obtained on Si(001) as described in Table 1. The peaks belonging to the Al holder have also been identified. The inset shows the room-temperature PL of Zn3N2 layers grown on 1.8 nm Au/Si(001) at 500°C using 50 sccms NH3 (CVD1068 lowest two traces), 450 sccms NH3 (CVD1069 mid two traces) and 450 sccms NH3:50 sccms H2 (CVD1070 top two traces). The bold traces shown in the inset correspond to Zn3N2 obtained closest to Zn, and the thin ones to Zn3N2 obtained further donwstream.
All of the Zn3N2 layers described above exhibited PL emission at 2.9 and 2.0 eV as shown in Figure 1. In particular, the Zn3N2 layers obtained on Au/Si(001) closest to the source of Zn had the strongest PL at 2.9 eV, while those further downstream from the source of Zn exhibited stronger emission at 2.0 eV. This was observed systematically and is similar to the case of ZnSe, where it was shown that the PL is strong at 450 nm under Zn-rich growth conditions and shifts to 650 nm when the Zn content is lower [19]. It should be noted that the PL at 2.9 eV is comparable to the value of 3.2 eV measured by Kuriyama et al. [20] who prepared Zn3N2 using NH3, while the PL at 2.0 eV is closer to 2.3 eV found by Futsuhara et al. [12]. Different PL and optical energy band gaps have, therefore, been obtained for Zn3N2 using different growth methods and conditions. Interestingly, the PL peak of the Zn3N2 layers at 2.9 eV shown in Figure 1 was enhanced by increasing the flow of NH3 or by adding H2 which also led to a suppression of the side emission at 2.0 eV. The same has also been observed in the growth of GaN NWs or the conversion of β-Ga2O3 into GaN NWs, where the band edge emission at 3.4 eV was boosted using a high flow of H2 along with NH3 since it passivates surface states or defects within the GaN NWs. Therefore, at first sight, it appears that the main band edge of the Zn3N2 layers grown here is ≈2.9 eV which is close to the PL of Zn3N2 layers obtained by a variety of other methods [21]. However, the energy band gap of Zn3N2 is still a controversial issue, and the optical band gap may not correspond to the fundamental energy gap as will be discussed later in more detail.
No Zn3N2 NWs were obtained on Au/Si(001) by changing the temperature between 500°C and 700°C, flow of NH3, or the thickness of Au between 0.9 and 19 nm while no deposition took place on plain Si(001). This is in direct contrast to the case of ZnO NWs which were obtained readily on Au/Si(001) at 500°C to 600°C by the reaction of Zn with residual O2 under an inert flow of 100 sccms Ar by reactive vapour transport or directly on Si(001) without any Au via a self-catalysed vapour solid mechanism. The ZnO NWs showed clear peaks in the XRD as shown in Figure 2, corresponding to the hexagonal wurtzite crystal structure of ZnO.
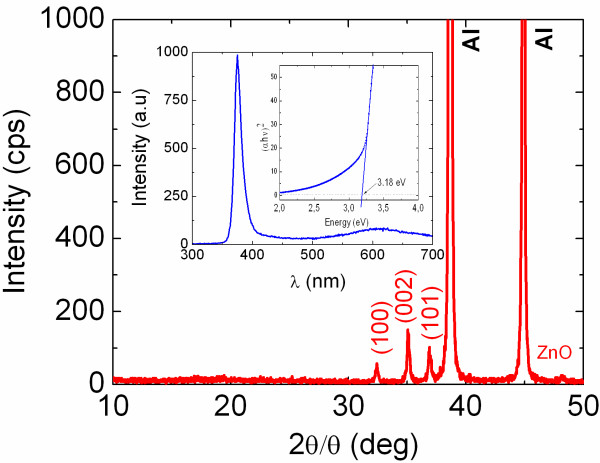
Figure 2.
XRD spectra of ZnO NWs’ lower trace. Inset shows the PL of the ZnO NWs and square of the absorption versus energy.
A typical PL spectrum of the ZnO NWs obtained on Au/Si(001) is shown in Figure 2 with a peak at 390 nm corresponding to 3.2 eV, which is in excellent agreement with the abrupt onset in the absorption measured from ZnO NWs grown on 1.0 nm Au/quartz, shown as an inset in Figure 2. Here, it should be noted that the broad PL of the ZnO NWs at ≈2.0 eV (≡600 nm) is attributed to the radiative recombination of the carriers' occupying defect states that are located energetically in the upper half of the energy band gap, as we have shown in the past for MO NWs such as SnO2 and β-Ga2O3 using ultrafast transient absorption-transmission pump-probe spectroscopy [5,22]. This broad PL is not desirable in optoelectronic devices as it represents a competing radiative recombination path which acts to reduce the main band-edge emission.
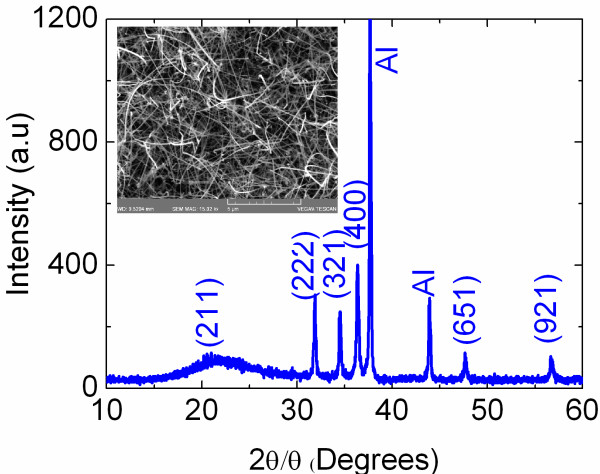
While we did not obtain any Zn3N2 NWs on Au/Si(001), we found that the reaction of Zn with 250 to 450 sccm NH3 including 50 sccm H2 over 1.0 nm Au/Al2O3 at temperatures between 500°C and 600°C led to the growth of Zn3N2 NWs with diameters of 50 to 100 nm and lengths of many tens of micrometres as shown in Figure 3. We should note that the Zn3N2 NWs probably follow a vapour-liquid-solid-like mechanism similar to the case of GaN NWs, since no deposition occurred on plain Si(001) or Al2O3. The XRD of the Zn3N2 NWs, also shown in Figure 3, is similar to that of the Zn3N2 layers prepared on Au/Si(001). In addition, we observed new peaks which are characteristic of Zn3N2 and, more importantly, do not belong to ZnO.
Figure 3.
XRD spectra of the Zn3N2 NWs grown on 1 nm Au/Al2O3 at 600°C under NH3:H2. Inset shows the SEM image of Zn3N2 NWs.
The absorption-transmission spectrum of the Zn3N2 NWs that were grown on 1.0 nm Au/Al2O3 was measured with a Perkin-Elmer Lamba 950 used to determine the optical band gap EOP according to αhν ∝ (hν − EOP)n by extrapolating the linear portion of the curve to zero absorption, where hν is the photon energy and n = 1 / 2 for direct transitions. A plot of the square of absorption versus energy for the Zn3N2 NWs grown here is shown as an inset in Figure 4 from which we find that EOP = 3.2 eV which is consistent with the PL of the Zn3N2 NWs of Zong et al. [8] and the PL emission of the Zn3N2 layers shown in Figure 1, as well as with the predictions of Long et al. [23] who suggested that optical gap energies measured in the range 2.12 to 3.2 eV correspond to band-to-band transitions.
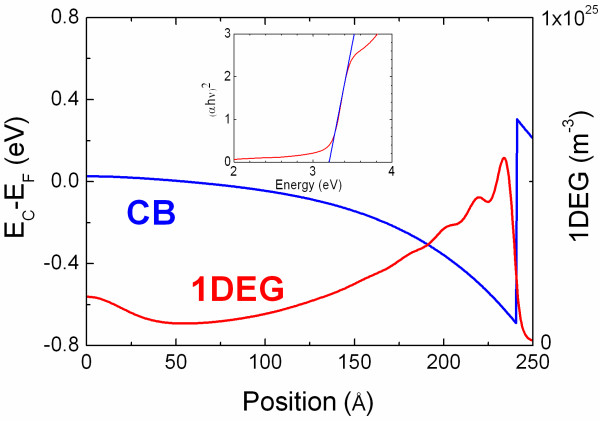
Figure 4.
Self-consistent conduction-band edge potential with respect to the Fermi level.EC − EF (EF = 0 eV) versus radial position for a 50-nm diameter Zn3N2/ZnO core-shell NW. The core has a radius of 24 nm. Inset shows the absorption squared versus energy for the Zn3N2 NWs grown on 1 nm Au/Al2O3.
However, according to the ab initio electronic structure calculations of Li et al. [17], the fundamental gap of Zn3N2 is 1.17 eV which is in agreement with the results of Suda and Kakishita [24] who found that the energy gap of polycrystalline Zn3N2 layers grown by molecular beam epitaxy on quartz is ≈1.0 eV and explained that large blue shifts of the EOP are due to the Burstein-Moss shift. In addition, the large carrier densities of 1019 to 1020 cm−3 measured by Suda and Kakishita [24] were attributed to oxygen contamination.
We ought to mention here that the growth conditions for the Zn3N2 NWs gave Zn3N2 layers on Au/Si(001), not ZnO NWs which would have been obtained if the oxygen background was substantial. Since no ZnO NWs were obtained, the oxygen background under the conditions used for the growth of the Zn3N2 is negligible, especially under the presence of H2.
In short, it is unlikely that the Zn3N2 NWs contain O from the main gas stream, while it is also unlikely that they contain O from the Al2O3 bonds which are extremely stable at 500°C to 600°C. However, it is known that Zn3N2 is sensitive to moisture in air [25], so one expects the formation of a Zn3N2/ZnO core-shell NW, but not the complete conversion of Zn3N2 into ZnO NWs since we observed peaks that are clearly related to Zn3N2 after exposure to air, as shown in Figure 3. Despite intensive investigations on the properties of ZnO, little is known about its surface properties. While a few claim that the Fermi level is pinned above the conduction band edge [26], others claim that the Fermi level is pinned below the conduction band edge [27]. Here, we take the Fermi level to be located below the conduction band edge as in the case of n-type ZnO NWs [28]. This is also in accordance with Long et al. [23] who suggested that Zn3N2 with N substituted by O (ON) is more stable than Zn replaced by O (OZn) or interstitial O (OI). In the case of ON, the Fermi level locates near the bottom of the conduction band, but in the cases of both OZn and OI, the Fermi level is pinned around the top of the valence band [23]. In other words, interstitial oxygen gives p-type Zn3N2, but since it is not energetically favourable, we expect to have the formation of n-type ZnO shell at the surface which surrounds an n-type Zn3N2 core.
The energy band diagram of a 50-nm diameter Zn3N2/ZnO core-shell NW determined from the self-consistent solution of the Poisson-Schrödinger equations (SCPS) in cylindrical coordinates and in the effective mass approximation is shown in Figure 4. In such a calculation, Schrödinger's equation is initially solved for a trial potential V, and the charge distribution ρ is subsequently determined by multiplying the normalised probability density, ∣ψk∣2, by the thermal occupancy of each sub-band with energy Ek using Fermi-Dirac statistics and summing over all k. The Poisson equation is then solved for this charge distribution in order to find a new potential V′, and the process is repeated until convergence is reached. A detailed description of the SCPS solver is given elsewhere [29,30].
In this calculation, we have taken into account the effective mass me* = 0.29 mo and static dielectric constant ϵr = 5.29 of Zn3N2[24,31], as well as me* = 0.24 mo and ϵr = 8.5 for ZnO [32,33]. In addition, we have taken into account the energy band gap of Zn3N2 to be 1.2 eV [17,24] and the Fermi level to be pinned at 0.2 eV below the conduction band edge at the ZnO surface [28]. A flat-band condition is reached at the centre of the Zn3N2/ZnO NW, and a quasi-triangular potential well forms in the immediate vicinity of the surface, holding a total of eight sub-bands that fall below the Fermi level. The one-dimensional electron gas (1DEG) charge distribution is confined to the near-surface region, has a peak density of 5 × 1018 cm−3 (≡5 × 1024 cm−3), as shown in Figure 4, and a 1DEG line density of 5 × 109 m−1.
Optical transitions in this case will occur between the valence band and conduction band states residing above the Fermi level similar to the case of InN [1]. Consequently, the optical and transport properties will depend strongly on the surface properties, but further investigations are required in order to follow up and confirm that the energy band gap of Zn3N2 is 1.2 eV [17,24] and if it is possible to obtain a p-type ZnO by thermal oxidation of the n-type Zn3N2 NWs which would be important for device applications.
Conclusion
Zn3N2 NWs with diameters of 50 to 100 nm and a cubic crystal structure have been grown on 1 nm Au/Al2O3 between 500°C and 600°C under a steady gas flow of NH3 containing H2. These exhibited a large optical band gap of 3.2 eV determined from absorption-transmission steady state spectroscopy. The surface oxidation of Zn3N2 is expected to lead to the formation of a Zn3N2/ZnO core-shell NW, the energy band diagram of which was calculated via the self-consistent solution of the Poisson-Schrödinger equations within the effective mass approximation by taking into account a fundamental energy band gap of 1.2 eV for Zn3N2. Uniform Zn3N2 layers were obtained on Au/Si(001), while no deposition took place on plain Si(001), in contrast to the case of ZnO NWs which grow with or without a catalyst on Si(001) via the reaction of Zn with O2.
Competing interest
The authors declare that they have no competing interests.
Authors’ contributions
MZ and CK carried out the synthesis, scanning electron microscopy and X-ray diffraction. The optical properties were measured by AO. The calculations were carried out by MZ who was also wrote the manuscript. All authors read and approved the final manuscript.
Contributor Information
Matthew Zervos, Email: zervos@ucy.ac.cy.
Chrystalla Karipi, Email: karipi.chrystalla@ucy.ac.cy.
Andreas Othonos, Email: othonos@ucy.ac.cy.
References
- Othonos A, Zervos M, Pervolaraki M. Ultra fast carrier relaxation of InN nanowires grown by reactive vapor transport. Nanoscale Res Lett. 2009;8:122. doi: 10.1007/s11671-008-9211-8. [DOI] [Google Scholar]
- Tsokkou D, Othonos A, Zervos M. Defect states of CVD grown GaN nanowires: effects and mechanisms in the relaxation of carriers. J Appl Phys. 2009;8:054311. doi: 10.1063/1.3212989. [DOI] [Google Scholar]
- Zervos M, Othonos A. Gallium hydride vapor phase epitaxy of GaN nanowires. Nanoscale Res Lett. 2011;8:262. doi: 10.1186/1556-276X-6-262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang ZL. Nanostructures of ZnO. Materials Today. 2004;8:26. [Google Scholar]
- Othonos A, Zervos M, Tsokkou D. Tin oxide nanowires: influence of trap states on ultra fast carrier relaxation. Nanoscale Res Lett. 2009;8:828. doi: 10.1007/s11671-009-9323-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zervos M, Othonos A. Synthesis of tin nitride nanowires by chemical vapor deposition. Nanoscale Res Lett. 2009;8:1103. doi: 10.1007/s11671-009-9364-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zervos M, Othonos A. Enhanced growth and photoluminescence properties of SnxNy (x > y) nanowires grown by halide chemical vapor deposition. J Crystal Growth. 2011;8:25. doi: 10.1016/j.jcrysgro.2010.12.029. [DOI] [Google Scholar]
- Zong F, Ma H, Ma J, Du W, Zhang X, Xiao H, Ji F, Xue C. Structural properties and photoluminescence of zinc nitride nanowires. Appl Phys Lett. 2005;8:233104. doi: 10.1063/1.2140086. [DOI] [Google Scholar]
- Zong F, Ma H, Xue C, Du W, Zhang X, Xiao H, Ma J, Ji F. Structural properties of zinc nitride empty balls. Mat Lett. 2006;8:905. doi: 10.1016/j.matlet.2005.10.044. [DOI] [Google Scholar]
- Khan WS, Cao C, Ping DY, Nabi G, Hussain S, Butt FK, Cao T. Optical properties and characterization of zinc nitride nanoneedles prepared from ball-milled Zn powders. Mat Lett. 2011;8:1264. doi: 10.1016/j.matlet.2011.01.040. [DOI] [Google Scholar]
- Khan WS, Cao C. Synthesis, growth mechanism and optical characterization of zinc nitride hollow structures. J Crystal Growth. 1838;8:312. [Google Scholar]
- Futsuhara M, Yoshioka K, Akai OT. Structural, electrical and optical properties of zinc nitride thin films prepared by reactive rf magnetron sputtering. Thin Solid Films. 1998;8:274. [Google Scholar]
- Kamińska E, Piotrowska A, Kossut J, Butkutė R, Dobrowolski W, Łukasiewicz R, Barcz A, Jakieła R, Dynowska E, Przeździecka E, Aleszkiewicz M, Wojnar P, Kowalczyk E. p-type conducting ZnO: fabrication and characterization. Phys Stat Sol. 2005;8:1119. doi: 10.1002/pssc.200460659. [DOI] [Google Scholar]
- Gao J, Zhang X, Sun Y, Zhao Q, Yu D. Compensation mechanism in N-doped ZnO nanowires. Nanotechnology. 2010;8:245703. doi: 10.1088/0957-4484/21/24/245703. [DOI] [PubMed] [Google Scholar]
- Yang X, Wolcott A, Wang G, Sobo A, Fitzmorris RC, Qian F, Zhang JZ, Li Y. Nitrogen-doped ZnO nanowire arrays for photoelectrochemical water splitting. Nano Lett. 2009;8:2331. doi: 10.1021/nl900772q. [DOI] [PubMed] [Google Scholar]
- Zervos M, Karipi C, Othonos A. The nitridation of ZnO nanowires. Nanoscale Res Lett. 2012;8:175. doi: 10.1186/1556-276X-7-175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z, Wang P, Chen H, Cheng X. Structural, electronic and thermodynamic properties of cubic Zn3N2 under high pressure from first-principles calculations. Physica B. 2011;8:1182. doi: 10.1016/j.physb.2011.01.001. [DOI] [Google Scholar]
- Partin DE, Williams DJ, O'Keeffe M. Synthesis, stoichiometry and thermal stability of Zn3N2 powders prepared by ammonolysis reactions. J Solid State Chem. 1997;8:56. doi: 10.1006/jssc.1997.7407. [DOI] [Google Scholar]
- Othonos A, Lioudakis E, Tsokkou D, Philipose U, Ruda HE. Ultrafast time-resolved spectroscopy of ZnSe nanowires: carrier dynamics of defect-related states. J Alloys Comp. 2009;8:600. doi: 10.1016/j.jallcom.2008.07.197. [DOI] [Google Scholar]
- Kuriyama K, Takahashi Y, Sunohara F. Optical band-gap of Zn3N2 films. Phys Rev B. 1993;8:2781. doi: 10.1103/PhysRevB.48.2781. [DOI] [PubMed] [Google Scholar]
- Ebru ST, Hamide K, Ramazan E. Structural and optical properties of zinc nitride films prepared by pulsed filtered cathodic vacuum arc deposition. Chin Phys Lett. 2007;8:3477. doi: 10.1088/0256-307X/24/12/051. [DOI] [Google Scholar]
- Othonos A, Zervos M, Christofides C. Carrier dynamics in β-Ga2O3 nanowires. J Appl Phys. 2010;8:124302. doi: 10.1063/1.3520589. [DOI] [Google Scholar]
- Long R, Dai Y, Yu L, Guo M, Huang B. Structural, electronic, and optical properties of oxygen defects in Zn3N2. J Phys Chem B. 2007;8:3379. doi: 10.1021/jp0667902. [DOI] [PubMed] [Google Scholar]
- Suda T, Kakishita K. Band-gap energy and electron effective mass of polycrystalline Zn3N2. J Appl Phys. 2006;8:076101. doi: 10.1063/1.2180541. [DOI] [Google Scholar]
- Bär M, Ahn KS, Shet S, Yan Y, Weinhardt L, Fuchs O, Blum M, Pookpanratana S, George K, Yang W, Denlinger JD, Al-Jassim M, Heske C. Impact of air exposure on the chemical and electronic structure of ZnO:Zn3N2 thin films. Appl Phys Lett. 2009;8:012110. doi: 10.1063/1.3056638. [DOI] [Google Scholar]
- Janoti A, Van de Walle CG. Fundamentals of zinc oxide as a semiconductor. Rep Prog Phys. 2009;8:126501. doi: 10.1088/0034-4885/72/12/126501. [DOI] [Google Scholar]
- Tisdale WA, Muntwiler M, Norris DJ, Aydil ES, Zhu XY. Electron dynamics at the ZnO (10-10) surface. J Phys Chem C. 2008;8:14682. doi: 10.1021/jp802455p. [DOI] [Google Scholar]
- Janotti A, Van de Walle CG. Fundamentals of zinc oxide as a semiconductor. Rep Prog Phys. 2009;8:126501. doi: 10.1088/0034-4885/72/12/126501. [DOI] [Google Scholar]
- Zervos M, Feiner LF. Properties of the ubiquitous p-n junction in semiconductor nanowires. J Appl Phys. 2004;8:1. doi: 10.1063/1.1631749. [DOI] [Google Scholar]
- Zervos M. Properties of the ubiquitous p-n junction in semiconductor nanowires. Semiconductor Sci Technol. 2008;8:075016. doi: 10.1088/0268-1242/23/7/075016. [DOI] [Google Scholar]
- Mohamed HA. Structure and optical constants of electron beam deposited zinc nitride films. Opt Adv Mater Rapid Comm. 2009;8:553. [Google Scholar]
- Oshikiri M, Imanaka Y, Aryasetiawan F, Kido G. Comparison of the electron effective mass of the n-type ZnO in the wurtzite structure measured by cyclotron resonance and calculated from first principle theory. Physica B. 2001;8:472. doi: 10.1016/S0921-4526(01)00365-9. [DOI] [Google Scholar]
- Morkoç H, Uzgür U. Zinc Oxide, Fundamentals. New York, Wiley: Materials and Device Technology; 2009. [Google Scholar]