Orphan spin operators enable the acquisition of multiple 2D and 3D magic angle spinning solid-state NMR spectra

Abstract

We propose a general method that enables the acquisition of multiple 2D and 3D solid-state NMR spectra for U-¹³C, ¹⁵N-labeled proteins. This method, called MEIOSIS (Multiple ExperIments via Orphan SpIn operatorS), makes it possible to detect four coherence transfer pathways simultaneously, utilizing orphan (i.e., neglected) spin operators of nuclear spin polarization generated during ¹⁵N-¹³C cross polarization (CP). In the MEIOSIS experiments, two phase-encoded free-induction decays are decoded into independent nuclear polarization pathways using Hadamard transformations. As a proof of principle, we show the acquisition of multiple 2D and 3D spectra of U-¹³C, ¹⁵N-labeled microcrystalline ubiquitin. Hadamard decoding of CP coherences into multiple independent spin operators is a new concept in solid-state NMR and is extendable to many other multidimensional experiments. The MEIOSIS method will increase the throughput of solid-state NMR techniques for microcrystalline proteins, membrane proteins, and protein fibrils.

INTRODUCTION

Solid-state NMR (ssNMR) is the method of choice for probing structure, dynamics, chemistry, and ligand binding of microcrystalline and membrane-bound proteins at the atomic resolution.¹ Sensitivity and resolution of the resonances (typically ¹H, ¹³C, and ¹⁵N) in multidimensional NMR spectra are fundamental requirements for protein structural analysis. In spite of the most recent progress, multidimensional ssNMR experiments still require many days or weeks of spectrometer time.

A central element in the ssNMR experiment is cross-polarization (CP), which enables the polarization transfer from high to low gyromagnetic ratio nuclei.² During CP, multiple spin nuclear excitation pathways are generated.³ However, only selected spin operators are transformed into detectable coherences, whereas several other pathways are discarded. While in liquid-state NMR there are several pulse sequences designed to detect discarded coherences via dual receivers or phase cycling schemes,⁴ in ssNMR there are only a few examples that utilize orphan (i.e., neglected) spin operators to boost sensitivity.^{5, 6, 7, 8, 9, 10, 11, 12, 13} In general, classical ssNMR pulse sequences eliminate orphan spin operators of magnetization either using z-filters or phase cycling schemes that suppress the spectral artifacts arising from undesired coherence transfer pathways.¹⁴ Recently, we proposed new pulse schemes to recover orphan spin operators originating from chemical shift or dipolar coupling Hamiltonians, and convert them into observable coherences to enhance the sensitivity of static ssNMR experiments.^{5, 6, 7, 8} For rotating solids, we developed the dual acquisition magic angle spinning (DUMAS) approach,^{9, 10} which uses simultaneous cross-polarization (SIM-CP) between ¹H, ¹³C, and ¹⁵N and enable the simultaneous acquisition of two 2D or 3D experiments.

In this article, we present a new method, MEIOSIS (Multiple ExperIments via Orphan SpIn operatorS) that enables one to simultaneously acquire multiple multidimensional NMR spectra of uniformly ¹³C, ¹⁵N-labeled proteins. This new method utilizes two elements that were instrumental for the DUMAS approach: SIM-CP and long-living ¹⁵N polarization. However, MEIOSIS also exploits the residual magnetization of NCA or NCO from specific-CP to generate phase-encoded coherence pathways that are decoded into four independent spectra using Hadamard transformations. To demonstrate the power of this method, we simultaneously acquired four 2D experiments (DARR,¹⁵ N(CA)CX, NCO, and CA(N)CO¹⁶) and three 3D experiments (NCACX, NCOCX, and CA(N)COCX^{17, 18}) on a U-¹³C, ¹⁵N-labeled microcrystalline ubiquitin. Hadamard decoding the coherences into multiple independent spin operators is a general concept in NMR and can be used to redesign many pulse sequences.

THEORY

The MEIOSIS method utilizes the polarization from four pathways generated during the specific-CP transfer between ¹⁵N and ¹³C nuclei. Not only does this new pulse scheme detect the transferred polarization from ¹⁵N to ¹³C and vice versa, but it also recovers the residual magnetization of ¹⁵N and ¹³C that is not transferred during the specific-CP. To encode the four different pathways, the ¹⁵N specific-CP pulse scheme is implemented with a phase alternation (+x, −x), resulting to two explicit acquisitions for each scan. The four polarization pathways are then decoded via Hadamard processing into multiple 2D or 3D experiments.

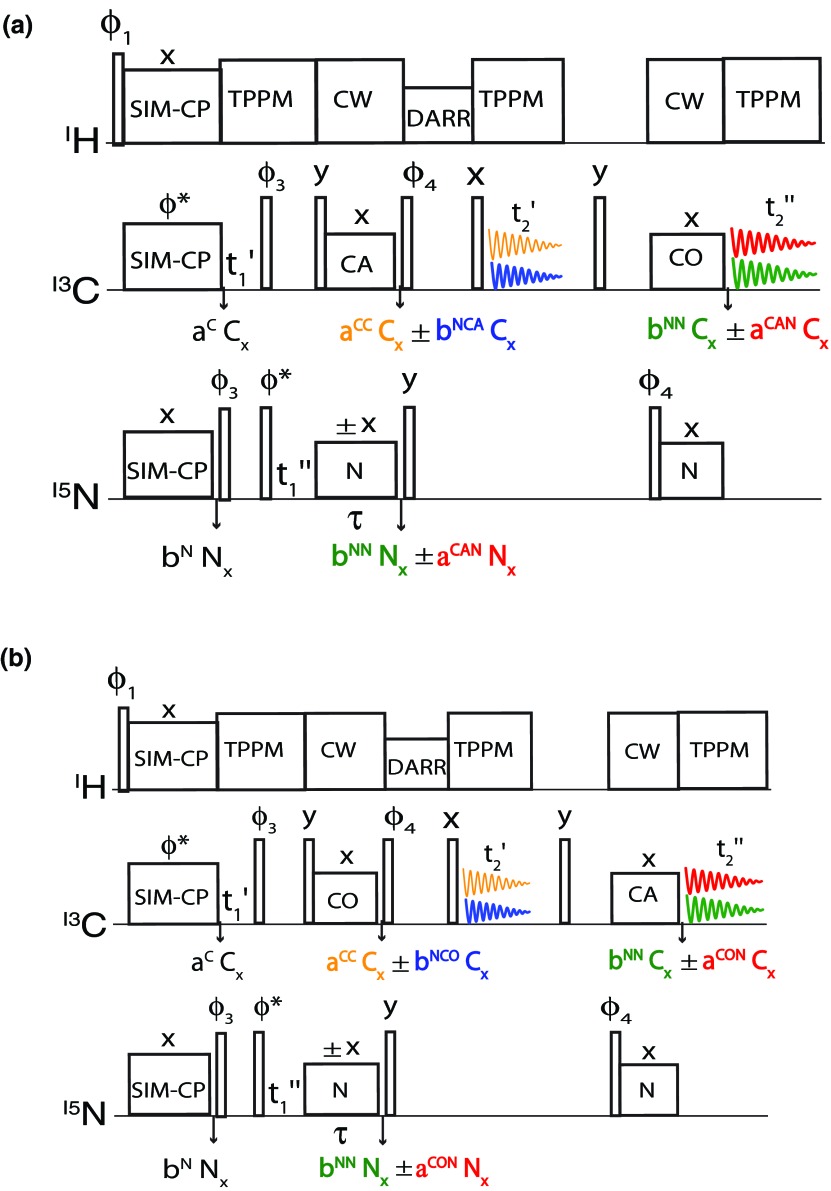
An example of a pulse sequence designed with this MEIOSIS scheme is reported in Fig. 1a. After a 90° pulse on ¹H, a SIM-CP sequence transfers the magnetization from ¹H to ¹³C and ¹⁵N. A 90° pulse with phase ϕ₃ brings the ¹⁵N magnetization in the z-direction, while ¹³C magnetization evolves during ${\mathrm{t}}_1^{\prime }$. A pair of 90° pulses on ¹³C and ¹⁵N aligns the ¹³C magnetization along z and tips the ¹⁵N magnetization in the x-axis, whose chemical shift evolves during ${\mathrm{t}}_1^{″}$ under ¹H decoupling. A 90° pulse tilts the ¹³C magnetization on the x-axis and a specific-CP¹⁹ is applied between ¹⁵N and ¹³Cα. The MEIOSIS method enables one to recover residual magnetization during the bidirectional polarization transfer⁹ from N to Cα and Cα to N (i.e., NCA/CAN transfer), which makes it possible to obtain multiple spectra simultaneously.

Figure 1.

(a) 2D MEIOSIS pulse sequence for simultaneous acquisition of four experiments: DARR, N(CA)CX, NCO, and CA(N)CO. (b) MEIOSIS pulse sequence with CON and CAN transfers inverted. The phase cycle of 2D MEIOSIS and conventional pulse sequences of Fig. 1S of the supplementary material³⁶ are given by: ϕ₁ = (y)₄, (−y)₄, ϕ₂ = (x, x, −x, −x)₂, ϕ₃ = (y, −y)₄, ϕ₄ = (y, y, −y, −y)₂, and ϕ_rec = (x, −x, −x, x, −x, x, x, −x). For indirect dimension, states mode acquisition is obtained by alternating the ϕ* between x and y.

Encoding four independent polarization pathways

To understand the theoretical basis of this method, we analyze the CP dynamics for a two-spin system (N-CA) in the double quantum (DQ), and zero quantum (ZQ) sub-spaces.³

Let N_i and ${\mathrm{C}}_{\mathrm{i}}^{\alpha }$ (i = x, y, z) be the Pauli spin matrices for ¹⁵N and ¹³C^α (or CA), respectively. In Fig. 1a at ${\mathrm{t}}_1^{\prime }=t_1^{″}=0$, the density matrix prior to NCA/CAN transfer is given by

$$\rho (t_1=0)\propto a^{C_{\alpha }}·C_x^{\alpha }+b^N·N_x,$$ (1)

where the a^Cα and b^N coefficients represent the initial ¹³C and ¹⁵N polarizations, respectively.

To describe the dipolar spin Hamiltonian during specific-CP of time τ, we consider on resonance continuous wave RF irradiations with phase +x on ¹³C and phase +x on ¹⁵N, and with RF amplitudes ω_1C and ω_1N, respectively. Under these conditions the Hamiltonian can be written as

$$H\left(\tau \right)=H_D\left(\tau \right)+H_{RF},$$ (2)

where $H_D\left(\tau \right)=D\left(\tau \right)·2C_z^{\alpha }{N}_z$ and $H_{RF}={\omega }_{1C}{C}_x^{\alpha }+{\omega }_{1N}{N}_x,$$D\left(\tau \right)={\sum }_{n=\pm 1,\pm 2}{D}_n·e^{in{\omega }_r\tau },$D_±1 = d¹·e^±iγ, D_±2 = d² · e^±i2γ, $d^1=\frac{d}{2\sqrt{2}}·\sin \left(2\beta \right),d^2=\frac{d}{4}·{\sin }^2\beta ,$ and $d=-\left(\frac{{\mu }_0}{4\pi }\right)\left(\frac{{\gamma }_C·{\gamma }_N·\hslash }{r^3}\right).$

The angles β and γ describe the orientation of the internuclear vector with respect to the rotor frame, d is the ¹⁵N-¹³C dipolar coupling constant, and ω_r is the MAS spinning frequency. In a doubly tilted rotating (DTR) frame defined by the operator U₁, the resultant Hamiltonian and density matrix are given by H^T and ${\rho }_{+}^T$:

$$\begin{array}{ccc}\hfill U_1& =& e^{-i\frac{\pi }{2}{C}_y^{\alpha }}·e^{-i\frac{\pi }{2}{N}_y},\hfill \\ \hfill H^T\left(\tau \right)& =& D\left(\tau \right)·2C_x^{\alpha }{N}_x+{\omega }_{1C}{C}_z^{\alpha }+{\omega }_{1N}{N}_z,\hfill \\ \hfill {\rho }_{+}^T& \propto & a^{C_{\alpha }}·C_z^{\alpha }+b^N·N_z,\hfill \end{array}$$ (3)

where the positive sign of ${\rho }_{+}^T$ indicates the +x phase of ¹⁵N spin lock during specific-CP. At the Hartmann-Hahn side band matching condition (ω_1c − ω_1N = ±ω_r or ± 2ω_r), the dipolar recoupling can be represented by transforming the time-dependent Hamiltonian into a time-independent Hamiltonian in the interacting frame U₂:¹⁹

$$\begin{array}{ccc}\hfill U_2& =& e^{-i{\omega }_{1C}{C}_z^{\alpha }\tau }·e^{-i{\omega }_{1N}{N}_z\tau },\hfill \\ \hfill {\rho }_{+}^{T^{*}}& =& U_2^{-1}·{\rho }^T·U_2={\rho }^T,\hfill \\ \hfill H^{T^{*}}& =& U_2^{-1}·H^T·U_2=d^n·e^{in\gamma }·2\left(C_x^{\alpha }{N}_x+C_y^{\alpha }{N}_y\right).\hfill \end{array}$$ (4)

To describe the density matrix evolution, we define the ZQ and DQ operators³ as follows:

$$\begin{array}{ccc}\hfill Z{Q}_x& =& 2C_x^{\alpha }{N}_x+2C_y^{\alpha }{N}_y,Z{Q}_y=2C_y^{\alpha }{N}_x-2C_x^{\alpha }{N}_y,\hfill \\ \hfill Z{Q}_z& =& C_z^{\alpha }-N_z,\hfill \\ \\ \hfill D{Q}_x& =& 2C_x^{\alpha }{N}_x-2C_y^{\alpha }{N}_y,D{Q}_y=2C_y^{\alpha }{N}_x+2C_x^{\alpha }{N}_y,\hfill \\ \hfill D{Q}_z& =& C_z^{\alpha }+N_z.\hfill \end{array}$$ (5)

Therefore, the density matrix and Hamiltonian can be expressed as

$$\begin{array}{c}{\rho }_{+}^T\propto \frac{a^{C_{\alpha }}.}{2}(Z{Q}_z+D{Q}_z)-\frac{b^N}{2}.(Z{Q}_z-D{Q}_z),\hfill \\ H^{T^{*}}=d^n.e^{in\gamma }·Z{Q}_x.\hfill \end{array}$$ (6)

During the specific-CP sequence of time τ, the DQ_z term does not evolve under the Hamiltonian, while ZQ_z evolves into ZQ_y. For a specific crystalline orientation (defined by the β and γ angles), the NMR signal for n = ±1 matching conditions oscillates with a frequency d¹, and for n = ±2 with frequency d². The resultant density matrix for all crystal orientations can be written as

$$\begin{array}{ccc}\hfill {\rho }_{+}^T& \stackrel{H^{T^{*}}\left(\tau \right)}{\to }& \frac{1}{2}\sum _{\beta ,\gamma }{a}^{C_{\alpha }}[Z{Q}_z\cos (d^n·\tau )\hfill \\ & & -Z{Q}_y\sin (d^n·\tau )+D{Q}_z]\hfill \\ & & -b^N[Z{Q}_z\cos (d^n·\tau )-Z{Q}_y\sin (d^n·\tau )-D{Q}_z].\hfill \end{array}$$ (7)

A ${90}_{-\mathrm{y}}^{\circ }$ rotation ($U_1^{-1}$) is applied to back transform the operators from the DTR frame to the rotating frame. The latter converts the C_z^α and N_z of Eq. 7 into single quantum (SQ) operators C_x^α and N_x. Considering only the contribution of single spin operators, Eq. 7 can be written as

$$\begin{array}{ccc}\hfill {\rho }_{+}\left(\tau \right)& \propto & \sum _{\beta ,\gamma }{a}^{C_{\alpha }}·\left[C_x^{\alpha }{\cos }^2\left(d^n·\frac{\tau }{2}\right)+N_x{\sin }^2\left(d^n·\frac{\tau }{2}\right)\right]\hfill \\ & & +b^N·\left[N_x{\cos }^2\left(d^n·\frac{\tau }{2}\right)+C_x^{\alpha }{\sin }^2\left(d^n·\frac{\tau }{2}\right)\right]\hfill \\ & \propto & a^{CC}·C_x^{\alpha }+a^{CAN}·N_x+b^{NN}·N_x+b^{NCA}·C_x^{\alpha },\hfill \end{array}$$ (8)

where a^CC and a^CAN represent the ¹³Cα residual (i.e., not transferred to ¹⁵N) and ¹⁵N transferred (from ¹³Cα to ¹⁵N) magnetization resulting from all crystal orientations; while b^NN and b^NCA represent the ¹⁵N residual and ¹³Cα transferred magnetization, respectively. Although experimentally detectable (Fig. 2), the residual and transferred magnetization is difficult to quantify theoretically using a two-spin model. In fact, the oscillations of the operators for multiple-spin systems are attenuated by several factors, including the ¹³C and ¹⁵N homo- and hetero-nuclear dipolar coupling network, insufficient ¹H decoupling power, T_1ρ relaxation, and RF inhomogeneity. Note that the density matrix in Eq. 8 is represented by four independent pathways encoded into single quantum coherences. After specific-CP, the polarization of four pathways is tilted along z direction by applying two 90° pulses on ¹⁵N and ¹³C. The longitudinal relaxation of ¹⁵N is long-living on the order of a few seconds. Therefore, the ¹⁵N polarization can be stored for several milliseconds without sensitivity loss. At the same time, the ¹³C polarization of CC and NCA pathways undergoes homonuclear spin exchange during the DARR mixing time, which is then detected by a 90° readout pulse followed by ${\mathrm{t}}_2^{\prime }$ acquisition. At zero DARR mixing period and ${\mathrm{t}}_2^{\prime }=0$, the density matrix becomes

$$\begin{array}{c}\hfill {\rho }_{+}\propto {\left(a^{CC}·C_x^{\alpha }+b^{NCA}·C_x^{\alpha }\right)}_{1st-acq}+\left(b^{NN}{N}_z+a^{CAN}{N}_z\right).\end{array}$$ (9)

The first term of Eq. 9 is acquired during ${\mathrm{t}}_2^{\prime }$, while the second term representing the ¹⁵N magnetization is stored along z. After the first acquisition, any longitudinal or transverse ¹³C magnetization is suppressed by a 3 ms period followed by a 90° pulse and another 3 ms period. At this point, a 90° pulse on ¹⁵N followed by NCO specific-CP transfers the magnetization from ¹⁵N to ¹³C′. The magnetization of both CAN and NN pathways is transferred to ¹³C′, which is recorded during the second acquisition period ${\mathrm{t}}_2^{″}$. The resultant density matrix (ρ₊) for each scan is the sum of two density matrices associated with 1st and 2nd acquisitions that are recorded in two different memory locations:

$$\begin{array}{ccc}\hfill {\rho }_{+}& \propto & {\left(a^{CC}{C}_x^{\alpha }+b^{NCA}{C}_x^{\alpha }\right)}_{1\mathrm{st}-\mathrm{acqu}}\hfill \\ & & +{\left(b^{N{N}^{*}}{C}_x^{\prime }+a^{CA{N}^{*}}{C}_x^{\prime }\right)}_{2\mathrm{nd}-\mathrm{acq}}\hfill \\ & \propto & {\left({\rho }^{CC}+{\rho }^{NCA}\right)}_{1\mathrm{st}-\mathrm{acqu}}+{\left({\rho }^{N{N}^{*}}+{\rho }^{CA{N}^{*}}\right)}_{2\mathrm{nd}-\mathrm{acqu}}.\hfill \end{array}$$ (10)

Due to the second specific-CP, the amplitudes of the spin operators a^CAN and a^NN are reduced by a factor of 2–3 and are marked with an asterisk in Eq. 10.¹⁸ In order to encode the operators of the density matrix in each acquisition, we record another scan with the phase of the ¹⁵N RF flipped to −x during first specific-CP, while that of ¹³C is kept at +x. The phase flip can either be incorporated in to Hamiltonian or in the initial density matrix. In the latter case, the operator formalisms of ZQ_z and DQ_z are inverted, and they become (C_z + N_z) and (C_z − N_z), respectively. By substituting these operators in Eq. 7 and considering only SQ coherences, the resultant density matrix, ρ₂, is

$$\begin{array}{ccc}\hfill {\rho }_{-}\left(\tau \right)& \propto & \sum _{\gamma }2a^{C_{\alpha }}\left[C_x^{\alpha }{\cos }^2\left(d^n\tau \right)-N_x{\sin }^2\left(d^n\tau \right)\right]\hfill \\ & & +2b^N\left[N_x{\cos }^2\left(d^n\tau \right)-C_x^{\alpha }{\sin }^2\left(d^n\tau \right)\right]\hfill \\ & \propto & a^{CC}{C}_x^{\alpha }-a^{CAN}{N}_x+b^{NN}{N}_x-b^{NCA}{C}_x^{\alpha }.\hfill \end{array}$$ (11)

In analogy with Eqs. 8, 9, 10, the resultant density matrix of two acquisitions is given by

$$\begin{array}{ccc}\hfill {\rho }_{-}& \propto & {\left(a^{CC}{C}_x^{\alpha }-b^{NCA}{C}_x^{\alpha }\right)}_{1\mathrm{st}-\mathrm{acqu}}\hfill \\ & & +{\left(b^{N{N}^{*}}{C}_x^{\prime }-a^{CA{N}^{*}}{C}_x^{\prime }\right)}_{2\mathrm{nd}-\mathrm{acq}}\hfill \\ & \propto & {\left({\rho }^{CC}-{\rho }^{NCA}\right)}_{1\mathrm{st}-\mathrm{acqu}}+{\left({\rho }^{N{N}^{*}}-{\rho }^{CA{N}^{*}}\right)}_{2\mathrm{nd}-\mathrm{acqu}}.\hfill \end{array}$$ (12)

As for Eq. 10, the first acquisition in Eq. 12 gives the ¹³C spectrum resulting from NCA and CC pathways, but with an inverted sign for the NCA transfer, and the second acquisition gives NN and CAN pathways, with an inverted sign for the CAN pathway. The free-induction decay (FID) signals (G_±) of the corresponding density matrices (ρ±) can be calculated as follows:

$$\begin{array}{ccc}\hfill {\rho }_{\pm }(t_2^{\prime },t_2^{″})& \propto & {\left[{\rho }^{CC}{(\mathrm{t}}_2^{\prime })\pm {\rho }^{NCA}\left(t_2^{\prime }\right)\right]}_{1\mathrm{st}-\mathrm{acqu}}\hfill \\ & & +{\left[{\rho }^{N{N}^{*}}{(\mathrm{t}}_2^{″})\pm {\rho }^{CA{N}^{*}}\left(t_2^{″}\right)\right]}_{2\mathrm{nd}-\mathrm{acqu}},\hfill \\ \hfill {\mathrm{G}}_{\pm }& \propto & Tr\left[C_x·{\rho }_{\pm }(t_2^{\prime },t_2^{″})\right].\hfill \end{array}$$ (13)

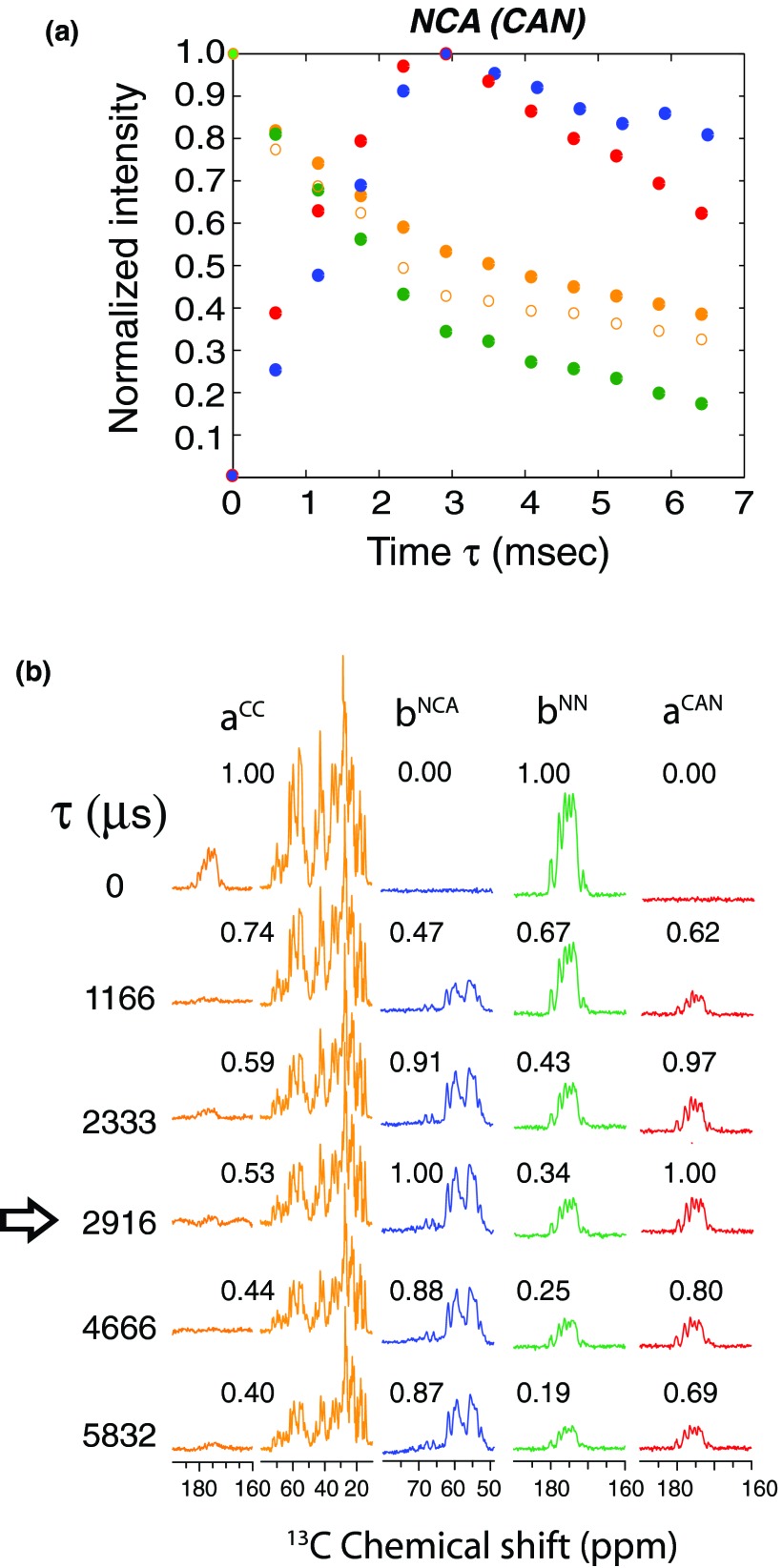
Figure 2.

(a) Experimental plot of ubiquitin showing the normalized intensities of four pathways during NCA (or CAN) transfer, as a function of specific-CP contact time (τ). Each data point is obtained by integrated intensities of the 1D spectra shown in (b), by using the pulse sequence of Fig. 1a with $t_1^{\prime }$, $t_1^{″}$, and DARR mixing period set to zero. The maximum intensity of each pathway is normalized to one. The data points (a) and the corresponding spectra in (b) are color-coded according to respective pathways shown in Fig. 1. Open and closed orange colored circles indicate Cα (50–75 ppm) and aliphatic carbon region (0–75 ppm) intensities. The arrow indicates the optimal contact time (2916 μs) for maximum NCA and CAN transfer. The residual magnetization at 2916 μs corresponds to ∼34% for ¹⁵N and ∼43% for the ¹³Cα (50–75 ppm) and 54% for ¹³C aliphatic (0–75 ppm) resonances. The residual magnetization of C′ region is less than 5% due to insufficient spin lock field.

Decoding the four independent pathways

In order to decode the four spin operators (CC, NCA, NN, and CAN, Fig. 1a), we need to consider the signs of four operators (Eqs. 10, 11, 12, 13) that resemble the rows of the four-dimensional Hadamard matrix. For the ¹⁵N spin-lock with phase +x (Eq. 10), the density matrices are +ρ^CC, +ρ^NCA, +ρ^NN, and +ρ^CAN; while for the −x phase (Eq. 12) the density matrices are +ρ^CC, −ρ^NCA, +ρ^NN, and −ρ^CAN. By summing the two data sets in the first acquisition, the two CC components are added, while the NCA operator cancels out. On the other hand, by subtracting the two data sets, the NCA transfer corresponds to the sum of the two NCA components, while the CC operator cancels out. Similarly, the addition and subtraction of two data sets for the second acquisition will give magnetization resulting from NN and CAN pathways, respectively. The decoded FID signal can be calculated as follows:

$$\begin{array}{ccc}\hfill G_{sum}& =& G_{+}+G_{-}=Tr\left\{{\left[2C_x·{\rho }^{CC}\left(t_2^{\prime }\right)\right]}_{1st\text{-}acqu}\right.\hfill \\ & & \left.+{\left[2C_x·{\rho }^{N{N}^{*}}\left(t_2^{″}\right)\right]}_{2nd\text{-}acqu}\right\},\hfill \\ \\ \hfill G_{diff}& =& G_{+}-G_{-}=Tr\left\{{\left[2C_x·{\rho }^{NCA}\left(t_2^{\prime }\right)\right]}_{1st\text{-}acqu}\right.\hfill \\ & & \left.+{\left[2C_x·{\rho }^{CA{N}^{*}}\left(t_2^{″}\right)\right]}_{2nd\text{-}acqu}\right\}.\hfill \end{array}$$ (14)

Note that G_sum and G_diff are decoded FID signals of two separate scans, G+ and G−.

For a 2D experiment with evolution time ${\mathrm{t}}_1^{\prime }$ or ${\mathrm{t}}_1^{″}$ and ¹³C homonuclear spin exchange during DARR mixing period, the density matrices become

$$\begin{array}{ccc}\hfill G_{sum}& =& G_{+}+G_{-}=\sum _{i}Tr\left\{{\left[2C_{ix}·{\rho }_i^{CC}(t_2^{\prime },t_2^{\prime })\right]}_{1st\text{-}acqu}^{DARR}\right.\hfill \\ & & \left.+{\left[2C_{ix}·{\rho }_i^{N{N}^{*}}(t_1^{″},t_2^{″})\right]}_{2nd\text{-}acqu}^{NCO}\right\},\hfill \\ \\ \hfill G_{diff}& =& G_{+}-G_{-}=\sum _{i}Tr\left\{{\left[2C_{ix}·{\rho }_i^{NCA}(t_1^{″},t_2^{\prime })\right]}_{1st\text{-}acqu}^{NCACX}\right.\hfill \\ & & \left.+{\left[2C_x·{\rho }_i^{CA{N}^{*}}(t_1^{\prime },t_2^{″})\right]}_{2nd\text{-}acqu}^{CANCO}\right\},\hfill \end{array}$$ (15)

where the summation index i represents each of the ith carbon spins that contribute to the signal.

In the above theoretical treatment, during NCA/CAN transfer we considered the residual magnetization for ¹³Cα and ¹⁵N only. However, as will be shown in the Results and Discussion section, in addition to Cα one can also obtain the residual magnetization for the carbonyl and side chain carbons. In other words, there will be a CC pathway associated with backbone and side-chain carbon atoms that will contribute to the DARR spectrum.

The 2D MEIOSIS method (Fig. 1a) can be extended to 3D experiments (Fig. 4a) by incorporating an additional ¹³C evolution period prior to the first and second acquisitions. Three 3D experiments, NCACX, NCOCX, and CA(N)COCX, are obtained from NCA, NN, and CAN pathways, respectively (Fig. 2). The ¹⁵N ${\mathrm{t}}_1^{\prime }$ evolutions of NCACX and NCOCX are synchronized with ¹³Cα ${\mathrm{t}}_1^{″}$ of CA(N)COCX, whereas ¹³Cα ${\mathrm{t}}_2^{\prime }$ evolution of NCACX is synchronized with ¹³CO ${\mathrm{t}}_2^{″}$ evolution of CA(N)COCX and NCOCX. Unlike 2D MEIOSIS, in the 3D experiment the residual ¹³C magnetization a^CC is discarded. In fact, the chemical shift of the CC pathway evolves similarly during ${\mathrm{t}}_1^{\prime }$ and ${\mathrm{t}}_2^{\prime }$, and at longer dwell times gives an aliased 2D DARR spectrum along the 2D plane formed by F1′-F2′ diagonal and F3 axis.

Figure 4.

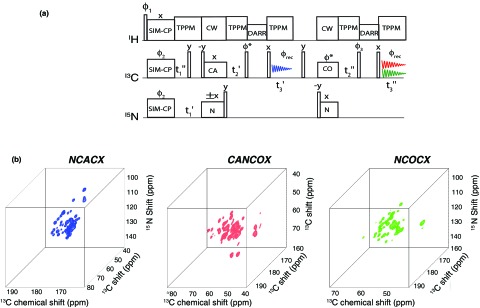
Three-dimensional MEIOSIS pulse sequence for simultaneous acquisition of three 3D spectra: NCACX, NCOCX, and CAN(CO)CX. The phase cycle is given by ϕ₁ = (y, −y)₂, ϕ₂ = x, x, −x, −x, and ϕ_rec = x, −x, −x, x. Sates mode acquisition of indirect dimensions is obtained by alternating ϕ₂, and ϕ* phases between x and y.

RESULTS AND DISCUSSION

To analyze the amplitudes of the four pathways as a function of NCA/CAN specific-CP contact time, we carried out a series of 1D experiments on U-¹³C, ¹⁵N ubiquitin using the pulse sequence shown in Fig. 1a without DARR mixing period, and ${\mathrm{t}}_1^{\prime }$ and ${\mathrm{t}}_1^{″}$ set to zero. Fig. 2 shows the amplitudes of the four pathways obtained from the integrated intensities of the 1D spectra at various specific-CP contact times. The data points and corresponding spectra in Figs. 2a, 2b are color-coded according to the individual pathways. The maximum of the NCA/CAN transfer occurs at approximately 3 ms contact time, and the residual magnetization corresponds to ∼34% for ¹⁵N, ∼43% for the ¹³Cα (50–75 ppm). Remarkably, the residual magnetization of the ¹³C aliphatic (0–75 ppm) resonances is ∼53%! During the NCA/CAN transfer, the ¹³C spin-lock sequence creates an effective field on the Cα region, while the carbonyl magnetization dephases due to insufficient RF amplitude of the spin-lock. Hence, the residual magnetization for ¹³C′ resonances is less than 5% (Fig. 2b). At the end of the τ period, all of the ¹³C resonances should be encoded into the C_x spin operators (Eq. 8). However, we detected a small C_y component (∼5%) for resonances in the frequency range corresponding to 0–30 ppm, which gives mixed phase (absorptive and dispersive) line shapes. The latter is due to an offset-dependent evolution of the magnetization during ¹³C spin-lock field applied at 60 ppm. To eliminate this out-of-phase C_y component, we applied a phase cycle ϕ₄, which allows the acquisition of pure absorptive lines. Note that in 2D experiments phase cycle ϕ₄ is not required as the DARR mixing period suppresses the C_y components.

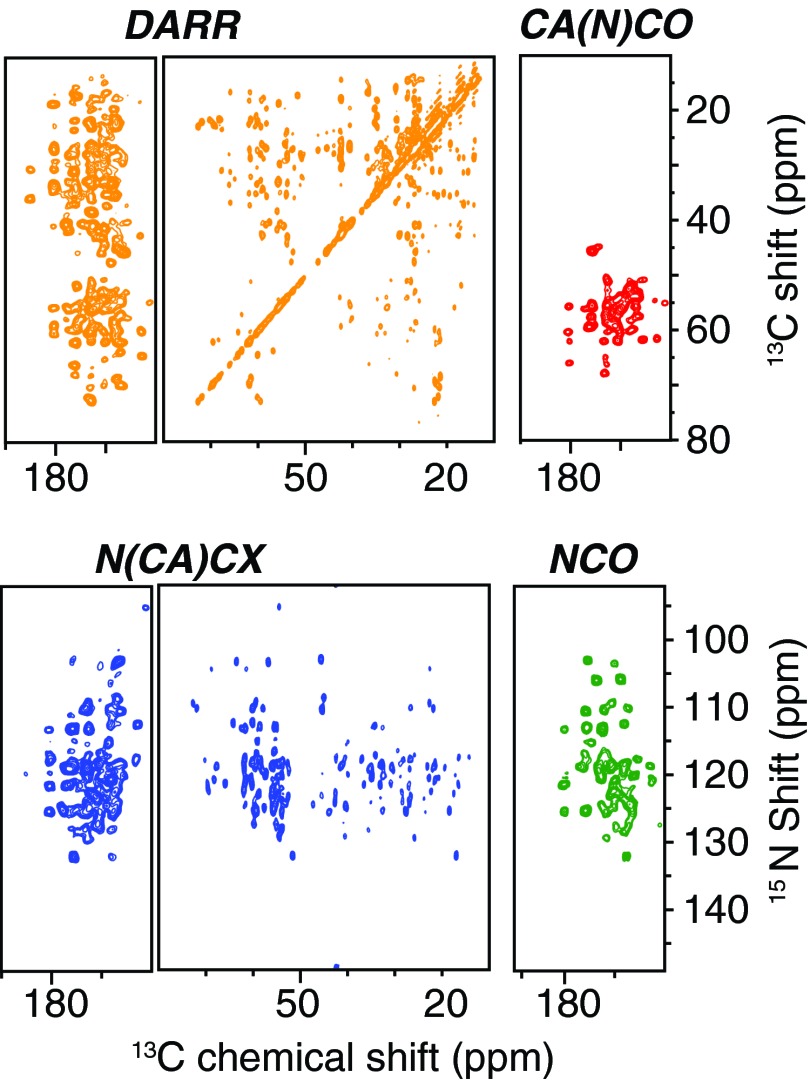
We tested the 2D MEIOSIS pulse sequence for the simultaneous acquisition of four 2D spectra of U-¹⁵N,¹³C labeled sample of microcrystalline ubiquitin (Fig. 3) and compared the results with conventional experiments (Fig. 1S of the supplementary material).³⁶ The total experimental time for conventional experiments was ∼62 h, with DARR and NCACX experiments lasting 7 and 22 h, respectively, and NCO and CA(N)CO experiments 3.5 and 28 h, respectively (Fig. 2S of the supplementary material).³⁶ Remarkably, the total experimental time for the four experiments acquired simultaneously with the MEIOSIS sequence was ∼29 h, cutting experimental time by more than 50%. The sensitivity of each of the four spectra obtained from MEIOSIS is similar to the corresponding conventional experiments, as demonstrated in both the 1D spectra and contour plots reported in Fig. 3S of the supplementary material.³⁶

Figure 3.

Simultaneous acquisition of four 2D spectra using the MEIOSIS pulse sequence reported in Fig. 1a.

The MEIOSIS experiment requires the optimization of indirect evolution times, taking into account both sensitivity and resolution of individual experiments. In 2D MEIOSIS, for instance, the ${\mathrm{t}}_1^{\prime }$ evolution for DARR and CA(N)CO are time shared, therefore, the indirect spectral widths for these two spectra are identical. Note that it is possible to reduce the spectral width in the ${\mathrm{F}}_1^{\prime }$ dimension (frequency domain of ${\mathrm{t}}_1^{\prime }$) by taking into account the aliasing of carbonyl resonances of the DARR spectrum. The ¹³C spectral width of DARR and CA(N)CO can be reduced by increasing the dwell time to 60–80 μs. The reduced ¹³C spectral width in the DARR experiment can be a significant advantage for MEIOSIS experiments, as during NCA specific-CP the residual magnetization of ¹³CO as well as aromatic resonances is reduced to ∼5% of total intensity (Fig. 2), which leads to negligible aliased peaks. However, for accurate comparison between conventional and 2D MEIOSIS experiments we used the full ¹³C spectral width (0–185 ppm) during ${\mathrm{t}}_1^{\prime }$.

The MEIOSIS scheme of Fig. 1a can also be reversed by setting the first and second specific-CP to NCO and NCA transfers, respectively (Fig. 1b). The resultant experiment allows simultaneous acquisition of the DARR, N(CO)CX, CO(N)CA, and NCA experiments. In the absence of DARR mixing time, the experimental amplitudes for the four pathways in the NCO/CON transfer with ${\mathrm{t}}_1^{\prime }={\mathrm{t}}_1^{″}=0$, are shown in Fig. 4S of the supplementary material.³⁶ The NCO/CON transfer, however, requires higher RF amplitudes for ¹³C (7/2ω_r = 45.5 kHz) compared to the NCA/CAN transfer (3/2ω_r = 19.5 kHz), and the ¹³C offset is now centered at the carbonyl region. As shown in Fig. 4S of the supplementary material,³⁶ the residual magnetization for ¹³C is ∼53% for the Cα region (50–75 ppm) and 46% for the aliphatic resonances (0–75 ppm), while the residual ¹⁵N magnetization is ∼33%. In contrast to NCA/CAN transfer, the residual ¹³CO magnetization of NCO/CON is about 40%.

The sensitivity of multidimensional ssNMR experiments decreases for longer DARR mixing periods. On the other hand, different DARR mixing periods are necessary to obtain short-, medium-, and long-range correlations for structure determination. Of course, it is preferable to combine experiments that are equally sensitive. Unfortunately the sensitivity for a given experiment depends on the building blocks used in the pulse sequence. The sensitivity of MEIOSIS experiments needs to be optimized using 1D spectra. For instance, as shown in Fig. 2, the intensity of the initial magnetization for CC and NCA pathways during the first acquisition is higher than that of the corresponding NN and CAN pathways detected during the second acquisition. Therefore, we designed the pulse sequence in such a way as to avoid a DARR mixing period prior to the second acquisition, finding the best compromise of sensitivity for the two acquisitions. However, it is possible to optimize the sensitivity of the experiments by applying a longer mixing period prior to the first acquisition (∼100 ms) and a much shorter mixing period (20 ms) prior to the second acquisition. In the latter case, we would obtain a MEIOSIS experiment consisting of four 2D spectra: DARR, N(CA)CX, CA(NCO)CX,¹⁷ and N(CO)CX. Fig. 4b shows the 3D spectra NCACX, NCOCX, and CA(N)COCX acquired simultaneously using the 3D MEIOSIS pulse sequence shown in Fig. 4a. The total acquisition time was 5 days.

The existence of residual ¹H polarization after ¹H-¹³C CP was first identified by Pines and co-workers²⁰ to enhance the sensitivity of 1D ¹³C spectra. However, this method requires the use of repetitive CP and continuous wave decoupling during the acquisition, giving poor resolution of the resonances. Later on, the ¹H residual polarization was also described qualitatively by Levitt and co-workers.³ In our implementation, we transform orphan spin operators into detectable coherences to either simultaneously acquire multiple experiments or to enhance the sensitivity of a single multidimensional experiment, thereby dramatically reducing the experimental time. We group these experiments in a category called polarization optimized experiments (POE). In static ssNMR, we designed POE to recover chemical shift or dipolar coupling coherences and convert them into observable terms to enhance the sensitivity of heteronuclear correlations (HETCOR) or separated local field experiments such as PISEMA (polarization inversion spin exchange at magic angle).^{5, 6, 7, 8, 21} We also developed the DUMAS approach,^{9, 10} which consists of using SIM-CP between ¹H, ¹³C, and ¹⁵N to store and utilize ¹⁵N magnetization, thus obtaining the simultaneous acquisition of two 2D experiments. Moreover, we discovered the possibility of transferring the magnetization simultaneously between ¹⁵N and ¹³Cα (or ¹³C′) and vice versa for the acquisition of two 3D experiments concurrently. The MEIOSIS method was developed using the POE philosophy, i.e., making the best out of nuclear polarization. Unlike classical ssNMR methods (including DUMAS), MEIOSIS exploits four different polarization pathways that are transformed into four individual spectra. We anticipate that several other orphan spin operators can be rescued using this approach, such as those generated by CP between HC or HN nuclei in protonated and perdeuterated samples. In fact, the specific-CP scheme is used in almost all ¹³C detected triple resonance experiments. Since the MEIOSIS scheme relies upon its ability to recover the lost polarization generated during specific-CP, this method is applicable to a multitude of pulse sequences. Moreover, variants of MEIOSIS could be designed using other homonuclear spin exchange schemes, such as DREAM (dipolar recoupling enhanced by amplitude modulation),²² SPC5 (supercycled POST-C5),²³ PAR (proton assisted recoupling),²⁴ etc. Additionally, although we assessed the performance of MEIOSIS for specific-CP ¹⁵N-¹³C transfer, we anticipate that it could also be extended to other ¹⁵N-¹³C polarization transfer schemes such as symmetry based transfer sequences,²⁵ PAIN-CP (proton assisted insensitive nuclei cross polarization), as well as optimal control based NC transfer.^{26, 27} As recently demonstrated for the DUMAS methods,²⁸ we anticipate that the variants of MEIOSIS pulse schemes will be implemented for the structural analysis of U-²H, ¹³C, ¹⁵N proteins with ¹H and ¹³C dual-receiver acquisition.

CONCLUSIONS

In conclusion, we present a new, powerful method that allows one to recover lost polarization in classical experiments using Hadamard decoding. We have demonstrated this approach for four of the most common pulse sequences used for structure determination. The 2D MEIOSIS experiments will enable rapid scanning of protein sample conditions and monitor ligand binding on multiple chemical groups, simultaneously. 3D MEIOSIS will dramatically reduce acquisition time for backbone and side chain assignments. Additionally, the concepts presented in this paper open up the possibility of developing a new class of multidimensional ssNMR experiments for higher dimensionality, thus speeding up the structure determination of biomacromolecules. MEIOSIS can also be applied with faster spinning speeds²⁹ and/or perdeuteration.³⁰ When applied in concert with other fast acquisition and sensitivity enhancement techniques (e.g., dynamic nuclear polarization,³¹ paramagnetic relaxation enhancements,³² and ¹H detection³³), this approach will dramatically increase the throughput of high-resolution structure determination by MAS ssNMR.

MATERIALS AND METHODS

All of the NMR experiments were performed using a VNMRS spectrometer operating at a ¹H Larmor frequency of 600 MHz. About 5 mg of U-¹³C, ¹⁵N ubiquitin was used to prepare the microcrystalline sample, which was then packed into a 3.2 mm rotor of BioMAS probe. A spinning rate (ω_r) of 13 kHz was used for all of the experiments, and the temperature was held constant at 5 °C. ¹⁵N RF carrier frequency was centered at 120 ppm, while ¹³C was centered at 100 ppm. The 90° pulse lengths for ¹H, ¹³C, and ¹⁵N were 2.5, 6, and 6 μs, respectively. During SIM-CP ¹³C and ¹⁵N RF amplitudes were set to 35 kHz, whereas ¹H RF amplitude was linearly ramped from 80% to 100% with the center of the slope set at 61 kHz. Based on the 1D calibration spectra, the Hartmann-Hahn contact time during SIM-CP was set to 300 μs. The sensitivity of ¹⁵N SIM-CP spectrum is 90% of that of double resonance CP, whereas ¹³C sensitivity is similar for CP and SIM-CP. It is to be noted that at higher spinning speeds (∼20 kHz) the sensitivity of ¹³C and ¹⁵N SIM-CP is almost identical to that of double resonance CP.³⁴ For specific-CP from ¹⁵N to ¹³Cα (or ¹³C′), the ¹³C offset was shifted to 60 (or 177) ppm. During specific-CP, the ¹⁵N RF amplitude was set to (5/2)·ω_r = 32.5 kHz, whereas ¹³C RF amplitude was set to (3/2)·ω_r (=19.5 kHz) and (7/2)·ω_r (=45.5 kHz) for ¹³Cα and ¹³C′ transfers, respectively. The specific-CP was implemented with an adiabatic ramp (Δ ∼ 1.6 kHz and β = 0.5 kHz). The specific-CP contact times for ¹³Cα and ¹³C′ transfers were set to 2916 and 2694 μs, respectively. For heteronuclear decoupling CW (continuous wave) or TPPM (two pulse phase modulation),³⁵¹H RF amplitude was set to 100 kHz. DARR mixing was applied for 20 ms with ¹H RF amplitude was set to 13 kHz (ω_r). For the 2D MEIOSIS experiment, t₁ dwell time (dw) of 36 μs and 288 μs were respectively used for ¹³C and ¹⁵N indirect evolutions. The numbers of increments (ni) and transients (nt) are optimized such that the product of “ni” and “nt” is constant for ¹³C and ¹⁵N t₁ evolutions represented by ${\mathrm{t}}_1^{\prime }$ and ${\mathrm{t}}_1^{″}$, respectively; ni(${\mathrm{t}}_1^{\prime }$) = 128, nt(${\mathrm{t}}_1^{\prime }$) = 96, ni(${\mathrm{t}}_1^{″}$) = 32, and nt(${\mathrm{t}}_1^{″}$) = 384 that gives the total t₁ evolution times of 4.57 and 8.92 ms for ¹³C and ¹⁵N, respectively.^{9, 10} For conventional experiments (Fig. 1S) dw(${\mathrm{t}}_1^{\prime }$), dw(${\mathrm{t}}_1^{″}$), ni(${\mathrm{t}}_1^{\prime }$), and ni(${\mathrm{t}}_1^{″}$) are identical to MEIOSIS; whereas the number of transients for DARR, N(CA)CX, CA(N)CO, and NCO were, respectively, set to 48, 152, 192, and 24. A recycle delay of 2 s was used in all experiments. For 3D MEIOSIS experiments, each of the indirect dimensions t₁ and t₂ use 21 increments, and a total of 56 scans were used. The dwell times of ¹³C and ¹⁵N were set to 150 and 300 μs, respectively, which corresponds to total evolution times of 3 and 6 ms for ¹³C and ¹⁵N, respectively. The ¹³C offset was centered at 60 ppm and the offset was moved to 170 ppm for ¹³C′ evolution during ${\mathrm{t}}_2^{″}$. This offset switching is achieved by phase modulation of ϕ₃ in synchrony with ${\mathrm{t}}_2^{″}$ evolution. The effective number of scans in 2D and 3D MEIOSIS experiments is twice the set number of scans (nt) due to the fact that two separate experiments are recorded with ¹⁵N phase +x and −x, respectively, which are then constructively added to obtain individual pathways. Therefore, we compare MEIOSIS to the conventional methods using the total experimental time required to collect the data rather than number of scans. The ¹³C spectra were referenced with respect to CH₂ resonance of adamantane at 40.48 ppm and indirectly to ¹⁵N using relative gyromagnetic ratio of ¹⁵N and ¹³C.

Possible drawbacks for the implementation of the MEIOSIS scheme may result from the increase of the RF duty cycles. However, we have found that, the performance of the pulse sequences described here is well within the capabilities of commercial ssNMR probes.