Measurement of breast tissue composition with dual energy cone-beam computed tomography: A postmortem study

Abstract

Purpose: To investigate the feasibility of a three-material compositional measurement of water, lipid, and protein content of breast tissue with dual kVp cone-beam computed tomography (CT) for diagnostic purposes.

Methods: Simulations were performed on a flat panel-based computed tomography system with a dual kVp technique in order to guide the selection of experimental acquisition parameters. The expected errors induced by using the proposed calibration materials were also estimated by simulation. Twenty pairs of postmortem breast samples were imaged with a flat-panel based dual kVp cone-beam CT system, followed by image-based material decomposition using calibration data obtained from a three-material phantom consisting of water, vegetable oil, and polyoxymethylene plastic. The tissue samples were then chemically decomposed into their respective water, lipid, and protein contents after imaging to allow direct comparison with data from dual energy decomposition.

Results: Guided by results from simulation, the beam energies for the dual kVp cone-beam CT system were selected to be 50 and 120 kVp with the mean glandular dose divided equally between each exposure. The simulation also suggested that the use of polyoxymethylene as the calibration material for the measurement of pure protein may introduce an error of −11.0%. However, the tissue decomposition experiments, which employed a calibration phantom made out of water, oil, and polyoxymethylene, exhibited strong correlation with data from the chemical analysis. The average root-mean-square percentage error for water, lipid, and protein contents was 3.58% as compared with chemical analysis.

Conclusions: The results of this study suggest that the water, lipid, and protein contents can be accurately measured using dual kVp cone-beam CT. The tissue compositional information may improve the sensitivity and specificity for breast cancer diagnosis.

INTRODUCTION

Currently, the standard imaging modality for early detection of breast cancer is mammography.^{1, 2, 3, 4, 5} Despite its technical advances, the positive predictive value from diagnostic mammography may be as low as 20% and benign findings account for a large portion of the biopsy results.⁶ Therefore, it is important to develop new image-based metrics to improve the predictive power for cancer diagnosis. A recent report suggests that high mass density (i.e., mammographic attenuation) is associated with increased likelihood of malignancy and should be considered a significant predictor of breast cancer.⁷ However, due to the 2D projection nature of mammography, the mammographic attenuation of a mass can sometimes be misleading. Therefore, we are investigating a more reliable tissue-based metric to improve the predictive capability, where chemical composition is determined from dual energy imaging.

Generally, a two-compartment model which assumes the breast is composed of fibroglandular and adipose tissues has been widely used to describe the composition of breasts.^{8, 9, 10} However, this model is limited for characterization of soft tissue lesions, which typically appear as high mammographic density masses in mammograms, because it cannot fully eliminate any of the three major components which are water, lipid, and protein. Moreover, the current two-compartment model suffers large uncertainty from system calibration¹¹ due to the wide variations in the chemical composition of the fibroglandular and adipose tissue.^{12, 13} For example, it has been reported that the water concentration in adipose tissue may vary between 11.4% and 30.5%.¹² It has been reported that malignant tissues have a significantly higher water fraction compared to normal tissues.^{14, 15} Additionally, lipid content can be used to identify certain benign lesions.¹⁶ These reports indicate the possibility to differentiate the malignant lesions from the healthy or benign tissues by characterizing the lesions according to their water, lipid, and protein composition. The three-compartment model may potentially improve the sensitivity and specificity of breast cancer detection and reduce the number of biopsies needed for suspicious lesions.

A new technique was recently reported that proposed a three-material compositional measure of water, lipid, and protein contents using dual energy mammography.¹⁷ Dual energy imaging is typically limited to quantifying two materials of interest unless additional a priori information is included through imposing a constraint in the calibration and measurement processes.¹⁸ In such a case, the total object thickness underneath each pixel would be incorporated to facilitate the extension to a three-material measurement. This idea was also implemented previously in order to isolate breast glandularity and better measure breast microcalcification mass.¹⁹ However, in order to carry out this type of measurement over the entire breast, a very accurate estimate of breast thickness is necessary at every point of the image. This represents a significant technical challenge in mammography where only 50% of the breast is considered uniformly thick. Peripheral areas must either be ignored or accommodated through additional algorithms and processing. Furthermore, issues such as paddle tilt challenge the assumption that any part of the image is of one uniform thickness. Several studies have addressed the effect of compression paddle tilt and proposed algorithm-based corrections for quantitative measurement.^{20, 21} While the technique has shown positive results in phantoms of fixed thicknesses, the technique's effectiveness in dealing with clinical mammograms is unclear due to the limited available data.

This technical challenge can be readily resolved by using a dual energy technique in conjunction with computed tomography (CT) where the image information is constrained into voxels of known areas and slice thicknesses. This could effectively overcome the thickness difficulty. The recent advancement of the dedicated breast CT systems based on flat panel detectors have demonstrated great potentials in breast imaging, using a dose level equivalent to a standard two view screening mammography exam.^{22, 23, 24, 25, 26} It has been reported that this technique has improved sensitivity due to its ability to provide 3D information about breast tissues. System parameters, including optimized spectra and gantry geometry, have been extensively investigated by several research groups.^{25, 27, 28, 29, 30, 31, 32} An initial clinical study suggests that the cone beam breast CT is significantly better than mammography for visualization of soft tissue lesions.²⁶ A recent clinical study has also shown that breast CT has a significantly lower anatomical noise than mammography and breast tomosynthesis, providing the ultimate solution to eliminate the anatomical noise induced by overlap of the breast tissue.³³ Therefore, with the help of the dedicated breast CT, it is possible to accurately characterize the chemical composition of a lesion in terms of water, lipid, and protein contents.^{34, 35, 36, 37} The proposed three-compartment measurement may be used in addition to diagnostic mammography to improve the positive predictive value in malignant tumor detection.

The purpose of this study was to evaluate the feasibility of a three-material compositional measure of water, lipid, and protein contents in breast tissue with a dual energy CT system based on dual kVp technique. The fundamental questions, regarding the implementation of this technique, are: First, what would be a reasonable beam spectra combination for implementing a dual kVp technique? Second, given that calibrating with a “pure-protein” reference material would be both challenging and difficult to implement, what impact does the use of polyoxymethylene plastic, as previously proposed, have as a surrogate for pure-protein calibration? Third, using previously proposed calibration materials, how accurately can we determine the breast tissue composition, in terms of water, lipid, and protein contents, with the proposed experimental technique? To answer the first two questions, an analytical simulation model was used to optimize the imaging parameters and to evaluate the error induced by calibration material selection. The third question was addressed with experimental imaging of 20 pairs of postmortem breasts. In order to validate the accuracy of the proposed dual kVp tissue compositional characterization, one would require a gold standard measurement, which was conducted through chemical analysis in the current study. Chemical analysis where individual water, lipid, and protein contents are isolated under controlled laboratory conditions has previously been studied as a means of validating breast density measurements with dual energy mammography.³⁸ In the current study, the use of a three-compartment model with the proposed dual kVp imaging technique would allow breast tissue to be characterized with the volumetric fractions of water, lipid, and protein contents. Therefore, it would provide a straightforward comparison between the image-based compositional measurement and the results from chemical analysis. The error in the proposed imaging technique can be accurately determined using the results from chemical analysis as a gold standard.

MATERIALS AND METHODS

Analytic simulation model

The analytical model described here has been previously reported.^{13, 34} The simulation traces the emission of photons from the x-ray source, their attenuation through the patient, and subsequent absorption in the detector. Based on this ray tracing, the x-ray attenuation coefficients for the lower and upper kVp beams, which will be referred to as the low and high energy in the following text, for each material in the study were calculated as were the recorded detector signals and their uncertainties due to statistical x-ray noise. These quantities were used to calculate quantities relevant to dual energy imaging, namely, the dual energy signal and uncertainty for each basis material (i.e., water, lipid, and protein) image.

Polyenergetic x-ray beams were simulated within the range of 40–140 kVp at intervals of 1 kVp. Spectra were provided by the TASMIP code.³⁸ A prefiltration of 2.0 mm aluminum was employed in the low kVp exposure. An additional 0.15 mm of Cu was added for the high kVp exposure to preharden the beam. This is similar to what has been implemented in other dedicated breast CT implementations.²⁶ The breast was modeled as a 14 cm thickness of adipose and mammary gland tissues with a breast density of 30%. Using the chemical composition data of Woodard and White¹² for adipose and mammary gland tissues, this composition corresponds to water, lipid, and protein volume fractions of 0.303, 0.611, and 0.083, respectively. The mean glandular dose (MGD) was taken as the measurement of radiation risk and was calculated using previously reported data generated from the Monte Carlo simulations.³⁹ The detector used in the simulation was a cesium iodide-based charge-integrating flat panel detector. The quantum detection efficiency of the detector has been considered in the simulation by estimating the photon absorption in cesium iodide with a mass density of 210 mg/cm².

The simulation was used to optimize the dual kVp imaging protocol, in terms of the selection of the low and high tube voltage and the corresponding dose allocation. For this purpose, all possible combinations of the low and high tube voltages from 40 to 140 kV with a step of 1 kV were tested. For each spectral combination, the dose distributions between the low and high energy beams were tested at an interval of 10% of the total dose. In each configuration, the dual energy signal-to-noise ratio (SNR), defined in Eq. 1, was calculated from the basis material thickness measurement.

$${\mathrm{SNR}}_i=\frac{t_i}{{\sigma }_i}.$$ (1)

Here, t_i and σ_i represent the simulated thickness signal and variance in thickness for material i, where i referring to water (w), lipid (l), or protein (p) contents. Although dual energy SNR calculations were performed for all three contents, the optimization used only information from lipid, as it accounts for the largest fraction of breast mass. Since the thickness signal (t_i) will be normalized in the simulation, the dual energy SNR of lipid was simply determined by the variance in thickness of lipid (${\sigma }_{\mathrm{l}}^2$), which can be written as

$$\begin{array}{ccc}& & {\sigma }_{\mathrm{l}}^2=\frac{\frac{{\left(\overline{{\mu }_{\mathrm{p}}\left(E_{\mathrm{H}}\right)-{\mu }_{\mathrm{w}}\left(E_{\mathrm{H}}\right)}\right)}^2}{{\mathrm{SNR}}_{\mathrm{L}}^2}+\frac{{\left(\overline{{\mu }_{\mathrm{p}}\left(E_{\mathrm{L}}\right)-{\mu }_{\mathrm{w}}\left(E_{\mathrm{L}}\right)}\right)}^2}{{\mathrm{SNR}}_{\mathrm{H}}^2}}{{\left(\left(\overline{{\mu }_{\mathrm{p}}\left(E_{\mathrm{L}}\right)-{\mu }_{\mathrm{w}}\left(E_{\mathrm{L}}\right)}\right)\left(\overline{{\mu }_{\mathrm{l}}\left(E_{\mathrm{H}}\right)-{\mu }_{\mathrm{w}}\left(E_{\mathrm{H}}\right)}\right)-\left(\overline{{\mu }_{\mathrm{p}}\left(E_{\mathrm{H}}\right)-{\mu }_{\mathrm{w}}\left(E_{\mathrm{H}}\right)}\right)\left(\overline{{\mu }_{\mathrm{l}}\left(E_{\mathrm{L}}\right)-{\mu }_{\mathrm{w}}\left(E_{\mathrm{L}}\right)}\right)\right)}^2}\hfill \end{array}$$ (2)

where μ_i(E_j) is the energy-dependent attenuation coefficient, with the subscript i referring to water (w), lipid (l), or protein (p), and the subscript j referring to either the low (L) or high (H) energy bins, respectively. SNR_j is the single energy signal SNR with the subscript j referring to the low (L) or high (H) energy detector signal. Details on the derivation of the dual energy basis material measurement uncertainty has previously been reported.⁴⁰

Finally, a figure-of-merit (FOM) was calculated to optimize the dual energy SNR with respect to the square root of the MGD, and was defined as

$$\mathrm{FOM}=\frac{{\mathrm{SNR}}_{\mathrm{l}}}{\sqrt{\mathrm{MGD}}}.$$ (3)

This definition of FOM permits the dual energy decomposition images to be compared at the same patient dose, which provides an easy comparison of the image qualities from the different configurations. The optimal combination of the low and high tube voltage, along with the corresponding ratio of the dose distribution, which resulted in the highest FOM was recorded and used to guild the following experiments.

Experimental calibration and tissue sample preparation

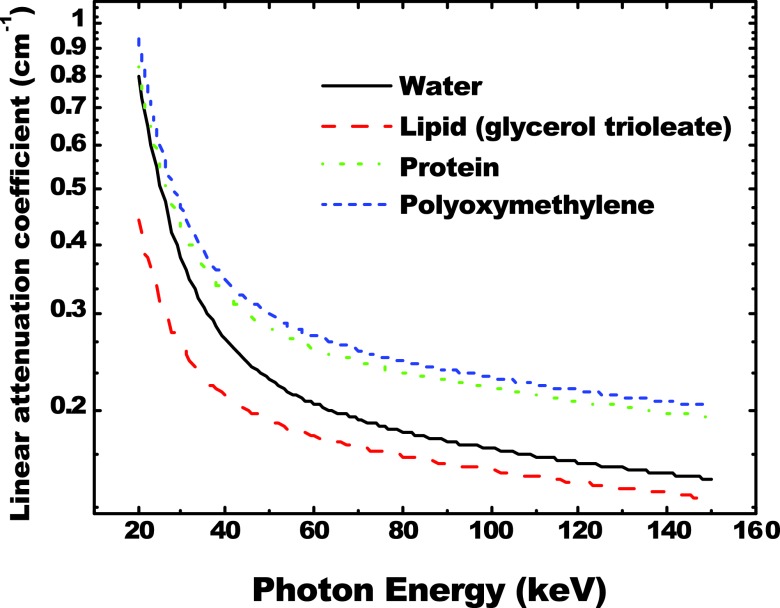
A calibration phantom was constructed from a 10.160 cm diameter cylinder of poly(methyl methacrylate) (PMMA) plastic (Mac Master Carr, Inc., Elmhurst, IL). Six holes, 1.905 cm in diameter each, were bored into the plastic cylinder. Two cylinders with a diameter of 1.905 cm, made from polyoxymethylene plastic (Delrin from Mac Master Carr, Inc., Elmhurst, IL), were used as insertions for two of the six holes. The rest were filled with water and vegetable oil, respectively. A photo of the calibration phantom and a reconstructed slice from a cone beam CT scan are shown in Fig. 1. For the material selection consideration, PMMA was used for its general similarity to breast tissue, in terms of x-ray attenuation and scattering. Water was its own representation while vegetable oil and polyoxymethylene represented lipid and protein, respectively. Vegetable oil contains primarily oleylic acid, which has a very similar elemental composition as steric acid that is the most common fatty acid found in human and animal tissue. Polyoxymethylene has been shown previously to be a good candidate for representing the x-ray attenuation properties of protein.^{17, 41} The calculated linear attenuation curves based on the molecular structure of the materials involved in this study are presented in Fig. 2, where a good agreement between protein and polyoxymethylene can be found in the energy range under investigation. Here, the elemental compositions of lipid and protein were determined based on previous report by Woodard and White.¹² The densities of the two materials were assumed to be 0.924 and 1.350 g/cm³, respectively. The suitability of polyoxymethylene as a protein-equivalent calibration material will be discussed later.

Figure 1.

(a) A photo of the three-material calibration phantom; (b) a CT image of the phantom. The locations of water (W), oil (O), and polyoxymethylene plastic (P) were noted on the image.

Figure 2.

The x-ray linear attenuation curves of water, lipid, protein, and polyoxymethylene. There is a good agreement between protein and polyoxymethylene.

Twenty pairs (left and right) of postmortem breast samples were acquired from the Willed Body Program in the School of Medicine at University of California, Irvine. The mass of the breast samples varies from 136 to 2330 g. The breast density, as estimated by using a standard single threshold segmentation technique from the cone beam CT slices, is approximately in range of 5%–70%. Postmortem breast samples were imaged including the skin. To prevent any water loss during the experiment, all samples were wrapped with a thin, very low attenuation, plastic film (GLAD cling wrap, The Glad Production Co., Oakland, CA). Once the samples were wrapped in plastic wrap, they were shaped into cylinders with a diameter of approximately 10 cm using white polystyrene foam which is almost transparent to x-ray. Before each CT scan, samples were kept at room temperature for at least 20 min to allow for tissue relaxation.

Image acquisition and processing

A cone-beam CT system was constructed to investigate breast CT imaging with a flat-panel detector. The system consisted of a tungsten target x-ray tube (Dynamax 78E) coupled to a Phillips Optimus M200 x-ray generator and a CsI indirect flat-panel detector (PaxScan 4030CB, Varian Medical Inc., Palo Alto, CA) mounted onto an optical bench. A high precision motor (Kollmorgen Goldline DDR D062M Danaher Motion, Wood Dale, IL) provided the rotational mechanism and also served as the platform on which the object was placed. A TTL-logic signal from the flat panel controlled the timing of the x-ray pulse. The synchronization of this signal with the x-ray pulse was implemented using a field programmable gate array (FPGA) and associated circuits. The detector had an intrinsic pixel pitch of 194 μm and was used with 2 × 2 hardware binning, which effectively increases the pixel size to 384 μm. The source-to-detector distance (SID) and the source-to-object distance (SOD) were 1.5 and 1.0 m, respectively. The flat-panel detector had a dimension of 40 × 30 cm². The flat-panel detector was operated at 7.5 frames/s and the motor was rotated at 1.0 rpm. A total of 462 frames were acquired for each scan with an angular increment of 0.78°. Image scans were acquired at beam energies of 50 and 120 kVp. A 2.00 mm Al was used as prefiltration for the 50 kVp scan, and an additional 0.15 mm Cu was inserted for the 120 kVp scan. The Entrance Skin Air Kerma (ESAK) of the low and high energy scans were measured with an ion chamber (Model 2026C, Radcal Corporation, Monrovia, CA) at the isocenter and were found to be about 4.44 and 3.29 mGy, respectively. For these imaging protocols, the MGD estimated from Monte Carlo simulations³⁹ for the total exposure of the two scans is approximately 6 mGy for a breast of 14 cm in diameter with 30% glandularity. The MGD allocation between the low and high energy beams is approximately 50:50.

Images were acquired and recorded onto a workstation using proprietary software (Varian VIVA). Subsequently, the raw data were preprocessed for beam hardening and glare corrections, which are discussed in the Appendix, with an open source image processing software package,⁴² followed by CT reconstruction using a Feldkamp-based filtered backprojection algorithm (Cobra, Exxim Computing Corporation, Pleasanton, CA). The CT images were reconstructed with a voxel size of 0.3 × 0.3 × 0.3 mm. The attenuation coefficient of each material was derived during the reconstruction process and presented in the final CT images. During the calibration process, the mean values and variations of the reconstructed attenuation coefficients for water, lipid, and protein calibration materials in the phantom need to be measured. This was accomplished with carefully hand-delineated circular regions of interests (ROI) of identical diameter. In order to minimize the partial volume effects, the size of the ROI has to be carefully determined. First, a large ROI was drawn to select the entire area containing only one calibration in the CT image, and the mean value in this ROI was measured. This process was repeated while decreasing the diameter each subsequent time until the measured mean values became saturated. This size was then used as the measurement standard for all other materials. In this study, the ROI size determined this way in the calibration phantom had a diameter of 13.5 mm and included 1597 pixels. The mean values of the reconstructed attenuation coefficients for water, lipid, and protein were further averaged over all slices, respectively, and were used for calibration. For the postmortem breast tissues samples, ROIs of the entire volumes in the reconstructed CT slices, including the skin, were selected through a carefully determined threshold in the histogram. For samples with discernible calcifications, voxels containing calcium were removed from the selected ROIs. Then, the mean values of the reconstructed attenuation coefficients for the low and high energy scans were measured within the selected ROIs and used for dual energy three-material decompositions.

Image based tissue composition measurement

The decomposition of measured linear attenuation into fractional measurements of tissue composition was based on the solution to a dual energy system of three equations and three unknowns:^{19, 34}

$$\left(\begin{array}{ccc}\hfill {\mu }_{\mathrm{W}}^{\mathrm{L}}& \hfill {\mu }_{\mathrm{L}}^{\mathrm{L}}& \hfill {\mu }_{\mathrm{P}}^{\mathrm{L}}\\ \hfill {\mu }_{\mathrm{W}}^{\mathrm{H}}& \hfill {\mu }_{\mathrm{L}}^{\mathrm{H}}& \hfill {\mu }_{\mathrm{P}}^{\mathrm{H}}\\ \hfill 1& \hfill 1& \hfill 1\end{array}\right)\left(\begin{array}{c}{f}_{\mathrm{W}}\\ f_{\mathrm{L}}\\ f_{\mathrm{P}}\end{array}\right)=\left(\begin{array}{c}{S}^{\mathrm{L}}\\ S^{\mathrm{H}}\\ 1\end{array}\right),$$ (4)

where ${\mu }_{\mathrm{W}}^i$, ${\mu }_{\mathrm{L}}^i,$and ${\mu }_{\mathrm{P}}^i$ are the linear attenuation coefficients of water, lipid, and protein, respectively, where i denotes for either low (L) or high (H) energy scans. f_W, f_L, and f_P were the volume fractions of water, lipid, and protein, respectively. S^L and S^H were the measured CT signals for the low and the high energy scans, respectively. The first two equations represent the fact that the measured log signal in the low or high energy scan is a linear combination of the attenuation coefficients of the three components, while the last equation comes from the CT voxel size constrain.

Although the theory of dual energy imaging is well represented in Eq. 4, some technical obstacles remain because of the use of polyenergetic spectra and the presence of the nonlinear artifacts. Instead of solving Eq. 4 directly, low-order polynomial approximations are usually used for generating the basis images from the measured signals.^{43, 44} In this study, limited by the number of calibration points, we chose a first order linear equation with the following form to approximate the inverse of Eq. 4:

$$f_i=a_0+a_1{S}^{\mathrm{L}}+a_2{S}^{\mathrm{H}}.$$ (5)

Solving for f_W, f_L, and f_P was a two-step process that was accomplished numerically by means least-squares fitting. The first step was substituting the known values and each respective image attenuation measurement of f_W, f_L, and f_P from the calibration phantom. Origin (OriginLab Co., Northampton, MA) was used to perform the linear fitting according to Eq. 5 and solve for the system matrix calibration coefficients, a₀, a₁, and a₂. After determining these coefficients, image attenuation measurements from the postmortem breast tissue samples with unknown compositions were substituted into the system to determine the image-based measurements of water, lipid, and protein contents.

Chemical analysis

In order to have a gold standard for the tissue compositional analysis, all postmortem breast samples were chemically decomposed into water, lipid, and protein contents right after the dual energy cone beam CT scan. The chemical analysis method was based on a standardized procedure devised by the United States Department of Agriculture to measure the content of water, lipid, lean, and mineral in a sample.⁴⁵

Each postmortem breast sample was weighed before and after the CT scan. The change in weight during the packing and imaging was assigned to water loss, and added into the final water fraction. Each postmortem breast, including the skin, was then cut into small cubical pieces of approximately 5 × 5 × 5 mm³ and placed into a vacuum oven maintained at approximately 95 °C for 48 h to evaporate all water content. The sample was removed from the vacuum and weighed once again. The lost mass during baking was assumed to be purely water. The dried sample was then mixed with petroleum ether, grounded into a slurry, and agitated at 30 °C for approximately 1 h to extract the lipid content of the fatty tissue into the ether solvent. The sample was then cooled at room temperature (approximately 20 °C) for 24 h. Next, the sample mixed in the solution was vacuum filtered through a Buchner funnel of known weight. An additional 1 liter of pure petroleum ether was passed over the sample to wash away any residual lipid content. Therefore, the petroleum ether solution was assumed to contain all the lipid content. This lipid content was then isolated from the solution by evaporating the petroleum ether with heat under vacuum distillation. The mass of the isolated lipid content was weighed, yielding the lipid mass. The dried sample after filtration contains mostly protein with a very small amount of minerals, such as Na, K, and Ca. To separate the pure protein mass, we followed the ashing procedure adapted from the Handbook of Food Analysis.⁴⁶ Each sample was placed in a crucible and baked in a furnace with excess air at 550 °C for 18 h, so that all carbon-based compounds was oxidized and removed in the ash. The weight difference before and after the high temperature baking was assigned to pure protein mass. Further analysis was also performed on the remaining ash to determine the amount of Ca in the tissue by removing the water soluble components. Finally, the measured mass of water, lipid, and protein was converted into volume, respectively, and the volumetric fractions of the three materials were used as the gold standard for the evaluation of the imaging-based dual energy decomposition. The accuracy and precision of the chemical analysis has been validated in our previous studies.¹³

RESULTS

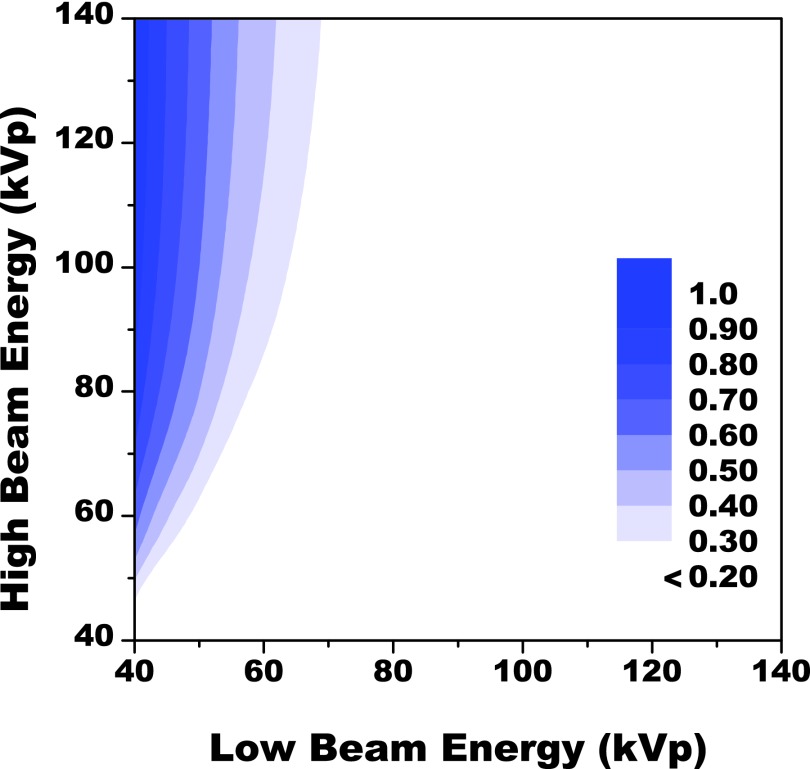
The results from the analytical simulation are presented in Fig. 3, as a two-axis contour plot showing the distribution of simulated FOM values as a function of the low and high beam energies. The simulation tested a range of dose distributions between the low and high energy beams for each dual kVp configuration, as discussed in Sec. 2A. For each dual kVp configuration, only the optimal dose distribution, which maximized the FOM, was recorded in the simulation result. Then, the corresponding FOM value was presented in Fig. 3. The FOM values were normalized to the peak value and were shown in gray scale. The simulated values were set to zero in the event that kVp of low energy beam is equal to or larger than that of the high energy beam. The maximum FOM derived from our simulation was found at the top left corner in the figure which corresponds to a dual kVp configuration of 40 and 140 kVp. The result suggested that maximum spectra separation was desired for water, lipid, and protein decomposition. The FOM may further increase outside the tested kVp range. However, the x-ray tube loading and the maximum available beam energy are out of the practical limitations. The corresponding dose distribution between the two beams, which was not shown in the figure, is approximately 50:50 according to the simulation results.

Figure 3.

A two axis contour plot showing the distribution of FOM values as a function of the low and high energy beams. The results are given in arbitrary units and normalized to the highest FOM observed in the study which was at a beam energy combination of 40 and 140 kVp. The optimal distribution of dose at this combination was approximately 50:50.

In the calibration phantom used in this study, wells of water and lipid, in the form of oil, represented themselves while polyoxymethylene represented protein. The suitability of this last selection was studied here. The impact this choice had on measurement accuracy could not be easily quantified with experiment but could be studied with a simple model. An approach equivalent to the one described in Sec. 2D was used with theoretically derived data. First, water, oil, and polyoxymethylene were used as the calibration materials. The system calibration coefficients used in Eq. 5 was calculated with theoretical attenuation values of the above three materials. Then three test materials: pure water, pure lipid, and pure protein, were decomposed with the proposed method to determine the respective fractional compositions in terms of water, lipid, and polyoxymethylene. The results from modeling calibration measurements with polyoxymethylene and pure-protein are shown in Fig. 4. The agreement between the known and the simulated fraction of water was nearly perfect, as was the agreement between those of lipid. The error in protein measurement was approximately −11.0%. Additionally, as seen in Fig. 4, residual protein signals appeared in measurements of pure water and pure lipid. The error in residual protein was −9.0% when measuring pure water and 21.0% when measuring pure lipid. No other residual errors were present. The root-mean-square (RMS) error due to calibration material mismatch was 14.6%.

Figure 4.

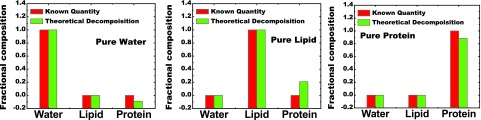
Data showing the comparison of composition fractions with the known data next to the data predicted from the simulation model which used polyoxymethylene as a calibration material for pure protein. Residual signals (errors) were only seen in the content of protein for all three pure materials. The average RMS error for all three samples was 8.5%.

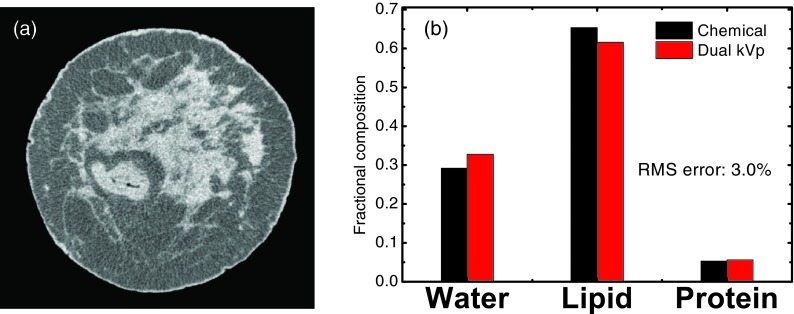
Although 40 and 140 kVp was suggested to be the optimal imaging configuration for the three-material decomposition, such parameters are difficult to implement in practice. Limited by the experimental conditions, we performed postmortem breast imaging at beam energies of 50 and 120 kVp, respectively. The experimental imaging configuration will be further discussed in Sec. 4. The low energy (50 kVp) CT image obtained from the flat panel-base cone beam system for one of the postmortem breast samples is shown in Fig. 5a. No cupping or streak artifacts were observed in the low energy CT images for any of the samples investigated in this study. Distribution of the glandular tissue can be identified in the center area, while the adipose tissues, are noticed mainly in the periphery. A thin layer of skin around the whole sample can be clearly observed. Although the separation of the two primary tissues is clear in the CT images, the segmentation of water, lipid, and protein contents is not straightforward. Such information may only be acquired with the dual energy decomposition using the proposed technique, as shown in Fig. 5b. The volumetric fractions of water, lipid, and protein contents obtained with the proposed dual kVp technique for the displayed sample were compared to the gold standard measured from chemical analysis. There is an excellent agreement between the image-based measurement and the true values for all three contents. The RMS error for the three-material decomposition for the displayed sample was estimated to be 3.0%.

Figure 5.

(a) A CT image reconstructed from low energy (50 kVp) scan for one postmortem breast sample. (b) Comparison of the composition measurements, in terms of water, lipid, and protein contents, between dual kVp CT and chemical analysis for the same sample. The RMS error for three-material decomposition is 3.0% for this sample.

The results of the tissue composition measurement of the postmortem breast samples are presented in Fig. 6 for water (a), lipid (b), and protein (c) contents. The volumetric fractions of the three components measured with the image-based dual energy technique were compared to the gold standards, which were obtained from the chemical analysis. The identity lines are shown in each plot for visual clarity. The correlation between the image-based measurement and the chemical analysis was estimated with a linear regression model. The fitted slopes were estimated to be 1.08 (±0.05), 1.09 (±0.04), and 1.06 (±0.16) for water, lipid, and protein contents, respectively. The p values determined in the paired t-test between the results from the chemical analysis and the dual energy decomposition for water, lipid, and protein contents were 0.59, 0.22, and 0.82, respectively. The statistical analysis suggests a good agreement between the measured and true values for all samples. It should also be noted that the three investigated contents are correlated to each other as well, since adipose tissue contains mostly lipid while glandular tissue consists of mainly water and protein. The RMS errors of the image-based decomposition with respect to the gold standard obtained from chemical analysis are estimated to be 4.7%, 4.2%, and 2.6% for water, lipid, and protein contents, respectively. The RMS errors of the three-material decomposition were also calculated for each sample, and plotted as a function of the sample weight in Fig. 6d. The RMS errors ranged from 0.9% to 8.5%, with an average value of 3.58% for all 40 samples.

Figure 6.

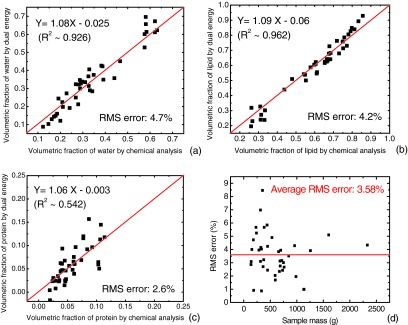
Results of the tissue compositional studies for all 40 samples. The volumetric fractions of water (a), lipid (b), and protein (c) contents measured with dual kVp technique are presented as a function of the results obtained from chemical analysis. Identity lines are drawn for visual guidance. Excellent correlations with slopes very close to one can be observed for all three contents. (d) The RMS errors of three-material decomposition for all 40 samples are plotted as a function of sample mass. The average RMS error of 3.6% is noted by the straight line.

Another interesting result is to investigate the correlation of the tissue composition measurements from the left and right breast of the same pair. This correlation is shown in Fig. 7 for the results obtained from both chemical analysis (a) and dual-energy decomposition (b). Here, we plot the correlation of the percent fibroglandular volume (%FGV) which is the total volumetric ratio of water and protein in the breast tissue. The identity lines are shown in red for visual guidance. It can be seen from the chemical analysis that the tissue composition has a good linear correlation, with a slope of 0.99, between the left and the right breast. Such correlation was preserved in the dual-energy decomposition studies, evidenced by the fitting slope of 1.03.

Figure 7.

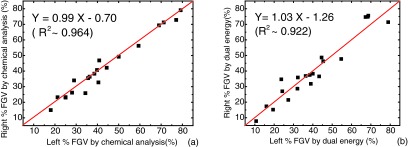
Correlation of the %FGV between left and right breast samples from the same pair for chemical analysis (a) and dual kVp CT decomposition (b). In both cases, the slopes are close to one, which suggest the similarity of the tissue composition in the same pair of breasts.

DISCUSSION

Previous studies suggest that the malignancy of lesions may be better characterized by their chemical compositions, in terms of water, lipid, and protein contents.^{7, 17} The fundamental question investigated in this study is to evaluate the feasibility of tissue composition measurement with spectral CT. In order to justify the accuracy of the three-material compositional measurement with such an imaging modality, chemical analysis which measured the volumetric fraction of water, lipid, and protein contents was used as the gold standard. The excellent agreement between the image-based measurement and the gold standard suggests that the proposed dual-energy technique can be implemented to characterize the tissue composition with high accuracy for suspicious lesions. Thus, it has the potential to improve the positive predictive values for malignancy detection and reduce the number of biopsies required. However, it should be noted that, rather than visual representations, the three-material characterization focuses more on the composition analysis of lesions. Since both tissue types are mixtures of water, lipid, and protein contents, the dual-energy decomposition images of the three contents may not be the best way to present the results. On the other hand, once a suspicious lesion is identified in a standard image, for example, from the low energy scan, its chemical composition, in terms of the volumetric fractions of water, lipid, and protein contents, can be accurately measured with the proposed technique. Such numeric results that characterize the lesion by its fundamental compositions may provide invaluable information for cancer diagnosis. It should be pointed out that the technique uses the low and high energy attenuation coefficients of the material instead of CT numbers as is the case for conventional CT. In principle, both representations can be used with Eq. 5 for dual energy decomposition, as the conventional CT numbers are simply obtained through normalization to the attenuation of water at the given beam energy. However, such transformations may reduce the relative difference between the low and high energy signals, which could potentially lead to increased error levels in the quantitative measurements.

Although data from simulation suggest that the FOM was maximized at a low beam energy of 40 kVp, imaging at such a low beam energy with the filtration used in this study would require a very high tube current to reach the expected dose distribution within an acceptably short scan time. It is thus impractical for clinical conditions, where thicker filtration and shorter scanning time can be expected. Therefore, for the low energy image, 50 kVp was selected for experimental studies since it might be more feasible for clinical implementation than 40 kVp. However, even higher beam energies will be necessary for larger breasts. Imaging at 50 kVp was also recommended by a previous study⁴⁷ that investigated the effect of CNR and noted that CNR was maximized at relatively low beam energies, but noted potential limitations due to tube power requirements. Conversely, a beam energy of 120 kVp was chosen for the high energy image due to experimental system limitations. Clearly, for this imaging task, the trend from the simulation results suggests that dual energy FOM is optimized when the low and high energies are separated as far as possible. The predicted FOM when imaging at 50 and 120 kVp was 0.64, a 36% reduction from the theoretical maximum at 40 and 140 kVp. As shown in the figure, this drop in performance mostly resulted from raising the low energy beam from 40 to 50 kVp, while the reduction of the high energy beam from 140 to 120 kVp accounted for a difference in FOM of less than 2%.

The current study investigated the feasibility to perform tissue compositional studies with dual kVp CT technique at an acceptable dose level determined by techniques seeking to match the dose of breast CT with the standard two view screening mammography.^{26, 48} In previous studies, the dose for the reference size breast used in this study was reported to be approximately 6 mGy for a dedicated breast CT based on flat-panel detectors at 80 kVp.⁴⁸ Therefore, the current study was carefully designed, so that the total dose from both low and high energy scans matches the desired level of approximately 6 mGy. As stated in Sec. 2, the dose was assessed using Monte Carlo simulation, validated previously by Boone et al.,⁴⁹ which calculates the dose deposition in breast of a given size relative to the ESAK, and was given in units of mGy per mGy of air kerma for the low and high energy beams, respectively. The final dose was calculated by multiplying the ESAK to MGD converting factor with the measured ESAK for each beam. The ESAK measured with an ion chamber was determined to be approximately 4.44 and 3.29 mGy for 50 and 120 kVp beams, respectively. The corresponding MGD was then estimated to be approximately 3.03 and 2.98 mGy, respectively, leading to a total dose level equivalent to 6.01 mGy. It is possible that further improvement in measurement precision might be limited by the dose requirements for dedicated breast CT.

An interesting observation from the postmortem study is the correlation of the chemical compositions between the left and right breast. Although some studies have suggested that the breast density may occasionally vary due to breast feeding or surgery, it is generally expected to have a similar tissue composition between left and right breast of the same individual. The chemical analysis on the postmortem breast samples investigated in current study corroborates the general expectations by comparing the %FGV between the same pair of samples. This information can then be used to evaluate the precision for breast composition measurement from an imaging modality in patient studies, where the true values of breast density or tissue compositions may not be easily obtained. In fact, the good correlation between left and right breasts with the image-based dual energy decomposition speaks to the excellent precision and reproducibility of the proposed technique.

Since the results from chemical analysis were used as the gold standard in this study, the potential errors from chemical analysis were first evaluated. The precision of the method was validated with repeated chemical composition measurements of different amounts of bovine tissue. The accuracy of the method has previously been reported,¹³ and was further validated in this study by comparing the total mass of the measured water, lipid, and protein contents to the original weight of the postmortem sample. The experimental errors from chemical analysis were approximately one tenth of a gram, which corresponds to a volumetric percentage error of less than 1%. It is therefore safe to conclude that the measurement from chemical analysis can be used as the gold standard for the tissue compositional analysis, since its errors are significantly less than the errors from dual energy decomposition.

When compared to the chemical analysis results, the image-based technique performed well. The average RMS error for three-material decomposition is less than 5%, with a single maximum error of 8.5%. The accuracy of the image-based decomposition for each component was very good, especially for water and lipid. The correlation of protein was slightly worse, which is mainly attributed to the relative low protein concentration and small range of the distribution among all samples. However, protein content contributes up to 10% in volume in normal breast tissue. It remains a critical component in the proposed three-compartment model. Ignoring protein in the decomposition process will result in large errors in the volumetric quantification of water and lipid. The error in the current study may come from several sources.

First, the simulation predicted that errors will be introduced when the plastic polyoxymethylene phantom was used as a protein surrogate calibration material. Interestingly, no single error from the experimental study reached the highest level predicted by the calibration model, which was seen at a value of 21% error for the amount of protein apparently present when pure lipid was measured. This may be explained by the fact that all breast tissue samples were mixtures of all three components, while the simulation was targeted at the pure materials. Since the simulated errors in protein fraction for pure water and lipid actually have the opposite sign, the total error induced by polyoxymethylene calibration phantom may to some extent cancel each other out in a mixture of the pure material.

Another important source of error comes from the presence of x-ray scatter induced by the sample. Scattered radiations are known to reduce the contrast of the image and usually lead to an underestimation of the x-ray attenuation coefficient. More importantly, in dual energy imaging, the modification of the attenuation coefficient induced by x-ray scatter is a nonlinear process for the low and high energy scans. Therefore, it may reduce the accuracy of material decomposition with the proposed technique. In the current study, x-ray scatter from the breast samples was not corrected. It is possible that the error level can be further reduced by scatter correction from the samples. However, one should also note that in current study, the size and the attenuation properties of the phantom used for dual kVp calibration were very similar to the postmortem breast samples that were all packed into a cylindrical shape of the same diameter. It is thus expected that the scatter effects were almost identical between the calibration scan and the sample measurement. The uncertainties induced by the scatter effect may be well included in the calibration. In addition, a large air gap was employed in the experiment to minimize the effect of scatter. In fact, the excellent agreement of the tissue composition measurement with respect to the gold standard suggested that errors induced by scatter have been effectively limited with the proposed calibration phantom design.

Further effort to improve the accuracy of the proposed technique can also be implemented with a more complex calibration fitting function. Equation 5 was derived for a linear system. The presence of the nonlinear factors, such as beam hardening and x-ray scatter, may limit its accuracy which may also be another source of error in this study. To accommodate such effects, nonlinear fitting functions may be introduced for more accurate tissue compositional studies.⁵⁰ However, this also means that the calibration function contains more terms and fitting parameters. It would thus require more calibration points than the three pure materials used in the current study.

In conclusion, the results of this study suggest that the water, lipid, and protein contents can be measured using dual energy CT with relatively good agreement. Further improvements in accuracy may be possible if a phantom, which better approximates the chemical composition of protein, is used. Thus, further research is merited to determine if this technique has the potential to better characterize suspicious lesions by their chemical compositions.

APPENDIX: IMAGE CORRECTIONS FOR CBCT

Beam hardening corrections

The experimental settings in this study involved polyenergetic beams that were attenuated by breast tissues approximately 10 cm thick. In this case, the harder components of the spectra will be attenuated less than the low energy photons. This effect is usually referred to as beam hardening, where the effective energy of the attenuated beam shifts towards high energy in comparison to the unattenuated one. As a result, the attenuation coefficients measured across a homogenous sample will vary from point to point, depending on the thickness of the sample and will typically be shown as cupping artifacts. In the current study, beam hardening artifacts were corrected in the projection domain for both the low and high energy beams with a method developed based on the previously reported signal-to-equivalent thickness calibration (STC).⁵¹ The calibration for beam hardening correction was performed with a set of BR12 slab phantoms (CIRS, Norfolk, VA) which closely simulates the x-ray attenuation properties of breast tissues. A sequence of projection images were acquired with the flat panel-based cone beam CT system for the BR12 phantoms of various thicknesses, ranging from 0.5 to 17.0 cm. The measured log signal values were calculated by taking the negative logarithm of each image. To estimate the signal without beam hardening artifacts, the expected log signal values were calculated as the production of the known phantom thickness and the log signal measured from 1 cm BR12 phantom, assuming that the beam hardening was negligible for such a thin absorber. Subsequently the correlation between the measured (S_m) and expected (S_e) signals were fitted by a nonlinear rational function shown in Eq. A1:

$$S_{\mathrm{e}}=\frac{a_0+a_1{S}_{\mathrm{m}}}{1+b_1{S}_{\mathrm{m}}}.$$ (A1)

Three fitting parameters (a₀, a₁, and b₁) were introduced to accommodate for the nonlinear relations between the expected and measured log signals. Once the two sets of the calibration parameters were determined for the low and high energy beams, respectively, Eq. A1 was applied to the raw projection images of the breast tissue images acquired in the corresponding exposures. This produced images that were corrected for beam hardening artifacts.

Flat panel scatter-glare corrections

Another common artifact involved in flat panel-based cone beam CT system is the x-ray scatter in the detector and its housing, which usually leads to superimposed low spatial frequency “glare” signal. The presence of such scatter causes underestimation of the true attenuation coefficients. Furthermore, the errors induced by scatter-glare can be independent in the low and high energy exposures for dual energy imaging, which results in great challenges for accurate material decomposition. In this study, we performed scatter-glare corrections for the raw tissue images in the projection domain following the methodology reported by Seibert et al.⁵², ⁵³ X-ray image signals were measured underneath lead disks of diameters 4.3, 5.2, 6.7, and 9.8 mm, which were placed directly on the detector surface. The lead disks were approximately 2 mm thick and were assumed to completely absorb any incident radiation. The measurement set was acquired for both low and high energy beams, respectively. The signals behind the lead disks were transformed to the log contrast ratio by taking the negative natural logarithm of the ratio between the attenuated and open field signals.

Values of the log contrast ratio were fit to a line as a function of disk radii. The resultant slope and intercept from the linear fit were used to calculate the scatter radial extent (ρ) and scatter fraction (k) of the x-ray scatter kernel, which can be expressed as

$$H\left(f\right)=\pi \frac{\rho }{\sqrt{1+{\left(2\pi kf\right)}^2}}+(1-\rho ),$$ (A2)

where f is the spatial frequency and H is the frequency domain representation of the point spread function (PSF). Specifically, the scatter radial extent was equal to the reciprocal of the slope and the scatter fraction was equal to the negative exponential of the intercept. The definition of these terms as well as the explicit derivation can be found in a previous report describing the characterization methodology for veiling glare.⁵² Finally, Eq. A2 was applied on the Fourier transform of the raw tissue images in the projection domain with the proper calibration parameters for the corresponding energies to remove the scatter-glare effects.