Toward a quantitative account of pitch distribution in spontaneous narrative: Method and validation

Abstract

Pitch is well-known both to animate human discourse and to convey meaning in communication. The study of the statistical population distributions of pitch in discourse will undoubtedly benefit from methodological improvements. The current investigation examines a method that parameterizes pitch in discourse as musical pitch interval H measured in units of cents and that disaggregates the sequence of peak word-pitches using tools employed in time-series analysis and digital signal processing. The investigators test the proposed methodology by its application to distributions in pitch interval of the peak word-pitch (collectively called the discourse gamut) that occur in simulated and actual spontaneous emotive narratives obtained from 17 middle-aged African-American adults. The analysis, in rigorous tests, not only faithfully reproduced simulated distributions imbedded in realistic time series that drift and include pitch breaks, but the protocol also reveals that the empirical distributions exhibit a common hidden structure when normalized to a slowly varying mode (called the gamut root) of their respective probability density functions. Quantitative differences between narratives reveal the speakers' relative propensity for the use of pitch levels corresponding to elevated degrees of a discourse gamut (the “e-la”) superimposed upon a continuum that conforms systematically to an asymmetric Laplace distribution.

INTRODUCTION

Variations in the pitch of the voice during speech comprise much of the overall “melody” (Wells, 2006) or “music” (Wennerstrom, 2001a) of human verbal communication. Suprasegmental pitch patterns that may be analogous to musical melodies are significant because they have been identified as mediating a variety of communicative functions at the lexical, utterance, and discourse level. Important questions arise as to how the pitches that appear in these patterns are statistically distributed. Such information would complement the extensive literature on pitch contour by providing insight into the range of pitches used by speakers and the shape of the distribution of frequency of occurrence across the pitch range. For example, one might ask: In a discourse is the population distribution of pitches symmetric, with equally frequent excursions to higher pitch as to lower, or alternatively, is the distribution skewed to preferentially higher pitches or to lower? Moreover, are the pitches continuously distributed or do they occur in clusters analogous to the degrees of a musical scale, or is the situation an admixture of continuum and discrete? To what extent do the excursions to higher pitch (or lower) associate with prominence assignment or some other linguistic function rather than occurring randomly? Such quantitative inquiries demand a rigorous and objective formalism for extracting the salient statistical information from the intonation contour of a discourse. This work proposes a robust analytical treatment of the peak pitches of words in a discourse that is grounded in the methods of time-series forecasting and digital signal processing and that provides the necessary information to answer such questions as posed above. Moreover, this work applies the formalism of this work to peak word-pitches—both simulated and actual pitch time series that are obtained from an ensemble of 17 spontaneous narratives dealing with an emotive topic. It is noteworthy that few a priori assumptions are made about the function of the modulations of pitch appearing in the narratives. The proposed method gives voice to the data but does not presume to speak for it.

The method, indeed, has general applicability, although it was developed to support a specific line of inquiry. The investigators were initially motivated to understand the functions of intonation, one core dimension of prosody, in natural narrative discourse (Wennerstrom, 2001a,b). In particular, the authors are interested in the paralinguistic (non-phonological) aspects (Wennerstrom, 2001a) or performance features (Wolfson, 1982) of intonation in which a narrator expresses his or her emotional involvement or attitude about the story events via an infinite variety of pitch manipulations. It has been hypothesized that degrees of pitch manipulation toward the extreme upper portion of a speaker's pitch range may be used by speakers as one of multiple linguistic and paralinguistic evaluative devices (Labov, 1972) that evaluate or add prominence, i.e., emphasis, to selected information in a discourse. Evidence of an association of elevated pitch extrema with a range of linguistic devices that have been independently characterized as evaluative (e.g., direct speech, marked lexical items, comparators) would suggest that many of these elevated pitch extrema may indeed be evaluative in nature (Wennerstrom, 2001b; Olness et al., 2010). In past research, these elevated pitch extrema have been operationalized as fundamental frequencies in the top 10% of a speaker's fundamental frequency range (Wennerstrom, 2001b). The current study is, in part, an attempt to refine the operationalization of these elevated pitch extrema.

Paralinguistic aspects of intonation may be contrasted with the phonological aspects of intonation, in which the same narrator also chooses from among a finite set of intonation forms and their corresponding functions available in a given language. These are outlined in Wennerstrom (2001a), using examples from English. Phonological aspects of intonation in English include: A fixed set of pitch accents used to indicate new lexical additions to the discourse information structure (e.g., Pierrehumbert and Hirschberg, 1990); a fixed set of pitch boundaries, phrase accents, or boundary tones, in which high versus low tones at the end of an utterance indicate the degree of dependency of that utterance on the next (e.g., Pierrehumbert and Hirschberg, 1990); a fixed set of utterance-initial pitch options, termed key, that express whether an utterance is contrastive, additive, or a foregone conclusion relative to the previous utterance (Brazil, 1985); and paratone, defined as an expansion of pitch range at the beginning of a new topic unit or structural element of the discourse, and a compression of pitch range at the end of the structural unit, wherein the structural element corresponds to a written paragraph. Wennerstrom (2001a,b) has suggested that fundamental frequency extremes in the top 10% of a speakers range may often be associated with the beginning of a new structural element in a narrative, i.e., they may be found in paratones. Presumably, however, most other phonological categories of intonation patterns such as pitch accents, pitch boundaries and key, and other utterance-level pitch change phenomena such as declination ('t Hart, 1986; Ladd, 1988; Liebermann, 1986) would be realized in the middle and lower portions of a speaker's pitch range. The operationalization of pitch distribution addressed in the current study characterizes the shape of the speakers' pitch distributions in naturally occurring narratives. Once the nature of this distribution has been characterized, future studies may then examine where phonological aspects of intonation, as well as declination, fall within this distribution.

One presumes that the phonological aspects of aspects of intonation use are language-specific. However, many scholars would agree that the paralinguistic, non-phonological, emotional, and expressive aspects of intonation use may not be language specific, but rather may “ride ‘on top of’ the phonological structure” (Wennerstrom, 2001b) and be “superimposed upon almost any utterance” (Shen, 1990) in a gradient fashion (Ladd, 1980). Such a stance is consistent with evidence of a relationship between emotional arousal (as in emotional states of anger or joy) and increased fundamental frequency (Bachorowski and Owren, 2008). A detailed account of the emotional, gradient uses of intonation is beyond the scope of the current study. However, an important motivation for the current study is the premise that paralinguistic, evaluative pitch manipulations are established not by their absolute pitch, but rather by their relatively elevated pitch in contrast to the characteristic global trend of the immediately preceding utterances. A detailed operational account of global approximations to this trend, and deviations from it—as outlined in the current study—provides a necessary foundation for future examinations of the paralinguistic, evaluative role of prosody as it contributes to discourse-level coherence.

A functional definition of pitch

While the meaning of “pitch” as used in this work, namely, musical pitch interval, will seem self-evident to many readers of this journal, this is not necessarily the case for others from different disciplines. In fact, Terken and Hermes have noted that a lack of consensus as to the appropriate metric for pitch has hampered the field of intonation studies (Terken and Hermes, 2000). The fundamental frequency F₀, a meaningful index of the pitch of a complex tone (Micheyl and Oxenham, 2010), is often used as the metric for pitch in intonation studies (Rietveld and Gussenhoven, 1985). In fact, Matteson and Lu found a remarkably harmonic spectrum, by use of precision spectral analysis of the overtone series of vowels for typically healthy human voices that often exhibited over 100 frequency components separated by the fundamental frequency and therefore was uniquely characterized by the F₀ of the series (Matteson and Lu, 2009). Other researchers in intonational studies have opted for the use of mel (or the ERB scale) that was introduced initially to map the pitch of pure tones onto the position of the stimulus on the Basilar membrane of the cochlea (Stevens et al., 1937). However, in the range of the fundamental frequency of human speech (namely, 64 to 512 Hz) mel is de facto a very nearly linear mapping of F₀. From a plot of the interpolation formulas of O'Shaughnessy (1987) or of Fant (1968) the authors observe that between 64 and 512 Hz the average absolute deviation (AAD) of a linear fit (mel = 1.14[F₀ + 34 Hz]) from the tabulated values of Beranek (1949) and of Umesh et al. (1999) is comparable to the AAD of O'Shaughnessy's interpolation (∼6%) and superior to Fant's earlier interpolation formula. Furthermore, several lines of evidence and inference, namely, music auditory perception (Shepard, 1964; Deutsch, 2002; Warren et al., 2003), vocal physiology (Titze and Hunter, 2004), and the psychoacoustics of speech perception and production (de Pijper, 1983; 't Hart et al., 1990; Wennerstrom, 2001a; Braun, 2002; Simpson, 2009; Deutsch, 2010) converge to support the contention that a more appropriate metric of pitch is the logarithmic transform of the fundamental frequency called the pitch interval, denoted in this investigation by H (Gough, 2007) (as in pitch “height”) and measured in units of cents (¢)

$$\mathcal{H}:F_{\text{reference}}\hspace{0.17em}=1200\hspace{0.17em}\text{cents}\hspace{0.17em}{\log }_2\left(\frac{F_0}{F_{\text{reference}}}\right).$$ (1a)

Or more conveniently written

$$\mathcal{H}\hspace{0.17em}=\hspace{0.17em}\frac{1200\hspace{0.17em}\text{cents}}{\log 2}\log \left(\frac{F_o}{1\hspace{0.17em}\text{Hz}}\right)\hspace{0.17em}\approx \hspace{0.17em}3986\hspace{0.17em}\text{cents}\hspace{0.17em}\log \left(\frac{F_0}{1\hspace{0.17em}\text{Hz}}\right).$$ (1b)

Thus, a pitch that has a fundamental frequency of 220 Hz (corresponding to the musical tone A₃, in the tenor or contralto range) will have a pitch (relative to 1 Hz) of 9337¢, while an octave below (A₂: 110 Hz, in the baritone range) will then lie 1200¢ lower at 8137¢. In this graduation, a cent, a unit introduced in 1885 by Ellis (Ellis, 1885), corresponds to a frequency ratio of 1.0005778 that in turn corresponds to a pitch interval of 1/100 of a semitone (in equal temperament). The cent is indeed sufficiently fine for all practical measurement, since the difference limen of musical pitch perception—while varying with frequency in the range of 100 to 1000 Hz—is generally a few cents (∼0.02 semitone) in the frequency range of human speech from 30 to 1000 Hz (Askenfelt, 1973). A musical interval is long established in musical acoustics as the appropriate metric of pitch. In intonational studies pitch ratio, that is, mel has often been the unit of choice. However, Deutsch (Deutsch, 2010) has pointed out that the pitch of complex tones involves the whole chain of the auditory perception, not just the cochlea. Indeed, many intonational phenomena demonstrate vividly the higher cortical functions in auditory perception, such as, for example, Shepard or difference tones that a listener perceives in complex harmonic tones but are in fact absent, that is, he does not actually hear (Shepard, 1964). Therefore, it should not be surprising that mel—a unit of pitch stimulus devised for pure tones—might be less helpful in parameterizing the pitch of complex tones vocalizations than pitch interval.

What is more, in previous intonational studies, 't Hart et al. (1990) proposed two decades ago a very similar pitch interval metric that they called “pitch distance” D and that they measured in units of semitones (STs). They exploited D extensively for the description of pitch in intonational studies, an analysis Couper-Kuhlen also continued in the interim (Couper-Kuhlen, 1996). Unfortunately, the relatively coarse unit of the “semitone” suffers from a measure of ambiguity, since in musical contexts a pitch distance of one ST will vary with the musical intonation schema; for example, while in 12 tone Equal Temperament (12-TET) a ST is indeed 100¢, in Just Intonation (JI) or in Pythagorean tuning it will range in size from 70¢ to 134¢, while the cent is invariant in all tunings (Truax, 1999). Therefore, the authors chose to use pitch interval as defined by Eq. 1 and graduated in units of cents rather than in ST.

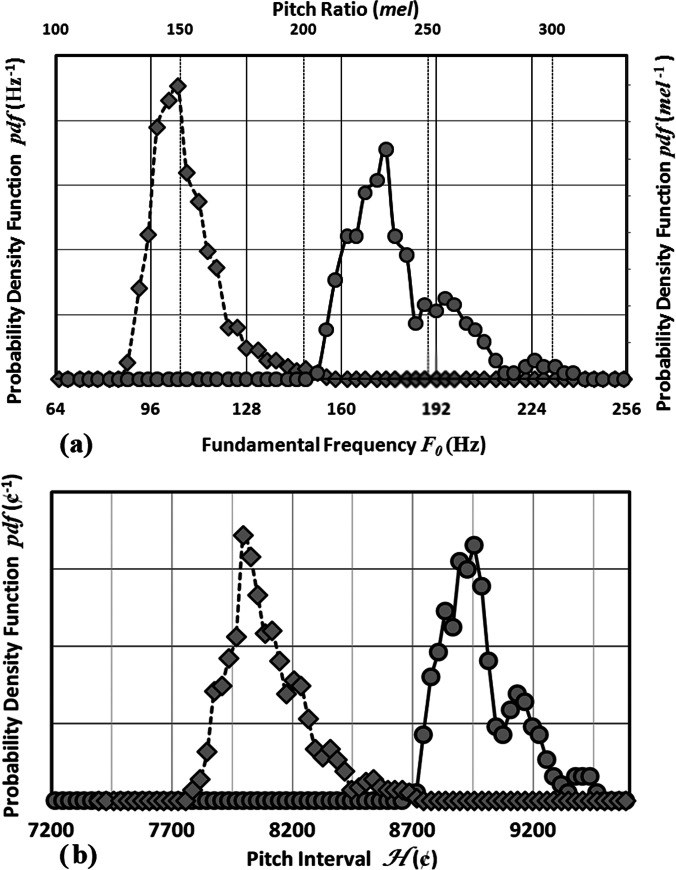
For qualitative relative comparisons it makes little difference if the pitch is parameterized linearly as F₀ (or equivalently as mel) or logarithmically by H, but it is, nevertheless, crucially important what acts as the metric for pitch if one seeks quantitative comparisons of distributions as is the case in this investigation. As a demonstration of this assertion consider two distributions: One obtained from a male speaker and the other a female speaker. In Fig. 1 the probability density function (PDF) for the two speakers appear (subjects E and N) for whom the gamut root (to be defined below) varied only slightly during the discourse and therefore permits a straightforward comparison of the distributions parameterized as fundamental frequency in hertz (and as mel) and as pitch interval in cents. In the first [Fig. 1a] the probability per unit frequency interval (in units of Hz⁻¹ or in units of mel⁻¹ on the secondary axis) is plotted versus fundamental frequency F₀ (in hertz) or as mel on the secondary horizontal axis and then in the lower panel [Fig. 1b] the probability per unit pitch interval (¢⁻¹) versus pitch interval H (in ¢) appears. Note that when logarithmically transformed to pitch interval, the shape and widths of the two distributions are much more similar than when expressed as F₀, (or mel) an observation that suggests that perhaps the male and female speakers favored similar pitch interval excursions in their narratives rather than similar excursions of frequency.

Figure 1.

PDFs for the peak word-pitch occurring in a discourse narrated by a male (lower frequency, mel and pitch) and female (higher frequency, mel and pitch) parameterized as fundamental frequency F₀ and mel (a) and as pitch interval H (b). In the pitch parameterization, the distributions appear more similar in shape and width than in terms of the fundamental frequency.

The peak word-pitch

In an utterance the fundamental frequency (and consequently the pitch) of the voice may rise and fall during a syllable, a word, or an intonational unit (IU) of variable length to produce the pitch contour of the utterance. However, because the motivation of this work lies in the future association of evaluative performance features of language (Wennerstrom, 2001a,b; Olness et al., 2010) with the highest or “peak pitch” of a word, the investigators identified the maximum fundamental frequency ${\left(F_0\right)}_n^{\max }$ and consequently the highest pitch occurring during the utterance of the nth word in the series as the peak word-pitch ${\mathcal{H}}_n$. This discretization was inspired by Wennerstrom's analysis of intonation and evaluation in oral narratives (Wennerstrom, 2001b). It employs the peak word-pitch as a single-pitch proxy representative of the whole of the word. Thus, the present investigation does not address the contour of a given word but rather looks to extract the statistical populations and distributions of the peak word-pitch thereof that a speaker deploys in a spontaneous narrative.

It should be noted that the methods detailed in this article are of more general application than only to the extraction of peak word-pitch distributions. The source of F₀ data could have been equal-time-interval-sampled frequencies or a word-averaged pitch or stylization as, for example, has been implemented by D'Alessandro and Mertens (1995). The subsequent methodology could then be applied otherwise unchanged. Nevertheless, the ultimate discourse analytical objectives drove the decision to examine the peak word-pitch as defined here.

A normalization for comparison: “Gamut root”

Early in their analysis of the distributions of peak word-pitch ${\mathcal{H}}_n$, the authors noted that the pitches used by an individual narrator in his or her discourse clustered about an idiosyncratic value, as seen, for example, as in Fig. 1, the distributions are unimodal or, at least they exhibit a strong central peak. The precise modal value, however, tended to wander or drift during the discourse. When viewed as a sequence, the values of the peak word-pitches in a given extract appeared to return again and again to the vicinity of this characteristic modal pitch. These initial observations led the authors to postulate the existence of a pitch level in reference to which the speaker gives context and significance to her utterances by pitch variation with respect to that reference pitch that might drift slowly during the discourse. In analogy to a musical scale (but without any a priori assumptions as to the existence of degrees or discrete levels) the authors propose the term “discourse gamut,” for the whole range of pitches used in a discourse, resurrecting from obsolescence the original meaning: “gamut… the ‘Great Scale’ (of which the invention is ascribed to Guido d'Arezzo)” (Oxford, 1989). The authors, furthermore, designate the empirically observed reference, to which pitch excursions are referenced, the gamut “root,” and—anticipating the observation of the preferential use of highly pitched excursions from the root—the authors also appropriate the term “e-la” defined originally as the highest degrees of the gamut of D'Arezzo (Oxford, 1989). Indeed, the term “gamut” has come to mean in common usage the complete range of something, while e-la denotes the highest portion of that range. In prior linguistic studies, investigators found an association between elevated pitches, notably Wennerstrom (Wennerstrom, 2001a,b) and the authors of this work (Olness et al., 2010). These researchers identified the “Pitch Peaks,” the highest 10% of the peak word-pitches, as candidate evaluative devices, i.e., a resource used to emphasize selected information in the discourse. In the current study pitches sufficiently elevated above the gamut root but not necessarily belonging to the top 10% may be significant. These—as yet untested—pitches will be designated as the e-la. Thus, the gamut in this context is defined as all of the pitches used by a speaker, whether continuously or discretely distributed and normalized to the modal pitch of the complete discourse, the gamut root. The gamut may contain high-pitched excursions, as well: The e-la, which may be continuously or discretely distributed and may have an important evaluative function.

Various earlier researchers have, furthermore, postulated the dichotomization of intonation into pitch fluctuations corresponding to “global” and “local” ('t Hart et al., 1990) processes. The gamut root proposed here is identified with these global trends. The global reference pitch (gamut root Γ_n) accounts for the postulated long-range (and therefore, slowly varying with word number n) pitch trend of words in the “time” series of the pitch interval ${\mathcal{H}}_n$ of the peak word-pitch versus the word sequence number n. Furthermore, the authors propose that, in a narrative, the speaker quickly chooses a register, a target, a “scale” or a “root” which is used as the reference for contrasts in pitch or intonation. This proposal is not altogether novel in discourse studies: For example, the pitch reference line and frequency code of Gussenhoven's analysis (Gussenhoven, 2004) implies the existence of a reference pitch level, and the controversy over the “look-ahead” preplanning of pitch range selection (Thorson, 2007) presupposes a pitch scaling, as well. Therefore, the gamut root Γ_n (where the subscript n references the value for the nth word in the sequence) as defined herein is a hypothetical frame of reference that is similar to but subtly different from the concept articulated by Wennerstrom of a “pitch range” (Wennerstrom, 2001b) or the notion of relative high, mid, and low “key” options, as conceptualized by Brazil (1985). The authors of this study define below quantitatively and precisely the gamut root and therefore introduce this term to distinguish it from prior qualitatively similar constructs that may or may not coincide with its meaning. The utility of normalizing the pitch distribution is persuasively illustrated by subtracting the value of the mode of the peak word-pitch distributions of Fig. 1 and plotting them on the same graph (Fig. 2). The two distributions have a remarkably similar shape: Skewed to higher pitches (the e-la) with secondary concentrations of pitches near 280¢ and 500¢. A convenient property of logarithms is that the subtraction of a constant is equivalent to a normalization of the argument. Thus, the root of the distribution is defined in this work to be associated with the mode of the overall distribution rather than another measure of central tendency, and subtraction of the gamut root pitch interval from the pitch interval data therefore normalizes it to the mode, the most used pitch, and consequently mitigates the differences between the pitch range of men and women, and young and old.

Figure 2.

The PDFs of the distributions appearing in Fig. 1, normalized to their respective modal pitches, that is, gamut root. Note that in the range of the fundamental frequencies of adult speakers, the mel scale is very nearly a linear mapping of frequency, that is, mel ≈ 1.14(F₀ + 34 Hz).

The task of extracting the (potentially) varying root from the peak pitch of each word is a formidable task. When the peak word-pitch data ${\mathcal{H}}_n$ are plotted as a sequence or series versus n the word sequence number, it becomes (at least formally) a “time series” and is, therefore, accessible to the tools of time series analysis (Box and Jenkins, 1976; Chatfield, 2000). In Sec. 2, the narrative of this paper lays out the procedural details and justification of each step used to extract what is called in time series analysis the “trend,” that is understood in this context to be related to the gamut root of the discourse. The trend is obtained by an average over a window of Q successive peak word-pitches as described in Sec. 2. Moreover, by subtracting the trend (that is, the gamut root) from the time series the procedure produces a “stationary” series whose mode is zero and for which the vagaries of potential drift in the root have been removed. That this is indeed the case, and that there is a necessity for the removal of root-drift is also documented in Sec. 2.

Distribution fitting models

The authors also noted that the distributions of peak word-pitches they extracted from the analysis of the narratives in this study, when quantified as pitch interval relative to the root, are often multimodal, comprising a strong central distribution associated with the root but with other clusters of higher and lower pitch, along with a significant background continuum. This observation led them to propose that the range of pitches used by the speaker, the gamut, might manifest degrees, not necessarily but possibly associated with standard harmonic intervals. Prior discourse studies have suggested that the highest pitch extrema—which the authors designated the e-la—may be associated with linguistic evaluative devices. In fact, the discourse intonation limen for discrimination was identified by 't Hart (1981) and is in line with recent Just Noticeable Difference (JND) data revealed by a “dual pair discrimination experiment” reported by McDermott et al. (2010). The JND extracted from figures in the latter work are, respectively, 317¢ ± 95¢ for non-musicians and 217¢ ± 167¢ for musicians for the limen for the discrimination of which two pair of tones are perceived as the same pitch while the other pair are perceived as different. Thus, it follows that degrees of the discourse gamut in this work that are less than 200¢ away from the gamut-root probably are not perceived as distinct, while those levels that differ by more than about 200¢ probably will be recognized as disparate. Moreover, there may exist distinct levels of elevated pitch extrema, which may lie at approximate multiples of the JND for discrimination and thus give a scale-like structure. Consequently, the authors define all of the peak word-pitch population lying higher than a critical value (typically 200¢) referenced to the gamut root as the e-la of the discourse gamut. Further studies are underway that will reveal to what extent there is an association of the use of these higher pitches with a linguistic evaluative function.

The suggestion that there might be clusters or discourse “degrees” of elevated intonation is plausible because of the competing principles of contrast and parsimony. One might naively expect the distribution of pitches in a discourse lacking significant modulation to be well described by a normal distribution for which small deviations in pitch execution occur randomly while the speaker articulates various phonemes (Lehiste, 1970). More generally, however, if the gamut root does indeed exist, then individuals could intentionally selectively highlight information in the narrative or denote emotion by uttering words with a pitch contrasting with the gamut root (Wennerstrom, 2001a). The pitch difference must be sufficiently large, however, to be recognized as intended in order to successfully highlight or add contrast to the discourse information marked by the elevated pitch.

Previous studies have reported that the threshold for discrimination of pitch differences—that is, the equivalent of the limen of pitch elevation for evaluative purposes—is conservatively somewhat less than 300¢ ('t Hart, 1981). The principle of parsimony, moreover, suggests that the majority of the pitch differences intended to denote evaluative prominence of the information marked with an elevated pitch will not lie much beyond the minimum deviation which is sufficient to assure recognition. This should result in a concentration of clustering of pitches just above the threshold for contrast recognition. What is more, studies have curiously suggested that pitch level changes corresponding to the pentatonic scale also occur (Schwartz et al., 2003; Kuiper and Tillis, 1985). This observation suggests that one should also look for clusters of pitches that approximate 386¢ and 702¢—the first two degrees of the pentatonic scale that exceed the limen of evaluative pitch elevation—even if one were not to observe precisely tuned intervals or levels (Frazer, 2004). On the other hand, as anyone who has listened to “karaoke night” can attest, even if pitch exactness is not universally achieved, nevertheless, the off key singer (or speaker) uses a scale, albeit idiosyncratic and poorly tuned (Pfordresher et al., 2010).

Alternatively, one might argue that there is no compelling reason to assume the existence of degrees of the gamut. Thus, as will be demonstrated in Sec. 2, a simple model of a “random walk” of pitch that exhibits a preferential bias to return to the gamut root will produce a continuous asymmetric double exponential (ADE) or asymmetric Laplace distribution, a function that is unimodal.

The fitting function must admit the possibility of both continuum and cluster processes, since a process omitted in the formulation of the fitting function will not spontaneously appear in the result. Thus, to account for possible clusters of pitches, the analysis included a Gaussian mixture model (GMM), similar to that which has been exploited in text-independent speaker recognition (Reynolds and Rose, 1995); in other words, the distribution was fit with the sum of several Gaussian peaks for which the clusters or levels in the discourse gamut coincide with the centroids of the subsidiary Gaussians in the fitted model with the addition of an ADE function to account for the continuous distribution. By comparing the relative contribution to the distribution of the GMM components and the ADE components the analyst can estimate the relative propensity of the narrator to use degrees of her idiosyncratic gamut versus a continuum of pitch.

Therefore, in the present study the authors propose an operationalization of peak word-pitch statistics that they have found powerful and illuminating and that has revealed remarkable general features in the structure of the distributions of peak word-pitches.

METHODOLOGY

As a test of the proposed protocol, a corpus of data was obtained for this study that comprises narratives from 17 individuals with over 7000 peak word-pitch samples. Narrative samples were purposefully selected to be narratives on an emotive topic: Personal narratives of a frightening experience. The analysis consists of four phases: (1) The determination of the maximal fundamental frequency ${\left(F_0\right)}_n^{\max }$ of each word that occurs in the discourse; (2) the scaling of pitch by the logarithmic metric of pitch interval as given by Eq. 1 and the arrangement of the pitch interval ${\mathcal{H}}_n$ versus the word sequence number n to form a time-series; (3) the determination and removal of the trend or gamut root Γ_n evaluated for each word; and (4) the fitting of the distributions of ${\mathcal{H}}_n^{*}$, the stationary relative pitch of the peak word-pitch time series, with a GMM plus an ADE model to identify the possible existence, propensity for, and location of degrees of the discourse gamut and the e-la. While these ideas have antecedents in a prior qualitative, descriptive analysis in the intonation literature, the concepts proposed herein are, in contrast to most prior work, quantitatively and objectively defined, and applied for the first time within natural discourse contexts which are purposefully selected to be emotive in content.

Participants

The participants in the methodological-validation study were 17 native English-speaking, middle-aged African-American adults residing in north-central Texas. Participants were originally recruited through referrals from friends and family members of other participants in a larger study on narrative discourse production of speakers with and without aphasia (Olness et al., 2010), and had been selected primarily for their demographic similarity to the individual participants with aphasia in that study, for matching purposes. The group of 17 participants comprised 6 males and 11 females. Their ages ranged from 44 to 66 yrs with a median age of 53 yrs. All but one had completed high school. Twelve of the 17 had been reared in urban, small-town or rural Texas for at least a portion of their childhood; an additional 5 had been reared elsewhere in the United States (East Coast, West Coast, Midwest, or West). Demographic characteristics of each participant are found in Table TABLE I..

TABLE I.

Discourse relevant demographic data. Education Level number corresponds to educational attainment: 1 = < 12th grade; 2 = high school graduate; 3 = associates degree; 4 = some college credit; 5 = baccalaureate degree; 6 = some graduate credit; 7 = graduate degree. Socioeconomic Status (SES) level estimated from occupation: Highest number (7) associated with highest SES [adapted from Featherman and Stevens (1980)].

ID	Age	Gender	Childhood Geo Origin	Adult Geo Origin	Education Level	SES
A	53	F	KY, CO, IN, DC (urban; sm town)	RI, TX (urban)	5	7
B	55	F	TX (rural)	TX (urban)	7	7
C	66	M	TX (urban)	TX (suburban)	3	3
D	56	F	IL (urban)	IL, TX (urban)	4	4
E	56	M	TX (urban)	TX (urban)	5	6
F	44	M	TX (urban)	TX (urban)	2	2
G	52	M	IA (sm town)	IL, TX (urban)	3	4
H	57	F	DC (urban)	TX (urban)	7	7
I	53	F	TX (sm town)	TX (urban)	1	3
J	52	F	TX (urban)	TX (urban)	7	7
K	47	F	TX (sm town)	TX (urban)	3	4
L	61	F	TX (sm town)	TX (urban)	3	3
M	52	M	TX (rural)	TX (urban)	4	4
N	45	F	CA (urban; rural)	CA, TX (urban)	5	4
O	46	F	TX (urban)	TX (urban)	2	4
P	56	F	TX (urban)	TX (urban)	4	7
Q	55	M	IL, IA, TX (urban; sm town)	IA, TX (urban; sm town)	2	4

The fact that all of the participants were African Americans provided some control for the potential effects of race and ethnicity on discourse (Johnson, 2000; Morgan, 2002). However, the complexities of assigning ethnic dialect status (Mufwene, 2001) were outside the bounds of the current study, especially given the possibility of code-switching between dialects. Moreover, there was group heterogeneity for multiple factors known to influence sociolinguistic variation, such as gender, geographic origin, population density in one's location of residence, education level, and socioeconomic status (Troutman, 2001; Bailey, 2001; Cukor-Avila, 2001). The authors worked under the assumption that it is not ethnicity alone that conditions the use of prosody for emotional expression in personal narratives, but rather that “expression of emotion in stories varies with genre…ethnicity, gender, geographic region, class, personal style…and other pragmatic factors” (Wennerstrom, 2001a). In many of these respects, the participant group in the current study was relatively heterogeneous, despite its apparent demographic homogeneity.

Narrative sampling

As already noted, two of the factors that influence the expression of emotion in stories are discourse genre and pragmatic factors (Wennerstrom, 2001a). The discourse elicitation context of the current study was designed to control for these factors. The context was designed specifically to elicit a personal narrative on an emotive topic in contrast to scripted speech, for example, so the participants' discourse samples would be relatively natural and include evaluative emphasis of information, and so responses of all participants would be in the same narrative discourse genre. Participants recounted a narrative of a frightening experience as one of five personal narratives told to an interested listener-interviewer (Labov, 1972) in the final portion of a larger discourse protocol. Each participant was interviewed by one of two African-American female adult interviewers from Texas (one in her thirties, one in her twenties; both from middle class backgrounds; and both with a master's degree in the field of communication sciences and disorders). The interviewer asked the participant-narrator to “… think of a time when you were frightened or scared” and to relate that event (“What happened?”). This elicitation was chosen for its ability to prompt a narrative with emotive content on a personally salient theme (Labov, 1972).

Recording and pitch sampling

The investigators audio recorded the narratives at a quiet location of each participant's choice (for example, residence, library, university) utilizing a Sony TCD-D100 digital audio tape-recorder (Sony Corp. of America, New York) equipped with a Sony ECM-F01 omni-directional electrets condenser microphone. While this choice prevented tight control on background noise and loudness level control, the psychological and affective advantages were worth the modest challenge it introduced in the subsequent analysis. Indeed, the small variations in volume and background noise did not prevent an accurate evaluation of the fundamental frequency of almost every word. Recordings were orthographically transcribed. The maximum fundamental frequency ${\left(F_0\right)}_n^{\max }$ in each word (the peak word-pitch) was determined using PRAAT software (Boersma, 2001) and ${\left(F_0\right)}_n^{\max }$ was converted to pitch interval ${\mathcal{H}}_n$ in cents as described in Eq. 1. In a few cases some sounds exhibited no distinct pitch, as in the situation of unvoiced incoherent utterances or some occasions of glottal fry. These were omitted from the time series. In addition, some subjects exhibited the phenomenon of period doubling (Menzer et al., 2006) that appears as sudden isolated drops in pitch by an octave (a factor of 2 in F₀) or equivalently by a drop in pitch interval of −1200¢. It should be emphasized that these pitch breaks are not artifacts but are actual unintentional pitch changes resulting from a non-linear physical process in phonation. These period doubled pitch breaks were retained in the data set but treated as outliers in the determination of the trend as described in this section.

Narrative length and content

The narratives ranged in length from 104 words to 1582 words, with a median length of 313 words. The duration of the narratives ranged from 64 s to 1340 s, with a median duration of 327 s. The narratives contained many pauses, both audible and silent. Consequently, the average rate of speech in these narratives ranged from 0.3 to 3.5 words/s with a median rate of approximately 1.3 words/s. The intonational analysis of selected discourses consistently revealed IUs comprised of 1 to 15 words with a median of approximately 5 words. Thus, a moving window of 31 words was exploited in the analysis described below and typically encompassed more than one IU at any given time. Furthermore, the peak word-pitches spanned an ambitus (a musical term for the pitch range lowest to highest of a tune or discourse) (Oxford, 2005) for the data set of from F₀ = 63 Hz (H = 7172¢) to F₀ = 528 Hz (H = 10852¢). The topics of all narratives involved threats to the health or welfare for the narrator or for a close relative or friend, including medical conditions, public and domestic violence, traffic and car-related accidents, dangerous situations at the workplace, encounters with threatening people or animals, and domestic accidents.

Analysis

In what follows the authors will first describe straightforwardly each of the steps used in the quantitative treatment of the data without any rationale or justification in order to provide a clearer overview of the procedure. Then, the presentation will return to each step with a discussion of the function and rationale for each step in the formalism. The authors will then demonstrate the efficacy of the protocol on a simulated data set possessing a well-determined (simulated) distribution before then applying the methodology to the empirical data.

Protocol

a. Frequency extraction and pitch calculation. The digital recording of the discourse was subjected to analysis by the software program PRAAT (Boersma, 2001) that uses an autocorrelation algorithm to extract the fundamental frequency of the sound (Boersma, 1993). The analyst selected the region of interest of the discourse occurring in a given voiced word by inspecting the graphic display of the pitch while listening to the audio transcript in conjunction with a manual orthographic transcription of the discourse. The maximum frequency utility of PRAAT then reported the peak frequency in this audio sample. Subsequent checks by multiple analysts confirmed the analyst-independence of the peak word-frequency determination. This frequency ${\left(F_0\right)}_n^{\max }$ was recorded in a spreadsheet as the peak word-frequency for the nth word in the discourse. The frequency was then transformed into the peak word-pitch interval by

$${\mathcal{H}}_n\hspace{0.17em}\equiv \hspace{0.17em}3986\hspace{0.17em}\text{cents}\hspace{0.17em}\log \left({\left(F_o\right)}_n^{\max }\hspace{0.17em}/1\hspace{0.17em}\text{Hz}\right).$$ (1c)

In what follows the reference frequency of 1 Hz will be tacitly assumed.

b. Gamut root determination. When the pitch is arrayed versus the word sequence number, the series is formally a “time-series” and, therefore, accessible to time-series forecasting tools (Box and Jenkins, 1976; Chatfield, 2000). A key approach in time-series analysis is the averaging over successive windows or sub-sets of the series. Consequently, the sequence was subjected to averaging in a moving window of width Q = 2q + 1 = 31. For each word the analyst computed the modified z-score to assess the divergence of the data point from its neighbors. The modified z-score z_n is given by Iglewicz and Hoaglin (1993),

$$z_n=0.6745\hspace{0.17em}\left|{\mathcal{H}}_n-\text{median}\left[{\mathcal{H}}_{n+q},{\mathcal{H}}_{n-q}\right]\right|/\text{MAD},$$ (2a)

where “MAD” represents the median absolute deviation from the median in the interval

$$\text{MAD}\hspace{0.17em}=\hspace{0.17em}\text{median}{\left[\left|{\mathcal{H}}_n-\text{median}\left[{\mathcal{H}}_{n+q,}{\mathcal{H}}_{n-q}\right]\right|\right]}_{n+q,n-q}.$$ (2b)

To assess the critical value z_critical of the modified z-score sufficient to detect outliers in the time series, the investigators temporarily interjected spurious artificial outliers by replacing approximately 10% of randomly selected points by their value, minus 1200¢, a simulation of period doubling. They adjusted the critical value of the modified z-score until 95% of the interjected outliers were flagged by the protocol. This critical value was then used in a subsequent analysis of the original, unaltered time series.

If the modified z-score exceeded the critical value of z_critical, the data point of the series was flagged by the protocol as an “outlier,” not belonging to the perimodal distribution, and was omitted from the computation of the “trimmed” mean ⟨${\mathcal{H}}_n^{†}$⟩ in the window, although all of the data were retained for all other steps in the analysis. Thus, the trimmed mean in the window from n − q to n + q, where Q = 2q + 1 is

$$\langle {\mathcal{H}}_n^{†}\rangle \hspace{0.17em}={\displaystyle \sum _{i=n-q}^{n+q}\left[{\epsilon }_i\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathcal{H}}_i\right]/}{\displaystyle \sum _{i=n-q}^{n+q}{\epsilon }_i},$$ (3)

where ε_i = 1, if the z-score is less than the critical value and ε_i = 0 if the z-score is equal to or greater than the critical value.

Furthermore, although the trend in this work, in common with traditional time series analysis, was initially computed by taking the mean in the window, the gamut root is identified with the mode of the relative pitch distribution. Therefore, the protocol calculated the reference pitch, the gamut root Γ_n, from the trimmed mean within the window n − q to n + q and the mean-mode distance of the complete relative pitch distribution

$${\Gamma }_n=\langle {\mathcal{H}}_n^{†}\rangle +{\Gamma }_0.$$ (4)

Such that the mode of the relative, stationary time series

$${\mathcal{H}}_n^{*}={\mathcal{H}}_n-{\Gamma }_n,$$ (5)

is zero. That is

$$\text{HSM}[{\mathcal{H}}_n^{*}]=0$$

and thus

$${\Gamma }_0=\mathrm{HSM}\left[{\left(\langle {\mathcal{H}}_n^{†}\rangle -{\mathcal{H}}_n\right)}_{I,N}\right].$$ (6)

The mean-mode offset Γ₀ was determined by the Half Sample Mode algorithm denoted as HSM (Bickel, 2002) applied to the difference between the trimmed mean and the data over the whole of the discourse. (Readers who wish a copy of the VBA-imbedded Excel^TM source code for the algorithms used in this work are encouraged to contact Samuel E. Matteson.)

c. PDF of relative stationary time series. Finally, the authors computed the PDF for the relative pitch in the discourse from a histogram extracted from the interpolated cumulative probability function (CPF). They fitted the resulting distributions with a GMM plus an ADE component using the software package Origin Pro 8 (Origin, 2011) that exploits a Levenberg-Marquardt algorithm (Levenberg, 1944; Marquardt, 1963) for non-linear fitting and by use of a manual Chi-squared minimization simplex procedure. The authors plotted the fitted distributions and examined the correspondences between the features of the various distributions. Explicitly, the fitting function was

$$f\left(h^{*}\right)=\hspace{0.17em}\frac{A_0}{{\lambda }_{+}+{\lambda }_{-}}{e}^{-\left|h^{*}\right|/{\lambda }_{+/-}}\hspace{0.17em}\hspace{0.17em}+{\displaystyle \sum _{k=1}^N\frac{A_k}{\sqrt{2\pi }{\sigma }_k}{e}^{-{\left(h^{*}-h_k\right)}^2/2{\sigma }_k^2}},$$ (7)

where λ_+/− represents either λ₊ or λ₋ depending on whether h* is greater or less than zero, respectively.

Rationale and demonstration

a. Pitch transformation. A central proposition of this work is that pitch interval H is more useful in the analysis of pitch than is fundamental frequency F₀. Figure 1 argues this contention by displaying the PDF of pitch parameterized in terms of F₀ and H for two narrators, a male (subject E with lower pitch) and female (subject N with higher pitch). As noted earlier, when evaluated as fundamental frequency [Fig. 1a], the distributions of the two subjects appear very different, while when the probability density is plotted versus the pitch interval H, the shape of their distributions appear much more alike [Fig. 1b]. The peak word-pitch similarity of the two distributions is highlighted further when one plots the distributions relative to the respective modes of the complete discourse distribution. The PDFs of the male and female narrators appear almost congruent when one plots them versus the relative pitch interval (Fig. 2), even exhibiting nearly coincident secondary peaks and shoulders.

A Chi squared (χ²) goodness of fit procedure affords a more quantitative comparison of the competing metrics of fundamental frequency F₀ (in hertz) and pitch interval H (in cents). After normalizing the distributions of Fig. 1 to their respective modes, the analysts computed the Chi squared deviation of the pair of distributions from their average (interpolating as needed from the originally lower pitched distribution) when the distributions were parameterized as frequency and as pitch interval. In the former case, that is, for F₀, χ² = 22.8 with 29 degrees of freedom and with p = 0.78, not a statistically significant fit. In the latter case of the pitch interval H parameterization, however, χ² = 14.3 with 33 degrees of freedom and with p = 0.998, a significantly better fit. Thus, the pitch interval parameterization is markedly superior in standardizing the distribution forms.

b. The peak word-pitch time series. The arrangement of the peak word-pitch interval values versus the word number (Fig. 3) bears an uncanny similarity to other time series such as daily high temperature that can be disaggregated into a climatic trend with a stationary daily (or hourly) temperature fluctuation distribution. The necessity of disaggregation is illustrated well by a Monte Carlo simulated distribution consisting of three randomly generated variables with Gaussian population distributions superimposed on a trend that changes once in the middle of the series. The times series that resulted provided a demonstration of the need for the determination of the gamut root and the validity of the pitch distribution extraction protocol. By comparing the extracted distributions to the original (known) distribution the authors demonstrated the validity of the method to determine the distributions in experimental time series for actual discourses. In Fig. 4 the histogram of the simulated time series appears with the simulated trend superimposed. No effort was made in the analysis of Fig. 4 to track the trend as it changed and, consequently, the shifting trend obscured the multimodal character of the distribution by conflating different parts of the stationary distribution, that is, the distribution from the first half of the time series was shifted and convoluted with the distribution of the latter half. The distribution thus extracted does not accurately represent the original distribution. Therefore, it is apparent that the trend should be subtracted from the time series point-by-point to mitigate the vagaries of the trend.

Figure 3.

Simulated time series of peak word-pitch versus word sequence number. The simulated discourse pitch distribution consists of three artificially produced populations (with high, middle, and low centroids) with relative statistical frequencies of 1:2:4, respectively superimposed on a trend with a single shift near the mid-point of the time series (solid line). In addition, randomly placed outliers have been introduced to test the robustness of the outlier detection protocol.

Figure 4.

(Color online) Histogram of simulated distribution of peak word-pitch time series shown in Fig. 3 normalized to the mode of the distribution of the whole time series. The histogram data do not well reproduce the original distributions when the analysis does not take into account shifts in the modal pitch, the gamut root.

c. The gamut root. Time series analysis traditionally computes the trend, the reference level in this work associated with the gamut root, from the mean in a moving window centered on the point. This choice takes advantage of the smaller standard error of the mean relative to the other measures of central tendency: ${\delta }_{\text{mean}}=\sigma /\sqrt{Q}$ for Q samples and a standard deviation of σ. The averaging over a window is a form of “spatial” filtering that removes rapid (short range) fluctuations and preserves slow (long range) drifts. This is precisely the dichotomy between the local and global fluctuations alluded to earlier: The local fluctuations are those changes in pitch that occur over the span of a word or a few words in an utterance and the global changes are those that occur over many words or a major fraction of the discourse. Therefore, it seems that the mean or the mean-determined mode of the distribution is an ideal index of the gamut root.

Unfortunately the mean is also susceptible to bias from outliers that have values far from the bulk of the distribution. A common technique for the identification of such outliers exploits the modified z-score as defined in Eq. 2 that is a measure of the absolute deviation from the median of the distribution relative to the median of the collection of absolute values of deviations from the median (the MAD). Since the median is less sensitive to the presence of outliers than is the mean, the modified z-score is a more robust metric for the identification of outliers than the standard z-score; yet it serves the same purpose. In realistic data, outliers do indeed occur. One such outlier-producing phenomenon that occurs more commonly in the discourses of older narrators (such as those in this study) as compared to the narration of younger speakers is period doubling pitch breaks (Menzer et al., 2006). Period doubling is an unintended drop by an octave (−1200¢) of the pitch due to a physiological non-linear process in phonation. Such events potentially will bias the value of the mean and were omitted from the computation of the trend, but otherwise included in the distribution. The investigators determined the optimal value of the critical modified z-score for outlier identification by inserting test outliers in real series at random points and adjusting the critical value of the modified z-score until 95% of the test outliers were detected. This value was then used to flag outliers in the original time series. In Fig. 3, the open, unfilled points are those in the simulated data that were identified as outliers due to their greater-than-critical modified z-score. These points were omitted from the trimmed mean determination in the moving window.

The procedure of averaging the values in a window to extract a trend is well-known in digital signal processing and is a type of Finite Impulse Response filter called a “Boxcar Filter” (Frerking, 1994). The Boxcar filter is a low pass filter, that is, “frequencies” lower than the reciprocal of the “period” of the averaging window are preserved, while higher frequencies are attenuated. In the present context the formal frequency corresponds to the cycle rate of pitch features that is, in turn, equal to the reciprocal of the pitch feature length in words. By “pitch feature” we mean a rise or fall in pitch that repeats with “a period” of so many words. The Fourier transform of the discourse is instructive. For example, if a declination-reset cycle of seven words re-occurs often in the discourse, then peaks in oscillatory strength will appear at the feature length (7.0 words) and harmonics of it (3.5 and 2.3 words) down to the Nyquist Criterion of 2 words, which is half the frequency of the sampling rate. Upon application of the Boxcar filter, the rapidly cycling features are filtered out of the trend and disaggregated into the gamut root and the relative stationary time series. Notably, when the simulated declination cycles are recreated by successive random selection of one high-pitch population member followed by two from the middle pitch population and four from the low range, the pattern persists in the stationary time series even after the trend is accounted for by subtraction.

The choice of the width of the window for averaging is an important decision, but its precise value is not critical; that is, the value of the window width only affects significantly the filtering of the features of approximately the same or smaller size; long cycle length features are retained in the gamut root while short cycle length features are filtered out of the gamut root. Furthermore, from a statistical point of view the window width Q should be chosen to be as large as possible to minimize the uncertainty of the mean since the standard error of the mean is inversely proportional to the square root of the number of samples averaged. Moreover, the width should also encompass several cycles of the intonational features that the analyst wishes to preserve in the stationary time series. Selected narratives used in this study were divided into IUs according to the definition and methodology described in Chafe (1993, 1994) and DuBois et al. (1993). Based on this analysis, the mean and modal lengths of substantive IUs were determined to be approximately six and four words, respectively; these values are consistent with those reported by Chafe (1994). What is more, cycles in peak word-pitch as yet unassociated with linguistic function appear in some discourses that exhibit a median feature length of 7 words but with some as long as 15. Thus, a window width of approximately 30—at several times the maximum feature length—appears to be a lower bound for a practical filter.

Conversely, since the shortest discourse was approximately 100 words in length and shifts in the gamut root may occur throughout the discourse, the investigators opted for a window width that permitted a segregation of the discourse into a minimum of three parts: A beginning, middle, and end. Consequently, a window of approximately 30 words appears to be a good, albeit somewhat arbitrary, upper bound for the window width and was used for analysis of all the discourses for consistency.

To avoid the introduction of an undesirable lag and to center the filtering on a given point, the width of the Boxcar filter must be an odd number. Thus, candidate values for Q near 30 (in particular 29, 31, and 33) were examined in detail. The transfer function of the Boxcar filter for these various widths revealed that the filtering was more uniformly low (∼3%) for features of from 1 to 7 words for a window width of Q = 31 words rather than the neighboring alternative values. Thus, a window width of 31 words was the best compromise between the lowest uncertainty and the best segregation between the long and short features. Incidentally, the gamut root for the first and last q + 1 (16) pitches in the time series is assigned the value of the sixteenth and last-but-sixteenth gamut root, respectively.

As has been shown earlier, the mode of the distribution is the most revealing measure of central tendency for the normalization of the various distributions. The investigators experimented exhaustively with directly estimating the mode of the distribution in each window of the time series. Unfortunately, all direct mode estimation techniques are themselves susceptible to bias for small samples, since in random samples runs can occur that do not faithfully represent the parent distribution. What is more, the direct mode estimate can change rapidly and consequently is inconsistent with the slowly varying character of the putative gamut root. Therefore, a hybrid method was developed by the authors that takes advantage of the established features of the moving mean or Boxcar filter but then normalizes the trimmed, windowed mean to the mode of the parent distribution by computing the distance between the mode and mean of the total stationary distribution. A robust algorithm called the HSM algorithm developed by Bickel and Frühwirth (2006) computes the mode of the distribution. The gamut root determined from the trimmed-mean-determined-mode for each word in the series was subtracted from the pitch to yield the relative, stationary time series ${{\mathcal{H}}_n}^{*}$ as detailed in Eq. 5, above. The relative pitch time series has a flat (with zero value) trend and a mode of zero, as well.

d. PDF. From the relative, stationary time series ${{\mathcal{H}}_n}^{*}$, the authors computed a CPF symbolized by F(${\mathcal{H}}^{*}$) representing the fraction of the data points that occur at or below the value of H*; they accomplished this task by ordering and enumerating the data and normalizing to the total number of points, removing duplications in the process. The PDF of the distribution represented by the symbol $f({\mathcal{H}}^{*})=d\mathit{F}/d\mathcal{H}*\approx \delta \mathit{F}/\delta {\mathcal{H}}^{*}$ was approximated by constructing a histogram of the distribution by interpolation of the empirical CPF to determine what fraction of the population (δF) lies in an interval from ${\mathcal{H}}^{*}-\delta h/2$ to ${\mathcal{H}}^{*}+\delta h/2$. Figure 5 displays the result of this analysis along with a smoothed line to guide the eye. The original distribution of simulation data points is superimposed for comparison. The agreement is excellent, particularly in light of the introduction of many spurious points, whose existence is revealed by the telltale peaks near −1200¢. The fitting of the data with a GMM is sensible if one anticipates a clustering. But what if there is also a continuous component? One can show that the ADE is an appropriate functional form that arises naturally from a simple model. The investigators tested the GMM and ADE alone and with other functional forms in fitting the data. The combination of GMM and ADE yielded better fits in all tests, as indicated by a lower mean square deviation.

Figure 5.

(Color online) PDF of simulated peak word-pitch time series of Fig. 3 with the original distribution superimposed (dashed curve). The agreement between the strength, width, shape, and position of the extracted peaks and the simulation is excellent; the data show less than a 1% change in the standard deviation of the peaks and a small error in peak position (−28¢ absolute and less than −11¢ relative to the modal peak), a value that is well within the estimated standard error of the measurement. Note the preservation of the distribution of outliers introduced in the simulation.

Envision the pitch sequence as a random walk in pitch h with steps (of constant magnitude) to greater or lesser pitch values for each successive word in the sequence. Moreover, assume that there is a bias for steps toward the gamut root (to lower pitch if h > 0 and to higher pitch if h < 0). Furthermore, consider the case where the distribution reaches stasis, that is, does not change with succeeding words. Then, the controlling probability density equation will be

$$\frac{\mathit{df}}{\mathit{dn}}=0={\pi }_{+}\hspace{0.17em}Rf\left(h-\delta h\right)+{\pi }_{-}\hspace{0.17em}Rf\left(h+\delta h\right)-Rf\left(h\right),$$ (8)

where π₊ and π₋ are the marginal probabilities of a step up (or no step) or down in pitch, respectively, and δh is the average pitch change between words, while R is the rate of pitch change per word. The first two terms are the gain in probability density from the adjacent PDF regions below and above a given region and the third term is the loss from the region due to departures. One can show that Eq. 8 is satisfied if

$$f\left(h\right)=\frac{A_0}{{\lambda }_{+}+{\lambda }_{-}}{e}^{-\left|h\right|/{\lambda }_{\pm }},$$ (9)

where the scaling length λ_± is given by

$${\lambda }_{+}=\frac{\delta h}{\text{ln}\left({\pi }_{-}/{\pi }_{+}\right)}\hspace{0.17em}\hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}h\ge 0$$ (10a)

and

$${\lambda }_{-}=\frac{\delta h}{\text{ln}\left({\pi }_{+}/{\pi }_{-}\right)}\hspace{0.17em}\hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}h<0.$$ (10b)

Since the probabilities for steps toward the gamut root rather than away from it may be different if the pitch is above or below the gamut root, the scaling lengths may be different. Such a contingency was comprehended in the fitting function.

The fraction 1−A₀ is an empirical measure of the propensity of the speaker to use degrees of the gamut or preferred clusters of pitches rather than an exclusively continuous distribution. By comparing the mean absolute deviation of the centroids of each of the subsidiary Gaussian peaks in the fits (h_k) to the values of normative musical scales (pentatonic, diatonic, and chromatic) with various intonation schemata (for example, 12-TET or JI, major and minor modes), the nearest equivalent musical scale to the discrete portion of the discourse gamut was identified.

RESULTS

The investigators applied the methodology that is described in Sec. 2 to the peak word-pitch time series of the 17 narratives of this study with the following general results. (1) The central working hypothesis that pitch is most usefully parameterized by pitch interval was supported by the intelligibility of these results and by the high level of common distribution structure found in the time series and distributions of the various narrators, irrespective of their fundamental frequency range or gender. (2) Most, but not all (12 of 17), of the time series contained significantly divergent outliers, but all were accommodated by the outlier identification analysis. (3) Many of the time series exhibited marked shifts in the gamut root sufficient to potentially conflate various parts of the distribution, a situation that was nevertheless corrected for by the gamut-root determination techniques described earlier. In other words, in most cases ignoring shifts in the gamut root spuriously combines populations that should be resolved because their respective reference changed during the time series. In fact, the ambitus of the gamut root varied from a low of 121¢ to a maximum of 1511¢ with a median value of 472¢, quite sufficient to obscure structure in the relative peak pitch distributions if not corrected. (4) All of the time series exhibited a prominent central tendency that provides support for the concept of the gamut root. (5) A few intonation contours unmistakably followed a classic declination-reset cycle that was preserved in the stationary relative peak word-pitch time series data. The present discourses, however, do not follow a general tendency to declination; in fact, some display the opposite tendency, what one might call “aclination” and reset. (5) Finally, all but one of the PDFs of the narratives, whether the individual was voluble and spoke with animation or was taciturn with a restricted affect, contain elevated pitches (the e-la), that are idiosyncratically shared between a continuum and a number of degrees or pitch clusters. The fraction of the distributions that could be accounted for by clustering ranged from 0% to 55% with a median value of 25%. The degrees, however, do not appear to conform to conventional scale intervals with any statistical significance.

Outliers and time series

As described in Sec. 2, the presence of outliers in the time series of the narratives was flagged by the divergence of the modified z-score for each point and its 30 neighbors in the averaging window. If the modified z-score exceeded a critical value, the point was flagged as an outlier and omitted from the average of the trend, but otherwise included in a subsequent analysis. The unique critical value of the modified z-score for each time series was determined using test outliers inserted into the time series. Five of the narratives required only relaxed values near the recommended value of 3.5 (Iglewicz and Hoaglin, 1993) while the remaining 12 narratives required a lower critical z-score (median near 1.2) to reliably flag outliers, primarily because of the relatively large fraction of outliers present in the narration.

Gamut root determination and filtering

Figure 6 shows the longest time series (subject B) in this study as an example that is nevertheless typical of gamut root variability and gamut root extraction in the presence of outliers as exhibited by other time series. Note that initially the speaker's voice experienced frequent period doubling pitch breaks that became less frequent as the speaker's voice gradually “warmed up.” The gamut root that is calculated from the trend of the time series is plotted as the solid line, and there it appears to track faithfully the densest part of the local distribution. Figure 7a is a closer look at the first 200 words of the time series in comparison to another narrative (subject F) of approximately 200 words [Fig. 7b] that has fewer outliers and is much more stable. In both cases the protocol accommodates outliers and reproduces well the gamut root even when the trend makes a marked change, as it occurs at n = 125 in Fig. 7a.

Figure 6.

Long time series for subject A with a significant number of outliers (open circles). The gamut root shown as the double line is computed from a moving average of the points in a moving window that have a modified z-score less than or equal to the critical value (z_critical = 0.89), a value that is unique to this discourse.

Figure 7.

Comparison of two peak word-pitch time series extracts illustrating the presence of outliers and gamut root variability. The narrative (a) above required a critical value of the modified z-score of 0.87 while that below (b) had a z_critical = 1.1. Outliers are identified as open circles and were omitted in the computation of the trend and gamut root.

An examination of the formal Fourier transform of the time series is helpful in the assessment of the appropriateness of the choice of window width in the determination of the gamut root (Q = 31). The Fourier transform provides information regarding the presence of intonational structures of various word lengths. Peaks in the fast Fourier transform (FFT) “spectrum” correspond to the presence of repetitive features and their harmonics. Figure 8a, as an example, plots the FFT of the first 1024 peak word-pitches in the time series shown in Fig. 6 (subject B) as a function of the feature length before filtering and after. What is notable about this plot are the many closely spaced peaks lying below 30 words in length. The “feature cycle length” corresponds formally to the wave length and thus the plot is reminiscent of “pink noise,” that is a random power spectrum that increases with wave length in a power law, as indicated by the superimposed line in this log-log plot (the slope of which is incidentally approximately 0.43). A striking lack of features around a feature length of 30 appears as well. To more fully assess the filtering effect of the averaging protocol using a window width of Q = 31, the authors computed the ratio of the FFT amplitude of the averaged spectrum and the relative pitch to the original FFT amplitude (or the so-called oscillator strength). The result, that is plotted in Fig. 8, indicates that features of lengths of approximately 40 or less are filtered out of the gamut root (have an amplitude of less than 20%) and persist in the relative pitch at 80% or more of their original oscillator strength, while features of length approximately 60 words or longer are similarly disaggregated into the gamut root with a filter factor of 80% or higher. In the range of features of from 40 to 60 words, the effects are shared more equally between the gamut root and the residual stationary distribution.

Figure 8.

(a) FFT amplitude versus intonation feature length for a sample of 1024 words in the time series of Fig. 6. Solid line is power law fit (power = 0.43). (b) Empirical Boxcar filter transfer function obtained from a ratio of oscillator strength in window-averaged (Boxcar filtered) FFT plot to the original oscillator strength (solid line) versus feature length. Also shown is the transfer function for the residual peak word-pitch time series.

Declination and reset

Declination is a much appreciated feature of many discourses ('t Hart, 1986; Ladd, 1988; Liebermann, 1986; Swerts et al., 1996), in which the pitch of successive words declines, then resets to a value near the initial pitch. While an exhaustive investigation of the presence of declination and reset is beyond the scope of this current work, the legitimate question arises as to whether such features of intonation contour are preserved by the proposed disaggregation methodology. The answer appears to be “yes,” declination—if present—persists in the relative stationary time series. In Fig. 9 the relative stationary peak word-pitch times series for one individual (subject F) displays classic declination and reset contours. A few of the declination features are marked by descending arrows with their respective resets marked by the broad upward pointing arrowhead.

Figure 9.

The relative stationary peak word-pitch time series (subject F) exhibiting declination and reset. Declination features are marked by descending arrows, while resets are indicated by upward-pointing broad arrowheads.

Not all time series, however, exhibit declination. Many narrative time series seem to peregrinate without clear pattern and, indeed, a few can be characterized as displaying aclination, the inverse of declination, as illustrated by the relative stationary peak word-pitch time series of Fig. 10 (subject J) where the pitch rises in each successive word (indicated by the rising arrows) then resets (as indicated by the downward pointing broad arrowhead). Whatever the reason for such correlated pitch movements or lack thereof, because they occur over the span of a few words, they persist in the relative pitch time series unfiltered by the Boxcar filter formed by the windowed average in the proposed methodology.

Figure 10.

A relative stationary peak word-pitch time series (subject J) demonstrating features that are the inverse of declination, so-called aclination features with reset. Aclination features are indicated by rising arrows while resets are marked by downward pointing broad arrowheads.

PDFs of peak word-pitch

One of the most important results of this study is the distribution of the pitches used by the speakers in their spontaneous narratives. The distributions of the pitches used in the discourse relative to the gamut root are represented by the PDF of the residual stationary time-series. The PDF of each of three are shown in Fig. 11 (subjects A, B, and Q) in order to graphically assess the quality of the fit. In each case the empirical data are fit by the fitting function of Eq. 7: The sum of a continuous ADE function and an ensemble of Gaussian peaks at discrete levels. The former function accounts for the continuum of pitches that might appear in the discourse gamut and the latter represents any degrees or levels. Table TABLE II. summarizes the extensive and varied findings. Notably, all but one of the PDFs is best fit with a combination of both continuous and discrete contributions. In Table TABLE II. the scale lengths of both the positive and negative parts of the exponential distribution appear, as well as the number of degrees and location of the three most prominent discrete components. The fraction of the distribution that arises from the continuous ADE function varies from 45% and 100% with a median value of 75%. The median (average) full width at half maximum for the ADE functions is 204¢ (210¢) with the “time constant” for positive values exceeding that for negative values by a median (average) value of 21¢ (29¢). Furthermore, for 12 of 17 the continuous distribution is positively skewed.

Figure 11.

Representative PDFs for narrators A, B, and Q with the fraction of the fit due to the ADE of 1.0, 0.95, and 0.45, respectively, show in the data as well as the fit.

TABLE II.

A summary of the quantitative findings of this investigation. The subject discourses are identified by the letters A through Q; columns 2 and 3 are the fraction of the probability density fit by the ADE function (A₀) along with the scale lengths λ. The number of Gaussian functions follows with the centroids of the three most prominent and the estimated error in the degree position.

ID	A0	λ− (¢)	λ+ (¢)	# °	h1 (¢) ± δh1 (¢)	h2 (¢) ± δh2 (¢)	h3 (¢) ± δh3 (¢)
A	1.00	129	129	0	—	—	—
B	0.94	210	272	3	−1139 ± 16.9	928 ± 11.9	1200 ± 10.5
C	0.86	189	186.5	3	−532 ± 10.5	780 ± 34.3	1862 ± 28.9
D	0.84	200	275	3	−240 ± 6.4	286 ± 28.7	870 ± 13.1
E	0.82	89	99	3	−158 ± 6.2	130 ± 7.7	303 ± 10.5
F	0.79	175	194	3	270 ± 14.3	859 ± 17.7	1252 ± 28.7
G	0.78	126	310	6	128 ± 6.1	274 ± 8.1	556 ± 7.6
H	0.75	135	160	2	−1284 ± 18.3	497 ± 21.7
I	0.75	125	125	4	−998 ± 23.1	166 ± 6.2	428 ± 9.1
J	0.73	100	172	4	−1145 ± 17.2	−290 ± 12.1	680 ± 11.3
K	0.71	157	85	3	−236 ± 8.1	136 ± 5.6	310 ± 18.4
L	0.71	141	169	6	−1249 ± 19.3	144 ± 11.6	462 ± 28.8
M	0.68	128	178	4	−181 ± 9.4	320 ± 14.9	515 ± 9.9
N	0.68	62	57	3	130 ± 8.9	250 ± 6.3	360 ± 10.4
O	0.64	160	167	7	169 ± 7.2	287 ± 6.5	540 ± 9.4
P	0.51	109	130	5	−174 ± 11.7	124 ± 3.4	284 ± 12.1
Q	0.45	97	120	6	139 ± 5.3	270 ± 4.2	640 ± 21.8

Figure 12 graphically illustrates both the qualitative diversity of the distributions of peak word-pitch and the power of the fitting stratagem of this work. The distributions appear in descending order (identified in the plot and Table TABLE II. by the letters A through Q) of the contribution of the continuous distribution function (the asymmetry double exponential function ranging from 100% to 45%). Thus, each successive plot contains a much greater contribution from the discrete component. By these fitting functions one can quantify the extent to which a discourse exhibits clustering of pitches rather than a continuous distribution. Therefore, the two-component fitting procedure processes an adequate flexibility and power to encompass what at first seems a bewildering array of disparate forms and reveals a common underlying statistical structure: A continuous plus a cluster distribution.

Figure 12.

Composite of all PDF distribution fits for all subjects A to Q arranged in descending order of continuum contributions from 100% (A) to 45% (Q). Note that the seemingly diverse ensemble is accommodated by a sum of the two fitting functions.

The form of the continuous component is especially unexpected. It is not a normal distribution but is an asymmetric form of the Laplace exponential form, as was shown to be plausible earlier.

Correlations of gamut degrees with musical intervals

In Fig. 11, an arrow indicates the position of a peak or cluster. In Table TABLE II. the three most prominent degrees are also indicated for all narratives (subjects A through Q), including those in Fig. 11. In general, there are discrete contributions at near plus and minus a semitone but often strong clustering occurs also at values greater than 250¢ and at higher values. The authors examined how closely the peak positions coincided with pitch intervals of the pentatonic, diatonic, and chromatic scales of the major and minor modes in 12-TET and JI. Of the 65 peaks in the 17 narratives, 30, that is, 43%, lay within ±20¢ of a conventional musical tone in a standard scale. This correspondence is only slightly larger than one would expect to occur due to random fluctuations; 40% of the tones are expected to lie in this interval, since the ratio of the acceptance interval to the average pitch interval between musical tones is 40¢/100¢. A Chi-squared test of these data yielded a χ² of 1.03 with 1 degree of freedom. According to standard statistical tables this case could have occurred randomly with a probability of 0.30. Thus, these data do not support a contention that the degrees correspond to musical intervals with any statistical significance, although the speakers may have intended to use musical tones but did so very imprecisely (Pfordresher et al., 2010).

The issue of the location of each cluster can be further elucidated by combining the discrete parts of all of the distributions by addition as in Fig. 13. Any shared concentration of pitches will manifest itself as a larger composite peak. In Fig. 13 the pitch intervals of a chromatic scale are superimposed with error bars of ±20¢ corresponding to the JND for non- musician pitch discrimination. This graph makes clear the lack of a statistically significant association between the peaks of the distributions and musical scale. Occasionally a peak will indeed align with a musical interval but the association appears only to be coincidental in these subjects. In fact, in many instances the degrees of the discourse gamut “lie in the cracks” midway between standard musical degrees. Notably the strong peak that appears is several PDFs at 280¢ qualitatively seems to correspond most closely to a minor third (at 316¢ in JI) but the correspondence is crude at best.

Figure 13.

Composite (sum) of the GMM component of all the distributions compared to degrees of the standard musical scale (bottom). Longer vertical markers indicate the “white” keys and the shorter the “black” keys in a chromatic scale. Some of the peaks of the distribution do coincide with musical degrees, but only incidentally, suggesting no statistical significance. The first order, second order, and third order thresholds for contrast are noted by horizontal bars.

Relationship of gamut degrees with threshold

The data suggest an alternative explanation for clustering. Note that many significant and ubiquitous cluster populations occur in three peaks: Near−100¢ and +100¢, both of which lie less than the JND for discrimination detection and a peak at +280¢, which is near the JND for discrimination of pitch contrast. The latter is a value cluster that could be discriminated by a listener as different from surrounding pitches, thus potentially functioning to highlight or add prominence to the discourse information marked by these elevated pitches. The authors conjecture that this is evidence for a parsimony-contrast model for cluster formation in the discourse gamut, a model which could be tested with future studies that relate pitches in various levels of the pitch distribution to the narrative structural transitions, narrative evaluative devices, and narrative content with which they are synchronous.

DISCUSSION AND CONCLUSIONS

Pitch interval and its distribution in natural discourse

The data of this study provide compelling evidence in support of the use of pitch interval in discourse studies, rather than the widespread practice of analyzing pitch as fundamental frequency (or mel). Indeed, a detailed inter-speaker analysis would have been impossible if the peak word-pitch had been left expressed as raw fundamental frequency F₀ (or mel). In contrast to analyses relying on fundamental frequency (or mel), an otherwise obscured systematic behavior emerges when the PDF is first converted to pitch interval H and then normalized to the gamut-root. Both various psycho-acoustical investigations and the present study demonstrate that the metric of pitch interval H measured in cents provides a powerful analytical tool for the investigation of pitch in speech.

Furthermore, the results of this study will suggest that at least the speakers of the demographic sample of this investigation relate the local pitch excursions of their narrative to a personal global trend pitch that the current work designates the gamut root. This reference level drifts and changes during the narrative but can be accurately tracked using a trend-determined mode-estimation procedure (the mean-mode procedure described above) that acts on an appropriately-sized window of the data.

Heretofore, researchers could only report that the distributions were approximately “log-normal” in F₀, that is, Gaussian in H, or “not precisely a normal distribution” (Sönmez et al., 1997). The present methodology permits the discourse analyst now to resolve the details that had been obscured by prior insufficient analysis. The current analysis demonstrates that the data conform more closely to a distribution described by a combination of ADE and GMM, rather than log-normal or a normal distribution. This study confirms that a disaggregation of the pitch-versus-word sequence (or time series) into a global (meso-scale) reference or trend (the gamut root) and a local (micro-scale) relative stationary pitch ${\mathcal{H}}^{*}$ time series is indeed possible, a process that exposes both the badly tuned but nonetheless musical scale-like gamut-degree structure and the glide-like intonation continuum. All but one of the speakers in this study showed some preference for discrete pitch levels or degrees. The particular preferred pitches, however, appear to be idiosyncratic and only approximately tuned to musical intervals for these subjects.

The finding that pitch is both distributed with discrete intervals (degrees of the discourse gamut) as well as in a smooth continuum extends in a different way the anticipatory results of Braun (2002) who found that in locally emphasized Dutch, speakers used a higher portion of musical tones than in normal speech. Moreover, the positively skewed pitch distributions (in 14 of 17 distributions in this study as presented in Sec. 3) arise from a general tendency for these speakers to use higher pitch levels relative to the gamut root more often than lower pitch intervals. The higher reaches of the pitch distribution, whether continuous or discrete in character—that the authors designate as the e-la—may correlate with linguistic phenomena that highlight or add prominence to discourse information (e.g., evaluative device) or that mark narrative structural transitions (e.g., discourse markers). This topic is the object of on-going research by the authors' research group.

The intonation continuum

The commonality that occurs in the continuous part of the distribution both in functional form and in scale across speakers with very different pitch ranges and narrative styles is an additional remarkable finding of this study. As suggested by the plausibility arguments that appear in the justification of the methodology, the functional form of an ADE may have its origin in the stochastic evolution of the peak word-pitch time series. The continuous distributions observed in these narratives may very well result from a very simple process controlled by a general tendency of the speaker to return to the gamut root. Confirmation of this highly suggestive hypothesis must await further analysis and more data on the evolution of the peak word-pitch time series and lies beyond the scope of the current study, which is focused on distributions rather than the evolution of contour. The finding is, nonetheless, provocative.

Estimated error in pitch determination

The uncertainty in the value of the gamut root plays an important role in the assessment of the quantitative reliability of the disaggregated distributions. The standard deviation of the peaks (the sample standard deviation) appearing in the gamut-root PDF provides a straightforward means to estimate the contribution of the uncertainty in the mode to the error in the computation of the normalized pitch interval (the standard error of the mean). From an elementary statistical analysis (Weisstein, 2011) the full width at half maximum of the individual peaks that appear in the PDF distribution of the gamut-root, that range from 80¢ to 120¢, correspond to a sample standard deviation ranging from 34¢ to 51¢. Assuming a sample of 31 points (the window width) the standard error of the mean for the gamut-root is, therefore, estimated to be 6¢ to 9¢, a small contribution to the overall uncertainty.

The PDFs clearly exhibited multiple peaks or degrees in the discourse gamut, even without disaggregation. These degrees do not correspond sharply or precisely to given pitches, but can be ascertained from the peak fits. The non-linear fitting software Origin 8 provides an estimate of the standard error in each of the determinations of the peak position, derived from the goodness of fit and the error matrix. The Pearson product-moment R² value was in excess of 0.98 in all cases with from 3 to 7 Gaussian fitting functions. The estimated uncertainty in the peak positions ranged from a low of approximately 1¢ to a maximum of 120¢ for a very broad and poorly resolved peak of low population, with the root-mean-square standard error for the combination of all peak determinations of approximately 27¢. This value is just below the threshold of discrimination for the untrained ear (McDermott et al., 2010).

Therefore, the random error in the pitch determination resulting from the method of this study, assuming that the errors in the gamut root and the peak fits are uncorrelated, was estimated conservatively to be 28¢, a value consistent with the resolution of the effective histogram bin width and the typical sample distribution widths.

Implications for discourse studies

The authors' earlier work (Olness et al., 2010) that follows Wennerstrom's intonational protocol, examined the hypothesis that the top 10% of the peak word-pitches used in a discourse are associated with linguistic features such as evaluative devices and discourse markers. In the present study the authors examined how closely this intuitively-assigned criterion of the 90th-plus percentile, that identifies the pitch peaks, to use Wennerstrom's phase, corresponds to utterances that are actually significantly higher than the gamut-root. The investigators found that for 14 of 17 or 82% of the spontaneous emotive narratives, the peak word-pitches in the 90th-plus percentile are estimated to be due almost totally to the highest pitches in the narrator's discourse gamut; that is, in these discourses the pitch peaks arise from the e-la (pitches greater than 300¢ above the gamut-root) with a probability of 99% or greater. The data suggest, however, that in the 3 discourses for which the 90th percentile occurred lower than 300¢ above the gamut-root, as much as 60% of the words in the pitch peaks category—as identified by the 90th percentile criterion—may potentially be misattributed since they actually are due to perimodal pitches but with an elevated gamut-root.

Indeed, while the arbitrary designation of the top 10% of pitches is convenient to apply and avoids the issues of choosing the appropriate metric for pitch, it begs the question of how often an individual exploits the e-la of his or her discourse gamut. If the speaker uses such devices more than 10% of the time then one should expect that the peak word-pitches in the top 90th percentile will be hypermodal words, identified in this work as the e-la. If the narrator uses e-la pitches with a statistical frequency of less than 10%, then perimodal pitches, that is, pitches not belonging to the e-la class, will be inadvertently included in the sample. These issues may account for some of the variability noted by Wennerstrom (2001b) in her results. Therefore, it seems prudent to revisit the criterion for the degree of association between evaluative devices and those pitches that are demonstrably higher than the gamut root, as well as the pitch peaks constituting the top 10% of the population. While such a linguistic investigation is beyond the scope of the present work, it is a promising area of inquiry for future research.

Implications for other intonational studies

The results of this study have further ranging implications, moreover, than just discourse studies. A quantitative account of statistical pitch distribution in discourse contexts will potentially inform the research of not only linguists, but also of other researchers engaged in analyzing, synthesizing, or recognizing realistic human speech. For example, cognitive neuroscientists who investigate the production and perception of pitch for their implications regarding the origins of language (for example, see Wilson et al., 2009) can compare the overall shape of pitch distributions in discourse to other vocal signaling distributions. For musical acousticians, the shape of the distribution may also illuminate the kinship of spoken pitch and sung pitch (for example, see Levitin, 1994); for instance, through the comparison of the distribution of pitch in discourse to the overall distribution of pitch in musical scales. Indeed, researchers of discourse have increasingly pointed out the connection between the pitch of words in natural discourse and musical pitch in song (Wennerstrom, 2001a; Deutsch, 2010; Braun, 2002). Likewise, speech synthesis researchers (for example, Prevost and Steedman, 1994) and speaker recognition technologists (Abberton and Fourcin, 1978) can exploit information about pitch distribution in discourse to mimic natural intonation more faithfully, or for potential applications to speaker recognition in naturalistic discourse contexts.

In view of the remarkable insight that accrues from the application of the quantification methods detailed in this work, the data compel the questions: “Are these results universal? Will the patterns observed in these data hold for other demographic groups, languages, or genres of discourse?” It remains to be seen, but in any case the quantitative tools that have been developed in this investigation are now ready at hand to equip such inquiries, by the current authors and by other investigators, as well.