Decoding Flexion of Individual Fingers Using Electrocorticographic Signals in Humans

Abstract

Brain signals can provide the basis for a non-muscular communication and control system, a brain-computer interface (BCI), for people with motor disabilities. A common approach to creating BCI devices is to decode kinematic parameters of movements using signals recorded by intracortical microelectrodes. Recent studies have shown that kinematic parameters of hand movements can also be accurately decoded from signals recorded by electrodes placed on the surface of the brain (electrocorticography (ECoG)). In the present study, we extend these results by demonstrating that it is also possible to decode the time course of the flexion of individual fingers using ECoG signals in humans, and by showing that these flexion time courses are highly specific to the moving finger. These results provide additional support for the hypothesis that ECoG could be the basis for powerful clinically practical BCI systems, and also indicate that ECoG is useful for studying cortical dynamics related to motor function.

1. Introduction

Brain-computer interfaces (BCIs) use brain signals to communicate a user’s intent [1]. Because these systems directly translate brain activity into action, without depending on peripheral nerves and muscles, they can be used by people with severe motor disabilities. Successful translation of BCI technology from the many recent laboratory demonstrations into widespread and valuable clinical applications is currently substantially impeded by the problems of traditional non-invasive or intracortical signal acquisition technologies.

Non-invasive BCIs use electroencephalographic activity (EEG) recorded from the scalp [2, 3, 1, 4, 5, 6, 7, 8]. While non-invasive BCIs can support much higher performance than previously assumed, including two- and three-dimensional cursor movement [5, 9, 8, 10], their use typically requires extensive user training, and their performance is often not robust. Intracortical BCIs use action potential firing rates or local field potential activity recorded from individual or small populations of neurons within the brain [11, 12, 13, 14, 15, 16, 17, 18, 19]. Signals recorded within cortex may encode more information and might support BCI systems that require less training than EEG-based systems. However, clinical implementations are impeded mainly by the problems in achieving and maintaining stable long-term recordings from individual neurons and by the high variability in neuronal behavior [20, 21, 22]. Despite encouraging evidence that BCI technologies can actually be useful for severely disabled individuals [6, 23], these issues of non-invasive and action potential-based techniques in acquiring and maintaining robust recordings and BCI control remain crucial obstacles that currently impede widespread clinical use in humans.

The capacities and limitations of different brain signals for BCI applications are still unclear, in particular in light of the technical and practical constraints imposed by the long-term clinical applications in humans that are the immediate goal of BCI research. The further development of most BCIs based on intracortical recordings is driven by the prevalent conviction [24, 25, 26, 27] that only action potentials provide detailed information about specific (e.g., kinematic) parameters of actual or imagined limb movements. It is argued that the use of such specific movement-related parameters can support BCI control that is more accurate or intuitive than that supported by BCIs that do not use detailed movement parameters. This prevalent conviction has recently been challenged in two ways. First, it is becoming increasingly evident that brain signal features other than action potential firing rates also contain detailed information about the plans for and the execution of movements. This possibility was first proposed for subdurally recorded signals by Brindley in 1972 [28]. More recently, several studies [29, 30, 31] showed in monkeys that local field potentials (LFPs) recorded using intracortical microelectrodes contain substantial movement-related information, and that this information “discriminated between directions with approximately the same accuracy as the spike rate” [29]. Furthermore, our own results in humans [32, 33, 34, 35, 36, 37] showed that electrocorticographic activity (ECoG) recorded from the cortical surface can give both general and specific information about movements, such as hand position and velocity. We also found that the fidelity of this information was within the range of the results reported previously for intracortical microelectrode recordings in non-human primates (Table 3 in [36]). These results have recently been replicated and further extended [38, 39]. There has even been some evidence that EEG and MEG carry some information about kinematic parameters [40]. Second, it is still unclear whether information about movement parameters does in fact extend the range of options for BCI research and application. Recent studies using EEG and ECoG in humans ([5, 8, 9, 10] and [41], respectively) used brain signals that did not reflect particular kinematic parameters. Nevertheless, these studies demonstrated BCI performance that was amongst the best reported to date. In summary, it has become clear that information about specific movement parameters is accessible to different types of signals recorded by different sensors, and there is currently little evidence that any sensor supports substantially higher BCI performance than the others.

Going forward, a critical challenge in designing BCI systems for widespread clinical application is to identify and optimize a BCI method that combines good performance with ease of use and robustness. Based on the studies listed above and others [32, 42, 43, 44, 41], ECoG has emerged as a signal modality that may satisfy these requirements. This notion has been supported in part by our previous study [36], in which we showed that ECoG can be used to decode parameters of hand movements. In the present study, we asked to what extent ECoG also holds information about movements of individual fingers. There is some evidence in the literature that supports this hypothesis. When monkeys were prompted to move individual fingers [45, 46, 47], neurons were found to change their activity in widely distributed patterns. In line with this finding, [48] did not find a focal anatomical representation of individual fingers in M1. This widely distributed and thus relatively large representation has also been shown in humans, e.g., in fMRI studies [49, 50], lesion studies [51, 52], and a MEG study [53]. Recent studies have already begun to attempt to differentiate activity associated with particular finger movement tasks: in humans, movements of the index finger could be discriminated from rest using EEG [54]; the laterality of index finger movements could be determined using EEG [55, 56], MEG [57], or ECoG [58]; MEG signals were found to correlate to velocity profiles of movements of one finger [59]; and studies even found some differences between movements of different fingers on the same hand using EEG [60], or more robust differences using ECoG [61, 62] and activity recorded from individual neurons in monkey motor cortex [63, 64, 65, 66].

In this study, we set out to determine whether it is possible to faithfully decode the time course of flexion of each finger, i.e., not only the laterality of finger movements or the type of finger, in humans using ECoG. We studied five subjects who were asked to repeatedly flex each of the five fingers in response to visual cues. The principal results show that it is possible to accurately decode the time course of the flexion of each finger individually. Furthermore, they confirm the finding of our previous study [36] that the most useful sources of information that can be recorded with subdural electrodes are the local motor potential (LMP) and ECoG activity in high frequency bands (i.e., from about 70 Hz to about 200 Hz) recorded from hand and other motor cortical representations. These results provide strong additional evidence that ECoG could be used to provide accurate multidimensional BCI control, and also suggest that ECoG is a powerful tool for studying brain function.

2. Methods

2.1. Subjects

The subjects in this study were five patients with intractable epilepsy who underwent temporary placement of subdural electrode arrays to localize seizure foci prior to surgical resection. They included three women (subjects A, C, and E) and two men (subjects B and D). (See Table 1 for additional information.) All gave informed consent. The study was approved by the Institutional Review Board of the University of Washington School of Medicine. Each subject had a 48- or 64-electrode grid placed over the fronto-parietal-temporal region including parts of sensorimotor cortex (Fig. 1). These grids consisted of flat electrodes with an exposed diameter of 2.3 mm and an inter-electrode distance of 1 cm, and were implanted for about one week. Grid placement and duration of ECoG monitoring were based solely on the requirements of the clinical evaluation, without any consideration of this study. Following placement of the subdural grid, each subject had postoperative anterior-posterior and lateral radiographs to verify grid location.

Table 1. Clinical profiles.

All subjects had normal cognitive capacity, and were literate and functionally independent.

Subject	Age	Sex	Handedness	Grid Location	Seizure Focus
A	46	F	L	left frontal	left frontal
B	24	M	R	right frontal	right medial frontal
C	18	F	R	left frontal	left frontal
D	32	M	R	left fronto-temporal	left temporal
E	27	F	R	left fronto-temporal	left temporal

Figure 1. Estimated locations of recorded electrodes in the five subjects.

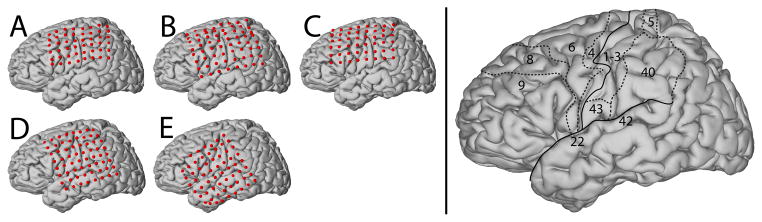
Subject B’s grid was located on the right hemisphere. We projected this grid on the left hemisphere. The brain template on the right highlights the location of the central sulcus and Sylvian fissure, and also outlines relevant Brodmann areas.

2.2. Experimental Paradigm

For this study, each subject was in a semi-recumbent position in a hospital bed about 1 m from a video screen. Subjects were instructed to move specific individual fingers of the hand contralateral to the implant in response to visual cues. The cues were the written names of individual fingers (e.g., “thumb”). Each cue was presented for 2 s. The subjects were asked to repeatedly flex and extend the requested finger during cue presentation. The subjects typically flexed the indicated finger 3–5 times over a period of 1.5–3 s. Each cue was followed by the word “rest,” which was presented for 2 s. The visual cues were presented in random order. Data were collected for a total period of 10 min, which yielded an average of 30 trials for each finger. The flexion of each finger was measured using a data glove (5DT Data Glove 5 Ultra, Fifth Dimension Technologies) that digitized the flexion of each finger at 12 bit resolution. The effective resolution (i.e., the resolution between full flexion and extension) averaged 9.6 bits for all subjects and fingers. Figure 2 shows an example of flexion patterns for the five fingers acquired using this data glove. These behavioral data were stored along with the digitized ECoG signals as described below, and were subsequently normalized by their mean and standard deviation prior to any subsequent analysis.

Figure 2. Example finger flexion.

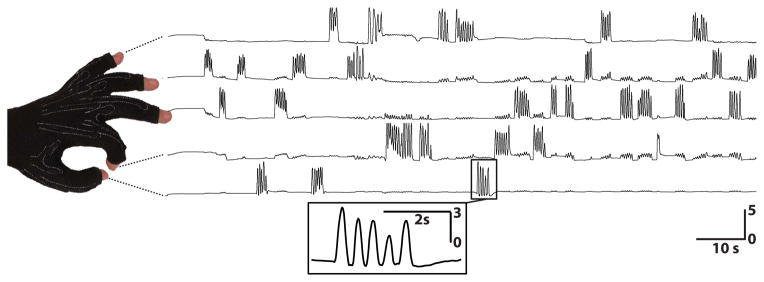
These traces show the behavioral flexion patterns for subject E and each of the five fingers over the first two minutes of data collection. Flexion consisted of movements of individual fingers, accompanied occasionally by minor flexion of other fingers. Horizontal bars give time and vertical bars give units of standard deviation.

2.3. Data Collection

In all experiments in this study, we presented the stimuli and recorded ECoG from the electrode grid using the general-purpose BCI2000 system [67] connected to a Neuroscan Synamps2 system. Simultaneous clinical monitoring was achieved using a connector that split the cables coming from the subject into one set that was connected to the clinical monitoring system and another set that was connected to the BCI2000/Neuroscan system. All electrodes were referenced to an inactive electrode. The signals were amplified, bandpass filtered between 0.15–200 Hz, digitized at 1000 Hz, and stored in BCI2000 along with the digitized flexion samples for all fingers [33]. Each dataset was visually inspected and all channels that did not clearly contain ECoG activity (e.g., such as channels that contained flat signals or noise due to broken connections — we did not notice and thus exclude channels with interictal activity) were removed prior to analysis, which left 48, 63, 47, 64, and 61 channels (for subjects A–E, respectively) for our analyses.

2.4. 3D Cortical Mapping

We used lateral skull radiographs to identify the stereotactic coordinates of each grid electrode with software [68] that duplicated the manual procedure described in [69]. We defined cortical areas using Talairach’s Co-Planar Stereotaxic Atlas of the Human Brain [70] and a Talairach transformation (http://www.talairach.org).

We obtained a template 3D cortical brain model (subject-specific brain models were not available) from source code provided on the AFNI SUMA website (http://afni.nimh.nih.gov/afni/suma). Finally, we projected each subject’s electrode locations on this 3D brain model and generated activation maps using a custom Matlab program.

2.5. Feature Extraction

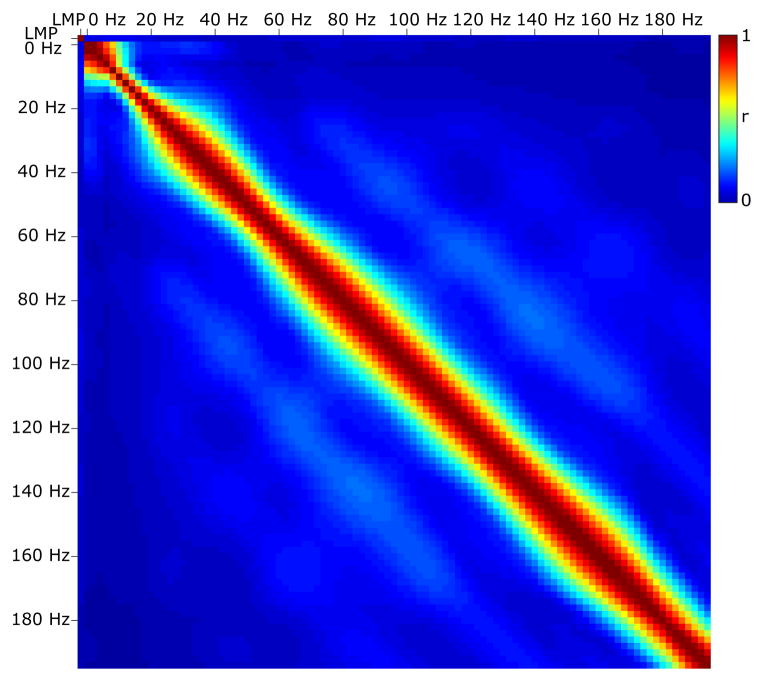
We first re-referenced the signal from each electrode using a common average reference (CAR) montage. To do this, we obtained the CAR-filtered signal $s_h^{\prime }$ at channel h using $s_h^{\prime }=s_h-\frac{1}{H}{\sum }_{q=1}^H{s}_q$. H was the total number of channels and s_h was the original signal sample at a particular time. For each 100-ms time period (overlapping by 50 ms), we then converted the time-series ECoG data into the frequency domain with an autoregressive model [71] of order 20. Using this model, we calculated spectral amplitudes between 0 and 200 Hz in 1-Hz bins. We also derived the Local Motor Potential (LMP), which was calculated as the running average of the raw unrectified time-domain signal at each electrode calculated for each 100-ms time window. Fig. 3 demonstrates that there was practically no (linear) relationship between the LMP and amplitudes in different frequencies, and generally little relation between different frequencies. We then averaged the spectral amplitudes in particular frequency ranges (i.e., 8–12 Hz, 18–24 Hz, 75–115 Hz, 125–159 Hz, 159–175 Hz). These bins are similar to what we used in our previous study [36], except that we abandoned the 35–70 Hz frequency range because it has been demonstrated to reflect conflicting spectral phenomena [72], and because its inclusion in preliminary tests decreased performance. Fig. 4 shows an example to demonstrate that our selected ECoG features at particular locations typically exhibited correlation with the flexion of individual fingers.

Figure 3. Correlation of features.

This figure shows the correlation coefficient r (color coded – see color bar), calculated for all data between the LMP and amplitudes in different frequency bands. r is very low for the LMP and amplitudes in different frequencies, and generally low for different frequencies.

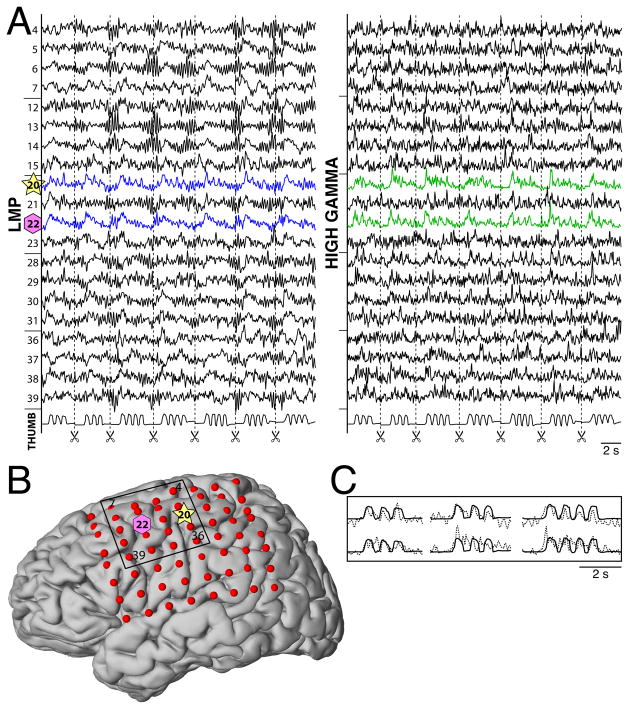
Figure 4. Example of ECoG features related to finger flexion in subject B.

A: Example traces of the LMP (left) and high gamma (75–115Hz, right), corresponding to the 20 locations indicated by the black rectangle shown in figure B. These traces show the time course of ECoG (top traces) as well as the behavioral trace for thumb flexion (trace on the bottom). The traces only show data for the movement periods, i.e., periods around thumb movements (see scissors symbols). Dashed lines indicate beginning/ends of movement periods. B: Locations of the electrodes on the grid shown on the 3D template brain model. The locations that showed correlations with thumb flexion in A, i.e., channels 20 and 22, are indicated with symbols. C: Magnification of the first three movement periods. The solid traces on top and bottom show thumb flexion, and the dotted traces on top and bottom give LMP and high gamma activity, respectively, at channel 20. The LMP and high gamma activity are correlated with flexion of the thumb.

In summary, we extracted up to 384 features (6 features – the LMP and 5 frequency-based features – at up to 64 locations) using 100-ms time windows from the ECoG signals. We then decoded from these features the flexion of the individual fingers. As shown later in this paper, we achieved optimal performance in decoding finger flexion when we used brain activity that preceded the actual movement by 50–100 ms. These features were submitted to a decoding algorithm that is described in more detail below.

2.6. Decoding and Evaluation

As described above, we first extracted several time- or frequency domain features from the raw ECoG signals. We then constructed one linear multivariate decoder for each finger, where each decoder defined the relationship between the set of features and flexion of a particular finger. Each decoder was computed from the finger movement periods. A movement period was defined as the time from 1000 ms prior to movement onset to 1000 ms after movement offset. Movement onset was specified as the time when the finger’s flexion value exceeded an empirically defined threshold. Movement offset was specified as the time when the finger’s flexion value fell below that threshold and no movement onset was detected within the next 1200 ms. This procedure yielded 25–48 (31 on average) movement periods for each finger. We discarded all data outside the movement periods so as to provide a balanced representation of movement and rest periods for the construction of the decoder.

For each finger, the decoder was constructed and evaluated using 5-fold cross-validation. To do this, each data set was divided into five parts, the decoders were determined from 4/5th of the data set (training set) and tested (i.e., the decoder was applied) on the remaining 1/5th (test set). This procedure was then repeated five times – each time, a different 1/5th of the data set was used as the test set. The decoder for the flexion of each finger was constructed by determining the linear relationship between ECoG features and finger flexion using the PaceRegression algorithm that is part of the Java-based Weka package [73]. Unless otherwise noted, we utilized feature samples that preceded the flexion traces to be decoded. Specifically, we used a window of 100 ms length that was centered at −50 ms with respect to the flexion trace, i.e., causal prediction. Thus, this procedure could be used to predict the behavioral flexion patterns of each finger in real time without knowledge of which finger moved or when it moved. (All decoded flexion traces shown in Fig. 7 and Fig. 8, and classification time courses shown in Fig. 11, are shifted back in time by the 50 ms offset used for decoding to highlight the fact that cortical signals precede the movements.)

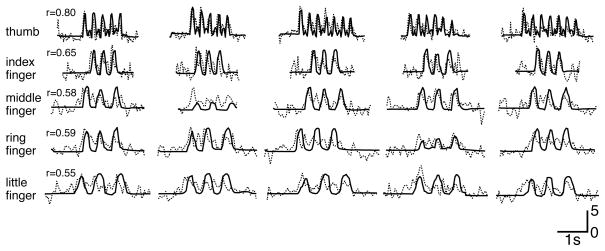
Figure 7. Examples for actual and decoded movement trajectories.

This figure shows, for the best cross validation fold for each finger and for subject A, the actual (solid) and decoded (dotted) finger flexion traces, as well as the respective correlation coefficients r. These traces demonstrate the generally close concurrence between actual and decoded finger flexion. They also show that this subject used different flexion rates for different fingers and/or cross validation folds, and that the decoded traces reflect these different rates. The horizontal bar gives time and the vertical bar gives units of standard deviation.

Figure 8. Average actual and decoded flexion traces for three different flexion speeds.

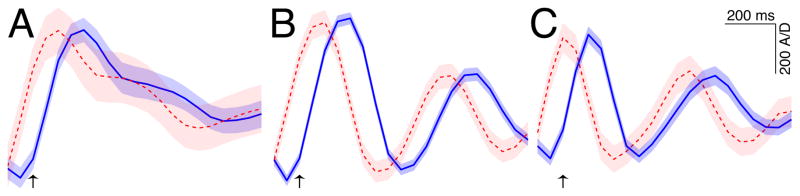
The traces in A, B, and C show actual (blue solid) and decoded (red dashed) flexion traces, averaged across all subjects and fingers, and corresponding to the 0–10th, 45–55th, and 90–100th percentile of flexion speeds, respectively. Shaded bands indicate the standard error of the mean. The minimum and maximum amplitudes of the average decoded traces were scaled to match those of the actual traces to facilitate comparison. All traces begin 100 ms prior to detected movement onsets (which are indicated with arrows). The decoded traces are shifted back in time by the 50 ms offset used for decoding to highlight the fact that cortical signals precede the movements.

Figure 11. Discrete classification of finger movements.

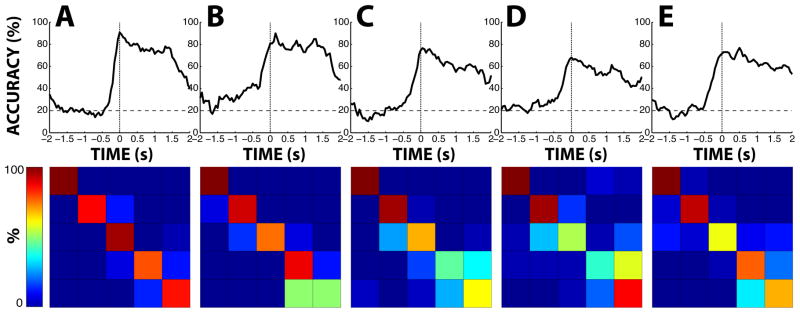
The top row shows the classification accuracy (i.e., the fraction of all finger movements that were correctly classified) for each subject A-E as a function of time relative to movement onset. Movement onset is marked by the dotted line. Accuracy due to chance (i.e., 20%) is marked by the dashed line. The bottom row shows the confusion matrix of classification at the time of the peak classification accuracy for each subject. In each matrix, each row represents the finger that actually moved (from top to bottom: thumb, index, middle, ring, and little finger). Each column represents the finger that we classified (from left to right: thumb, index, middle, ring, and little finger). In each cell, the color indicates the fraction of all movements of a particular finger that was assigned to the particular classified finger.

We then computed the Pearson’s correlation coefficient r between the actual and decoded flexion traces for each test set. Finally, we derived a metric of decoding performance for each subject and finger by averaging the r values across the five test sets.

3. Results

3.1. Brain Signal Responses to Finger Movements

We first characterized the brain signal responses to finger flexion. These responses were assessed by determining the correlation of ECoG features with the task of resting or moving a finger. The rest dataset included all data from 1800 ms to 1200 ms before each movement onset. For each subject, finger, and feature, we then calculated the value of r² between the distribution of feature values during rest and the distribution of feature values for each time point from 600 ms before to 600 ms after movement onset. Fig. 5 shows the results for flexion of the thumb for all subjects.

Figure 5. Brain signal changes between rest and thumb movement for all subjects.

Each column (A–E) gives data for the respective subject. Plots on top show brain signal changes in frequencies between 0 and 200 Hz over time (horizontal axis from 600 ms prior to 600 ms after movement onset). These changes are given in color-coded values of r² (see colorbars). Plots on the bottom show changes (expressed as r² values) in the LMP feature over time. Blue traces on the bottom right of each brain indicate the average actual thumb flexion trace. Insets show magnifications of the areas shown by black rectangles. High frequencies in the ECoG and the LMP give substantial information about the movement, and some of this information appears to precede the actual movement.

The time-frequency plots on top show that in each subject the amplitudes at particular locations and frequencies (in particular at frequencies >50 Hz) hold substantial information (up to an r² of 0.66) about whether or not the thumb was flexed. This information was highly statistically significant: when we ran a randomization test, r² values of less than 0.02 were significant at the 0.01 level for any subject and time-frequency or LMP feature. This information about finger flexion was localized to one or only a few electrode locations. Furthermore, it is also evident from these plots that ECoG changes preceded the actual movement. The traces on the bottom show that the LMP also changed substantially (i.e., up to an r² of 0.60) with the movement, and that, again, some of the changes preceded the actual movement. Activity changes for different fingers (see Fig. 1 in the Supplementary Material) showed the same general topographical and spectral characteristics as shown here for the thumb movement. At the same time, each finger showed its own distinctive pattern (e.g., time-frequency changes). As shown later in Section 3.6, these different patterns allowed for accurate classification of individual fingers.

Fig. 5, Supplementary Figure 1, and the Supplementary Movie illustrate qualitatively how ECoG signals differ between rest and finger movement. We also quantitatively assessed these changes by determining how many electrodes showed significant activity changes for the high gamma (75–115Hz) band and the LMP^‡. We applied a three-way ANOVA to determine which factors (subject, finger, or feature) were related to the number of channels with significant signal changes (N_s). The results showed that N_s was not related to the subjects (p = 0.20) or the different fingers (p = 0.77). However, the number of significant electrodes significantly differed for the LMP (17% of all channels) and high gamma features (5% of all channels) (p < 0.0001). Notably, we did not find a difference when we compared N_s for the thumb versus the other fingers (p = 0.21). This suggests that a potential difference in the size of the cortical representation of the thumb versus other fingers is smaller than the spatial resolution (1 cm) available in this study.

In summary, changes in the LMP and amplitudes at frequencies higher than 50 Hz over hand area of motor cortex are associated with flexion of individual fingers with different changes for different fingers. Some of these changes preceded finger flexion. Furthermore, the LMP feature is spatially broader than the high gamma feature. The analyses in the next section determined how well each feature was related to the degree of finger flexion.

3.2. Relationship of ECoG Signals with Finger Flexion

To further characterize the relationship of the ECoG features with finger flexion, we correlated, for all movement periods, the time course of the flexion with the time course of each feature for each finger. We then computed one measure of the correlation coefficient r and its significance p (determined using the F-test) for each subject, finger, and cross-validation fold. To get these two measures for each finger of each subject, we used the results from the four (out of five) cross validation folds with the highest r values. We then converted the associated p values into indices of confidence c_i (c_i =− log₁₀(p)), and averaged those across the four cross validation folds.

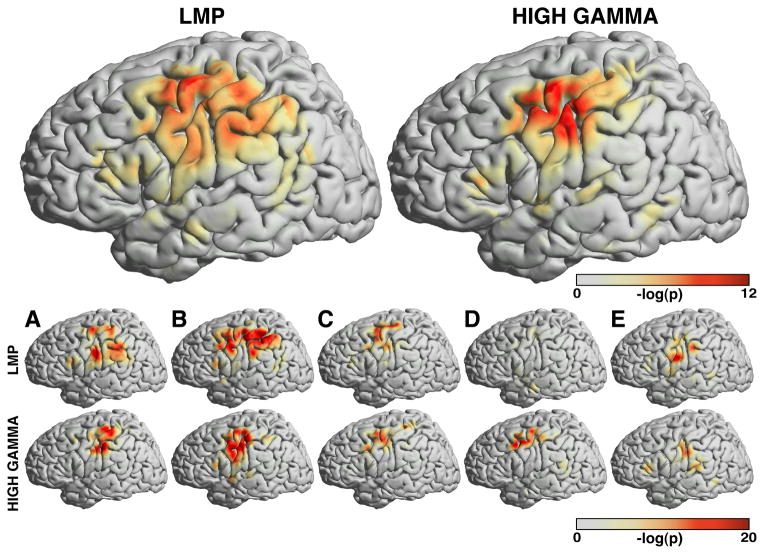
The results of the analyses for thumb flexion are shown in Fig. 6. They are representative of the results achieved for the other fingers, which indicates that the brain signal changes associated with specific flexion values largely overlap for the different fingers. The two large brain images on top show the confidence indices for the LMP and 75–115 Hz (i.e., high gamma), averaged across all subjects. The ten smaller brain images on the bottom show results for individual subjects A–E and the LMP (upper row) and high gamma (lower row) features.

Figure 6. Relationship of brain signals with thumb flexion.

This figure shows the spatial distribution of the confidence index c_i for the LMP (top left) or 75–115 Hz high gamma band (top right), and for each subject and the LMP or high gamma feature (ten brains on the bottom). The confidence indices are color coded (see colorbars).

The high values of the confidence indices over primarily different motor cortical areas and for the LMP and high gamma features again document the important role of these locations and ECoG features, respectively. Similar to our previous study [36], the topographies of the confidence indices differ between the LMP and high gamma (see Fig. 5 in [36]), and are more diffuse for the LMP. Interestingly, the patterns of confidence indices shown here are spatially much more widespread than the information shown before in Fig. 5 that differentiates movement from rest. See Section 4 for further discussion of this topic. Also, the spatial distribution of the LMP and high gamma features for subjects A and B appears to be more spatially widespread than that for the other three subjects. This is interesting, as subjects A and B used their non-dominant hand for the finger movement task. The next section demonstrates how this information about finger flexion supported the successful decoding of individual finger flexion movements.

3.3. Accurate Decoding of Finger Flexion

Table 2 and Fig. 7 show the principal results of this study. Table 2 gives the correlation coefficients calculated for all finger movement periods (see Section 2.6 for a description of how these periods were determined) between actual and decoded flexion traces. The given correlation coefficients represent the mean, minimum, and maximum correlation coefficients calculated for a particular subject and finger and across all cross validation folds. When averaged across subjects, the correlation coefficients range from 0.42–0.60 for the different fingers. When averaged across fingers, the correlation coefficients range from 0.41–0.58 for the different subjects. As reported in Table 2, the average decoding performance (i.e., correlation coefficient averaged across all subjects and fingers) was 0.52. We also computed this average decoding performance for individual features, as well as for the set of all frequency-based features. This resulted in 0.40 (LMP), 0.19 (8– 12 Hz), 0.25 (18–24 Hz), 0.45 (75–115 Hz), 0.40 (125–159 Hz), 0.33 (159–175 Hz), and 0.49 (all frequency features). Furthermore, and in contrast to our previous study [36], the application of the CAR filter had only a modest effect: e.g., for the LMP alone, we achieved 0.40/0.41 (with CAR/without CAR, respectively); for all features, we achieved 0.52/0.54 (with CAR/without CAR, respectively).

Table 2. Decoding performance for all subjects and fingers.

This table lists correlation coefficients r, calculated between the actual and decoded flexion time courses for the indicated finger. The three values for each combination of subject and finger represent the mean, minimum, and maximum value of r for all cross validation folds. These results demonstrate that reconstruction of the flexion of each of the five fingers is possible using ECoG signals in humans.

Subj.	Thumb	Index Finger	Middle Finger	Ring Finger	Little Finger	Avg.
A	0.75/0.71/0.80	0.61/0.53/0.65	0.49/0.40/0.58	0.54/0.50/0.59	0.43/0.33/0.55	0.57
B	0.66/0.62/0.74	0.61/0.53/0.68	0.51/0.37/0.57	0.58/0.46/0.66	0.53/0.47/0.60	0.58
C	0.60/0.51/0.66	0.62/0.51/0.67	0.60/0.55/0.64	0.49/0.44/0.52	0.39/0.34/0.44	0.53
D	0.37/0.32/0.42	0.55/0.50/0.58	0.54/0.44/0.64	0.36/0.22/0.43	0.23/0.14/0.33	0.41
E	0.42/0.29/0.52	0.60/0.43/0.65	0.56/0.43/0.63	0.54/0.49/0.61	0.54/0.49/0.58	0.53
AVG	0.56	0.60	0.54	0.50	0.42	0.52

These results demonstrate that it is possible to accurately infer the time course of repeated, rhythmic finger flexion using ECoG signals in humans. Results shown later in this paper also show that these flexion patterns are highly specific to the moving finger. Furthermore, for a particular subject and finger, the correlation coefficients only modestly varied across cross-validation folds. This indicates that the decoding performance is robust during the whole period of data collection. Fig. 7 shows examples for actual and decoded flexion traces. Because the calculation of decoding parameters only involved the training data set, but not the test data set, similar results can be expected in online experiments, at least for durations similar to those in this study.

3.4. Decoding Finger Flexion for Different Flexion Speeds

While this study was not designed to systematically vary the speed of the finger flexions, the subjects varied that speed substantially for different fingers and/or at different times (see traces for the thumb and little fingers in Fig. 7). To study decoding at different flexion speeds, we first estimated the speed for each movement period by calculating the period from the onset of the movement (that was detected as described earlier in the paper) to the offset of the first flexion (which was detected as the first time the flexion value fell below the same threshold that was used for detecting the onset). We then compiled the flexion speeds from all subjects, fingers, and movement periods, and selected the flexion patterns according to flexion speeds in three categories. These categories corresponded to the 0–10th, 45–55th, and 90–100th percentile of estimated flexion speeds. Fig. 8A–C shows the averaged flexion traces (solid) and corresponding averaged decoded traces (dashed) for the three different speed bins, respectively. These results demonstrate that the decoded traces accurately track the flexion dynamics at different flexion speeds. They also show that the brain signals precede the actual flexion by approximately 100 ms.

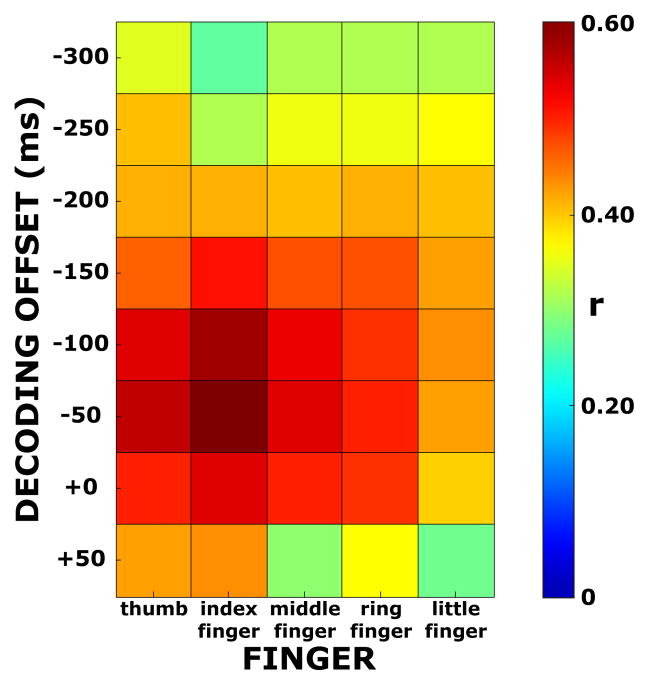
3.5. Optimal Decoding Offset

We also studied the effect of the decoding offset, i.e., the temporal offset of the 100 ms window that was used for decoding the flexion of a particular finger at a particular time. Unless otherwise noted, we used an offset of−50 ms for the analyses throughout the paper, i.e., brain signals from a 100-ms window centered at 50 ms prior to time t was used to decode finger flexion at time t. We evaluated the effect of that offset (−300, −250, 200, −150, −100, −50, 0, +50 ms) on decoding performance by calculating the resulting correlation coefficient r for a particular subject, finger, and cross validation fold. We then averaged these correlation coefficients across subjects and cross validation folds. The color-coded r values are shown in Fig. 9 for each finger. They show that for the different fingers, decoding performance (i.e., the averaged value of r) peaked around −100 to −50 ms. (In this figure, the values at −50 ms correspond to the values of r averaged across subjects in Table 2.) These results provide support for the hypothesis that the ECoG features we assessed were related primarily to movement and not to sensory feedback produced by the moving fingers.

Figure 9. Correlation coefficients for different fingers and decoding offsets.

Correlation coefficients r (color coded and averaged across subjects and cross validation folds) for different decoding offsets and fingers. The highest correlation coefficients are achieved when we used a 100 ms window that preceded the decoded flexion values by 50–100 ms.

3.6. Information About Individual Fingers

We finally studied the amount of information that is captured in the ECoG about different fingers, because the results shown up to this point (except for the finger-specific ECoG responses shown in the Supplementary Figure) do not exclude the possibility that our decoding results simply detected movement of any finger. We investigated this possibility in two ways.

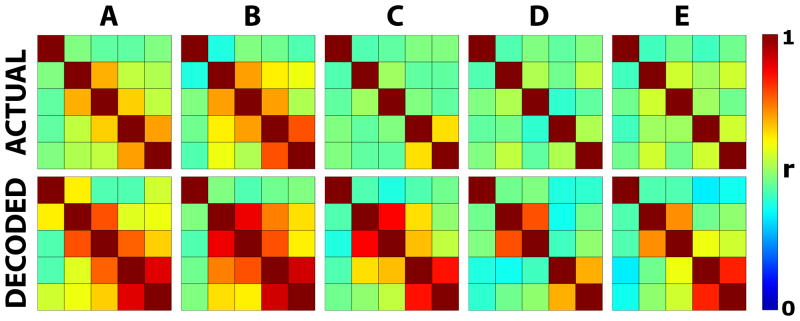
First, we determined the degree of interdependence of finger flexion for the actual and decoded flexion, respectively. To do this, we calculated the correlation coefficient r for the actual (i.e., behavioral) or decoded movement traces between all pairs of fingers. The results are shown in confusion matrices in Fig. 10. Each of the color-coded squares gives, for the indicated subject and for actual (top) or decoded (bottom) flexion, the correlation coefficient r calculated for the whole time course of finger flexion for a particular combination of fingers. The thumb and little finger correspond to the leftmost and right-most columns, and to the top-most and bottom-most rows, respectively. If the actual or decoded movements of the different fingers were completely independent of each other, one would expect a correlation coefficient of 1 in the diagonal running from top-left to bottom-right, and a correlation coefficient of 0 in all other cells. The results on top show that there was some degree of interdependence between the actual movements of the different fingers, in particular between index finger and middle finger and between ring finger and little finger. The results for decoded flexion on the bottom show a similar pattern, although the degree of interdependence of the decoded movements was modestly higher than that calculated for actual movements.

Figure 10. Interdependence of actual and decoded finger flexion.

Each of the ten figures shows color-coded correlation coefficients, calculated for actual and decoded finger flexion time courses for the indicated subject across all finger combinations (thumb: first row/column, little finger: last row/column).

Second, we also determined to what extent it is possible to determine from the ECoG signals which finger was moving. We did this using a five-step procedure: 1) We first detected movement onsets for each finger using the procedure described earlier in this paper, and labeled the period from 2 s before to 2 s after movement onset as the movement period of that finger. 2) We then decoded flexion traces for each finger using the 50 ms offset used for other analyses in this paper, and normalized the decoded traces for each finger by subtracting each trace’s mean and dividing the result by the standard deviation. 3) We then smoothed each trace using a zero delay averaging filter of width 500 ms. 4) We then classified, at each time during each movement period, the smoothed decoded flexion values into five finger categories by simply determining which of the five decoded flexion values (i.e., the five values corresponding to the five fingers) was highest at that point in time. 5) We finally determined classification accuracy by calculating the fraction of all trials in which the actual and classified finger matched. The results are shown in Fig. 11. The maximum classification accuracies (i.e., the classification accuracy at the best time for each subject) were 90.6%, 89.9%, 76.4%, 68.1%, and 76.7% for each subject, respectively. The average of those accuracies is 80.3% (accuracy due to chance is 20%). The best times were 0 ms, +150 ms, +50 ms, +0 ms, and +500 ms relative to movement onset, for each subject, respectively. When we used the same common optimal offset for each subject (i.e., without optimizing for each subject individually), the mean accuracy was 77.3% at +150 ms, and the median accuracy was 76.4% at +50 ms relative to movement onset. The mean accuracy at 0 ms was 77.1%. When we did not smooth the decoded traces prior to classification, the mean accuracy at 0 ms was 67.5%. In summary, our results show conclusive evidence that ECoG signals hold substantial information about the time course of the flexion of each individual finger.

4. Discussion

In this study, we showed that ECoG signals can be used to accurately decode the time course of the flexion of individual fingers in humans. The information in the ECoG that was most reflective of the movement preceded it by 50–100 ms. The results presented in this paper also further support the findings of our previous study [36] — in particular, that the Local Motor Potential (LMP) and amplitudes in the high gamma range hold substantial movement-related information. This information allowed us to accurately decode the flexion of each finger, even at different flexion speeds, using short windows of 100 ms. These results provide further evidence to support the hypothesis that the movement information encoded in ECoG signals exceeds that provided by EEG (see also Fig. 7 in [40]). Furthermore, our results suggest that both the fidelity of movement-related information in ECoG and its potential clinical practicality should position ECoG well for neuroprosthetic applications. In particular, previous efforts to classify finger movements used activity recorded sequentially from individual neurons (i.e., in successive recordings) in non-human primates [63, 64, 65, 66]. These studies demonstrated robust but only discrete decodings, i.e., inferring which finger flexed or extended but not the temporal flexion patterns of each finger as we showed here. The results in our present study are particularly appealing given that the patients in this study were under the influence of a variety of external factors, and that the experiments did not control for other relevant factors that may increase signal variance, such as eye position, head position, posture, etc.

The successful decoding of finger movements achieved in this study depended substantially on the LMP component and on amplitudes in gamma bands recorded primarily over hand-related and other areas of motor cortex. This is similar to the findings reported in two recent studies that decoded kinematic parameters related to hand movements using ECoG [36, 38]. In contrast to the cosine tuning reported for hand movements in humans using ECoG [36] or EEG/MEG [40], in the present study we assessed the linear relationship of ECoG features with finger flexion. We did this because auxiliary analyses demonstrated that a linear function was better able to explain the relationship of ECoG features with finger flexion compared to a cosine function or finger velocity.

In this study, we found that gamma band activity differed markedly between movement of a particular finger and rest in one or only a few electrodes (e.g., Fig. 5, Supplementary Figure 1). This is in contrast to the spatial distribution of the LMP feature that tended to be more broad. These differences support the hypothesis that the LMP and amplitudes in gamma bands are governed by different physiological processes. The information shown in Fig. 5 is also different from the spatial distribution of the information related to the degree of finger flexion shown in Fig. 6. This discrepancy suggests that the brain represents the general state of finger movement (i.e., any flexion or rest) differently from the specific degree of flexion. While the LMP component appears to be a different phenomenon from frequency-related components (see Fig. 3, Fig. 5, and Fig. 6 in this paper, and Fig. 5 in [36]), the physiological origin of the LMP component is still unclear. Thus, further studies are needed to determine the origin of the LMP and its relationship to existing brain signal phenomena, in particular to activity in the gamma band. While activity in the gamma band has been related to motor or language function in several studies, there still exists considerable debate about its physiological origin [74, 75].

In our experiments, subjects were cued to move only one finger at a time. Thus, aside from residual movements of other fingers that were due to mechanical or neuromuscular coupling [76, 77, 78], the subjects moved each finger in isolation. It is not clear whether the results presented in the paper would generalize to more natural and completely self-paced movements. Because ECoG detects mainly neuronal activity close to the cortical surface, rather than subcortical structures or the spinal cord, it is likely that the performance of decoding of particular parameters of movements will depend to what extent the cortex is involved in preparing for and executing these movements. Thus, successful BCI- or motor-related studies, and practical implementations derived from those studies, will depend on the design of protocols that appropriately engage sizable areas of cortex.

The present paper confirms and significantly extends the results presented in recent studies [32, 36, 39, 38], which demonstrated that ECoG holds information about position and velocity of hand movements, by showing that it is possible to derive detailed information about flexion of individual fingers in humans using ECoG signals. This information could be used either in an open-loop fashion to provide a real-time assessment of actual or potentially even imagined or intended movements, or in a closed-loop fashion to provide the basis for a brain-computer interface system for communication and control.

In this study, we showed that recordings from electrodes with relatively coarse spacing (1 cm) in patients who are under the influence of medications and a variety of other external influences can provide detailed information about highly specific aspects of motor actions in relatively uncontrolled experiments. While such results are appealing, this situation is most likely substantially limiting the potential information content and usefulness of the ECoG platform for BCI purposes. Clinical application of ECoG-based BCI technology will require optimization of several parameters for the BCI purpose and also evaluation of other important questions. Such efforts should include: optimization of the inter-electrode distance (there is evidence that much smaller distances may be optimal [79, 43]) and recording location (i.e., subdural vs. epidural, different cortical locations); long-term durability effects of subdural or epidural recordings; and the long-term training effects of BCI feedback.

In summary, the results shown in this paper provide further evidence that ECoG may support BCI systems with finely constructed movements. Further research is needed to determine whether ECoG also gives information about different fingers in more complex and concurrent finger flexion patterns, and to determine the optimum for different parameters such as the recording density. We anticipate that such studies will demonstrate that ECoG is a recording platform that combines high signal fidelity and robustness with clinical practicality.