Abstract
Lysosomes must maintain an acidic luminal pH to activate hydrolytic enzymes and degrade internalized macromolecules. Acidification requires the vacuolar-type H+-ATPase to pump protons into the lumen and a counterion flux to neutralize the membrane potential created by proton accumulation. Early experiments suggested that the counterion was chloride, and more recently a pathway consistent with the ClC-7 Cl–/H+ antiporter was identified. However, reports that the steady-state luminal pH is unaffected in ClC-7 knockout mice raise questions regarding the identity of the carrier and the counterion. Here, we measure the current–voltage characteristics of a mammalian ClC-7 antiporter, and we use its transport properties, together with other key ion regulating elements, to construct a mathematical model of lysosomal pH regulation. We show that results of in vitro lysosome experiments can only be explained by the presence of ClC-7, and that ClC-7 promotes greater acidification than Cl–, K+, or Na+ channels. Our models predict strikingly different lysosomal K+ dynamics depending on the major counterion pathways. However, given the lack of experimental data concerning acidification in vivo, the model cannot definitively rule out any given mechanism, but the model does provide concrete predictions for additional experiments that would clarify the identity of the counterion and its carrier.
INTRODUCTION
Lysosomes must maintain an acidic luminal pH (pHL) to activate hydrolytic enzymes and degrade internalized macromolecules (De Duve and Wattiaux, 1966; Lloyd and Mason, 1996). Acidification results from the action of a vacuolar-type H+-ATPase (V-ATPase), which uses the free energy of ATP hydrolysis to pump protons into the lumen of the lysosome. The process of proton pumping generates a large, lumen-positive voltage (the pump is electrogenic), inhibiting further pumping. Thus, the free energy of ATP is used to move both protons against their chemical gradient and against the inside-positive voltage that is generated. Because even small imbalances in ionic charge give rise to huge membrane potentials, another ion, or ions, must move across the organelle membrane to dissipate the membrane potential generated by the V-ATPase and facilitate bulk proton transport. This secondary ion movement is a process referred to as the “counterion flux” (Dell’Antone, 1979; Ohkuma et al., 1982, 1983; Harikumar and Reeves, 1983).
The role of counterions in facilitating organellar acidification has long been appreciated, and movement of either or both anions (entering the lumen) and cations (leaving the lumen) have been proposed (Mindell, 2012). Evidence is plentiful for a counterion role for Cl–; early lysosomal acidification studies highlighted the importance of Cl– availability in the external (cytosolic) medium (Cuppoletti et al., 1987; Van Dyke, 1993), which suggests a role for this abundant anion in the counterion flux, but these experiments did not directly demonstrate Cl– permeability, and they did not identify the molecular basis of the observed Cl– effects. Subsequent genetic experiments indicated that ClC-7, a member of the CLC family of chloride channels and transporters, was a likely candidate for the Cl– pathway in lysosomes, as ClC-7 knockout mice develop a lysosomal storage disease and osteopetrosis (Kornak et al., 2001; Kasper et al., 2005; Steinberg et al., 2010; Weinert et al., 2010), a disease associated with improper acidification of the lysosomaly derived ruffled border of osteoclasts. These results are supported by in vitro experiments demonstrating that the Cl– permeability of HeLa cell lysosomes is primarily mediated by ClC-7 (Graves et al., 2008). However, other work reported that lysosomal pH is unperturbed in ClC-7 knockout mice (Kornak et al., 2001; Kasper et al., 2005; Lange et al., 2006; Steinberg et al., 2010; Weinert et al., 2010), leaving uncertainty regarding the protein’s role in acidification. Cation permeabilities have also recently been proposed to mediate the counterion flux (Van Dyke, 1993; Steinberg et al., 2010; Weinert et al., 2010; Scott and Gruenberg, 2011), and several candidate cation channels are targeted to the lysosomal membrane; however, patient cells and knockout animals lacking candidate cation channels do not show consistent acidification defects (Zeevi et al., 2007; Cang et al., 2013).
Generally, the counterion flux has been presumed to result from conductance of ions through an ion channel; however, recent demonstrations that ClC-7 is not a channel but is instead a transporter, exchanging Cl– for protons, suggest a wider range of possible activities that might account for the counterion flux. In the simplest terms, a channel is a protein that forms a continuous aqueous pore across the membrane; by nature such a structure permits only dissipative flux of ions down their electrochemical gradients. In contrast, a transporter harnesses free energy (from ATP or from an ion gradient) to move another ion or small molecule uphill, against its electrochemical gradient. Notably, though the CLC family includes both ion channels (conducting Cl–) and transporters, all of the CLC family members thought to localize to endocytic organelles belong to the transporter branch of the family and are Cl–/H+ exchangers (antiporters). ClC-7 moves two Cl– ions into the lumen for each H+ removed (Graves et al., 2008), an action that appears counterproductive because it would reduce net acidification. However, because each turnover of ClC-7 only removes one H+ while bringing in two Cl– ions, the antiporter lowers the membrane potential and can facilitate continued proton pumping via the V-ATPase. A naive analysis suggests that a single turnover of the ClC-7 would allow the V-ATPase to subsequently pump in three more H+ ions without a net change to the membrane potential; and therefore, the entire cycle would result in the net accumulation of two H+. Is the antiport activity essential for a counterion conductance? Could a Cl– channel serve equally well as a counterion pathway? Recent genetic experiments suggest that a channel-like mutant of ClC-7 cannot fully recapitulate the acidification observed in the presence of the antiporter form of the protein (Weinert et al., 2010). Why not? How does this scheme compare with other possible counterion pathways?
It is not currently possible to answer these questions experimentally given the available techniques for quantitative measurements of the biophysical properties of lysosomes. To our knowledge, there are no simultaneous quantitative measurements of both pHL and the membrane potential, which are both necessary to calculate the proton motive force. Thus, even the most careful studies of lysosomal ion regulation involve unknown quantities. To explore the capabilities and limitations of different possible acidification systems, we built a mathematical model that incorporates the salient features of the acidification process. Our model is an extension of an earlier study used to explore endosomal maturation (Grabe and Oster, 2001).
MATERIALS AND METHODS
Plasmid DNA mutagenesis and transfection
Plasmid vectors (pCMV6_ENTRY) contained a cytomegalovirus promoter upstream of gene inserts encoding the open reading frame for CLCN7, isoform a (Homo sapiens) and OSTM1 (H. sapiens) followed by a C-terminal Myc/DDK tag, 30 amino acids long (OriGene). Mutations in the ClC-7 sorting motifs (LL23/24AA and LL68/69AA; Leisle et al., 2011) were made by site-directed mutagenesis of CLCN7 using custom mutagenic primers (Life Technologies) and a QuikChange II Site-Directed Mutagenesis kit (Agilent Technologies). A plasmid containing the open reading frame for EGFP (Green Lantern plasmid; Life Technologies) was cotransfected to identify transfected cells. Lipofectamine LTX and Plus reagent (Life Technologies) were mixed with a DNA mixture of ClC-7, Ostm-1, and EGFP plasmids (15:15:1 mass ratio, respectively). The transfection complex was incubated with HeLa cells growing on broken glass coverslips. Patch clamp experiments were conducted 24–36 h after transfection.
Electrophysiology
An Axopatch 200B Patch Clamp Amplifier (Molecular Devices) was used for voltage clamp. Data were acquired with a Digidata 1322A 16-bit A/D converter and Clampex 9.2 software (Molecular Devices). Recordings were filtered at 1 kHz with a Bessel low-pass filter and sampled at 5 kHz. Current was evoked with a holding voltage of +20 mV followed by test voltage steps from −140 mV to +100 mV in 20-mV increments for 1,600 ms followed by a constant voltage of +60 mV for 0.5 ms to observe tail current (voltages were reported using the cytoplasm as ground convention as discussed in the text). Bath recording solution was 130 mM NaCl, 5 mM KCl, 1 mM MgCl2, 1 mM CaCl2, 10 mM glucose, and 20 mM Hepes, pH titrated to 7.4 with 8.5 mM NaOH, and osmolality adjusted to 305 mmole/kg with sucrose. Pipette solution was 110 mM CsCl, 10 mM NaCl, 0.5 mM CaCl2, 10 mM EGTA, and 40 mM Hepes, pH titrated to 7.1 with 11.75 mM NaOH and osmolality adjusted to 299 mmole/kg with sucrose. Pipettes were fabricated from borosilicate glass capillaries (1.5 OD × 0.86 ID with filament; Harvard Apparatus) using a P-97 micropipette puller (Sutter Instrument) and had a resistance of 2–4 MOhm in the bath recording solution.
A general model of organelle pH regulation
Grabe and Oster (2001) developed a general continuum model of organelle pH regulation that is based on membrane biophysics and showed that it can adequately represent pH regulation in endosomes and Golgi. Here, we modify this model by removing the Na+/K+-ATPase, incorporating a calibrated description of the ClC-7 antiporter, and tuning other lysosome-specific parameters. Our model incorporates the salient features of the acidification process as shown in Fig. 1 A, and tracks the total number of ions in the lumen over time. Each ion type is represented by a time-dependent variable, and its change is governed by a differential equation. For instance, the number of protons in the lumen is given by H+, and the rate of change is determined by the proton flux across the membrane facilitated by proton channels and transporters. The differential equation describing the change in the number of luminal H+ is:
| (1) |
where JV is the proton pumping rate of a single V-ATPase (defined as positive when H+ enter the lysosome), JClC is the proton removal rate by ClC-7, and NV and NClC are the number of V-ATPases and ClC-7 antiporters, respectively. The last term of Eq. 1 is the passive, non–voltage-activated proton leak with a permeability PH+ per unit area. The surface area of the compartment is S, and U is the reduced membrane potential, ΔΨ/kBT, where kBT is a thermal energy unit, and ΔΨ is the membrane potential arising from charge imbalance in the organelle. kB is the Boltzmann constant and T is the temperature measured in Kelvin. The subscripts C and L denote a cytosolic or luminal quantity, respectively. Similar to Eq. 1, the differential equation describing the rate of change of luminal chloride ions, Cl–, is:
| (2) |
Figure 1.
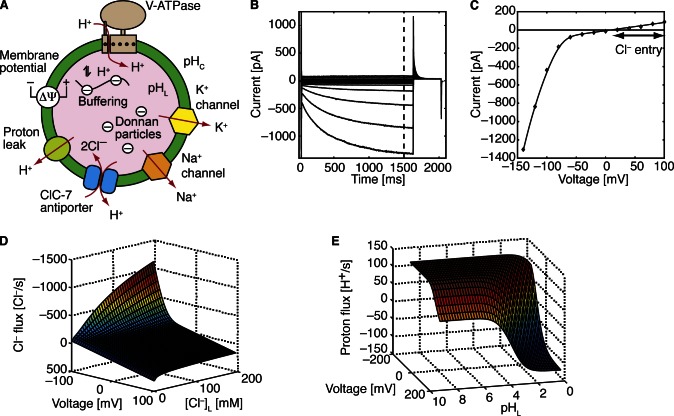
A model of lysosomal acidification and the key ionic currents. (A) Factors involved in lysosomal acidification and illustration of the mathematical model. Effective lysosomal acidification requires the V-ATPase, counterion flows, and other factors. First, proton leak has been identified as an important determinant of pHL in lysosomes (Van Dyke, 1993) and organelles along the secretory pathway (Wu et al., 2001). The molecular identity of this leak channel in lysosomes is unknown, but the nonselective cation channel TRP-ML1 has been implicated (Soyombo et al., 2006), and the voltage-gated Hv1 proton channel (Ramsey et al., 2006; Sasaki et al., 2006), found in phagosomes (Ramsey et al., 2009), is also a potential candidate. Second, lysosomal acidification can be influenced by Donnan particles, which are negatively charged proteins and molecules trapped in the lumen of the organelle that affect ion homeostasis through the membrane potential (Moriyama et al., 1992). Third, the buffering capacity of the luminal contents can drastically affect the rate of pH changes as well as the total charge composition (Grabe and Oster, 2001). Finally, it has been suggested that chloride, potassium, and/or sodium ions may serve as counterions during lysosomal acidification (Henning, 1975; Casey et al., 1978; Ohkuma et al., 1982; Moriyama, 1988; Van Dyke, 1993; Kiselyov et al., 2005; Soyombo et al., 2006; Steinberg et al., 2010). (B) ClC-7 antiporter whole cell current recordings. Starting from a resting potential of +20 mV, we applied a pulse protocol that stepped to a holding voltage ranging from –140 mV to +100 mV for 1,600 ms before returning to the original resting potential. (C) Current–voltage curve for the ClC-7 antiporter. The steady-state currents at 1,500 ms in B were used to create the current–voltage curve under conditions that slightly favor Cl– exit (H+ entry) from what would be the lysosomal lumen (diamonds). The solid line is the model fit from Eq. 3 in the Materials and methods. (D) Chloride pumping profile for a single ClC-7 antiporter. This pumping surface was created using Eq. 3 in the Materials and methods. Single transporter fluxes are not known, so this surface is based on estimates of single transporter turnover as well as the global fit shown in C. (E) Proton pumping profile for the V-ATPase. This surface is based on an earlier model (Grabe et al., 2000). For D and E, positive values indicate ions entering the lysosome.
The first term on the right-hand side of Eq. 2 is the Cl– flux due to ClC-7, and the second term is a passive Cl– leak characterized by a permeability per unit area PCl–. The coefficient n in Eq. 2 determines the stoichiometry of ClC-7, which is known to be 2 (2 Cl–:1 H+), but changing n makes it possible to explore hypothetical situations.
Flux characteristics of V-ATPase and ClC-7
The ability of our computational model to have real predictive power hinges on accurately representing the flux characteristics of each channel and transporter present in the cellular compartment. Here, JV is given by a detailed mechanochemical model of the V-ATPase, which was calibrated against experimental current–voltage data (Grabe and Oster, 2001). This flux depends on pHL and ΔΨ according to the performance surface shown in Fig. 1 E. We characterized the ClC-7 antiporter turnover rate, JClC, by constructing an empirical function that fits the current–voltage (I-V) curve in Fig. 1 C. The I-V curve has two distinct regimes: one that is linear at positive voltages and a second region that is cubic at negative voltages (Fig. 1 C, diamonds). Therefore, we fit the experimental data to an equation that transitions from being linear to cubic as a switching function x goes from being zero at negative ΔΨ to 1 at positive ΔΨ. However, rather than writing JClC as a function simply of ΔΨ, we chose to express it as a function of the driving force for ClC-7 turnover, ΔμClC, for reasons that follow. Thus, the ClC-7 turnover rate is written as:
| (3) |
where
and
In the equations above, e is an elementary charge unit, n is the ClC-7 stoichiometry, x is the switching function, and a and b are constants. The quantity kBT/e is equal to RT/F, where R is the gas constant and F is Faraday’s constant. At room temperature (25°C), RT/F = 25.69 mV, which is the value used in all numerical simulations. Expressing the ClC-7 turnover rate as a polynomial function of the driving force automatically enforces detailed balance, as when ΔμClC is zero both the linear and cubic terms in Eq. 3 are zero. Thus, the antiporter stops transporting ions when the driving force is zero. We determined the value of the constants a = 0.3 and b = 1.5 × 10−5 by fitting Eq. 3 (solid curve) to the experimental measured macroscopic currents reported in picoAmps (Fig. 1 C, diamonds). Coincidentally, using these numeric values for a and b closely reproduces the experimental estimates for single antiporter rates measured in ions per second for a bacterial homologue of ClC-7 (Walden et al., 2007). Thus, we simply multiplied Eq. 3 by –2, giving –2 × JClC, to produce the single antiporter Cl– performance surface in Fig. 1 D.
Membrane potential
Our model incorporates a physical model of the membrane potential (Rybak et al., 1997), which depends on the net accumulation of charged ions in the lumen of the compartment described by the following equation:
| (4) |
where C0 is the membrane capacitance, S is the surface area, V is the lysosomal volume, i and j run over all cation and anion species, ni and nj are their respective valences, β is the buffering capacity, B is the luminal concentration of impermeant charges, which are primarily fixed negative protein charges trapped in the lumen, and V0 is the initial lysosomal volume. Because B does not vary with V, B must be multiplied by V0 when V is not constant. By convention, the membrane potential is negative when there are more negatively charged ions inside the compartment relative to outside.
The total membrane potential, ΔΨTotal, is the membrane potential caused by the charge imbalance shown in Eq. 4 plus the potentials caused by the intrinsic charge on the outer and inner leaflets of the lysosomal membrane: ΔΨTotal = ΔΨ + (ΨOut − ΨIn), where ΨOut and ΨIn are the outer and inner leaflet potentials, respectively. To start each simulation, B in Eq. 4 was adjusted to set the initial ΔΨTotal to 0 mV or other values indicated in the text.
To account for the effects of surface charge on the ionic concentrations at the membrane, the ion concentration values used in Eqs. 1, 2, 3, and 5 are modified by a Boltzmann factor that depends on the leaflet potentials as follows:
where [Ci]L and [Ci]C are luminal and cytosolic concentrations of the ion i, respectively. The surface concentrations are denoted by a zero subscript and the valence and charge of the ion are indicated by zi. Importantly, surface potentials do not modify the concentration values used to compute the membrane potential, as these values represent the total luminal charge.
Flux of passive water
Ionic concentration differences across a bilayer give rise to an osmotic pressure difference that drives the flow of water in the direction of higher osmolyte concentrations. Thus, as ions enter or leave the lysosome during acidification, water will enter or leave the lysosome, respectively. Ignoring any differences in hydrostatic pressure across the membrane, the flux of water can be modeled as (Verkman, 2000):
where the sum runs over all luminal ion species, ϕi is the osmotic coefficient of ionic species i, ΦC is the osmolarity of the cytoplasm, PW is water permeability of the membrane, S is surface area, and νW is the partial molar volume of water (18 cm3/mol). All simulations started from osmotic equilibrium, which we obtained by adjusting ΦC.
Parameter values
As displayed in Table 1, we used experimentally determined parameter values whenever possible. In the simulations we report, the buffering capacity was kept constant at 40 mM/pH, but we performed additional simulations in which we varied the buffering capacity and found that these changes did not alter our conclusions. An early study reported a lysosomal proton permeability value of 2.9 × 10−4 cm/s (Van Dyke, 1993). From fits in Fig. 2 A, we estimated PH+ to be five times smaller at 6 × 10−5 cm/s, and we used this value in all simulations. We performed additional simulations using the larger PH+ value, and the primary difference is an increase in the number of V-ATPases required to achieve a low pHL. For all simulations in Fig. 2, we assumed that the lysosomes are at a quasi-steady-state before the addition of valinomycin. In the presence of ClC-7 and a small proton leak (Fig. 2 A), this is a very easy constraint to satisfy because ClC-7 cannot initiate transport without the counterion flow provided by K+ entry. However, for all other panels (Fig. 2, B–D) this adds a serious constraint to the initial ionic balance because the membrane potential must be very close to the Nernst potential for H+. In fact, this constraint could not be met in Fig. 2 D using the experimentally measured ionic conditions. For simulations including water flow, we used the passive membrane permeability, PW, measured for endosomes, which is 0.052 cm/s (Lencer et al., 1990). We assumed that the osmotic coefficient was 0.73 for all charged solutes (Kielland, 1937), and while the cytoplasmic/external osmolyte concentration, ΦC, was adjusted to maintain equilibrium, it was typically ∼290 mM.
Table 1.
Model parameters
| Description | Units | Symbol | Value | Reference |
| Cytosolic pH | pHC | 7.2 | Roos and Boron, 1981; Wu et al., 2000 | |
| Cytosolic potassium concentration | mM | [K+]C | 145 | Alberts et al., 2008 |
| Cytosolic sodium concentration | mM | [Na+]C | 10 | Alberts et al., 2008 |
| Cytosolic chloride concentration | mM | [Cl–]C | 5–50 | Sonawane et al., 2002; Alberts et al., 2008 |
| Luminal pH (initial) | pHL | 7.4 | Alberts et al., 2008a | |
| Luminal potassium concentration (initial) | mM | [K+]L | 5 | Alberts et al., 2008a |
| Luminal sodium concentration (initial) | mM | [Na+]L | 145 | Alberts et al., 2008a |
| Luminal chloride concentration (initial) | mM | [Cl–]L | 110 | Alberts et al., 2008a |
| Proton permeabilityb | cm/s | PH+ | 6 × 105 | |
| Potassium permeability | cm/s | PK+ | 7.1 × 107 | Hartmann and Verkman, 1990 |
| Sodium permeability | cm/s | PNa+ | 9.6 × 107 | Hartmann and Verkman, 1990 |
| Chloride permeability | cm/s | PCl− | 1.2 × 105 | Hartmann and Verkman, 1990 |
| Bilayer capacitance | µF/cm2 | C0 | 1 | Hille, 2001 |
| Lysosome diameter | µm | 0.68 | Van Dyke, 1993 | |
| Lysosome volumec | L | V | 1.65 × 1016 | |
| Lysosome surface areac | cm2 | S | 1.45 × 108 | |
| Buffering capacityd | mM/pH | β | 40 | |
| Osmotic coefficient | ϕ | 0.73 | Kielland, 1937 | |
| Water permeability | cm/s | PW | 0.052 | Lencer et al., 1990 |
| Partial molar volume of water | cm3/mol | νW | 18 | Verkman, 2000 |
| Cytoplasmic osmolyte concentratione | mM | ΦC | 290 |
These are typical extracellular values. Values in nascent lysosomes are not known.
This value was estimated based on fits to data in Fig. 2 A. An experimental estimate based on measurements from rat liver lysosomes is 2.9 × 10−4 cm/s (Van Dyke, 1993).
These values are calculated for a sphere of diameter 0.68 µm.
Buffering capacity varies with the pHL. An earlier study reported a value of 60 mM/pH at pHL 6.8, which gradually decreased to 20 mM/pH at pHL 5.2 (Van Dyke, 1993). A recent study reports a value of 61.5 mM/pH for pHL 4.5–5.0 (Steinberg et al., 2010). We use a constant buffering capacity that falls in between these reported values and gives a best fit value to the in vitro data in Fig. 2 A.
290 mM was a typical value, which was adjusted to maintain initial osmotic equilibrium.
Figure 2.
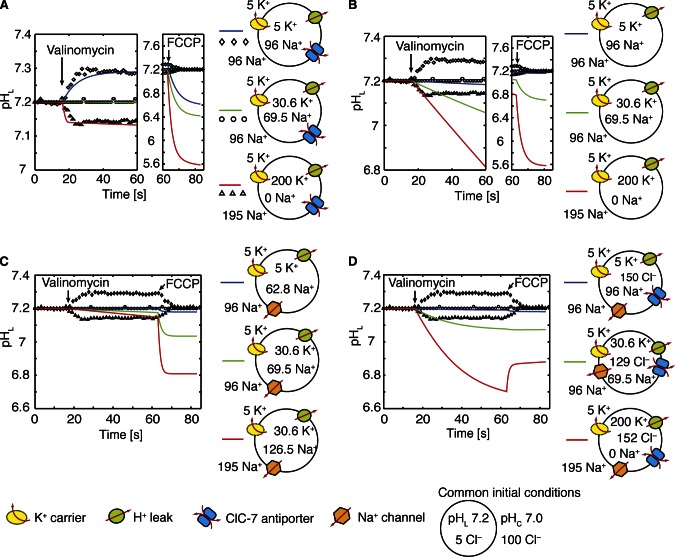
Regulation of lysosomal pH in the absence of V-ATPases. Time-dependent changes in pHL from the model (blue, green, and red lines) are plotted along with the corresponding experimental recordings (diamonds, circles, and triangles; Graves et al., 2008) for three different ionic conditions. (A) A model with ClC-7 antiporters, a K+ carrier, and a minor proton leak. For all scenarios, the initial ionic conditions (in millimolar) and putative ion pathways used in each scenario are displayed to the right of each panel, and the experimental conditions are the same as in A. Valinomycin was added at 16 s, and FCCP at 63 s. There is no K+ pathway before the addition of valinomycin, at which the potassium permeability is set to 7.1 × 10−7 cm/s. The proton permeability (PH+) was increased to 1 cm/s upon addition of FCCP. The model with ClC-7 matches the initial experimental pHL changes, but predicts luminal acidification after addition of FCCP rather than a return to the starting pHL. PH+ was 6 × 10−5 cm/s. (B) A model with a K+ carrier and a proton leak. The addition of valinomycin only causes acidification, even under experimental conditions that alkalinize the lysosome (diamonds). PH+ was 2.9 × 10−3 cm/s. (C) pHL changes elicited by K+ and Na+ channels and a proton leak. Low [K+]L levels (blue curve/diamonds) failed to alkalinize the lumen as in B. PH+ was 2.9 × 10−3 cm/s. (D) A model with ClC-7 antiporters, a K+ carrier, Na+ channels, and a proton leak. As in scenarios B and C, this model only causes luminal acidification. PH+ was 2.9 × 10−3 cm/s. In B–D, the concentration of Donnan particles was adjusted to set the initial total membrane potential to 11.8 mV in order to place the system in steady state at the start of the simulations. In some cases, steady state could only be achieved by changing the initial ionic concentrations from the experimental values given in A. The leaflet potentials were –50 mV outside and 0 mV inside, and the buffering capacity was 40 mM/pH.
Numerical solutions
A system of equations for the model lysosome with V-ATPase, 2 Cl–:1 H+ ClC-7 antiporter, K+ and Na+ channels, H+ leak channels, and water flux are as follows:
| (5) |
These equations were numerically solved with Berkeley Madonna using the Rosenbrock method for stiff differential equations or a fourth-order Runge-Kutta method when water flux was included.
Online supplemental material
Fig. S1 shows the time course for all simulations used to produce the data in Fig. 7. We also provide the basic Berkeley Madonna model. Online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201210930/DC1.
Figure 7.
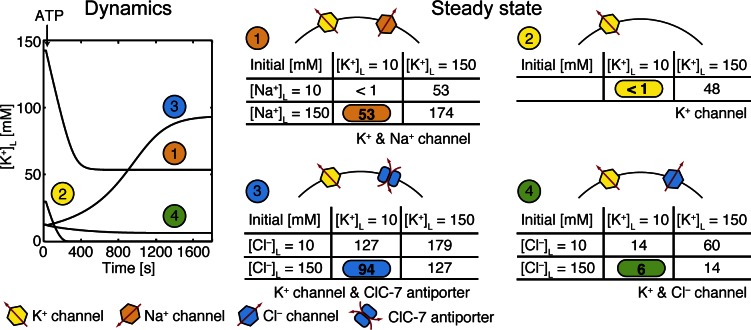
Changes in K+ concentration levels during lysosomal acidification depend on the molecular identity of the counterion pathway. Four model lysosomes were considered, each containing a set of counterion pathways as labeled. For each scenario we performed a simulation with a low initial internal concentration of the permeant ion (10 mM) and a second simulation with a high concentration (150 mM) to determine if this unknown variable greatly affected the final steady-state [K+]L values listed in the four tables on the right. Scenarios 1, 3, and 4 involved two permeant ions, and required four calculations to explore all combinations of ionic conditions, whereas scenario 2 required only two simulations. The final steady-state [K+]L value is listed for each simulation, and the full time courses corresponding to the color-coded simulation conditions are shown on the left. Each time course uses initial luminal values closest to typical extracellular values listed in Table 1. Acidification was initiated at 25 s by turning on the V-ATPases, which corresponds to adding ATP to the solution. Before the addition of ATP, the system was allowed to reach steady state, which in some cases resulted in initial [K+]L values different from those stated in the tables. For instance, scenario 1 (orange) shown on the graph starts with an initial [K+]L of 10 mM (see the corresponding table on the right), yet the time dependent curve shows [K+]L starting at 140 mM. This is due to a large increase in [K+]L during the initial equilibration in the absence of ATP. The full time courses for all 14 simulations are shown in Fig. S1. Only the ClC-7–containing lysosome undergoes an increase in [K+]L as K+ enters the lumen along with the pumped Cl–. The three other scenarios show a marked decrease in K+ as the organelle acidifies, and the K+ channel-only scenario reaches a final [K+]L in the millimolar range. All simulations included PH+ of 6 × 10−5 cm/s and 300 V-ATPases. Simulations with ClC-7 antiporters included 5,000 transporters. All other parameter values are given in Table 1.
RESULTS
Central to our approach is the use of experimentally calibrated ion pumping surfaces, as shown in Fig. 1 E for the V-ATPase, in an attempt to approximate the true lysosomal conditions as closely as possible. A model loosely based on our earlier work (Grabe and Oster, 2001) was recently used to examine lysosomal acidification (Weinert et al., 2010), but this study lacked detailed representations of the V-ATPase and ClC-7 transporters, and it considered only a limited number of potential transport proteins under a restricted range of environmental conditions. Here, we broaden the scope of the Weinert et al. (2010) study by simulating a large number of scenarios and exploring the influence that increased biophysical accuracy has on the conclusions.
To address this gap in the literature, we experimentally determined the current–voltage properties of the ClC-7 antiporter. We expressed rat ClC-7 in HeLa cells with a mutation that facilitates trafficking of the antiporter to the plasma membrane at levels high enough to permit electrophysiological recordings in whole cell patch clamp recordings (Leisle et al., 2011; Fig. 1 B). The usual electrophysiological convention is to consider the voltage on the extracellular side of the membrane to be zero (ground). Here, however, we remain consistent with other studies of organellar channels/transporters (Ohkuma et al., 1982; Harikumar and Reeves, 1983; Cuppoletti et al., 1987; Van Dyke, 1993; Grabe and Oster, 2001; Dong et al. 2010; Weinert et al., 2010) and use the opposite convention; we call the voltage at the cytosol zero, and positive ions flowing into the lumen is a positive current. With our convention, Fig. 1 C shows that ClC-7 is a strong inward rectifier. Inward rectification indicates that the primary direction of H+ flow is into the lumen and Cl– flow is out of the lumen, which is the wrong direction to act as a counterion flow but may aid in acidification. Therefore, to reduce the membrane potential, ClC-7 must operate in the direction that produces a small flux of current (Leisle et al., 2011). We constructed the analytic function in Eq. 3 (see Materials and methods), which is an excellent fit to the data (Fig. 1 C, solid curve), and which automatically enforces the correct reversal potential for all ionic conditions. In Fig. 1 D we computed the Cl– pumping rate surface for a single antiporter by scaling the current to give a maximum single transporter turnover of 1,000 s−1, as reported by Walden et al. (2007) for ClC-ec1, a bacterial homologue of ClC-7. For a more detailed mathematical description, including how the ClC-7 and V-ATPase pumping profiles are incorporated into the model, refer to the Materials and methods.
It is important to highlight that the currents measured in the whole cell recordings at positive voltages are within the range of the baseline currents measured in nontransfected cells (Fig. 1 B). Thus, we cannot unambiguously determine if Cl– exit from the cytosol (into the lysosome) is possible, nor can we determine the magnitude of the current. ClC-7 antiporter turnover in this direction is essential in our simulations, as counterion compensation is entirely dependent on Cl– carried into the lysosome in the very shallow portion of the current–voltage curve (Fig. 1 C). However, because we scale ClC-7 currents by a parameter corresponding to the number of antiporters, the exact magnitude of the current is not important. Until we have a specific pharmacologic inhibitor, we have no tools to more accurately assess the background currents in ClC-7 plasma membrane–expressing cells. However, as discussed in the next subsection, previously published results suggest that ClC-7 is indeed capable of carrying Cl– both into and out of lysosomes isolated from native tissue (Graves et al., 2008). Should ClC-7 prove to be an ideal rectifier, carrying no current at luminal positive voltages, our models would have to be reconsidered.
ClC-7 explains in vitro acidification changes in the absence of ATP
We first considered lysosomes that lack the full acidification machinery, as this allows us to focus on the accuracy of the remaining elements such as the Cl– transport pathway. In particular, we examined in vitro experiments performed on rat liver lysosomes incubated in the absence of ATP to prevent V-ATPase–dependent proton pumping. Using this system, Graves et al. (2008) showed that an imposed Cl– gradient can drive V-ATPase–independent changes in pHL and suggested that this is caused by the ClC-7–mediated coupled antiport of H+ and Cl– across the lysosomal membrane (Graves et al., 2008). To quantitatively evaluate this hypothesis, we performed a series of simulations under the same ionic conditions (Fig. 2). As in the experiments, we imposed an initial Cl– gradient with low internal Cl– to drive Cl– entry when the membrane potential is small and Cl– exit when the membrane potential is large and negative. We controlled the membrane potential by varying the initial luminal concentration of K+ ([K+]L), while leaving the cytosolic concentration unchanged. Addition of the K+ carrier valinomycin pushes the membrane potential toward the reversal potential for K+, EK, which is 0 mV (diamonds), −46 mV (circles), or −92 mV (triangles) for the three conditions simulated. We represented the addition of valinomycin through the activation of a K+-specific permeability at 16 s. All experiments were terminated by the addition of carbonyl cyanide p-trifluoromethoxyphenylhydrazone (FCCP; Graves et al., 2008), which we modeled by introducing a large, passive proton permeability at 63 s.
Initially, pHL is constant both in the model (solid curves) and the experiments (symbols). In the model this occurs because a substantial membrane potential builds up almost instantaneously to oppose the Cl– gradient and stop transport via ClC-7 (Fig. 3). When EK is −92 mV, the addition of valinomycin drives the membrane potential negative and forces luminal Cl– to exit and cytosolic H+ to enter via ClC-7, acidifying the lysosome (Fig. 2 A, red curve/triangles). However, when there is no K+ gradient, valinomycin draws the membrane potential toward zero, causing Cl– to enter and H+ to exit, resulting in alkalinization (Fig. 2 A, blue curve/diamonds). A K+ gradient that sets the membrane voltage to EClC, the ClC-7 reversal potential, leads to no net change in pHL (Fig. 2 A, green curve/circles). Before the addition of FCCP, our simulations are in excellent agreement with the experiment. Based on our fits, the passive H+ permeability (PH+) of the lysosome is 6 × 10−5 cm/s, which is five times smaller than previous estimates (Van Dyke, 1993); however, H+ flux mediated by the ClC-7 antiporter may have led to overestimates of PH+ in past studies. Additionally, we estimate that there are 5,000 ClC-7 antiporters in each lysosome, occupying roughly 3–5% of the surface area. Once PH+ and buffering capacity values have been set, the fits in Fig. 2 A are robust to the choice of model parameters. The magnitudes of the changes depend only on the ClC-7 transport stoichiometry. Thus, our model supports the hypothesis that ClC-7 is present in lysosomes and that it influences the ionic homeostasis of the organelle.
Figure 3.
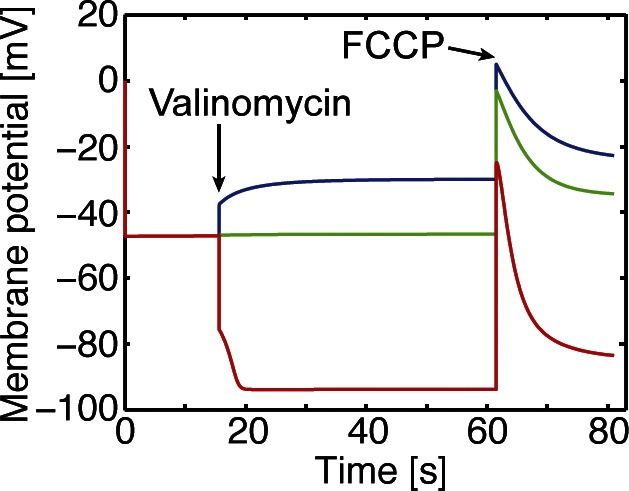
Predicted lysosomal membrane potential. Simulations and color coding are identical to those described in Fig. 2 A for a model containing ClC-7 antiporters, a K+ carrier, and a minor proton leak, but no V-ATPases. The red curve was simulated with a high initial [K+]L (200 mM), the green curve with moderate [K+]L (30.6 mM), and blue curve with low [K+]L (5 mM). Initially, the membrane potential is enforced to be zero, but quickly becomes –45 mV, which stops ion transport via ClC-7 and brings the system to a steady state. Valinomycin was added at 16 s, at which point the potassium permeability was increased from 0 to 7.1 × 10−7 cm/s to account for this additional pathway. The membrane potential changed according to whether K+ exited or entered the lysosome. In all cases, the membrane potential remained negative during this period. FCCP was added at 63 s, which was modeled by increasing PH+ from 6 × 10−5 cm/s to 1 cm/s. This caused a spike in the membrane potential due to an inward flux of H+.
We also considered the possibility that changes to pHL depend on ion fluxes other than Cl–. We modeled lysosomes that contain only H+ leak channels (Fig. 2 B), Na+ and H+ channels (Fig. 2 C), and Na+ and H+ channels along with ClC-7 antiporters (Fig. 2 D). In the presence of a H+ leak alone, we could only observe pHL changes by significantly increasing PH+ by a factor of 10 over the experimentally reported value (Van Dyke, 1993) and >50 times the best-fit value used in Fig. 2 A. Even with this large increase, this minimal model fails to describe the data (Fig. 2 B). We then included Na+ and H+ channels, but this additional consideration also failed to describe the experimental pHL changes (Fig. 2 C). Finally, we considered a model lysosome containing all three pathways: ClC-7 antiporters, Na+ channels, and H+ channels. This model also failed to describe the observed changes in pHL (Fig. 2 D). In summary, cation channels alone or K+, Na+, and H+ channels combined with ClC-7 cannot explain the observed lysosomal pH changes (Graves et al., 2008). However, a lysosome containing a ClC-7 antiporter and a small-conductance H+ channel fits the initial dynamics and magnitudes very well.
Surprisingly, all tested scenarios failed to match the changes in pHL caused by the addition of FCCP, which dissipated the accumulated pH gradient as if clamping the voltage near zero. Just before FCCP addition, the model predicts negative membrane potentials for all scenarios (Fig. 3). The negative membrane potential causes luminal acidification after FCCP addition rather than the return to baseline observed experimentally. For the ClC-7 model considered in Fig. 2 A, the fit between the simulated and the observed magnitudes of the pHL changes strongly, which indicates that the model is predicting the true membrane potential once valinomycin is added, and raises the question as to why adding a protonophore did not cause acidification in the experiments. We were unable to improve the quality of the fits by varying model parameters or by including voltage-gated Na+ channels or voltage-gated ClC-7 antiporters (unpublished data). The model can describe the data if the experimentally measured ionic concentrations are incorrect, but it is also possible that we are missing some regulatory element, further highlighting the need for well-controlled in vitro experiments that quantitatively measure key values. A possible explanation of this discrepancy with the experiment is that the addition of FCCP to valinomycin-treated lysosomes induces a nonspecific leak in the organelle membrane, which pulls the potential toward 0 mV. To prevent this uncertainty from undermining our current study, in the simulations that follow, we explored a wide range of environmental variables relevant to lysosomal pH regulation.
ClC-7 promotes robust acidification
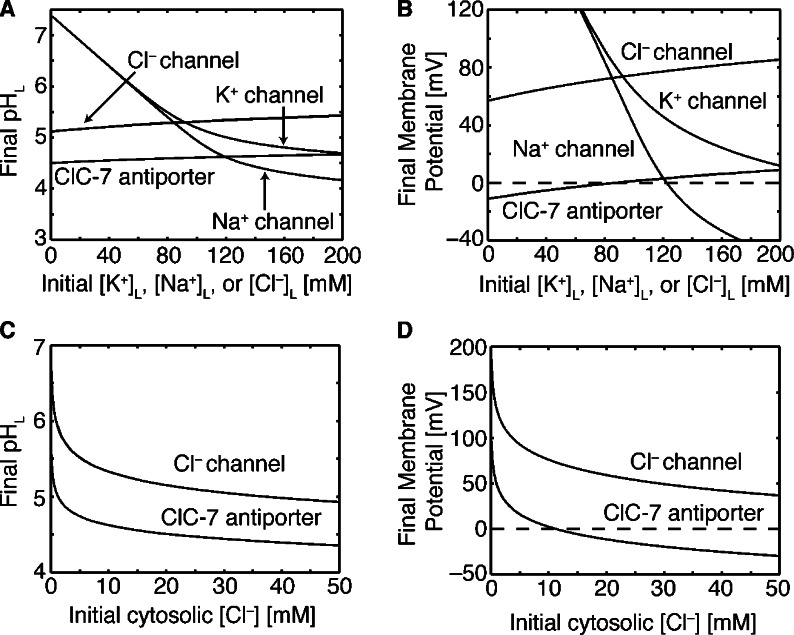
The major focus of our work is to understand how steady-state pHL values are influenced by counterion identity for lysosomes undergoing active acidification via the V-ATPase proton pump. Recent studies suggest that K+ and/or Na+, instead of Cl–, could be the primary counterions (Steinberg et al., 2010; Weinert et al., 2010). We explored this hypothesis by comparing the effectiveness of K+ channels, Na+ channels, Cl– channels, and ClC-7 antiporters in creating an acidic lysosomal interior. For this set of simulations, we used the proton permeability value determined by fitting the in vitro data in Fig. 2 A, and with this value of PH+, 300 V-ATPases were needed to achieve a low pHL. The initial luminal concentrations of ions inside nascent organelles are poorly characterized, and to address this uncertainty, we assessed a wide range of initial ionic conditions for their influence on steady-state pHL. Using 5,000 antiporters, determined from our analysis in the next subsection, we see that ClC-7 promotes robust acidification across the entire initial chloride concentration range investigated (Fig. 4 A). Additionally, ClC-7 achieves pHL that is ∼1/2 a unit lower than a Cl– channel. This result corroborates modeling performed by Weinert et al. (2010) for one particular condition, but further demonstrates that ClC-7 is effective over a large range of luminal chloride concentrations.
Figure 4.
Steady-state pHL in the presence of the V-ATPase proton pump. (A) Steady-state pHL as a function of initial luminal concentration for four different counterion flows: ClC-7 antiporter, Cl–, K+, or Na+ channel. For each curve, the initial concentration of the ion being transported was varied from 1 to 200 mM. Thus, for simulations including Cl– channels, the initial [Cl–]L was varied from 1 to 200 mM, and the steady-state pHL was determined for each concentration. (B) The steady-state membrane potentials for the simulations in A. (C) Steady-state pHL as a function of cytosolic Cl– concentration for models containing either Cl– channels or ClC-7 antiporters. (D) The steady-state membrane potentials for the simulations in C. All simulations included PH+ of 6 × 10−5 cm/s and 300 V-ATPases. Simulations with ClC-7 antiporters included 5,000 transporters, and the model lysosome was spherical with a diameter of 0.68 µm (Van Dyke, 1993). In all simulations, the initial luminal concentrations of ions were equal to typical extracellular values, except for the concentrations being explicitly varied along the x axes. All other parameter values are given in Table 1.
Cation channels, however, only allow acidification less than pHL 5.0 if the initial luminal concentration of the permeant cation is >100 mM (Fig. 4 A). The K+ concentration values necessary for effective acidification are far greater than typical extracellular K+ values (5 mM), but are close to extracellular Na+ concentrations (145 mM; Alberts et al., 2008). However, there are few experimental estimates of lysosomal cation concentrations, and those that do exist are not in agreement. For instance, Steinberg et al. (2010) predict [K+]L and [Na+]L to be 50 mM and 20 mM, respectively, at pHL 6.0 in macrophages, whereas in HEK293T cells Wang et al. (2012) argue that Na+ is 100-fold higher than K+ (Wang et al., 2012). According to our model, these former concentrations at pHL 6.0 are too small to allow effective acidification unless both K+ and Na+ channels are present (Fig. 5). It is difficult to judge the result from Wang et al. (2012) because their measurements are presumably performed on lysosomes that have already achieved an acidic lumen. However, lysosomes containing K+ and Na+ channels that acidify from the initial luminal concentrations suggested by Steinberg et al. (2010) give rise to steady-state luminal cation concentrations that do not match the values from the Wang et al. (2012) study (partly Fig. 5, but not all data are shown), potentially pointing to a discrepancy between the Steinberg and Wang studies.
Figure 5.
Dynamics of lysosomal acidification for two different counterion pathway models. The top curve is from a model containing only K+ and Na+ channels, and the bottom curve is from a model that has both cation channels in addition to ClC-7 antiporters. The initial conditions were set to [K+]L = 50 mM, [Na+]L = 20 mM, [Cl–]L = 1 mM, and pHL 6.0 as reported by Steinberg et al. (2010). For these values, cation channels alone can achieve a pHL of 5.0, but the addition of ClC-7 lowers the pH another 1/2 unit. Both simulations included PH+ of 6 × 10−5 cm/s and 300 V-ATPases. The simulation with ClC-7 antiporters included 300 transporters. The buffering capacity was 40 mM/pH, and all other parameter values are given in Table 1.
The steady-state membrane potential values corresponding to Fig. 4 A are shown in Fig. 4 B. ClC-7 antiporters result in lower membrane potentials than Cl– channels, which explains their ability to facilitate greater acidification. K+ channels alone only result in positive membrane potentials, and for Na+ or K+ channels, if the initial luminal concentrations are <60 mM, the final membrane potential is >120 mV, showing how cations require high numbers to allow acidification below pHL 6.0. We also explored the influence of organelle size on the steady-state properties, and we determined that the pH and membrane potential were unaffected by changes in lysosomal diameter from 0.2 to 1 µm (unpublished data).
We also examined how the cytosolic Cl– concentration ([Cl–]C) impacted the resting membrane potential and pH of lysosomes containing ClC-7 antiporters and Cl– channels. The majority of the calculations presented here assume a [Cl–]C value of 10 mM (Alberts et al., 2008), but recent measurements indicate that the value is 45 mM (Sonawane et al., 2002). As expected, the steady-state pHL is more acidic at [Cl–]C of 50 mM than it is at 10 mM because the driving force for Cl– entry into the lysosome is larger at 50 mM (Fig. 4 C). However, the difference is <0.5 pH units, indicating again that the resting pHL is relatively insensitive to chloride levels. In fact, the ClC-7 antiporter aids acidification to pHL 5.0 even at a [Cl–]C of 1 mM, which shows that ClC-7 antiporters could successfully aid acidification even in dialysis experiments that remove cytosolic Cl– if trace amounts of chloride remain. The resting membrane potential for ClC-7–containing lysosomes is predicted to be positive for [Cl–]C values <10 mM, whereas Cl– channel containing lysosomes have positive membrane potentials across the entire range (Fig. 4 D).
The simulations shown in Fig. 4 are based on a constant buffering capacity of 40 mM/pH, but the lysosomal buffering capacity changes with pH. Thus, we also explored the effect of varying buffering capacity on the steady-state pH and membrane potential. Lowering the buffering capacity shifts both the steady-state pH curves and the steady-state membrane potential curves for K+ and Na+ channels in Fig. 4 (A and B) to the left, making these channels more effective at promoting acidification. The steady-state pH values of ClC-7– and Cl– channel–mediated counterion models are insensitive to changes in buffering capacity, although the steady-state membrane potential values become slightly more negative than those shown in Fig. 4 B. The question remains as to the true buffering capacity of the lysosome. Van Dyke (1993) reported a small value of 20 mM/pH at pH 5.25, but a much larger value of 60 mM/pH at pH 6.75, and we used a value of 40 mM/pH for our simulations, which falls in the middle of this range. However, Steinberg et al. (2010) reported a buffering capacity of 61.5 mM/pH in the pH 4.5–5.0 range. Thus, it is likely that the value we used in our simulations is an underestimate of the true buffering capacity value, and the true value is likely to make it even more difficult for cation channels alone to facilitate acidification.
Differential changes in volume
Regardless of the identity of the counterion pathway, acidification must be accompanied by a large change in ionic conditions, which will impact the osmolarity of the lysosomal compartment. In the case of ClC-7 or a passive Cl– channel, large quantities of Cl– will enter the lumen to offset the accumulation of protons; however, if the pathway is dominated by cations, then K+ or Na+ will exit the lysosome. The vast majority of the protons that enter the lysosome are buffered, and therefore do not contribute to the osmolarity. Thus, anion entry will increase the osmolarity and cause the lysosome to expand, while cation exit will cause the lysosome to shrink. We recalculated the acidification simulations in Fig. 4 A this time, including a term for the corresponding water flux. Interestingly, the steady-state pH values are nearly identical to those presented in Fig. 4 A (not depicted), but the compartments do change volume as hypothesized. ClC-7 antiporters or Cl– channels cause the lysosomes to swell by 33–35% or 22–28%, respectively (Fig. 6). Depending on the quantity of cations that leave the compartment, and correspondingly the degree of acidification, K+ or Na+ exit cause a 0–25% or 0–29% reduction in volume, respectively. For the parameters used here, our results indicate that the percent change in lysosomal volume is quite similar, regardless of the counterion. Moreover, the volume changes are so small that it is unclear if direct visualization with light microscopes commonly used in these experiments could identify swelling from shrinking.
Figure 6.
Different counterion pathways have different effects on lysosomal volume. The simulations reported are identical to those shown in Fig. 4 A except for the initial lysosomal volume and the inclusion of water flux. For each counterion pathway, the initial concentration of the ion being transported was varied from 1 to 200 mM, and the percentage change in the steady-state volume relative to the initial volume was calculated. The initial volume and surface area were set to 3.3 × 10−17 L and 6.2 × 10−9 cm2, respectively. The lysosome with ClC-7 resulted in the greatest increase in volume as it acidifies, and the final volume was close to the volume of the sphere with the same surface area as the initial value.
Different counterion pathways have distinct kinetic signatures
Potentially the most promising experiments for identifying the counterions and their carriers involve the use of quantitative fluorescent dyes to track the changes in Cl–, K+, or Na+ during acidification. Although the Verkman laboratory has performed seminal studies measuring chloride changes in nascent endosomes (Sonawane et al., 2002; Sonawane and Verkman, 2003), reliable cation and anion dyes are not readily available at present, and no such experiments have been performed on lysosomes. In anticipation of a reliable K+ dye becoming publically available, we simulated the time-dependent change in [K+]L as well as the steady-state [K+]L during acidification of a lysosome starting from steady state (Fig. 7). Both the dynamics and steady-state values depend on counterion pathways and initial ionic conditions. Thus, we performed simulations of a lysosome containing a K+ channel alone as well as in combination with a Na+ channel, Cl– channel, or ClC-7 antiporter. For each of the four combinations of counterion pathways, the simulations were performed with high (150 mM) or low (10 mM) permeant ion concentrations. This resulted in four simulations for the scenarios involving two permeant ions and two simulations for the scenario involving only K+ channels. The steady-state [K+]L values for all simulations are given in the tables in Fig. 7. We color-coded the simulation for each scenario that corresponds to typical extracellular values and showed the corresponding dynamics on the graph to the left. Unlike all other scenarios, lysosomes containing ClC-7 antiporters resulted in an increase in [K+]L once acidification was initiated by the addition of ATP (Fig. 7, blue 3 in graph). This increase in [K+]L occurs for all simulations in scenario 3 that contain ClC-7 and none of the simulations that lack ClC-7 antiporters (Fig. S1). Additionally, the ClC-7 antiporter produces steady-state [K+]L values at or above 100 mM for all initial conditions, unlike all other simulations except for scenario 1, with high initial luminal [K+]L and [Na+]L. With regard to this later scenario, there is no data to suggest that nascent, or pre-acidified, lysosomes contain such high levels of both Na+ and K+. Therefore, we believe that a measurement of resting lysosomal [K+]L near or above 100 mM is a strong indication that ClC-7 antiporters are active in the lysosomal membrane. Because the K+ dynamics and steady-state properties elicited by ClC-7 antiporters are distinct from the other putative counterion pathways, it is possible that even a qualitative [K+]L fluorescence measurement could identify the counterion and its pathway.
Changes in ClC-7 stoichiometry affect steady-state pH
Our in silico system allows us to assess the role of stoichiometry in the ability of ClC-7 to facilitate lysosomal acidification. We can manipulate the stoichiometry of the antiporter at will, an operation not experimentally possible. To see how these changes influence the lysosome, we performed simulations with stoichiometries of 3 Cl–:1 H+, 2 Cl–:1 H+, and 1 Cl–:1 H+ (Fig. 8, A and B). Under a wide range of initial [Cl–]L, a hypothetical antiporter with a 1:1 Cl–/H+ coupling ratio permits the greatest acidification followed by a 2:1 ratio and finally a 3:1 ratio, which is least effective (Fig. 8 A). To illustrate these differences in another manner, we consider the time-dependent acidification of a vesicle aided by a ClC-7 antiporter with a hypothetical 3:1 ratio (Fig. 8 B). For the parameters outlined in the caption, this system reaches a steady-state pHL of ∼5, but changing the stoichiometry to 2:1 at that point allows acidification by an additional 0.25 pH units, and then finally changing the stoichiometry to 1:1 permits acidification by another 0.5 units down to pHL 4.25. In each case, changing the coupling ratio allows the ClC-7 antiporter to further reduce the membrane potential and achieve a lower pHL value. Stoichiometric ratios of 1 Cl–:2 H+ and 1 Cl–:3 H+ produced nearly identical steady-state pH values as the 1 Cl–:1 H+ antiporter. However, in simulations where the proton leak was very small, the 1 Cl–:1 H+ ClC-7 antiporter produced the most acidic interior (unpublished data). At first glance, it appears counterintuitive that a hypothetical ClC-7 with a 1:1 coupling ratio permits greater acidification than antiporters with larger coupling ratios because fewer Cl– are imported during each transport cycle, resulting in less neutralization of the membrane potential. We resolve this apparent contradiction in the Discussion.
Figure 8.
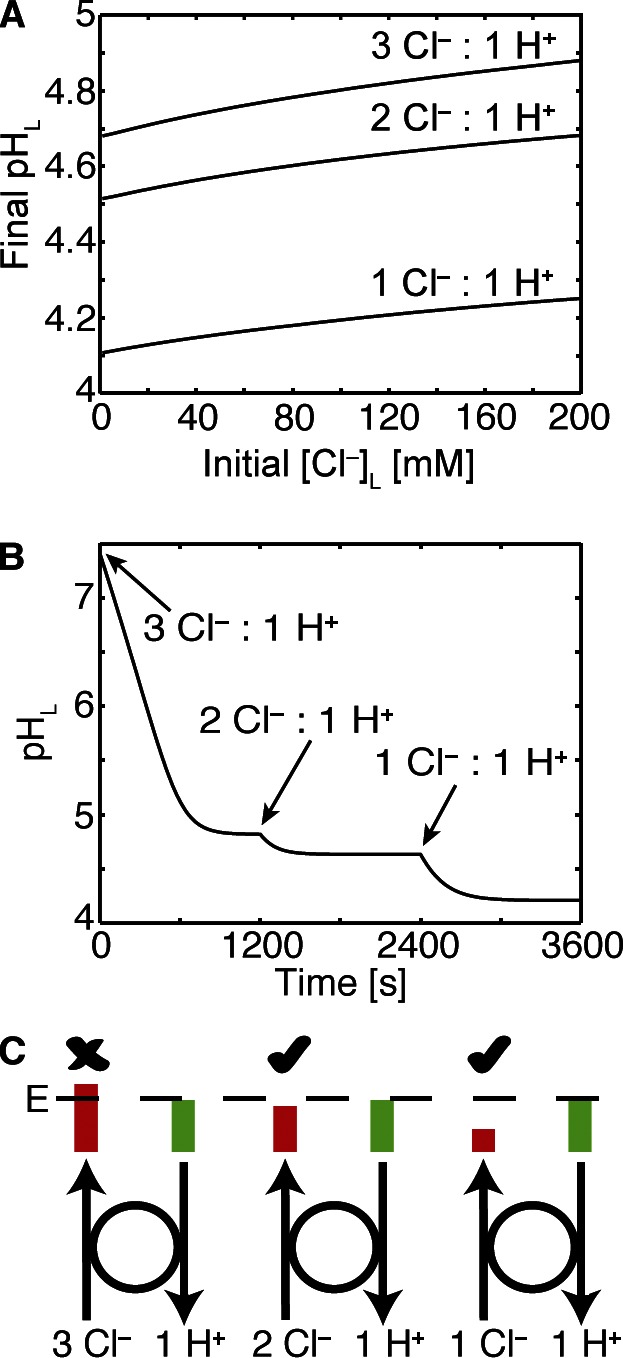
The influence of ClC-7 antiporter stoichiometry on acidification. (A) Steady-state pHL values over a range of initial [Cl–]L values are plotted for a model lysosome containing 300 V-ATPases, PH+ of 6 × 10−5 cm/s, and 5,000 ClC-7 antiporters of varying stoichiometry. A putative antiporter with a 1:1 stoichiometric ratio gives rise to the greatest acidification. (B) Time-dependent change in pHL was calculated, starting with the stoichiometry of 3 Cl–:1 H+. After the pH reached steady state, the stoichiometric ratio was changed to 2 Cl–:1 H+ and then to 1 Cl–:1 H+. After each change, the system achieved a lower pHL. (C) At a given pH gradient, the antiporter has a fixed amount of energy (E) provided by the proton movement during one cycle (green bars). If the transport is 3:1, the energy required for Cl– movement against their gradient (red bars) is greater than the energy provided by proton movement, and transport will not happen (indicated by the X). When the ratio is 2:1, the antiporter is close to stalling, but there is just enough energy to complete the cycle and pump Cl– into the lumen, which will subsequently allow further acidification by the V-ATPase (check mark). When the ratio is 1:1, there is ample energy to allow Cl– transport into the lumen (check mark). All other parameter values are given in Table 1.
DISCUSSION
Role of ClC-7 in lysosomal pH regulation and ion homeostasis
Our study suggests a crucial role for the ClC-7 antiporter in lysosomal pH regulation and ion homeostasis. We showed that both ClC-7 antiporters and Cl– channels are the only counterion pathways that promote robust lysosomal acidification over a broad range of initial luminal and cytosolic ion concentrations. But ClC-7 antiporters are more effective than Cl– channels and are the only counterion pathway that explains the in vitro lysosomal acidification changes (Graves et al., 2008). The current–voltage curve indicates that ClC-7 is a strong inward rectifier, allowing Cl– to flow out of the lysosome at high rates while moving Cl– inward at a very slow rate. Paradoxically, to act as a counterion pathway, ClC-7 must move Cl– into the lumen in the direction that produces very slow turnover (Fig. 1 C). Nonetheless, the antiporter is extremely effective at aiding acidification because the turnover rate of the V-ATPase is relatively slow; even the low Cl– fluxes predicted for positive voltages are sufficient to dissipate the V-ATPase–generated membrane potentials. We also found that the most important characteristic of our calibrated ClC-7 antiporter model is the requirement to obey detailed balance; all of our results are insensitive to the exact shape of the ClC-7 performance surface in Fig. 1 D (unpublished data). Importantly, a model with Cl– as the primary counterion agrees well with seminal studies of lysosomal acidification, which also highlighted the importance of Cl– (Ohkuma et al., 1982; Cuppoletti et al., 1987; Van Dyke, 1993).
Cation channels as counterion pathways
In recent years several cation channels, such as TRP-ML1 (Kiselyov et al., 2005) and Na+-selective two-pore channels (TPC; Wang et al., 2012; Cang et al., 2013), have been identified in lysosomes. It was suggested that TRP-ML1 may be the proton leak pathway, as lysosomes of TRP-ML1−/− cells hyperacidify (Soyombo et al., 2006); however, TRP-ML1 is a nonselective cation channel, so it may permeate Na+ and K+ (LaPlante et al., 2002). The identification of these channels in lysosomes corroborates claims that K+, or possibly Na+, act as counterions during acidification (Steinberg et al., 2010). One of the strongest arguments from the Steinberg et al. (2010) study is that macrophages harvested from ClC-7 knockout mice have virtually identical lysosomal pH to wild-type littermates (4.73 and 4.72, respectively). Similar results have been reported for lysosomes in neurons and fibroblasts of ClC-7 knockout mice (Kasper et al., 2005; Weinert et al., 2010). However, these results clash with the finding that small interfering RNA (siRNA) knockdown of ClC-7 in HeLa cells results in a marked reduction in lysosomal acidity as determined by qualitative fluorescence measurements (Graves et al., 2008). The Steinberg et al. (2010) study also found that lysosomes were able to acidify in cells dialyzed to remove cytosolic chloride and that isolated lysosomes held in Cl–-free medium were able to acidify with K+ acting as a counterion (Steinberg et al., 2010). This latter finding is consistent with our results if a K+ channel is present and starting luminal K+ levels are high (Fig. 4 A). But we suggest that the former result must be taken cautiously, as the Steinberg et al. (2010) study reports 8.5 mM residual Cl– remaining in their “Cl–-free” cells, and we show in Fig. 4 C that ClC-7 and Cl– channels are both effective at aiding acidification with trace amounts of cytosolic chloride.
Our results indicate that Na+ and K+ can bring about effective acidification, but their ability to do so is highly dependent on the initial luminal concentrations. Using the luminal K+ and Na+ concentrations determined by Steinberg et al. (2010), our model predicts that the presence of ClC-7 antiporters will always promote greater acidification (Fig. 5). However, lysosomal cation concentrations have been poorly characterized, and Steinberg et al. (2010) have determined values that appear to conflict with the values determined by Wang et al. (2012). It is hard to judge the role of cations during acidification until their concentration values and dynamics are better understood.
It is possible that luminal ionic concentrations are precisely balanced before lysosomal maturation such that all counterion pathways are able to effectively contribute to the counterion movement. In this case, acidification may be unaffected by the removal of any particular counterion pathway. Furthermore, compensatory changes in expression of one or more transporters, as have been observed in ClC-7 knockout mice (Poët et al., 2006), may mask the effects of knocking out crucial counterion transporters. Another possibility that we have not considered is that ion stores are continually delivered to the lysosome during acidification, providing a source of counterions for efflux, though this would need to be through bulk processes, like fusion with ion-laden vesicles, as cation transport directly across the lysosomal membrane would increase the counterion requirement.
Membrane potential and K+ dynamics as indicators of counterion pathways
A recent estimate of the steady-state membrane potential of the lysosome is between +30 and +110 mV (Dong et al., 2010), and our results indicate that lysosomes containing ClC-7 antiporters produce more negative resting membrane potentials in the range of –10 to +10 mV (Fig. 4 B). If the buffering capacity is higher than our assumed value of 40 mM/pH, then our simulations predict that ClC-7 antiporters would result in more positive membrane potentials closer to the experimental range (unpublished data). The model shows that a pure Cl– channel produces membrane potentials in the experimental range. Interestingly, the resting membrane potential and steady-state pHL are very sensitive to the initial luminal cation concentrations when the counterion pathway is mediated by Na+ or K+ channels (Fig. 4, A and B). This sensitivity makes it difficult to determine whether models containing cation channels are consistent with the membrane potential measurements. Conversely, ClC-7 antiporters and Cl– channels produce steady-state pHL and membrane potential values in a narrow range regardless of the initial internal ion concentrations. Given that the luminal contents of nascent lysosomes are subject to stochastic variation, the robust acidification property of anion pathways is appealing, as it indicates that lysosomes will always achieve the desired pHL value needed to function properly.
We predict that lysosomes with and without ClC-7 antiporters will have different steady-state pHL values (Fig. 5) and, if K+ channels are present, different [K+]L levels (Figs. 6 and 7). The latter finding may partly explain why ClC-7 knockout mice express lysosome-related disorders despite apparently normal pHL values (Kornak et al., 2001; Kasper et al., 2005; Weinert et al., 2010), as lysosomal dysfunction may be the result of changes in other ionic conditions such as K+ levels. Wang et al. (2012) predict that lysosomal [K+]L is low (1–2 mM), and our modeling shows that there are only a few mechanisms for achieving low [K+]L levels: either there is no K+ conductance and Cl– is the counterion (Fig. 4 A) or ClC-7 is not active in the lysosome and initial [K+]L is low (Fig. 7). A measurement of the K+ dynamics during acidification would distinguish between these two possibilities.
ClC-7 stoichiometry
The counterintuitive result that ClC-7 antiporters with the known 2:1 Cl–/H+ stoichiometric ratio are less effective at acidification than antiporters with a 1:1 ratio can be understood through an equilibrium analysis of the energy of transport. Such analysis is possible because the antiporter is close to reversible equilibrium, or mechanical stall, as the system approaches steady state. ClC-7 stops transport when the energy gained by removing a single proton from the lumen is equal to the energy required to import the number of chloride ions specified by the stoichiometric ratio. Thus, when the proton gradient provides enough energy to pump two chloride ions but not three, only antiporters with a 2:1 or 1:1 stoichiometry can turn over, reduce the membrane potential, and aid acidification (Fig. 8 C). Likewise, as the chloride gradient increases, there will be a point at which a ClC-7 with a 2:1 ratio will stop working, and only a hypothetical antiporter with a 1:1 ratio will continue to promote acidification. Although there is a bacterial ClC antiporter that exchanges 1 F– for 1 H+ (Stockbridge et al., 2012), there is no ClC antiporter that exchanges 1 Cl– for 1 H+. There are, however, antiporters with higher coupling ratios, namely the unc ClC-7 mutant antiporter that uncouples H+ and Cl– movement. Our model predicts that lysosomes with such mutant antiporters would be less acidic, which is not supported by in vitro experiments (Weinert et al., 2010), but does explain why mice carrying the unc ClC-7 mutation have osteopetrosis, similar to, but milder than, that seen in ClC-7 knockout mice (Weinert et al., 2010).
Our quantitative model sheds light on known experiments; however, given the current uncertainty in lysosomal biology, it is not possible to make concrete predictions concerning the true nature of the counterion and its pathway. As shown in Fig. 2 A, some in vitro studies can only be understood through the inclusion of ClC-7 antiporters, and antiporters also allow for proper acidification in a robust manner (Fig. 4, A and C). Nonetheless, cation channels on their own can facilitate proper acidification under the right conditions (Fig. 4 A), and there are an increasing number of channels being identified in the lysosome. Regardless, our results suggest new kinetic and steady-state experiments that will help delineate the key components required for lysosomal acidification and ionic regulation. It is possible that lysosomes contain combinations of these counterion pathways, and other pathways yet unknown, which may explain the difficulty in ascribing known experiments to one candidate or another. This possibility is highlighted by the recent work of Cang et al. (2013) showing that an ATP-sensitive Na+ channel opens and closes in response to changes in the extracellular environment, giving rise to changes in the steady-state membrane potential and pH of endolysosomes (Wang et al., 2012; Cang et al., 2013). The sensitivity of the lysosome to changes in the environment may also help rationalize the difference between in vivo and in vitro experiments as well as differences in results between laboratories. However, such complexity further highlights the need for a mathematical model, such as ours, to interpret data and make new predictions.
Supplementary Material
Acknowledgments
We would like to thank Lily Jan (Howard Hughes Medical Institute/University of California, San Francisco), Kenton Swartz (National Institutes of Health), and Jianmin Sun (University of Pittsburgh) for their comments on this manuscript. We appreciate the technical assistance of Daniel Silverman. We also appreciate technical discussions with Marcel Bruchez (Carnegie Mellon University) concerning fluorescent technologies. George Oster (University of California, Berkeley), Robert Macey (University of California, Berkeley), and Mike Gittelsohn provided technical support concerning ongoing development of Berkeley Madonna.
We are grateful for financial support from National Institutes of Health grant R21GM100224-01 (to M. Grabe and S. Nayak) and the National Institute of Neurological Disorders and Stroke Intramural program (J.A. Mindell).
Christopher Miller served as editor.
Footnotes
Abbreviations used in this paper:
- FCCP
- carbonyl cyanide p-trifluoromethoxyphenylhydrazone
- pHL
- luminal pH
- V-ATPase
- vacuolar-type H+-ATPase
References
- Alberts B., Johnson A., Lewis J., Raff M., Roberts K., Walter P. 2008. Molecular Biology of the Cell. Fifth edition. Garland Science, New York: 1,601 pp [Google Scholar]
- Cang C., Zhou Y., Navarro B., Seo Y.J., Aranda K., Shi L., Battaglia-Hsu S., Nissim I., Clapham D.E., Ren D. 2013. mTOR regulates lysosomal ATP-sensitive two-pore Na(+) channels to adapt to metabolic state. Cell. 152:778–790 10.1016/j.cell.2013.01.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casey R.P., Hollemans M., Tager J.M. 1978. The permeability of the lysosomal membrane to small ions. Biochim. Biophys. Acta. 508:15–26 10.1016/0005-2736(78)90185-2 [DOI] [PubMed] [Google Scholar]
- Cuppoletti J., Aures-Fischer D., Sachs G. 1987. The lysosomal H+ pump: 8-azido-ATP inhibition and the role of chloride in H+ transport. Biochim. Biophys. Acta. 899:276–284 10.1016/0005-2736(87)90409-3 [DOI] [PubMed] [Google Scholar]
- De Duve C., Wattiaux R. 1966. Functions of lysosomes. Annu. Rev. Physiol. 28:435–492 10.1146/annurev.ph.28.030166.002251 [DOI] [PubMed] [Google Scholar]
- Dell’Antone P. 1979. Evidence for an ATP-driven “proton pump” in rat liver lysosomes by basic dyes uptake. Biochem. Biophys. Res. Commun. 86:180–189 10.1016/0006-291X(79)90398-X [DOI] [PubMed] [Google Scholar]
- Dong X.P., Wang X., Xu H. 2010. TRP channels of intracellular membranes. J. Neurochem. 113:313–328 10.1111/j.1471-4159.2010.06626.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabe M., Oster G. 2001. Regulation of organelle acidity. J. Gen. Physiol. 117:329–344 10.1085/jgp.117.4.329 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabe M., Wang H., Oster G. 2000. The mechanochemistry of V-ATPase proton pumps. Biophys. J. 78:2798–2813 10.1016/S0006-3495(00)76823-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graves A.R., Curran P.K., Smith C.L., Mindell J.A. 2008. The Cl-/H+ antiporter ClC-7 is the primary chloride permeation pathway in lysosomes. Nature. 453:788–792 10.1038/nature06907 [DOI] [PubMed] [Google Scholar]
- Harikumar P., Reeves J.P. 1983. The lysosomal proton pump is electrogenic. J. Biol. Chem. 258:10403–10410 [PubMed] [Google Scholar]
- Hartmann T., Verkman A.S. 1990. Model of ion transport regulation in chloride-secreting airway epithelial cells. Integrated description of electrical, chemical, and fluorescence measurements. Biophys. J. 58:391–401 10.1016/S0006-3495(90)82385-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henning R. 1975. pH gradient across the lysosomal membrane generated by selective cation permeability and Donnan equilibrium. Biochim. Biophys. Acta. 401:307–316 10.1016/0005-2736(75)90314-4 [DOI] [PubMed] [Google Scholar]
- Hille B. 2001. Ion Channels of Excitable Membranes. Third edition. Sinauer, Sunderland, MA: 814 pp [Google Scholar]
- Kasper D., Planells-Cases R., Fuhrmann J.C., Scheel O., Zeitz O., Ruether K., Schmitt A., Poët M., Steinfeld R., Schweizer M., et al. 2005. Loss of the chloride channel ClC-7 leads to lysosomal storage disease and neurodegeneration. EMBO J. 24:1079–1091 10.1038/sj.emboj.7600576 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kielland J. 1937. Individual activity coefficients of ions in aqueous solutions. J. Am. Chem. Soc. 59:1675–1678 10.1021/ja01288a032 [DOI] [Google Scholar]
- Kiselyov K., Chen J., Rbaibi Y., Oberdick D., Tjon-Kon-Sang S., Shcheynikov N., Muallem S., Soyombo A. 2005. TRP-ML1 is a lysosomal monovalent cation channel that undergoes proteolytic cleavage. J. Biol. Chem. 280:43218–43223 10.1074/jbc.M508210200 [DOI] [PubMed] [Google Scholar]
- Kornak U., Kasper D., Bösl M.R., Kaiser E., Schweizer M., Schulz A., Friedrich W., Delling G., Jentsch T.J. 2001. Loss of the ClC-7 chloride channel leads to osteopetrosis in mice and man. Cell. 104:205–215 10.1016/S0092-8674(01)00206-9 [DOI] [PubMed] [Google Scholar]
- Lange P.F., Wartosch L., Jentsch T.J., Fuhrmann J.C. 2006. ClC-7 requires Ostm1 as a beta-subunit to support bone resorption and lysosomal function. Nature. 440:220–223 10.1038/nature04535 [DOI] [PubMed] [Google Scholar]
- LaPlante J.M., Falardeau J., Sun M., Kanazirska M., Brown E.M., Slaugenhaupt S.A., Vassilev P.M. 2002. Identification and characterization of the single channel function of human mucolipin-1 implicated in mucolipidosis type IV, a disorder affecting the lysosomal pathway. FEBS Lett. 532:183–187 10.1016/S0014-5793(02)03670-0 [DOI] [PubMed] [Google Scholar]
- Leisle L., Ludwig C.F., Wagner F.A., Jentsch T.J., Stauber T. 2011. ClC-7 is a slowly voltage-gated 2Cl(-)/1H(+)-exchanger and requires Ostm1 for transport activity. EMBO J. 30:2140–2152 10.1038/emboj.2011.137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lencer W.I., Weyer P., Verkman A.S., Ausiello D.A., Brown D. 1990. FITC-dextran as a probe for endosome function and localization in kidney. Am. J. Physiol. 258:C309–C317 [DOI] [PubMed] [Google Scholar]
- Lloyd J.B., Mason R.W. 1996. Biology of the Lysosome. Plenum Press, New York: 416 pp [Google Scholar]
- Mindell J.A. 2012. Lysosomal acidification mechanisms. Annu. Rev. Physiol. 74:69–86 10.1146/annurev-physiol-012110-142317 [DOI] [PubMed] [Google Scholar]
- Moriyama Y. 1988. Potassium ion dependent proton efflux and depolarization from spleen lysosomes. Biochem. Biophys. Res. Commun. 156:211–216 10.1016/S0006-291X(88)80826-X [DOI] [PubMed] [Google Scholar]
- Moriyama Y., Maeda M., Futai M. 1992. Involvement of a non-proton pump factor (possibly Donnan-type equilibrium) in maintenance of an acidic pH in lysosomes. FEBS Lett. 302:18–20 10.1016/0014-5793(92)80274-K [DOI] [PubMed] [Google Scholar]
- Ohkuma S., Moriyama Y., Takano T. 1982. Identification and characterization of a proton pump on lysosomes by fluorescein-isothiocyanate-dextran fluorescence. Proc. Natl. Acad. Sci. USA. 79:2758–2762 10.1073/pnas.79.9.2758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohkuma S., Moriyama Y., Takano T. 1983. Electrogenic nature of lysosomal proton pump as revealed with a cyanine dye. J. Biochem. 94:1935–1943 [DOI] [PubMed] [Google Scholar]
- Poët M., Kornak U., Schweizer M., Zdebik A.A., Scheel O., Hoelter S., Wurst W., Schmitt A., Fuhrmann J.C., Planells-Cases R., et al. 2006. Lysosomal storage disease upon disruption of the neuronal chloride transport protein ClC-6. Proc. Natl. Acad. Sci. USA. 103:13854–13859 10.1073/pnas.0606137103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsey I.S., Moran M.M., Chong J.A., Clapham D.E. 2006. A voltage-gated proton-selective channel lacking the pore domain. Nature. 440:1213–1216 10.1038/nature04700 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsey I.S., Ruchti E., Kaczmarek J.S., Clapham D.E. 2009. Hv1 proton channels are required for high-level NADPH oxidase-dependent superoxide production during the phagocyte respiratory burst. Proc. Natl. Acad. Sci. USA. 106:7642–7647 10.1073/pnas.0902761106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roos A., Boron W.F. 1981. Intracellular pH. Physiol. Rev. 61:296–434 [DOI] [PubMed] [Google Scholar]
- Rybak S.L., Lanni F., Murphy R.F. 1997. Theoretical considerations on the role of membrane potential in the regulation of endosomal pH. Biophys. J. 73:674–687 10.1016/S0006-3495(97)78102-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sasaki M., Takagi M., Okamura Y. 2006. A voltage sensor-domain protein is a voltage-gated proton channel. Science. 312:589–592 10.1126/science.1122352 [DOI] [PubMed] [Google Scholar]
- Scott C.C., Gruenberg J. 2011. Ion flux and the function of endosomes and lysosomes: pH is just the start: the flux of ions across endosomal membranes influences endosome function not only through regulation of the luminal pH. Bioessays. 33:103–110 10.1002/bies.201000108 [DOI] [PubMed] [Google Scholar]
- Sonawane N.D., Verkman A.S. 2003. Determinants of [Cl-] in recycling and late endosomes and Golgi complex measured using fluorescent ligands. J. Cell Biol. 160:1129–1138 10.1083/jcb.200211098 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sonawane N.D., Thiagarajah J.R., Verkman A.S. 2002. Chloride concentration in endosomes measured using a ratioable fluorescent Cl- indicator: evidence for chloride accumulation during acidification. J. Biol. Chem. 277:5506–5513 10.1074/jbc.M110818200 [DOI] [PubMed] [Google Scholar]
- Soyombo A.A., Tjon-Kon-Sang S., Rbaibi Y., Bashllari E., Bisceglia J., Muallem S., Kiselyov K. 2006. TRP-ML1 regulates lysosomal pH and acidic lysosomal lipid hydrolytic activity. J. Biol. Chem. 281:7294–7301 10.1074/jbc.M508211200 [DOI] [PubMed] [Google Scholar]
- Steinberg B.E., Huynh K.K., Brodovitch A., Jabs S., Stauber T., Jentsch T.J., Grinstein S. 2010. A cation counterflux supports lysosomal acidification. J. Cell Biol. 189:1171–1186 10.1083/jcb.200911083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stockbridge R.B., Lim H.H., Otten R., Williams C., Shane T., Weinberg Z., Miller C. 2012. Fluoride resistance and transport by riboswitch-controlled CLC antiporters. Proc. Natl. Acad. Sci. USA. 109:15289–15294 10.1073/pnas.1210896109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dyke R.W. 1993. Acidification of rat liver lysosomes: quantitation and comparison with endosomes. Am. J. Physiol. 265:C901–C917 [DOI] [PubMed] [Google Scholar]
- Verkman A.S. 2000. Water permeability measurement in living cells and complex tissues. J. Membr. Biol. 173:73–87 10.1007/s002320001009 [DOI] [PubMed] [Google Scholar]
- Walden M., Accardi A., Wu F., Xu C., Williams C., Miller C. 2007. Uncoupling and turnover in a Cl-/H+ exchange transporter. J. Gen. Physiol. 129:317–329 10.1085/jgp.200709756 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X., Zhang X., Dong X.P., Samie M., Li X., Cheng X., Goschka A., Shen D., Zhou Y., Harlow J., et al. 2012. TPC proteins are phosphoinositide-activated sodium-selective ion channels in endosomes and lysosomes. Cell. 151:372–383 10.1016/j.cell.2012.08.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinert S., Jabs S., Supanchart C., Schweizer M., Gimber N., Richter M., Rademann J., Stauber T., Kornak U., Jentsch T.J. 2010. Lysosomal pathology and osteopetrosis upon loss of H+-driven lysosomal Cl- accumulation. Science. 328:1401–1403 10.1126/science.1188072 [DOI] [PubMed] [Google Scholar]
- Wu M.M., Llopis J., Adams S., McCaffery J.M., Kulomaa M.S., Machen T.E., Moore H.P., Tsien R.Y. 2000. Organelle pH studies using targeted avidin and fluorescein-biotin. Chem. Biol. 7:197–209 10.1016/S1074-5521(00)00088-0 [DOI] [PubMed] [Google Scholar]
- Wu M.M., Grabe M., Adams S., Tsien R.Y., Moore H.P., Machen T.E. 2001. Mechanisms of pH regulation in the regulated secretory pathway. J. Biol. Chem. 276:33027–33035 10.1074/jbc.M103917200 [DOI] [PubMed] [Google Scholar]
- Zeevi D.A., Frumkin A., Bach G. 2007. TRPML and lysosomal function. Biochim. Biophys. Acta. 1772:851–858 10.1016/j.bbadis.2007.01.004 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.