A fully scalable online pre-processing algorithm for short oligonucleotide microarray atlases

Abstract

Rapid accumulation of large and standardized microarray data collections is opening up novel opportunities for holistic characterization of genome function. The limited scalability of current preprocessing techniques has, however, formed a bottleneck for full utilization of these data resources. Although short oligonucleotide arrays constitute a major source of genome-wide profiling data, scalable probe-level techniques have been available only for few platforms based on pre-calculated probe effects from restricted reference training sets. To overcome these key limitations, we introduce a fully scalable online-learning algorithm for probe-level analysis and pre-processing of large microarray atlases involving tens of thousands of arrays. In contrast to the alternatives, our algorithm scales up linearly with respect to sample size and is applicable to all short oligonucleotide platforms. The model can use the most comprehensive data collections available to date to pinpoint individual probes affected by noise and biases, providing tools to guide array design and quality control. This is the only available algorithm that can learn probe-level parameters based on sequential hyperparameter updates at small consecutive batches of data, thus circumventing the extensive memory requirements of the standard approaches and opening up novel opportunities to take full advantage of contemporary microarray collections.

INTRODUCTION

Accumulation of research data in in-house and public repositories, such as the ArrayExpress (1) and Gene Expression Omnibus (2), has created data collections that include tens of thousands of microarray experiments from standardized measurement platforms (1). By combining data from hundreds of studies and thousands of commensurable microarray experiments, it is possible to overcome some of the inherent biases that are associated with meta-analyses involving multiple measurement platforms (3,4) to obtain a more holistic picture of genome function or carry out comprehensive investigations on targeted model systems and diseases that can benefit from large sample sizes provided by the new data collections (5,6). A major portion of the data in contemporary microarray collections originates from short oligonucleotide microarrays (7) whose applications range from gene expression profiling (1) to alternative splicing and phylogenetic profiling of microbial communities (8–10). With >30 000 studies and a million assays in public repositories (6), being able to combine and analyse very large sets of arrays together is a key challenge with a variety of applications (5,11–13).

Reliable pre-processing of the data is central for investigations. Multi-array preprocessing techniques that combine information across multiple arrays to quantify probe effects have led to improved preprocessing performance (14), but the applicability of the standard multi-array techniques, such as Robust Multiarray Averaging (RMA) (15), GC-RMA (16), Model-based expression indices (MBEI) (17) and Probe Logarithmic Intensity Error (PLIER) (18), has been limited to a few thousand arrays at most owing to the considerable memory requirements associated with processing up to a million probe-level features per a single array. This has formed a bottleneck for large-scale analysis of contemporary microarray data collections. Scalable preprocessing approaches have been recently developed to tackle these shortcomings. The scalable reference-RMA (refRMA) (19) and frozen RMA (fRMA) (20) algorithms rely on pre-calculated probe effect terms that are estimated from restricted reference training sets and then extrapolated to preprocess further microarray data. The applicability of these methods has, however, been limited to few specific microarray platforms with pre-calculated probe effect terms: the scalable fRMA algorithm is currently available only for altogether six Affymetrix platforms from human and mouse (21,22), whereas the ArrayExpress database lists >200 short oligonucleotide platforms from Affymetrix, Agilent, Nimblegen and other providers. Dozens of these platforms cover already thousands of samples in public databases, and the data collections are constantly accumulating (6). Hence, there is a need for platform-independent pre-processing techniques that can extract and use probe-level information across large microarray data collections in a fully scalable manner.

To overcome the key limitations of the current approaches, we introduce a fully scalable algorithm for multi-array preprocessing based on Bayesian online-learning, in which the model parameters can be sequentially updated with new observations based on a rigorous probabilistic model. The new algorithm extends the Robust Probabilistic Averaging (RPA) framework introduced in (23) by providing a model for probe affinities and by incorporating prior terms to provide the basis for scalable online-learning through sequential hyperparameter updates. The resulting algorithm allows rigorous pre-processing of very large microarray atlases on an ordinary desktop computer in small consecutive batches with minimal memory requirements and in linear time with respect to sample size. In contrast to the currently available alternatives, the proposed model provides the means to integrate probe-level information across tens or hundreds of thousands of arrays and a general-purpose preprocessing method for data sets of any size. In addition, the analysis of probe performance can now be based on the most comprehensive collections of microarray data to guide microarray design and quality control. To our knowledge, this is the only probe-level pre-processing approach, which is both fully scalable and applicable to all short oligonucleotide platforms, providing new tools to take full advantage of the contemporary, rapidly expanding microarray data collections.

MATERIALS AND METHODS

Probe-level procedures that combine information across multiple arrays have been found to improve pre-processing performance (14), but their applicability to large sample collections has been limited owing to huge memory requirements associated with increasing sample sizes. The available solutions have been based on learning and extrapolation of probe-level effects from smaller reference training sets (19,20). In this section, we outline an alternative online-learning procedure that can extract and use probe-level information across very large microarray collections in a fully scalable manner with minimal memory requirements and in linear time with respect to sample size based on Bayesian hyperparameter updates.

Scalable preprocessing with online-learning: an overview

In the following, let us outline the proposed online-learning procedure and provide details of parameter estimation. Assuming that appropriate microarray quality controls have been applied before the analysis (18), the standard steps of background correction, normalization and probe summarization are applied to consecutive batches of the data in three sweeps over the data collection:

• Step 1: Background correction and quantile basis estimation. In the first step, each individual array is background-corrected. In the present work, we use the standard RMA background correction (15). The background corrected data are stored temporarily on hard disk to speed up pre-processing. The basis for quantile normalization is then obtained by averaging sorted probe-level signals from background-corrected data (14). For scalable estimation of the base distribution, we average over the estimates from individual batches to obtain the final quantile base distribution as in parallel implementations of RMA (24). The final base distribution is identical with the one, which would be obtained by jointly normalizing all arrays in a single batch. Optionally, other standard approaches for background correction and normalization could be used in combination with our model (25).

• Step 2: Hyperparameter estimation. The key novelty of our approach is in introducing the scalable approach for estimating the probe-level hyperparameters. This is achieved based on Bayesian online-learning where consecutive batches of data are used to update the hyperparameters of the model. Before hyperparameter estimation, each batch is background-corrected, quantile-normalized and log-transformed. At the first batch, the model can be initialized by giving equal priors for the probes if no probe-specific prior information is available. The probe-level hyperparameters are then updated at each new batch and provided as priors for the next batch. The final probe-level parameters are obtained after processing the complete data collection. Ideally, the fully scalable parameter estimation through consecutive hyperparameter updates will yield identical results with a single-batch approach.

• Step 3: Probe summarization. The final probe-level parameters from the second step are used to summarize the probes in each batch, yielding the final preprocessed data matrix.

The probe-level model

Let us first summarize the probe-level model for a fixed probeset with J probes across 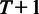arrays. The model assumes background-corrected, normalized and log-transformed probe-level data. The algorithm is based on a Gaussian model for probe effects, where the signal 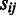of probe 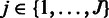in sample is modelled as a sum of the underlying target signal 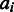and Gaussian mean and variance parameters 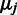, 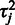that are directly interpretable as constant affinity 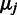and stochastic noise 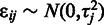, respectively:

(1)

In this model, the residual variance 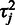of a probe with respect to the estimated target signal is used to quantify the reliability, or accuracy of the probe: the lower the variance, the more reliable the probe (23). In the following, let us outline the estimation procedure for the model parameters , , 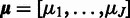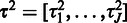. We start by estimating the variance parameters 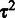of this model by following (23) and additionally incorporate Bayesian prior terms in the model to obtain a fully scalable algorithm. Affinity estimation (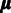) relies on the final probe-specific variance estimates. The final probeset-level summaries are obtained after estimating the probe-specific affinity and variance parameters.

Incorporating prior information of the probes

Estimation of the probe-specific variance parameters is based on probe-level differential expression signal 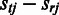between each sample 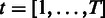and a randomly selected reference sample . Then, given Equation (1), the unidentifiable affinity parameters 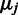cancel out, yielding 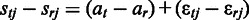. Following (23), let us denote , 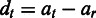and apply the vector notation 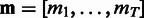, 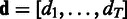. Then, the full posterior density for the model parameters 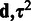is obtained with the Bayes’ rule as

(2)

The reference effects are marginalized out in the model, and the choice of the reference sample does not affect the final variance estimates 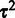(23). Assuming independent observations 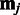, given the model parameters, and marginalizing over the 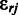, the likelihood term in Equation (2) is (23):

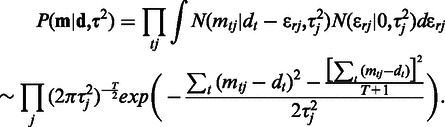(3)

With non-informative priors for 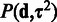, the posterior of Equation (2) would reduce to maximum-likelihood-estimation of Equation (3) as in (23). In this article, we take full advantage of the prior term to construct the scalable Bayesian online-learning version. Application of the prior forms the basis for sequential updates of the posterior in Equation (2). Assuming independent prior terms, a non-informative prior 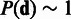, and inverse Gamma conjugate priors for 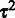with hyperparameters 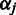and 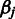(26), the prior takes the form

(4)

The posterior in Equation (2) is now fully specified given the likelihood [Equation (3)], the prior [Equation (4)], and the probe-specific hyperparameters , .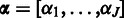

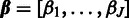Our primary interest is in estimating the probe-specific variances 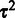, whereas 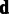is a nuisance parameter that could be marginalized out from the model to obtain more robust estimates of 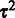. As no analytical solution is available, and sampling-based marginalization approaches would slow down computation, we obtain a single point estimate for the joint posterior in Equation (2) as a fast approximation by iteratively optimizing 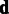and 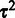. A mode for 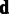, given 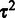, is searched for by standard quasi-Newton optimization (27). 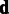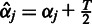Then, given , the variance follows inverse Gamma distribution with hyperparameters and 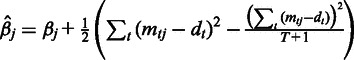. This specifies the prior

(5)

The point estimate for 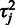is given by the mode at 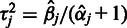. The parameters 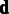and 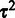are iteratively updated until convergence ( 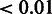change in parameter values in our experiments). The inverse Gamma hyperparameters corresponding to the final 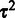can be retrieved as 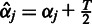and .

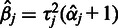Online-learning of variance hyperparameters

The aforementioned formulation allows incorporation of prior information of the probes in the analysis and sequential updates where the updated hyperparameters 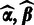from the previous batch provide priors for the next batch through Equation (2) and the prior in Equation (4). In the absence of prior information, we shall give equal weight for all probes 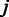at the first batch by setting 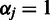; 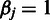for all 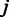. The final probe-level hyperparameters are obtained by updating 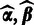with new observations at each batch until scanning through the complete data collection.

Affinity estimation

The remaining task after learning the probe-specific variances 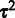is to estimate the probeset-level signal 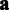and probe affinities 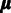in Equation (1). Unidentifiability of probe affinities is a well-recognized issue in microarray preprocessing (15), and further assumptions are necessary to formulate an identifiable model. A standard approach, used in the widely used RMA algorithm (15) is to assume that the probes capture the underlying signal correctly on average and the probe affinities sum to zero: 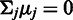. We propose a more flexible probabilistic approach where this hard constraint is replaced by soft priors that keep the expected probe affinities at zero but allow higher deviations for the more noisy probes that have a higher residual variance 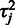. To implement this, we apply a Gaussian prior 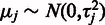for the affinities. This allows greater affinity values for the more noisy probes, which yields a better fit between the probeset-level signal estimate 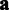and the less noisy probes with smaller 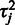and corresponds to the assumption that probes with increased or decreased affinities are likely to have the highest residual variance. This is supported by previous observations that probes with higher signal levels tend to have also a higher variance (28); on the other hand, it has been suggested that intensities in low affinity probes may be saturated by background noise (29). Our model accommodates both of these observations. Alternatively, the affinity priors could be determined based on known probe-specific factors, such as GC-content, which is a key element in probe affinity estimation in the GC-RMA algorithm (16). As probe performance is affected by a number of factors, however, we prefer the data-driven approach, which can accommodate noise from various, potentially unknown sources. This model yields a preliminary estimate for the probeset-level summaries. Based on Equation (1), we have 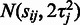. A maximum-likelihood estimate for 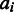is obtained as a weighted sum of 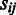over the probes 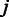, weighted by the inverse variances: 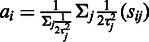. The corresponding maximum-likelihood estimate for 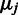at sample is then given by . 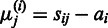Averaging of the affinity estimates across multiple samples yields the maximum-likelihood estimate for the affinities .

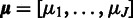Probe summarization

The final affinity and variance estimates can be used to summarize the probes according to Equation (1). The probeset-level signal 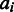is now readily obtained by Equation (1) as the weighted sum of over the probes 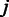, weighted by the inverse variances: .

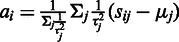Alternative approaches for scalable pre-processing

Alternative approaches for scalable preprocessing can be classified in (i) traditional single-array preprocessing methods and (ii) frozen multi-array techniques. In single-array algorithms, pre-processing is performed separately for each array. Such approaches are fully scalable but cannot combine probe-level information across multiple arrays, limiting their accuracy compared with multi-array procedures (14). We include the MAS5 algorithm (18) as the reference as one of the most well-known single-array pre-processing techniques. The frozen multi-array techniques include the refRMA (19) and fRMA (20) algorithms. To our knowledge, fRMA (20), which incorporates ideas from refRMA (19), is the only available algorithm for scalable multi-array preprocessing of large-scale microarray collections. The fRMA is based on a standardized database of pre-calculated probe effects, which are applied to pre-process new arrays. The estimation procedure for probe effects is not scalable, however, and fRMA is currently readily applicable to only three Affymetrix platforms for which the pre-calculated probe-effect terms are available. In addition to the standard ‘single-array’ fRMA model, we consider a second variant, which includes an additional model for batch effects (fRMA-batch). This incorporates additional experiment-specific information to the analysis, which cannot be used by the other methods. Although this can improve pre-processing performance, batch information is not necessarily available for heterogeneous microarray collections, and its incorporation will set additional requirements on the application of the fRMA-batch procedure. Finally, we include in the comparisons the widely used RMA algorithm (15). In contrast to the other approaches considered in this work, RMA is not fully scalable, but the RMA pre-processed version of the human gene expression atlas data set (5) is readily available, and as one of the most widely used standard pre-processing algorithms, it is a relevant reference model.

Data

We investigate the model performance by comparisons to alternative pre-processing methods based on standard benchmarking procedures with AffyComp spike-in data sets (25) and a large-scale human gene expression atlas (5).

AffyComp spike-in experiments

The AffyComp website [http://affycomp.biostat.jhsph.edu; (25)] provides standard benchmarking tests for microarray pre-processing based on spike-in experiments on the Affymetrix HG-U95av2 and HG-U133A_tag platforms. The tests quantify the relative sensitivity and accuracy of a pre-processing algorithm based on known target transcript concentrations. We focus here on the scalable MAS5, fRMA and RPA algorithms, as most other methods at the AffyComp website have been designed for moderately sized data sets and have therefore a different scope than the scalable approaches. However, fRMA is not applicable to the spike-in data sets, as pre-calculated probe-effect vectors are not available for the AffyComp platforms. Therefore, we have included the widely used RMA algorithm, which is widely used and has a closely related probe-level model. All arrays were pre-processed in a single batch with RPA. The score components in Figure 1 correspond to the following benchmarking statistics: (i) median SD across replicates; (ii) inter-quartile range of the log-fold-changes from genes that should not change; (iii) 99.9% percentile of the log-fold-changes if from the genes that should not change; (iv) 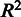obtained from regressing expression values on nominal concentrations in the spike-in data; (v) slope obtained from regressing expression values on nominal concentrations in the spike-in data; (vi) slope from regression of observed log concentration versus nominal log concentration for genes with low intensities; (vii) same for genes with medium intensities; (viii) same for genes with high intensities; (ix) slope obtained from regressing observed log-fold-changes against nominal log-fold-changes; (x) slope obtained from regressing observed log-fold-changes against nominal log-fold-changes for genes with nominal concentrations ≤2; (xi) area under the receiver operating characteristic (ROC) curve (AUC; up to 100 false positives) for genes with low intensity standardized so that the optimum is 1; (xii) AUC for genes with medium intensities; (xiii) AUC for genes with high intensities; (xiv) a weighted average of the ROC curves 11–13 with weights related to amount of data in each class. For full details, see (25).

Figure 1.

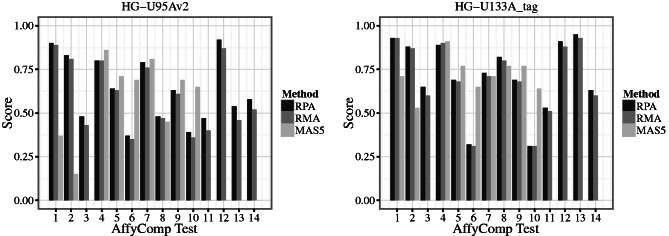
The benchmarking statistics for the AffyCompIII spike-in data for RPA, RMA and MAS5 for the HG-U95Av2 and HG-U133A_tag platforms. RPA and MAS5 represent fully scalable algorithms, and the standard RMA algorithm has been included as a benchmark, as its fully scalable extension, fRMA, is not available for the spike-in platforms. For clarity of presentation, we have transformed the scores 1–3 with so that the score value of 1 corresponds here to ideal performance at all 14 scores. For a full description of the 14 benchmarking components, see ‘Materials and Methods’ section.

Human gene expression atlas

We have selected for comparisons a reasonably large, well-annotated and quality assessed microarray data set including 5372 human samples from a versatile collection of 369 cell and tissue types, disease states and cell lines from 206 public experiments and 162 laboratories, measured with the Affymetrix HG-U133A microarray (5). The biological groups are of varying sizes and include 150 classes with only one sample (singleton classes); the annotations describing the group of each sample in the data set can be retrieved from the ArrayExpress archive (accession number: E-MTAB-62) (http://www.ebi.ac.uk/gxa/experimentDesign/E-MTAB-62). This data set is ideal for benchmarking of scalable preprocessing methods, as the alternative fRMA pre-processing model depends on the availability of pre-calculated probe effect terms, which are available for this platform. Moreover, sufficient sample metadata is available to include batch effects in the fRMA model. In addition, despite the heterogeneous origin of the data set, which made it unfeasible to obtain ‘batches’ in strictly the same manner as defined in (20), we could approximate them with the following approach. For each array within each experiment in the data set, we retrieved the creation date of the CEL file from its HEADER section, under the DatHeader TAG, and assigned to the same batch those arrays from the same experiment (and laboratory) that were scanned on the same day. Thus, it was possible to assess the two available versions of fRMA, the ‘single-array’ and ‘batch-of-arrays’. Moreover, the sample size allows comparisons with the standard and widely used RMA algorithm (15). In addition to the standard Affymetrix probe sets, we have included in the comparisons alternative probe sets based on updated Ensembl gene mappings available through the hgu133ahsensgcdf (14.1.0) annotation package (30). The reference probe effects for fRMA and the alternative mapping of probes to genes were built with frmaTools (21).

RESULTS

We assess the performance of the new algorithm by investigating the scalability and parameter convergence of the model and by comparisons to alternative approaches based on standard AffyComp benchmarking experiments based on spike-in data sets as well as sample classification and correlation of technical gene replicates across a large-scale human gene expression atlas. For details of the data and experiments, see ‘Materials and Methods’ section.

Scalability and parameter convergence

Ideally, the online-learning procedure is expected to yield identical results with the single-batch algorithm. We confirmed this by comparing the results obtained with the single-batch and online-learning versions of RPA at a moderately sized data set of 300 randomly selected samples. The probeset-level signal estimates correlated to a high degree (Pearson correlation 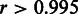; P < 10⁻⁶) between the single-batch and online-learning versions. The results were also robust to varying batch sizes of 20, 50, 100 and 300 samples; the probeset-level summaries obtained with these batch sizes were highly correlated (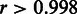; P < 10⁻⁶). In further experiments, we use a batch size of 50 samples. The high correspondence between the single-batch and online-learning models and between the different batch sizes confirms the technical validity of the implementation. Parameter convergence in general depends on the versatility of the data collection and the overall probe-specific noise, which can vary between probesets. More versatile data collections that cover a number of different biological conditions are in general more informative of probe performance than smaller data sets (6,20). For certain probesets, the probe parameters start to convergence only after 2000–3000 samples, indicating that the sample sizes of ∼1000 arrays typically applied with fRMA (20,21) may in some cases be too low to ensure convergence (Supplementary Figure S1). Although our model is applicable to data collections of any size, it provides favourable performance compared with the alternatives including the standard RMA algorithm, already on the moderately sized data sets as demonstrated by the AffyComp spike-in experiments with 42 (HG-U133A_tag) and 59 and (HG-U95Av2) samples.

The scalability of Online-RPA was investigated by pre-processing up to 20 000 HG-U133A CEL files from ArrayExpress. The model scales up linearly with respect to sample size (Supplementary Figure S2), with 8 h for 20 000 CEL files on a Z400 desktop with four 3.06 GHz processor cores.

Spike-in experiments

The Figure 1 summarizes the 14 AffyComp benchmarking tests for MAS5, RMA and RPA. Comparisons to further pre-processing algorithms are available on the AffyComp website (http://affycomp.biostat.jhsph.edu/AFFY3/comp_form.html). RPA outperformed RMA in 13 and 11 tests (of 14) on the HG-U95Av2 and HG-U133A_tag data sets, respectively (Figure 1), in particular with respect to bias (tests 5–10; Supplementary Figure S3) and the true positive/false positive detection rate, quantified by AUC/ROC analysis (tests 11–14); the differences between RPA and the other methods were particularly salient with low concentration targets (Figure 2). In the other tests, RPA and RMA had comparable performance. Interestingly, MAS5 had the smallest bias (tests 5–10), although RPA and RMA in general outperformed this method in the other tests, and in certain tests, such as ROC/AUC analysis (tests 11–14), MAS5 failed to distinguish the spike-in transcripts from noise. At the AffyComp benchmarking tests, RPA was in general outperformed by certain methods, including the Factor Analysis for Robust Microarray Summarization (FARMS) (31) and GCRMA (16). These methods have a more limited scalability than RPA, however, and hence a different scope. In summary, RPA had a similar or improved pre-processing performance in spike-in data sets compared with the standard RMA and Microarray Suite 5.0 (MAS5) algorithms, and a wider scope than the only scalable probe-level alternative, fRMA, which is not available for the spike-in platforms (21).

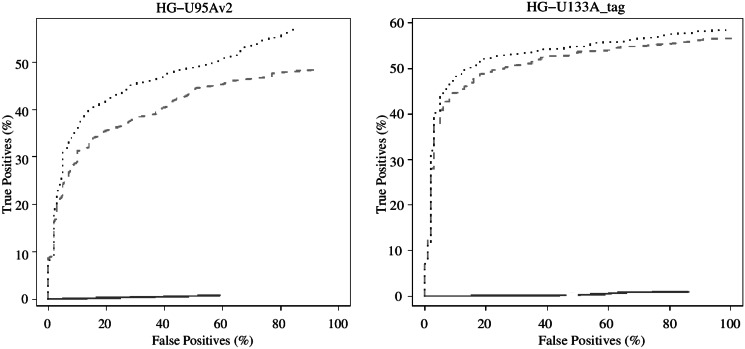
Figure 2.

Average ROC curves for low-abundance targets with nominal concentrations at most 4 picoMolar and nominal fold changes at most 2 in the AffyCompIII spike-in data for MAS5 (solid line), RMA (dashed line) and RPA (dotted line) on the HG-U95Av2 (left) and HG-U133A_tag (right) platforms. The figure has been adapted from AffyCompIII comparison Figure 5C. For details, see (25).

Classification performance

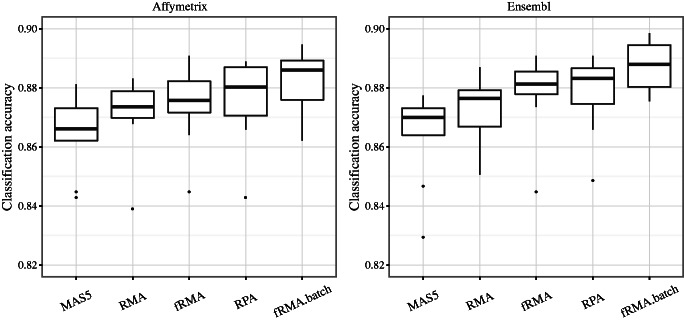
We investigated the sample classification performance in the human gene expression atlas of 5372 samples from 369 cell and tissue types, disease states and cell lines (5); (Figure 3). A random forest classifier (32) was trained to distinguish between these classes based on 1000 randomly selected probe sets and 500 trees at 10 cross-validation folds, where the data were split into training (90%) and test (10%) sets. The singleton classes (150 samples) were excluded. The comparisons were performed with both the standard Affymetrix probe sets and alternative probesets based on the Ensembl Gene identifiers. RPA outperformed RMA and MAS5 (P < 0.05; paired Wilcoxon test). Differences between RPA and fRMA were not significant, and the fRMA with batch effects (fRMA-batch) outperformed the other methods (P < 0.05). However, fRMA and fRMA-batch have a considerably more limited scope than Online-RPA. For further details on the data, class and batch definitions, see ‘Materials and Methods’ section.

Figure 3.

Classification performance in Lukk et al. (5) data set for the comparison algorithms. The 5372 samples were classified into 369 cell and tissue types, and after excluding the singleton classes, the classification performance was quantified by random forest classifier based on 10-fold cross-validation. Online-RPA outperforms RMA and MAS5 (P < 0.05). Differences between RPA-online and fRMA are not significant, and fRMA-batch outperforms the other methods (P < 0.05).

Correlation between technical gene replicates

The standard Affymetrix arrays contain multiple probesets for certain transcripts. As the final benchmarking test, we compared the probeset-level summaries for such technical gene replicates on the Lukk et al. (5) human gene expression atlas as in (23,33). Pearson correlation was calculated for each Affymetrix probeset pair sharing the same EnsemblID (Bioconductor package hgu133a.db). The average correlations over all pairs were as follows: MAS5 0.46, RMA 0.53, fRMA 0.51, fRMA.batch 0.55 and RPA 0.54. The differences between the methods were significant (paired Wilcoxon test P < 0.01). In this comparison, RPA outperformed MAS5, RMA and fRMA (Supplementary Figure S4).

Frozen parameter estimates

A frozen RPA (fRPA) model with fixed probe effects can be constructed analogously to refRMA (19) and fRMA (20). In this model, probe effects are estimated with an appropriate reference training set and then applied to pre-process new arrays. The advantage of frozen methods is that the pre-processing will consistently yield the same results, regardless of the other arrays in the processed set, and the data collection can be incrementally accumulated without the need to jointly pre-process the whole collection whenever new samples are added (19,20). Our fully scalable algorithm now makes it possible to estimate probe effects from a considerably larger reference training set than in fRMA. To assess the frozen version in the context of a smaller study, we derived RPA probe parameters from the Lukk et al. (5) data set, which has 5372 samples on Affymetrix HG-U133A platform, and applied these parameters (Supplementary data set 1) to pre-process the Symatlas data (34) (accession number: E-AFMX-5), which has 158 samples from 79 human tissues and cell types, each with two biological replicates. A best match for each sample was identified between the two sets of biological replicates based on Spearman correlation, and match between samples from the same tissue was considered a correct match. A jackknife analysis, where 20% of the probesets were randomly selected for the analysis at each iteration, yielded the following average classification performance across 1000 iterations: MAS5 (71.1%), RMA (90.69%), RPA (91.02%), fRMA (91.47%), fRPA (91.9%). The differences were significant (paired one-sided Wilcoxon test, P < 10⁻⁶).

DISCUSSION

The lack of scalable preprocessing techniques has formed a bottleneck for large-scale meta-analyses of contemporary microarray collections. High memory requirements of the standard pre-processing techniques for short oligonucleotide arrays have limited their applicability to moderately sized data sets with at most a few thousand samples. The frozen RMA (20) can be used to preprocess larger collections, but its applicability is currently limited to only a few Affymetrix platforms (HG-U133Plus2.0, HG-U133A, MG-430 2.0, MG-430A 2.0, HuGene-1.0-st-v1, and HuEx-1.0-st-v2) (21,22), as it requires pre-calculated calibration sets that are not available for most platforms. The ArrayExpress database contains dozens of additional short oligonucleotide platforms that each cover hundreds of studies and thousands of samples, including Arabidopsis (ATH1-121501), Human (HG-U95A; HG-U95Av2), Mouse (MG-U74Av2), Rat (RG-U34A; RAE230A, Rat2302), Drosophila (Drosophila-2), Yeast (Yeast-2; YG-S98), Barley (Barley-1), Porcine (Porcine), Rice (Rice), Zebrafish (Zebrafish) and so forth. In total, >200 distinct short oligonucleotide platforms from Affymetrix, Nimblegen and Agilent for gene expression, exon analysis and phylogenetic profiling are available, and these data collections are rapidly accumulating as journals routinely require the deposition of raw data in public repositories, and microarrays currently remain the major source of new data submissions (6). Hence, fRMA and other frozen methods have a considerably more limited scope than our model that can be used to preprocess data collections of any size from all these platforms. Although certain methods, such as FARMS (31) and GCRMA (16) with more detailed probe-level models outperformed RPA in spike-in experiments, their scalability and hence the scope are more limited.

We have introduced the first fully scalable online-learning algorithm that overcomes the key scalability limitations of the current pre-processing techniques and can extract and use individual probe effects across very large microarray collections by learning probe-level parameters based on sequential hyperparameter updates at small consecutive data batches. This provides novel tools to take advantage of the full information content in contemporary microarray data collections. With nearly a million arrays in the ArrayExpress database, being able to combine and analyse very large sets of arrays together is a key challenge with a variety of applications ranging from gene expression profiling (1,5,11–13) to alternative splicing and phylogenetic profiling of microbial communities (8–10). The model extends the framework introduced in (23) by adding a model for affinity estimation and incorporating prior terms to achieve a scalable algorithm that is applicable to contemporary microarray collections that can involve tens of thousands of samples.

The new online-learning algorithm can be used as a standard pre-processing technique for short oligonucleotide collections of any size: in moderately sized data sets, it outperforms the standard RMA model, and, in particular, for many existing large-scale collections that cover a thousand or more arrays and hence approach the scalability limits of standard techniques, this remains the only available probe-level model. We have also demonstrated that frozen calibration sets can be derived with our method across considerably larger data collections than in the alternative fRMA model, which may lead to potentially improved pre-processing performance also on those platforms where alternative frozen methods are available. Although our previous work (23) demonstrates that the proposed probe-level model can improve comparability also across platforms, our model is primarily intended for meta-analysis within a single platform as different platforms introduce different biases that are more challenging to model (3,4). The RPA Bioconductor package provides standard routines for preprocessing Affymetrix CEL files, which present a major source of microarray data in public repositories. In addition, general-purpose analysis routines are available, making the model applicable to the over 200 short oligonucleotide platforms listed in ArrayExpress. Although application on other than standard Affymetrix CEL files will require some more effort as background correction and normalization have to be carried out in separate steps with dedicated tools, we have already used the standard RPA in this way to pre-process custom Agilent HITChip microarrays for which no other probe-level pre-processing algorithms are currently available (35). We are looking forward to add routines for further platforms in future versions of the package.

In contrast to the alternatives Online-RPA is applicable to all short oligonucleotide platforms, as its application does not depend on pre-calculated probe effect terms. The model scales up linearly with respect to sample size, with 8 h running time for 20 000 CEL files in our experiments. The running time could be further accelerated by optimizing the implementation, using more efficient processors and parallelizing with multiple cores (24). As described in ‘Materials and Methods’ section, the affinity estimates are calculated as a post-processing step, following weighted averaging of the probes based on the estimated probe-specific variances. Interestingly, we noticed that incorporating the affinity estimates in the final probeset-level summaries did not significantly improve the performance compared with weighted averaging of the probes based on the probe-specific variance estimates provided by the model. This highlights the importance of modelling probe-specific stochastic noise parameters and indicates that the application of fixed affinity terms in probe summarization could be omitted to speed up computation without compromising pre-processing performance. Both options are available with a comparable performance; the latter option has been used for the experiments in this article. The probe-specific affinity and variance estimates could also be used to investigate the relative contributions of different probe-level noise sources both within and between platforms to guide probe design and analysis.

The widely used RMA algorithm can be seen as a special case of our single-batch model, assuming that all probes within a probeset have identical variances and the affinities sum to zero. The recent scalable extension, fRMA (20), has a more detailed model for probe effects. Although RPA was comparable with the standard fRMA algorithm, the fRMA-batch, which uses additional sample metadata, outperformed RPA. The modelling of batch effects in fRMA is only possible, however, when sufficient sample metadata is available, which is not always the case with large and heterogeneous microarray collections. Moreover, batch effects could be modelled as a separate step as suggested previously (36,37). However, comparison of the various modelling techniques for batch effects is out of the scope of the present work. In analogy to fRMA, our model also allows the utilization of estimated model parameters as priors to pre-process further data sets. This can provide the advantages of single-chip methods and fRMA of not having to recompute the whole pre-processing procedure when new arrays are included in the data collection. If probe parameters from previous studies are used as priors to preprocess new samples in our model, this will correspond to analysing the new samples together with the previous ones in a single batch and the parameters will converge more rapidly. Providing frozen parameter estimates can not only speed up computations but also allow reproducible analysis of single arrays for diagnostic and other purposes, as suggested in (20), as the probe summaries obtained with frozen probe parameters do not depend on the other arrays in the preprocessed data set. Our fully scalable model allows the estimation of probe effects from larger data collections than in fRMA. The favourable performance of fRPA in our experiments based on a reference training set of 5372 samples suggests that estimating probe effects from a larger data collection may lead to improved pre-processing performance. A more comprehensive validation with multiple platforms and benchmarking measures is needed, however, to compare the general performance and relative merits of fRPA and fRMA. A full development and validation of fRPA calibration sets for the most popular platforms is a promising direction for further work.

Probe performance is affected by RNA degradation, non-specific hybridization, GC- and SNP-content, annotation errors and other, potentially unknown factors. Although modelling of the probe effects have been shown to yield improved probeset-level estimates of the target signal (15,17), the various sources of probe-level noise and their relative contributions remain poorly understood. With the fully scalable extension, the analysis of probe performance can now be based on the most comprehensive data collections. As such, Online-RPA can assist in nailing down individual probes affected by various sources of noise and biases, giving tools to guide microarray pre-processing and probe design in future studies and industry standards [19].

CONCLUSION

The introduced online-learning algorithm is the first fully scalable general-purpose method for probe-level pre-processing and analysis of short oligonucleotide collections. It can be applied to data sets of any size, ranging from moderately sized standard data sets to very large gene expression atlases involving tens or hundreds of thousands of samples. In contrast to the alternatives, the model is readily applicable to all short oligonucleotide microarray platforms, and it compares favourably to the currently available alternatives. This provides new tools to scale up investigations to take full advantage of the information content in the rapidly expanding data collections. The implementation is freely available through R/Bioconductor at http://bioconductor.org/packages/devel/bioc/html/RPA.html.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Figures 1–4 and Supplementary Data Set 1.

FUNDING

Academy of Finland [256950 to L.L., 127575, 218591 to L.L.E.]; Alfred Kordelin foundation (to L.L.); Ramón Areces Foundation [to A.T.]; European Community’s Seventh Framework Programme [FP7/2007-2013], ENGAGE Consortium [HEALTH-F4-2007-201413 to J.R.]. Funding for open access charge: Academy of Finland [256950 to L.L.].

Conflict of interest statement. None declared.