Genetic Algorithm Reveals Energy-Efficient Waveforms for Neural Stimulation

Abstract

Energy consumption is an important consideration for battery-powered implantable stimulators. We used a genetic algorithm (GA) that mimics biological evolution to determine the energy-optimal waveform shape for neural stimulation. The GA was coupled to NEURON using a model of extracellular stimulation of a mammalian myelinated axon. Stimulation waveforms represented the organisms of a population, and each waveform’s shape was encoded into genes. The fitness of each waveform was based on its energy efficiency and ability to elicit an action potential. After each generation of the GA, waveforms mated to produce offspring waveforms, and a new population was formed consisting of the offspring and the fittest waveforms of the previous generation. Over the course of the GA, waveforms became increasingly energy-efficient and converged upon a highly energy-efficient shape. The resulting waveforms resembled truncated normal curves or sinusoids and were 3–74% more energy-efficient than several waveform shapes commonly used in neural stimulation. If implemented in implantable neural stimulators, the GA optimized waveforms could prolong battery life, thereby reducing the costs and risks of battery-replacement surgery.

I. Introduction

Implantable neural stimulators assist thousands of individuals with neurological disorders. These devices are battery-powered, and when the battery is depleted, the entire device must be replaced through an invasive and expensive surgery. The frequency of battery-replacement surgeries could be reduced by increasing the energy efficiency of stimulation, which is dependent upon stimulation parameters such as pulse width (PW) and waveform shape.

The relationship between energy efficiency and PW of rectangular pulses is well documented [1–5], but the relationship between energy efficiency and waveform shape is not as straightforward. The energy-optimal waveform shape cannot be determined analytically due to the complexity and non-linearity of the equations that define the excitable membrane. Also, since the number of possible waveform shapes is infinite, the energy-optimal shape cannot be determined through a “brute force” method of testing every possibility. For problems such as these, solutions may be found using numerical methods known as global optimization algorithms. The goal of this study was to seek the energy-optimal waveform shape for neural stimulation using a genetic algorithm (GA). This algorithm was applied in a computational model of extracellular stimulation of a mammalian myelinated axon for a wide range of PWs. The outcome of these simulations was a set of waveform shapes that were more energy-efficient than several waveforms commonly used in neural stimulation. The GA waveforms could prolong the lifetime of implantable stimulators, thus reducing the costs and risks of battery-replacement surgery.

II. Methods

A. Overview of Genetic Algorithms

Genetic algorithms seek optimal solutions through a process that mimics biological evolution. The first generation of a GA begins with a population of candidate solutions, which are analogous to organisms, and the “genes” of each solution are the parameters that define the solution. Then, the fitness of each solution is evaluated with a cost function specific to the optimization problem. Next, the solutions “mate” with one another, producing offspring solutions that possess a combination of the parents’ genes. Then, the genes of the offspring are mutated. Both the mating process and mutations promote a wide exploration of the solution space to increase the chance of discovering the global optimum rather than a local optimum. At the end of each generation, the population is partially or entirely replaced by the offspring. Over time beneficial genes remain in the gene pool of the population while unfavorable genes are weeded out. This process of selection and mating is repeated either for a fixed number of generations or until the solutions converge upon a fitness value, and the solution with the greatest fitness is the resulting estimate of the optimum solution.

B. Specific Implementation of the Genetic Algorithm

We designed a GA to seek the energy-optimal waveform shape in a computational model of nerve fiber stimulation. Simulations of extracellular stimulation of a single myelinated mammalian peripheral axon were run in NEURON [6] using the MRG model (fiber diameter = 11.5 μm) [7]. Stimulation was delivered through a current-regulated point source located within a conductive medium (300 Ω-cm) at a distance of 1 mm directly above the center node of the fiber.

Each generation of the GA consisted of a population of 50 stimulation waveforms with fixed pulse width (PW). Waveforms were discretized in time using a time step equal to that of the computational model (dt = 0.002 ms), and the amplitude at each time step was represented by a gene (e.g. the genes of an increasing ramp waveform would increase in value at a constant rate [0 1 2…]). The values of the genes of the waveforms of the first generation were chosen randomly from a uniform distribution between 0 and two times the cathodic threshold of stimulation with a rectangular waveform at equivalent PW. The cost function, F, of each waveform equaled the energy consumed by the stimulation pulse, E, plus a considerable penalty if the waveform failed to elicit an action potential:

$$F=E+\mathit{Penalty}$$ (1)

$$E={\int }_0^{PW}P(t)dt={\int }_0^{PW}{I}^2(t)Z(t)dt=dt\ast \sum _{n=1}^N{I}_n^2{Z}_n$$ (2)

where P is instantaneous power, t is time, I is current, Z is load impedance, and N is the number of discretizations (genes) of a stimulation waveform. In our simulations, the output impedance was assumed to be linear:

$$E\propto dt\ast \sum _{n=1}^N{I}_n^2$$ (3)

Penalty was 0 if the waveform elicited an action potential, and 1 nJ/ohm (2 to 3 orders of magnitude larger than E) if it did not.

F was not used to select parents for mating but was used to select waveforms to survive to the next generation. Each waveform had an equal chance of being selected as a parent to promote a wide search of the solution space. Each offspring was produced by combining the genes of two parents through two crossover points. Then, each gene was mutated by scaling the value by a random value chosen from a normal distribution (μ = 1, σ² = 0.025). Amplitudes were never allowed to be positive, thus restricting waveforms to monophasic cathodic pulses. At the end of each generation, all but the top 10 fittest waveforms (i.e. smallest F) in the population were replaced by offspring waveforms.

The GA was run multiple times using several different parameters. To determine whether the outcome of the GA was dependent on PW, we ran the GA for a wide range of PWs (0.02, 0.05, 0.1, 0.2, 0.5, 1, and 2 ms). For each PW, the GA was run for 5 independent trials, each for 10,000 generations and with different initial populations. For each trial, we recorded the most energy-efficient waveform of the final generation (GA waveform) and the energy consumed by the most energy-efficient waveform of each generation (generation energy). For each PW, we calculated the mean and standard error of the energy consumed by the GA waveforms across trials, and these values of energy were used to construct an energy-duration curve. The GA energy-duration curve was compared to energy-duration curves of waveform shapes commonly used in neural stimulation: square, increasing/decreasing ramp, increasing/decreasing exponential, and sinusoid.

C. Population Model

The GA waveforms were tested in a model of a population of axons consisting of 100 parallel MRG axons (11.5-μm diameter) distributed uniformly within a cylinder with 3-mm diameter. Extracellular stimulation was delivered through a point source electrode located at the center of the cylinder. For each PW (0.02, 0.05, 0.1, 0.2, 0.5, 1, and 2 ms), 10 random axon populations were chosen. Then, for each population, input/output (I/O) curves of the number of fibers activated vs. energy consumed were constructed. Amplitudes were adjusted by scaling the entire waveform. For each I/O curve, the energy required to activate 50% of the entire population was calculated, and the means and standard errors of these values across the 10 axon populations were computed. I/O curves were also generated for the same populations using square, increasing/decreasing ramp, increasing/decreasing exponential, and sinusoid waveforms, and the energy efficiencies of these waveforms and the GA waveforms were compared.

III. Results

A. Genetic Optimization of Stimulus Waveform

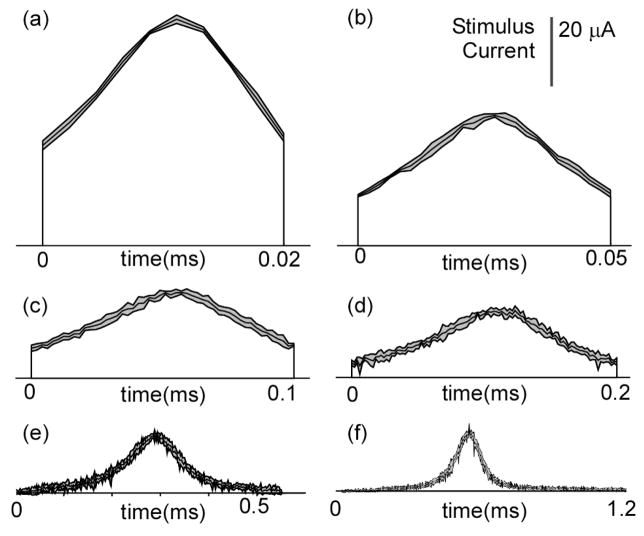
By the end of each trial, the GA had converged upon a highly energy-efficient waveform shape. The generation energy was within 1% of the final generation energy by 5000 generations for PW ≤ 0.5 ms and by 9000 generations for PW = 1 and 2 ms. For each PW, the GA waveforms were very similar across trials, and across PWs the shapes of the GA waveforms were also quite similar (Fig. 1). For PW ≤ 0.2 ms, the shapes of these waveforms resembled truncated normal curves or sinusoids, with the peak near the middle of the pulse. For PW ≥ 0.5 ms, the shapes of the GA waveforms also resembled truncated normal curves or sinusoids but with leading and/or trailing tails of negligible amplitude. As PW increased, the smoothness of the GA waveforms decreased.

Fig. 1.

Energy-optimal stimulation waveforms determined with a genetic algorithm for different PWs: 0.02, 0.05, 0.1, 0.2, and 0.5 ms (a–e, respectively). f) Waveforms for PW = 1 and 2 ms combined. For PW ≥ 0.5 ms, the peaks of the waveforms were aligned and leading/trailing tails of low amplitude were excluded for plotting. Curves within the gray regions represent the means of the resulting waveforms across 5 trials, and the upper and lower curves define 95% confidence intervals.

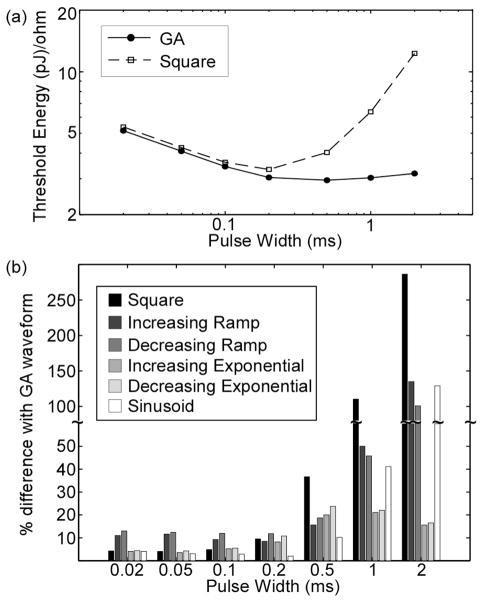
Compared to commonly-used waveforms in neural stimulation, the GA waveforms were more energy-efficient for all PWs. The energy-duration curve of the GA waveforms was concave up (Fig. 2a), and the minimum energy of this curve was less than the minimum energies for the other waveform shapes. For PW ≤ 0.2 ms, the GA waveforms were slightly more energy-efficient (<15%) than the other waveform shapes (Fig. 2b). Of these other shapes, the shape that most resembled the GA waveforms—the sinusoid—was the most energy-efficient. Between PW = 0.2 ms and 0.5 ms, the differences in energy-efficiency between GA waveforms and the other shapes increased considerably for all shapes, and the differences increased further with PW for all but the exponential waveforms.

Fig. 2.

Energy efficiency of the GA waveforms in single axon model. a) Energy-duration curves for GA waveforms (mean, n=5; SE was negligible) and square waveform. b) Energy efficiency of GA waveforms compared to waveform shapes commonly used in neural stimulation.

Results of the GA were mostly insensitive to variations in the algorithm parameters. Neither doubling nor halving the number of waveforms in each generation or waveforms that survived to the next generation had substantial effects on the shape of the GA waveforms or their energy efficiencies (< 0.1% difference). As well, the amplitudes of the waveforms in the initial generation were scaled between 0.4 – 1.6 times the original amplitudes. Scaling factors < 0.6 resulted in initial waveforms that were all below threshold, and the GA did not produce an energy-efficient waveform. However, scaling factors > 0.8 had little effect on the shape and energy efficiency (<0.1% difference) of the GA waveforms. Further, the variance of the normal distribution used in mutations was varied between 0 – 4 times the original variance. With variance = 0 (no mutations), the GA quickly converged on an energy-inefficient waveform. For all other variances, the GA resulted in approximately the same shape and energy efficiency (<0.4% difference) of the GA waveform. One factor that had a substantial effect on energy efficiency—but not the overall shape of the GA waveform—was the time step, dt. Smaller values of dt resulted in more energy-efficient GA waveforms for PW ≤ 0.5 ms, as a result of finer resolution of waveform shape; and less energy-efficient GA waveforms for PW ≥ 1 ms, due to the increased difficulty of generating smooth waveforms.

B. Population Model

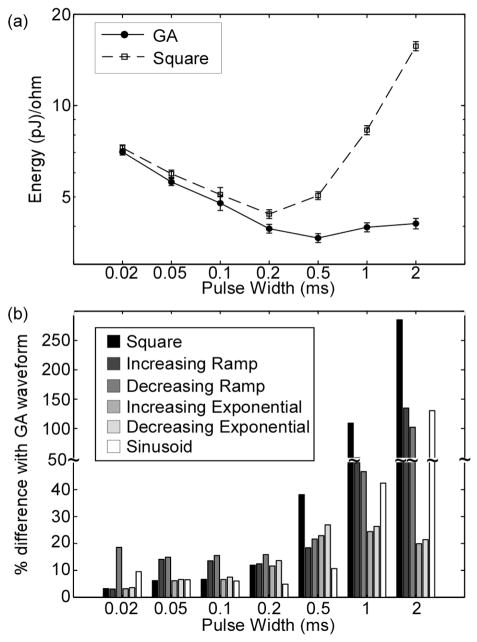
As in the single axon model, the GA waveforms were more energy-efficient than the commonly-used waveform shapes in the population model. The most energy-efficient GA waveform for each PW was used in the population model. The resulting energy-duration curve of the GA waveforms was concave up with the minimum at PW = 0.5 ms (Fig. 3a). The GA waveforms were more energy-efficient than the commonly-used waveform shapes for all PWs, and differences in energy efficiency were approximately equal to the differences in the single axon model with a few exceptions (Fig. 3b). These results demonstrated that the superior energy efficiency of the GA waveforms compared to the other waveform shapes was independent of the position of the electrode with respect to the axon.

Fig. 3.

Energy efficiency of GA waveforms in population model. a) Energy-duration curves for activation of 50% of axons in randomly-selected populations (mean +/− SE; n=10). b) Energy efficiency of GA waveforms compared to waveform shapes commonly used in neural stimulation (mean, n=10; SE was negligible).

IV. Discussion

A genetic algorithm was used to seek the energy-optimal waveform shape for neural stimulation. In an optimization problem where analytical methods were impossible and brute force methods were impractical, the GA succeeded in revealing highly energy-efficient waveforms. The resulting waveforms of the GA resembled truncated normal distributions or sinusoids and were more energy-efficient than waveforms commonly used in neural stimulation. For short PWs, improvements in energy efficiency were small, but for long PWs, improvements were more substantial. With more energy-efficient waveforms, the lifetime of implantable stimulators could be extended, which would reduce the risks and costs of battery-replacement surgeries.

For many optimization problems, including the present problem, it is impossible to prove that a solution is globally optimal. However, the results of this study provide strong evidence that the GA waveforms are the most energy-efficient shapes. For all trials, the generation energy was within 1% of the final generation energy for >1000 generations, indicating that each trial had converged upon at least a locally-optimal solution. As well, for each PW, all 5 independent trials of the GA converged to approximately the same shape (Fig. 1) and the same energy efficiency (Fig. 2a). Across PWs, all GA waveforms resembled normal curves or sinusoids that were truncated at different points. Finally, variations in the parameters of the GA either had negligible effects on the solutions or resulted in less energy-efficient waveforms. Although these findings do not constitute a proof of the GA waveforms being globally optimal, they do suggest that the GA waveforms were more than just locally optimal.

Although the GA was mostly effective, a minor shortcoming was the lack of smoothness of the resulting waveforms. The GA waveforms were often jagged, leading to slight reductions in energy efficiency. The waveforms would likely have become smoother and more energy-efficient if the GA had run for a greater number of generations. The lack of smoothness was especially a problem for GA waveforms with long PWs on the leading and trailing tails with low amplitude. All GA waveforms with PW = 1 and 2 ms were still able to elicit an action potential when the tails were removed, indicating that the tails were superfluous (data not shown). However, the GA prevented the amplitude from reaching 0. The lack of smoothness of the GA waveforms with long PWs led to the energy-duration curve being concave up (Fig. 2a). Theoretically, as PW increased, the energy should have either continued to decrease or plateaued because any GA waveform generated at a given PW could be generated with a longer PW. Despite the lack of smoothness of the GA waveforms, the GA still revealed highly energy-efficient waveform shapes.

Several issues should be considered before the GA waveforms are implemented. As calculated in this study, the energy efficiency did not take into account the energy consumed by the electronic circuitry that would be required to generate the GA waveforms. When this circuitry is considered, the GA waveforms may not be energy-optimal. Another consideration is the charge efficiency of the GA waveforms. The charge and charge density delivered during a stimulus pulse are cofactors in tissue damage [8, 9] and electrode corrosion. If the GA waveforms required excessive charge, then they would not be clinically useful, no matter how energy-efficient they were. A third consideration is whether the GA waveforms would still be energy-efficient when delivered as one phase of a biphasic pulse. Clinically, neural stimulation is most often delivered as biphasic pulses. The charge recovery pulse can affect the threshold of the primary pulse, and it is unclear if changes in threshold are dependent on the waveform shape of the primary pulse. The GA could be run again with biphasic pulses to determine if the GA produces the same resulting waveforms.