Identity by Descent: Variation in Meiosis, Across Genomes, and in Populations

Abstract

Gene identity by descent (IBD) is a fundamental concept that underlies genetically mediated similarities among relatives. Gene IBD is traced through ancestral meioses and is defined relative to founders of a pedigree, or to some time point or mutational origin in the coalescent of a set of extant genes in a population. The random process underlying changes in the patterns of IBD across the genome is recombination, so the natural context for defining IBD is the ancestral recombination graph (ARG), which specifies the complete ancestry of a collection of chromosomes. The ARG determines both the sequence of coalescent ancestries across the chromosome and the extant segments of DNA descending unbroken by recombination from their most recent common ancestor (MRCA). DNA segments IBD from a recent common ancestor have high probability of being of the same allelic type. Non-IBD DNA is modeled as of independent allelic type, but the population frame of reference for defining allelic independence can vary. Whether of IBD, allelic similarity, or phenotypic covariance, comparisons may be made to other genomic regions of the same gametes, or to the same genomic regions in other sets of gametes or diploid individuals. In this review, I present IBD as the framework connecting evolutionary and coalescent theory with the analysis of genetic data observed on individuals. I focus on the high variance of the processes that determine IBD, its changes across the genome, and its impact on observable data.

The descent and ancestry of DNA

At a given location in the genome, the descent of DNA as described by Mendel’s first law (Mendel 1866) provides the framework for analyses of the genetic consequences of coancestry among individuals. This fundamental law of inheritance is phrased in probabilistic terms. In a diploid individual, at each location in the genome, a random one of the two homologous copies of the DNA at that location is the DNA copied to the offspring gamete. Additionally, all meioses are independent; the random choice is made independently for each offspring, independently in the two parents of an individual, and independently from generation to generation in an ancestral lineage.

DNA in different current gametes that is a copy of a single piece of DNA in some ancestral individual is said to be identical by descent or IBD from that ancestor. There is no absolute measure of IBD; IBD is always relative to some ancestral reference population. Many experimental or agricultural populations have a natural founding stock, as do some natural populations, and IBD may be measured relative to this founder population. More generally, IBD may be measured relative to the population at some past time point, with the implication that more remote coancestry of current gametes is ignored. In pedigrees, IBD is well defined relative to the specified founders of the pedigree. The fact of IBD does not depend on whether pedigree relationships are known. Specification of a pedigree relationship merely imposes a specific prior distribution on the probabilities of IBD among individuals and across the genome.

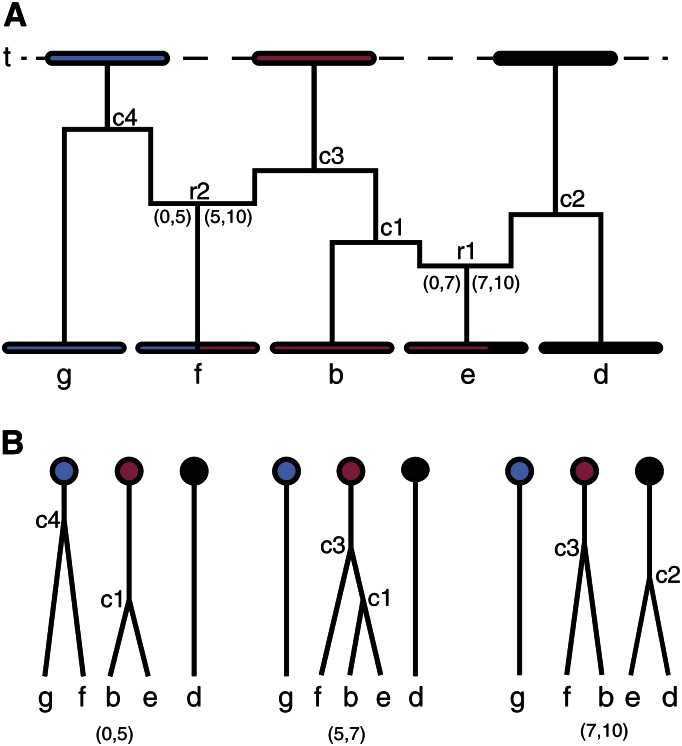
At a point in the genome, the coalescent ancestry of a sample of gametes (Kingman 1982) defines the partition of n gametes into the subsets that are IBD. The ancestral recombination graph or ARG (Hudson 1991; Griffiths and Marjoram 1996) is the most complete description of the ancestry of the DNA of a set of n gametes, defining the coalescents across the genome and hence the IBD partitions relative to any past time point. Conversely, the sequence of IBD partitions across the genome and over all time depths relative to which IBD may be defined determine the sequence of coalescents across the genome. Figure 1A shows the recent ARG ancestry of a DNA segment in n = 5 current gametes back to time point t. There are two recombination events in the recent ancestry of these gametes, at genome locations 5 and 7. Each recombination changes the IBD partition relative to time t. Specifically, in region (0, 5) the IBD partition is {(g, f), (b, e), (d)}; in (5, 7) it is {(g), (f, b, e), (d)}; in (7, 10) it is {(g), (f, b), (e, d)}. The ordering of the subsets, and the ordering of elements within them, is irrelevant. The corresponding coalescents are shown in Figure 1B.

Figure 1.

Partial ancestral recombination graph to reference time t, showing the successive IBD segments among five current gametes. The chromosome is 10 cM and indexed by a continuous range of positions from 0 to 10. The four coalescent events are marked as c₁ to c₄. Two recombination events occur in the ancestry of these chromosomes, at positions 5 and 7. These events are marked as r₁ and r₂.

Inheritance of segments of DNA

Generation to generation, DNA is inherited in large segments of order 100 centimorgans (cM). Over successive generations, recombination events break up these segments. In reverse time, recombination events change the coalescent ancestry of a sample of gametes and the IBD partitions relative to any specified past time point t (Figure 1). In populations with no natural founding time point, lengths of segments shared IBD between a pair of gametes provide a useful calibration of the time depth of the common ancestor to whom that IBD traces. For example, a time depth of 25 generations, resulting in a separation of 50 meioses, gives segments of expected length 2 cM. More generally, a separation of m meioses provides segment lengths that are exponentially distributed with mean 100/m cM.

Sved (1971) considered segments of genome unbroken by recombination descending to a pair of gametes from the most recent common ancestor (MRCA) of this segment. For example, in Figure 1, the segment (5, 7) descends unbroken to f and e from the MRCA at coalescent event c₃. Hayes et al. (2003) defined a segment to be IBD between a pair of gametes if it descends in this way unbroken by recombination. However, at any point in the genome, the MRCA of a pair of current gametes is within some segment of genome unbroken by recombination; thus, defining IBD in this way requires some choice of minimal segment length that is no less arbitrary than choice of a defining time depth t. Several recent authors in effect define IBD by a time depth such that pairwise IBD segments deriving from that time depth are long enough to be detectable given the available density of genetic marker or sequence data (Browning and Browning 2010; Huff et al. 2011). However, there is high variance in the exponentially distributed lengths of IBD segments deriving from a MRCA at a given time depth t.

The generalization to a set of gametes would be to define a given segment of genome in the given set to be IBD if and only if it has a single coalescent ancestry. In this case, IBD at any single point always occurs, and pointwise IBD is characterized by the length of the segment around the point that shares the identical coalescent ancestry. However, the segment shared by all of a set of gametes becomes shorter as more gametes are included. More importantly, the basic premise that IBD is an equivalence relation dividing a set of gametes into IBD subsets is violated if IBD is defined in terms of a shared segment length rather than a time depth. For example, in Figure 1, f and b are IBD over (5, 10), b and e are IBD over (1, 7), but f and e are IBD only over (5, 7). With, for example, a threshold length of 3, this last IBD between f and e would not be recognized, although it would be determined that f and b, and b and e were IBD in this region. While analysis of segments of DNA descending unbroken by recombination is an important tool, only the ARG relative to some time depth provides a consistent definition of an IBD process across the genome.

Coancestry and allelic associations

DNA that is IBD relative to some recent time point has very high probability of being of the same allelic type. As compared to individuals randomly chosen from the population, individuals who share DNA IBD at the locus or loci relevant to a phenotype will show similarity for that phenotype. Thus, phenotypic correlations among individuals result from IBD, and conversely allelic or phenotypic similarity provides evidence of IBD. Correlations in allelic type have long been used to measure relatedness among individuals (Wright 1922). Powell et al. (2010) argue that the definition of IBD relative to a time point is in conflict with coalescent theory (Kingman 1982) and propose definition of IBD in terms of current allelic correlations. However, these allelic correlations are a statistic reflecting coancestry rather than being that coancestry.

Linkage disequilibrium (LD) is the name given to associations in allelic type across linked loci. Associations due to coancestry result broadly from two causes. A new variant arising on a specific local haplotypic background creates a strong association (LD) with the alleles of that background. Eventually, the initial LD is broken down by recombination, but if the loci are tightly linked this may take thousands of generations. Second, there are associations due to population substructure. Random genetic drift will result in different allele frequencies in different subpopulations. Even if there is no LD within subpopulations, there will be allelic associations between loci in the combined population. This LD is also a reflection of coancestry: individuals within subdivisions are more closely related than are individuals in different subdivisions. As with allelic associations among individuals, LD is not IBD, but is a reflection of IBD.

Given genetic marker data on members of an extant population, IBD can be detected. A set of individuals sharing a haplotype that, due to its population frequency, is not expected to be shared by a set of individuals of this size randomly chosen from the population is evidence of IBD. The smaller the probability that this haplotype sharing would occur “by chance,” the stronger the evidence of IBD. Longer haplotypes (of length >1 Mbp, say) have lower population frequencies, and so, when shared, provide clearer evidence of more recent IBD. At shorter distances, LD becomes an important factor in assessing the population frequencies of observed haplotypes, and hence the evidence for IBD when these haplotypes are shared. Thus, at short distances LD becomes a confounding factor in the detection of IBD, and IBD of short segments of DNA cannot be detected from common SNP variation.

The scope of this review

In this review we focus only on within-species genetic variation and so the time depth of coancestry of interest is also that within species. The focus is on human populations, and our view of IBD is that of coancestry relative to some time depth. This time depth will depend on the population and the goal of the analysis, but will normally be <100 generations (see Rare variants in human populations). The remainder of this review is divided into four main sections.

In The Processes of Identity by Descent we consider the random processes that give rise to IBD itself. Specifically, we consider probabilities of IBD, models for the partition of gametes into IBD subsets, and the probability distributions of proportions of IBD genome and of lengths of IBD segments. Although we make links between IBD and the coalescent ancestry of a set of gametes, it is not possible to give a full description of coalescent theory (Kingman 1982; Hudson 1991; Griffiths and Marjoram 1996), nor to review evolutionary aspects of this theory such as those developed by Neuhauser and Krone (1997) and by Hein et al. (2005).

In Phenotypic Similarity and Allelic Variation we explore the relationship between IBD and the consequent phenotypic similarity of related individuals and consider measures of allelic variation and association in relation to coancestry and IBD. Our discussion of allelic correlations focuses on their use as measures of relatedness among individuals. We consider the pedigree-based numerator relationship matrix (Henderson 1976) and the corresponding data-based genetic relatedness matrix (Visscher et al. 2006). Although IBD is the foundation of phenotypic similarities at the population level as well as the individual level and has links to analyses of extant allelic associations in populations (Ardlie et al. 2002; Wellcome Trust Case Control Consortium 2007), we do not cover the extensive literature on population structure (Pritchard et al. 2000; Falush et al. 2003). Our focus is on measures of similarity among individuals, rather than on population-level measures.

In Inference of Relationships, Relatedness, and IBD Segments we consider the estimation of relationships and relatedness and the inference of IBD in individuals not known to be related. We do not cover estimation of admixture (McKeigue 1998) or inference of hybrids (Anderson and Thompson 2002) or the use of inferred ethnic ancestry in admixture mapping (Patterson et al. 2004; McKeigue 2005). The methods used in this area have many similarities to inference and use of inferred IBD segments. They differ in that, compared to IBD genome segments, the degree of haplotypic similarity within segments of given ethnicity is less, while the segments of a specific ethnic origin are typically longer. The focus of admixture analysis is to detect segments of genome of a specified ethnic ancestry in an individual, rather than shared ancestry among individuals.

Finally, in Use of Inferred IBD in Genetic Analysis we review the uses of inferred IBD in the analysis of genetic data both in pedigrees and in populations. This includes a review of genetic linkage mapping in terms of IBD and the use of coalescent approaches to fine-scale mapping (Gene mapping using IBD in pedigrees and Association and ancestry in fine-scale mapping). We review briefly the increasing literature on the use of observed allelic associations in the analysis of quantitative genetic variation (Association mapping and heritability) and the adjustments for coancestry needed to interpret these allelic associations (Adjusting for relatedness in population-based genetic mapping). We consider the direct use of IBD in mapping from population data (Population-based IBD mapping) and briefly review recent literature on the use of inferred IBD in analyses of population demographic history (Evolutionary and demographic inferences).

The Processes of Identity by Descent

In this section we assume that there is an accepted founder population relative to which IBD is to be measured, whether founder members of a defined pedigree or a population existing at some time point in history.

Sources of variance in identity by descent

The probabilistic process of Mendelian segregation results in variance, across loci, among individuals and over realizations of a population process. Before considering these processes in more detail, we consider a simple example to illustrate aspects of variation in IBD. First, consider Mendelian segregation at a single locus and within a defined pedigree. If the marginal probability of IBD between two gametes at a single genome location is ψ, the variance in realized IBD is ψ(1 − ψ), and the variance in the proportion of n such realizations that result in IBD is ψ(1 − ψ)/n. For example, at any genome location, a pair of maternal first cousins share their maternal genome IBD with probability 0.25. In a set of 120 first-cousin pairs, the expected proportion sharing genome IBD at a location is 0.25 and the standard deviation of that proportion is ∼0.04. In 5% of such sets of 120 pairs, the proportion may be as high as 33% or as low as 17%.

A second dimension is the genome. In terms of genetic distance, crossovers in the process of meiosis occur at a rate of 1/M or 1/100 cM: on average, 1 cM is ∼10⁶ bp. The outcomes of meiosis at nearby chromosomal locations are therefore strongly positively correlated. In a pair of first cousins, segments of IBD genome have an expected length of 25 cM. In a genome of length 3000 cM, the expected proportion of genome IBD is 0.25, and the standard deviation of that proportion is ∼0.04. In 5% of first-cousin pairs, the proportion may be as high as 33% or as low as 17%. For the variance of genome IBD between first cousins, the 3000-cM genome is “equivalent to” to 120 independent realizations.

The inbreeding coefficient of an individual is the probability that, at any point in the genome, it carries two IBD genes. To avoid confusion we use the classical term autozygosity for the event of IBD between the two homologs of an individual. The inbreeding coefficient of the offspring of first cousins is 0.0625. Consider a set of 120 individuals, each the offspring of a first-cousin marriage. At any location in the genome, the expected proportion who are autozygous is 0.0625 and the standard deviation is ∼0.022. In 5% of such sets the proportion may be as high as 10.5% or as low as 2%. In a genome of length 3000 cM, the expected proportion of genome IBD is 0.0625, and the standard deviation of that proportion is ∼0.018. In 5% of offspring of first-cousin marriages, the proportion may be as high as 9.8% or as low as 2.7%. Note that, whereas for the variance of IBD between cousins the genome is equivalent to 120 independent realizations, for the variance of autozygosity in their offspring this is no longer the case.

A third dimension is the population, in which not only autozygosity but also the inbreeding coefficient has variance. Consider first a population with a proportion α of offspring of independent first-cousin marriages and the remainder having negligible inbreeding coefficients. The mean inbreeding coefficient in the population is 0.0625α, and the standard deviation across population members is $0.0625\sqrt{\alpha \left(1-\alpha \right)}$. In a sample of n individuals from this population, the expected average inbreeding coefficient is 0.0625α, and the standard deviation of this average is $0.0625\sqrt{\alpha \left(1-\alpha \right)/n}$.

Finally, consider a population consisting of 30 sets of 4 offspring of independent first-cousin marriages. Now every individual has inbreeding coefficient 0.0625, but the population structure affects the variance in IBD. Instead of 120 independent realizations, we now have 30. Within each set, there is no IBD with probability 3/4, while with probability 1/4, each of the 4 offspring has probability 1/4 of autozygosity independently of its siblings. The standard deviation of the proportion of the 120 individuals who are autozygous at a location increases from 0.018 to 0.028, due to the within-family correlation in IBD.

In natural populations all the above sources of variance have effects. In a given population, with a given population pedigree, not all individuals have the same ancestry; some will have higher inbreeding coefficients, and some lower. Due to random events in meiosis, individuals with the same ancestral pedigree, and hence the same inbreeding coefficient, will vary in the proportion of their genome that is IBD. Likewise, for an individual with a given ancestral pedigree, different genome locations will vary in the realized IBD.

Coancestry at a single locus

We first review the probabilities, expectations, and variances of IBD at a single point in the genome. The probability of IBD between a pair of segregating gametes is the kinship coefficient, ψ(B, C) between the pair of individuals, B and C, segregating the gametes (Wright 1922). Equivalently, this is the inbreeding coefficient, f(D), of the offspring D of B and C. The independence of meioses provides that, provided B is not C nor an ancestor of C,

$$f\left(D\right)=\psi \left(B,C\right)=\left(\psi \left(M_B,C\right)+\psi \left(F_B,C\right)\right)/2\hspace{1em}\text{and}\hspace{1em}\psi \left(D,D\right)=\left(1+\psi \left(B,C\right)\right)/2,$$ (1)

where M_B and F_B are the parents of B. For a founder A who is not an ancestor of B,

$$\psi \left(A,B\right)=0\hspace{1em}\text{and}\hspace{1em}\psi \left(A,A\right)=1/2.$$

Whether based on matrix methods and forward computation from the founders to the descendants (Quaas 1976), ancestral path-tracing methods (Wright 1922; Stevens 1975), recursive methods (Karigl 1981), or some combination of these approaches, methods for computation of kinship coefficients use Equation 1.

To consider even a pair of individuals, it is necessary to consider larger numbers of gametes. For pedigree relationships, Cotterman (1940) and Malécot (1948) first developed probabilities of IBD among the four parental gametes transmitted to a pair of individuals. In this case there are 15 possible partitions of these four gametes (Table 1). For a larger set of n-labeled genes, Nadot and Vayssiex (1973) provided a method with which to index the IBD states and to compute the count of these partitions into IBD subsets. These counts are the Bell numbers (Bell 1940) and increase very rapidly with n. The properties of the Bell numbers are still of mathematical interest (Berend and Tassa 2010).

Table 1. The IBD states among the four genes of two individuals.

IBD Statea				State Descriptions
B1		B2		Partition	Ewens	Probabilityb
a	b	c	d	z	(a1, a2, a3, a4)	Jacquard	k
1	1	1	1	(a, b, c, d)	(0,0,0,1)	Δ1	—
1	1	2	2	(a, b)(c, d)	(0,2,0,0)	Δ2	—
1	1	1	2	(a, b, c)(d)	(1,0,1,0)	Δ3	—
1	1	2	1	(a, b, d)(c)	(1,0,1,0)
1	1	2	3	(a, b)(c)(d)	(2,1,0,0)	Δ4	—
1	2	1	1	(a, c, d)(b)	(1,0,1,0)	Δ5	—
1	2	2	2	(a)(b, c, d)	(1,0,1,0)
1	2	3	3	(a)(b)(c, d)	(2,1,0,0)	Δ6	—
1	2	1	2	(a, c)(b, d)	(0,2,0,0)	Δ7	k2
1	2	2	1	(a, d)(b, c)	(0,2,0,0)
1	2	1	3	(a, c)(b)(d)	(2,1,0,0)	Δ8	$k_1$c
1	2	3	1	(a, d)(b)(c)	(2,1,0,0)
1	2	2	3	(a)(b, c)(d)	(2,1,0,0)
1	2	3	2	(a)(b, d)(c)	(2,1,0,0)
1	2	3	4	(a)(b)(c)(d)	(4,0,0,0)	Δ9	k0

The two gametes of individual B₁ are denoted a and b, and the two gametes of B₂ are c and d.

^aThe pattern is defined by the labeling developed by Nadot and Vayssiex (1973).

^bThe total probability of each subset of genotypically equivalent states is given on the first row. For example, Δ₃ is the combined probability of states (11 12) and (11 21).

^cNote that Cotterman (1940) and some later authors use 2k₁ instead of k₁ for this probability.

In considering only a pair of individuals, it is usually unnecessary to distinguish the maternal and paternal origins of the two homologs within each individual, and the 15 possible IBD partitions reduce to nine state classes (Table 1). This provides the now generally accepted formulation of the nine IBD states on a pair of relatives due to Jacquard (1974). Despite the simplicity of the law of single-locus Mendelian segregation, computation of the probabilities of these nine state classes on an arbitrary pedigree remains a challenge. Methods based on extensions of Equation 1 to larger numbers of genes were developed by Karigl (1981), and the same approach provides methods for the computation of other probabilities of gene ancestry and gene extinction within defined pedigrees (Thompson 1983). For relationship between a pair of noninbred individuals, the IBD states are much simpler. The two individuals share 2, 1, or 0 genes IBD at any locus, with probabilities k₂, k₁, and k₀, respectively (Table 1).

Inbreeding and kinship coefficients, and more generally probabilities of any IBD state, are expectations of random variables that indicate IBD at a given point in the genome. These random variables also have variance. Conceptually, the pedigree-based inbreeding coefficient of an individual may be thought of as the proportion of between-homolog IBD over descents within the same pedigree at an infinite number of unlinked loci. Different members of the population share some part of their ancestry, with resulting correlations in realized IBD. Within a given pedigree there are both positive and negative correlations affecting the variance of the IBD indicators. For example, consider only the descent from a maternal grandparental couple to a set of siblings. There is positive correlation in the maternal DNA received by the siblings due to their shared descent from grandparents to mother. There is negative correlation between the grandparents and also between the two homologs within each grandparent in their descent to the grandchildren, since each grandchild receives one and only one of these four at a single locus.

As the examples in Sources of variance in identity by descent show, within a finite population there is variation both in the event of IBD (for example, autozygosity) and also in the probabilities of such events (for example, inbreeding coefficients). In addition to the variation resulting from randomness in meiosis and from the different ancestral pedigrees of individuals within a given population, we may also consider variation among replicate population realizations under a given population process such as random mating (Cockerham and Weir 1983). If f is the overall probability of IBD between random gametes in the total collection of population replicates, the total variance is f(1 − f). Cockerham and Weir (1983) partition this total variance into the variance within a population $\left({\sigma }_{\text{w}}^2\right)$ and that between population replicates $\left({\sigma }_{\text{b}}^2\right)$. The component ${\sigma }_{\text{b}}^2$ reflects the variation in IBD among replicate populations due to genetic drift. It is also the covariance in IBD within a population relative to the total: the larger the variance between, the greater the covariance within, relative to the total collection. If a sample of n individuals is taken from a population, their average autozygosity has expectation f and variance ${\sigma }_{\text{w}}^2/n+{\sigma }_{\text{b}}^2$. As discussed by Cockerham and Weir (1983), increasing n does not affect the component of variance due to replication of the population process.

Coalescent IBD and Ewens’ sampling formula

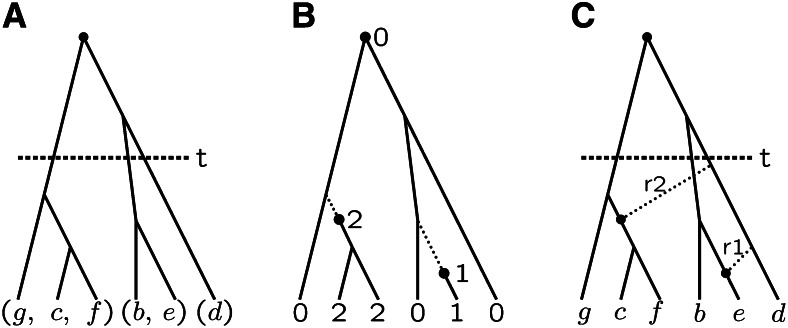
At a point in the genome, IBD among a set of n gametes relative to time t ago is most easily thought of in terms of the coalescent ancestry (Kingman 1982). If IBD is measured relative to a time point at which there were k ancestral lineages, the n gametes are partitioned into k IBD subsets. As a function of the reference time t, the coalescent imposes structure on the sequence of IBD partitions, since each coalescent event can only merge two lineages. In the example of Figure 2A, the n = 6 gametes are partitioned into k = 3 groups, and the IBD partition is ((g, c, f), (b, e), (d)). A partition may be characterized by the number a_j of IBD groups of size j, where $n={\displaystyle {\sum }_{j}j{a}_j}$, and $k={\displaystyle {\sum }_j{a}_j}$. In the example, a₃ = a₂ = a₁ = 1.

Figure 2.

IBD: (A) in the coalescent ancestry relative to time depth t, (B) relative to mutational origins on the coalescent ancestry, and (C) changing due to recombination. For details, see text.

In terms of the time process, the coalescent is considered backward from the present time, with the next coalescent events occurring between a random pair of lineages at rate proportional to ℓ(ℓ − 1)/2 when there are ℓ such lineages. The process may equally be viewed forward in time. Each coalescent event between a random pair among ℓ + 1 lineages (backward) corresponds to bifurcation of a random one of the ℓ lineages (forward). The two processes differ in the distribution of time between events, but both give the same distribution of tree topologies (Kingman 1982), and hence the same distribution of {a_j}. The probability distribution of tree shapes generated by this random bifurcating tree (RBT) process was considered by Harding (1971).

The Ewens sampling formula (ESF) (Ewens 1972) also provides a model for the partition of n gametes into IBD subsets. Developed originally to model allelic variation, this model has more general applications (Tavaré and Ewens 1997) and has been used to model IBD in forensic applications (Balding and Nichols 1994) and in the inference of IBD from population data (Brown et al. 2012). A key advantage of this model as a description of IBD among n gametes is that a single parameter θ determines the full distribution. In particular, the probability that any two of gametes are IBD is β = 1/(1 + θ). Thus the parameter serves as a surrogate for the time depth t relative to which IBD is measured. Under the ESF, the distribution of the number of subsets k depends on θ but the distribution of {a_j} given k does not.

Each of the RBT and ESF models has a Polya urn interpretation, which provides additional insights into the probabilities of IBD partitions: details are given in the Appendix. While there are close parallels in the processes which give rise to the IBD partitions, the distributions of the number {a_j} of groups of size j are different. The sizes of subsets in an RBT partition tend to be more balanced than those for the ESF. For example, when k = 2, with a_x = a_n−x = 1 for x = 1,2, … [n/2], the RBT distribution is uniform over x, while that for the ESF is proportional to (x(n − x))⁻¹. An example for the case n = 8 and k = 4 is given in Table 2. Note in particular the differences between the balanced a₂ = 4 with higher probability under RBT and the extreme a₅ = 1, a₁ = 3 with higher probability under ESF.

Table 2. States with n = 8 and k = 4 and their conditional probabilities given k under RBT and ESF.

Partition					Probability
a1	a2	a3	a4	a5	RBT	ESF
3	0	0	0	1	0.114	0.199
2	1	0	1	0	0.343	0.371
2	0	2	0	0	0.171	0.165
1	2	1	0	0	0.343	0.248
0	4	0	0	0	0.029	0.016

There is also a coalescent interpretation for the partition distributions under the ESF (Ewens 2004). This is that, backward in time, each extant lineage is terminated by a mutation at a constant rate θ/2, while nonterminated lineages coalesce according to the standard neutral coalescent (Figure 2B). From this viewpoint, the ESF may be a more appropriate model when considering descent from novel mutations, for example, in analyses of IBD of haplotypes carrying recent rare variants. Note that this infinite-alleles ESF version of the coalescent with mutation differs from the infinite-sites version of Griffiths and Tavaré (1994) in which mutations are randomly placed on a preformed coalescent ancestry.

In the example of Figure 2, A and B, the two partitions of the n = 6 gametes into k = 3 groups have the same configuration a₁ = a₂ = a₃ = 1. Note, however, that the subgroups are distributed quite differently on the tree, and in Figure 2B the group of size 3 reflects lineages unmutated since the tree origin. For larger n, if θ is small or β = 1/(1 + θ) is large, so that k ≪ n, this group of unmutated lineages will be large. However, if βn < 1 so that k and n are of the same order of magnitude, the ESF provides a useful prior for the probabilities of IBD in the inference of IBD from genetic marker data (see Inference of IBD segments).

Along a chromosome, the IBD partition of a set of n gametes changes due to recombination. Figure 2C shows two potential such recombination events. From the original partition ((g, c, f), (b, e), (d)) of Figure 2A, recombination r1 would result in ((g, c, f), (b), (e, d)), while r2 would result in ((g), (b, e), (c, d, f)). The close parallel of Figure 2, B and C, suggests that the ESF will also be a useful model for the IBD of novel local haplotypes generated by recombination events. The equivalence of the processes of formation and subsequent descent of recombination breakpoints (junctions) and of point mutations (Figure 2B) were first used by Fisher (1954) in considering lengths of IBD segments (see The IBD process in a genome continuum).

Identity by descent at linked loci

There is positive correlation in meiosis between genes at linked loci, but there is also high variance in the recombination process. In the absence of genetic interference, over a descent line of k meioses, the distance to the next recombination point is exponentially distributed with mean 1/k Morgans (M); exponential distributions have a standard deviation equal to the mean.

Equation 1 may be extended to compute the probabilities of IBD at two linked loci in any defined pedigree (Thompson 1988). Pedigree relationships that have the same single-locus IBD probability may have different two-locus IBD probabilities: the simplest example is a pair of half-sisters and an aunt–niece pair. Relationships such as these, which give the same probability of joint genotypes at single loci but different two-locus genotype probabilities, in principle are distinguishable on the basis of data at linked loci.

Consideration of the variance in proportion of genome-shared IBD by relatives requires only two-locus IBD probabilities. If I(x) denotes the event of IBD at position x in the genome, the proportion of a genome length L that is IBD is $\left(1/L\right){\displaystyle {\int }_0^{L}I\left(x\right)dx}$, which directly provides that the expected proportion of IBD is the pointwise probability, ψ. The variance is

$$E\left({\left(\left(1/L\right){\displaystyle {\int }_0^{L}I\left(x\right)dx}\right)}^2\right)-{\left(E\left(\left(1/L\right){\displaystyle {\int }_0^{L}I\left(x\right)dx}\right)\right)}^2={\left(1/L\right)}^2{\displaystyle {\int }_{x=0}^L{\displaystyle {\int }_{y=0}^L\text{Pr}\left(I\left(x\right)=I\left(y\right)=1\right)dx\hspace{0.17em}dy-{\psi }^2}}$$

(Guo 1995). To compute the variance, the joint probability of IBD at both genome locations x and y is required. This probability depends only on the recombination fraction between x and y and on the pedigree relationship between the individuals. Hill and Weir (2011) have given a detailed recent treatment of this variance in the proportion of genome shared by relatives of a given degree. Guo (1995) also considers the mean and variance of the proportion of genome shared IBD by all of a larger target group of relatives.

The IBD process in a genome continuum

Across the genome, changes in the IBD partition in a set of gametes result from recombination events in the meioses of the ancestral lineages. Fisher (1949, 1954) considered these recombination breakpoints or junctions in the descent of DNA. Once formed, junctions segregate as any variant allele, allowing much population-genetic theory to be applied to their survival and frequencies. This leads to results on the distribution of proportions of genome that is autozygous in individuals (Franklin 1977; Stam 1980) and of segments of IBD among individuals in populations (Chapman and Thompson 2003).

Both in known pedigrees and under population models, the IBD process has high variance (Donnelly 1983). The probability that two relatives share genome IBD from an ancestor m generations ago at a specified point in the genome is β = 2^−(2m−1), while the probability that they share any of an autosomal genome length L M is ∼1 − exp(−(2m − 1)Lβ). But given that they do share at a specified point, the expected length of genome shared is (2m)⁻¹ M. For example, for a pair of relatives separated by 12 meioses, the probability of IBD at any point in the genome is 0.0005, but the probability of sharing some segment of autosomal genome is 0.148, while the expected length of a segment shared IBD is 8.5 cM. Where the expected segment lengths are substantially less than the length of a chromosome, the partition of the genome into chromosomes has very little impact on these results (Stam 1980; Donnelly 1983).

Where IBD segments are small and few, the distribution of their number is approximately Poisson; Poisson distributions have equal mean and variance. The second-order effect is of clumping of segments of IBD, since the chance that the next recombination event in the chain of connecting meioses reverses the change that broke the IBD is of order m⁻¹ while the overall probability of IBD decays exponentially in m (Donnelly 1983). The Poisson clumping heuristic (Aldous 1989) provides an approach to closer approximations to the distribution of the extent of IBD genome (Bickeböller and Thompson 1996a,b). An approach to obtaining exact distributions of the proportion of genome shared IBD, to arbitrary accuracy, was provided by Stefanov (2000, 2002, 2004).

There is considerable diversity in the recent literature in discussion of the lengths of segments of IBD and the relationship of length to either the defining time depth of IBD or to the time depth to the MRCA (the “age”) of the segment (Browning and Browning 2010; Huff et al. 2011; Palamara et al. 2012). First is simply the well-known effect of size-biased sampling (Cox 1962). Whereas, across the genome, lengths of IBD segments tracing to an ancestor at time depth t are exponentially distributed, conditioning on IBD at a point in the genome gives a surrounding IBD segment that is the sum of two such exponential lengths. Second is the distinction between age (the MRCA) and the time depth for defining IBD. A pair of cousins will have long segments of IBD tracing to their shared grandparents. In a finite population, their genomes may additionally be IBD for smaller segments, tracing to more distant common ancestors. As the defining time depth t is increased, there will be many more and smaller such segments. Additionally, the large segments the cousins share IBD from their grandparents will be made up of multiple small segments of the genomes that existed in ancestors at time depth t. Third, discussions of age and length are often confused by the variance of the processes involved. The length of an IBD segment descended to two extant gametes from a single common ancestor 25 generations ago (50 meioses separation) has an expected length of 2 cM, but the number of meioses corresponding to a median length of 2 cM is about 35. With probability 10% only 6 meioses will provide a recombination breakpoint within 2 cM, while with the same probability it may take as many as 115 meioses to obtain this breakpoint. Conversely, given an exact segment length of IBD, estimation of the number of meioses of separation has high uncertainty.

The distribution of lengths of IBD segments at the population level provides another dimension. The pointwise probability of IBD between two gametes increases with the time depth t relative to which IBD is measured. For a randomly mating population, relative to time depth t generations, the pointwise pairwise probability of IBD is

$$\beta \left(t\right)=1-{\displaystyle \prod _{s=1}^t\left(1-{\left(2N_{\text{e}}\left(s\right)\right)}^{-1}\right)},$$ (2)

where N_e(s) is the effective population size at time depth s. Through a given line of descent, lengths of segments decrease with increasing time depth, but the overall IBD level is higher. Thus, at greater time depths there must be many more IBD segments, resulting from the many more alternative lines of descent.

The calibration of time depth in terms of lengths of IBD segments is also affected by this greater number of older segments. Although the mean length of older segments is less, the variance in length is such that a proportion of these segments will be long: for example, longer than 1 cM. In considering the age of IBD segments of length 1 cM, the larger numbers of older segments will weight the distribution toward older ages. The mean age may be much larger than the 50-generation time depth (100 meiosis separation) that is expected to give rise to segments of length 1 cM. The number of segments and overall level of IBD will depend on the population size and history (Equation 2), and thus the magnitude of this effect will be population dependent.

Phenotypic Similarity and Allelic Variation

Phenotypic similarities among relatives

Explicit use of identity by descent in computing phenotypic probabilities for relatives is generally attributed to Cotterman (1940) and Malécot (1948), but the idea is implicit much earlier. Pearson (1904) considered the phenotypic correlations between siblings resulting from their shared inheritance and the randomness of Mendelian segregation. Fisher (1918), in considering phenotypic correlations among more general relatives, likewise placed these within the framework of Mendelian segregation. Wright (1922) defined and computed inbreeding coefficients and went on to develop the theory of allelic correlations in uniting gametes and similarities among relatives, but did not explicitly use the concept of identity by descent. Only in later writing (Wright 1969) did he explicitly connect the two approaches, providing the fundamental result that for related individuals in an infinite population the single-locus probability of IBD between gametes is equal to the correlation in allelic type.

A pedigree relationship gives rise to probabilities of different IBD states among the parental gametes in a set of observed individuals. The joint probabilities of observed phenotypes on a set of relatives depends on the pedigree only through the probabilities of these IBD states. For pedigree relationships between a pair of individuals, the probabilities of IBD states at a single locus are the Jacquard coefficients of Table 1. The probabilities of a pair of genotypes under each of the nine states are given in Table 3. The assumption underlying these probabilities is that IBD DNA is of the same allelic type, while non-IBD DNA is of independent allelic type and that population allele frequencies provide the type probabilities.

Table 3. Probabilities of each genotype combination when the two individuals are in each of the nine genotypic state classes.

Genotypes of individuals
B1	bibi	bibi	bibi	bibj	bibj	bibi	bibj	bibj	bibj
B2	bibi	bjbj	bibj	bibi	bibj	bjbk	bkbk	bibk	bkbl
State:
1	pi	0	0	0	0	0	0	0	0
2	$p_i^2$	pipj	0	0	0	0	0	0	0
3	$p_i^2$	0	pipj	0	0	0	0	0	0
4	$p_i^3$	$p_i{p}_j^2$	$2p_i^2{p}_j$	0	0	2pipjpk	0	0	0
5	$p_i^2$	0	0	pipj	0	0	0	0	0
6	$p_i^3$	$p_i^2{p}_j$	0	$2p_i^2{p}_j$	0	0	2pipjpk	0	0
7	$p_i^2$	0	0	0	2pipj	0	0	0	0
8	$p_i^3$	0	$p_i^2{p}_j$	$p_i^2{p}_j$	pipj(pi + pj)	0	0	pipjpk	0
9	$p_i^4$	$p_i^2{p}_j^2$	$2p_i^3{p}_j$	$2p_i^3{p}_j$	$4p_i^2{p}_j^2$	$2p_i^2{p}_j{p}_k$	$2p_i{p}_j{p}_k^2$	$4p_i^2{p}_j{p}_k$	4pipjpkpl

The state classes are numbered as in Table 1. The alleles b_i, b_j, b_k and b_l are distinct, with population frequencies p_i, p_j, p_k and p_l. For markers with only two alleles, such as SNPs, only the first five genotype combinations apply.

The overall probability of genotypes G₁ and G₂ is

$${\displaystyle \sum _{j=1}^9{\Delta }_j\text{Pr}\left(G_1,G_2|\text{IBD}\hspace{0.17em}\text{state}\hspace{0.17em}j\right)}.$$ (3)

For two noninbred relatives, only the last three states, with probabilities k₂, k₁, and k₀, apply (Table 1). These correspond to the individuals sharing 2 IBD as do monozygous twins (MZ), 1 as do parent and offspring (PO), or 0 as for unrelated individuals (U). Thus the probability of data on the pair is the weighted average of the probabilities for MZ, PO, and U, with weights k₂, k₁, and k₀. Once k = (k₀, k₁, k₂) is known, the pedigree relationship is no longer relevant (Thompson 1975).

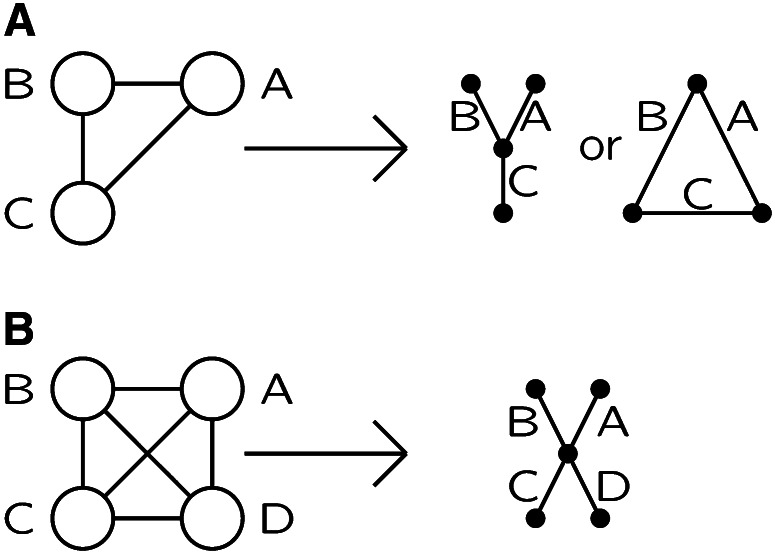
The same principles apply to larger groups of individuals and more complex patterns of IBD. The probability of phenotypes is the weighted sum of the probabilities given each IBD state. A useful way to represent a general single-locus IBD state is via an IBD graph (Thompson 2011). An example is shown in Figure 3. The edges of the graph correspond to individuals observed for a phenotype of interest that is determined probabilistically by the allelic types of the DNA that the individual carries at this locus. This DNA is represented by the nodes of the graph, and where the individuals share DNA IBD, their edges connect at that shared DNA node. The labeling of the nodes is arbitrary, although in the pedigree context, a node may represent a founder genome that descends to observed individuals (Sobel and Lange 1996).

Figure 3.

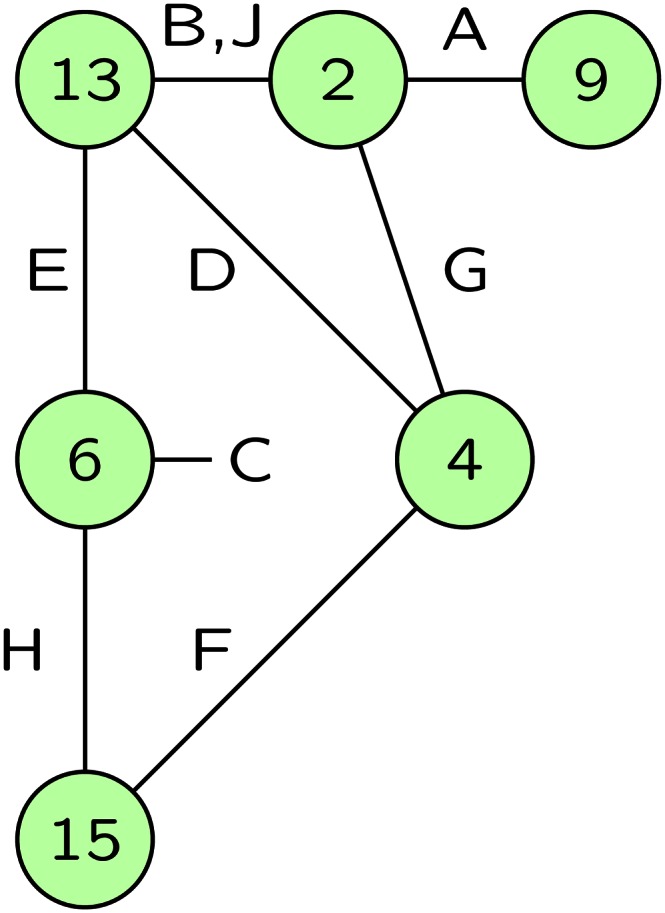
The IBD graph at a single genome location on nine observed individuals, labeled by letters A, B, …. The numbered nodes represent distinct non-IBD DNA at this locus, and the individual edges connect the two DNA nodes that an individual carries. Individuals C is autozygous, carrying two copies of the DNA-node 6. Individuals B and J share both their genomes IBD at this locus.

The state-dependent pairwise genotype probabilities of Table 3 can be generalized to joint phenotypes and IBD graphs. Given the IBD graph, the overall probability of the phenotype data Y on the observed individuals is

$$\text{Pr}\left(Y|\text{IBD}\right)={\displaystyle \sum _{\mathcal{A}\left(g\right)}\left({\displaystyle \prod _m\text{Pr}\left(Y_m|\mathcal{A}\left(g^{\left(m,1\right)}\right),\mathcal{A}\left(g^{\left(m,2\right)}\right)\right)}\right)}\cdot \left({\displaystyle \prod _{g}p\left(\mathcal{A}\left(g\right)\right)}\right).$$ (4)

Here Y_m is the phenotypic observation on individual m, which has a probability dependent on the allelic types of the two genome nodes g^(m,1) and g^(m,2), which m carries at this locus. Each node g represents distinct (non-IBD) DNA, so is modeled as of independent allelic type; p((g)) is the population allele frequency of the allelic type assigned to node g. The summation is over all assignments 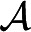of allelic types to each node g. The disjoint components of IBD graphs are often small, so that computation using Equation 4 can be far more efficient than direct computation on a pedigree structure. In fact, it is often feasible to compute phenotype probabilities for phenotypes determined jointly by IBD graphs at two or more genome locations (Su and Thompson 2012).

Just as for the IBD states of Equation 3, the IBD graph separates the phenotype data from any data used to infer the IBD. For example, a pedigree provides probabilities of each possible IBD graph. Given these probabilities, the pedigree is no longer relevant; joint phenotype probabilities depend only on these IBD graphs. The generalization of Equation 3 to computing the probability of phenotypes Y on any set of individuals is

$$\text{Pr}\left(Y\right)={\displaystyle \sum _{\text{IBD}}\text{Pr}\left(Y|\text{IBD}\right)\text{Pr}\left(\text{IBD}\right).}$$ (5)

A version of this equation will be important in Use of Inferred IBD in Genetic Analysis in discussion of the IBD framework for genetic mapping.

Covariances for a quantitative trait

In the classical variance component approach to the analysis of quantitative genetic traits and their heritability, a key step is the computation of probabilities of IBD among the observed individuals given their pedigree relationships. For example, the covariance between phenotypic measurements Y_B and Y_C on the two individuals B and C may be modeled as

$$\text{Cov}\left(Y_1,Y_2\right)=2\psi \left(B,C\right){\sigma }_{\text{A}}^2+k_2\left(B,C\right){\sigma }_{\text{D}}^2,$$ (6)

where ${\sigma }_{\text{A}}^2$ and ${\sigma }_{\text{D}}^2$ are the additive and dominance variances (Falconer and Mackay 1996), and ψ and k₂ are the IBD probabilities in Equation 1 and Table 1. For an additive genetic model, we require only the numerator relationship matrix (Henderson 1976), which is the expected proportion of genome-shared IBD and equal to twice the matrix of pairwise kinship coefficients ψ. Other models may require more IBD states to be considered, for example, the vector of probabilities k = (k₀, k₁, k₂) that two noninbred individuals share 0, 1, or 2 genes IBD at a locus. For such a pair of noninbred individuals, the kinship coefficient is ψ = (k₁/4 + k₂/2).

In an analysis of the heritability of height, Visscher et al. (2006, 2008) propose replacing pedigree-based kinship coefficients (Equation 6) with an estimate of the realized proportions of genome shared IBD. The assumption underlying this approach is only that the additive genetic covariance between relatives is proportional to this realized IBD fraction. This genetic relatedness matrix (GRM) is estimated as follows. At any SNP locus l, suppose p_l is the frequency of a designated one of the two alleles, and in an individual i suppose x_il denotes the number of copies (0, 1, or 2) of this allele carried by i at locus l. Under a model of sampling alleles from the current population, x_il has expectation 2p_l and variance 2p_l(1 − p_l). For two individuals i and j, the (i, j) entry of the GRM is the empirical correlation between the allele counts x of i and j,

$$A_{ij}=\frac{1}{L}{\displaystyle \sum _{l=1}^L\frac{\left(x_{il}-2p_l\right)\left(x_{jl}-2p_l\right)}{2p_l\left(1-p_l\right)},}$$ (7)

where L is the total number of loci genotyped.

Powell et al. (2010) propose that, rather than considering IBD relative to some past time point, IBD should be defined via the correlations in allelic type among gametes or individuals relative to the current population (Equation 7). Rousset (2002) makes similar arguments, suggesting that inbreeding coefficients, for example, should be defined through allelic state similarities rather than in terms of descent. Although the GRM (7) provides an estimate of the realized proportion of IBD over chromosomes or genome regions, it does not take the segmental nature of inheritance of DNA into account. Note that permutation of the loci will not affect the GRM.

There is a close parallel between the partition of IBD and partitions of the allelic variation or the variance for quantitative traits among individuals and among populations. While Cockerham and Weir (1983) partitioned total inbreeding within and between pedigrees (Coancestry at a single locus), Crow and Kimura (1970) had provided analogous formulae for the moments of allele frequency distributions. In highly structured pedigreed populations, the hierarchy of IBD in descent to individuals is reflected in the phenotypic distribution. For example, Avery and Hill (1979) partitioned the variance for a quantitative trait among full sibships, among half sibships, among full sibs within half sibships, and among individuals within full sibships. They applied their results also to derive expressions for the variance among individuals in heterozygosity over the genome. These expressions are analogous to those for variance in IBD.

Allelic and haplotypic variation

A fundamental result is that for related individuals in an infinite population the single-locus probability of IBD between gametes is equal to the correlation in allelic type (Wright 1969). For pairs of loci, similar results hold, and Sved (1971) used probabilities of IBD to establish that the expected value of the squared allelic correlation r² between two loci is the probability that the segment of DNA between the two loci descends unbroken by recombination from a common ancestor to two randomly chosen current gametes. Note that while this approach relates the IBD segments of Hayes et al. (2003) to population-based allelic associations, it is not here a definition of IBD.

Sved (1971) used this IBD approach to establish the well-known formula for the equilibrium level of allelic association between alleles at different loci on a single haplotype,

$$r^2=1/\left(1+4Nc\right),$$ (8)

where N is the effective population size and c the recombination fraction between the two loci. Sved (1971) also notes the similarity of both the derivation and the result to the analogous result for homozygosity at a single locus with mutation due to Kimura and Crow (1964), following Fisher (1954) in citing the parallels in the processes of descent of recombination breakpoints and of point mutations.

The probabilities of Table 3 and more generally Equation 4 made two basic assumptions. The first is that IBD DNA is of the same allelic type. Although this ignores mutation, this is usually a reasonable assumption; mutation can be accommodated through an error model for the observed allelic types. The second is that non-IBD DNA is of independent allelic type. This is far more problematic, since it ignores all sources of dependence other than the IBD considered, including remote coancestry and population structure, and requires “population” frequencies of alleles or haplotypes to be assigned to these “non-IBD” entities.

Consider first a single locus and IBD defined via the ancestral coalescent relative to some time point t. Our model assumes that the ancestral lineages at time t, which are, by definition, non-IBD, are of independent allelic types. However, in reality, these lineages have a more remote ancestry resulting in some being more closely related in that ancestry and, therefore, being of correlated allelic types. For single SNP or even multiallelic microsatellite markers such correlations are slight, and the independence model is a good approximation.

A bigger issue is the population allele frequencies that are used to assign probabilities to the types of these ancestral lineages. In practice, allele frequencies estimated from current population samples are used. For very small populations, such as in a highly endangered species, founder allele frequencies have little meaning: all current copies of an allele may be IBD and its current frequency simply represent the reproductive success of the founder and its descendants (Geyer et al. 1989). In a larger population, currently rare alleles are likely young, and those observed now will be those that have, by chance, increased in frequency from even lower frequencies (see Rare variants in human populations). However, for common allelic variants in populations of substantial size, relative to a time depth of tens of generations, use of current allele frequencies provides a useful probability model for the allelic types of ancestral lineages.

Allelic associations across loci raise greater problems, and the assumption of independent local haplotypes among the ancestral lineages at time t is an approximation. The more remote coancestry of these lineages and the inheritance of small chromosome segments over this remote coancestry will result in LD in the population at ancestral time t. The use of current local haplotype frequencies to model the haplotypes of the population at time t will result in the sharing of such haplotypes among current individuals not being recognized as IBD, even when it results from coancestry more recent than time t. Conversely, ignoring LD in the current population and using only allele frequencies in assigning probabilities will result in shared current haplotypes being interpreted as IBD, even when in reality the coancestry is more remote than t.

In a simulation study, Brown et al. (2012) examined the inference of IBD using a model that did not allow for LD and compared results with those of BEAGLE fastIBD (Browning and Browning 2011c), where fitting an LD model is is a key part of the method. The simulation was of a population over 200 generations, so many of the actual segments shared IBD by current individuals were short. For longer segments of genome of length >1 cM, an order of magnitude longer than the range of the population LD, there was little difference between the two approaches. However, when the level of LD in the founder population was high, the approach that did not allow for LD inferred many short false-positive IBD segments. Conversely, the BEAGLE approach had a much higher false-negative rate, failing to detect true short IBD segments, since it could not distinguish these shorter shared haplotypes from the background LD its model had fit. In any natural population, LD will place a lower bound on the length of IBD segments that can be reliably identified, or equivalently on the time depth of IBD it is reasonable to consider.

Models for haplotypic variation and allelic association (LD) are key to methods for phasing haplotypes from genotypic data and for imputing missing genotypes in population samples. These methods for phasing and imputation have played a major role in the analysis of SNP data (International HapMap Consortium 2005): Browning and Browning (2011a) have provided a recent review. While the models need not explicitly consider IBD, many of the approaches do take IBD as the underlying framework of their methods.

The model that underlies the phasing method of Scheet and Stephens (2006) explicitly considers “founder” haplotypes that become modified by mutation and recombination. More recent methods, designed to address the computational challenges of genome-wide analyses, are more empirical, but retain the segmental nature of haplotypic variation that results from coancestry. For example, Browning and Browning (2009) use a fitted BEAGLE model (Browning 2006) to model each of the two haplotypes that together define the genotype of an individual. Other recent approaches using haplotypic variation (Howie et al. 2009; Li et al. 2010) aim to address phasing and imputation of next-generation sequence variants as well as SNP genotypes.

Methods for phasing that are based on population haplotypic variation model the marker-to-marker sequence of alleles along a chromosome. Where there is no LD, for example, due to a recombination hotspot, phase information is lost. There is no way to phase haplotypes across the hotspot. More generally, the procedures are subject to switch errors (Lin et al. 2002). By contrast, the IBD resulting from gene descent within a pedigree provides information on the parental origin of alleles on each haplotype of an individual. If the parental origins of alleles at two markers is known, so also is the phase of these markers, even if there are intervening markers that cannot be phased. The same “long-range” phasing is possible also in small populations, where there are long segments of IBD resulting from recent coancestry among individuals, resulting in long haplotypes shared among multiple individuals. While not modeling the IBD directly, Kong et al. (2008) makes use of long shared haplotypes to provide very effective methods for IBD detection, long-range phasing, and haplotype imputation.

Rare variants in human populations

In the last 2000 years the human population has undergone explosive growth (Cohen 1995). In this period, many rare variants now being revealed by sequencing (Gusev et al. 2009; Coventry et al. 2010) have become established. Many of these variants were unknown from previous SNP discovery approaches, since 96% of individuals in large case-control studies are of European origin (Need and Goldstein 2009), and variants arising over the past 2000 years will normally be geographically localized and may be rare even within local populations. This will make any association of these variants with disease hard to detect, despite the hypothesis that many of these recent variants may be mildly deleterious (Coventry et al. 2010). An approach to detecting genes that may harbor such variants is IBD-based mapping (see Population-based IBD mapping). This approach is dependent on the power to detect increased IBD around such genes among affected individuals, which is in turn dependent on both the age and the local counts of the relevant variant alleles. Young variants with sizeable counts provide the best opportunity, since these will show longer segments of IBD among larger numbers of individuals.

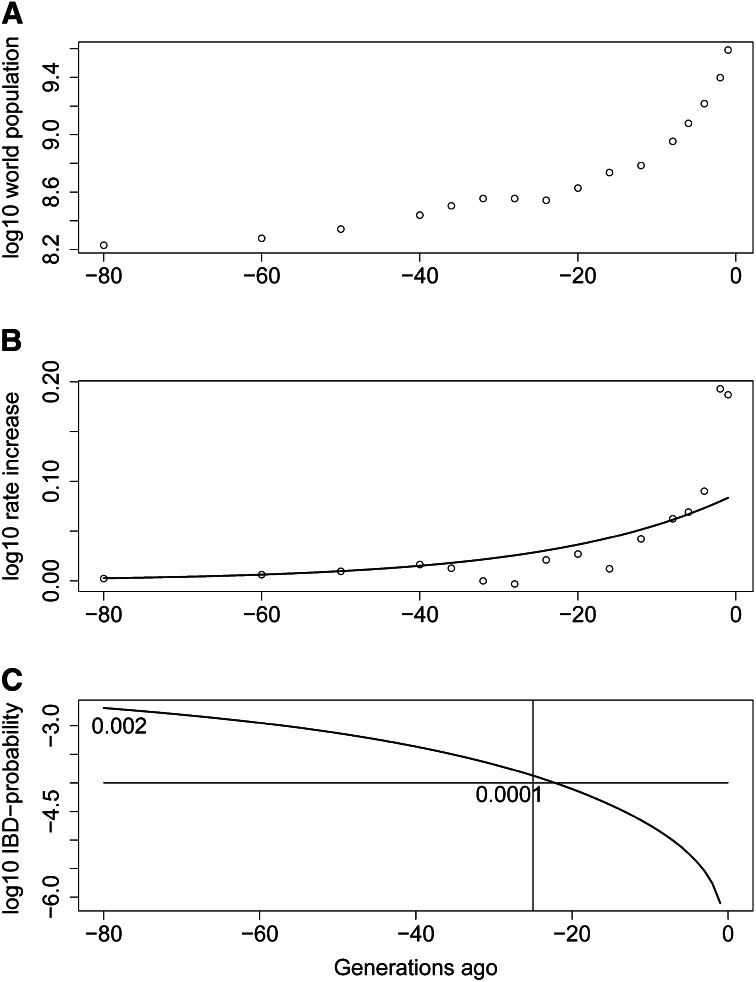
It is, therefore, important to assess the age and count distribution of new variant alleles in a human population. To quantify the discussion, we use data from Cohen (1995) (Figure 4A) to fit world population growth over the past 2000 years and assume 25 years per generation. Broadly, a linear fit to the log-log rate of increase fits the data, with a slope of 0.019 per generation. That is, the rate of increase r(t) at t generations ago is fit as

$${\text{log}}_{10}\left({\text{log}}_{10}\left(r\left(t\right)\right)\right)=-1.06-0.019t.$$ (9)

In the past century the rate has been higher, while ca. 1400 A.D. the world population fell due to the Black Death and in the 17th century the increase was also low compared to (9), but overall the equation provides reasonable fit (Figure 4B). Note that Equation 9 gives a total population growing as exp(exp(exp(⋅))) in time.

Figure 4.

The effect of explosive population growth on the proportion of IBD genome. (A) Human world population growth over the past 2000 years. (B) The increasing rate of increase of the human population. (C) The pointwise probability of genome-shared IBD in randomly sampled chromosomes, relative to past time points.

To relate this growth to pointwise probability of IBD, assumptions must be made about effective population size (Equation 2). The prehistoric effective population size that explains current levels of SNP variation and LD is of the order of 10⁴ (Ardlie et al. 2002; Schaffner et al. 2005). For purposes of demonstration, assume this value for the effective population size of some population 80 generations ago, and that growth has followed the rates given by Equation 9. The pairwise probability, β, of IBD relative to t generations ago between two random gametes sampled from the current population can then be computed (Figure 4C).Note that at 25 generations depth, when IBD segments are expected to be of length 2 cM, the probability is somewhat over 0.0001. Some broad confirmation of these figures is given by the fact that Browning and Browning (2010) found approximately this rate of overall IBD when seeking segments of this size in European samples (Wellcome Trust Case Control Consortium 2007).

Figure 4C provides an example of the population-level balance between increasing IBD and shorter segments of IBD relative to increasing time depths discussed in The IBD process in a genome continuum. Relative to time depth 22, β = 0.0001, and the expected length of segments from a common ancestor at this time depth is ∼4.5 cM. Relative to time depth 80, β = 0.002, but the expected length of a segment tracing to common ancestry at this time depth is only 1.25 cM. Of course, in each case, some part of the IBD will trace to more recent ancestry, with longer expected segment lengths, but generally higher IBD probability and shorter segments imply the existence of more segments.

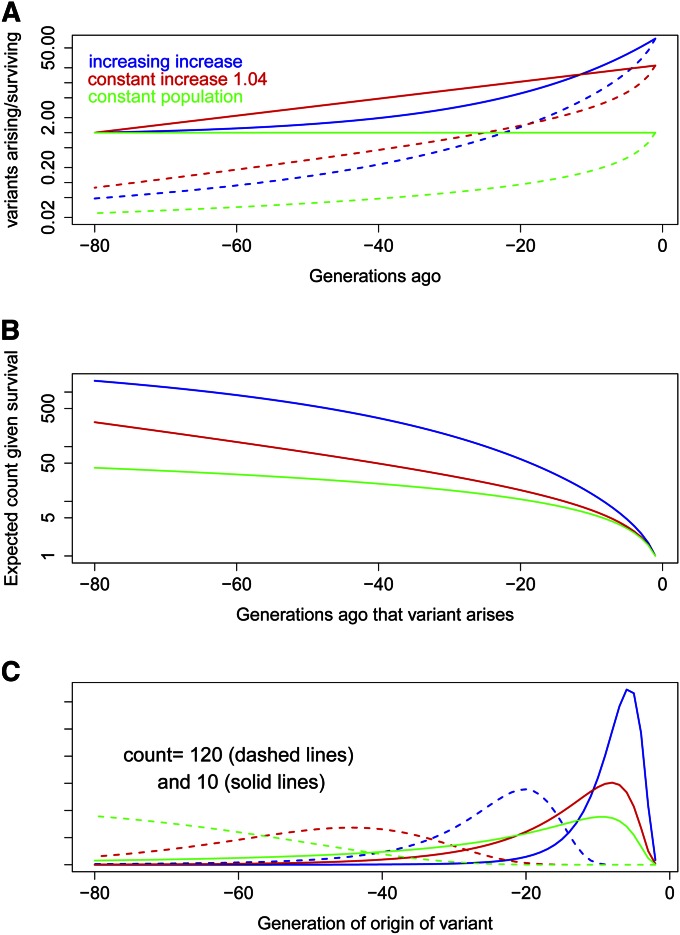
The study of survival of new variants using branching process models dates back to Fisher (1922), while the population genetics of recent, geographically localized, variants has been studied under the heading of Private Polymorphisms (Neel 1978; Slatkin 1985). We here apply that approach to variants arising in a population with a growth pattern like that of Figure 4. In an expanding population, the survival probability of new mutations is increased, but a much greater effect is the larger numbers arising. Using a branching process model with a Poisson offspring distribution, Figure 5A shows the relative numbers of mutations arising t generations ago and surviving to the present under the three scenarios: a population with the growth of Figure 4, a constant rate of increase of 4% per generation equivalent to the same growth over 80 generations, and a constant population. All counts are given relative to one variant arising in any of the three populations 80 generations ago.

Figure 5.

The effect of explosive population growth on the numbers and counts of newly arising variants, under three population scenarios: explosive population growth (blue), equivalent exponential growth (red), and in a constant population (green). (A) Variants arising (solid lines) and surviving (dashed lines) as a function of time of origin. (B) Expected numbers of copies of each surviving variant as a function of time of origin. (C) The age probability distributions of variants currently present in 10 (solid lines) and 120 (dashed lines) copies.

Expected counts increase proportionately with population growth, but lower survival probabilities also increase expected counts for those variants that survive. Suppose the population size at some past time is M, the current population is N, and the probability of survival to the present of a new mutant arising at that past time is Q. Then overall, the expected number of current copies of a given variant is N/M, and among variants that survive it is N/MQ. Figure 5B gives the expected count of copies of a variant arising at past times and surviving to the present under the three population scenarios of Figure 5A. However, summing over variants provides a different picture. The number of variants arising is proportional to M, and the number surviving is proportional to MQ. Hence the total number of all copies of all surviving variants that arose at any given past time is independent both of M and of Q, and hence of that past time. In any population there are fewer older variants in more copies but within smaller IBD segments and more younger variants each in fewer copies carried in larger IBD segments.

Conditional upon survival, there is a rapid increase in the count of a new alleles (Thompson and Neel 1996). The expected number of copies of a surviving variant is proportional to 1/Q, where Q is the survival probability. Many variants become extinct by chance in only a few generations; those that do not, have high counts (Figure 5B). For example, even in a constant population (green curve) variants surviving even 5 generations are expected to have at least 5 copies. Conversely, variants present in a population at significant counts are often young, particularly in a population exhibiting strong growth. Figure 5C shows the age distributions of a variant present in only 10 copies and of a variant present in 120 copies. In all cases, the former is likely to be quite young. For the variant with 120 copies, the three population scenarios give quite different distributions (dashed lines). For explosive growth the variant is likely to be only between 15 and 25 generations old, while for exponential growth from 30 to 70 generations old. However, in a constant population, the variant is likely to be at least 50 generations old and could be much older. The youth of rare variants present in substantial counts in human populations will be reflected in large segments of IBD sharing among the individuals who carry them.

There are close parallels between the processes of recombination and mutation in the ancestry of a set of chromosomes (Figure 2). Both processes occur at rate ∼10⁻⁸/meiosis/bp. Thus mutations introduce point changes of state in a chromosome at roughly the rate that recombination creates potentially novel local haplotypes. Once formed, these recombination breakpoints segregate according to the same model as a variant allele (Fisher 1954). Thus the same arguments that apply to the distribution of rare variants apply also to novel haplotypes; many will be young and geographically localized. A novel haplotype shared by descendants of a recombination breakpoint will provide clear evidence of IBD among the chromosomes that carry it. Additionally, the chromosomes will show IBD to either side of the breakpoint with the more broadly distributed ancestral haplotypes from which the novel haplotype was formed, enabling these ancestral recombinations to be detected (Chapman and Thompson 2003).

Inference of Relationships, Relatedness, and IBD Segments

Estimation of relationships

Pedigree relationships ℛ provide probabilities of IBD states z at a locus, denoted π(z|ℛ). These in turn provide probabilities of phenotypic data (Phenotypic similarities among relatives). Conversely, it has long been recognized (Edwards 1967) that phenotypic data provide information about latent IBD and hence about pedigree relationships. The simplest approaches consider genotypic data at independently segregating loci on pairs of individuals. The likelihood of a relationship ℛ is then

$$L\left(ℛ\right)={\displaystyle \prod _{j=1}^{\ell }\text{Pr}\left(G_{1,j},G_{2,j}|ℛ\right),}$$

where G_h,j is the genotype of individual h at locus j, and

$$\text{Pr}\left(G_{1,j},G_{2,j}|ℛ\right)={\displaystyle \sum _{\text{z}}\text{Pr}\left({\text{G}}_{\mathrm{1,\; j}},{\text{G}}_{\mathrm{2,\; j}}|\text{z}\right)\pi \left(\text{z}|ℛ\right)}.$$

For a general pair of individuals, the probabilities π(z|ℛ) are the Jacquard coefficients (Equation 3), while if the individuals are assumed noninbred they are the probabilities k = (k₀, k₁, k₂) of sharing 0, 1, or 2 genes IBD at a locus. The probabilities of each genotype pair under each IBD state were given in Table 3, and in estimating relationship ℛ the population allele frequencies are assumed known.

Relationship estimation on the basis of L(ℛ) was considered by Thompson (1975), restricting attention to relationships ℛ in which the two individuals are not inbred. Milligan (2003) revisited this approach, while Anderson and Weir (2007) address the case in which the individuals may be inbred and there may be underlying structure in the population. Since L(ℛ) depends on ℛ only through the probabilities π(z|ℛ), relationships ℛ that give the same π(z|ℛ), such as half-sib and avuncular relationships, can never be distinguished on the basis of data at independently segregating loci. Although a highly polymorphic multiallelic locus can give an accurate estimate of the IBD state z at that locus, large numbers of independently segregating loci are required to provide an accurate estimate of π(z|ℛ), and relationships that give similar values of π(z|ℛ) are not easily distinguished. The number of independently segregating loci in the human genome is quite limited, so that this classical approach cannot extend beyond distinguishing the simplest relationships of parent–offspring, sib, half sib, and unrelated.

There is also information about relationships in the lengths of segments in a given IBD state z, and methods for computing likelihoods of relationships using data at linked loci (Boehnke and Cox 1997; Abecasis et al. 2002) make implicit use of this information. Now, not only the allele frequencies but also the genetic linkage map must be known. Relationships such as half sibs and aunt–niece that provide identical single-locus IBD state probabilities differ in their two-locus probabilities and so have different likelihoods on the basis of data at linked loci. However, other distinct relationships may provide identical IBD state probabilities at two or even three loci (Thompson 1988). Even where relationships are identifiable, information is again limited by the variance of the underlying IBD process, and in practice usefulness is limited to detection of non-sib pairs in sib-pair studies (Guo 1994; Olson 1999) or to cases in which there are very specific alternative hypotheses of relationship. More individuals provide more information (McPeek and Sun 2000; Sieberts et al. 2002), and validation from marker data of the stated relationships in genetic epidemiological studies is standard (Boehnke and Cox 1997; Sun et al. 2002). However, there is insufficient information for reliable relationship estimation beyond one generation of unobserved individuals.

The availability of dense SNP data has renewed interest in the estimation of pedigree relationships. It is indeed the case that such data provide accurate estimates of IBD genome segments. For close relatives who share several segments of autosomal genome IBD with high probability, this provides estimates of degree of relationship (Huff et al. 2011) or even information to correct misspecified pedigrees (Han and Abney 2011). However, inferences are limited by the finite length and polymorphism of the human genome and the variation in realized IBD over realizations in any pedigree. Moreover, the issues of identifiability of general relationships are complex. From an infinitely long and infinitely informative genome, the exact probability distribution of IBD states and segment lengths could be determined. Even then, the pedigree might not be determined by this distribution (Steel and Hein 2006).

Estimators of relatedness

Although there is insufficient information for the general reconstruction of pedigrees from genetic marker data, estimation of more limited parameters of relationship is more feasible and may suffice. For example, in analyses of quantitative genetic traits only kinship coefficients ψ and pairwise probabilities of IBD k are needed (Equation 6).

In livestock populations, where relationships are known, pedigree-based values of k and ψ are available, but in natural populations a variety of estimators based on allelic identity have been developed. The majority of these are moment-based estimators derived from expectations of allelic identity at single markers (Queller and Goodnight 1989; Ritland 1996; Lynch and Ritland 1999; Wang 2002). Despite the superior performance of maximum-likelihood estimators (Milligan 2003) these less-biased estimators of relatedness are often preferred in the estimation of heritability (Thomas 2005). Since unrelated individuals have kinship coefficient 0, the maximum-likelihood estimator can never be unbiased, whereas moment-based estimators that permit negative estimates can be so. The use of these estimators reinforces the interpretation of relatedness as a (potentially negative) correlation rather than as a (necessarily positive) probability (see Covariances for a quantitative trait). Toro et al. (2011) provide a recent discussion of the estimation of genealogical coancestry from molecular markers.

With the advent of genome-wide SNP variants, the use of genome-wide marker-based estimates of relatedness has also entered the human genetic literature. Estimators of k can be used to detect closely related individuals in case-control studies (Voight and Pritchard 2005; Sun and Dimitromaniakis 2012). The empirical genetic relatedness matrix or GRM (Equation 7) may be used as an estimator of the pedigree-based numerator relationship matrix (Equation 6). Even where the pedigree relationship is known, a marker-based estimate of relatedness may be preferred, since the realized proportion of genome-shared IBD varies among pairs of individuals with the same pedigree relationship (Identity by descent at linked loci). In known sib pairs, using the variation in realized IBD contributes to analyses of heritability (Visscher et al. 2006). Additionally, partitioning the analysis by chromosome provides estimates of the contributions of each chromosomes to phenotypic variation (Visscher et al. 2007). Using an even more local set of genetic markers provides estimates of IBD in small genomic regions for purposes of gene mapping (Day-Williams et al. 2011).

Despite the strong parallels in the patterns of variance and covariance (Phenotypic Similarity and Allelic Variation), the generation-to-generation processes for population levels of IBD and for allelic similarities are not strongly correlated (Cockerham 1969; Nei et al. 1977). Although IBD DNA is, with high probability, of the same allelic type, each set of IBD gametes has an allelic type in accordance with population allele frequencies. For example, in a single individual, autozygosity implies homozygosity, but homozygosity is not a strong indicator of autozygosity. Any marker-by-marker moment-based estimator, for example, the GRM (7), takes no account of the genome locations of markers. To gain information across linked markers, Day-Williams et al. (2011) use a smoothing method. An alternative approach is to consider haplotypic rather than allelic similarity and model the segments of IBD across a chromosome. This is the approach considered in the following section.

Inference of IBD segments

Similarity of haplotype markedly above that expected in individuals randomly sampled from the population provides evidence that the corresponding segments of DNA are IBD from a recent common ancestor. The longer such near-identical haplotypes extend, the more recent on average is that common ancestor (Coancestry and allelic associations). Because the lengths of IBD segments decrease only as m⁻¹ with increasing number of meioses of separation, even common ancestry at a depth of 50 generations will give rise on average to a segment of length 1 cM (Inheritance of segments of DNA). Failure to take the segmental nature of IBD into account when inferring relatedness results in loss of power (Albrechtsen et al. 2009).

Browning and Browning (2012) have provided a recent thorough review of methods for the detection of IBD segments from similarity of marker haplotypes. Broadly, methods may be divided into two groups. Rule-based methods can provide rapid searches for shared haplotypes in large population samples on a genome-wide scale. Such methods include GERMLINE (Gusev et al. 2009), the approach of Kong et al. (2008), and the more recent BEAGLE fastIBD method of Browning and Browning (2011c). The alternative is to take a model-based approach to inference of IBD segments, and we limit discussion here to the development of these probability models. We consider IBD relative to a time point sufficiently recent that the haplotypic similarity due to IBD is distinguishable from population-level LD.

Model-based approaches to the detection of IBD segments in individuals not known a priori to be related all use hidden Markov models (HMM) to model the latent IBD. Using genotypic data on single individuals, Leutenegger et al. (2003) used a two-state HMM to model the IBD/non-IBD between the two homologous chromosomes of offspring individuals to detect unspecified relationships between their parents. Browning (2008) used the same two-state IBD-model for pairs of phased haplotypes sampled from a population.

The first model for inferring IBD segments between pairs of diploid individuals was that implemented in PLINK (Purcell et al. 2007). This approach modeled the IBD as that of two independent pairs of haplotypes, each following a model equivalent to that of Leutenegger et al. (2003). The IBD state is summarized as 0, 1, or 2 shared IBD between the two individuals. However, the inbreeding coefficient of offspring is the kinship coefficient of parents, and in most populations IBD within individuals is at least as great as IBD between. The approach of Browning and Browning (2010) also seeks only IBD between individuals and uses only two latent IBD states: any-IBD and no-IBD. In contrast, Han and Abney (2011) provide an estimate of the probability of each of the nine genotypically distinguishable states (Table 1) at each marker location using individual-specific transition rates. However, the HMM transitions are not based on any model of descent; if a transition occurs the next state is a realization of the marginal probabilities specific to the pair of individuals.

Thompson (2008) provided a Markov model for transitions along a chromosome among the 15 states of IBD of the four gametes of two individuals (Table 1). A generalization of this model applicable to any number of gametes has the Ewens sampling formula (Equation A.1) as the pointwise model for the partition of n gametes into IBD subsets. Transitions among the IBD states approximate those expected to occur due to recombination events in their coalescent ancestry (Figures 1 and 2C), and hence this model provides a useful prior for the IBD. This model has been in implemented in the IBD_Haplo software and tested in estimating IBD segments among sets of four gametes (pairs of individuals) in a simulated population of 200 generations time depth using either haplotypic or genotypic data (Brown et al. 2012). Moltke et al. (2011) have also provided a model for any number of gametes, but, to facilitate MCMC sampling of IBD, their latent IBD model is simplified, both in its pointwise state probabilities and in its permitted transitions.

All the above methods use similar data models. Basically, IBD DNA is of the same allelic type, while non-IBD DNA is of independent allelic types. The models require allele frequencies. Since we seek IBD relative to a recent reference time depth t, for common variants it can be assumed that the allele and local haplotype frequencies at ancestral time depth t do not differ widely from those in the current population. Thus allele frequencies and local LD structure can be estimated from large samples from current populations. While sharing of rare variants may provide strong evidence of coancestry, the absence of population-level data on the frequencies of such rare alleles or haplotypes makes the reliable quantitative assessment of this IBD evidence problematic. The data model of Purcell et al. (2007) is slightly different in that it uses the population sample directly, rather than using estimated allele frequencies. The alleles of the population sample are assigned without replacement to non-IBD DNA within each pair of individuals, resulting in negative correlations in the allelic types of these non-IBD gametes.

Allowance for genotyping error is important (Leutenegger et al. 2003), and this is also accommodated in other recent articles (Browning and Browning 2010; Moltke et al. 2011; Brown et al. 2012). An error model can accommodate mutation, recognizing haplotypic similarity and shared descent even when mutations have occurred. While most of the methods consider the data input as genotypic, the methods of Thompson (2008) and Brown et al. (2012) allow for either phased or unphased data on individuals, or for phase information only in specified chromosomal regions. Generally, knowledge of the phased haplotypes provides more accurate estimates of the IBD partition, since alternate uncertain phasings generate uncertainty in IBD state conditional on marker data. An exception is where the model badly misspecifies local haplotype frequencies, for example, by ignoring LD (Brown et al. 2012).

In earlier models (Leutenegger et al. 2003; Purcell et al. 2007), LD is not accommodated; the data at each locus depend only on the latent IBD state at that locus. Albrechtsen et al. (2009) extended the basic data model to allow for pairwise LD among loci, and Han and Abney (2011) use a version of this model, conditioning their HMM emission probabilities on genotypes at either single or multiple previous loci. The approach of Browning (2008) and Browning and Browning (2010) uses a full LD model. In this case, allele frequencies are not used directly, but only through the haplotype clusters of the BEAGLE model fitted empirically to a large population sample (Browning and Browning 2007). A model that incorporates LD more closely approximates local haplotype frequencies and thus increases specificity, but an approach that too closely fits the observed haplotype frequencies among a small set of individuals will lose power to detect IBD among them (Brown et al. 2012).

At any location in the genome, the ancestral coalescent partitions a set of chromosomes into the disjoint subsets that are IBD relative to a past time t (The descent and ancestry of DNA). This partition is an equivalence relationship; if ≡ denotes IBD, then among three gametes, b, c, and d, b ≡ c and c ≡ d implies b ≡ d. Without this consistency, joint phenotype probabilities (Equation 4) are undefined. In a defined pedigree, any pattern of inheritance of DNA will always provide an IBD graph (Phenotypic similarities among relatives), and hence a jointly consistent pattern of IBD. However, pairwise estimates of IBD among chromosomes or among individuals need not be jointly consistent. Joint consistency is ensured only by the construction of an IBD graph from these pairwise estimates (Glazner and Thompson 2012).

Consider, for example, three diploid individuals with each pair sharing just one gamete IBD. This IBD can be resolved in one of two ways: all three individuals share the same gamete IBD, or there are three distinct IBD nodes each shared by a different pair (Figure 6A). Suppose now a fourth individual also shares just one gamete IBD with each of the other three. Then this is possible only through all four individuals sharing a single gamete (Figure 6B). There are also constraints in the changes in IBD graph across the genome. Suppose at the first locus, each pair of three individuals shares one gamete IBD, and at a very closely linked locus, a fourth individual shares also with each of the other three. In this case, at the first locus, the IBD should resolve as the three individuals sharing a single gamete IBD and not as the three pairs (Figure 6). Generally, the constraints both at a locus and across loci make construction of IBD graphs from pairwise estimates a complex task.

Figure 6.

Resolving components of IBD graphs from pairwise IBD. (A) For three individuals A, B, and C, with each pair sharing a gamete IBD, the joint sharing can be resolved in two ways. (B) If D also shares a gamete IBD with each of A, B, and C, then all four individuals must share a single gamete.

Use of Inferred IBD in Genetic Analysis

In this section we review the use of IBD, primarily in locating the genes of causal effect on a trait of interest relative to the increasing mass of mapped allelic marker variation, from the first DNA markers (Botstein et al. 1980) to millions of SNPs (1000 Genomes Project Consortium 2010) and next-generation sequence data. Whether in pedigrees (Gene mapping using IBD in pedigrees) or in populations (Association and ancestry in fine-scale mapping), implicitly (Association mapping and heritability and Adjusting for relatedness in population-based genetic mapping) or explicitly (Population-based IBD mapping), all approaches depend on IBD. Finally, in Evolutionary and demographic inferences we very briefly review other applications of IBD in inference from human genetic data.

Gene mapping using IBD in pedigrees

Pedigree-based linkage analyses directly models inheritance of DNA at locations across the genome. The classical pedigree-based linkage LOD score (Smith 1953) uses a joint model-based probability of marker genotypes Y_M and trait phenotypes Y_T to assess co-inheritance at (hypothesized) trait and (known) marker loci. As a function of trait data and model, this joint probability is proportional to the conditional probability Pr(Y_T|Y_M), which may be expressed directly in terms of IBD among observed individuals using a slight generalization of Equation 5,

$$\text{Pr}\left(Y_{\text{T}}|Y_{\text{M}}\right)={\displaystyle \sum _{\text{IBD}}\text{Pr}\left(Y_{\text{T}}|\text{IBD}\right)\text{Pr}\left(\text{IBD}|Y_{\text{M}}\right)},$$ (10)

where the summation is over the states of IBD at a hypothesized trait locus among individuals observed for the trait. Given chromosome-wide genetic marker data Y_M on pedigree members, joint IBD graphs across the chromosome may be realized from Pr(IBD|Y_M). Whether the IBD is expressed in terms of inheritance (Lange and Sobel 1991) or directly in terms of an IBD graph (Thompson 2011), averaging the values of Pr(Y_T|IBD) over realizations of IBD at each hypothesized trait locus provides a Monte Carlo estimate of Pr(Y_T|Y_M) and hence of linkage LOD scores.

Other classical linkage mapping designs make more explicit use of the pedigree-based probabilities of IBD, in case-only designs such as affected sib-pair methods (Suarez et al. 1978), homozygosity mapping (Lander and Botstein 1987), and other affected relative pair methods (Weeks and Lange 1988). Ascertainment of affected relatives increases the probabilities of IBD at causal genome locations. Additionally, because prior probabilities of IBD are smaller in remote relatives, IBD in more remotely related affected individuals provides a strong signal. With modern genome-wide dense markers, using marker-based inferred IBD among cases in pedigrees remains a powerful tool, but direct pedigree-based computations are often infeasible. Albers et al. (2008) have developed a method that approximates IBD probabilities among remotely related case individuals in pedigrees and used these to provide accurate estimates of LOD scores or other linkage detection statistics. Thomas et al. (2008) have also developed methods with which to use segments of IBD inferred from dense marker data among members of extended pedigrees to map causal loci.

Quantitative trait mapping using an IBD framework also has a long history. Haseman and Elston (1972) relate the dissimilarity between sibs to the inferred IBD at given points in the genome inferred from marker data. Goldgar (1990) and Schork et al. (1993) extend these ideas to more individuals and more complex models, while Guo (1994) considers the mean and variance of IBD in specified chromosomal regions conditional on marker data. Modern dense genome-wide SNP data provide the information to estimate both pointwise probabilities and genome-wide proportions of IBD sharing between pairs of individuals. Han and Abney (2011) suggest that their estimates of realized IBD across the genome could be used in follow-up QTL mapping studies.

An advantage of an IBD framework for linkage analysis is that IBD within pedigrees may be combined with IBD inferred between members of different pedigrees using a population-based model. The within-pedigree analysis also provides phase information on observed individuals, increasing the information for the between-pedigree inferences (Brown et al. 2012). Specifically, combined IBD graphs jointly over observed individuals and across a chromosome may be estimated conditional on marker data and used in Equation 10 to estimate LOD scores that include information from unknown between-pedigree relationships. Combining inheritance information within the pedigrees of a genetic epidemiological study with inferred IBD among members of different pedigrees has the potential to increase both the power and resolution of linkage mapping (Glazner and Thompson 2012).

Association and ancestry in fine-scale mapping

Pedigree-based methods of gene mapping have high power, if the assumed pedigree relationship is correct. However, they have low resolution due to the limited number of meioses in which recombination events are reflected in observable data (Boehnke 1994). This recognition has led to genome-wide association studies (GWAS), in which LD between a marker and a causal locus provides the mapping signal (Risch and Merikangas 1996). An association test makes no explicit use of IBD, but its success is dependent on the LD that arises from coancestry, and its success is often limited by the effects of population-level relatedness that also create LD (Coancestry and allelic associations). Initial optimism regarding association mapping (Glazier et al. 2002) was tempered by failures to detect known genes (van Heel et al. 2002) and failures to replicate findings (Elbaz et al. 2006). Only with much larger-scale GWAS (Wellcome Trust Case Control Consortium 2007) and better methods with which to control for population structure (see Adjusting for relatedness in population-based genetic mapping) did GWAS start to have major successes in mapping causal trait loci.

In an association test the genetic linkage among markers and the relatedness of individuals are ignored. However, the haplotypic variation in a population sample has both dependence across loci within a haplotype and dependence among haplotypes resulting from their ARG. These dependencies provide the basis for IBD-based methods for using LD for fine-scale mapping. The earliest methods for LD mapping (Terwilliger 1995; Xiong and Guo 1997) used the genetic marker map, but were based on a combination of local single-marker likelihoods and implicitly assumed a “star phylogeny” in which alleles descend independently from the root. Other approaches (Kaplan et al. 1995; Graham and Thompson 1998; Rannala and Slatkin 1998) take the coalescent ancestry structure of the sample into account but not the dependence along the chromosome. In the ancestry of a haplotype carrying a disease allele, when a recombination occurs between the causal locus and a genetic marker, the marker allele acquired on the haplotype is modeled as randomly sampled according to population frequencies. McPeek and Strahs (1999) take the orthogonal approach, modeling the decay of haplotype IBD along the chromosome, but using only the pairwise covariance structure among haplotypes to take the coancestry into account. McPeek and Strahs (1999) also provides an excellent review of earlier articles.

Generalization of these models, taking both coalescent ancestry and the segmental structure of this coancestry into account in LD-based mapping, has proven difficult. Analysis using the full ARG is computationally intensive (Kuhner et al. 2000; Kuhner and Smith 2007), as are the approaches to fine-scale mapping that use it Larribe et al. (2002). One approach is that of Zöllner and Pritchard (2005), which models the local coalescent process across a few markers and seeks clustering of similar phenotypes within this local coalescent at specific genome locations. Use of the sequential Markov approximation to the ARG (McVean and Cardin 2005) may prove more tractable, and an approach using heuristic ARG estimates has been scaled up to analyze thousands of individuals jointly (Minichiello and Durbin 2006). However, even in this case, ARG-based analyses are limited to short genomic regions.

Association mapping and heritability

GWAS are having increasing success, with many hundreds of causal genes detected and results replicated, but the proportion of trait heritability accounted for by these genes is often very low (Manolio et al. 2009), and this is nowhere more apparent than in the many studies of the additive genetic variance of human height. Height is a trait not only easily measured, and with apparently high heritability, but one in which genetic effects are broadly distributed over the genome. Studies of close relatives based on Equation 6 provide an estimate of heritability of the order of 80%, although this may be inflated by effects of shared environment or by epigenetic factors that also contribute to correlations in relatives.

Lango Allen et al. (2012) undertook a meta-analysis of 46 earlier studies, with a combined total of data on >183,000 individuals. Their approach selected SNPs representing 180 loci, each showing a robust significant signal of association with human height. In their analysis, these SNPs explain only 10% of the phenotypic variation in height, while they estimate that unidentified common variants of similar effect size would increase this to 16%. However, this would still be only 20% of the presumed heritable variation.

Yang et al. (2010) took a different approach in which SNP effects are treated as random effects, and the total additive genetic contribution of all SNPs across the genome is thereby estimated. The model implies a vector of genetic values based on the SNP genotypes of each individual, where the variance of this vector is the genetic relatedness matrix or GRM (Equation 7 in Covariances for a quantitative trait). The goal is to use not only SNPs identified as tagging loci with significant effects, but all SNPs across the genome. Using a variance matrix based on 294,831 SNPs in 3925 individuals they explain 45% of the phenotypic variance. They suggest that the remaining missing heritability is due to incomplete linkage disequilibrium between causal variants and genotyped SNPs. It is important to note that Yang et al. (2010) excluded close relatives from their study. Whether the pedigree relatedness (Equation 6) or the GRM (Equation 7) is used to model the variance of individual effects, any additive effects shared by close relatives will contribute to the estimate of heritability.

Rather than estimation of heritability, or within-sample variance explained, the approach of de los Campos et al. (2010) is that of whole-genome prediction. The test of a prediction method is not the within-sample variance explained, but out-of-sample predictive accuracy. This is generally assessed by cross-validation, with the measure being the proportion of variance explained (R²) in the regression of observed values on the prediction. Heritability provides an upper bound on predictive R², but there is a large difference due to variance in the estimators of SNP effects (Visscher et al. 2010). Ultimately, if large enough samples of individuals are available to estimate all effects without error, R² should approach the heritability bound. In practice, the very large numbers of SNP effects contributing to a trait such as height means that predictive accuracy remains stubbornly low (Makowsky et al. 2011). Samples containing a significant proportion of close relatives provide much higher whole-genome predictive accuracy (Makowsky et al. 2011). If the goal is prediction, the fact that correlations in close relatives may not reflect true additive genetic heritability is not a concern.

Whether for heritability estimation or genomic prediction, there is no intrinsic difference between using a pedigree-based numerator relationship matrix (Equation 6) and using the GRM based on SNP markers (Equation 7). Also, other estimates of relatedness could be used. For example, methods that use haplotypic rather than marker-by-marker similarities (Inference of IBD segments) provide more accurate estimates of local IBD. However, while pedigree-based kinship (Equation 6) and empirical correlations (Equation 7) always produce a positive semi-definite covariance matrix, other methods of estimating genome-wide pairwise IBD may not.

The approach of Yang et al. (2010) for quantitative traits has been extended by Lee et al. (2011) to case-control studies by transforming the trait status to a quantitative liability scale. They account for a significant proportion of the heritability estimated from family studies. It remains a question whether the remaining “missing” additive genetic variance is truly missing and due to rare alleles of small effect (Lee et al. 2011). Alternatively, or in part, the “missing” heritability may be a “phantom” resulting from gene–environment interactions and epistasis (Zuk et al. 2012) or epigenetic factors.

Adjusting for relatedness in population-based genetic mapping

In any genetic mapping method, the base point for comparison must be chosen. The linkage LOD score (Smith 1953) compares the data probabilities with the trait locus at some hypothesized genome location with the probability of the same data under the same trait and marker model, but the trait locus being at some genome location unlinked to the genetic markers. By contrast, methods developed for the mapping of QTL (Lander and Botstein 1989) compare the model of some nonzero effect at a specific location with the null model of no effect. The same question of the null hypothesis arises in population-based approaches to genetic mapping. For example, in admixture mapping, Patterson et al. (2004) develop both a case-only test comparing ancestry at each location to a genome-wide value for the same individual and a case-control test in which ancestry measures at specific genome locations are compared between cases and controls. The first approach requires a genetic model, while the latter assumes absence of systematic differences between cases and controls.

In case-control studies, it is necessary to control for differences between the case population and the control population, with regard both to their allele and haplotype frequencies that affect allelic associations with a trait phenotype and to their degree of relatedness that affects genotypic and phenotypic covariances within them. Genomic control (Devlin et al. 2001) uses the genome-wide distribution of test statistics to provide a correction factor for significance of signals at specific genome locations. Alternatively, this approach can be used to detect whether stratification exists, and principal components (PC) analysis can then be used to correct for it (Price et al. 2006). The coefficients of the top PCs are used as fixed-effect covariates to correct for stratification, but this does not account for relatedness among individuals. While Lee et al. (2011) used the GRM (Equation 7) to estimate heritability and 20 PCs to adjust for stratification, Kang et al. (2010) used a model including a random-effects covariance matrix based on the GRM to correct for relatedness. Both relatedness of individuals and case-control population differences are reflections of coancestry, and both inflate heritability estimates if not adjusted for. However, the same covariance information cannot simultaneously estimate heritability and correct for structure and relatedness. Browning and Browning (2011b) give additional discussion of this issue, while a recent review of this area has been given by Price et al. (2010).

Difficulties in identifying the loci underlying phenotypic variance and covariance increase in non-Caucasian populations (Need and Goldstein 2009), due to genetic diversity and to the effects of rare causal variants. Both allele frequencies and haplotype frequencies (LD structure) differ among populations. In an attempt to replicate GWAS results on asthma and allergic diseases, Yoon et al. (2012) considered 46 strong SNP associations found in 12 independent GWAS. Of the 32 that were polymorphic and of sufficient quality in their Korean population, only 6 showed effects in their study. Wang et al. (2012) also ascribe some part of the missing heritability to differences in LD structure across populations, noting that standard methods of meta-analysis assume homogeneity of LD across the studies. They have proposed a new method to combine across ethnic groups allowing for LD differences, and in a study of type 2 diabetes their approach finds novel variants in addition to confirming others previously found.

Population-based IBD mapping

It has been proposed that rare variants arising in the last 80 generations of explosive human population expansion may underlie many current common genetic diseases (Rare variants in human populations). Despite the development of association-based tests to address problems of allelic heterogeneity (Li and Leal 2008; Madsen and Browning 2009), there is very low power for detecting geographically localized rare causal variants. Whereas association approaches will fail, the patterns of genome shared IBD among cases at causal may be well differentiated from those in noncausal regions (i.e., genomic control) and from those among controls. These ideas underlie the recent development of population-based IBD mapping.

Ascertaining via disease in geographically localized populations increases the potential to detect the presence of rare causal variants in segments of IBD inferred among such groups of case individuals. The methods of Leutenegger et al. (2003) (Inference of IBD segments) were developed with the goal of increasing information for genetic linkage mapping in a population in which relationships between parents of affected individuals were often underrecorded. Detection of IBD segments between the two homologs of these affected individuals, without knowledge of the ancestry, has led to identification of the relevant recessive gene (Edery et al. 2011). More generally, Albrechtsen et al. (2009) have used a population-based method of inferring IBD segments among affected individuals and demonstrated the increased power relative to association mapping methods. The same power that is gained by considering remotely related affected individuals in known pedigrees (Weeks and Lange 1988; Albers et al. 2008) applies also to the population-based approach.

In population samples, detection of segments of IBD enables association tests either to use (Browning and Browning 2010) or to adjust for (Choi et al. 2009) this coancestry in association methods of gene mapping. Alternatively, inferred IBD may be used directly in methods of population-based IBD mapping under the basic premise that, collectively, there will be a higher probability of IBD among cases at causal locations. Browning and Thompson (2012) have shown that where there are multiple rare causal variants, IBD-based mapping can have very substantially greater power than association mapping in a case-control study. The pairwise methods of Browning and Thompson (2012) may be extended to larger sets of gametes or individuals. For example, ESF (Coalescent IBD and Ewens’ sampling formula) provides one model for the subsets of IBD gametes, parametrized in terms of pairwise IBD probability β = 1/(1 + θ) (see Equation A.1). Since the number of IBD subsets, k, is a sufficient statistic for θ and hence of β (Ewens 1972), tests of different values of β in different population samples based on the varying values of k and n can be easily derived.

In pedigree-based linkage analyses, several IBD-based test statistics have been considered: for a review and comparison see McPeek (1999). Location-specific IBD among case individuals is often scored pairwise, but other statistics include the sizes of groups of cases sharing haplotypes IBD. Once the IBD graph is inferred from genetic marker data, the source of the IBD inference is irrelevant to the analysis of trait phenotypes (Phenotypic similarities among relatives). Thus, all these test statistics can equally be applied in population samples. Figure 7A shows a small collection of IBD graph components that might be inferred at a particular locus in a case-control study. There would be many additional unconnected individuals. This sample would indicate more IBD among cases (A) than among controls (U) and includes one pair of affected individuals who share both their gametes IBD. Alternatively, a model-based statistic such as the probability of trait phenotypes conditional on IBD (Equation 4) can be used. Figure 7B shows the same IBD graphs, but now with a quantitative phenotype for each individual shown; a value ≥4.0 corresponds to case status. The clear correlations among individuals sharing genome IBD at this locus show how a model-based approach may significantly increase power.

Figure 7.

Possible components of an IBD graph used in genetic mapping, showing only individuals involved in some IBD sharing. The IBD graph may derive from the analysis of marker data on a pedigree or on individuals samples from a population. (A) A binary trait with affected (A) and unaffected (U) individuals. (B) A quantitative trait, with the trait values of individuals shown. In both cases, at this hypothesized locus, phenotypic similarity is associated with IBD.

In pedigree-based linkage analysis, test statistics that increase power rely on the particular patterns of IBD that are expected under given trait models. One example is the autozygosity used in homozygosity mapping of rare recessive traits (Smith 1953; Lander and Botstein 1987). Rather than being autozygous, case individuals sampled from a population may often be compound heterozygotes, carrying two different but nonnormal alleles. Such situations are well known in the case of “Mendelian” traits such as the first to be positionally cloned, the cystic fibrosis transmembrane conductance regulator locus, where now hundreds of alleles that have different geographic origins are known (Estivill et al. 1997), and in their various combinations have multiple trait effects (Chillón et al. 1995). Many Mendelian disorders caused by variants in one or both homologs of a single gene have eluded pedigree-based linkage mapping due to their rarity. Test statistics that exploit the expected IBD pattern will have high power in this situation.

While analogous IBD-based test statistics may be used in pedigrees and in populations, procedures for testing will differ. A pedigree provides a strong prior distribution on null patterns of IBD at and across test locations in the genome. Rejection of the null distribution leads to inference of a causal location. In population samples there is no such well-defined null distribution. Testing-inferred IBD against a null distribution such as that of the ESF (Equation A.1) may show that the IBD does not follow this distribution, but this may be for reasons of population structure and history unrelated to the trait phenotype of interest. In population-based IBD mapping, as in GWAS, permutation of case-control labels, or more generally of quantitative phenotypes, is feasible and effective. These permutations provide a null distribution for the hypothesis that case-control status or phenotypic value is unrelated to the IBD state at the test location. Also, as in GWAS, adjustment can be made for genome-wide differences in the patterns of IBD in case and control populations (Browning and Thompson 2012). By contrast, in human pedigree studies the constraints of pedigree structure make effective permutation testing impossible, although it is possible and effective for some designed crosses in experimental populations (Churchill and Doerge 1994).

Evolutionary and demographic inferences

Population genetics theory makes many predictions as to the allelic and haplotypic variation to be expected in a populations as a result of drift, selection, mutation, migration, and recombination. With the advent of genome-wide informative genetic marker data, many advances in methods have made evolutionary and demographic inferences from these data. An early example is the use of Equation 8 to provide the now standard estimate of 10⁴ for the ancient effective human population size (Ardlie et al. 2002), while Hayes et al. (2003) use lengths of segments of shared haplotypes to estimate effective population sizes at various past times.

As with other aspects of IBD, the processes involved have high variance, and over the evolution of a population the processes of allelic association (or LD) and IBD are not closely correlated (Cockerham 1969; Thompson 1976; Nei et al. 1977). The sharing of common alleles provides little evidence for IBD. In a review of more recent studies of the relationship between heterozygosity and fitness, Szulkin et al. (2010) make the same point in connection with multilocus patterns of LD. While earlier methods for detecting selection in human populations focused on allelic variation (Bowcock et al. 1991) more recent approaches make use of the haplotypic variation (Sabeti et al. 2002). Albrechtsen et al. (2010) develop a method for detecting genome regions that have undergone strong recent selection. Their approach explicitly relates the resulting reduced haplotypic variation to high levels of IBD sharing among individuals.

Under the assumption that the majority of the human genome, and in particular the noncoding sequences, has not been subject to strong selection, haplotypic variation and structure provide information about demographic history (Pluzhnikov et al. 2002). This haplotypic structure is a result of segments of IBD. SNP variants have low mutation rates, so much of the common allelic variation within and among human populations dates back tens of thousands of years. Haplotypic variation reflects lesser but still substantial time depths. A DNA length of say 10⁵ bp will undergo recombination at a rate of order 0.001 per meiosis. Thus most of the common haplotypic variation exhibited in patterns of LD of this extent was established at least 500 generations (12,000 years) ago. The patterns of genetic variation within and among populations, given the wealth of data now available, can provide a much more detailed picture of the major demographic events in human prehistory (Gutenkunst et al. 2009).

Data on chromosome segments provide much stronger evidence than allelic variation at single loci for two reasons. For short segments, within the range of population LD, the haplotype acts as a single “rare allele.” The relative rarity of particular haplotypes can suggest coancestry, but again time-depth information is scant. Longer shared haplotypes across several megabase pairs are a strong signal of recent IBD. Segments of allelic identity of this length are likely to have descended from a recent common ancestor, unbroken by recombination events. The length of shared segments provide some information on the likely time depth, although there is high variance. Population size, patterns of growth, and also patterns and time depth of subdivision all have impacts on the lengths and counts of IBD segments in a population (Chapman and Thompson 2002).

The many new rare variants being uncovered by sequencing genomes from a global array of human populations (1000 Genomes Project Consortium 2010) are providing new information for inferences of the demographics history of populations and the coancestry among them. In the past 2000 years the human population has undergone explosive growth (Cohen 1995). In this period, many rare variants now being revealed by sequencing (Coventry et al. 2010) have become established. Sharing of these rare variants, whether detected directly or via the local haplotypic background on which they arise, provides powerful evidence of coancestry (see Rare variants in human populations). The site-frequency spectra of variants and the sharing of alleles among populations provide new scope for inferences of human demographic history (Gravel et al. 2011). At shorter time depths, long-range haplotype sharing within and across populations provide more detailed demographic evidence. The distributions of segment lengths of inferred IBD can provide a time depth to patterns of changing population size or bottleneck events (Gusev et al. 2012; Palamara et al. 2012).

Summary

Coancestry underlies genetically mediated patterns of similarity among individuals and among populations. The most complete description of the coancestry among a set of gametes is their ARG, but more limited summaries of the ancestry are useful. For each past time point t, and at each point in the genome, the ARG provides the partition of gametes into subsets each descending from a single lineage existing at time t. This is the IBD partition relative to time t. This partition changes along the chromosome due to recombination events more recent than time t in the ancestral lineages. The ARG also defines the segments of genome that descend from the most recent common ancestor of a set of gametes unbroken by recombination. Although analysis of such segments has provided fundamental results on the relationships between IBD and genetic variation (Sved 1971), in terms of defining, inferring, and using IBD, this summary of the ARG seems less useful.

Backward in time, the time to the next coalescent event is exponentially distributed. Across the genome, the genetic distance to the next recombination event is exponential. Exponential distributions have standard deviations equal to their mean. Accordingly the processes of IBD have high variance, across the genome, within defined pedigrees, and in populations. While the probability of IBD at a point in the genome decays exponentially with the number of meioses of separation, m, the length of an IBD segment decreases only linearly in m. Thus in remote relatives, IBD segments are rare but not short (Donnelly 1983). At the population level, probabilities of IBD relative to a past time t increases with t, but the expected lengths of segments decrease, resulting in many more older segments, shorter in length in expectation but again having high variance. This leads to striking differences between the length distribution at given m, and the number of meioses separation among segments of the given length.

At a point in the genome, relative to a recent time point t (perhaps 1200 years or 50 generations), IBD DNA has very high probability of being of the same allelic type, whereas the types of non-IBD DNA are effectively independent. The joint probability of phenotypes of a set of related individuals may thus be expressed as linear weighted sums over the probabilities of IBD states. Jointly among individuals, a consistent pattern of IBD at a locus can be expressed in terms of the IBD graph. Given the IBD graph, or a set of realized IBD graphs, a joint probability of the phenotypes of related individuals can be similarly computed. Whereas pedigree-based probabilities of IBD are the expected proportions of genome IBD, allelic covariances provide estimates of the realized proportions. There are close parallels between the partitioning of variance in IBD and the partitioning of realized allelic variation, both among individuals and among populations.

Across the genome, there is dependence of allelic types (LD) resulting from population structure or remote coancestry. This affects the frame of reference required to define the independence in allelic type of non-IBD DNA. Sharing of a haplotype that is rare in the population is a signal of coancestry or IBD, but there is no absolute measure of haplotypic rarity that defines IBD. For common haplotypic variation, use of current haplotypic frequencies in assessing IBD provides a framework for inferring coancestry, as well as for phasing and imputation. Rare variants can provide a strong signal of coancestry, but provide little time-depth information. With the explosive growth of the human population, there are many young rare variants, typically geographically localized. Many will have arisen more recently than the time depth of IBD typically of interest. Recombination breakpoints creating novel local haplotypes have the same distribution of survival and replication as do these novel variants (Fisher 1954). The common haplotypic variation surrounding a (typed or untyped) novel variant or recombination breakpoint provides information both on IBD and on its likely time depth.

Since IBD gives rise to allelic and phenotypic correlations, it is possible to infer IBD from observed patterns of similarity. For close relatives, pedigree relationships may be estimated or validated from genetic marker data. For more remote relatives, the segmental nature of IBD is key to inference, and longer shared haplotypes provide evidence of recent coancestry. However, even recent coancestry may, by chance, provide only short shared haplotypes; there is no hard threshold length between the longer segments of IBD of recent coancestry and the shorter-range haplotypes that reflect the LD of more remote coancestry. Segment lengths of a given time depth have a high variance in length. Shared segments of a given length can have very different depths of coancestry. There are many recent methods for inference of IBD; most of these focus on pairwise estimation. To obtain a full IBD graph that can be used in a joint analysis of trait data, the pairwise inferences must be combined consistently, not only at each locus but also across loci.

Despite the high variance of the processes involved, and the caveats regarding too close an identification of allelic and descent identity, modern SNP data and now sequencing data are providing a wealth of information. There are many ways in which to measure the processes and probabilities of IBD (The Processes of Identity by Descent). There are many ways to use IBD to analyze patterns of phenotypic variation among related individuals in a defined pedigree or from a population (Phenotypic Similarity and Allelic Variation). There are many ways to estimate relationship and measure relatedness and to detect IBD segments (Inference of Relationships, Relatedness, and IBD Segments). Finally, and most importantly, an IBD approach unifies genetic mapping in pedigrees and populations and across genomic scales from a SNP at a single base pair to haplotypes over several million base pairs. It provides a framework with which to address the heritability of phenotypes, and quantitative variation in populations, and to address the demographic and evolutionary history of our species.

Appendix: Models for IBD Partitions

Each of the ESF and RBT models has a Polya urn interpretation, which provides additional insights into the distributions of the number {a_j} of groups of size j. That for the ESF is due to Hoppe (1984) and provides the formula for the probability of any partition z of the n labeled objects in which there are a_j groups of size j,

$${\pi }_n\left(z\right)={\theta }^{k-1}{\displaystyle \prod _{j=1}^n{\left(\left(j-1\right)!\right)}^{a_j}}/{\displaystyle \prod _{j=1}^{n-1}\left(\theta +j\right)},$$ (A.1)

where ${\displaystyle {\sum }_{j}j{a}_j=n}$ and ${\displaystyle {\sum }_j{a}_j=k}$. Conditional on the number of subsets k

$${\pi }_n\left(z|k\right)={\displaystyle \prod _{j=1}^n{\left(\left(j-1\right)!\right)}^{a_j}}/S_{n,k}\propto \prod _{j=1}^n{\left(\left(j-1\right)!\right)}^{a_j,}$$ (A.2)

where S_n,k is the coefficient of θ^k−1 in (θ + 1)(θ + 2) … (θ + n − 1) (Ewens 2004).

For the Polya urn model for the RBT, we start with an urn with k balls of different color and sample a ball (n − k) times, each time replacing it together with an additional ball of the same color. Hence a particular sequence s of choices resulting in a_j subsets of size j has probability

$${\pi }_n\left(s|k\right)=\left(k-1\right)!{\displaystyle \prod _{j=1}^n{\left(\left(j-1\right)!\right)}^{a_j}}/\left(n-1\right)!\propto {\displaystyle \prod _{j=1}^n{\left(\left(j-1\right)!\right)}^{a_j}.}$$ (A.3)

The apparent similarity of Equations A.2 and A.3 is misleading if the distribution of interest is that of the {a_j}. In the ESF case there are $n!/{\displaystyle {\prod }_j{\left(j!\right)}^{a_j}{a}_j!}$ partitions z with given {a_j} (Hoppe 1984). This provides the ESF result

$${\pi }_n\left(a_1,\dots ,a_n|k\right)=n!{\left(S_{n,k}{\displaystyle \prod _j{j}^{a_j}{a}_j!}\right)}^{-1}.$$ (A.4)

For the RBT, the (j − 1) samplings of each of the a_j colors resulting in a group of size j may be arbitrarily ordered among the (n − k) samplings. Additionally, the k original lineages are unordered. Thus there are $\left(k!/{\displaystyle {\prod }_j{a}_j!}\right)\left({\left(n-k\right)!/{\displaystyle \prod \left(\left(j-1\right)!\right)}}^{a_j}\right)$ sequences resulting in a_j groups of size j, providing for the RBT

$${\pi }_n\left(a_1,\dots ,a_n|k\right)=k!{\left(\left(\begin{array}{c}n-1\\ k-1\end{array}\right){\displaystyle \prod _j{a}_j!}\right)}^{-1}.$$ (A.5)

From Equations A.4 and A.5 we see that the ESF partitions tend to be far more unbalanced than those of the RBT. Due to the extra factors $j^{a_j}$ in the denominator of Equation A.4, the ESF gives higher probabilities of more extreme group sizes, while the RBT gives rise to more balanced group sizes.