Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 May 28;3:1900. doi: 10.1038/srep01900

Graphene/elastomer composite-based photo-thermal nanopositioners

James Loomis 1, Xiaoming Fan 1, Farhad Khosravi 1, Peng Xu 1, Micah Fletcher 1, Robert W Cohn 2, Balaji Panchapakesan 1,a
PMCID: PMC3664893  PMID: 23712601

Abstract

The addition of nanomaterials to polymers can result not only in significant material property improvements, but also assist in creating entirely new composite functionalities. By dispersing graphene nanoplatelets (GNPs) within a polydimethylsiloxane matrix, we show that efficient light absorption by GNPs and subsequent energy transduction to the polymeric chains can be used to controllably produce significant amounts of motion through entropic elasticity of the pre-strained composite. Using dual actuators, a two-axis sub-micron resolution stage was developed, and allowed for two-axis photo-thermal positioning (~100 μm per axis) with 120 nm resolution (feedback sensor limitation), and ~5 μm/s actuation speeds. A PID control loop automatically stabilizes the stage against thermal drift, as well as random thermal-induced position fluctuations (up to the bandwidth of the feedback and position sensor). Maximum actuator efficiency values of ~0.03% were measured, approximately 1000 times greater than recently reported for light-driven polymer systems.

In recent years, nanopositioning systems have impacted areas as diverse as scanning probe microscopy1,2, metrology3,4, advanced manufacturing4,5, biological processes6, materials science7, high density storage/memory8,9, and precision machining10,11. The most common nanopositioning systems are capable of positioning below ~1 nm and employ piezoactuated flexure-based systems with feedback control12,13. Nanopositioning systems based on ferroelectric actuators14, shape memory alloys15, magnetic levitation16,17,18, laser interferometry12,19,20, ultrasonic actuators21,22, and electro-thermal actuators23 have also been demonstrated. While these types of systems are impressive, new types of positioners that employ novel actuation technologies can expand the scope of high-performance and low-cost nanopositioning and nanomanipulation applications.

Since 2004, atomically thin carbon films (graphene) have been the subject of intense research due to remarkable properties such as high mechanical strength, thermal conductivity, electrical conductivity, and quantum Hall effect at room temperature24,25,26,27. Because of these properties, graphene presents an intriguing material in high performance polymer composites. For example, graphene/polymer composites are gaining attention for use in light-weight applications including sports equipment, wind turbines, aircraft composites, and medical implants28. Recent work in the area of graphene nanoplatelet (GNP, ~3–5 layer stacks of graphene)-based photo-actuators has shown an optical-to-mechanical energy conversion factor of 7 MPa/W, reversible actuation, high actuator stresses, saturable absorption, layer and dimensional state dependent mechanical stiffness, low fabrication costs, and ability to integrate with existing commercial electronics and optics29,30,31. Here we demonstrate a novel two-axis nanopositioner based on a simple graphene-elastomer model system that could find utility in future photo- and electro-thermal actuation technologies.

In general, light driven actuators have several advantages including wireless/remote actuation, displacement control using infrared (IR) intensity modulation (controlling number of photons), low noise, massively parallel actuation of positioner arrays from a single light source, and electrical/mechanical decoupling. Past research on photo-mechanical actuators has demonstrated applications in micro-electro-mechanical system (MEMS)-based micro-grippers for manipulation of micro-scale objects32,33, photonic switches34, robotics35, plastic motors36, and adaptive micro-mirrors37. These applications, combined with recent research in carbon nanotube (CNT)/elastomer38,39,40,41,42,43 and graphene/elastomer photo actuators29,30,31 have generated renewed excitement in photo-active materials and their use as micro-/nano-optomechanical systems.

Results

Principle of GnP/elastomer photo-thermal actuation

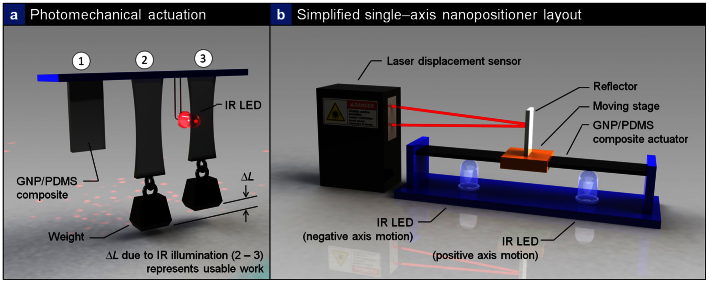
Figure 1(a) presents a schematic demonstrating the principle GNP/elastomer photo-thermal actuation. Unrestricted elastomeric composites with graphene additives (sample [1]) have random polymeric chain arrangement/entanglement. Addition of weight (sample [2]) to the free-end stretches the composites and induces a pre-strain. As entangled polymeric chains are pulled into a more ordered arrangement, system entropy is reduced. When the pre-strained composite sample is heated via IR illumination (sample [3]), light is absorbed by the GNPs within the polydimethylsiloxane (PDMS) matrix; and optical energy is efficiently transduced into thermal energy through phonons in the sp2 graphene sheets44. Due to the high macroscopic thermal conductivity of graphene films45 (300 W/m·K) and intimate dispersion of GNPs within the PDMS matrix, heat is percolated through the matrix causing polymeric chain contraction. Increasing polymeric chain temperature results in an associated increase in spring constant46. Since there is constant force applied (suspended weight), contraction in the composite occurs (following Hooke's law) and lifts the weight, resulting in usable work done through the system by so called “rubbery elasticity”. The large amplitudes of actuation obtainable in graphene/elastomer and nanotube/elastomer systems are directly as a result of the sp2 bonding in the nano-carbons. In general, strong covalent sp2 bonds result in efficient heat transfer by lattice vibrations in the GNPs, and therefore allow for large amplitudes of photo-thermal actuation accomplished through heat transduction from the lattice into the polymeric chains. This thereby enables a unique photo-thermal actuation mechanism in nano-carbon/elastomer composites. In pristine nanotubes and single layer graphene, all bonds are strong sp2 covalent bonds that result in high intrinsic thermal conductivity27,44,47, while reduced graphene oxide is a mixture of sp2 and sp3 bonds. Finally, amorphous carbon and diamond-like carbon contain a large fraction of sp3 bonds that lower system thermal conductivity44. All of these forms can be useful for application-specific tunable photo-thermal actuation amplitudes in carbon/elastomer composites.

Figure 1. Photo-thermal overview.

Figure 1

Open in a new tab

(a) Photo-thermal actuation schematic. Three thin GNP/PDMS composite strips are mounted with their upper ends fixed to a rigid plate. The free end of sample [1] is unrestricted, while samples [2] and [3] have a weight attached, thus inducing pre-strain into the composite actuator. [3] Illumination via an IR LED results in energy transduction to the polymeric chains, causing a contraction in the actuator (and thus usable work). (b) Simplified single-axis nanopositioner layout. A laser displacement sensor is used to measure stage position. Independently controlled diodes on either side of the stage allow for differential positive or negative axis stage motion.

Photo-thermal nanopositioning system

Figure 1(b) presents a simplified model of a single-axis photo-thermal nanopositioning system. In this setup, a thin GNP/PDMS composite strip is held at a fixed pre-strain, a nanopositioning stage is mounted in the composite center, and IR light-emitting diodes (LEDs) placed on either side for differential control via both positive and negative stage actuation (only one LED per side is shown for clarity, real system encompasses three LEDs per side, or six per axis). Illumination of the left LED results in localized heating of the GNP/PDMS composite around the light spot, causing polymeric chain contraction in that region and subsequent stage translation to the left. Conversely, energizing the LED on the right side will cause the stage to translate right. By dynamically modulating IR intensity, a force balance can be enacted on either side of the stage to maintain it in a desired displacement. However, even when the stage is at a set position, LED intensity is still being continuously tuned via a proportional-integral-derivative (PID) control loop which monitors stage position and compensates for thermal drift. This highly dynamic process achieves nanopositioning by controlling polymeric chain extension/contraction through rapidly modulating thermal energy input. Stage displacement is measured with the aid of high speed laser displacement sensor (120 nm resolution) and a reflective element placed on the stage.

GNP/PDMS actuator fabrication and characterization

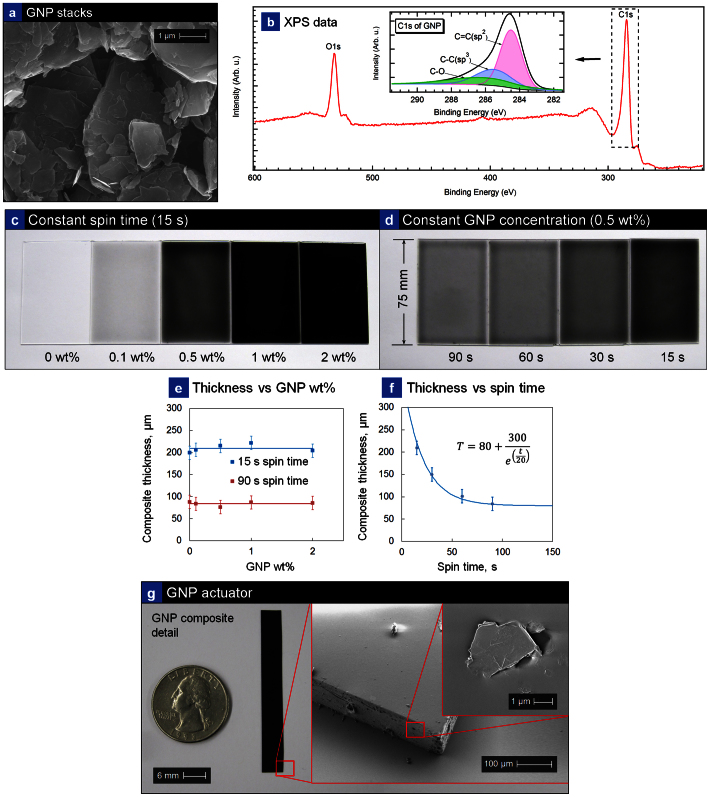
Figure 2(a) presents a scanning electron microscope (SEM) image of GNPs deposited on a silicon wafer. GNPs were verified to be 3–5 layers, with diameters ranging from 1–2 μm. Figure 2(b) presents the photoelectron spectroscopy (XPS) of GNPs. The XPS C1s spectra shows the different binding energy values for different carbon bonds, namely sp3 C-C or C-H (285.5 eV), single C-O bonds (286.1 eV), and sp2 C = C bonds (284.5 eV). Figure 2(b) shows the high levels of deoxygenated sp2 carbon bonds that exist in GNPs, signaling high intrinsic thermal conduction well-suited for photo-thermal actuators presented here. The intensity of sp2 C = C is much higher than the sp3 C-C bonds and C-O bonds. GNPs are still slightly oxidized on the surface as one can see the oxidized C-O bonds.

Figure 2. GNP/PDMS composite characterization.

Figure 2

Open in a new tab

(a) SEM of plain GNP powder (not mixed with PDMS). (b) XPS data. (c) Changes in composite opacity as GNP loading is increased from 0 to 2 wt%. In all five slides, spin time is constant at 15 s. (d) Series of four slides with identical GNP loading (0.5 wt%), but decreasing spin times. (e) GNP/PDMS composite thicknesses are shown as a function of GNP wt% loading. Curves for a 15 s spin time as well as 90 s spin time are displayed. (f) Composite thickness as a function of spin time is shown. Composite samples were fabricated with spin casting times between 15 s to 90 s. (g) Sample GNP composite actuator (2 wt%) used in our two-axis nanopositioners. The first inset is a SEM image showing a corner of the composite strip, and the second insert is a detail of a GNP stack sticking out of the polymer.

Investigating effects of varying fabrication parameters, Figure 2(c) is a series of five slides showing increasing composite opacity with a corresponding increase in GNP loading (from 0 to 2 wt%). In all five slides, spin times and thus composite thickness are constant. Conversely, Figure 2(d) presents a series of four slides, all with identical GNP loading (0.5 wt%), but decreasing spin times. The longest spin time sample (90 s) is the thinnest and the most transparent, while the shortest spin time (15 s) is the thickest and most opaque. Compared to carbon counterparts such as single layer graphene (derived from reduced graphene oxide) and CNTs, GNPs are easy to disperse uniformly and thus are ideal for use in advanced polymer composites. The high level of sp2 carbon bonds, ease of dispersion in polymers via shear mixing, ability to spin-coat, and compatibility with MEMS lithographic processes makes GNP/PDMS more favorable for low-cost commercial manufacturing as compared to all other graphene/polymer composites. Quantitatively, Figure 2(e) shows curves of GNP/PDMS composite thicknesses as a function of GNP wt% loading for 15 s and 90 s spin times. GNP wt% was not observed to have a significant impact on thickness, rather it was observed to be spin time and spin speed-dependent, as shown in Figure 2(f). Finally, Figure 2(g) presents a GNP/PDMS composite actuator prior to mounting in the nanopositioner enclosure (a coin is shown for size comparison). The first inset in this figure is a SEM image showing the composite smooth surface with several nanoplatelet flakes protruding from the cut edges. The second inset shows a detail of a single nanoplatelet stack and the GNP-polymer interface. Figure S1 in the supplementary information (SI) presents further microscopic investigation into differences in the GNP-polymer interface in cross-sections of 0, 1, and 2 wt% composites. Fabrication of the polymer composites consisted of shear mixing GNPs in PDMS, spin-coating large area thin films, polymerization, and cutting 50 mm × 6 mm actuator strips (strained 50% to 75 mm for use in nanopositioners).

Nanopositioner system integration

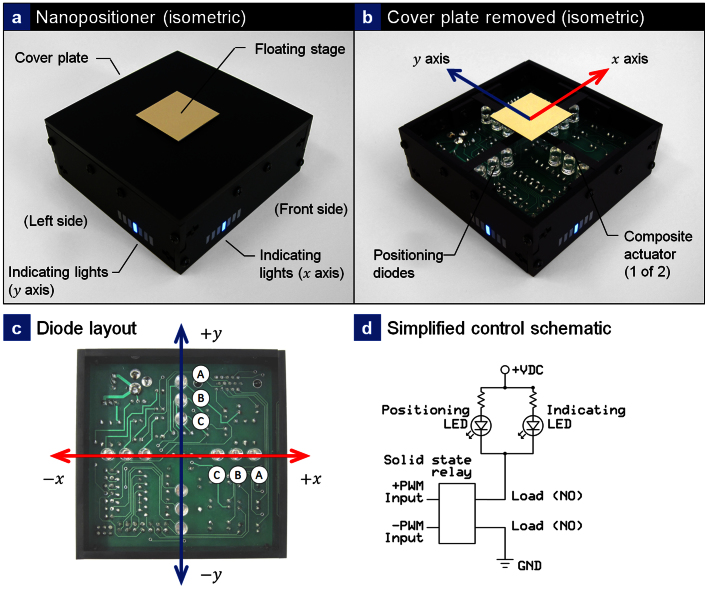
Following fabrication and characterization of graphene/elastomer composite actuators, they are integrated into a compact nanopositioning system incorporating a laser-cut enclosure housing multiple IR LEDs, custom electronics, and control software. Figure 3(a) presents an isometric overview of a fully assembled two-axis nanopositioner (82 mm × 82 mm × 30 mm). A removable cover plate encloses two GNP/PDMS actuators and their respective positioning diodes. A cutout in the cover plate allows for mounting a floating stage on the actuators underneath. Indicating lights on the front (x axis) and the left side (y axis) provide a visual operator tool by displaying positioning diode status. A single blue LED is illuminated on each axis indicating the nanopositioner is powered, since no other lights are lit the floating stage is in the home position (0,0). Details regarding the control system setup can be found in the SI.

Figure 3. Nanopositioner overview.

Figure 3

Open in a new tab

(a) Isometric of fully assembled nanopositioner. (b) Nanopositioner with cover plate removed, showing positioning diodes and dual GNP/PDMS composite actuators. (c) Top view of the nanopositioner with the actuators removed, clearly showing diode layout. (d) Simplified control schematic for a single positioning diode.

In Figure 3(b), the cover plate has been removed, exposing two GNP/PDMS composite actuators and their associated IR positioning LEDs. Six positioning diodes are mounted underneath each strained GNP/PDMS composite actuator strip (12 total for the two-axis system). The diode arrangement allows for independent differential stage control along both the x and y axes. While positioning diodes and GNP actuators are mounted to the top of the printed circuit board (PCB), all other electronics are mounted on the bottom side. Figure 3(c) presents a clarified top view of the nanopositioner with the cover plate and GNP actuators removed to show the diode layout. This orientation shows differential arrangement between positive and negative positioning diodes. Along their respective axes, IR LEDs closest to the home position [origin of (0,0)] were designated as “C”, those in the middle as “B”, and the diodes farthest away as “A”. Figure 3(d) shows a simplified electrical schematic for a single positioning diode. A pulse-width modulation (PWM) signal drives a solid state relay that turns the positioning diode on/off. Visible wavelength indicating diodes from the position sensor serve as an operator feedback tool and are electrically connected in parallel and mounted externally on the nanopositioner to duplicate positioning diode intensity. To precisely control energy transduction to the polymeric chains and thus stage position, continuous high-speed intensity tuning of each diode is required. Therefore diode control for each axis was allocated to an independent PID controller, which was chosen due to ease of implementation and widespread industrial use. A discussions regarding PID loop implementation can be found in the SI.

Kinetics of photo-thermal nanopositioners

In order to determine stage kinetics, diode maximum displacement tests were conducted on various GNP wt% composites (of identical thicknesses). Figure 4(a) shows maximum displacement testing results as a function of GNP wt% loading for two different positioning diode types (coarse adjust, high-power IR diode and fine adjust, low-power diode). A discussion in the SI provides insight as to the advantages and tradeoffs of selecting high power vice low power IR diodes. While there was initially a sharp increase in maximum displacement with increasing GNP concentration, loadings beyond ~0.75 wt% resulted in negligible additional stage travel demonstrating saturation of the photo-thermal response. The maximum displacement (xmax) responses as a function of GNP wt% were fit to equation (1) for both low power and high power diode, where δ is the displacement coefficient, and ϕ the load adjustment factor. Figures S3(a) and (b) in the SI present detailed displacement versus time data during a single run. While high power IR diodes enable large actuator displacements, for a fixed number of intensity steps, lower power diodes allow for finer temperature control and resolution, resulting in more accurate stage positioning.

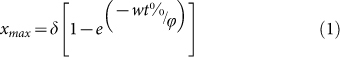graphic file with name srep01900-m1.jpg

Having witnessed the effect of high and low power diodes on maximum stage displacements, composites thickness was also found to affect overall stage kinetics. Figure 4(b) shows stage displacement responses for 90 μm and 210 μm thick composites (thinnest and thickest films made). Curves shown were fit to the raw data using equation (2), where t is the time, τ is a time constant, and β is a drift adjustment factor.

graphic file with name srep01900-m2.jpg

Interestingly, thinner composites actuated faster, yet had lower maximum displacements than their thicker counterparts. With a fixed number of diode intensities available by our control setup, a composite with a larger displacement also had lower resolution. Conversely, while thinner samples have smaller maximum displacements, they also have finer control steps. The curve fitting in equation (2) to the experimental data show that the actuation and relaxation followed simple Debye characteristics and therefore a unique actuation mechanism29. Unlike CNT/PDMS actuators which follow a compressed exponential function for actuation29, GNP/PDMS actuators were found to not only follow a simple exponential function during both actuation and relaxation, but also exhibit about a three times faster response29. While for the same wt% loading, photo-thermal amplitude of CNT/PDMS composites is larger than the GNP/PDMS system, however large amplitudes are only realized with efficient dispersion that results in high energy percolation within the composites. As CNTs are difficult to separate into individual nanotubes (vice bundles) and disperse uniformly within the polymeric matrix, CNT/PDMS composite fabrication is highly labor intensive with low yields making them expensive to produce. Conversely, GNPs are quite easy to disperse due to their rigid morphology, number of graphitic layers, and lack of adhesion or clumping between individual stacks.

Figure 4. Positioning diode response characterization.

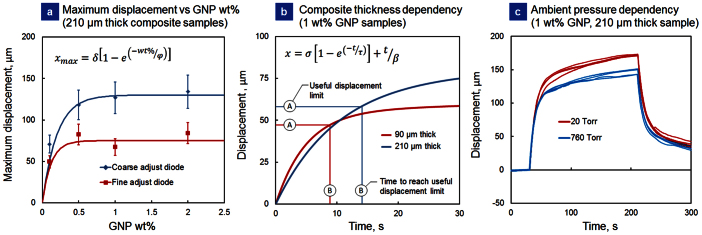
Figure 4

Open in a new tab

(a) Maximum stage displacement as a function of GNP wt% loading for coarse adjust and fine adjust positioning diodes. (b) Displacement kinetics as a function of composite actuator thickness for a 1 wt% GNP sample. Useful displacement limit and time are also indicated. (c) Displacement versus time curves shown for a 1 wt% GNP sample at ambient pressure (760 Torr) and at medium vacuum (20 Torr).

Useful displacement versus maximum displacement

While curves in Figure 4(a) show maximum displacement as a function of GNP wt%, these reported values are steady-state equilibrium positions reached only after relatively long time periods (~180 s). While possible to achieve these displacements, due to long wait times required, they are not necessarily useful for practical nanopositioning applications. Therefore, additional criteria were set to determine useful displacement versus maximum displacement. This was achieved via selection of a tripwire value for slope of the displacement versus time curve. It was determined that when the displacement curve slope equaled 2 represented the best balance between (1) quick actuation times; (2) a large portion of maximum possible displacement; and (3) still allowed ample additional displacement control for maintaining the stage in position. Therefore, taking the derivative of the displacement [equation (2)], setting it equal to 2, and solving for time (t) yields equation (3).

graphic file with name srep01900-m3.jpg

Applying this constraint to the plots in Figure 4(b), the displacement curve for the thin (90 μm) composite sample reached a slope of 2 at 8.5 s, representing a displacement of ~47.2 μm (~50% of maximum displacement). For the thicker sample (210 μm), a slope of 2 was reached at 14 s, representing a displacement of ~58 μm, or ~60% of maximum. Thereby, a two-axis nanopositioner outfitted with the thin composite would have a total travel of ~94 μm per axis (2 × 47.2 μm), and outfitted with the thick composite would have a total travel of 116 μm per axis (2 × 58 μm). Finally, actuation speed was calculated by dividing the usable displacement by the time required to reach those values yielded velocities of ~5.5 μm/s (90 μm “thin” composite) and ~4.1 μm/s (210 μm “thick” composite). These velocity values can be improved significantly through use of much thinner composite actuators (<1 μm). However, such ultra-thin composites will need new preparation steps as they are difficult to handle. One such solution is integration of thinner films onto MEMS substrates with on-chip positioning stages to improve photo-thermal actuation velocity.

Vacuum dependency of photo-thermal nanopositioner

Many systems that utilize micro- and nanomanipulation technologies require operation in a vacuum. Therefore, in order to evaluate feasibility of photo-thermal nanopositioners as replacement actuation systems for work in vacuum environments, stage response pressure dependency was measured. Figure 4(c) presents displacement versus time curves for a 1 wt% 210 μm thick composite sample at atmospheric pressure (760 Torr), as well as in a medium vacuum (20 Torr). Interestingly, at lower pressure (20 Torr), displacement was ~30% higher than at atmospheric pressure, indicating as pressure decreases there is an associated drop in composite heat loss due to natural convection. Simply stated, as pressure is reduced, convective heat loss is minimized and identical diode intensity results in larger displacement. As pressure (P) is reduced, density of the fluid (ρ) follows, as equation (4) shows, where R is the specific gas constant. Since the heat transfer coefficient is proportional to fluid (air) density, as pressure decreases, so does the heat transfer coefficient [equation (5)]. Since 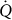Inline graphic, A, and T∞ remain constant, composite temperature must increase, as equation (6) shows. Since the pre-strained composite temperature is increasing, additional actuation is realized resulting in larger stage displacement under vacuum conditions. For future scaled-down photo-thermal systems that utilize actuators with submicron thicknesses, as ambient pressure decreases stage velocities are expected to increase due to lowered friction between gas molecules.

graphic file with name srep01900-m4.jpg
graphic file with name srep01900-m5.jpg
graphic file with name srep01900-m6.jpg

While initial results are promising, further testing and characterization are required to determine nanopositioner suitability for use in high vacuum systems (such as in an SEM). Furthermore, one must consider that under vacuum, the positioning resolution of a given diode decreases (larger overall displacement for the same number of available PWM steps). Scaling effects also significantly affect heat loss versus heat generation in a vacuum environment at micro and nanometer length scales, and warrants further investigation. Finally, material properties of polymers and their outgassing rates should be determined before practical development of nanopositioners for vacuum environments. Therefore, vacuum-rated photo-thermal nanopositioners will require additional investigation before practical implementation to maintain the same performance characteristics as their ambient pressure-operated counterparts.

Accuracy and resolution

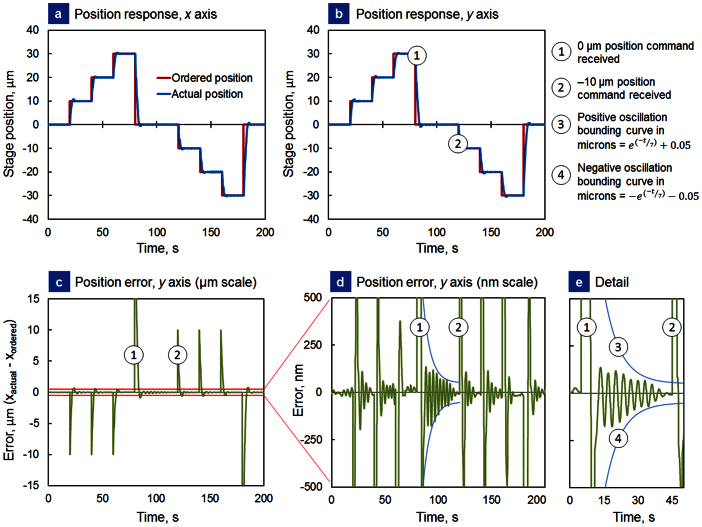
Nanopositioner ability to accurately respond to and maintain ordered positions was evaluated with x and y axes set to automatic (PID loop) control. Nanopositioners were given a sequence of ordered commands, and automated stage response monitored. Figures 5(a) and (b) show positioner response to a command sequence for x and y axes. Stage response (blue curve) is plotted against position command (red curve). Figures 5(c)–(e) show error between ordered and actual position with scale bars in μm and nm respectively. Large spikes are due to mismatch between actual and ordered positions upon new command receipt (annotations [1] and [2]). Figure 5(e), clearly shows the error spike [1] as the new position command is received, and the subsequent decay of the bounding oscillations (curves [3] and [4]). These oscillations although smaller than 120 nm are a result of filtering/averaging within the laser control head. While in reality, true resolution of the displacement sensor could be less than 120 nm, the manufacturer's specification on the laser displacement sensor used for stage position feedback is 120 nm, therefore we consider this the resolution limit for our nanopositioner. In follow-on generations, incorporation of capacitive displacement to monitor stage position (vice the current laser displacement system) can potentially increase positioner resolution to sub-10 nm48. Armed with increased resolution, stage positioning accuracy can be improved further through modifications such as (1) PID loop tuning, (2) incorporation of coarse adjust as well as fine adjust diodes into a single axis, and (3) higher frequency PWM control with a larger number of intensity steps.

Figure 5. Stage response and stability in automatic control mode to position requests for both the x and y axes (1 wt% GNP composite).

Figure 5

Open in a new tab

Ordered and actual (a) x axis and (b) y axis positions. Stage was ordered to sequentially move to positions +10 μm, +20 μm, +30 μm, and then −10 μm, −10 μm, −10 μm. Annotations [1] and [2] indicate position commands for 0 μm and −10 μm respectively. (c) Sample positioning error (xactual − xordered) with μm scale. Spikes are due to mismatch between actual and ordered position when the control loop receives a new position request. (d) Sample positioning error (xactual − xordered) with nm scale. (e) Detail of position response and subsequent stage oscillations. Positive and negative oscillation bounding curves are indicated by annotations [3] and [4] respectively.

Ideal for use in systems requiring precise positioning control/manipulation, such as probe stations and optical microscopes, photo-thermal nanopositioners were evaluated for use in several real-world tasks. For example, a nanopositioner was mounted to an optical microscope (Nikon Eclipse L150) for microsphere positioning. Figure 6 shows a sequence as the spheres are moved to positive and negative x and y axes displacement limits (arrows show the direction of movement). For clarification, a microsphere has been circled in red, clearly showing ~100 μm per axis photo-actuated positioning.

Figure 6. Actual stage response under optical microscope.

Figure 6

Open in a new tab

Sequence of four images show the nanopositioner moving microspheres along the −x, +x, −y, and +y axes. A single microsphere is circled in red, and crosshairs have been added for clarity.

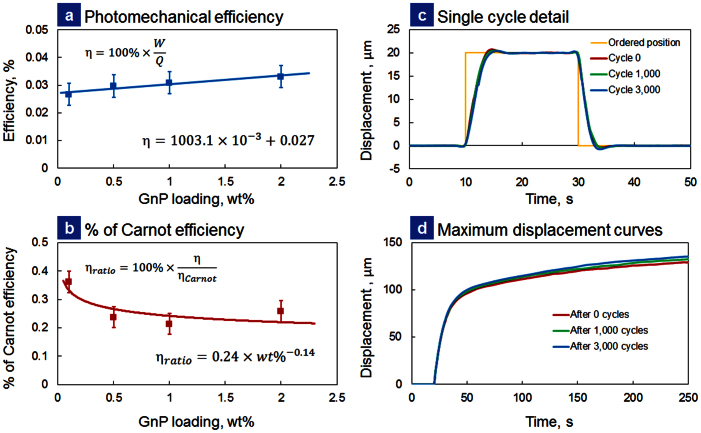
Energy conversion efficiency

Graphene addition to elastomers not only creates high mechanical strength composites and photo-thermal actuation, but also could potentially be viable system for energy harvesting49. An important nanopositioner aspect is energy efficiency at converting IR illumination into (x,y) stage movement. Therefore, efficiency (η) of the GNP composites to a known IR illumination source was evaluated. Figure 7(a) presents the efficiency relationship as a function of GNP loading. Interestingly, a slight increase in efficiency with increased GNP loading was found, which ranged from ~ 0.027% (0.1 wt% GNPs) to ~0.033% (2 wt% GNPs). Efficiency calculation details can be found in the SI. Since graphene-elastomer photo-thermal actuation system is an example of a heat engine, measured efficiency was compared to maximum possible Carnot efficiency, 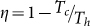Inline graphic. While an identical IR illumination source was used, due to varying GNP loadings in the composites different Th temperatures were realized. For example, a 0 wt% GNP sample (optically clear50) experienced negligible temperature change, while 2 wt% GNP samples showed ~50°C change. Because of the larger temperature change, higher wt% composites had a larger maximum possible Carnot efficiency. Likewise, they also did more work and had a larger measured efficiency than their lower wt% counterparts. However, the looming question was – did the higher wt% composites use a larger portion of the available Carnot efficiency? Therefore, a ratio of measured to Carnot efficiency was determined [equation (7)] and simplified [equation (8)].

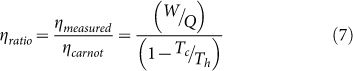graphic file with name srep01900-m7.jpg
graphic file with name srep01900-m8.jpg

Figure 7. Photo-thermal efficiency and long-term degradation.

Figure 7

Open in a new tab

(a) Photo-thermal efficiency versus GNP loading. (b) Photo-thermal efficiency divided by Carnot efficiency. (c) Stage position versus time curves are plotted for 0 cycles, 1,000 cycles, and 3,000 cycles. (d) Maximum displacement curves shown were conducted before the 1st cycle, the 1,000th cycle, and the 3,000th cycle.

As Figure 7(b) shows, while just a small amount of GNPs (0.1 wt%) resulted in a small composite temperature change, it was most efficient at transduction of this temperature change into useful work. By 0.5 to 2 wt%, the ηratio was approximately equal. To summarize, incorporation of a small amount of GNPs into a composite results in an actuator that uses the largest percentage of maximum possible efficiency, this low wt% composite also results in the smallest amount of work in response to the same IR illumination source. In comparison, past–light driven actuators based on polyvinyledene difluoride (PVDF) have demonstrated an efficiency value of ~8.3 × 10−5% under quasi-static motion51, about three orders of magnitude less efficient than our graphene-elastomer systems (~3 × 10−2%). Furthermore, improvements in efficiency for graphene-elastomer composites might be possible by using single layer graphene fillers and nanoscale thickness composite actuators.

Long-term cycling and composite actuator degradation response

Experiments were also conducted to determine composite degradation as a function of repeated cycling. Figure 7(c) is a plot showing this 1st cycle, the 1,000th cycle, and the 3,000th cycle. In order to monitor composite degradation, every 250 cycles the positioner performed a maximum displacement test. Figure 7(d) show the results of a maximum displacement test after 0, 1,000 and 3,000 cycles. As these plots show, even after 3,000 cycles, there was minimum-observed degradation, which demonstrates high lifetime of composite actuators. Additionally, a supplementary study was conducted which evaluated the incident on/off frequency dependence of the actuator (results are presented in Figures S4 and S5 in the SI). Actuator stage peak-to-peak amplitude was seen to decay exponentially with increasing IR illumination cycling frequency (up to 5 Hz). Future device miniaturization can enable high frequency operation of photo-thermal nanopositioners which could be useful for on-chip scanning nanomanipulation applications with enhanced signal to noise ratio.

Discussion

This work introduces a new class of nanopositioners that exploit photo-thermal actuation mechanism in graphene-elastomer composites. Compared to electro-mechanical transduction, photo-mechanical/photo-thermal actuation offers an alternative way to couple energy into actuator structures offering distinctive advantages such as wireless actuation, remote controllability, electrical-mechanical decoupling, low noise, and scalability through existing MEMS processing technology. Unfortunately, few material systems have been shown to exhibit photo-mechanical actuation properties and are often not compatible with complementary metal-oxide-semiconductor (CMOS)/MEMS processing techniques. For example, photo-mechanical actuation has been achieved in PVDF52, azobenzene53, shape memory polymers54, liquid crystal elastomers55, and chalcogenide glasses56. However, practical nanopositioner systems based on the previously mentioned technologies are rare. The system presented here is simple, low-cost, and could be integrated with myriad of systems such as optical microscopes and probe stations. Furthermore, numerous properties such as distribution of graphene networks, percolation threshold, elastomer matrix material, polymer chain segmental length, and composites thickness can be tuned to enable higher levels of control in future nanopositioning systems with a wide variety of application-specific tailorable parameters.

While at first it may seem that polymers are not an ideal material system for positioning applications due to thermal drifts, these drifts are corrected for using the differential dynamic photon-intensity modulation setup presented. Furthermore, ability to transduce photon energy into thermal energy that can change polymer chain mobilities at rapid pace to produce reversible actuation makes this system interesting to study. Tunability of sp2/sp3 graphene bonds in polymer composites could potentially result in extraordinary research systems with high mechanical strength, high intrinsic thermal conductivity, excellent electrical properties, and fast photo-thermal actuation. The uniqueness of our system – ability to dynamically tune IR intensity/temperature to change mechanical stiffness of the polymer chains in localized composite areas – makes this nanopositioner highly internally dynamic. One drawback of this work is that resolution of the feedback system limits the nanopositioner resolution to ~120 nm, however this is still better than the ~170 nm resolution recently reported for a polysilicon-based thermal nanopositioners23. Current photo-thermal nanopositioner resolution limitations are due to the feedback system employed, not the actuators themselves. Hence next generation devices could incorporate capacitive as well as interferometric feedback resulting in much finer control, and achieve sub-10 nm resolution similar to recently demonstrated on-chip electro-thermal nanopositioning systems57. Further development of graphene/polymer composite–based nanopositioners will extend the promising potential of graphene-based actuation technologies and will serve as a catalyst to inspire continued research into energy efficient transduction systems.

Methods

General setup

Research grade GNPs were purchased from Cheap Tubes, Inc. (>700 m2/g surface area, <3 nm thickness, <4 layers) and were used in original form and not surface modified at any time. PDMS silicone elastomer obtained from Dow Corning (Sylgard 184) was used as the host matrix. PDMS is a two-part solvent-free flexible silicone organic polymer in the form of a base compound with a separate hydrosilane curing agent that acts as a crosslinker. Composite actuators were fabricated on Fisherbrand 50 × 75 mm glass slides. All experiments were conducted in a climate-controlled laboratory.

GNP/PDMS composite actuator fabrication

Standard MEMS processes were used to spin cast large area thin composite films on glass substrates. These films were subsequently cut into 50 mm long by 6 mm wide strips for use as actuators [as Figure 2(g) shows, strained 50% to 75 mm when mounted in the nanopositioner]. Composite actuators were fabricated with GNP loadings from 0 to 2 wt% and thicknesses from 90 μm to 210 μm. Film thickness (T) was dependent on spin time (t), as shown by equation (9).

graphic file with name srep01900-m9.jpg

Amount of absorbed IR light dictates actuator displacement and kinetics. At constant spin time, wt% and opacity are directly proportional, while at constant wt%, opacity and spin time are inversely proportional.

GNP/PDMS composites were fabricated by weighing the desired amount of GNPs and adding to the PDMS base compound. The additive/base compound combination was shear mixed for 5 min to facilitate carbon distribution. Taking into account the GNPs, crosslinker was added at a ratio of 1:10 (to the PDMS base compound) and further shear mixed for 5 min. To remove trapped air pockets, prepared polymers were degassed for 30 min. Small amounts (~3 g/slide) of liquid polymer mixtures were deposited on the glass slides. Standard spin coating processing (750 rpm, 15 to 90 s) was used to produce thin films on the glass slides. The slides were then cured at 65°C for 4 h to finish the cross-linking process in the polymer. Once cured, GNP/PDMS films were cut into 6 mm wide strips in preparation for mounting in the nanopositioner housing.

Nanopositioner fabrication

A custom control PCB was design in-house and sent out for fabrication. The nanopositioner frame was assembled from matte finish black acrylic sheet. Mechanical design was completed in SolidWorks and actual acrylic pieces cut using an Epilog laser cutter. Electronic components were sourced from Mouser, with final nanopositioner soldering and assembly completed in the Small Systems Laboratory. LabVIEW-based control software was written that allowed for a variety of control modes and characterization sequences (Figure S6 in the SI is a software screenshot and associated description).

Nanopositioner testing

A high speed laser displacement sensor (MTI Instruments, Microtrak II, LTC-025-02) was used as position feedback. Detailed information regarding test sequencing and data analysis can be found in the “test sequencing” section of the SI.

Author Contributions

J.L. and B.P. designed the experiments and wrote the manuscript. J.L. designed the nanopositioner and wrote the software. X.F. and P.X. conducted XPS spectroscopy. F.K. assisted with SEM imaging. R.C. assisted with experimental concepts and discussions. M.F. of the Math Science Technology (MST) program at Manual High School (Louisville, KY) assisted J.L. with conducting experiments.

Supplementary Material

Supplementary Information

Supplementary Info

srep01900-s1.pdf (2.1MB, pdf)

Acknowledgments

Funding for this work was supported by NSF awards ECCS 1202190 and CMMI 1233996, for one of the authors (B.P.).

References

  1. Binnig G. & Rohrer H. Scanning Tunneling Microscopy. Helv Phys Acta. 55, 726–735 (1982). [Google Scholar]
  2. Binnig G., Quate C. F. & Gerber C. Atomic Force Microscope. Phys Rev Lett. 56, 930–933 (1986). [DOI] [PubMed] [Google Scholar]
  3. Yoshida S. Nanometrology. Metrologia. 28, 433–441 (1992). [Google Scholar]
  4. Nakayama K., Tanaka M., Shiota F. & Kuroda K. Precision Physical Measurements and Nanometrology. Metrologia. 28, 483–502 (1992). [Google Scholar]
  5. Feinberg B. Dimensional Metrology in Manufacturing - Need for Relevance. Manuf Eng Manage. 70, 27–30 (1973). [Google Scholar]
  6. Shao Z. F., Yang J. & Somlyo A. P. Biological atomic force microscopy: From microns to nanometers and beyond. Annu Rev Cell Dev Bi. 11, 241–265 (1995). [DOI] [PubMed] [Google Scholar]
  7. Brown N. M. D. Scanning Probe Microscopies-Applications in Material Science. Advances in Engineering Materials. 99–1, 161–168 (1995). [Google Scholar]
  8. Esch J. Prolog to High-density data storage based on the atomic force microscope - An introduction to the paper by Mamin, Ried, Terris, and Rugar. P Ieee. 87, 1012–1013 (1999). [Google Scholar]
  9. Mamin H. J., Ried R. P., Terris B. D. & Rugar D. High-density data storage based on the atomic force microscope. P Ieee. 87, 1014–1027 (1999). [Google Scholar]
  10. Elmustafa A. A. & Lagally M. G. Flexural-hinge guided motion nanopositioner stage for precision machining: finite element simulations. Precision Engineering-Journal of the International Societies for Precision Engineering and Nanotechnology. 25, 77–81 (2001). [Google Scholar]
  11. Schumacher H. W., Keyser U. F., Zeitler U., Haug R. J. & Eberl K. Controlled mechanical AFM machining of two-dimensional electron systems: fabrication of a single-electron transistor. Physica E. 6, 860–863 (2000). [Google Scholar]
  12. Yeh H. C., Ni W. T. & Pan S. S. Digital closed-loop nanopositioning using rectilinear flexure stage and laser interferometry. Control Eng Pract. 13, 559–566 (2005). [Google Scholar]
  13. Shim J. Y. & Gweon D. G. Piezo-driven metrological multiaxis nanopositioner. Rev Sci Instrum. 72, 4183–4187 (2001). [Google Scholar]
  14. Weinacht M., Martin G., Tarakanov E. A. & Yushin N. K. Ferroelectric Actuators with Precision Displacement Control. Russ Ultrason. 25, 30–33 (1995). [Google Scholar]
  15. Ganor Y., Shilo D., Messier J., Shield T. W. & James R. D. Testing system for ferromagnetic shape memory microactuators. Rev Sci Instrum. 78, (2007). [DOI] [PubMed] [Google Scholar]
  16. Verma S., Kim W. J. & Gu J. Six-axis nanopositioning device with precision magnetic levitation technology. Ieee-Asme T Mech. 9, 384–391 (2004). [Google Scholar]
  17. Gu J., Kim W. & Verma S. Nanoscale motion control with a compact minimum-actuator magnetic levitator. J Dyn Syst-T Asme. 127, 433–442 (2005). [Google Scholar]
  18. Verma S., Shakir H. & Kim W. J. Novel electromagnetic actuation scheme for multiaxis nanopositioning. Ieee T Magn. 42, 2052–2062 (2006). [Google Scholar]
  19. Yeh H. C., Ni W. T. & Pan S. S. Real-time motion control with subnanometer heterodyne interferometry. Int J Mod Phys D. 11, 1087–1099 (2002). [Google Scholar]
  20. Lazar J., Klapetek P., Cip O., Cizek M. & Sery M. Local probe microscopy with interferometric monitoring of the stage nanopositioning. Meas Sci Technol. 20 (2009). [Google Scholar]
  21. Snitka V. Ultrasonic actuators for nanometre positioning. Ultrasonics. 38, 20–25 (2000). [DOI] [PubMed] [Google Scholar]
  22. Fan K. C. & Lai Z. F. An intelligent nano-positioning control system driven by an ultrasonic motor. Int J Precis Eng Man. 9, 40–45 (2008). [Google Scholar]
  23. Hubbard N. B. & Howell L. L. Design and characterization of a dual-stage, thermally actuated nanopositioner. J Micromech Microeng. 15, 1482–1493 (2005). [Google Scholar]
  24. Novoselov K. S. et al. Electric field effect in atomically thin carbon films. Science. 306, 666–669 (2004). [DOI] [PubMed] [Google Scholar]
  25. Lu Q., Arroyo M. & Huang R. Elastic bending modulus of monolayer graphene. Journal of Physics D-Applied Physics. 42, (2009). [Google Scholar]
  26. Gusynin V. P. & Sharapov S. G. Unconventional integer quantum Hall effect in graphene. Physical Review Letters. 95, (2005). [DOI] [PubMed] [Google Scholar]
  27. Balandin A. A. et al. Superior thermal conductivity of single-layer graphene. Nano Lett. 8, 902–907 (2008). [DOI] [PubMed] [Google Scholar]
  28. Kuilla T. et al. Recent advances in graphene based polymer composites. Prog Polym Sci. 35, 1350–1375 (2010). [Google Scholar]
  29. Loomis J. et al. Graphene-nanoplatelet-based photomechanical actuators. Nanotechnology. 23, (2012). [DOI] [PubMed] [Google Scholar]
  30. Loomis J., King B. & Panchapakesan B. Layer dependent mechanical responses of graphene composites to near-infrared light. Appl Phys Lett. 100, (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Loomis J. & Panchapakesan B. Dimensional dependence of photomechanical response in carbon nanostructure composites: a case for carbon-based mixed-dimensional systems. Nanotechnology. 23, (2012). [DOI] [PubMed] [Google Scholar]
  32. Lu S. X. & Panchapakesan B. Nanotube micro-optomechanical actuators. Appl Phys Lett. 88, (2006). [Google Scholar]
  33. Lu S. X., Liu Y., Shao N. & Panchapakesan B. Nanotube micro-opto-mechanical systems. Nanotechnology. 18, (2007). [Google Scholar]
  34. Comstock M. J. et al. Measuring reversible photomechanical switching rates for a molecule at a surface. Appl Phys Lett. 92, (2008). [Google Scholar]
  35. Uchino K., Poosanaas P. & Tonooka K. Photostrictive actuators - New perspective. Ferroelectrics. 264, 1961–1966 (2001). [Google Scholar]
  36. Yamada M. et al. Photomobile polymer materials: Towards light-driven plastic motors. Angew Chem Int Edit. 47, 4986–4988 (2008). [DOI] [PubMed] [Google Scholar]
  37. Lu S. & Panchapakesan B. All-optical micromirrors from nanotube MOMS with wavelength selectivity. J Microelectromech S. 16, 1515–1523 (2007). [Google Scholar]
  38. Ahir S. V. & Terentjev E. M. Photomechanical actuation in polymer-nanotube composites. Nature Materials. 4, 491–495 (2005). [DOI] [PubMed] [Google Scholar]
  39. Ahir S. V. & Terentjev E. M. Fast relaxation of carbon nanotubes in polymer composite actuators. Phys Rev Lett. 96, (2006). [DOI] [PubMed] [Google Scholar]
  40. Lu S. X. & Panchapakesan B. Optically driven nanotube actuators. Nanotechnology. 16, 2548–2554 (2005). [Google Scholar]
  41. Lu S. X. & Panchapakesan B. Photomechanical responses of carbon nanotube/polymer actuators. Nanotechnology. 18, (2007). [Google Scholar]
  42. Lu S. X., Ahir S. V., Terentjev E. M. & Panchapakesan B. Alignment dependent mechanical responses of carbon nanotubes to light. Appl Phys Lett. 91, (2007). [Google Scholar]
  43. Ahir S. V., Terentjev E. M., Lu S. X. & Panchapakesan B. Thermal fluctuations, stress relaxation, and actuation in carbon nanotube networks. Phys Rev B. 76, (2007). [Google Scholar]
  44. Balandin A. A. Thermal properties of graphene and nanostructured carbon materials. Nature Materials. 10, 569–581 (2011). [DOI] [PubMed] [Google Scholar]
  45. Wu H. & Drzal L. T. Graphene nanoplatelet paper as a light-weight composite with excellent electrical and thermal conductivity and good gas barrier properties. Carbon. 50, 1135–1145 (2012). [Google Scholar]
  46. James E. Mark B. E. Rubberlike Elasticity, A Molecular Primer. (Cambridge University Press, 2007). [Google Scholar]
  47. Choi S. U. S., Zhang Z. G., Yu W., Lockwood F. E. & Grulke E. A. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl Phys Lett. 79, 2252–2254 (2001). [Google Scholar]
  48. Xia S. & Nihtianov S. Power-Efficient High-Speed and High-Resolution Capacitive-Sensor Interface for Subnanometer Displacement Measurements. IEEE Trans. Instrum. Meas. 61, 1315–1322 (2012). [Google Scholar]
  49. Gabor N. M. et al. Hot Carrier-Assisted Intrinsic Photoresponse in Graphene. Science. 334, 648–652 (2011). [DOI] [PubMed] [Google Scholar]
  50. Cai D. K., Neyer A., Kuckuk R. & Heise H. M. Optical absorption in transparent PDMS materials applied for multimode waveguides fabrication. Optical Materials. 30, 1157–1161 (2008). [Google Scholar]
  51. Sarkisov S. S. et al. Light-driven actuators based on polymer films. Opt Eng. 45, (2006). [Google Scholar]
  52. Sarkisov S. S., Curley M. J., Fields A., Sarkisov S. S. & Adamovsky G. Photomechanical effect in films of polyvinylidene fluoride. Appl Phys Lett. 85, 2747-2749 (2004). [Google Scholar]
  53. Seki T. & Tamaki T. Photomechanical Effect in Monolayers of Azobenzene Side-Chain Polymers. Chem Lett 1739–1742 (1993). [Google Scholar]
  54. Lendlein A., Jiang H. Y., Junger O. & Langer R. Light-induced shape-memory polymers. Nature. 434, 879–882 (2005). [DOI] [PubMed] [Google Scholar]
  55. Ikeda T., Mamiya J. & Yu Y. L. Photomechanics of liquid-crystalline elastomers and other polymers. Angew Chem Int Edit. 46, 506–528 (2007). [DOI] [PubMed] [Google Scholar]
  56. Stuchlik M., Krecmer P. & Elliott S. R. Opto-mechanical effect in chalcogenide glasses. Journal of Optoelectronics and Advanced Materials. 3, 361–366 (2001). [Google Scholar]
  57. Zhu Y., Bazaei A., Moheimani S. O. R. & Yuce M. R. A Micromachined Nanopositioner With On-Chip Electrothermal Actuation and Sensing. Ieee Electr Device L. 31, 1161–1163 (2010). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Info

srep01900-s1.pdf (2.1MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES