Spatial variation of permittivity of an electrolyte solution in contact with a charged metal surface: a mini review

Abstract

Contact between a charged metal surface and an electrolyte implies a particular ion distribution near the charged surface, i.e. the electrical double layer. In this mini review, different mean-field models of relative (effective) permittivity are described within a simple lattice model, where the orientational ordering of water dipoles in the saturation regime is taken into account. The Langevin-Poisson-Boltzmann (LPB) model of spatial variation of the relative permittivity for point-like ions is described and compared to a more general Langevin-Bikerman (LB) model of spatial variation of permittivity for finite-sized ions. The Bikerman model and the Poisson-Boltzmann model are derived as limiting cases. It is shown that near the charged surface, the relative permittivity decreases due to depletion of water molecules (volume-excluded effect) and orientational ordering of water dipoles (saturation effect). At the end, the LPB and LB models are generalised by also taking into account the cavity field.

1. Introduction

The functional activity of cells in contact with an implant is determined by the physical properties of the cell membrane (Boulbitch et al. 2001) and the material characteristics of the implant (Gongadze et al. 201 lb). The most widely used implant material is titanium (Gongadze et al. 2011b), because it is not rejected by the body. The interactions between the charged metal implant surface and the surrounding bone tissue are essential for the successful integration of the bone implant. It was indicated recently that the strength of interaction between a charged titanium surface and osteoblast cells strongly depends on the properties of the intermediate electrolyte (Teng et al. 2000; Oghaki et al. 2001; Smith et al. 2004; Kabaso et al. 2011). Contact between a charged metal implant or electrode surface and an electrolyte implies a particular ion distribution near the charged surface, i.e. the electrical double layer (EDL) which is the subject of this work.

Helmholtz (1879) treated the double layer mathematically as a capacitor, based on a physical model in which a layer of ions of opposite charge (counterions) with a single shell of hydration around each ion (the so-called Helmholtz layer) is adsorbed at the oppositely charged surface and neutralises its charge. Gouy (1910) and Chapman (1913) also considered the thermal motion of ions and pictured a diffuse double layer composed of counterions attracted to the surface and ions of the same charge (co-ions) repelled by it, embedded in a dielectric continuum of constant permittivity. Such a distribution of ions in the EDL can be described within the mean-field Poisson-Boltzmann (PB) theory (Gouy 1910; Chapman 1913; Stern 1924; McLaughlin 1989; Safran 1994; Kralj-Iglič and Iglič 1996; Lamperski and Outhwaite 2002; Manciu and Ruckenstein 2002; Bivas 2006; Bivas and Ermakov 2007; Bazant et al. 2009), expressing the competition between electrostatic interactions and the configurational entropy of ions in the solution. The Gouy-Chapman diffuse double layer is more extended than the single molecular Helmholtz layer.

Within the standard PB theory (Cevc 1990), the finite size of ions is not taken into account (except by the Stern distance of closest approach); therefore, the number density of counterions at the charged surface may exceed the upper value corresponding to their close packing. Different attempts have been made to incorporate steric effects into a modified PB theory in order to prevent the prediction of an unrealistically high number densities of counterions close to the charged surface.

The first attempt to include the finite size of ions in PB theory was made by Stern (1924) who combined Helmholtz (1879) and Gouy–Chapman models (Gouy 1910; Chapman 1913). In its simplest version, the Stern model considers only the finite size of the counterions whose centres can approach the charged surface only to a certain distance, the so-called outer Helmholtz plane (Butt et al. 2003).

Later Bikerman (1942) proposed a modified PB model (Bikerman model) to account for the finite size of ions and solvent molecules. Bikerman's modified PB equation and the corresponding Fermi–Dirac-like distribution of ions has been later derived and justified using other different methods (Grimley and Mott 1947; Grimley 1950; Freise 1952; Dutta and Sengupta 1954; Eigen and Wicke 1954; Wiegel and Stating 1993; Kralj-Iglič and Iglič 1996; Lamperski and Outhwaite 2002). Among others, Freise (1952) introduced the finite size of ions by a pressure-dependent potential, while Eigen and Wicke (1954) used a thermodynamic approach. More recently, Bikerman's predictions have been reformulated within the PB theory based on a lattice statistics model and density functional theory (Kralj-Iglič and Iglič 1996). The finite size of ions has also been described by other density functional approaches (Trizac and Raimbault 1999; Barbero et al. 2000) and by considering the ions and solvent molecules as hard spheres (Lamperski and Outhwaite 2002; Biesheuvel and van Soestbergen 2007). Also Monte Carlo simulations are widely used in order to describe the finite-sized counterions (Biesheuvel and van Soestbergen 2007; Tresset 2008; Ibarra-Armenta et al. 2009; Zelko et al. 2010).

An oft-stated assumption in most PB models is that the relative permittivity in the electrolyte is constant (McLaughlin 1989; Cevc 1990; Hianik and Passechnik 1995; Lamperski and Outhwaite 2002; Butt et al. 2003). But actually, close to the charged surface the water dipoles cannot move as freely as further away from it. Besides, due to accumulation of counterions near the charged metal surface, the water molecules are partially depleted from this region (see e.g. Gruen and Marcelja 1983; Butt et al. 2003; Iglič et al. 2010; Gongadze et al. 2011a, 2011c). In addition, the dipole moment vectors of water molecules at the charged metal surface are, due to the strong electric field of the charged surface, partially oriented towards the surface, while all orientations of water dipoles further away from the charged surface are equally probable. The water orientation near the charged membrane surface is important for many biological processes such as binding of ligands to active sites of enzymes, transport of ions through channel proteins or adhesion of cells to an implant surface (McLaughlin 1989; Cevc 1990; Israelachvili and Wennerström 1996; Butt et al. 2003; Arsov et al. 2009; Gongadze et al. 2011a, 2011b; Kabaso et al. 2011).

As shown in the past, the properties of the EDL may be influenced by the ordering of water molecules in the region of the EDL (Gruen and Marcelja 1983; Outhwaite 1983; Cevc 1990; Coalson and Duncan 1996; Israelachvili and Wennerström 1996; Butt et al. 2003; Manciu and Ruckenstein 2004; Arsov et al. 2009) and the depletion of water molecules (Gongadze et al. 2011a). Close to the charged surface the orientation of water molecules may result in spatial variation of permittivity (Outhwaite 1976; Gongadze et al. 2011a, 2011b; Butt et al. 2003). However, in the absence of an explicit consideration of the orientational ordering of water molecules, the assumption of constant permittivity is largely a consequence of the constant number of water molecules in PB theory. Considering this effect, Outhwaite developed a modified PB theory of the EDL composed of a mixture of hard spheres with point dipoles and finite size ions (Outhwaite 1976, 1983). The problem was also considered within lattice statistics (Iglič et al. 2010; Gongadze et al. 2011a).

In this mini review, we describe the mean-field density functional theory of spatial variation of permittivity of an electrolyte solution in contact with a charged surface by taking into account the orientational ordering of water molecules within the lattice statistical mechanical approach, assuming that ions and solvent molecules occupy sites in a square lattice. In the model, the relative permittivity is consistently related to the spatial distribution of electric field strength and the distribution of ions. The finite volume of ions and water molecules (Lamperski and Outhwaite 2002; Iglič et al. 2010) in the electrolyte solution is taken into account. Accordingly, the number density of water is not constant in the whole electrolyte solution (Iglič et al. 2010; Gongadze et al. 2011a).

In the present article, we compare the predictions of the mean-field lattice EDL model considering the orientational ordering of water molecules (Figure 1) in the Langevin-Bikerman (LB) model for finite-sized ions and in the Langevin-Poisson-Boltzmann (LPB) model for pointlike ions. The Bikerman model for finite-sized ions and zero dipole moments of water molecules (Bikerman 1942) is derived as a limiting case of the LB model. The interplay between water ordering and the volume-excluded effect in the decrease of permittivity near the charged surface is discussed. The dependence of the relative permittivity and the electric potential on the distance from the charged plane in the vicinity of charged surface is compared in different models. Comparison between the predictions of both Langevin models and the Stern model is discussed. In the LB and LPB models (Iglič et al. 2010; Gongadze et al. 2011a), the cavity and reaction field as well as the structural correlations between water dipoles (Onsager 1936; Kirkwood 1939; Booth 1951; Fröhlich 1964; Franks 1972) are not taken into account. Therefore, at the end of the article, generalisation of the LPB and LB models by taking into account the cavity field in the saturation regime (Booth 1951) (i.e. at high values of electric field strength) is presented within the Booth–Poisson–Boltzmann (BPB) model for point-like ions and within the modified Langevin-Bikerman (MLB) model for finite-sized ions (Gongadze and Iglič 2012).

Figure 1.

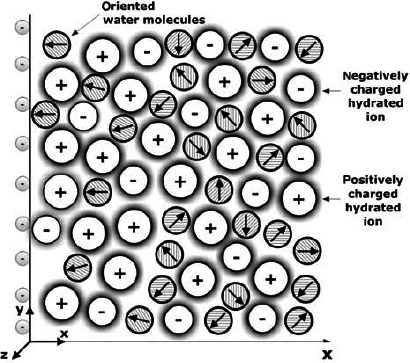
Schematic figure of an EDL near a negatively charged planar surface. The water dipoles in the vicinity of the charged surface are partially oriented towards the surface.

2. LB model considering the finite size of ions and spatial variation of the relative permittivity

We consider a planar uniformly charged surface in contact with a solution of monovalent ions (counterions and coions) and water dipoles of finite size. The charged surface bears a charge with a surface charge density σ. The x-axis of the Cartesian coordinate system points in a direction from the charged plane to the bulk solution (Figure 1). The water molecules are assumed to have non-zero dipole moments (p). A lattice with an adjustable lattice site is introduced in order to describe the system of water dipoles and salt ions. All lattice sites are occupied by ions or water dipoles. For the sake of simplicity, we assume that a single lattice site is occupied by only one ion or water. No empty lattice sites are allowed in the model. If the volume of one lattice site is closer to the volume of a single water molecule than to the volume of a single ion, this means that we allow partial overlapping of the ions at number densities which are close to the saturation densities of the ions. Oppositely, if the volume of the lattice site is closer to the volume of a single ion, this means the water dipole describes a cluster of water molecules.

The free energy of the system (functional) F can be written as

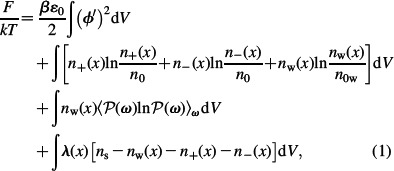where the first term in Equation (1) corresponds to the energy of the electrostatic field. Here, ∊₀ is the permittivity of free space, kT is the thermal energy, β = 1/kT, ϕ(x) is the electric potential, n₀ is the bulk number density of ions, ϕ′ is the first derivative of ϕ with respect to x, dV = Adx is the volume element with thickness dx, where A is the area of the charged surface. The second line in Equation (1) accounts for the contribution to the free energy due to configurational entropy of the positive and negative salt ions (see Appendix), n₊ and n₋ are the number densities of positively and negatively charged ions, respectively (taking into account n_w(x) = n_s – n₊(x) – n_–(x)), n_w is the number density of water dipoles, n_s is the number density of lattice sites, n₀ is the bulk number density of positively and negatively charged ions, while n_0w is the bulk number density of water dipoles. We assume ϕ(x→ ∞) = 0. The third line of Equation (1) accounts for the orientational contribution of water dipoles to the free energy. ℘(x) is the probability that the water dipole located at x is oriented at an angle ω with respect to the normal to the charged surface, i.e. ω is the angle between the dipole moment vector p(x) and the vector ∇ϕ/|∇ϕ|. Here, averaging over all angles, ω is defined as

where dΩ is the element of solid angle 2πsinωdω. The last line in Equation (1) is the constraint due to the finite size of particles within lattice statistics (Kralj-Iglič and Iglič 1996):

imposing the condition that each site of the lattice is occupied by only one particle (co-ion, counterion or water), λ(x) is the local Lagrange parameter, n_s = 1/a³, where a is the width of a single lattice site. In bulk solution, Equation (3) transforms into:

where n_0w is the bulk number density of water dipoles. In the limit of small n₊(x), n_–(x) and n₀, everywhere in the solution the configurational entropy of ions (the second line in Equation (1)) transforms into:

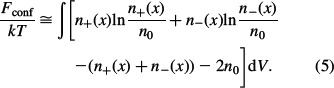At any position x we require the normalisation condition:

to be fulfilled. The above expression for the free energy can be rewritten in the form:

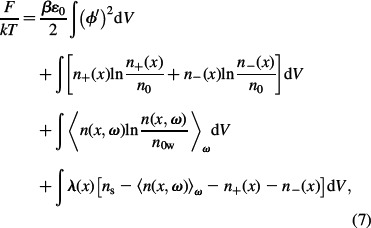where the distribution function of water dipoles n(x, ω) is defined as:

and where the validity of Equation (6) was taken into account in the third line of Equation (7), as well as in the fourth line of Equation (7) where

In most EDL models, the relative permittivity is taken into account a priori rather than deriving it as in the present work. For this purpose, the average microscopic volume charge density ρ(x) should be considered by including the contribution of the local net ion charges and the dipole moments, presented by the polarisation P (see e.g. Evans and Wennerström 1994; Jackson 1999):

The polarisation P(x) is given by

where p is the water dipole moment, angle ω describes the orientation of the dipole moment vector with respect to vector ∇ϕ/|∇ϕ| and < p(r, ω)_B is its average (at coordinate x) over the angle distribution in thermal equilibrium. In our case σ < 0; therefore, the projection of polarisation vector P on the x-axis points in the direction from the bulk to the charged surface. Hence P(x) is considered negative. According to the Boltzmann distribution law (Safran 1994), the relative probability of finding a water dipole in an element of solid angle dΩ = 2πsinωdω is proportional to the Boltzmann factor exp(–W_d/kT), where

is the energy of the water dipole p in the electric field E = – ∇ϕ, p₀ is the magnitude of the water dipole moment and ω is the angle between the dipole moment vector p and the vector ∇ϕ/|∇ϕ| (i.e. the x-axis in our case of negative σ. Hence:

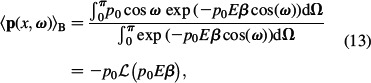where p₀ is the magnitude of the water dipole moment and E = |ϕ∇| is the magnitude of the electric field strength. For σ < 0, it follows that E = |ϕ∇| = |ϕ∇|. The function ℒ(u) = (coth(u) – 1/u) is the Langevin function. The Langevin function ℒ(p₀Eβ) describes the average magnitude of the water dipole moments for given E(x). In our derivation, we assume azimuthal symmetry, i.e. we assume that for given ω the dipole moment vector p orients itself uniformly around the x-axis.

In thermal equilibrium F adopts a minimum with respect to the functions n₊(x), n₋(x) and n(x, w). The results of the variational procedure are (Iglič et al. 2010):

Inserting Equations (14)–(16) into the constraint (3) and taking into account n_w(x) = 〈n(x, ω)〉_ω (Equation (9)) yields the local Lagrange parameter λ(x):

where the function H is related to the finite particle size:

In the above derivation of λ(x) we took into account:

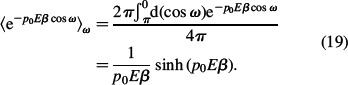Using Equations (9) and (16), we get the following expression for the number density of water dipoles n_w(x):

Taking into account Equations (17)–(19) it follows from Equations (14), (15) and (20) that:

Combining Equations (11), (13) and (23) yields the polarisation:

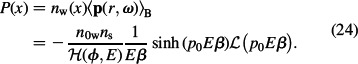Using the definition

Equation (24) can be rewritten as:

Using Equation (26) and the distribution functions (21) and (22), the expression for the average microscopic volume charge density of electrolyte solution (Equation (10)) reads:

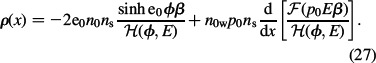Inserting the volume charge density (27) into the Poisson equation (Jackson 1999)

where ϕ″ is the second derivative of ϕ with respect to x, we get:

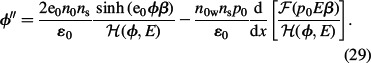The differential equation (29) has two boundary conditions, where the first is obtained by integration of the differential equation (29):

Here, the condition of electro-neutrality of the whole system was taken into account. The second boundary condition is:

Equations (29) and (30) can be rewritten in more general form as (Iglič et al. 2010)

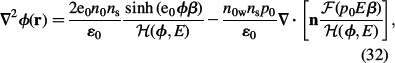where n = ∇ϕ/∇ϕ| = ∇ϕ/E. Equation (32) may be further rearranged as:

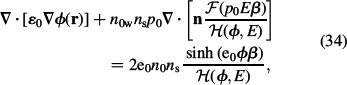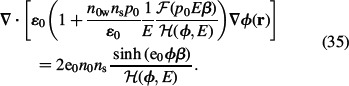The above Equation (35) can be finally written in the LB form of the Poisson equation as (Gongadze et al. 2011a, 2011b)

where ρ_free(r) is the macroscopic (net) volume charge density of co-ions and counterions (see also Equations (21) and (22)):

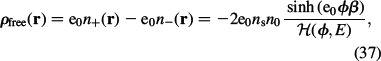while ∊_r(r) is the relative permittivity of the electrolyte solution in contact with the charged surface:

The above expression for ∊_r(r) (Equation (38)) is consistent with the usual definition of relative permittivity (Gongadze et al. 2010, 2011a):

where P is the polarisation vector. Also the boundary condition (33) can be further rearranged as follows:

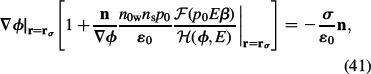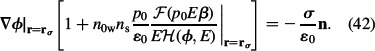Using the definition of the relative permittivity (Equation (38)), the above boundary condition can be finally written as

or

The second boundary condition is:

In this paper, the LB Equation (37) was solved numerically for planar geometry using the finite element method (FEM) within the Comsol Multiphysics 3.5a Software program package (COMSOL AB, Stockholm, Sweden). The space dependence of ∊_r(r) (Equation (38)) in Equation (36) was taken into account in an iterative procedure, where the initial value of ∊_r(r) is constant equal to the permittivity of the bulk solution. The boundary conditions (44) and (45) are taken into account.

Figure 2 shows the calculated spatial dependence of ∊_r(r) for three values of the surface charge density σ. The decrease in ∊_r(r) towards the charged surface for larger values of |σ| is a consequence of the increased orientational ordering of water dipoles (saturation effect) and the increased depletion of water molecules (Figure 3) near the charged surface due to accumulation of counterions (Figure 3).

Figure 2.

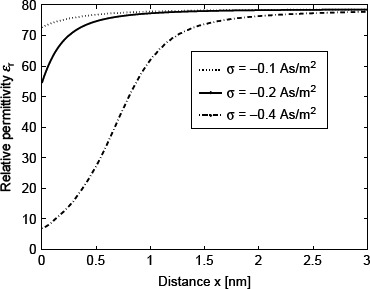
Relative permittivity ∊_r (Equation (38)) as a function of the distance from the charged surface x within the LB model for finite-sized ions. Three values of surface charge density were considered: σ = —0.1 As/m², σ = −0.2 As/m² and σ = –0.4 As/m². Equation (36) was solved numerically as described in the text. The dipole moment of water p₀ = 4.794 D, bulk concentration of salt n₀/N_A = 0.15 mol/1, bulk concentration of water n₀/N_A = 55 mol/1, where N_a is the Avogadro number.

Figure 3.

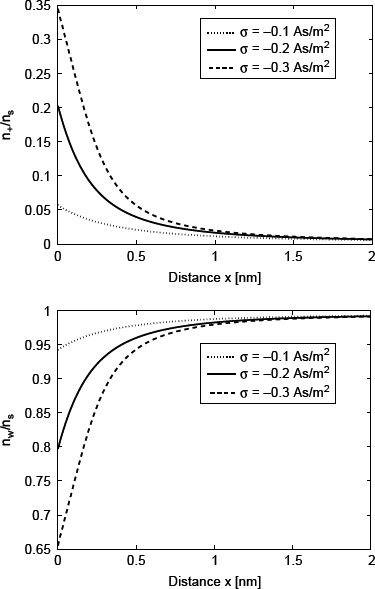
Therelativenumberdensityofcounterions(n₊/n_s) and water Langevin dipoles (n_w/n_s) as a function of the distance from the charged surface x (calculated using Equations (21) and (23), respectively) within the LB model for finite-sized ions. Three values of surface charge density were considered: σ = −0.1 As/m², σ = −0.2 As/m² and σ = −0.3 As/m². Equation (36) was solved numerically as described in the text. The other values of the model parameters are the same as in Figure 2.

The distribution functions (21)–(23) can also be derived without minimisation of the system free energy by using only Boltzmann factors within lattice statistics (Gongadze et al. 2011c). Here again the finite size of molecules is considered by assuming that ions and water dipoles are distributed in a lattice, where each lattice site is occupied by only one of the three molecular species (cations, co-ions and water molecules).

Since in the bulk solution, i.e. far away from the charged surface, the number densities of water molecules (n_0w), counterions (n₀) and co-ions (n₀) are constant, their number densities can be expressed in a simple way by calculating the corresponding probabilities that a single lattice site is occupied by one of the three particle types in the electrolyte solution (counterions, co-ions and water molecules):

where n_s = 2n₀ + n_0w as defined before (see Equation (4)). Closer to the charged surface, the number densities of ions and water molecules are influenced by the charged surface so the probabilities that the single lattice site is occupied by one of the three kinds of particles should be corrected by the corresponding Boltzmann factors (Gongadze et al. 2011c):

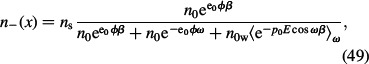where 〈e^{−p₀E cos ωβ}〉_ω (Equation (19)) is the dipole Boltzmann factor after rotational averaging over all possible angles ω. Using the definition of ℋ (Equation (18)), we can rewrite Equations (48)–(50) in the form of Equations (21)–(23).

3. Bikerman and PB models

In the limit of p₀ → 0, the particle distribution functions (21)–(23) transform into Fermi-Dirac-like distributions in the form (Bikerman 1942; Grimley and Mott 1947; Grimley 1950; Freise 1952; Dutta and Sengupta 1954; Eigen and Wicke 1954; Wiegel and Strating 1993; Iglič and Kralj-Iglič 1994; Kralj-Iglič and Iglič 1996):

while the LB equation for finite-sized ions (Equation (29)) transforms into the Bikerman equation:

where we made the transformation ∊₀ → ∊_r∊₀ with ∊_r = 78.5. In the limit of small e₀ϕβ, where the finite size of molecules can be neglected, the above Fermi-Dirac-like distributions of ions and water molecules yield Boltzmann distribution functions for ions and a constant distribution for water molecules (Gouy 1910; Chapman 1913; McLaughlin 1989; Cevc 1990; Bivas 2006):

while Equation (54) transforms into the PB equation (Gouy 1910; Chapman 1913; McLaughlin 1989):

where we took into account n₀ ≪ n_0s and therefore n_s ≈ n_0w.

4. LPB model considering spatial variation of the relative permittivity for point-like ions

In this section, we describe the LPB mean-field model of the EDL for point-like ions, where the spatial variation of permittivity (i.e. orientational ordering of water dipoles) is taken into account. Again we consider a planar-charged surface with surface charge density σ in contact with a water solution of monovalent ions (counterions and co-ions). Unlike in Section 2, the finite volume of ions and water in the electrolyte solution is not taken into account. Accordingly, the volume density of water is constant in the whole electrolyte solution (Equation (57)) (Kralj-Iglič and Iglič 1996), while the configurational entropy of the ions can be expressed by Equation (5). Therefore, the free energy of the system F can be written as (see also Equation (1))

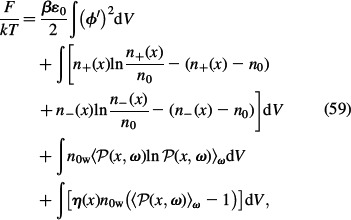where n_0w is the constant number density of water dipoles. The first term in Equation (59) corresponds to the energy of the electrostatic field. The second and the third line in Equation (59) account for the free energy contribution due to the configurational entropy of counterions and co-ions (Equation (5)). Again we assume ϕ(x→∞) = 0. The fourth line in Equation (59) accounts for the orientational contribution of water dipoles to the free energy. ℘(x, ω) is the probability that the water dipole located at x is oriented at an angle ω with respect to n = ∇ϕ/|∇ϕ|. The last line is the local constraint for the orientation of water dipoles valid at any position x (Equation (6)). The results of the variation of the above free energy give the Boltzmann distributions for counterions and co-ions:

and the orientational probability density:

where Λ(x) is a constant for given x. According to Equation (62), the polarisation value (Equation (11)) can be calculated as follows:

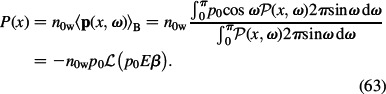The Langevin function ℒ(p₀Eβ) describes the average magnitude of the water dipole moments at given x. In our derivation, we assumed an azimuthal symmetry. Inserting the Boltzmann distribution functions of ions (Equations (60) and (61)) and the expression for polarisation (Equation (63)) into Equation (10), we get the expression for the volume charge density in an

Inserting the above expression for volume charge density ρ(x) (Equation (64)) into the Poisson Equation (Equation (28)), we get the LPB equation for point-like ions (Gongadze et al. 2010; Gongadze et al. 2011a):

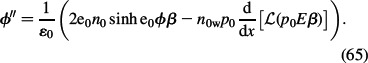The LPB differential equation for point-like ions (65) is subject to two boundary conditions. The first is obtained by integrating the differential equation (65):

The condition requiring electro-neutrality of the whole system was taken into account in the derivation of Equation (66). The second boundary condition is (31). Similarly as we did in the case of the LB model for finite-sized ions, also Equations (65) and (66) can be rewritten in the more general form of the LPB equation as

where ρ_free(r) is the macroscopic (net) volume charge density of co-ions and counterions (see also Equations (60) and (61)):

and ∊_r(r) is the relative permittivity of the electrolyte solution in contact with the charged surface:

The corresponding boundary condition at the charged surface is

where the relative permittivity ∊_r(r) is defined by Equation (69). The second boundary condition is

The above-defined relative permittivity ∊_r(r) is consistent with the definition (Gongadze et al. 2010; Gongadze et al. 2011a):

where P is the polarisation. Equation (69) describes the dependence of the relative permittivity ∊_r on the magnitude of the electric field strength E calculated within the presented LPB model which takes into account the orientational ordering of water dipoles near the charged surface (Figure 1). The finite size of ions is not taken into account in Equation (69).

The LPB Equation (37) was solved numerically for planar geometry using the FEM within the Comsol Multiphysics 3.5a Software program package as already described above. The space dependence of ∊_r(r) (Equation (69)) in Equation (67) was taken into account in an iterative procedure, where the initial value of ∊_r(r) is constant and equal to the permittivity of the bulk solution. The boundary conditions (70) and (71) are taken into account.

Figure 4 shows the spatial dependence of ∊_r(r) calculated within the LPB model for point-like ions (Equation (69)) using two values of the surface charge density σ. The decrease in ∊_r towards the charged surface is now a consequence of the increased orientational ordering of water dipoles near the charged surface only. Therefore, it is less pronounced than in the case of the LB model for finite-sized ions (Figure 2), where the depletion of water molecules near the charged surface additionally decreases ∊_r(r).

Figure 4.

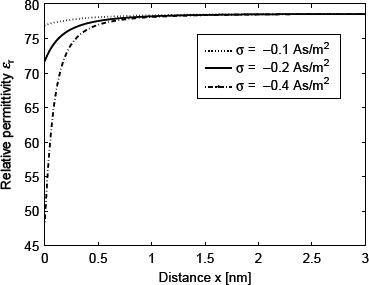
Relative dielectric permittivity ∊_r (Equation (69)) as a function of the distance from the charged surface x within the LPB model for point-like ions. Three values of surface charge density were considered: σ = −0.1 As/m², σ = −0.2 As/m² and σ = −0.4 As/m². The LPB equation (67) was solved numerically as described in the text. The dipole moment of water p₀ = 4.794 D, bulk concentration of salt n_0w/N_a = 0.15 mol/1, bulk concentration of water n_0w/N_a = 55 mol/1, where N_a is the Avogadro number.

For p₀Eβ < 1, we can expand the Langevin function in Equation (72) into a Taylor series up to the cubic term: ℒ(u) ≈ u/3 − u³/45 to get:

It can be seen in Equation (73) that ∊_r decreases with increasing magnitude of electric field strength E. Since the value of E increases towards the charged surface (see e.g. McLaughlin 1989), ∊_r decreases towards the charged surface. It is therefore plausible that due to preferential orientation of water dipoles in the close vicinity of the charged surface, the relative permittivity of the electrolyte ∊_r near the charged surface is reduced relative to its bulk value as shown in Figure 4.

In the approximation of a small electrostatic energy and small energy of dipoles in the electric field compared to thermal energy, i.e. small e₀ϕβ and small p₀Eβ, also the relative permittivity within the LB model for finite-sized ions (Equation (38)) can also be expanded into a Taylor series to get:

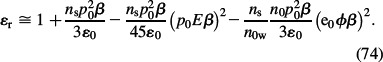Assuming n_s ≈ n_0w it follows from Equation (74) that:

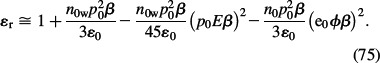In the limit of vanishing electric field strength (E → 0) and zero potential (ϕ → 0), Equations (73) and (75) predict:

5. Comparison of LPB and LB models

Comparison of the approximative expression for the relative permittivity ∊_r, calculated within the LB model for finite-sized ions (Equation (75)) and within LPB theory for point-like ions (Equation (73)), we can see that the first three terms in the expansions are equal in both models. The third term represents the effect of orientation of water molecules in the electric field near the charged membrane surface. The fourth term in Equation (75) describes the decrease in ∊_r near the charged membrane surface due to depletion of water dipoles, because of the accumulation of counterions. Based on Equations (75) and (73), it can be concluded that the relative permittivity of the electrolyte near the charged membrane surface is reduced relative to its bulk value due to preferential orientation of water molecules and due to depletion of water molecules in the close vicinity of the charged surface.

Figure 5 shows the electric potential as a function of the distance from the charged planar surface (x) calculated within the LPB model and the LB model. It can be seen that the potential drop near the charged surface is largest in the LB model which takes into account the finite size of ions, while in the LPB model for point-like ions the potential drop is smaller; this can be explained by the larger value of ∊_r(r) near the charged surface for point-like ions than for finite-sized ions, as shown in Figures 2 and 4.

Figure 5.

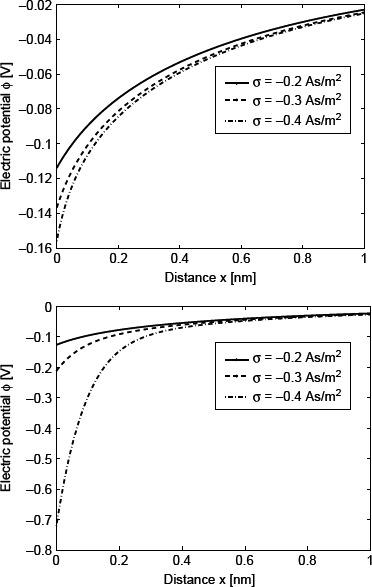
Electric potential ϕ as a function of the distance from the charged planar surface x within the LPB model for point-like ions (upper figure) and within the LB model for finite-sized ions (lower figure) for three values of the surface charge density; σ = −0.2 As/m², σ = −0.3 As/m² and σ = −0.4 As/m². The dipole moment of water p₀ = 4.794 D, bulk concentration of salt n₀/N_a = 0.15 mol/1 and bulk concentration of water n_0w/N_a = 55mol/1.

6. Stern model and the distance of closest approach

6.1. Stern model

Within the Stern model (Stern 1924; Butt et al. 2003), the concentration of charged ions obeys the Boltzmann distribution law (Equations (55) and (56)), while the electrostatic potential is determined by the PB equation (Equation (58)). What makes the Stern model different from the usual PB (Gouy-Chapman) theory for point-like ions (Gouy 1910; Chapman 1913; McLaughlin 1989; Safran 1994) is the distance of closest approach of ions (b) to the charged surface, so the PB Equation (58) in the simplest version of the Stern model is replaced by

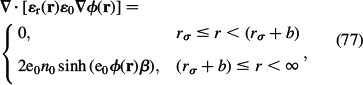where the relative dielectric permittivity ∊_r(r):

is constant over the whole space.

6.2. Stern–Langevin–Poisson–Boltzmann and Stern–Langevin–Bikerman models

Generalisation of the above Stern model within LPB theory for point-like ions includes the orientational ordering of water dipoles, while the ions are still considered as point-like particles as described in Section 4:

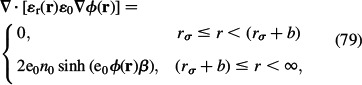where the relative permittivity ∊_r(r) is defined by Equation (69):

Note that we assumed the validity of Equation (80) also for r < (r_σ + b).

A further generalisation of the Stern model is the Stern-Langevin-Bikerman (SLB) model for finite-sized ions (Section 2):

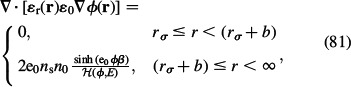where the relative permittivity ∊_r(r) is defined by Equation (38):

Note that for the sake of simplicity, the validity of Equation (82) is assumed also for r < (r_σ + b).

6.3. SLB model with a step function

In order to better capture the discrete character of the thin layer of ordered water molecules at the charged surface, the continuous dependence of relative permittivity ∊_r(r) (Equation (82)) in the region r_σ ≤ r < (r_σ + a), where a = n_s^−1/3 is the width of a single lattice site, may be described by a step function. Hence

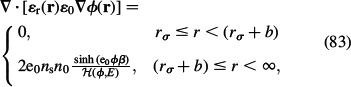where the relative permittivity ∊_r(r) is defined (based on Equation (82)) as

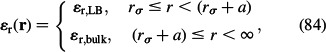where 0 ≤ c ≤ a. The parameter a thus defines the region of preferentially oriented water molecules (Figure 6).

Figure 6.

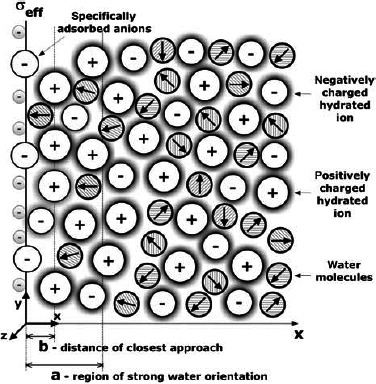
Charge distribution SLB model (Gongadze et al. 2011c), where in the interval 0 < x < a is the region of strong water orientation and b is the distance of closest approach. The surface charge density σ = σ_eff incorporates the negatively charged metallic surface, as well as the specifically bound negatively charged ions (Butt et al. 2003).

6.4. Boundary conditions

As already shown above, the boundary conditions at the charged surface r = r_σ are consistent with the condition of electro-neutrality of the whole system:

The validity of Gauss's law at r = r_σ + b is fulfilled by:

The electric potential should also be continuous at r = r_σ + b:

In the case of the SLB model, the validity of Gauss's law should be fulfilled not only at r_σ + b but also at r_σ + a:

where also

Due to the screening effect of the negatively charged surface caused by the accumulated cations, far away from the charged metal surface the electric field strength tends to zero, which means that the electric potential is constant. As already taken into account in the above derivations (see e.g. Equation (31)), we assume:

6.5. Spatial variation of electric potential in different models

Figure 7 shows the electric potential as a function of the distance from the charged planar surface (x) calculated within the classical Stern model, the Stern-Langevin-PB (SLPB) model, the SLB model and the SLB model with the relative permittivity represented as a step function. The potential drop near the charged surface is the smallest in the Stern model where ∊_r(r) is constant everywhere in solution and equal to its bulk value. As expected, the electric potential changes linearly in the region 0 < x < b, but then for x > b the slope (i.e. the electric field strength) changes substantially (see Figure 7). The main reason for such behaviour is that the electric field strength close to the charged surface in the region 0 < x < b (where the free ions are depleted) is determined by the boundary condition at the charged metal surface (at x = 0). Therefore, in this region the electric field strength is E = −ϕ′ = − σ/∊_r(x = 0)∊₀.

Figure 7.

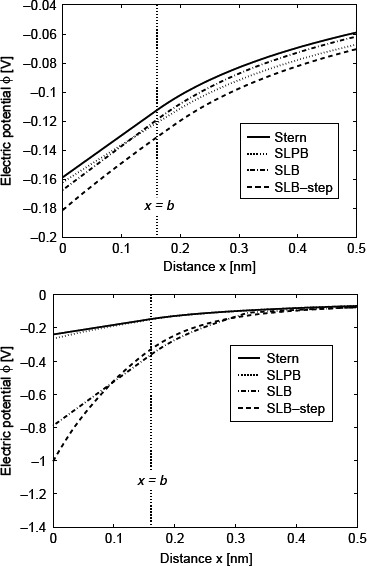
Electric potential ϕ as a function of the distance from the charged planar surface x (r_σ = 0) within the Stern model (Equation (77)), the SLPB model for point-like ions (Equation (79)), the SLB model for finite-sized ions (Equation (81)) and the SLB model with a step function for finite-sized ions (Equation (83)) for c = 0, where in all four cases the distance of closest approach b = a/2 = n_s^−1/3/2 ≈ 0.16 nm was taken into account. The value of the surface charge density was considered to be: σ = −0.2 As/m² (upper figure) and σ = −0.4 As/m² (lower figure). The remaining parameters used are dipole moment of water, p₀ = 4.794 D; bulk concentration of salt, n₀/N_a = 0.15 mol/1 and bulk concentration of water, n_0w/N_a = 55 mol/1, where N_a is Avogadro number.

7. Cavity and reaction field

The effective dipole moment of the water molecule should be known before a satisfactory statistical mechanical study of water and aqueous solutions is possible (Adams 1981). The dipole moment of a water molecule in liquid water differs from that of the isolated water molecule because each water molecule is further polarised (i.e. the dipole moment is further increased) and orientationally perturbed by the electric field of the surrounding water molecules (Adams 1981). Accordingly, in the above-described treatment of water ordering close to the saturation limit at high electric field within the LPB and LB models, the effective dipole moment of water p₀ = 4.79 Debye (D) is larger than the dipole moment of an isolated water molecule (p₀ = 1.85 D). However, it is also larger than the dipole moment of a water molecule in clusters (p₀ = 2.7 D) and the dipole moment of an average water molecule in the bulk (p₀ = 2.4 – 2.6 D) (Dill and Bromberg 2003) since the cavity and reaction fields as well as structural correlations between water dipoles (Fröhlich 1964; Franks 1972) were not explicitly taken into account in the LPB and LB models.

In the past treatment of the cavity and reaction fields and the correlations between water dipoles in the Onsager (1936), Kirkwood (1939) and Fröhlich (1964) models were limited to the case of small electric field strengths, i.e. far away from saturation limit considered in the LB model and also in the LPB model. Generalisation of the Kirkwood–Onsager–Fröhlich theory in the saturation regime was performed by Booth (1951). However, Booth's model does not consider the excluded volume effect in an electrolyte solution near a charged surface as described in the LB model and is therefore appropriate only for the LPB model. Therefore in this section, first the LPB model (Gongadze et al. 2011a) is generalised to take into account the cavity field, as well as the structural correlations between the water dipoles close to the saturation regime by utilising the Booth expression for relative permittivity. At the end, generalisation of LB model is also given by taking into account the cavity field (but not the structural correlations between water dipoles) in the saturation regime important in consideration of an electrolyte solution in contact with highly charged surface (Gongadze and Iglič 2012).

7.1. BPB model

To take into account the cavity field, as well as structural correlations between water dipoles within the LPB model, the LPB equation for point-like ions (see Equations (67) and (68)):

can be modified by taking into consideration (instead of Equation (69)) the Booth expression for the relative permittivity of pure water in the saturation regime (Booth 1951):

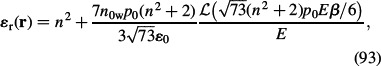which is also valid in the saturation regime of water polarisation at high values of E. Here, ℒ(u) is again the Langevin function, n = 1.33 is the optical refractive index of water, p₀ ≈ 2 D (Booth 1951) is the water dipole moment and n_0w is the number density of water molecules. In the approximation of small energy of dipoles in the electric field compared to the thermal energy, the relative permittivity within the BPB model for point-like sized ions (Equation (93)) can be expanded in a Taylor series to get

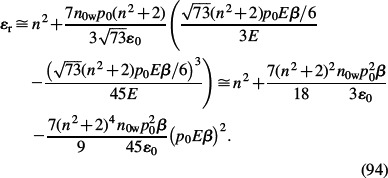In the limit of zero electric field the above equation transforms into:

It follows from Equation (95) that the value of the dipole moment of water p₀ = 2.03 predicts a bulk permittivity ∊_r = 78.5 (see also Figure 8). The boundary condition at the charged surface is:

where the relative permittivity ∊_r(r) is now defined by Equation (93). The second boundary condition is:

Figure 8.

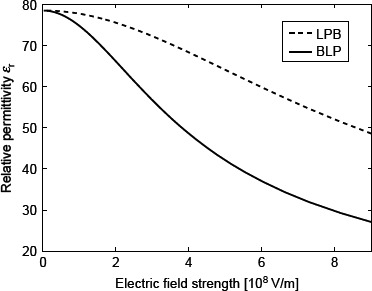
Relative permittivity ∊_r as a function of the magnitude of electric field strength (E) within the LPB model (Equation (69)) and BLP model (Equation (93)) for point-like ions and n_0w/N_a = 55 mol/1, where N_a is the Avogadro number. In the case of the LPB model, the effective dipole moment of water p₀ = 4.794 D, while in the BLP model the dipole moment of water p₀ = 2.03 D and n = 1.33.

Figure 8 shows the relative permittivity ∊_r as a function of the magnitude of the electric field strength (E) within the LPB and Booth-Langevin-Poisson (BLP) models, both for point-like ions. It can be seen that in the two models ∊_r decreases with increasing E; however in the BLP, it drops already at around 0.5V/nm to a half of its bulk value. Obviously, including the cavity field and structural correlations between water dipoles leads to a stronger saturation of the relative permittivity than by only considering the orientational ordering of water molecules.

7.2. MLB model

In the model, electronic polarisation is taken into account by assuming that the point-like rigid (permanent) dipole embedded in the centre of the sphere with a volume equal to the average volume of a water molecule in the electrolyte solution. The permittivity of the sphere is taken to be n², where n = 1.33 is the optical refractive index of water. The relative (effective) permittivity of the electrolyte solution (∊_r) can be then expressed as

where P is the polarisation vector due to net orientation of permanent point-like water dipoles having dipole moment p. The external dipole moment (p_e) of a point-like dipole at the centre of the sphere with permittivity n² can be then expressed in the form (Fröhlich 1964):

whence it follows:

In our analysis, short-range interactions between point-like rigid dipoles are neglected. The local electric field strength at the centre of the sphere at the location of the permanent (rigid) point-like dipole is (Fröhlich 1964):

where the first term represents the field inside a spherical cavity with dielectric permittivity n² embedded in the medium with permittivity ∊_r and the second term gp is the reaction field acting on p (due to the dipole moment p of the point-like dipole itself). In the following, Equation (101) is simplified in the form (strictly valid for ∊_r ≫ n² only):

The energy of the point-like dipole p in the local field E_c may be then written as

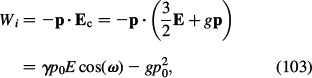where p₀ is the magnitude of the dipole moment p_e, ω is the angle between the dipole moment vector p and the vector −E and

The polarisation P(r) is given by (see also Equation (11)) (Gongadze and Iglič 2012)

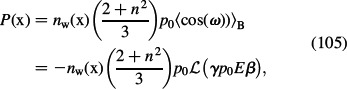where

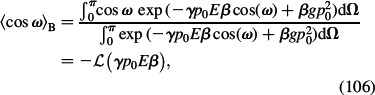and dΩ = 2πsinωdω is an element of solid angle. Since σ < 0, the projection of polarisation vector P on the x-axis points in the direction from the bulk to the charged surface and P(x) is considered negative. A similar procedure as in the case of the LB model (see Equations (48)–(50)) leads to ion and water dipole distribution functions (Gongadze and Iglič 2012):

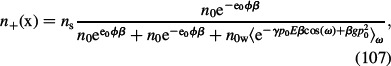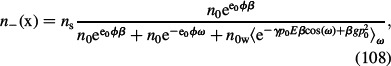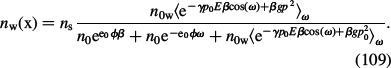For simplicity we neglect βgp₀²:

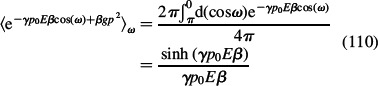is the dipole Boltzmann factor after rotational averaging over all possible angles ω. Equations (107)–(110) can be rewritten as (Gongadze and Iglič 2012):

where:

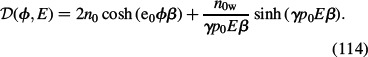Combining Equations (105) and (113) gives the polarisation in the form:

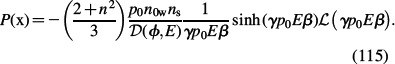Using the definition of the function F(u) (Equation (25)), Equation (115) transforms to:

Combining Equations (98) and (116) yields the relative (effective) permittivity (Gongadze and Iglič 2012):

Following a similar procedure as in Section 2, we can then write the MLB form of the Poisson equation as

where ρ_free(r) is the macroscopic (net) volume charge density of co-ions and counterions (see also Equations (111) and (112)):

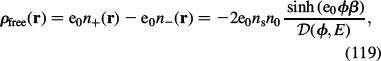while ∊_r(r) is defined by Equation (117). The boundary conditions are:

In the approximation of small electrostatic energy and small energy of dipoles in the electric field compared to thermal energy, i.e. small e₀ϕβ and small γp₀Eβ, the relative permittivity within the MLB model for finite-sized ions (Equation (117)) can be expanded into a Taylor series (assuming n_s ≈ n_0w) to get (Gongadze and Iglič 2012):

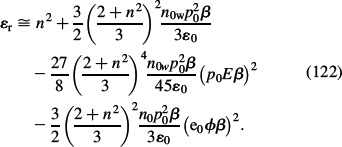In the limit of vanishing electric field strength (E → 0) and zero potential (ϕ → 0), the above equations give the Onsager expression for permittivity:

In the above-derived expression for the relative (effective) permittivity (Equation (117)), the value of the dipole moment p₀ = 3.1 D predicts a bulk permittivity ∊_r = 78.5. This value is considerably smaller than the corresponding value in the LB model (p₀ = 4.79 D) (see Figure 2 and Equation (38)) which does not take into account the cavity field.

The value p₀ = 3.1 D is also close to the experimental values of the effective dipole moment of water molecules in clusters (p₀ = 2.7 D) and in bulk solution (p₀ = 2.4 – 2.6 D) (Dill and Bromberg 2003). The MLB model does not, however, neglect the main (qualitative) predictions of the LB model where all the equations (including the expression for the relative permittivity) have a similar structure as in the MLB, only the effective value of the water dipole moment (p₀) is larger. Moreover, for γ → 1 and n → 1, the equations of the above described MLB model transform into equations of LB model.

Figure 9 shows the calculated spatial dependence of relative number density of counter ions (n₊/n_s), water dipoles (n_w/n_s) and ∊_r(x) within MLB model in planar geometry for two values of the surface charge density σ. The decrease in ∊_r(x) towards the charged surface is pronounced with increasing σ and is a consequence of the increased depletion of water molecules near the charged surface (due to excluded volume effect as a consequence of counterions accumulation near the charged surface) and increased orientational ordering of water dipoles (saturation effect). Comparison between the predictions of the LB model and the presented MLB model shows the stronger decrease in relative permittivity of the electrolyte solution near the highly charged surface stronger in MLB model.

Figure 9.

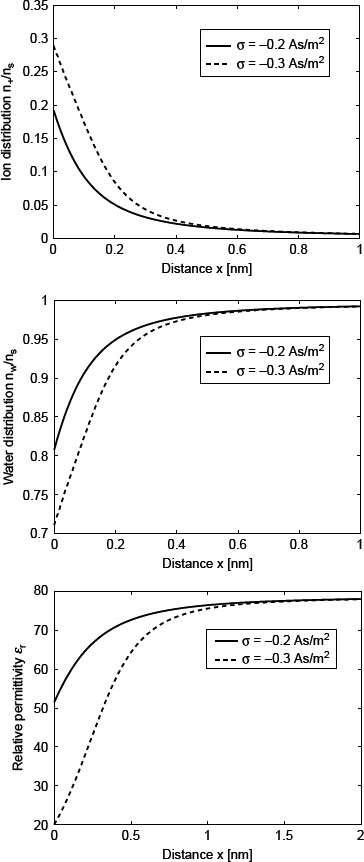
The relative number density of counter ions (n₊/n_s), water dipoles (n_w/n_s) (calculated using Equations (111) and Equation (113) and relative permittivity ∊_r (Equation (117)) as a function of distance from a planar-charged surface x (adapted from Gongadze and Iglič 2012). Two values of surface charge density were considered: σ = −0.2 As/m² and σ = −0.3 As/m². Equation (118) was solved numerically taking into account the boundary conditions (120) and (121) as described in the text. Values of parameters assumed are dipole moment of water, p₀ = 3.1 D; bulk concentration of salt, n₀/N_a = 0.15 mol/l; optical refractive index, n = 1.33; bulk concentration of water, n_0w/N_a = 55 mol/1, where N_a is Avogadro number.

8. Conclusions

To conclude, in this work we described different modifications of the PB model of the EDL by introducing the orientational ordering of water molecules (also close to the saturation regime) and the finite size of molecules. The corresponding LPB model for point-like ions and the LB model and generalised Stern model for finite-sized ions were derived. The Bikerman model is derived as the limiting case of the LB model for finite-sized ions. It is shown that due to the increased magnitude of the electric field in the vicinity of the charged surface in contact with the electrolyte solution, the relative permittivity of the electrolyte solution in this region is decreased. The predicted decrease in the relative permittivity relative to its bulk value is the consequence of the orientational ordering of water dipoles in the vicinity of the charged surface (saturation effect). Due to accumulation of counterions near the charged surface, the number density of water molecules near the charged surface is decreased and as a result the relative permittivity is additionally decreased (excluded volume effect).

The electric field may influence the dipole moment of the water in two ways. First, it perturbs the average orientation of the water dipole, and second, it induces an increase in the magnitude of the water dipole moment, mainly by elastic displacement of the atomic electrons relative to their respective nuclei (Fröhlich 1964). The magnitude of the induced water dipole moment is determined by the polarisability of the molecule, i.e. the proportionality coefficient between the induced dipole moment and ∊₀E_c, where E_c is the local electric field strength as defined above (Equation (101)).

In order to (partially) capture these two effects in our theoretical description of the permittivity of water, we applied the concept of the cavity field (Onsager 1936; Fröhlich 1964) in the MLB (Gongadze-Iglič) model (valid also in the saturation limit) by simultaneously taking into account the volume-excluded effect. To our knowledge this was done for the first time. The corresponding analytical expression for the spatial dependence of the relative (effective) permittivity of the electrolyte solution near the charged surface was derived (Gongadze and Iglič 2012).

Appendix: Configurational entropy of electrolyte solution

We consider the configurational entropy of the solution composed of counterions and co-ions. Following the classical well-known approach (Hill 1986), the finite sizes of ions (macroions) are considered within the lattice model (Kralj-Iglič and Iglič 1996). The system is divided into cells of equal volume ΔV. In the particular cell chosen, there are N₊ counterions and N₋ co-ions. The number of spatial arrangements of non-interacting counterions and co-ions in a small cell with M lattice sites is (Hill 1986):

and can be rewritten into

where

The configurational (translational) entropy of the mixed system of the single cell S_cell is (Hill 1986):

Using the Stirling's approximation for large N_i : ln N_i! ≃ N_i ln N_i − N_i, i = {+, −}, the expression for In W transforms into (Hill 1986):

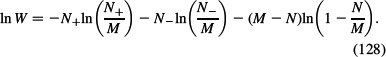To take into account the excluded volume effect, we assume that each lattice site with volume ν₀ can be occupied only by one ion. The volume of the cell with M sites is given by ΔV = Mν₀. The number density of counterions is defined as n₊ = N₊/ΔV, while the number density of co-ions is n₋ = N₋/ΔV. The configurational entropy of the whole system is obtained by integration over all cells of the system:

where S_cell is given by Equation (127). We insert Equation (128) into Equation (127) to get:

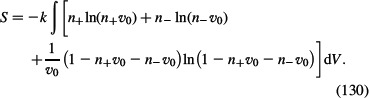Equation (130) takes into account the finite size of ions. In the following, the entropic part of the free energy = – TS is calculated from the Equation (130):

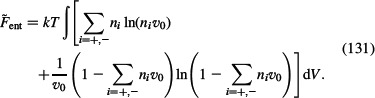We need to subtract the reference free energy (Kralj-Iglič and Iglič 1996). The difference between the entropic part of the free energy and the reference entropic part of the free energy F_ref is:

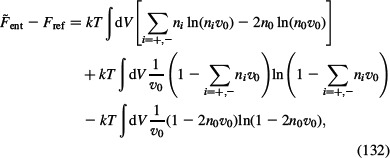where n₀ is the bulk number density of ions. Assuming

and taking into account ln(n₀ν₀) = const. and ln(1 – 2n₀ν₀) = const. we obtain the entropic part of the free energy in the form:

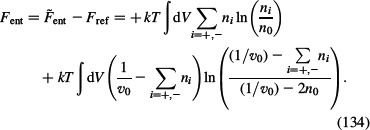In our model, the number density of lattice sites n_s = 1/ν₀ = 1/a³, where we define a as a lattice constant (width of a single lattice site). All lattice sites are occupied by either solvent molecules or macroions, therefore:

where n_w is the number density of lattice sites occupied by solvent (water) molecules, n₊ is the number density of counterions and n_– is the number density of co-ions. By taking into account Equation (135), we may rewrite Equation (134) in the well known form (see for example Dill and Bromberg 2003):

where n_0w is the bulk number density of water.

If we assume that n₊ ≪ 1, n₋ < 1, everywhere in the solution, as well as n₀ ≪ 1, we can expand the third term in Equation (136) up to quadratic terms to get (see for example Kralj-Iglič and Iglič 1996):

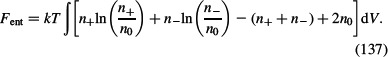Equation (137) describes the configurational entropy of electrolyte solution where the excluded volume is not taken into account.