An efficient sampling and inference procedure for studies with a continuous outcome

Abstract

To characterize the relation between an exposure and a continuous outcome, the sampling of subjects can be done much as it is in a case-control study, such that the sample is enriched with subjects who are especially informative. In an outcome dependent sampling (ODS) design, observations made on a judiciously chosen subset of the base population can provide nearly the same statistical efficiency as observing the entire base population. Reaping the benefits of such sampling, however, requires use of an analysis that accounts for the ODS design. In this report, the authors examined the statistical efficiency of a plain random sample analyzed with standard methods, compared with that of data collected with an ODS design and analyzed by either of two appropriate methods. In addition, three real datasets were analyzed using an ODS approach. The results demonstrate the improved statistical efficiency obtained by using an ODS approach and its applicability in a wide range of settings. An ODS design, coupled with an appropriate analysis, can offer a cost-efficient approach to studying the determinants of a continuous outcome.

A simple and well known outcome dependent sampling design is the case-control study. The case-control study design is logistically and economically appealing because observations made on a judiciously chosen subset of the population base provide nearly the statistical efficiency of observing the entire population base ¹. The principal idea of the case-control design and its subsequent extensions such as case-cohort and two-stage designs^{e.g.2,3,4,5,6,7}, is to concentrate resources on observations carrying the greatest amount of information. Related ideas of response based sampling have also be developed in economics and survey sampling^8,9,10.

An unique property of the case-control design is that under the logistic regression model with a binary Y, the estimated regression parameter (the odds ratio) for the exposure is the same under retrospective sampling as it is under a cohort study, with the effect of sampling confined to the intercept^2,4. i.e., analyzing the a data set from case-control study as if it were from a cohort study will only affect the intercept. This property does not hold for a continuous response variable or if the regression model is not logistic. While designs for studying dichotomous outcomes have continued to develop, for studies of continuous outcomes analogous work has lagged. As the scope of epidemiologic inquiry grows, so does the need for efficient approaches to studying the determinants of a continuous outcome’s level. This need is especially clear when the measurement of exposure is expensive.

As an example, the authors wanted to study background-level in utero exposure to the neurodevelopmental toxicant polychlorinated biphenyls (PCBs) in relation to performance on the Bayley Scale of Infant Development (BSID). Maternal pregnancy serum was available from a previously completed cohort study in which BSID had been measured, and PCB concentration in the maternal serum could provide a good surrogate measure of in utero exposure.

In studies of the relation between a relatively expensive exposure measure and the level of a continuous outcome, one approach has been to dichotomize the outcome and conduct a nested case-control study^11,12. Dichotomizing a continuous outcome, however, could cause the estimand to be different and usually will result a loss of information as a lower order scale for the response is used ¹³.

To reap the benefits of a reduced sample size, one can employ case-control-like sampling adapted for continuous outcomes, outcome dependent sampling (ODS). Zhou et al.¹⁴. proposed an new ODS scheme that allows for two components. First, an overall random sample (SRS) of the population base is taken. Second, one or more supplementary random samples are taken, in which (as with case-control sampling) the probability of selection depends on the level of the outcome variable. For example, supplementary random samples might be taken only from the tails of the distribution of outcome. In most settings, by oversampling subjects in the tails, greater efficiency can be achieved than with a plain random sample of the same total sample size as the ODS sample, because the “tail” observations can provide greater influence on the parameter under study. Unlike the case-control study, failure to account for the biased sampling scheme with a continuous response in the statistical analysis will led to biased estimates for the regression parameters. In oder to consistently estimate the same estimand as the cohort study, the sampling scheme must be accounted for properly in the analysis. One commonly used method that can be adapted to our setting is to conduct a weighted analysis (weighted estimating equation approach), with weights inversely proportional to the probability of being sampled (IPW) ^e.g.,15. Another alternative is the weighted pseudo-likelihood method¹⁰, which requires that one correctly specify all the underlying distributions. Misspecification of these distributions will lead to biased and erroneous conclusions. These methods, however, are all accounting the sampling scheme in an approximate way. A more efficient analysis that based on a likelihood function that truly reflect the biased sampling design¹⁴ has been recently developed. The likelihood function used in (14) reflects all observed data and characteristics of the ODS sampling design. No additional distribution assumptions about the exposure variable are needed, nor is enumeration of the base population required (as is the case with the IPW method).

The present report builds on our previous, technically-oriented piece¹⁴ in several ways. First, we provide a more intuitive explanation for why our ODS estimator is more statistically efficient than the alternatives. Our simulation study shows this efficiency under a wide range of exposure distributions, and translates the gain in efficiency into the reduction in sample sizes that yield equivalent statistical power. The simulation also explores the impact of various options in sampling and expresses results in terms of statistical power. The real data examples demonstrate the wide applicability and special advantages of the proposed ODS design and estimator.

MATERIALS AND METHODS

A Semiparametric Inference Procedure for ODS with a Continuous Outcome

In this section, we give a brief overview of the ODS design Zhou et al.¹⁴ proposed and their method for statistical inference under such a design. Let Y denote the continuous outcome variable and X denote the exposure. Assume that each Y falls into one of three mutually exclusive intervals: a lower tail strata, a middle section strata, and a upper tail strata. The general structure of the proposed design consists of two components: an overall random sample (SRS), and a supplement random sample from each of the three strata of Y. Let C_k, k = 1, 2, 3, denote the strata in Y. The observed data structure in the above ODS design is as follows: one observes the supplement random samples conditional on Y being in strata C_k, i.e., {Y_ki,X_ki|Y ∈ C_k}, where i = 1, 2, …, n_k; One also observes an overall SRS sample whose individuals are denoted by {Y_0i, X_0i} where i = 1, 2, …, n₀. The total sample size in the ODS sample is therefore n = n₀ + n₁ + n₂ + n₃, where any of the n_k, k = 0, 1, 2, 3 can be zero. The above general sampling strategy encompasses several special cases, e.g., when n₁ = n₂ = n₃ = 0, then the ODS design reduces to the simple random sample design or cohort design; when Y is binary and n₀ = 0, the ODS design reduces to the usual case-control design.

Denote by f_β(Y|X) the conditional density function for the population, where β is the vector of regression coefficients that links exposure X and the outcome Y. Let G and g denote the cumulative distribution and density functions of X, respectively. The joint likelihood function, L(β), of the observed ODS data is

$$=\left[\prod _{i=1}^{n_0}{f}_{\beta }(Y_{0i},X_{0i})\right]\left[\prod _{k=1}^3\prod _{i=1}^{n_k}{f}_{\beta }(Y_{ki},X_{ki}|Y_{ki}\in C_k)\right]=\left[\prod _{i=1}^{n_0}{f}_{\beta }(Y_{0i}|X_{0i})g(X_{0i})\right]\left[\prod _{k=1}^3\prod _{i=1}^{n_k}{f}_{\beta }(Y_{ki},X_{ki}|Y_{ki}\in C_k)\right].$$ (1)

The component in the first bracket is data contribution to the likelihood from the SRS sample, the second bracket is the contribution from each of the supplement samples. An important feature of this likelihood is easier to appreciate if it is re-expressed. From Bayes formula,

$$f_{\beta }(Y_{ki},X_{ki}|Y_{ki}\in C_k)=I[Y_{ki}\in C_k]\frac{f_{\beta }(Y_{ki}|X_{ki})g(X_{ki})}{\mathit{\text{Pr}}(Y_{ki}\in C_k)},$$ (2)

where I is an indicator function for stratum membership, Pr(Y_ki ∈ C_k) involves both g and β through Pr(Y_ki ∈ C_k) = ∫ fβ(Y_ki|x)g(x)dx. Plugging equation (2) into equation (1), the likelihood function we began with, denoted as L(β,G) now to reflect the dependence on the unknown distribution of X, can be rewritten as

$$L(\beta ,G)=\left[\prod _{k=0}^3\prod _{i=1}^{n_k}{f}_{\beta }(Y_{ki}|X_{ki})\right]\left[\prod _{k=0}^3\prod _{i=1}^{n_k}g(X_{ki})\right]\left[\prod _{k=1}^{K}P{(Y_{ki}\in C_k)}^{-n_i}\right].$$ (3)

L(β, G) now has three components: the specified regression model fβ(Y|X) in the first bracket, the unspecified g(X) in the second bracket, and the ODS sampling induced probability P(Y_ki ∈ C_k) that ties fβ(Y|X) and g(X) together in the third bracket. The first component would be the usual likelihood function for observed data, had the sampling been simple random sampling. The last component reflects the biased sampling nature of the ODS design and ignoring it in analysis would result in biased β estimates. Hence g(X), or G, in the second bracket cannot be simply factored out as would be the case with a simple random sample design. Statistical inference about β using the standard maximum likelihood estimation method will depend on a known or a parameterized G. In practice, however, G is rarely known. Misspecification of the distribution could lead to an erroneous conclusion and bias the parameter estimation. Consequently, statistical approaches that do not rely on the extra parameterization of G are desirable.

To estimate β without specifying G(X), Zhou et al. ¹⁴ developed a maximum likelihood based approach that maximizes L(β, G) by modeling G nonparametrically. They used the profile likelihood idea where it (a) fixes β in equation (3) and solve for an empirical likelihood estimate Ĝ(β) from a constrained likelihood function, constraints placed on Ĝ that reflect its properties of being a discrete distribution function, using the Lagrange multiplier technique. An explicit solution for Ĝ(β) can be obtained. (b) Plugging Ĝ(β) into equation (3), the Zhou et al. estimator β̂_Z can be obtained, using the Newton-Raphson procedure, by maximizing the resulting likelihood. An explicit standard error formula based on an asymptotic distribution is given in Zhou et al.. The statistical program for this analysis can be obtained from the web page (www.bios.unc.edu zhou) or from the authors.

The inverse probability weighted approach of Horvitz and Thompson¹⁵ can also be adapted in this situation by crudely treating all observed data, including the SRS sample, as if it were sampled from three strata, each with a given selection probability. Like the Zhou et al.. estimator, the IPW approach also yields a consistent estimate for β. The IPW method is commonly used with data from a two-stage study^{e.g. 16,17} If all N individuals were fully observed in the entire population, the log likelihood function would be ${\sum }_{i=1}^N\text{log}P(y_i|x_i;\beta )$. An estimate of this quantity is obtained if we use the completely observed individuals and weight their contributions inversely according to their selection probability into the second stage. Th IPW estimator β̂_IPW is the solution to following weighted score equation

$$\frac{1}{N}\sum _k\sum _{i\in C_k}\frac{1}{p_k}\frac{\frac{\partial }{\partial \beta }{P}_{\beta }(y_i|x_i)}{P_{\beta }(y_i|x_i)}=0.$$

where p_k can be estimated by $\frac{n_k}{N_k}$ if there is a complete information. Note that the IPW actually need more information than the likelihood approach employed by the Zhou et al. method since it requires the sampling probabilities to be known. However, since the IPW approach is based on crudely accounting for the sampling scheme and is based on estimating equations approach, it may not be as efficient as a likelihood based estimator. It has been shown that when the number of bins to group Y is not fine enough (when the number of categories of Y is small), the method is not efficient¹⁸. The realistic settings for the ODS design we considered had k between 2 to 4.

A SIMULATION STUDY

We designed a simulation to study the efficiency of different methods under a variety of conditions that mimic situations one might face in real applications. The basic simulation setting is modeled after a real study by Daniels et al.¹⁹, of prenatal exposure to low levels of PCB in relation to mental and motor development, where an ODS design was used in the data collection. The data were generated according to the following model,

$$Y={\beta }_0+{\beta }_1{X}^p+{\beta }_2{Z}_1+{\beta }_3{Z}_2+{\beta }_4{Z}_3+e,$$

where X is the exposure variable that takes on several distributions, p = 1 indicates a linear dose-response relationship and p = 2 represents a nonlinear relationship for E[Y|X], the Zs are independent covariate variables, and e is a standard normal random error. We generate X from several distributions that includes normal, exponential, lognormal, and Bernoulli. These selections reflect possible real situations where X could be a rare-binary variable, a continuous variable, or a skewed variable. We generated Z₁ from a binary distribution (Bernoulli(0.45)), Z₂ from a log-normal distribution (LN(0, 0.25)), and Z₃ from a three level polynomial distribution (P(n, 0.3, 0.7)).

In our simulation, we first generated a cohort with 100, 000 individuals according to the above model and drew ODS samples from this cohort. We drew an overall random sample of size n₀, where we observed {Y,X,Z₁,Z₂,Z₃}. We also drew a supplement random sample of size n₁ from the lower tail of Y defined by {Y < Ȳ − a * σ_Y} and a supplement random sample of size n₃ from the upper tail of Y defined by {Y > Ȳ + a * σ_Y}, where σ is the standard deviation of Y and a is a known constant. In addition to various configurations for the parameter values, we investigated the effect of varying the value of cut point a on the performance of the methods. We also investigated the impact on statistical power of varying the contribution to the total sample size from the overall random sample and the supplement random samples (ρ = n₀/(n₀+ n₁ + n₃)). Note n₂ = 0 here does not reduce the generality.

Under each setting, we compared the Zhou et al. estimator, denoted by β̂_Z, with four other estimators: (i) the naive maximum likelihood estimator, β̂_N, based on the observed ODS data but ignoring the sampling scheme; (ii) an inverse probability weighted estimator (β̂_IPW); (iii) the maximum likelihood estimator based on a plain random sample of the same size as the ODS sample (β̂_P); (iv) two logistic regression estimators (β̂_Lk) based on dichotomizing a continuous Y by defining the outcome D as D = 1 if Y > mean(Y)+k * σ_Y and D = 0 otherwise, where k = 0, 1. The weight used in calculating β̂_IPW is the inverse of the observed probability of being sampled in the respective strata of Y. The β_N and β_P estimates are the same as the ordinary least square estimates in our simulation setting. Each set of simulations generated 1000 data sets.

SIMULATION STUDY RESULTS

Table 1 shows the simulation results for a = 1, and (n₀, n₁, n₃) = (200, 100, 100) (hence ρ = 0.5) for various exposure effects. The mean estimate given by β̂_N is biased for estimating β₁ in the simulation. Thus, ignoring the sampling scheme (β̂_N) leads to a biased estimate for the exposure effect. It is also clear from Table 1 that different dichotomization of a continuous Y will lead to inconsistent, and different, estimates (β̂_L0 and β̂_L1) of the β₁. Perhaps more importantly, the logistic estimators can be less able to detect the true underlying relationship, as reflected by corresponding p values of 0.08 for β̂_L1, compared with p < 0.05 for all other methods using continuous response. We do not present results for these two estimators in future comparisons. The other three methods all yielded consistent estimates of β₁. The actual coverage of their nominal 95 percent confidence intervals coverage (95% CI Coverage) are all close to 95 percent, indicating that a good approximation to the asymptotic normality is achieved with this sample size, and the estimated standard errors (SE) are close to the true standard deviations. Under the setting considered, β̂_Z has the smallest SE while b β̂_P has the largest SE. Because β̂_N is a biased estimator and its SE underestimates the true variation, we excluded it from the further studies of sample size and power below. The above observations are consistent across different exposure effects listed in Table 1. Under the same linear model but when the X term is quadratic, β̂_Z is again more efficient.

Table 1.

Simulation results for different exposure effects with α = 1 and ρ = 0.5

Term of X in the model	(n0, n1, n3)	β 1	Methods	Mean	SE	$\widehat{\text{SE}}$	95% C.I. Coverage
Linear X	(200,100, 100)	0.1	βN	0.167	0.066	0.051	0.671
X ~ N(0, 1)			βP	0.099	0.051	0.051	0.950
			βIPW	0.101	0.048	0.047	0.938
			βZ	0.101	0.040	0.040	0.947
			βL0	0.237	0.113	0.107	0.756
			βL1	0.221	0.131	0.128	0.852
Quadratic X2	(200,100,100)	0.1	βN	0.156	0.042	0.034	0.587
X ~ N(0,1)			βP	0.100	0.035	0.036	0.961
			βIPW	0.101	0.034	0.041	0.975
			βZ	0.100	0.029	0.029	0.950
Linear	(200,100,100)	0.1	βN	0.137	0.026	0.021	0.554
X ~ LN(0,1)			βP	0.100	0.025	0.025	0.953
			βIPW	0.102	0.023	0.028	0.977
			βZ	0.101	0.020	0.020	0.947
Linear	(200,100,100)	0.1	βN	0.166	0.299	0.234	0.863
X ~ Bernoulli(0.05)			βP	0.110	0.237	0.234	0.948
			βIPW	0.103	0.224	0.220	0.930
			βZ	0.102	0.183	0.184	0.961

NOTE: Results are based on the model Y = β₀+β₁X+β₂Z₂+β₃Z₃+β₄Z₄+e, where e ~ N(0, 1),β₀ = 1.5, β₂ = −0.5, β₃ = 0.02 and β₄ = 0.05. β_N is the estimator based on ignoring the ODS sampling scheme. β_P is the maximum likelihood estimator based on a plain random sample of the same sample size. β_IPW is the inverse probability weighted estimator and β_Z is the Zhou et al. estimator. β_L1 is estimator from a logistic regression analysis where outcome variable to be one if Y ≥ mean(Y) + σ_Y and 0 otherwise. β_L2 is estimator from a logistic regression analysis where outcome variable to be one if Y ≥ mean(Y) and 0 otherwise.

Results in the lower panels of Table 1 provide the contrast for the normally distributed X to extreme X, namely a skewed exposure (Lognormal) and a rare binary exposure (Bernoulli(.05)). When compared to the Normal distributed exposure, the SE for β_Z is even smaller SE in the skewed exposure situations. For the rare binary exposure case, results in Table 1 demonstrate that β̂_Z is still the most efficient overall, though the sample size considered was not sufficiently large enough for any of them. This is reflected in the fact that the estimated standard errors are bigger than the estimates of the slope. This is not surprising because with the distribution of a rare binary X, there may not be enough information in the data set as X = 1 could be sparse. Future development of a modified ODS design for this situation is certainly warranted.

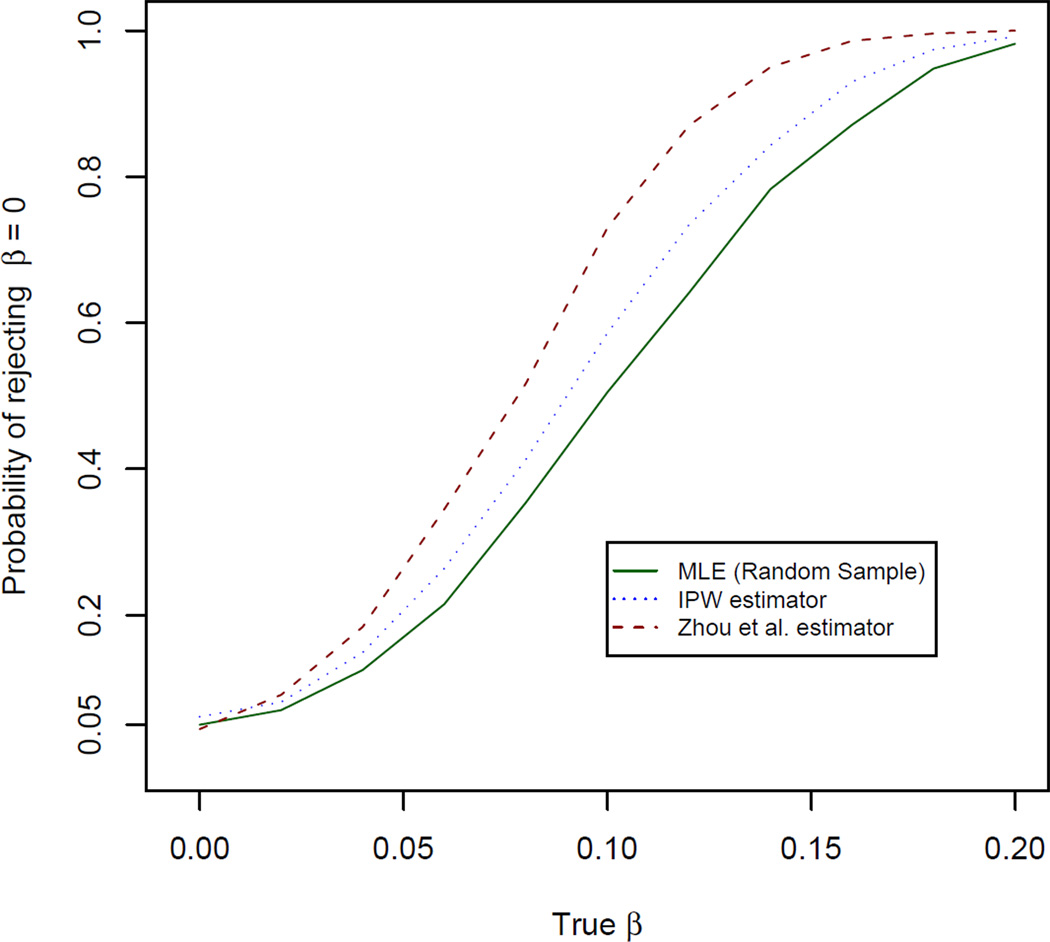
Figure 1 shows the power for testing H₀ : β1 = 0 v.s. H₁ : β₁ = true value, for n = 400 and type I error fixed at 5 percent. The points corresponding to the true value of β₁ = 0 shows the empirical type I error rate for each test. All three methods yield close to 5 percent type I error. For all three estimators, as β₁ increases, so does the statistical power, and the power of β̂_Z > β̂_IPW > β̂_P.

Figure 1.

Simulation results for the power of testing H₀ : β₁ = 0. v.s. H₁ : β₁ = true value under the model in the top panel of Table 1. The results are based on 1000 simulations with n₀= 200 and n₁ = n₃ = 100.

Table 2 shows the sample sizes required to achieve a given statistical power for three values of β₁ according to type of estimator under the same settings used in the top panel of Table 1. Use of ODS with an appropriate estimator requires a smaller sample size. In this setting, the β̂_Z method on average needs about 60 percent of the subjects who would be needed if the study were conducted with a simple random sampling scheme and the β̂_IPW method needs about 83 percent. Further, for a given power, as the true value of β₁ is farther away from 0, relatively fewer subjects are needed to achieve the same power with β̂_Z as compared with β̂_P. i.e., efficiency increased as β₁ is farther away from 0.

Table 2.

Sample size needed for testing H₀ : β₁ = 0 for a given statistical power. The results are based on 1000 simulations with α = 1.0, ρ = 0.5 and n₁ = n₂.

		Sample Sizes for
Power	Trueβ1	βP	βIPW	βZ
0.80	0.05	3000	2500	1900
	0.10	790	670	470
	0.15	360	310	220
0.85	0.05	3600	2900	2250
	0.10	960	780	530
	0.15	400	340	245
0.90	0.05	4200	3400	2500
	0.10	1070	870	630
	0.15	485	400	280
0.95	0.05	5100	4300	3080
	0.10	1320	1080	770
	0.15	625	510	350

NOTE: X follows a log-normal distribution, other details see footnote to Table 1.

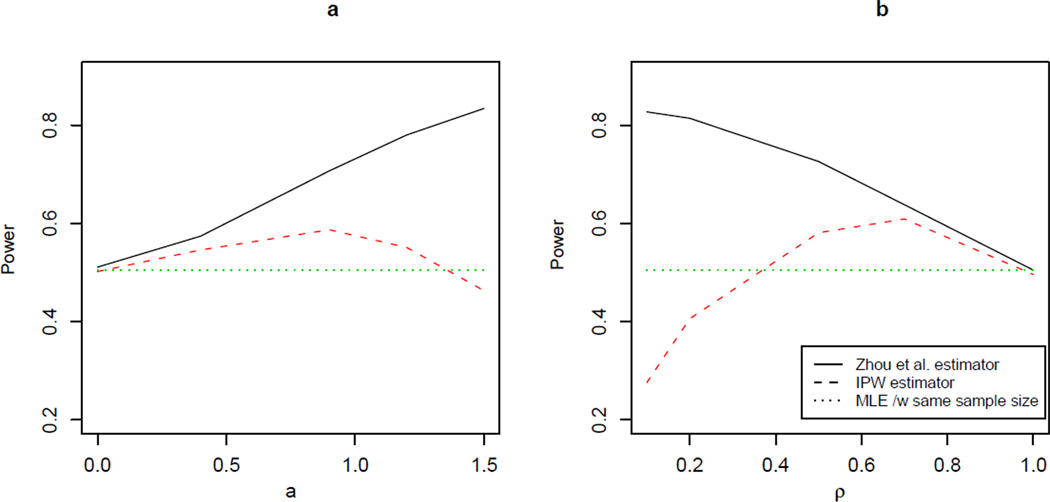
Figure 2 shows the impact of two factors in a given ODS setting. The impact of varying a, the cut-point that determined the strata of Y where the supplement random samples were drawn, is shown in the left graph. a = 0 means there was only plain random sampling and in this instance all three methods had the same power. As a increases, however, β̂_Z (solid line) has better power than the other two. With β̂_Z, the increase in power appears to be monotonic in a. The graph on the right of Figure 2 shows the impact of ρ, the fraction of the overall random sample in the total ODS sample (ρ = n₀/(n₀+n₁+n₃)). At ρ = 1, there is no supplement sample and the ODS samples are plain random samples. However, as ρ decreases to below 0.7, β̂_Z (solid curve) is again the most powerful of the three estimators.

Figure 2.

The power for the testing H₀: β₁ = 0. v.s. H₁ : β₁ = 0.1. (a). The power as a, cut-point for defining the strata in term of σ_Y, varies with sample size (n₀, n₁, n₂) = (200, 100, 100); (b). The power as ρ, the fraction of SRS sample, varies with n = 400, n₁ = n₂, and a = 1.

Table 3 investigates different ODS allocations when the exposure variable is skewed (X ~ lognormal). Compared with the results in the lognormal panel of Table 1, we see that allocating more of the ODS sample to the upper tail of Y improves the efficiency. The standard error of the slope estimator decreases as more of the ODS sample is shifted from the lower tail to the upper tail, i.e. 0.0222 → 0.0201 → 0.0192 as the ODS allocation changes from (200, 150, 50) → (200, 100, 100) → (200, 50, 150).

Table 3.

Simulation study for different ODS allocation with skewed exposure effect.

(n0,n1,n3)	β1	Methods	Mean	SE	$\widehat{\text{SE}}$	95% C.I.
(200; 50; 150)	0.1	βN	0.116	0.021	0.019	0.850
		βP	0.100	0.025	0.025	0.953
		βIPW	0.102	0.023	0.028	0.986
		βZ	0.100	0.019	0.019	0.947
(200,150,50)		βN	0.147	0.031	0.025	0.503
		βP	0.100	0.025	0.025	0.953
		βIPW	0.102	0.025	0.031	0.977
		βZ	0.101	0.022	0.022	0.943

Real Data Example 1

In the motivating example noted in the Introduction, the setting was like one where if the outcome has been dichotomous a nested case-control study would have been implemented. However, the outcome of interest, the score on the Bayley Scale of Infant Development (BSID), was a continuous variable, and, as noted above, treating it as a dichotomous variable would have resulted in a loss of statistical power. Measurements of the exposure of interest here, polychlorinated biphenyls, are expensive, thus minimizing sample size while maintaining power was especially important. Thus, the authors drew drew a random sample of cohort members and two additional random samples, one from each tail of the outcome distribution¹⁹. Using the inverse probability weighted estimator, the estimated β̂_IPW was 0.47 BSID units/µg/L PCB with estimated SE as 0.32 (p = 0.14)¹⁴. Using the Zhou et al. estimator, the estimated β̂_Z was 0.44 with SE = 0.22 (p = 0.02). Using the SRS data alone, the β̂_N was 0.29 (SE = 0.29, p = 0.32). Daniels et al. also examined and confirmed the shape of the dose-response relation in both the ODS and the SRS samples. The example demonstrates the improved efficiency obtained by the Zhou et al. estimator.

Real Data Example 2

Rissanen et al.²⁰ examined the relation of serum lycopene concentration to the thickness of carotid arteries among 1028 men in Finland. Using their data, we selected samples of total n=400 in two ways. First, we selected a random sample with n=400. Second, we selected a random sample of n=200, and, among those with carotid artery thickness above the 90th percentile we selected a random sample of n=100, and among those with carotid artery thickness below the 10th percentile we selected a random sample of n=100. We then analyzed the data using ordinary least squares with n=1028, and with the 400 all selected at random. In addition, we analyzed the 200-100-100 sample using inverse variance weights and then with the Zhou et al. estimator. In all models the lycopene results were adjusted for the same covariates (age, year, and sonographer). Results are given in Table 4. With n=1028 (the full data), the estimated coefficient for lycopene was −0.14 with an estimated SE at 0.04 and p = 0.0011. With n=400 (all random), the estimated effect β̂_P = −0.10, with SE = 0.06 and p = 0.096. With the 200-100-100 sample, we had β̂_IPW = −0.19 with SE = 0.08, p = 0.017 and β̂_Z = −0.24, SE = 0.07 and p = 0.0009. This example suggests that use of an outcome-dependent sampling scheme and the Zhou et al. estimator obtained nearly as much power as analysis of the full dataset. Furthermore, the greater efficiency of the Zhou et al. estimator compared with IPW approach is clear. The larger β’s obtained using outcome dependent sampling and estimators reflect the shape of the dose-response curve, which had larger negative slopes near the tails of the outcome. While we focused on analyzing the lycopene association as linear (trend test type approach), clearly a curvilinear approach would better describe the relation and could be easily accommodated with either the IPW or the Zhou et al. estimators.

Table 4.

Results of fitting adjusted models of the carotid artery thickness in relation toserum lycopene concentration, according to sampling method and method of data analysis.

Sampling method	n	Analysis method	β̂1	SE(β)	p
All available subjects	1028	OLS	−0.14	0.04	0.0011
Random sample	400	OLS	−0.10	0.06	0.096
Random sample plus outcome tail samples2	400	weighted OLS	−0.19	0.08	0.017
Random sample plus outcome tail samples2	400	Zhou et al. estimator	−0.24	0.07	0.0009

NOTE:

¹Units are mm per mol/L, adjusted for age, year, and sonographer.

²200 subjects selected at random, 100 with carotid artery thickness above the 90th percentile selected a random, and 100 with carotid artery thickness below the 10th percentile selected a random (see text).

Real Data Example 3

Korrick et al.²¹ conducted a case-control study of hypertension and bone lead level.x For logistic reasons the sampling probabilities for cases and controls could not be determined. Measurements of blood pressure were available. The example, which is presented in the online supplementary material, shows that with their data, the proposed ODS approach could be used to estimate the coefficient for bone lead in a model of blood pressure.

DISCUSSION

Our results show that for a fixed total number of observations used to examine the linear relation between a continuous exposure and a continuous outcome, the ODS design is more efficient than a plain random sample design. An intuitive and simple expression of the benefit of the ODS approach using the Zhou et al. estimator was found in the simulations showing that it yields the same estimand as that from the underlying cohort study and that for a given desired statistical power, the number of observations needed could be reduced by about 40 percent compared with a plain random sample. This work shows that the benefits of outcome dependent sampling apply to continuous outcomes, not just to dichotomous ones through case-control designs. For binary response variable, our approach is equivalent to the case-control analysis²².

To implement the weighted method, one needs to know or estimate the weights which requires at least empirical data about the distribution of Y. This may not be a problem for nested studies; however, it can be difficult to calculate the weight for studies that are not nested. The difficultly arises because good quality data on the distribution of Y, and an enumeration of potential subjects, may not be available for the base population. The IPW suffers from the fact that in the typical ODS setting the natural choice of number of categories of Y is not large enough to yield the variability in weights that would make it efficient¹⁸. Some recently developed methods may help to identify even more optimal weights^18,23. The Zhou et al. method, on the other hand, does not used the selection probability and hence does not need to enumerate the base population.

Our results showed that with a up to about 1 and ρ near 0.5 and a total sample size of 400, ODS analysis conducted using the estimator of Zhou et al. increased power about twice as much as the weighted estimating equation approach (Figure 2). With larger values of a or smaller values of ρ, the advantage of the Zhou et al. estimator was greater. This reflects a greater influence on the regression parameters for data from the tail areas than the middle areas. In general, the efficiency gain of the IPW method over the simple random sample analysis is notable, thus we would suggest in practice that one should at least do the weighted analysis if one cannot implement the Zhou et al. method.

If an ODS procedure is to be used, questions will arise regarding the optimal choice of a and ρ. For example, consider an examination of the serum level of contaminant X among pregnant women in relation to a continuous outcome in offspring. Subject matter considerations might support large values of a, e.g., greater than 1, so that it corresponds to a clinically abnormal value. Values of a greater than 1 might seem appealing because of the resulting increase in power, especially with the Zhou et al. estimator (Figure 2). But the reward from choosing a relatively large value of a depends on an assumption about fβ(Y|X) across the range of Y. If, e.g., Y is intelligence quotient (IQ), and a is set at 2.5, and the only supplement sample is of those with IQ’s less than 100 - 2.5 * SE_IQ, or 62.5, then the mentally retarded population in the supplement sample will include a larger proportion of genetically-determined retardation, on whom X might have essentially no effect. This “dilution” of the supplement sample with the “doomed” (or “immune”) means estimates of fβ(Y|X) will be attenuated in proportion to the dilution. Smaller values of a, e.g., 1–1.5 would guard against such dilution while allowing one to get much more power with the Zhou et al. estimator than would be possible with the weighted estimated equation. Similarly, choice of ρ > 0 has several advantages over ρ = 0 (14), since including an overall random sample provides the flexibility of a cohort study and allows for model checking. In general, choosing a ρ from the range of [.2, 0.5] allows one to get much improved power with the Zhou et al. estimator than would be possible with the weighted estimated equation estimator, while still allocating enough observations to the SRS sample.

Similarly, the relative size of n₁ and n₃ might be affected by several factors that will vary across studies. For example, if the exposure variable is known to be skewed with a long tail to the right and β is known to be either zero or positive, then increasing the size of n₃ relative to n₁ would be sensible. A large n₃ relative to n₁ would also make sense when there is little interest in the determinants of a low value of the outcome variable.

Prospective designs coupled with relatively expensive measures of exposure are being used with increasing frequency in epidemiologic research. Furthermore, the scope of epidemiologic research increasingly includes outcomes best measured on a continuous scale. Given these trends, methods that allow cost cutting while maintain statistical efficiency are likely to see greater use. Recently, similar ideas using the ODS design has been extended to the situation where in addition to the ODS sample, information other than exposure variable are also available for the rest of the base population²⁴. Methods have been developed that account for an ordinal outcome variables in a generalized linear model setting, as have been methods that incorporate auxiliary information about the exposure variable that is available for the entire base population²⁵. Much work, however, remains to be done, e.g., how to use ODS with longitudinal data is still an open question. A survey of the statistical research on ODS design can be found in Zhou and You²⁶.

Abbreviations

BSID

Bayley Scale of Infant Development

CI

Confidence interval

IQ

intelligence quotient

ODS

outcome dependent sampling

SE

standard error