Meta-Analysis of Rare Binary Adverse Event Data

Abstract

We examine the use of fixed-effects and random-effects moment-based meta-analytic methods for analysis of binary adverse event data. Special attention is paid to the case of rare adverse events which are commonly encountered in routine practice. We study estimation of model parameters and between-study heterogeneity. In addition, we examine traditional approaches to hypothesis testing of the average treatment effect and detection of the heterogeneity of treatment effect across studies. We derive three new methods, simple (unweighted) average treatment effect estimator, a new heterogeneity estimator, and a parametric bootstrapping test for heterogeneity. We then study the statistical properties of both the traditional and new methods via simulation. We find that in general, moment-based estimators of combined treatment effects and heterogeneity are biased and the degree of bias is proportional to the rarity of the event under study. The new methods eliminate much, but not all of this bias. The various estimators and hypothesis testing methods are then compared and contrasted using an example dataset on treatment of stable coronary artery disease.

1 INTRODUCTION

The use of meta-analysis for research synthesis has become routine in medical research. Unlike early developments for effect sizes based on continuous and normally distributed outcomes (Hedges and Olkin, 1985), applications of meta-analysis in medical research often focus on the odds ratio (Engles et. al, 2000 and Deeks, 2002) between treated and control conditions in terms of a binary indicator of efficacy and/or the presence or absence of an adverse drug reaction (ADR). The two most widely used statistical methods for meta-analysis of a binary outcome are the fixed-effect model (Mantel and Haenszel (MH), 1959) and the random-effect model (DerSimonian and Laird (DSL), 1986). A special statistical problem arises when the focus of research synthesis is on a rare binary events, such as a rare ADR.

The literature of fixed-effect meta-analysis for sparse data provides a solid guideline for both continuity correction and methods to use. The standard use of a continuity correction for binary data may not be appropriate for sparse data as the number of zero cells for such data become large. Sweeting et.al. (2004) showed via simulation that for sparse data with homogeneous treatment effect, the “empirical correction” which incorporates information on odds ratios from other studies, and the “treatment arm correction” that uses the reciprocal of the size from the other arm, perform better than the constant 0.5 correction for both the MH and inverse variance weighted methods. Their investigation reveals that for fixed-effect models, the MH method performs consistently better than the inverse variance weighted method for imbalanced group sizes and all continuity corrections. They found that the Peto method is almost unbiased for balanced group sizes and the bias increases with respect to the group imbalance.

Bradburn et. al, (2007) have performed an extensive simulation study to compare a number of fixed-effect methods of pooling odds ratios for sparse data meta-analysis. They considered balanced as well as highly imbalanced group sizes and used a constant 0.5 zero-cell correction only when required. Their investigation revealed that most of the well known meta-analysis methods are biased for sparse data. They found that the Peto method is the least biased and the most powerful for within-study balanced sparse data which matches the findings of Sweeting et al. (2004). Whereas, for unbalanced cases, the MH without zero-correction, logistic regression and the exact method have similar performance and are less biased than the Peto method. They concluded that the method of analysis should be chosen based on the expected treatment effect size, imbalance of the study arms and the underlying event rates. The general recommendation is to use the MH method with an appropriate continuity correction and avoid the inverse variance weighted average and DSL methods when dealing with sparse data with homogeneous treatment effect.

Relatively less attention has been paid to heterogeneous treatment effects or moment-based meta-analysis with random-effects for sparse data. Sweeting, et al. (2004) performed a limited simulation study using random-effects models to combine odds ratios for sparse data. In 95% of the cases they did not get valid estimates (i.e. positive estimates) of the between-study variance. As a consequence, their results for random-effects models were close to those of the fixed-effects model. For random-effects meta-analysis, Shuster (2010) showed via simulation that inverse variance weighted average estimates including the DSL method are highly biased. Based on his findings, he strongly advocated for the simple (unweighted) average estimate for random-effects meta-analysis.

Available random-effect methods consistently underestimate the heterogeneity parameter (DerSimonian and Kacker, 2007). The random-effects meta-analysis also requires an appropriate continuity correction to estimate the treatment effect. Although Sweeting, et al. (2004) showed that the empirical and treatment arm corrections performed better than 0.5 cell correction for fixed-effect models, they cautioned against the applicability of the empirical continuity correction for the random-effects model, as for such models the underlying treatment effect varies between studies.

The focus of this article is on random-effects meta-analysis for sparse data. We first look for a continuity correction to make our moment based estimate of the treatment effect asymptotically unbiased for a single study. Next we extend this concept of bias correction for multiple studies and propose an asymptotically unbiased estimate which matches with the finding of Shuster (2010). We organize the article as follows. In Section 2 we discuss various meta-analytic methods for estimating relevant model parameters. In this section, we propose two new methods: one for estimating the treatment effect and the other for estimating the heterogeneity parameter. In Section 3 we investigate hypothesis testing problems for these parameters. For the heterogeneity parameter we show standard testing procedures have very poor power. Using the concept of parametric boot-strapping, we propose a testing procedure for the heterogeneity parameter that provides better power. In Section 4 we compare performances of several methods via simulation and show that our proposed methods provide very satisfactory results. In Section 5 we illustrate our results with an example of Percutaneous Coronary Intervention (PCI) versus medical treatment alone (MED) in the treatment of patients with stable coronary artery disease. We conclude with a discussion of our results in Section 6.

2 Estimation of Model Parameters

Consider a meta-analysis consisting of k randomized studies. In the ith study, n_it subjects are randomly assigned to the treatment group, and the remaining n_ic subjects are assigned to the control group. The outcome variable is characterized as a success or failure and accordingly assign a value of 1 or 0. Let x_it and x_ic be respectively the numbers of observed events of interest in the treatment and control groups of the ith study. One general approach to model the between study variation is to use a binomial-normal hierarchical model. Let p_it and p_ic be respectively the probabilities of observing an event in the treatment and control groups. The model can be expressed as:

$$x_{ic}~B(p_{ic},n_{ic}),x_{it}~B(p_{it},n_{it}),\mathit{\text{log}}it(p_{ic})={\mu }_i,\mathit{\text{log}}it(p_{it})={\mu }_i+\theta +{\epsilon }_i,\mathit{\text{ln}}\left\{\frac{p_{it}/q_{it}}{p_{ic}/q_{ic}}\right\}=\theta +{\epsilon }_i,,\text{and}{\epsilon }_i~N(0,{\tau }^2),$$ (1)

where q_it = 1 − p_it and q_ic = 1 − p_ic. The primary focus of this article is on estimation and testing of the treatment effect (θ) and heterogeneity parameter (τ²).

We start by reviewing the moment-based estimators that form the basis of current routine practice in this area (e.g., the Cochrane Reviews). As we will show, the moment-based estimators can result in quite biased estimates of the overall treatment effect in the presence of heterogeneity of the treatment effect across studies. We study the bias of these estimators and propose new alternative moment-based methods that improve overall performance and testing.

The MH and empirical logit (EL) methods (also known as the inverse variance method) used for estimating the odds ratios are moment-based approaches which ignore heterogeneity among studies. The DSL method incorporates the between-study variability in the weighted average estimate of θ assuming τ² is known. When the binary outcome is rare, and one or more cells in a study are zero, traditional moment-based approaches such as EL and DSL break down as it becomes impossible to compute the odds ratio. Several numeric adjustments to correct this problem have been suggested. Haldane (1955) added 1/2 to the observed frequencies to estimate the treatment effect for a single study, whereas for multiple studies Cox (1970) added −1/2 to estimate the same parameter. Both of the authors proved that for fixed-effect models their estimates are optimal in terms of reducing the bias to the first order approximation. For studies of rare events, when a large number of observed frequencies are zero, the empirical and treatment arm corrections proposed by Sweeting et.al. (2004) provide better results than the constant 0.5 correction for fixed-effect meta-analysis. In what follows we discuss our approach to select the continuity correction for random-effects meta-analysis with sparse data.

We first add a positive constant a to the observed frequencies and estimate the treatment effect for the model defined in (1) and then determine the optimal value of a to make the estimate unbiased. Let θ̂_ia be an estimate of the treatment effect based on the ith study.

$${\widehat{\theta }}_{ia}=\mathit{\text{ln}}\left\{\frac{x_{it}+a}{n_{it}-x_{it}+a}\right\}-\mathit{\text{ln}}\left\{\frac{x_{ic}+a}{n_{ic}-x_{ic}+a}\right\},$$ (2)

where x_ij and n_ij are respectively the observed number of events and total sample size in the jth group, j = t, c, of the ith study. Using Result 1 provided in Appendix 1 we compute the following expression for the expected value of θ̂_ia.

$$E({\widehat{\theta }}_{ia})=\theta +\left(\frac{\frac{1}{2}-a}{n_{it}}\right)[e^{\mu +\theta +{\tau }^2/2}-e^{-\mu -\theta +{\tau }^2/2}]-\left(\frac{\frac{1}{2}-a}{n_{ic}}\right)[e^{\mu }-e^{-\mu }]+O(n^{-2}).$$ (3)

Inspecting the right hand expression in (3), we see that the first order term of bias (i.e. terms of order n⁻¹) will vanish if a = 1/2. The implication of this result is that the estimate θ̂_i1/2 is unbiased up to the order of n⁻¹, and hence the simple average estimate ${\widehat{\theta }}_{s1/2}={\sum }_{i=1}^k\frac{{\widehat{\theta }}_{i1/2}}{k}$ is also unbiased. We now explore the properties of the weighted average estimate. The variance of θ̂_i1/2 shown in Appendix 2 to be:

$$V({\widehat{\theta }}_{i1/2})=\frac{1}{n_{it}}[e^{\mu +\theta +\frac{{\tau }^2}{2}}+e^{-\mu -\theta +\frac{{\tau }^2}{2}}]+\frac{1}{n_{ic}}[e^{\mu }+e^{-\mu }]+\frac{2}{n_{it}}+\frac{2}{n_{ic}}+{\tau }^2+O(n^{-2}).$$ (4)

In the right side of (4), the quantity $\frac{1}{n_{it}}[e^{\mu +\theta +\frac{{\tau }^2}{2}}+e^{-\mu -\theta +\frac{{\tau }^2}{2}}]+\frac{1}{n_{ic}}[e^{\mu }+e^{-\mu }]+\frac{2}{n_{it}}+\frac{2}{n_{ic}}$ is the expression for the within-study variance, and τ² is the between-study variance. Thus V(θ̂_i1/2) is the sum of the within- and between-study variances. Note that

$$E_{\epsilon }(\frac{1}{n_{it}{p}_{it}{q}_{it}}+\frac{1}{n_{ic}{p}_{ic}{q}_{ic}})=\frac{1}{n_{it}}[e^{\mu +\theta +\frac{{\tau }^2}{2}}+e^{-\mu -\theta +\frac{{\tau }^2}{2}}]+\frac{1}{n_{ic}}[e^{\mu }+e^{-\mu }]+\frac{2}{n_{it}}+\frac{2}{n_{ic}}.$$ (5)

Hence, the quantity $\frac{1}{n_{it}{p}_{it}{q}_{it}}+\frac{1}{n_{ic}{p}_{ic}{q}_{ic}}+{\widehat{\tau }}^2$ is unbiased for V(θ̂_i1/2), provided that τ̂² is unbiased for τ̂². A usual estimate of V(θ̂_i1/2) denoted by V̂(θ̂_i1/2) is

$$\widehat{V}({\widehat{\theta }}_{i1/2})={\widehat{\sigma }}_i^2({\widehat{\tau }}^2)=\frac{1}{n_{it}{\widehat{p}}_{it}{\widehat{q}}_{it}}+\frac{1}{n_{ic}{\widehat{p}}_{ic}{\widehat{q}}_{ic}}+{\widehat{\tau }}^2,$$ (6)

where ${\widehat{p}}_{it}=\frac{x_{it}+1/2}{n_{it}+1}\text{and}{\widehat{p}}_{ic}=\frac{x_{ic}+1/2}{n_{ic}+1}$. The study-specific estimate of variance of the treatment effect recommended by DSL has the same expression as in the right side of (6). Let ${\widehat{w}}_i({\tau }^2)=\frac{1}{{\widehat{\sigma }}_i^2({\tau }^2)}$. The weighted average estimate of θ denoted by θ̂_wa is

$${\widehat{\theta }}_{wa}({\tau }^2)=\frac{{\sum }_{i=1}^k{\widehat{w}}_i({\tau }^2){\widehat{\theta }}_{ia}}{{\sum }_{i=1}^k{\widehat{w}}_i({\tau }^2)}.$$ (7)

When τ² is assumed to be 0, the estimate in equation (7) is known as the EL or inverse variance estimator of common log odds ratio. By contrast, the MH estimate of the common odds ratio, which also assumes τ² = 0, is given by ${\widehat{\theta }}_{MH}={\sum }_{i=1}^K\frac{x_{it}(n_{ic}-x_{ic})}{n_{it}+n_{ic}}/{\sum }_{i=1}^K\frac{x_{ic}(n_{it}-x_{it})}{n_{it}+n_{ic}}$.

Note that (i) the weights ŵ_i(τ²) are biased (Bohning et al., 2002; Malzahn et al., 2002), and (ii) ŵ_i(τ²) and θ̂_ia are correlated (as p̂_i and $\frac{1}{{\widehat{p}}_i{\widehat{q}}_i}$ are correlated). Shuster (2010) proved that when estimated effect size and empirically derived weights are correlated, the weighted average estimate from the random effects model provided in (7) is biased. In Appendix 5 we show that θ̂_wa has the following bias:

$$\mathit{\text{Bias}}({\widehat{\theta }}_{wa})=E(\frac{E\{\frac{\widehat{w}}{n}|\epsilon \}}{E\{\frac{\widehat{w}}{n}\}}{L}_a(x)-L(p))=H(p_t,q_t,p_c,q_c),$$ (8)

where L_a(x) = θ̂_wa, L(p) = E_x(L_a(x)), $H(p_{t|\epsilon },q_{t|\epsilon },p_c,q_c)=-\frac{(p_{t|\epsilon }-q_{t|\epsilon })}{n(q_{t|\epsilon }{p}_{t|\epsilon })}\{a+\frac{p_c{q}_c-p_{t|\epsilon }{q}_{t|\epsilon }}{2(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}\}+\frac{(p_c-q_c)}{n(p_c{q}_c)}\{a+\frac{p_{t|\epsilon }{q}_{t|\epsilon }-p_c{q}_c}{2(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}\}$ and H(p_t, q_t, p_c, q_c) = E(H(p_t|ε, q_t|ε, p_c, q_c)). We see in Figure 1b and 1c that for studies of rare events, this bias is usually positive and is an increasing function of both τ² and a. As a result, the bias of the weighted average method does not vanish even after adding 1/2 as it does for the simple average method. It is a well known result in linear models that the weighted average estimate (when weights are inversely proportional to variance) is the best linear unbiased estimate (BLUE) for the mean effect. However, the concept of the BLUE is not applicable in the current context as the weights are biased and correlated. Shuster (2010) strongly recommended using the simple average (unweighted) estimate for the random-effects model as the correlation between the weights and effect size produces serious bias to the weighted average estimate. The estimated variances of θ̂_s1/2 and θ̂_w1/2 are respectively

$$\widehat{V}({\widehat{\theta }}_{s1/2})=\frac{{\sum }_{i=1}^k{\widehat{\sigma }}_i^2({\tau }^2)}{k^2},\text{and}\widehat{V}({\widehat{\theta }}_{w1/2})=\frac{1}{{\sum }_{i=1}^k{\widehat{w}}_i({\tau }^2)}.$$ (9)

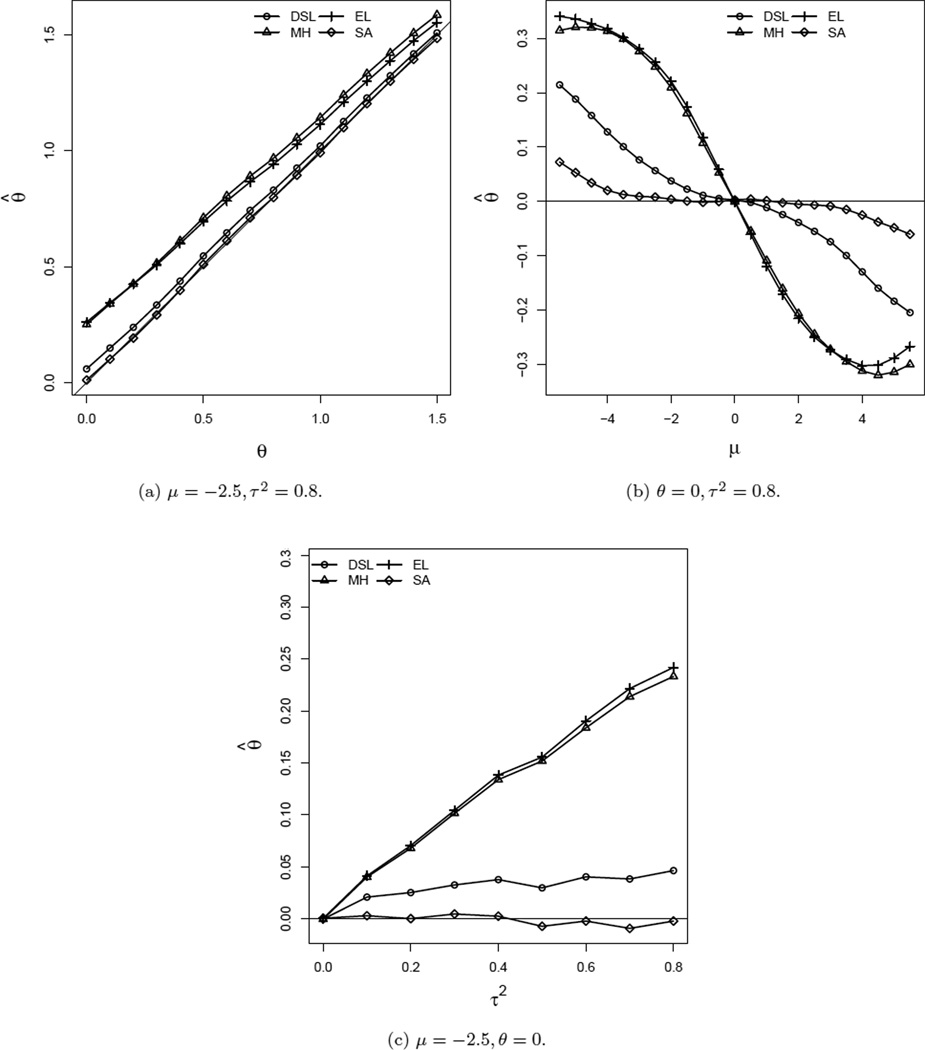
Figure 1.

Comparison of estimates of θ for n ~ U(50, 1000) and k = 20.

Note that V̂(θ̂_s1/2) ≥ V̂(θ̂_w1/2) because the arithmetic mean is larger than the harmonic mean. However, this ordering of the variance estimates may not hold for the true variances. In our case the study specific estimate of θ and the estimate of its variance are statistically dependent, hence E(ŵ_i(τ²)θ̂_i1/2) ≠ E(ŵ_i(τ²))E(θ̂_i1/2) (as p̂_i and $\frac{1}{{\widehat{p}}_i{\widehat{q}}_i}$ are correlated). Consequently, the exact variance of the weighted average estimate is not $\frac{1}{{\sum }_{i=1}^k{w}_i({\tau }^2)}$. Therefore, in such situations, not only is the weighted average estimate biased but also the superiority of the weighted average estimate in terms of its smaller variance compared to that of the simple average estimate is questionable.

2.1 Estimation of τ²

In practice, τ² has primarily been estimated using the method of moments and likelihood-based methods. Following Cochran’s (1954) Q-statistics, DerSimonian and Laird (1986) proposed a moment-based estimator for an τ² that is easy to compute and has been used extensively. Hardy and Thompson (1996) explored the DSL procedure in connection with constructing a confidence interval for θ for unknown τ². They concluded that the likelihood-based method outperforms the DSL method because it incorporates extra variability due to the estimation of τ². In the context of a mixed-effects linear meta-analysis model, Sidik and Jonkman (2007) compared seven different estimators of the heterogeneity in a simulation study. To obtain confidence intervals for the variance components, Viechtbauer (2007) compared those seven approaches with a new method and showed that the new method had the correct coverage probability. Alternatively, the I² statistic is used to quantify the impact of heterogeneity on the treatment effect (Higgins and Thompson, 2002). From the inferential point of view, I² and Q have been shown to have similar performance (Huedo-Medina et al., 2006).

To illustrate, we use results from the previous section to find the DSL estimator of τ². We take the within-study estimates of variance and corresponding weights to be

$${\widehat{\sigma }}_i^2(0)=\frac{1}{n_{it}{\widehat{p}}_{it}{\widehat{q}}_{it}}+\frac{1}{n_{ic}{\widehat{p}}_{ic}{\widehat{q}}_{ic}},\text{and}{\widehat{w}}_i(0)=\frac{1}{{\widehat{\sigma }}_i^2(0)}.$$ (10)

Let

$$Q=\sum _{i=1}^k{\widehat{w}}_i(0){({\widehat{\theta }}_{i1/2}-{\widehat{\theta }}_{w(0)1/2})}^2,$$ (11)

where θ̂_w(0)1/2 is a weighted average estimate of θ defined in (7). Note that the weight function does not include the between-study variability. The DSL (1986) estimate of τ² is

$${\widehat{\tau }}_{DSL}^2=\frac{Q-(k-1)}{{\sum }_{i=1}^k{\widehat{w}}_i(0)-{\sum }_{i=1}^k{\widehat{w}}_i^2(0)/{\sum }_{i=1}^k{\widehat{w}}_i(0)}.$$ (12)

This estimator has two drawbacks. First, in the presence of the heterogeneity, ${\widehat{\tau }}_{DSL}^2$ is a biased estimate (Bohning et al., 2002; Malzahn et al., 2002; Sidik, 2005). Second, the weights ŵ_i(0) assume that τ² = 0 and hence the between-study variability is not included in it. Incorporating estimates of the proper weights ${\widehat{w}}_i^2({\tau }^2)$, DerSimonian and Kacker (2007) proposed a two-step procedure to estimate τ²: (i) use the within-study weights described in equation (10) to compute ${\widehat{\tau }}_{DSL}^2$ as described in (12), (ii) compute adjusted weights that incorporate the DSL estimate of between-study variance, ${\widehat{w}}_i({\widehat{\tau }}_{DSL}^2)$, and use these in equations (10) and (12) to compute the adjusted estimate ${\widehat{\tau }}_{DSK}^2$. Theoretical properties of this two-step method have not been well studied. We have numerically investigated the properties of ${\tau }_{DSK}^2$ and found that for rare events this estimate has considerable downward bias.

Another procedure for estimating τ² was proposed by Paule and Mandel (1982) (${\tau }_{PM}^2$) and it is based on the following estimating equation.

$$F({\tau }^2)=\sum _i{w}_i({\tau }^2){[{\theta }_i-{\theta }_{w({\tau }^2)}]}^2-(k-1)=0.$$ (13)

A unique solution of equation (13), ${\tau }_{PM}^2$, can be determined by numerical iteration starting with τ² = 0. If F(τ²) is negative for all positive τ², ${\widehat{\tau }}_{PM}^2$ is set to 0. Note that ${\widehat{\tau }}_{PM}^2$ is based on σ̂_i(0) which varies from study to study. The variance estimator may be improved by borrowing strength from all studies when estimating each within-study variance ${\widehat{\sigma }}_i^2$

$${\widehat{\sigma }}_i^2(*)=\frac{1}{(n_{it}+1)}\left[\mathit{\text{exp}}\right(-\widehat{\mu }-{\widehat{\theta }}_{sa}+\frac{{\tau }^2}{2})+2+\mathit{\text{exp}}(\widehat{\mu }+{\widehat{\theta }}_{sa}+\frac{{\tau }^2}{2}\left)\right]+\frac{1}{(n_{ic}+1)}[\mathit{\text{exp}}(-\widehat{\mu })+2+\mathit{\text{exp}}(\widehat{\mu })].$$ (14)

We propose a new estimator, denoted ${\widehat{\tau }}_{IPM}^2$, that is the solution to a modified version of equation (13), where the weights w_i(τ²) are replaced by the shared-strength weights $w_i(*)=\frac{1}{{\tau }^2+{\widehat{\sigma }}_i^2(*)}$. We numerically compare the performance of ${\tau }_{PM}^2\text{and}{\tau }_{IPM}^2$ in Section 4.

3 HYPOTHESIS TESTING

In addition to parameter estimation, an equally important problem in meta-analysis is hypothesis testing regarding θ and τ². A large sample test for θ using θ̂_w1/2 and test for τ² using a mixture of chi-square distributions are available (see Hartung, Knapp and Sinha (2008), Sapiro (1985), and Self and Liang (1987)). In this section we explore some tests for both of these parameters.

3.1 Testing the Treatment Effect

Hartung et al. (2008) constructed the following test statistic for testing the null hypothesis H₀ : θ = 0.

$$T_1=\frac{{\widehat{\theta }}_{{\widehat{w}}_i({\widehat{\tau }}^2)}-0}{\sqrt{\frac{1}{{\sum }_{i=1}^k{\widehat{w}}_i({\widehat{\tau }}^2)}}}.$$ (15)

Even though asymptotically T₁ follows a t distribution with k − 1 degrees of freedom (df), i.e., T₁ ~ t_k−1, its small sample property has not been well studied, particularly for moderate values of τ² (say .5 ≤ τ² ≤ 1.5). As the bias of θ̂_w1/2 is significant even for moderate τ², a natural question to ask is how good the performance of T₁ will be in terms of controlling type I error rates for small to large within-study sample sizes (n = 50, ⋯ , 1000). Based on the unbiased simple average estimate θ_s1/2 we construct the following test statistic

$$T_2=\frac{k({\widehat{\theta }}_{s1/2}-0)}{\sqrt{{\sum }_{i=1}^k{\widehat{\sigma }}_i^2({\widehat{\tau }}^2)}}.$$ (16)

In Section 4.2 we investigate the performance of T₁ and T₂ numerically and provide guidelines for application.

3.2 Testing the Heterogeneity Parameter

In practice, we use the likelihood ratio test or Wald’s test to determine whether the heterogeneity parameter is zero, i.e. H₀ : τ² = 0. This puts the variance component on the boundary of the parametric space defined by the alternative hypothesis. Under this scenario, the limiting distribution of the likelihood ratio test statistic −2ln(LR) under the null hypothesis does not follow a χ² distribution. Shapiro (1985) derived the asymptotic distribution of −2ln(LR) as a mixture of χ² distributions, when τ² falls on the boundary. Self and Liang (1987) generalized these results. The general conclusion is that standard tests for H₀ : τ² = 0 are too conservative in terms of controlling type I error rates (α) and exhibit inadequate power in the neighborhood of the null hypothesis. We propose two tests for τ². The first test is based on the Q statistic:

$$Q({\widehat{\tau }}^2)=\sum _{i=1}^k{\widehat{w}}_i({\tau }^2){[{\widehat{\theta }}_{i1/2}-{\widehat{\theta }}_{w({\tau }^2)1/2}]}^2.$$

As shown in Appendix 4, an estimate of the variance of the Q statistic is:

$$\widehat{\mathit{\text{Var}}}(Q({\widehat{\tau }}^2))=2\sum _{i=1}^k{\widehat{w}}_i^2({\widehat{\tau }}^2){[{\widehat{\tau }}^2+{\widehat{\sigma }}_i^2(0)+\frac{1}{{\sum }_{i=1}^k{\widehat{w}}_i({\widehat{\tau }}^2)}-\frac{2{\widehat{w}}_i({\widehat{\tau }}^2)({\widehat{\tau }}^2+{\widehat{\sigma }}_i^2(0))}{{\sum }_{i=1}^k{\widehat{w}}_i({\widehat{\tau }}^2)}]}^2.$$ (17)

Cochran (1950) showed that the asymptotic distribution of Q(τ̂²) is χ² with degrees of freedom (k − 1), which is a gamma distribution. Krishnamoorthy, Mathew and Mukherjee (2008), and Bhaumik, Kapur, and Gibbons (2009) observed that the normal distribution approximation is better for a standardized log-transformed gamma distribution than the standardized gamma distribution. Based on this result, we propose the following test for H₀ : τ² = 0.

$$T_3=\frac{(k-1)[\mathit{\text{ln}}(Q({\widehat{\tau }}^2))-\mathit{\text{ln}}(k-1)]}{\sqrt{\widehat{\mathit{\text{Var}}}[\mathit{\text{ln}}(\widehat{Q}(0))]}}.$$ (18)

In (18) the variance of ln(Q(τ̂²)) is computed using the delta method and $\widehat{\mathit{\text{Var}}}[\mathit{\text{ln}}(Q(0))]$ is obtained by substituting τ̂² = 0 in the expression of $\widehat{\mathit{\text{Var}}}[\mathit{\text{ln}}(Q({\widehat{\tau }}^2))]$. For many situations T₃ performs extremely well in terms of controlling type I error rates. Our simulation results show that for extremely rare events, this test has inflated type I error rates. The simulated results are not reported here. Our second proposed test for τ² = 0 is based on the simple average estimate of θ, which is specifically designed for rare events. Let y_i = (θ̂_i1/2 − θ̂_s1/2)². Under the null hypothesis, an estimate of the mean of y_i denoted by B_i is $\frac{k-2}{k}{\widehat{\sigma }}_i^2(0)+\frac{{\sum }_{i=1}^k{\widehat{\sigma }}_i^2(0)}{k^2}$. An estimate of the variance of y_i is Σ̂_i, where Σ̂_i = 2B_i. The second proposed test for H₀ : τ² = 0 is

$$T_4=\frac{{\sum }_{i=1}^k(y_i-B_i)}{\sqrt{{\sum }_{i=1}^k{\widehat{\mathrm{\Sigma }}}_i}}.$$ (19)

Even though the asymptotic distribution of T₄ is standard normal, for small samples its distribution is not known. In Section 4 we show that for finite samples this test is very conservative. To maintain the proper type I error rate, we propose to determine the critical value using the parametric bootstrapping technique as follows:

1. For a given dataset of sample size n, estimate θ and μ by the simple average method. For large n, θ̂ and μ̂ are consistent estimators for θ and μ. In the following we replace θ̂ by θ and μ̂ by μ.

2. Using θ̂, μ̂ (obtained from step 1) and τ₀, generate k studies each of size (n_t, n_c) from B(n_t, p_t) and B(n_c, p_c) for treatment and control groups respectively under the null hypothesis.

3. Compute y_i and B_i.

4. Compute T₄ using equation (19)

5. Repeat steps 2–4 for 10000 times.

6. Find the 100(1 − α)th percentile point T₄(α) from the generated $T_4^{\prime }s$.

7. Reject H₀ if T₄ > T₄(α) where T₄ is obtained from (19) for the original data.

We investigate the performance of T₄ in Section 4.

4 SIMULATION STUDY

In this section, we describe the results of a simulation study designed to compare several methods for evaluating (i) performance of moment-based estimates of θ, (ii) the type I error rates and power functions for testing θ, (iii) performance of estimates of τ², and (iv) the type I error rates and power functions for testing τ². All the simulation studies were performed using the R software.

4.1 Performance of Estimates of θ

We compare the performance of the overall treatment effect estimate θ via simulation for four different estimation procedures, (a) simple average (SA), (b) DSL with estimated ${\tau }_{DSL}^2$, (c) empirical logit (EL), and (d) Mantel-Haenszel (MH). For this comparison we set θ = 0, 0.5, 1.0, ⋯ 2.5; k = 20; μ = −5.5, −5, ⋯ , 0, ⋯ , 5, 5.5; ${\sigma }_{\mu }^2=0.5$ and τ² = 0, 0.2, 0.4, 0.6, 0.8. The number of subjects in each arm was chosen independently by rounding random draws from a uniform distribution with min(n) = 50 and max(n) = 1000, i.e. n_t and n_c ~ U(50, 1000). Next, we generated the responses x_ic for the control group based on a binomial distribution B(n_ic, p_ic) for i = 1, ⋯ , k, where p_ic is computed as $\frac{\mathit{\text{exp}}(\mu +{\epsilon }_1)}{1+\mathit{\text{exp}}(\mu +{\epsilon }_1)}$. The responses x_it for the treatment group were drawn from a binomial distribution B(n_it, p_it) for i = 1, ⋯ , k with $p_{it}=\frac{\mathit{\text{exp}}(\mu +{\epsilon }_1+\theta +{\epsilon }_2)}{1+\mathit{\text{exp}}(\mu +{\epsilon }_1+\theta +{\epsilon }_2)}$, ε₁ ~ N(0, 0.5) and ε₂ ~ N(0, τ²). Inclusion of ε₁ in p_ic and ε₂ in p_it imply that both the control and treatment groups have varying rates of events. We have added 0.5 correction when necessary for EL, DSL and MH, whereas for SA estimates we have added 0.5 correction for all studies. We simulated 1000 replications for each combination of k, n, θ, μ and τ².

Figure 1 compares various estimates of the overall treatment effect. Panel (a) reveals that the MH and EL methods overestimate the overall treatment effect. This figure also suggests that SA estimates are less biased for all values of the treatment effect under consideration. For moderate overall treatment effects, DSL and SA estimates are comparable. Panel (b) exhibits the effect of the background incidence rate in estimating the overall treatment effect. It is evident from this figure that MH, EL and DSL estimates are biased when μ ≠ 0 (i.e. mean (p_c) ≠ 0.5). The SA estimate, on the other hand, is almost unbiased for moderate background incidence rates (i.e. −4 ≤ μ ≤ 4). Also, the bias of the SA estimate for rare event cases is comparatively smaller. Panel (c) shows the effect of heterogeneity of treatment effects across studies on the estimate of the overall treatment effect. It is apparent that bias of the SA estimate in the presence of even significant heterogeneity is minimal compared to the other estimators (EL, DSL, and MH) under consideration.

In addition, we have used the “empirical continuity correction” suggested by Sweeting et al. (2004) for all moment-based estimators. We observe that moment-based estimates of θ with this continuity correction are more biased than 0.5 correction for rare events in the presence of noticeable heterogeneity. This is not surprising as Sweeting et al. (2004) have pointed out the non-applicability of empirical continuity correction for random-effects models.

In this context it is important to mention that theoretical properties of simple average estimate of θ is derived under the fixed response rate in the control group but its properties are studied via simulation under both fixed (not reported here) and random response rates in the control group. In both cases we observe that the simple average estimate performs better than MH, EL and DSL.

4.2 Performance of Tests for Treatment Effect

In Section 3, we discussed the general testing procedure for H₀ : θ = 0 against the alternative H₁ : θ ≠ 0. In this section, we use a simulation study to compare the performance of three tests: (a) z-test based on the EL estimate of θ in equation (15), i.e. T₁, with τ̂² = 0, (b) z-test based on the DSL estimate of θ including τ² in (15), i.e. T₁, with ${\widehat{\tau }}^2={\widehat{\tau }}_{DSK}^2$, and (c) z-test based on the simple average estimate of θ, i.e., T₂, with ${\widehat{\tau }}^2={\widehat{\tau }}_{IPM}^2$. Our Monte Carlo simulation is based on 10000 replications with τ²=0.8, k=20, and a nominal significance rate of α= 0.05. Figure 2 graphically presents the results of our simulation study.

Figure 2.

Comparison of type I error rates and power curves for testing θ. μ = −2.5, τ² = 0.8, n ~ U(50, 1000), and k = 20.

Figure 2(a) displays the estimated significance level of each test when the underlying incidence rate is varied, and when the null hypothesis (i.e θ = 0) is true. Although DSL performs quite well when μ is in the neighborhood of zero, the type I error of DSL is inflated (to almost 20%) for extreme values of μ. Type I error rates of EL and MH are highly inflated for all values of μ. On the other hand, the SA based test has type I error rates close to the nominal level regardless of the background incidence rates.

Next we numerically study the power functions of these tests varying θ = 0, 0.1, ⋯ , 1.5, μ = −2.5 (i.e., mean (p_c) = 0.08), and n_c, n_t ~ U(50, 1000). We present these results in Figure 2(b). The SA test demonstrates a desirable power curve that controls the type I error rate at the nominal level and grows to the power close to one for an effect size close to 0.6. On the contrary, power curves of EL and MH are overlapping in the figure. Both EL and MH have highly inflated type I error rates (close to one) and hence naturally they have deceptively high power.

4.3 Performance of Estimates of the Heterogeneity Parameter τ²

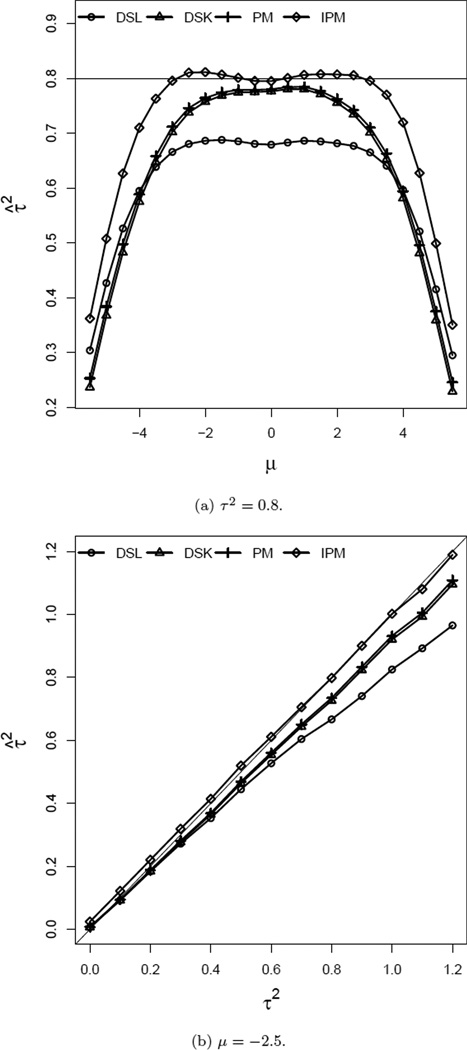
In order to study the performance of estimates of τ², we simulate data sets following the same procedure described in the first paragraph of Section 4.1. For this simulation, values of τ² are set between 0 and 1.2. In order to demonstrate the effect of rare events as well as prevalent events on the estimates of τ², the values of μ are varied from −5.5 (0.4%) to 5.5 (99%). For this comparison we set θ at 0 and the number of studies were set to 20. Sample sizes in each treatment arm were drawn from U(50, 1000). Figure 3(a) shows that for extremely rare (or prevalent) cases, moment-based estimates by PM and DSK fail to detect the presence of heterogeneity (τ² = 0.8) in the treatment effect across studies. This figure also illustrates the reduction of bias achieved by the IPM procedure compared to DSL, DSK, and PM for −4 ≤ μ ≤ 4. Figure 3(b) shows that the IPM approach performs the best among all four methods for all values of 0 < τ² ≤ 1.2 when μ is set at −2.5, (i.e. a moderate background rate of 7.5%).

Figure 3.

Comparison of Estimates of τ². θ = 0, n ~ U(50, 1000), and k = 20.

4.4 Performance of tests of the Heterogeneity Parameter

In this section we compare the performance of Cochran’s Q, and Parametric boot-strapping (PB) statistics for testing H₀ : τ² = 0, against H₁ : τ² > 0. For the current simulation we follow the same parametric conditions as described in Section 4.1. For this study we set μ = −4.5 and −2.5 along with θ = 0, k = 20 and the n ~ U(50, 1000). We present the power curves in Figure 4. Figures 4a and 4c reveal that Cochran’s Q has lower power compared to PB for both event rates −4.5 and −2.5. It is clear from the comparison of these two figures that for moderate event rates (i.e. μ = −2.5) the performance of both the tests have improved significantly. In Figure 4a we see that for a rare event case (μ = −4.5), the power of Q is extremely poor. The new test PB also performs poorly for smaller values of τ² but for τ² > 0.6 it performs far better than Q.

Figure 4.

Comparison of power curves for testing τ². μ = −2.5, θ = 0, n ~ U(50, 1000), and k = 20.

For μ = −4.5, τ² = 0.6 plays an important role, as for this value of τ², the proportion of between studies variance (I²) exceeds 40% of the total variance (see Figure 4b). Higgins and Thompson (2002) suggest that any value of I² less than 30% indicates only for a mild heterogeneity. Following their tentative rule, we can infer that τ² ≤ 0.6 indicates only mild heterogeneity (see Figure 4b). For a significant heterogeneity (when I² ≥ 50%, or in the current context τ² ≥ 0.6), PB outperforms Q in terms of power (see Figure 4a). In Figure 4(d) we see that the power of each test depends on the number of studies included in the meta-analysis. The power curve of Q grows with a slower rate compared to that of PB. To attain 80% power, PB requires about 125 studies, whereas for the same power, Q needs almost 450 studies.

4.5 Correlated Arms

In Figure 1, we observed that all methods overestimated the treatment effect. In order to give a definite answer to the question when moment-based estimates will underestimate the treatment effect, we perform a simulation study with correlated arms (i.e. we assume that ε₁ and ε₂ are correlated and the data were generated accordingly for this simulation study). Figure 5 shows that usual moment-based methods run into even more problems when the event rates of the control and treatment are correlated. For larger negative correlations (i.e. ρ < −.5), treatment shows a protective effect and for larger positive correlations (i.e. ρ > .5), it shows a harmful effect when the generating parameters are under the null. The performance of the simple average is better compared to its counterparts DSL, MH and EL even for correlated arms. We have extended our simulation study for a wide range of θ ( −.4 ≤ θ ≤ 1.0 ) and observed the same pattern. For negative correlations, θ is under estimated and for positive correlations, it is over estimated on average. The SA method always has better performance.

Figure 5.

Estimate of θ for correlated background rates and treatment effects. Parameters: μ = −2.77, θ = 0, ${\sigma }_{\mu }^2=1.2$, τ² = 0.45, n ~ U(50, 1000), and k = 17.

4.6 Some Results for Extreme Rare Events

As we have mentioned earlier in Section 2, a special statistical problem arises when the focus of research synthesis is on a rare binary event. Our simulation studies show that moment-based estimates have undesirable statistical properties when the event is very rare or very frequent. We noted in Figure 1b that the bias of the overall treatment effect estimate is attenuated for very rare cases. One explanation for this undesirable behavior is when events are rare, estimates and inferences are unduly influenced by the factor used for continuity correction. One way to avoid this is to conduct larger studies each with more samples. Our simulation results conducted for rare events (mean (p_c) = 2/1000), show that the moment-based estimates produce significant biases for sample sizes smaller than 400, and only the SA estimate converges asymptotically to the true value. The DSL estimate shows very weak convergence, and MH and EL estimates fail to converge to the true value even for a sample size as large as 2400 in each arm. Our simulation also shows that for rare event studies all available estimating methods fail to adequately estimate the heterogeneity parameter for random treatment effects. However, as we have seen in Figures 1c and 2a for fixed-effect models, biases and type I error rates can be severely affected depending on the magnitude of the true heterogeneity. Our simulation shows that for rare events the parametric bootstrap method outperforms the Q statistic. When the number of studies are fairly large (k ≥ 40), our proposed tests for the treatment effect maintain nominal type 1 error rates and provide adequate power.

Zero Studies: For extremely rare events, a large proportion of studies tends to have zero events in both arms. It has been argued by various authors that the zero studies do not contribute to the odds ratio estimation and hence should not be included in the analysis. The contrasting argument in support of inclusion of those studies in order to take an advantage is also found in the literature (Whitehead and Whitehead, 1991). We have performed an extensive simulation study to examine the effects of inclusion (with 0.5 correction) and exclusion of zero studies in the estimation of both the treatment effect parameter (θ) and the heterogeneity parameter (τ²). We find that as the proportion of zero studies increases the discrepancy in the estimation of θ also increases. It reveals that estimates with the inclusion of zero cells have smaller bias compared to estimates without zero cells. The SA estimator is least affected by the proportion of zero studies. It also reveals that exclusion of zero studies improves our ability to estimate τ². In summary, we have two contradictory results. First, the inclusion of zero studies with 0.5 continuity correction helps us estimating θ more accurately. Second, an exclusion of zero studies is helpful in estimating τ². Therefore, two separate strategies are needed to be implemented when estimating these two parameters.

5 ILLUSTRATION

Coronary artery disease is the single largest killer of American men and women (Rosamond et.al., 2007). In 2004 in the U.S., there were 840,000 cases discharged with the diagnosis of acute coronary syndrome, most of them with acute myocardial infarction (MI). Percutaneous coronary intervention or PCI (commonly known as angioplasty) is increasingly being used in patients with various manifestations of coronary artery disease. PCI is an established treatment strategy that improves overall survival and survival time free of recurrent MI for patients with acute coronary disease; however, less is known about the effects of PCI in the treatment of patients with stable coronary artery disease. Research in this area has been limited for two reasons. First, patients with stable coronary artery disease have a very good prognosis and large sample size studies are required to assess potential differences in treatments regarding rare events (Rihal et.al., 2003; Timmis et.al., 2007). Second, there is a period of early risk associated with PCI, which requires longer follow-up periods when compared to medical treatment alone (MED) to offset this early excess risk.

In an effort to better study the efficacy of PCI versus MED, Schomig et.al., (2008) conducted a meta-analysis of 17 randomized clinical trials (RCTs) that compared PCI to MED in patients with stable coronary artery disease. They studied a total of 7513 patients (3675 PCI and 3838 MED). Overall, the average age of the patients was 60 years, 18% of them were women, 54% had incurred MI, and the average length of follow-up was 51 months. Ninety-two percent of the patients in the PCI-based strategy group received revascularization (43% balloon angioplasty, 41% stents, and 8% CABG). In the PCI group, 271 patients died and in the MED group 335 died. Among the 13 studies that reported cardiac mortality, the PCI and MED arms had a combined 115/2814 and 151/2805 cardiac deaths, respectively. Finally, myocardial infarction rates (MI) were provided in all 17 studies, reporting 319 in the PCI group and 357 in the MED group. The original authors used Cochran’s Q-test to assess heterogeneity and performed Mantel and Haenszel (MH) and Dersimonian and Laird (DSL) methods to estimate the overall treatment effect. The Test of heterogeneity (Cochran’s Q statistic) was not significant for total mortality (p=.263) or cardiac mortality (p=.161), but was significant for MI (p=.003). The fixed-effect (MH) model showed a significant protective effect of PCI on total mortality (OR = 0.80, CI = 0.68–0.95), and cardiac mortality (OR = 0.74, CI = 0.57–0.96), and approached significance for MI (OR = 0.91, CI = 0.77–1.06). The random-effect (DSL) model showed a significant protective effect of PCI on total mortality (OR = 0.80, CI = 0.64–0.99), an effect that approached significance for cardiac mortality (OR = 0.74, CI = 0.51–1.06), and a non-significant effect for MI (OR = 0.90, CI = 0.66–1.23) that was in the same protective direction as the other effects. On the basis of these results, the authors concluded that a PCI-based invasive strategy may improve long term survival compared with a medical treatment in patients with stable coronary artery disease.

To illustrate the performance of the moment-based approaches, we reanalyzed these data for all three outcomes (total mortality, cardiac mortality, and MI). For MI, there are 17 studies with an average of 200 subjects per arm. Table 1 presents the estimates of the treatment effects and Table 2 presents the corresponding heterogeneity parameter estimates. Inspection of Table 2 reveals the significance of the heterogeneity. The IPM provides a significantly larger estimate of the heterogeneity parameter. The SA estimate of the treatment effect is positive in contrast to the other estimators. All estimators (SA, MH, and DSL) indicate that PCI has a non-significant effect for MI. We notice the reversal of bias in this example when compared to the figure presented earlier (Figure 1). Our simulation shows (in Figure 5) that such reversal occurs when there is a strong negative correlation between background event rates and treatment effects across studies.

Table 1.

Analysis of PCI vs MED for Myocardial Infarction data

Estimate	θ̂	Std. err	p-val
SA	0.284	0.482	0.221a
MH	−0.096	0.080	0.230b
DSL	−0.106	0.155	0.493b

^a(T₂) was used to perform the test

^b(T₁) was used to perform the test

Table 2.

Analysis of PCI vs MED for Myocardial Infarction data

Estimate	τ̂2	p-val
DSL	0.168	0.003a
DSK	0.175	0.003a
IPM	0.358	< 0.05b

^aCochran’s Q was used to perform the test

^bParametric bootstrapping (T₄) was used to perform the test

For the cardiac death data none of the methods (DSL, DSK, and IPM) found significant heterogeneity, consistent with the findings of Schomig et al (2008). Estimates of heterogeneity by DSL, DSK, and IPM for the all cause mortality data were also non-significant. Hence to estimate the treatment effect for the cardiac death and all cause mortality data our recommendation is to use the MH method using the continuity correction proposed by Sweeting et al.(2004). Our analysis by MH method with empirical continuity correction shows non-significant protective effects of PCI on both total mortality and cardiac mortality.

6 DISCUSSION

It is with some trepidation that we present our findings on the limitations of the most commonly used methods for research synthesis of rare events. These methods (MH and DSL) have been routinely used for decades to advise physicians of the best evidence based practice (e.g., Cochrane Reviews - http://www.cochrane.org/), and to identify potential adverse reactions of pharmaceuticals. For example, the U.S. Food and Drug Administration (FDA) used the MH test to perform an analysis of risk of suicidal thoughts and behaviors associated with antidepressant medications in children, which led to a black box warning that is now present on every antidepressant medication and was further extended to young adults http://www.fda.gov/Drugs/DrugSafety/InformationbyDrugClass/ucm096352.htm. Our findings reveal that these methods in particular and moment-based methods in general can be quite limited in their ability to detect heterogeneity in treatment effect, and in the presence of such heterogeneity can yield biased estimates of overall treatment effects and corresponding tests of hypotheses. In some cases, these biases can be large enough to even change the direction of the overall treatment effect. Furthermore, our simulations indicate that sample size requirements for very rare outcomes are enormous, and generally require hundreds of studies each with hundreds of patients per treatment arm. In practice, such studies are rarely of sufficient size or number to provide anything close to these requirements. Finally, the need to discard studies with zero events in both arms and/or impute a constant for studies with zero events in a single arm, further limits our ability to estimate and test heterogeneity, which in turn biases estimation and testing of the overall treatment effect.

In summary, research synthesis of rare binary event data appears to be more complicated than traditional meta-analysis for continuous outcomes where more traditional effect size estimates are available from a series of studies. The non-linear form of the models produces more complicated relationships between the overall average treatment effect and its variance than for the case of meta-analysis based on linear models. Bias of moment-based estimates is a complicated function of the degree to which the treatment effect varies across studies and the volume of data analyzed. Furthermore, there are a number of different moment-based approaches for estimating the combined treatment effect and heterogeneity, and depending on the combination of the above factors, some work better than others.

In the absence of heterogeneity, the MH method with the empirical continuity correction performs well, and is to be recommended for moment-based fixed-effects meta-analysis. The three new methods developed in this paper ( SA for estimating the overall treatment effect, IPM for estimating heterogeneity, and PB for testing heterogeneity ) perform reasonably well. We recommend the SA with the 0.5 continuity correction for sparse data with heterogeneity. To estimate the heterogeneity parameter our recommendation is to use the IPM. We recommend the PB for testing the heterogeneity parameter. Finally, it should be noted that we have not considered full likelihood approaches to the problem of parameter estimation and hypothesis testing in connection with random-effects meta-analysis. Research along these lines is currently underway.

Appendix 1

Expectation of θ̂_ia:

$$\mathit{\text{ln}}\left(\frac{p_{it}|{\epsilon }_i}{1-p_{it}|{\epsilon }_i}\right)=\mu +\theta +{\epsilon }_i,\mu =\mathit{\text{ln}}\left(\frac{p_{ic}}{1-p_{ic}}\right),{\epsilon }_i~N(0,{\tau }^2).$$

From Gart 1985,

$$E_{x|\epsilon }\left\{\mathit{\text{ln}}\right(\frac{x_{it}+a}{n_{it}-x_{it}+a}\left)\right\}=\mathit{\text{ln}}\left(\frac{p_{it|{\epsilon }_i}}{q_{it|{\epsilon }_i}}\right)+\frac{(p_{it|{\epsilon }_i}-q_{it|{\epsilon }_i})(\frac{1}{2}-a)}{n_{it}{p}_{it|{\epsilon }_i}{q}_{it|{\epsilon }_i}}+O(n^{-2}).$$

Then,

$$E_x\left\{\mathit{\text{ln}}\right(\frac{x_{ic}+a}{n_{ic}-x_{ic}+a}\left)\right\}=\mathit{\text{ln}}\left(\frac{p_{ic}}{q_{ic}}\right)+\frac{(p_{ic}-q_{ic})(\frac{1}{2}-a)}{n_{ic}{p}_{ic}{q}_{ic}}+O(n^{-2}).$$

Thus,

$$E[{\widehat{\theta }}_{ia}]=E_{\epsilon }[E_{x|\epsilon }[{\widehat{\theta }}_i]]=E_{\epsilon }\left\{\mathit{\text{ln}}\right(\frac{p_{it|{\epsilon }_i}}{q_{it|{\epsilon }_i}}\left)\right\}+\frac{(\frac{1}{2}-a)}{n_{it}}{E}_{\epsilon }\{\frac{1}{q_{it|{\epsilon }_i}}-\frac{1}{p_{it|{\epsilon }_i}}\}+O(n^{-2})-E_{\epsilon }\left\{\mathit{\text{ln}}\right(\frac{p_{ic}}{q_{ic}}\left)\right\}-\frac{(\frac{1}{2}-a)}{n_{ic}}{E}_{\epsilon }\{\frac{1}{q_{ic}}-\frac{1}{p_{ic}}\}+O(n^{-2})=E_{\epsilon }\{\mu +\theta +{\epsilon }_i\}+\frac{(\frac{1}{2}-a)}{n_{it}}{E}_{\epsilon }\{\frac{1}{q_{it|{\epsilon }_i}}-\frac{1}{p_{it|{\epsilon }_i}}\}-\mu -\frac{(\frac{1}{2}-a)}{n_{ic}}\{\frac{1}{q_{ic}}-\frac{1}{p_{ic}}\}+O(n^{-2})=\theta +\frac{(\frac{1}{2}-a)}{n_{it}}{E}_{\epsilon }\{1+e^{\mu +\theta +{\epsilon }_i}-1-e^{-\mu -\theta -{\epsilon }_i}\}-\frac{(\frac{1}{2}-a)}{n_{ic}}\{e^{\mu }-e^{-\mu }\}+O(n^{-2})=\theta +\frac{(\frac{1}{2}-a)}{n_{it}}\left\{e^{\mu +\theta +{\tau }^2/2}-e^{-\mu -\theta +{\tau }^2/2}\right\}-\frac{(\frac{1}{2}-a)}{n_{ic}}\{e^{\mu }-e^{-\mu }\}+O(n^{-2}).$$

$$\text{Bias of}{\widehat{\theta }}_{ia}=\frac{(\frac{1}{2}-a)}{n_{it}}\{e^{\mu +\theta +{\tau }^2/2}-e^{-\mu -\theta +{\tau }^2/2}\}-\frac{(\frac{1}{2}-a)}{n_{ic}}\{e^{\mu }-e^{-\mu }\}+O(n^{-2}).$$

Appendix 2

Variance of ${\widehat{\theta }}_{i\frac{1}{2}}$:

$$V({\widehat{\theta }}_{ia})=E_{\epsilon }V({\widehat{\theta }}_{ia}|\epsilon )+V_{\epsilon }E({\widehat{\theta }}_{ia}|\epsilon )=E_{\epsilon }\{\frac{1}{n_{it}{p}_{it|{\epsilon }_i}{q}_{it|{\epsilon }_i}}+\frac{1}{n_{ic}{p}_{ic}{q}_{ic}}\}+V_{\epsilon }\left\{E_{x|\epsilon }\right(\mathit{\text{ln}}\frac{{\widehat{p}}_{it|{\epsilon }_i}}{{\widehat{q}}_{it|{\epsilon }_i}}-\mathit{\text{ln}}\frac{{\widehat{p}}_{ic|{\epsilon }_i}}{{\widehat{q}}_{ic|{\epsilon }_i}}\left)\right\}=E_{\epsilon }\{\frac{1}{n_{it}{p}_{it|{\epsilon }_i}{q}_{it|{\epsilon }_i}}+\frac{1}{n_{ic}{p}_{ic}{q}_{ic}}\}+V_{\epsilon }\{\mathit{\text{ln}}\frac{p_{it|{\epsilon }_i}}{q_{it|{\epsilon }_i}}-\mathit{\text{ln}}\frac{p_{ic}}{q_{ic}}+\mathit{\text{const}}\},$$

where, $\mathit{\text{const}}=\frac{(\frac{1}{2}-a)}{n_{it}}\{\frac{1}{q_{it|{\epsilon }_i}}-\frac{1}{p_{it|{\epsilon }_i}}\}-\mu -\frac{(\frac{1}{2}-a)}{n_{ic}}\{\frac{1}{q_{ic}}-\frac{1}{p_{ic}}\}+O(n^{-2})$. Then,

$$V({\widehat{\theta }}_{i\frac{1}{2}})=\frac{1}{n_{it}}{E}_{\epsilon }\{e^{\mu +\theta +{\epsilon }_i}+e^{-\mu -\theta -{\epsilon }_i}+2\}+\frac{1}{n_{ic}}\{e^{\mu }+e^{-\mu }+2\}+V_{\epsilon }\{\mathit{\text{ln}}\frac{p_{it|{\epsilon }_i}}{q_{it|{\epsilon }_i}}-\mathit{\text{ln}}\frac{p_{ic}}{q_{ic}}\}=\frac{1}{n_{it}}\{e^{\mu +\theta +{\tau }^2/2}+e^{-\mu -\theta +{\tau }^2/2}\}+\frac{1}{n_{ic}}\{e^{\mu }+e^{-\mu }\}+\frac{2}{n_{it}}+\frac{1}{n_{ic}}+V_{\epsilon }(\theta +{\epsilon }_i)=\frac{1}{n_{it}}\{e^{\mu +\theta +{\tau }^2/2}+e^{-\mu -\theta +{\tau }^2/2}\}+\frac{1}{n_{ic}}\{e^{\mu }+e^{-\mu }\}+\frac{2}{n_{it}}+\frac{2}{n_{ic}}+{\tau }^2.$$

Appendix 3

Expression of τ²

$$\text{Let},{\widehat{\theta }}_{ia}~𝒩(\theta ,{\tau }^2+{\sigma }_i^2),\tilde{\theta }=\frac{{\sum }_{i=1}^k{\widehat{w}}_i{\widehat{\theta }}_{ia}}{{\sum }_{i=1}^k{\widehat{w}}_i},{\widehat{w}}_i=\frac{1}{{\widehat{\sigma }}_i^2},\text{note that}{\widehat{w}}_i\stackrel{p}{\to }{w}_i.$$

$$\text{Then},V(\tilde{\theta })=\frac{{\sum }_{i=1}^k{w}_i^2({\tau }^2+{\sigma }_i^2)}{{({\sum }_{i=1}^k{w}_i)}^2}={\tau }^2\frac{{\sum }_{i=1}^k{w}_i^2}{{({\sum }_{i=1}^k{w}_i)}^2}+\frac{1}{{\sum }_{i=1}^k{w}_i}.Q=\sum _{i=1}^k{w}_i{({\widehat{\theta }}_{ia}-\tilde{\theta })}^2.$$

$$E[Q]=\sum _{i=1}^k{w}_{i}E{({\widehat{\theta }}_{ia}-\tilde{\theta })}^2=\sum _{i=1}^k{w}_{i}V({\widehat{\theta }}_{ia}-\tilde{\theta })=\sum _{i=1}^k{w}_i[V({\widehat{\theta }}_{ia})+V(\tilde{\theta })-2\mathit{\text{Cov}}({\widehat{\theta }}_{ia},\tilde{\theta })]=\sum _{i=1}^k{w}_i[{\tau }^2+{\sigma }_i^2+{\tau }^2\frac{{\sum }_{i=1}^k{w}_i^2}{{({\sum }_{i=1}^k{w}_i)}^2}+\frac{1}{{\sum }_{i=1}^k{w}_i}-2\mathit{\text{Cov}}({\widehat{\theta }}_{ia},\tilde{\theta })]=\sum _{i=1}^k{w}_i[{\tau }^2+{\sigma }_i^2+{\tau }^2\frac{{\sum }_{i=1}^k{w}_i^2}{{({\sum }_{i=1}^k{w}_i)}^2}+\frac{1}{{\sum }_{i=1}^k{w}_i}-2\frac{w_i({\tau }^2+{\sigma }_i^2)}{{\sum }_{i=1}^k{w}_i}]={\tau }^2\sum _{i=1}^k{w}_i-{\tau }^2\frac{{\sum }_{i=1}^k{w}_i^2}{{\sum }_{i=1}^k{w}_i}+(k-1).$$

Thus

$${\tau }^2=\frac{E[Q]-(k-1)}{{\sum }_{i=1}^k{w}_i-\frac{{\sum }_{i=1}^k{w}_i^2}{{\sum }_{i=1}^k{w}_i}}.$$

The DSL estimate of τ², denoted by ${\tau }_{DSL}^2$ has the following expression

$${\tau }_{DSL}^2=\frac{\widehat{Q}-(k-1)}{{\sum }_{i=1}^k{\widehat{w}}_i-\frac{{\sum }_{i=1}^k{\widehat{w}}_i^2}{{\sum }_{i=1}^k{\widehat{w}}_i}}.$$

Appendix 4

Estimate of $V[\widehat{Q({\tau }^2)}]$

$$Q({\tau }^2)=\sum _{i=1}^k{w}_i({\tau }^2){({\widehat{\theta }}_{ia}-{\tilde{\theta }}_{w({\tau }^2)})}^2,w_i({\tau }^2)=\frac{1}{{\tau }^2+{\sigma }_i^2},V[Q({\tau }^2)]=\sum _{i=1}^k{[w_i({\tau }^2)]}^{2}V{({\widehat{\theta }}_{ia}-{\tilde{\theta }}_{w({\tau }^2)})}^2.$$

Since, $({\widehat{\theta }}_{ia}-{\tilde{\theta }}_{wa({\tau }^2)})~𝒩(0,A_i^2)$, where $A_i^2=E{[{\widehat{\theta }}_{ia}-{\tilde{\theta }}_{w({\tau }^2)}]}^2=({\tau }^2+{\sigma }_i^2)(1-2\frac{w_i({\tau }^2)}{{[{\sum }_{i=1}^k{w}_i({\tau }^2)]}^2})+\frac{1}{{\sum }_{i=1}^k{w}_i({\tau }^2)}$, and E[θ̂_ia − θ̃_w(τ²)]⁴ = 3A⁴ (using the recursive relation of moment of a normal distribution). Then,

$$V[Q({\tau }^2)]=\sum _{i=1}^k{[w_i({\tau }^2)]}^2\{E{({\widehat{\theta }}_{ia}-{\tilde{\theta }}_{w({\tau }^2)})}^4-{[E{({\widehat{\theta }}_{ia}-{\tilde{\theta }}_{w({\tau }^2)})}^2]}^2\}=\sum _{i=1}^k{[w_i({\tau }^2)]}^2\{3A_i^4-{[A_i^2]}^2\}=\sum _{i=1}^k{[w_i({\tau }^2)]}^2(2A_i^4).$$

$$\text{Hence},V[\widehat{Q({\tau }^2)}]=\sum _{i=1}^k{[\widehat{w}{({\tau }^2)}_i]}^2(2{\widehat{A}}_i^4).$$

Appendix 5

Bias of θ̂_wi

Recall that ${\widehat{\upsilon }}_t=\frac{(x_t+a)(n_t-x_t+a)}{n_t+2a}\text{and}{\widehat{\upsilon }}_c=\frac{(x_c+a)(n_c-x_c+a)}{n_c+2a}$, where υ̂_t and υ̂_c are the estimates variance of log odds of treatment and control groups respectively. Then $\widehat{w}=\frac{1}{{\widehat{\upsilon }}_t+{\widehat{\upsilon }}_c}$ and for A₁ = a/n_t + p_t|εq_t|ε, A₂ = a/n_c + p_cq_c, B₁ = q_t|ε − p_t|ε, B₂ = q_c − p_c, e₁ = p̂_t − p_t|ε and e₂ = p̂_c − p_c, we have

$$f({\widehat{p}}_{t|\epsilon },{\widehat{p}}_c)=\frac{\widehat{w}}{n}=\frac{n}{n+2a}\left\{\frac{(A_1+B_1{e}_1-e_1^2)(A_2+B_2{e}_2-e_2^2)}{(2A+B(e_1+e_2)-(e_1^2+e_2^2)}\right\}.$$

Expanding f(p̂_t|ε, p̂_c) in a Taylor’s series about p̂_t|ε, p̂C = (p_t|ε, p_c), we can write,

$$\frac{\widehat{w}}{n}=\frac{a}{n}+\frac{(p_{t|\epsilon }{q}_{t|\epsilon })(p_c{q}_c)}{p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c}+\frac{(q_{t|\epsilon }-p_{t|\epsilon })(p_c^2{q}_c^2)}{{(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}^2}{e}_1+\frac{(q_c-p_c)(p_{t|\epsilon }^2{q}_{t|\epsilon }^2)}{{(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}^2}{e}_2-\{\frac{2(p_c^2{q}_c^2)}{{(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}^2}+\frac{2{(p_{t|\epsilon }-q_{t|\epsilon })}^2(p_c^2{q}_c^2)}{{(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}^3}\}{e}_1^2-\{\frac{2(p_{t|\epsilon }^2{q}_{t|\epsilon }^2)}{{(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}^2}+\frac{2{(p_c-q_c)}^2(p_{t|\epsilon }^2{q}_{t|\epsilon }^2)}{{(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}^3}\}{e}_2^2+\left\{\frac{2(q_{t|\epsilon }-p_{t|\epsilon })(q_c-p_c)(q_{t|\epsilon }{p}_{t|\epsilon }{q}_c{p}_c)}{{(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}^3}\right\}{e}_1{e}_2.$$

$$E(\frac{\widehat{w}}{n}|\epsilon )=\frac{(p_{t|\epsilon }{q}_{t|\epsilon })(p_c{q}_c)}{p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c}+\frac{1}{n}\{\frac{a-2(q_{t|\epsilon }{p}_{t|\epsilon }{q}_c{p}_c)[{(p_{t|\epsilon }-q_{t|\epsilon })}^2(p_c{q}_c)+{(p_c-q_c)}^2{p}_{t|\epsilon }{q}_{t|\epsilon }]}{{(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}^3}-\frac{2(q_{t|\epsilon }{p}_{t|\epsilon }{q}_c{p}_c)}{p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c}\}.$$

$$\text{Let},L_1(x)=\mathit{\text{ln}}\left(\frac{x_{it}+a}{n_{it}-x_{it}+a}\right)\text{and}{L}_2(x)=\mathit{\text{ln}}\left(\frac{x_{ic}+a}{n_{ic}-x_{ic}+a}\right).$$

And, l(p_t|ε) = E_x(L₁(x)) and l(p_c) = E_x(L₂(x)), then

$$L_a(x)=L_1(x)-L_2(x)=l(p_{t|\epsilon })+B_{(t)0}+\sum _{t=1}^{\infty }{B}_{(t)i}{e}_1^i-[l(p_c)+B_{(c)0}+\sum _{i=1}^{\infty }{B}_{(c)i}{e}_2^i]=l(p_{t|\epsilon })-l(p_c)+B_{(t)0}-B_{(c)0}+\sum _{i=1}^{\infty }{B}_{(t)i}{e}_1^i-\sum _{i=1}^{\infty }{B}_{(c)i}{e}_2^i.$$

Thus, if L(p) = E_x(L_a(x)), then

$$E\{\frac{\widehat{w}}{n}{L}_a(x)|\epsilon \}=E\{\frac{\widehat{w}}{n}|\epsilon \}L(p)+E\{\frac{\widehat{w}}{n}|\epsilon \}[B_{(t)0}-B_{(c)0}]+\frac{(q_{t|\epsilon }-p_{t|\epsilon })(p_c^2{q}_c^2)}{n{(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}^2}-\frac{(p_{t|\epsilon }-q_{t|\epsilon })(p_c{q}_c)}{2n(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}-\frac{(q_c-p_c)(p_{t|\epsilon }^2{q}_{t|\epsilon }^2)}{n{(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}^2}+\frac{(q_c-p_c)(p_{t|\epsilon }{q}_{t|\epsilon })}{2n(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}=E\{\frac{\widehat{w}}{n}|\epsilon \}[L(p)+(B_{(t)0}-B_{(c)0})]+H(p_{t|\epsilon }{q}_{t|\epsilon }{p}_c{q}_c),$$

where,

$$B_{(·)i}=\sum _{j=0}^{\infty }{B}_{ij}/n^j.$$

All the B_ij are constant with respect to n. In particular,

$$B_{(c)0}=-a(p_c-q_c)/(n_c{p}_c{q}_c)+O(n^{-2}),B_{(c)1}=1/(p_c{q}_c)-a(p_c^2+q_c^2)/\left\{n_c{(p_c{q}_c)}^2\right\}+O(n^{-2}),B_{(c)2}=\frac{1}{2}(p_c^2-q_c^2)/{(p_c{q}_c)}^2-a(p_c^3-q_c^3)/\left\{n_c{(p_c{q}_c)}^3\right\}+O(n^{-2}),B_{(t)0}=-a(p_{t|\epsilon }-q_{t|\epsilon })/(n_t{p}_{t|\epsilon }{q}_{t|\epsilon })+O(n^{-2}),B_{(t)1}=1/(p_{t|\epsilon }{q}_{t|\epsilon })-a(p_{t|\epsilon }^2+q_{t|\epsilon }^2)/\left\{n_t{(p_{t|\epsilon }{q}_{t|\epsilon })}^2\right\}+O(n^{-2}),B_{(t)2}=\frac{1}{2}(p_{t|\epsilon }^2-q_{t|\epsilon }^2)/{(p_{t|\epsilon }{q}_{t|\epsilon })}^2-a(p_{t|\epsilon }^3-q_{t|\epsilon }^3)/\left\{n_t{(p_{t|\epsilon }{q}_{t|\epsilon })}^3\right\}+O(n^{-2}).$$

Then,

$$E(\frac{E\{\frac{\widehat{w}}{n}|\epsilon \}}{E\{\frac{\widehat{w}}{n}\}}{L}_a(x)-L(p))=E(-\frac{(p_{t|\epsilon }-q_{t|\epsilon })}{n(q_{t|\epsilon }{p}_{t|\epsilon })}\{a+\frac{p_c{q}_c-p_{t|\epsilon }{q}_{t|\epsilon }}{2(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}\}+\frac{(p_c-q_c)}{n(p_c{q}_c)}\{a+\frac{p_{t|\epsilon }{q}_{t|\epsilon }-p_c{q}_c}{2(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}\left\}\right)=E\{H(p_{t|\epsilon },q_{t|\epsilon },p_c,q_c)\}$$

where $H(p_{t|\epsilon },q_{t|\epsilon },p_c,q_c)=-\frac{(p_{t|\epsilon }-q_{t|\epsilon })}{n(q_{t|\epsilon }{p}_{t|\epsilon })}\{a+\frac{p_c{q}_c-p_{t|\epsilon }{q}_{t|\epsilon }}{2(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}\}+\frac{(p_c-q_c)}{n(p_c{q}_c)}\{a+\frac{p_{t|\epsilon }{q}_{t|\epsilon }-p_c{q}_c}{2(p_{t|\epsilon }{q}_{t|\epsilon }+p_c{q}_c)}\}$. Note that H is a continuous function of $\frac{p_{t|\epsilon }}{n}$, and $\frac{p_{t|\epsilon }}{n}\stackrel{p}{\to }\frac{e^{\mu +\theta +{\tau }^2/2}}{1+e^{\mu +\theta +{\tau }^2/2}}/n$. Let $p_t=\frac{e^{\mu +\theta +{\tau }^2/2}}{1+e^{\mu +\theta +{\tau }^2/2}}$. Then,

$$E(\frac{E\{\frac{\widehat{w}}{n}|\epsilon \}}{E\{\frac{\widehat{w}}{n}\}}-L(p))=H(p_t,q_t,p_c,q_c).$$