Stronger neural dynamics capture changes in infants’ visual working memory capacity over development

Abstract

Visual working memory (VWM) capacity has been studied extensively in adults, and methodological advances have enabled researchers to probe capacity limits in infancy using a preferential looking paradigm. Evidence suggests that capacity increases rapidly between 6 and 10 months of age. To understand how the VWM system develops, we must understand the relationship between the looking behavior used to study VWM and underlying cognitive processes. We present a dynamic neural field model that captures both real-time and developmental processes underlying performance. Three simulation experiments show how looking is linked to VWM processes during infancy and how developmental changes in performance could arise through increasing neural connectivity. These results provide insight into the sources of capacity limits and VWM development more generally.

Introduction

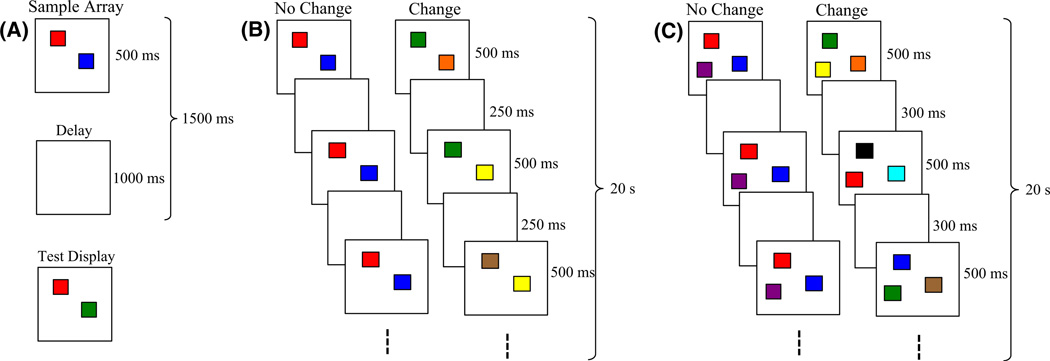
Working memory plays a crucial role in cognitive functioning. One hallmark of working memory is its limited capacity. For instance, adults have a visual working memory (VWM)¹ capacity of 3–4 simple objects (Luck & Vogel, 1997). VWM capacity is typically estimated in a change-detection task designed to isolate this form of memory. In this task (Figure 1A), participants briefly view a set of items (e.g. colored squares). The items disappear for a short delay, then reappear, and participants identify whether the items remained the same or one has changed. Capacity is computed from the proportion of changes detected versus falsely reported across trials (Pashler, 1988).

Figure 1.

Behavioral tasks used to test capacity. (A) The change-detection task, which is used primarily with adults. (B) The change-preference task, modeled after the change-detection task for studying capacity in infants. (C) All-change condition.

The past decade has seen an increase in research investigating the development of VWM capacity. Understanding VWM processes during development is important because poor VWM abilities are associated with a number of neuropsychological disorders, including childhood schizophrenia (Cullen, Dickson, West, Morris, Mould, Hodgins, Murray & Laurens, 2010) and attention-deficit ⊇ hyperactivity disorder (Willcutt, Doyle, Nigg, Faraone & Pennington, 2005). Reliable early assessment of VWM might foster interventions to enhance memory abilities before maladaptive behaviors become problematic.

One challenge in studies on VWM capacity development is that tasks designed to isolate VWM in adulthood are inappropriate early in development, forcing researchers to adapt suitable tasks to probe infants’ working memory (e.g. Feigenson & Carey, 2003; Rose, Feldman & Jankowski, 2001; Ross-Sheehy, Oakes & Luck, 2003). Once the task has changed, how can we be sure we are measuring the same construct?

Theoretical models can help address this issue. The goal of the present paper is to illustrate this approach. We begin with our previous work using dynamic neural fields (DNFs) to capture and predict adults’ performance in change detection (Johnson, Spencer, Luck & Schöner, 2009a; Johnson, Spencer & Schöner, 2009b). We then adapt the model to capture infants’ looking and memory performance from recent studies of VWM capacity development. This establishes how visual memory is involved in both the adult and infant tasks. It also allows us to probe candidate mechanisms of developmental changes in VWM capacity.

Multiple paradigms have been used to probe the development of VWM capacity (e.g. Feigenson & Carey, 2003; Rose et al., 2001). We focus here on the change-preference task from Ross-Sheehy and colleagues (2003) because it isolates VWM well. In this task (Figure 1B), infants view two displays that simultaneously present the same number of colored squares briefly, followed by a short delay. When the images reappear, the no-change display remains the same, while one item on the change display switches to a new color. These "blinks" continue for 20 s per trial, with one color on the change display replaced each time. This paradigm capitalizes on infants’ preference to look at displays that contain dynamic elements or impose a greater informational load (Cohen, 1991; Shaddy & Colombo, 2004). If infants can hold items in memory over the delay, they will be able to determine that only one display is changing. This will drive a preference to look at the change display. Capacity is estimated as the largest set size at which infants exhibit a significant change preference. Ross-Sheehy et al. found that 6-month-olds exhibited a change preference only for set size 1 (SS1), whereas 10-month-olds showed change preferences at SS1–4. Thus, capacity increases to adult-like levels between 6 and 10 months.

Here we use DNFs to address three key questions that arise from use of the change-preference paradigm. First, how does looking behavior relate to capacity? To show a preference, infants must detect the difference between the change and no-change displays. But what, precisely, are they remembering across "blinks"? Are they able to encode and store multiple items, and do they store items for both the no-change and change displays? Answering these questions is critical to understanding how VWM changes between infancy and adulthood. Second, what are infants comparing across blinks and displays? For instance, do infants need to remember the position of each item (i.e. establish feature-location bindings) across "blinks" to detect change (see Oakes, Ross-Sheehy & Luck, 2006)? Finally, what mechanism underlies improved performance over development? If this improvement is evidence of increased memory capacity, what mechanism enables infants to go from a capacity of 1 at 6 months to 3–4 at 10 months?

In the section that follows, we present an overview of our DNF model. We then present three simulation experiments that capture performance from 14 conditions across two age groups in infancy. These simulation experiments (1) explain how looking is related to memory formation and maintenance in the change-preference paradigm, (2) clarify how different experimental manipulations probe the VWM system, and (3) show that a simple neural mechanism – increasing the strength of neural interactions – can yield an increase in capacity.

Dynamic neural field model overview

DNFs belong to a larger class of bi-stable attractor networks (Amari, 1977) that have been used to capture neural population dynamics (Bastian, Schöner & Riehle, 2003) and the link between cognitive and behavioral dynamics (Simmering, Schutte & Spencer, 2008; Spencer et al., 2009). Here we explain the real-time neurodynamic processes underlying looking and memory formation using DNFs. We explain how the model looks back and forth between displays in the change-preference task, and how memory formation for items on the no-change display and the detection of changes on the change display create a change preference.

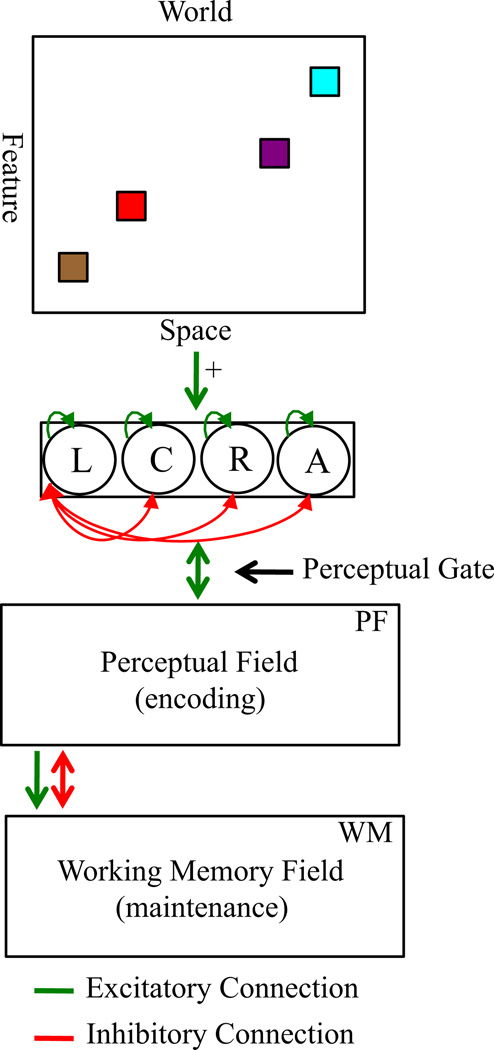
Figure 2 shows the model architecture proposed by Johnson and colleagues (e.g. Johnson et al., 2009a; see Appendix). The model consists of a perceptual field (PF) with a population of neurons with receptive fields tuned to continuous feature dimensions (e.g. color). This field encodes multiple items in parallel, forming peaks of activation that estimate specific color values. Note that we use a single dimension to represent color, in part because its three constituent dimensions are perceived in an integrated fashion (e.g. Garner & Felfoldy, 1970) and in part because neurophysiological and simulation studies suggest that cortical maps reduce these dimensions into a lower-dimensional feature space (Farley, Yu, Jin & Sur, 2007).

Figure 2.

DNF model architecture. The top panel shows the ‘world’ at which the model looks, which can contain the multiple features on the change and no-change displays at left and right locations in the task space. The presence of these displays signals to the fixation system that a stimulus is present in the task space (green ⊇ excitatory arrow to fixation system), biasing the system to look left or right (L = left; R = right; C = center; A = away). Fixating a display acts as a perceptual gate, allowing the metric details of the stimulus at the fixated location to excite neurons within the cognitive system (green bi-directional arrow). The cognitive system includes two excitatory layers, the perceptual field (PF) and working memory field (WM), which are coupled to an inhibitory layer (Inhib, not shown). Activity in PF sustains looking and also passes activation to WM (green arrow from PF to WM). Strong WM peaks suppress activity in PF via Inhib (red bi-directional arrow), weakening support for fixation. Activation in PF and WM is strengthened via Hebbian learning, which strengthens excitatory connections among previously active neurons. Functionally, this facilitates encoding in PF and the maintenance of items in WM.

Above-threshold (> 0) peaks in PF excite similarly tuned neurons in a working memory layer (WM). Stronger neural interactions in WM enable maintenance of peaks in the absence of perceptual stimulation (e.g. during delays). Interactions between PF and WM are set such that strong activation in WM inhibits similarly tuned neurons in PF (via a separate inhibitory layer, not shown). This inhibition suppresses activity generated by incoming inputs that match remembered items, providing a visual recognition mechanism (for behavioral tests of this mechanism, see Johnson et al., 2009a).

To capture infants’ performance, we made two additions to the Johnson et al. model. First, we added a simple fixation system (e.g. Robertson, Guckenheimer, Masnick & Bachner, 2004) that stochastically looks among left and right locations where the change and no-change displays appear, a center location where an attention-getter appears, and an away location with no task-relevant stimulation. The presence of stimuli at left and right locations biases the fixation system to look to the displays. Fixating one of these locations opens a perceptual gate and the color-specific information at the fixated location is input to PF and WM. Encoding (> 0 PF activation) helps maintain continued fixation through reciprocal excitation between PF and the fixation system. Suppression of PF activation by the formation of WM peaks leads to release from fixation. Our second modification to Johnson et al.’s model is the addition of Hebbian layers coupled to PF and WM. These instantiate a form of Hebbian learning to capture changes that occur with repeated presentation of items across a trial. These layers strengthen encoding of previously encoded items in PF and facilitate the maintenance of items in WM.

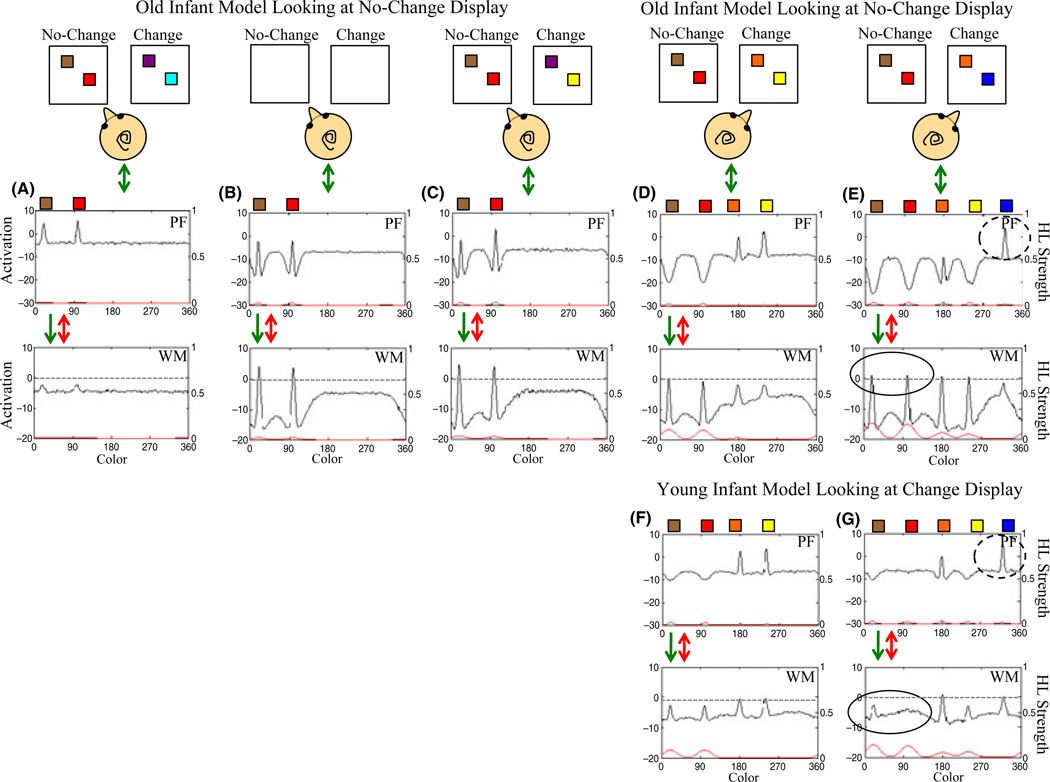
Figure 3A–E shows a simulation of the model to explain how a change preference can arise. The top row shows the change and no-change displays for SS2 as they appear during a segment of one trial; the infant head indicates which display the model is fixating. Initially, the model looks at the no-change display (3A), and the two colors (brown, red) excite neurons in PF. Local excitatory ⊇ lateral inhibitory interactions within PF create peaks, which serve three functions. First, they support continued looking to the stimulus by passing excitation to the fixation system. Second, they enable Hebbian learning on active neural sites to occur, which primes previously excited neurons to respond more robustly (red line, right y-axis shows Hebbian contribution to PF). Third, they excite similarly tuned neurons in WM, helping to form WM peaks associated with these colors.

Figure 3.

Illustration of the mechanisms underlying change preferences and development. Panels A–E show the old infant model while looking at the no-change (A–C) and change (D–E) displays, and panels F–G show the young infant model while looking at the change display. Along the x-axis of PF and WM is the color value (in degrees). The left y-axis shows activation in PF and WM, and the right y-axis shows the Hebbian contributions to PF and WM. Initially, the old infant model is looking at the no-change display (A) and begins to encode and form WM peaks for the two items on the display. This supports fixation through activation in PF feeding excitation back to the fixation system. During the delay (B), the model is maintaining the items on the no-change display in WM. This inhibits associated neural sites in PF, which continues when the no-change display reappears (C) and leads to little support for fixation. When the model looks to the change display (D), it encodes the two items not held in memory. The related activity in PF supports fixation. When the change display reappears (E), one item has changed. The model encodes the novel item, continuing to support fixation. Note that the old model maintains items from the no-change display while looking at the change display. Stochastic looking between the two displays results in recognition of the items on the no-change display and encoding of novel items on the change display, giving rise to a change preference. For the young model, the processes of encoding items on the no-change and changes displays are comparable to the old infant model (see A–C). When the young model looks at the change display (F–G), however, the WM peaks maintaining the items from the no-change display spontaneously decay. This arises due to implementation of the Spatial Precision Hypothesis, specifically, weaker excitatory and inhibitory interactions for the young model. In contrast to the old model, the young model must re-encode items on the no-change display upon re-fixation. This leads to no preference across displays.

Once peaks have built in WM, strong local excitatory ⊇ lateral inhibitory interactions enable these peaks to remain active during the delay (3B). Hebbian learning also occurs among active sites in WM (red line, right y-axis), which facilitates peak formation and maintenance. The maintenance of peaks in WM inhibits similarly tuned neurons in PF, which then suppresses activation associated with the re-presentation of the same items in 3C (see suppressed encoding of the brown color). Consequently, the re-presentation of familiar items provides little support for fixation, and the model looks away.

After another delay (not shown) the displays reappear (3D). Now, the model fixates the change display, encoding (see PF) and forming WM peaks for the orange and yellow squares, supporting continued fixation. After another delay (not shown), the display reappears with blue replacing yellow. The model detects the change – it forms a new peak in PF (dashed circle in 3E) – which supports continued fixation. Note that the model also actively maintains items from the no-change display in WM (solid circle in 3E). If the model spontaneously switches gaze to the no-change display, activation in PF will be weak (as in 3C), providing little support for fixation. Change preferences emerge in the model through the balance between these two mechanisms: detection of ‘change’ in the change display, and memory for ‘same’ in the no-change display.

To capture developmental changes in capacity, we implemented the Spatial Precision Hypothesis (SPH) (e.g. Schutte & Spencer, 2009). The SPH posits that neural interactions strengthen over development. Thus, we created a young (6 months) and old (7.5–10 months) model where the old model had stronger excitatory and inhibitory interactions within PF and WM. Stronger neural interactions are associated with faster WM peak formation, more effective suppression of encoding by WM peaks, and more robust responsiveness to novelty (Perone & Spencer, 2011).

A key consequence of the SPH is that WM peaks are less stable in early development (Schutte & Spencer, 2009), leading to spontaneous de-stabilization of WM peaks. This is illustrated in Figure 3F–G, which shows a simulation of the young model while looking at the change display; note that 3F–G shows the model after it has encoded and formed memories for items on the no-change display (as in 3A–C). When the young model switches gaze to look at the change display (3F), it encodes the two previously unseen colors (orange, yellow). Notice that the WM peaks associated with the colors on the no-change display (brown, red) are sub-threshold. These peaks were spontaneously destabilized when the model encoded the new item on the change display. Figure 3G shows the model after a delay (not shown) when the yellow item has changed to blue. The young model detects this change (dashed circle). However, WM peaks associated with the colors on the no-change display (brown, red) are absent (see solid circle). Consequently, the young model will not recognize ‘same’ when it re-fixates the no-change display, resulting in no preference.

We tested whether the model can capture infants’ performance in the change-preference task in three simulation experiments. In each case, we situated the model in the experimental design that infants completed. Sets of model parameters were simulated in batches of 200 ‘participants’, which is sufficient to produce robust results in the presence of stochastic fluctuations (i.e. noise added to the fixation system and fields at each time step). In each experiment, infants were tested across six 20 s trials (in the model, 1 time step = 2.5 ms). Change preference scores for the model were calculated in the same manner as for infants: dividing total time looking at the change display by total looking across the change and no-change displays on each trial, then averaging across trials to the same set size.

For the simulations presented here, parameters were fit by hand to the means from the infant experiments through trial-and-error to produce the qualitative pattern of performance shown by 6-month-olds in Ross-Sheehy et al.’s (2003) Experiment 1. We avoided tuning to exact values because behavioral replications of the same conditions show variation across different groups of infants (see Ross-Sheehy et al., 2003). Once a range of acceptable parameters was identified for the young infants’ performance, we scaled a fixed set of parameters specified by the SPH to capture 10-month-old infants’ performance.

Next, we tested the range of young infant parameters in a second simulation experiment (Ross-Sheehy et al., 2003, Experiment 4), eliminating parameter sets that could not capture the full range of performance. We further tested the model by showing that developmental increases in capacity captured by the parameters from simulation Experiments 1 and 2 were sufficient to qualitatively capture performance from a third experiment – a recent probe of color-location binding (Oakes, Messenger, Ross-Sheehy & Luck, 2009). Finally, we optimized this parameter set across the full set of behavioral conditions, selecting parameters that provided the best fit across all three (see Table A1). To quantify the fit of the model to the infant data, we calculated the root mean squared error (RMSE) for 14 mean change preference scores and 14 standard deviations across simulation experiments. RMSE equaled 0.042 for the mean change preference scores and 0.072 for the standard deviations. The final model parameters fit the empirical data very well (see Appendix for additional simulation details).

Simulation Experiment 1

Ross-Sheehy et al. (2003) reported that 6-month-olds showed a change preference only at SS1, whereas 10-month-olds exhibited a change preference at SS1–3 (Experiment 1). We situated the young and old models in the change-preference task with the same procedural details as infants. The model was presented with each set size twice, randomized across six trials. For each trial, colors were randomly selected from a set of nine color values. The color inputs into PF were Gaussian distributions centered at specific values along a single color dimension and equally separated. Inputs were presented for 500 ms, followed by a 250 ms delay, reappeared for 500 ms, and so on for 20 s. On each reappearance, one randomly selected color on the change display was replaced with another randomly selected color not already present on that display.

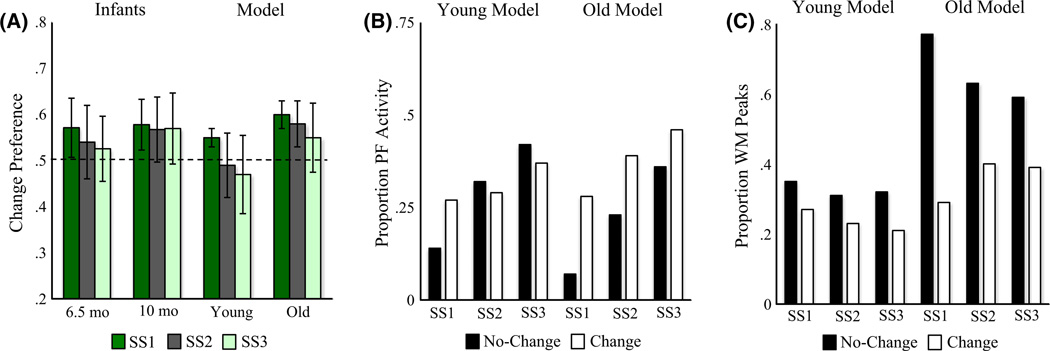
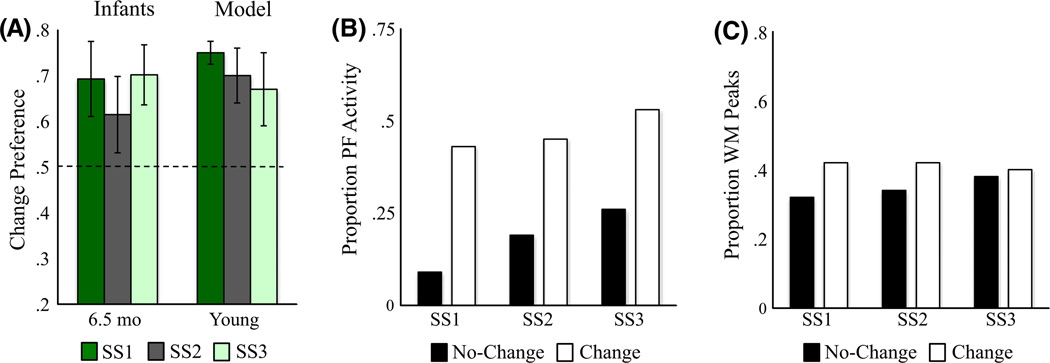
Figure 4A shows the mean preference scores for SS1–3 for the young and old models, alongside data from Ross-Sheehy et al. (2003). Like infants, the young model exhibited a change preference only at SS1, but the old model exhibited a change preference at SS1–3. This pattern emerged from relative differences in the input to the fixation system when the model looked at the change and no-change displays. Figure 4B shows the proportion of total looking time when there was strong input from PF to the fixation system for looks to each display. There was stronger support for continued fixation when the young model looked at the change display at SS1 relative to the no-change display. Critically, there was less of a difference across displays at SS2–3. For the old model, by contrast, there was support for continued fixation for all set sizes.

Figure 4.

Results of Simulation Experiment 1. (A) Change preference scores for infants in Ross-Sheehy et al. (2003) Experiment 1 and our DNF model (error bars show one standard deviation). The x-axis shows the age of infants or developmental stage of the model, the y-axis shows change preference scores (chance = 0.50), and bars represent different set sizes. (B) The proportion of time strong activation (> .5) from PF is feeding into the fixation system while looking at the change (white bars) and no-change (black bars) displays relative to total looking across both displays, averaged across simulations. The x-axis shows set sizes separately for the young versus old model. (C) The proportion of WM peaks maintaining items across delays for the change (white bars) and no-change (black bars) displays, averaged across simulations. The x-axis shows set sizes separately for the young versus old model. Note that the maximum number of items that can be maintained for the no-change display is equal to the set size. As set size increases, the same proportion of items maintained in WM reflects a higher number of items. The maximum number of unique items that can be maintained for the change display is on average slightly less than the set size because, on each "blink", colors were randomly selected from a set of nine. Occasionally, one or more items present on the change display were also on the no-change, which were not included when calculating the number of items maintained for the change display.

What is the origin of this differential support from PF to the fixation system? Figure 4C shows the proportion of WM peaks that the model maintained across delays out of the total number of unique colors present on each display.² As expected, the old model maintained more WM peaks overall, proportionally more items on the no-change display, and proportionally fewer items as set size increased (reflecting a capacity limit). Note that the proportion is near 0.6 for the no-change display at SS3. Thus, the old model remembered 2 out of 3 colors, suggesting that the maximum set size at which infants show a significant change preference overestimates infants’ capacity. In contrast to the old model, the young model maintained very few items on each display, although it maintained proportionally more items at SS1 than at higher set sizes.

Ross-Sheehy et al. (2003) also tested 10-month-olds at SS2–6 to probe the upper limits of capacity. Infants showed a change preference at SS2 (.56), SS4 (.58), but not SS6 (.52). Similarly, the old model shows a change preference at SS2 (.59) and SS4 (.55), but not SS6 (.50). Thus, the DNF model captures the developmental change in capacity from 6 to 10 months.

Simulation Experiment 2

To probe whether capacity limits at 6 months arise from an inability to remember items over the delay, Ross-Sheehy et al. (2003) presented 6-month-olds with a change-preference task with the delays between blinks removed. Six-month-olds showed significant change preferences at SS1–3. We probed whether the DNF model can capture this dramatic shift in performance.

The absence of a delay should minimize the de-stabilization of WM peaks since there is more perceptual support for their continued maintenance. This, in turn, should facilitate the detection of ‘same’ on the no-change display. Figure 5A shows that the young model, like infants, exhibits change preferences across set sizes in the no-delay task. Inspection of 5C partially explains why: relative to Simulation 1, the young model does, in fact, maintain proportionally more WM peaks. Interestingly, however, this increase occurred for both no-change and change displays. Why, then, did the model show a change preference in all conditions?

Figure 5.

Results of Simulation Experiment 2. Panels are the same as in Figure 4. Note that the proportion of WM peaks across SS1–3 for the no-change display is comparable to the proportion of WM peaks for the no-change display across SS1–3 in Simulation Experiment 1 for the same young infant model. However, the proportion of WM peaks for the change display increased, due both to the absence of a delay and a small bias to look at the change display (see text for additional details).

Two factors contribute to the change preference. First, in the no-delay task, the fixation system receives more stimulus input on the change display. Although both displays share low-level visual properties that signal the presence of a display on the left and the right, only the change display has transient onsets that occur each time an item changes color. This small, differential input biases the young model to look more at the change display. The second factor that contributes is shown in Figure 5B: when the model looks to the change display, PF provides strong support to maintain fixation. This occurs because the WM peaks that the young model forms are unable to suppress PF in this task context. Thus, a small difference in input leads to large differences in behavior.

Simulation Experiment 3

Oakes et al. (2009) suggested that VWM capacity increases from 1 to 3 items as infants gain the ability to establish feature-location bindings in VWM. In this view, 6-month-olds exhibit a change preference for SS1 because location information is irrelevant. By contrast, they do not exhibit change preferences for SS2–3 because they are unable to align their percept of each colored square to the correct memory representation for comparison across delays. Essentially, 6-month-olds detect ‘changes’ on the no-change display due to mismatches between memory and perceptual input.

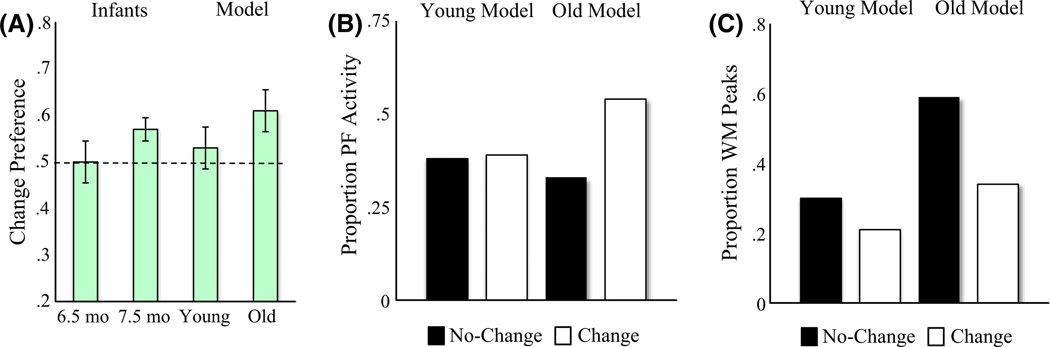
The binding account leads to a radical prediction: 6-month-olds should fail to detect change with multi-item displays even when every item changes at every blink (Figure 1C). This is remarkable because 6-month-olds detect changes with single-item displays, and remembering a single item from the change display should be sufficient to drive a change preference in the ‘all-change’ task. If, however, 6-month-olds cannot bind features and locations, they should fail in the all-change task because they cannot align the remembered and perceived items. Oakes et al. (2009) tested this prediction. As predicted by the binding account, 6-month-olds did not show a change preference while 7.5-month-olds did (Figure 6A).

Figure 6.

Results of Simulation Experiment 3. Panels are the same as in Figures 4 and 5.

Simulation Experiments 1–2 demonstrate that the DNF model offers an explanation of developmental change in infants’ performance in the change preference task. Critically, however, the model does not bind colors and locations (although see Johnson, Spencer & Schöner, 2009c, for a DNF model of feature-space binding). We asked, then, whether the model could capture performance in the all-change condition.

We tested the young and old models in the Oakes et al. (2009) task. Consistent with empirical results, only the old model exhibited a robust change preference (6A). Figure 6B shows that PF activity helped maintain fixation when the old model looked at the change display. This occurred less frequently when the old model looked at the no-change display due to the robust WM peaks evident in 6C. The young model, by contrast, shows a weak change preference (comparable to 6-month-old infants’ performance) because it maintains very few colors in WM.

These results demonstrate the utility of having a formal process model of infants’ performance: results reveal that the developmental difference between 6 and 7.5 months in the all-change task does not require a change in binding – an improvement in capacity is sufficient to explain infants’ performance. As discussed below, other tasks appear to require color-location binding (Oakes et al., 2006). DNF models can provide a critical tool as future work clarifies how capacity and binding co-develop during the first year.

Discussion

Studies of working memory development often aim to investigate the origins of this central cognitive process. It is not immediately obvious, however, how the tasks and behavioral measures used to test infants’ VWM relate to work with adults. Here, we showed that the same processes in a DNF model used to capture adults’ performance in a change-detection task can also capture infants’ performance in the change-preference task. The DNF model captures basic cognitive processes that have long been assumed to underlie infant looking while also specifying the processes that govern where infants look, how they encode and remember fixated items, how fixation is released, and how familiar and novel items are compared in a neural process model (for similar models, see Schelesinger, Amso & Johnson, 2007; Sirois & Mareschal, 2004). This specificity enables the DNF model to provide a mechanistic explanation of how VWM is related to a particular behavioral measure in infancy under specific task conditions.

The central concepts of the DNF model are shared by many conceptual (Hunter & Ames, 1988) and formal (French, Mareschal, Mermillod & Quinn, 2004) models of infant memory – for example, infants compare percepts with memory to recognize items, leading to reduced looking, and detect novelty, leading to increased looking. However, our model differs from existing models in an important way: it actively looks back and forth between displays, allowing it to capture the second-to-second connection between looking and learning. This is a substantive contribution because a major challenge in empirical investigations of the early development of VWM is specifying how VWM processes and behavior are linked. This feature of the DNF model enables us to test competing theoretical explanations of the same phenomenon. For instance, we showed here that this link led to a novel interpretation of the processes driving performance in the Oakes et al. (2009) all-change condition.

The DNF model also offers unique insights into the development of VWM capacity. We were able to capture differences in performance between 6 months and 7.5–10 months by implementing the SPH, that is, through strengthening excitatory and inhibitory neural connections. As a result, WM peaks were more robust in the old model, the model was able to maintain more peaks, and the model preferred to look at the change display even at higher set sizes. Thus, a small, quantitative increase in excitatory ⊇ inhibitory strength is sufficient to increase the number of items able to be maintained. Note that we implemented our mechanism for developmental changes in capacity ‘by hand’, strengthening excitatory and inhibitory connections within PF and WM in a uniform manner (i.e. the same changes were made to all nodes within a given layer). Critically, this approach was constrained by previous work showing that the SPH can capture changes in children’s spatial cognitive abilities (e.g. Schutte & Spencer, 2009). Here, we showed that the SPH can be generalized to capture infants’ capacity, suggesting that a common mechanism might underlie changes across two developmental periods and seemingly different domains.

Developmental changes in infants’ performance in the change-preference task are likely influenced by a confluence of changes in neural interaction strength in the visual processing pathways (for reviews, see Shatz, 2002; Stiles, 2008). In particular, there are dramatic developmental changes in the visual processing pathways projecting to and from the lateral geniculate nucleus that have been proposed to underlie developmental change in visual processing speed (for a review, see Colombo, 1995). Moreover, these early visual processing pathways project to primary visual cortex which is involved in processing higher-level visual information such as color. It is notable that strong neural activity in higher primary visual cortical areas is associated with robust working memory for visual features in adults (Sligte, Scholte & Lamme, 2009). It is possible that the SPH captures experience-dependent changes that arise within the visual processing pathways and within higher-level cortical fields tuned to specific feature dimensions. For example, Hebbian learning processes are likely involved in adjusting the strength of projections among cortical layers as these layers are repeatedly used to encode and remember the metric features of objects (Abbott & Regehr, 2004; see also Murphy, Beston, Boley & Jones, 2005; Shatz, 2002). Dimension-wide changes in connection strength might reflect the accumulation of such changes across the longer timescales of development (e.g. months and years). This is consistent with recent studies showing that experience with particular stimuli can generalize beyond the specifics of experience. For instance, infants’ experience with particular exemplars enhances memory for other items within that category (e.g. Kovack-Lesh, Horst & Oakes, 2008).

Although our simulations provide support for the SPH, they cannot definitively rule out alternative explanations. A host of proposals have been put forth to explain why performance in working memory tasks improves over development. Interestingly, many of these explanations focus on mechanisms other than working memory capacity, including attention (e.g. Cowan, Morey, AuBuchon, Zwilling & Gilchrist, 2010; see also Ross-Sheehy, Oakes & Luck, 2010), cognitive control (e.g. Marcovitch, Boseoyski, Knapp & Kane, 2010), and strategic processes like chunking ⊇ grouping (e.g. Ryan, 1969) or rehearsal (e.g. Hitch, Halliday, Schaafstal & Schraagen, 1988). Our account showed that changes in the capacity of the underlying memory system alone can capture infants’ data from Ross-Sheehy et al. (2003) and Oakes et al. (2009). Note, however, that our account also shows that performance does not directly reveal capacity because the model can show a preference in SS3 while maintaining fewer than three peaks.

Recently, Ross-Sheehy et al. (2010) provided evidence that attentional control influences performance in the change-preference task. In particular, they showed that young infants looked longer to SS3 displays in which the changing item was cued, compared to similar displays in which a non-changing item was cued. Thus, young infants can show a preference at SS3 if they attend to the changing item. It is unlikely, however, that such changes in attention would explain older infants’ preference for changing displays because the changing location is randomly selected on each "blink". As a consequence, infants’ likelihood of attending to the correct object on any given fixation would be at chance (i.e. 33% in SS3). Even with more developed attentional abilities at 10 months, the task was designed such that attention to a single item within a display would be an unlikely source of a robust preference.

The final contributions of the present report are the insights gained into a promising task for studying visual memory development – the change-preference task. Perhaps most notably, Simulation Experiment 3 shed light on when binding is needed and when it is not. Although the DNF model captured results from Oakes et al. (2009), our model does not explain 7.5-month-olds’ change preference in a binding task where the colors on the change display remain the same but swap positions (Oakes et al., 2006). These results indicate that 7.5-month-olds can detect changes in which colors were where. Future model development can help clarify precisely what type of change 7.5-month-olds are detecting, as well as how detection of change results in a change preference in the context of memory for the no-change display. Such insights are central if we are to understand how changes in capacity and binding are related.

Appendix

Dynamic neural field (DNF) models are formal implementations of a set of theoretical concepts described by the dynamic field theory (DFT) of embodied cognitive dynamics (for reviews see Schöner, 2009; Spencer et al., 2009; Spencer, Simmering, Schutte & Schöner, 2007). The centerpiece of the DFT is to embrace the use of complex, dynamic neural networks to capture brain–behavior relations. Other computational approaches have captured neural dynamics and cognitive dynamics within neurally inspired neural network models, but they have only captured a limited view of brain–behavior relations. For example, biophysical approaches have made some strides on this front, with neurally realistic models of single neurons that capture key elements of neuronal firing, neurotransmitter action, and so on (e.g. Salinas, 2003). Such models can be coupled together into populations and populations coupled together to capture cortical–cortical connections. The goal of these models is often to capture neural behavior within and across cortical regions as well as aspects of behavioral performance (e.g. reaction time). Critically, biophysical models have led to new insights into brain function and neural dynamics, but they have rarely attempted to capture the flexibility and variety of human behavior in context. This is, by contrast, a central goal of the DFT.

DNFs belong to a larger class of bi-stable attractor networks (Amari, 1977; Wilson & Cowan, 1972), and have been used to capture the mapping between real-time neural population dynamics and behavior in a variety of domains: the planning and execution of eye movements (Kopecz & Schöner, 1995; Wilimizig, Schneider & Schöner, 2006); the planning of reaching movements (Bastian et al., 2003); visual working memory for features (Johnson et al., 2009b; see also Johnson et al., 2009a); and spatial cognition (see Spencer et al., 2007 for a review). DNFs have also effectively captured the co-development of neural and behavioral processes in the Piagetian A-not-B task (Thelen, Schöner, Scheier & Smith, 2001) and spatial working memory tasks (Schutte & Spencer, 2009; Schutte, Spencer & Schöner, 2003; Simmering et al., 2008; Simmering & Spencer, 2008). These previous applications demonstrate that DNFs provide an effective set of concepts that link cognition and behavior in real-time, over learning, and over development (Lipinski, Simmering, Johnson & Spencer, 2010; Lipinski, Spencer & Samuelson, 2010; Schöner & Thelen, 2006).

DNFs consist of layers of neurons organized by functional topography along continuous, metric dimensions (e.g. color). Neuronal activation in DNFs is based on the space code principle from neurophysiology in which neighboring neurons mutually excite each other. In addition, active excitatory neurons stimulate similarly tuned inhibitory interneurons, implementing a form of lateral or surround inhibition. This creates a local excitatory ⊇ lateral inhibitory activation profile, a ubiquitous form of neural interaction that stabilizes motor behavior and neural representations within the cognitive system (Fuster, 2003). Neuronal activation in DNFs evolves continuously in time, and the state of a DNF at any point in time depends on its own intrinsic dynamics and the inputs impinging on them. Amari (1977) originally analyzed five qualitatively different attractor states that DNFs can enter. These attractor states can be used to implement various cognitive functions, and constrain the parameter values tested in our simulation experiments (described further below).

Model architecture and equations

The core architecture of our model consists of three layers, or fields, of neurons selectively tuned to a continuous color dimension: a perceptual field (PF) in which stimuli are encoded, a working memory field (WM) in which stimuli can be maintained in the absence of perceptual stimulation, and a field of inhibitory interneurons (Inhib) through which PF and WM interact. Each excitatory layer (PF, WM) is also reciprocally coupled to a Hebbian layer. When there is suprathreshold (> 0) activation in an excitatory layer, a Hebbian trace accumulates over a slow timescale (see below). These traces then feed back into the excitatory layer, effectively strengthening local excitatory connections at previously active sites. Functionally, in PF this strengthens encoding – the neural response to the re-presentation of the same stimulus – and in WM helps peaks sustain suprathreshold activity. Finally, PF is reciprocally coupled to a fixation system that stochastically looks among left and right locations at which task-relevant stimuli appear, and to center and away locations at which no task relevant stimuli appear. All elements of the model are formally described below.

Perceptual Field (PF)

The equation for PF (u) is:

$${\tau }_{\mathit{\text{excite}}}\mathit{u̇}(x,t)=-u(x,t)+h_u+S_l(x,t)\mathrm{\Lambda }(\mathit{\text{fl}})+S_r(x,t)\mathrm{\Lambda }(\mathit{\text{fr}})+{\displaystyle \int }{c}_{\mathit{\text{uu}}}(x-x\prime ){\mathrm{\Lambda }}_{\mathit{\text{uu}}}(u(x\prime ,t))\mathit{\text{dx}}\prime -{\displaystyle \int }{c}_{\mathit{\text{uv}}}(x-x\prime ){\mathrm{\Lambda }}_{\mathit{\text{uv}}}(v(x\prime ,t))\mathit{\text{dx}}\prime +{\displaystyle \int }{c}_{\mathit{\text{uhl}}}(x,x\prime ){\mathit{\text{hl}}}_u(x,t)\mathit{\text{dx}}\prime +c_{\mathit{\text{uf}}}\mathrm{\Lambda }(\mathit{\text{fl}})+c_{\mathit{\text{uf}}}\mathrm{\Lambda }(\mathit{\text{fr}})+\mathit{\text{noise}}$$

where u(x,t) is the rate of change of activation for each neuron across the continuous dimension, x, as a function of time, t, and τ_excite is the time constant along which activation evolves. Note that each layer consisted of 360 neurons.

Activation at each site in PF is influenced by multiple factors including the current state, − u(x, t), and a negative resting level, h_u. Note that at every time step, white noise was added to h_u to reflect stochastic fluctuations in baseline activation within the neural population. Also note that h_u was weighted by c_u, which was equal to 1 when stimuli in the task space were present and 2 when absent (h_u is assigned a negative value). This boosts the resting state of PF when displays in the task space are present relative to inter-stimulus intervals when, typically, the experimental setting is dimly lit.

Next, activation in PF is influenced by input on the left, S_l(x, t), and right, S_r(x, t), displays. Input took the form of a Gaussian distribution:

$$S_l(x,t)=c\text{ exp }\left[-\frac{{(x-x_{\mathit{\text{center}}})}^2}{2{\sigma }^2}\right]X(t)$$

with the positions of colors centered at x_center, input widths of σ, and strengths c. The gating function, X(t), denotes that the stimulus input is weighted with a 1 during time intervals when the stimulus is "on" and 0 otherwise. For each stimulus, σ was set to 3 and c was set to 17. Note that the stimulus on a particular display is only input into to PF when that location is fixated. This gating is achieved by weighting the stimulus input by the thresholded activation of the fixation system (described below), for example, weighting S_l by the thresholded activation of the left fixation node, S_l(x, t)Λ(fl). This sets S_l (x, t) to 0 when the fixation system is not looking left, that is, when activation of the left node is below 0.

Next, activation in PF is influenced by excitatory within-layer neural interactions, ∫ c_uu (x − x′)Λ_uu(u(x′, t))dx′. These interactions are specified by the convolution of a Gaussian local excitation profile, c_uu(x − x′), and a sigmoidal threshold function. The Gaussian was defined as:

$$C(x-x\prime )=c\text{ exp }\left[-\frac{{(x-x\prime )}^2}{2{\sigma }^2}\right]-k$$

where σ determines the neighborhood across which neural interactions propagate, c determines the strength, and k sets the resting level. Note that the resting level was set to 0 for all convolutions except from Inhib to PF, where this value was set to .27 (see below). Only neurons with above-threshold activation (i.e. above 0) participate in local neural interactions as determined by a sigmoidal function:

$$\mathrm{\Lambda }(u)=\frac{1}{1+\text{exp}[-\beta u]\prime }$$

where β is the slope of the sigmoid. β was set to .05.

In addition to local excitatory interactions, activation in PF is also influenced by an inhibitory projection from Inhib (described below), − ∫ c_uv(x − x′)Λ_uv(v(x′, t))dx′. As with excitatory interactions, inhibitory interactions in PF are projected across a neural neighborhood specified by a Gaussian, c_uv(x − x′), and only neurons with above-threshold activity in Inhib, Λ_uv(v(x′, t)), contribute to interactions.

Activation in PF is influenced by input from a Hebbian layer, ? c_uhl(x, x′)hl_u(x, t)dx′. This input is determined by the convolution of a Gaussian projection, c_uhl(x, x′), which determines the neural neighborhood across which Hebbian traces have an influence, and the strength of the trace within the Hebbian layer, hl_u(x, t) (described below).

The next contribution to activation in PF is an excitatory input from the fixation system, c_uf, which affects all sites in PF uniformly when either the left or right node is suprathreshold.

Finally, activation in PF is influenced by the addition of spatially correlated noise:

$$q{\displaystyle \int }{g}_{\mathit{\text{noise}}}(x-x\prime )\xi (x\prime ,t)\mathit{\text{dx}}\prime$$

Noise was presented to PF by convolving a field of white noise, ξ(x′, t), with a Gaussian kernel, g_noise(x − x′). σ_noise was set to 1 and q (the noise strength) was set to 0.12.

Working Memory (WM)

The equation for WM (w) is:

$${\tau }_{\mathit{\text{excite}}}\mathit{ẇ}(x,t)=-w(x,t)+h_w+{\mathit{\text{cS}}}_l(x,t)\mathrm{\Lambda }(\mathit{\text{fl}})+{\mathit{\text{cS}}}_r(x,t)\mathrm{\Lambda }(\mathit{\text{fr}})+{\displaystyle \int }{c}_{\mathit{\text{wu}}}(x-x\prime ){\mathrm{\Lambda }}_{\mathit{\text{wu}}}(u(x\prime ,t))\mathit{\text{dx}}\prime +{\displaystyle \int }{c}_{\mathit{\text{ww}}}(x-x\prime ){\mathrm{\Lambda }}_{\mathit{\text{ww}}}(w(x\prime ,t))\mathit{\text{dx}}\prime -{\displaystyle \int }{c}_{\mathit{\text{wv}}}(x-x\prime ){\mathrm{\Lambda }}_{\mathit{\text{wv}}}(v(x\prime ,t))\mathit{\text{dx}}\prime +{\displaystyle \int }{c}_{\mathit{\text{whl}}}(x,x\prime ){\mathit{\text{hl}}}_w(x,t)\mathit{\text{dx}}\prime +\mathit{\text{noise}}$$

This equation is identical to PF with two exceptions. First, direct stimulus input into WM, S_l(x, t)Λ(fl) and S_r(x, t)Λ(fr), is weakened relative to PF by scaling it by a strength parameter, c, which was set to 0.05. Second, WM receives an excitatory projection from PF, ∫ c_wu(x − x′)Λ_wu(u(x′, t))dx′, given by the convolution of a Gaussian projection and the sigmoidal threshold function.

Inhibitory Layer (Inhib)

Activation in PF and WM is mediated by a shared layer of inhibitory interneurons. The equation for Inhib (v) is:

$${\tau }_{\mathit{\text{inhib}}}\mathit{v̇}(x,t)=-v(x,t)+h_v+{\displaystyle \int }{c}_{\mathit{\text{vu}}}(x-x\prime ){\mathrm{\Lambda }}_{\mathit{\text{vu}}}(u(x\prime ,t))\mathit{\text{dx}}\prime +{\displaystyle \int }{c}_{\mathit{\text{vw}}}(x-x\prime ){\mathrm{\Lambda }}_{\mathit{\text{vw}}}(w(x\prime ,t))\mathit{\text{dx}}\prime +\mathit{\text{noise}}$$

Inhib receives excitatory projections from PF, ∫ c_vu(x − x′)Λ_uv(u(x′, t))dx′, and WM, ∫ c_vw(x − x′)Λ_vw(w(x′, t))dx′. These inputs are projected across a neural neighborhood specified by a Gaussian projection, c(x′ − x′). As above, only above-threshold neurons in PF and WM contribute to these cross-layer interactions as determined by the sigmoidal threshold function, Λ.

Hebbian layers (HL)

Activation within PF and WM is influenced by traces in associated Hebbian layers. The equation for the Hebbian layer associated with PF is:

$$h{\mathit{l̇}}_u(x,t)=\{\begin{array}{cc}\frac{1}{{\tau }_{\mathit{\text{build}}}}[-{\mathit{\text{hl}}}_u(x,t)+{\mathrm{\Lambda }}_{\mathit{\text{hlu}}}(u(x,t))]\hfill & \text{if }u(x,t)\ge 0\hfill \\ \frac{1}{{\tau }_{\mathit{\text{decay}}}}[-{\mathit{\text{hl}}}_u(x,t)]\hfill & \text{otherwise}\hfill \end{array}$$

where hl̇_u(x, t) is the rate of change of activation for each site in the Hebbian layer, x, as a function of time, t. The constants τ_build and τ_decay set the time scale during which activation traces accrue and decay, respectively. Activation in the Hebbian layer only accrues when neurons in PF are above threshold, u(x, t) ? 0.

Fixation system

The fixation system consists of four bi-stable nodes that stochastically look about the task space, exploring left, right, center, and away locations. A node is in the fixation state when it shows above-threshold activity (> 0). The nodes are all mutually inhibitory, implementing a winner-takes-all fixation system.

Left and right nodes

The equations for the left and right nodes are identical. We present the equation for the left node, which is:

$${\tau }_{\mathit{\text{excite}}}\mathit{ḟ}l(t)=-\mathit{\text{fl}}+h_{\mathit{\text{fl}}}+c_{\mathit{\text{ff}}}{\mathrm{\Lambda }}_{\mathit{\text{fl}}}(\mathit{\text{fl}})+c_b+c_s+c_t-c_{\mathit{\text{ci}}}{\mathrm{\Lambda }}_{\mathit{\text{fc}}}(\mathit{\text{fc}})-c_{\mathit{\text{ci}}}{\mathrm{\Lambda }}_{\mathit{\text{fr}}}(\mathit{\text{fr}})-c_{\mathit{\text{ci}}}{\mathrm{\Lambda }}_{\mathit{\text{fa}}}(\mathit{\text{fa}})+{\mathrm{\Lambda }}_{\mathit{\text{fl}}}(\mathit{\text{fl}}){\displaystyle \int }{c}_{\mathit{\text{fu}}}{\mathrm{\Lambda }}_{\mathit{\text{ul}}}(u(x\prime ,t))\mathit{\text{dx}}\prime$$

where the time scale of the activation variable, fl, is set by the constant, τ_excite. The rate at which activation in the left node changes is influenced by its current state, −fl, and its negative neuronal resting level, h_fl (described below).

The left node has a self-excitatory component, c_ff. This input is gated by the thresholded activation of the left node, Λ_fl(fl), which sets the input to be 0 when the node is below threshold. When the left node is in the "on" state (above 0), c_ff biases the node to remain in the "on" state.

The left node receives three excitatory stimulus inputs that are dictated by the timing parameters of the procedure. First, c_b is an input that is present during the first 125 ms (50 time steps) of each 20 s (8000 time step) trial. This indicates that something has just appeared at the left location in the task space. The second input, c_s, is a low-level input that signals the continued presence of the left display. This input is present during the entire trial. The last input, c_t, is an input associated with the re-appearance of the colored squares following each delay (i.e. on every "blink"). This input was present for 250 ms (100 time steps). Note that in the no-delay condition (Simulation 2), c_t was set to zero for the no-change display because the display remained constant during each trial. On the change display, by contrast, a new item appeared every 500 ms (200 time steps) causing a "flicker" that was captured by maintaining the same value of c_t used for all other conditions (see Table A1).

The left node receives inhibitory input from the current activity of other nodes, for example, c_ciΛ_fr(fr), which is the thresholded activation of the right node weighted by c_ci. When the right node, via noise, spontaneously pierces threshold, it has an inhibitory effect on the state of the left node. When activation in the left node is relatively weak, this can cause the left node to enter the "off" state. When activation in the left node is relatively strong, however, inhibition from activation of the right node is unlikely to cause a shift to the "off" state.

The left node receives excitatory input from PF, Λ_fl(fl) ∫ c_fuΛ_u(u(x′, t))dx′, which is the sum of above-threshold activation in PF across all sites, x, at time t, and is gated by the thresholded activation in the left node, Λ_fl(fl). Thus, activation in PF only contributes to the left node when the left node is in the "on" state. This sum has a weighted strength, c_fu.

Finally, the left node has a dynamic resting level that facilitates transitions between "on" and "off" states. In particular, the resting level of the fixation system, h_f, is governed by the following equation:

$${\tau }_{\mathit{\text{excite}}}{\mathit{ḣ}}_{\mathit{\text{fl}}}(t)=-h_{\mathit{\text{fl}}}+h_{\mathit{\text{rest}}}+h_{\mathit{\text{down}}}{\mathrm{\Lambda }}_{\mathit{\text{fl}}}(\mathit{\text{fl}})$$

The resting level of the left node decreases toward a low attractor, h_down, when the current activation of the node is above threshold, and it moves toward the baseline level, h_rest, when activation in the node is below threshold. Thus, the left node is biased toward the "off" state when in the "on" state, and it is biased toward the "on" state when in the "off" state. These dynamics are similar to a dynamical systems model used by Robertson et al. (2004) to capture looking and looking away of young infants. Note that the resting level equations for center, away, and right nodes are identical.

Center node

In preferential looking tasks, infants are typically presented with a salient stimulus (e.g. blinking light) at a center location prior to stimulus presentation. This ‘attention getter’ effectively orients infants toward a central location between the left and right locations at which task-relevant stimuli will appear. The equation for the center node is:

$${\tau }_{\mathit{\text{excite}}}\mathit{ḟ}c(t)=-\mathit{\text{fc}}+h_{\mathit{\text{fc}}}+c_{\mathit{\text{ff}}}{\mathrm{\Lambda }}_{\mathit{\text{fc}}}(\mathit{\text{fc}})+c_{\mathit{\text{ag}}}-c_{\mathit{\text{ci}}}{\mathrm{\Lambda }}_{\mathit{\text{fl}}}(\mathit{\text{fl}})-c_{\mathit{\text{ci}}}{\mathrm{\Lambda }}_{\mathit{\text{fr}}}(\mathit{\text{fr}})-c_{\mathit{\text{ci}}}{\mathrm{\Lambda }}_{\mathit{\text{fa}}}(\mathit{\text{fa}})$$

This equation is identical to the left and right nodes except that it only has one input, the transient attention getting input, c_ag. Note that because there are no task-relevant features associated with the attention getter, activation in PF does not contribute to the activation of the center node.

Away node

The equation for the away node is:

$${\tau }_{\mathit{\text{excite}}}\mathit{ḟ}a(t)=-\mathit{\text{fa}}+h_{\mathit{\text{fa}}}+c_{\mathit{\text{ff}}}{\mathrm{\Lambda }}_{\mathit{\text{fa}}}(\mathit{\text{fa}})+c_{\mathit{\text{sa}}}-c_{\mathit{\text{ci}}}{\mathrm{\Lambda }}_{\mathit{\text{fl}}}(\mathit{\text{fl}})-c_{\mathit{\text{ci}}}{\mathrm{\Lambda }}_{\mathit{\text{fr}}}(\mathit{\text{fr}})-c_{\mathit{\text{ci}}}{\mathrm{\Lambda }}_{\mathit{\text{fc}}}(\mathit{\text{fc}})$$

This equation is identical to the center node except that it only has a static input, c_sa, that specifies the presence of task-irrelevant stimuli during the entire experimental session. Looking time to a particular location was calculated as the number of time steps in which the node associated with that location was above threshold. For the left and right nodes, this corresponds to the time in which the model looked at either the change or no-change display, thereby allowing the input on the display to project into PF. To calculate a change preference, the number of time steps in which the model was looking to the change display was divided by the number of time steps looking to the change and no-change displays (cf. Ross-Sheehy et al., 2003).

Model parameters

The values of the model parameters follow some general constraints found in other instantiations of three-layer DNF models as applied to visuo-spatial cognition (Johnson et al., 2009; Lipinski et al., 2010; Schutte & Spencer, 2009; Simmering et al., 2008). First, the time constant, τ, was smaller ⊇ faster for the inhibitory layer than the excitatory layers. Second, the resting level for the inhibitory layer was lower than the excitatory layer resting levels. Third, the width or spread of the inhibitory projection was much broader to WM than to PF (i.e. σ_wv > σ_uv); in addition, these inhibitory projections were broader than the excitatory projections within and between all layers (i.e. σ_−v > σ_−u, σ_−w). Fourth, both local excitatory and lateral inhibitory interactions were stronger in WM than in PF (e.g. c_ww > c_uu). Finally, the rate at which activation built in the Hebbian layers was much faster than its decay (i.e. τ_build < τ_decay). These constraints on the parameters ensure that the three-layer architecture will operate within the dynamic regime necessary to capture the cognitive processes of interest here.

Table A1.

Model parameters

PF(u)			WM(w)			Inhib(v)			Fixation(f)			Time scales (τ)		Hebbian learning (hl)
	young	old		young	old		young	old
hu	−5	–	hw	−5	–	hv	−10.5	−12.5	cci	2.5	τexcite	80	chl	0.25
cuu	1.232	1.7	cww	5.04	7.4088	cuv	1.701	2.7641	cff	2	τinhib	10	σuhl	5
σuu	3	–	σww	3	–	σuv	10	–	cfu	0.295	τbuild	5000	cwhl	0.25
			cwu	1.2	–	cvu	0.2	–	cuf	1	τdecay	25000	σwhl	15
			σwu	5	–	σvu	5	–	cb	1
						cwv	1.215	2.2781	cag	5.5
						σwv	25	–	cs	5.6
						cvw	5	–	csa	5.6
						σvw	5	–	ct	0.4
									hrest	−5
									hdown	−3.1

To get the model to produce the appropriate pattern of performance in the infant task, we ran simulations in batches of 200 ‘participants’, that is, 200 runs with the same parameter settings. We tuned the model’s performance by adjusting parameter values in small increments until the model showed the same qualitative pattern as in the infant data. Specifically, for Simulation Experiment 1 we began with the mean preference scores for 6-month-olds in Ross-Sheehy et al.’s (2003) Experiment 1 as a goal, aiming for the model to produce preference scores above 0.55 for the one mean that was significantly higher than chance and preference scores less than 0.55 for the remaining means.

Once a range of parameter values was identified that could produce this pattern of performance over set sizes for the young model, we adjusted a small subset of parameters to approximate older infants’ behavior. Following previous implementations of the Spatial Precision Hypothesis (Schutte & Spencer, 2009), we increased the strength of local excitatory (c_uu, c_ww) and lateral inhibitory (c_uv, c_wv) projections over development. Additionally, simulations revealed that we needed to lower the resting level of the inhibitory layer (h_v) to capture the performance of older infants. This change balances the boost in inhibition that occurs as the strengths of the Gaussian convolutions from Inhib to PF and WM increase. We tested a range of scaling values on these five parameters to identify a set of values that could produce the qualitative pattern shown by 10-month-olds in Ross-Sheehy et al.’s (2003) Experiment 1, that is, mean preference scores above 0.55 for all three set sizes.

With these parameters as a starting point, we then tested the model in Experiment 2 and then in Experiment 3, eliminating parameter values as needed until the model could produce the qualitative pattern of performance across all conditions and age groups. Finally, we optimized the parameters to reduce RMSE (see text). The final parameter settings for the young and old infant models – those that provided the best fit across all three simulation experiments – are shown in Table A1. Parameters in bold are those manipulated to capture development. Dashes indicate that the parameter value was identical for the young and old infant models.