A Neurobehavioral Model of Flexible Spatial Language Behaviors

Abstract

We propose a neural dynamic model that specifies how low-level visual processes can be integrated with higher level cognition to achieve flexible spatial language behaviors. This model uses real-word visual input that is linked to relational spatial descriptions through a neural mechanism for reference frame transformations. We demonstrate that the system can extract spatial relations from visual scenes, select items based on relational spatial descriptions, and perform reference object selection in a single unified architecture. We further show that the performance of the system is consistent with behavioral data in humans by simulating results from 2 independent empirical studies, 1 spatial term rating task and 1 study of reference object selection behavior. The architecture we present thereby achieves a high degree of task flexibility under realistic stimulus conditions. At the same time, it also provides a detailed neural grounding for complex behavioral and cognitive processes.

People use spatial language in impressively flexible ways that can sometimes mask the complexity of the underlying cognitive system. The capacity to freely establish appropriate reference points using objects in the local environment is a critical component of this flexibility. The description, “The keys are to the right of the laptop,” for example, uses the relational information in the visible scene to ground the location of the keys relative to the laptop. Conversely, listeners easily use such relational spatial descriptions to establish reference points in the local environment, thus enabling them to comprehend and act on such messages (e.g., to locate the keys). The purpose of this article is to give a detailed theoretical account of the cognitive processes—described at the level of neural population dynamics—necessary to generate and understand relational spatial descriptions.

To this end, our neural dynamic model addresses two key goals. First, we seek to ground spatial language behaviors in perceptual processes directly linked to the visible world. Second, we seek to establish a single, integrative model that generalizes across multiple spatial language tasks and experimental paradigms. We specifically address three spatial language behaviors that we consider foundational in real-world spatial communication: (a) Extracting the spatial relation between two objects in a visual scene and encoding that relation with a spatial term, (b) guiding attention or action to an object in a visual scene given a relational spatial description, and (c) selecting an appropriate reference point from a visual scene to describe the location of a specified object.

To formulate a process model of these basic spatial language behaviors, it is useful to consider the underlying processing steps. According to Logan and Sadler (1996; see also Logan, 1994, 1995), the apprehension of spatial relations requires the following: (a) the binding of the descriptive arguments to the target and reference objects (spatial indexing), (b) the alignment of the reference frame with the reference object, (c) the mapping of the spatial term region (e.g., the spatial template for above) onto the reference object, and (d) the processing of that term as an appropriate fit for the spatial relation. These elements may be flexibly combined in different ways to solve different tasks (Logan & Sadler, 1996). In a standard spatial term rating task, for example, in which individuals are asked to rate the applicability of a spatial term as a description of a visible spatial relation (e.g., “The square is above the red block”), individuals would first bind the arguments (“the square” and “the red block”) to the objects in the scene. With the items indexed, the reference frame can then be aligned with the reference object, the given spatial term can be mapped to scene, and the ratings assessment can be given.

It is important to note that these elements need not always be strictly sequential or independent. In a more open-ended spatial description task, for example, reference frame selection is tightly interlinked with spatial term selection. To select an appropriate reference object, one must consider which choice will allow for a simple and unambiguous spatial description of the desired target. On the other hand, the spatial description cannot be determined before the reference point is fixed. This interrelation is highlighted by recent experimental results from Carlson and Hill (2008) showing that the metric details of object arrangement in a scene strongly influence reference object selection: Individuals were more likely to select a nonsalient object as a referent when it provided a better match to axially based projective terms (e.g., above, right) than a salient candidate reference object.

The link between visual information of object positions and the relational spatial descriptions of those positions is a central element of Logan and Sadler's (1996) conceptual model and of all the tasks we consider here. Describing the position of an object relative to another one is equivalent to specifying that position in an object-centered frame of reference centered on the selected reference object. This requires a reference frame transformation from the retinal frame in which the objects are initially perceived onto an object-centered reference frame.¹ Different positions within this object-centered frame can then be linked directly to different projective spatial terms. To date, there are no formal theories that specify how spatial language behaviors are grounded in such lower level perceptual processes, yet still retain the hallmark of human cognition—behavioral flexibility.

In the present article, we describe a new model of spatial language behaviors that specifies how lower level visual processes are linked to object-centered reference frames and spatial semantics to enable behavioral flexibility. In addition, we show how this goal can be achieved while bridging the gap between brain and behavior. In particular, the model we propose is grounded both in neural population dynamics and in the details of human behavior. We demonstrate the latter by quantitatively fitting human performance from canonical tasks in the spatial language literature. This leads to novel insights into how people select referent objects in tasks where they must generate a spatial description. The model also shows how the processing steps specified by Logan and Sadler (1996) can be realized in a fully parallel neural system. Indeed, the parallel nature of this system is critical to the range of behaviors we demonstrate, consistent with work suggesting that flexibility can emerge from dynamic changes of active representational states that are coupled to the world through sensory inputs (see Barsalou, 2008; Beer, 2000; Schöner, 2008; Sporns, 2004; Thelen & Smith, 1994; Tononi, Edelman, & Sporns, 1998).

To achieve our central goals, we use the framework of Dynamic Field Theory (DFT; Erlhagen & Schöner, 2002; Spencer, Perone, & Johnson, 2009). The DFT is a theoretical language based on neural population dynamics that has shown promise for bridging the gap between brain and behavior (Schöner, 2008; Spencer & Schöner, 2003). In particular, DFT has successfully captured human performance in quantitative detail (Johnson, Spencer, Luck, & Schöner, 2009; Schutte & Spencer, 2009; Simmering & Spencer, 2009) and aspects of this approach have been directly tested using multiunit neurophysiology (Bastian, Schöner, & Riehle, 2003; Erlhagen, Bastian, Jancke, Riehle, & Schöner, 1999) as well as ERPs (McDowell, Jeka, Schöner, & Hatfield, 2002). Critically, the present article also builds on insights of other theories, including the Attentional Vector-Sum model (Regier & Carlson, 2001), which has been used to quantitatively capture human performance in spatial ratings tasks, and recent work in theoretical neuroscience examining reference frame transformations (Pouget & Sejnowski, 1997; Salinas & Abbott, 2001; Zipser & Andersen, 1988). These neural models use population codes to represent object locations and other metric features like current eye position, and they detail how mappings between different spatial representations can be realized by means of synaptic projections.

To maintain strong ties to the empirical literature on spatial language, we focus only on spatial relations in a two-dimensional image and consider only those cases where an object-centered reference can be achieved by shifting the reference frame in the two-dimensional image plane (for treatments of reference frame rotation and intrinsic object axes in spatial language see, e.g., Carlson, 2008, and Levinson, 2003). Furthermore, we concentrate on the four projective terms left, right, above, and below. These spatial terms have been studied extensively in the two-dimensional plane across differing tasks (e.g., Carlson & Logan, 2001; Landau & Hoffman, 2005; Logan, 1994, 1995; Logan & Sadler, 1996; Regier & Carlson, 2001) and thus provide a rigorous basis for assessing the behavioral plausibility of our model.

To preview our results, we show that our integrated neural dynamical system can generate a matching spatial description for specified objects, rate the applicability of a spatial term for the relation between two objects, localize and identify an item in a scene based on a spatial description, and autonomously select an appropriate reference point to describe an object location. The ratings and spatial description demonstrations are particularly important because they include quantitative fits to published empirical findings. Through these demonstrations, we show that our system can provide an integrated account for a large range of qualitatively different spatial language behaviors. At the same time, we establish a strong connection to theoretical neuroscience by grounding these behaviors in a formal neural dynamic model that describes the transformation of low-level visual information into an object-centered reference frame.

Toward a Neurobehavioral Account of Spatial Language Behaviors

Before describing our theory, it is useful to place this work in the context of the current theoretical literature. Thus, the following sections focus on two exemplary models in spatial cognition. The first is the Attentional Vector-Sum (AVS) model (Regier & Carlson, 2001), a neurally inspired model that accounts for a range of spatial language ratings data for axial spatial terms (left, right, above, below; for recent extensions of this model, see Carlson, Regier, Lopez, & Corrigan, 2006). The second is a neural population-based approach to reference frame transformation proposed by Pouget and colleagues (Deneve, Latham, & Pouget, 2001). As we shall see, although neither approach by itself enables the range of flexible spatial language behaviors we pursue here, each model reveals key insights into the operations supporting object-centered spatial language behavior. Our neural dynamic framework shows how the insights of each of these models can be integrated to yield a behaviorally flexible spatial language system.

The Attentional Vector-Sum Model

The Attentional Vector-Sum (Regier & Carlson, 2001) model provides an appropriate starting point for our discussion for several reasons. First, it is a formalized model and thus avoids interpretative ambiguities. Second, many of its properties are motivated by research examining neural population dynamics. Finally, it provides good fits to empirical data from several experiments, offering a parsimonious account of these data.

The AVS model builds on two independently motivated observations. First, spatial apprehension and, therefore, the rating of a spatial relationship requires attention to be deployed on the relevant items (Logan, 1994, 1995). Second, the neural encoding of directions can be described by a weighted vector sum (Georgopoulos, Schwartz, & Kettner, 1986). Specifically, when nonhuman primates perform pointing or reaching tasks, individual neurons in both the premotor and motor cortex show different preferred movement directions. Each of these neurons is most strongly activated for movements in a certain range of directions but shows lower activity for other movements. When the vectors describing each neuron's preferred direction are scaled with the neuron's activation, the vector sum across the neural population predicts the direction of an upcoming reach.

Regier and Carlson (2001) applied the concept of vector sums to spatial relations by defining a vector from each point in the reference object to the target location. These vectors are then weighted according to an “attentional beam,” which is centered on that point of the reference object that is closest to the target. The orientation of the sum of attentionally weighted vectors (more precisely, its angular deviation from a cardinal axis) forms the basis for computing ratings of spatial term applicability. A second, independent component in computing the rating is height, which gauges whether the target object is higher, lower, or on the same level as the top of the reference object.

AVS has captured a host of empirical results probing how factors such as reference object shape, orientation, and the horizontal grazing line influence the applicability of spatial descriptions to the layout of objects in a scene. In particular, AVS accounts for the finding that above ratings are independently sensitive to deviations from (a) the proximal orientation (the direction of the vector connecting the edge of the target object with the closest point of the reference object) and (b) the center-of-mass orientation (the direction of the vector connecting the center of mass of the reference object to the center of mass of the target object).

Although AVS incorporates key aspects of attention and neural population vector summation, it is not itself a neural model. It does not use population codes to perform computations and it does not specify the source of the attentional weighting that it employs. For instance, the model does not specify how a neural system could determine the vectors that connect reference and target objects based on actual visual input—a key aspect of the spatial indexing function outlined by Logan and Sadler (1996). We aim to develop a neural implementation that provides this grounding in perceptual processes while at the same time retaining the commitment of AVS to capturing human ratings responses using concepts from neural population approaches.

A Neural Network Model of Reference Frame Transformations

To ground flexible spatial language behaviors in perceptual processes requires specifying how a neural system perceives objects in a retinal frame and then maps these neural patterns into an object-centered frame centered on a reference object. The second class of exemplary models we consider specifies a neural mechanism for reference frame transformations. The first such model was proposed by Zipser and Andersen (1988). They described a mechanism for mapping location information from a retinocentric to a head-centered representation, based on the observed properties of gain-modulated neurons in the parietal cortex. Pouget and Sejnowski (1997) presented a formalized version of this model (described as a radial basis function network), which was later extended to explain multisensory fusion (Deneve, Latham, & Pouget, 2001; for review, see also Pouget, Deneve, & Duhamel, 2002). We will look at the Deneve, Latham, & Pouget (2001) model more closely because it combines several characteristics that make it relevant for the domain of spatial language. In particular, it can be generalized to object-centered representations,² and it is flexible with respect to the direction of reference frame transformation, which offers insights into how different spatial language tasks may be solved within a single architecture.

The neural network model by Deneve, Latham, & Pouget (2001) describes the coordination between three different representations dealing with spatial information: an eye-centered layer, which represents the location of a visual stimulus in retinal coordinates; an eye-position layer, which describes the current position of the eye (i.e., the gaze direction) relative to the head; and a head-centered layer, which represents the location of a stimulus in head-centered coordinates. Each of these layers can serve both as an input and as an output layer. In addition, there is an intermediate layer, which is reciprocally connected to each of the input/output layers and conveys interactions between them. All information within this network is represented in the form of population codes. Each layer consists of a set of nodes with different tuning functions, that is, each node is most active for a certain stimulus location or eye position, respectively, and its activity decreases with increasing deviation from that preferred value.

Initially, the activity of all input/output layers reflects the available sensory information. For example, let us assume that we have the location of a visually perceived object encoded in the eye-centered layer (by a hill of activity covering a few nodes) and that we are also given the current eye position, but we have no explicit information about the location of the object in the head-centered coordinate frame. In this case, the eye-centered and eye-position layers will project specific input into the intermediate layer, while the head-centered layer provides no input. The intermediate layer combines all inputs in a higher dimensional representation and projects back to all input/output layers. In an iterative process, the nodes in the head-centered layer are then driven by this activity in the intermediate layer to form a representation of the object location relative to the head, while the initial representations in the eye-centered and eye-position layers are retained and sharpened.

Because all connections in the model are bidirectional, it can flexibly be applied to a range of other tasks by simply providing different initial activity patterns. For any combination of inputs, the mechanism will work toward producing a consistent set of representations, filling out missing information, solving ambiguities between different inputs or sharpening the representations in all input/output layers. In the context of spatial language, an analogous mechanism can be used to combine the three variables of target position, reference position, and the spatial relation between the two. This might, for example, enable a system to locate a target item in a visual scene, given a reference object, and a spatial relation, or to determine a spatial relation, given the reference object and the target object.

The Deneve, Latham, & Pouget (2001) model offers a flexible transformation mechanism. It also captures a range of neural data. Nevertheless, it does not capture the behavior of people—the model does not generate overt behavior. To use a mechanism like this in a model of human spatial language behaviors, we need additional structures that process a diverse array of verbal and visual information (Chambers, Tanenhaus, Eberhard, Filip, & Carlson, 2002; Spivey, Tyler, Eberhard, & Tanenhaus, 2001; Tanenhaus, Spivey-Knowlton, Eberhard, & Sedivy, 1995), provide the appropriate spatial representations, link them to spatial term semantics, and generate the required responses. We describe a model that accomplishes this goal and builds on the insights of AVS and the Deneve, Latham, & Pouget model below.

A Neurobehavioral Model Using Dynamic Neural Fields

In this section, we introduce a dynamic neural field model that bridges the gap between brain and behavior, providing both a neural process account and strong ties to flexible, observable spatial language behaviors. We begin by describing each core element in the model. We then test the viability of our system by demonstrating how a suite of spatial language behaviors arise from the same unified model using a single parameter set (see Supplemental Materials).

Dynamic Neural Fields

Dynamic Neural Fields (DNFs) are a class of biologically plausible neural processing models (Amari, 1977; Wilson & Cowan, 1973). They are based on the principle that biological neural systems represent and process information in a distributed fashion through the continuously evolving activity patterns of interconnected neural populations. The Dynamic Field Theory (e.g., Erlhagen & Schöner, 2002) builds upon this principle by defining activation profiles over continuous metric feature dimensions (e.g., location, color, orientation), emphasizing attractor states and their instabilities (Schöner, 2008). Activations within dynamic fields are taken to support a percept or action plan (Bastian, Schöner, & Riehle, 2003) and thus incorporate both representational and dynamical systems properties (Schöner, 2008; Spencer & Schöner, 2003). Because an activation field can be defined over any metric variable of interest, this approach allows for a direct, neurally grounded approach to understanding the processes that underlie a broad range of behaviors (for recent empirical applications, see Johnson, Spencer, & Schöner, 2008; Lipinski, Simmering, Johnson, & Spencer, 2010; Lipinski, Spencer, & Samuelson, 2010a; Schutte, Spencer, & Schöner, 2003; Spencer, Simmering, & Schutte, 2006; Spencer, Simmering, Schutte, & Schöner, 2007).

Neural populations processing metric features may represent a theoretically infinite number of feature values (e.g., angular deviations of 0°–360°). We therefore describe the activity level of the neural population as a time-dependent distribution over a continuous feature space (see Figure 1a). This activation distribution, together with the neuronal interactions operating on it, constitutes a Dynamic Neural Field. One may think of this field as a topo-graphical map of discrete nodes, in which each node codes for a certain feature value (analogous to the representations used by Pouget and colleagues). Conceptually, however, we treat the activity pattern in the field as a continuous distribution.

Figure 1.

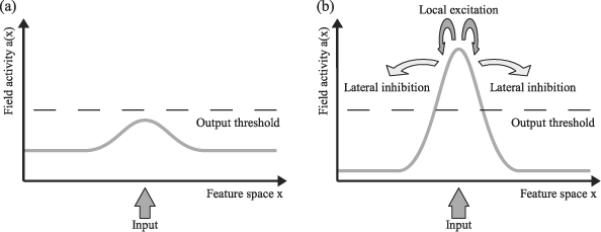
Dynamic neural fields. Dynamic neural fields represent metric information through a continuous distribution of activity (gray line) over a feature space (plotted along the x-axis). Panel (a) shows a hill of activity formed by localized external input. Panel (b) illustrates the effects of the local excitation/lateral inhibition interactions in the field triggered when the input drives activity beyond a (smooth) output threshold (dashed line).

Activity patterns in a DNF change continuously over time and are coupled to external input (e.g., sensory input). In a field defined over visual space, for example, presentation of a visual stimulus will give rise to increased activation at the stimulus position (see Figure 1a). With sufficient activation, stimulated nodes will begin to generate an output signal and interact with other nodes in the field. These interactions generally follow the biologically plausible pattern of local excitation and lateral inhibition (Wilson & Cowan, 1973) shown in Figure 1b. Local excitation means that activated nodes stimulate their neighbors, leading to a further increase in the localized activation. Lateral inhibition, on the other hand, means that activated nodes inhibit distant neighbors, thereby reducing activation in the field (see Figure 1b). Together, these interactions promote the formation of a single activity peak. Once a peak is formed, these interactions work to stabilize the peak against fluctuations.

System Architecture

Activation peaks in DNFs form the basis for cognitive decisions and representational states (Spencer, Perone, & Johnson, 2009; Spencer & Schöner, 2003). To explain complex spatial language behaviors, we use an architecture composed of multiple DNFs, each of which takes a specific role in the processing of visual and semantic information. In this architecture, local decisions—peaks within specific DNFs—are bound together by means of forward and backward projections between them.

Most of the DNFs represent spatial information. Fields that are close to the visual input represent the two-dimensional space of the input image (corresponding to the retinal image in the human visual system). At a later stage, spatial information is transformed into an object-centered reference frame using a mechanism inspired by the Deneve, Latham, & Pouget (2001) model. The object-centered representation is then used to anchor spatial semantics in the visual scene. We further represent object color as a simple visual feature that is used to identify the items involved in a task (e.g., “which object is to the right of the green object?”; see General Discussion for extension to other features). One set of DNFs in our architecture combines color and spatial information, thus allowing us to “bind” an object's identity to a location and vice versa. Color, as well as different spatial semantics, are treated as categorical features and are represented by discrete nodes instead of continuous fields.

The visual input for our system comes either from camera images of real-world scenes or from computer-generated schematic images as used in psychophysical experiments. The camera images are taken with a Sony DFW-VL500 digital camera mounted on an articulated robot head, which is part of the Cooperative Robotic Assistant (CoRA) platform (Iossifidis et al., 2004). Our model is able to flexibly solve different tasks defined by a sequence of context-carrying and control inputs, which reflect the components of verbal task information. Figure 2 shows a schematic overview of our architecture. We describe each component in turn below.

Figure 2.

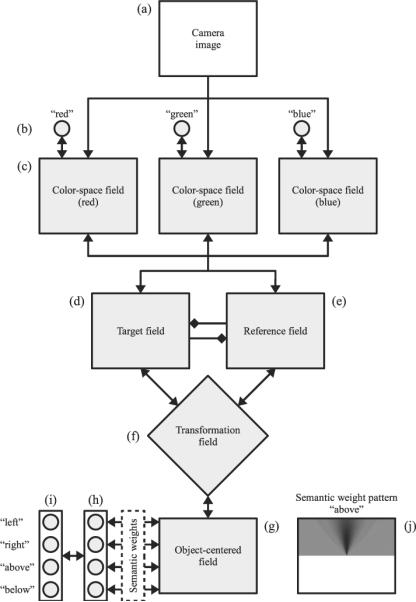
Architecture overview. The camera image (a) is the primary input to our mechanism. All elements shown in gray below it are dynamic neural structures: Gray circles are discrete nodes representing color terms (b), spatial relations (h), or spatial terms (i) that follow the same dynamic principles as the fields. Gray rectangles (c, d, e, and g) are dynamic neural fields defined over a two-dimensional space. The transformation field (f) is a higher dimensional dynamic neural field. Excitatory interactions between elements are indicated by arrows. These interactions are typically bidirectional in our architecture, shown as double arrows. Diamond-shaped links (d and e) represent inhibitory projections. The connections between the object-centered field (g) and the spatial relation nodes (h) depend on custom semantic weights, shown exemplarily for the above relation (j). The semantic weight patterns describe how well a certain position in the object-centered field matches the meaning of a spatial term (darker colors mean higher weights).

Color-space fields

A set of color-space fields (see Figure 2c) provides a simplified, low-level representation of the visual scene. We use a fixed set of discrete colors; and, for each of them, a DNF is defined over the two-dimensional space of image positions. Each point in the image that contains salient color information provides a local excitatory input to the color-space field of the matching color. The resulting activity pattern in this set of fields then reflects the positions and shapes of all colored objects in the scene.

Color term nodes

Each of the color-space fields is connected to a single color term node (see circles, Figure 2b) which receives the summed output from its associated field. Each node is thereby activated by any object-related activity in the field independent of object position. In turn, the output of the color term node homogeneously activates, or “boosts,” the color-space field to which it is coupled. The color term nodes can also be activated by direct external input, corresponding to verbal information identifying an object in the task (e.g., “the green object”). Likewise, system responses regarding object identity are read out from these nodes. Each color term node therefore functions as a connectionist-style, localist color term representation. To produce unambiguous responses, each node has a self-excitatory connection as well as inhibitory connections with the remaining nodes. These interactions amplify small differences in activation level and ensure that only a single node is strongly active at a given time.

Target field

The target field (see Figure 2d) represents the position of the target object, that is, the object whose location is described by the spatial term in a given spatial language task. Like the color-space fields, the target field is defined over the same two-dimensional space of image (“retinal”) positions. Each color-space field projects to the target field in a topological fashion. This means that output from one position in a color-space field excites the corresponding position in the target field. The output from the target field is projected back into each color-space field in the same fashion and, thus, increases activation at the corresponding location. In addition, the output from the target field mildly suppresses all activity in those color-space field locations that do not match the active target field regions. This combined excitation and inhibition enhances activation at the target position while reducing activation at competing “distractor” locations. The target field is also bidirectionally coupled to the transformation field (see below).

Interactions within the target field are governed according to a strong local excitation/ lateral inhibition function. This ensures that only a single activity peak forms in this field, even if it receives multiple target location inputs from the color-space fields. This peak formation corresponds to the selection of a single target object. Once the selection decision is made, the interactions within the field stabilize the peak.

Reference field

The reference field represents the position of the reference object identified by the spatial term (see Figure 2e). Like the target field, it receives topological input from all color-space fields and projects back to them. The reference field is also similarly coupled bidirectionally to the transformation field (see below) and it incorporates the same strong interaction function as the target field, leading to selective behavior. Finally, there is a local inhibitory connection between the target and referent fields (diamond-shaped connections in Figures 2d and 2e). Thus, high activity at one position in the target field suppresses the corresponding position in the reference field (and vice versa). This ensures that a single item cannot act as both target and referent.

Object-centered field

The target and reference fields contain all the location information needed for our tasks. However, these locations are defined in image-based (i.e., retinal) coordinates. Consequently, one cannot easily read out the position of the target object relative to the reference object nor can one process an object-centered location description. We therefore introduce the object-centered field (see Figure 2g). This field is defined over the two-dimensional space of positions relative to the reference object location.

The object-centered field receives input from, and projects back to, the transformation field. It is through this field that the object-centered field interacts with the target and reference fields. In addition, the object-centered field provides input to, and receives input from, the spatial relation nodes (see Figure 2h; see below). The object-centered field does not use strong neural interactions; thus, the field holds broadly distributed activity patterns instead of narrow peaks.

Spatial relation nodes

Activity in different parts of the object-centered field directly corresponds to different spatial relationships between the target and reference objects. The spatial relation nodes capture the categorical representation of these relationships. The current framework has one discrete node for each of the four spatial terms defined here: left, right, above, and below (see Figure 2h). Each node is bidirectionally connected to the object-centered field. The pattern of connection weights between spatial term nodes and the field is shown for one exemplary relation—the above relation—in Figure 2j. The connection pattern is determined from the combination of a Gaussian distribution in polar coordinates (compare O'Keefe, 2003) and a sigmoid (step-like) function along the vertical axis. Additional relational terms beyond the four projective relations may easily be added to this network (see the General Discussion section).

Each node receives summed, semantically weighted output from the object-centered field. Conversely, node activation projects back to the object-centered field according to the same semantic weights. The spatial relation nodes have moderate self-excitatory and mutually inhibitory interactions. They produce a graded response pattern reflecting the relative position of the target to the reference object. For example, both the right and above nodes may be activated to different degrees if the target is diagonally displaced from the reference object.

Spatial term nodes

The spatial term nodes turn the graded activation patterns of the spatial relation nodes into a selection of a single term (see Figure 2i). There is one node for each of the four spatial terms. Each spatial term node receives excitatory input from the corresponding spatial relation node and projects back to it in the same fashion. There are strong lateral interactions among the spatial term nodes (self-excitation and global inhibition), leading to pronounced competition between them. In effect, only one of them can be strongly activated at any time, even if the activity pattern in the less competitive spatial relation nodes is ambiguous. Like the color term nodes, the spatial term nodes can be activated directly by external input (e.g., verbal instruction) and can be used to generate overt responses.

Reference frame transformation field

The transformation field (see Figure 2f) converts location information between the image-based and object-centered reference frames—it is at the heart of our framework. The transformation mechanism that we employ is similar to the one described by Deneve, Latham, & Pouget (2001). In our specific instantiation, the transformation field is defined over the space of all combinations between target and reference positions. We first describe the transformation process with a simplified case where the target, reference, and object-centered fields are all one-dimensional and the transformation field is two-dimensional (see Figure 3).

Figure 3.

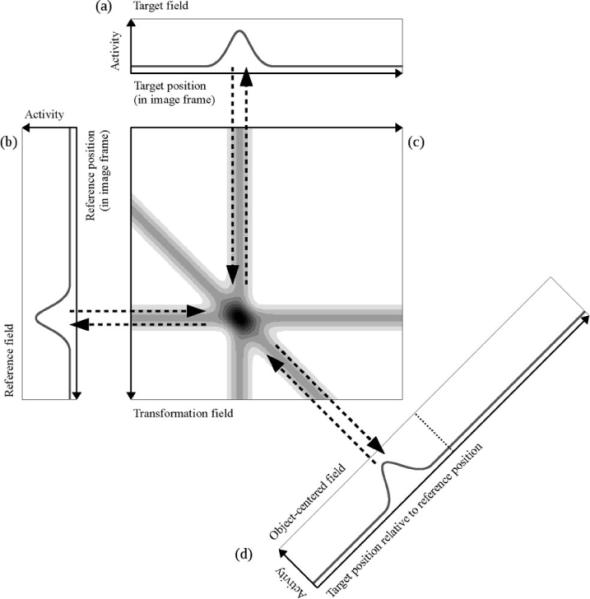
Reference frame transformation for one-dimensional inputs through a two-dimensional transformation field. The target field (a) and the reference field (b) represent object position in the image frame. The transformation field (c) is defined over the space of all combinations of target and reference position and it links the target and reference field with the object-centered field (d). The activity distribution within the transformation field is indicated by different shades of gray, with darker shades meaning higher activity. The target field is aligned with the horizontal target position axis of the transformation field. The reference field is aligned with the vertical reference position axis (this axis is inverted for reasons of visualization). The object-centered field is shown tilted by 45°. All projections between a one-dimensional field and the transformation field run orthogonally to the position axis of the respective one-dimensional field (bidirectional dashed arrows). The inputs from the three one-dimensional fields produce the three visible activity ridges in the transformation field. The output from the intersection point of these ridges projects back to the peak positions in the one-dimensional fields. The diagonal projection to the object-centered field connects all combinations of target and reference position to the matching relative position in the object-centered field. The dotted line in the object-centered field represents the center of this field, which is by definition aligned with the reference object.

The target field in Figure 3 is shown aligned with the horizontal axis of the transformation field and defines the target location in the image-based frame. The reference field is shown aligned with the vertical axis of the transformation field and defines the reference location in the image frame. Each activated node in the reference field drives the activity of all nodes in the transformation field that correspond to that same reference position, that is, all nodes in the same horizontal row in Figure 3. This gives rise to a horizontal activity ridge. The input from the target field acts analogously, forming a homogeneous, vertical activity ridge. The intersection of these two ridges leads to an increased activity level, and substantial output from the transformation field is generated only at this intersection. The transformation field employs moderate global inhibition that softly normalizes overall field activity.

What does the intersection point in the transformation field signify? It captures the target and reference locations in a single, combined representation. This representation implicitly yields the specific spatial relation between target and reference objects, which is simply the difference between the two locations. Given this, we can implement the transformation by setting up an excitatory connection from every point in the transformation field to the position in the object-centered field that corresponds to this difference. In other words, all target-referent location combinations that have the same position difference (say, +30° of visual angle) have an excitatory connection to the place in the object-centered field which represents that specific relation. This gives rise to a simple geometric connection pattern in which all points in the transformation field that correspond to the same target-referent relation lie on a diagonal line. This can be seen as follows: If the reference point on the vertical axis moves by a certain value, the target position on the horizontal axis must move by that same value to keep the relative position constant.

In our framework, this transformation field is dynamically and bidirectionally coupled to the target, reference, and object-centered fields. Transformations are, thus, not fixed to a single directional flow. Specifically, the object-centered field projects activation back into the transformation field along the same diagonal axis from which it receives input (see diagonal activity ridge, Figure 3c). In turn, the transformation field projects back to the target and reference fields along the vertical and horizontal axes, respectively. Thus, if a reference position is given together with a desired relative position in the object-centered field, the transformation field will activate the appropriate region in the target field. In the context of spatial language, this means that a reference object and a spatial term can be used together to specify a target location. This multidirectionality does not require any switching in the interactions between these fields. Instead, the dynamic coupling between them smoothly drives the activation in the fields toward a consistent pattern (analogous to Deneve, Latham, & Pouget, 2001). This dynamic flexibility allows for the generation of different spatial language behaviors within a single, unified architecture.

To use this transformation mechanism with actual image positions, we extend the target, reference, and object-centered representations to two dimensions. The transformation field in our implementation is then defined over a four-dimensional space, spanning two dimensions of target position and two dimensions of reference position. Functionally, the mechanism is equivalent to the simplified version described here.

Demonstrations

In this section, we detail five demonstration sets testing our system's capacity for flexible behavior. In Demonstration 1, the system must select a spatial term describing the relation between a specified target and reference object (“Where is the green item relative to the red item?”). Demonstration 2 substantiates the plausibility of this spatial semantic processing by simulating empirical above ratings performance from Experiments 1, 2, and 4 of Regier and Carlson (2001). In Demonstration 3, the system selects the color of the target object given a reference object and a descriptive spatial term (“Which object is above the blue item?”). In Demonstration 4, the system must describe the location of a specified target object by selecting both a reference object color and a descriptive spatial term (“Where is the green item?”). Demonstration 5 substantiates the plausibility of this spatial description process by simulating empirical results from the reference object selection task reported in Experiment 2 of Carlson and Hill (2008). The different types of information flow in these demonstrations capture key aspects of the apprehension of spatial relations and the use of spatial language in real-world communication.

Demonstrations 1, 3, and 4 use images of real-world scenes of a tabletop workspace containing three everyday objects of comparable size. In Demonstrations 2 and 5, we use computer-generated colored rectangles as visual inputs to allow an enhanced degree of stimulus control. Both types of stimuli are processed in precisely the same way in our system. We use the same architecture with identical parameter values across all five demonstration sets. To define each task and generate responses on each trial, additional inputs that reflect the task structure were applied sequentially to specific elements of the system. We assume that the required sequence of inputs is generated from a semantic analysis of the verbally posed request, for example, “What is to the right of the blue item?”

We discriminate between two types of task information. The first type provides concrete content information, specifying either the identity of an object (“the blue item”) or a spatial relationship (“to the right”). This can be conveyed to our system by activating a single color or spatial term node. The second type of information specifies the roles of these content-carrying inputs and the goal of the task. Both are conveyed in speech through sentence structure and keywords (such as “what,” “where,” “of,” and “relative to”). This type of task information is transmitted to the system in the form of homogeneous boost inputs, which raise the activity level of a whole field or a set of nodes. These boosts do not supply any specific information about object locations or identities, but they structure the processing within the dynamic architecture. The responses for each task are read out from the color, the spatial term, or the spatial relation nodes after a fixed number of time steps (which is identical for all tasks), when the sequence of task inputs is completed and the dynamical system has settled into a stable state.

A detailed description of the input sequences used for each task is given below. In most cases, this input sequence approximately follows the typical order in which pieces of information are provided in spatial language utterances. Although we use a fixed sequence here, our system has a high degree of flexibility with respect to the exact timing and the order of different inputs. We note, however, that the semantic analysis of the verbal information that leads to the input sequence is a complex cognitive task of its own that we do not address. In our view, the ability to create an appropriate sequence of content-carrying and control inputs is what constitutes an understanding of a task, something which is beyond the scope of this article. Note that the same sequences or sequence elements may also be used in conjunction with our architecture to solve other spatial cognition tasks that do not necessarily involve any verbal input.

Demonstration 1: Spatial Term Selection

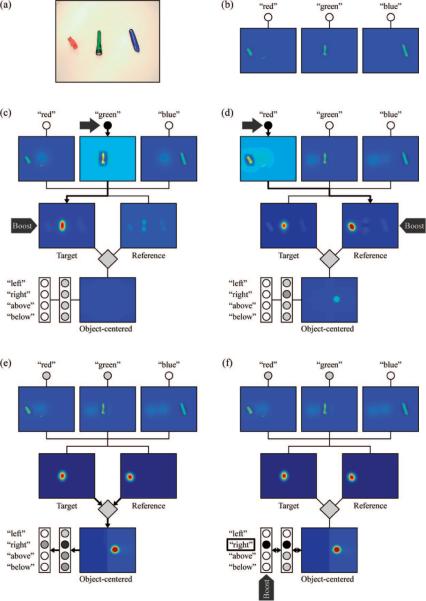
The selection of a spatial relation term is a critical component of any spatial description (e.g., Franklin & Henkel, 1995; Hayward & Tarr, 1995). Demonstration 1 shows how our system handles spatial term selection. We presented a red tape dispenser, a small green flashlight, and a blue box cutter aligned horizontally in the image plane (see Figure 4a). In addition, we presented a sequence of task inputs corresponding to the question “Where is the green flashlight relative to the red tape dispenser?” To respond correctly, the system must activate the right spatial term node. Note that this response can only be obtained if the flashlight's position is taken relative to the specified reference object: The green flashlight is neither to the right in the image (it is slightly to the left of the center) nor to the right of the alternative referent, the blue box cutter.

Figure 4.

Activation sequence for spatial term selection in Demonstration 1. Panel (a) shows the camera input for this task. Panels (b)–(f) show activity distributions at different points in the task. Field activity levels are color-coded (dark blue = lowest activity, dark red = highest activity). Activity of discrete nodes (circles) is coded by lightness (darker shades = higher activity). The activity in the high-dimensional transformation field (grey rhombus) is not represented. Bold connections with arrows between the fields highlight dominant directions of information flow in the task. Block arrows indicate current task input. Panel (b): the scene representation in the color-space fields before the task. Panel (c): target object selection by activating the green color node and boosting the target field. Panel (d): reference object selection by activating the red color node and boosting the reference field. Panel (e): emergence of a peak in the object-centered field representing the target object location relative to the selected reference object. The right spatial relation node activity is also increased (dark gray node). Panel (f): boost of spatial term nodes to prompt the response right (box).

Results and discussion

The three objects in the workspace generate activation profiles in each of the respective color-space fields at their location in the image space (see Figure 4b). This activity is driven by the continuously provided visual input. Such image-based color-space field activation forms the basis of the simple neurally grounded scene representations used in all tasks. The color-space fields project weakly to the target and the reference fields as well as to the color term nodes, although the activity in these parts of the system remains well below the output threshold. The remaining downstream fields therefore remain silent as well.

We begin the task by specifying the green flashlight as the target object. To do this, we activate the green color term node, which uniformly raises the activation of the green color-space field (see Figure 4c). This amplifies the output at the location of the green flashlight (see Figure 4c). At the same time, we uniformly boost the target field. The target field receives positive activation from the color-space fields, and the boost leads to the formation of a peak at the location of the strongest input. In this case, then, the target field peak corresponds to the location of the green item. After the target position is set, the green node input is turned off and the target field is de-boosted to an intermediate resting level. The target object peak is nonetheless stably maintained because of the neural interactions within the field. This stabilized peak also inhibits the corresponding region of the reference field (see the slightly darkened reference field regions in Figures 4c and 4d). This prevents the selection of that same location as the reference position.

Having presented the target item information (i.e., “Where is the green flashlight?”), we next provide the reference object information by activating the red color term node and boosting the reference field (see Figure 4d). The activation of the color term node homogeneously increases the red color-space field activation. As a result, the activation profile from the red tape dispenser is increased and the boosted reference field forms a robust peak at the dispenser's location (see Figure 4d). Analogous to the target field, the reference field peak stably represents the reference object location even after we de-boost the field to an intermediate resting level and remove the red node input. We note that the order in which target and reference objects are defined can be reversed in this mechanism without changing the outcome, thus providing a fair degree of flexibility in line with the variability of natural communication.

With peaks established in both the target and reference fields, these fields now provide strong input into the transformation field (see arrows, Figure 4e). A high level of activation, therefore, arises autonomously at the “intersection” of these inputs in the transformation field. This intersection represents the combination of the target and reference object positions in a single, four-dimensional representation (not shown). From the intersection point, activation is propagated to one location in the object-centered field. This location represents the target object's position relative to the reference object. An activity peak forms autonomously at this location in the object-centered field (see Figure 4e).

The formation of the object-centered peak propagates activation to the spatial relation nodes. Because the peak has formed in the right part of the object-centered field, it most strongly activates the right node (see darker shading of the right relation node, Figure 4e). The spatial term nodes receive input from the spatial relation nodes. In the present case, the right node has the highest activity, but the activity level is low overall. To unambiguously select one spatial term, we homogeneously boost the spatial term nodes to prompt the system to respond. Due to the strong self-excitatory and global inhibitory interactions among nodes, the right node becomes more strongly activated and suppresses all other nodes (see Figure 4f), thus producing the correct response for the task.

It is important to observe that this spatial term selection behavior does not depend on a target object location that perfectly corresponds to a single spatial term. For example, in Figure 5 we used the same task structure as the preceding demonstration, but shifted the flashlight (see Figure 5a) to a position that is both above and to the right of the red tape dispenser; it is neither perfectly to the right nor perfectly above the red reference object. As before, with the target and reference object locations established, a peak representing the target object relation forms in the object-centered field. This peak, which is now to the right and above the center of the field, provides comparable activation input into both the right and above spatial relation nodes (see Figure 5b). Nevertheless, after boosting the spatial term nodes, the slightly elevated activation of the right node together with the competitive inhibitory interactions among nodes leads to the complete suppression of the above node and, ultimately, the selection of right as the descriptive spatial term (see Figure 5c).

Figure 5.

Activation sequence for spatial term selection in Demonstration 1 with imperfect correspondence to spatial terms. Panel (a) shows objects in the camera input. Panels (b) and (c) show activity distributions at different points in the task. Panel (b): With target object (green flashlight) and reference object (red tape dispenser) already established, a peak representing the target object relation forms in the object-centered field. The peak provides comparable activation input into both the right and above spatial relation nodes (dark gray nodes). Panel (c): Boosting the spatial term nodes prompts competition between these nodes, leading to the generation of the response right (box).

Note that although the system dynamics currently force the selection of only a single spatial term, the activation of multiple spatial relation nodes signals the potential for the system to generate multiple terms (e.g., “to the right and above”; see, e.g., Carlson & Hill, 2008; Hayward & Tarr, 1995). Thus, while we have not yet implemented a sequencing mechanism that permits the sequential selection of multiple spatial terms, our model already incorporates the semantic sensitivity needed to structure such a sequence.

Demonstration 2: Simulating Empirical Spatial Term Ratings

In this demonstration, we test whether the neural dynamic system which accomplished spatial term selection in Demonstration 1 can also account for the details of human spatial term use. To this end, we examine the model's performance in a set of spatial language ratings tasks, in which the system rates the applicability of a spatial term to the relation between two items in a visual scene. Ratings performance represents a key test of this model because such tasks have played a prominent role in spatial semantic processing research to date (e.g., Carlson-Radvansky & Logan, 1997; Carlson-Radvansky & Radvansky, 1996; Coventry, Prat-Sala, & Richards, 2001; Hayward & Tarr, 1995; Lipinski, Spencer, & Samuelson, 2010b). We simulate a subset of the ratings tasks that Regier and Carlson (2001) used to establish AVS.

Method

Materials

We used computer-generated scenes containing one larger, green reference object in a central location, and a smaller, red target object. The target was located at different positions around the referent. The shape and placements of target and reference objects were based on the stimulus properties reported for Experiments 1, 2, and 4 from Regier and Carlson (2001). Note, however, that we had to modify the sizes of some objects given the relatively simple visual system that we used. This ensured that small items could still generate a sufficient response from the color-space fields, while large items did not dominate the system's response for color terms. Furthermore, we had to scale the distances between items in some instances to fit the object array within the fixed dimensions of our input image. These modest constraints could certainly be relaxed with a more sophisticated visual system. That said, we viewed the simplicity of the visual system as a plus because it highlights that our model does not depend on sophisticated, front-end visual processing to show the types of flexibility shown by humans.

Procedure

Each ratings trial began by first establishing the target and reference object locations as described in Demonstration 1. In contrast to Demonstration 1, however, we did not boost the spatial term nodes here, and we did not use their output as the basis for the response. Instead, we recorded the output of the spatial relation nodes at the end of the demonstration (using the same total number of iterations as above). We then scaled this output (which is in the range of 0 to 1) to the range used in the experiments (0 to 9) to obtain a rating response.

Demonstration 2a: Sensitivity to proximal orientation

This demonstration had two goals. The first was to test whether the same model that produced the spatial term selection behaviors in Demonstration 1 could also capture empirical spatial language ratings performance. In particular, above ratings should be highest for locations lying along the positive region of the vertical axis, systematically decrease as the target location deviates from the vertical axis, and then sharply decline for targets at or below the horizontal axis.

The second goal was more focused. Recall that Regier and Carlson (2001) observed that there are two distinct orientation measures that influence spatial language ratings data. The first is proximal orientation, the orientation of a vector that points to the target from the closest point within the reference object (shown as gray lines in Figure 6). The second is center-of-mass orientation, the orientation of a vector that connects the reference object's center of mass with the target (black lines in Figure 6).³ The influence of the proximal orientation was investigated in Regier and Carlson's Experiment 1. In this task, individuals rated the relation between a small target object and a rectangular reference object. Critically, this rectangle was presented in either a horizontal or a vertical orientation. By rotating the rectangular reference object but holding the target object location constant, they were able to change the proximal orientation without altering the center-of-mass orientation (compare Figures 6a and 6b). Empirical results showed that ratings for the vertical terms (above, below) in the tall condition were lower than those in the wide condition. Conversely, ratings for the horizontal terms (left, right) were higher in the tall condition. Thus, spatial term ratings were sensitive to changes in proximal orientation. Here we test whether our model is also sensitive to changes in proximal orientation.

Figure 6.

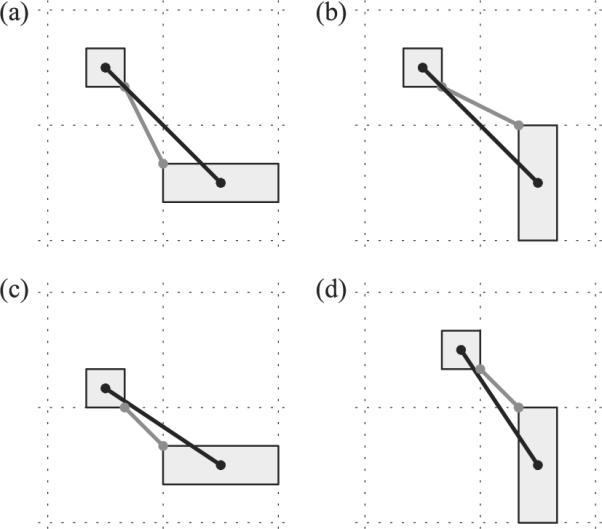
Proximal orientation vectors (gray lines) and center-of-mass orientation vectors (black lines). Panels (a) and (b) depict a change in the proximal orientation vector from the Wide (a) to the Tall (b) reference object condition as in Demonstration 2a, while the center-of-mass orientation remains the same. Panels (c) and (d) depict a change in the center-of-mass orientation vector from the Wide (c) to the Tall (d) reference object condition while the proximal orientation is held constant, corresponding to the situation in Demonstration 2b.

Materials

The input image was divided into a (hypothetical) 5 × 5 grid of square cells (with borders remaining on the left and on the right portion of the image). The rectangular reference object was centered in the central cell of the grid. The reference object was either vertically oriented (Tall condition) or horizontally oriented (Wide condition). The small square target object was placed centrally in each of the other cells in successive trials.

Results

Table 1 shows the model's above ratings for each position of the target object for each of the two orientation conditions. Results for the Tall condition are broadly consistent with the Experiment 1 response profile (in parentheses) reported by Regier and Carlson (R² = .98, RMSD = .55). In particular, ratings are highest for target locations along the positive portion of the vertical axis, systematically decline as the target deviates from this axis, and then sharply decline for targets placed along the horizontal axis. The model's ratings for the Wide condition also follow the empirical profile (in parentheses; R² = .97, RMSD = .6).

Table 1.

Demonstration 2a: Above Ratings for Each Position of the Target Object in Simulations (Empirical Results in Parentheses)

	Column
Condition and row	1	2	3	4	5
Tall
1	6.0 (6.7)	8.3 (7.4)	8.8 (8.9)	8.3 (7.4)	6.0 (6.8)
2	5.4 (5.6)	7.3 (6.6)	8.6 (8.9)	7.3 (6.2)	5.4 (6.0)
3	0.9 (0.9)	0.9 (0.9)		0.9 (1.0)	0.9 (1.3)
4	0.0 (0.6)	0.0 (0.3)	0.0 (0.6)	0.0 (0.4)	0.0 (0.6)
5	0.0 (0.4)	0.0 (0.4)	0.0 (0.3)	0.0 (0.6)	0.0 (0.3)
Wide
1	5.9 (6.5)	8.3 (7.3)	8.8 (8.9)	8.3 (7.0)	5.9 (6.9)
2	5.5 (6.2)	7.6 (6.4)	8.6 (8.4)	7.6 (6.9)	5.5 (6.2)
3	0.9 (0.7)	0.9 (0.8)		0.9 (0.7)	0.9 (0.8)
4	0.0 (0.4)	0.0 (0.5)	0.0 (0.3)	0.0 (0.4)	0.0 (0.3)
5	0.0 (0.4)	0.0 (0.4)	0.0 (0.4)	0.0 (0.3)	0.0 (0.3)

Note. Columns and rows refer to the 5 × 5 grid of square cells used in Demonstration 2a. Empirical results from Regier and Carlson (2001, Experiraent 1).

We also tested whether the ratings were sensitive to changes in proximal orientation. As in Regier and Carlson (2001), we compared the mean above ratings for the oblique target locations between the Wide and the Tall condition. If our model is sensitive to changes in proximal orientation, then above ratings for the oblique target locations in the Wide condition should be higher than those in the Tall condition. Results showed a mean rating of 6.825 for the Wide condition and a mean of 6.75 for the Tall condition, a difference of .075. Thus, our neural dynamic framework is sensitive to changes in proximal orientation. Note that the magnitude of this difference was comparable to that for the empirical data (.093) and the AVS model (.092).

Demonstration 2b: Sensitivity to center-of-mass orientation

Regier and Carlson (2001, Experiment 2) also showed in a very similar setting that spatial term ratings were sensitive to change in the center-of-mass orientation. As before, the rectangular reference object was rotated into either a Wide or a Tall orientation. In this task, however, the placement of the target object within a cell was varied between the Tall and Wide conditions to maintain a constant proximal orientation (illustrated in Figures 6c and 6d; compare gray line orientations). As a result, the center-of-mass orientation between target and reference object changes between the two conditions. In general, the center-of-mass orientation becomes more vertically aligned in the Tall condition compared to the Wide condition (compare black lines, Figures 6c and 6d). Regier and Carlson showed that this led to higher mean above ratings for the Tall condition. Here we test whether our model shows the same sensitivity to changes in center-of-mass orientation.

Materials

Stimuli were the same as in Demonstration 2a with one exception. Here, target placements were varied within each cell between the Tall and Wide conditions such that the proximal orientation between the target and reference object was held constant across rotations of the referent. The center-of-mass orientation, therefore, varied across rotations of the rectangle.

Results

Table 2 shows the above ratings results. As before, the simulated ratings followed the empirical profile (Tall: R² = .99, RMSD = .65; Wide: R² = .96, RMSD = .92). To test whether our model captures sensitivity to changes in the center-of-mass orientation, we compared the mean ratings for the oblique target locations. If our model is sensitive to these changes, then above ratings for the oblique target locations in the Tall condition should be higher than those in the Wide condition. Results showed a mean rating of 7.675 for the Tall condition and a mean of 5.975 for the Wide condition, a difference of 1.7. Our model is therefore sensitive to changes in the center-of-mass orientation, consistent with the empirical data. Note that the obtained effect is larger than that reported by Regier and Carlson (2001) in Experiment 2 (0.114).

Table 2.

Demonstration 2b: Above Ratings for Each Position of the Target Object in Simulations (Empirical Results in Parentheses')

	Column
Condition and row	1	2	3	4	5
Tall
1	7.4 (6.6)	8.6 (7.3)	8.8 (8.7)	8.6 (7.7)	7.4 (6.9)
2	6.3 (6.3)	8.4 (6.7)	8.6 (8.6)	8.4 (7.0)	6.3 (6.3)
3	0.9 (1.2)	1.1 (1.1)		1.1 (1.5)	0.9 (1.2)
4	0.0 (0.3)	0.0 (0.4)	0.0 (0.5)	0.0 (0.4)	0.0 (0.4)
5	0.0 (0.5)	0.0 (0.4)	0.0 (0.3)	0.0 (0.3)	0.0 (0.5)
Wide
1	6.3 (6.7)	8.0 (7.0)	8.8 (9.0)	8.0 (7.4)	6.3 (7.1)
2	3.9 (5.9)	5.7 (.6.8)	8.4 (8.9)	5.7 (6.7)	3.9 (6.4)
3	0.9 (1.1)	0.9 (1.2)		0.9 (1.2)	0.9 (1.6)
4	0.1 (0.6)	0.0 (0.6)	0.0 (0.4)	0.0 (0.7)	0.0 (0.7)
5	0.0 (0.6)	0.0 (0.5)	0.0 (0.9)	0.0 (0.9)	0.1 (0.9)

Note. Columns and rows refer to the 5 × 5 grid of square cells used in Demonstration 2b. Empirical results from Regier and Carlson (2001, Experiment 1).

Demonstration 2c: Center-of-mass versus reference object midpoint

In Experiment 3 of Regier and Carlson (2001), wider rectangles were used to probe different regions directly above the referent. Results replicated the center-of-mass effect. However, the midpoint and center of mass were at the same location. Thus, in Experiment 4, Regier and Carlson separated out the possible contribution of the midpoint to the center of mass effect by replacing the wide rectangle with a wide triangle and probing ratings at three critical points⁴ (A,B,C; see Figure 7). If the target's position relative to the midpoint was the critical relation, the above ratings should have peaked at B (right above the midpoint) and showed comparably lower values for A and C. Instead, empirical above ratings were similar for positions A and B and lower for location C, consistent with a dominant influence of the center-of-mass orientation and the predictions of the AVS model. Here we test whether our neural dynamic system can simulate these results.

Figure 7.

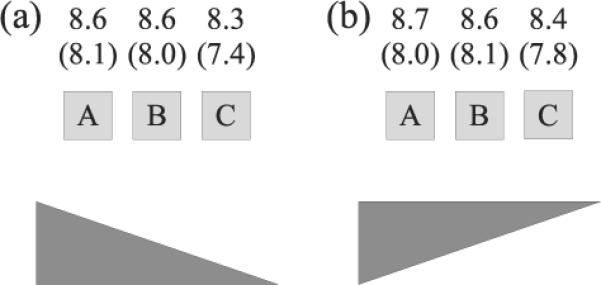
Demonstration 2c target object positions for the upright (a) and inverted (b) triangle reference objects, with results of the ratings simulations. Empirical data in parentheses from Experiment 4, Regier and Carlson (2001), Grounding spatial language in perception: An empirical and computational investigation. Journal of Experimental Psychology: General, 130, p. 285. doi:10.1037/0096-3445.130.2.273

Method

We used the same square targets as in Demonstrations 2a and b, and a wide upright or inverted triangle as a reference object. The referent's size was smaller than that used in the original experiment to accommodate the constraints of our visual system. Nevertheless, all qualitative properties of the spatial relationship between target and reference object for positions A to C were retained.

Results

Figure 7 shows the results of the ratings simulations and the empirical data (in parentheses). For the upright triangle (see Figure 7a), Points A and B both yielded higher ratings than Point C. Points A and B also yielded identical ratings and there was no evidence of a ratings peak at Point B. Simulated ratings for the inverted triangle also replicated this general pattern (see Figure 7b; combined R²= .79; RMSD = .65). The mean ratings for Points A and B (averaged across the upright and inverted conditions) exceeded Point C ratings by a mean of .28. This magnitude is comparable to the mean difference observed in the empirical data (.45).

Discussion

The results from Demonstrations 2a–c confirm that our neural dynamic model can account for details of human spatial language behavior. For the majority of the tested conditions, the model provides a good quantitative fit to the empirical data. To understand how sensitivity to the different orientation measures arises in our framework, it is necessary to consider what factors determine the precise position of the reference field peak. The first and dominant factor is the position and shape of the reference object in the scene, transmitted via the color-space fields. Each point in the color-space fields that is sufficiently activated creates an excitatory output signal to the reference field. These signals are spatially smoothed by a Gaussian filter to reflect the spread of synaptic projections in real neural systems. With every point of the reference item projecting broadly into the reference field, the resulting activity distribution in this field takes the form of a smooth hill with its maximum marking the approximate location of the reference item's center of mass. The activity peak in the reference field forms around this maximum, thus explaining our system's sensitivity to the center-of-mass-orientation observed in Demonstrations 2b and 2c.

Importantly, however, the activity pattern in the reference field still reflects the (smoothed) item shape, and it is still sensitive to modulations of its input after the peak has formed. In particular, peaks in the target and reference fields project broad activation back to the color-space fields, strengthening the output from the corresponding locations. This can be interpreted as a form of spatial attention, directed to both the target and reference item. If the two items are close to each other, the two peaks can interact via this form of spatial attention. Specifically, in Demonstration 2a, the back-projection from the target field can modulate the representation of the reference object in the color-space fields, strengthening the output to the reference field from those parts that are closest to the target. This has a biasing effect on the reference peak, pulling it toward the target location. The position of this peak, however, is still restricted by the rectangular shape of the visual input, and it will move significantly only along the rectangle's longer axis (where the input gradient is more shallow). Thus, if the reference object is horizontally oriented and the target is in an oblique relation above it, the reference peak will drift horizontally toward the target. This increases the verticality of the spatial relation, thus leading to a higher above rating. In contrast, if the reference object is vertically oriented, the peak will be pulled upward in the same situation, thus decreasing the verticality and the above rating. Note that this mechanism is largely analogous to the explanation in the AVS model. In AVS, the location of the target object determines the focus of spatial attention within the reference object, and thereby determines how different parts of this object are weighted in calculating the vector sum (a more general comparison of our model to AVS is given in the General Discussion).

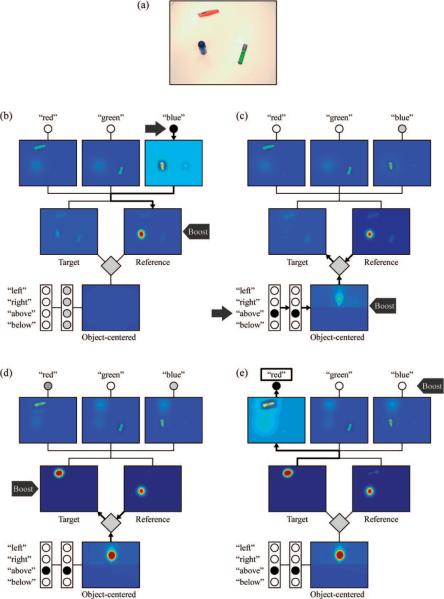
Demonstration 3: Target Object Identification

To establish the behavioral flexibility of our neural system beyond spatial term semantic behaviors, we test whether the system can describe the target object at a location specified by a spatial description. In particular, we placed a blue deodorant stick, a red box cutter, and a green highlighter in the visible workspace (see Figure 8a). We then provided task input specifying the blue deodorant stick as the reference object and above as the spatial relation, thereby posing the question “Which object is above the blue deodorant stick?” To respond correctly, the system must activate the red color term node.

Figure 8.

Activation sequence for target object identification in Demonstration 3. Panel (a) shows objects in the camera input. Panel (b), reference object selection by activating the blue node and boosting the reference field. Panel (c), above node activation through task input and boost to the object-centered field, leading to activation of the upper part of the object-centered field (lighter blue region above the reference location). Panel (d), target field boost leading to the formation of a peak at the target object location. Panel (e), the color of the corresponding target object is queried by boosting the color nodes, leading to the red response (box).

Results and discussion

With the three items placed in the workspace, we first specify the reference object information by simultaneously activating the blue color term node and boosting the reference field. This leads to a stronger activation at the blue object's location in the blue color-space field and the subsequent formation of a peak at that location in the reference field (see Figure 8b). We then remove the blue node input and de-boost the reference field to an intermediate resting level. As before, this reference peak is stably maintained at the position of the blue item (see Figure 8c).

We then specify the desired spatial relation by simultaneously activating the above spatial term node and boosting the object-centered field (see Figure 8c). The spatial term node first activates the corresponding spatial relation node, which further projects to the object-centered field. This generates an activation profile in the object-centered field that mirrors the above semantic weight pattern (see Figure 8c). Because the object-centered field is simultaneously boosted, its output is amplified and its spatially structured activity pattern is projected into the transformation field. Within the transformation field, the input from the object-centered field effectively intersects with the reference field input. Consequently, the transformation field propagates activation into the target field (see arrows Figure 8d). This input corresponds to a shifted version of the above activity pattern in the object-centered field, now centered at the reference object position in the image-based frame. Consequently, the region in the target field above the blue deodorant stick becomes moderately activated.

Next, we select a target object by homogeneously boosting the target field (see Figure 8d). At this point, the target field receives excitatory input from two sources: the broad spatial input pattern from the transformation field and the more localized color-space field inputs representing the object locations. When the target field is boosted, the activity hills formed by the color-space field inputs compete with each other through lateral interactions. Because the activity hill corresponding to the red box cutter lies in the preactivated region above the referent location, it has a clear competitive advantage, leading to a peak at this location (see Figure 8d).

Once the target peak forms, it projects activation back into all the color-space fields. This input is not sufficient to produce any significant output by itself, but it amplifies the output of the red box cutter's representation in the red color space field. Consequently, there is stronger input to the red color term node (see Figure 8e). When we then uniformly boost all color term nodes to generate an object description, this elevated activity provides a competitive advantage for the red node (see Figure 8e), leading to a red response.

Demonstration 4: Spatial Term and Reference Object Selection

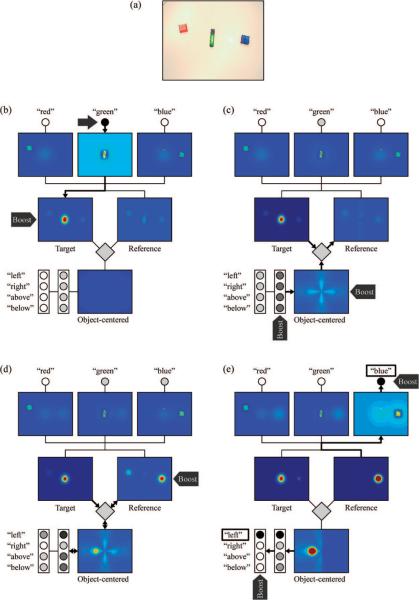
Demonstration 3 showed how specifying the reference object and a spatial term can cue a form of attention to a semantically defined spatial region. Spatial language tasks are not always so well defined however. For example, if one wishes to describe the location of a target object—a coffee cup—on a crowded desk, one needs to select both the spatial term and the reference object. Does the functionality of our neural system generalize to situations in which only a single piece of information—the identity of the target item—is specified?

We tested this by presenting a stack of red blocks, a green highlighter, and a stack of blue blocks (see Figure 9a), but only designated the green item as the target object. The task structure is, therefore, equivalent to asking “Where is the green highlighter?” To complete the task, the system must generate a description of the object's location by selecting both a reference object and an appropriate object-centered spatial term. Success in this task would constitute a fourth qualitatively different behavior performed by this system using precisely the same parameters.

Figure 9.

Activation sequence for spatial term and reference object selection in Demonstration 4. Panel (a) shows the objects in the camera input. Panel (b), the green highlighter is defined as the target object (whose position is to be described) by activating the green node and boosting the target field. Panel (c), both the spatial relation nodes and the object-centered field are boosted. The semantically structured activation profiles in the object-centered field are then transmitted through the transformation field to the reference object field. Panel (d), reference field boost leading to the selection of a reference object location. Panel (e), boosts of both the color and spatial term nodes. The boost of the color term nodes leads to the selection of the blue node (box) as the reference object identifier. The boost to the spatial term nodes leads to the selection of the left node (box) as the target object's relation to the blue reference object.

Results and discussion

To establish the target object (green highlighter) location, we first activate the green color term node while simultaneously boosting the target field (see Figure 9b). After the peak forms at the target object location, we turn off the color term input and reduce the target field boost to an intermediate level. Next, we prepare the selection of a reference object by boosting all spatial relation nodes as well as the object-centered field (see Figure 9c). As a result, the weight patterns of the modeled spatial relations begin to simultaneously shape the activation profile of the object-centered field. This semantically structured activation is then transmitted through the transformation field to the reference object field. Consequently, certain regions of the reference field become more activated, particularly those whose spatial relation to the specified target object fits well with one of the spatial terms.

Next, we uniformly boost the reference field to form a peak and thereby force a selection of a reference object (see Figure 9d). This selection depends both on preactivation from the transformation field and on the properties of the visual input: A large and salient object may be selected even if it is located in a less favorable location simply because it produces stronger activation in the color-space field and, as a result, stronger input to the reference field. The target object itself cannot be selected as a referent due to the mutual local inhibition between target and reference fields (see Figure 9c). In the current example, the candidate reference objects are of comparable size. Ultimately, the blue stack of blocks that lies just to the right of the target (green highlighter) gets selected over the red stack of blocks that is both somewhat to the left and somewhat above the target (see Figure 9d). This selection of the blue blocks as the reference tips the activity distribution in the spatial relation nodes in favor of the left node—the node that captures the spatial relation between the target and the selected referent. Note that by this process, the selection of the reference object and the spatial relation are mutually and dynamically dependent: Reference object selection depends on the degree of semantic fit and the semantic fit depends on the selected reference object.

The system can now produce a response by boosting the color and spatial term nodes (see Figure 9e). The boost of the color term nodes leads to the selection of the blue node, because the location of the blue stack is most strongly activated by the back projection from the reference field. Among the spatial term nodes, the left node wins the competition because the left spatial relation node is strongly activated. These two components yield the response “to the left of the blue item,” which describes the green highlighter's location.

Demonstration 5: Simulating Empirical Reference Object and Spatial Relation Selection

Because the generation of spatial descriptions is so central to human spatial communication, it is important to consider how well the model's performance in Demonstration 4 maps onto human performance. Recent research by Carlson and Hill (2008) provides a basis for this evaluation. In their Experiment 2, participants were shown visual scenes containing photographs of two or three real-world items. Participants described the location of the specified target object (which they referred to as the located object) by completing a phrase of the form “The target is ____.” The second item, referred to as the reference object, was more salient (i.e., larger and of a different shape) than the target item. Finally, a portion of the trials also contained a third, distractor object which was of similar shape and size to the target.⁵

Results showed that while greater saliency can increase the likelihood of selection as a referent, this selection process is also influenced by the placement of the nonsalient item. Indeed, in some instances the less salient distractor item was chosen as the referent on a majority of trials. Here, we show that our model can capture the reported reference object selection patterns in all eight conditions tested by Carlson and Hill (2008) in Experiment 2, including the critical six conditions containing two potential reference objects. We then explain how visual saliency and spatial arrangement act together in the selection of the reference object in our neural system.

Materials

To more carefully control stimulus size and, hence, saliency, we presented colored squares of different sizes rather than photographs of real objects as the visual input. The size of the located and distractor objects was 10 × 10 pixels, and the salient referent was 14 × 14 pixels. This proportion of 1:1.96 approximates the mean proportion of target-to-reference object sizes in Carlson and Hill (1:1.74). Throughout the simulations, we used red for the target object, green for the salient reference object, and blue for the nonsalient distractor object.

Items were presented according to the eight arrangements in the experimental study (see Figure 10). For these arrangements, the input images were divided into a 5 × 3 grid of square cells. The reference object was then placed in either the center cell of the bottom row or in the rightmost cell of the bottom row. The target and the distractor objects were placed in different combinations in the corner cells or in the center cell of the top row (see Figure 10). Carlson and Hill (2008) designated the different arrangements by the applicability of the above relation to the located (target) object and the distractor object relative to the referent. They distinguished between three regions: a good region (exactly above the reference object), an acceptable region (diagonally above), and a bad region (to the left or right of the reference object). Conditions were then labeled according to the placement of the located target object (L) in the good (LG) or acceptable (LA) above regions and the placement of the nonsalient distractor object (D) in the good (DG), acceptable (DA), or bad (DB) above regions.

Figure 10.

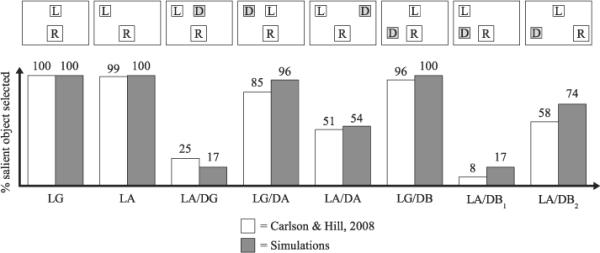
Reference object selection results for Demonstration 5. The bars show the percentage of trials in which the more salient object (R) was chosen over the distractor (D) as the reference object in describing the position of the located target object (L). The arrangement of objects in the scene for each stimulus condition is depicted on top. Object labels in the figure were chosen to maintain consistency with the preferred terminology in Experiment 2 from Carlson and Hill, 2008, Processing the presence, placement, and properties of a distractor in spatial language tasks. Memory & Cognition, 36, 240–255. Conditions were labeled according to the placement of the located target object in the good (LG) or acceptable (LA) above regions and the placement of the nonsalient distractor object in the good (DG), acceptable (DA), or bad (DB) above regions. doi:10.3758/MC.36.2.240.

Method

The generation of a location description proceeded exactly as described in Demonstration 4, with the red square defined as the target object. To produce a probabilistic reference object selection, we added noise to the activities of all fields and nodes throughout each simulation. The strength of the noise was treated as an additional free parameter, which was adjusted to fit the experimental results (although this parameter value was identical for all stimulus conditions). We then ran 100 trials for each stimulus condition and recorded how often the system selected the green salient item and the blue distractor item as the referent.

Results and discussion

In all trials for each of the stimulus conditions, our system produced a valid description of the target object's location. Note that for oblique spatial relations between two objects, there are two possible terms (e.g., above and left) that were considered correct. As can be seen in Figure 10, the rates of selecting the salient object as the referent are clearly dependent on the arrangement of the items in the visual scene for both the empirical data (white bars) and the simulation results (dark). The model captures the empirical results well.

How do these different reference selection rates arise in our model? In the noiseless version of the model, reference object selection is fully determined by the strengths of the visual inputs and the strength of the projections from the spatial relation nodes—the peak in the reference field will always form at that location driven to a higher activity level by the combination of these two inputs. Consequently, for a fixed visual and task input, the same object will always be selected as the referent. With noise, however, the field location receiving weaker inputs can reach higher activity levels during the course of competition. In such cases, the alternative item will be selected as the reference object. The probability for selecting one object over the other reflects the difference in input strength at the two locations. If one location receives significantly more input than the other, it will be selected in the majority of trials. If, on the other hand, the input levels are quite similar, the selection rates for both candidates will approach chance level. The strength of the noise determines how large the absolute difference of activity levels has to be to reach a certain preference for one object. This parameter therefore determines the relative impact of the stochastic component of the model and cannot be derived from the properties of the deterministic elements. Note that the noise level can only drive selection rates globally either toward chance levels or toward a deterministic response, but it does not selectively affect the outcome in any single condition.

Comparing the simulation results with the empirical data (see Figure 10), we find that our model effectively captures the reference object selection preferences of all eight tested conditions (R²= .96, RMSD = 8.3). Because the selection patterns in the two-item LG and LA conditions are straightforward (there is only one possible referent), we concentrate on the pattern of results from the remaining three-item conditions.

In the LA/DG condition, the located target object (L) is situated exactly to the left of the nonsalient distractor (D), while it sits neither perfectly above nor perfectly to the left of the salient object (R). The more salient object is therefore selected in a minority of the empirical (25%) and simulated trials (17%). Our model details the neural dynamics producing this outcome. When the spatial relation nodes are boosted (see Demonstration 4), they ultimately project to the reference field and most strongly activate those areas that lie on the cardinal axes extending through the target location. In the LA/DG case, the distractor (D) location receives more input than the salient object (R) location. This semantically based input is sufficient to overcome the stronger visual input from the larger, more salient object on most of the trials.

In the LG/DA condition, the distractor and the salient object offer an equally good match to a single descriptive term: The located target object (L) is directly right of the distractor (D), and directly above the more salient (R) object. For this reason, both object locations in the reference field receive comparable input from the spatial relation nodes. Reference object selection is, thus, based largely on visual saliency, leading to a preference for the salient object (simulations: 96%; empirical: 85%).

In the LA/DA condition, the arrangement of items is similar to the LA/DG condition; however, the distance between the distractor and the located object is now increased. This is relevant because the semantic weight patterns are distance sensitive, in accordance with the boundary vector cell semantic distributions from O'Keefe (2003). Accordingly, the location of the distractor object receives weaker spatial semantic input than it does in the LA/DG condition. Nonetheless, the semantic input is sufficient to balance out the stronger visual input for the larger, more salient alternative. The nonsalient and the salient objects are selected with approximately equal probability (simulations: 54%; empirical: 51%).

For condition LG/DB, the visual saliency and spatial relation both favor the selection of the salient object, consistent with the empirical (96%) and simulated (100%) preferences. Condition LA/DB₁ is somewhat similar to LA/DG, with the located target object (L) again in a good spatial relation (directly above) to the nonsalient distractor (D) but in an oblique relation to the salient object (R). As before, the better match of a spatial term leads to a strong selection preference for the nonsalient distractor over the salient object (simulations: 17%; empirical: 8%).

Finally, in the LA/DB₂ condition, the located target object (L) lies in an oblique relation to both the distractor (D) and the salient object (R), thus providing for only “acceptable” spatial term relations. Consequently, the locations of both items in the reference field receive the same amount of input from the spatial relation nodes (via the object-centered and transformation fields). Visual saliency therefore dominates and the larger, salient object (R) is selected on the majority of trials (simulations: 74%; empirical: 58%). Interestingly, in both the empirical data and in our simulations, the degree of preference for the salient object is lower here than in the LG/DA condition. In that condition, the target object (L) was located in a direct (i.e., “good”) spatial relation to both the distractor (D) and the salient (R) objects. Thus, both of the item locations received the same support from the spatial relation nodes just as they did in the current LA/DB₂ condition. Given this equivalent spatial relation support within each of these conditions, why does visual salience dominate reference object selection more in the LG/DA condition? Because of the reduced semantic support, specific location input in the LA/DB₂ condition is lower compared to LG/DA. In combination with the output nonlinearity of the dynamic fields, the lower overall activity levels in condition LA/DB₂ allow the noise to exert a greater influence on the referent selection. This brings the selection rates closer to chance. In contrast, the stronger inputs in the LG/DA condition reduce the relative impact of noise and, in effect, magnify the impact of the salience difference.

In summary, our integrated neural system captures the key properties of the experimental results and, moreover, provides the first formal, process-based explanation for the pattern of results. Furthermore, when considered in the context of Demonstrations 1–4, this second fit to empirical data shows impressive generality across different spatial language behaviors. We know of no other theoretical framework in the spatial language domain that has achieved this level of generality, while still retaining specification of precise empirical detail.

General Discussion

The goal of the present work was to enhance our understanding of the neural processes underlying flexible spatial language behaviors, with a focus on linking lower level visual processes with object-centered spatial descriptions. We began by considering Logan and Sadler's (1996) theoretical framework outlining the core functions required for spatial apprehension, noting that no current theory has effectively integrated all functions within a single system. Across five demonstrations, we showed that our dynamic neural system using simple, real-world visual input and a neurally grounded reference frame transformation process provides an integrated account of these functions and their interactions in the service of flexible spatial language behaviors. Our demonstrations show how the goals of rigorous, formalized models of empirical behavior (e.g., Regier & Carlson, 2001) and the neural foundations of reference frame transformations (Deneve, Latham, & Pouget, 2001; Pouget, Deneve, & Duhamel, 2002) can be simultaneously realized within a single unified system.

The spatial term selection task in Demonstration 1 showed that our neural dynamic system can spatially index visual input and map spatial semantic terms to an object-centered reference frame. To substantiate these processes as a model of human spatial language performance, Demonstration 2 simulated empirical results from three spatial term ratings tasks from Regier and Carlson (2001). Our simulations captured the canonical ratings profiles and also revealed a fine-grained sensitivity to changes in both the center-of-mass orientation and the proximal orientation. By explicitly instantiating the neural dynamic processes that underlie ratings responses, we showed how these subtle attentional effects first highlighted by Regier and Carlson can emerge from interactive neural dynamics linked to simple visual inputs.

Demonstration 3 showed a flexible extension to a third task, illustrating how our system can extract target object information (color) at a linguistically cued location. Demonstrations 4 and 5 provided perhaps the strongest tests of our framework, revealing that our system can generate a spatial description given only visual input and the target specification. Critically, probes of this process were consistent with empirical results testing the contribution of salience and object location to reference object and spatial term selection behaviors. To our knowledge, this is the first formalized model of these effects. In sum, our neural dynamic model generated four qualitatively different behaviors and simulated empirical results from two different experimental tasks and 11 different experimental conditions without changes to the architecture or the parameter settings.

We draw attention to several key aspects of the model's performance. First, each of these tasks demanded the satisfaction of all four spatial apprehension functions previously detailed by Logan and Sadler (1996). Our results show that satisfying these functions within a single neural dynamic framework can provide for the generation of different spatial language behaviors across varying visual and linguistic contexts. This lends considerable support to Logan and Sadler's framework. Second, by simulating empirical findings from two different tasks (spatial language ratings and reference object selection), our model reveals how human behaviors in these different tasks may be rooted in the same interactive dynamic processes. Furthermore, because we have a process-based model, we are able to pinpoint the source of sometimes subtle empirical effects, such as attentional weighting and changes in the preference for visually salient reference objects.

Finally, by focusing simultaneously on reference frame transformations and representational integration, we developed a flexible system that brings together low-level visual representations using real visual input with spatial semantics in an object-centered reference frame. Neural dynamic approaches are thus capable of instantiating behavioral flexibility across domains (Cassimatis, Bello, & Langley, 2008) without sacrificing explicit links to empirical results. By providing an explicit link between empirical data and neural mechanisms for processing spatial information, we highlighted how empirical research on spatial language behaviors can contribute to our understanding of the neural basis of spatial cognition. Future probes of the reference frame transformation mechanism in our system may, for instance, provide novel insights into the processing of spatial information in the brain and, more generally, help reveal how cognitive operations emerge from, and are coupled to, perceptual processes.

Comparisons With AVS

The goal and scope of the present model differs markedly from that of the AVS model that was initially proposed to explain performance in ratings tasks. Nevertheless, because of the relative simplicity, small number of parameters, and broad applicability of the AVS model, it is informative to examine the relationship between its algorithmic calculation of ratings and our neural dynamic mechanism.

The basis for computing ratings in AVS is an attentionally weighted sum of vectors pointing from the reference object to the target object. The same information that this vector provides can also be found in the activation profile of the object-centered field that emerges after specifying the target and the reference objects. This field can be interpreted as representing the endpoints of vectors that connect the reference location with the target location. The common starting point of these vectors is the center of the object-centered field (the representation in this field is, by definition, centered on the reference object). In this view, a peak in the left part of the object-centered field, for example, corresponds to a vector from the reference to the target location that is pointing leftward. This property of the object-centered field representation is achieved through the reference frame transformation mechanism. The projection from the object-centered field to the spatial relation nodes, mediated by the semantic weight patterns, then provides a neural dynamic instantiation of the vector-based ratings calculation in AVS.

Because the activity peaks in the target and reference fields extend over a small area and loosely reflect the object dimensions, there is an averaging effect in our model similar to AVS. The peak in the object-centered field, therefore, does not reflect a single vector but a collection of vectors from different points in the reference object to different points in the target object. As discussed in Demonstration 2, the precise position of the reference peak can be influenced by the location of the target peak. This is comparable to the attentional weighting employed by AVS.

Although in many ways we provide a dynamic instantiation of the mechanisms outlined by AVS, AVS also explains ratings effects that we have not yet addressed. For instance, AVS accounts for the empirical grazing line effect in which above ratings drop substantially when the target object falls below the highest point of the reference object. Our model does not represent the extreme points of the reference object in any precise way and doing so would again require a more intricate visual system that goes beyond the scope of our present focus. We note, however, that if a target is below some part of the reference object (and thus below the grazing line), this would activate the below relation node in our model. Inhibitory interactions would then reduce the above node's activity. These interactions also play a significant role in shaping the rating responses in the different conditions tested in Demonstration 2. These considerations notwithstanding, the empirical grazing line effect does warrant further treatment in our model.

Despite these differences, our model is nonetheless highly compatible with the AVS model, showing how the neural population coding of location central to AVS can support behavioral flexibility when extended to the level of neural dynamic processes.

Neural Plausibility

The system we presented is implemented as a single, integrated dynamic neural system fully specifying the processes that lead from real visual input to the selection of spatial descriptions. We contend that this architecture is neurally plausible on two levels. First, the neural dynamics in our model operate according to established principles of neural information processing. In particular, our system recognizes the continuously changing activity profiles of neural populations as the predominant way of representing and processing perceptual information. It also employs directed, weighted projections between these populations that are either excitatory or inhibitory. Furthermore, it makes use of empirically confirmed interaction patterns, namely local excitation and surround inhibition (Amari, 1977; Douglas & Martin, 2004; Erlhagen et al., 1999; Jancke et al., 1999; Pouget, Dayan, & Zemel, 2000; Wilson & Cowan, 1973). Second, the architecture that we present preserves the functional organization of the visuospatial processing pathway. It is composed of several elements with specific functionality which can be flexibly combined to solve different tasks (Damasio, 1989; Fuster, 2003; Tononi, Edelman, & Sporns, 1998; Tononi & Sporns, 2003). We will briefly discuss how each of those elements is related to components of the visual-spatial pathway in the human brain.

The first step of visual processing in our model is the set of color-space fields. This is functionally similar to early visual areas (like V1 and V2). These areas provide a topographically organized map of retinal space (Gardner, Merriam, Movshon, & Heeger, 2008) with intermingled representations of edge orientation, spatial frequency, and color that can be functionally described as a high-dimensional representation of visual input with two spatial and multiple feature dimensions (Swindale, 2000). In our model, we selected color as the sole feature dimension and discretized it into three categories. These differences in arrangement, however, do not influence the basic functional properties of the underlying representations.

The activity patterns in early visual areas of the brain are not fully determined by retinal input but can be modulated in different ways by cognitive processes. Spatial attention can enhance neural responses to stimuli in a specific part of a visual scene and suppress activity for other regions (Somers, Dale, Seiffert, & Tootell, 1999). This attentional effect corresponds directly to the influence of the target and reference field back-projections onto the color-space field, raising the activity level for those spatial regions with a task-relevant object and mildly decreasing activity elsewhere. Likewise, feature attention can increase the response to specific features irrespective of their location in a scene. This effect has first been described for area V4 (Chelazzi, Miller, Duncan, & Desimone, 2001), but an effect on even earlier visual areas has recently been described in an EEG study by Müller, Andersen, Trujillo, Valdès-Sosa, Malinowski, & Hillyard, (2006). They found an increase in the visual evoked potential for stimuli of one color over another, depending on task instructions. This is very similar to the modulation of the color-space fields by input from the color term nodes in our system, which likewise raises the strength of the response for visual stimuli of a certain color.

The color term nodes themselves serve as a placeholder for a much more complex system. In effect, they replace the complete ventral stream of visual processing, or what pathway (Goodale & Milner, 1992; Ungerleider & Mishkin, 1982). Their purpose is to produce a very limited form of object identification given the visual scene. We kept object recognition as simple as possible here to concentrate on spatial processing (see below for possible extensions).

The remaining dynamic fields in our architecture—target, reference, transformation, and object-centered fields— can be equated to different elements of the dorsal stream of visual processing, or where pathway (Ungerleider & Mishkin, 1982). This pathway spans the occipital and parietal lobes and is assumed to be concerned with spatial cognition and sensory-motor coordination. The target and reference fields in our model represent object location in the reference frame of the visual system (i.e., image-based), abstracted from any feature information. Corresponding spatial representations in retinocentric coordinates can be found throughout the dorsal stream (Colby & Goldberg, 1999; Gardner et al., 2008; Patel, He, & Corbetta, 2009).

The transformation field that we used for the mapping between different reference frames is modeled after the properties and conjectured function of gain-modulated neurons in the parietal cortex (Colby & Goldberg, 1999). Our model of this process provides the same level of detail as previous approaches that are explicitly designed as neural models (Deneve, Latham, & Pouget, 2001), but it achieves a higher level of neural realism in some respects (e.g., we use lateral inhibition instead of an algorithmic normalization of field activities). These previous approaches predominantly dealt with the transformation from retinocentric to head- or body-centered representations (for a review, see Andersen, Snyder, Bradley, & Xing, 1997). However, spatial representations in multiple frames of reference have been found in the same area, and evidence for neural populations coding object position in an object-centered reference frame has been described by Chafee, Averback, and Crowe (2007; Crowe, Averback, & Chafee, 2008). It is reasonable to assume that object-centered transformations draw on analogous neural mechanisms.

The spatial relation and spatial term nodes, as well as the color nodes, provide a way of representing discrete linguistic categories in a way easily integrated into our dynamic neural architecture. Such localist word representations have frequently been used in linguistic modeling (e.g., Dell, Schwartz, Martin, Saffran, & Gagnon, 1997; McLeod, Plunkett, & Rolls, 1998). These nodes, of course, are a substantial simplification of the real neural system supporting language, but they do incorporate some basic neural concepts including information integration from multiple sources, restricted connectivity patterns, and the capacity for Hebbian learning (Elman, Bates, Johnson, Karmiloff-Smith, Parisi, & Plunkett, 1996). More importantly, the semantic roots of these nodes in the nonlinguistic processing systems of our network (e.g., color terms linked to color-space fields) reflect an emerging view that semantic processing is tied to neural activity in those sensory-motor brain regions that directly represent the perception of the original stimulus (Barsalou, 2008; Barsalou, Simmons, Barbey, & Wilson, 2003; Damasio, 1989; Rogers & McClelland, 2004). The linguistic representations in our system are, therefore, analogous to cortically distributed functional word webs (Pülvermuller, 2001, 2002).

Limits and Outlook

As with any theoretical model, we made several simplifications when implementing our dynamic neural architecture (for discussion of the role of simplifications in modeling, see McClelland, 2009). Perhaps the most obvious was the restricted number of spatial terms. Our limited vocabulary was a function of the extensive empirical research on projective terms, their known behavioral properties, and the set of spatial terms used to probe the AVS model. Nonetheless, the spatial term network needs to be extended to include different classes of terms. The immense challenge of using neural dynamics to instantiate 3–D visual perception using a 2–D visual image currently precludes some topological terms (e.g., in,into). The descriptor between is also challenging because two peaks in the reference field are required (although dynamic fields can support multiple peaks; see Johnson et al., 2009). Despite such limits, we can still dramatically increase the size of our network through the addition of topological terms “by,” “far,” “near,” “next to,” and “beside,” which are sensitive to metric changes in 2–D perceptual space. Terms related to those tested here (e.g., “over,” “under,” “in front,” “behind”) can also be easily added.

A second obvious limit is that the identification of items in the scene is based exclusively on object color, allowing us neither to differentiate between items of the same color nor to use colorless objects. As noted before, we view the current mechanism as a placeholder, and any more elaborated object recognition system can take its place if it supports two basic operations. First, it must be able to identify an item at a location highlighted by spatial attention, and second, it must be able to find a specified object in a scene and highlight its location in a spatial representation. Faubel and Schöner (2009) have presented a DNF-based object recognition architecture that fulfills both conditions. Starting from a set of simple feature maps over space (comparable to the color-space fields), this system allows the identification and localization of learned objects based on a combination of shape information and color histograms. An extension of our mechanism which provides a more specific object identification may also allow us to incorporate findings of object identity and function influencing the outcome of spatial language tasks (Carlson-Radvansky & Radvansky, 1996; Coventry & Garrod, 2004; Coventry, Prat-Sala, & Richards, 2001).

A further limit is that we do not incorporate working memory or longer term memory into the tasks. This is important for spatial language because people often depend on remembered rather than visible relations. However, dynamic neural field models have been used to quantitatively simulate spatial working memory for both children and adults (Schutte & Spencer, 2009; see also Simmering, Schutte, & Spencer, 2008). Recent modeling and empirical work (Lipinski, Spencer, & Samuelson, 2006, 2009, 2010b; Spencer, Simmering, & Schutte, 2006) also indicates that the spatial language dynamics are tightly coupled to these memory processes. Moreover, recent investigations show that neural dynamic fields can also account for novel, long-term memory effects in spatial recall (Lipinski et al., 2010; Lipinski, Spencer, & Samuelson, 2010a). Thus, while practical constraints limited the scope of the present article, our present framework is not theoretically restricted in this regard.

Conclusion

The neural dynamic processes supporting reference frame transformations and behavioral flexibility are central issues in spatial cognition research. By bringing the insights of theoretical neuro-science to bear in the domain of spatial language, we proposed a novel system that succeeds in a range of tasks using real world visual input. The same model also captured empirical results in precise detail, offering the first formalized account of the complex reference object and spatial term selection preferences established by Carlson and Hill (2008). The success of our framework in these rigorous natural and experimental tests corroborates the plausibility of our system as a model of human spatial language behaviors and demonstrates how cognitive flexibility can be realized in a system grounded in both neural dynamics and behavioral details.