A MULTI-PATCH MALARIA MODEL WITH LOGISTIC GROWTH POPULATIONS

Abstract

In this paper, we propose a multi-patch model to study the effects of population dispersal on the spatial spread of malaria between patches. The basic reproduction number ${\mathcal{R}}_0$ is derived and it is shown that the disease-free equilibrium is locally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$. Bounds on the disease-free equilibrium and ${\mathcal{R}}_0$ are given. A sufficient condition for the existence of an endemic equilibrium when ${\mathcal{R}}_0>1$ is obtained. For the two-patch submodel, the dependence of ${\mathcal{R}}_0$ on the movement of exposed, infectious, and recovered humans between the two patches is investigated. Numerical simulations indicate that travel can help the disease to become endemic in both patches, even though the disease dies out in each isolated patch. However, if travel rates are continuously increased, the disease may die out again in both patches.

1. Introduction

Malaria is a parasitic vector-borne disease caused by the Plasmodium, which is transmitted to people via the bites of infected female mosquitoes of the genus Anopheles. People with malaria often experience fever, chills, and flu-like illness. If not treated promptly or effectively, an infected individual may develop severe complications and die. Vaccines for malaria are under development, with no approved vaccine yet available. About half of the world's population is at risk of malaria. This leads to an estimated 225 million malaria cases and nearly 781, 000 deaths worldwide in 2008, the vast majority are children under five in Africa region (WHO [48]).

Following the pioneering work of Ross [35] and Macdonald [24, 25, 26], mathematical modelling of malaria transmission has been developed rapidly. Among these, we would like to mention Dietz et al. [12], Aron and May [4], Nedelman [30], Koella [22], Gupta et al. [16], Ngwa and Shu [33], Ngwa [32], Chitnis et al. [7, 8], Ruan et al. [36], Lou and Zhao [23], and the references cited therein.

In paper [33] (also Ngwa [32]), Ngwa and Shu introduced a compartmental model described by ordinary differential equations (ODEs) for the spread of malaria involving variable human and mosquito populations, in which the human population is classified as susceptible, exposed, infectious and recovered and the mosquito population is divided into classes containing susceptible, exposed and infectious individuals. They established a threshold below which the disease-free equilibrium is stable and above which the disease can persist. Chitnis et al. [7, 8] extended the model in Ngwa and Shu [33] and Ngwa [32] to generalize the mosquito biting rate, include human immigration and exclude direct infectious-to-susceptible human recovery. They presented a bifurcation analysis in [7], defined a reproductive number and showed the existence and stability of the disease-free and endemic equilibria. To determine the relative importance of model parameters in disease transmission and prevalence, sensitivity indices of the reproductive number and the endemic equilibrium were computed in [8].

Malaria varies greatly in different regions in the vectors that transmit it, in the species causing the disease and in the level of intensity. It can be easily transmitted from one region to other regions due to extensive travel and migration (Martens and Hall [27], Tatem et al. [41]). This leads to new outbreaks in some former malaria-free or lower transmission areas. For instance, even though malaria has been eliminated in the United States since 1950's, about 1,500 malaria cases are diagnosed every year in this country, of which approximately 60% are among US travelers (Newman et al. [31]). Thus it is necessary to distinguish the regions and understand the influence of population dispersal on the propagation of the disease between regions, which may improve malaria control programs.

Multi-patch models have been developed to study the spatial spread of infectious diseases by many researchers over the past three decades. In particular, models of malaria in this direction include Dye and Hasibeder [13], Hasibeder and Dye [17], Torres-Sorando and Rodriguez [44], Rodriguez and Torres-Sorando [34], Smith et al. [38], Auger et al. [5], Cosner et al. [9], Arino et al. [3], etc. For references on general epidemic models in a patchy environment, we refer the reader to two review articles by Wang [46] and Arino [2]. Most of these studies focus on evaluating the basic reproduction number R₀ and establishing the existence and stability of the disease-free and endemic equilibria. One of the goals in considering multi-patch epidemic models is to study how the dispersal of individuals, in particular of the exposed and infectious individuals, contributes to the spread of diseases from regions to regions. Mathematically, one way to investigate this problem is to determine how R₀ depends on model parameters, especially those describing the movement of exposed and infectious individuals. This indeed is a very interesting and challenging problem and there are very few results on this aspect (see Theorem 4.2 in Hsieh et al. [20] and Lemma 3.4 in Allen et al. [1]). The reason is that for a multi-patch model R₀ usually cannot be expressed analytically in terms of model parameters and the monotone dependence of R₀ on model parameters is very complicated.

In this paper, based on the model of Ngwa and Shu [33] (also Ngwa [32] and Chitnis et al. [7, 8]), we propose a multi-patch model to examine how population dispersal affects malaria spread between patches. The paper is organized as follows. In next section, we describe our model in detail. The basic reproduction number ${\mathcal{R}}_0$ is derived and shown to be a threshold in section 3. In section 4, we analyze the dependence of ${\mathcal{R}}_0$ on the model parameters, in particular on the travel rates of exposed, infectious, and recovered humans, for the two-patch submodel using the matrix theory. In section 5, numerical simulations are performed to investigate the effects of human movement on disease dynamics. Section 6 gives a brief discussion of main results and future work.

2. Model formulation

We model the transmission dynamics of malaria between humans and mosquitoes within a patch and the spatial dispersal between n patches. Within a single patch, our model is based on that of Ngwa and Shu [33] (also Ngwa [32] and Chitnis et al. [7, 8]) with an SEIRS structure for humans and an SEI structure for mosquitoes. Hereafter, the subscript i refers to patch i and the superscript h/v refers to humans/mosquitoes. Let $S_i^h\left(t\right)$, $E_i^h\left(t\right)$, $I_i^h\left(t\right)$ and $R_i^h\left(t\right)$ denote, respectively, the number of susceptible, exposed, infectious, and recovered humans in patch i at time t. The total human population in patch i at time t is $N_i^h\left(t\right)=S_i^h\left(t\right)+E_i^h\left(t\right)+I_i^h\left(t\right)+R_i^h\left(t\right)$. Similarly, $S_i^v\left(t\right)$, $E_i^v\left(t\right)$ and $I_i^v\left(t\right)$ denote, respectively, the number of susceptible, exposed, and infectious mosquitoes in patch i at time t. The total mosquito population in patch i at time t is $N_i^v\left(t\right)=S_i^v\left(t\right)+E_i^v\left(t\right)+I_i^v\left(t\right)$. The mosquito population has no recovered class since we assume that the mosquito's infective period ends with its death.

For patch i, all newborns in both populations are assumed to be into the susceptible class (no vertical transmission). Susceptible humans, $S_i^h$, may become exposed when they are bitten by infectious mosquitoes. The exposed humans, $E_i^h$, become infectious as the incubation period ends. Infectious humans, $I_i^h$, either reenter the susceptible class or recover into the immune compartment, $R_i^h$, where they remain for the period of their immunity before returning to the susceptible class. Susceptible mosquitoes, $S_i^v$, can be infected when they bite infectious or recovered humans and once infected they progress through the exposed, $E_i^v$, and infectious, $I_i^v$, classes. Both human and mosquito populations follow a logistic growth and migrate between patches, with humans having additional disease-induced death. The flowchart of malaria transmission for patch i omitting density-dependent death and travel is illustrated in Fig 2.1. Solid arrows denote within-species progression while dotted arrows denote interspecies transmission.

Fig. 2.1.

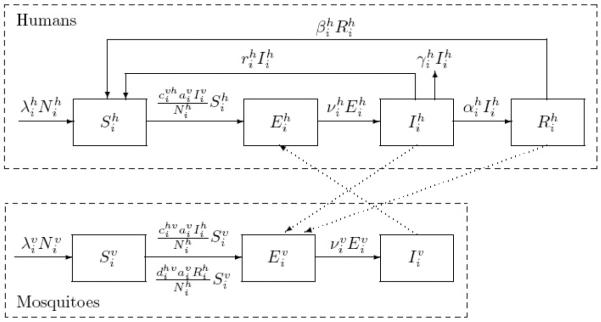
Flow diagram of the mosquito-borne model in patch i.

The interactions between humans and mosquitoes in patch i (with i = 1, 2, …, n) based on the above assumptions are then described by the following differential equations with non-negative initial conditions satisfying $N_i^h\left(0\right)>0$:

$$\begin{array}{cc}\hfill \frac{{\mathrm{dS}}_i^h}{\mathit{dt}}& ={\lambda }_i^h{N}_i^h+{\beta }_i^h{R}_i^h+r_i^h{I}_i^h-\frac{c_i^{\mathit{vh}}{a}_i^v{I}_i^v}{N_i^h}{S}_i^h-f_i^h\left(N_i^h\right)S_i^h+\sum _{j=1}^n{\phi }_{\mathit{ij}}^S{S}_j^h,\hfill \\ \hfill \frac{{\mathrm{dE}}_i^h}{\mathit{dt}}& =\frac{c_i^{\mathit{vh}}{a}_i^v{I}_i^v}{N_i^h}{S}_i^h-({\nu }_i^h+f_i^h(N_i^h\left)\right)E_i^h+\sum _{j=1}^n{\phi }_{\mathit{ij}}^E{E}_j^h,\hfill \\ \hfill \frac{{\mathrm{dI}}_i^h}{\mathit{dt}}& ={\nu }_i^h{E}_i^h-(r_i^h+{\alpha }_i^h+{\gamma }_i^h+f_i^h(N_i^h\left)\right)I_i^h\sum _{j=1}^n{\phi }_{\mathit{ij}}^I{I}_j^h,\hfill \\ \hfill \frac{{\mathrm{dR}}_i^h}{\mathit{dt}}& ={\alpha }_i^h{I}_i^h-({\beta }_i^h+f_i^h(N_i^h\left)\right)R_i^h+\sum _{j=1}^n{\phi }_{\mathit{ij}}^R{R}_j^h,\hfill \\ \hfill \frac{{\mathrm{dS}}_i^v}{\mathit{dt}}& ={\lambda }_i^v{N}_i^v-\frac{c_i^{\mathit{hv}}{a}_i^v{I}_i^h}{N_i^h}{S}_i^v-\frac{d_i^{\mathit{hv}}{a}_i^v{R}_i^h}{N_i^h}{S}_i^v-f_i^v\left(N_i^v\right)S_i^v+\sum _{j=1}^n{\psi }_{\mathit{ij}}^S{S}_j^v,\hfill \\ \hfill \frac{{\mathrm{dE}}_i^v}{\mathit{dt}}& =\frac{c_i^{\mathit{hv}}{a}_i^v{I}_i^h}{N_i^h}{S}_i^v+\frac{d_i^{\mathit{hv}}{a}_i^v{R}_i^h}{N_i^h}{S}_i^v-({\nu }_i^v+f_i^v(N_i^v\left)\right)E_i^v+\sum _{j=1}^n{\psi }_{\mathit{ij}}^E{E}_j^v,\hfill \\ \hfill \frac{{\mathrm{dI}}_i^v}{\mathit{dt}}& ={\nu }_i^v{E}_i^v-f_i^v\left(N_i^v\right)I_i^v+\sum _{j=1}^n{\psi }_{\mathit{ij}}^I{I}_j^v,\hfill \end{array}$$ (2.1)

where

• $f_i^h\left(N_i^h\right)={\mu }_i^h+{\rho }_i^h{N}_i^h$ is the density-dependent death rate for humans;

• $f_i^v\left(N_i^v\right)={\mu }_i^v+{\rho }_i^v{N}_i^v$ is the density-dependent death rate for mosquitoes;

• ${\lambda }_i^h$ is the birth rate of humans;

• ${\lambda }_i^v$ is the birth rate of mosquitoes;

• $a_i^v$ is the mosquito biting rate;

• $c_i^{\mathit{vh}}$ is the probability that a bite by an infectious mosquito on a susceptible human will transfer the infection to the human;

• $c_i^{\mathit{hv}}$ is the probability that a bite by a susceptible mosquito on an infectious human will transfer the infection to the mosquito;

• $d_i^{\mathit{vh}}$ is the probability that a bite by a susceptible mosquito on a recovered human will transfer the infection to the mosquito;

• ${\nu }_i^{\mathit{h}}$ is the progression rate that exposed humans become infectious;

• ${\nu }_i^v$ is the progression rate that exposed mosquitoes become infectious;

• $r_i^h$ is the recovery rate that infectious humans become susceptible;

• ${\alpha }_i^h$ is the recovery rate that infectious humans become recovered;

• ${\gamma }_i^h$ is the disease-induced death rate for humans;

• ${\beta }_i^h$ is the rate of loss of immunity for humans;

• ${\phi }_{\mathit{ij}}^K\ge 0$ for K = S, E, I, R is the immigration rate from patch j to patch i for i ≠ j of susceptible, exposed, infectious, and recovered humans, respectively;

• ${\psi }_{\mathit{ij}}^L\ge 0$ for L = S, E, I is the immigration rate from patch j to patch i for i ≠ = j of susceptible, exposed, and infectious mosquitoes, respectively;

• $-{\phi }_{\mathit{ii}}^K\ge 0$ for K = S, E, I, R is the emigration rate of susceptible, exposed, infectious, and recovered humans in patch i, respectively;

• $-{\psi }_{\mathit{ii}}^L\ge 0$ for L = S, E, I, is the emigration rate of susceptible, exposed, and infectious mosquitoes in patch i, respectively.

For simplicity, death rates and birth rates of the individuals during travel are ignored. Thus, we have

$${\phi }_{\mathit{ii}}^K=-\sum _{\underset{j\ne i}{\overset{j=1}{}}}^n{\phi }_{\mathit{ji}}^K,K=S,E,I,R,\text{and}{\psi }_{\mathit{ii}}^L=-\sum _{\underset{j\ne i}{\overset{j=1}{}}}^n{\psi }_{\mathit{ji}}^L,L=S,E,I,1\le i\le n.$$

Unless otherwise indicated, the travel rate matrices ${\left({\phi }_{\mathit{ij}}^K\right)}_{n\times n}$ for K = S, E, I, R and ${\left({\psi }_{\mathit{ij}}^L\right)}_{n\times n}$ for L = S, E, I are assumed to be irreducible. Here the movement of humans and mosquitoes between patches is governed by the Eulerian approach (Cosner et al. [9]), that is, humans and mosquitoes change their residences when they move from one patch to another patch. It is worth noting that they may have different spatial scales because humans can travel much longer distances than mosquitoes.

In the absence of disease and dispersal, both human and mosquito populations in each patch are modeled by the logistic growth. For the persistence of the dispersal system, we assume that

$$s\left({\left(\right({\lambda }_i^h-{\mu }_i^h){\delta }_{\mathit{ij}}+{\phi }_{\mathit{ij}}^S)}_{n\times n}\right)>0\text{and}s\left({\left(\right({\lambda }_i^v-{\mu }_i^v){\delta }_{\mathit{ij}}+{\psi }_{\mathit{ij}}^S)}_{n\times n}\right)>0,$$

where s denotes the spectral bound of a matrix which is the largest real part of any eigenvalue of the matrix and δ_ij denotes the Kronecker delta (i.e. 1 when i = j and 0 otherwise), or else they will die out in all patches. This implies that ${\lambda }_i^h>{\mu }_i^h$ and ${\lambda }_j^v>{\mu }_j^v$ for some i and j.

Furthermore, it is assumed that all parameters in the model are strictly positive with the exception of the travel rates.

Let $N^h\left(t\right)={\sum }_{i=1}^n{N}_i^h\left(t\right)$ and $N^v\left(t\right)={\sum }_{i=1}^n{N}_i^v\left(t\right)$. The following theorem demonstrates that model (2.1) is mathematically well-posed and epidemiologically reasonable.

Theorem 2.1. Consider model (2.1) with non-negative initial conditions satisfying $N_i^h\left(0\right)>0$ for i = 1, … , n. Then the system has a unique solution and all disease state variables remain non-negative for all time t ≥ 0. Moreover, both the total human population N^h(t) and the total mosquito population N^ν(t) are bounded.

Proof. The vector field defined by (2.1) is continuously differentiable, so the initial value problem has a unique solution which exists for all t ≥ 0. The non-negative property of state variables can be easily verified.

Denote ${\chi }^v=\underset{1\le i\le n}{\max }({\lambda }_i^v-{\mu }_i^v)>0$ and ${\rho }^v=\underset{1\le i\le n}{\min }{\rho }_i^v$. Then

$$\begin{array}{cc}\hfill \frac{{\mathit{dN}}^v}{\mathit{dt}}& =\sum _{i=1}^n({\lambda }_i^v{N}_i^v-f_i^v(N_i^v\left)N_i^v\right)=\sum _{i=1}^n\left(\right({\lambda }_i^v-{\mu }_i^v)N_i^v-{\rho }_i^v{\left(N_i^v\right)}^2)\hfill \\ \hfill & \le {\chi }^v\sum _{i=1}^n{N}_i^v-{\rho }^v\sum _{i=1}^n{\left(N_i^v\right)}^2\le {\chi }^v\sum _{i=1}^n{N}_i^v-{\rho }^v{\left(\sum _{i=1}^n{N}_i^v\right)}^2∕n\hfill \\ \hfill & ={\chi }^v{N}^v-{\rho }^v{\left(N^v\right)}^2∕n=({\chi }^v-{\rho }^v{N}^v∕n)N^v.\hfill \end{array}$$

Hence, by a comparison theorem, N^ν(t) is bounded from above by max{nχ^ν/(ρ^ν, N^ν(0)}. Similarly, we can find an upper bound for N^h(t). The proof is complete.

3. Threshold dynamics

We first show the existence of a disease-free equilibrium (DFE) for (2.1), then calculate the basic reproduction number ${\mathcal{R}}_0$ and give an estimate of it. Uniform persistence of the disease and the existence of an endemic equilibrium are discussed at the end of this section.

3.1. Disease-free equilibrium

A disease-free equilibrium is a steady state solution of system (2.1) where there is no disease, namely, $S_i^h=S_i^{h\ast }>0$, $S_i^v=S_i^{v\ast }>0$, and all other variables $E_i^h$, $E_i^v$, $I_i^h$, $I_i^v$, $R_i^h=0$ for i = 1, 2, … , n. The partially immune human, $R_i^h$, is regarded as infected because individuals in this status are still infective to susceptible mosquitoes. Mathematically, if $E_i^h=E_i^v=I_i^h=I_i^v=0$ for all i at a steady state, then by summing the fourth equation of (2.1) up from 1 to n, we have

$$-\sum _{i=1}^n({\beta }_i^h+f_i^h(N_i^h\left)\right)R_i^h+\sum _{i=1}^n\sum _{j=1}^n{\phi }_{\mathit{ij}}^R{R}_j^j=-\sum _{i=1}^n({\beta }_i^h+f_i^h(N_i^h\left)\right)R_i^h+\sum _{i=1}^n\sum _{j=1}^n{\phi }_{\mathit{ji}}^R{R}_i^h=0.$$

Hence, $-{\sum }_{i=1}^n({\beta }_i^h+f_i^h(N_i^h\left)\right)R_i^h=0$. This implies $R_i^h=0$ for i = 1, 2, … , n.

Let $S^{h\ast }=(S_1^{h\ast },S_2^{h\ast },\dots ,S_n^{h\ast })$ and $S^{v\ast }=(S_1^{v\ast },S_2^{v\ast },\dots ,S_n^{v\ast })$. Thus there is a DFE for (2.1) if and only if S^h* and S^ν* are positive equilibria to the subsystems

$$\frac{{\mathrm{dS}}_i^h}{\mathit{dt}}={\lambda }_i^h{S}_i^h-f_i^h\left(S_i^h\right)S_i^h+\sum _{j=1}^n{\phi }_{\mathit{ij}}^S{S}_j^h,1\le i\le n$$ (3.1)

and

$$\frac{{\mathit{dS}}_i^v}{\mathit{dt}}={\lambda }_i^v{S}_i^v-f_i^v\left(S_i^v\right)S_i^v+\sum _{j=1}^n{\psi }_{\mathit{ij}}^S{S}_j^v,1\le i\le n,$$ (3.2)

respectively. They are guaranteed by the following lemma.

Lemma 3.1. Let $\text{Int}{\mathbb{R}}_{+}^{\mathrm{n}}$ be the interior of ${\mathbb{R}}_{+}^n$. For system (3.1), there is a unique nonzero equilibrium $S^{h\ast }\in \text{Int}{\mathbb{R}}_{+}^{\mathrm{n}}$ which is globally asymptotically stable with respect to ${\mathbb{R}}_{+}^n\backslash \left\{0\right\}$. Moreover, if ${\lambda }_i^h>{\mu }_i^h$ for 1 ≤ i ≤ n, we have

$$P^h\equiv \underset{1\le i\le n}{\overset{\min }{}}\frac{K_i^h}{L_i^h}\cdot L^h\le S^{h\ast }\le Q^h\equiv \underset{1\le i\le n}{\overset{\max }{}}\frac{K_i^h}{L_i^h}\cdot L^h,$$

where $K_i^h=\frac{{\lambda }_i^h-{\mu }_i^h}{{\rho }_i^h}$ for 1 ≤ i ≤ n, and $L^h=(L_1^h,\dots ,L_{n-1}^h,L_n^h)$ is the unique solution to

$$\sum _{j=1}^n{\phi }_{\mathit{ij}}^S{S}_j^h=0,i=1,\cdots ,n,\mathit{and}{S}_n^h=1$$

with $L_i^h>0$ for 1 ≤ i ≤ n − 1 and $L_n^h=1$. Similar result holds for system (3.2).

Proof. It is easy to see that system (3.1) is cooperative and irreducible. The existence, uniqueness and global asymptotic stability of S^h* can be proved by applying Theorem 6.1 in Hirsch [18] or Corollary 3.2 in Zhao and Jing [50].

Let $L^h=(L_1^h,\dots ,L_{n-1}^h,L_n^h)$ be the right eigenvector of the irreducible matrix ${\left({\phi }_{\mathit{ij}}^S\right)}_{n\times n}$ corresponding to the principal eigenvalue 0 normalized so that its last entry equals 1. The existence, uniqueness and positivity of L^h is proved in Lemma 1 of Cosner et al. [9] or Lemma 2.1 of Guo et al. [15]. We denote by f^h the vector field defined by (3.1) and let ${\varphi }_t^h$ denote the corresponding flow. Then the ith component of f^h evaluated at mL^h satisfies

$$\begin{array}{c}\hfill {\lambda }_i^h\left({\mathit{mL}}_i^h\right)-f_i^h\left({\mathit{mL}}_i^h\right)\cdot {\mathit{mL}}_i^h+\sum _{j=1}^n{\phi }_{\mathit{ij}}^S{\mathit{mL}}_j^h={\lambda }_i^h\left({\mathit{mL}}_i^h\right)-f_i^h\left({\mathrm{mL}}_i^h\right)\cdot {\mathit{mL}}_i^h\hfill \\ \hfill =m\left(\right({\lambda }_i^h-{\mu }_i^h)-{\rho }_i^h{\mathit{mL}}_i^h)L_i^h=m{\rho }_i^h{L}_i^h(\frac{{\lambda }_i^h-{\mu }_i^h}{{\rho }_i^h{L}_i^h}-m)L_i^h=m{\rho }_i^h{L}_i^h(\frac{K_i^h}{L_i^h}-m)L_i^h\hfill \end{array}$$

for m > 0 and i = 1, … , n. Thus f^h(mL^h) ≥ 0 for $m\le \underset{1\le i\le n}{\min }\frac{K_i^h}{L_i^h}$ and f^h(mL^h) ≤ 0 for $m\ge \underset{1\le i\le n}{\max }\frac{K_i^h}{L_i^h}$. In particular, f^h(P^h) ≥ 0 and f^h(Q^h) ≤ 0. It follows from the theory of monotone dynamical systems (Smith [39]) that ${\varphi }_t^h\left(P^h\right)$ is non-decreasing and ${\varphi }_t^h\left(Q^h\right)$ is non-increasing for t ≥ 0. Since both ${\varphi }_t^h\left(P^h\right)$ and ${\varphi }_t^h\left(Q^h\right)$ converge to S^h*, we have P^h ≤ S^h* ≤ Q^h.

3.2. The basic reproduction number

To derive the basic reproduction number ${\mathcal{R}}_0$ for (2.1), we order the infected variables first by disease state, then by patch, i.e.,

$$E_1^h,E_2^h,\dots ,E_n^h,E_1^v,E_2^v,\dots ,E_n^v,I_1^h,I_2^h,\dots ,I_n^h,I_1^v,I_2^v,\dots ,I_n^v,R_1^h,R_2^h,\dots ,R_n^h$$

and follow the recipe from van den Driessche and Watmough [45] to obtain

$$F=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill A_{64}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill A_{73}\hfill & \hfill 0\hfill & \hfill A_{75}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\text{and}V=\left[\begin{array}{ccccc}\hfill A_{11}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill A_{22}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill -A_{31}\hfill & \hfill 0\hfill & \hfill A_{33}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill -A_{42}\hfill & \hfill 0\hfill & \hfill A_{44}\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -A_{53}\hfill & \hfill 0\hfill & \hfill A_{55}\hfill \end{array}\right],$$

where

• $$A_{11}={\left({\delta }_{\mathit{ij}}\right({\nu }_i^h+f_i^h\left(S_i^{h\ast }\right))-{\phi }_{\mathit{ij}}^E)}_{n\times n}={\left({\delta }_{\mathit{ij}}\right({\nu }_i^h+{\mu }_i^h+{\rho }_i^h{S}_i^{h\ast })-{\phi }_{\mathit{ij}}^E)}_{n\times n},$$
• $$A_{22}={\left({\delta }_{\mathit{ij}}\right({\nu }_i^v+f_i^v\left(S_i^{v\ast }\right))-{\phi }_{\mathit{ij}}^E)}_{n\times n}={\left({\delta }_{\mathit{ij}}\right({\nu }_i^v+{\mu }_i^v+{\rho }_i^v{S}_i^{v\ast })-{\phi }_{\mathit{ij}}^E)}_{n\times n},$$
• $$A_{31}={\left({\delta }_{\mathit{ij}}{\nu }_i^h\right)}_{n\times n}=\text{diag}\{{\nu }_1^h,{\nu }_2^h,\dots ,{\nu }_n^h\},$$
• $$\begin{array}{cc}\hfill A_{33}& ={\left({\delta }_{ij}\right(r_i^h+{\alpha }_i^h+{\gamma }_i^h+f_i^h\left(S_i^{h\ast }\right))-{\phi }_{\mathit{ij}}^I)}_{n\times n}\hfill \\ \hfill & ={\left({\delta }_{\mathit{ij}}\right(r_i^h+{\alpha }_i^h+{\gamma }_i^h+{\mu }_i^h+{\rho }_i^h{S}_i^{h\ast })-{\phi }_{\mathit{ij}}^I)}_{n\times n},\hfill \end{array}$$
• $$A_{42}={\left({\delta }_{\mathit{ij}}{\nu }_i^v\right)}_{n\times n}=\text{diag}\{{\nu }_1^v,{\nu }_2^v,\dots ,{\nu }_n^v\},$$
• $$A_{44}={\left({\delta }_{\mathit{ij}}{f}_i^v\right(S_i^{v\ast })-{\psi }_{\mathit{ij}}^I)}_{n\times n}={\left({\delta }_{\mathit{ij}}\right({\mu }_i^v+{\rho }_i^v{S}_i^{v\ast })-{\phi }_{\mathit{ij}}^I)}_{n\times n},$$
• $$A_{53}={\left({\delta }_{\mathit{ij}}{\alpha }_i^h\right)}_{n\times n}=\text{diag}\{{\alpha }_1^h,{\alpha }_2^h,\dots ,{\alpha }_n^h\},$$
• $$A_{55}={\left({\delta }_{\mathit{ij}}\right({\beta }_i^h+f_i^h\left(S_i^{h\ast }\right))-{\phi }_{\mathit{ij}}^R)}_{n\times n}={\left({\delta }_{\mathit{ij}}\right({\beta }_i^h+{\mu }_i^h+{\rho }_i^h{S}_i^{h\ast })-{\phi }_{\mathit{ij}}^R)}_{n\times n},$$
• $$A_{64}={\left({\delta }_{\mathit{ij}}{c}_i^{\mathit{vj}}{a}_i^v\right)}_{n\times n}=\text{diag}\{c_1^{\mathit{vh}}{a}_1^v,c_2^{\mathit{vh}}{a}_2^v,\dots ,c_n^{\mathit{vh}}{a}_n^v\},$$
• $$A_{73}={({\delta }_{\mathit{ij}}{c}_i^{\mathit{hv}}{a}_i^v{S}_i^{v\ast }∕S_i^{h\ast })}_{n\times n}$$
• $$A_{75}={({\delta }_{\mathit{ij}}{d}_i^{\mathit{hv}}{a}_i^v{S}_i^{v\ast }∕S_i^{h\ast })}_{n\times n}.$$

The terms A₆₄, A₇₃ and A₇₅ are named after the partial derivatives of the vector fields of susceptible humans to infectious mosquitoes, susceptible mosquitoes to infectious humans, and susceptible mosquitoes to recovered humans, respectively.

Since A_ii for i = 1, … , 5, is a strictly diagonally dominant matrix, by the Gershgorin circle theorem, the real parts of its eigenvalues are positive and therefore $A_{\mathit{ii}}^{-1}$ exists. So the inverse of V exists and equals

$$V^{-1}=\left[\begin{array}{ccccc}\hfill A_{11}^{-1}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill A_{22}^{-1}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill A_{33}^{-1}{A}_{31}{A}_{11}^{-1}\hfill & \hfill 0\hfill & \hfill A_{33}^{-1}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill A_{44}^{-1}{A}_{42}{A}_{22}^{-1}\hfill & \hfill 0\hfill & \hfill A_{44}^{-1}\hfill & \hfill \hfill \\ \hfill A_{55}^{-1}{A}_{53}{A}_{33}^{-1}{A}_{31}{A}_{11}^{-1}\hfill & \hfill 0\hfill & \hfill A_{55}^{-1}{A}_{53}{A}_{33}^{-1}\hfill & \hfill 0\hfill & \hfill A_{55}^{-1}\hfill \end{array}\right].$$

Thus, the next generation matrix (see Diekmann et al. [11]) is

$${\mathit{FV}}^{-1}=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill M^{\mathit{vh}}\hfill & \hfill 0\hfill & \hfill A_{64}{A}_{44}^{-1}\hfill & \hfill 0\hfill \\ \hfill M^{\mathit{hv}}\hfill & \hfill 0\hfill & \hfill (A_{73}+A_{75}{A}_{55}^{-1}{A}_{53})A_{33}^{-1}\hfill & \hfill 0\hfill & \hfill A_{75}{A}_{55}^{-1}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],$$

where $M^{\mathit{vh}}=A_{64}{A}_{44}^{-1}{A}_{42}{A}_{22}^{-1}$ and $M^{\mathit{hv}}=(A_{73}+A_{75}{A}_{55}^{-1}{A}_{53})A_{33}^{-1}{A}_{31}{A}_{11}^{-1}$. Note that M^ν and M^hν account for new human infections due to each infectious mosquito and new mosquito infections due to each infectious or recovered human, respectively.

By calculating (FV⁻¹)², we find the basic reproduction number

$${\mathcal{R}}_0=\sqrt{\rho \left(M\right)},$$

where ρ denotes the spectral radius and M is the product of M^νh and M^hν, i.e.,

$$\begin{array}{cc}\hfill M& =M^{\mathit{vh}}{M}^{\mathit{hv}}=A_{64}{A}_{44}^{-1}{A}_{42}{A}_{22}^{-1}(A_{73}+A_{75}{A}_{55}^{-1}{A}_{53})A_{33}^{-1}{A}_{31}{A}_{11}^{-1}\hfill \\ \hfill & =A_{64}{A}_{44}^{-1}{A}_{42}{A}_{22}^{-1}{A}_{73}{A}_{33}^{-1}{A}_{31}{A}_{11}^{-1}+A_{64}{A}_{44}^{-1}{A}_{42}{A}_{22}^{-1}{A}_{75}{A}_{55}^{-1}{A}_{53}{A}_{33}^{-1}{A}_{31}{A}_{11}^{-1}.\hfill \end{array}$$

The first term in M represents infections related to infectious humans, while the second one describes infections related to recovered humans who survive the infectious class and acquire partial immunity.

Theorem 3.2. The disease-free equilibrium of (2.1) is locally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$.

Proof. To prove the stability of DFE, we need to check the hypotheses (A1)–(A5) in van den Driessche and Watmough [45]. (A1)–(A4) are easily verified while (A5) is satisfied if all eigenvalues of the 7n × 7n matrix

$$J=\left[\begin{array}{cc}\hfill -V\hfill & \hfill 0\hfill \\ \hfill J_3\hfill & \hfill J_4\hfill \end{array}\right]$$

have negative real parts. Here J₃ is a 2n × 5n matrix and J₄ = diag{Df^h(S^h*), Df^ν(S^ν*)} where f^ν denotes the vector field defined by (3.2). By Lemma 3.1, s(J₄) < 0. So is s(J).

Remark 3.3. The basic reproduction number for the ith patch in isolation (i.e., there is no travel between patch i and other patches) is given by

$${\mathcal{R}}_0^{\left(i\right)}=\sqrt{\frac{c_i^{\mathit{vh}}{\left(a_i^v\right)}^2{\nu }_i^v\left(c_i^{\mathit{hv}}\right({\beta }_i^h+{\lambda }_i^h)+d_i^{\mathit{hv}}{\alpha }_i^h){\nu }_i^h({\lambda }_i^v-{\mu }_i^v){\rho }_i^h}{{\lambda }_i^v({\nu }_i^v+{\lambda }_i^v)(r_i^h+{\alpha }_i^h+{\gamma }_i^h+{\lambda }_i^h)({\beta }_i^h+{\lambda }_i^h)({\nu }_i^h+{\lambda }_i^h)({\lambda }_i^h-{\mu }_i^h){\rho }_i^v}}.$$ (3.3)

This is slightly different from Ngwa and Shu's [33] which is ${\left({\mathcal{R}}_0^{\left(i\right)}\right)}^2$.

It is easy to see that in calculating ${\mathcal{R}}_0$, the matrix M is a positive matrix (all entries are positive) and hence ρ(M) is an eigenvalue of M and it is simple. In fact, it follows from Corollary 3.2 in Smith [39] that $A_{\mathit{ii}}^{-1}$, i = 1, … , 5, is a positive matrix. Moreover, as a consequence of Theorem 2.5.4 in Horn and Johnson [19], we know the determinants of both $A_{\mathit{ii}}^{-1}$ for i = 1, … , 5 and $A_{73}+A_{75}{A}_{55}^{-1}{A}_{53}$ are positive. So is M. In particular, M has two distinct positive eigenvalues when n = 2. This fact will be used later.

Similar to Theorem 2.3 in Salmani and van den Driessche [37] and Theorem 3.2 in Hsieh et al. [20], we have the following result which gives bounds on the basic reproduction number.

Theorem 3.4. $\underset{1\le i\le n}{\max }{\left({\tilde{\mathcal{R}}}_0^{\left(i\right)}\right)}^2\le {\mathcal{R}}_0^2\le \underset{1\le i\le n}{\max }{\left({\widehat{\mathcal{R}}}_{01}^{\left(i\right)}\right)}^2+\underset{1\le i\le n}{\max }{\left({\widehat{\mathcal{R}}}_{02}^{\left(i\right)}\right)}^2$, where

$$\begin{array}{cc}\hfill {\left({\tilde{\mathcal{R}}}_0^{\left(i\right)}\right)}^2& =c_i^{\mathit{vh}}{a}_i^v{({\mu }_i^v+{\rho }_i^v{S}_i^{v\ast }-{\psi }_{\mathit{ii}}^I)}^{-1}{\nu }_i^v{({\nu }_i^v+{\mu }_i^v+{\rho }_i^v{S}_i^{v\ast }-{\psi }_{\mathit{ii}}^E)}^{-1}\hfill \\ \hfill & \cdot (\frac{c_i^{\mathit{hv}}{a}_i^v{S}_i^{v\ast }}{S_i^{h\ast }}+\frac{d_i^{\mathit{hv}}{a}_i^v{S}_i^{v\ast }}{S_i^{h\ast }}{({\beta }_i^h+{\mu }_i^h+{\rho }_i^h{S}_i^{h\ast }-{\phi }_{\mathit{ii}}^R)}^1{\alpha }_i^h)\hfill \\ \hfill & \cdot {(r_i^h+{\alpha }_i^h+{\gamma }_i^h+{\mu }_i^h+{\rho }_i^h{S}_i^{h\ast }-{\phi }_{\mathit{ii}}^I)}^{-1}{\nu }_i^h{({\nu }_i^h+{\mu }_i^h+{\rho }_i^h{S}_i^{h\ast }-{\phi }_{\mathit{ii}}^E)}^{-1},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\left({\widehat{\mathcal{R}}}_{01}^{\left(i\right)}\right)}^2& =c_i^{\mathit{vh}}{a}_i^v{({\mu }_i^v+{\rho }_i^v{S}_i^{v\ast })}^{-1}{\nu }_i^v{({\nu }_i^v+{\mu }_i^v+{\rho }_i^v{S}_i^{v\ast })}^{-1}\frac{c_i^{\mathit{hv}}{a}_i^v{S}_i^{v\ast }}{S_i^{h\ast }}\hfill \\ \hfill & \cdot {(r_i^h+{\alpha }_i^h+{\gamma }_i^h+{\mu }_i^h+{\rho }_i^h{S}_i^{h\ast })}^{-1}{\nu }_i^h{({\nu }_i^h+{\mu }_i^h+{\rho }_i^h{S}_i^{h\ast })}^{-1},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\left({\widehat{\mathcal{R}}}_{02}^{\left(i\right)}\right)}^2& =c_i^{\mathit{vh}}{a}_i^v{({\mu }_i^v+{\rho }_i^v{S}_i^{v\ast })}^{-1}{\nu }_i^v{({\nu }_i^v+{\mu }_i^v+{\rho }_i^v{S}_i^{v\ast })}^{-1}\frac{d_i^{\mathit{hv}}{a}_i^v{S}_i^{v\ast }}{S_i^{h\ast }}{({\beta }_i^h+{\mu }_i^h+{\rho }_i^h{S}_i^{h\ast })}^{-1}\hfill \\ \hfill & \cdot {\alpha }_i^h{(r_i^h+{\alpha }_i^h+{\gamma }_i^h+{\mu }_i^h+{\rho }_i^h{S}_i^{h\ast })}^{-1}{\nu }_i^h{({\nu }_i^h+{\mu }_i^h+{\rho }_i^h{S}_i^{h\ast })}^{-1}.\hfill \end{array}$$

Proof. The lower bound can be proved by applying Fischer's inequality (see Theorem 2.5.4(e), Horn and Johnson [19]) to estimate the diagonal entries of matrix $A_{\mathit{ii}}^{-1}$, i = 1, … , 5. In fact, for example, let A₁₁ = (a_ij)_n×n and $A_{11}^{-1}={\left({\alpha }_{\mathit{ij}}\right)}_{n\times n}$, then 1/a_ii ≤ α_ii for i = 1, … , n and therefore

$$0\le \text{diag}\{1∕a_{11},\dots ,1∕a_{\mathit{nn}}\}\le \text{diag}\{{\alpha }_{11},\dots ,{\alpha }_{\mathit{nn}}\}\le A_{11}^{-1}.$$

To establish the upper bound of ${\mathcal{R}}_0$, observe that, for example,

$$\overrightarrow{1}\left(A_{44}{B}_{44}^{-1}\right)=\overrightarrow{1}\Rightarrow \overrightarrow{1}\left(B_{44}{A}_{44}^{-1}\right)=\overrightarrow{1},$$

where $\overrightarrow{1}={(1,1,\dots ,1)}_{1\times n}$ and $B_{44}=A_{44}-{\left({\psi }_{\mathit{ij}}^I\right)}_{n\times n}=\text{diag}\left\{f_1^v\right(S_1^{v\ast })\dots ,f_n^v(S_n^{v\ast }\left)\right\}$. This implies that the spectral radius of $B_{44}{A}_{44}^{-1}$ is 1 and hence

$$\rho \left(A_{44}^{-1}\right)=\rho \left(B_{44}^{-1}{B}_{44}{A}_{44}^{-1}\right)\le \rho \left(B_{44}^{-1}\right)\rho \left(B_{44}{A}_{44}^{-1}\right)=\rho \left(B_{44}^{-1}\right).$$

Finally, the proof is complete with the properties ρ(M₁M₂) = ρ(M₂M₁) and ρ(M₁ + M₂) ≤ ρ(M₁) + ρ(M₂) for any square matrices M₁, M₂ with the same order.

Remark 3.5. The trick in finding an upper bound for the basic reproduction number seems very useful for general epidemic patch models. With such a trick, one can prove the upper bound in Theorem 2.3 of Salmani and van den Driessche [37] without any additional restriction on the parameters which is a nice improvement. Also, the trick can be used to prove the upper bound in Theorem 3.2 of Hsieh et al. [20] without assuming that d_i = d for i = 1, 2, … , n.

Remark 3.6. When ${\lambda }_i^h>{\mu }_i^h$ and ${\lambda }_i^v>{\mu }_i^v$ for 1 ≤ i ≤ n, a combination of Lemma 3.1 and Theorem 3.4 yields an estimation of ${\mathcal{R}}_0$ which only depends on model parameters. However, this result might have little use, because we omitted some terms in the process of estimation.

3.3. Uniform persistence and the endemic equilibrium

Under certain conditions, we can use the techniques of persistence theory (Freedman et al. [14], Thieme [43], Cantrell and Cosner [6], Smith and Thieme [40]) to show the uniform persistence of the disease and the existence of at least one endemic equilibrium when ${\mathcal{R}}_0>1$. The proof is similar to Theorem 2.3 in Wang and Zhao [47] and Theorem 3.2 in Lou and Zhao [23]. For convenience, we denote the vector $\left(S_1^h\right(t),\dots ,S_n^h(t\left)\right)$ by S^h(t) for t ≥ 0. E^h(t), I^h(t), R^h(t), S^ν(t), E^ν(t) and I^ν(t) can be introduced similarly.

Theorem 3.7. Let ε₁₁ denote the disease-free equilibrium of (2.1), W^s(ε₁₁) be the stable manifold of ε₁₁, and X₀ be ${\mathbb{R}}_{+}^n\times \mathrm{Int}{\mathbb{R}}_{+}^{3n}\times {\mathbb{R}}_{+}^n\times \mathrm{Int}{\mathbb{R}}_{+}^{2n}$. Suppose that ${\mathcal{R}}_0>1$, then we have W^s(ε₁₁) ∩ X₀ = ∅. If, in addition, assume that

• (i)${\lambda }_i^h-{\mu }_i^h-{\gamma }_i^h>0$ for i = 1, 2, … , n;
• (ii)${\phi }_{\mathit{ij}}^K>0$ for K = S, E, I, R, i, j, = 1, 2, … , n, i ≠ j;
• (iii)${\lambda }_i^v-{\mu }_i^v>0$ for i = 1, 2, … , n (or ${\psi }_{\mathit{ij}}^S={\psi }_{\mathit{ij}}^E={\psi }_{\mathit{ij}}^I$ for i, j = 1, 2, … , n).

Then the disease is uniformly persistent among patches, i.e., there is a constant κ > 0 such that each solution Φ_t(x₀) ≡ (S^h(t), E^h(t), I^h(t), R^h(t), S^ν(t), E^ν(t), I^ν(t)) of system (2.1) with X₀ ≡ (S^h(0), E^h(0), I^h(0), R^h(0), S^ν(0), E^ν(0), I^ν(0)), ∈ X₀ satisfies

$$\underset{t\to \infty }{\text{lim inf}}\left(E^h\right(t),I^h(t),R^h(t),E^v(t),I^v(t\left)\right)>{(\kappa ,\kappa ,\dots ,\kappa )}_{1\times 5n},$$

and (2.1) admits at least one endemic equilibrium.

Proof. We show first that W^s(ε₁₁) ∩ X₀ = ∅ whenever ${\mathcal{R}}_0>1$. Define

$$\Delta =\left[\begin{array}{ccccc}\hfill {\left({\delta }_{\mathit{ij}}{\rho }_i^h\right)}_{n\times n}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\left({\delta }_{\mathit{ij}}{c}_i^{\mathit{vh}}{a}_i^v\right)}_{n\times n}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\left({\delta }_{\mathit{ij}}{\rho }_i^v\right)}_{n\times n}\hfill & \hfill {\left({\delta }_{\mathit{ij}}{c}_i^{\mathit{hv}}{a}_i^v\right)}_{n\times n}\hfill & \hfill 0\hfill & \hfill {\left({\delta }_{\mathit{ij}}{d}_i^{\mathit{hv}}{a}_i^v\right)}_{n\times n}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\left({\delta }_{\mathit{ij}}{\rho }_i^h\right)}_{n\times n}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\left({\delta }_{\mathit{ij}}{\rho }_i^v\right)}_{n\times n}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\left({\delta }_{\mathit{ij}}{\rho }_i^h\right)}_{n\times n}\hfill \end{array}\right]$$

and M_∊ = F − V − ∊Δ. It follows from Theorem 2 in van den Driessche and Watmough [45] that ${\mathcal{R}}_0>1$ if and only if s(F − V) > 0. Thus, there exists an ∊₁ > 0 such that s(M_∊) > 0 for ∊ ∈ [0, ∊₁]. Let | · | be the Euclidean norm in ${\mathbb{R}}^{7n}$. Choose η small enough such that

$$\frac{S_i^v\left(0\right)}{N_i^h\left(0\right)}\ge \frac{S_i^{v\ast }\left(0\right)}{S_i^{h\ast }\left(0\right)}-{∊}_1,\frac{S_i^h\left(0\right)}{N_i^h\left(0\right)}\ge 1-{∊}_1,N_i^h\left(0\right)\le S_i^{h\ast }+{∊}_1\text{and}{N}_i^v\left(0\right)\le S_i^{v\ast }+{∊}_1$$

for i = 1, 2, … , n, |x₀ − ε₁₁| ≤ η. We now show that

$$\underset{t\to \infty }{\text{lim sup}}\mid {\Phi }_t\left({\mathrm{x}}_0\right)-{\mathcal{E}}_{11}\mid >\eta \text{for}{\mathrm{x}}_0\in X_0.$$

Suppose, by contradiction, that there is a T > 0 such that |Φ_t(x₀) − ε₁₁| ≤ η for t ≥ T. Pick Φ_T (x₀) ∈ X₀ as new x₀, then |Φ_t(x₀) − ε₁₁| ≤ η for t ≥ 0 and

$$\frac{{\mathit{dE}}_i^h}{\mathit{dt}}\ge c_i^{\mathit{vh}}{a}_i^v{I}_i^v(1-{∊}_1)-({\nu }_i^h+f_i^h(S_i^{h\ast }+{∊}_1\left)\right)E_i^h+\sum _{j=1}^n{\phi }_{\mathit{ij}}^E{E}_j^h,$$

$$\frac{{\mathit{dE}}_i^v}{\mathit{dt}}\ge c_i^{\mathit{hv}}{a}_i^v{I}_i^h(\frac{S_i^{v\ast }}{S_i^{h\ast }}-{∊}_1)+d_i^{\mathit{hv}}{a}_i^v{R}_i^h(\frac{S_i^{v\ast }}{S_i^{h\ast }}-{∊}_1)-({\nu }_i^v+f_i^v(S_i^{v\ast }+{∊}_1\left)\right)E_i^v+\sum _{j=1}^n{\psi }_{\mathit{ij}}^E{E}_j^v,$$

$$\frac{{\mathit{dI}}_i^h}{\mathit{dt}}\ge {\nu }_i^h{E}_i^h-(r_i^h+{\alpha }_i^h+{\gamma }_i^h+f_i^h(S_i^{h\ast }+{∊}_1\left)\right)I_i^h+\sum _{j=1}^n{\phi }_{\mathit{ij}}^I{I}_j^h,$$

$$\frac{{\mathit{dI}}_i^v}{\mathit{dt}}\ge {\nu }_i^v{E}_i^v-f_i^v(S_i^{v\ast }+{∊}_1)I_i^v+\sum _{j=1}^n{\psi }_{\mathit{ij}}^I{I}_j^v,$$

$$\frac{{\mathit{dR}}_i^h}{\mathit{dt}}\ge {\alpha }_i^h{I}_i^h-({\beta }_i^h+f_i^h(S_i^{h\ast }+{∊}_1\left)\right)R_i^h+\sum _{j=1}^n{\phi }_{\mathit{ij}}^R{R}_j^h.$$

Consider an auxiliary system

$$\frac{d\omega \left(t\right)}{\mathit{dt}}=M_{{∊}_1}\omega \left(t\right).$$ (3.4)

Note that M_∊1 is an irreducible, cooperative matrix for sufficiently small ∊₁. Using the Perron-Frobenius theorem, s(M_∊1) > 0 is a simple eigenvalue associated to a positive eigenvector. It then follows that any solution of (3.4) with positive initial value goes to infinity as t → ∞. By the comparison theorem, we have

$$\underset{t\to \infty }{\text{lim}}\left(E_i^h\right(t),E_i^v(t),I_i^h(t),I_i^v(t),R_i^h(t\left)\right)=(\infty ,\infty ,\infty ,\infty ,\infty ),i=1,2,\dots ,n.$$

Suppose (i) and (ii) hold. Let $X=\{{\mathrm{x}}_0\in {\mathbb{R}}_{+}^{7n}:N_i^h(0)>0\text{for}i=1,2\dots ,n\}$. We now claim that there exist n + 1 positive constants ζ₁, ζ₂, … , ζ_n and Λ such that

$$\tilde{X}=\{{\mathrm{x}}_0\in X:N_i^h(0)\ge {\zeta }_i\text{for}i=1,2,\dots ,n\text{and}{N}^h(0)\ge \Lambda \}$$

is closed positively invariant and each orbit of (2.1) starting in X eventually enters into $\tilde{X}$. The proof of this claim is straightforward, but tedious, we refer to Theorem 2 of Cui and Chen [10] for the approach.

Let ${\tilde{X}}_0=\{{\mathrm{x}}_0\in \tilde{X}:E_i^h(0),I_i^h(0),R_i^h(0),E_i^v(0),I_i^v(0)>0\text{for}i=1,2,\dots ,n\}$, and $\partial {\tilde{X}}_0=\tilde{X}{\tilde{X}}_0$. It is sufficient to prove that system (2.1) is uniformly persistent with respect to $({\tilde{X}}_0,\partial {\tilde{X}}_0)$.

Obviously, ${\tilde{X}}_0$ is relatively open in $\tilde{X}$. It is easy to check that ${\tilde{X}}_0$ is positively invariant. Theorem 2.1 implies that system (2.1) is point dissipative. Define

$$M_{\partial }=\{{\mathrm{x}}_0\in \partial {\tilde{X}}_0:{\Phi }_t({\mathrm{x}}_0)\in \partial {\tilde{X}}_0,\forall t\ge 0\},$$

$$D_1=\{{\mathrm{x}}_0\in \tilde{X}:E_i^h(0)=I_i^h(0)=R_i^h(0)=E_i^v(0)=I_i^v(0)=0,\forall i\in \{1,2,\dots ,n\left\}\right\},$$

$$D_2=\{{\mathrm{x}}_0\in \tilde{X}:S_i^v(0)=E_i^v(0)=I_i^v(0)=0,\forall i\in \{1,2,\dots ,n\left\}\right\}.$$

We claim that M_∂, = D₁ ∪ D₂. Clearly, D1 ∪ D₂ ⊂ M_∂. It suffices to show that M_∂ ⊂ D₁ ∪ D₂. For any ${\mathrm{x}}_0\in \partial {\tilde{X}}_0\backslash (D_1\cup D_2)$, we have $N_i^h\left(0\right)>0$, i = 1, 2, … , n, and

$$\sum _{i=1}^n\left(E_i^h\right(0)+I_i^h(0)+R_i^h(0)+E_i^v(0)+I_i^v(0\left)\right)>0,\sum _{i=1}^n\left(S_i^v\right(0)+E_i^v(0)+I_i^v(0\left)\right)>0.$$

By the form of (2.1) and the irreducibility of travel rate matrices, it follows that ${\Phi }_t\left({\mathrm{X}}_0\right)\in {\tilde{X}}_0\text{for}t>0$. Hence x₀ ∉ M_∂ and the claim is proved.

Let $\overrightarrow{0}={(0,0,\dots ,0)}_{n\times n}$. It is easy to verify that there are exactly two equilibria in M_∂, i.e., ${\epsilon }_{10}=(S^{h\ast },\overrightarrow{0},\overrightarrow{0},\overrightarrow{0},\overrightarrow{0},\overrightarrow{0},\overrightarrow{0})$ and ${\epsilon }_{11}=(S^{h\ast },\overrightarrow{0},\overrightarrow{0},\overrightarrow{0},S^{v\ast },\overrightarrow{0},\overrightarrow{0})$. Clearly, the total mosquito population N^ν(t) is permanent with respect to X₀ provided that (iii) holds, and hence there is a δ > 0 such that

$$\underset{t\to \infty }{\text{lim sup}}\mid {\Phi }_t\left({\mathrm{x}}_0\right)-{\mathcal{E}}_{10}\mid \ge \delta \text{for}{\mathrm{x}}_0\in X_0.$$

Consequently, both {ε₁₀} and {ε₁₁} are isolated invariant sets in X, W^s(ε₁₀) ∩ X₀ = ∅ and W^s(ε₁₁) ∩ X₀ = ∅. Notice that every trajectory in M_∂ converges to either ε₁₀ or ε₁₁, and {ε₁₀} and {ε₁₁} are acyclic in M_∂. It follows from Theorem 4.6 in Thieme [43] that system (2.1) is uniformly persistent with respect to $({\tilde{X}}_0,\partial {\tilde{X}}_0)$.

A well-known result in uniform persistence theory says that a bounded and uniformly persistent system has at least one interior equilibrium (see Hutson and Schmitt [21] or Theorem 2.4 in Zhao [49]). Since system (2.1) is bounded and uniformly persistent, we conclude that it has an equilibrium $\tilde{\epsilon }\equiv ({\tilde{S}}^h,{\tilde{E}}^h,{\tilde{I}}^h,{\tilde{R}}^h,{\tilde{S}}^v,{\tilde{E}}^v,{\tilde{I}}^v)\in {\tilde{X}}_0$. By the first and fifth equations of (2.1), we find that ${\tilde{S}}^h\in \mathrm{Int}{\mathbb{R}}_{+}^n$ and ${\tilde{S}}^v\in \mathrm{Int}{\mathbb{R}}_{+}^n$ which indicates that $\tilde{\epsilon }$ is an endemic equilibrium of (2.1).

Remark 3.8. For n = 1, the theorem is an improvement of Proposition 3.3 of Ngwa and Shu [33]. By using the method in this proof, one can get similar or better results for some other epidemic metapopulation models such as those in Hsieh et al. [20] and Salmani and van den Driessche [37].

4. The dependence of ${\mathcal{R}}_0$ on parameters

In an epidemic model, once the basic reproduction number is calculated and shown to be a threshold for the dynamics of the disease, a natural question about disease control is how the reproduction number depends on the model parameters. Is the dependence in a monotone way (Müller and Hadeler [29])? For a very special case of a two-patch epidemic model, Hsieh et al. [20] showed that (Theorem 4.2) R₀ decreases when the travel rate of infected individuals increases. See also Allen et al. [1] (Lemma 3.4). In general there are very few results on this aspect. For model (2.1), it is easy to see that all parameters are directly or indirectly contained in ${\mathcal{R}}_0$. Obviously, ${\mathcal{R}}_0$ increasing with respect to $c_i^{\mathit{vh}}$, $c_i^{\mathit{hv}}$, $d_i^{\mathit{hv}}$ or $a_i^v$. By Theorem 2.5.4 in Horn and Johnson[19], an increase in ${\beta }_i^h$, $r_i^h$ or ${\gamma }_i^h$ will decrease ${\mathcal{R}}_0$. The dependence of ${\mathcal{R}}_0$ on other parameters is more complicated. For example, unlike in the single patch model, the following result indicates that in a multi-patch model the parameters ${\nu }_i^h$ or ${\nu }_i^v$ can decrease or increase ${\mathcal{R}}_0$ and even more complicated dependence may exist. Recall that ${\mathcal{R}}_0^2=\rho \left(M\right)$, where ρ denotes the spectral radius and $M=A_{64}{A}_{44}^{-1}{A}_{42}{A}_{22}^{-1}(A_{73}+A_{75}{A}_{55}^{-1}{A}_{53})A_{33}^{-1}{A}_{31}{A}_{11}^{-1}$. Only A₃₁ and A₁₁ contain ${\nu }_i^h$ while only A₄₂ and A₂₂ contain ${\nu }_i^v$. Then we have $\rho \left(M\right)=\rho \left(A^h{A}_{31}{A}_{11}^{-1}\right)=\rho \left(A^v{A}_{42}{A}_{22}^{-1}\right)$, where $A^h=A_{64}{A}_{44}^{-1}{A}_{42}{A}_{22}^{-1}(A_{73}+A_{75}{A}_{55}^{-1}{A}_{53})A_{33}^{-1}$ and $A^v=(A_{73}+A_{75}{A}_{55}^{-1}{A}_{53})A_{33}^{-1}{A}_{31}{A}_{11}^{-1}{A}_{64}{A}_{44}^{-1}$ are positive matrices with positive determinants. For n = 2, that is for the two-patch submodel, the question is reduced to a matrix problem.

Proposition 4.1. Let $A=\left[\begin{array}{cc}\hfill e\hfill & \hfill f\hfill \\ \hfill g\hfill & \hfill h\hfill \end{array}\right]\left[\begin{array}{cc}\hfill v_1\hfill & \hfill \hfill \\ \hfill \hfill & \hfill v_2\hfill \end{array}\right]{\left[\begin{array}{cc}\hfill v_1+a_1+k_1\hfill & \hfill -k_2\hfill \\ \hfill -k_1\hfill & \hfill v_2+a_2-k_2\hfill \end{array}\right]}^{-1}$, where all involving parameters are positive and satisfy eh > fg. Then ρ(A) is decreasing in ν₁ if

$$\left(\right(1+\frac{a_2}{v_2}\left)\right(e+g)-f-h)k_1^2+(e-h+2g+\frac{a_2+k_2}{v_2}(e+g)+\frac{a_2}{v_2}g)a_1{k}_1+(1+\frac{a_2+k_2}{v_2})a_1^{2}g<0$$

and increasing otherwise.

Proof. The matrix A is the product of three matrices which correspond to A^h, A₃₁ and $A_{11}^{-1}$ (or, A^ν, A₄₂ and $A_{22}^{-1}$) in M, respectively. So here ν_i represents ${\nu }_i^h\left(\text{or}{\nu }_i^v\right)$ and k_i represents ${\phi }_{\mathit{ij}}^E\left(\text{or}{\psi }_{\mathit{ji}}^E\right)$ for i, j = 1, 2 and i ≠ j.

Note that A has two distinct positive eigenvalues and the inverses of the eigenvalues of A are the eigenvalues of A⁻¹. Thus it suffices to consider the monotonicity of the smaller eigenvalue λ₁ = 1/ρ(A) of A⁻¹ on ν₁.

Let ${\stackrel{‒}{a}}_1=a_1+k_1$ and ${\stackrel{‒}{a}}_2=a_2+k_2$, and let $\left[\begin{array}{cc}\hfill x\hfill & \hfill -y\hfill \\ \hfill -z\hfill & \hfill w\hfill \end{array}\right]={\left[\begin{array}{cc}\hfill e\hfill & \hfill f\hfill \\ \hfill g\hfill & \hfill h\hfill \end{array}\right]}^{-1}$, then x, y, z, w > 0 and xw > yz. The characteristic equation of matrix A⁻¹ is ${\lambda }^2-\mathcal{P}\lambda +\mathcal{Q}=0$, where

$$\mathcal{P}=\text{tr}\left(A^{-1}\right)=x(v_1+{\stackrel{‒}{a}}_1)∕v_1+{\mathit{yk}}_1∕v_1+{\mathit{zk}}_2∕v_2+w(v_2+{\stackrel{‒}{a}}_2)∕v_2,$$

$$\mathcal{Q}=\text{det}\left(A^{-1}\right)=(\mathit{xw}-\mathit{yz})\left(\right(v_1+{\stackrel{‒}{a}}_1\left)\right(v_2+{\stackrel{‒}{a}}_2)-k_1{k}_2)∕\left(v_1{v}_2\right).$$

Thus, ${\lambda }_1=(\mathcal{P}-\sqrt{{\mathcal{P}}^2-4\mathcal{Q}})∕2$ and $\partial {\lambda }_1∕\partial v_1=(\stackrel{.}{\mathcal{P}}-\mathcal{P}\stackrel{.}{\mathcal{P}}-2\stackrel{.}{\mathcal{Q}})∕\sqrt{{\mathcal{P}}^2-4\mathcal{Q}}∕2$, where $\stackrel{.}{\mathcal{P}}=\partial \mathcal{P}∕\partial v_1=-(x{\stackrel{‒}{a}}_1+{\mathit{yk}}_1)∕v_1^2<0$ and $\mathcal{Q}=\partial \mathcal{Q}∕\partial v_1=-(\mathit{xw}-\mathit{yz})\left({\stackrel{‒}{a}}_1\right(v_2+{\stackrel{‒}{a}}_2)-k_1{k}_2)∕\left(v_1^2{v}_2\right)<0$. Then

$$\partial {\lambda }_1∕\partial v_1>0\iff \mathcal{P}\stackrel{.}{\mathcal{P}}-2\stackrel{.}{\mathcal{Q}}<0\text{and}{\left(\stackrel{.}{\mathcal{P}}\right)}^2\mathcal{Q}+{\left(\stackrel{.}{\mathcal{Q}}\right)}^2-\mathcal{P}\stackrel{.}{\mathcal{P}}\stackrel{.}{\mathcal{Q}}>0.$$

The second inequality is equivalent to

$$({\mathit{yv}}_2+{\mathit{wk}}_2)k_1^2+({\mathit{xv}}_2+{\mathit{zk}}_2){\stackrel{‒}{a}}_1{k}_1>(z{\stackrel{‒}{a}}_1+{\mathit{wk}}_1)(v_2+{\stackrel{‒}{a}}_2){\stackrel{‒}{a}}_1.$$ (4.1)

Claim: (4.1) implies $\mathcal{P}\stackrel{.}{\mathcal{P}}-2\stackrel{.}{\mathcal{Q}}<0$. In fact, we have

$$\begin{array}{cc}\hfill -\mathcal{P}\stackrel{.}{\mathcal{P}}{v}_1^2& =\left(x\right(1+{\stackrel{‒}{a}}_1∕v_1)+{\mathit{yk}}_1∕v_1+{\mathit{zk}}_2∕v_2+w(1+{\stackrel{‒}{a}}_2∕v_2\left)\right)(x{\stackrel{‒}{a}}_1+{\mathit{yk}}_1)\hfill \\ \hfill & >(x+{\mathit{zk}}_2∕v_2+w(1+{\stackrel{‒}{a}}_2∕v_2\left)\right)(x{\stackrel{‒}{a}}_1+{\mathit{yk}}_1)\hfill \\ \hfill & =\left(\right(\mathit{xv}+{\mathit{zk}}_2)+w(v_2+{\stackrel{‒}{a}}_2\left)\right)({\stackrel{‒}{a}}_1{k}_1+{\mathit{yk}}_1^2∕x)x∕\left(k_1{v}_2\right)\hfill \\ \hfill & >\left(\right({\mathit{yv}}_2+{\mathit{wk}}_2)k_1^2+({\mathit{xv}}_2+{\mathit{zk}}_2){\stackrel{‒}{a}}_1{k}_1-{\mathit{wk}}_2{k}_1^2+w(v_2+{\stackrel{‒}{a}}_2\left){\stackrel{‒}{a}}_1{k}_1\right)x∕\left(k_1{v}_2\right)\hfill \\ \hfill & >\left(\right(z{\stackrel{‒}{a}}_1+{\mathit{wk}}_1\left)\right(v_2+{\stackrel{‒}{a}}_2){\stackrel{‒}{a}}_1-{\mathit{wk}}_2{k}_1^2+w(v_2+{\stackrel{‒}{a}}_2\left){\stackrel{‒}{a}}_1{k}_1\right)x∕\left(k_1{v}_2\right)\text{by}\left(4.1\right)\hfill \\ \hfill & >\left(2w\right(v_2+{\stackrel{‒}{a}}_2){\stackrel{‒}{a}}_1{k}_1-{\mathit{wk}}_2{k}_1^2)x∕\left(k_1{v}_2\right)=\left(2\mathit{xw}{\stackrel{‒}{a}}_1\right(v_2+{\stackrel{‒}{a}}_2)-{\mathit{xwk}}_1{k}_2)∕v_2\hfill \\ \hfill & >2(\mathit{xw}-\mathit{yz})\left({\stackrel{‒}{a}}_1\right(v_2+{\stackrel{‒}{a}}_2)-k_1{k}_2)∕v_2=-2\stackrel{.}{\mathcal{Q}}{v}_1^2.\hfill \end{array}$$

The proof is complete by substituting ${\stackrel{‒}{a}}_1=a_1+k_1$ and ${\stackrel{‒}{a}}_2=a_2+k_2$ into (4.1).

Remark 4.2. The biological interpretation of the inequality in Proposition 4.1 is not easy. However, if the emigration rate k₁ = 0, then the inequality is always failed and ρ(A) is consistently increasing in ν₁. So, the decreasing phenomenon is due to the emigration of the corresponding exposed class and shortening the exposed period (1/ν₁) makes them migrate less to the other patch.

In the rest of this section, we will study the dependence of ${\mathcal{R}}_0$ on the movement of exposed, infectious, and recovered humans for the two-patch case. As far as we know, there are very few results on this topic (Theorem 4.2 in Hsieh et al. [20], see also Allen et al. [1]). Note that only A₁₁ contains ${\phi }_{\mathit{ij}}^E$ and only A₃₃ contains ${\phi }_{\mathit{ij}}^I$. We know $\rho \left(M\right)=\rho \left(A^E{A}_{11}^{-1}\right)=\rho \left(A^I{A}_{33}^{-1}\right)$, where $A^E=A_{64}{A}_{44}^{-1}{A}_{42}{A}_{22}^{-1}(A_{73}+A_{75}{A}_{55}^{-1}{A}_{53})A_{33}^{-1}{A}_{31}$ and $A^I=A_{31}{A}_{11}^{-1}{A}_{64}{A}_{44}^{-1}{A}_{22}^{-1}(A_{73}+A_{75}{A}_{55}^{-1}{A}_{53})$ are positive matrices with positive determinants. We first consider the case when the travel rates of exposed, infectious, and recovered humans from one patch to the other depend on both the residence and disease status. The question then becomes a matrix problem as follows.

Proposition 4.3. Let $A=\left[\begin{array}{cc}\hfill e\hfill & \hfill f\hfill \\ \hfill g\hfill & \hfill h\hfill \end{array}\right]{\left[\begin{array}{cc}\hfill a_1+k_1\hfill & \hfill -k_2\hfill \\ \hfill -k_1\hfill & \hfill a_2+k_2\hfill \end{array}\right]}^{-1}$, where all involving parameters are positive and satisfy eh > fg. Then ρ(A) is decreasing in k₁ if (e + g)/a₁ > (f + h)/a₂ and increasing otherwise.

Proof. The matrix A is the product of two matrices which correspond to A^E and $A_{11}^{-1}$ (or, A^I and $A_{33}^{-1}$) in M, respectively. Here k_i represents ${\phi }_{\mathit{ji}}^E$ (or ${\phi }_{\mathit{ji}}^I$) for i, j = 1, 2 and i ≠ j.

It suffices to consider the monotonicity of the smaller eigenvalue λ₁ = 1/ρ(A) of A⁻¹ on k₁.

Let $\left[\begin{array}{cc}\hfill x\hfill & \hfill -y\hfill \\ \hfill -z\hfill & \hfill w\hfill \end{array}\right]={\left[\begin{array}{cc}\hfill e\hfill & \hfill f\hfill \\ \hfill g\hfill & \hfill h\hfill \end{array}\right]}^{-1}$. Then x, y, z, w > 0 and xw > yz. The characteristic equation of matrix A⁻² is ${\lambda }^2-\mathcal{P}\lambda +\mathcal{Q}=0$

$$\mathcal{P}=\text{tr}\left(A^{-1}\right)=x(a_1+k_1)+{\mathit{yk}}_1+{\mathit{zk}}_2+w(a_2+k_2),$$

$$\mathcal{Q}=\text{det}\left(A^{-1}\right)=(\mathit{xw}-\mathit{yz})\left(\right(a_1+k_1\left)\right(a_2+k_2)-k_1{k}_2).$$

Thus, ${\lambda }_1=(\mathcal{P}-\sqrt{{\mathcal{P}}^2-4\mathcal{Q}})∕2$. Direct calculation yields $\partial {\lambda }_1∕\partial k_1=(\stackrel{.}{\mathcal{P}}-(\mathcal{P}\stackrel{.}{\mathcal{P}}-2\stackrel{.}{\mathcal{Q}})∕\sqrt{{\mathcal{P}}^2-4\mathcal{Q}})∕2$, where $\stackrel{.}{\mathcal{P}}=\partial \mathcal{P}∕\partial k_1=x+y$ and $\stackrel{.}{\mathcal{Q}}=\partial \mathcal{Q}∕\partial k_1={(\mathit{xw}-\mathit{yz})}_{a2}$. Then

$$\partial {\lambda }_1∕\partial k_1>0\iff \mathcal{P}\stackrel{.}{\mathcal{P}}-2\stackrel{.}{\mathcal{Q}}\le 0\text{or}{\left(\stackrel{.}{\mathcal{P}}\right)}^2\mathcal{Q}+{\left(\stackrel{.}{\mathcal{Q}}\right)}^2-\mathcal{P}\stackrel{.}{\mathcal{P}}\stackrel{.}{\mathcal{Q}}<0,$$

which is equivalent to

$$\left(x\right(a_1+k_1)+{\mathit{yk}}_1+{\mathit{zk}}_2+w(a_2+k_2\left)\right)(x+y)-2(\mathit{xw}-\mathit{yz})a_2\le 0$$ (4.2)

or

$$({\mathit{xk}}_2+y(a_2+k_2\left)\right)\left(\right(x+y)a_1-(z+w\left)a_2\right)(\mathit{xw}-\mathit{yz})<0.$$ (4.3)

Since xk₂ + y(a₂ + k₂) > 0 and xw > yz, (4.3) is reduced to (x + y)a₁ < (z + w)a₂. It is easy to verify that (4.2) implies (4.3). Therefore, when (x + y)a₁ < (z + w)a₂, i.e., (f + h)/a₂ < (e + g)/a₁, ρ(A) is decreasing in k₁.

Remark 4.4. The conclusion in Proposition 4.3 still holds if e, h, a₁, a₂ > 0, f, g, k₁, k₂ ≥ 0, eh > fg, and hk₂ + f(a₂ + k₂) > 0 (namely, k₂ > 0 or f > 0 which implies that there is also infected (exposed, infectious, or recovered) human or infected mosquito migration from patch 2 to patch 1). In particular, when only the two classes associated to k₁ and k₂ travel between patches, ρ(A) is decreasing in k₁ if $(g+e)∕a_1=e∕a_1={\mathcal{R}}_0^{\left(1\right)}>(f+h)∕a_2=h∕a_2={\mathcal{R}}_0^{\left(2\right)}$. Biologically, this means that the disease outbreak becomes less severe if more people migrate from the high transmission area to the low transmission area.

Remark 4.5. If hk₂ + f(a₂ + k₂) = 0, namely k₂ = 0 and f = 0, which means no infected (exposed, infectious, or recovered) human or infected mosquito migrates from patch 2 to patch 1, then

$$A=\left[\begin{array}{cc}\hfill e\hfill & \hfill 0\hfill \\ \hfill g\hfill & \hfill h\hfill \end{array}\right]{\left[\begin{array}{cc}\hfill a_1+k_1\hfill & \hfill 0\hfill \\ \hfill -k_1\hfill & \hfill a_2\hfill \end{array}\right]}^{-1}=\left[\begin{array}{cc}\hfill e∕(a_1+k_1)\hfill & \hfill 0\hfill \\ \hfill ({\mathit{ga}}_2+{\mathit{hk}}_1)∕\left(\right(a_1+k_1\left)a_2\right)\hfill & \hfill h∕a_2\hfill \end{array}\right].$$

We have ρ(A) = max{e/(a₁ + k₁), h/a₂} which is non-increasing in k₁.

The following result assumes that the travel rates of exposed, infectious, and recovered humans depend on disease states but are independent of residences (i.e., the travel rate matrices ${\left({\phi }_{\mathit{ij}}^E\right)}_{n\times n}$ and ${\left({\phi }_{\mathit{ij}}^I\right)}_{n\times n}$ are symmetric).

Proposition 4.6. Let $A=\left[\begin{array}{cc}\hfill e\hfill & \hfill f\hfill \\ \hfill g\hfill & \hfill h\hfill \end{array}\right]{\left[\begin{array}{cc}\hfill a_1+k\hfill & \hfill -k\hfill \\ \hfill -k\hfill & \hfill a_2+k\hfill \end{array}\right]}^{-1}$, where all involving parameters are positive and satisfy eh > fg. Then ρ(A) is decreasing in k if (e+f)/a₁ > (g+h)/a₂ and (e + g)/a₁ > (f + h)/a₂, or (e + f)/a₁ < (g + h)/a₂ and (e + g)/a₁ < (f + h)/a₂; and increasing otherwise.

Proof. We use the same notations as in Proposition 4.3 and consider the monotonicity of the smaller eigenvalue λ₁ = 1/ρ(A) of A⁻¹ on k. The characteristic equation of matrix A⁻¹ is ${\lambda }^2-\mathcal{P}\lambda +\mathcal{Q}=0$, where $\mathcal{P}=x(a_1+k)+\mathit{yk}+\mathit{zk}+w(a_2+k)$ and $\mathcal{Q}=(\mathit{xw}-\mathit{yz})\left(\right(a_1+k\left)\right(a_2+k)-k^2)$.

Obviously, $\stackrel{.}{\mathcal{P}}=\partial \mathcal{P}∕\partial k=x+y+z+w$ and $\stackrel{.}{\mathcal{Q}}=\partial \mathcal{Q}∕\partial k=(\mathit{xw}-\mathit{yz})(a_1+a_2)$. Then

$$\partial {\lambda }_1∕\partial k_1>0\iff \mathcal{P}\stackrel{.}{\mathcal{P}}-2\stackrel{.}{\mathcal{Q}}\le 0\text{or}{\left(\stackrel{.}{\mathcal{P}}\right)}^2\mathcal{Q}+{\left(\stackrel{.}{\mathcal{Q}}\right)}^2-\mathcal{P}\stackrel{.}{\mathcal{P}}\stackrel{.}{\mathcal{Q}}<0,$$

which is equivalent to

$$\left(x\right(a_1+k)+\mathit{yk}+\mathit{zk}+w(a_2+k\left)\right)(x+y+z+w)\le 2(\mathit{xw}-\mathit{yz})(a_1+a_2)$$ (4.4)

or

$$-\left(\right(x+z)a_1-(y+w\left)a_2\right)\left(\right(x+y)a_1-(z+w\left)a_2\right)(\mathit{xw}-\mathit{yz})<0.$$ (4.5)

Since xw > yz, the solutions to (4.5) satisfy (x + z)a₁ < (y + w)a₂ and (x + y)a₁ < (z + w)a₂, or (x + z)a₁ > (y + w)a₂ and (x + y)a₁ > (z + w)a₂. It is easy to verify that (4.4) implies (4.5). The proof is complete.

Remark 4.7. The monotonicity of ρ(A) is still true if e, h, a₁, a₂ > 0, f, g, k ≥ 0 and eh > fg. Epidemiologically, this means that the disease trend depends on a double-side effect. If f = g = 0, ρ(A) is always non-increasing in k which means that travel can reduce the disease severity when only the two classes associated to k migrate between patches.

So far all our analyses are carried out for all three classes of humans: exposed, infectious and recovered. However, one would expect that the effect of the recovered human movement is different from that of the other two classes. In fact, the last two propositions do not work for the movement of recovered humans $R_i^h$ which is related to different matrices, i.e., $\left[\begin{array}{cc}\hfill e\hfill & \hfill f\hfill \\ \hfill g\hfill & \hfill h\hfill \end{array}\right]\left(\left[\begin{array}{cc}\hfill d_1\hfill & \hfill \hfill \\ \hfill \hfill & \hfill d_2\hfill \end{array}\right]{\left[\begin{array}{cc}\hfill a_1+k_1\hfill & \hfill -k_2\hfill \\ \hfill -k_1\hfill & \hfill a_2+k_2\hfill \end{array}\right]}^{-1}\right)$ and $\left[\begin{array}{cc}\hfill e\hfill & \hfill f\hfill \\ \hfill g\hfill & \hfill h\hfill \end{array}\right]\left(\left[\begin{array}{cc}\hfill d_1\hfill & \hfill \hfill \\ \hfill \hfill & \hfill d_2\hfill \end{array}\right]+{\left[\begin{array}{cc}\hfill a_1+k\hfill & \hfill -k\hfill \\ \hfill -k\hfill & \hfill a_2+k\hfill \end{array}\right]}^{-1}\right)$, where all parameters are positive and eh > fg. A tentative analysis suggests that similar, but more complicated, results may hold for the recovered class.

Therefore, for the two-patch submodel, the basic reproduction number ${\mathcal{R}}_0$ varies monotonically with the travel rates of exposed, infectious, and recovered humans depending on their disease states. This demonstrates that if there is enough travel of humans between the two regions malaria can be sustained in the region with lower or no transmission. Screening at borders usually can help to identify infected individuals with symptoms but not those individuals with subpatent parasitaemia or those with only liver stage infections (exposed). The analysis in this section shows that the travel of the infected individuals, with or without symptoms, can contribute to the spread of the disease from one patch to another. Thus, as far as malaria is concerned, screening at borders is not an effective control measure.

These results can be applied to general multi-patch models when the impact of population dispersal on the spatial spread of an infectious disease is concerned. When the travel rate is independent of the disease state, but may or may not be independent of residence, the relationship between ${\mathcal{R}}_0$ and the travel rates of exposed, infectious and recovered humans becomes even more complicated and non-monotone dependence can occur. We will investigate these situations by presenting some examples in next section.

5. Numerical simulations

In the case when two patches are concerned, we study the effects of population dispersal on disease dynamics by performing numerical simulations. Some of the parameter values are chosen from the data in Chitnis et al. [8] and the references therein.

Example 5.1. To compare the importance of human movement of different exposed, infectious and recovered classes in the geographical spread of the disease, we need to do sensitivity analysis of the basic reproduction number ${\mathcal{R}}_0$ on the dispersal rates ${\phi }_{\mathit{ij}}^E$, ${\phi }_{\mathit{ij}}^I$ and ${\phi }_{\mathit{ij}}^R$, respectively.

Assume parameters in system (2.1) are as follows: ${\lambda }_i^h=5.5\times {10}^{-5}$, ${\mu }_i^h=8.8\times {10}^{-6}$, ${\rho }_i^h=2.0\times {10}^{-7}$, ${\lambda }_i^v=0.13$, ${\mu }_i^v=0.033$, ${\rho }_i^v=4.0\times {10}^{-5}$, ${\nu }_i^h=0.1$, ${\nu }_1^v=0.083$, $r_i^h=2.2\times {10}^{-3}$, ${\alpha }_i^h=4.8\times {10}^{-3}$, ${\gamma }_i^h=2.0\times {10}^{-5}$, ${\beta }_i^h=3.5\times {10}^{-3}$, $a_i^v=0.14$, for i = 1,2, and $c_1^{\mathit{vh}}=0.11$, $c_1^{\mathit{hv}}=0.08$, $d_1^{\mathit{hv}}=0.02$, $c_2^{\mathit{vh}}=0.02$, $c_2^{\mathit{hv}}=0.337$, $d_2^{\mathit{hv}}=0.06$. These parameters yields the respective basic reproduction numbers in isolation of ${\mathcal{R}}_0^{\left(1\right)}=1.0127>1$ and ${\mathcal{R}}_0^{\left(2\right)}=0.8535<1$ Thus, malaria is endemic in patch 1 and dies out in patch 2.

With migration between patches, we take the same travel rate for mosquitoes from one patch to the other, namely, ${\psi }_{12}^S={\psi }_{12}^E={\psi }_{12}^I={\psi }_{21}^S={\psi }_{21}^E={\psi }_{21}^I=0.01$. For human movement, we assume that the travel rates are independent of residences and choose ${\phi }_{12}^S={\phi }_{21}^S=0.15$ for the susceptible. Now we keep two of the three travel rates, i.e., ${\phi }_{12}^E={\phi }_{21}^E=k$, ${\phi }_{12}^I={\phi }_{21}^I=0.1k$ and ${\phi }_{12}^R={\phi }_{21}^R=0.4k$, fixed with k = 0.1 and let the remaining one decrease with k from 0.1 to 0. For example, if the first two travel rates are fixed with k = 0.1 and the remaining one decreases with k from 0.1 to 0, then ${\phi }_{12}^E={\phi }_{21}^E=0.1$ and ${\phi }_{12}^I={\phi }_{21}^I=0.01$, and ${\phi }_{12}^R={\phi }_{21}^R=0.4k$, k ∈ [0, 0.1]. The curves of ${\mathcal{R}}_0$ against k are illustrated in Fig 5.1(a). The monotonicity of the curves is predicted by Proposition 4.6. Since ${\mathcal{R}}_0=1.0006>1$ as k = 0.1, the disease is endemic in both patches by Theorem 3.7. To eradicate the disease, it is more effcient to restrict the travel of infectious humans in case we can only control the travel of one of the exposed, infectious and recovered human classes.

Fig. 5.1.

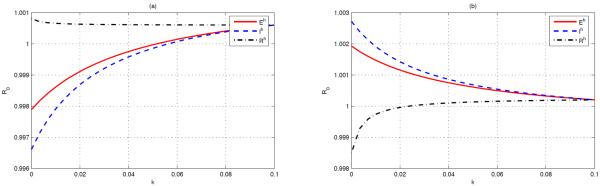
The basic reproduction number ${\mathcal{R}}_0$ in terms of k. (a) ${\mathcal{R}}_0=1.0006$ as k = 0.1, the optimal strategy for reducing ${\mathcal{R}}_0$ to be less than 1 is to restrict the travel of infectious humans. (b) ${\mathcal{R}}_0=1.0002$ as k = 0.1, the optimal strategy for reducing ${\mathcal{R}}_0$ to be less than 1 is to restrict the travel of recovered humans.

However, the optimal control strategy is changed if the parameter values are varied. For example, taking the same parameters as above except that $c_2^{\mathit{hv}}=0.23$ and $d_2^{\mathit{hv}}=0.1365$, then ${\mathcal{R}}_0^{\left(1\right)}=1.0127>1$, ${\mathcal{R}}_0^{\left(2\right)}=0.8497<1$, and ${\mathcal{R}}_0=1.0002>1$ as k = 0.1. From Fig 5.1(b), the only choice is to strictly control the travel of the recovered humans while travel restriction on the exposed and infectious humans has an adverse influence on disease control.

Example 5.2. For model (2.1, we present an example where the disease dies out or persists in each isolated patch but becomes endemic or extinct, respectively, when there is suitable migration between them. In fact, such a scenario may happen even for two identical patches from the aspect of ecology and epidemiology.

Case 1: ${\mathcal{R}}_0^{\left(1\right)}<1$ and ${\mathcal{R}}_0^{\left(2\right)}<1$, but ${\mathcal{R}}_0>1$. For i = 1, 2, suppose ${\lambda }_i^h=5.5\times {10}^{-5}$, ${\mu }_i^h=8.8\times {10}^{-6}$, ${\rho }_i^h=2.0\times {10}^{-7}$, ${\lambda }_i^v=0.13$, ${\mu }_i^v=0.033$, ${\rho }_i^v=4.0\times {10}^{-5}$, ${\nu }_i^h=0.1$, ${\nu }_i^v=0.083$, $r_i^h=2.1\times {10}^{-3}$, ${\alpha }_i^h=4.8\times {10}^{-3}$, ${\gamma }_i^h=1.8\times {10}^{-5}$, ${\beta }_i^h=2.7\times {10}^{-3}$, $a_i^v=0.14$, $c_i^{\mathit{vh}}=0.11$, $c_i^{\mathit{hv}}=0.08$, $d_i^{\mathit{hv}}=0.008$. We choose the travel rates as follows: ${\phi }_{12}^S=k$, ${\phi }_{12}^E={\phi }_{12}^I={\phi }_{12}^R=0.2k$, ${\phi }_{21}^S=0.5k$, ${\phi }_{21}^E={\phi }_{21}^I={\phi }_{21}^R=0.3k$ and ${\psi }_{12}^S={\psi }_{12}^E={\psi }_{12}^I={\psi }_{21}^S={\psi }_{21}^E={\psi }_{21}^I=0$, where k increases from 0 to 0.10. Note that the travel rates of exposed, infectious and recovered humans are independent of disease states but depend on their residences and there is no mosquito migration between patches.

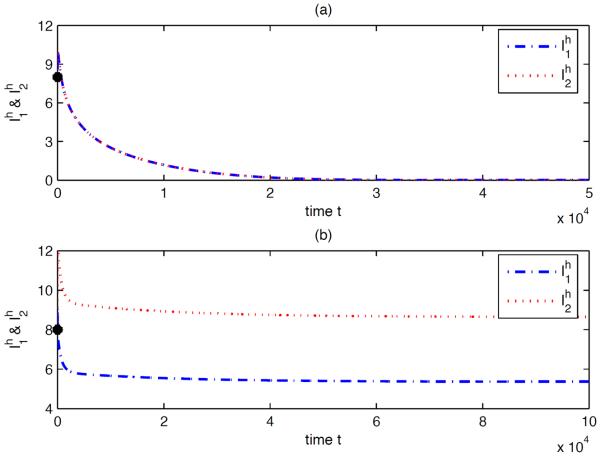
For the above parameter values, the dependence of ${\mathcal{R}}_0$ on k is shown in Fig 5.2. In particular, we have ${\mathcal{R}}_0^{\left(1\right)}={\mathcal{R}}_0^{\left(2\right)}=0.9557$ and the disease can die out in each isolated patches (see Fig 5.3(a)). When humans move between these two patches, even for very small travel rate (k > 10⁻⁵), ${\mathcal{R}}_0$ exceeds 1 and the disease becomes endemic in both patches (see Fig 5.3(b)) which is coincident with Theorem 3.7.

Fig. 5.2.

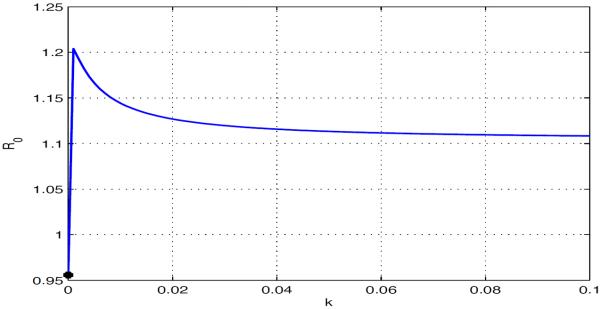
${\mathcal{R}}_0$ as a function of $k={\phi }_{12}^S$ with ${\mathcal{R}}_0^{\left(1\right)}={\mathcal{R}}_0^{\left(2\right)}=0.9557$. The disease dies out in each isolated patch, but it becomes endemic in both patches even when there is small human movement.

Fig. 5.3.

Numerical solutions of system (2.1) with (a) k = 0 (no human movement) and (b) k = 0.06 (the corresponding ${\mathcal{R}}_0=1.1116$), respectively. In both situations, the initial conditions are $S_i^h\left(0\right)=187$, $E_i^h\left(0\right)=3$, $I_i^h\left(0\right)=8$, $R_i^h\left(0\right)=9$, $S_i^v\left(0\right)=2310$, $E_i^v\left(0\right)=10$, $I_i^v\left(0\right)=4$ for i = 1, 2. The solution in (a) approaches the disease-free equilibrium, while the solution in (b) approaches the endemic equilibrium. Note that the two trajectories in (a) coincide completely because they have the same initial values and the two patches have the same parameter values.

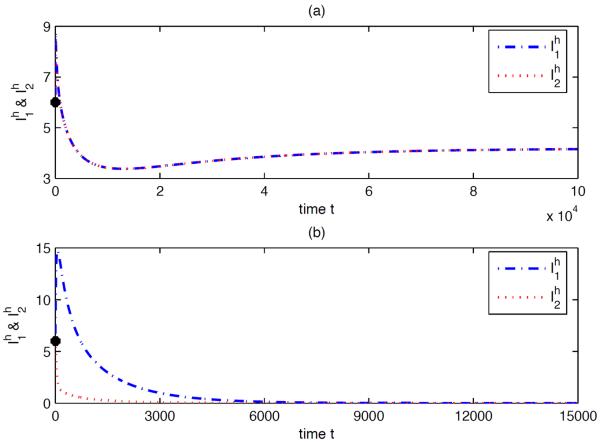
Case 2: ${\mathcal{R}}_0^{\left(1\right)}>1$ and ${\mathcal{R}}_0^{\left(2\right)}>1$, but ${\mathcal{R}}_0<1$. Use the same parameter values as in Case 1 except that $a_1^v=a_2^v=0.15$ and the travel rates. We choose ${\phi }_{12}^S=k$, ${\phi }_{12}^E={\phi }_{12}^I={\phi }_{12}^R=0.6k$, ${\phi }_{21}^S=0.5k$, ${\phi }_{21}^E={\phi }_{21}^I={\phi }_{21}^R=0.05k$, and ${\psi }_{12}^S={\psi }_{12}^E={\psi }_{12}^I={\psi }_{21}^S={\psi }_{21}^E={\psi }_{21}^I=0$, where k varies from 0 to 0.10. Thus,${\mathcal{R}}_0^{\left(1\right)}={\mathcal{R}}_0^{\left(2\right)}=1.0240$ and the dependence of ${\mathcal{R}}_0$ in k is shown in Fig 5.4. Suitable human movement may result in the extinction of the disease in both patches, even though the disease persists in each isolated patch (see Fig 5.5).

Fig. 5.4.

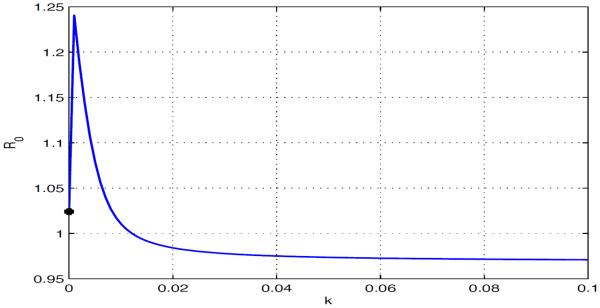
${\mathcal{R}}_0$ in terms of $k={\phi }_{12}^S$ with ${\mathcal{R}}_0^{\left(1\right)}={\mathcal{R}}_0^{\left(2\right)}=1.0240$. The disease persists in each isolated patch, but it becomes extinct in both patches when there is suitable human movement.

Fig. 5.5.

Numerical solutions of system (2.1) with (a) k = 0 (no human movement) and (b) k = 0.06 (the corresponding ${\mathcal{R}}_0=0.9727$), respectively. In both situations, the initial conditions are $S_i^h\left(0\right)=221$, $E_i^h\left(0\right)=3$, $I_i^h\left(0\right)=6$, $R_i^h\left(0\right)=4$, $S_i^v\left(0\right)=2150$, $E_i^v\left(0\right)=8$, $I_i^v\left(0\right)=7$ for i = 1, 2. The solution in (a) approaches the endemic equilibrium, while the solution in (b) approaches the disease-free equilibrium. Note that the two trajectories in (a) coincide completely because the two patches have the same parameter values and the initial data are same.

In studying how travel affects the spatial spread of certain disease, Hsieh et al. [20] considered two patches, a low prevalence patch with a minor disease outbreak (basic reproduction number in isolation is less than 1) and a high prevalence patch with endemic disease (basic reproduction number in isolation is greater than 1). They numerically demonstrated the possibility that for the low prevalence patch open travel with a high prevalence patch could lead to the disease becoming endemic. However, for a high prevalence patch open travel with a low prevalence patch could eradicate the disease. Our simulations in Example 5.2 present more interesting scenarios. Case 1 indicates that if both patches have low prevalence of the disease, travel of the exposed and infectious individuals from one patch to another would increase the chances of infecting the susceptible individuals in the second patch, travel of susceptible individuals from one patch to another patch would give them more opportunities to be infected in the second patch, and vice versa. These travels would make the disease more likely to be endemic in both patches. Such a situation has also been observed in Cosner et al. [9] for a two-patch Ross-Macdonald malaria model. Case 2 is an ad hoc and probably less likely scenario which could occur when all exposed and infectious individuals from one patch moved to another patch while all the susceptible individuals in the second patch move to the first patch. This dilution of the overall prevalence could lessen the severity of the disease so that it becomes minor in both patches.

Example 5.3. Assume all parameters are as in Case 1 of Example 5.2 except that $c_1^{\mathit{vh}}=0.118$, $c_1^{\mathit{vh}}=0.08$, $d_1^{\mathit{hv}}=0.008$, $c_2^{\mathit{vh}}=0.012$, $c_2^{\mathit{hv}}=0.50$, $d_2^{\mathit{hv}}=0.176$, and the travel rates. This means that the two patches differ only in infectivity, namely, one with higher mosquito infectivity but lower human infectivity and the other with lower mosquito infectivity but higher human infectivity. Using formula (3.3), we obtain the respective basic reproduction numbers ${\mathcal{R}}_0^{\left(1\right)}=0.9899<1$ and ${\mathcal{R}}_0^{\left(2\right)}=0.9250<1$ for both patches in isolation. So the disease dies out in each isolated patch.

Next, when the patches are connected, we fix the travel rates of mosquitoes and susceptible humans by letting ${\psi }_{12}^S={\psi }_{12}^E={\psi }_{12}^I={\psi }_{21}^S={\psi }_{21}^E={\psi }_{21}^I=0.002$, ${\phi }_{12}^S={\phi }_{21}^S=0.15$ and want to see the effects of exposed, infectious and recovered human movement on the disease dynamics. If the travel rates of exposed, infectious and recovered humans are independent of residences and disease states, i.e., ${\phi }_{12}^E={\phi }_{12}^I={\phi }_{12}^R={\phi }_{21}^E={\phi }_{21}^I={\phi }_{21}^R=k$, then Fig 5.6 shows how ${\mathcal{R}}_0$ varies with k from 0 to 0.10.

Fig. 5.6.

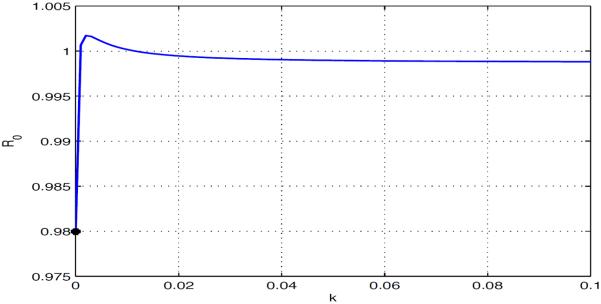
Relationship between ${\mathcal{R}}_0$ and $k={\phi }_{12}^E={\phi }_{12}^I={\phi }_{12}^R={\phi }_{21}^E={\phi }_{21}^I={\phi }_{21}^R$. The disease dies out when the exposed, infectious and recovered human travel rate is small or large, it persists otherwise.

The disease may die out if the exposed, infectious and recovered human movement is weak. Stronger travel of exposed, infectious and recovered humans between patches can lead to the disease becoming endemic in both patches. However, if the travel rate keeps increasing, the disease may again die out in both patches. This implies that inappropriate border control on exposed, infectious and recovered humans could have negative feedback. Observe that it is also an example where ${\mathcal{R}}_0$ is not monotone in the exposed, infectious and recovered human travel rate which is independent of residence and disease state.

6. Discussion

Malaria is one of the world's most common infectious diseases and it is a major cause of child death and poverty in Africa. This issue may become even more serious due to many factors such as the rapid expansion of modern transportation, urbanization in developing countries, deforestation and so on. In this paper, taking the transmission heterogeneity into account, we proposed a multi-patch model to study the impact of mobility of vector and host populations on malaria transmission. We have discussed the existence and stability of the disease-free equilibrium of the model and obtained a formula for the basic reproduction number ${\mathcal{R}}_0$. By applying some matrix inequalities, bounds on ${\mathcal{R}}_0$ were given. A sufficient condition was obtained to guarantee the existence of an endemic equilibrium. Then the dependence of ${\mathcal{R}}_0$ on the model parameters was analyzed. In particular, for a two-patch model, we studied the monotonicity of ${\mathcal{R}}_0$ in terms of the travel rates of exposed, infectious and recovered humans. Our analysis indicates that ${\mathcal{R}}_0$ varies monotonously with the movement of exposed, infectious and recovered humans which depends on the disease state. We should mention that the monotonicity also holds for mosquito movement. Finally, three numerical examples were given to illustrate the impact of population dispersal for the disease spread. The first example explores the role of different exposed, infectious and recovered classes in the disease propagation. The second one shows that suitable human movement can both intensify and mitigate the disease spread even for two identical patches. In the last example, two patches which only differ in infectivity of humans and mosquitoes are concerned. Non-monotonicity of ${\mathcal{R}}_0$ in the exposed, infectious and recovered human travel rate which is independent of the residence and disease state is observed. These results suggest that human movement is a critical factor in the spatial spread of malaria around the world. Since the travel of exposed (latently infected) human individuals can also spread the disease geographically and screening at borders usually can only help to identify those infected with symptom, inappropriate border control may make the disease transmission even worse and to control or eliminate malaria we need global and regional strategies (Tatem and Smith [42]). Accordingly, a full understanding of movement is important in designing effective anti-malaria measures.

There is still much work to do with our model. First of all, we are interested in the global stability of the disease-free equilibrium when ${\mathcal{R}}_0<1$. Unfortunately, it is difficult to give an explicit formula for the disease-free equilibrium (even for n = 2), so is ${\mathcal{R}}_0$. Even if we obtained such a formula, it is too complicated to use it directly. Unlike models in Salmani and van den Driessche [37] and Hsieh et al. [20], here we cannot use a comparison theorem for the vector-host model using their methods. Secondly, the existence, uniqueness and stability of the endemic equilibrium is in general unclear. Thirdly, the dependence of ${\mathcal{R}}_0$ on travel rates for three or more patches submodels would be extremely complicated since the interaction networks are more complex. However, at least we can do some numerical simulations. Furthermore, it is interesting to test our model with field data and carry out sensitivity analysis to develop efficient intervention strategies.

We remark that there are many possibilities to generalize the ODEs model studied here to increase realism. For example, in the model it is assumed that all parameters are constant. In fact, the biological activity and geographic distribution of malaria parasite and its vector are greatly influenced by climatic factors such as rainfall, temperature and humidity (Martens et al. [28], Smith et al. [38]). The impact of climate change can be investigated by assuming that some parameters to be time or temperature dependent. It is also important to consider stochastic versions of these models. The basic modeling approach of dividing the population into subclasses according to their locations and then observing their moving behavior can be viewed as a Markov process with random coefficients (Langevin formulation) or with known transition probabilities between regions. We leave all these for future consideration.