Adaptation maintains population homeostasis in primary visual cortex

Abstract

Sensory systems exhibit mechanisms of neural adaptation, which adjust neuronal activity based on recent stimulus history. In primary visual cortex (V1), in particular, adaptation controls the responsiveness of individual neurons and shifts their visual selectivity. What benefits does adaptation confer to a neuronal population? We measured adaptation in the responses of populations of cat V1 neurons to stimulus ensembles with markedly different statistics of stimulus orientation. We found that adaptation serves two homeostatic goals. First, it maintains equality in the time-averaged responses across the population. Second, it maintains independence in selectivity across the population. Adaptation scales and distorts population activity according to a simple multiplicative rule that depends on neuronal orientation preference and on stimulus orientation. We conclude that adaptation in V1 acts as a mechanism of homeostasis, enforcing a tendency towards equality and independence in neural activity across the population.

Sensory systems constantly exhibit perceptual adaptation, which goes unnoticed in our daily experience but becomes apparent after prolonged exposure to a given stimulus. Visual perception, for instance, can be profoundly affected after viewing steady motion^1,2 or constant orientation^3,4. Such perceptual phenomena are thought to arise from adaptation mechanisms that adjust neuronal activity based on recent stimulus history.

Sensory systems, indeed, exhibit various forms of neural adaptation^5-14. In primary visual cortex (V1), in particular, adaptation controls the responsiveness of individual neurons^6,15-20 and shifts their visual selectivity^{6,15,16,21,22}. While the first effect is akin to general neural fatigue, the second suggests a more specific adjustment of stimulus representation. However, sensory processing is mediated by neuronal populations²³, and the overall effects of adaptation on population activity have been hypothesized^2,24-26 but not measured. What benefits does adaptation confer to a neuronal population?

Results

To characterize coding and adaptation in a large population of cortical neurons, we recorded spiking activity from the primary visual cortex (V1) of anesthetized cats using 10 ×10 electrode arrays (Fig. 1b). We characterized responses as a function of stimulus orientation²⁷ using sequences of static gratings with random orientation and phase, each presented for 32 ms (Fig. 1a). We considered stimulus ensembles with two statistical distributions^5,7-10: uniform and biased. In the uniform case, the probability of each orientation was equal²⁷. In the biased case, the probability of one orientation was markedly higher than the others.

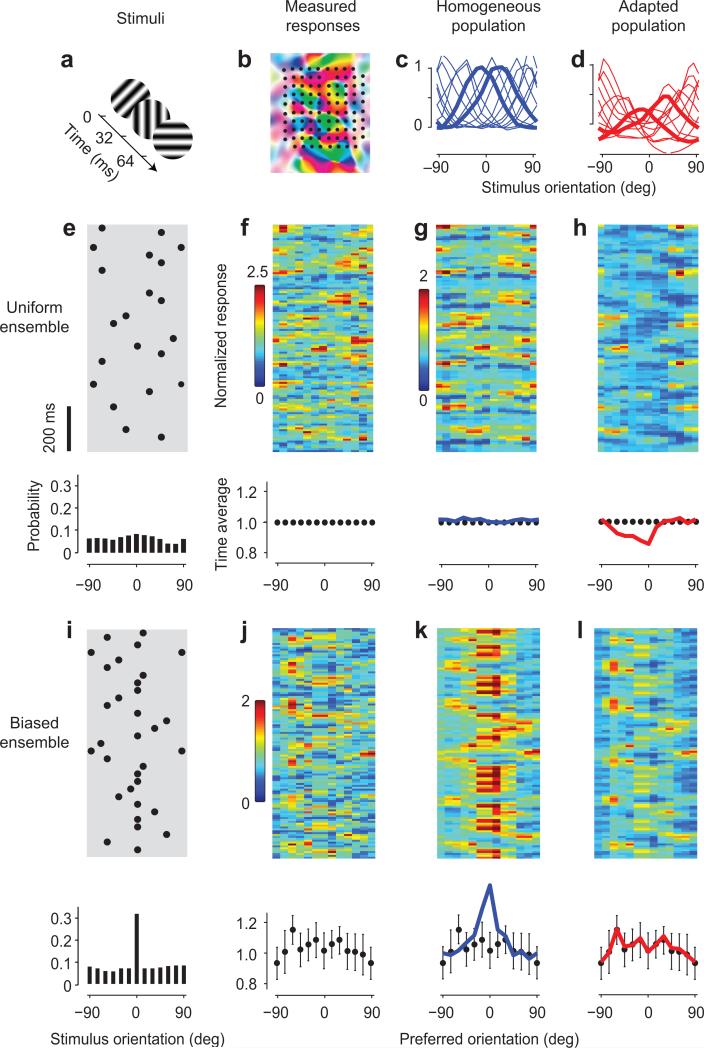
Fig. 1. Adaptation in visual cortex prevents biases in the population.

a: Stimuli were sequences of gratings with random orientation.

b: Layout of a 10×10 electrode array aligned with a map of preferred orientation (replotted from Ref. 49).

c: Tuning curves of neurons grouped by preferred orientation, measured with a uniform stimulus. Responses are scaled to the values of 1 at the preferred orientation and 0 at the orthogonal orientation.

d: Tuning curves measured with a biased stimulus, where the orientation of 0 deg was presented more often than the others. Thicker curves in c and d are tuning curves of neurons selective for -15 deg and +15 deg.

e: A segment of the stimulus sequence in the uniform ensemble. Each dot symbolizes a grating. In the whole sequence, the probability of presentation across orientations is flat (bottom panel).

f: Responses to the sequence in e. Each orientation bin is normalized to its own time average (bottom panel).

g: Fitted responses using the homogeneous tuning curves. Time averages are in bottom panel, blue line.

h: Simulation made using the adapted tuning curves. Time averages are in bottom panel, red line.

i-j: Same as e-f, but for a biased stimulus ensemble. Responses have the same scaling factor as those in f.

k: Simulation made using the homogeneous tuning curves.

l: Fitted responses using the adapted tuning curves.

Data in this figure are from experiments 75-6-2+3, with adaptor probability of 35%. Error bars in J-l bottom panels, ± 1 s.d.

As shown previously²⁷, population responses to stimuli with uniform statistics could be accurately fitted on the basis of the tuning curves of the neurons. We illustrate this with the results of a typical experiment (Fig. 1c, e-g). The stimulus was a time series of orientations (Fig. 1e) and the population responses varied as a function of time and of the preferred orientation of the neurons (Fig. 1f). We divided the axis of preferred orientation evenly into bins, each pooling the activity of neurons with similar orientation preferences. The population activity tracked the stimulus closely. By applying simple regression to these responses, we obtained tuning curves for each of the bins of preferred orientation (Fig. 1c). These tuning curves are homogeneous: they are similar to each other except for their preferred orientation. As expected²⁷, the tuning curves could be used to fit the population responses to the stimulus sequence through summation (Fig. 1g). This simple operation (followed by a mild nonlinearity²⁷) captured a high proportion (63%) of the explainable variance in the population responses in this experiment. A similar result was observed in 5 other experiments (Suppl. Fig. 1a).

When we changed the statistics of the stimulus ensemble, the cortex displayed a remarkable ability to adapt (Fig. 1i-k). We biased the stimulus sequence markedly in favor of one orientation (the “adaptor”), presenting it three times more often than the rest (Fig. 1i). Based on the tuning curves obtained with the uniform stimulus ensemble (Fig. 1c) the neurons selective for the adaptor orientation should respond on average much more than the others (Fig. 1k). The actual response of the population, instead, showed no such bias: the average over time of the cortical response to the biased stimulus ensemble did not show significant variation across neurons differing in preferred orientation (Fig. 1j). From the cortical responses it was not apparent that one orientation was shown three times more than the others. Evidently the neurons in visual cortex had adapted to the biased ensemble, and their adaptation had been strong enough to completely counteract the bias in the ensemble. Moreover, this adaptation was not so strong as to overcompensate, i.e. as to create a “hole” in the population responses.

The effects of adaptation were well described by a new set of tuning curves, one that was tailored for the biased ensemble (Fig. 1d,l). We obtained these adapted tuning curves (Fig. 1d) by applying regression on the population responses to the biased ensemble (Fig. 1j). Applying these tuning curves to the biased stimulus ensemble (Fig. 1i) yielded a fit (Fig. 1l) that resembled closely the measured population responses (Fig. 1j). This fit captured 40% of the explainable variance in the responses, significantly higher than the 22% captured by the homogeneous tuning curves. This increase in predictive power was observed in 4 other experiments (Suppl. Fig. 1c,d). In particular, the adapted tuning curves correctly captured how the average population response would show no trace of the bias in the stimulus (Fig. 1l, bottom).

The adapted tuning curves were significantly different from those measured during the presentation of the uniform ensemble, both in this experiment (Fig. 1c, d) and the others (Suppl. Figs. 2 and 3). Indeed, if one used the adapted tuning curves to simulate the responses to the uniform ensemble, one would grossly underestimate the responses of some of the neurons (Fig. 1h, and Suppl. Fig. 1b).

Similar results were obtained in 9 experimental sessions in 3 cats (Fig. 2). To pool the results across sessions we gave the orientation of the adaptor the nominal value of 0 deg, and the average response to the uniform ensemble the nominal value of 1 (Fig. 2a). The average population response to the biased ensemble was flat (Fig. 2d), showing neither a peak nor a trough for the responses of neurons tuned to the adaptor. Looking at these average responses, it would be impossible to tell that the adaptor had been shown 3-5 times more than the other orientations. Indeed, there was no statistical difference between the average responses of neurons selective for the adaptor (0 deg) and for the orthogonal orientation (t-test, p=0.98). As we have seen in the example experiment (Fig. 1), therefore, adaptation changed the tuning curves just as needed to counter the bias in the stimulus ensemble – neither too much nor too little.

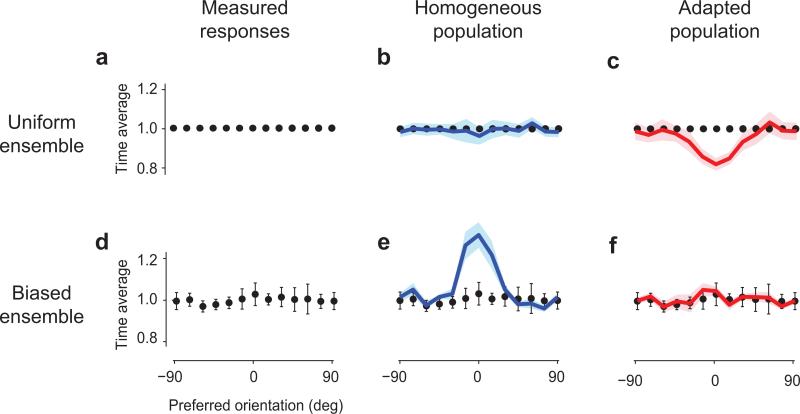
Fig. 2. Adaptation equalizes population responses.

a: The time average of the population responses to uniform stimulus ensembles was normalized to 1.

b: Time averages of fits by homogeneous tuning curves, averaged across 5 experiments (blue curve, shaded area ± 1 s.e.).

c: Time averages of predictions by adapted tuning curves, averaged across 5 experiments (red curve).

d-f: Same as a-c in responses to stimuli in biased ensembles. Data and error bars (± 1 s.e., n=4) illustrate equalization, and are repeated in each panel. The homogeneous tuning curves incorrectly predict a large peak (e), whereas the fits by the adapted tuning curves correctly capture equalization (f).

Just as we have seen in the example data set (Fig. 1), achieving this equalization requires significant changes in tuning curves (Fig. 2). In other words, no single set of tuning curves could predict the measured responses to both the uniform and biased stimulus ensembles. For instance, the responses to the biased ensemble (Fig. 2d) could be fitted by the adapted tuning curves (capturing 54%±20% of the explainable variance, SE, n = 4, Fig. 2f), but could not be obtained from the homogeneous tuning curves, which predicted a non-existing peak in the population responses at the orientation of the adaptor (16%±12% of the explainable variance, Fig. 2e). Conversely, the responses measured with the uniform stimulus ensemble could be fitted by the homogeneous tuning curves (88%±16% of the explainable variance, n = 8, Fig. 2b), but could not be obtained with the adapted tuning curves, which predicted a non-existing hole in the population responses at the orientation of the adaptor (capturing 48%±11% of the explainable variance, Fig. 2c).

This analysis, therefore, reveals that adaptation maintains equality in the time-average activity of different neurons, in the face of biases in the stimulus ensemble. Achieving this equality requires appropriate calibration: if adaptation were stronger or weaker there would be a valley or a mountain in the population responses, and instead there is neither. Equality, however, can only be maintained for a range of stimulus biases. At the extreme, if a single orientation were shown 100% of the time (as is typically the case in previous studies of adaptation) one would expect the neurons selective for that orientation to respond more than the rest. Indeed, while we saw complete equalization when the probability of the adaptor was 30-40% (Fig. 2e), equalization was less perfect when we increased this probability to 50% (Suppl. Fig. 4).

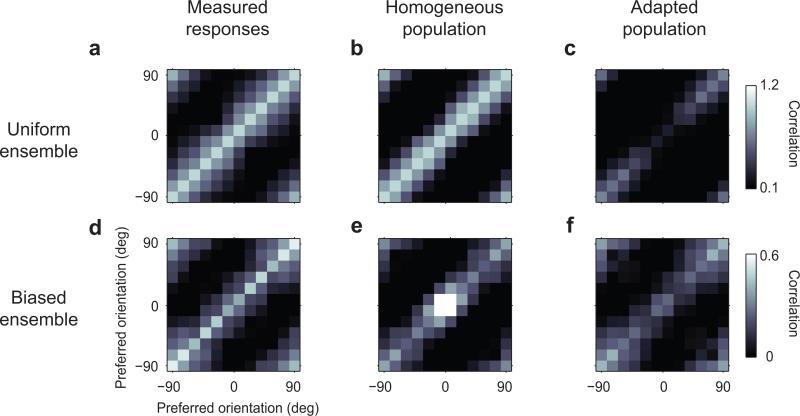
In addition to equalization, adaptation helped maintain decorrelation across the population (Fig. 3). Because of the width of the tuning curves, a biased stimulus sequence tends to engage not only the neurons selective for the adaptor orientation but also those selective for nearby orientations. In the absence of adaptation, the activity of these neurons would therefore become highly correlated (a “correlation catastrophe”). To look for these effects, we computed the correlation coefficients between pairs of bins, for each combination of orientation preference. These are known as “signal” correlations²⁸, and they reflect the similarity in tuning curves. As expected, the matrix of correlations in the uniform case was diagonal (Fig. 3a). The tuning curves obtained in this condition capture this diagonal aspect (Fig. 3b), but they also predict that in the responses to the biased stimulus ensemble there should be a strong central peak in the matrix (Fig. 3e): the “correlation catastrophe”. Instead, the population responses to the biased stimulus ensemble (Fig. 3d) showed a diagonal structure of correlations that is similar to the one seen with the uniform stimulus ensemble (Fig. 3a). Consistent with a longstanding theoretical proposal^24,29-31, therefore, adaptation prevented responses of cortical neurons from becoming more correlated.

Fig. 3. Adaptation decorrelates population responses.

a: Correlation coefficients between pairs of neuronal bins measured with the uniform stimulus ensemble (n=5). The values on the diagonal are scaled to 1. The subsequent panels have the same scaling factors.

b-c: Correlation coefficients of responses fitted by uniform tuning curves (b) and predicted by adapted tuning curves (c).

d-f: Same as a-c for responses to stimuli in the biased ensemble. The homogeneous tuning curves incorrectly predict a central peak in correlation (b) whereas the fits by the adapted tuning curves correctly capture a diagonal matrix (c).

This effect of decorrelation could be captured by the adapted tuning curves: running the biased stimulus ensemble through these adapted curves resulted in a diagonal matrix of correlations without a central peak (Fig. 3f). The adapted tuning curves, instead, would not have been appropriate in response to the uniform stimulus ensemble, as they would have caused a large central hole in the matrix of correlations (Fig. 3c).

Taken together, these results indicate that adaptation provides two homeostatic effects to the population, maintaining equality not only in the first order statistics, but also in the second order statistics. These effects are achieved quickly, with an average time constant of 1.7 ± 0.4 s (s.d., Suppl. Fig. 5). In such a short interval the cortex was able to engage adaptation mechanisms that effectively counteracted the bias in the stimulus ensemble, both in terms of first and of second order statistics. However, adaptation is known to operate on more than one time scale^6,32,33. Perhaps a relevant determinant of time scale is the number of stimuli that adaptation mechanisms need to observe to be fully engaged. In our experiments, 1.7 s correspond to ~53 stimuli. It was sufficient for V1 to observe the same orientation in 16-26 of those stimuli to drastically adapt its responsiveness and selectivity.

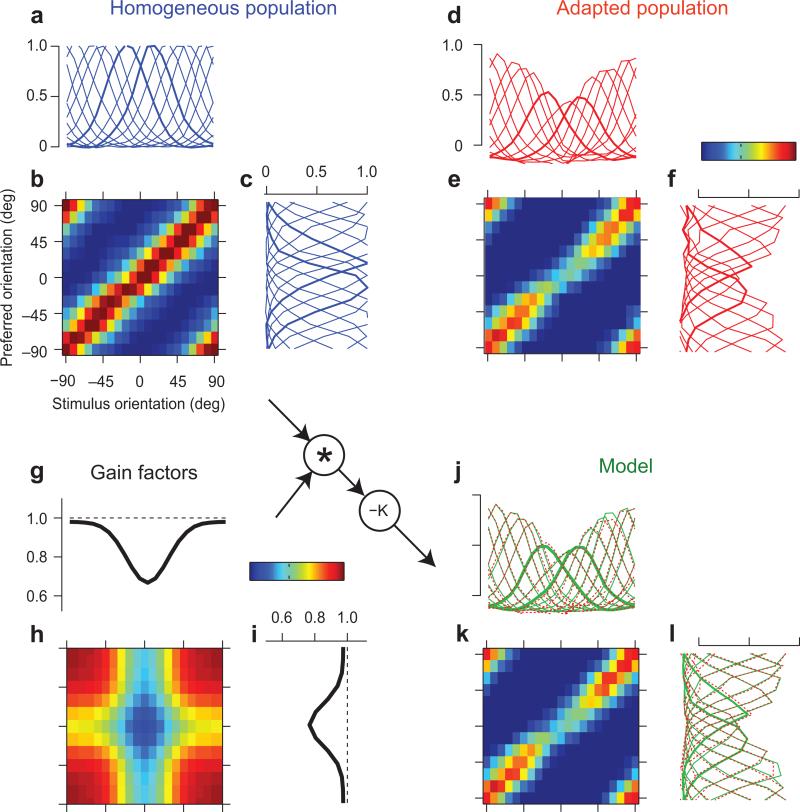
What does adaptation change in a population to allow it to discount these stimulus statistics? Since the effects of adaptation are captured by changes in tuning curves, the answer lies in the attributes of these tuning curves (Fig. 1c,d). To characterize these tuning curves, and to reveal more detailed effects, we examined the full matrix of responses to individual flashing gratings, averaging the results of all our experiments (Fig. 4a-c). This response matrix (Fig. 4b) depends both on the preferred orientation of the neurons (rows) and on the orientation of the stimulus (columns). Taking sections across the rows yields the familiar tuning curves of each preference bin (Fig. 4a). Taking sections across columns instead yields population response profiles, one for each stimulus orientation (Fig. 4c).

Fig. 4. Neuron-specific and stimulus-specific components of adaptation.

a: Tuning curves measured with uniform stimulus ensembles, averaged over all 11 sessions in 4 cats. As elsewhere, zero indicates the orientation of the adaptor.

b: Matrix of responses to individual gratings, as a function of preferred orientation and stimulus orientation.

c: Population response profiles in response to stimuli of different orientations.

d-f: same as a-c, measured in responses to stimuli with biased statistics.

g-i: A simple multiplicative model of adaptation, based on two gain factors, one dependent on stimulus orientation (g) and one dependent on neuronal preferred orientation (i). Their product is a gain matrix (h).

j-l: Model fits. Format is as in d-f. The predicted response matrix (k) is, obtained by multiplying the gain matrix by the response matrix measured with the uniform ensemble (inset). Predicted tuning curves (j) and population response profiles (l) closely resemble the measured ones (replotted in red).

The response matrix measured with the biased ensemble summarizes the effects of adaptation (Fig. 4d-f). A qualitative look at these tuning curves and population responses indicates that adaptation had two main effects. The first effect was an offset: a small reduction of all responses, regardless of orientation preference (Fig. 4d) and of stimulus orientation (Fig. 4f). We will model this effect with a simple subtractive shift. The second effect was a marked reduction in amplitude of the tuning curves, which as strongest for the tuning curves of neurons with orientation preference near zero, the nominal orientation of the adaptor (Fig. 4d). This effect amounted to creating a hole in the diagonal of the matrix (Fig. 4e).

There are two simple ways to creating such a hole along the diagonal of the response matrix (Fig. 4e): across rows and across columns. The first possibility is intuitive and rests on neuron identity: adaptation would reduce mostly the responses of the neurons selective for the adaptor (Fig. 4d). The second possibility is less intuitive, and rests on the stimuli rather than on the neurons: adaptation would control the population responsiveness to different stimuli, reducing it most strongly for stimuli with the same orientation as the adaptor (Fig. 4f).

Both descriptions are rooted in studies of adaptation in single neurons. The neuron-specific description of adaptation evokes simple forms of neural fatigue, and agrees with the view of adaptation as controlling a neuron's responsiveness or sensitivity^18-20. The stimulus-specific description involves fatiguing stimuli (rather than neurons), reducing their effectiveness in driving the cortex. This description agrees with the stimulus-specific effects of adaptation that have been reported in single neurons ^6,15-17,34.

To resolve the dichotomy in these descriptions, we designed a simple model that includes both neuron-specific and stimulus-specific factors (Fig. 4g-i). In the model, the response matrix is scaled by two multiplicative gain factors. One of these factors specifies how much to reduce the responsiveness of each neuron (Fig. 4i) and the other specifies how much to reduce the responses to each stimulus (Fig. 4g). We described the gain factors as Gaussians peaking at zero (the orientation of the adaptor and the preferred orientation of neurons tuned for the adaptor). The two Gaussians are multiplied to obtain a matrix of gain factors (Fig. 4h). In practice, the model works as follows: take the response matrix measured with the uniform stimulus ensemble (Fig. 4b), multiply it pointwise by the matrix of gain factors (Fig. 4h), and subtract a constant offset. The model is defined by only five parameters: the two widths and two amplitudes of the Gaussians, and the constant offset.

This simple model described accurately the effects of adaptation (Fig. 4j-l). The fitted model predicted a response matrix (Fig. 4k) that was extremely similar to the actual one (Fig. 4e), explaining 89.3% of the variance in this matrix. This similarity is confirmed by plotting the tuning curves on top of the measured ones (Fig. 4j) or by plotting the population response profiles on top of the measured ones (Fig. 4l). Similar results were obtained when working with matrices obtained separately from the experiments with adaptor probability of 30-40% (n=6, 80.0% of the variance) and with adaptor probability of 50% (n=5, 86.7% of the variance).

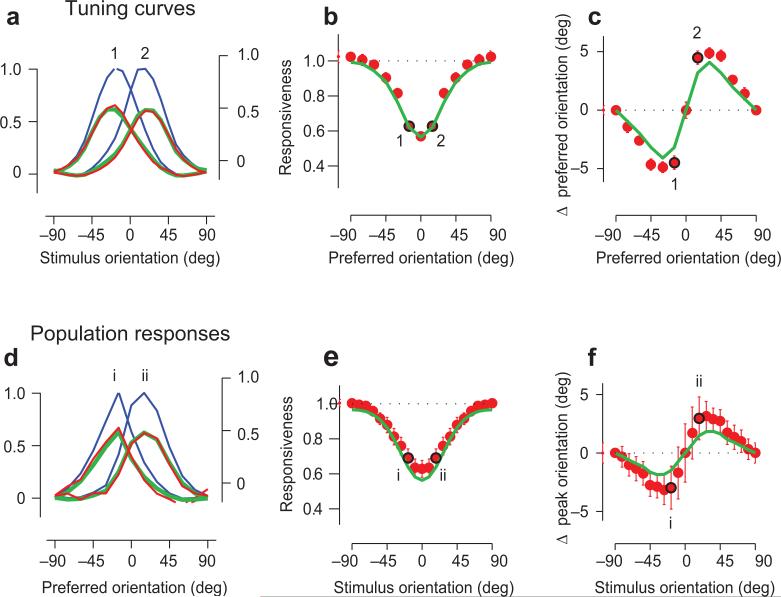
In particular, the model correctly predicted that adaptation would reduce the tuning curves and repel them away from the adaptor orientation (Fig. 5a-c). Because one of the gain factors depends on stimulus orientation (Fig. 4g), it scales the tuning curves more on the flank towards the adaptor than on the other flank, pushing them away from the adaptor orientation (Fig. 5a). The result is that tuning curves are reduced^6,18-20 (Fig. 5b) and change in preferred orientation^15,16,21,22 (Fig. 5c). Our simple model captures these effects very precisely (Fig. 5a-c, green curves).

Fig. 5. Effects of adaptation on tuning curves and population responses.

a: Tuning curves of neurons selective for +15 deg and -15 deg relative to adaptor, measured with uniform stimuli (blue curves, left scale), with biased stimuli (red curves, right scale). Green curve shows model fit.

b: Changes in tuning curve amplitude as a function of preferred orientation. Red dots are data, green curve is the model fit. Points marked 1 and 2 indicate the examples in a.

c: Same as b, but for changes in preferred orientation.

d-f: Same as a-c, but for population response profiles.

In addition, the model makes a novel prediction: that adaptation should not only reduce population response profiles but also repel them away from the adaptor (Fig. 5p-r). The second gain factor depends on preferred orientation (Fig. 4i), so it scales the population profiles more on the flank where neurons are selective for the adaptor than on the opposite flank, pushing them away from the adaptor orientation. These predictions are verified in the data: population responsiveness is reduced (Fig. 5e) and the peak of the population response profile is pushed away from the adaptor orientation (Fig. 5f). The model predicts these effects (Fig. 5d-f, green curves).

Because it accounts for responses simultaneously recorded from a population, the model allows us to measure the relative importance of stimulus-specific adaptation and neuron-specific adaptation. Remarkably, the less intuitive component of the model, the one that is stimulus-specific (Fig. 4g) was even stronger than the neuron-specific one (Fig. 4i). The reduction in stimulus-specific gain was consistently larger than the reduction in neuron-specific gain, both in individual experimental sessions and in averages across sessions (Suppl. Fig. 6). The most important effect of adaptation is therefore the one that is stimulus-specific, as if adaptation had reduced the effective strength of stimuli with orientation near the adaptor.

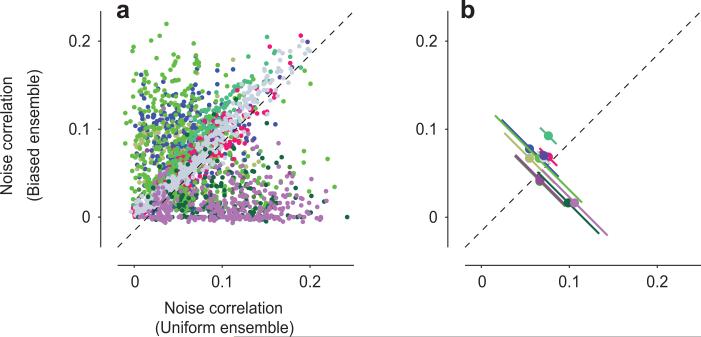
Our analysis of the effects of adaptation at the level of populations has concerned the average responses that the neurons give to repeated stimulus presentations (commonly termed “signal”), and not the trial-by-trial deviations from these average responses (“noise”). Measurements performed in awake primates following traditional, prolonged adaptation to single stimuli suggest that adaptation reduces the correlation among these deviations (“noise correlations”, Ref. 28) in neuronal pairs³⁵. Under our experimental conditions, however, we found little evidence for such an effect (Fig. 6). Indeed, adaptation to a biased ensemble reduced noise correlations in some pairs, but increased it in others (Fig. 6a). The overall effect seemed to vary across data sets (Fig. 6b): in some, adaptation slightly reduced noise correlations (6/11 with p<0.05: Wilcoxon rank sum test), and in others it slightly increased them (4/11), or showed no significant difference (1/11). On average, however, noise correlations stayed quite constant: the average difference in noise correlation between experiments with biased statistics and experiments with uniform statistics was a negligible 0.02±0.06 (s.d., N = 69,596 pairs). Similar effects were seen when the spike binning was shifted relative to the stimulus refresh times (not shown), and when noise correlations were computed over longer time intervals (2 s bins rather than 32 ms bins, Suppl. Fig. 7). We then asked whether adaptation might influence noise correlations more for pairs that are selective for certain orientations than for others³⁵. The results were negative, with similarly low effects of adaptation on noise correlations regardless of the preferred orientation in a pair, relative to the adaptor (Suppl. Fig. 8). These results indicate that under our experimental conditions the effects of adaptation on the population code can be fully summarized by the effects on average signals and signal correlations, with little effect on trial-by-trial deviations from these signals.

Fig. 6. Adaptation to biased ensembles does not affect pairwise noise correlations.

a: Noise correlations between pairs of units in response to uniform and biased ensembles. Colors distinguish data sets (n=11). For graphical purposes, only a randomly selected 5% of the 69,596 pairs are displayed.

b: The same data, averaged within each data set (n = 11, each with 1,892-9,120 pairs). The error bars indicate ± 1 s.d. of the difference in noise correlations in responses to the uniform and biased ensembles.

Discussion

To summarize, we discovered that primary visual cortex displays a remarkable ability to counteract biases in the stimulus ensemble, by rapidly introducing the appropriate opposing biases in the responsiveness and selectivity of neurons. These adaptation phenomena are due to homeostatic mechanisms that have two simple goals: to maintain equality in the time-averaged responses across the population, and to enforce independence in selectivity across the population.

These results provide experimental evidence for prescient previous proposals. The first goal, equalization, is consistent with proposals made by psychophysicists of adaptation being a “graphic equalizer” to counteract changes in the statistics of the environment¹. It also echoes proposals that adaptation may act to “centre” a population response by subtracting the responses to the prevailing stimulus distribution²⁵, or to scale responses so that the average of a measured signals is always mapped onto a fixed internal representation²⁶ . The second goal, independence, was predicted by a longstanding proposal concerning the role of adaptation in maintaining decorrelation in cortex^24,25,29,30.

We were able to understand the goals of these homeostatic mechanisms because we measured responses in a whole population, and because we measured activity concurrently with changes in stimulus statistics^5,7-10. Recording from a whole population is a promising technique to study adaptation³⁶. The key technical innovation here, however, lies in the choice of stimuli. These stimuli allowed us to observe the homeostatic mechanisms achieve their stable (and arguably intended) effects rather than their fleeting (and arguably unintended) aftereffects. By contrast, previous studies of adaptation in V1 used the traditional adapt-test technique⁶ developed in psychophysics^1,3,37-41, where the phases of adaptation and response measurement are distinct. This technique can only reveal adaptation's aftereffects, those that persist after a change in stimulus properties even though they are no longer needed.

We further discovered that adaptation in primary visual cortex follows a very simple arithmetical rule to shape the population responses. At the heart of this rule is multiplication with two gain factors, one that depends on stimulus attributes and one that depends on neuronal preference. This rule provides a unified framework that encompasses the known effects of adaptation on responsiveness and orientation selectivity of individual V1 neurons. Having this arithmetical rule, in turn, can guide and constrain research into the underlying circuits and mechanisms. These could involve synaptic depression^42,43 and fatigue at a prior cortical stage ³⁴. For instance, since our recordings mostly targeted layer 2/3, the adaptation we measured there could be at least partially inherited from inputs from layer 4.

The mechanisms we have discovered may well operate in the whole cortex, but for now we can only demonstrate that they do so in primary visual cortex, and specifically in the processing of stimulus orientation. Future work could establish the degree to which our observations generalize to other stimulus variables beyond orientation, and to other cortical areas beyond V1. Further work is also required to understand how the effects of adaptation in one sensory area cascade into subsequent ones, leading to compounding perceptual effects ⁴⁴. For instance, the effects of adaptation observed in primary visual cortex appear to be quite distinct from those observed in cortical area MT (Refs. 34,45). It is not entirely clear to what degree these differences can be explained by inheritance. Moreover, though it is possible that the effects of adaptation in area MT would be consistent with those that we propose, this needs to be established experimentally, for instance by adapting MT neurons to aspects of the stimuli that do not elicit selective responses in V1.

Adaptation is thought to be a mechanism constantly at work throughout cortex. We tend to notice its perceptual effects only when it does not work properly, or rather when it is catching up with a marked change in stimulus statistics^1-4. The simple arithmetical rules that we have uncovered to describe neural adaptation may guide future work to study this perceptual adaptation. Moreover, they provide a framework to link adaptation with other mechanisms of homeostasis, such as the ones at work during plasticity and development⁴⁶. Meanwhile, the results we have observed in primary visual cortex offer a promising first glimpse at how an entire cortical population adapts to the statistics of its inputs.

Methods

Experiments were carried out at the Smith-Kettlewell Eye Research Institute, under the supervision of the local Institutional Animal Care and Use Committee. They were performed in the same animals and with the same methods as in our previous study²⁷.

Briefly, 4 young adult female cats (2-4 Kg) were anesthetized with ketamine and xylazine during surgical procedures and with sodium pentothal and fentanyl during electrical recordings. A neuromuscular blocker was administered to prevent eye movements. The animals were respirated and the depth of anesthesia carefully monitored and adjusted by following EEG and vital signs. Utah probes (Blackrock, Utah) were inserted in area V1 with a pneumatic device to minimize tissue damage, and covered in 2% agar to improve stability. The probes consisted of a grid of 10×10 silicon electrodes with 400 μm spacing and 1.5 mm electrode length. Insertion depths were about 0.8–1 mm, resulting in recordings confined mostly to layers 2/3. Receptive fields were typically on the vertical meridian, indicating that the electrodes were placed at the border between areas 17 and 18, which together form cat area V1.

Stimuli were presented to the contralateral eye on a CRT monitor (refresh rate 120 Hz, mean luminance 32 cd/m²). They consisted of large, stationary gratings (30 deg in diameter) flashed in random sequence for 32 ms each. Each grating had one of 4 spatial phases and one of 6-12 orientations. The orientations could occur either with equal probability or with a biased statistics, where the ‘adaptor’ orientation had a higher probability of occurrence (p = 0.30, 0.35, 0.40, or 0.50). Grating contrast was typically 50-80% and spatial frequency was 0.2 cycles/deg. This spatial frequency was empirically determined to be effective in activating the recorded neurons, and is visible to neurons in both area 17 and 18 (Ref. ⁴⁷). Sequences were broken into 4–8 segments lasting 6-20 s each. Additional control segments were measured in response to gray screen. Segments were presented in random order and each block of segments was generally presented ten times.

Well-tuned multiunit activity was typically recorded from most of the 96 electrodes. Traces were acquired at 12 kHz and firing rates were obtained by low-pass filtering the spike trains with a cutoff at 25 Hz. Firing rates were then resampled at 32 ms intervals (the duration of our flashed gratings). To identify multi-unit activity (MUA) we set thresholds at 4 s.d. of the background noise in each of the 96 channels of the multielectrode array.

Population responses were computed by binning sites (15 deg bin width) according to their preferred orientation. Such preferred orientation was determined in the first experiment of the series with an unbiased stimulus sequence using event-related analysis²⁷. Binned responses in subsequent experiments with a biased stimulus ensemble where normalized to the time averages of responses to the first experiment. To compute correlation coefficients, instead, responses were normalized to the standard deviation over time.

To study the effects of adaptation we could not use the traditional method of event-related analysis²⁷ because this method works only for random stimuli whose distribution is uniform and spherical⁴⁸. We therefore measured a neuron's filter (or receptive field) F(τ, θ)in time τ and orientation θ as the least-square solution to the equation r(t) = Σ_θΣ_τS(t – τ, θ)F(τ, θ), where r(t) is the response of the neuron at time t and S(t – τ, θ) is the stimulus at time t – τ and orientation θ (a matrix of zeros and ones). We solved the equation in Matlab version R2012a using the pseudoinverse operator pinv. In the case of uniform stimuli, this procedure is analogous to simple stimulus-triggered averaging (Suppl. Fig. 9). Other aspects of the LN model, including the static nonlinearity, are as in our previous study²⁷. The static nonlinearity was imposed to be the same when modeling the responses to uniform and biased stimuli; this ended up being an excellent approximation as the fits barely improved if we allowed two different nonlinearities in the two adaptation conditions.

Only experiments with average responses r(t) having a mean over variance (s/n) significantly lower at times before the stimulus onset than at times during peak response (~40 ms after stimulus onset) were considered for further analysis.

The filters F(τ, θ)were matrices of size 12 × 8, where 12 was the number of preferred orientations and 8 the number of time steps in the past (Suppl. Fig. 9a). From these matrices we obtained one-dimensional tuning curves by considering the time at which the filter attained its maximal value.

To study how adaptation affected the correlations between stimuli (Fig. 3) we first averaged responses across stimulus repetitions. Then, we normalized the data by the standard deviation over time of the responses in the uniform-ensemble condition. Finally, we computed the covariance between pairs of orientation bins: cov = E[(R_i – E(R_i))(R_j – E(R_j))], where E is the expectation operator, and R_i(t) and R_j(t) are the responses of neurons in bins i and j.

The model of adaptation (Fig 4g-l) specifies the responses to individual gratings of neurons selective for orientation θ_p to stimulus with orientation θ_s. The response of the neurons when the stimulus ensemble is uniform is R_uniform(θ_s, θ_p), and the responses when the stimulus ensemble is biased is R_biased(θ_s, θ_p).

The model can be written as follows

$$R_{biased}({\theta }_s,{\theta }_p)=\alpha S({\theta }_s-{\theta }_a)P({\theta }_p-{\theta }_a)R_{uniform}({\theta }_s,{\theta }_p)-K,$$

where θ_a is the adaptor orientation. In this equation, α is an overall gain factor, K is a subtractive term, and S and P are terms that govern the stimulus-specific adaptation and the neuron-specific adaptation:

$$\begin{array}{cc}\hfill S({\theta }_s-{\theta }_a)& =1-a_{s}G({\theta }_s-{\theta }_a,28.3),\hfill \\ \hfill P({\theta }_p-{\theta }_a)& =1-a_{p}G({\theta }_p-{\theta }_a,28.3),\hfill \end{array}$$

where G(μ, σ) is a circular Gaussian with mean μ and standard deviation σ. The value of 28.3 deg was simply obtained by fitting a Gaussian function to the tuning curves. In other words:

$$R_{uniform}({\theta }_s,{\theta }_p)\approx G({\theta }_s-{\theta }_p,28.3).$$

The subtractive baseline K can be taken to be a constant or, for improved fits, to be a function of stimulus orientation as follows:

$$K({\theta }_s-{\theta }_a)=kG({\theta }_s-{\theta }_a,{\sigma }_k).$$

Here, the parameters k and σ_k determine the strength and tuning of the subtractive term. In the fits, the latter came out to be very large, leading to an almost flat curve, i.e. almost a constant.

The model, therefore, has five free parameters: the three multiplicative gain factors α, a_s, and a_p, and the two parameters of the subtractive baseline, k and σ_k.

To compute noise correlations, we measured multiunit activity on 44-96 responsive recording sites per experiment. Sites were considered responsive if their mean response explained at least 10% of the variance across repeats. We divided time in 32 ms or 2 s bins and represented the spike count at time t of the i^th site to the n^th repeat of a stimulus sequence as r_i,n(t). The noise correlations between a pair of sites i and j are calculated as the Pearson's linear correlation coefficient between (r_i,n(t) – r̂_i(t)) and (r_j,n(t) – r̂_j(t)), where r̂_k (t) is the mean response of site k across all stimulus repeats. We also considered the time bins 1.5 s after stimulus onset, to allow for the effects of adaptation to stabilize.