Abstract
Several quantitative MRI-based protocols have been developed for measuring the volume of entorhinal (ERC), perirhinal (PRC), and posterior parahippocampal (PPHC) cortex. However, since the volume of a cortical region is a composite measure, relating directly to both thickness and surface area, it would be ideal to be able to quantify all of these morphometric measures, particularly since disease-related processes, such as Alzheimer’s disease (AD), may preferentially affect thickness. This study describes a novel protocol for measuring the thickness, surface area, and volume of these three medial temporal lobe (MTL) subregions. Participants included 29 younger normal subjects (ages 18–30), 47 older normal subjects (ages 66–90), and 29 patients with mild AD (ages 50–96). Cortical surface models were reconstructed from the grey/white and grey/cerebrospinal fluid boundaries, and a hybrid visualization approach was implemented to trace the ERC, PRC, and PPHC using both orthogonal MRI slice- and cortical surface-based visualization of landmarks. Anatomic variants of the collateral sulcus (CS) were classified in all 105 participants, and the relationship between CS variants and corresponding morphometric measures was examined. One CS variant–a deep, uninterrupted CS not connected with nearby sulci–was the most common configuration and was associated with thinner cortex within the ERC and PRC regions. This novel protocol enables the reliable measurement of both the thickness and surface area of ERC, PRC, and PPHC.
1. Introduction
The entorhinal cortex (ERC), perirhinal cortex (PRC), and posterior parahippocampal cortex (PPHC) are anatomic regions in the medial temporal lobe (MTL) that are critical for memory function (Amaral and Insausti, 1990; Squire and Zola, 1996)Witter et al., 2000), and which have been implicated in early Alzheimer’s disease (AD) (Hyman et al., 1984; Braak and Braak, 1991; Arriagada et al., 1992; Braak and Braak, 1995; Gomez-Isla et al., 1996). Recently, quantitative protocols have been developed to study ERC and PRC volumes using MRI and validated against cytoarchitectural features (Insausti et al., 1998b). Since then, a variety of modifications to this fundamental methodology have been developed (Honeycutt et al., 1998; Killiany et al., 2000; Goncharova et al., 2001), and methods have been proposed for the measurement of PPHC volume as well (Pruessner et al., 2002).
Studies applying these volumetric protocols have demonstrated atrophy in groups of patients with AD, and in groups of individuals with mild cognitive impairment (MCI) who convert within a few years to a diagnosis of AD, suggesting that in vivo MTL cortical volumetric measurements are capable of identifying anatomic changes in the earliest stages of AD prior to dementia (Juottonen et al., 1998; Bobinski et al., 1999; Killiany et al., 2000; Xu et al., 2000; Dickerson et al., 2001; Du et al., 2001; Pruessner et al., 2002). It is controversial whether ERC atrophy is present in normal aging (Insausti et al., 1998a; Du et al., 2003; Raz et al., 2004). It is possible that the ERC atrophy effects observed in clinically normal older groups result from the presence of subclinical AD pathology, which may be more or less frequent depending on the sample, but it is also possible that measurement of the volume of the ERC may not be the best way to distinguish the process of AD from that of normal aging.
The volume of the ERC or any other bounded cortical region is a composite measure that relates directly to both cortical thickness and surface area. It is impossible from previous studies to ascertain whether reduced ERC volume is the result of cortical thinning, reduction in surface area, or both. Furthermore, there is a great deal of variability in definitions of the boundaries of ERC, PRC, and PPHC. The collateral sulcus (CS), which is the major macroscopic landmark used to define one border of the ERC, PRC, and PPHC (Insausti et al., 1998b), varies greatly across individuals (Ono et al., 1990), and may be challenging to identify in some cases from coronal MRI slices.
In this study, we developed a novel protocol for measuring the volume, thickness, and surface area of the ERC, PRC, and PPHC. To do so, we employed a novel semiautomated method augmented with manual operator tracing to identify boundaries. A hybrid visualization approach involving both typical MRI slices as well as a cortical surface model enabled visualization of gyral and sulcal topography, which was used as a basis for identifying the landmarks for boundary definition, the protocol for which was a slight variation on previously described anatomic protocols for these regions. As part of this study, we classified anatomic variants of the CS in 105 participants to investigate potential effects of these variants on morphometric measures of the ERC, PRC, and PPHC. Here we describe the protocol, our reliability analyses, and the CS anatomic variant study, while in an accompanying paper we apply this method to study the effects of aging and AD on MTL regional morphometry (Dickerson et al., submitted).
2. Methods
2.1. Participants
The data reported here were acquired from 105 individuals subdivided into three groups: 29 cognitively normal younger individuals (20f/9m, ages 18–30, mean: 23.55 ± 3.68), 47 cognitively normal older individuals (30f/17m, ages 66–90, mean: 76.2 ± 6.8), and 29 patients diagnosed with very mild or mild dementia of the Alzheimer’s type (referred to here as clinically diagnosed Alzheimer’s disease (AD); 18f/11m, ages 56-90, mean: 73.8 ± 11.7, CDR = 0.5 (very mild AD dementia) or 1 (mild AD dementia)). Clinical evaluation and scanning of participants were performed at Washington University (St. Louis, MO). All participants consented to participation in accordance with guidelines of the Washington University Human Studies Committee. Please see the accompanying manuscript (Dickerson et al., submitted) for detailed clinical and demographic data on the participants (the data presented in the present study is derived from the same participants as that of the accompanying study).
2.2. Image Acquisition
Structural MR images were acquired on a 1.5 T imaging system (Siemens Vision, Erlangen, Germany). Three to four acquisitions of a T1-weighted MPRAGE sequence (repetition time [TR] 9.7 msec, echo time [TE] 4 msec, flip angle [FA] 10, inversion time [TI] 20 msec, delay time [TD] 200 msec, 256 x 256 [1 mm x 1 mm] in-plane resolution, 128 sagittal 1.25 mm slices without gaps, time per acquisition 6.6 minutes) were acquired from each subject and averaged together in order to optimize signal-to-noise ratio for the use of gray-white contrast for segmentation.
2.3. Image Processing
All images were processed using Freesurfer’s (Massachusetts General Hospital, Boston, MA; http://surfer.nmr.mgh.harvard.edu, (Dale et al., 1999; Fischl et al., 1999a; Fischl et al., 1999b; Fischl and Dale, 2000; Fischl et al., 2001; Segonne et al., 2004)) cortical processing stream. Each average MR image was segmented into gray and white matter. Models for each of the gray matter and white matter surfaces were created from the corresponding MR image. Thus, both the typical MRI data as well as a model of the cortical surface can be visualized for each individual subject, enabling relationships to be appreciated between anatomic features within the native MRI (e.g., lateral geniculate nucleus (LGN)) and anatomic features on the cortical surface (e.g., CS morphology, see Figure 2). Manual tracings and morphometric computations were performed on the model by one rater. The dura layer that is present superficially to the ERC was removed using manual editing to ensure accurate measurement of regional cortical thickness. One rater (E.F.) performed all the manual procedures.
Figure 2.
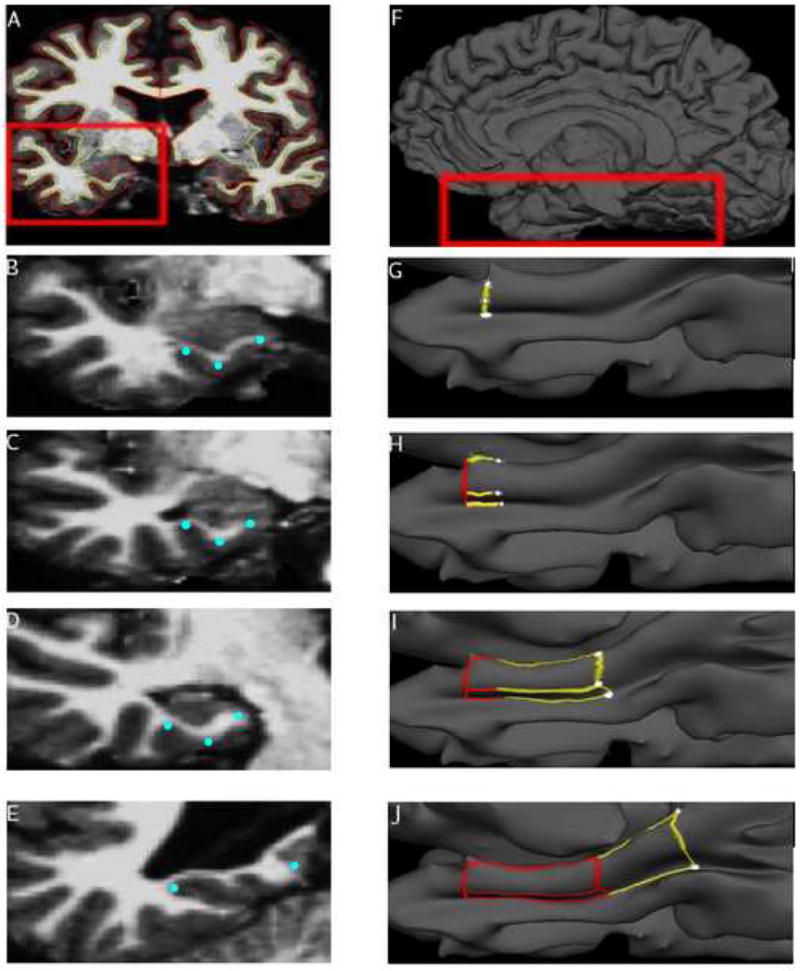
Step-by-step illustration of manual cortical surface-volume tracing protocol. Points, shown in blue, selected on the volume (left), were matched to points along the surface (right), shown in white. These points were used to delineate the borders of each region. (B, G) The rostral border of the ERC/PRC was traced first. (C, H) Tracing continues caudally, with the dorsomedial and ventrolateral borders of ERC/PRC delineated. To increase reliability, the paths are only drawn to the midpoint. (D, I) ERC/PRC borders are fully traced. (E, J) Tracing of the PPHC borders extends from the ERC/PRC dorsomedial and ventrolateral borders.
2.4. Development of Protocols
A novel surface-volumetric protocol for delineating the ERC, PRC, and PPHC was developed in part based on previous work (Dickerson et al., 2001; Goncharova et al., 2001). This protocol makes use of a novel visualization approach for enabling the operator to see and delineate cortical ROI boundaries. That is, anatomic landmarks that are inherently part of the deeper tissue (e.g., LGN) can be viewed within the MR image (in traditional orthogonal planar views) and anatomic landmarks that are part of the cortical surface (e.g., collateral sulcus) can be viewed in their native or inflated configuration on the model of the cortical surface. The location of these features can be mapped back and forth between the surface and native MR data: for example, the coronal slice from the MRI on which the LGN appears can be marked in the native image and mapped to the surface for visualization, or the surface point on which the CS forks can be marked on the surface and mapped to the MR image for visualization (see Figure 2). We used all the information available from both of these visualization methods to determine the boundaries for the regions, as described below.
2.5. ERC, PRC, and PPHC boundary definitions
The outlines of the ERC, PRC, and PPHC on coronal sections of a T1-weighted MPRAGE MRI image are shown in Figure 1. These boundary definitions, which are based on previous work by our group and others, are not novel in themselves, but will be summarized here for clarity.
Figure 1.
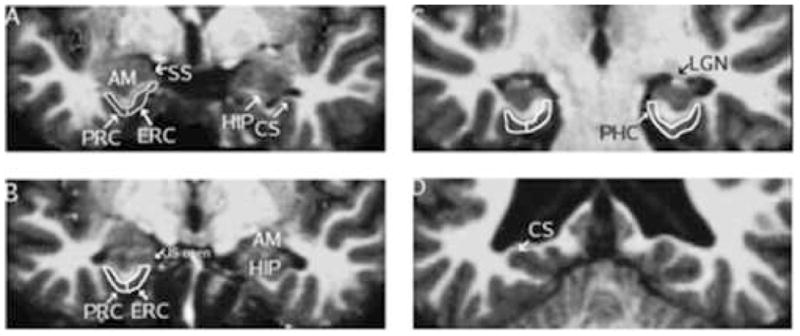
Representative coronal MRI slices illustrating boundaries of perirhinal, entorhinal, and posterior parahippocampal cortex. (A) The rostral border of the entorhinal (ERC) and perirhinal (PRC) regions, shown on the left hemisphere, is defined 3 mm rostral to the appearance of the hippocampus (HIP). The shoulder of the collateral sulcus (CS) defines the ventrolateral border of the ERC, while the PRC ventrolateral boundary is defined by the fundus of the CS. (B) The dorsomedial limit of the ERC is defined by the uncal sulcus (US) in more caudal slices. (C) The ERC/PRC caudal limit and rostral border of the posterior parahippocampal cortex (PHC) is defined 3mm caudal to the first appearance of the lateral geniculate nucleus (LGN). (D) The PHC caudal boundary is defined by the first caudal slice where the HIP is not present. Note that, in this figure, the subject’s head is rotated slightly such that the right side (image right) is at a slightly more caudal position than the left side.
The rostral boundary of the ERC and PRC was defined as 3 millimeters rostral to the slice where the hippocampus could first be seen (Fig. 1A). The amygdala, white matter of the PHG, gyrus ambiens, and sulcus semianularis were also visible. As described above, this location was identified in the MRI slice data and mapped to the surface. The caudal boundary of the ERC and PRC was defined as 3 millimeters caudal to the slice where the LGN could first be seen (moving from rostral to caudal in the coronal plane). In the section shown in Figure 1C, the LGN is just appearing in the right hemisphere, whereas in the left hemisphere, the LGN was present three slices rostrally. The caudal boundary for the ERC and PRC is also the rostral boundary for the PPHC, which is shown in Figure 1C on the left hemisphere. The last slice where the hippocampus appears (Fig. 1D) was used as the caudal limit of the PPHC.
In rostral slices (Fig. 1A), the dorso-medial boundary for the PPHC and ERC is determined by the tip of the angular bundle of the PHG white matter. Unfortunately, the software used in this study is unable to accurately assess cortical thickness dorsal to the angular bundle at this rostral level. As a result, a small dorsal and rostral portion of the ERC is not included in the label. Moving caudally, the dorso-medial limit is defined by the uncal sulcus after it opens (Fig. 1B). After the uncus disappears (Fig. 1C), the subiculum becomes the dorso-medial border for the ERC and PPHC.
Ventro-laterally, the limit of the ERC is determined by the medial branch of the collateral sulcus (see Figs. 1A–1C). The lateral border of the ERC is highly variable among individuals, and its location is also controversial among authors (Honeycutt et al., 1998; Insausti et al., 1998b; Goncharova et al., 2001; Pruessner et al., 2002). We defined the lateral border at the shoulder of the medial bank of the collateral sulcus, without extending the ERC boundary into the collateral sulcus. This location then served as the medial boundary for the PRC.
The ventro-lateral border for the PRC and PPHC is defined by the lateral branch of the collateral sulcus (see Figs. 1A–1C), and localized at the fundus of the collateral sulcus.
2.6. Manual Cortical ROI Tracings
The implementation of the MTL ROI boundary tracings within the hybrid surface-volume visualization system is novel and will be described here. The MTL regions were traced in a rostral to caudal direction on the reconstructed gray/white and gray/CSF surfaces. These surfaces were constructed by determining and then integrating the boundary between gray and white matter (shown in Fig. 2A as a yellow line) and the boundary between gray matter and CSF (shown in Fig. 2A as a red line). The points of maximum and minimum curvature along the collateral sulcus were determined using the reconstructed gray/CSF surface, known as the pial surface (Fig. 2F).
Each vertex in this surface is matched to a single voxel along the gray/CSF boundary (Dale et al., 1999; Fischl et al., 1999a) (more than one vertex may be matched to a single voxel). Boundaries for the ERC, PRC, and PPHC were generated by selecting key anatomic landmarks in the MR image, and matching those voxels to vertices in the cortical model (see Figs. 2B–2J). The surface was partially inflated so that the depths of sulci could be better seen, enabling the location of these points to be determined quickly and accurately (Figs. 2G–2J). Once a series of points on the surface is marked, a path bordering one or more of the MTL regions can then be generated automatically by the software to connect the points.
The rostral boundary of the PRC and ERC was traced by selecting three key points in a slice 3mm rostral to the appearance of the hippocampus: the tip of the angular bundle, the point of sharpest curvature along the dorso-medial bank of the collateral sulcus, and the point of maximum curvature at the fundus of the collateral sulcus (Fig. 2B). Each voxel is then referenced to a vertex in the surface and a path is drawn through them (Fig. 2G).
Three points were also selected part way between the rostral and caudal limits of the ERC and PRC in the slice where the US opens: the point ventral to the US, and the points of maximum and sharpest curvature along the collateral sulcus (Fig. 2C). The corresponding vertices were used to draw paths connecting the rostral boundary with these points (Fig. 2H). That is, a series of points were placed by the operator and each one was connected to the previous one by a line 1) spanning the fewest number of vertex points on the surface and 2) following the line of curvature, so as to keep the line consistent with cortical topography.
Three points were selected from the slice 3mm caudal to the appearance of the LGN to determine the caudal limit of the PRC and ERC (Fig. 2D). The junction between cortex and subiculum (at the dorsomedial shoulder of the parahippocampal gyrus), and the points of maximum and minimum curvature were used to draw the caudal boundary, and complete the dorsolateral and ventromedial borders of the ERC and PRC (Fig. 2I).
This boundary also represented the rostral limit of the PPHC. The first coronal slice caudal to the disappearance of the hippocampal tail was used as a caudal limit for the PPHC. The point of maximum curvature within the CS and the junction between cortex and the dorsal-medial shoulder of the CS (Fig. 2E) were selected and marked on the surface in order to delineate the caudal boundary of the PPHC (Fig. 2H).
The quantitative measures of each cortical ROI are calculated as follows. First, note that the model of the cortical surface is a mesh of tessellated triangles. Each entorhinal ROI, for example, includes approximately 200–400 triangles. The area of each triangle is calculated (1/2 * base * height). The total surface area of an ROI is defined by the sum of the area of each of the triangles within the ROI. Each triangle is present on both the grey-white surface and the pial surface and has three vertex points, each of which are connected by lines. Thus, this shape is a triangular prism. The distance between the vertex points is calculated and averaged for a given triangle to derive the mean cortical thickness at that triangle (the length of the triangular prism). The mean thickness of a cortical ROI is the average thickness of all of the triangular thickness measures. The volume of each one of these triangular prisms is equal to the surface area multiplied by the length. The volume of a cortical ROI is derived by summing the volumes of all the triangular prisms within the ROI.
2.7. Individual CS anatomic variability
The collateral sulcus varies greatly between individuals, and even within individuals between hemispheres. Ono (Ono et al., 1990) categorized three primary types of variants that can occur along the anterior CS: connections to the lateral occipitotemporal sulcus (LOTS), connections to the rhinal sulcus (RS), and interruptions within the collateral sulcus. Ono also noted that these interruptions can occur along the medial-lateral axis. As a result, one branch of the CS can overlap with the other. The classification system we developed differs from Ono in that we classified 1) the depth of the sulcus and 2) types of connections and interruptions. Each feature was localized along the antero-posterior axis (rostral, middle, or caudal) with respect to MR anatomic landmarks.
Using the surface-volume visualization methods described above, we developed a novel protocol for categorizing CS variants based on Ono’s work (Ono et al., 1990). Visualization of the cortical surface enables the operator to directly see the contiguity (or lack thereof) of the CS, which was used (as it was from post-mortem brain tissue by Ono and colleagues) for the classification of variants of the CS. Then, using key subcortical landmarks from the MRI image (as would be done in sectioned brain tissue), the rostrocaudal location of any given CS variant could be indexed.
The CS was divided into three sections. The rostral section was limited caudally by the appearance of the uncal hippocampus, which was also the rostral limit of the middle section. The caudal limit of the middle section was marked by the appearance of the LGN. The caudal section, whose rostral limit was also marked by the LGN, was limited caudally by the most caudal slice of the hippocampus.
First, we classified the depth of the CS by smoothing along the cortical surface with a kernel of 7.4 mm full-width half-maximum and determining if the CS was still visible (this smoothing step was done purely to assist with visualization of the quantitative depth measure for classification of CS variants and was separate from any morphometric measurments). The CS was classified as deep if it was still visible on the smoothed surface; if the CS was no longer visible after smoothing, it was classified as shallow. This corresponds to a deep CS being > 4 mm deep, while a shallow CS is < 4mm deep.
Second, we classified interruptions of the CS and its connections with the LOTS. Anatomic variants were determined for each section by tracing the CS and LOTS along the pial surface. We did not identify connections to the RS, because the sulcus was not consistently identified on the surface (in part because it may be very shallow).
The study of CS anatomic variants was useful during the development of our measurement protocol of primarily the PRC, and to a lesser degree the ERC, given the impact of atypical CS variants on the boundaries of these ROIs. In subjects where a “double collateral sulcus” was present, we used the surface model to determine that the double sulcus was, in fact, an interrupted and overlapped single collateral sulcus, most commonly involving a rostral branch that was more medially located, but interrupted, with a caudal branch that was more laterally located. In coronal MRI sections in which the slice plane intersected both branches, it would appear that there were two collateral sulci. In these subjects, we used the surface model to demarcate an interpolated path from one branch of the sulcus to the other.
2.8. Statistical Analysis
To assess the reproducibility (reliability) of the boundary definitions, analysis data from 15 subjects were repeated in a blinded manner (identifiers were coded by another investigator). Using the intraclass correlation method (Shrout and Fleiss, 1979), the reproducibility of the dura edits were assessed. Semi-processed (see reliability results section below for details) data was replicated. The rater then removed the dura and subsequently reproduced the surface models from the MR volume. Reliability of the dura edits was assessed separately for the morphometric measures of each region using the same ICC method. The rater (E.F.) then repeated the cortical surface labeling of the ERC, PRC, and PPHC ROIs. Reliability was assessed separately for the volume, surface area, and thickness of each region.
For the CS variant frequency analysis, between-group differences of CS variant frequency were evaluated using the Chi square test. In the case of a significant finding, two-way ANOVAs and ANCOVAs were used to calculate, for each subject group, the effects of categorical CS variant type on morphometric measures derived from the cortical surface model. For variant effects found in all three groups, two factor ANOVAs and ANCOVAs were used to assess the significance of the variant effect independent of diagnostic criteria. All statistical procedures were performed in SPSS 11.0 (Chicago, IL).
3. Results
3.1. Reliability of measurements
Table 1 shows the demographic and clinical characteristics of participants. The reliability of the measurements was assessed using the intraclass correlation (ICC) method, modified for an experimental design where one fixed rater makes repeated measurements on a subset of subjects (Shrout and Fleiss, 1979). Two different procedures were performed on 15 subjects to assess the reliability of 1) the generation of the pial surface from the MRI data, and 2) the manual tracings of ERC, PRC, and PPHC boundaries on the cortical surface.
Table 1.
Demographics and clinical characteristics of participants.
| Group | N | Gender | Age | MMSE | CDR (0/0.5/1) |
|---|---|---|---|---|---|
| Younger normals | 29 | 20f/9m | 23.5 ± 3.7 | N/A | N/A |
| Older normals | 47 | 30f/17m | 76.2 ± 6.8 | 29 ± 1.3 | 47/0/0 |
| Mild AD | 29 | 18f/11m | 74.3 ± 10.2 | 22.9 ± 3.8 | 0/7/22 |
F = female; m = male; MMSE = Mini Mental State Examination; CDR = Clinical Dementia Rating; Values for age and MMSE are mean ± standard deviation
As described above (Section 2.3), the pial surface is generated in an automated fashion, visualized as an overlay on the MRI data, and checked by a manual operator to ensure that the pial surface did not include dura (which closely overlies the crown of the parahippocampal gyrus, typically where the ERC is located). The operator removes the dura from the gray matter before regenerating the surfaces. Variability may be present in the automated surface generation and/or in the manual editing to remove dura. To assess reliability of surface generation, these steps were repeated on 15 subjects. To remove the effects of variability in ERC/PRC/PPHC boundary tracing (which is assessed separately below), the manual boundary tracings were then copied from the original dataset.
Thus, the intraclass correlation coefficient for dura edit reliability is a test of the reproducibility of the location of the pial surface in a manner that reproduces the same thickness estimate (for all 3 ROIs), and is also a test of the manual operator’s ability to repeatedly perform edits to the grey matter in order to remove dura (for the ERC only, since PRC and PPHC do not typically include overlying dura, and so are not affected by this manual editing procedure). This intra-class coefficient enables the assessment of reliability of the dura edits and for the automated surface generation algorithim.
The second reliability assessment was performed to determine the level of reproducibility of the manual tracing of boundaries demarcating ERC, PRC, and PPHC on the cortical surface. This reliability assessment was done by retracing (on 15 subjects) the regional parcellations made on the surface, in a blinded manner, without regenerating the surfaces. Measurements for the specific regions were then derived from this subset and compared to the originals. Since the surfaces were not regenerated, this intra-class coefficient enables the assessment of reliability of cortical ROI boundary tracing.
The reliability coefficients calculated from the subset are presented in Table 2. All reliability coefficients were greater than 0.81 (F=12, P < 0.001), which can be interpreted as indicating that the procedures are “almost perfect” and acceptable for other data analysis that test significance at p < .05 corrected with 80% power (Landis and Koch, 1977; Eliasziw et al., 1994).
Table 2.
Reliability assessments for MTL regional morphometric protocol.
| Morphometric measure | Cortical ROI tracing reliability (ICC) | Dural edit and surface generation reliability (ICC) |
|---|---|---|
| PRC surface area | 0.90 | 0.90 |
| PRC thickness | 0.96 | 0.95 |
| PRC volume | 0.95 | 0.94 |
| ERC surface area | 0.91 | 0.90 |
| ERC thickness | 0.99 | 0.96 |
| ERC volume | 0.94 | 0.93 |
| PPHC surface area | 0.95 | 0.95 |
| PPHC thickness | 0.99 | 0.97 |
| PPHC volume | 0.98 | 0.97 |
For each measure, degrees of freedom = (1, 29)
Values given are expressed as ratio of between-subject variance to total variance.
3.2. CS variant analysis
Using our CS categorization protocol, we classified CS variants across the entire dataset, and analyzed the frequency of each variant within and across subject groups. Illustrations of the differing CS variants are shown in Figure 3. Overall, CS variance was similar between left and right hemispheres, with deep, single-branch CS being the most common variant. The rostral and caudal sections had very little variance across the entire dataset, with a deep uninterrupted and unconnected CS indentified in more than 75 percent of all hemispheres. The middle section had the greatest number of variants, evenly split between shallow and deep, connected and interrupted sulci, with deep, unconnected, uninterrupted sulci being the most frequent variant, appearing in more than 30 percent of all surfaces.
Figure 3.
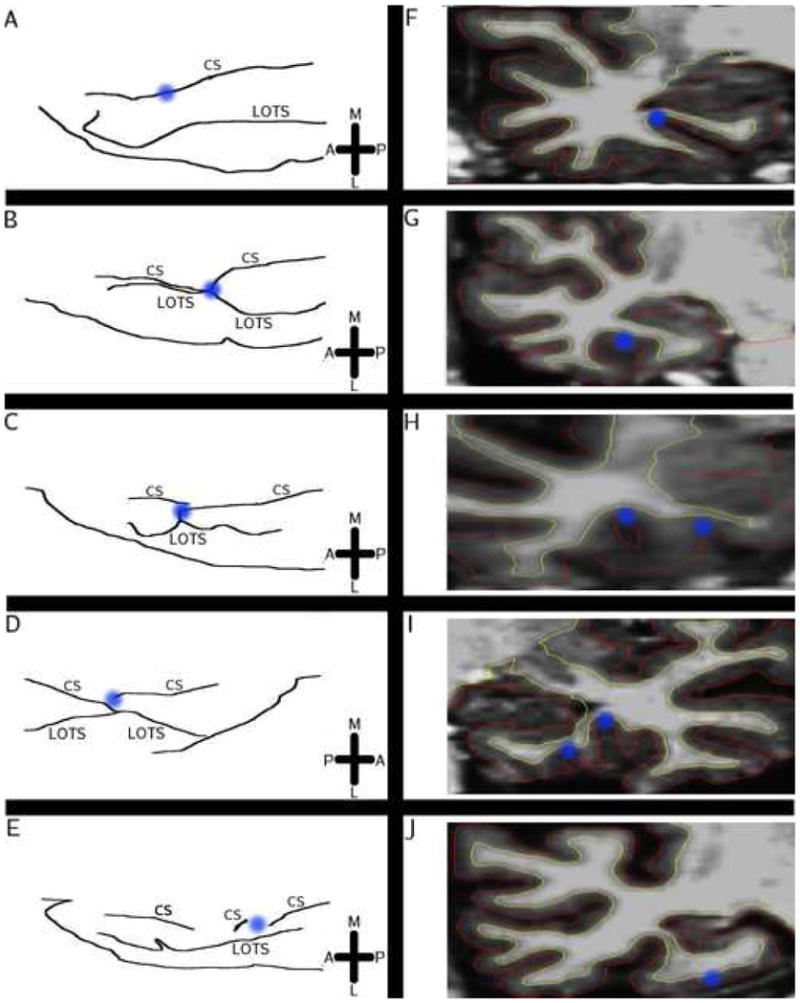
Illustration of types of CS variants. A = anterior, P = posterior, M = medial, L = lateral, CS = collateral sulcus, LOTS = lateral occipitotemporal sulcus. Blue points on the sketches (left) refer to the blue points on the MRI slice (right), which indicate the CS. (A, F) Sketch of deep, unconnected and uninterrupted CS, with example of MRI slice shown on the right. (B, G) Variant where a deep CS connects to the lateral occipitotemporal sulcus (LOTS). (C, H) Sketch of interrupted and unconnected CS. The two CS branches also overlap each other, as shown in the volume. (D, I) Sketch of interrupted and connected CS. The CS branches overlap and the lateral-anterior CS branch connects with the LOTS. (E, H) Double interrupted variant, where the CS is interrupted twice. The MRI slice depicts the second interruption. No overlap occurs.
Frequency differences between AD and control groups in the middle sections were also observed (see Figure 4). In the right hemisphere, 43.3 percent of AD subjects had a single, deep, unconnected, and uninterrupted CS. By way of comparison, 34 percent of older normals and 20.4 percent of younger normals were identified with the same variant type. In the left hemisphere, 56.7 percent of AD subjects had a single, deep, unconnected, and uninterrupted CS, whereas only 29.8 percent of older normals and 27.6 percent of younger normals possessed this variant. These frequency distributions were further evaluated using Chi square tests. For the right hemisphere, the between group differences were found to be non-significant (Chi square = 3.459, p = 0.177). However, in the left hemisphere analysis, the between group differences were significant (Chi square = 7.144, p < 0.03). Table 3 presents the raw values for thickness, surface area, and volume subdivided by CS variant type.
Figure 4.
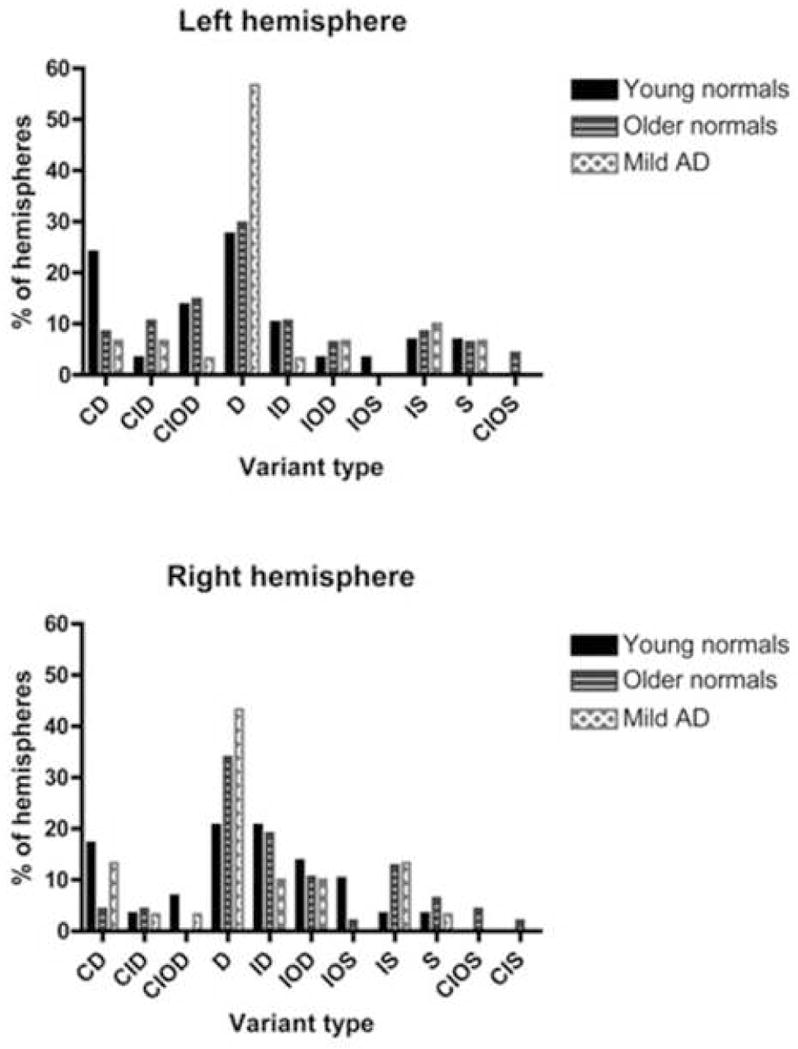
Distribution of CS variants (middle section of rostrocaudal extent), separated by hemisphere and diagnostic criteria. A combination of five letters denotes each unique variant type: D = deep, S = shallow, C = connected, I = interrupted, O = overlapped. Values expressed as a percentage of total hemispheres within each cohort.
Table 3.
Raw morphometric measurements subdivided by major collateral sulcus variant types.
| Thickness (mm) | Surface area (mm2) | Volume (mm3) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||
| YN | ON | AD | YN | ON | AD | YN | ON | AD | ||
| ERC | D | 2.94(0.37) | 2.61(0.38) | 2.28(0.40) | 171(36) | 164(57) | 139(41) | 823(118) | 691(252) | 486(182) |
| ID | 2.67(0.28) | 2.54(0.40) | 2.03(0.23) | 227(56) | 175(54) | 175(75) | 965(170) | 694(228) | 535(208) | |
| CD | 2.88(0.24) | 2.76(0.30) | 2.24(0.25) | 198(37) | 259(47) | 169(43) | 950(187) | 1116(273) | 577(171) | |
| other | 2.65(0.37) | 2.68(0.28) | 2.19(0.45) | 192(50) | 162(43) | 166(54) | 820(222) | 705(194) | 568(256) | |
|
| ||||||||||
| PRC | D | 1.80(0.23) | 1.91(0.38) | 1.76(0.41) | 247(73) | 253(60) | 252(84) | 524(151) | 548(153) | 489(184) |
| ID | 2.47(0.58) | 2.17(0.29) | 1.82(0.27) | 190(65) | 207(44) | 175(53) | 521(100) | 630(155) | 373(28) | |
| CD | 1.99(0.40) | 1.93(0.29) | 1.87(0.18) | 303(82) | 294(78) | 283(107) | 691(239) | 545(154) | 598(134) | |
| other | 2.20(0.35) | 2.25(0.40) | 2.03(0.37) | 207(55) | 191(64) | 186(79) | 530(143) | 499(192) | 481(235) | |
|
| ||||||||||
| N | D | 14 | 30 | 30 | ||||||
| ID | 9 | 14 | 4 | |||||||
| CD | 12 | 6 | 6 | |||||||
| other | 23 | 44 | 18 | |||||||
D = deep; ID = interrupted deep; CD = connected deep; YN = younger normals; ON = older normals; AD = Alzheimer’s disease; ERC = entorhinal cortex; PRC = perirhinal cortex; N = number of participants with each variant type
3.3. Effects of deep single branch CS on EC and PRC volume, surface area and cortical thickness
To assess whether this left hemisphere CS variant had an effect on standard morphometric measures (e.g. surface area, volume, and cortical thickness) in the left hemisphere, analysis of variance (ANOVA) and covariance (ANCOVA) were performed within each subject group. Between group differences of morphometric measures are discussed in the accompanying paper (Dickerson et al., submitted). For thickness measurements, ANOVAs were carried out for each diagnostic group to assess for differences in thickness between subjects with deep, single branch CS vs. those without such a CS. For surface and volume based measurements, ANCOVAs were performed with estimated total intracranial volume (eTIV) measurements included as a covariate to control for head size. ETIV measurements were not incorporated into the thickness analysis because head size has no effect on MTL cortical thickness. The morphometry of the PPHC was not examined because the PPHC is not located in the middle section of the CS, which is where these variants were observed.
For the left hemisphere ERC analysis, a significant variant effect was seen in the mild AD group [F(1,26) = 5.57, p < 0.03, Cohen’s d = 0.79] and a trend was observed in the younger normals [F(1,26) = 3.34, p < 0.08, d = 0.82] for surface area. This indicates that left ERC surface area was smaller in AD and younger individuals who had a deep single branch CS, compared to subjects with one of the less common variants. No other variant effects were found in any of the other ERC morphometric measures.
The left hemisphere PRC analysis revealed a strong variant effect of PRC thickness within younger [F(1,27) = 8.69, p < 0.008, d = 1.46], older [F(1,45) = 5.82, p < 0.03, d = 0.74], and mild AD [F(1,27) = 11.58, p < 0.003, d = 1.24] groups. A two factor ANOVA test of diagnostic group and variant type demonstrated that the between-variant effect on PRC thickness was independent of the diagnostic criteria [F(1,99) = 24.17, p < 0.001, d = 1.11], indicating that regardless of diagnostic group, PRC thickness was reduced in individuals with a deep single branch CS. These results are displayed in Figure 5. No other variant effects were observed in the PRC analysis.
Figure 5.
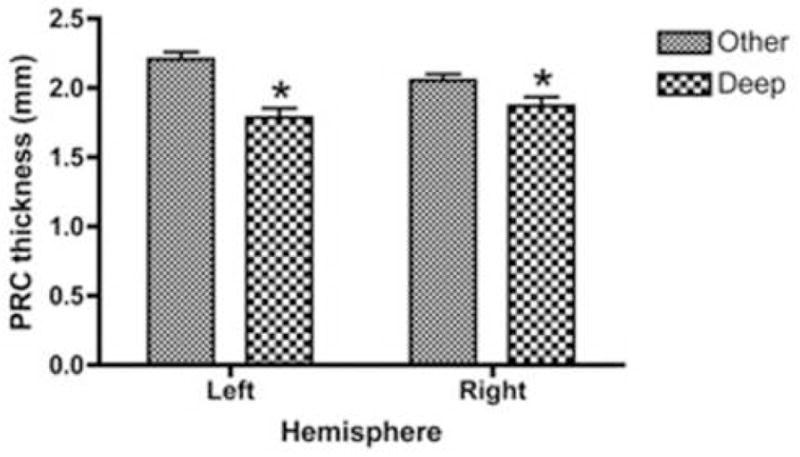
Effect of the presence (deep) or absence (other) of a deep single-branch (uninterrupted) CS on PRC thickness. * indicates the effect is statistically significant (p < 0.05). Error bars represent standard error of mean, values are given in millimeters.
To examine whether this effect on PRC thickness also occurred in the right hemisphere, a two-factor ANOVA test, with diagnostic group and right hemisphere variant type as the two factors, was used. These results are displayed in Figure 5. For the analysis, a significant variant [F(1,99) = 5.48, p < 0.03, d = 0.58] effect and group [F(1,99) = 2.610, p < 0.079] trend was observed, with no interaction between them, demonstrating that PRC thickness, irrespective of group and hemisphere, was reduced in individuals with a deep single branch CS.
4. Discussion
In this study, we developed a novel semi-automated method for reliably measuring thickness, surface area, and volume of the ERC, PRC, and PPHC. This method employs the use of a hybrid visualization approach involving both typical MRI slices, allowing for identification of subcortical landmarks, as well as a cortical surface model, which enables clear visualization of gyral and sulcal topography. As part of this study, we classified and investigated the frequency of anatomic variants of the CS to investigate potential effects of these variants on morphometric measures of the ERC, PRC, and PPHC. We found that the most frequent variant of the CS—an unconnected, uninterrupted, and deep sulcus as depicted in Figure 3A—was associated with thinner ERC and PRC cortical measurements.
4.1 The value of a protocol to measure MTL cortical thickness and surface area
Protocols have been developed for reliably measuring the volumes of cortical MTL regions—including ERC, PRC, and PPHC—from in vivo MRI data (Honeycutt et al., 1998; Insausti et al., 1998b; Goncharova et al., 2001; Pruessner et al., 2002). Yet the volume of a bounded cortical region is a product of the thickness of that region and its surface area (i.e., larger volume of a cortical region is present for regions that are thicker or have larger surface area). It is possible that factors associated with reduced volume of cortical regions, such as aging or neuropsychiatric disorders, may exert differential effects on thickness or surface area. For example, in an accompanying paper, we show that although both aging and AD are associated with reduced ERC, PRC, and PPHC volume, aging primarily effects surface area while AD is associated with large reductions in thickness of these regions (Dickerson et al., submitted).
Although further study is needed of the histologic correlates of these MRI-derived morphometric measures, previous stereologic investigations of mild AD have shown that thickness within specific laminae of the ERC is markedly reduced in conjunction with neuronal loss (Gomez-Isla et al., 1996). Thus, MRI-derived measures of cortical thickness likely reflect, at least in part, the integrity of cellular elements within the cortical mantle. The surface area of a given cortical gyrus or sulcus may reflect the size of intracortical elements, but may also relate to local subcortical factors, such as the volume of white matter subjacent to the gyrus, or to global factors, such as the size of various compartments of the brain (grey matter, white matter, or ventricular size) or to head size. Advances in MRI technology that enable the direct visualization of cellular elements, such as entorhinal islands, will likely enable improved measurements of these brain regions (Augustinack et al., 2005).
4.2 Strengths of this protocol
Through the use of this semi-automated protocol, we take advantage of computational algorithms for the identification of boundaries that may be difficult for a manual operator to delineate, such as the grey-white matter boundary (the deep boundary of the cortical surface) and the grey matter-cerebrospinal fluid boundary (the superficial boundary of the cortical surface). Furthermore, the use of the cortical surface model enables the calculation of thickness and surface area measures in the setting of gyral and sulcal curvature that would make these measures very difficult for a manual operator to make from MRI slice data. The reliability data presented here demonstrate the high level of precision achievable using this method.
We do not employ a fully automated approach in this protocol because of two major steps, which we believe are better performed by a manual operator, at least using the current generation of software. First, the gyral and sulcal boundaries of these small cortical ROIs have been difficult to reproduce using automated atlas-based approaches, in part due to individual differences in gyral and sulcal anatomy (variants). The use of a boundary definition protocol that includes options for different anatomic variants enables a manual operator to delineate these boundaries reliably. Second, with the use of MRI data at the current resolution, it can be difficult for computational algorithms to exclude the dural layer that typically overlies the crown of the parahippocampal gyrus, potentially artificially thickening the estimate of ERC thickness. In our hands, manual verification and, if necessary, editing of this region results in more visually accurate pial surface localization and highly reliable thickness estimates.
The hybrid cortical surface-MRI volume visualization approach is useful for the manual steps described in this protocol. The software used in the present study enables the operator to simultaneously view the cortical surface model and the MRI slice data, and to mark a point in one and see its location in the other. Thus, the operator can view MRI slice data to identify subcortical landmarks that are important in rostrocaudal ROI boundary definition and mark their location on the cortical surface model. The operator can view the cortical surface model to identify the contiguity or lack of contiguity of sulci (i.e., the CS in this case) for the purposes of mediolateral ROI boundary definition. The shoulder and fundus of the CS are easily identified along the surface by visualizing curvature information, so the surface is used to demarcate medial and lateral boundaries. And the operator can overlay surface boundaries or cortical ROI labels on MRI slice data to verify the location of surfaces or labels with respect to anatomic landmarks in the orthogonal slice planes traditionally used in anatomic atlases.
4.3 Validity of this protocol with respect to others
Our protocol for defining the boundaries of the ERC and PRC differs from some previously published methods primarily with respect to the definition of the lateral border. Some authors have defined the lateral border of the ERC differentially based on the depth of the CS (Insausti et al., 1998b), while others have extended the lateral ERC boundary to the fundus of the CS (Honeycutt et al., 1998). Our methodology is consistent with approaches that label the lateral ERC border at the ventromedial shoulder of the collateral sulcus; this approach does not result in substantially different measurements compared to Insausti et al.’s method (Goncharova et al., 2001; Pruessner et al., 2002).
One additional strength of the present approach to ROI boundary definitions involves the visualization of the CS and its anatomic variants. All of the aforementioned authors labeled the ERC lateral border with respect to the first visible sulcus moving laterally along the parahippocampal gyrus (Honeycutt et al., 1998; Insausti et al., 1998b; Goncharova et al., 2001; Pruessner et al., 2002). This becomes an important issue when there is a “double collateral sulcus” (Insausti et al., 1998b), which results from an interruption in the contiguity of the CS with overlap between the two branches. By using the cortical surface model, we were able to visualize the contiguity of the CS and any interruptions and overlap in branches. When there were interruptions or overlap, we interpolated a line from one branch to the other, attempting to maintain the trajectory of the major branch of the CS.
4.4 Anatomic variants of the CS
There are few investigations of inter-individual anatomic variation of MTL structures, and, to our knowledge, there have been no studies of the effects of variants on morphometric properties of MTL regions. Ono et al. developed a classification system to describe anatomic variants of the CS, and analyzed the frequency of variants within a sample of 20 cadaveric brains (Ono et al., 1990). We developed a system of CS variant classification modeled after Ono et al.’s system, with the incorporation of subcortical landmarks visualized from MRI (e.g., LGN) to further localize the variants in a manner that would relate to typical localizations of ERC, PRC, and PPHC. Ono et al. were unable to differentiate variants in this way because of the use of uncut post-mortem brain tissue. Ono et al. divided connections and interruptions into psuedo and true variants based on small gyral convolutions within the CS (Ono et al., 1990). On the other hand, we were unable to employ Ono et al.’s system for classifying connections and interruptions into psuedo or true variants because we could not reliably visualize the small gyral convolutions within the CS that were used for this classification. As a result, Ono et al.’s approach was able to classify a greater number of types surface variants, while our system was able to classify surface variants in a manner relating to subcortical anatomic landmarks.
Anatomic variants of the CS have not been well studied, despite the heavy use of this sulcus in quantitative MRI protocols for measuring the ERC in studies attempting to identify individuals with early AD pathology. We applied our CS variant classification system to a large group of 105 individuals, including cognitively intact younger and older individuals, as well as AD patients, and found that the deep single branch CS was more frequent in the AD patient group. It is possible that the deep single branch CS variants are more common in the demented population because the interruptions and connections are reduced by the widening of the CS, which accompanies atrophy (Thompson et al., 2001)Pruessner et al., 2002).
Variability in sulcal morphology may also affect morphometric measurements. Our classification system revealed a variant effect on bilateral PRC thickness and left ERC surface area, independent of diagnosis. To our knowledge, only one other study has demonstrated an effect of sulcal morphology on cortical morphometry (Kippenhan et al., 2005). Future studies may elucidate whether there is any relation between particular individual variants of CS configuration and memory performance or AD pathology. Regardless, this study has demonstrated that such a classification system provides a practical tool for examining the relationship between cortical folding and morphometry.
Acknowledgments
This study was supported in part by the National Institute on Aging (K23-AG22509, P50-AG05681, P01-AG03991), the National Center for Research Resources (P41-RR14075, R01 RR16594-01A1, the NCRR BIRN Morphometric Project BIRN002, U24 RR021382 & U24-RR021382), and the Mental Illness and Neuroscience Discovery (MIND) Institute. Additional support was provided by the National Institute for Biomedical Imaging and Bioengineering (R01 EB001550), the National Institute for Neurological Disorders and Stroke (R01 NS052585-01) and the National Alliance for Medical Image Computing (NAMIC), funded by the National Institutes of Health through the NIH Roadmap for Medical Research, Grant U54 EB005149.
We thank Dr. Randy Buckner and Dr. John Morris for providing the data. We also express special appreciation to the participants in this study for their valuable contributions, without which this research would not have been possible.
Footnotes
Disclosure Statement
There are no actual or potential conflicts of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Amaral D, Insausti R. Hippocampal Formation. In: Paxinos G, editor. The human nervous system. San Diego: Academic Press; 1990. pp. 711–755. [Google Scholar]
- Arriagada PV, Growdon JH, Hedley-Whyte ET, Hyman BT. Neurofibrillary tangles but not senile plaques parallel duration and severity of Alzheimer’s disease. Neurology. 1992;42:631–639. doi: 10.1212/wnl.42.3.631. [DOI] [PubMed] [Google Scholar]
- Augustinack JC, van der Kouwe AJ, Blackwell ML, Salat DH, Wiggins CJ, Frosch MP, Wiggins GC, Potthast A, Wald LL, Fischl BR. Detection of entorhinal layer II using 7Tesla [correction] magnetic resonance imaging. Ann Neurol. 2005;57:489–494. doi: 10.1002/ana.20426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bobinski M, de Leon MJ, Convit A, De Santi S, Wegiel J, Tarshish CY, Saint Louis LA, Wisniewski HM. MRI of entorhinal cortex in mild Alzheimer’s disease. Lancet. 1999;353:38–40. doi: 10.1016/s0140-6736(05)74869-8. [DOI] [PubMed] [Google Scholar]
- Braak H, Braak E. Neuropathological stageing of Alzheimer-related changes. Acta Neuropathol (Berl) 1991;82:239–259. doi: 10.1007/BF00308809. [DOI] [PubMed] [Google Scholar]
- Braak H, Braak E. Staging of Alzheimer’s disease-related neurofibrillary changes. Neurobiol Aging. 1995;16:271–278. doi: 10.1016/0197-4580(95)00021-6. discussion 278–284. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Dickerson BC, Goncharova I, Sullivan MP, Forchetti C, Wilson RS, Bennett DA, Beckett LA, deToledo-Morrell L. MRI-derived entorhinal and hippocampal atrophy in incipient and very mild Alzheimer’s disease. Neurobiol Aging. 2001;22:747–754. doi: 10.1016/s0197-4580(01)00271-8. [DOI] [PubMed] [Google Scholar]
- Dickerson BC, Feczko E, Augustinack JC, Pacheco J, Morris JC, Fischl B, Buckner RL. Differential effects of aging and Alzheimer’s disease on medial temporal lobe cortical thickness and surface area. Neurobiol Aging. doi: 10.1016/j.neurobiolaging.2007.07.022. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du AT, Schuff N, Zhu XP, Jagust WJ, Miller BL, Reed BR, Kramer JH, Mungas D, Yaffe K, Chui HC, Weiner MW. Atrophy rates of entorhinal cortex in AD and normal aging. Neurology. 2003;60:481–486. doi: 10.1212/01.wnl.0000044400.11317.ec. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du AT, Schuff N, Amend D, Laakso MP, Hsu YY, Jagust WJ, Yaffe K, Kramer JH, Reed B, Norman D, Chui HC, Weiner MW. Magnetic resonance imaging of the entorhinal cortex and hippocampus in mild cognitive impairment and Alzheimer’s disease. J Neurol Neurosurg Psychiatry. 2001;71:441–447. doi: 10.1136/jnnp.71.4.441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eliasziw M, Young SL, Woodbury MG, Fryday-Field K. Statistical methodology for the concurrent assessment of interrater and intrarater reliability: using goniometric measurements as an example. Phys Ther. 1994;74:777–788. doi: 10.1093/ptj/74.8.777. [DOI] [PubMed] [Google Scholar]
- Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proceedings of the National Academy of Sciences of the United States of America. 2000;97:11050–11055. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis. II: Inflation, flattening, and a surface-based coordinate system. Neuroimage. 1999a;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Fischl B, Liu A, Dale AM. Automated manifold surgery: constructing geometrically accurate and topologically correct models of the human cerebral cortex. IEEE Trans Med Imaging. 2001;20:70–80. doi: 10.1109/42.906426. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Tootell RB, Dale AM. High-resolution intersubject averaging and a coordinate system for the cortical surface. Hum Brain Mapp. 1999b;8:272–284. doi: 10.1002/(SICI)1097-0193(1999)8:4<272::AID-HBM10>3.0.CO;2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gomez-Isla T, Price JL, McKeel DW, Jr, Morris JC, Growdon JH, Hyman BT. Profound loss of layer II entorhinal cortex neurons occurs in very mild Alzheimer’s disease. J Neurosci. 1996;16:4491–4500. doi: 10.1523/JNEUROSCI.16-14-04491.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goncharova, Dickerson BC, Stoub TR, deToledo-Morrell L. MRI of human entorhinal cortex: a reliable protocol for volumetric measurement. Neurobiol Aging. 2001;22:737–745. doi: 10.1016/s0197-4580(01)00270-6. [DOI] [PubMed] [Google Scholar]
- Honeycutt NA, Smith PD, Aylward E, Li Q, Chan M, Barta PE, Pearlson GD. Mesial temporal lobe measurements on magnetic resonance imaging scans. Psychiatry Res. 1998;83:85–94. doi: 10.1016/s0925-4927(98)00035-3. [DOI] [PubMed] [Google Scholar]
- Hyman BT, Van Hoesen GW, Damasio AR, Barnes CL. Alzheimer’s disease: cell-specific pathology isolates the hippocampal formation. Science. 1984;225:1168–1170. doi: 10.1126/science.6474172. [DOI] [PubMed] [Google Scholar]
- Insausti R, Insausti AM, Sobreviela MT, Salinas A, Martinez-Penuela JM. Human medial temporal lobe in aging: anatomical basis of memory preservation. Microsc Res Tech. 1998a;43:8–15. doi: 10.1002/(SICI)1097-0029(19981001)43:1<8::AID-JEMT2>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- Insausti R, Juottonen K, Soininen H, Insausti AM, Partanen K, Vainio P, Laakso MP, Pitkanen A. MR volumetric analysis of the human entorhinal, perirhinal, and temporopolar cortices. AJNR Am J Neuroradiol. 1998b;19:659–671. [PMC free article] [PubMed] [Google Scholar]
- Juottonen K, Laakso MP, Insausti R, Lehtovirta M, Pitkanen A, Partanen K, Soininen H. Volumes of the entorhinal and perirhinal cortices in Alzheimer’s disease. Neurobiol Aging. 1998;19:15–22. doi: 10.1016/s0197-4580(98)00007-4. [DOI] [PubMed] [Google Scholar]
- Killiany RJ, Gomez-Isla T, Moss M, Kikinis R, Sandor T, Jolesz F, Tanzi R, Jones K, Hyman BT, Albert MS. Use of structural magnetic resonance imaging to predict who will get Alzheimer’s disease. Ann Neurol. 2000;47:430–439. [PubMed] [Google Scholar]
- Kippenhan JS, Olsen RK, Mervis CB, Morris CA, Kohn P, Meyer-Lindenberg A, Berman KF. Genetic contributions to human gyrification: sulcal morphometry in Williams syndrome. J Neurosci. 2005;25:7840–7846. doi: 10.1523/JNEUROSCI.1722-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977;33:159–174. [PubMed] [Google Scholar]
- Ono M, Kubik S, Abarnathey CD. Atlas of the Cerebral Sulci. Stuttgart: Thieme; 1990. [Google Scholar]
- Pruessner JC, Kohler S, Crane J, Pruessner M, Lord C, Byrne A, Kabani N, Collins DL, Evans AC. Volumetry of temporopolar, perirhinal, entorhinal and parahippocampal cortex from high-resolution MR images: considering the variability of the collateral sulcus. Cereb Cortex. 2002;12:1342–1353. doi: 10.1093/cercor/12.12.1342. [DOI] [PubMed] [Google Scholar]
- Raz N, Rodrigue KM, Head D, Kennedy KM, Acker JD. Differential aging of the medial temporal lobe: a study of a five-year change. Neurology. 2004;62:433–438. doi: 10.1212/01.wnl.0000106466.09835.46. [DOI] [PubMed] [Google Scholar]
- Segonne F, Dale AM, Busa E, Glessner M, Salat D, Hahn HK, Fischl B. A hybrid approach to the skull stripping problem in MRI. Neuroimage. 2004;22:1060–1075. doi: 10.1016/j.neuroimage.2004.03.032. [DOI] [PubMed] [Google Scholar]
- Shrout PE, Fleiss JL. Intraclass correlation: uses in assessing rater reliability. Psychol Bull. 1979;86:420–428. doi: 10.1037//0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
- Squire LR, Zola SM. Memory, memory impairment, and the medial temporal lobe. Cold Spring Harb Symp Quant Biol. 1996;61:185–195. [PubMed] [Google Scholar]
- Thompson PM, Mega MS, Woods RP, Zoumalan CI, Lindshield CJ, Blanton RE, Moussai J, Holmes CJ, Cummings JL, Toga AW. Cortical change in Alzheimer’s disease detected with a disease-specific population-based brain atlas. Cereb Cortex. 2001;11:1–16. doi: 10.1093/cercor/11.1.1. [DOI] [PubMed] [Google Scholar]
- Witter MP, Wouterlood FG, Naber PA, Van Haeften T. Anatomical organization of the parahippocampal-hippocampal network. Ann N Y Acad Sci. 2000;911:1–24. doi: 10.1111/j.1749-6632.2000.tb06716.x. [DOI] [PubMed] [Google Scholar]
- Xu Y, Jack CR, Jr, O’Brien PC, Kokmen E, Smith GE, Ivnik RJ, Boeve BF, Tangalos RG, Petersen RC. Usefulness of MRI measures of entorhinal cortex versus hippocampus in AD. Neurology. 2000;54:1760–1767. doi: 10.1212/wnl.54.9.1760. [DOI] [PubMed] [Google Scholar]


