The Impact of Individual Biases on Consensus Formation

Abstract

Social groups of interacting agents display an ability to coordinate in the absence of a central authority, a phenomenon that has been recently amplified by the widespread availability of social networking technologies. Models of opinion formation in a population of agents have proven a very useful tool to investigate these phenomena that arise independently of the heterogeneities across individuals and can be used to identify the factors that determine whether widespread consensus on an initial small majority is reached. Recently, we introduced a model in which individual agents can have conservative and partisan biases. Numerical simulations for finite populations showed that while the inclusion of conservative agents in a population enhances the population's efficiency in reaching consensus on the initial majority opinion, even a small fraction of partisans leads the population to converge on the opinion initially held by a minority. To further understand the mechanisms leading to our previous numerical results, we investigate analytically the noise driven transition from a regime in which the population reaches a majority consensus (efficient), to a regime in which the population settles in deadlock (non-efficient). We show that the mean-field solution captures what we observe in model simulations. Populations of agents with no opinion bias show a continuous transition to a deadlock regime, while populations with an opinion bias, show a discontinuous transition between efficient and partisan regimes. Furthermore, the analytical solution reveals that populations with an increasing fraction of conservative agents are more robust against noise than a population of naive agents because in the efficient regime there are relatively more conservative than naive agents holding the majority opinion. In contrast, populations with partisan agents are less robust to noise with an increasing fraction of partisans, because in the efficient regime there are relatively more naive agents than partisan agents holding the majority opinion.

Introduction

An intriguing feature of social groups is the ability of interacting agents to efficiently coordinate in the absence of a central authority. The widespread availability of social networking technologies has increased the success and impact of decentralized coordination, as e.g. during the “Arab Spring” [1] or the Spanish protests in 2011 that simultaneously started in 60 different towns known as the 15M movement [2]. Interestingly, decentralized coordination arises in spite of the heterogeneities across the individuals comprising these social systems and the initial opinions held by those individuals [3], [4]. Individual and group biases, however, can polarize public opinion on controversial matters, undermining society's ability to reach effective policy solutions [5], [6] and often completely changing the dynamics of the process [7], [8]. Thus, a fundamental question is how individual biases affect the efficiency of the collective in reaching consensus.

To explore these questions, we recently introduced a model in which agents may have conservative or partisan biases toward one of the two possible opinions. These agents update their opinions using a modified local majority rule that takes into account the potential effect of noise in the communication channel and the personal bias of each agent [9], [10]. In this model, the noise in the communication channel accounts for any external factor that might lead to an agent misinterpreting another agent's opinion, for instance an ambiguity in the conversation or a simple misunderstanding.

Numerical simulations for finite populations show that when the population is exclusively composed of naive agents, i.e. agents that follow a simple majority rule, the population can reach consensus on the initial majority opinion in the presence of noise [9]. Interestingly, including conservative agents who have a bias toward their current opinion enhances the population's efficiency in reaching consensus when noise is present, whereas even a small fraction of partisan agents who have a bias toward the opinion opposite to the one held by the majority of the agents, would be enough to draw the population into the consensus on the opinion of the minority.

Here, we investigate the model analytically using a mean-field approximation and show that results from model simulations can be interpreted in terms of the stability of the efficient steady-state solution of the model, i.e. the regime in which a majority of the population converges to the same opinion. We distinguish two cases: i) agents with no opinion bias, in which agents do not have an a priori bias toward one of the two opinions and where it turns out to be a continuous transition along the noise axis from an efficient regime to a regime in which the population settles into deadlock; ii) agents with an opinion bias, in which agents have a bias toward a specific opinion and as a result there is a discontinuous transition between an efficient regime and a partisan regime which draws the population into a consensus opposite to the opinion held initially by the majority of the agents. Interestingly, in the latter case, the noise amplitude at which the transition occurs depends on the initial density of agents holding the majority opinion. Furthermore, the analysis of the steady-state solution close to the transition point can shed light onto the mechanisms responsible for the higher robustness of systems of agents with an increasing fraction of conservatives against noise amplitude and the decrease in robustness of a population with an increasing fraction of partisans.

Background

The theoretical study of consensus formation in a population has received attention in the modeling community, especially because simple spin models already display consensus formation in a similar way to that observed in real social systems. In such systems, agents(spins) can hold two possible opinions 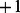or 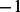and update their opinions according to some rule. Moreover, the opinion update rules in these models can be easily modified to mimic real situations. The most studied of these models is the voter model [11], [12] in which at each step, an agent picks a neighbor at random and updates her opinion to the opinion of the neighbor. The mean field approximation predicts that this model has two absorbing solutions in which the whole population adopts the same opinion 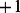or 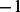. If the network of connections between agents has the topological features present in empirical social networks – high-clustering and the small-world property – then, a finite population reaches consensus in a shorter time than in regular lattices [13]–[16]. However, if one organizes the population into loosely connected topological communities, then each community may reach their own independent consensus [17], [18].

With the aim of depicting more realistic dynamics, studies in the literature have incorporated a number of features such as majority update rules that resemble more how the social environment influences individual preferences [9], [10], [19]–[24], or the presence of noise in the information transfer channel [9]–[11], [25], which is critical for the system to reach consensus.

Among the features with the largest impact in the system's dynamics is the introduction of agent bias [8], [10], [20], [22], [26]–[28]. Differently to other studies, our model [10] considers agents that have a bias with strengths that can vary and introduces noise in the channel of information transfer between agents. The introduction of conservative agents can help the population in the coordination task without the need of a central authority, whereas the inclusion of even a very small fraction of partisan agents prevents the system from coordinating.

Our interest is to study whether a small initial opinion imbalance toward one opinion ends up in the strengthening of that opinion (efficient regime), deadlock (non-efficient regime), or in the majority of agents adopting the opinion held initially by a minority of partisans (partisan regime). Because the steady-state solution of the model does not necessarily correspond to a pure consensus in which all the agents converge toward the same opinion, we look at the efficiency or capacity of the population to amplify an initially small majority. In particular, we study the transition between the different regimes in the mean-field approximation and show how the observed phenomena in numerical simulations can be understood in terms of the set of steady-state solutions to the model when agents with different biases are present in the population. For some cases, we provide the analytical solution for the transition line and characterize the effect of the fraction of non-naive agents on the coordination efficiency when we vary the noise amplitude in the communication channel.

Results

Model

Consider a population of 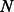agents that hold binary opinions 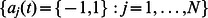. Further, assume that each agent has 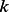neighbors and a preference toward a specific state 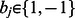. We define two broad classes of agents: “well-intentioned” agents who prefer the opinion they currently hold, so that 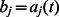, and “partisan” agents who have a fixed preferred opinion so that 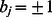. Each agent also has a bias strength 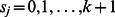toward her preferred opinion. 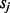specifies the agent's ability to counter peer pressure, that is, 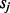specifies how strong the social pressure of the social neighborhood needs to be for the agent to adopt his non-preferred opinion. If 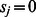, then a well-intentioned agent is naive, otherwise the agent is conservative. As a result, while all types of agents may change their state in response to peer pressure, a partisan agent will defect back to his preferred state if peer pressure decreases below a threshold value.

At each time step, agent 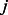takes into account his own opinion and the current opinion of his 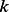neighbors and updates his opinion following a generalized majority rule that depends on 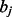and ,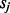

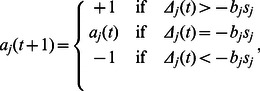(1)

where,

(2)

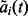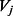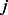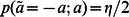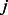and is the perceived opinion of neighbor and is the set of neighbors of agent . Because the communication channel between agents is noisy, with probability agent perceives the opinion of neighbor as being the opposite to the one he currently holds. Note that if the sum of perceived opinions of the agent's neighbors overcomes the strength of his bias to a specific opinion, then the agent will defect from his preferred opinion.

Mean-field approximation

Our goal is to find the steady-state efficiency of the system

(3)

where 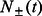is the number of agents holding opinion 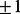at time , and 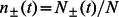. In what follows, we denote 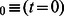and as the steady-state value of the efficiency.

At each time step , agent 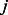will change opinions at a rate 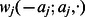, where expresses de dependency of the rate on 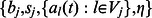. The expected change in 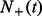is then

(4)

The next step is to find an expression for 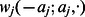. Assume we pick an agent 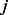at random. In the mean-field approximation, agent 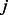is surrounded by an average neighborhood in which each neighbor holds opinion 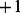with probability 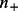and opinion 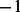with probability 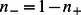. Thus, the probability 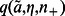of agent 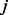perceiving a neighbor holding opinion is the same for all agents,

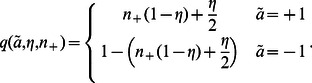(5)

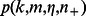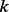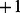Equation (5) enables us to obtain the probability that an agent with neighbors will perceive neighbors holding opinion and 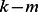neighbors holding opinion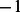

(6)

where we have used that .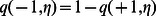

Consider an agent holding opinion 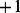. From Eq. (1), we see that for a well-intentioned agent (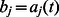) with bias strength to change her opinion to 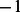, she needs to perceive at least 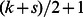agents holding the opposite opinion 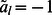. The rate at which a well-intentioned agent changes opinions is thus

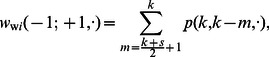(7)

where 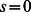corresponds to a naive agent and 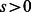corresponds to a conservative agent (see Table 1).

Table 1. Summary of transition rates for each agent type.

agent type	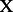bias strength
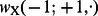
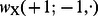
naive	s = 0
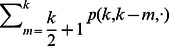
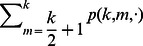
conservative	s = s
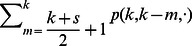
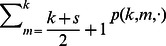
neg. partisan	s = s
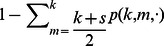
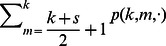
pos. partisan	s = s

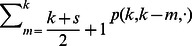
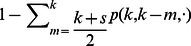
Note that, for a positive partisan (that is, 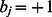) holding opinion 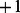, the rate of changing opinions is that of a well-intentioned agent with the same bias strength 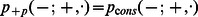. A negative partisan (that is, with 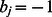), however, will always adopt opinion 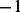, unless he perceives 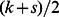agents as holding opinion 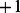. Thus, the rate at which a negative partisan holding opinion 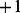changes opinions is

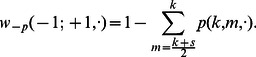(8)

Similar rules apply for agents changing from opinion 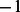to opinion 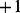(see Table 1).

Consider a mixed population of 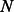agents in which there are 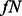non-naive agents with a fixed bias strength and 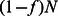naive agents. Further assume that 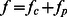, where 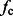is the fraction of conservative agents and 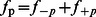is the total fraction of partisan agents, both negative and positive. Because agents do not change type, that is 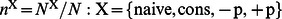is constant, and the rate of change depends on the type of agent 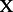, we can rewrite Eq. (4) as follows

(9)

(10)

A steady-state solution to Eq. (10) is one that satisfies 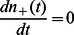. In the following, we distinguish two families of solutions: symmetric and non-symmetric.

Agents with no opinion bias: conservatives and equal fractions of negative and positive partisans

Consider a population comprised entirely of well-intentioned agents i.e., either naive (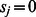) or conservative (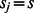) agents with a bias toward the opinion they currently hold. Because there is no a priori bias against a particular opinion, the solution 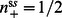is always a solution to the steady state condition 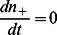. It is easy to check that the zero efficiency solution is a solution to both naive and conservative populations and is thus a solution of a system comprising both. However, this solution is not stable for low values of noise.

For simplicity, let us consider a population of well-intentioned agents of the same type and assume that 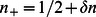with 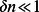. Straightforward algebra yields

(11)

where 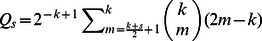and .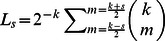

The condition 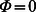yields the value at which the transition between efficient and non-efficient regimes occurs, 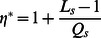. For 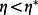, 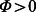and the solution 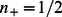is not stable. In this regime, there are two stable symmetric solutions for 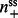, one such that 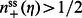that yields an efficiency 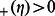, and another one such that 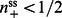that yields an efficiency 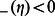(Fig. 1). As 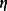increases, these two solutions approach the unstable solution 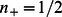. For 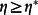, all solutions merge, and there is only one stable solution for the efficiency 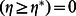. Therefore, in the mean-field approximation, a system comprised of naive agents with an initial condition of 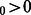(see dotted blue line in Fig. 1), will transition from an efficient regime (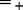) for 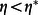, to an inefficient regime (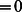) for .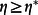

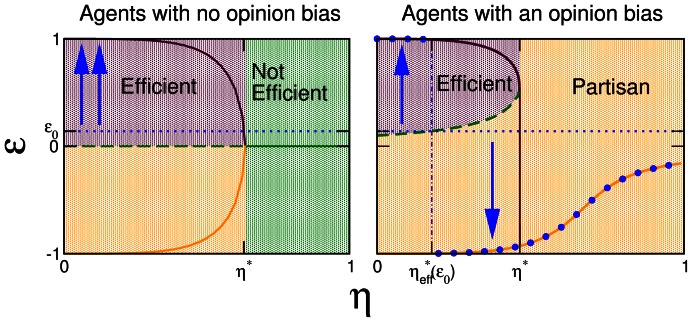
Figure 1. Mean-field solution for a mixed population of agents.

For a fixed fraction 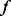of non-naive agents we plot the steady-state efficiency 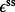versus the noise amplitude 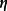. We consider two scenarios: (a) agents with no opinion bias and (b) agents with an opinion bias (see text). Continuous lines show stable solutions, and discontinuous lines show unstable solutions. The maroon regions show the set of initial conditions 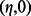for which 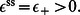The orange region covers 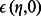for which 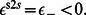The green region covers initial conditions 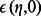for which 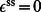. In (b), blue dots show 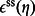for the initial condition indicated by the dotted blue line. Blue arrows indicate the steady-state solution that corresponds to the initial condition represented by the blue dotted line.

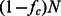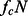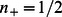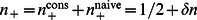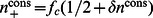One can generalize this result to a mixed population of naive agents and conservative agents with fixed bias strength . Because is a steady state solution for both kinds of agents, we assume that the solution can be written as with and 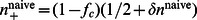. We obtain the following transition line 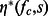(see Methods for a derivation)

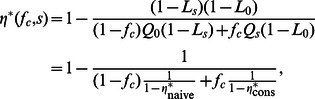(12)

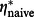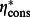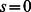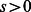where and are the solutions for the case with a single type of well-intentioned agents for and , respectively (see Fig. 2).

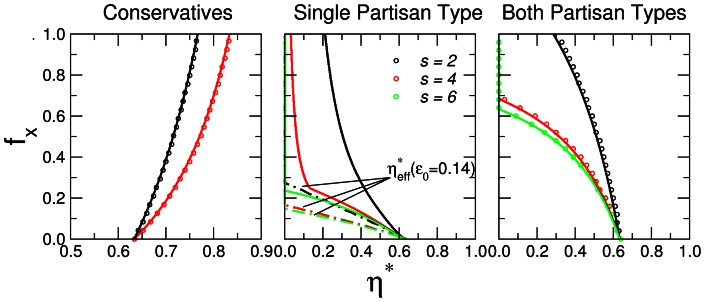
Figure 2. Transition line for the mean-field solution for a mixed population of agents with.

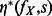
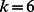We plot the noise amplitude 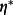at which the positive efficiency solution ceases to be stable (see Fig. 1) for a fraction 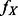of non-naive agents and for different bias strengths 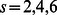(see text for the conservative case and 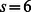). Solid lines show the numerical solution for the steady state condition and dots show the theoretical values from Eqs. (12) (conservatives) and (14) (both types of partisans). For the symmetric cases, those with conservatives and both types of partisans, the line separates the efficient regime for low values of noise amplitude from the non-efficient regime. In the case in which there are only negative partisans, the line separates the efficient regime from the partisan regime in which the system is drawn into a consensus on the opinion held by the initial minority opinion. Note how in the symmetric case 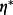is independent of , the efficiency of the system at time zero. However, in the non-symmetric case of only negative partisans, the transition line depends on the initial efficiency 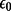. As a guide we show transition lines for 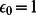(solid lines) and 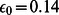(dotted lines).

Note that, because 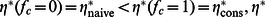grows with the fraction of conservatives, indicating that the presence of conservatives makes the system more robust to perturbations for all 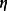(Fig. 2). In fact, if we look at the relative fraction of agents of each type in excess of 1/2, 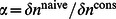(see Methods), we find that

(13)

which shows that for 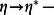, close to the transition between efficient and inefficient regimes, there are more conservative agents holding the majority opinion than naive agents.

Note that for 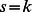the system is not symmetric. Because partisan agents settle into their preferred opinion, if there is a bias in the initial distribution of opinions (that is, 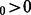), then, the efficiency of the system is always positive.

Agents with an opinion bias: negative partisans

Because partisans have a preference toward a fixed opinion, 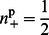is not a solution of 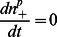, thus there is no stable non-efficient regime for high noise amplitudes. For the case in which there is a small fraction of negative partisans 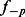, for low values of noise, there are still two stable 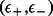steady-state solutions with positive and negative efficiencies (Fig. 1), and an unstable solution with 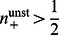. At 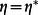the positive efficiency solution merges with the unstable solution and becomes marginally stable. Thus, for 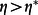the only stable solution is a “partisan” solution in which the majority of agents adopt the opinion of the partisan minority regardless of the initial majority opinion.

For a population with an initial majority holding opinion 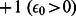there is thus a discontinuous transition from an efficient regime to a partisan regime. The transition point 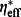depends on 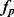and ; when 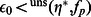(see crossing between dotted blue line and green line in Fig. 1b), then the population transitions into the partisan regime. Interestingly, 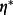decreases with 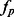and for 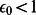there is a finite 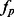at which the system can no longer be efficient (Fig. 2b). This finding is in agreement with the results for numerical simulations of the model for finite populations (see [10] and Fig. 3) and with the solution of the voter model when “zealots” (agents that are always in state 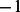) are present in the population [26], [27]. In the voter model, a small fraction of zealots is enough to throw the system into a negative efficiency value.

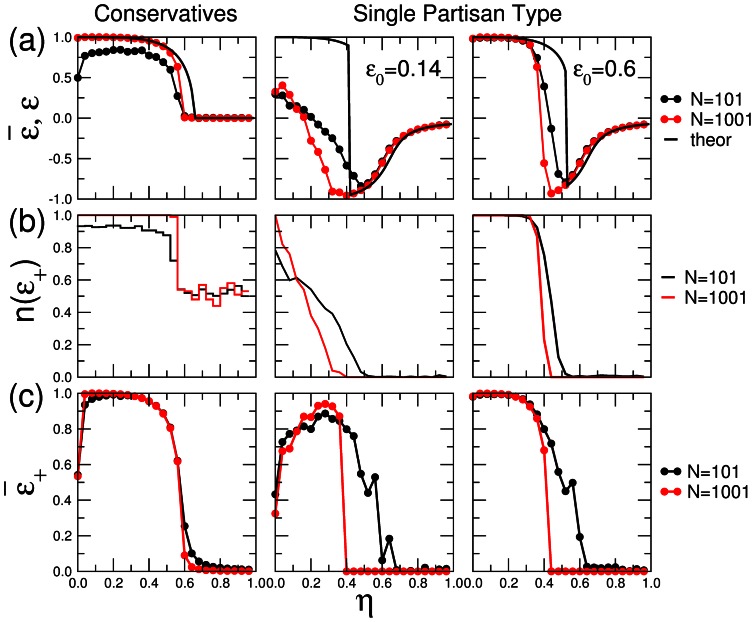
Figure 3. Comparison between model simulations for finite system sizes and the mean-field results.

We consider populations of naive agents with 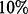of conservatives or negative partisan agents with bias strength 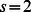. We build a network following the model proposed by Watts and Strogatz [30] using the same parameters as in [10]– 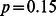and 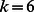. Once the system has reached a steady-state we obtain: (a) , the average efficiency, (b) 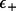, the average efficiency for the realizations with positive efficiency, and (c) 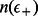the fraction of realizations in which is positive. We show results for populations of 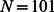(black) and 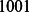(red) agents a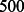nd and 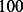realizations, respectively. In the top row, solid black lines indicate the solution to the mean-field model 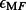. In the case of negative partisans, we show results for two initial conditions 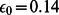and 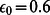. Note how in the case of conservative agents there is a good agreement between simulations and the mean-field expectation. There is a transition from a regime in which almost all realizations have 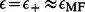to a regime for 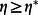, in which the population ends half of the time with 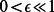. In the case with partisan agents, we show how the initial condition affects the behavior of the system as predicted. Note how there is a transition between a region in which some realizations have 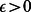, to a partisan regime in which no realizations have 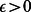and the efficiency is very similar to that of the mean-field approximation.

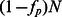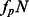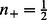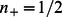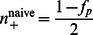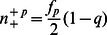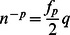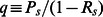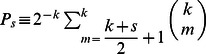If the population contains a mixture of naive agents and partisan agents with equal fractions of positive and negative partisans, then one recovers as a solution to Eq. (4). Note that in such case the steady-state solution corresponds to , and , with where and .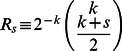

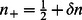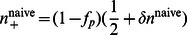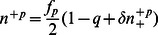Similarly to the case of well-intentioned agents, one can assume that close to the transition the solution is where , , and 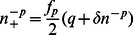to obtain the following transition line that separates efficient and non-efficient regimes (see Methods)

(14)

where 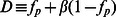and 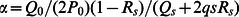. In fact, 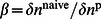is the relative fraction of agents holding the majority opinion in excess of the stable solution for 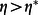. Note that 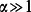– actually 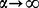for 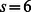, so that, close to the transition, the number of agents holding opinion 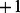can only increase through the change of opinions of naive agents. Therefore, the introduction of both types of partisan agents has the opposite effect of the introduction of conservative agents. Whereas having some conservative agents results in a system whose efficiency in reaching consensus is more robust to noise, introducing partisan agents reduces the ability of the system to reach consensus as the noise amplitude increases. In fact, the larger the fraction of partisans and the stronger their bias strength, the lower the efficiency in reaching consensus as 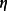increases (Fig. 2).

Discussion

Our work is the first to produce analytical results on the noise driven transition between efficient and non-efficient/partisan regimes when agents with bias are present in a model for consensus formation.

Seaver et al. [10] used numerical simulations to show the effect that including conservative or partisan agents in a population of naive agents has in the reaching of consensus in the absence of a central authority when noise is present. In here, we investigate the same model analytically in the mean-field approximation. We show that the mean-field solution can fully capture the transition from an efficient to an inefficient/partisan regime observed in numerical simulations of finite populations in [10]. Figure 4a compares the mean-field theoretical solution for the population efficiency to the average efficiency of a finite population with a finite number of neighbors in a Watts-Strogatz rewired network as in [10]. For most of the cases we study, we find that as the system size increases, the average efficiency approaches the mean-field solution, demonstrating that our results are a good approximation to numerical simulations of more realistic models for both the average efficiency values and the noise amplitude 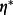at which the change of regime takes place. Even for small population sizes one can observe the signatures of the transition both when conservatives and negative partisans are present. Note that in the case of a small initial majority 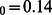, the average efficiency for 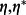is lower than expected. This is because most configurations end up having a negative efficiency for 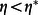(Fig. 3b). If we take into account configurations that end up with a positive efficiency (Fig. 3c), we observe how the efficiency approaches the theoretical one as population size increases. In the other cases, this has no effect since for 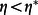most configurations have a positive efficiency.

Interestingly, our calculations uncover the mechanisms that drive these transitions and show how the microscopic differences in agent bias relate to the macroscopic differences observed in the efficiency to reach consensus. Importantly, the results in Fig. 3 indicate that these mechanisms are also responsible for the transition observed in more realistic numerical simulations for finite populations. In the case of a system of naive and conservative agents, the fraction of conservative agents holding the majority opinion in excess of 1/2 (efficient regime) for 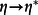is larger than that of naive agents. As a consequence, as the fraction of conservative agents increases, the transition shifts to larger values of 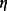, meaning that the ability of the system to reach consensus increases.

The inclusion of equal fractions of both types of partisans has the opposite effect. Since the relative fraction of naive agents holding the majority opinion in excess of 1/2 (efficient regime) for 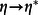is much larger than that of partisan agents, as the fraction of partisans increases the system becomes less robust to noise and the transition shifts to smaller values of 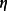. In fact, this last result highlights the importance of introducing naive agents in a biased population to guarantee a democratic outcome as it has been recently shown in communities of animals [29]. Our results thus add additional insights into the mechanisms behind opinion formation dynamics and could be useful for the future analysis of more complicated models.

Methods

Agents with no opinion bias: conservatives

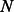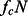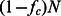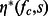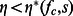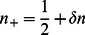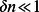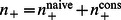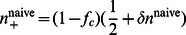Consider a mixed system of agents composed of conservative agents with fixed bias strength and naive agents. To obtain the transition line between efficient and non-efficient regimes, we assume that since the system is symmetric, the solution to Eq. (10) close to the transition for is with . Without loss of generality we can assume that with and 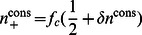. Introducing these solutions into Eq. (10) for each type of agent we obtain the following expressions

(15)

(16)

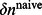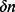By imposing the steady-state condition on Eqs. (15) and (16), we find the relationship between and 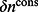, and and 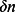, respectively. Noting that 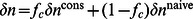, we obtain the following expression for Eq. (9)

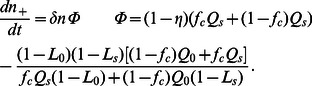(17)

Which setting 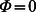so that the steady state condition is fulfilled for all 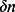yields the expression for 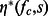in Eq. (12). Note that by imposing the steady-state condition on Eqs. (15) and (16), we can also find the expression for 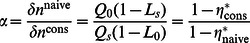in Eq. (13).

Agents with no opinion bias: both types of partisans

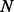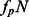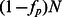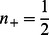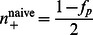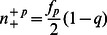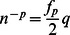Consider a mixed population of agents composed of partisan agents with fixed bias strength and equal fractions of negative and positive partisans, and naive agents. 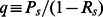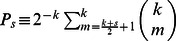As already explained in the main text, while this is a symmetric problem with a non efficient solution , the relative fraction of the number of agents holding the majority opinion depends on the type of agent so that , and , with where and .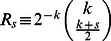

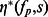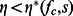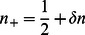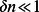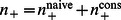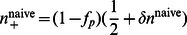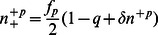To obtain the transition line between efficient and non-efficient regimes, we thus assume that the solution to Eq. (10) close to the transition for is with . Without loss of generality, we can assume that with , , and 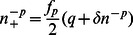. Introducing these solutions into Eq. (10) for each type of agent we obtain the following expressions

(18)

(19)

(20)

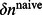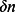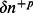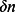By imposing the steady-state condition on Eqs. (18-20), we find the relationship between and , and 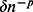and and 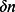, respectively. Note that because Eqs. (19) and (20) are the same, 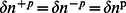. This means that the deviations from the steady state solution in which there are many more positive than negative partisans holding the majority opinion are the same for both types of partisans. Using that 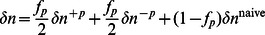, we obtain the following expression for Eq. (9)

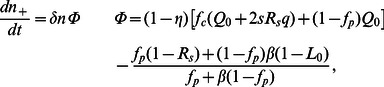(21)

where 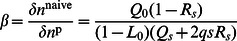. Setting 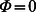so that the steady state condition is fulfilled for all , we obtain the expression for 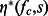in Eq. (14).

Funding Statement

MS-P and LANA acknowledge the support from SciSIP 0830388 from the National Science Foundation. M S-P acknowledges the support of the Spanish Ministerio de Ciencia e Innovación (MICINN) Grant FIS2010-18639, James S. McDonnell Foundation Research Award, European Union Grant PIRG-GA-2010-268342. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.