Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 May 29;3:1909. doi: 10.1038/srep01909

Digital optical phase conjugation for delivering two-dimensional images through turbid media

Timothy R Hillman 1, Toyohiko Yamauchi 2, Wonshik Choi 3, Ramachandra R Dasari 1, Michael S Feld 1,5, YongKeun Park 4,a, Zahid Yaqoob 1,b
PMCID: PMC3665964  PMID: 23714766

Abstract

Optical transmission through complex media such as biological tissue is fundamentally limited by multiple light scattering. Precise control of the optical wavefield potentially holds the key to advancing a broad range of light-based techniques and applications for imaging or optical delivery. We present a simple and robust digital optical phase conjugation (DOPC) implementation for suppressing multiple light scattering. Utilizing wavefront shaping via a spatial light modulator (SLM), we demonstrate its turbidity-suppression capability by reconstructing the image of a complex two-dimensional wide-field target through a highly scattering medium. Employing an interferometer with a Sagnac-like ring design, we successfully overcome the challenging alignment and wavefront-matching constraints in DOPC, reflecting the requirement that the forward- and reverse-propagation paths through the turbid medium be identical. By measuring the output response to digital distortion of the SLM write pattern, we validate the sub-wavelength sensitivity of the system.

Optical imaging and spectroscopy of biological cells and tissue provide a tremendous amount of information that can be utilized for diagnostic and therapeutic purposes. However, the sample depth from which the information can be successfully retrieved is fundamentally limited by multiple scattering effects, mainly due to refractive index variations on a length scale comparable to the optical wavelength. Scattering is the dominant extinction process, accounting almost exclusively for the limited imaging depth range. For example, the absorption coefficient μa of gray matter is only 0.2 cm−1, yet the scattering coefficient μs for the same tissue is equal to 77 cm−1 at the wavelength of 800 nm 1.

One class of techniques to suppress sample turbidity involves wavefront shaping – the manipulation of the optical wavefront prior to sample illumination, pre-scrambling it in such a way to counter the effects of scattering2. The value of such methods is attested by recent work demonstrating a high degree of control over the scattered optical wavefields in space3, time4,5,6, wavelength7,8, polarization9,10, transmitted energy11, and in the near-field (at sub-wavelength scales)12. Recently, it has also been shown that the penetration depth of optical coherence tomography can be increased using wavefront shaping13. Other approaches utilize the transmission matrix, the linear transformation relating the incident wavefields to transmitted wavefields, in order to deliver optical images through highly turbid media14,15,16.

Optical phase conjugation (OPC) is an elegant technique for reversing the effects of multiple scattering. Its first demonstration of image transmission through diffusing media was performed using photorefractive crystals as the phase-conjugate mirrors17. Our group collaborated in using conventional, crystal-based OPC to achieve turbidity suppression in biological samples18. A three-dimensional hologram of the light scattered from the sample was recorded in the crystal, which permitted a “time-reversed” version of the original scattered wave to be generated when the crystal was illuminated with an appropriate “conjugate-reference” beam. The time-reversal property was most dramatically evidenced when the phase-conjugate reconstructed wave encountered the turbid sample, leading to the reconstruction of the original, complex sample structure.

Recent advances in OPC utilize a digital implementation of the technique for turbidity suppression in biological tissues19,20. In digital optical phase conjugation (DOPC), the “phase-conjugate mirror” operation is performed by two distinct devices, a sensor and an actuator19. The former is used to acquire the complex-scalar transverse field distribution of the scattered light wave, and the latter, to generate the complex-conjugate, reverse-propagating reconstruction of this distribution. In practice, a CCD camera is used as the sensor, upon which a digital hologram is recorded in order to obtain the original complex amplitude distribution. The actuation step is performed using a liquid-crystal based device21, such as an SLM, which imparts a user-controllable phase distribution to the light wave reflected from it. This approach has been adopted by Cui and Yang19; other work by Hsieh et al. demonstrates DOPC using the second-harmonic-generated field from an illuminated nanoparticle20,22. Recently, DOPC in combination with ultrasonic modulation has enabled high-resolution deep-tissue fluorescent imaging23,24 and it has been shown that DOPC can be performed with respect to a fluorescence signal from turbid media25.

DOPC has a number of advantages over non-digital approaches, some of which are described in Ref. 19. A stored digital hologram is a permanent record of the scattered light wave, and it is not limited by the recording efficiency or recording lifetime of a photorefractive crystal. Additionally, the ability to digitally control the reconstruction wavefront provides the flexibility to modify it, in order to achieve an enhanced reconstruction, or to scan a focused spot over a limited range26. However, the implementation of DOPC presents a challenging system alignment problem because the sensor and actuator are decoupled in space, and the propagation paths for the original scattered wave and its phase-conjugate reconstruction are necessarily different. Yet the two waves must overlap precisely at the location of the scattering sample. Also, the restricted numerical aperture applied to the collected wavefields limits the quality of the reconstruction, a point we shall return to in the following section. Most likely for reasons such as these, full-field imaging through turbidity using DOPC has not been yet demonstrated to our knowledge; reconstructions have been limited to a single point recovery (scanned or stationary). In this Letter, we report a DOPC design implementation that permits the wide-field image reconstruction of a complex target through a highly scattering medium using digitally controlled, “time-reversed” light. We also characterize the sub-wavelength sensitivity of the system.

Results

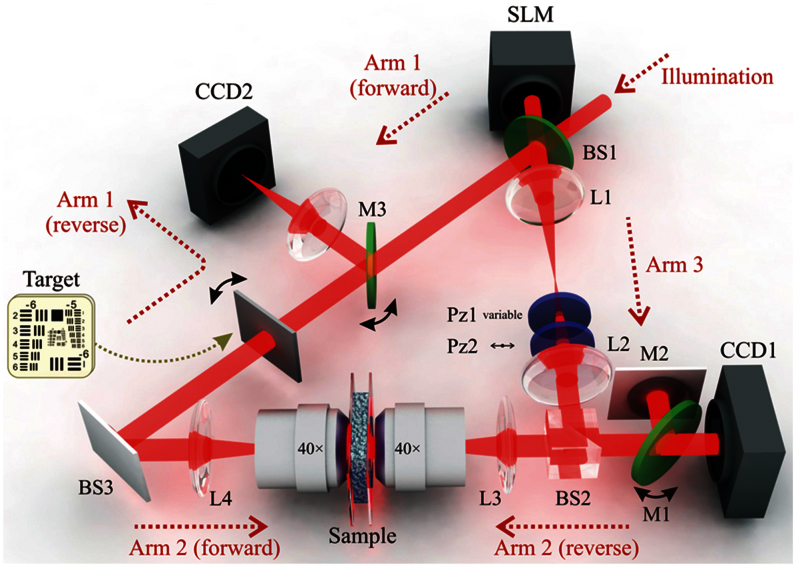
The experimental interferometer setup features a Sagnac-like ring design, so that light can propagate in either direction through the turbid medium (sample). It is depicted in Fig. 1, with the three distinct arms of the ring labeled. The basic actions of operating the sensor and the actuator can be described as the acquisition and reconstruction steps, respectively, and they are described in the Supplementary information. The essence of our approach is as follows: The complex amplitude distribution of the light scattered by the turbid medium (in the forward direction) is holographically captured by CCD1. The SLM is used to generate the phase-conjugate reconstructed wavefront, which back-propagates through the turbid medium, suppressing the multiple-light-scattering effects in a time-reversal manner. To record the hologram, we used a hybrid off-axis/phase-stepping approach (see Supplementary information).

Figure 1. Optical schematic for our ring-interferometer DOPC approach.

Figure 1

Open in a new tab

BS: beam-splitter; CCD: charge-coupled device camera; L: lens; Pz: polarizer; SLM: spatial light modulator. The double-headed black arrows at M1, M3 and the target indicate flip stages. Horizontally polarized illumination enters from the top-right.

Our highly turbid medium comprised a layer of 200-nm (average diameter) ZnO particles spray-painted onto a standard glass microscope cover slip. The thickness of the layer was 11.3 μm; its transport mean-free path was 0.7 ± 0.2 μm. The turbid sample was buffered between two thin strips of polydimethylsiloxane (PDMS), and sandwiched between the two identical objective lenses (Zeiss, FLUAR 40×/1.3 oil). A negative USAF target (Edmund Optics Inc.) was utilized for the purpose of generating a two-dimensional wide-field image pattern. Figure 2(a) shows the average of multiple intensity images (at CCD2), generated by transmitting different speckle illumination patterns (generated with different SLM patterns) in the reverse direction through the sample followed by the target. This gives a representation of the reconstructed image we wish to achieve by DOPC. Accordingly, Figs. 2(b)–(d) each represent images obtained when the target was “flipped down”, so that it was no longer in the beam path. The first of these, Fig. 2(b), presents the reconstruction when no phase control is applied to the SLM; the turbid sample is illuminated (in the reverse direction) by a plane wave. As a result, a speckle pattern with homogeneous size statistics is observed. Figure 2(c) shows the result when the DOPC reconstruction pattern is written to the SLM without incorporating the “fine-tuning” phase adjustment (see Supplementary information). Although a “pure” speckle pattern is no longer observed and a vague semblance of the structures becomes visible, the quality of the reconstruction is dramatically improved in Fig. 2(d), for which the fine-tuning step has also been included. Note that signal level for the image of Fig. 2(a) is much lower than that of Fig. 2(d). This is because the former is generated by merely blocking a broad beam with the target mask, but the latter by using wavefront control to reconstruct the image utilizing the full power of the beam (and no target mask).

Figure 2. Detected intensity reconstruction in output (CCD2) plane.

Figure 2

Open in a new tab

In (a), the target was included in the beam path, It was illuminated (in reverse) by five different speckle patterns (generated by random SLM patterns), and the average result is shown. In (b)–(d), the target was removed from the beam path (flipped down), in order to generate a reconstruction by DOPC alone. Considering the individual cases: (b) No SLM control, resulting in turbid sample illumination with a plane wave; (c) Optimized SLM control in the absence of “fine-tuning”; (d) Optimized, fine-tuned SLM control. Scale: each element-5 bar has (long-dimension) length 1.57 mm. Consistent but arbitrary intensity units are utilized in the images.

We address the sensitivity of the system to systematic distortions of the phase-conjugate SLM write patterns. As noted previously, precise control of the pattern is a fundamental advantage of the digital form of OPC. Specifically, we observe the effect of translating the reconstruction patterns by one, two, and three pixels from the optimized location (Fig. 3). A one-pixel shift corresponds to 20-μm translation in the SLM plane, but due to demagnification of the beam, only approximately 100-nm lateral beam translation upon encountering the sample. Yet even a two- or three-pixel translation, corresponding to less than half of one wavelength at the sample, is sufficient to destroy the quality of the reconstruction almost entirely, demonstrating the required precision of the phase-conjugate reconstruction for highly turbid samples. This observation can be supported by inspecting a plot of the modulus of the complex autocorrelation function of the optimized phase pattern written to the SLM (see Supplementary Fig. 5).

Figure 3. The “optimum” reconstruction is the same as in Fig. 2(d).

Figure 3

Open in a new tab

The other reconstructions are generated by translating the SLM pattern by the specified number of pixels in the same direction. The effective translation (mismatch), Δx, of the reconstruction beam with respect to the scattering sample is indicated, subject to the qualification given in the text. The value of η corresponding to each reconstruction is calculated, also subject to a qualification given in the text. The image SNR is also calculated by comparing the reconstructed image with the image obtained in the absence of the scattering medium. The images are plotted using a linear grayscale, with intensity value 0 as the lower limit. Scale: each element-5 bar has (long-dimension) length 1.57 mm.

Discussion

To systematically address the fundamental factors that limit the quality of the reconstruction, we consider the wavefield scattered by the sample at the acquisition stage. It can be expressed as a two-dimensional field vector, S = (S1,S2), corresponding to two orthogonal polarization states. However, only a limited portion of this scattered wave, for one polarization state, is collected by the optical system, and therefore is available to generate the reconstruction. The holographically recorded field can be denoted as

graphic file with name srep01909-m1.jpg

where ΩR is the accessible solid-angle range. The quality of the reconstruction will depend on the relative optical powers of the total “signal” and “noise” contributions of SR, defined with respect to the “target” signal S. We define the reconstruction efficiency η to be equal to the ratio of the “signal” to the “total power”, so that:

graphic file with name srep01909-m2.jpg

The inner product used in the equation is defined:

graphic file with name srep01909-m3.jpg

where the differential solid angle dΩ = sinθdθdφ in a spherical coordinate system, and the optical powers of the scattered and reconstruction waves are equal to P = 〈S,S〉 and PR = 〈SR,SR〉, respectively. In our case, for which the components of SR are either equal to those of S or zero, the reconstruction efficiency can be expressed as:

graphic file with name srep01909-m4.jpg

Even though η is defined at the acquisition stage, it legitimately describes (or sets an upper limit to) the quality of the final reconstruction, since the DOPC signal is generated based on the acquired hologram.

We assume that the scattering medium thoroughly scrambles the incoming signal, so that the fraction of the scattered wave's total power that is incident upon CCD1 is essentially independent of the specific structural form of the wave that is incident upon the medium. Therefore, the complex correlation coefficient between S and SR, given by 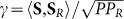Inline graphic, and hence also 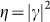Inline graphic, will remain constant over the ensemble of possible incoming-signal distributions. We also assume that the spatial distribution of the “noise” component of the signal at the reconstruction stage is essentially independent of its particular input distribution. This means that the background noise level captured by CCD2 at this stage is dependent only on the total power of the reconstruction wave incident on the reverse side of the scattering medium. Taking these statements together, we conclude that the ratio of the “signal” power to “total” power in the reconstructed image remains constant for any original target illumination pattern. Indeed, it depends only on the fundamental characteristics of the recording system such as the numerical aperture for collection of the scattered light (and to some degree, the angular scattering characteristics of the sample). The ratio could also be improved by incorporating polarization-sensitivity into the system.

As we have noted, the value of η calculated according to fraction of the scattered light collected at the acquisition stage is only an upper limit to the actual “reconstruction efficiency” (at CCD2), since the “true” quantity depends on our ability to effectively construct the phase-conjugate beam and back-propagate it through the system. We observe that the aim of the correction steps, detailed in the Supplementary information, was to precisely match the phase profiles of scattered and reconstruction wavefronts up to phase conjugation. A technical factor that diminishes the effective value of γ is the fact that we utilize phase control only (not amplitude control) in generating the reconstruction wave. Assuming that the amplitude distribution across the recording-plane field of view obeys Rayleigh statistics, then this effect decreases γ by a factor of 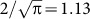Inline graphic, with a consequent reduction in η by the square of this value.

Having established that η is not dependent on the structure or power of the original target beam, but only upon the system characteristics, we now consider the visibility of a target reconstruction. The visibility can be defined as the extent to which the reconstruction (at CCD2) is distinguishable from the background noise, the ratio of the average image intensity level (above the noise floor) in the region corresponding to the transparent area of the mask, to the background intensity level. It depends primarily on the spatial extent of the reconstruction pattern (or the mask area). This is because a structure-independent signal power level (relative to the background) is dispersed over this area. Accordingly, the broader the target pattern, the greater the system η required to reconstruct it to high fidelity. This observation explains why a single point target can be much more easily reconstructed than a complex image: even if the reconstruction efficiency η is low, the visibility may still be extremely high given that the signal component of the reconstruction is concentrated to a focused spot, but the noise component is spread over a large scattering solid angle. The high-quality reconstruction obtained in Ref. 18 can be accounted for due to the high system η: the scattering medium was in direct contact with the recording crystal, so that virtually all of the forward-scattered light contributed to the hologram. Moreover, the holographic reconstruction provided by the 3D recording medium was a faithful representation of the scattered wavefield. These system characteristics permitted a high-visibility reconstruction of the large target area to be obtained.

The unusual feature of our DOPC system, that image fidelity depends on the spatial extent of the target pattern, is similar in nature to that of the related technique of Ref. 3. In this paper, when an SLM-pattern optimization routine is used to generate multiple high-intensity focused spots in a recording plane located behind a scattering sample, then the total optical power of the signal-carrying component of the light is the same as for the generation of a single spot, but it is divided between the spots.

In Fig. 3, we have stated representative (effective, reconstruction-plane) values of η calculated by dividing the measured power in the “signal” region of the image (corresponding to the transparent region of the mask) to the sum of this and the measured power in the “background” region (elsewhere, including a larger field of view not included in the cropped depictions of the figures). Because the optical imaging system at CCD2 has a limited collection aperture, the contribution of light scattered at large off-axis angles is not included in the calculation, so the reported values are overestimates. However, the error in measured background power will be a systematic (constant) scaling factor. The visibility is also reported in the figure. Because it is based on intensity measurements, not total power measurements, it can be determined more accurately. Note that since a single mask pattern is used, there is a direct correspondence between visibility and η. (It is not strict proportionality, because the term on the denominator of η is total power, not “background” or noise power.) The reconstruction quality (as evaluated by inspection, or by measured visibility), can be very good despite the fact that the η values are low (substantially less than 1 even in the optimum case). We reiterate that this is because the “signal-bearing” component of the scattered light is concentrated in a small area, whereas the “noise” component is diffused over a large area.

In summary, we have experimentally demonstrated wide-field imaging through a highly scattering sample using DOPC employing a ring interferometer configuration. The challenging optical alignment problem of matching the forward- and reverse-propagating wavefields has effectively been solved. The SLM used as the phase-conjugate-mirror “actuator” was capable of being directly imaged onto the CCD used as “sensor” in the ring interferometer, the key to the sub-wavelength accuracy attained in the optical alignment. Our work provides a means to implement a robust and practical DOPC system for biophotonic applications where multiple light scattering is a limiting factor, including optical deep-tissue imaging and photodynamic therapy.

Methods

Experimental setup

In our DOPC system, an EM-CCD camera (CCD1 in Fig. 1, Photon Max 512, Princeton Instruments, New Jersey, USA) and a SLM (Hamamatsu, LCOS-SLM X10468-02, Japan) constitute the sensor and actuator, respectively. A phase profile (pixelated over an 800 × 600 grid, total dimensions 16 × 12 mm) is applied to the beam incident on the SLM. Full phase control is permitted for each pixel independently, and performed using a computer. The liquid crystal pixels of the SLM are aligned horizontally, mandating that horizontally polarized light be incident upon it to achieve phase-only control. Highly coherent light from a tunable laser source (Xperay Tunable Laser, General Microtechnology and Photonics, Switzerland), operating at 831 nm, is coupled into a single-mode fiber that is further connected to an optical-fiber-based polarization controller. This permits the source to be easily interchanged with a visible-light fiber-coupled laser, for the purpose of system alignment. After exiting the fiber, the beam is expanded and collimated; in Fig. 1, it is shown entering the system from the top-right.

Sample preparation

The scattering layer was prepared by spray-painting ZnO particles (an average diameter of 200 nm) on a standard glass microscope cover slip. The transport mean free path of the sample was measured as 0.7 ± 0.2 μm at a wavelength of 632.8 nm and the thickness of the sample was 11.3 μm. The turbid sample was positioned at the common focal plane of the two microscope objectives.

Author Contributions

T.R.H., Y.P. and Z.Y. designed experiments, performed research, analyzed the data and wrote the paper; T.Y. and W.C. provided advice and assistance at the early stages of the project; R.R.D. and M.S.F. provided advice and were responsible for obtaining financial support for the project. All surviving authors reviewed the manuscript.

Supplementary Material

Supplementary Information

supplementary info

srep01909-s1.doc (8.7MB, doc)

Acknowledgments

This work was supported by The National Institute of Biomedical Imaging and Bioengineering (9P41-EB015871-26A1), Hamamatsu Photonics (Japan), Samsung Advanced Institute of Technology, KAIST Institute for Optical Science and Technology, and the Korean Ministry of Education, Science and Technology (MEST) grant No. 2009-0087691 (BRL) and National Research Foundation (2012R1A1A1009082, 2012K1A31A1A09055128, M3C1A1-048860, 2013M3C1A3000499). TRH acknowledges support from the Singapore-MIT alliance fund (SMA2). YKP acknowledges support from TJ ChungAm Foundation. We thank Dr. Allard Mosk (University of Twente, The Netherlands) for providing the scattering samples.

References

  1. Vo-Dinh T. Biomedical photonics handbook. Journal of Biomedical Optics 9, 1110 (2004). [Google Scholar]
  2. Mosk A. P., Lagendijk A., Lerosey G. & Fink M. Controlling waves in space and time for imaging and focusing in complex media. Nat. Photonics 6, 283–292 (2012). [Google Scholar]
  3. Vellekoop I. & Mosk A. Focusing coherent light through opaque strongly scattering media. Optics Letters 32, 2309–2311 (2007). [DOI] [PubMed] [Google Scholar]
  4. McCabe D. J. et al. Spatio-temporal focusing of an ultrafast pulse through a multiply scattering medium. Nature Communications 2, 447 (2011). [DOI] [PubMed] [Google Scholar]
  5. Katz O., Small E., Bromberg Y. & Silberberg Y. Focusing and compression of ultrashort pulses through scattering media. Nature photonics 5, 372–377 (2011). [Google Scholar]
  6. Aulbach J., Gjonaj B., Johnson P. M., Mosk A. P. & Lagendijk A. Control of light transmission through opaque scattering media in space and time. Phys. Rev. Lett. 106, 103901 (2011). [DOI] [PubMed] [Google Scholar]
  7. Park J. H., Park C. H., Yu H., Cho Y. H. & Park Y. K. Active spectral filtering through turbid media. Opt. Lett. 37, 3261–3263 (2012). [DOI] [PubMed] [Google Scholar]
  8. Small E., Katz O., Guan Y. & Silberberg Y. Spectral control of broadband light through random media by wavefront shaping. Optics Letters 37, 3429–3431 (2012). [DOI] [PubMed] [Google Scholar]
  9. Park J.-H., Park C., Yu H., Cho Y.-H. & Park Y. Dynamic active wave plate using random nanoparticles. Opt. Express 20, 17010–17016 (2012). [Google Scholar]
  10. Guan Y., Katz O., Small E., Zhou J. & Silberberg Y. Polarization control of multiply-scattered light through random media by wavefront shaping. Optics Letters 37, 4463–4665 (2012). [DOI] [PubMed] [Google Scholar]
  11. Kim M. et al. Maximal energy transport through disordered media with the implementation of transmission eigenchannels. Nature photonics 6, 581–585 (2012). [Google Scholar]
  12. Park J. H. et al. Subwavelength light focusing using random nanoparticles. Nature photonics (2013). [Google Scholar]
  13. Jang J. et al. Complex wavefront shaping for optimal depth-selective focusing in optical coherence tomography. Optics Express 21, 2890–2902 (2013). [DOI] [PubMed] [Google Scholar]
  14. Popoff S., Lerosey G., Fink M., Boccara A. C. & Gigan S. Image transmission through an opaque material. Nature Communications 1, 81 (2010). [DOI] [PubMed] [Google Scholar]
  15. Popoff S., Lerosey G., Fink M., Boccara A. & Gigan S. Controlling light through optical disordered media: transmission matrix approach. New Journal of Physics 13, 123021 (2011). [Google Scholar]
  16. Choi Y. et al. Overcoming the diffraction limit using multiple light scattering in a highly disordered medium. Physical Review Letters 107, 23902 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Leith E. N. & Upatnieks J. Holographic imagery through diffusing media. J. Opt. Soc. Am. A 56, 523–523 (1966). [Google Scholar]
  18. Yaqoob Z., Psaltis D., Feld M. & Yang C. Optical phase conjugation for turbidity suppression in biological samples. Nature photonics 2, 110 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Cui M. & Yang C. Implementation of a digital optical phase conjugation system and its application to study the robustness of turbidity suppression by phase conjugation. Optics Express 18, 3444–3455 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hsieh C. L., Pu Y., Grange R., Laporte G. & Psaltis D. Imaging through turbid layers by scanning the phase conjugated second harmonic radiation from a nanoparticle. Optics Express 18, 20723–20731 (2010). [DOI] [PubMed] [Google Scholar]
  21. Garibyan O. et al. Optical phase conjugation by microwatt power of reference waves via liquid crystal light valve. Opt Commun 38, 67–70 (1981). [Google Scholar]
  22. Grange R., Lanvin T., Hsieh C. L., Pu Y. & Psaltis D. Imaging with second-harmonic radiation probes in living tissue. Biomedical optics express 2, 2532–2539 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Yang Y. M., Judkewitz B., A D. C. & Yang C. Deep-tissue focal fluorescence imaging with digitally time-reversed ultrasound-encoded light. Nature Communications 3, 8 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Si K., Fiolka R. & Cui M. Fluorescence imaging beyond the ballistic regime by ultrasound-pulse-guided digital phase conjugation. Nature photonics (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Vellekoop I. M., Cui M. & Yang C. Digital optical phase conjugation of fluorescence in turbid tissue. Appl Phys Lett 101, 081108–081108–081104 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Vellekoop I. M. & Aegerter C. M. Scattered light fluorescence microscopy: imaging through turbid layers. Opt. Lett 35, 1245-1247 (2010). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

supplementary info

srep01909-s1.doc (8.7MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES