Experimental basis of the hypotheses on the mechanism of skeletal muscle contraction

Summary

With time clever hypotheses may be accepted as “facts” without being supported by solid experimental evidence. In our opinion this happened with muscle contraction where pure suggestions still occupy the scene and delay the progress of the research. Among these suggestions are: 1. the believe that viscosity is irrelevant in the economy of muscle contraction, 2. the concept of the drag stroke, 3. some interpretations of the significance of the Huxley-Simmons manoeuvre, 4. the definition of the load as a force/cross-section without taking into consideration the possible, divergent effects of the infinite mass x acceleration couples.

Technical questions are also raised since it is apparent that measuring equipments interfere with the measure itself.

Introduction

Here are sketched the principal contributions to the study of muscle contraction. Some of these contributions will be critically considered.

The force-velocity curve

The bequest of the four decades of the monumental Hill’s work is summarized by the concept that the shape of the force-velocity curve of frog muscle is connected with the heat that it produces. A concept expressed by the Hill’s equation:

$$(\text{P}+\text{a})\hspace{0.17em}(\text{v}+\text{b})=({\text{P}}_0+\text{a})\hspace{0.17em}\text{b},$$

where, v, is the contraction velocity, P, is the tension, P₀, is the tension produced when there is no shortening (that is, in an isometric contraction), and, a, and, b, are constants (1).

Hill provided the accurate description of the variation of the heat rate, h, with the load for frog muscle:

$$\text{h}=(0.18\hspace{0.17em}{\text{P}}_0+0\hspace{0.17em}16\hspace{0.17em}\text{P})\hspace{0.17em}\text{v}+\text{f}(\text{t})$$

Of the two terms of the right-hand side of the equation the first represents the “shortening heat” rate and the second, f(t), the “maintenance heat” rate (2).

Furthermore, Hill A.V. defined precisely the efficiency of the mechanical power during frog muscle shortening and in relation to load (3).

In all Hill’s work continuous attempt was made to provide a full description of muscle activity by the concomitant measure of contraction velocity, tension, work produced and muscle power output.

The sliding filament model

The unraveling of the microscopic anatomy of the contractile apparatus (4, 5) focused deeply the interest toward the molecular mechanisms of the contraction with the introduction of the sliding filament model.

In this respect very provocative was the model proposed by A. F. Huxley (6), with the presentation of the following hypotheses: 1. the execution of the power stroke was conditioned by the stretching of an elastic element, the stretching being performed by thermal motions; 2. a linear elasticity was assigned to both detached and attached cross-bridge; 3. At the maximum velocity of shortening, since tension equals zero, the net positive force exerted by myosin heads attached in the power stroke must equal the net negative force exerted by heads that have been carried into the drag-stroke region.

To insure that the force-generating mechanism works equally well over a considerable range of inter-filament spacing (this spacing changes considerably with sarcomere length) H.E. Huxley (7) proposed that the actual force-generating structure (the myosin head) is attached to the backbone of the myosin filaments by a linkage, 40 nm long, with flexible couplings at either end. The force-generating structure can therefore attach itself to the actin filament, in a constant configuration, and undergo exactly the same structural changes, independently of the inter-filament spacing.

This idea prompted A.F. Huxley to formulate a further model to explain force generation in striated muscle. In the model cross-bridge attachment was placed under the control of thermal motion. After attachment the cross-bridges was assumed to rotate, relatively to the thin filament, from one to the next of a few positions with progressively lower potential energy while stretching the, 40 nm long, elastic linkage. At the end of the rotation, the detachment of myosin head from the thin filament was prompted by a process involving the hydrolysis of ATP (8).

The alternative model of Eisenberg et al. (1980)

According to Huxley and Simmons (8) there is no relation between the 40 nm long, elastic element and the chemical changes occurring elsewhere in the attached cross-bridge. As a consequence the elastic element must be stretched by one-dimensional fluctuations (Brownian motion) before any chemical change in state may occur. Furthermore the rates of transition between the attached states are linked to the amount the elastic element must be stretched by one-dimensional Brownian motion. To make these transition rates realistic, three or more attached states are necessary in the Huxley-Simmons model.

On the contrary, according to Eisenberg et al. (9), elasticity and chemical changes of state are linked. This means that the conformational change of the attached cross-bridge affects 1. the free energy of the cross-bridge and its optimal angle of attachment to actin; 2. the state of the bound nucleotide and the force exerted by the cross-bridge.

The model of Eisenberg et al. (9), is a four state model: two unattached (refractory and non refractory) and two attached (AM⁺.D.Pi and AM*.D) cross-bridge states. The attached cross-bridge can exist in two conformational states with different optimal attachment angle: in the 90° conformation the cross-bridge exerts zero force when it is attached to actin at a 90° angle, whereas in the 45° conformation the cross-bridge exerts zero force when it is attached at a 45° angle. In both conformational states the cross-bridge exerts positive force when it rotates to a larger angle than its optimal angle, and negative force when it rotates to a smaller angle than its optimal angle. The predictions of the model are in agreement with the well documented relationship between the in vitro actomyosin ATPase activity and the velocity of muscle contraction in vivo (10, 11). The prediction is also made that the number of the attached cross-bridges (and not their force) decreases with the shortening velocity.

The power stroke

According to Huxley H.E. (12) for the same output of mechanical energy the cross-bridges might move either (a) with a weak force over a relatively large distance, or (b) with a strong force over a short distance, or (c) with variable force/distance relationship, depending on the mechanical load against which they operate. Huxley A.F. (6) clearly selected the first possibility since, as it was pointed out by Civan and Podolsky (13), his mathematical model was based on a long distance, weak force mechanism. The choice was made explicit by Huxley and Simmons (8) with their ∼10 nm power stroke, deduced from the decrease in tension after rapid changes in muscle-fibre length.

The third possibility, namely a variable force/distance relationship, depending on the mechanical load, was first formulated theoretically by Worthington and Elliott (14), then, experimentally, by Piazzesi et al. (15) who proposed the step size to decrease from 7 nm at zero load to 4 nm at 80% of the isometric load. In these experiments, performed with 150 μs force steps, the elastic response was separated from the subsequent early rapid component of filament sliding which was attributed to the working stroke in the attached myosin heads.

While Huxley (6), Cooke (16) and Piazzesi et al., (15) think that the force delivered by each attached motor decreases with sliding velocity, Eisenberg et al. (9) propose that it is the number of the attached motors to decrease with the increase of contraction velocity. Furthermore, according to Piazzesi et al. (17), any attached motor delivers the same force, ∼6 pN and displays the same strain, ∼1.7 nm, both in the isometric and in the isotonic conditions.

Higuchi and Goldman (18), in skinned fibres, directly estimated the proportion of simultaneously attached actomyosin complexes and their ATP use. They found an interaction distance of ∼40 nm, drag distance included. The step size of the power stroke was estimated not only from mechanic experiments but also from kinetic and energetic data (19, 20).

Pate et al. (19) deduced the average step size of the power stroke from the rate of head dissociation and the velocity of filament sliding. This procedure was especially successful at low substrate concentration, where the rate of head dissociation is almost proportional to substrate concentration (21, 22). Interestingly, in this model, the calculation of the step size does not require knowledge of either the fraction of the attached cross-bridges or the ATPase rate per working head.

Barclay et al. (20) estimated the steady state working stroke, defined as the distance the filaments move while a cross-bridge is attached. This distance is determined by dividing the contraction velocity by the time for which a cross-bridge is attached. This latter is the product of the time of the ATPase cycle by the fraction of the attached cross-bridge. According to Barclay et al. (20) the steady state working stroke increases from zero in the isometric contraction to 12 nm at 0.2 Vmax and to ∼20 nm at the Vmax.

The quick release and the early force recovery

Huxley and Simmons (8) applied a small, very rapid, length change to a single muscle fibre in the isometric state (quick release) then measured the subsequent rapid tension recovery at fixed sarcomere length. To explain the early force recovery Huxley and Simmons assumed that the cross-bridge is composed by two structural elements, an elastic one (link AB) and a visco-elastic one capable of readjusting the tension of the system. It was also assumed that the attached cross-bridge performs work in a small number of steps, from one to the next of a series of stable positions with progressively lower potential energy. At the end of the series the cross-bridge can be detached from the thin filament by a process involving the hydrolysis of ATP. Thus the early force recovery is due to the tendency of the myosin head to rotate toward positions of lower potential energy.

The cross-bridge was assumed to perform work in more than one step because the one-step model was not sufficient to justify the actual force delivered by a real fibre. The multi-step model was also selected because it makes faster and easier the cross-bridge attachment by decreasing its thermally driven deflection. The multistep model was adopted by many authors (20, 23–27). According to Linari et al. (27) a multi-step power stroke offers an increasing detachment probability above 6 nm. The same authors calculated that the energy for the first step (∼2.8 nm) is 3 k_BT at 5°C. This value is compatible with thermal motion that, according to A.F. Huxley (6) is required to stretch the elastic element.

For Huxley and Simmons (8) the rapid force recovery is due to the action of already attached cross-bridges. This idea, shared also by Barclay et al. (20), is based on the consideration that the rate of force recovery is ∼3 orders of magnitude faster than a single cross-bridge cycle.

Considerations on the mechanism of muscle contraction

Here we will provide evidence that some of the topics illustrated in the previous section are open to criticism. Our arguments are the followings: 1. In the classic studies on muscle contraction the water-protein interactions are almost completely overlooked; 2. The viscous hindrance in the sliding of the thin past the thick filament is not properly considered; 3. Proper consideration of the viscous contribution casts doubt on the reality of the drag stroke; 4. The interpretation of the Huxley – Simmons manoeuvre; 5. Suspects are raised that the measuring equipment interferes with the measurements.

Water and muscle contraction

The partition of the free energy among contractile proteins cannot be determined unless the non-ideality of the contractile system is recognized (28–29). Reasoning on non-ideal systems requires the knowledge of activity. Determination of activities requires an osmotic approach to the system. In fact the change of the chemical potential of the solute is obtained by combining the two equations:

$$\begin{array}{l}\mathrm{\Delta }{\mu }_1={\mu }_1-{\mu }_1\circ =-\pi \hspace{0.17em}V\\ {({\text{n}}_1\hspace{0.17em}\text{d}{\mu }_1+{\text{n}}_2\hspace{0.17em}\text{d}{\mu }_2)}_{\text{T},\text{P},\text{n}2}=0\end{array}$$

where n₁ and n₂ are the number of moles of water and of the solute, μ₁ and μ₂ are the chemical potentials of water and of the solute, V is the volume of one mole of water, 18 cm³, and π is the osmotic pressure.

In a binary solution the activity coefficient of the solute, γ₂, is given by,

$$\text{ln}[{\gamma }_2]={\int }_0^{m_2}\frac{(\varphi -1)}{m_2}{dm}_2+(\varphi -1).$$

(30), where, m₂, is the molality of the solute and, Φ, is the molal osmotic coefficient. Thus, by measuring the osmotic pressure, the free energy change and the activity of the solute can be determined. In some cases these rules can be extended to systems more complex than binary solutions (31).

Following this pathway protein osmotic pressure is found to influence the behaviour of the cross-bridge since it determines 1. its free energy minimum (28); 2. its stiffness and 3. its contractile force (32).

Osmotic studies unravel protein cross talking trough chemiosmotic coupling. As an example, the addition of MgADP perturbs both the chemical and the osmotic equilibria of myosin solutions. The resulting free energy changes are associated with the perturbation of the hydration shell of myosin, waves of water chemical potential are generated which, in muscle, can be sensed by the surrounding proteins, that compete with myosin for water. Therefore MgADP and, eventually, MgATP may indirectly regulate the functioning of proteins of the contractile machinery, which, per se, may even be insensitive to MgADP or to MgATP (33).

In muscle there is a huge number of distinct reaction systems which, in the relaxed state, are ‘embedded’ in water at the same chemical potential. During the power stroke, the formation and the transitions of the actomyosin intermediates are accompanied by changes of the protein solvation water and, consequently, by the transfer of water among the protein solvation shells of the different systems. This means that each actomyosin reaction center behaves as an open system, which exchanges water and small electrolytes with the surroundings. Since both mechanical strain and formation of the attached states influence the local water chemical potential (34), during the power stroke spikes of the water chemical potential are generated.

From a thermodynamic point of view these spikes are mostly due to sudden changes of the water activity coefficient.

From a physical point of view these spikes are due to the sudden conversion of solvation layers of water into bulk water and vice versa. The conversion is sensed either as a positive or as a negative compression and is transmitted like a sound wave in water (rate ∼1400 m/s). This means that the waves of the water chemical potential propagate at the rate of ∼1.4 μm/ns, a rate which is orders of magnitude faster than the power stroke. In spite of their swiftness these waves are likely to play a role in the regulation and in the energetic of muscle contraction (33).

The transition of polymers into a network of polymers alters per se the water activity: in fact the macromolecular osmotic pressure of water increases (water chemical potential decreases) as a consequence of the cross-linking. This means that the water of hydration is held more tightly and more work is needed to remove a mol of water from the network than from the free polymer chains. This also means that, at the same solid mass concentration, the elastic stress on the network is larger than the elastic stress on the free polymer chains. In muscle, the network formed by the cyclic interaction of thick and thin filament decreases, per se, the water chemical potential and increases the elastic stress on the structures involved. This is a possible further mechanism of regulation of muscle contraction. In fact, not only the stiffness and the force generated by the cross-bridge are a function of the intrinsic protein osmotic pressure generated by the cross-bridge itself (32), but cross-bridge attachment promotes, per se, the increase of the stiffness of the structure. We are thus in the presence of a fine interplay of regulating factors, all based on subtle changes of the water activity (35).

The viscous hindrance and the sliding of the thin past the thick filament

Many studies were devoted to understand the importance of viscous hindrance in the economy of muscle contraction. The general tendency was to exclude that viscous hindrance influences significantly muscle contraction.

The hydrodynamic viscous coefficient of a single myosin filament in a model half-sarcomere was calculated by Huxley (36) that proposed the viscous drag force to be 10⁻⁴ times lower than the isometric force. Schoenberg (38) individuated in the rapid equilibrium between the attached and detached states of the cross-bridge a mechanism sufficient to generate a visco-elastic behavior without postulating a viscous component.

From the other side activated fibers were shown to display a significant internal viscosity (38, 39). Furthermore Elliott and Worthington (40) calculated for the actin filament of frog muscle during contraction a hydrodynamic viscous drag of 6 10⁻⁵ kg s⁻¹, the same order of magnitude of the isometric force.

As a matter of fact bona fide values for the viscous hindrance of the sliding of the thin past the thick filament in active muscle are not available. According to Poiseuille, the steady flux of a liquid in a tube depends on the viscous coefficient, η (m l⁻¹ t⁻¹), on the hydrostatic pressure difference at the ends of the tube, on the length of the tube and on a geometrical factor, related to section of the tube. For a circular section the geometrical factor is π r⁴/8. Unfortunately, in muscle, the shape of the section is so complex that the related geometrical factor is not available so the calculation of a viscous coefficient is precluded.

To overcome the difficulty a conventional viscosity coefficient, β (m l⁻² t⁻¹) was introduced (41) and was defined as the ratio of the viscous component of the load to the stretching velocity (39).

While dealing with viscosity in muscle we must be aware that muscle is a highly non-ideal solution (28). From a thermodynamic point of view this means that water activity is lower than expected from the water molar fraction. From the modeling point of view this means that bulk water decreases in favor of hydration water, that thickness of the water protein shell increases, that the boundaries of the hydrated proteins are getting closer and that their mutual friction increases.

From this point of view criticism must be raised both to T.L. Hill (42) for his sliding filament model of contraction of striated muscle and to Schoenberg (37) for postulating that rapid cross-bridge equilibrium between attached and detached cross-bridge states is sufficient to generate visco-elastic behaviour without a viscous component attributable to the solution.

For T.L. Hill (42) the free energy of detached cross-bridges does not change when the sarcomere is stretched. This is not correct. In fact, if the contribution of water to the system is explicitly considered, it turns out that the perturbation of water equilibrium alters the free energy of all the other species of the system, detached cross-bridges included (28, 32). It was also shown that the stretching itself of the attached cross-bridges perturbs water equilibrium Furthermore, the lowering of the cross-bridge deformation by applying a stretching force, decreases the water activity coefficient. This indicates that new water-myosin interactions are formed or preexisting water-myosin interactions are strengthened, or both (34, 43). In any case the fraction of structural water increases and viscosity also increases, a conclusion in keeping with Bird et al. (44) which relates the increase of viscosity to the decrease of the water activity. For these reasons it is expected the viscous hindrance to be very significant in contracting muscle.

The drag stroke

The concept of drag stroke was proposed by A.F. Huxley (6) to justify the zero force output from muscle fibres contracting at maximal velocity. The concept is in use from more than fifty years without any real attempt to prove its factual reality (16, 18, 19, 45).

In essence it is assumed that cross-bridges produce a positive force (power stroke) that causes the relative sliding of the thin past the thick filament and the consequent fibre contraction. The sliding itself pulls the still attached cross-bridges in the zone of negative force where they resist the sliding and oppose muscle contraction (drag stroke). The idea is that, at the maximum velocity, the positive force delivered by the power strokes equals that delivered by the drag strokes, the net force being zero.

In fact there is not a rational hiatus between the maximal velocity and all the other isotonic contraction velocities. In all the cases the velocity of the contraction is constant thus the resultant of the forces, including the load, must be zero. The only difference is that, under maximal velocity conditions, the system deals only with a very tiny internal load, the fibre, while, in all the other isotonic conditions, an external load adds to the internal one.

The real question is whether the forces produced by the working stroke, by the eventual drag stroke and by the loads (internal and external) are the only forces involved. According to A.F. Huxley (6) there are no other forces since viscosity is ignored.

It is true that we do not possess a definite figure for the viscosity of the active muscle but it is also true that the strict interaction of water with the protein of the contractile apparatus determines a viscous behaviour opposing muscle contraction. We propose, therefore, that most of the force assigned to the drag stroke originates, on the contrary, from the viscous hindrance due to the sliding of the thin past the thick filament.

In the classic view attached cross-bridges produce force as linearly elastic elements (i.e., force is proportional to strain) and the elastic modulus is the same for both positive and negative values of x.

We think, on the contrary, that in the “zone of negative force” the stiffness of the cross-bridges, still attached, fades since they have already delivered their energy. We cannot ignore 1. that the power stroke rely on the stiffness acquired by the contractile structure and 2. that stiffness acquisition depends on the energy delivered by ATP. It seems therefore correct the idea that, once the energy of ATP has been used up, its “product”, the stiffness, is also gone. If this is true the elastic modulus of the attached cross-bridge should not be the same for both positive and negative values of x, but the modulus for the positive side should be larger than that for the negative side. Moreover, we also doubt that the contractile force is a linear function of the deformation, x, since the “length-force constant” changes significantly with the deformation of the cross-bridge (34, 46).

The interpretation of the Huxley - Simmons manoeuvre

We have already discussed the classic interpretation of the Huxley-Simmons manoeuvre (47) with particular reference to the following points:

The reallocation of the energy associated to the elastic component of the Huxley-Simmons manoeuvre

If the rapid release is an elastic phenomenon some of the energy involved in the process must be available for further events such as the early force recovery as it was shown by a modelled elastic system (47). This feature was recognized also by Woledge et al. (26) who claimed, however, that the elastic energy stored was only 0.8 k_BT, i.e. ∼1/30 of the energy provided by the splitting of one ATP molecule. On this basis they assumed that “the cross-bridge is recharged with work a number of times within each ATPase cycle”.

The relationship between the rate of the quick release and the rate of the early force recovery

We pointed out already (47) that, if part of the early recovery is generated by the kinetic energy accumulated in the course of the quick release, a relationship should be found between the rates of the quick release and of the early force recovery. This relation is in fact observed in experiments where the length changes are complete in a fixed time (15, 23, 48). Under this condition the rate of shortening (and the kinetic energy) increase with the length of the step. This feature was never recognized before. Furthermore, while formulating their cross-bridge model, Piazzesi and Lombardi (23) assumed the step-length change to be complete in zero time while, in fact, it was complete in 120 μs. This “simplification” would have never been proposed if the authors had appreciated the importance of the kinetic energy of the quick release in the economy of the Huxley-Simmons manoeuvre.

The kinetic energy is dissipated in the measure

The analysis of Figure 14 of Ford et al. (41) shows that at the end of the experimental quick release of 6 nm per half sarcomere the kinetic energy available is only 0.97 nJ out of the 81.6 nJ found while modeling a purely elastic process. This means that the kinetic energy was largely dissipated in the experimental procedure. In fact, to allows the sudden stop of fibre shortening, the setting of the measuring equipment had to be changed (47).

All the components of the attached cross-bridge participate to the quick release

The quick release is a sequence of events that involve the actin filament, the force-generating structure of the cross-bridge, a 40 nm linkage and, finally, the backbone of the thick filament. All these structures are in series thus the associated force must fade concomitantly with the quick release. Furthermore, as shortening readjustment proceeds, the change in length must be shared by the two components of the cross-bridge, in reason of their respective stiffness. There is in fact no reason to associate the quick release to the elastic element only (47).

Technical questions

Nowadays the equipments of muscle physiologists have reached a high degree of sophistication with time resolution approaching the microsecond. These equipments are also very versatile and shift easily from either the fixed end mode or the force clamp mode or the length clamp mode. The reader understands the meaning of these expressions but he does not know their physical equivalence. He ignores which physical parameters are changed to shift, as an example, from the fixed end to the force clamp mode and so on.

In the experiments on muscle contraction the system is composed by the muscle fibre and by the load, nothing else. So every thing that is not the muscle fibre is the load, equipment included. This is the reason why the reader must know exactly, in physical terms, what happens to the equipment when the mode is changed. The possibility must be excluded that, by changing the mode, the load is surreptitiously changed.

The equipment interferes with the evaluation of the rapid release

If indeed the quick release is an elastic process, it should be possible to reproduce its time course for both force and length decreases, provided that the isometric tension and the stiffness of muscle fibre are known. However this is not so. The data of Figure 14 of Ford et al. (41) allow to calculate that the spontaneous release of the fibre should require ∼43 μs (47). On the contrary the observed release takes place in ∼180 μs (41). Similar conclusions are drawn here from the work of other authors.

In Figure 5 of Linari et al. (48), the isometric tension of 160.87 kN/m² is reduced to zero in 110 μs by a quick release of 3.9 nm/half sarcomere. However, by modeling the rapid release as a purely elastic phenomenon (Appendix A) it is found that the event should take place in only 9.9 μs.

In Figure 2A of Piazzesi et al. (15) the isometric tension of 176 kN/m² is reduced to zero in 150 μs by a quick release of 3.73 nm per half sarcomere. Again, by modeling the rapid release as a purely elastic phenomenon (Appendix A), it is found that the shortening of the half sarcomere by 3.73 nm should take place in only 9.07 μs. In Piazzesi et al. (24) the isometric tension of 146 kN/m² is reduced to zero in 110 μs by a quick release of 3.77 nm per half sarcomere while the theory predicts that the reduction to zero of the force should take place in only 40.87 μs.

Interestingly, in all the cases by properly increasing the mass, the rate of the phenomenon can be delayed to the experimental values without affecting the associated kinetic energy which, at the peak, equals 0.3938 J (Fig. 1, lower part). So the quick release in Ford et al. (41) is delayed to 180 μs by increasing the “fibre mass” by 17.45 fold; in Linari et al. (48) the reduction to zero of the force is obtained in 110 μs provided that the “fibre mass” is increased by 124 times; in Piazzesi et al. (15) the reduction to zero of the force can be delayed to 150 μs by increasing the “fibre mass” by 274 fold (Tab. 1).

Figure 1.

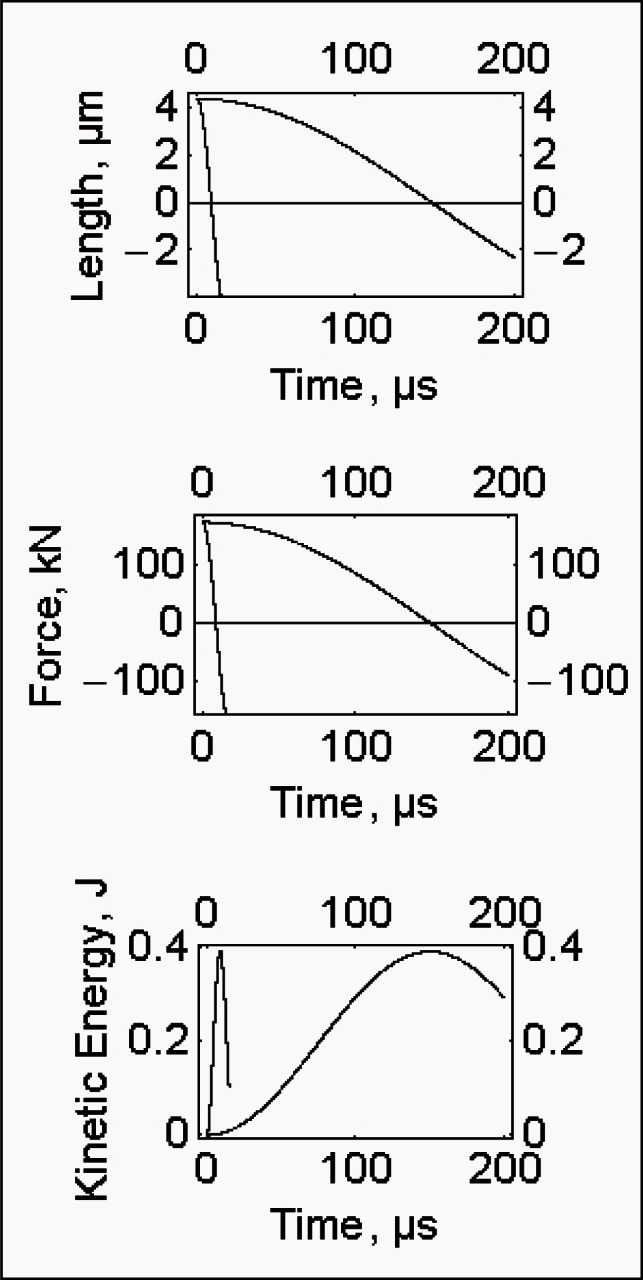
Length, force and kinetic energy of a muscle flbre in the course of the quick release.

Upper figure: fibre length as a function of time. Left: the theoretical curve crosses the abscissa axis at 9.07 μs, right: the theoretical curve crosses the abscissa axis at 150 μs after increasing the “fibre mass” by 274 fold. Middle figure: force as a function of time. Left: the theoretical curve crosses the abscissa axis at 9.07 μs, right: the theoretical curve crosses the abscissa axis at 150 μs after increasing the “fibre mass” by 274 fold.

Lower figure: kinetic energy as a function of time. The peak of the two curves is at 0.3938 J.

Data are taken from Fig. 4 of Piazzesi et al. (2003).

T₀, 146 kN/m², fibre length 5.17 10⁻³ m, sarcomere length 2.11 10⁻⁶ m, duration of step 110 μs, stiffness referred to the half sarcomere 146000 N / 3.77 10⁻⁹ m, temperature 2.1 °C.

Table 1.

The theoretical time of the quick release is converted into the experimental time by multiplying the “fibre mass” by a proper factor.

T0, kN/m2	Fibre length, mm	Fibre stiffness	Time to reduce force to zero (theory) μs	Time to reduce force to zero (experiment) μs	Mass factor
270*	5.34	8.427 109	43.13	180	17.45
160.87**	1.27	3.312 1010	9.9	110	124
176***	1.27	3.938 1010	9.07	150	274
146****	5.17	7.9 109	40.87	110	7.25

^*)Ford et al. (1977), fibre density 1190 kg/m³, fibre mass 6.3546 kg/cross-section of 1 m², sarcomere length 2 μm;

^**)Linari et al. (1998), fibre density 1.035 kg/m³, fibre mass 1.314 kg/cross-section of 1 m², sarcomere length 2.04 μm;

^***)Piazzesi et al. (2002), fibre density 1035 kg/m³, fibre mass 1.314 kg/m³, sarcomere length 2.12 μm;

^****)Piazzesi et al. (2003), fibre density 1035 kg/m³, fibre mass 5.35 kg/m³, sarcomere length 2.11 μm.

It is clear that the estimate of the mass of the fibre cannot be subjected to such a large errors. Evidently the extra mass is a load imposed surreptitiously by the measuring equipment. This seems to be confirmed by the fact that the divergence of the theory form the experiment is larger at the lowest fibre (or fibre segment) length where technical difficulties seems to be more likely (Tab. 1).

Pitfalls of the model we are using seem to be excluded. In the model only the elastic force of the fibre is considered. Shortening of the fibre occurs by the uniformly accelerated motion thus in the absence of any hindrance as for a pure elastic phenomenon should be. In the essence a simple harmonic motion is generated.

We are forced to conclude that measurements interfere with the phenomena that are measured. These drawbacks could probably be overcome by the proper description of the physical parameters of the equipment while measurements are performed.

The acceleration of the load

We turn now our attention to the effect of the acceleration of the load on the economy of muscle contraction. The importance of the acceleration of the load was very clear in the early studies on muscle contraction. The “balanced mass” apparatus (49) and the “heavy flywheel” (50) were constructed to measure the maximum work developed by a contracting muscle. The function of these devices was to retard the shortening of the muscle to various degrees, by causing it to accelerate “equivalent masses” of different sizes and to control the rate of shortening. In all these studies it was always possible to trace the contribution of both the mass and of the acceleration of the load.

More recently the load was provided by linear motors, the technical features of the equipment were always detailed but no information was provided on the mass and of the acceleration of the load in the single experiments. The force is the product of the mass by the acceleration, thus the same force is generated by an infinite number of mass and acceleration couples and each one of these couples displays different physical and biological effects. Therefore, the load must be defined both by the mass and by the acceleration.

This topic is addressed by making use of a model of muscle contraction that relates the experimental power output to the experimental speed of contraction by means of the hindrance of the contractile system, expressed by the constant, 1/k (s⁻¹) (51). The model shows that, at constant load force, the decrease of the acceleration of the load: 1. slows down the pre-steady state of the contraction; 2. decreases the apparent stiffness of the active half sarcomere; 3. decreases the constant, 1/k (s⁻¹) (52). These effects are the direct consequence of the equation of motion used where the relevance of the acceleration of the load is recognized,

$${\text{a}}_{\text{d}}=({\text{F}}_1-{\text{F}}_2)/({\text{m}}_1+{\text{m}}_2)$$

a_d, driving acceleration; F₁, contractile force; F₂, force associated to the load; m₁, mobile mass of the contractile apparatus; m₂, mass of the load.

According to the model the acceleration of the load determines the time course of the generation of the isometric tension (53). The model shows also that, to reproduce the rapid release, it is not necessary a distinct elastic elements in the contractile machinery (41, 54). The same result is obtained if, in the course of the isometric contraction, the contractile structures increase their rigidity. This idea is quite old (55) and is also substantiated by our studies on the relationship between protein osmotic pressure, stiffness of the cross-bridge components and contractile force of skeletal muscle (32, 34).

Conclusion

In this work we dealt with some concepts more open to criticism but others may deserve consideration. Unfortunately the general tendency is to put forward models of increasing complexity and not always grounded on a solid basis. Sometime simple models, built on a purely physical basis, may help to address and sometime to answer questions so far unresolved. We urge that the interference of the measuring equipment is more carefully considered.

APPENDIX A.

The model reproduces the pure elastic shortening of a muscle fibre.

The shortening of the whole fibre (or fibre segment) that bring tension to zero, dl_T, is

$${\text{dl}}_{\text{T}}=\text{dl}\hspace{0.17em}2\hspace{0.17em}\text{lsf}\hspace{0.17em}/\text{ls}$$

where, dl, is the shortening of the half sarcomere that bring tension to zero; lsf, is the fibre length and, ls, is the sarcomere length.

A single force, F_E, is considered which, in muscle fibre, is represented by the product of the isometric tension, T₀, time the cross-section of the fibre, sec,

$${\text{F}}_{\text{E}}={\text{T}}_0\hspace{0.17em}\text{sec}$$

The driving acceleration of the process is

$${\text{a}}_{\text{d}}={\text{F}}_{\text{E}}/\text{m}$$

m, the mass of the fibre, equals,

$$\text{m}=\text{d}\hspace{0.17em}\text{sec}\hspace{0.17em}\text{lsf}$$

where, d = 1035 kg / m³ is the density of frog sartorius muscle (56).

The fibre shortens by uniformly accelerate motion, thus the instantaneous rate, v, is

$${\text{v}}_{(\text{i})}={\text{v}}_{(\text{i}-1)}+{\text{ad}}_{(\text{i}-1)}\hspace{0.17em}{\text{t}}_{\text{A}}$$

and the length traveled in the time, t_A, is

$${\text{l}}_{\text{A}}=\text{ad}/2\hspace{0.17em}{{\text{t}}_{\text{A}}}^2+\text{v}\hspace{0.17em}{\text{t}}_{\text{A}}$$

So at any time, t_A, dl_T decreases by, l_A,

$${\text{dl}}_{\text{T}\hspace{0.17em}(\text{i})}={\text{dl}}_{\text{T}\hspace{0.17em}(\text{i}-1)}-{\text{l}}_{\text{A}}$$

The force decreases linearly with shortening,

$${\text{F}}_{\text{E}}=\text{stiffness}\hspace{0.17em}{\text{dl}}_{\text{T}}$$

where stiffness is, of course, referred to the fibre (or segment) length.

The kinetic energy accumulated in the course of shortening is,

$$\text{ke}=\text{m}\hspace{0.17em}{\text{v}}^2/2.$$

Where, v, is the velocity of shortening.

The program is operated by the Mathematica 4 software. Data are taken from Piazzesi et al. 2002:

• T₀ = 176000 N/m²; sec = 1; d = 1035 kg / m³; ls = 2.12 10⁻⁶ m;

• lsf = 1.27 10⁻³ m; dl = 3.73 10⁻⁹ m; stiffness = 3.93827 10¹⁰ N/m;

• t_A = 10⁻⁸ s;

• F_E = T₀ sec;

• dl_T = dl 2 lsf /ls;

• m = d sec lsf;

• a_d = F_E / m;

• l_A = 0; v = 0; ke = 0;

• a1 = Table[{ i,

• l_A = a_d / 2 t_A² + v t_A;

• dl_T= dl_T – l_A;

• v = v + ad t_A;

• F_E = stiffness dl_T;

• a_d = F_E / m;

• ke = m v² / 2;

• t_T = i t_A;

• t_T, dl_T, F_E, ke}, {i, 1, 3000}].