Analysing panel count data with informative observation times

Summary

In this paper, we study panel count data with informative observation times. We assume nonparametric and semiparametric proportional rate models for the underlying event process, where the form of the baseline rate function is left unspecified and a subject-specific frailty variable inflates or deflates the rate function multiplicatively. The proposed models allow the event processes and observation times to be correlated through their connections with the unobserved frailty; moreover, the distributions of both the frailty variable and observation times are considered as nuisance parameters. The baseline rate function and the regression parameters are estimated by maximising a conditional likelihood function of observed event counts and solving estimation equations. Large-sample properties of the proposed estimators are studied. Numerical studies demonstrate that the proposed estimation procedures perform well for moderate sample sizes. An application to a bladder tumour study is presented.

1. Introduction

In longitudinal studies of serial events such as repeated tumour occurrences or graft rejection episodes the cumulative number of these events experienced by each subject may be observed only at several distinct and random observation times, specific to each subject. Data of this type are commonly referred to as panel count data; see Thall & Lachin (1988) and Balshaw & Dean (2002). Statistical methodology for panel count data has developed slowly. Sun & Kalbfleisch (1995) derived a one-sample nonparametric maximum pseudolikelihood estimator of the rate function for the serial event process. Wellner & Zhang (2000) studied the asymptotics of the nonparametric maximum pseudolikelihood estimator and showed that it is less efficient than the nonparametric maximum likelihood estimator through some simulation studies. For semiparametric modelling, the derivation of the semiparametric maximum likelihood estimator is computationally intensive, and Zhang (2002) proposed an inference procedure based on a semiparametric pseudolikelihood function. Wellner et al. (2004) compared the large-sample properties of the semiparametric maximum pseudolikelihood estimator with the semiparametric maximum likelihood estimator, and showed that the former can be very inefficient when the distribution of the number of observation times is heavy-tailed. Sun & Wei (2000) formulated estimation equations for regression parameters in the semiparametric proportional rate models. However, the Sun–Wei estimator is inefficient as it ignores correlations among event counts in the estimation equations, and its validity relies heavily on correct modelling of the observation pattern.

Most proposed statistical models for panel count data assume that the observation times are independent of the serial events, conditioning on observed covariates such as treatment assignments. However, such an assumption can be violated in many applications. No existing method can handle panel count data with informative observation times. Motivated by Wang et al. (2001), we study nonparametric and semiparametric models that allow observation times to be correlated with the event process, where the correlation is induced by a frailty variable. Estimation procedures that require no parametric assumption about the distributions of the frailty variable and the observation time process are proposed for nonparametric and semiparametric models.

2. Notation and models

This paper focuses on statistical inference for the rate function for the underlying event process in a fixed time interval [0, τ]. Let N(t) denote the number of serial events that have occurred at or before time t, and assume that observations on a subject are collected at K random time points 0<t₁< … <t_K≤τ, where K is a random variable that takes positive integer values and y = t_K is the last observation time, i.e. the censoring time. Let m_j= N(t_j)−N(t_j−1) be the number of serial events in the time interval (t_j−1, t_j] and m = N(y) the total number of events observed in [0, τ]. We denote the observed data by D = {t₁, t₂, …, t_K, K, y; m₁, m₂, …, m_K, m}.

We consider the following nonparametric model for the event process N(·).

Model 1

Let Z be a nonnegative latent variable with E(Z)=1, so that, given Z=z, N(·) is a nonhomogeneous Poisson process with intensity function

$$\lambda (t\mid z)=z{\lambda }_0(t),t\in [0,\tau ],$$

where λ₀(t) is an unspecified function. Given Z, the event process N(·) is independent of K and the random observation times {t₁, …, t_K}.

Define the function ${\mathrm{\Lambda }}_0(t)={\int }_0^t{\lambda }_0(u)du$. Model 1 implies that the cumulative rate function of the event process in the disease population is given by E(Z)Λ₀(t)=Λ₀(t). Under Model 1, the event process N(·) and the observation times {t₁, …, t_K} are correlated through the frailty variable Z. Unlike most frailty models in the literature, Model 1 makes no parametric assumption about the distribution of Z.

Let x be a p×1 vector of covariates. When the effects of x on the rate function of the event process are of interest, a semiparametric extension of Model 1 for the event process N(·) is given below.

Model 2

There exists a nonnegative latent variable Z with E(Z|x)=1 so that, conditioning on x and Z=z, N(·) is a nonhomogeneous Poisson process with intensity function

$$\lambda (t\mid x,z)={ze}^{x^{\prime }\beta }{\lambda }_0(t),t\in [0,\tau ],$$

where β is a p×1 vector of parameters and λ₀(t) is unspecified. Moreover, given x and z, the event process N(·) is independent of the number of observation time points, K, and the observation times {t₁, …, t_K}.

In our formulation the distribution of the frailty variables and the conditional distribution of the observation times given the frailty can be arbitrary and are left unspecified.

3. The estimators and their asymptotic properties

3·1. Estimation procedure for model 1

We use subscript i for a subject, i=1, …, n. Let z_i be the individual frailty value, k_i the number of observation times and t_ij the jth observation time for the ith subject, where j=1, …, k_i and 0≡t_i0< … <t_iki≤τ. Let y_i denote the last observation time point, that is, y_i=t_iki. Let N_i be the underlying individual counting process and let m_ij= N_i(t_ij)−N_i(t_ij−1) be the number of serial events in the time interval (t_ij−1, t_ij]. Finally, let m_i = N(y_i) be the total number of events occurring during follow-up. For ease of notation we use m_ij and m_i to represent both random variables and realisations. We denote the observed data of the ith subject by D_i={t_i1, t_i2, …, t_iki, k_i, y_i; m_i1, m_i2, …, m_iki, m_i}, for i=1, 2, …, n, and assume that D₁, …, D_n are independent and identically distributed copies of D.

Model 1 implies that, given m_i and y_i, the m_i event times are order statistics of independent and identically distributed random variables with density function z_iλ₀(t)/z_iΛ₀(y_i). The likelihood of the event times is proportional to the truncation likelihood given in Wang et al. (2001). If we further condition on {t_ij, j=1, …, k_i}, the conditional likelihood function can be derived by integrating out the probability density function of the order statistics. Assuming that Λ₀(τ) is bounded, we define the shape function for the event process N(·) on [0, τ] as F(t)=Λ₀(t)/Λ₀(τ), for t≤τ. Thus F defines a proper cumulative distribution function on [0, τ] with F(τ)=1. The conditional likelihood function, conditioning on z_i, k_i, m_i and {t_ij, j=1, …, k_i}, is

$$Q\propto \prod _{i=1}^n\prod _{j=1}^{k_i}{\left\{\frac{{\mathrm{\Lambda }}_0(t_{ij})-{\mathrm{\Lambda }}_0(t_{ij-1})}{{\mathrm{\Lambda }}_0(y_i)}\right\}}^{m_{ij}}=\prod _{i=1}^n\prod _{j=1}^{k_i}{\left\{\frac{F(t_{ij})-F(t_{ij-1})}{F(y_i)}\right\}}^{m_{ij}}.$$ (1)

Interestingly, no information from the frailty variable Z is required to form (1). Note that, if ${\sum }_{j=1}^{k_i}{m}_{ij}=1$, the right-hand side of (1) is exactly the likelihood function of a set of independent interval censored and right-truncated data. Therefore, the estimation of F(t) in (1) can be implemented by the self-consistency algorithm proposed by Turnbull (1976).

Turnbull’s self-consistency algorithm is equivalent to the Expectation-Maximisation algorithm. When applied to the conditional likelihood function Q, the E-step and M-step have simple closed solutions as described below. Let $0\equiv t_0^{\ast }<t_1^{\ast }<\dots <t_L^{\ast }\le \tau$ be the ordered and distinct observation times from {t_ij; k_i>1, 1≤i≤n, 1 ≤ j ≤k_i}. For 1≤ l ≤L, define $p_k=F(t_k^{\ast })-F(t_{k-1}^{\ast })$. We maximise Q subject to the constraint ${\sum }_{k=1}^L{p}_k=1$. Define a_ijk=1 if $[t_{k-1}^{\ast }{t}_k^{\ast }]\subseteq [t_{ij-1},t_{ij}]$ and 0 otherwise. Additionally, we define b_ik=1 if $t_k^{\ast }\le y_i$ and 0 otherwise. Given the estimates $p_k^{(l)}(k=1,\dots ,L)$ in the lth iteration, the E-step is to compute

$$d_k^{(l)}=\sum _{i=1}^n\sum _{j=1}^{k_i}{m}_{ij}\left\{\frac{a_{\mathit{ijk}}{p}_k^{(l)}}{{\sum }_{h=1}^L{a}_{\mathit{ijh}}{p}_h^{(l)}}+\frac{(1-b_{ik})p_k^{(l)}}{{\sum }_{h=1}^L{b}_{ih}{p}_h^{(l)}}\right\},$$

where ${\sum }_{h=1}^L{b}_{ih}{p}_h^{(l)}={\widehat{F}}_n^{(1)}(y_i)$ in the lth iteration. Given the updated $d_k^{(l)}$, in the M-step we update the estimate of p_k with $p_k^{(l+1)}=d_k^{(l)}/{\sum }_{h=1}^L{d}_h^{(l)}$. Note that $d_k^{(l)}$ is the expected number of events in the time interval [ $t_{k-1}^{\ast },t_k^{\ast }$] and ${\sum }_{h=1}^L{d}_h^{(l)}={\sum }_{i=1}^n{m}_i/{\widehat{F}}_n^{(l)}(y_i)$ is the projected total number of serial events in the time interval [0, τ]. Finally, the estimate of F(t) is updated with ${\widehat{F}}_n^{(l+1)}(t)={\sum }_{t_h\le t}{d}_h^{(l)}$. We alternate between the E-step and M-step until convergence to obtain the estimate F̂_n of F.

The cumulative rate function Λ₀(t) is related to F through the equation Λ₀(t)= F(t)Λ₀(τ), where Λ₀(τ) is interpreted as the expected number of serial events occurring in the time interval [0, τ]. If we condition on z_i and y_i, m_i has the expected value E(m_i|z_i, y_i) = z_iΛ₀(y_i) = z_iF(y_i)Λ₀(τ). Thus we have E{m_iF(y_i)⁻¹}=Λ₀(τ), since E(Z)=1; that is, the ratio of m_i to F(y_i) projects the number of events in [0, τ]. If we substitute F with F̂_n, an estimator of Λ₀(τ) is given by ${\widehat{\mathrm{\Lambda }}}_n(\tau )=n^{-1}{\sum }_{i=1}^n{m}_i/{\widehat{F}}_n(y_i)$. Hence Λ₀(t) can be estimated by Λ̂_n(t)=F̂_n(t)Λ̂_n(τ).

Let 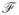be the class of functions defined by

$$ℱ=\{\mathcal{F}:[0,\tau ]\to [0,1]\mid F\text{is}\text{nondecreasing},F(0)=0\text{and}F(\tau )=1\}.$$

Then the L₂(ν) metric d on 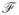is defined as

$$d^2(F_1,F_2)=\int {\mid F_1(t)-F_2(t)\mid }^{2}dv(t)=E\left(E\left[\sum _{j=1}^K{\{F_1(t_j)-F_2(t_j)\}}^2\mid K\right]\right)$$

where

$$v(t)=\sum _{k=1}^{\infty }\text{pr}(K=k)\sum _{j=1}^k\text{pr}(t_{ij}\le t\mid K=k).$$

The strong consistency property of Λ̂₀ is stated in Theorem 1 with the following conditions.

• Condition 1. There exists an integer k₀<∞ such that the number of observation times, K, satisfies pr(K ≤ k₀) = 1 and pr(K>1)>0.

• Condition 2. The cumulative rate function Λ₀ satisfies Λ₀(τ)≤M for some M ∈ (0, ∞).

• Condition 3. The random function $M_0={\sum }_{j=1}^k{m}_{j}log(m_j)$ satisfies E[M₀]<∞.

  Condition 4. There exists a τ₁>0 such that pr(Y ≥τ₁)=1 and Λ₀(τ₁)≥C* for some C*>0.

Theorem 1

We assume that Conditions 1–4 hold. Define τ₂=sup{t: pr(Y ≥t)>0}. Then, for every t such that t ≤τ₂, d(Λ̂_n1_[0,t], Λ₀1_[0,t])→0 almost surely when n → ∞.

Since the estimation of Λ₀ shares similarities with the estimation of a distribution function under random interval censoring and truncation, the convergence rate of Λ̂_n(t) is expected to be nonregular, i.e. not of n^1/2-convergence rate. For the purpose of systematically studying the convergence rate of Λ̂_n(t), we consider the following technical conditions.

• Condition 5. There exists a constant η>0 such that adjacent observation times are separated by η, that is t_j−t_j−1≥η for j=1, 2, …, K.

• Condition 6. The baseline cumulative rate function Λ₀∈C¹[0, τ] and there exists a constant γ>0 such that ${\mathrm{\Lambda }}_0^{\prime }(t)\ge \gamma$ for t ∈ [0, τ].

  Condition 7. For any α=o_P(1), there exists a constant C** such that E(zⁱe^αz)≤C** for i =0, 1, 2.

Theorem 2

We assume that Conditions 1–7 hold, and we suppress the indicator, 1_[0,t], in our expression by assuming that the metric d is defined with t ≤τ₂. Then we have that n^1/2 d(Λ̂_n, Λ₀)=O_p(1).

The proofs of the theorems are sketched in the Appendix using modern empirical process theory. We leave the study of the asymptotic distribution of Λ̂ to future research.

Remark

Conditions 1–7 are sufficient, but may not all be necessary. In particular, Condition 7 may be stronger than necessary, but it does hold for the Gamma frailty variable.

3·2. Estimation procedure for model 2

Under Model 2 the conditional likelihood for the ith individual, given z_i, x_i, k_i, m_i and observation times {t_i1, …, t_iki}, is proportional to

$$\prod _{j=1}^{k_i}{\left\{\frac{z_i{e}^{x_i^{\prime }\beta }{\mathrm{\Lambda }}_0(t_{ij})-z_i{e}^{x_i^{\prime }\beta }{\mathrm{\Lambda }}_0(t_{ij-1})}{z_i{e}^{x_i^{\prime }\beta }{\mathrm{\Lambda }}_0(y_i)}\right\}}^{m_{ij}}=\prod _{j=1}^{k_i}{\left\{\frac{F(t_{ij})-F(t_{ij-1})}{F(y_i)}\right\}}^{m_{ij}},$$

where F(t)=Λ₀(t)/Λ₀(τ). Note that the unobserved frailty z_i and the observed covariates x_i are cancelled out in the formula, yielding the same conditional likelihood function given by (1) in § 3·1. Thus the baseline cumulative rate function can be estimated in the same way as that in Model 1. Intuitively, if all subjects are under observation up to time τ the total number of events of each subject contains all the information about β. Note that $E\{m_i{F}^{-1}(y_i)\mid x_i,y_i,z_i\}=z_i{\mathrm{\Lambda }}_0(\tau )e^{x_i^{\prime }\beta }$. Following E(z_i|x_i)=1 we have

$$E\{m_i{F}^{-1}(y_i)\mid x_i\}={\mathrm{\Lambda }}_0(\tau )e^{x_i^{\prime }\beta };$$

that is, the ratio of m_i to F(y_i) projects the number of events in [0, τ]. We can derive the inferential results for β based on a class of unbiased estimating equations given by

$$n^{-1}\sum _{i=1}^n{w}_i{x}_i^{{\ast }^{\prime }}\{m_i{F}^{-1}(y_i)-e^{x_i^{{\ast }^{\prime }}\gamma }\}=0,$$ (2)

where $x_i^{\ast }={(1,x_i^{\prime })}^{\prime }$, γ = (η,β′)′, η=log Λ₀(τ), and w_i is a weight function depending on (x_i, β, Λ₀). If Λ₀ is a known function, the optimal weight is given by

$$e^{x_i^{{\ast }^{\prime }}\gamma }/E[{\{m_i{F}^{-1}(y_i)-e^{x_i^{{\ast }^{\prime }}\gamma }\}}^2]$$

(Godambe, 1960). In practice, however, F is estimated with a convergence rate of n^1/3, and hence the efficiency gain is unknown when F̂_n is used to replace F in the optimal weight function.

We denote the solutions of (2), with F replaced by F̂_n, by $\widehat{\gamma }={({\widehat{\eta }}_n,{\widehat{\beta }}_n^{\prime })}^{\prime }$. In the Appendix we show that, under Conditions 1–4, |β̂_n−β|²→0 almost surely as n→∞, where |·| represents the usual Euclidean L₂-norm. Moreover, using the estimator obtained by solving (2), we estimate the baseline cumulative rate function Λ₀(t)=F(t)Λ₀(τ) by Λ̂_n(t)=F̂_n(t)e^η̂n. The estimator Λ̂_n satisfies the following strong consistency property: d(Λ̂_n1_[0,t], Λ₀1_[0,t])→0 almost surely for all t∈[0, τ₂] as n→0. The derivation of the asymptotic distribution of β̂_n and Λ̂_n(t) is a challenging problem and is left for future research.

4. Simulations and data analysis

4·1. Monte Carlo simulations

Four sets of simulation studies with moderate, n=100, and large, n=1000, sample sizes were conducted to evaluate the performance of the proposed nonparametric and semiparametric estimators. We used Λ₀(t)=2t for t∈[0, 10] and conducted the simulations using 1000 replications. The first simulation study compared the efficiency of the proposed nonparametric estimator to that of the nonparametric maximum likelihood estimator (Wellner & Zhang, 2000) and the nonparametric maximum pseudolikelihood estimator (Sun & Kalbfleisch, 1995) under the assumption of independent observation process. To be specific, we set z≡1 and generated K from a discrete uniform distribution on {1, 2, …, 6}. The K distinct observation times t₁, …, t_K were order statistics of independent and identically distributed uniform random variables on [0, 10], and observation times were rounded to the second decimal place. The second set of simulation studies examined the bias in these three nonparametric estimators when the independence assumption is violated. Let $z~\text{Ga}(2,\frac{1}{2})$. For z>1, K was generated from a discrete uniform distribution on {1, 2, …, 8} and t₁, …, t_K were order statistics of K independent and identically distributed exponential random variables with mean 2; for z≤1, K was generated from a discrete uniform distribution on {1, …, 6} and t₁, …, t_K were order statistics of K independent and identically distributed uniform random variables on [0, 10]. Thus, subjects with z>1 have a higher event rate and tend to be observed more frequently than patients with z≤1.

Table 1 gives the Monte Carlo bias and standard error estimates of these three nonparametric estimators at selected time points. Table 1(a) shows that the bias in these three nonparametric estimators is very small when observation times are independent of the event process. The proposed estimator Λ̂_n(t) is more efficient, with smaller Monte Carlo standard errors, than the nonparametric maximum pseudolikelihood estimator, and is slightly less efficient than the nonparametric maximum likelihood estimator. When the sample size is large, the proposed estimator is highly efficient relative to the nonparametric maximum pseudolikelihood estimator. In Table 1(b), where the pattern of observation is correlated with the distribution of serial events, the nonparametric maximum likelihood estimator and the nonparametric maximum pseudolikelihood estimator are substantially biased, while the proposed estimator still gives valid results.

Table 1.

Simulation results for nonparametric estimators under the assumptions of independent and informative observation times

(a) Independent observation times
n	t	Λ0(t)	Proposed		NPMLE		NPMPLE
			Bias	SE	Bias	SE	Bias	SE
100	1·0	2	−0·031	0·397	−0·030	0·392	−0·060	0·418
	3·0	6	−0·006	0·488	−0·019	0·476	−0·058	0·633
	5·0	10	−0·024	0·542	−0·047	0·505	−0·063	0·723
	7·0	14	−0·015	0·654	−0·055	0·559	−0·065	0·844
	9·0	18	0·004	0·804	−0·051	0·643	−0·045	0·904
1000	1·0	2	0·011	0·156	0·010	0·154	0·007	0·200
	3·0	6	0·005	0·202	−0·002	0·189	−0·017	0·276
	5·0	10	0·014	0·210	−0·002	0·193	−0·030	0·336
	7·0	14	0·011	0·241	−0·009	0·211	−0·019	0·374
	9·0	18	0·025	0·277	−0·003	0·218	−0·023	0·408

(b) Informative observation times
n	t	Λ0(t)	Proposed		NPMLE		NPMPLE
			Bias	SE	Bias	SE	Bias	SE
100	1·0	2	−0·009	0·271	0·015	0·271	0·447	0·454
	3·0	6	−0·007	0·553	−0·040	0·512	0·361	0·795
	5·0	10	0·049	0·874	−0·543	0·722	−1·183	0·949
	7·0	14	0·008	1·198	−1·699	0·859	−3·395	1·067
	9·0	18	0·127	1·532	−2·987	1·021	−5·324	1·349
1000	1·0	2	0·000	0·104	0·021	0·101	0·484	0·194
	3·0	6	0·015	0·214	−0·021	0·182	0·431	0·345
	5·0	10	0·031	0·343	−0·509	0·258	−1·157	0·407
	7·0	14	0·035	0·459	−1·580	0·309	−3·321	0·459
	9·0	18	0·038	0·564	−2·901	0·340	−5·448	0·508

NPMLE, nonparametric maximum likelihood estimator; NPMPLE, nonparametric maximum pseudolikelihood estimator; Bias and SE are the Monte Carlo sample mean and standard deviation of the 1000 estimates of Λ₀(t).

We evaluated the performance of the proposed semiparametric estimator in the last two sets of simulation studies. The covariate x was generated from a Ber(0·5) random variable, and z was from a Ga(2, 0·5) distribution. We set the cumulative intensity function to be ze^xβΛ₀(t) with β=−1. In the third simulation study we compared the efficiency of the proposed semiparametric estimator to that of the Sun–Wei estimator under the assumption that the observation time process is a nonhomogeneous Poisson process with cumulative intensity function given by log(1+2t)e^x/2. Thus, the observation pattern depends only on observed covariates but not on the subject’s risk of serial events. The proposed semiparametric estimation procedure, with unit weights, w_i=1, in the estimating equations (2), and the Sun–Wei estimator, with and without assuming that the observation process follows a proportional rate model, were applied to each simulated dataset. Table 2 gives the Monte Carlo bias and standard error of the estimated β, and Table 3 gives estimates of Λ₀(t) at selected time points using the proposed semiparametric method. As shown in Table 2, both estimators have small biases; moreover, the proposed semiparametric estimator outperforms the Sun–Wei estimators in that it gives smaller Monte Carlo standard errors.

Table 2.

Bias and standard error of β̂ using the proposed semi-parametric method and the Sun–Wei estimators when the observation time process depends only on observed covariates

	n=100			n=1000
	Proposed	SWa	SWb	Proposed	SWa	SWb
Bias	−0·005	0·464	−0·036	−0·003	0·460	−0·040
SE	0·161	0·219	0·191	0·052	0·067	0·059

SW^a, the Sun–Wei estimator of β without modelling the observation pattern; SW^b, the Sun–Wei estimator with modelling the observation pattern; Bias and SE, Monte Carlo sample mean and standard deviation for the 1000 estimates.

Table 3.

Bias and standard error of Λ̂₀(t) using the proposed semiparametric method when the observation time process depends only on observed covariates

t	Λ0(t)	n=100		n=1000
		Bias	SE	Bias	SE
1·0	2	0·005	0·394	0·006	0·136
3·0	6	0·024	0·879	0·004	0·301
5·0	10	0·093	1·352	0·033	0·464
7·0	14	0·175	1·887	0·073	0·594
9·0	18	0·204	2·550	0·082	0·814

Bias and SE, the Monte Carlo sample mean and standard deviation of the 1000 estimates of Λ₀(t).

The last simulation study examined the validity of the two semiparametric estimators in a setting where both the event process and the observation pattern are correlated with z. For x=1 and z>1, K was generated from a discrete uniform distribution on {1, 2, …, 8} and t₁, …, t_K were order statistics of K independent and identically distributed exponential random variables with mean 2; otherwise, K was generated from a discrete uniform distribution on {1, …, 6} and t₁, …, t_K were order statistics of K independent and identically distributed uniform random variables on [0, 10]. Tables 4 and 5 show that bias in the proposed estimator is almost ignorable, while the Sun–Wei estimators yield substantial bias in estimating regression parameters.

Table 4.

Bias and standard error of β̂ from the proposed semiparametric method and the Sun–Wei estimators when the observation times are informative

	n=100			n=1000
	Proposed	SWa	SWb	Proposed	SWa	SWb
Bias	−0·009	0·246	0·932	−0·001	0·245	0·928
SE	0·123	0·153	0·153	0·033	0·049	0·048

SW^a, the Sun–Wei estimator without modelling the observation pattern; SW^b, the Sun–Wei estimator with modelling the observation pattern; Bias and SE, Monte Carlo sample mean and standard deviation for the 1000 estimates of β.

Table 5.

Bias and standard error of Λ̂₀(t) using the proposed semiparametric method when the observation times are informative

t	Λ0(t)	n=100		n=1000
		Bias	SE	Bias	SE
1·0	2	0·001	0·525	−0·005	0·132
3·0	6	0·045	1·698	0·003	0·220
5·0	10	0·088	2·560	0·036	0·296
7·0	14	0·142	3·663	0·010	0·375
9·0	18	0·217	4·529	0·033	0·463

Bias and SE, the Monte Carlo sample mean and standard deviation of the 1000 estimates of Λ₀(t).

4·2. Data analysis

We used a subset of data from the bladder tumour study conducted by the Veterans Administration Cooperative Urological Research Group (Byar, 1980) to illustrate the proposed methods. All the recruited patients had superficial bladder tumours before entering the study, and were randomly allocated into one of the three treatment groups; namely placebo, thiotepa and pyridoxine. Many patients experienced multiple tumour occurrences after enrolment, and new tumours were removed at follow-up clinic visits. We set τ=30 months and compared the thiotepa group with the placebo group in tumour occurrence rate during the first 30 months.

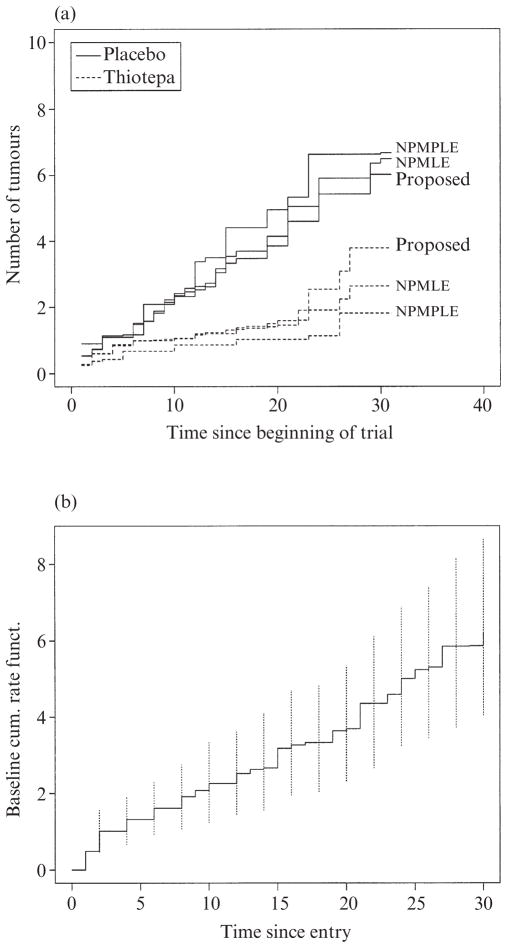
Figure 1(a) shows the estimated cumulative rate function for placebo and thiotepa groups using the proposed nonparametric method, the nonparametric maximum likelihood estimator and the nonparametric maximum pseudolikelihood estimator. Patients treated with thiotepa had a lower tumour occurrence rate, indicating the effectiveness of thiotepa in the first 30 months. Next, we applied the proposed semiparametric method and the Sun–Wei estimators to the bladder tumour data, with x an indicator of whether or not a patient was in the thiotepa group. With the proposed method, the estimate of the regression coefficient of the treatment indicator is −0·62 with a bootstrap standard error of 0·43, yielding an estimated tumour occurrence rate in the thiotepa group of 0·54=e^−0·62 times that of the placebo group during the first 30 months of follow-up. The estimated baseline cumulative rate function with 95% pointwise bootstrapped confidence interval at selected time points is given in Fig. 1(b). With the Sun–Wei estimators, the estimated coefficient of the treatment indicator is −0·88 with a bootstrap standard error of 0·41 under the assumption that the observation pattern is the same for both treatment groups, and is −1·48 with a bootstrap standard error of 0·40 under the assumption that the observation process follows a proportional rate model. The proposed method estimates a smaller treatment effect in the tumour occurrence rate than do the Sun–Wei estimators.

Fig. 1.

Bladder tumour study. (a) Nonparametric estimation of cumulative rate function by treatment group; (b) Semiparametric estimation of baseline cumulative rate function with pointwise bootstrap 95% confidence intervals.

5. Final remarks

We have applied our method to data generated from other than the working Poisson process, and concluded that the inferential results, not shown here, are still valid. Moreover, the Poisson process assumption is not required in our proof for the strong consistency. This indicates that the proposed methods have the same robustness property as those proposed by Wellner & Zhang (2000) and Zhang (2002), namely that the validity of the proposed methods does not depend on the underlying counting process conditioning on the frailty variable under Model 1 or conditioning on the frailty variables and covariates under Model 2. We have also considered in our simulation studies scenarios where the scheduled visits are fixed by design and the chance of missing a visit depends on the frailty z. The results, not shown, suggest that the proposed method gives valid results, while the nonparametric maximum likelihood estimator and the nonparametric pseudolikelihood estimator are substantially biased.

The standard asymptotic theory applies to the proposed method when the schedules of visits are fixed by study design: instead of maximising a nonparametric conditional likelihood with infinite-dimensional parameters, the proposed estimation procedure maximises a conditional likelihood with finite number of parameters. This asymptotic normality with a convergence rate of n^1/2 is expected for the proposed estimators.

It is important to indicate that the proposed methodology relies on the assumption that the effect of frailty on the intensity function is multiplicative. This assumption is widely used in modelling clustered survival times, where a parametric assumption for the frailty distribution is usually required for statistical inference. The estimation procedure proposed in this paper does not rely on the frailty distribution and hence is more robust against departure from the true frailty distribution. While the use of multiplicative frailty is crucial to our methodology, the technique for checking the multiplicative assumption needs to be developed in future research.

Appendix

Proofs

Sketch proof of Theorem 1

We only state the main results for the proof of Theorem 1. Readers are referred to the technical report available at http://www.bepress.com/jhubiostat/paper90 for details. The proof of strong consistency of F̂_n closely follows Wellner & Zhang (2000). Arguing as in the proof of Theorem 4·2 in Wellner & Zhang (2000), we can show that d(F̂_n1_[0,t], cF1_[0,t])→ 0 almost surely for any t ∈ [0, τ₂], where τ₂=sup{t : pr(Y ≥t)>0} and c is a fixed constant.

Now we prove that Λ̂_n(t) is a consistent estimator of Λ₀(t) for t in [0, τ₂]. We write

$${\widehat{\mathrm{\Lambda }}}_n(\tau )-\frac{1}{c}{\mathrm{\Lambda }}_0(\tau )=\frac{1}{n}\sum _{i=1}^n{m}_i\left\{\frac{1}{{\widehat{F}}_n(y_i)}-\frac{1}{cF(y_i)}\right\}-\frac{1}{cn}\sum _{i=1}^n\left\{\frac{m_i}{F(y_i)}-{\mathrm{\Lambda }}_0(\tau )\right\}=\text{I}+\text{II}.$$

Let 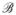denote the Borel sets in 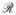. We define a new measure ν₂ on ([τ₁, τ], 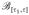) by ν₂(B)=E1_[yi∈B]. Obviously, ν₂ is dominated by the measure ν. For a δ_n>0 with δ_n→0 as n → ∞, we define a class 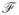={ f : f (t)=N(t){g⁻¹(t)−c⁻¹F⁻¹(t)}, where g is nondecreasing and nonnegative with positive lower bound in [τ₁, τ] and d(g1_[0,tau;], cF1_[0,tau;])≤δ_n. For a sufficiently large n,

$$\begin{array}{l}\left|n^{-1}\sum _{i=1}^n{m}_i\{{\widehat{F}}_n^{-1}(y_i)-c^{-1}{F}^{-1}(y_i)\}\right|\le \underset{g\in \mathcal{F}}{sup}\left|n^{-1}\sum _{i=1}^n{m}_i\{g^{-1}(y_i)-c^{-1}{F}^{-1}(y_i)\}\right|\\ \le \underset{f\in \mathcal{F}}{sup}\mid Pf\mid +{\left|\right|{\mathbb{P}}_n-P\left|\right|}_{\mathcal{F}},\end{array}$$

where ℙ_n denotes the empirical measure and P denotes the probability measure.

Under Condition 4 and applying Theorems 2·7·5 and 2·4·1 in van der Vaart & Wellner (1996), we can show that 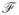is a Glivenko–Cantelli class. Thus ||ℙ_n−P||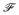→0 almost surely. Moreover,

$$\underset{f\in \mathcal{F}}{sup}\mid Pf\mid =E[{\mathrm{\Lambda }}_0(\tau )F(y_i)\{g^{-1}(y_i)-c^{-1}{F}^{-1}(y_i)\}]\mid \le c{\delta }_n$$

for some c>0 following from the fact that ν₂ is dominated by ν and the Hölder inequality. This implies that I→0 almost surely. The quantity II converges to 0 almost surely because E{m_i/F(y_i)}=Λ₀(τ) and by the law of large numbers. Thus we show that Λ̂_n(τ)−c⁻¹Λ₀(τ) converges to 0 almost surely. It is easy to see that Λ̂_n(t)−Λ₀(t)→0 almost surely for ν-almost-all t∈[0, τ₂], and it follows from the dominated convergence theroem, with dominating functions Λ₀(τ₂) since ν is a finite measure, that d(Λ̂_n1_[0,t], Λ₀1_[0,t])→0 almost surely for any t∈[0, τ₂].

Sketch proof of Theorem 2

We apply Theorem 3·2·5 of van der Vaart & Wellner (1996) to derive the rate of convergence. To do so, we verify that the conditions of that theorem hold in our problem with Conditions 1–7.

We rewrite $q(\mathrm{\Lambda };D)={\sum }_{j=1}^k{m}_{j}log\{\mathrm{\Lambda }\ast (t_j)-\mathrm{\Lambda }\ast (t_{j-1})\}$, where Λ*(t_j)=Λ(t_j)/Λ(y) for j=1, 2, …, k. We define

$$\text{M}(\mathrm{\Lambda })=Pq(\mathrm{\Lambda };D)=E\left\{\sum _{j=1}^k\mathrm{\Delta }{\mathrm{\Lambda }}_0(t_j)log\mathrm{\Delta }\mathrm{\Lambda }\ast (t_j)\right\},$$ (A1)

where ΔΛ₀(t_j)=Λ₀(t_j)−Λ₀(t_j−1) and ΔΛ*(t_j)=Λ*(t_j)−Λ*(t_j−1).

First, we show that performing Taylor expansion on the right-hand side of (A1) along with Conditions 5 and 6 yields $\text{M}({\mathrm{\Lambda }}_0)-\text{M}(\mathrm{\Lambda })\ge CE[{\sum }_{j=1}^k{\{\mathrm{\Lambda }(t_j)-{\mathrm{\Lambda }}_0(t_j)\}}^2]={Cd}^2(\mathrm{\Lambda },{\mathrm{\Lambda }}_0)$ for any Λ in a neighbourhood of Λ₀. Here C represents a generic constant.

Next, we consider a class 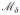={q(Λ; D)−q(Λ₀; D) : d(Λ, Λ₀)<δ} for some δ>0 and δ=o(1). For any f=q(Λ; D)−q(Λ₀; D)∈ 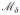, using Conditions 1 and 7, we can obtain || f ||_P,B≤Cδ, where ||·||_P,B is the Bernstein norm defined as || f ||_P,B={2P(e^|f|−1−| f |}^1/2. Hence, by Lemma 3·4·3 of van der Vaart & Wellner (1996),

$$E_P{\left|\right|\surd n({\mathbb{P}}_n-P)\left|\right|}_{{\mathcal{M}}_{\delta }}\le C{\stackrel{\sim }{J}}_{[]}(\delta ,{\mathcal{M}}_{\delta },{\left|\right|·\left|\right|}_{P,B})\left\{1+\frac{{\stackrel{\sim }{J}}_{[]}(\delta ,{\mathcal{M}}_{\delta },{\left|\right|·\left|\right|}_{P,B})}{{\delta }^2{n}^{1/2}}\right\},$$

where J̃ _[](δ, 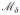, ||·||_P,B) is the bracketing integral of the class of functions 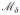and is defined by

$${\stackrel{\sim }{J}}_{[]}(\delta ,{\mathcal{M}}_{\delta },{\left|\right|·\left|\right|}_{P,B})={\int }_0^{\delta }{\{1+log{N}_{[]}(\epsilon ,{\mathcal{M}}_{\delta },{\left|\right|·\left|\right|}_{P,B})\}}^{1/2}d\epsilon .$$

Finally, using Conditions 5–7, we can argue that the ε-bracketing number of class 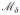with Bernstein norm is controlled by e^1/ε, that is N_[](ε, 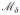, ||·||_P,B) = O(ε^1/ε). Hence

$${\stackrel{\sim }{J}}_{[]}(\delta ,{\mathcal{M}}_{\delta },{\left|\right|·\left|\right|}_{P,B})\le C{\int }_0^{\delta }{\{1+log(1/\epsilon )\}}^{1/2}d\epsilon \le C{\int }_0^{\delta }{\epsilon }^{-1/2}d\epsilon \le C{\delta }^{1/2}.$$

This implies that the function φ_n(δ), which is critical for the rate of convergence based on Theorem 3·2·5 of van der Vaart & Wellner (1996), is given by

$${\phi }_n(\delta )={\delta }^{1/2}\left(1+\frac{{\delta }^{1/2}}{{\delta }^2{n}^{1/2}}\right)={\delta }^{1/2}+{\delta }^{-1}/n^{1/2}.$$

It can be easily verified that φ_n(δ)/δ is a decreasing function of δ and n^2/3φ_n(n^−1/3)=2n^1/2, so that n^1/3d(Λ̂_n, Λ₀)=O_P(1) because of Theorem 3·2·5 of van der Vaart & Wellner (1996). %

Consistency of β̂_n

The consistency of F̂_n under Model 2 can be established by arguing in the same way as described above, except for replacing z_i with $z_{i}exp(x_i^{\prime }\beta )$. We now examine the consistency of β ^_n obtained by solving the estimating function (2). The consistency property of the estimator obtained from the alternative estimating function can be proven using a similar argument. Define the function $U(\gamma )=n^{-1}{\sum }_{i=1}^n{w}_i{x}_i^{{\ast }^{\prime }}\{m_i{\widehat{F}}_n{(y_i)}^{-1}-e^{x_i^{{\ast }^{\prime }}\gamma }\}$. It can be shown that the function U converges to 0 almost surely when evaluated at γ=(log{Λ₀(τ)/c}, β′) ′. Furthermore, it is easy to see that the derivative of U evaluated at (log{Λ₀(τ)/c}, β ′) ′ is negative definite. Applying Taylor expansion to U(γ), one can show that the solution of (2), that is $\widehat{\gamma }={({\widehat{\eta }}_n,{\widehat{\beta }}_n^{\prime })}^{\prime }$, converges to γ=(log{Λ₀(τ)/c}, β ′) ′ almost surely. Thus we prove that β̂_n converges to β almost surely.

Based on the above sketch proof, η̂_n converges to log{Λ₀(τ)/c} almost surely. Along with the fact that d(F̂_n1_[0,t], cF1_[0,t])→ 0 almost surely for any t∈[0, τ₂], it can be shown that d(Λ̂_n1_[0,t], Λ₀1_[0,t])=d(F̂_n1_[0,t]e^η̂_n, Λ₀1_[0,t])→0 for any t∈[0, τ₂].