Abstract
Tailoring the hydrodynamic boundary condition is essential for both applied and fundamental aspects of drag reduction. Hydrodynamic friction on superhydrophobic substrates providing gas–liquid interfaces can potentially be optimized by controlling the interface geometry. Therefore, establishing stable and optimal interfaces is crucial but rather challenging. Here we present unique superhydrophobic microfluidic devices that allow the presence of stable and controllable microbubbles at the boundary of microchannels. We experimentally and numerically examine the effect of microbubble geometry on the slippage at high resolution. The effective slip length is obtained for a wide range of protrusion angles, θ, of the microbubbles into the flow, using a microparticle image velocimetry technique. Our numerical results reveal a maximum effective slip length, corresponding to a 23% drag reduction at an optimal θ ≈ 10°. In agreement with the simulation results, our measurements correspond to up to 21% drag reduction when θ is in the range of −2° to 12°. The experimental and numerical results reveal a decrease in slip length with increasing protrusion angles when θ ≳ 10°. Such microfluidic devices with tunable slippage are essential for the amplified interfacial transport of fluids and particles.
Despite more than two decades of intense research on hydrodynamic slippage on substrates with various physicochemical properties (1–4), tuning the hydrodynamic slippage remains a challenge, especially for microfluidic laminar flow. The slip length—quantifying the slippage—ranges from a few nanometers for flat hydrophobic substrates to several micrometers for superhydrophobic substrates with hybrid (liquid–gas and liquid–solid) interfaces (4). Hydrophobic microstructures containing trapped gas bubbles have been shown to be advantageous for drag reduction (5–11). Their orientation with respect to the flow direction (12–16) and the geometry of gas–liquid menisci (11–14, 17) has been demonstrated to affect the slippage. In particular, microscale bubbles transverse to the flow direction can alter the flow resistance, depending on the protrusion of the bubbles into the flow. Moreover, transition from slippage to friction has been predicted for trapped bubbles perpendicular to the flow in theoretical (14, 18) and numerical studies (12, 13, 19, 20). The presence of such a critical protrusion angle highlights the feasibility of manipulating the flow resistance via bubble geometry. One recent experimental study suggests that for flow over a hydrophobic surface with trapped passive microbubbles, there is a transition from an enhanced slippage state to the frictional state at a large protrusion angle, in an estimated range of 30°–60° (20). However, there has been no experimental investigation of flow past a hydrophobic surface with transversely embedded microbubbles for a wide range of protrusion angles at high resolution. In this paper, we report on integrated microfluidic devices that permit the presence of stable and controllable microbubbles at the boundary of hydrophobic microchannels. We further examine in detail the effect of geometry of the microbubbles transverse to a pressure-driven flow on the effective slippage.
Results and Discussion
We designed and fabricated microfluidic devices consisting of two main parallel microchannels for separate liquid and gas streams, connected by an array of side channels in between (Fig. 1). To prevent the side channels from wetting, the original hydrophilic silicon microchannels are hydrophobized on the basis of silane chemistry, using perfluorinated octyltrichlorosilane (21). Due to the hydrophobicity of the surface and for sufficiently large applied gas pressure Pg, the bridging side channels are filled with gas. The control of the gas pressure results in tunable protrusion angles θ of the microbubbles and will compensate for gas dissolution into the fluid (Fig. 1 B and C). Establishing stable and controllable bubbles is crucial in this study, which currently is attained by active control of gas pressure. In contrast, trapped passive bubbles are unstable as shown in previous studies (6, 11). The shape and the stability of the interface are determined by capillary forces and the pressure difference between the gas and liquid phases (8).
Fig. 1.
Controllable microfluidic bubble mattress and computational bubble unit cell. (A) Optical image of the microfluidic device with integrated gas (G) and liquid (L) channels, with the inlets and outlets indicated. (B) Scanning electron microscopy image of a representative microfluidic device, showing two main microchannels for gas 
and liquid 
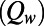streams connected by gas-filled side channels. (C) Bright-field microscopy image of bubbles protruding 35° ± 3.3° into the liquid microchannel with a height, H. Here, the shear-free fraction, φ, is defined as 
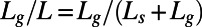, where 
is the width of the gas gap, and 
is the width of the solid boundary. (D) Numerical results of the pressure-driven flow over a microbubble unit, using the same experimental parameters. The color bar refers to the velocity, which is given in meters per second. Here φ = 0.38 and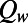 
= 45 μL/min.
This fluidic configuration allows for easy and precise control of the gas–liquid interface curvature. It also enables visualization of both the interface geometry and the flow field near the bubble surfaces by direct velocity measurements of a steady, laminar flow past the microbubbles, using microparticle image velocimetry (μPIV) (22).
Numerically we study the effect of the interface shape on slippage, using 2D finite-element methods (Comsol Multiphysics). We solve for the pressure-driven flow of water for the flow settings used in the experiments with a computational domain representing the experimental geometric parameters (Fig. 1D). Shear-free boundary conditions are applied along the gas protrusions, whereas no-slip boundary conditions are imposed on the solid walls. Fig. 1D represents the computed flow field for θ ≈ 35° over a bubble unit with length L, consisting of one no-slip (solid–liquid) and one shear-free (gas–liquid) boundary condition.
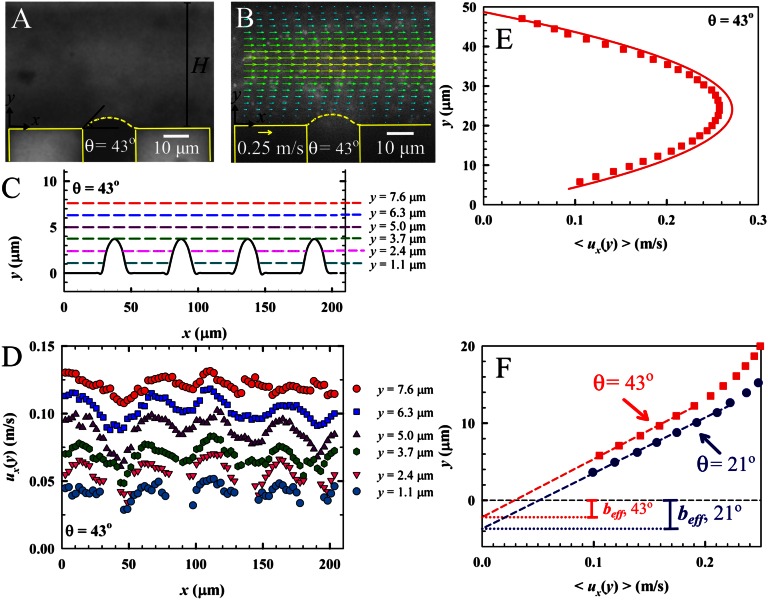
In Fig. 2, we present the flow velocity profiles measured in the middle of the microchannel depth by μPIV, providing direct quantification of effective slippage for varying geometric parameters: the protrusion angle, θ and the shear-free fraction, φ. In Fig. 2A, a representative bright-field image of a bubble unit with a protrusion angle of θ ≈ 43° is presented. Fig. 2B represents the velocity field for θ ≈ 43° protruding curved gas–liquid menisci, superimposed on a correspondent raw μPIV image. The bubble position and bubble curvature are depicted by dashed lines (Fig. 2 A and B). The curvature of the bubbles is calculated by circular arc estimation. The bubbles are stable and symmetric during the experiments due to sufficiently low capillary and Weber numbers [capillary (Ca) ≈ 5 × 10−3, Weber (We) ≈ 6 × 10−3]. The bubbles’ protrusion angles were accurately measured from the corresponding bright-field images with ImageJ analysis. The error bars were calculated from the standard deviation of θ for each bubble. The locations and profiles of four successive bubbles, having protrusion angles of 43°, are represented in Fig. 2C. The curved gas–liquid interfaces protrude ∼3.7 μm into the microchannel in the y direction. A series of detailed velocity profiles, ux(y), at different channel heights, y, is presented in Fig. 2D. The presence of the microbubbles has a strong effect on the detailed velocity field. Near the wall, the variation of velocity field reflects the local variation of the hydrodynamic boundary condition. Even at y = 0.15H (y = 7.6 μm), the effect of the bubbles on the flow field is still observed. Large protruding bubbles, as in this case (θ ≈ 43°), can act as obstacles to the flow. Indeed, a slight deceleration of the flow is observed in front of the bubbles. Right behind the bubble, the loss in velocity is recovered and higher velocities are achieved. The overall average velocity in this case is still higher than that for nonslippery walls. These observations are consistent with the numerical findings of Hyväluoma et al. (13).
Fig. 2.
Velocity profiles measured by μPIV. (A) Bright-field image of a bubble unit with a protrusion angle of θ = 43° ± 6°. (B) Velocity field measurement for bubbles at θ = 43° ± 6° superimposed on its raw μPIV image. In A and B, the dashed lines represent the bubble curvature and the solid lines represent the no-slip solid walls. (C) Liquid–gas interfaces showing the bubbles having protrusion angles of θ = 43° ± 6°. The curvature of the bubbles is calculated by circular arc estimation. Colored lines indicate the vertical positions of the velocity measurements presented in D. (D) Detailed streamwise velocity profiles,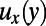 
, at different channel heights y, indicated by the corresponding dashed lines in C. (E) Average velocity profile for θ = 43° ± 6° (experimental, 
; and numerical, —). (F) Experimental average velocity profiles for θ = 43° ± 6° at a shear-free fraction φ = 0.38 (
) and θ = 21° ± 3° at a shear-free fraction φ = 0.54 (●), near the wall with attached bubbles. The dashed lines represent the linear fits for the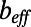 
evaluations.
Fig. 2E presents the experimental and numerical velocity profiles obtained by the streamwise average of local velocity profiles. The measured and computed velocity profiles agree very well. The average velocity profiles near the hybrid wall are presented in Fig. 2F for the same experiment with θ = 43° ± 6° and for another experiment with θ = 21° ± 3°. Near the hydrophobic surface embedded with curved gas–liquid interfaces, the velocity profiles exhibit a linear relation between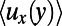 
and y. The effective slip length, 
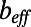, based on the average velocity profiles is calculated using Navier’s slip boundary condition (4): 
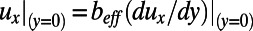. To obtain 
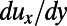, a least-squares linear fitting was performed for the data below 
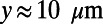. The effective slip length calculation is graphically represented in Fig. 2F. The effective slip length for bubbles protruding 43° is smaller than that for those protruding 21°. Although slight deceleration of the flow is observed in front of 43° protruding bubbles (Fig. 2D), the effective slip length is found to be 1.8 ± 0.1 μm for this θ, showing that 43° protruding bubbles still contribute to enhanced slippage. The numerical effective slip lengths were evaluated using the same approach with the local velocity gradients being calculated at y = 6.5 μm.
To further verify our methods, we compare our results with the analytical asymptotic solutions of the slip length for Stokes flow past periodically alternating, flat (protrusion angle θ = 0°) shear-free and no-slip regions transverse to the flow (5) (with details provided in Appendix). Both the experimental and the numerical results of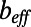 
at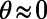 
are consistent with the predictions of the analytical asymptotes of the ratio of shear-free fraction.
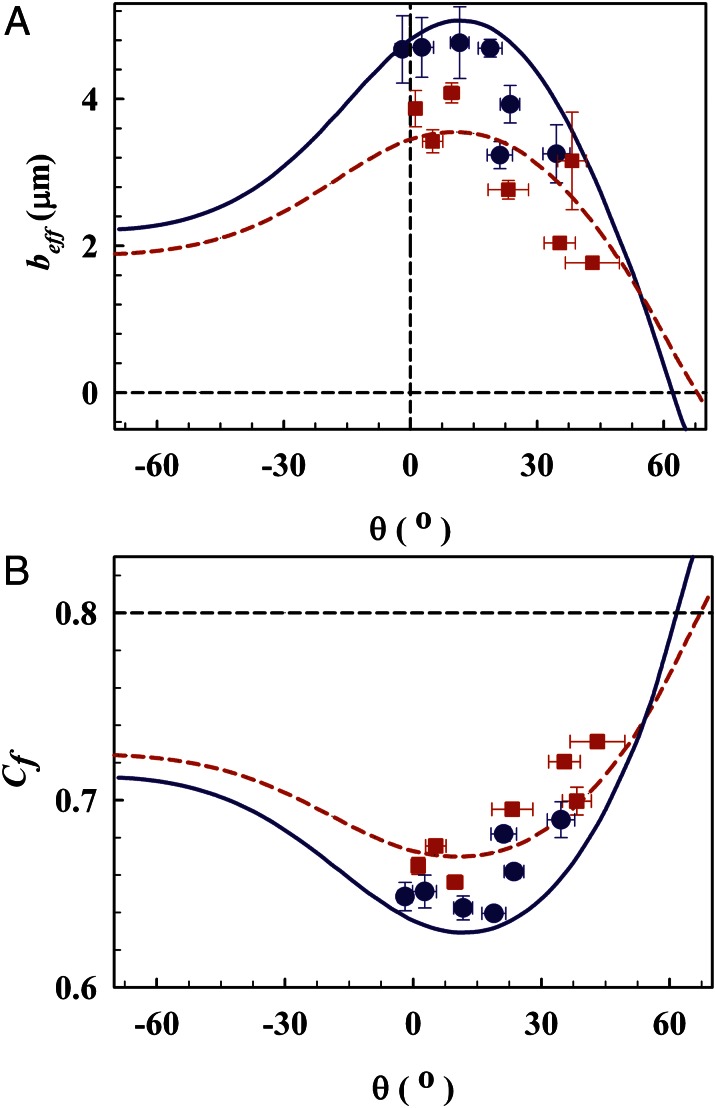
In Fig. 3A, the first measurements of effective slip lengths for a wide range of protrusion angles θ are presented and compared with the numerical results. Our measurements clearly demonstrate the dependence of the effective slip length on both θ and φ. When the fraction of the surface covered by bubbles is φ = 0.54, a maximum effective slip length of 4.8 ± 0.1 μm was measured at θ = 12° ± 2°. In addition, the experimental results reveal a decrease in the effective slip length with increasing protrusion angles when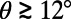 
. A similar trend was observed for φ = 0.38. For larger protrusion angles, 
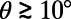, the measured effective slip length decreases with increasing protrusion angle, implying an increasing flow resistance due to larger protrusions. There is good quantitative agreement with the numerical results.
Fig. 3.
Effective slip length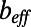 
and effective friction factor 
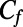as a function of the protrusion angle θ obtained by μPIV measurements and numerical calculations. (A) Experimental and numerical 
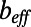results for φ = 0.54 and φ = 0.38. (B) Experimental and numerical 
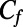results for φ = 0.54 and φ = 0.38. In A and B, the solid line (—) and the circles (●) indicate the numerical and experimental results for φ = 0.54. The dashed line (---) and the squares (
) indicate the numerical and experimental results for φ = 0.38. The horizontal black dashed line represents the value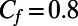 
obtained for the no-slip condition b = 0.
Our simulations reveal an asymmetry in the effective slip length between positive and negative protrusion angles, affirming previous reports (13, 14, 18–20). Consistent with the experimental results, the numerical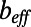 
increases with increasing protrusion angle to a maximum value at θ = 11° and subsequently decreases with further increases in θ for all φ. A peak position of 
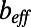was also encountered at a similar θ ≈ 10° in the theoretical solutions provided in refs. 14 and 18 and highlighted as an optimum angle in ref. 14. The effective slip length becomes zero at a critical protrusion angle, 
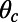, above which the microbubbles exhibit negative slip length, revealing a transition from slippage to extra friction. Our simulations yield 
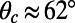and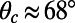 
for φ = 0.54 and φ = 0.38, respectively, which are quantitatively consistent with the results of previous theoretical and numerical studies (13, 14, 18–20).
Our numerical data indicate that for θ beyond the value θ = 11° giving maximal slip length, higher bubble fractions (here φ = 0.54) follow a steeper decrease in the effective slip length than lower ones (here φ = 0.38).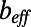 
is smaller for φ = 0.54 (with a smaller 
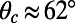) than for φ = 0.38 when 
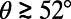(Fig. 3A). The increase in protrusion angle alters the flow cross-sectional area. When the typical length scales of the system are comparable with the scale of bubble units, the changes in the flow cross-sectional area and the interface curvature have effects on the velocity field. These observations are consistent with the previous studies, suggesting the significant role of confinement effects on slippage over gas–liquid interfaces longitudinal to flow direction (11, 12).
Our findings suggest that the confinement effects and the gas–liquid interface geometry of the microbubbles have a strong effect on the effective slip length. Furthermore, the experimental results imply the possibility of engineering hydrodynamic slippage/drag by controlling the shape of the gas–liquid meniscus via external means.
To highlight the capability of tailoring the effective boundary condition in our microfluidic devices, we recast the experimental and numerical data in terms of the Fanning friction factor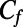 
, which for a fully developed, steady, laminar flow in a smooth rectangular duct of hydraulic radius 
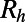is (23)
 |
Here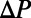 
(Pa/m) is the pressure gradient, ρ is the liquid density, and 
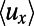is the mean velocity. Solving 2D Stokes flow for a rectangular duct using Navier’s slip condition at y = 0, we obtain an expression for the pressure drop along the microchannel length:
 |
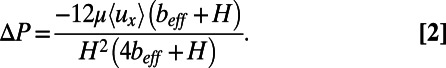Here, μ is the dynamic viscosity of the liquid. Using our experimental and numerical results, we calculate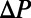 
from Eq. 2 to evaluate the friction factors for pressure-driven flow of water past microbubbles in our microfluidic devices. In Fig. 3B, we present the effective friction factor values for varying protrusion angles of microbubbles for φ = 0.38 and φ = 0.54.
The friction factor is a direct measure of the pressure loss due to hydrodynamic drag. The effective friction factors of our microbubble mattress should be less than that of a rectangular duct with no-slip walls for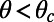 
. The analytical model reduces to 
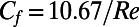for a straight rectangular channel 
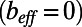with a width-to-height aspect ratio of 2, corresponding to our microchannels. The analytical Cf value for 
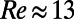, as in our μPIV experiments and numerical simulations, is calculated as 0.8 for a nonslippery microchannel. This analytical friction coefficient, depicted by the dashed line in Fig. 3B, is larger than the friction coefficients of our hydrophobic microchannels with embedded microbubbles for 
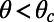. At a critical 
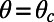, the numerical results of 
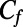are equal to the analytical friction factor 
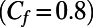for no-slip walls. When 
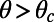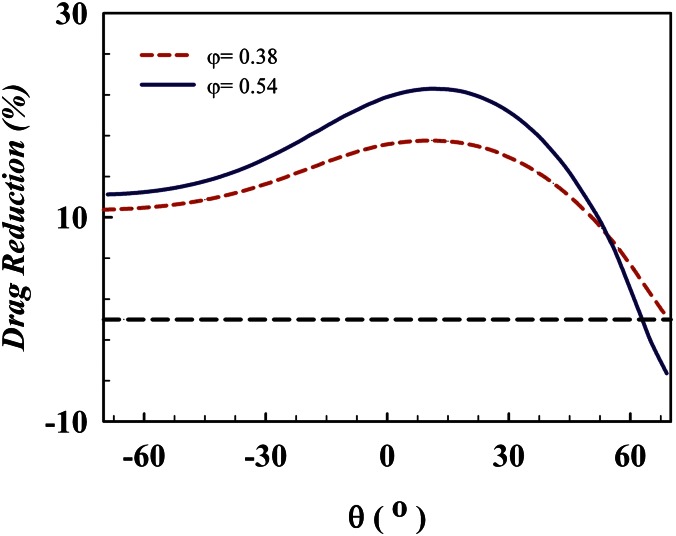
, a higher friction factor appears, revealing a transition from slippage to extra friction. Fig. 3B emphasizes the significant effect of the interface menisci curvature on the hydrodynamic slippage. The numerical results show when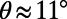 
, 18% and 23% drag reductions are achieved for φ =0.38 and φ =0.54, respectively, compared with the flow in a nonslippery microchannel at the same flow rate. In good agreement with the numerical results, experimental drag reductions of 19% and 21% are obtained for φ =0.38 and φ =0.54, respectively, when θ is in the range of −2° to 12°.
In conclusion, we present a hydrophobic microfluidic device that allows for the manipulation of flow resistance. The proposed design of the microfluidic device allows for the formation of stable and controllable microbubbles that are perpendicular to the pressure-driven flow in the microchannels. Our experimental measurements, which cover a wide range of protrusion angles, reveal a strong dependence of the effective hydrodynamic slip on the gas–liquid interface curvature. Our experimental results confirm the numerical simulations for effective slip length and the effective friction factor. Our microfluidic device allows for the tuning of the convective flow throughput and, hence, the control of flow resistance. This active control is of paramount importance for microfluidic applications aiming to amplify the transport of fluids and particles at interfaces, which is driven by a convection–diffusion mechanism (24).
Materials and Methods
Experimental Setup.
Silicon microchannels were fabricated by photolithography followed by a deep reactive ion etching process. The microchannels were sealed by anodic bonding to glass. The width of the main microchannels, H, is 50 μm. The width of the gas-filled side channels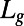 
was kept constant at 20 μm and the length of the liquid-solid interface 
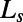was varied (30 μm and 20 μm, respectively). The periodic bubble unit length is given as 
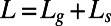. The shear-free fraction (surface porosity) is defined as 
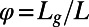(Fig. 1C). The ratio of the bubble unit cell length L to the channel hydraulic radius 
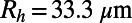is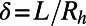 
. The effective slip length was quantified for different shear-free fractions φ (∼0.38 and ∼0.54) and spatial periods normalized by the hydraulic radius, 
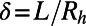(= 1.5 and = 1.2). The protrusion angles of the microbubbles were varied over a wide range (−2° to 43°) with small gas pressure changes applied (0.29–0.34 bar) for a liquid flow rate of 45 μL/min. We operated at a sufficiently small capillary number, 
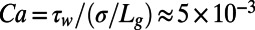, and Weber number, 
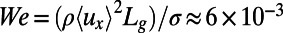, to ensure symmetric microbubbles pinned at the sharp corners of the side channels. Here 
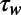is the shear stress imposed by the liquid on the hybrid wall and σ is the interfacial tension of the air–water interface.
μPIV.
Steady, laminar velocity profiles at the focal plane in the middle of the microchannel depth were measured using a μPIV technique, as described in ref. 11. Milli-Q water seeded with 1-μm diameter fluorescent particles was used as the working fluid. A dual-cavity Nd:YAG laser at 532 nm was used for channel illumination. Image pairs with a delay time of 7 μs between two exposures were recorded using a double-shutter PCO Sensicam camera with a resolution of 1,376 × 1,040 pixels × 12 bits. To enhance particle visibility and the signal-to-noise ratio of the correlation map, image preprocessing was performed before cross-correlation. Averaged mean intensity images were calculated and subtracted from the image pairs. The particle image density was artificially increased by using a consecutive sum of five images in a row to increase the resolution of the final vector field. The interrogation view of the μPIV images was ∼222 μm × ∼167 μm. A multigrid ensemble correlation averaging method was used for 195 image pairs. When processing the data, the interrogation window size was decreased in steps to a size of 32 × 16 pixels (∼5.2 μm × 2.6 μm) to achieve a high spatial resolution for the detailed velocity profiles. Our data have high signal-to-noise ratios. Therefore, no smoothing needed to be applied to the velocity fields. For each measurement, bright-field images were acquired to determine the protrusion angle and to define the locations of the bubbles and walls on the raw μPIV images.
Numerical Analysis.
The effective slip length was also numerically calculated using a 2D finite-element method (Comsol Multiphysics v4.1) that solved the Navier–Stokes equations for a steady pressure-driven flow of water in a microchannel consisting of 15 successive bubble units at the bottom surface. A two-bubble-unit cell length was required for the entrance/outlet effects and developing flow effects. The bubbles are pinned and approximated as rigid circular arcs calculated by the projected diameter of bubble,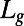 
, and the protrusion angle θ. The bubble interface curvature is parameterized by the protrusion angle θ. A perfect slip boundary condition for the bubble surfaces and a no-slip boundary condition for solid walls were assumed. The upper solid wall is a nonslipping wall at a distance 
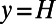. Pressure-driven flow was produced by applying a laminar flow with a mean velocity of 0.2 m/s as the inlet condition. The effective slip length for all θ is calculated at an evaluation line, 
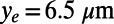, due to the protrusion depth of bubbles in the y direction into the channel. The evaluation line at height 
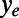is sufficiently above the bubble surfaces for all θ. The effective slip length is calculated on the basis of Navier’s slip boundary condition. The ratio of the velocity 
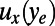to the tangential shear rate at 
, 
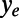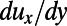, is integrated along x over the middle 11 bubble units, and 
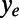is subtracted from the resultant value to obtain 
.
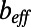Derivation.
To obtain the Fanning friction factor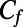 
, the 2D, steady, fully developed Stokes flow between parallel plates was analytically solved using the no-slip boundary condition at the upper plate, 
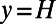, and the full-slip boundary condition at the bottom plate, y = 0. Due to the protrusion depth of bubbles in the y direction, the effective hydrodynamic boundary position depends on y. We incorporate the effective slip length 
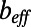, using a linear approximation of velocity in the close proximity of the solid wall, 
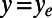, yielding the following relation between the slip velocity at y = 0 and the velocity at 
:
 |
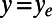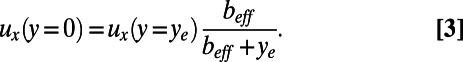Thereby,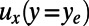 
can be expressed as 
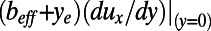, and the pressure drop can be expressed in terms of 
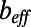(Eq. 2). For a fully developed, steady laminar flow, the shear stress is given as 
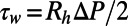. The definition of the Fanning friction factor 
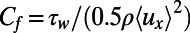then immediately yields Eq. 1. It is worth noting that for the case of a straight rectangular duct 
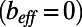, Eq. 2 reduces to plane Poiseuille flow 
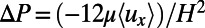, which can be further used in Eq. 1 to derive 
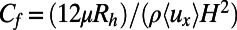. For a rectangular duct with an aspect ratio of 2, corresponding to our microchannels, 
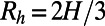, yielding 
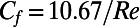for a smooth, nonslippery rectangular duct. Hydrodynamic drag reductions can be calculated for different protrusion angles in comparison with nonslippery microchannels. In Fig. 4, we show the extent of drag reduction that can be tuned by controlling the shape of the gas–liquid menisci curvature. Here the black dashed line represents a microchannel with nonslippery walls (
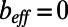and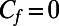 
).
Fig. 4.
Drag reduction as function of the protrusion angle θ obtained by simulations. The solid line (—) and the dashed line (---) represent the results for φ = 0.54 and φ = 0.38, respectively. The horizontal black dashed line represents the no-slip condition (b = 0 and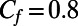 
).
Appendix
To further validate our experimental and numerical results for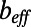 
presented in Fig. 3A, we compare these results with the analytical asymptotic solutions of ref. 5. Three distinct asymptotic limits for 
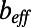are considered, as suggested in ref. 5:
 |
 |
 |
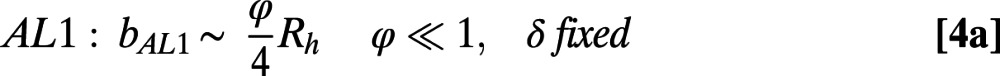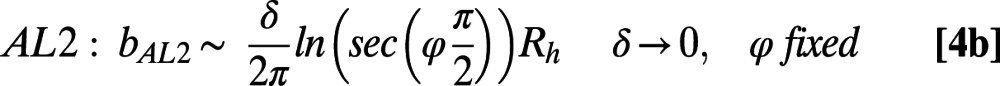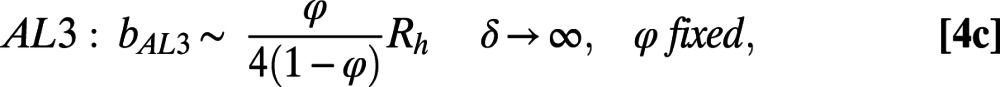where 
is the hydraulic radius, and 
. The first asymptotic limit (Eq. 4a) describes the limit at which the bubble fraction goes to zero for a given ratio of bubble unit length to hydraulic radius. The second (Eq. 4b) and the third (Eq. 4c) asymptotes describe the limits at which δ goes to zero and infinity, respectively, for a given φ. In Table 1, we compare our numerical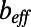 
values obtained at θ = 0° and our experimental 
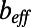values measured at θ = 1.2° ± 0.3° and θ = −1.9° ± 0.5° for φ = 0.38 and 0.54, respectively, with the predictions resulting from Eqs. 4a–4c. Indeed, the results of effective slip length obtained from both the μPIV measurements and the numerical simulations agree well with the asymptotic prediction of the analytical solution, Eq. 4a. The slight discrepancy can be explained by the asymptotic limit of small φ for a constant δ of 
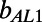. The asymptotic solutions 
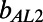and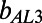 
refer to the minimum and maximum slip lengths for the asymptotic extremes in δ. Table 1 indicates that for all φ, 
< 
< 
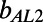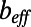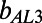, which further validates the consistency of our experimental and numerical effective slip length results evaluated for an intermediate δ.
Table 1.
Comparison of effective slip length results with the asymptotic results of ref. 5
 |
||||||
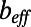| φ | δ | μPIV | Numerical |  |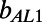
 |
 |
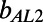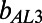| 0.38 | 1.5 | 3.9 ± 0.3 | 3.5 | 3.2 | 1.5 | 5.1 |
| 0.54 | 1.2 | 4.7 ± 0.5 | 4.9 | 4.5 | 2.6 | 9.8 |
Acknowledgments
The authors thank S. Schlautmann (University of Twente) for technical support in the cleanroom fabrication and E. Charlaix for valuable discussions. Grants from The Netherlands Organization for Scientific Research–ACTS for a doctoral fellowship (to E.K.) (Process on a Chip Project 053.65.007), from Fundamental Research on Matter for doctoral funding of C.W.V., and from European Research Council (a starting grant to R.G.H.L.) are gratefully acknowledged.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.Tretheway DC, Meinhart CD. Apparent fluid slip at hydrophobic microchannel walls. Phys Fluids. 2002;14(3):L9. [Google Scholar]
- 2.Joseph P, Tabeling P. Direct measurement of the apparent slip length. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;71(3 Pt 2A):035303. doi: 10.1103/PhysRevE.71.035303. [DOI] [PubMed] [Google Scholar]
- 3.Choi C-H, Westin KJA, Kenneth SB. Apparent slip flows in hydrophilic and hydrophobic microchannels. Phys Fluids. 2003;15(10):2897–2902. [Google Scholar]
- 4. Lauga E, Brenner MP, Stone HA (2007) Handbook of Experimental Fluid Dynamics, eds Tropea C, Yarin A, Foss JF (Springer, New York), Chap 19.
- 5.Lauga E, Stone HA. Effective slip in pressure-driven Stokes flow. J Fluid Mech. 2003;489:55–77. [Google Scholar]
- 6.Byun D, Kim J, Ko HS, Park HC. Direct measurement of slip flows in superhydrophobic microchannels with transverse grooves. Phys Fluids. 2008;20:113601. [Google Scholar]
- 7.Choi C-H, Kim CJ. Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface. Phys Rev Lett. 2006;96(6):066001. doi: 10.1103/PhysRevLett.96.066001. [DOI] [PubMed] [Google Scholar]
- 8.Rothstein JP. Slip on superhydrophobic surfaces. Annu Rev Fluid Mech. 2010;42:89–109. [Google Scholar]
- 9.Ou J, Perot B, Rothstein JP. Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys Fluids. 2004;16(12):4635–4643. [Google Scholar]
- 10.Ou J, Rothstein JP. Direct velocity measurements of the flow past drag-reducing ultrahydrophobic surfaces. Phys Fluids. 2005;17:103606. [Google Scholar]
- 11.Tsai P, et al. Quantifying effective slip length over micropatterned hydrophobic surfaces. Phys Fluids. 2009;21:112002. [Google Scholar]
- 12.Teo CJ, Khoo BC. Flow past superhydrophobic surfaces containing longitudinal grooves: Effects of interface curvature. Micro-Nanofluidics. 2010;9:499–511. [Google Scholar]
- 13.Hyväluoma J, Kunert C, Harting J. Simulations of slip flow on nanobubble-laden surfaces. J Phys Condens Matter. 2011;23(18):184106. doi: 10.1088/0953-8984/23/18/184106. [DOI] [PubMed] [Google Scholar]
- 14.Ng C, Wang CY. Effective slip for Stokes flow over a surface patterned with two- or three-dimensional protrusions. Fluid Dyn Res. 2011;43:065504. [Google Scholar]
- 15.Schmieschek S, Belyaev AV, Harting J, Vinogradova OI. Tensorial slip of superhydrophobic channels. Phys Rev E Stat Nonlin Soft Matter Phys. 2012;85(1 Pt 2):016324. doi: 10.1103/PhysRevE.85.016324. [DOI] [PubMed] [Google Scholar]
- 16.Bocquet L, Barrat J-L. Flow boundary conditions from nano- to micro-scales. Soft Matter. 2007;3:685–693. doi: 10.1039/b616490k. [DOI] [PubMed] [Google Scholar]
- 17.Chen H, Li J, Chen D. Study of drag forces on a designed surface in bubbly water lubrication using electrolysis. J Fluids Eng. 2006;128:1383–1389. [Google Scholar]
- 18.Davis AMJ, Lauga E. Geometric transition in friction for flow over a bubble mattress. Phys Fluids. 2009;21:011701. [Google Scholar]
- 19.Hyväluoma J, Harting J. Slip flow over structured surfaces with entrapped microbubbles. Phys Rev Lett. 2008;100(24):246001. doi: 10.1103/PhysRevLett.100.246001. [DOI] [PubMed] [Google Scholar]
- 20.Steinberger A, Cottin-Bizonne C, Kleimann P, Charlaix E. High friction on a bubble mattress. Nat Mater. 2007;6(9):665–668. doi: 10.1038/nmat1962. [DOI] [PubMed] [Google Scholar]
- 21.Maboudian R, Ashurs WR, Carraro C. Self-assembled monolayers as anti-stiction coatings for MEMS: Characteristics and recent developments. Sens Actuators A Phys. 2000;82:219–223. [Google Scholar]
- 22. Raffel M, Willert C, Wereley S, Kompenhans J (2007) Particle Image Velocimetry (Springer, Berlin)
- 23. Cengel Y (2007) Heat and Mass Transfer: A Practical Approach (McGraw–Hill, New York)
- 24.Bocquet L, Lauga E. A smooth future? Nat Mater. 2011;10(5):334–337. doi: 10.1038/nmat2994. [DOI] [PubMed] [Google Scholar]