Salts drive controllable multilayered upright assembly of amyloid-like peptides at mica/water interface

Abstract

Surface-assisted self-assembly of amyloid-like peptides has received considerable interest in both amyloidosis research and nanotechnology in recent years. Despite extensive studies, some controlling factors, such as salts, are still not well understood, even though it is known that some salts can promote peptide self-assemblies through the so-called “salting-out” effect. However, they are usually noncontrollable, disordered, amorphous aggregates. Here, we show via a combined experimental and theoretical approach that a conserved consensus peptide NH₂-VGGAVVAGV-CONH₂ (GAV-9) (from representative amyloidogenic proteins) can self-assemble into highly ordered, multilayered nanofilaments, with surprising all-upright conformations, under high-salt concentrations. Our atomic force microscopy images also demonstrate that the vertical stacking of multiple layers is highly controllable by tuning the ionic strength, such as from 0 mM (monolayer) to 100 mM (mainly double layer), and to 250 mM MgCl₂ (double, triple, quadruple, and quintuple layers). Our atomistic molecular dynamics simulations then reveal that these individual layers have very different internal nanostructures, with parallel β-sheets in the first monolayer but antiparallel β-sheets in the subsequent upper layers due to their different microenvironment. Further studies show that the growth of multilayered, all-upright nanostructures is a common phenomenon for GAV-9 at the mica/water interface, under a variety of salt types and a wide range of salt concentrations.

A better understanding of the self-assembly of highly ordered peptide nanostructures is critical because it not only helps to uncover the pathogenesis of various neurodegenerative diseases (1) but provides an attractive “bottom-up” nanotechnology for de novo nanodevice design (2) and fabrication (3). In addition to a series of factors (4–6) previously discovered to modulate peptide self-assembly, solid substrates have been found to drive this process directly acting as templates (7, 8), controlling both assembly kinetics and morphology of amyloid peptide aggregates (8–11). These findings emphasize the importance of the substrate surface, whether it be a cellular membrane or an inorganic solid surface, on the assembly of various peptides, which is critical in many biological processes. It has been shown recently that fibrous nanostructures form a fundamental framework ubiquitous in normal cellular metabolism, including cell division and signaling, as well as in over 27 different human amyloid diseases and 9 in animals (12).

Due to the complexity of cellular membranes and associated physiological conditions (13, 14), hydrophilic mica and hydrophobic highly oriented pyrolytic graphite (HOPG) are the two commonly used model substrates for the investigation of surface effects (10, 11, 15). For example, it was found that amyloid-β (Aβ) peptide formed oligomeric protofibrillar aggregates on mica but only 1D nanofilaments on HOPG (8, 16). In contrast, protein α-synuclein (α-syn) grew epitaxially into β-sheet–like structures on mica but not on HOPG (10). Surface dependence of peptide assembly has also been reported on other surfaces, such as the micelle surface in incubation solution (17) and the contact surface of test tube materials and stir beads (11).

Recently, we have investigated the effects of solid substrates on the assembly of an amyloid-like peptide, NH₂-VGGAVVAGV-CONH₂ (GAV-9), representing the conserved consensus of three neurodegenerative disease-related proteins, α-syn, Aβ-protein, and prion protein, with a sequence of NH₂-VGGAVVAGV-CONH₂ (18). We have shown that GAV-9 peptide can epitaxially self-assemble into 1D nanofilaments with an “upright” conformation on mica surface but a “flat” conformation on the surface of HOPG (7).

Meanwhile, salts are often recognized as another important modulator for peptide and protein self-assembly. Salt ions, with their ubiquitous presence in physiological environments, play a critical role in both assembly dynamics and structure (19–24). In addition to the nonspecific Debye–Hückel screening, specific ionic interactions (i.e., electroselective series) and indirect/direct effects from water structure (i.e., Hofmeister series) have been explored extensively to interpret salt effects (19–24). For example, the α-syn fibrillization follows the Hofmeister series but not the electroselective series (19), whereas the opposite seems to be true for other proteins, such as glucagon (21), β2-microglobulin (20), and mouse prionic protein (24), indicating the complex nature of the salt effect on molecular assembly.

In this paper, we report a unique fibrous assembly of GAV-9 peptides consisting of multilayered nanofilaments with surprising all-upright conformations at the mica/water interface under high-concentration salt solutions using in situ atomic force microscopy (AFM). For example, with 100 mM MgCl₂, our in situ AFM images showed a uniform ∼6-nm-high nanostructure on mica, indicating a potential double-layered upright structure, because each peptide stretches ∼3 nm. Delicate AFM nanomechanical manipulations confirmed that it is indeed a double-layered assembly with both upright conformations. Our atomistic molecular dynamics simulations then revealed a parallel β-sheet structure, with the N termini pointing to the mica surface for the first monolayer and an antiparallel one for the second monolayer. This indicates that the detailed layer structures (parallel or antiparallel β-sheets) of the self-assembled nanofilaments can be sensitive to their local molecular environment, such as template surfaces (on mica and on subsequent peptide surfaces) and salt concentrations. Further studies with a variety of salt types and a wide range of salt concentrations indicate that this is a common phenomenon, with even higher numbers of upright layers (triple, quadruple, or even quintuple layers) possible.

Results and Discussion

Self-Assembly of Double-Layered Upright GAV-9 Peptides in 100 mM MgCl₂.

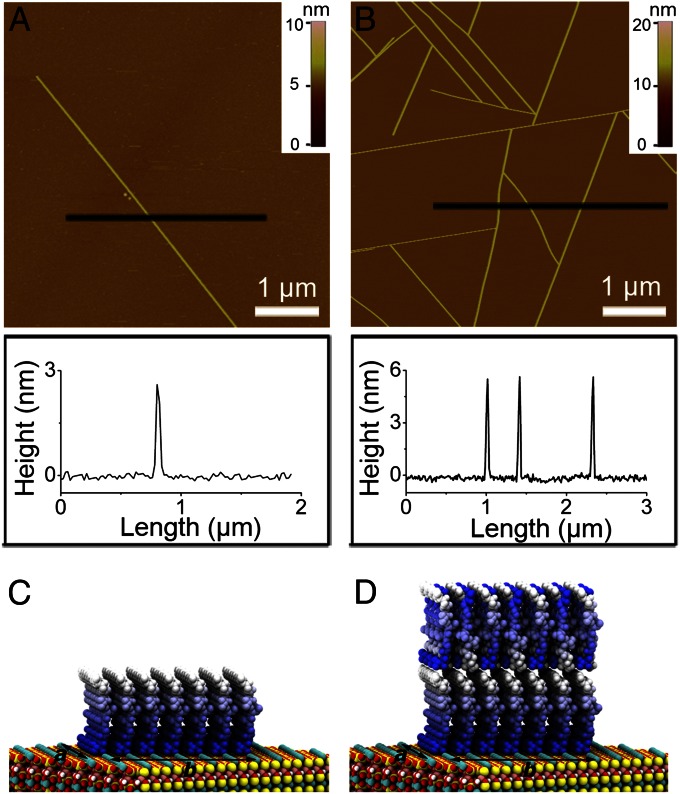
In situ AFM images show that GAV-9 peptides self-assemble to form nanofilaments on mica under either pure water or a high-salt solution (Fig. 1). Despite the apparent similarity in their morphologies, detailed section analysis distinguishes them by their heights. Under a high-salt concentration (e.g., 100 mM MgCl₂), the height of nanofilaments is about 5.8 ± 0.3 nm, whereas it is only 3.0 ± 0.2 nm in pure water.

Fig. 1.

Representative AFM images (Upper) and section analysis (Lower) of the self-assembled GAV-9 nanofilaments on mica substrates under pure water (A) and aqueous solution containing 100 mM MgCl₂ (B), respectively. Molecular structures of monolayered (C) and double-layered (D) upright-oriented peptides on mica surface. The peptides are decorated with a color gradient ranging from blue to white for N-to-C directions. Arrows indicate two surface crystallographic directions (a and b) of mica. Peptides are placed on epitaxial binding sites along a- and b-directions, respectively, spaced at 0.52 nm and 0.92 nm (Fig. S5).

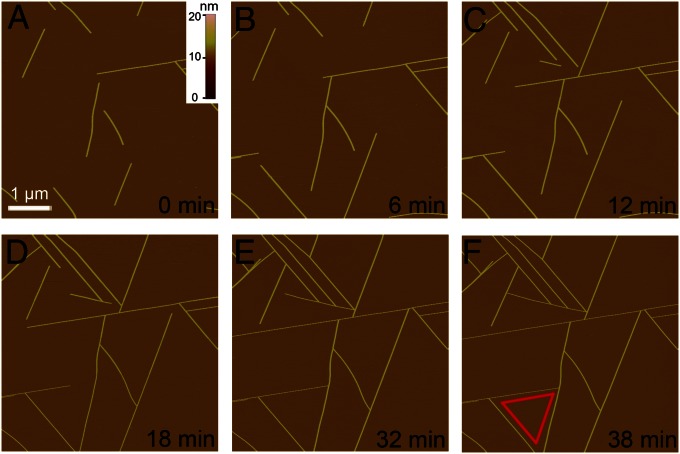
Fig. 2 shows the in situ growth dynamics of the nanofilaments on mica under 100 mM MgCl₂ solution. These nanofilaments grow bidirectionally, extending to lengths up to tens of micrometers as long as they do not encounter other filaments or blockers. Their growth directions are restricted approximately to three epitaxial orientations positioned 120° to each other (Fig. 2F). The growth rate varies somewhat from filament to filament at different locations, which may be due to the different local environment. However, in general, increasing the peptide concentration results in an increase in the growth rate as well as in the number of nanofilaments on the surface. Except for assembly height, growth dynamics and morphology are very similar to those in pure water, implying that the contact mode of the basal peptides to the substrate surface might not be much altered in this environment. Previous studies have shown that the 3-nm height in water originates from the fully stretched upright peptide conformations, stabilized by the strong electrostatic interactions between the positively charged GAV-9 N terminals and the negatively charged surface cavities (K⁺-vacant sites) on mica (7). Molecular dynamics simulations also revealed that GAV-9 and its shortened analog both form well-ordered β-stranded structures along the crystallographic b-direction [i.e., direction of longer distance (0.92 nm) epitaxial binding sites] of mica surface (25, 26).

Fig. 2.

In situ AFM observation of the assembly of GAV-9 peptide on mica surface under 100 mM MgCl₂. (A–F) Series of snapshots of the extending nanofilaments with a height of 6 nm. The edges of the equilateral triangle in F indicate three preferred directions along which peptides assembled into nanofilaments. The same scale bar used in A applies to all AFM images.

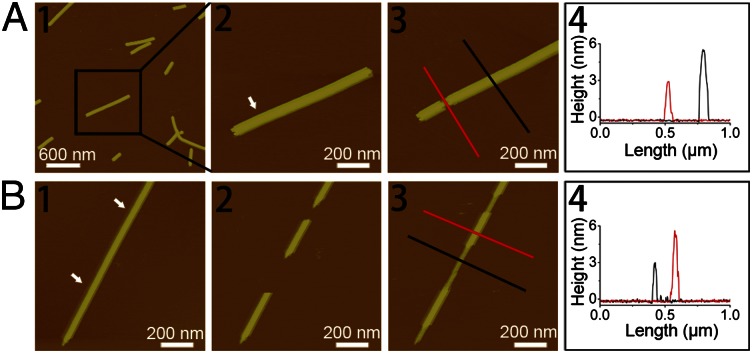
One plausible explanation for the ∼6-nm nanofilament height might be due to the additional GAV-9 peptide layer with the same upright conformation on top of the first monolayer. To confirm this hypothesis, we performed some delicate AFM nanomechanical manipulations on the ∼6-nm nanofilaments (27). We first started with a “top-down” approach: Only the top layer was selectively removed by the tip of the atomic force microscope (Fig. 3A). The resulting sublayer was exactly 3 nm in height. We then tried another bottom-up approach: One long ∼6-nm-high nanofilament was cut in the middle using the tip of the atomic force microscope, leaving several small gaps along the filament (Fig. 3B). It is interesting to observe that the gaps were refilled with the ∼3-nm-high structure (Fig. 3 B2 and B3) in some cases (single layer) and with the ∼6-nm-high structure in other cases (double layer) (Fig. S1). These findings unambiguously suggest that GAV-9 peptides indeed form a double-layered nanostructure in 100 mM MgCl₂, with both layers in the upright conformation.

Fig. 3.

(A) AFM height images and section analysis indicating a height of ∼3 nm of the sublayer after removing the top layer by AFM mechanical manipulation. (A1 and A2) Original double-layered GAV-9 nanofilaments. (A3) Top layer was removed by AFM manipulation. (A4) Section analysis of the sublayer and the double-layered nanofilaments as indicated by lines in A3. (B) Tapping-mode AFM height images indicating the extension of GAV-9 nanofilaments with a height of ∼3 nm after removing two parts of preformed nanofilaments with a height of ∼6 nm. (B1) Original double-layered GAV-9 nanofilaments. (B2) Two gaps appeared on the original nanofilament after AFM mechanical manipulation. (B3) GAV-9 molecules filled the gaps, resulting in formation of a sublayer with a height of ∼3 nm. (B4) Section analysis of the sublayer and the double-layered nanofilaments is shown as indicated with lines in B3. The arrows in A2 and B1 indicate the positions on the preformed peptide nanofilaments mechanically manipulated by the tip of atomic force microscope. Both of the experiments were carried out on mica under aqueous solution containing 50 mM MgCl₂.

Molecular Mechanism and Atomic Structure of the Peptide Layers.

The above in situ AFM experiments strongly suggest that the observed GAV-9 double-layered structure in 100 mM MgCl₂ is constructed by piling up two upright peptide conformations, each measuring ∼3 nm in height. However, it is currently not possible to reveal the detailed molecular structures of these layers in AFM, due to the limited experimental resolution. In this particular case, we are especially interested in whether the assembly patterns and structures in various layers are the same or not. If not, why not? In addition, what is the main driving force for the structural variations?

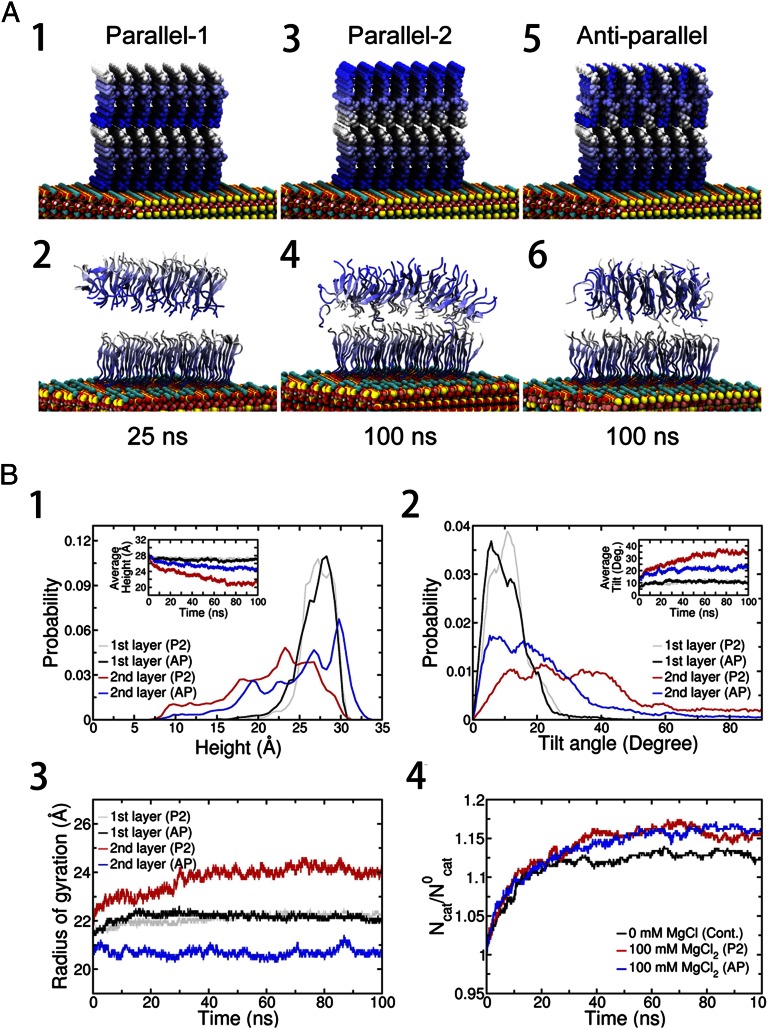
To investigate this with atomic details, we use molecular dynamics simulations to examine all possible assembly models of the double layer. As we already know from previous studies, the first sublayer is a parallel monolayer with the N terminus pointing to the mica surface (more discussion below), which leaves us only three major choices (models) focusing on the orientations and patterns of the second layer. In the first model, named the P1 (parallel 1) model, the peptides are configured in parallel, with the N-terminal end facing the C termini of the first layer, hoping the abundant 200 mM Cl⁻ counter-ions can effectively screen out the repulsive interactions between these positively charged N termini at the interface, thus demonstrating consistency with the first layer in terms of peptide orientation (both pointing from N termini to C termini from the substrate). In the second model, named the P2 (parallel 2) model, the peptides are configured in parallel, with the C-terminal end facing the C termini of the first layer, leaving the charged N-terminal residues exposed to the solvent, which is energetically favorable in general. For the third model, named the AP (antiparallel) model, the peptides in the second layer are configured in an antiparallel orientation and then stacked onto the first layer, which is parallel, resulting in a hybrid (parallel + antiparallel) nanostructure. Of the three models, the first model, the P1 model, seems to be most intuitive due to its simplicity and beauty. All three models were constructed in this study and then simulated with molecular dynamics for at least 100 ns each in 100 mM MgCl₂ (more details are provided in Materials and Methods).

Fig. 4A shows representative structures for each model. Interestingly, the top layer of the P1 model begins to detach from the sublayer at about 15 ns in our simulation, and it separates completely at about 25 ns, albeit with a still well-ordered internal structure after detaching. Even with abundant counter-ions (Cl⁻) near the interface, they do not seem to be sufficient to screen out the repulsive interactions effectively between the positively charged N-terminal groups in proximity. The burial of a large amount of charges at the interface is also unfavorable, due to the desolvation penalty. This is quite different from the first layer, where GAV-9 peptides tightly bind onto the mica through the strong electrostatic interactions between the positive N termini and the negative surface cavities (K⁺-vacant site) on mica, hence enabling stable accumulation of a large number of positively charged N termini by knocking out K⁺ ions (25, 26). Therefore, the P1 model is energetically unfavorable. Interestingly, both the P2 and AP models show that they can stay stably on top of the sublayer over the duration of the simulation but with slightly different morphologies. The N-terminal side of the P2 model (top surface, exposed to water) is seen to widen significantly during the simulation due to the strong electrostatic repulsions (Fig. 4A4). This widening again emphasizes that the counter-ions (even with 200 mM Cl⁻) are not enough to screen out the electrostatic repulsions among the N termini (of the second layer) in the parallel assemblies (more details are provided below). Another difficulty with the P2 model is that once a third layer is deposited, the charged N termini of the second layer will all have to be buried, which will result in a large desolvation penalty, similar to that in P1 model. On the other hand, the AP model avoids the strong repulsion from immediate neighbors and shows a stable layer structure via hydrogen bonding with the C-terminal −CONH₂ groups of the first layer. No widening of the top or bottom surface has been observed in the AP model.

Fig. 4.

(A) Representative structures from molecular dynamics simulation. Three different models, the P1, P2, and AP models, were configured. The blue gradient is diminished from the N-terminus to C-terminus of the peptide. In all three models, the 7 × 7 peptides in the sublayer are configured in parallel on the mica surface (Fig. S3) and the positive N-terminal NH3⁺ ions are compensated for by a corresponding number of Cl⁻ ions in the initial structure. Then, the whole system is immersed in 100 mM MgCl₂ explicit water solution. (A1) In the P1 model, the 7 × 7 GAV-9 peptides in the top layer are configured in parallel with their N termini touching C termini of the sublayer. (A2) P1 model after 25 ns. (A3) In the P2 model, the 7 × 7 GAV- 9 peptides in the top layer are configured in parallel. In contrast to the P1 model, the C termini touch the C termini of the sublayer. (A4) P2 model after 100 ns. (A5) In the AP model, the 7 × 7 GAV-9 peptides in the top layer are configured antiparallel. (A6) AP model after 100 ns. Average heights (B1), tilting angles (B2), Rgs (B3), and excess cation density on mica surface (B4) of the peptide assemblies. Cont., control system; Deg., degree; N_cat, number of adsorbed cations (K⁺ or Mg2⁺) on the mica surface at a given moment; N⁰_cat, number of stoichiometric cations (only K⁺ ) that neutralize the mica surface after GAV-9 peptides are adsorbed on it. Simulations start with randomly distributed K⁺ ions, which are detached from the mica surface due to GAV-9 adsorption.

Detailed structural analyses indicate that the AP model is more stable than the P2 model as well (Fig. 4B). The radius of gyration (Rg) of the second layer in the P2 model is Rg ≈ 24 Å, whereas it is only Rg ≈ 20.7 Å in the AP model, indicating a more compact structure in the AP model. As for reference, the Rg of the first layer is Rg ≈ 22 Å, which is slightly larger than the top layer in the AP model, probably due to its “mandatory” surface mapping with mica. This suggests that the antiparallel packing provides a more stable and robust assembly template for the second layer (and other top layers). The height and tilt angle also support the AP model. Although the first layers are more or less similar in both configurations (∼2.7 nm in height and ∼11° tilted), the upper layers seem to differ more. Peptides in the AP model tend to make more straight conformations with perpendicular orientations from the surface [2.48 (±0.01) nm and 21.6 (±0.3)° tilted], whereas peptides in the P2 model are more likely to stay away from the straight-up conformation [2.13 (±0.03) nm and 34.0 (±0.5)° tilted], with a broader distribution in both height and angle. The combined heights of the double layer from the mica substrate are 5.06 ± 0.04 nm, and 5.67 ± 0.02 nm for the P2 and AP models, respectively, indicating a better consistency with the observed height from in situ AFM (i.e., 5.8 ± 0.3 nm) for the AP model.

Our hypothesis on the top layer morphology is further validated by potential of mean force (PMF) calculations. We studied the dissociation of a single peptide from a well-formed 7 × 7 GAV-9 island [previously used for a monolayer growth mechanism in pure water (26)] with two different assembly models (P2 and AP models) using steered molecular dynamics (SMD) simulations and the Jarzynski equation for PMF (28, 29) (more details are provided in Fig. S2). With an aggregate of 1.7 μs of SMD simulations, we found that peptide bindings on hydrophobic (H) sides are significantly more stable than bindings on hydrophilic (P) sides, which is concordant with our previous findings that the hydrophobic interaction dominates the longitudinal growth of GAV-9 nanofilaments on mica (26). This significance of hydrophobic interactions (and lowering of the desolvation penalty) was also emphasized in the studies on charged amyloid peptides aggregation of Thirumalai and coworkers (30, 31). The binding free energies are also comparable on the H edges for both the AP and P2 models (ΔG_bind ≈ −32 kcal/mol). On the contrary, interactions along the hydrophilic edges (i.e., transversal lateral directions) are more sensitive to the peptide arrangement. The AP model stabilizes the binding by ∼12 kcal/mol for a single peptide, whereas the P2 model stabilizes binding by only ∼4 kcal/mol. This indicates that the ionic strength (i.e., ∼6 Å of Debye length) might not be enough to screen out electrostatic repulsion in the P2 model between short-distanced (<5 Å) peptides along the transversal hydrophilic sides (linked by backbone hydrogen bonds), although for the relatively long-distanced (∼10 Å) peptides along the longitudinal direction (due to bulky side chains), the electrostatic repulsion is no longer a major force due to the longer distance and more effective screening; thus, both the AP and P2 models give similar binding affinities due to their comparable hydrophobic interactions (30, 31). Our PMF results therefore further support that the AP model is thermodynamically more stable than the P2 model for the upper layers, which largely comes from the aid of a more supportive transversal lateral interaction in its antiparallel arrangement.

As mentioned above, we have assumed that the first layer assembles in parallel on mica even under 100 mM MgCl₂, the same as with no salt (25, 26). However, one might question whether increasing ionic strength might influence the aggregation pattern for the first sublayer. A careful examination of the first layer under 100 mM MgCl₂ shows that the parallel assembly is still more favorable than the antiparallel assembly on mica (Fig. S3), verifying that our earlier assumption was correct. Indeed, it is difficult to alter the parallel assembly, powered by the stable registration of positive N termini on negative mica surface cavities, for the first layer (25). This also supports previous views (20–22, 32) that peptide self-assembly is strongly influenced by its microenvironment. Even with the same bulk salt solution, parallel assembly was favored for the first layer (due to the attractive interaction with the mica surface), whereas the antiparallel assembly was favored for the second layer. For the second layer and above, the attractive electrostatic interactions from the mica surface decay significantly due to longer distances (even more so in a high-salt concentration due to screening), which are insufficient to hold the N termini from the top layers. Rather, the antiparallel assembly is preferred not only to reduce the strong repulsions between immediate neighboring N-terminal groups but to facilitate the energetically more stable antiparallel β-sheet conformation often found in amyloid oligomers (33).

On the other hand, given that the electrostatic screening enhances hydrophobic interactions to promote peptide aggregation, the double-layered formation under high-salt concentrations might be better understood by combining surface reaction kinetics. Under the condition of no external salt in the solution, the epitaxial binding sites on the mica surface are in equilibrium between the K⁺-occupied and K⁺-vacant states (our molecular dynamics simulations indicate that 52.3% of K⁺ sites are open in pure water, in agreement with previous experimental findings), where GAV-9 may readily react (adsorb) onto the K⁺-vacant sites [for the K⁺-occupied sites, on the other hand, it needs to go through ion exchange reactions (34, 35)]. However, once a high concentration of salt (e.g., MgCl₂) is added into the solution, the above equilibrium is shifted toward the K⁺-occupied states (or Mg²⁺-occupied states) (36, 37). This can be clearly seen from the excess cation density on the mica surface in our simulation (Fig. 4B4). Compared with the no-salt control case, the 100-mM MgCl₂ solution displays a significantly higher surface cation coverage with both K⁺ and Mg²⁺ (with a roughly 36:1 ratio for K⁺/Mg²⁺). In essence, this excess of cations on the mica surface reduces the negatively charged surface cavities (K⁺-vacant sites) available for GAV-9, which promotes the assembly of a second layer on top of the first one, instead of generating a new first layer.

Multilayered Assembly Is a General Phenomenon for GAV-9 with a Wide Range of Salt Concentrations and a Variety of Salt Types.

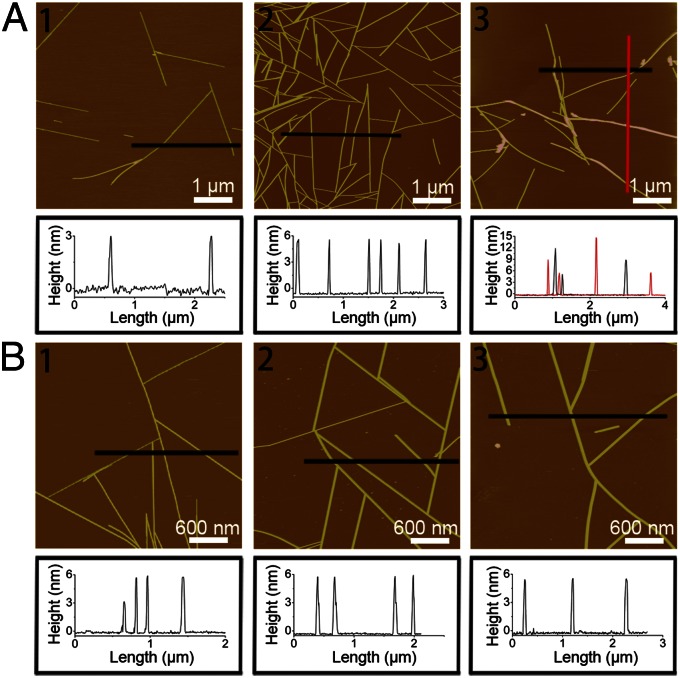
In the above discussions, we focused on the double-layered formation in the 100-mM MgCl₂ solution; however, the multilayered assembly is not limited to this particular concentration or salt type. Rather, we found that the multilayered nanostructure is a progressive process in a wide range of salt concentrations (Fig. 5A and Fig. S4). Under a very-low-salt concentration (i.e., <5 mM MgCl₂), single-layered structures are dominant, similar to those in pure water. With the salt concentration increased to 5–60 mM MgCl₂, coexistence of single- and double-layered structures is observed, with heights of ∼3 nm or ∼6 nm, but none in-between. With the concentration further increased to 60–150 mM MgCl₂, a relatively uniform double-layered structure is seen, as discussed above. Once beyond 150 mM MgCl₂, higher order layers with heights of ∼9, ∼12, and ∼15 nm (triple, quadruple, and quintuple layers) have been observed. It is interesting to note that as the salt concentration increases, the enhanced vertical nanofilament growth is accompanied by a reduction in the longitudinal length growth and an increase of off-epitaxial binding (i.e., no longer positioned at the optimal 120° to each other) (23), which further suggests that the available K⁺-vacant sites on the mica surface are more likely to be blocked by the increased Mg²⁺ ions, thus shifting the assembly toward vertical stacking.

Fig. 5.

AFM height images and section analysis of the GAV-9 assemblies under aqueous solutions containing different concentrations of MgCl₂: 5 mM (A1), 100 mM (A2), and 250 mM (A3), respectively. AFM height images and section analysis of the GAV-9 assemblies under aqueous solutions containing 100 mM NaCl (B1), 100 mM KCl (B2), and 100 mM MgSO₄ (B3), respectively.

Furthermore, the multilayered GAV-9 peptide assembly is also found in other salt types like NaCl, KCl, and MgSO₄. Fig. 5B shows double-layered GAV-9 nanofilaments in 100 mM NaCl, KCl, and MgSO₄, respectively, indicating that the multilayered structure is a general phenomenon for GAV-9 peptides on mica under high-salt concentrations. However, it is noteworthy that different salt types may display a different efficiency in the multilayered formation. For example, the double-layered structures are predominant in 100-mM KCl, MgCl₂, and MgSO₄ solutions, whereas a mixture of single- and double-layered structures is observed in 100 mM NaCl. This can be explained by differences in their ion-exchange capacity on mica, where Mg²⁺ can adsorb onto mica with higher strength and lower mobility than K⁺ and H₃O⁺ (36, 37), whereas Na⁺ has lower binding affinity than K⁺ on mica (38). Specifically, there is a cation order of Mg²⁺ > K⁺ > Na⁺ in its enhancement for the multilayered formation with the increase of the salt concentration, following an exact reverse order of the Hofmeister series for cations.

Conclusion

We have investigated the formation of multilayered nanofilaments of the amyloidal peptide GAV-9 on the surface of mica under high-salt concentrations with both experimental and theoretical approaches. In situ AFM images and delicate nanomechanical manipulation experiments show that GAV-9 peptide exhibits a very strong tendency to assemble uniformly into a double-layered nanostructure with all-upright conformations in 100-mM MgCl₂ solutions. This layer-by-layer assembly of the upright-oriented peptides can be modulated by adjusting the salt concentration (i.e., the ionic strength). Our molecular dynamics simulations and PMF calculations suggest a parallel β-sheet conformation for the first layer but an antiparallel β-sheet for the second layer and beyond. The more stable antiparallel conformation for the second-layer peptide is a result of balanced complex interactions between peptide and peptide, peptide and water, and peptide and mica, which are also more consistent with the findings of the current AFM experiment as well as with the commonly observed antiparallel amyloid fibril structures. The different assembly patterns for the first and second layers also emphasize the importance of the microenvironment, such as template surfaces (i.e., on mica, on peptide surface) even under the same salt solution. Further studies with a variety of salt types (e.g., KCl, NaCl, MgSO₄) and a wide range of salt concentrations (0–250 mM) indicate that this is a common phenomenon, with an even higher number of well-ordered upright layers (three, four, or five layers) possible. Compared with previous self-assemblies of other peptides and proteins with indefinite morphologies (39), the current study with GAV-9 peptides indicates that highly ordered, controllable nanostructures can be achieved through careful sequence design, substrate lattice matching, and ionic strength tuning.

Materials and Methods

Peptide and Salts.

The peptide GAV-9 (NH₂-VGGAVVAGV-CONH₂) was synthesized using the t-Butyloxy carbonyl (Boc) solid-phase method and cleaved from the resin with hydrogen fluoride. The sample had a purity of 98.8% m/m, which was verified by HPLC and was further characterized using a mass spectrum (9). Before use, freeze-dried peptide powder was dissolved to a concentration of ∼3 mM in aqueous solutions of certain salts. The salts MgCl₂⋅6H₂O (≥98%), NaCl (≥99.5%), MgSO₄ (≥98%), and KCl (≥99.5%) were purchased from Sinopharm Chemical Reagent Co., Ltd.

AFM.

All in situ AFM operations were performed in a liquid cell on a commercial AFM instrument (Nanoscope V; Veeco/Digital Instruments) equipped with a 100-μm scanner. Experiments were performed in tapping mode. Silicon nitride cantilevers with a nominal spring constant of 0.24 N/m (SNL-10; Bruker) were used. Muscovite mica [KAl₂(Si₃Al)O₁₀(OH)₂; Ya'an KF Electrical Material Co., Ltd.] was used as the inorganic substrate, which was freshly cleaved by adhesive tape before each experiment.

Molecular Dynamics Simulation.

In our simulations, the mica surface was constructed using double-layered muscovite (001) [KAl₂(Si₃Al)O₁₀(OH)₂] with the Clay force field (CLAYFF) (40) based on the monoclinic C2/c 2M₁ crystal structure (41) and the Al-avoidance (i.e., Loewenstein’s) rule (42) (further details are provided in Fig. S5). For the first layer, 49 GAV-9 peptide chains were loaded on every possible binding site along 7 × 7 crystallographic rectangular lattices on a 89.7 × 106.4-Ų mica surface so as to contact each other in an optimally packed configuration (25, 26). The stability of the first layer was evaluated with a single-layered peptide on mica with both parallel and antiparallel configurations.

For the second layer, three possible models were examined on top of the first parallel layer: (i) P1 model, in which a parallel assembly of 49 GAV-9 peptides was loaded in the N-terminal–to–C-terminal (N-to-C) peptide direction, the same as the sublayer; (ii) P2 model, in which a parallel assembly of 49 GAV-9 peptides was loaded in the C-to-N peptide direction, opposite to the first layer; and (iii) AP model, in which 49 GAV-9 peptides were configured in an antiparallel orientation on top of the first layer. All the positive N-terminal groups in GAV-9 were neutralized with counter-ions (Cl⁻).

The single- and double-layered systems were then immersed in water boxes with >18,000 and >25,000 TIP3P water molecules (43), respectively. The 100-mM MgCl₂ salt concentration was set up by replacing some water molecules with Mg²⁺ and Cl⁻ ions. All our molecular dynamics simulations were performed with the NAMD2 package (44) optimized on an IBM Bluegene supercomputer (45). Molecular dynamics simulations have been widely used to complement experiments (46–53), which can provide atomic details that are often inaccessible in experiments due to resolution limits, even with the most sophisticated experimental techniques currently available. The long-range electrostatic interactions were calculated with the particle mesh Eward method (54), whereas the nonbonding dispersion interactions were treated with a smooth cutoff at 12.0 Å. Each system was first minimized for 20,000 steps to remove the bad contacts with the CHARMM22 (Chemistry at Harvard Macromolecular Mechanics) force field (55), and was then equilibrated for 0.5 ns with a 0.5-fs time step in the isobaric and isothermal (NPT) ensemble at 1 atm and 310 K. In production runs, trajectories proceeded with a 2-fs time step for ∼100 ns.

The peptide binding free energies (PMFs) for the upper layers were calculated by separate SMD simulations (more details are provided in Fig. S2). Using a similar 7 × 7 GAV-9 island as in the previous study for monolayer growth in pure water (26), four test peptides were selected to be pulled off from each side of the island for both the P2 and AP models. The selected peptides were pulled off along the surface normal by means of an external spring (k = 5 kcal/mol) on the center-of-mass of the peptide with a constant velocity of 0.5 Å/ns, whereas the rest of the island was restrained by harmonic constraints on C_α atoms (k = 5 kcal/mol). Each peptide was simulated five times, with an aggregate of >1.7 μs of molecular dynamics simulation time. The PMFs were calculated for both H and P edges by averaging over all trajectories obtained from the same edge type using the Jarzynski equation (28, 29).