CORaL: Comparison of Ranked Lists for Analysis of Gene Expression Data

Abstract

Because a very large number of gene expression data sets are currently publicly available, comparisons across experiments between different laboratories have become a common task. However, most existing methods of comparing gene expression data sets require setting arbitrary cutoffs (e.g., for statistical significance or fold change), which could select genes according to different criteria because of differences in experimental protocols and statistical analysis in different data sets. A new method is proposed for comparing expression profiles across experiments by using the rank of genes in the different datasets. We introduce a maximization statistic, which can be calculated recursively and allows for efficient searches on a large space (paths on a grid). We apply our method to both simulated and real datasets and show that it outperforms other existing rank-based algorithms. CORaL is a novel method for comparison of gene expression data that performs well on simulated and real data. It has the potential for wide and effective use in computational biology.

1. Introduction

In the past several years, many gene expression datasets have been made publicly available, in part for the purpose of comparison with each other and with newly produced data. The most common method for comparing two gene expression experiments is to consider the two experiments separately and then find the genes that are determined to be significant in both experiments. This method depends on applying cutoffs for test statistics such as p value (statistical significance) and fold change (average expression in treatment divided by average expression in control). Using cutoffs introduces uncertainty, as cutoffs are generally set arbitrarily.

To avoid using cutoffs that select some genes while arbitrarily excluding others, rank-based methods have been developed. For example, the algorithms behind Gene Set Enrichment Analysis (Subramanian et al., 2008) and GOrilla (Eden et al., 2009) rank genes by fold change to estimate enrichment of gene sets. Eden et al. (2007) use ranked lists to compare experimental samples of immunoprecipitation data with background. Jurmen et al. (2007) and Boulesteix and Slawski (2009) compare the algebraic stability between ranked lists of genes.

This article describes a new rank-based comparison-analysis method based on a maximization statistic that is calculated using a recursive algorithm.

There are two existing algorithms for comparison of gene expression data using ranked lists. The algorithm of Plaisier et al. (2010), called Rank-Rank Hypergeometric Overlap (RRHO), focuses on visual representations of the similarities between two ranked lists, using a mathematical model similar to ours. The algorithm of Yang et al. (2006), called OrderedList, focuses on using a similarity score to evaluate whether two lists have significant similarity. These algorithms will be compared with our method in detail in the Results section.

Our new algorithm improves and extends an algorithm we have presented in Antosh et al. (2011). The model for calculation of p value has been improved, and the method has been extended to allow for the more general case where the two experiments have a different number of differentially expressed genes.

2. Methods

2.1. Model

In our model, we first group genes into two sets: genes that change from control and genes that do not. We presume that most of the genes that change from control have higher fold changes than most of the nonchanging genes; that is, the biological change generally is higher than the noise. Based on this, the genes that change in both experiments will overlap (be highly ranked in both experiments)—this is because the genes that change in both experiments will be near the top of a list of genes ranked by fold change in each experiment. We further presume that this overlap drops off at the point in the ranked lists where most of the genes do not change. The genes above this drop-off point in the ranked list are referred to as the significant set.

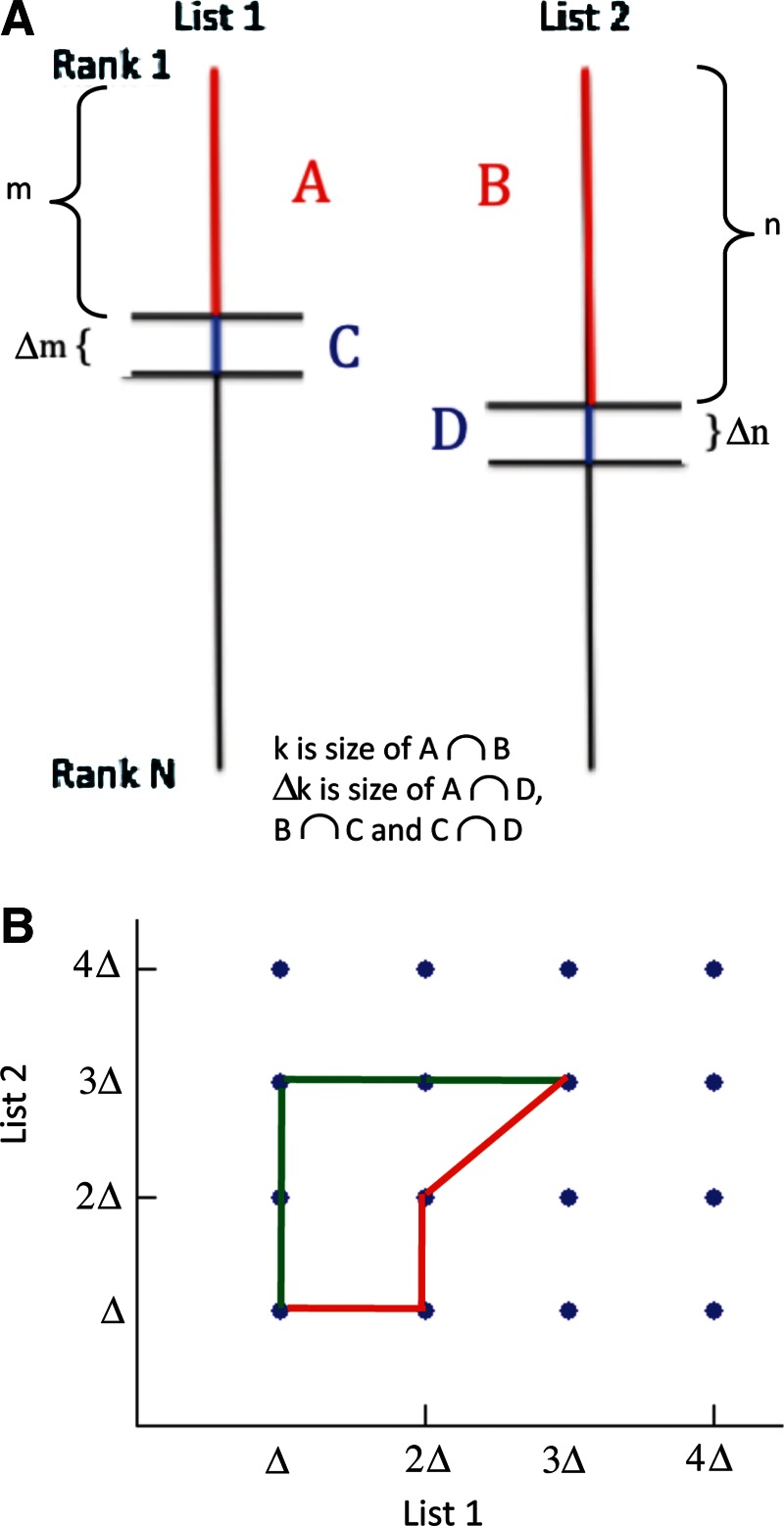
In the algorithm, the genes are ranked by fold change. The lists are analyzed starting from the top by adding groups of genes in incremental steps. As shown in Figure 1A, the top m elements in list 1 and the top n elements in list 2 have an overlap of k elements. Also, k increases by a value Δk when m increases by a step-size Δm and n increases by a step-size Δn. The statistical significance (p value) of each step is the probability that the additional Δk genes found in the step is significantly more than the Δk that would be expected randomly. These statistical significance values are used in a maximization function, defined below, to determine the optimal set sizes in each list.

FIG. 1.

Illustration of method. (A) Sections of ranked lists: k_AB is the overlap of red sections A and B, and Δk is the sum of the overlaps between sections A and D (k_AD), sections B and C (k_BC), and blue sections C and D (k_CD). (B) Illustration of grid search and of two possible paths from (Δ,Δ) to (3Δ,3Δ).

The maximization process can be thought of as a search on a grid, with an example grid illustrated in Figure 1B. Each point on the grid is a possible significant set size, with the significant set size in each list being a multiple of the step-size Δ. Using the strategy of a grid search, we want to maximize the likelihood of both reaching a point and of stopping the search at that point. We define the statistic to be maximized, L, as the measure of the probability of reaching a point on the grid and then stopping at that point. It is thus the product of the likelihood of reaching each point, defined as T, and the likelihood of stopping at that point, defined as S:

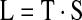(1)

Both T and S depend on the probability of the individual steps taken in the grid, as illustrated in Figure 1B, and are formally defined in Section 2.3.

2.2. Calculation of step p values

The overlaps between the regions of the list shown in Figure 1A step can be represented using a 3 × 3 contingency table (Table 1). In this table, four different variables combine to make up the variables k and Δk shown in Figure 1A. This is because the different sections of lists produce distinct overlaps. In the table, k_AB is the overlap between section A and section B in Figure 1, k_AD is the overlap between sections A and D, and so on. Δk is thus equal to the sum of k_AD, k_BC, and k_CD, and k is equal to k_AB. Also, Δm is the step size in list 1, and Δn is the step size in list 2. Ghent (1972) derived an exact equation for the probability of a 3 × 3 contingency table; specifically, the statistical probability that an exact set of overlaps (k_AB, k_AD, k_BC, k_CD) is found. This probability is given in Equation (2). For shortness of annotation, C_ij is introduced to represent the entry in the ith row and jth column in Table 1. The denominator is thus N factorial times the factorial of each element in the 3 × 3 table.

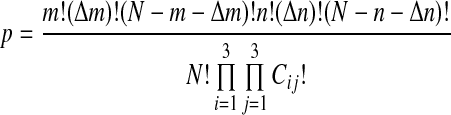(2)

Table 1.

3 × 3 Contingency Table Applied to Ranked List Steps

	List 1 index
		1 to m	(m+1) to (m+Δm)	(m+Δm+1) to N	Total
	1 to n	kAB	kBC	n−kAB−kBC	n
List 2 Index	(n+1) to (n+Δn)	kAD	kCD	Δn−kAD−kCD	Δn
	(n+Δn+1) to N	m−kAB−kAD	Δm−kBC−kCD	N−m−n−Δn−Δm+kAB+kAD+kBC+kCD	N−n−Δn
	Total	m	Δm	N−m−Δm	N

2.2.1. Normalizing for k_AB

The 3 × 3 contingency table (Table 1) represents the probability that an exact set of k happens—meaning the exact combination (k_AB, k_AD, k_BC, k_CD). The probabilities will only add up to one over all possible combinations of the four k variables. However, only the case where k_AB equals the actual found value of k_AB is relevant to this problem, because the overlap k_AB at the first point in the step is considered to be known and fixed, and thus has only one allowed value. The probability calculated in Equation (2) can be normalized to eliminate other possible values of k_AB by dividing by the probability of finding an overlap of magnitude k_AB between regions A and B. This probability is the Fisher's exact test and is given by Equation (3).

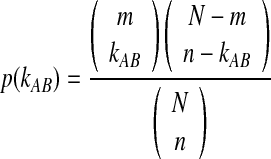(3)

2.2.2. Summation over probabilities to calculate p value

The step p value is the probability that Δk is greater than or equal to the value of Δk found. This is a sum over Equation (2) divided by Equation (3) for all values of Δk greater than or equal to the value found. This involves a sum over k_AD, k_BC, and k_CD. However, the sum is shortened by some constraints, given in inequalities 4.

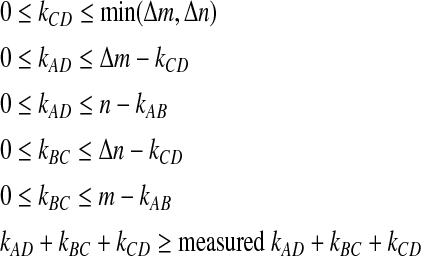(4)

For k_CD, the first constraint is that the overlap (between sections C and D in Fig. 1) cannot be greater than the total number in the smaller of the step sizes—it is the overlap of segments the size of the step sizes. For k_BC, the first constraint is that only so many elements in section C are left to overlap with section B in Figure 1 because some of the elements in section C could be in the overlap with section D, k_CD. The second constraint on k_BC is the number of elements left to overlap in section B because some of the elements in section B could be in the overlap with section A, k_AB. The constraints on k_AD are analogous to those on k_BC. The final constraint is the actual p value constraint.

If Δn = Δm, the number of terms in the sum before constraint is equal to (Δm)³. Thus if Δm = 100, that number is 1 million. However, the second and fourth constraints alone remove roughly 60 percent of the terms. The speed of calculation is aided by the use of a table of factorial values instead of recalculating the factorial values in each term. Additionally, terms that stay the same throughout (e.g., N!) are only calculated once.

2.2.3. Summary

In summary, the step p values are calculated in the following manner. First, the step is modeled as a 3 × 3 contingency table, which has a calculable probability (Eq. 2) for each combination of overlaps (k_AB, k_AD, k_BC, k_CD). The value of k_AB is considered a fixed point (because we know where the step is starting), and the calculated probabilities are normalized (using Eq. 3) to eliminate all other values of k_AB. The step p value is equal to the sum over all 3 × 3 table probabilities where k_AB is the measured value of k_AB, and k_BC, k_AD, and k_CD satisfy inequalities (4).

2.3. Maximization approach to determining optimal overlap size

As stated in Section 2.1, the maximization approach is analogous to a grid search, with an example grid shown in Figure 1B. Allowed step directions are forward by one step in one list or the other, or forward in both lists. Using the strategy of a grid search, we want to maximize the likelihood of both reaching a point and of stopping the search at that point.

The maximization statistic in Equation (1) can be computed recursively for all (i,j) in the grid illustrated in Figure 1B. The total probability (T) in Equation (1) for a given point (i,j) on the grid is the sum over all possible paths from (0,0) to (i,j) of the probability of that path, R_path [Equation (5)].

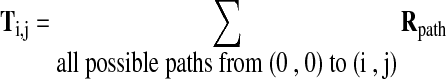(5)

The probability R_path of a given path depends on the length of the path and the probability p_step that the step will be taken (Eq. 6). P_step is defined as one minus the step p values computed in Equations (1) to (3). A small p value indicates a step that adds a comparatively large overlap (Δk), and a large p value indicates a step that adds a comparatively small overlap. Thus we presume that the smaller the p value, the more likely the step is to be taken. Hence, the path probability can be computed as follows:

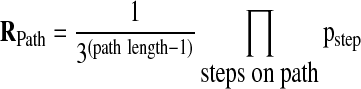(6)

The factors of 1/3 come from the three possible steps (we are allowing only forward steps in the x direction, the y direction, or both) at each grid point. To choose the direction that each path takes, the other two directions must be discarded (for that particular path). The probability of choosing any of the three directions randomly is 1/3. This is true with one exception. The first step has to be from (0,0) to (1,1), because a step to (0,1) or (1,0) will have a zero overlap by definition. Thus, the first step has no factor of 1/3, producing the 1/3 to the power of path length minus 1. The step probabilities are corrected for multiple testing using the Benjamini–Yekutieli method (Benjamini and Yekutieli, 2001), which controls the false discovery rate under arbitrary interdependence of the steps.

The likelihood of stopping, S, shown in Equation (7), is the product of the step probabilities (p_step) of not taking a step forward in any of the three given directions (first three terms in the product) and the probability of taking the three forward steps up to the point (last three terms). Any steps that would go off of the grid are not considered.

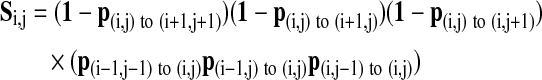(7)

Using the grid of possible set sizes, the point with the maximum value of L is chosen. Once this point is chosen, the statistical significance of the overlap at that point is evaluated and ruled significant if Fisher's exact test (a sum over k_AB in Eq. 3, with k_AB ranging from the measured value of k_AB to the smaller of the two significant set sizes found in the optimization) gives a p value less than 0.05. Note that T can be computed recursively because T_i,j depends only on the sums of probabilities for the steps leading up to (i,j). Pseudocode for the recursive algorithm used to compute it is presented in the Supplementary Material (Supplementary Material is available online at www.liebertonline.com/jcb).

2.4. Existing methods testing

We compared the results of our algorithm with the results of algorithms developed by Plaisier et al. (2010) and Yang et al. (2006). The algorithm developed by Yang et al., OrderedList, was applied using their software package in R. Simulations were run using the rank-input commands compareLists and getOverlap, and the biological data comparisons were done using the command OrderedList. Default values were used, including for the parameter alpha that determines candidate values for significant set size.

The algorithm developed by Plaisier et al. (2010), RRHO, was implemented using their web-based interface. The step size matched the step sizes used in CORaL. A step size of 100 was generally used, which matches the recommended step size listed. Overlaps and set sizes were considered from the regions referred to as A (genes upregulated in both lists) and B (genes downregulated in both gene sets). Overlaps with p value less than 0.05 were ruled nonsignificant. We coded Plaisier's method into the statistical computing language R for the simulations; the code is available in the Supplementary Material.

In simulations, the same data were used for all three methods. In real data, the same genes were used for all three methods.

3. Results

CORaL (our algorithm), OrderedList (Yang et al., 2006), and RRHO (Plaisier et al., 2010) were implemented on simulated data as well as data used in Bauer et al. (2010) and Pearson et al. (2008).

3.1. Simulated data

The goal of the simulated data is to produce data that are realistic and also have a predictable result. For inputs of list length N and desired overlap k, the simulation procedure is as follows:

• To start, the two lists will each contain N “fold changes” covering the values 1 through N. The element in each list with fold change N will have the best rank.

• Select k elements in the two lists to become the overlap. In list 1, give these elements the k best fold changes (i.e., fold changes between N and N − k + 1).

• Temporarily set up the k elements in the overlap to have perfect correlation—order the fold changes for the overlap elements in each list such that the element in list 1 that has the best fold change of the overlap elements also has the best fold change of the overlap elements in list 2, and so on down the list.

• Randomly distribute the rest of the fold changes in the list.

• Subtract from each fold change the absolute value of randomly drawn, normally distributed noise with the standard deviation of the noise specified as a simulation parameter.

• Run the analysis methods (CORaL, RRHO, OrderedList) on the fold changes.

The realistic nature of this simulation method is verified by attempting to reproduce data with behavior similar to the comparison of genes upregulated from control in two dietary restriction data sets from Bauer et al. (2010). Running CORaL on these data resulted in the parameters k = 3290, N = 5700. A simulation using those parameters resulted in data that fit the real data based on the overlap fraction diagnostic plot described in Figure 1 of Antosh et al. (2011). Using the same notation as Equation (3), that plot is the fraction of overlap (k_AB/m, keeping m = n for a diagnostic) versus m/N. The diagnostic plot is shown in the Supplementary Material, along with an illustration of the simulation method.

In the simulation, we used two levels of noise—a realistic noise amount and zero noise. The realistic noise was determined by examination of the diagnostic plots (included in the Supplementary Material); the desired result was a smooth curve where k/m did not significantly decrease with increasing values of m/N. The zero noise level was included in order to have some results that were completely predictable.

Two overlap simulations were performed: k = 400, N = 1200 and a two-dimensional simulation where 200 overlap elements receive the 200 best fold changes in list 1 and 200 of the top 400 best fold changes in list 2 (so that for the significant set sizes, m = 200, n = 400 in our notation). The second simulation is to test the effectiveness of the method in a situation where m and n should not be equal. A step size of 50 was used in these simulations.

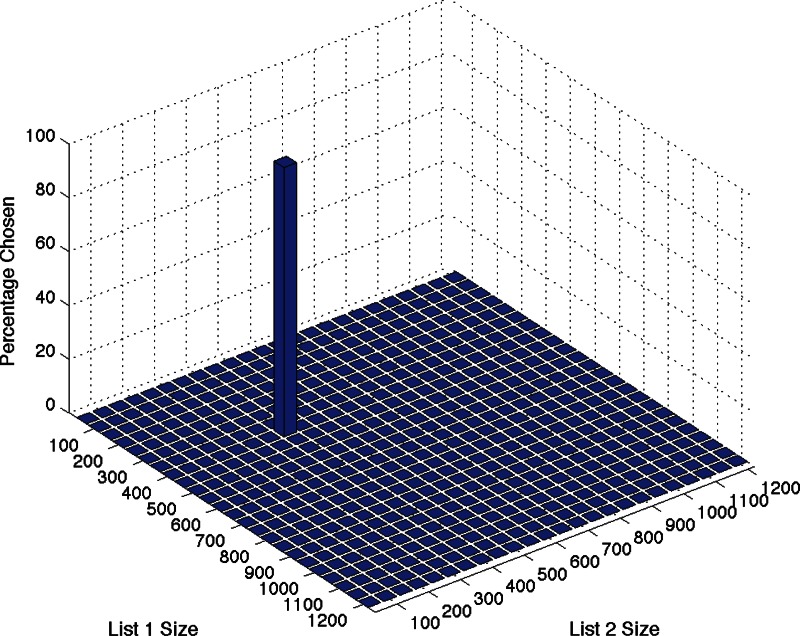
With zero noise, CORaL chooses the expected answers. It chooses m = n = k = 400 in each of 100 simulations with k = 400, N = 1200, and it chooses m = 200, n = 400, k = 200 in the second simulation (which has desired result m = 200, n = 400). The choice of m and n from the second simulation is shown in Figure 2.

FIG. 2.

Simulation results for m = 200, n = 400, k = 200, N = 1200, Δ = 50. About 100 data sets were simulated, and the probability of selecting each set size is displayed.

In the noisy, more realistic simulations, the k overlap elements have spread out, and the important measure is how many of the elements can be recovered. It is not expected to recover all of the elements, because some will have been altered significantly. In the k = 400, N = 1200 simulation with noise of standard deviation 300, CORaL chooses significant set sizes that retain an average of 327 ± 21 of the original 400 overlap elements, finding on average an additional 26 elements that were not in the original overlap before noise. Variation in the results is a result of variation between the 100 simulated data sets; the result of CORaL on the same data is always the same.

In the m = 200, n = 400 simulation with noise of standard deviation 150, CORaL chooses significant set sizes that retain an average of 167 ± 18 of the original 200 overlap elements, finding on average an additional 21 elements that were not in the original overlap before noise.

As a negative control, 100 simulations were run with random data (m = n = k = N = 1200). CORaL chose the smallest possible set size.

3.2. Results on real data sets

Pearson et al. (2008) produced a data set consisting of three treatments given to mice (dietary restriction, a high dose of resveratrol, and a low dose of resveratrol) with samples from four different tissues (heart, liver, fat, and muscle). The effects of these treatments should be somewhat specialized by tissue, because the biological properties of the tissues tested differ significantly.

Using each method, all possible pair-wise comparisons were run between the treatments; the total gene overlap was used to cluster the treatments hierarchically (average linkage method). CORaL shows a complete clustering effect with tissue, with the following mean number of genes in common between treatments on the same tissue: 6315 for fat, 798 for heart, 3125 for liver, and 3078 for muscle (actual overlaps shown in Supplementary Material tables). Pearson et al. (2008) finds the correlation of gene expression pathways to be significantly less strong in the heart data than in the other tissues; this is supported by the heart overlap being significantly smaller than the other tissues in our results. As a measure of effectiveness in determining the existence of significant overlaps, CORaL found a significant overlap in 49 of the 66 possible pair-wise comparisons between the 12 Pearson et al. data sets (three treatments and four tissues).

3.3. Comparison with existing methods

In the comparison with the methods of Plaisier et al. (2010; RRHO) and Yang et al. (2006; OrderedList), it is important to note the similarities and differences in approach and goals between the methods. The foremost goal of Yang et al. is to determine whether or not there was any statistically significant similarity between the two ranked lists. The foremost goal of Plaisier et al. is to visualize “the strength, pattern and bounds of correlation” through a graphical map of the statistical significance of the overlap between different subsets of the ranked lists. The foremost goal of our algorithm is to estimate the significant set in each of the two lists.

Yet, all three methods share two general goals: determining whether or not there is a statistically significant similarity between the two ranked lists, and determining the size of a significant set. The methods of Yang et al. (2006) and Plaisier et al. (2010) for detecting similarity was described in the paragraph above. Yang et al. also looks for a significant set size, justifying the need for it by saying that “A priori, we do not know how deep inside the lists we must look to detect a biologically relevant signal. This calls for an algorithm that calibrates α adaptively to the gene lists of interest.”Alpha is their parameter for decay of the exponential term in the similarity score, determining how much weight the lower parts of the list have on the similarity score and thus how far down the list the similarity score is significant. Their process for finding how deep to go in the list is based on partial areas under receiver operating curves, and is described in Section 2.3 of their article. It is true that they emphasize the overall similarity, but the process of finding the significant set is necessary for their algorithm as well. Plaisier et al. use corrected Fisher test p values to determine quantitatively whether or not there is similarity between the lists, and they approach finding the significant set on the way to summarizing their visual map, stating that “the most straightforward summary statistic of a rank–rank hypergeometric map is the point with the maximum absolute log p value, which represents the rank threshold pair that gives the most significant hypergeometric overlap in the experiments being compared.” Thus, Plaisier et al. also make an attempt at labeling significant sets, although it is important to remember that Plaisier et al. are attempting to summarize their visualization, whereas we are attempting to find precision in the significant set sizes.

In producing their visualization, Plaisier et al. (2010) compute the hypergeometric probability based on Fisher's exact test (a sum over k_AB in Eq. 3) for every possible combination of significant set sizes in each list (m genes from experiment 1, n genes from experiment 2, overlap k and total number of genes N). They then summarize this visualizing by selecting the set (m,n) that gives the minimum p value as the location of the significant sets. They do allow for two selections: one representing the overlap between genes up and one representing the overlap between genes down. They allow correction of these p values for multiple hypothesis testing (although this should not affect which values are minimum, only their significance level).

The choice of minimum p value as their analog of the significant set makes an implicit assumption that the point with the highest significance is the end of the significant correlation between the two lists, whereas our algorithm looks for the point that is most likely to be reached and stopped at in a grid search.

In the simulated data, the method of Plaisier et al. (2010) underestimates in the noisy simulations. In both of the zero-noise simulations, it chooses the expected results. In the noisy simulations, it finds significantly fewer genes than CORaL: 250 ± 26 of the 400 elements in the k = 400, N = 1200 simulation and 130 ± 29 of the 200 elements in the m = 200, n = 400 simulation. Thus, compared with the CORaL result, the result of Plaisier's method is a point in the lists where statistically significant steps are left untaken. In both of these results, there were fewer nonoriginal overlap elements than found by CORaL (three elements in the first simulation and five elements in the second simulation), but this is likely a result of the significantly smaller set sizes chosen.

With the Pearson et al. (2008) data sets, Plaisier's (2010) method shows very distinct tissue clusters. However, the number of significant genes is very large: the mean number of genes in common between treatments on a given tissue is 11,144 for fat, 9141 for heart, 10,032 for liver, and 9483 for muscle (actual overlaps shown in Supplementary Tables). In particular, the average overlap of treatments in the heart is approximately 8300 genes larger as the average overlap found by our method, and no longer smaller than the other tissues (as found by our method and by Pearson). These results suggest an overestimation. We could identify a possible cause in the way Plaisier's p values were computed, specifically by including the full list of genes in their computation, as opposed to the subset of genes up- and downregulated that we utilize in our method. This will result in consistently lower p values, and some comparisons being labeled as significant that would otherwise not be. The primary goal of Plaisier's method is to provide assess similarities between ranked lists of genes, without a specific focus on the accuracy on the number of overlapping genes, and this might have played a role in their choice of a less strict model for the computation of the p values. Of the 66 possible pair-wise comparisons, Plaisier's method finds 61 to have a significant overlap.

As mentioned previously, Yang's (2006) method uses a similarity score, shown in Equation (8).

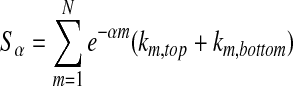(8)

For a given ranked list index m, the score is the overlap of the top and bottom m genes in each list multiplied by an exponential decay term. Here, k represents an overlap, and α is a tuning parameter. The choice of α is analogous to choosing the significant set sizes in our method, because the score is set to zero when the exponential factor reaches a certain magnitude. α is determined by calculating the similarity score for permutations of the data and fashioning the results into a receiver operating curve for several trial values of α.

This approach to determining both significance and significant sets has several important differences when compared with our method. Yang's (2006) method fixes the top and bottom significant sets in each list (four total significant sets) to all be the same size, whereas our method provides a more general solution in allowing the four sets to all be of different sizes. Both methods essentially step down the list, but only our method looks at the probabilities of the individual steps.

In the simulated data, Yang's (2006) method often overestimates. For k = 400, N = 1200 simulation with zero noise, a set size of m = n = 1000 is chosen in all simulations. With realistic noise, 398 ± 7 of the 400 original overlap elements are chosen, but so are on average 205 nonoriginal overlap elements. For m = 200, n = 400 simulation with zero noise, a set size of m = n = 1000 is chosen the majority of the time. With realistic noise, 176 ± 44 elements are chosen. This result is similar to that of CORaL, although the result has a higher standard deviation. The result in this simulation for total overlap genes (original plus extra) is 165 ± 81 elements.

One stated goal of Yang's (2006) method is to test for the existence of significant overlap between data sets. Of the 66 pair-wise comparisons in the Pearson et al. (2008) data set, only 11 were determined to have significant overlap. This is significantly fewer than the 49 found by CORaL. In addition to this, Yang's method of finding significant sets results in no distinct tissue clusters by tissue. Because of the process in OrderedList where replicates are ignored, it was only possible to run OrderedList with an extra sample added to the fat and liver control samples as well as the fat dietary restriction samples. This extra sample consisted of the mean expression of the other samples.

3.4. Determining step size

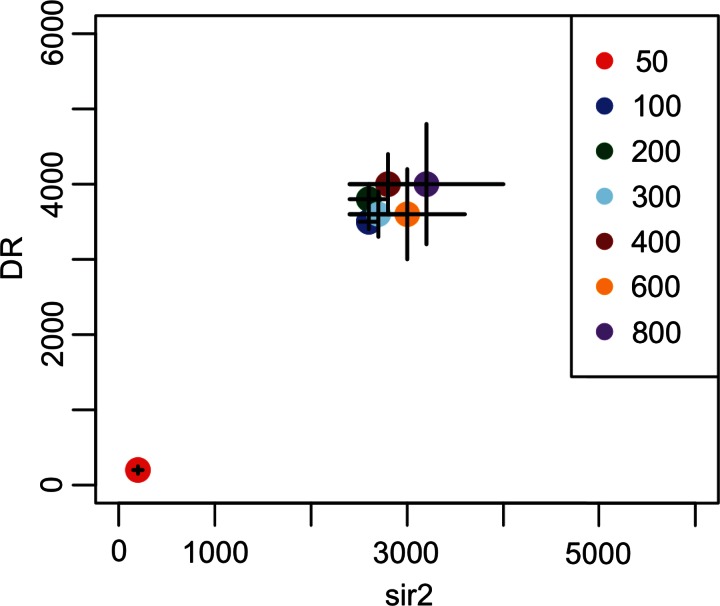
The only adjustable parameter in our method is the step size (Δm or Δn), which sets the size of the grid describing the data (as in Fig. 1). The Δm and Δn are allowed to be two possible values: 0 or an overall step size Δ (the allowance of 0 is to create the steps in only one list or the other list). Figure 3 illustrates the effect of step sizes on a comparison of genes upregulated from control in the sir2 mutation and dietary restriction data sets from Bauer et al. (2010). As shown in the figure, Δ = 50 and Δ = 100 choose smaller significant set sizes than those chosen by larger values of Δ, while step sizes of 200 and larger choose the same point to within one step. It appears that Δ = 50 stops because of random fluctuations in the data. The smaller the step size, the more likely it is that random fluctuations will happen. The larger step sizes will jump past small random fluctuations.

FIG. 3.

Illustration of different step-size results. Black lines represent the size of each step. The result from Δ = 200 is within one step size of the results of every larger step size; demonstrating the method is step-size independent for step sizes above the value needed to skip random fluctuations.

Thus, we propose to handle fluctuations by testing multiple step sizes and finding the step size that no longer increases the resulting set sizes. For a set of step sizes such as (50, 100, 200, 400, 800), where the step sizes increase by a common factor (2), the best step size is the first to have the step size after it selects the same set size to within one step.

Applied to these data, RRHO selects (m,n) = (2600, 3500), the same result CORaL at that step size. OrderedList selects (0,0). The results of CORaL and RRHO that DR (n) has a larger set size than sir2 (m) is consistent with sir2 being a smaller-scale effect as compared with DR, which was the conclusion reached in Bauer et al. (2010).

4. Conclusions

This article introduces a comparison analysis algorithm for gene expression data that does not depend on arbitrary cutoffs for such statistics as fold change and p value (statistical significance).

CORaL is a new algorithm for comparing gene expression data based on (1) comparing lists of genes ranked by fold change and then (2) maximizing the statistical likelihood of reaching a given significant set size, using the overlaps between sections of the ranked lists. There are two innovations in the method: finding the p value for a given step in the list and the use of these p values to determine the point of significance. There is only one parameter, the step size, and multiple step sizes can be used to find an appropriate step size. The maximization statistic used can be calculated recursively and allows for efficient searches on a large space (paths on a grid).

The method performs as expected on simulated data, always choosing the end of the significant sets. Results of data from Pearson et al. (2008) and Bauer et al. (2010) produce conclusions that make sense biologically, including a tissue-specific effect in the data of Pearson et al. and the relative sizes of the effects of sir2 and dietary restriction in the data of Bauer et al.

The use of contingency tables in our method (as well as in the Fisher's test in the method of Plaisier et al. (2010)) makes an implicit approximation that genes are behaving independently. This is of course not always true. However, correcting the p values with the Benjamini–Yekutieli correction (Benjamini and Yekutieli, 2001) controls the false discovery rate in arbitrary dependencies, and the method has been shown to work satisfactorily on simulated and real data that is partially correlated. The Supplementary Material shows the level and significance of correlation between the ranks of the overlap genes in the Pearson data for the significant overlaps chosen by CORaL.

Our method is shown to perform equally well or better than the existing algorithms for comparison of ranked list gene expression data that attempt to determine significant set size and the existence of significant correlation. The significant set size determination method of Yang et al. (2006) often overestimates and is shows a greater variance than CORaL in simulations, and finds significantly fewer similarities between the datasets from Pearson et al. (2008). The summary of visualization in Plaisier et al. (2010) recovers fewer overlap genes than CORaL in realistic simulations. It effectively clusters the data of Pearson et al. by tissue, but chooses extremely large overlaps that are likely the result of an overestimation. It equals the result of our method on the data from Bauer et al. (2010).

With the growing number of gene expression datasets, comparisons between datasets will become increasingly important. This method is an improvement on existing ranked list methods and could be applicable to data from fields outside of gene expression and biology.

Acknowledgments

This work was supported by NIA Grant AG028753 to N.N. The Pearson et al. data set is available as GSE11845 in the Gene Expression Omnibus Repository.

Author Disclosure Statement

No competing financial interests exist.