An ab-initio Computational Method to Determine Dielectric Properties of Biological Materials

Abstract

Frequency dependent dielectric properties are important for understanding the structure and dynamics of biological materials. These properties can be used to study underlying biological processes such as changes in the concentration of biological materials, and the formation of chemical species. Computer simulations can be used to determine dielectric properties and atomic details inaccessible via experimental methods. In this paper, a unified theory utilizing molecular dynamics and density functional theory is presented that is able to determine the frequency dependent dielectric properties of biological materials in an aqueous solution from their molecular structure alone. The proposed method, which uses reaction field approximations, does not require a prior knowledge of the static dielectric constant of the material. The dielectric properties obtained from our method agree well with experimental values presented in the literature.

Frequency dependent dielectric properties can be used to characterize biological materials, determine the concentration of chemical mixtures and detect the formation of new products from biological processes. Computer simulations can be used to determine dielectric properties of aqueous solutions of biological materials and atomic details of bio-molecules that are usually inaccessible via experimental methods. In bio-molecular aqueous solutions, water molecules form hydration shells around ionic compounds and charged chemical species. The bio-molecules, water molecules in the hydration shell and water molecules in the bulk affect the structure and dynamics of other molecules¹. The dielectric properties of bio-molecules in aqueous solution are different from those of pure water, and change with the chemical structure and dynamics of water in the hydration shells around charged chemical species. In the literature, dielectric properties of amino acids in organic solvents or aqueous solutions with different concentrations have been studied experimentally¹,²,³. Also, the dipole moment, polarizability of chemical species such as amino acids and dielectric constants of proteins have been studied theoretically⁴,⁵.

In theoretical computer simulations, an accurate description of the aqueous environment is desirable for realistic bio-molecular modeling, but unfortunately this is not possible and in many cases computationally expensive. For example, a medium-size protein usually requires thousands of discrete water molecules to be placed around it⁶. Alternatively, the reaction field approximation, where a continuum reaction field beyond the cutoff sphere is used has many computational advantages over other methods⁶,⁷. The distortive periodicity beyond the cutoff sphere is avoided because the long range electrostatic interactions are represented by the reaction field and the computational cost is reduced⁶,⁷. Unfortunately the reaction field values are usually unknown. In some studies, the dielectric constant of the continuum is set to the static dielectric constant of the material, however this approach does not consistently provide accurate results of dielectric properties. To date, there is no unified method that permits one to calculate dielectric properties over frequency of a chemical species in solution from its molecular structure alone, without prior knowledge of its static dielectric constant using reaction field approximations. In this paper, a method is described that permits one to determine the dielectric properties of a chemical species in aqueous solution which does not require any prior knowledge of the static dielectric constant.

The proposed method to calculate the frequency dependent permittivity involves the following steps. (i) The dielectric constant of the bulk material in the reactive field outside the cutoff sphere is obtained from an iterative method using MD simulations. (ii) DFT calculations are used to obtain the polarizability of molecular clusters and to calculate the dielectric constant at infinite frequency. (iii) The total dipole moment fluctuations are obtained from MD simulations to calculate the static dielectric constant and relaxation time constant. (iv) This is then incorporated into a Debye model to obtain the frequency dependent complex permittivity. In order to confirm the accuracy of our methodology, the frequency dependent permittivity of well known materials such as water, methanol and ethanol are obtained and compared with the theoretical and experimental values presented in the literature. Here an extensive series of simulations are reported which demonstrate consistent and accurate results can be obtained by our method. In this paper, the method described is applied to obtain the dielectric properties of aqueous solutions of biological materials such as amino acids (L-alanine, L-glycine, L-glutamic acid), and neurotransmitters (γ-aminobutyric acid, dopamine).

Results

The dielectric properties were obtained using a reaction field approximation where the sample is embedded in a dielectric continuum (please refer Supplementary Materials for more details). The dielectric constant of the continuum ε_RF is used to represent the bulk dielectric for modeling the reactive field outside the cut-off radius. In previous studies this value is set to the static dielectric constant of the material. To set this value one requires prior knowledge of the dielectric properties of the molecules or materials under study. Here, we propose an iterative approach using Eq. (1) (see Method) to obtain ε_RFwhich does not require any prior knowledge of the static dielectric constant.

The dielectric constant at infinite frequencies can be obtained from Eq. (3) (see Supplementary Materials) using the static polarizability and ε_RF. It has been shown that DFT is able to predict accurately the polarizability of molecules when using appropriate exchange correlation potentials and basis sets⁸,⁹,¹⁰. We obtained the mean polarizabilities from DFT calculation using VWN exchange-correlation functional (Local Vosko, Wilk and Nusair correlation) and auxiliary function density (A2 Auxis set). The accuracy of polarizability values obtained using VWN, which is based on local density approximations (LDA), is compared with generalized gradient approximations (GGA) methods implemented in deMon2k¹¹ (see Supplementary Materials, Fig. S1–S2). The error in polarizability values using LDA is within 10%, GGA within 17%, when compared to the experimental values. In subsequent analysis VWN exchange-correlation functional is used.

The mean polarizability of water, methanol and ethanol clusters increases linearly with cluster size. Figure 1 (a) shows the mean polarizability of ethanol clusters and Fig. 1 (b) shows the mean polarizability per ethanol molecule. The polarizability per molecule saturates with increasing cluster size. Thus, for larger numbers of molecular clusters, this method provides a convenient means of determining polarizability. The calculated dielectric constant at infinite frequency using this method is summarized in Table 1.

Figure 1. (a) The mean polarizability and (b) the polarizability per molecule of ethanol clusters.

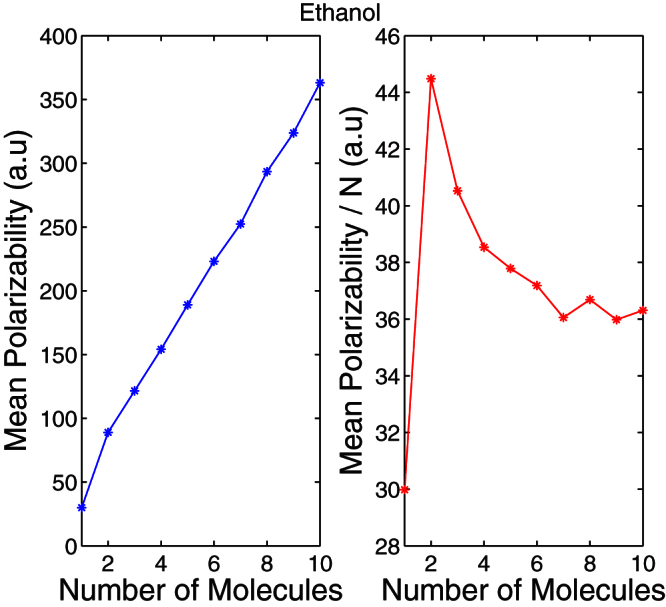
Table 1. The Debye model parameters of water, methanol and ethanol.

	Theoretical
	In this Study (T = 300 K)			Previous Studies (T = 298 K)			Experimental13 (T = 298 K)
Material	ε∞	ε0	τD(ps)	ε∞	ε0	τD (ps)	ε∞	ε0	τD (ps)
Water	1.37	81.2 ± 3	8.8 ± 0.6		66.7	6.17	4.9	78.4	8.23
Methanol	2.05	35.5 ± 1	48.3 ± 2.8		27.8	14.77	5.3	32.6	46.8
Ethanol	2.04	17.52 ± 0.5	148.4 ± 3.7	1	16	4912	3.9	23.7	145.1

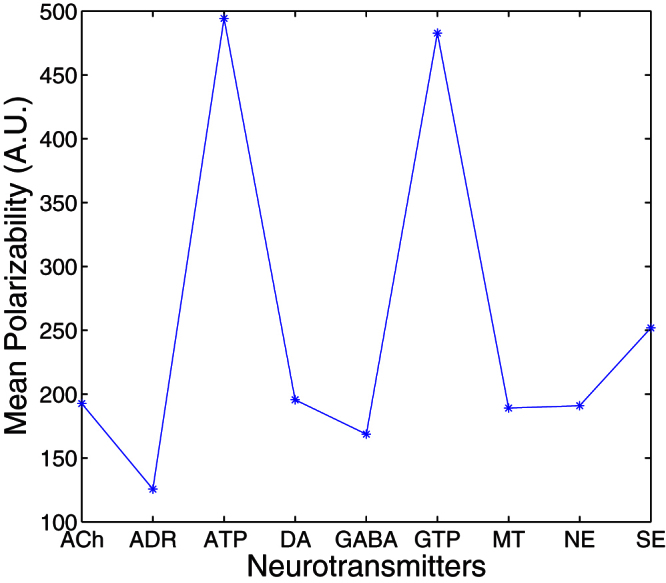
The polarizability of neurotransmitters (ACh - acetylcholine, ADR - adrenaline, ATP - adenosine triphosphate, DA - dopamine, GABA - γ aminobutyric acid, GTP - guanosine triphosphate, MT - melatonin, NE - norepinephrine, SE - serotonin) is shown in Fig. 2. As for water and alcohols, the polarizability of varying number of neurotransmitter and amino acid molecules can be determined to calculate the dielectric constant at infinite frequency. However, obtaining the polarizability of biomolecule-water mixtures is computationally expensive. Thus, in this study, the dielectric constant at infinite frequency of aqueous solutions of amino acids and neurotransmitters is assumed to be equal to that of water.

Figure 2. The mean polarizability of neurotransmitters (ACh - acetylcholine, ADR - adrenaline, ATP - adenosine triphosphate, DA - dopamine, GABA - γ aminobutyric acid, GTP - guanosine triphosphate, MT - melatonin, NE - norepinephrine, SE - serotonin).

The total dipole moment of the molecular clusters shown in Table 3 was obtained by the trajectories produced by the MD simulations (see Method). The static dielectric constant was calculated using the fluctuations in the total dipole moment [Eq. (2) (see Supplementary Materials)] and ε_RF. The normalized autocorrelation function of the total dipole moment was fitted to exp(−t/τ) to obtain the Debye relaxation time using Eq. (4) (see Supplementary Materials). The real and imaginary parts of the complex permittivity were obtained by fitting the dielectric constant at zero and infinite frequencies, and relaxation time to the Debye model. The permittivity of water, ethanol and methanol obtained from DFT and MD simulations were compared with the theoretical and experimental values presented in the literature and are shown in Table 1. Table 2 provides a comparison of the static dielectric constant and relaxation time constant of amino acids and neurotransmitters obtained in this study with the experimental values presented in the literature.

Table 2. The static dielectric constant and relaxation time constant of amino acids and neurotransmitters.

		Theoretical (T = 298 K)		Experimental (T = 298 K)
Material	In Zwitterion Form	ε0	τD(ps)	ε0	τD(ps)
Gly 1 M	NH3+- CH2- COO−	97.36 ± 3.7	20.81 ± 2.6	100.44	22.73
Ala 1 M	CH3- CH- NH3+- COO−	89.52 ± 2.5	33 ± 2.4	103.54	30.871
Glu 1 M	COOH - CH2 - CH2 - NH3+- COO−	105.5 ± 1.3	155.5 ± 6
Gaba 1 M	NH3+ - CH2 - CH2 - CH2- COO−	120.72 ± 1.7	126.55 ± 2.6	128	11714
Dopamine 1 M	C6H3(OH)(O−) - CH2 - CH2 - NH3+	102.7 ± 3.9	137.52 ± 5.2

Table 3. A summary of the molecular structures used for the simulations.

Material	Nmat (mol)	Nwat (mol)	L (Å)	Material	Nmat (mol)	Nwat (mol)	L (Å)
Water		240	20.8	Ala 1 M	4	208	19.09
Methanol	180		18.5	Glu 1 M	4	200	18.81
Ethanol	180		23.3	GABA 1 M	4	222	21.28
Gly 1 M	4	212	19.98	Dopamine 1 M	4	195	18.71

Discussion

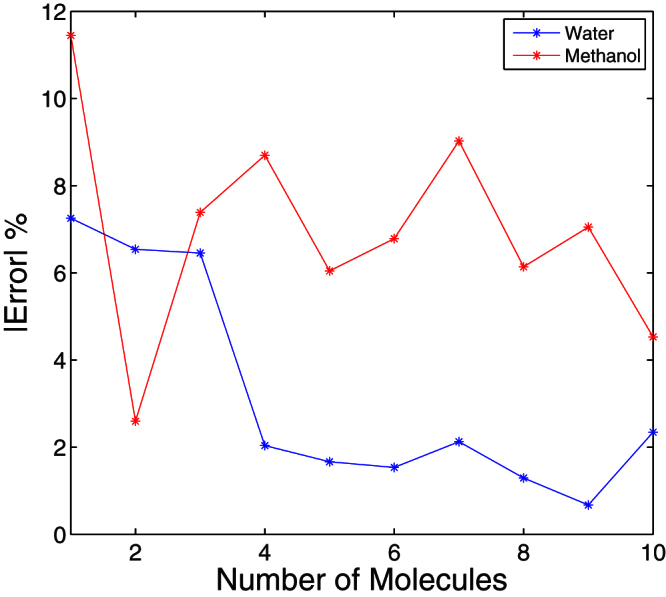
In this paper, we compared the accuracy of the predicted mean polarizabilities obtained using VWN exchange-correlation functional (Local Vosko, Wilk and Nusair correlation) and auxiliary function density (A2 Auxis set) with previously reported values in the literature. The polarizability of water clusters obtained using Hartree-Fock (HF) levels and 6-31++G(d,p) basis set in Ref. 8, and the polarizability of methanol clusters calculated using B3LYP/6-31++G(d,p) method in Ref. 9, correspond with the polarizabilities obtained in this study, confirming our methodology. Figure 3 shows the mean polarizability of water and methanol comparing our method with the results in Ref. 8 and Ref. 9. The calculated polarizabilities are within 10% error. We also determined the polarizability of amino acids and compared with the results available in the literature¹⁰. In Ref. 10, the polarizability was obtained using QZ4P ZORA basis set and LB94 exchange correlation potential. The values reported there agreed with the experimental values and our results are within 10% error of those reported in Ref. 10. In our results (Table 1), the dielectric constant at infinite frequency, as calculated using the polarizability of molecular clusters, deviates from experimental values. The accuracy however improves as the number of atoms in a molecule increases.

Figure 3. The error percentage in determining polarizability of water and methanol clusters.

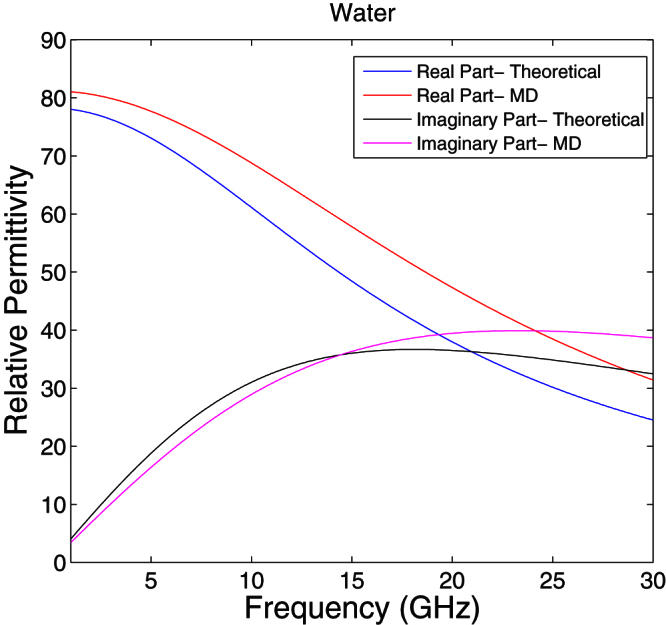
The total dipole moment, obtained from MD simulations, was used to estimate the static dielectric constants and relaxation time constants and these parameters of water, ethanol and methanol were compared with the experimental values as shown in Table 1. Our results compared favorably to experimental results in contrast to previously reported theoretical values. In Ref. 7, they have used applied field method and NPT (constant number of molecules, pressure and temperature) conditions for the simulations. The dielectric data of water obtained in Ref. 7 is comparable with the results presented in the literature using fluctuation method and NPT conditions. Although, the static dielectric constant of methanol obtained in Ref. 7 better matches experimental values compared to data presented in the literature using fluctuation method and NVT (constant number of molecules, volume and temperature) conditions, a disparity exists. In our simulations we used ε_RFobtained from Eq. (1), rather than the static permittivity of the materials that have been used in previous studies. The accuracy of permittivity values suggests that Eq. (1) is better suited for obtaining the dielectric constant of the continuum and does not require a prior knowledge of the material's static dielectric constant. Figure 4 shows the frequency dependent complex permittivity of water compared with the experimental results reported in the literature. This demonstrates that, even though there is an error in the estimation of the dielectric constant at infinite frequencies, the frequency dependent permittivity estimated from MD simulations agrees well with the experimental values.

Figure 4. The frequency dependent complex permittivity of water.

The dielectric properties of glycine 1 M (Gly 1 M), alanine 1 M (Ala 1 M) and gamma-aminobutyric acid (GABA 1 M) obtained using the method described in this paper compared favorably with experimental values in Table 2. The predominant form of amino acids in aqueous solution is the zwitterion that requires water molecules to stabilize it. The electrostatic interactions between these amino acid dipolar ions and water molecules are strong because the dipole moment of amino acid dipolar ion is much greater than that of ordinary polar molecules¹. This causes an increase in the dielectric constant of aqueous solutions of amino acid and neurotransmitters. The relaxation time constants of bio-molecular aqueous solutions increase relative to those of pure water. This indicates that the absorption peak of bio-molecular aqueous solutions has been shifted to a lower frequency. These larger values of relaxation times seems to indicate the formation of hydrogen bonds where water forms a hydration region with enhanced relaxation times around the solute¹.

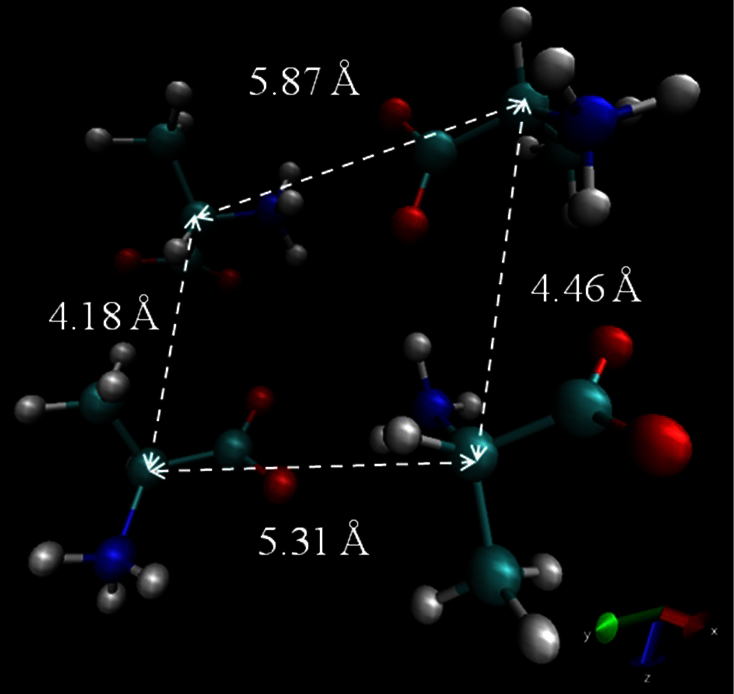
The dielectric properties of water, alcohols, amino acids, and neurotransmitters obtained from MD simulations agreed well with the values presented in the literature confirming our methodology. These properties provide information on biological materials and can be used to estimate parameters such as the concentration and structure of molecules. Further, this method can be used to analyze binary mixtures and mixture of many compounds. However, the dielectric properties obtained from MD simulations show the dependence on the orientation of the molecules and the distance between the molecules in addition to the cluster size. The Ala 1 M was created using 4 alanine molecules and when the molecules are oriented as in Fig. 5 (average root mean square distance per Ala residue = 0.33 Å) the static dielectric constant is 93 and the relaxation time is 30 ps whereas when the molecules are oriented as in Fig. 6 (average root mean square distance per Ala residue = 0.42 Å), the static dielectric constant is 102 and the relaxation time constant is 58.9 ps. The orientation of other bio-molecules in aqueous solution, that are studied in this paper, is shown in Supplementary Materials (Fig. S3–S7). Thus, using our method, we can verify the structure of the biological materials. In future work this method will be studied in cases where biological materials are under the influence of external electric fields.

Figure 5. The orientation of alanine molecules in alanine 1 M aqueous solution that result in ε₀ = 86, and τ_D = 29 ps.

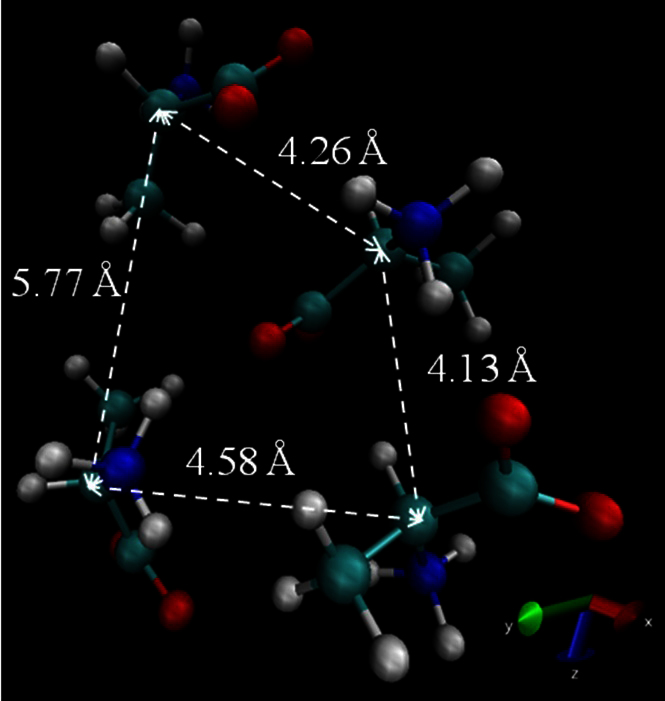
Figure 6. The orientation of alanine molecules in alanine 1 M aqueous solution that result in ε₀ = 102, and τ_D = 58.9 ps.

Methods

MD simulations to optimize the molecular structure

The molecular clusters were created using VEGA ZZ software¹⁵ and a summary of number of molecules in the clusters and the lengths of the cubic cells are presented in Table 3. The molecular structures of amino acids and neurotransmitters shown in Supplementary Materials (Fig. S3–S7) were used to create their aqueous solutions. The trajectories were generated using NAMD software¹⁶ and the simulations were performed using the standard CHARMM force fields. Periodic boundary conditions were used and the systems were simulated in NVT ensembles. The temperature was maintained at 300 K. The damping coefficient was 5 ps⁻¹ and the integration time was 1 fs. The maximum interaction cutoff was set as r_c = L/2 where the length of the cubic basic cell is L (see Table 3). In order to ensure continuity of Van der Waals and electrostatic interactions, a switching function was used. This was defined in NAMD by enabling the switching parameter with the switchdist parameter to cutoff (r_c) − 1 Å. In NAMD, the pairlist distance was set to √2L such that atoms do not move more than pailistdist - cutoff (r_c). This ensured energy conservation and efficiency. The dielectric constant in the simulation was set to the dielectric constant of the continuum (ε_RF) and it can be obtained as follows.

Computation of static dielectric constant of the continuum ε_RF

The sensitivity of static dielectric constant to ε_RFwas analyzed by obtaining ∂ε₀/∂ε_RFfrom Eq. (2) (see Supplementary Materials) as ∂ε₀/∂ε_RF = [8π(<M²> − <M>²)/3ε_ak_bTV(1 − ε_∞) − 2(4π(<M²> − <M>²)/3ε_ak_bTV)²]/[1 + 2ε_RF − 4π(<M²> − <M>²)/3ε_ak_bTV]² ∞ [(<M²> − <M>²) − (<M²> − <M>²)²]/[ε_RF − (<M²> − <M>²)]² where ε₀is the static dielectric constant, M is the total dipole moment, ε_∞is the dielectric constants at infinite frequencies, V is the volume of the system, k_bis the Boltzmann constant, T is the temperature in Kelvin and ε_ais the permittivity of vacuum. We obtained the variation in the total dipole moment of water using VMD software¹⁷ by varying ε_RF from 1 to 100. An equilibration simulation of 1 ps and subsequently, a 20 ps production run were performed at T = 300 K and V = 8990 ų. The total dipole moment was saved at every 10 fs. Although, the variation in total dipole moment (<M²> − <M>²) becomes a constant after a certain ε_RF (Fig. 7(a)), Fig. 7(b) (∂ε₀/∂ε_RFverses ε_RF) shows that the calculated static dielectric constant of water using Eq. (2) is sensitive to dielectric constant of the continuum (ε_RF). Thus, it is important to estimate the external dielectric constant of the continuum ε_RF accurately. In many of the previous studies ε_RFis taken as the static dielectric constant of the material which require a prior knowledge of the material's static permittivity. Here, we proposed an approach to obtain the dielectric constant of the continuum.

Figure 7.

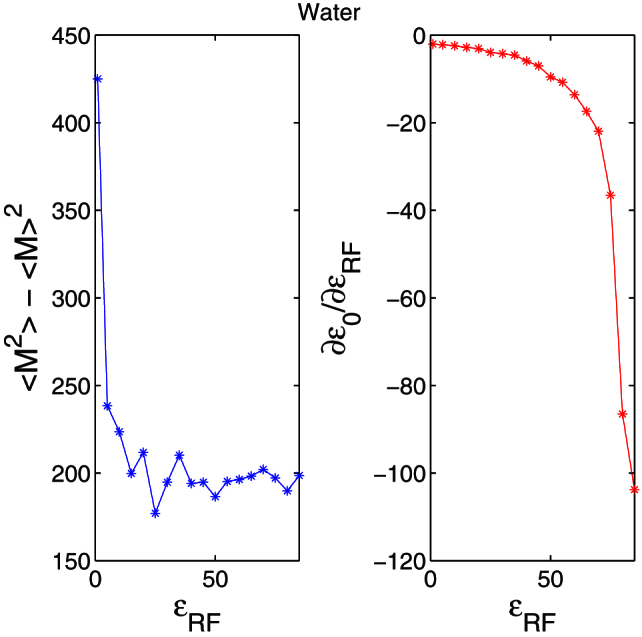
(a) The variation of the total dipole moment of water with ε_RF.(b) The sensitivity of static dielectric constant to dielectric constant of the continuum, ∂ε₀/∂ε_RF.

The dielectric constant in the reaction field ε_RF was set to 1, 50, 100 and the simulations were separately performed for each ε_RF. An equilibration simulation of 1 ps and subsequently, a 20 ps production run was performed for each ε_RFby applying harmonic constraints. Then the static dielectric constant of the continuum was calculated from,

MD simulations to obtain static dielectric constant ε₀ and relaxation time constant τ_d of the molecular Clusters

The molecular clusters were minimized for 100 ps and subsequently, a 1 ns production run was performed. The dielectric constant of the simulation was set to ε_RFand harmonic constraints were applied. The occupancy column of the PDB file was used for the harmonic constraint force constant and this column was set to 1. The root mean square distance (RMSD) and radial distribution function (RDF) were analyzed using VMD. We observed from RMSD that the final 900 ps simulation of the 1 ns production run was equilibrated. The RDF of each residue in the cluster with water shows that the clusters have highly symmetric structures. The total dipole moment of the systems was obtained using VMD software. The equilibrium properties were averaged over 45 blocks of 20 ps, for a total of 900 ps to obtain the static dielectric constant and the relaxation time from Eq. (2) and Eq. (4) (see Supplementary Materials). Each simulation was repeated many times (5) and the mean and standard deviation of the dielectric properties were computed.

DFT to obtain ε_∞

The molecular clusters (1 to 10 number of molecules) were obtained using VEGA ZZ and the geometries were optimized using DFT (deMon2k¹¹). The DFT calculations were performed using Restricted Kohn Sham (RKS) Self -Consistent Field (SCF) method which is applicable for closed shell systems. The static polarizability of molecules were obtained using VWN exchange-correlation functional and auxiliary function density (A2 Auxis set) for the calculation of the exchange-correlation energy and matrix elements of the exchange-correlation potential. The polarizability tensor was calculated numerically with a finite field method where the applied field strength was set to 0.01 a.u. Since performing DFT for a large number of molecules is computationally expensive we obtained the polarizability of 1 to 10 number of molecules and observed the variation of polarizability per molecule by dividing the mean polarizability from the number of molecules in the cluster. Since after some number of molecules in the cluster the polarizability per molecule saturates, the polarizability of a larger molecular clusters can be obtained straightforwardly. Using the polarizability values in Eq. (3) (see Supplementary Materials), the dielectric constant at infinite frequency can be obtained. However, this method is not applicable for mixtures.

Author Contributions

C.D.A. and E.S. wrote the main manuscript text. M.N.H. and P.M.F. helped to prepare the figures and proofread the manuscript. All authors reviewed the manuscript.

Supplementary Material

Supplementary Information

An ab-initio Computational Method to Determine Dielectric Properties of Biological Materials