Abstract
Optical frequency combs have become an essential tool for distance metrology, showing great advantages compared with traditional laser interferometry. However, there is not yet an appropriate method for air refractive index correction to ensure the high performance of such techniques when they are applied in air. In this study, we developed a novel heterodyne interferometry technique based on two-colour frequency combs for air refractive index correction. In continuous 500-second tests, a stability of 1.0 × 10−11 was achieved in the measurement of the difference in the optical distance between two wavelengths. Furthermore, the measurement results and the calculations are in nearly perfect agreement, with a standard deviation of 3.8 × 10−11 throughout the 10-hour period. The final two-colour correction of the refractive index of air over a path length of 61 m was demonstrated to exhibit an uncertainty better than 1.4 × 10−8, which is the best result ever reported without precise knowledge of environmental parameters.
An optical frequency comb emits an evenly spaced ultra-short pulse train with a broad spectrum consisting of discrete, uniform mode-spacing narrow lines. When its mode frequencies are referenced to a frequency standard, the optical frequency comb becomes an ultra-stable ruler in the space, time and frequency domains1. Due to such inherent advantages, optical frequency combs have enabled revolutionary progress in distance metrology2. Since the first demonstration conducted by Minoshima et al.3, many important advances have been made in distance metrology using frequency combs4,5,6,7,8,9,10,11, such as large dynamic range measurements of absolute distance (from zero to kilometers) with high precision or resolution (nanometer-level) at high speed (kilohertz-level)9,10. Such performances, which are inaccessible to traditional laser interferometry, are promising for ultra-precision engineering, light detection and ranging (LIDAR), geodetic surveying and so on. However, as mentioned by Newbury12, when such state-of-the-art techniques are applied in air, there is still a limitation, indeed the only limitation, of measurement accuracy caused by the uncertainty in the refractive index of air. Consequently, it is absolutely essential that a high-accuracy correction method for air refractive index be developed to overcome such a limitation, allowing for real breakthroughs to be made in practical distance metrology measurement.
Conventionally, empirical equations13,14 are used for air refractive index corrections based on the knowledge of environmental parameters such as air temperature, pressure, humidity and CO2 concentration. The accuracy of these empirical equations is in the order of 10−8, which represents the best performance for distance measurements performed in air. However, the accuracy with which the refractive index of air is corrected is sensitive to the accuracy with which environmental parameters are measured. Normally, air temperature and pressure are the most critical parameters, e.g., either an uncertainty of 0.1 K in air temperature or 0.4 hPa in air pressure will cause an uncertainty of 1 × 10−7 in the refractive index of air. Unfortunately, due to air turbulence or the non-uniformity of environmental conditions, it is very difficult to obtain an accurate distribution of these parameters along real optical paths in distance measurements, especially in the case of long-distance measurements.
Alternatively, the two-colour method proposed by Bender and Owens15,16 can realize air refractive index correction without precise knowledge of environmental parameters3,17,18,19,20,21. The basic principle of the method is to employ lights with two different wavelengths to measure the same geometrical distance D and thus obtain two optical distances D1 and D2. The geometrical distance D obtained after correcting the refractive index of air can be given by
where A is a coefficient regarded as a constant when the two wavelengths are fixed20. Therefore, air refractive index correction is realized only by considering the results of optical measurement. However, applying the two-colour method to high-accuracy measurements has the following fundamental drawback. Normally, A is very large, e.g., A≈141, for wavelengths of 1560 and 780 nm, and the uncertainty in D2 − D1 will be magnified by A times, thereby decreasing the accuracy of D. In other words, if we expect the same level of correction accuracy offered by the empirical equations, the accuracy of measurements of D2 − D1 must reach the 10−11 regime. Therefore, the main challenge of the two-colour method is determining how to measure D2 − D1 with extremely high accuracy. Such a severe requirement may be potentially fulfilled by making full use of the extremely high accuracy offered by frequency comb technology.
We have previously reported on the setup for homodyne20 and heterodyne21 interferometry using optical frequency combs for the two-colour correction of the refractive index of air. However, the demonstrated distances are short and the accuracy is not sufficiently high relative to the potential of the technique. Here, we introduce a novel heterodyne interferometry technique that fully utilizes the ultra-stability of frequency combs for air refractive index correction. The interferometers were adaptively designed so that inherent noises and drift are compensated for nearly perfectly. Finally, we obtained the best results for air refractive index correction without precise knowledge of environmental parameters ever reported, which nearly match the uncertainty of the empirical equations. Such a breakthrough can allow for the best performance of any well-established distance metrology tool in air, as well as of the metrology of the refractive index of air itself.
Results
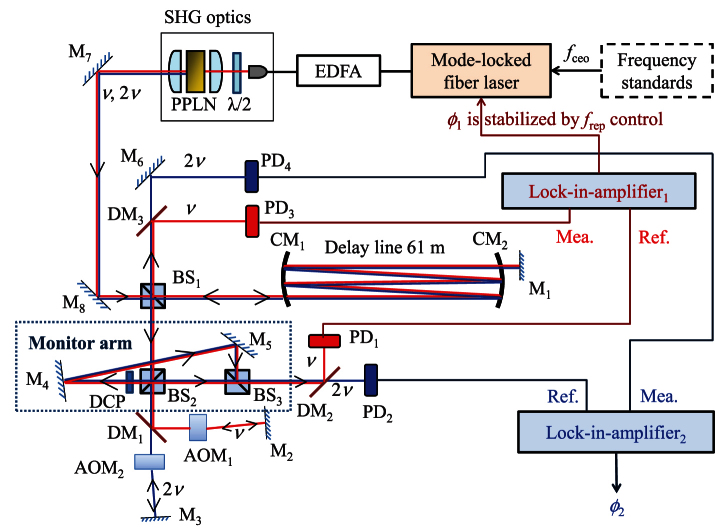
A home-made mode-locked Er:fiber ring laser, the same employed in previous studies20,21, was used as the frequency comb source (Fig. 1). The carrier-envelope-offset frequency (fceo) of the laser was stabilized and referenced to a hydrogen maser. The repetition frequency (frep) of the comb is variable near 54.0 MHz, and the corresponding optical distance between adjacent pulses is Dp-p = 5.55 m. The output of the fiber comb is amplified by an Er-doped fiber amplifier (EDFA) and is then introduced into a piece of a periodically poled LiNbO3 (PPLN) crystal for second harmonic (SH) generation. Consequently, the unconverted fundamental (ν) and the SH (2ν) are coaxially introduced into an unbalanced long-path interferometer (Fig. 1). The transmitted beams from the beam splitter (BS1) are introduced into a probe arm consisting of an optical delay line and a mirror (M1). The delay line is a folded-path setup consisting of two concave mirrors (CM1 and CM2), each of which has a small hole in it. The incident beams pass through the hole in CM1, are reflected 34 times between CM1 and CM2 and then leave the delay line through the hole in CM2. The emergent beams are reflected back along the same path by M1, then enter the delay line again and finally travel through the hole in CM1 to go back to BS1. The total path length of the probe arm is more than 61 m.
Figure 1. Schematic of experimental setup.
BS1–3: Beam splitter; DM1–3: Dichroic mirror; M1–8: Mirror; PD1–4: Photodetector; DCP: Dispersion compensation plate. SHG: Second harmonic generation.
The beams reflected by BS1 are divided by another beam splitter (BS2) into two parts: the transmitted beams from BS2 are introduced to the reference arm; the reflected beams from BS2 are introduced into the monitor arm. In the reference arm, the fundamental and SH are separated by a dichroic mirror (DM1) and then diffracted by two acousto-optic modulators (AOM1 and AOM2, respectively). The two diffracted beams are reflected back along the same paths by two mirrors (M2 and M3) and diffracted by the two AOMs again. The beams overlap at DM1 and are both divided by BS2 into two parts: the reflected beams overlap with the beams from the monitor arm (reflected by two mirrors M4 and M5) at BS3, and the interference signals for the fundamental and SH are separated by DM2 and detected by two photodetectors (PD1 and PD2, respectively); the transmitted beams overlap with the beams from the probe arm, and the interference signals for the fundamental and SH are separated by DM3 and detected by another two photodetectors (PD3 and PD4, respectively).
The path-length difference between the probe arm and the reference arm is preset to 11 times Dp-p, i.e., 61.1 m. The path lengths of the reference arm and monitor arm are set to make the pulse-to-pulse interferences between the reference arm and probe arm and those between the reference arm and monitor arm occur simultaneously (refer to “methods” section for details). The driven signals for AOM1 and AOM2 are 160 MHz and 80 MHz, respectively, such that the frequency shifts generated by the two AOMs (diffracted twice) for the fundamental and SH are 320 MHz and 160 MHz, respectively. Considering that the mode interval of the frequency comb is 54 MHz, it is easy to use low-pass-filters to obtain heterodyne signals of 4 MHz for the fundamental and 2 MHz for the SH (refer to “methods” section for details). The phases of the heterodyne interference signals detected by PD1 and PD2 reflect the optical path-length differences between the probe arm and reference arm at the two wavelengths. Normally, these differences can be treated as the final target optical distances (D1, D2). However, the fundamental and SH do not share a common path in the reference arm; thus, air fluctuations and the mechanical drift of the mirrors in the reference arms will cause noise and drift in the measurement of D2 − D1. Moreover, the thermal expansions of the two AOMs will cause different optical path-length changes and phase drift in their diffracted beams, which will impact the stability of D2 − D1 significantly. Here the setup was adaptively designed to utilize the monitor arm to resolve the problem. The signals from PD1 and PD2 are sent to the reference ports of the two lock-in amplifiers (SR844, Stanford Research Systems Inc.), whereas the signals from PD3 and PD4 are sent to the measurement ports. Consequently, the phase output (φ1 and φ2) is irrelevant to the optical path-length change in the reference arm such that the phase noise and drift caused by introducing separate reference paths consisting of two AOMs are compensated for.
The optical path length measured is long in the current system, causing the interferometric phase to change easily over several cycles when the refractive index of air changes. To avoid the ambiguity of phase unwrapping, the interferometric phase of the fundamental (φ1) was stabilized to zero by the feedback control of the repetition frequency of the comb such that the detected SH interferometric phase (φ2) reflects only the optical path-length difference between the fundamental and SH wavelengths, i.e., D2 − D1 (refer to “methods” section for details). This configuration cancels out the common noises between two-colour signals; therefore, extremely high measurement stability is achieved. Moreover, an extremely high measurement accuracy that is only sensitive to the difference between two-colour signals is realized. It should be noted that such phase stabilization achieved using feedback was not possible in the previous system using a shutter-based monitor interferometer21.
Short-term stability
To evaluate the accuracy of the method, we first tested the short-term performance of the system in the measurement of D2 − D1. Considering that in a short period the dispersion effect on changes in the refractive index of air is negligible, we can compare the results of D2 − D1 with a constant to evaluate the system's accuracy. The fundamental and SH interferometric phases were recorded continuously for 500 s. The optical path-length variation corresponding to the fundamental interferometric phase (φ1) was stabilized to zero with a standard deviation of 0.8 nm (Fig. 2a), which shows that such stabilization is effective. The optical path-length variation corresponding to the SH interferometric phase (φ2) was also constant (Fig. 2b). As mentioned above, the SH interferometric phase reflects D2 − D1, and the corresponding path-length variation shows a standard deviation of 1.0 nm over a period of 500 s. Furthermore, to cancel out the residual noise due to imperfect stabilization, we still used the difference between the optical path lengths corresponding to φ2 and φ1 as the final D2 − D1. The variation was observed to constant with a standard deviation of 0.6 nm (Fig. 2c), which represents 1.0 × 10−11 of the measured path length of 61.1 m. Such accuracy is one order of magnitude higher than that reported in our previous studies20,21, which indicates that our adaptively designed system combined with interferometric phase stabilization functions well in improving the measurement accuracy. As mentioned above, the extremely high accuracy achieved in the measurement of D2 − D1 is essential for the high-accuracy correction of the refractive index of air by the two-colour method.
Figure 2. Short-term interferometric measurements of two-colour frequency combs.
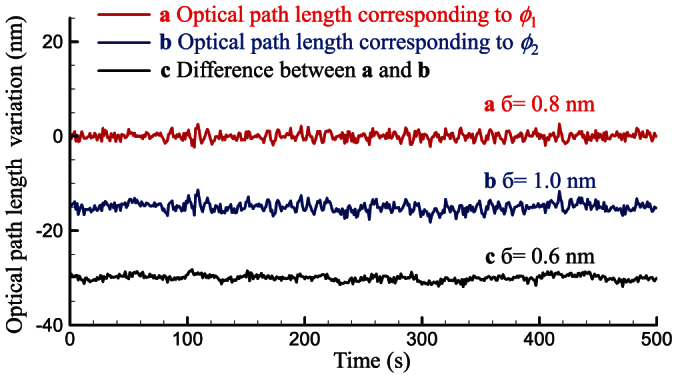
The vertical origins of plots (b) and (c) are shifted to −15 nm and −30 nm, respectively, for clarity.
Long-term performance in two-colour correction of refractive index of air
To further evaluate the current method, long-term continuous measurements were carried out for air refractive index correction. According to equation (1), the relative variation in the distance after refractive index correction ΔD/D can be given by:
where the small second-order term is neglected. To test the efficacy of the method, we performed a distance measurement using a stationary target and investigated the level of stability in the value of ΔD/D obtained by equation (2). In this test, the concave mirrors (CM1 and CM2) of the delay line were placed on a low-thermal-expansion board (the coefficient of thermal expansion of the board was 1.3 × 10−6), and the interferometer setup was placed in a thermally isolated box in a temperature-controlled room. Consequently, the geometric distance D was held constant. Furthermore, the environmental parameters could be recorded with high accuracy such that the results obtained from the well-established refractive index equation could be used to evaluate the results of phase measurements using the current system, e.g., D2 − D1. Moreover, in the case of perfect correction, the corrected distance D should be constant, i.e., ΔD should be zero. Hence, the accuracy of the final air refractive index correction can be evaluated without using an empirical equation because the stability of ΔD/D will reflect the accuracy of the current method.
Long-term evaluation was accomplished in two steps. First, the relative variations in D2 − D1, i.e., Δ(D2 − D1)/D, which are equal to the variations in the difference between the two-colour refractive indices of air Δ(n2 − n1), were compared with the results obtained from Ciddor's equation14 to evaluate the accuracy of the long-term measurement of D2 − D1. Figure 3 shows the results of continuous 10-hour measurements. The variations in D2 − D1 were obtained according to the interferometric phases φ1 and φ2, and the corresponding variations in n2 − n1 were determined by assuming that the geometrical distance D remained constant (Fig. 3a). The results indicate that the variations in n2 − n1 were of the order 10−8 over 10 hours. The environmental parameters were recorded during the measurements, so that n2 − n1 could also be calculated using Ciddor's equation (Fig. 3b). The measurement and calculation results were nearly in perfect agreement throughout the 10-hour period, and their difference remained constant with a standard deviation of 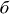 = 3.8 × 10−11 (Fig. 3c). Compared with our previous results20,21, the long-term accuracy was also improved by one order of magnitude. Such high-consistency results demonstrate that the developed technique can realize extremely precise measurements of D2 − D1, which is the key point of the high-accuracy two-colour method.
= 3.8 × 10−11 (Fig. 3c). Compared with our previous results20,21, the long-term accuracy was also improved by one order of magnitude. Such high-consistency results demonstrate that the developed technique can realize extremely precise measurements of D2 − D1, which is the key point of the high-accuracy two-colour method.
Figure 3. Long-term variations in the difference between the two-colour refractive indices of air (n2 − n1).
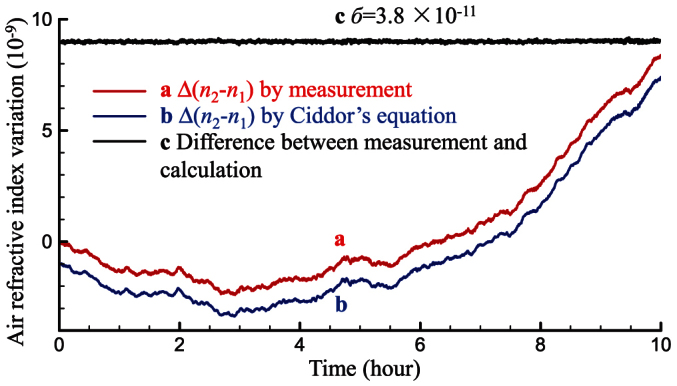
(a) Obtained by the measured D2 − D1. (b) Calculated using Ciddor's equation with environmental parameters. (c) Their difference. The vertical origins of plots b and c are shifted to −1 and 9, respectively, for clarity.
In the second step of the evaluation, the refractive index of air was corrected according to equation (2) to obtain ΔD/D. During the long-term measurement, the variation in A was small with a standard deviation of ΔA = 0.0012, and (D2 − D1)/D was smaller than 1.9 × 10−6. Consequently, the third term on the right-hand side of equation (2) was smaller than 2.3 × 10−9, which is negligible compared with the final value obtained for ΔD/D. Therefore, equation (2) can be modified as follows:
The final correction of the refractive index of air was performed according to equation (3). Because the fundamental interferometric phase is stabilized, the variation in D1 can be calculated as follows:
where c is the speed of light in vacuum. During our long-term experiment, frep was measured continuously by a frequency counter (Agilent 53132A) referenced to a hydrogen maser so that a precise measurement of ΔD1 could be obtained. The relative variation in the measurement ΔD1/D is shown in Fig. 4a. The difference between the measured ΔD1/D and the variation in the refractive index Δn1, which was calculated using environmental parameters by assuming constant D is 1.4 × 10−8. The coefficient A can be easily calculated to be A = 140.49, and the results of A· Δ(D2 − D1)/D are shown in Fig. 4b. The corrected distance is shown in Fig. 4c, which is shown to be constant with a standard deviation of б = 1.4 × 10−8, whereas the relative change in the optical distance itself was nearly 1.5 × 10−6 over the same period, mainly due to changes in air pressure (Fig. 4a).
Figure 4. Correction of the refractive index of air by two-colour method.
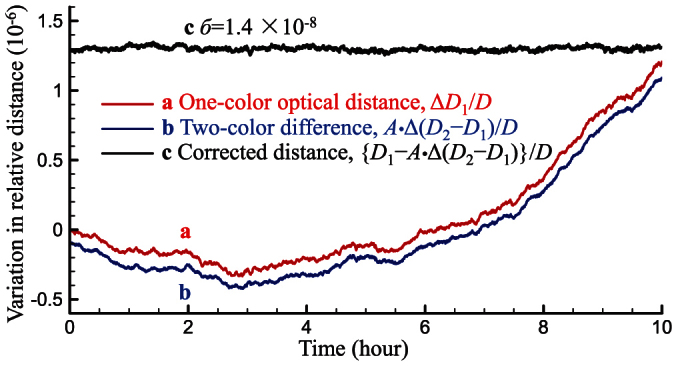
(a), The relative variations in the optical distance of the fundamental. (b) The relative variations in the difference between the optical distances corresponding to two colours with a zoom factor A. (c) The relative variation in the geometrical distance. The vertical origins of plots (b) and (c) are shifted to −0.1 and 1.3, respectively, for clarity.
Discussion
In two-colour methods, refractive index correction is described by the second term of equation (1), A(D2 − D1)/D. In this study, the standard uncertainty in the measurement of Δ(D2 − D1)/D was on the order of 10−11. Even when hampered by factor A, the uncertainty was still of the order 10−9. Thus, our two-colour method can potentially realize a 10−9 level correction of the refractive index of air, which is better than that achieved by the empirical equations. However, it is necessary to note that geometric distance D is not ideally constant during long-term measurement. The change in the geometric distance is detected as ΔD1/D, i.e., ΔD/D, because it is the real physical value being measured. Therefore, in the current case, the accuracy of correction is underestimated (i.e., uncertainty is overestimated) to be 1.4 × 10−8, mainly due to the real instability in the distance D. This discussion is supported by the fact that the difference between the measured ΔD1/D and calculated refractive index variation Δn1 is also 1.4 × 10−8. Although a low-thermal-expansion board was used for the delay line, a temperature change of 0.01 K could cause the total path length to change by a factor of 10−8. Moreover, the deformation of the holders of the concave mirrors in the delay line also affects the variation in D. Therefore, a better evaluation method, e.g., one using better experimental conditions, is necessary to evaluate the real accuracy of the current method. Nevertheless, data with a proven accuracy better than 1.4 × 10−8 still represent the best results obtained without precise knowledge of environmental parameters.
It is also necessary to note that mechanical vibration was not a severe factor in the present experiment. As discussed in our previous report21, when ΔD/D is smaller than 10−5, the uncertainty in the measurement of Δ(D2 − D1)/D is negligible. Therefore, the impact of mechanical vibration on the measurement of D2 − D1 (the key factor in the two-colour method) is normally negligible. In the measurement of D1, the impact of mechanical vibration was canceled out to a great extent by using a lock-in amplifier for the interferometric phase measurement. Therefore, we only placed the experimental setup on an air-floating optical table, and no additional vibration control was required.
In conclusion, we have developed a novel heterodyne interferometry based on two-colour frequency combs for air refractive index correction. Benefitting from the adaptive design of interferometers and consequent interferometric phase stabilization using frequency comb lines, extremely high-accuracy measurement of optical path lengths was realized. Finally, we achieved extremely high-accuracy corrections of the refractive index of air, potentially on the scale of 10−9. The current method is a powerful tool not only for air refractive index correction in distance metrology but also for the metrology of the refractive index of air itself, e.g., for the evaluation and improvement of the corresponding empirical equations.
Methods
Path-length setting for reference and monitor arms
The path-length difference between the probe arm and the reference arm was preset to 11 times Dp-p, i.e., 61.1 m. Considering that the optical path lengths for the fundamental and SH in the probe arm show minor differences due to the dispersion effects of the optics and air, the same differences were set between the optical path lengths for the fundamental and SH in the reference arms. Meanwhile, a dispersion compensation plate (DCP) was used in the monitor arm to make the dispersion in the arm the same as that in the probe arm, and the optical path length of the monitor arm was set equal to that of the reference arm. Consequently, pulse-to-pulse interferences between the reference arm and probe arm and also between the reference arm and monitor arm could occur simultaneously.
Heterodyne signal generation
The frequency shifts generated by the two AOMs for the fundamental and SH (marked as fΔ1 and fΔ2) were 320 MHz and 160 MHz, respectively. In the fundamental frequency domain, the kth mode of the comb in the reference arm can be expressed by
The kth mode of the comb in the probe arm and monitor arm can be expressed by
Therefore, when the reference beam meets the probe or monitor beam, the frequency of the beat signal for the fundamental can be expressed by N · frep − fΔ1 = (N ·54 − 320) MHz (N is an integer). The lowest-frequency beat signal (6frep − fΔ1 = 4 MHz), which is the beat of fref.(k) and fprobe, monit.(k + 6), is selected by a low-pass-filter as the heterodyne signal for the fundamental. Likewise, the heterodyne signal for the second harmonics expressed by 3frep − fΔ2 = 2 MHz is obtained.
Stabilization of the fundamental interferometric phase
The fundamental interferometric phase was stabilized to zero by the feedback control of the repetition frequency of the comb such that changes in the optical path length were canceled out. Such stabilization was achieved as follows. The analog output of lock-in amplifier1 (proportional to phase output φ1) was stabilized to a zero voltage by a proportional–integral–derivative controller (PID controller, SIM960, Stanford Research Systems). The error signal was applied to the PZT-driven fiber stretcher in the laser oscillator. The servo bandwidth was limited by the response time of the PZT driver, which is on the order of kHz. Simultaneously, the interferometric phase of SH φ2 was measured by lock-in amplifier2. All of the wavelengths of the comb modes in air, which are the products of the wavelengths in vacuum and the refractive indices of air, were stabilized accordingly if the dispersion of the air refractive index was negligible7. In other words, if an interference signal change is observed at the other wavelength, it is due to dispersion; therefore, we can precisely measure only the difference between the refractive indices of air corresponding to the two colours. In our experiment, because the variation in the fundamental interferometric phase caused by the changes in the optical path length at the fundamental wavelength was canceled by feedback, the detected SH interferometric phase reflected only the optical path-length difference between the fundamental and SH wavelengths, i.e., D2 − D1.
Author Contributions
K.M. designed and supervised the study; G.W. and K.M. designed the experimental setup; K.A., H.I. and K.M. designed and constructed the two-colour comb source; G.W., M.T. and K.M. constructed the setup, performed experiments and collected and analyzed data; G.W. and K.M. interpreted the data and wrote the paper.
Acknowledgments
This work was supported by the System Development Program for Advanced Measurement and Analysis (Program-S), Development of Systems and Technology for Advanced Measurement and Analysis, Japan Science and Technology Agency (JST). We also thank support by Grants-in-Aid for Scientific Research No. 25286076 from the Ministry of Education, Culture, Sports, Science, and Technology of Japan. The support from the Special-funded Program on National Key Scientific Instruments and Equipment Development of China (2011YQ120022) and Tsinghua University Initiative Scientific Research Program (2011Z02166) are also acknowledged.
References
- Cundiff S. T. & Ye J. Colloquium: Femtosecond optical frequency combs. Rev. Mod. Phys. 75, 325–342 (2003). [Google Scholar]
- Kim S.-W. Combs rule. Nature Photon. 3, 313–314 (2009). [Google Scholar]
- Minoshima K. & Matsumoto H. High-accuracy measurement of 240-m distance in an optical tunnel by use of a compact femtosecond laser. Appl. Opt. 39, 5512–5517 (2000). [DOI] [PubMed] [Google Scholar]
- Ye J. Absolute measurement of long, arbitrary distance to less than an optical fringe. Opt. Lett. 29, 1153–1155 (2004). [DOI] [PubMed] [Google Scholar]
- Schuhler N., Salvade Y., Leveque S., Dandliker R. & Holzwarth R. Frequency-comb- referenced two-wavelength source for absolute distance measurement. Opt. Lett. 31, 3101–3103 (2006). [DOI] [PubMed] [Google Scholar]
- Joo K.-N. & Kim S.-W. Absolute distance measurement by dispersive interferometry using a femotsecond pulse laser. Opt. Express 14, 5954–5960 (2006). [DOI] [PubMed] [Google Scholar]
- Schibli T. R. et al. Displacement metrology with sub-pm resolution in air based on a fs-comb wavelength synthesizer. Opt. Express 14, 5984–5993 (2006). [DOI] [PubMed] [Google Scholar]
- Cui M. et al. High-accuracy long-distance measurements in air with a frequency comb laser. Opt. Lett. 34, 1982–1984 (2009). [DOI] [PubMed] [Google Scholar]
- Coddington I., Swann W. C., Nenadovic L. & Newbury N. R. Rapid and precise absolute distance measurements at long range. Nature Photon. 3, 351–356 (2009). [Google Scholar]
- Lee J., Kim Y.-J., Lee K., Lee S. & Kim S.-W. Time-of-flight measurement with femtosecond light pulses. Nature Photon. 4, 716–720 (2010). [Google Scholar]
- Van den Berg S. A., Persijn S. T. & Kok G. J. P. Many-wavelength interferometry with thousands of lasers for absolute distance measurement. Phys. Rev. Lett. 108, 183901 (2012). [DOI] [PubMed] [Google Scholar]
- Newbury N. R. Searching for applications with a fine-tooth comb. Nature Photon. 5, 186–188 (2011). [Google Scholar]
- Boensch G. & Potulski E. Measurement of the refractive index of air and comparison with modified Edlén's formulae. Metrologia 35, 133–139 (1998). [Google Scholar]
- Ciddor P. E. Refractive index of air: new equations for the visible and near infrared. Appl. Opt. 35, 1566–1573 (1996). [DOI] [PubMed] [Google Scholar]
- Bender P. L. & Owens J. C. Correction of optical distance measurements for the fluctuating atmospheric index of refraction J. Geophys. Res. 70, 2461–2462 (1965). [Google Scholar]
- Owens J. C. The use of atmospheric dispersion in optical distance measurement. Bull. Geod. 89, 277–291 (1968). [Google Scholar]
- Matsumoto H. & Honda T. High-accuracy length-measuring interferometer using the two-colour method of compensating for the refractive index of air. Meas. Sci. Technol. 3, 1084–1086 (1992). [Google Scholar]
- Zeng L., Seta K., Matsumoto H. & Iwashaki S. Length measurement by a two-colour interferometer using two close wavelengths to reduce errors caused by air turbulence. Meas. Sci. Technol. 10, 587–591 (1999). [Google Scholar]
- Meiners-Hagen K. & Abou-Zeid A. Refractive index determination in length measurement by two-colour interferometry. Meas. Sci. Technol. 19, 084004 (2008). [Google Scholar]
- Minoshima K., Arai K. & Inaba H. High-accuracy self-correction of refractive index of air using two-color interferometry of optical frequency combs. Opt. Express 19, 26095–26105 (2011). [DOI] [PubMed] [Google Scholar]
- Wu G., Arai K., Takahashi M., Inaba H. & Minoshima K. High-accuracy correction of air refractive index by using two-color heterodyne interferometry of optical frequency combs. Meas. Sci. Technol. 24, 015203 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]