Comparison of Ultrasound Attenuation and Backscatter Estimates in Layered Tissue-Mimicking Phantoms among Three Clinical Scanners

Abstract

Backscatter and attenuation coefficient estimates are needed in many quantitative ultrasound strategies. In clinical applications, these parameters may not be easily obtained because of variations in scattering by tissues overlying a region of interest (ROI). The goal of this study is to assess the accuracy of backscatter and attenuation estimates for regions distal to nonuniform layers of tissue-mimicking materials. In addition, this work compares results of these estimates for “layered” phantoms scanned using different clinical ultrasound machines. Two tissue-mimicking phantoms were constructed, each exhibiting depth-dependent variations in attenuation or backscatter. The phantoms were scanned with three ultrasound imaging systems, acquiring radio frequency echo data for offline analysis. The attenuation coefficient and the backscatter coefficient (BSC) for sections of the phantoms were estimated using the reference phantom method. Properties of each layer were also measured with laboratory techniques on test samples manufactured during the construction of the phantom. Estimates of the attenuation coefficient versus frequency slope, α0, using backscatter data from the different systems agreed to within 0.24 dB/cm-MHz. Bias in the α0 estimates varied with the location of the ROI. BSC estimates for phantom sections whose locations ranged from 0 to 7 cm from the transducer agreed among the different systems and with theoretical predictions, with a mean bias error of 1.01 dB over the used bandwidths. This study demonstrates that attenuation and BSCs can be accurately estimated in layered inhomogeneous media using pulse-echo data from clinical imaging systems.

Introduction

Attenuation and scattering are important properties of tissue that contribute to diagnostic information in medical ultrasound. In conventional gray-scale imaging, these tissue characteristics are gleaned from variations in image brightness. However, signals displayed on clinical ultrasound systems also depend on operator settings and system-dependent factors, so that attenuation and scattering can only be assessed in a qualitative fashion. In contrast, quantitative ultrasound (QUS) methods are being developed that display properties of tissue on an absolute scale.

Earlier QUS work has demonstrated potential for characterizing diffuse disease and for diagnosing focal lesions. For example, ultrasound attenuation was used to differentiate fatty liver from normal liver,^1,2 characterize bones,^3,4 and assess breast masses of different pathology.^5-7 Spectral analysis of backscattered echo signals has been used to differentiate benign from malignant masses in the eyes⁸ and lymph nodes,^9,10 and to assess thyroid nodules¹¹ and liver masses.¹² Glomerular and arteriole sizes in kidneys were successfully estimated from backscattered echo data using a scatterer size estimator, resulting in the potential to detect renal transplant rejection and monitor glomerular hypertrophy.¹³ Furthermore, effective scatter size estimates from backscattered echo signals clearly differentiated rat mammary fibroadenomas from 4T1 mouse carcinomas.¹⁴

For QUS to translate into clinical practice, the accuracy and system independence of attenuation and backscatter coefficient (BSC) estimates need to be demonstrated on clinical imaging devices. These factors have been partially addressed in a number of laboratory intercomparison studies.^15-18 Most of these investigations applied apparatus with single-element transducers, obtaining measurements of scattering and attenuation properties of well-characterized tissue-mimicking materials. Madsen et al.¹⁵ and Wear et al.¹⁶ included results from one modified clinical ultrasound system in their eight-laboratory intercomparison studies.

More recently, it has been shown that the attenuation and BSC of samples can be estimated using echo data acquired from clinical imaging systems that are supplied with research interfaces.^19-21 To do so, however, factors such as the frequency-dependent sensitivity of the transducer, beam-focusing patterns, and time-gain compensation (TGC) must be accounted for during the data analysis. A reference phantom method (RPM)²² is a straightforward way to account for these system-dependent factors. In this method, ratios of the echo signal power spectrum from a region of interest (ROI) in the sample to the spectrum from the same depth in a well-characterized reference medium yield values that depend only on the attenuation and backscatter properties of the sample and reference. Because the properties of the reference are known, acoustic properties of the sample can be derived.

One of the challenges for QUS in vivo is correcting for inhomogeneous tissue paths between the ultrasound transducer and the ROI. Attenuation competes with backscattering to affect the detected echo signals, and spatial variations in both properties along the propagation path complicate the estimation of the attenuation and BSCs for any ROI distal to such inhomogeneous regions. Although previous studies^19,21 demonstrated that QUS parameters could be accurately estimated from in vivo rodent tumors using clinical imaging systems, the tumors were superficial, protruded from the body wall, and the very thin skin and fat layers likely had little influence on QUS parameter estimate accuracy. The goal of the work reported herein was to assess the accuracy of backscatter and attenuation estimates from ROIs within simple, “layered phantoms” that represent basic, but important, first approximations to the inhomogeneous tissue propagation path in vivo. In addition, multiple clinical ultrasound systems were used to acquire the data to assess imaging system independence under these conditions.

Methods

Tissue-Mimicking Layered Phantoms

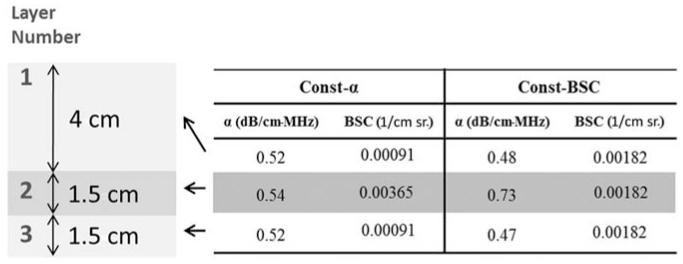
Two tissue-mimicking phantoms having spatial variations in backscatter and attenuation were constructed. Each phantom consisted of three layers differing either in attenuation but not in backscatter, or in backscatter but not in attenuation (see Figure 1). A “Constant attenuation” (Const-α) phantom was designed to have a uniform attenuation coefficient in all layers, but the middle layer had 6 dB higher backscatter than the other two layers. Similarly, a “Constant backscatter” (Const-BSC) phantom was designed to have three layers with equivalent BSCs, but the middle layer had higher attenuation than the other two layers. The specific properties attenuation and backscatter of these phantoms are presented in Figure 1.

Figure 1.

Description of Const-α and Const-BSC phantoms. (BSC at 7 MHz from Faran’s theory²³ is presented here.)

Const-α = constant attenuation; Const-BSC = constant backscatter.

Both phantoms consist of gelatin with ultrafiltered milk added to control the amount of attenuation and 5 to 43 μm diameter glass microspheres (Spheriglass® 3000E, Potters Industries, Valley Forge, Pennsylvania) to provide scattering.²⁴ The scatterer concentrations and volume ratios of molten gel-to-filtered milk are detailed in Table 1. The layered surfaces are bonded together, and because the media are nearly identical in density and sound speed, reflection losses at the interfaces are negligible. The top layer, middle layer, and the bottom layer of the phantoms in the order as shown in Figure 1 are defined as “Layer 1,” “Layer 2,” and “Layer 3,” respectively. The phantoms are rectangular cuboids, 9 cm (laterally) × 9 cm (elevationally) × 7 cm (axially). For scanning and storage, they were submerged in oil within a plastic container.

Table 1.

Composition of Layered Phantoms

	Const-α			Const-BSC
	Layer 1	Layer 2	Layer 3	Layer 1	Layer 2	Layer 3
Scatterer concentration (g/L)	2	8	2	4	4	4
Volume ratio of molten gelatin to ultrafiltered milk	2.1:1	2.1:1	2.1:1	2.85:1	1:1	2.85:1

Const-α = constant attenuation; Const-BSC = constant backscatter.

Speeds of sound, attenuation coefficients, and BSCs of the phantom layers were estimated using 2.5-cm-thick cylindrical test samples of the layer materials, manufactured during construction of the phantoms. Test samples have two parallel transmission windows of 25-μm-thick Saran Wrap® (Dow Chemical, Midland, Michigan). A narrow band substitution technique¹⁶ with matching pairs of unfocused transducers was applied to measure attenuation coefficients over the 3.5 to 10 MHz frequency range and speeds of sound at 3.5 MHz. (Sound speed measurement at a single frequency is sufficient because dispersion is negligible in these materials.) Sound speed of all sections of both phantoms was within the range of 1550 ± 5 m/s, except Layer 2 of the Const-BSC phantom, where the sound speed was 1564 m/s. Attenuation coefficients were fit to linear functions of frequency, and the slopes of the attenuation coefficients versus frequency (dB/cm-MHz) were obtained over 3.5 to 10 MHz. These attenuation measurement results are presented in the numerical data in Figure 1 for each section of both phantoms.

The BSC of each layer was computed by applying the theory of Faran,²³ in which the first 25 terms of the Faran model (with the corrections to (30) noted by Hickling²⁵) were used. Input parameters for the model included the microsphere mass density (2.38 g/cc), Poisson’s ratio for the glass (0.210), the speed of sound in both glass (5572 m/s) and the background, and the microsphere diameter distribution. The diameter distribution was obtained by measuring the sizes of a sample of 200 microspheres using an Olympus BH-2 microscope (Tokyo, Japan) equipped with a video camera that fed into a Cue-Micro-100 video caliper (Mercer Scientific, Trenton, New Jersey) and into a video monitor. The distribution of these microspheres has been previously reported.¹⁷ A BSC was computed for each diameter taking into account the microsphere concentration and the diameter distribution to determine the number per unit volume in the layer. The BSC of each layer was then obtained by summing the contributions for each diameter. Theoretical predictions were plotted along with experimental results.

Ultrasound Clinical Scanners and Data Collection

Three clinical scanning systems, each providing radio frequency (RF) echo data through a research interface, were used to image the tissue-mimicking layered phantoms. The three clinical systems are an UltraSonix RP (Ultrasonix Medical Corporation, Richmond, British Columbia), a Siemens Acuson S2000 (Siemens Medical Solutions USA, Inc., Malvern, Pennsylvania), and a VisualSonics Vevo 2100 (VisualSonics, Inc., Toronto, Ontario, Canada). For each system, the individual transducers, the nominal excitation frequencies used, and the data acquisition digitization rates are summarized in Table 2.

Table 2.

Summary of Clinical Imaging Systems and the Respective Nominal Excitation Frequencies Used with the RF Data Collection (Note, the VisualSonics Data Are Baseband Quadrature Components)

System	Transducer	Nominal Excitation Frequency (MHz)	Sampling Frequency (MHz)
UltraSonix RP	L14-5/38	6	40
Siemens Acuson S2000	18L6	10	40
	9L4	9
VisualSonics Vevo 2100	MS200	15	40

RF = radio frequency.

Echo signals from a reference phantom were used to account for imaging system-dependent factors that affect the RF echo data, as described by Yao et al.²² The reference medium used in this study was Layer 1 of the Const-BSC phantom after rotating it 90 degrees to gain access to this uniform volume over an 8-cm-depth range (Figure 2).

Figure 2.

Phantom orientation used for reference scans.

Prior to RF data acquisition, the imaging system settings, including TGC, overall gain, transmit focus position, and transmit power level, were established for each phantom scan by adjusting controls until a uniform gray level over the entire depth of the phantom image was observed on the scanner’s B-mode image display. The same settings were then used to scan the reference medium. Each system was used to scan the layered phantoms and reference medium with the array transducer placed in contact with the media. In each case, three to five frames of RF echo data were acquired, with an elevational translation or rotation of the transducer between each frame to obtain statistically independent echo signals. Transducers used with the Siemens and the UltraSonix imaging systems were applied to scan the phantoms from the top as visualized in Figure 1, whereas the VisualSonics probes were applied to scan from the bottom layer. Scanning from the bottom provided a shorter propagation path to the mid layer for that system’s high-frequency probes. In each case, the reference data were obtained as illustrated in Figure 2.

Attenuation Estimation

For each of the imaging systems, a separate team of researchers collected and analyzed that system’s data. In every case, the RPM was applied to estimate the slope of the attenuation coefficient versus frequency for each section of both phantoms. Specific analysis parameters and details on RPM implementation were determined independently by each team.

For a ROI with Const-BSC properties, the RPM estimates the attenuation of the sample using

$${\alpha }_{\text{sample}}\left(f\right)=-\frac{\ln \left(\frac{S_{\text{sample}}(z,f)}{S_{\text{ref}}(z,f)}\right){\mid }_{z_2}-\ln \left(\frac{S_{\text{sample}}(z,f)}{S_{\text{ref}}(z,f)}\right){\mid }_{z_1}}{4(z_2-z_1)}+{\alpha }_{\text{ref}}\left(f\right),$$ (1)

where the S_sample and S_ref are the power spectra for the sample and reference, respectively; α_sample and α_ref are the attenuation coefficients of the sample and reference, at frequency f, respectively; and z₂ and z₁ are depths in the ROI, where z₂ > z₁.

Analysis parameters used for each system’s RF echo data are summarized in Table 3. Each team applied a tapering window to compute the echo signal power spectrum. The squared magnitude of the Fourier transform of the signal from each window was averaged with those from adjacent scan lines at each depth to estimate the power spectrum. Adjacent windows were overlapped both axially and laterally. The spatial extent of the “spectral window” is defined as the axial length of the tapering window and the lateral extent of the adjacent scan lines used for power spectra averaging. The slope of the attenuation coefficient versus frequency (“α0” in α(f) = α0f) was obtained over an “attenuation estimation distance,” defined as the axial length of linear regression distance to estimate the attenuation coefficient (dB/cm) at each frequency.

Table 3.

Parameters for the Spectral Analysis Used for the Estimations of Attenuation Coefficient Slope versus Frequency and BSC

	UltraSonix	VisualSonics	Siemens
Spectral window size (axial  × lateral)	4 mm × 10 mm for αo	2 mm × 5 mm for αo	3-5 mm × 5 mm
	3.8 mm × 3.8 mm for  BSC	1.5 mm × 1.5 mm for BSC
Tapering function	Rect for αo	Rect for αo	Hann window
	Hann for BSC	Hann for BSC
Spectral window overlap  ratio (axial × lateral)	50% × 50% for αo	50% × 50% for αo	75% × 75%
	75% × 75% for BSC	75% × 75% for BSC
Attenuation estimation  distance	10 mm	5 mm	6-8 mm
Attenuation estimation  distance overlap ratio	50%	50%	0-85%
Signal processing bandwidth	4-8 MHz (Layer 1)	7.2-12.2 MHz (Layer 1)	4-10 MHz (Layer 1)
	3.6-6.5 MHz (Layer 2)	8.5-13 MHz (Layer 2)	4-8 or 3-8.5 MHz  (Layer 2)
	3.3-6 MHz (Layer 3)	9.1-14.7 MHz (Layer 3)	4-6 or 3-7 MHz (Layer 3)
Bandwidth selection  criterion	−6 dB	−6 dB	5-10 dB above noise  floor

BSC = backscatter coefficient. “Rect” and “Hann” refer to the rectangular and Hann time-gating functions, respectively,

BSC Estimation

BSCs also were estimated using the reference phantom technique.²² σ_sample, the BSC of the sample, was estimated using

$${\sigma }_{\text{sample}}(z,f)=\frac{S_{\text{sample}}(z,f)}{S_{\text{ref}}(z,f)}\times {\sigma }_{\text{ref}}(z,f)\times \exp \left[-4{\int }_0^z\left({\alpha }_{\text{ref}}\right(z;f)-{\sigma }_{\text{sample}}(z;f\left)\right)dz\prime \right],$$ (2)

where the S_sample and S_ref are the power spectra for the sample and reference, respectively; σ_ref is the BSC of the reference medium; z is the depth of interest; and α_sample and α_ref are the attenuation coefficients of the sample and reference, at frequency f, respectively.

The power spectra of sample and reference signals were calculated in the same way as that used for attenuation estimations. The power spectra from the sample and reference were corrected for the attenuation losses along the sample path and the reference phantom path, using the slope of the attenuation coefficient versus frequency for each layer estimated by the laboratory measurement and presented in Figure 1. The BSCs obtained from each spectral window (as defined above) over the ROI were spatially averaged. Parameters used for BSC estimations are also summarized in Table 3. The estimated BSCs based on this average were compared with the predictions from Faran’s scattering theory.²³

Analysis of the BSC estimates was performed to determine the level of agreement with theoretical predictions. For this analysis, the bias with respect to Faran (B_Faran) was computed as the ratio of the BSC estimate (σ_sample(f)) from all transducers to the Faran prediction (σ_Faran(f)) at the same frequency. This is expressed as

$$B_{\text{Faran}}\left(f\right)=10\times {\log }_{10}\frac{{\sigma }_{\text{sample}}\left(f\right)}{{\sigma }_{\text{Faran}}\left(f\right)}.$$ (3)

The B_Faran value for the BSC estimate from each system was computed over each available bandwidth and averaged over the frequency points within the analysis bandwidth (see Table 3).

Results

Slope of the Attenuation Coefficient versus Frequency

Attenuation coefficient slope estimates obtained with each clinical system are presented in Table 4. There is close agreement among the results generated by these imaging systems, particularly for Layer 2 from both phantoms. To inspect further, percent errors of the estimated slope of the attenuation coefficient versus frequency were computed, using the laboratory characterization of each layer as the gold standard. These results are shown in Table 5 for the different systems. The percent errors sorted by the location of the ROI, that is, as “proximal,” “mid,” and “distal” layers, help illustrate the accuracy of attenuation estimates for the nonuniform paths. The minimum and maximum (magnitude) percent errors were 1.8% and 40.4%, respectively, for the Const-α phantom, and 0% and 12.8%, respectively, for the Const-BSC phantom. The maximum errors were from the distal layers of both phantoms. However, note that most of the errors were less than 10%. Mean percent errors over all three layers among three imaging systems were −4.9% for the Const-α phantom and −4.4% for the Const-BSC phantom.

Table 4.

Mean Attenuation Coefficient versus Frequency Slope Values (dB/cm-MHz) Estimated Using the Three Clinical Ultrasound Imaging Systems

		Layer 1 (dB/cm-MHz)		Layer 2 (dB/cm-MHz)		Layer 3 (dB/cm-MHz)
Clinical System	Transducer	Const-α	Const-BSC	Const-α	Const-BSC	Const-α	Const-BSC
Lab characterization		0.52	0.48	0.54	0.73	0.52	0.47
UltraSonix RP	L14-5/38	0.46	0.46	0.48	0.64	0.31	0.41
Siemens Acuson S2000	18L6	0.48	0.48	0.53	0.71	0.44	0.43
	9L4	0.49	0.5	0.52	0.7	0.55	0.45
VisualSonics Vevo 2100	MS200	0.67	0.46	0.55	0.69	0.53	0.5

Const-α = constant attenuation; Const-BSC = constant backscatter. The mean value was obtained by averaging estimates from different alpha-estimation blocks and from uncorrelated image frames for each layer. For the UltraSonix and Siemens systems, the transducers were placed in contact with Layer 1 and then directed to the more distal layers; for the high-frequency VisualSonics, the transducer was in contact with Layer 3, providing a shorter path to the distal layer (see Figure 1).

Table 5.

Percent Error (Magnitude) of the Slope of the Attenuation Coefficient versus Frequency for Each Layer of the Const-α Phantom and Const-BSC Phantom

		Proximal Layer (% error)		Mid Layer (% error)		Distal Layer (% error)
Clinical System	Transducer	Const-α	Const-BSC	Const-α	Const-BSC	Const-α	Const-BSC
UltraSonix RP	L14-5/38	−11.5	−4.2	−11.1	−12.3	−40.4	−12.8
Siemens Acuson  S2000	18L6	−7.7	0	−1.8	−2.7	−15.4	−8.5
	9L4	−5.8	4.2	−3.7	−4.1	5.8	−4.2
VisualSonics  Vevo 2100	MS200	1.9	−6.4	1.8	−5.5	28.8	4.2

Const-α = constant attenuation; Const-BSC = constant backscatter. The layers are identified (“proximal,” “mid,” and “distal”) according to their position with respect to the transducer during scanning.

BSC versus Frequency

BSCs estimated using the clinical systems were plotted as a function of frequency, and the results are presented in Figure 3. Each plot also shows results from predictions using Faran’s theory. Visually, the BSC estimates from the different systems agreed with theoretical predictions except for small offsets. The best overall agreement was exhibited in the results from the mid layer of the Const-BSC phantom.

Figure 3.

BSC estimates for (a) Const-α phantom and (b) Const-BSC phantom; from the top to the bottom, the BSC estimates for proximal layer, mid layer, and distal layer are presented. The layers are named after their position with respect to the transducer during scanning.

Const-α = constant attenuation; Const-BSC = constant backscatter.

To quantify the accuracy of backscatter determinations by each system, the bias error, B_Faran (see (3)) was determined for the BSC estimates from each phantom layer. The results of this analysis, averaged over frequency, are presented in Figure 4. Generally, it can be observed that results were more accurate for shallow layers. However, even after traversing the more highly attenuating mid layer, accurate BSCs were obtained.

Figure 4.

Average values of B_Faran over each used bandwidth for the estimated BSCs from various systems for (a) Const-α phantom and (b) Const-BSC phantom (error bars indicate one standard deviation) in dB. The layers are named after their position with respect to the transducer during scanning.

Const-α = constant attenuation; Const-BSC = constant backscatter.

BSC estimates from the layers were in agreement with predictions from Faran’s theory to within 2.5 dB, with most imaging system estimates within about 1 dB. Based on the results in Table 5 and Figure 4, in most cases, errors in the estimation of the slope of the attenuation coefficient and BSC of the distal layers were larger than those corresponding to the proximal and mid layers.

Discussion

The RPM provides accurate results for attenuation coefficients and BSCs estimated from measurements in homogeneous regions using clinical ultrasound equipment.^19-21,26 The focus of this article was on attenuation and BSC estimates when the ROI is located distal to inhomogeneous layers, mimicking the common clinical challenge of QUS in an organ distal to a fat and/or muscle layer. Phantoms exhibiting one-dimensional variations in backscatter and attenuation were used in the study. “Proximal,” “mid,” and “distal” layers were intended to mimic ROI locations in vivo that might correspond, for example, to sites in subcutaneous fat, muscle, and the liver or kidney (equivalently, these could be subcutaneous fat, glandular and retromammary layers of the breast).

The attenuation estimates were generated for ROIs that did not span the boundaries between layers. However, they represent values generated through layers with different attenuation and backscatter properties, a first approximation to dealing with inhomogeneous tissue paths. Additional strategies would need to be applied to use the spectral difference analysis approach to recognize scattering gradients when measuring attenuation in the presence of such tissue features.²⁷

The attenuation and backscatter estimates from the distal layers were less precise than those from the proximal and mid layers. The mean error (among all systems) in each layer was 3.7%, 4.9%, and 5.3% for the proximal, mid, and distal layers, respectively. However, the standard deviations among these measurements (in each layer) were 5.3%, 4.7%, and 19.9%, respectively. This can be attributed to a general reduction of the signal-to-noise ratio (SNR) at large depths when using higher frequency transducers. When scanning with the UltraSonix and the Siemens systems, the distal layer corresponded to Layer 3 as defined in Figure 1. Therefore, the acoustic pulses from these two systems had to traverse the 4-cm-thick Layer 1 and the 1.5-cm-thick Layer 2 before reaching the distal Layer 3. In the same way, echoes backscattered from the distal layer had to penetrate through these layers on their way back to the transducer. As a consequence, the total attenuation from Layers 1 and 2 severely reduced the SNR of echoes from Layer 3 compared with the SNR from echoes from shallower layers.

In spite of this, the mean percent errors of the attenuation estimates from the three systems over the three layers were 4.9% and 4.4% for Const-α phantom and Const-BSC phantom, respectively. Comparing our results with those reported for an interlaboratory study by Wear et al.¹⁶ where they estimated the attenuation from three homogeneous phantoms, their agreement was within 0.2 dB/cm-MHz, whereas ours are within 0.24 dB/cm-MHz (combining the results from the UltraSonix L14-5/38 and the Siemens 9L4 for Layer 3 of the Const-α phantom). It also should be noted that attenuation estimates done using the three imaging systems were obtained from backscattered echoes, whereas Wear et al.¹⁶ reported attenuation estimates obtained by insertion-loss with through-transmission.

Attenuation estimates have shown potential to classify diseases and differentiate tumors.^1,5 The study by D’Astous and Foster⁵ demonstrated that infiltrating ductal carcinoma could be differentiated from fat. The mean attenuation values of carcinoma and fat were about 0.96 and 0.48 dB/cm-MHz at 5MHz. Fujii et al.¹ showed that fatty livers and normal livers had mean attenuation values of 0.80 and 0.59 dB/cm-MHz (using a 3.75-MHz-sector array transducer), respectively. The differences between normal and disease cases in these two studies are greater than the attenuation errors shown here.

Regarding the BSC estimates, the agreement between measurements and theory as well as the agreement among all systems are within one order of magnitude. This level of accuracy is comparable with results of other interlaboratory studies.^16-18 Again, the latter studies were conducted on samples measured in well-controlled laboratory settings, whereas the present results report values generated using clinical imaging systems, so we are encouraged by our results. Estimation of an effective scatterer size has been shown to be a valuable approach to evaluate the degree of agreement between the frequency dependence of backscatter determined among different measurement groups.¹⁹ This was not performed here because the value of ka (where k is the wave number and a is the scatterer radius) for the glass bead scatterers in our phantoms was too low (0.1-0.6 for the mean bead diameter of 24 μm and echo signals spanning the 2-12 MHz range) for accurate estimation of effective scatterer diameter.²⁸

Intersystem variations of BSC estimates from both phantoms could be caused in part by the uncertainty in accounting for the total attenuation through the various layers. Accuracy variations in BSC and attenuation estimates were observed among imaging systems. Although the BSC and attenuation coefficients were estimated using the RPM, there were different SNR levels in RF signals from different imaging systems. Moreover, the RPM was implemented independently by the research teams using their own signal analysis parameters. In the future, the standardization of estimation processes will be investigated to reduce the variation among systems.

In this experiment, the attenuation compensation for BSC estimation was performed using laboratory estimates of the attenuation coefficients. This approach, however, is not practical for in vivo applications. To overcome this limitation, various algorithms have been designed to estimate the total attenuation from the backscatter echo signals.^29,30 The performance of these algorithms will ultimately affect the accuracy and precision of in vivo BSC estimates. This topic is currently being explored.

Conclusions

Slopes of the attenuation coefficient versus frequency computed using echo data from clinical imaging systems are in excellent agreement with laboratory results for tissue-mimicking phantoms having layers that exhibit depth-dependent variations in backscatter and attenuation. BSC estimates for each layer were in good agreement (often within about 1 dB) among systems as well as with theoretical predictions. This study demonstrates that attenuation and BSCs can be accurately estimated in layered media using pulse-echo data from clinical imaging systems.