Spatial telomere organization and clustering in yeast Saccharomyces cerevisiae nucleus is generated by a random dynamics of aggregation–dissociation

The 32 telomeres of budding yeast form clusters, yet whether clusters are due to random localization or telomeric interactions is unclear. Data from live-cell imaging are compared with a biophysical model of telomere dynamics. Direct molecular interaction between telomeres is the key parameter that regulates telomere clustering.

Abstract

Spatial and temporal behavior of chromosomes and their regulatory proteins is a key control mechanism in genomic function. This is exemplified by the clustering of the 32 budding yeast telomeres that form foci in which silencing factors concentrate. To uncover the determinants of telomere distribution, we compare live-cell imaging with a stochastic model of telomere dynamics that we developed. We show that random encounters alone are inadequate to produce the clustering observed in vivo. In contrast, telomere dynamics observed in vivo in both haploid and diploid cells follows a process of dissociation–aggregation. We determine the time that two telomeres spend in the same cluster for the telomere distribution observed in cells expressing different levels of the silencing factor Sir3 protein, limiting for telomere clustering. We conclude that telomere clusters, their dynamics, and their nuclear distribution result from random motion, aggregation, and dissociation of telomeric regions, specifically determined by the amount of Sir3.

INTRODUCTION

The nucleus is spatially and functionally organized, and its architecture is a key contributor to genomic function (Gotta et al., 1996; Heard and Bickmore, 2007; Misteli, 2007; Hübner and Spector, 2010), yet the underlying principles are poorly understood. The clustering of specific DNA sequences forming subnuclear compartments in which specific factors concentrate is a process conserved through evolution (de Laat, 2007). In budding yeast, the 32 telomeres of a haploid cell can associate in several clusters, leading to the unequal distribution of telomeres and telomere-associated factors (Taddei et al., 2010). Understanding the principles of telomere organization in yeast is a key step to elucidating the general mechanisms governing chromosome trans-interactions in eukaryotes.

In vivo studies show that telomeric foci undergo fusion and fission events over a time scale of minutes (Schober et al., 2008), but the physical principles underlying telomere dynamics are elusive. Of interest, interactions between subtelomeres have been proposed to be nonspecific and governed only by some structural constraints, including chromosome structure, attachment to the spindle pole body, and nuclear crowding (Therizols et al., 2010; Zimmer and Fabre, 2011; Wong et al., 2012).

To investigate the mechanisms underlying cluster formation and their overall dynamics, we analyze data from live-cell imaging, using a novel stochastic model that we built based on a coarse-grained description of telomere motion, aggregation, and dissociation. Finite dissociation–aggregation systems were analyzed at a molecular level by using a stochastic description (Lushnikov, 1978; Edelstein-Keshet and Ermentrout, 1998; Aldous, 1999; Wattis, 2006). We first show that random encounter of telomeres does not account for the observation that telomere clusters are observable for minutes (Schober et al., 2008). To resolve this issue, we account for direct molecular interactions between telomeres and estimate the number and size of clusters in experimental and simulation histograms that agree. This result shows that dissociation/association of telomeres moving by random motion on the nuclear surface explains the formation of visible clusters. Whereas the association rate depends on geometrical parameters such as telomere diffusion and the physical properties of the nucleus, the dissociation rate that we estimate here is regulated by the local organization of telomeres in clusters and the Sir proteins mediating interactions between telomeres. Indeed, telomere clustering can be modulated by changing the cellular amount of Sir3 molecules (Ruault et al., 2011). Of importance, our model is able to predict telomere distribution when changing the geometry of the nucleus or when varying the affinity between telomeres. These predictions agree with experimental data obtained in vivo in diploids cells (data that we present here for the first time) or by varying the number of Sir3 molecules engaged in telomere clustering.

Moreover, we obtain several refined quantifications regarding cluster dynamics. We estimate the mean time that two telomeres spend in the same cluster (while the cluster changes identity by accepting or losing telomeres) and the mean time that two telomeres meet again after they separate from a given cluster. These two characteristic times give precise quantification parameters that could be used to analyze the dynamics of telomere interactions observed in vivo (Schober et al., 2008; Therizols et al., 2010). In summary, this overall analysis represents a first attempt to model and quantify telomere organization, clustering, and dynamics in Saccharomyces cerevisiae based on elementary physical properties.

RESULTS

Random encounter does not account for the dynamics of telomere foci observed in vivo

To test whether telomere foci observed in vivo could result from the random encounters of telomeres at the nuclear periphery, we first generated a stochastic simulation of noninteracting telomeres, described as 32 independent Brownian particles diffusing on the periphery of a nucleus of radius 1 μm, excluding the nucleolus, which occupies about one-third of the total surface.

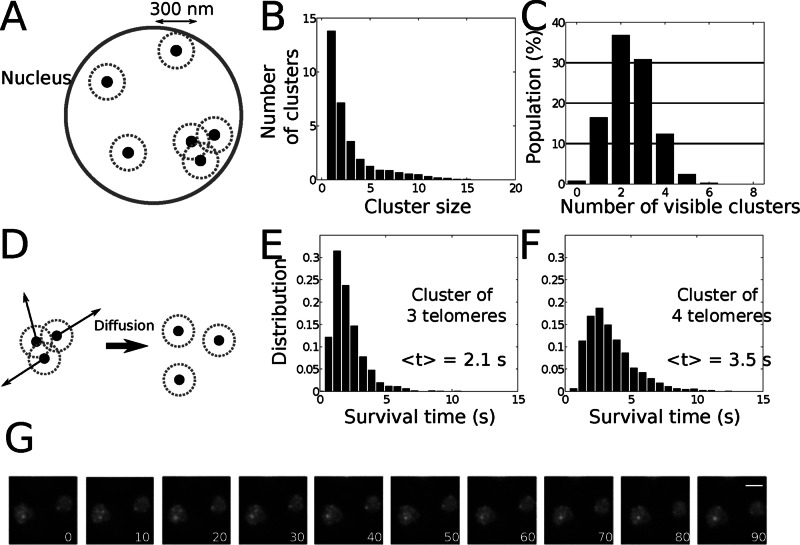
We used 300 nm as the distance to define the upper size of a telomere cluster (Materials and Methods and Figure 1A). As the simulations were running, we counted at each moment of time the number of spots generated by telomeres within a size of 300 nm. We found that on average, 13.7 telomeres were isolated, 7.2 telomeres were in pairs (3.6 pairs), and the remaining 11 telomeres were in clusters of three or more (Figure 1B). To compare this numerical simulation with live-cell imaging data monitoring the telomeric protein Rap1 fused to green fluorescent protein (GFP), we used our previously estimated detection threshold for telomere cluster of N = 2 (Ruault et al., 2011). We thus retained only clusters containing at least three telomeres (which we call observable clusters). After running the numerical simulations, we ordered the distribution of cells according to their number of observable clusters (Figure 1C) and obtained a mean of 2.5 ± 1.1 (SD), in agreement with the experimental observations (Schober et al., 2008; Ruault et al., 2011; see later discussion of Figure 3B). The similarity between the histograms for the percentage of cells according to their number of observable clusters was evaluated as the maximum of the absolute difference of the experimental and simulated cumulative distribution functions for the number of clusters (distribution error function, DE). We found DE = 0.24, which could support at this stage the hypothesis of noninteracting telomeres. We next extracted the cluster dynamics from the simulations; we simulated the motion of telomeres found within a 300-nm disk (Figure 1D) and computed the time these telomeres need to spread apart and become non­observable. Using the motion parameters described, we obtained that clusters of three or four telomeres would be observable only for few seconds (Figure 1, E and F). This result is in contrast with in vivo observations of telomere foci over minutes (Schober et al., 2008; Figure 1G and Supplemental Movies S1 and S2). We thus conclude that telomere clusters cannot result simply from the transient encounter of independent telomeres moving by random motion. To resolve this issue, we now show that telomere clustering dynamics is driven by diffusion–aggregation–dissociation.

FIGURE 1:

Model of random encounter of telomeres. (A) Schematic representation of randomly located telomeres at the nuclear periphery. Two telomeres at a distance <300 nm are considered to belong to the same cluster. (B) Mean number of clusters of a given size (n = 5000). On average, 20.9 telomeres are isolated or in pairs and are thus nonobservable. (C) Number of clusters per cell containing more than three telomeres (n = 5000). Mean ± SD, 2.5 ± 1.1. (D) Schematic representation of the dispersion of a telomere focus. The telomeres start at the same initial position and diffuse on the surface of a sphere (D = 0.005 μm²/s). The mean separation time for three (E) or four (F) telomeres is, respectively, <t> = 2.1 or 3.5 s (n = 1500). (G) Rap1-GFP fluorescence images extracted from Supplemental Movie S1. yAT340 was grown in glucose complete medium. The z-stack images were acquired every 10 s for 100 times. Bar, 2 μm.

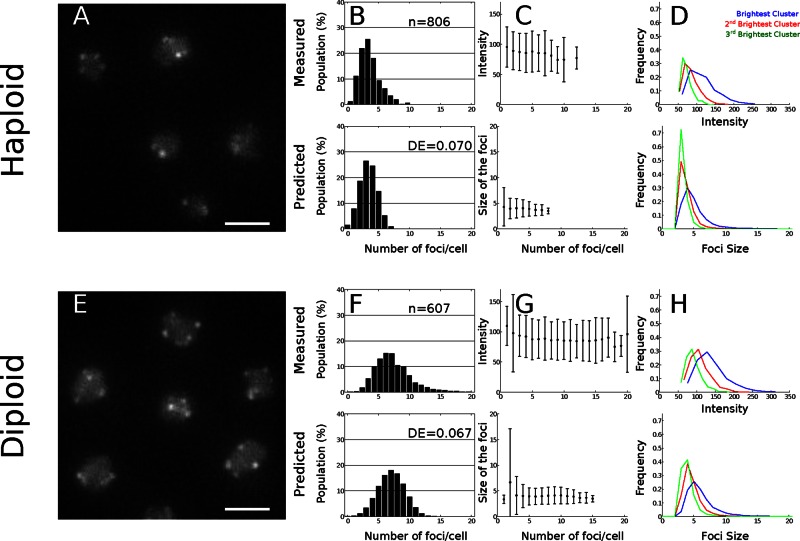
FIGURE 3:

Comparison of experimental and simulation results of telomeres clustering in yeast. (A, E) Live-cell imaging of telomere clusters. Representative fluorescence image of the telomere-associated protein Rap1 tagged with GFP (scale bar, 2 μm) in haploid (yAT340) and diploid cells (yAT352). (B, F) Histogram of the number of clusters per cell. (C, G) Mean ± SD of the intensity distributions of the clusters in live cells and distribution of the cluster size in the Brownian simulations. In the haploid cells, clusters are made of four telomeres, with a small dispersion that does not depend on the cluster number. (D, H) Fluorescence intensity (experiments) and sizes defined as the number of telomeres per cluster (simulations) for the three brightest clusters. The frequency of occurrence (y-axis) of a given cluster size is plotted as a function of the intensity of a cluster (x-axis), proportional to the telomere number.

Coarse graining the motion of telomeres at the nuclear envelope in a dissociation–aggregation model

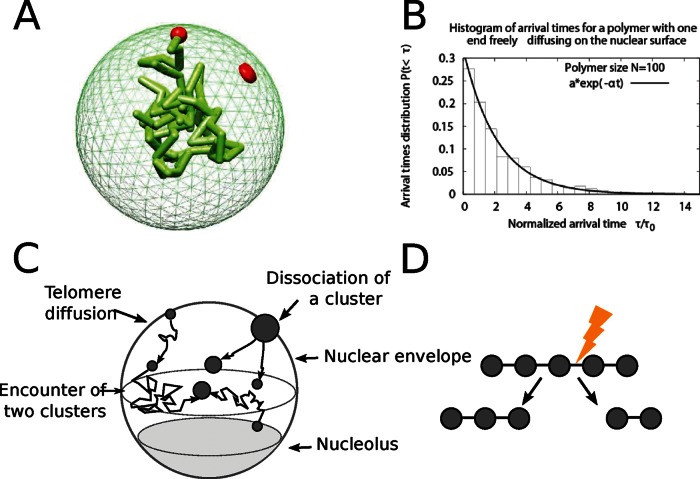
We first show that telomere clustering can be studied by coarse graining the polymer dynamics into an equivalent Brownian particle. The physical reason is that the arrival time to a cluster (which occupies a small fraction of the surface) is a rare event and takes a long time (Schuss et al., 2007). To validate the coarse graining description of a telomere, we ran a Brownian simulation of a Rouse polymer, which models the chromosome dynamics (Supplemental Information, Polymer Simulations). In this simulation, the telomere motion occurs on the surface of a sphere, which represents the nuclear surface (Figure 2A), whereas the remainder of the monomers in the chain evolve inside the nucleus. We found that the distribution of telomere arrival time to a small target, which can represent another telomere or a small cluster, is well approximated by a single exponential (Figure 2B). This result shows that the encounter rate of telomeres at the nuclear periphery can be characterized by a single parameter (the arrival rate or equivalently by an effective diffusion constant): even though telomere motion involves complex polymer chains accounting for the physical chromosomal chain, encounter is a rare event, and its rate is Poissonian. Consequently, to model clustering, we use this property to approximate the arrival time of a chromosome to a small cluster by the Poissonian dynamics, as long as the chromosome length does not restrict the motion of the telomere on the nuclear surface. Two telomeres encounter at a Poissonian rate k_f.

FIGURE 2:

Computational model of telomere cluster formation. (A) Snapshot from a Brownian dynamics simulation of a polymer with one end anchored on the nuclear surface. The polymer is composed of 100 monomers with average distance between monomers of l₀ = 50 nm, and the nucleus is a reflecting sphere of size R = 250 nm. (B) Histogram of the arrival times for a polymer of size 100 monomers freely diffusing in the nucleus and one end constrained to the surface. A fit of the form f(t) = a exp(−bt) gives a = 1.014 and b = 0.76. (C) The diffusion–aggregation–dissociation model of telomere organization. Telomeres are represented as Brownian particles diffusing on the nuclear surface, and two telomeres coalesce with a rate k_f and a cluster of n splits at a rate (n − 1)k_b. (D) Schematic representation of the cluster dissociation model, in which a cluster of n telomeres has n − 1 bonds. Any of these bonds can break at a rate k_b, and the cluster effective dissociation rate is (n − 1)k_b.

We conclude from the polymer simulations (Figure 2B) that we can simulate the arrival time of a telomere to a cluster using a Poissonian distribution approach. In that case, we can restrict our study to the dynamics of 32 stochastic particles (Figure 2C). Thus, using a molecular dynamics simulation of two Brownian particles on the surface of a sphere (Carlsson et al., 2010), we ran simulations for a Brownian motion occurring on the two-dimensional sphere except for a region of the size of the nucleolus (see earlier discussion). We obtained an approximation for the forward rate of k_f ≈ 1.9 × 10⁻³ s⁻¹, where the encounter disk is of radius δ = 0.015 μm and the effective diffusion constant is D = 0.005 μm²/s (Bystricky et al., 2004). When a telomere aggregates to a cluster, it only slightly varies in size. Indeed, in the complex environment of the nuclear surface, the diffusion constant varies with the log of the radius of the effective diffusing particle. Thus any changes in the radius will result only in a small change in the diffusion coefficient. We neglected any possible changes in the scattering cross section and motility, which could modify the forward binding rate (Hozé and Holcman, 2012). Thus the encounter rate between clusters or telomeres will be approximated by a constant independent of the size.

In the absence of specific information about the molecular organization of clusters, we tested several dissociation rules and found that only the one described later could account for the experimental observations (data not shown). In this model, a cluster containing n telomeres can dissociate with a Poissonian rate of (n − 1)k_b, where k_b is the dissociation rate between two telomeres (Figure 2D). This rate implies that a possible telomere organization in a cluster consists of a linear succession of telomeres in which each of them is connected to its two closest neighbors. Such organization is an ideal abstraction, and the true organization would require a spatial resolution that is not yet accessible. Thus any dissociation event gives rise to two clusters of random size p and n − p, respectively, where the dissociation probability is uniform.

In the present model, free telomeres can bind together to form clusters with a forward rate k_f and dissociate with a backward rate k_b. The ratio a = k_f/k_b defines the equilibrium parameter. Because the association and dissociation rates are Poissonian, to study the cluster distributions, we simulated telomere dynamics using the classic Gillespie algorithm (Supplemental Information, Numerical simulations of telomere dynamics using Markovian equations).

Live-cell data agree with the stochastic aggregation of telomeres

To validate our aggregation–dissociation model for telomere organization, we compared our stochastic simulations (see Supplemental Information) with live-cell imaging data (Figure 3A). We first determined the dissociation rate k_b by comparing the experimental and simulation histograms for the number of clusters containing more than two telomeres (Figure 3B). The optimal value of the DE score was 0.11, which was obtained for k_b = 2.4 ×10⁻² s⁻¹. However, to account for the higher variance observed in the histogram of the experimental number of clusters, we introduced a fluctuation in the dissociation rate k_b of each cell. We generated random values of k_b following a Gaussian distribution, k_b = 2.3 × 10⁻² ± 1.3 × 10⁻² s⁻¹ (mean ± SD), which corresponds to a ratio of a = k_f/k_b = 0.083 ± 0.031, and we obtained an optimal fit for the distribution of the number of clusters (see Supplemental Table S1 for the parameters). We also tested initially the effect of varying k_b across clusters and observed a distribution similar to the ones obtained for simulations in which we chose a single value (the mean value) of dissociation k_b: this is thus equivalent to making a simulation with no variation in k_b. Thus we conclude that the only way to introduce a variability in the cluster number is by assigning a random value for k_b to each cell and then performing the statistic analysis. Simulations show an excellent adequacy to the experimental cluster distribution (Figure 3B), size (Figure 3C), and size distribution (Figure 3D), with a DE score of 0.07. In addition, we observed an average of three detectable clusters per cell and very few cells with more than eight clusters. Of interest, in our simulations, we found that half of the telomeres are not in visible clusters: indeed, 10.1 are isolated and 8.4 are in pairs. In addition, the number of telomeres per cluster obtained in our simulations reflects very well the cluster intensity obtained experimentally: in both simulated and experimental data, we found that the average cluster intensity does not vary with the number of clusters per cell (Figure 3C). Because there are 32 telomeres and the intensity is an increasing function of the number of telomeres, we conclude that there is on average no more than four telomeres per cluster. Consistently, the median/average number of telomeres per observable cluster was 3/3.4 ± 1.4 (SD) in our simulations. To get better precision on the cluster distribution, we plotted the distribution of the first three brightest clusters for both experimental and simulated data (Figure 3D) and found that in both cases the three brightest clusters contain four telomeres. We also found from our modeling and numerical simulations that the clusters contain on average four telomeres. This small number is a result of the association/dissociation kinetics at equilibrium but is not imposed by direct physical constraints. Indeed, a cluster containing four telomeres dissociates on average in 15 s, much faster than the mean time for two clusters to associate (9 min for two clusters).

In addition, we estimated the influence of chromosome arm lengths on the telomere aggregation–dissociation process, using an extension of our simulations (Supplemental Figure S2), and found cluster distributions similar to the ones described previously. Thus we conclude that geometrical and motility parameters, such as number of telomeres, nucleus radius, exclusion from the nucleolus, telomere physical properties, and diffusion constant, determine the association rate k_f (Holcman and Schuss, 2004). All these factors, together with the dissociation rate k_b, shape the number and average size of the clusters (four telomeres per cluster), and the equilibrium parameter a = k_f/k_b integrates all the determinants of telomere distribution.

The organization of telomeres in diploid cells confirms the aggregation–dissociation model of clustering

Our model predicts the effect of the equilibrium parameter on the telomere distribution. To test the robustness of our model, we checked whether it could account for the organization of telomeres in diploid cells in which nuclear volume (nucleus radius, 1.25 μm) and number of telomeres are doubled. These changes in the cell geometry affect the forward rate, which we recomputed from Brownian simulations and found for the association rate k_f = 1.1 × 10⁻³ s⁻¹. Considering that the backward rate is unchanged and taking the value found in the preceding section, we obtained for the new equilibrium constant the value a = 0.047 ± 0.017 (compared with 0.083 ± 0.031 for the haploid). We next imaged telomere foci in diploid cells (Figure 3E) and found that the number of telomere foci obtained by simulation is similar to the number measured in live cells. They have on average six clusters containing three to six telomeres per cell (Figure 3, F and G). We found also that the light intensity and telomere distribution of measured and simulated telomeres per cluster were very similar (Figure 3, F–H). Indeed, the DE score for the histograms describing the number of observable foci per cell was 0.067 (Figure 3F), and the predicted distribution of foci intensity was in good agreement with the experimental data. Of interest, the median cluster size is four in both haploid and diploid cells, that is, there are four telomeres per cluster, suggesting that the number of telomeres per cell does not influence the number of telomeres per cluster. Furthermore, according to our simulations, in diploid cells, telomeres cluster in five to nine foci containing three to six telomeres, whereas 18.7 telomeres are single and 16.4 are in pairs. The match between the experimental data and our numerical simulations confirms the robustness of the model to parameter changes while the physical properties of the telomeres and the cluster dissociation rate were fixed.

The aggregation model accounts for telomere distribution for two levels of Sir3 overexpression

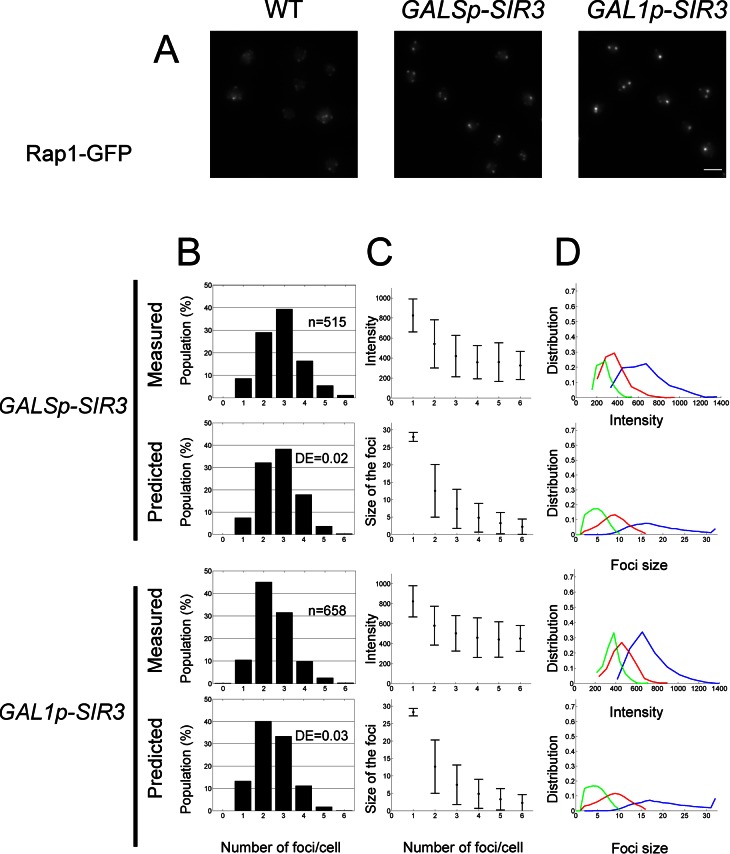
The present model predicts that molecular factors physically link telomeres in a reversible manner. Any changes in this factor concentration should thus directly affect the number of clusters and telomeres per cluster. One candidate to link telomeres together is the silencing factor Sir3, which was shown to be limiting for telomere clustering (Ruault et al., 2011). To further test the robustness of our model, we sought a value for the equilibrium parameter a that could account for the telomere foci distribution observed in vivo in cells expressing different levels of SIR3. We previously showed that overexpressing by 6- or 12-fold the endogenous level of Sir3 protein, induced, respectively, by the GALS and GAL1 promoters, leads to a higher degree of telomere clustering, with clusters mainly found in the nuclear interior (Figure 4A; Ruault et al., 2011). We thus fitted the parameter a to the experiments and found that increasing a = 0.083 ± 0.031 (wild type) to a = 5.9 (GALS) and a = 8.3 (GAL1) allows us to reproduce the histogram of number of observable foci per cell obtained in vivo (DE scores, 0.02 and 0.03). To estimate the corresponding detachment rate k_b, we had to take into account the rate of cluster formation in the nuclear interior. To this aim, we ran a three-dimensional Brownian simulation inside the nucleus and estimated the forward association rate to be k_f^3D = 9.0 × 10⁻⁴ s⁻¹ (recall that in the wild-type case, we found that the forward constant is k_f^2D = 1.9 × 10⁻³ s⁻¹, which was estimated for telomeres moving on the nuclear periphery). As expected, the encounters are less frequent in three versus two dimensions, and this is quantified by the ratio k_f^3D/k_f^2D = 0.48.

FIGURE 4:

Telomere hyperclustering under Sir3 overexpression. (A) Fluorescence images of the telomere-associated protein Rap1 tagged with GFP in wild-type, GALSp-SIR3 (yAT369), and GAL1p-SIR3 (yAT370) cells after 8 h in raffinose plus galactose medium. Bar, 2 μm. (B) Histogram of the number of clusters per cell. (C) Intensity distributions of the clusters in live cells and in simulations (mean ± SD). (D) Size distribution for the first three brightest clusters. The frequency of occurrence of a given cluster size is plotted as a function of the intensity of a cluster, proportional to the number of telomeres.

From this, we deduced that there is a large increase of the binding time, k_b⁻¹ = 109 min for GALSp and k_b⁻¹ = 154 min for GAL1p, in strains overexpressing Sir3 compared with WT, k_b⁻¹ = 43.5 s (Figure 4B).

Of importance, due to the detection threshold, the simulation histograms for wild-type and GALSp are similar, although they are obtained for very different values of the equilibrium ratio a, which changes by a factor of 100. This increase is associated with the formation of much bigger clusters when SIR3 is overexpressed under the GALS promoter (the average cluster size is 1.8 in wild type vs. 10.7 for GALSp), consistent with the variation of intensity observed in vivo. Similarly, the size of clusters predicted in our model is consistent with the intensity observed when SIR3 expression is driven by the stronger GAL1 promoter. Thus our model was also able to reproduce the distribution of clusters in both cases of Sir3 overexpression (GALSp and GAL1p, Figure 4B).

Unlike wild-type cells, some GALSp and GAL1p cells contain a single, large visible “hypercluster” containing 28 ± 1 telomeres for GAL1p strains (Supplemental Table S1).

Plotting the distribution of the first three brightest clusters (Figures 3D and 4D) reveals that our simulations could accurately reproduce the experimental intensity. Whereas in wild-type cells the three brightest clusters have almost the same number of telomeres, this distribution is much more spread for GALSp or GAL1p.

Thus our model accounts not only for telomere distributions observed in wild-type cells, but also for two biological situations in which the backward rate is decreased by overexpressing different amounts of Sir3.

The aggregation model further accounts for telomere clustering when amount of Sir3 available for telomere clustering varies

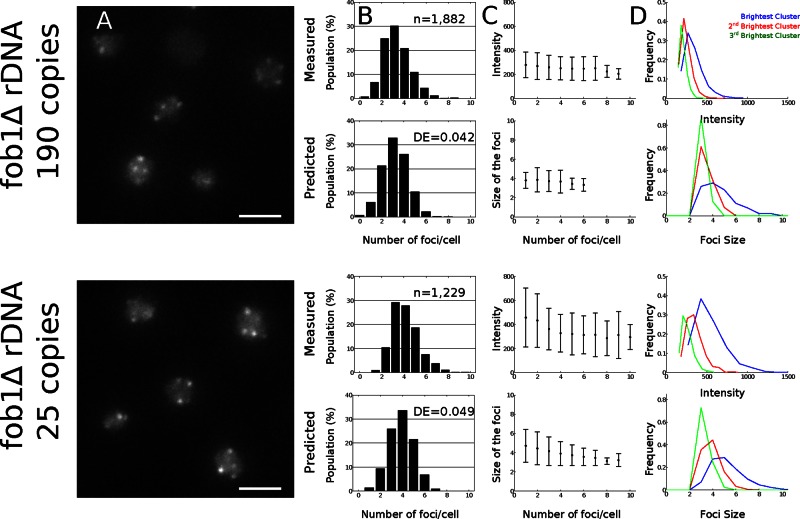
We then sought to study natural variations of k_b by varying the number of Sir3 molecules engaged in telomere clustering. Sir3 was shown to associate not only at telomeres, but also at the ribosomal DNA (rDNA) locus, the size of which is variable and contains on average 150 repeats of 9.1 kb coding for rRNA (Radman-Livaja et al., 2011). We reasoned that strains containing a small rDNA should have more Sir3 available for telomere clustering. We thus monitored telomere distribution in strains that have a fixed number of repeats (Cioci et al., 2003; 190 repeats = long rDNA; 25 repeats = short rDNA) and quantified the intensity and number of telomere foci in these strains (Figure 5A). In the case of short rDNA, we obtained more clusters (4.0 ± 1.4) and clusters brighter than in the wild-type case, which suggests that Sir3 is liberated and redistributed to telomeres.

FIGURE 5:

Comparison of the experimental and simulation results of telomeres clustering in strains with a short or a long rDNA array. (A) Live-cell imaging of telomere clusters. Representative fluorescence image of the telomere-associated protein Rap1 tagged with GFP (scale bar, 2 μm) in a fob1Δ strain with a long rDNA (yAT1782) and in a fob1Δ strain with a short rDNA (yAT1783). The rest of the information is the same as for Figure 3.

Using our simulations, we found that these results are obtained from our model with a new equilibrium constant a = 0.12, which implies that the dissociation time is 1.5 times longer in the short-rDNA case than in the wild-type case. Of interest, the long-rDNA and wild-type cases are very similar (Figures 3B and 5B), although we noticed a higher variance in the number of clusters in the wild-type case that could be related to the variability in the rDNA tandem repeat number in strains with a wild-type FOB1 gene. The cluster sizes were very similar in numerical simulations and experiments (Figure 5, C and D).

Mean time two telomeres spend in the same cluster and before they meet again for the first time

To further investigate the cluster dynamics in which telomeres are constantly exchanged between these clusters, we looked for quantities that could be conserved during cluster dynamics. We studied the colocalization time T_C that two telomeres spend in the same cluster (including cluster of two telomeres), where they can potentially exchange factors or share or compete for similar regulation processes. This time is not equal to the classic dissociation time, which represents the lifetime of a bond between two telomeres (1/k_b = 43.5 s), because it accounts for all events of binding and unbinding leaving the two telomeres inside the same cluster (Figure 6). For an average of four telomeres per cluster, using the dissociation rate (n − 1)k_b, we find that the mean time until the cluster splits into two is 1/3k_b ≈ 14.5 s. Using our stochastic simulations, we found that the colocalization time T_C is ∼23.4 s (n = 500 runs; Supplemental Table S1), which is in perfect agreement with in vivo data monitoring association between various pairs of telomeres (Bystricky et al., 2004; Schober et al., 2008; Therizols et al., 2010).

FIGURE 6:

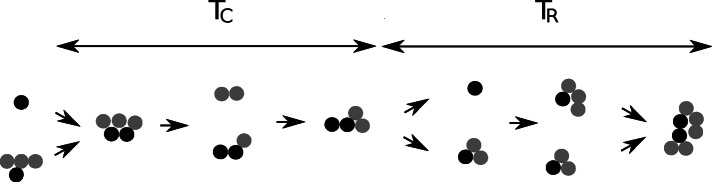
Schematic representation of cluster formation and dissociation. The colocalization time T_C is the mean time two specific telomeres (black) spend in the same cluster. Before they separate, they can form clusters with other telomeres (gray). The recurrence time T_R is the mean time the two telomeres are separated.

Another significant and complementary quantity is the recurrence time T_R, which is the mean time for two telomeres to meet again in a cluster after they separate. This recurrence time T_R is the sum of the time that both telomeres spend separately in different clusters plus the time to travel between clusters until they meet again as a pair or in an observable cluster (Figure 6). Using our Gillespie simulations, we found that T_R = 480 s ≈ 8 min (n = 500 runs; Supplemental Table S1). Surprisingly, the recurrence time is shorter than the forward time k_f⁻¹ = 526 s (n = 500), indicating that clustering favors the encounter of telomeres. Therefore, although the backward and forward rates characterize classical chemical reactions, they are not well suited to describe the clustering dynamics: two telomeres colocalized in the same cluster undergo events such as clustering with other telomeres or dissociations that do not separate them. Finally, we estimated from the simulations the probability to find two given telomeres in the same cluster (including in a pair), which is equal to the ratio of times, P₂ = T_C/(T_C + T_R).

This probability is ∼0.047, consistent with the result of Therizols et al. (2010), where the probabilities for two telomeres to belong to the same cluster were determined experimentally to be mostly in the range 0.04–0.09 (Supplemental Table S1).

In cells overexpressing SIR3 under the GAL1p, we estimated the equilibrium probability to find two telomeres in the same cluster (Supplemental Table S1) to be 53%, again in agreement with experimental data (Ruault et al., 2011). Remarkably, although the present model was designed to account for the spatial distribution of telomeres, it also predicts accurately the dynamics of telomere interactions in different experimental contexts.

DISCUSSION

We showed that the dynamics of telomere clusters observed in vivo cannot result simply from the transient stochastic encounter of independent telomeres. Instead, clustering dynamics appears to be driven by aggregation and dissociation. We propose an aggregation–dissociation model that accounts for the distribution of telomeres but also their dynamics as monitored in living cells. In our model, free telomeres can bind together to form clusters with a forward rate k_f and dissociate with a backward rate k_b. The ratio of these two constants defines an equilibrium parameter, the ratio a = k_f/k_b. This equilibrium constant is sufficient to characterize both the distribution and dynamics of telomere foci observed in wild-type cells. Furthermore, we found specific values for the equilibrium parameter a that reflect the variation of telomere clustering observed when varying the amount of Sir3 available for binding at telomeres (Figure 7A). This can be achieved either by varying the size of the rDNA that competes with telomeres for Sir3 binding or artificially increasing Sir3 cellular levels. It thus came as a surprise that so many different situations could be accounted for by varying a single parameter, a = k_f/k_b. Given that the forward rate k_f can be deduced from the motion of telomeres measured in vivo, the geometry of the nucleus, and the number of telomeres, the only free variable is the backward rate, k_b, which we showed to be directly related to the amount of Sir3 available for binding at telomeres (Figure 7). We also showed that although telomere motion results from the complex behavior of the chromosomal polymer, the arrival time of a telomere to a cluster is Poissonian and can thus be characterized by the encounter rate.

FIGURE 7:

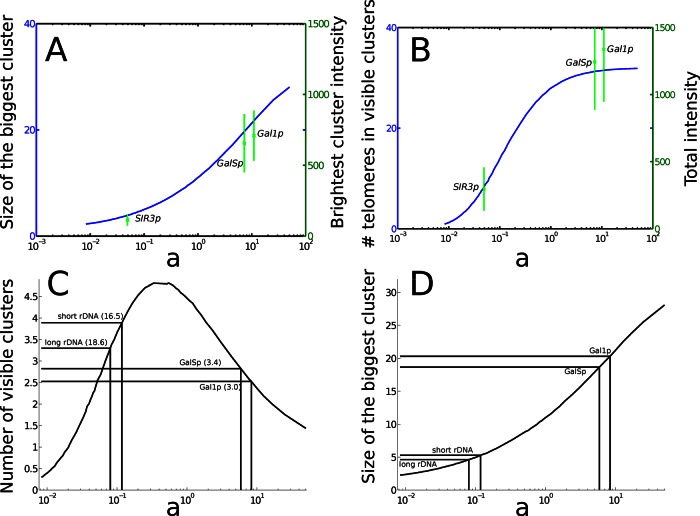
Influence of the equilibrium parameter a on clustering organization. (A) Comparison of the intensity of the brightest foci and the maximal size of the clusters in the simulations. The intensity of the brightest foci is reported on the right y-axis in arbitrary units, with the corresponding values of a. (B) The sum of foci intensity compared with the total number of visible telomeres in the simulations. The number of observed clusters (C) and the size of the largest cluster (D) are represented as a function of the equilibrium ratio a (logarithmic scale). An increase in the amount of Sir3 in cells corresponds to an increase of a. The number of visible clusters is equal to 0 for a = 0, tends to 1 (a hypercluster containing all the telomeres) for large a, and reaches a maximum at a = 0.51, corresponding to an intermediate level of Sir3 proteins. The number in parentheses is the total number of clusters, including isolated telomeres and pairs of telomeres. Although wild-type and GALSp cells contain the same number of clusters, the structure of the clusters is very different (D). The size of the biggest cluster is ∼5 for wild-type cells, 19 for GALSp, and 21 for GAL1p.

Our modeling approach allows us to report for the first time that the dissociation rate of a telomere pair is k_b = 2.3 × 10⁻² s⁻¹ and the association rate of a telomere to a cluster is independent of the cluster size and is k_f ≈ 1.9 × 10⁻³ s⁻¹. Our model also predicts that the recurrence time for two telomeres to return in the same cluster is of the order of 480 s, whereas they stay together in a given cluster for 23 s only, consistently with experimental observations (Therizols et al., 2010). Furthermore, in our simulations one telomere spends ∼30% of the time in a visible cluster, in agreement with the dynamics of telomere Tel14L observed in vivo (Schober et al., 2008).

We propose that telomere organization in wild-type cells results from three physical processes: aggregation mediated by direct interactions between telomeres, dissociation resulting from the separation from a cluster, and telomere random motion located on the nuclear envelope. In this model, clusters are constantly reshaped due to binding and unbinding, leading on average to three to five detectable foci of four telomeres.

Levels of Sir3 available for telomere clustering govern telomere distribution and dynamics

At the molecular level, telomeres are brought to the nuclear surface by telomere-associated proteins interacting with components of the nuclear envelope (for review see Taddei and Gasser, 2012), whereas the silencing factor Sir3 contributes to telomere clustering (Ruault et al., 2011). Indeed, Sir3 overexpression affects drastically the organization and the composition of the telomere clusters. In our simulation, cells with a unique cluster (Figure 4C) contain around 25 telomeres, which is more than five times higher than in the haploid case. This result suggests that by invading subtelomeric regions (Hecht et al., 1996), Sir3 can generate an increased binding region (gluing zone) promoting telomere/telomere interactions. However, Sir3 spreading in subtelomeric regions is not necessary to promote telomere clustering, as shown for a specific sir3 mutant (Ruault et al., 2011). It is thus possible that Sir3 not only spreads on subtelomeric regions when overexpressed, but also accumulates at the tip of telomeres and form multimers that allow binding of telomeres to each other. In both cases, increasing the amount of cellular Sir3 proteins leads to additional interacting bonds between telomeres. We also report that the size of the rDNA affects telomere distribution, probably by affecting the amount of Sir3 available for telomere clustering. Interestingly, spontaneous variations of rDNA size are observed in vivo in wild-type cells (Michel et al., 2005) and could be responsible for the variation of telomere clustering observed in different strains or backgrounds (Supplemental Movies S1 and S2), as we accounted for here by considering that the dissociation rate k_b varies according to a Gaussian law centered around the mean (Figure 3).

It would be interesting to refine the model by accounting for the precise structure of the telomere and derive the expression for the binding rate constant. Furthermore, the present model could also be used to study other long-range interactions that affect genomic functions in many organisms. This model could be further used to analyze how silent chromatin clustering can be modulated in response to change in environmental conditions. Interestingly, similar clustering of telomeres occurs in the parasite Plasmodium (Scherf et al., 2008) and regulates the expression of its virulence factors. In summary, understanding the principles of telomere organization in yeast might help to elucidate general mechanisms governing chromosome trans-interaction in eukaryotes.

To conclude, the model developed here accounts for self-organization principles that can be modulated by controlling protein-driven interactions. Consistent with this idea, we observed different levels of clustering in different genetic backgrounds and in different growth conditions (M. Guidi and A. T., unpublished results). The plasticity of the telomere organization might allow the cell to adapt rapidly to environmental changes, a question that will be important to explore in the future.

MATERIALS AND METHODS

Media and growth conditions

Yeast cells were grown in synthetic medium (yeast nitrogen base; MP Biomedicals, Solon, OH) supplemented with 2% glucose (wt/vol) and a complete supplement mixture (BIO 101). Liquid synthetic media were enriched for complete synthetic medium (2× complete synthetic medium as final concentration). For galactose induction (GAL1p-SIR3 and GALSp-SIR3 strains), cells were precultured in synthetic medium containing 2% raffinose (wt/vol), and galactose was added to a final concentration of 2% (wt/vol) to start the induction. Induction was carried out for 8 h. All the strains were grown at 30°C around OD_{600 nm} of 2–3.

Yeast strains

Strains derived from the W303 background: yAT340 MATα ade2-1::ADE2 his3-11 his3-15 leu2-3 leu2-112 rap1::GFP-RAP1(LEU2) sik1::SIK1-mRFP(KanMX); yAT352 MATa/α ade2-1::ADE2/ade2-1::ADE2 his3-11/his3-11 his3-15/his3-15 leu2-3/leu2-3 leu2-112/leu2-112 rap1::GFP-RAP1(LEU2)/rap1::GFP-RAP1(LEU2) sik1::SIK1-mRFP(KanMX)/sik1::SIK1-mRFP(KanMX). Strains with different sizes of rDNA array are derived from NOY1064 and NOY1071 from the Nomura laboratory (University of California, Irvine, Irvine, CA; Cioci et al., 2003): yAT1782 MATa ade2-1 his3-11 his3-15 leu2-3 leu2-112 rap1::GFP-RAP1(ADE2) sik1::SIK1-mRFP(KanMX) fob1∆::HIS3 rDNA copy number 190; yAT1783 MATa ade2-1 his3-11 his3-15 leu2-3 leu2-112 rap1::GFP-RAP1(ADE2) sik1::SIK1-mRFP(KanMX) fob1∆::HIS3 rDNA copy number 25.

Strain derived from JS306 (J. D. Boeke laboratory, Johns Hopkins University School of Medicine, Baltimore, MD): yAT1565 MATa his3∆200 leu2∆1 met15∆0 trp1∆63 ura3-167 RDN1::Ty1-MET15 mURA3/HIS3 rap1::GFP-RAP1(LEU2).

Strains derived from the YPH499 background: yAT369 MATa adh4::URA3-TEL ppr1∆::HIS3 rap1::GFP-RAP1(LEU2) sir3::GALSp(KanMX) VR::ADE2-TEL; yAT370 MATa adh4::URA3-TEL ppr1∆::HIS3 rap1::GFP-RAP1(LEU2) sir3::GAL1p(KanMX) VR::ADE2-TEL

Microscopy

Live-cell images were acquired using a wide-field microscopy system based on an inverted Nikon TE2000 (Nikon, Melville, NY) equipped with a 100×/1.4 numerical aperture (NA) oil immersion objective, a charge-coupled device (CCD) camera (CoolSNAP HQ2; Photometrics, Tucson, AZ), a xenon arc lamp for fluorescence (Lambda LS; Sutter Instruments, Novato, CA), a collimated white light-emitting diode for transmission, ultraviolet filter (LP 400, GG400; Nikon), and a filter set adapted to green fluorescence (GFP; excitation bandpass, 465–500 nm; dichroic, 506 nm, emission bandpass, 516–556 nm; Semrock, Rochester, NY). The theoretical resolution of the system (1.4 NA; emission wavelength, 528 nm; refractive index, 1.515) is 200 nm in x and y and 400 nm in z. The depth of a voxel (along the z-dimension) has typically only half of the resolution of the pixel in the x- and y-dimensions. All fluorescence live-cell images are presented as maximal intensity projection of three-dimensional stack images. The axial (z) step is 200 nm.

The movies were obtained using a spinning-disk confocal microscope (Revolution XD Confocal System; Andor Technology, South Windsor, CT) equipped with a spinning-disk unit (CSU-X1; Yokogawa, Tokyo, Japan), a microscope (Ti 2000; Nikon) with a 100 Å∼/1.4 NA oil immersion objective, and an electron-multiplying CCD camera (iXON DU-885; Andor Technology). The axial (z) step is 300 nm. A z-stack was acquired every 10 s for 100 times.

Foci quantification

Quantification of telomere clusters on live-cell images was performed using a home-made Matlab (MathWorks, Natick, MA) application (Q-foci; Ruault et al., 2011). Images were deconvolved before quantification using the Meinel algorithm in MetaMorph (eight iterations; sigma, 0.8; frequency, 3; MDS Analytical Technologies, Sunnyvale, CA), nuclei were segmented by Otsu thresholding, and local intensity maxima were detected in segmented nuclei. Each local intensity maximum was considered as a potential telomere cluster candidate. Because Rap1-GFP foci brightness is highly variable, depending on the number of telomeres in the cluster, the results did not show a clear cut-off in scores between small clusters and false positives. Consequently the threshold for classification of a possible telomere cluster (candidate) was set manually based on the control experiments (wild type). This threshold was used for other data sets.

Abbreviation used:

rDNA

ribosomal DNA