Modeling sequence evolution in HIV-1 infection with recombination

Abstract

Previously we proposed two simplified models of early HIV-1 evolution. Both showed that under a model of neutral evolution and exponential growth, the mean Hamming distance (HD) between genetic sequences grows linearly with time. In this paper we describe a more realistic continuous-time, age-dependent mathematical model of infection and viral replication, and show through simulations that even in this more complex description, the mean Hamming distance grows linearly with time. This remains unchanged when we introduce recombination, though the confidence intervals of the mean HD obtained ignoring recombination are overly conservative.

1. Introduction

The theory of population genetics has been applied to a vast number of organisms, from primates to bacteria and virus. Combined with coalescent theory and phylogenetic methods, it can trace back in time the dynamics and evolution of species. Previously (Lee et al., 2009; Giorgi et al., 2010), we developed an intra-host evolutionary model for HIV-1 during early infection, and tested the genetic diversity of early HIV-1 samples against a null model of neutral evolution. The method allows one to distinguish infections that are established by a single virus from those initiated by multiple viruses. It also allows one to estimate the time since infection and the onset of immune selection. Though the model is now widely used and performs well on different datasets (Keele et al., 2008; Wood et al., 2009; Keele et al., 2009), including very large ones obtained through 454 sequencing (Fischer et al., 2010), the viral lifecycle described in Lee et al. (2009) was a simplification of the underlying biology. Here we study a more realistic model of HIV replication and how the new approach affects the results.

Following in Sewall Wright’s footsteps, Kimura (1968) used the Fokker-Planck equation to develop a continuous time model of population genetics. This was later expanded by Gillespie (1984) who developed explicit simulation frameworks for continuous time stochastic models in population genetics.

In the first part of this paper, we develop a continuous time, age-dependent model to describe the genetic drift in a growing viral population. We use a deterministic approach and derive a model using the Von Foerster equation and renewal condition with age-dependent birth and death rates. We then expand this into a completely stochastic model using the Fokker-Planck equation and follow, through simulation, the variation in genetic distances across a finite population of viral sequences. We measure genetic distances in the sample using Hamming distances (HD), defined as the number of base positions at which two sequences differ. Model simulations show that even in this fully randomized model, the growth in mean HD, averaged over multiple runs, is linear in time, and that different choices of birth and death rates only affect the rate of the growth but not this behavior.

In the second part of the paper we study how recombination affects the results. Genetic recombination takes place when a newly constructed nucleic acid molecule arises from multiple template strains. Recombination events in HIV-1 are common (Onafuwa-Nuga et al., 2009; Robertson et al., 1995; Wooley et al., 1997; Sabino et al., 1994) and result from multiple infections of the same target cell (Chen et al., 2005; Dang et al., 2004; Jung et al., 2002; Levy et al., 2009). A number of studies have indicated that the HIV recombination rate is several times larger than its mutation rate (Batorsky et al., 2011; Jetzt et al., 2000; Levy et al., 2009; Shriner et al., 2004; Suryavanshi et al., 2007; Neher et al., 2010; Zhang et al., 2010), and that recombinants reach fixation and undergo a rapid expansion in the population, thus representing an evolutionary shortcut (Ramirez et al., 2008).

Previous recombination studies have suggested that recombination affects a virus’s ability to escape CTL responses (Mostowy et al., 2011) and has a significant impact on the emergence of drug resistance (Althaus et al., 2005; Fraser, 2005; Kouyos et al., 2009; Moutouhet al., 1996; Vijay et al., 2008). In Vijay et al. (2008) the authors use a simulation to study the effects of recombination on the changes in mean Hamming distance with time. However, in the works cited above, it is assumed that the host’s immune response plays a major role in defining the fitness of the viral strains. In this paper, we address recombination in our original model of exponential viral growth with no positive selection pressure from the environment, a scenario that is relevant to early dynamics of viral growth in the acute phase of HIV infection prior to the initiation of an effective adaptive immune response. Under this scenario, we see that recombination does not affect the linearity in time of the mean HD growth, though it does change the growth of the variance of the HD distribution.

2. Results

2.1. Continuous time model of viral evolution

In Lee et al. (2009) we described two simplified models of viral evolution, where cell infection and cell death happen at fixed, discrete times. In this section we present a more realistic model based on a continuous time birth and death process. We also introduce age-dependency in the model, where age represents the time since a cell was infected. The corresponding stochastic formulation is presented in Appendix A.

As stated in Lee et al. (2009), we assume that one unique genetic strain, called the transmitted/founder virus, initiates the infection. In general, it takes some time before the host’s immune response kicks in, and since during the early phase of the infection the viral population is much smaller than the target cell population, we assume that viral evolution is initially driven by exponential growth and random accumulation of mutations at allowed sites (Ribeiro et al., 2010). Genetic diversity can also be achieved through recombination, which takes place when two or more distinct strains infect one cell and give rise to new, recombined genomes. However, when the viral population is sufficiently small with respect to the target cell population, the effect of recombination during this initial phase of the infection should be negligible. Under these hypotheses, mutations from the founder strain accumulate randomly following a Poisson distribution (Lee et al., 2009).

In all our analyses, we ignore the presence of proteins such as APOBEC, which results in hypermutated sequences and can modify the mutation rate. We have included the capability to identify and exclude APOBEC mediated hypermutation in previous implementations of our model (Giorgi et al., 2010).

Once a virion enters a cell, the HIV enzyme reverse transcriptase transcribes the viral RNA into DNA, which is then integrated into the host genome. A viral genome integrated into the DNA of the host cell is called a provirus. The time from viral entry into a target cell until the first virions start budding out (called the eclipse phase) has been estimated to last about 24 hours (Perelson et al., 1996; Markowitz et al., 2003), although in some cases the virus can lie dormant inside the cell for years. The infected cell will on average survive another 24 hours while producing virus (Markowitz et al., 2003), and during this time it will produce tens of thousands of new viral particles (Chen et al., 2007). HIV is rapidly cleared from circulation, with an average half-life of roughly 45 minutes (De Boer et al., 2010; Ramratnam et al., 1999), and on average, in early infection, between 6 and 10 virions go on to successfully infect new cells (Ribeiro et al., 2010). The number of virions that successfully infect new cells in this initial phase is called the basic reproductive ratio, usually denoted R₀.

In all that follows, we neglect the time a virus spends outside a cell and choose to follow provirus instead. We only consider mutations that may occur during reverse transcription, and neglect the extremely rare mutations that happen after integration in the cell’s genome.

Given this framework, we let I(a, g, t) be the number of infected cells that at time t are of age a (i.e. a represents the time elapsed since the cell was infected) and generation g (i.e. the genome it carries has undergone g infection cycles since the transmitted virus, with one reverse transcription event occurring at each infection). Here a and t are non-negative, real variables, and g is a non-negative integer.

We assume that both the birth rate α(a) (the number of cells infected by each cell of age a per unit time) and death rate β(a) (the number of cells of age a that die per unit time) are functions that depend only on the age of the infected cell, a, and not on time t. Notice that α(a) is in fact an infection rate. Here we choose to call it birth rate to show that the classic birth and death process provides a good infection model when neglecting the time the virus spends outside the cell. Let Λ denote the lag before new virions start budding out of the infected cell (i.e. the length of the eclipse phase) and impose that α(a) = 0 for a ≤ Λ. In the discussion that follows, we implicitly assume that all functions evaluate to zero on negative arguments.

It has been shown (Von Foerster, 1959; Nisbet et al., 1982; Huddleston et al., 1983) that the dynamics of an age-structured birth and death system is determined by the following differential equations, called the Von Foerster equation and the renewal condition, respectively:

$$\begin{array}{c}\frac{\partial }{\partial t}I(a,g,t)+\frac{\partial }{\partial a}I(a,g,t)=-\beta (a)I(a,g,t)\\ I(0,g+1,t)={\int }_0^{t}I(a,g,t)\alpha (a)da\end{array}$$ (1)

with initial conditions

$$I(a,g,0)=\{\begin{array}{cc}{I}_0& \text{if}a=g=0\\ 0& \text{otherwise}.\end{array}$$ (2)

The first equation in (1) describes how infected cells are lost via death, whereas the second one describes how newly infected cells are formed via births. This is a classic age-structured birth and death system (Murray, 2002; Kevorkian, 2002), with the addition of the parameter g for generation cycles. Such models are called age-maturity structured and have been described in the context of cell kinetics, where the parameter g in that case represents the number of cell divisions (Bernard et al., 2003; Zilman et al., 2010).

Let $f(a)=\alpha (a){\text{e}}^{-{\int }_0^a\beta (s)ds}$. Notice that ${\text{e}}^{-{\int }_0^a\beta (s)ds}$ can be interpreted as the expected fraction of cells whose age at death is greater than a. Therefore, f(a) represents the expected rate at which an infected cell survives up to age a and starts new infections. Let f̃ be the Fourier transform of f, i.e.

$$\stackrel{\sim }{f}(k)={\int }_{\mathrm{\Lambda }}^{\infty }f(a){\text{e}}^{\mathit{ika}}da.$$ (3)

We assume that β(a) is a strictly positive function with lim_a→∞ β(a) ≠ 0 and such that lim_a→∞ f (a) = 0. It follows (see Appendix B) that a closed solution of Eq. (1) is given by

$$I(g,t)=\frac{I_0}{2\pi }{\int }_0^t{e}^{-{\int }_0^a\beta (s)ds}{\int }_{-\infty }^{\infty }\stackrel{\sim }{f}{(k)}^g{\text{e}}^{-ik(t-a)}dkda$$ (4)

2.2. Mean Hamming Distance

In Keele et al. (2008) we attained plasma samples from HIV-1 subjects early after infection, from which viral sequences were derived. Roughly 80% of those subjects were infected by a single viral strain, and we called those infections homogeneous. Under our model of neutral exponential growth, mutations from the founder strain accumulate randomly following a Poisson distribution due to reverse transcription errors introduced when the virus infects a cell. As mutations accumulate, the mean of the Poisson distribution grows with time. Therefore, given a sample of viral sequences taken from a homogeneously infected subject, it is possible to count the number of mutations across all pairs of sequences, fit a Poisson distribution to the frequency counts, and use the mean of the Poisson to estimate how much time has elapsed since the beginning of the infection.

The Hamming distance (HD) between two genetic sequences is defined as the number of bases at which the two differ. In our original model (Lee et al., 2009; Giorgi et al., 2010), we showed that for homogeneous infections, in the absence of selection, the mean HD is given by

$$E[HD](t)=\sum _{d}dP(HD=d\mid t)\approx \sum _d\frac{{\sum }_{g}I(g,t)P_{\mathit{Binom}}(d;2{gN}_B,\epsilon )}{{\sum }_g{I}_g(t)}$$ (5)

where ε is the viral mutation rate per base per generation, N_B is the length of the sequences, and g is the number of generation steps since the most recent common ancestor, or MRCA. P_Binom(d; n, p) is the binomial distribution with parameters n and p:

$$P_{\mathit{Binom}}(d;n,p)=\left(\begin{array}{c}n\\ d\end{array}\right)p^d{(1-p)}^{n-d}.$$

Here we are neglecting the possibility of multiple mutations at the same site, as these are expected to be very rare in early HIV infection (Lee et al., 2009).

In the synchronous infection model described in Lee et al. (2009), we assume that each provirus produces R₀ new proviruses and that all infected cells are of the same generation and are born and die synchronously. We calculated Eq. (5) for $I(g,t)=R_0^g$ (synchronous model) and for a slightly more complicated, but still simplified, scenario in which cells produce virions in two synchronous bursts, as a first approximation to an asynchronous infection. In both cases we saw that the mean HD (calculated over all pairs of sequences in a given sample) grows linearly with time and is proportional to 2gεN_B. In Lee et al. (2009) we showed that the MRCA is at most a couple of generations away from the transmitted/founder strain, and it coincides with the transmitted/founder strain in most cases. Since, in HIV infections, one replication cycle is roughly two days (Markowitz et al., 2003), we can use this result to estimate the time since the MRCA in early homogeneous infections (Keele et al., 2008; Wood et al., 2009; Keele et al., 2009).

We now show that the linearity in time of the mean HD growth remains unchanged when substituting the more general expression of I(g, t) from Eq. (4) into Eq. (5). We first derive the expression of the mean HD at generation g when the death rate is constant, i.e. β(a) = β₀ for all a > 0, and the birth rate is a piecewise linear function in age of the form α(a) = 0 for all a ≤ Λ, and α(a) = α₀(a − Λ) for all a > Λ. Expanding Eq. (4) using these particular birth and death rates, one obtains

$$I(g,t)=I_0\frac{{\alpha }_0^g}{(2g)!}\left[{(t-\mathrm{\Lambda }g)}^{2g}-{(\mathrm{\Lambda }g)}^{2g}\right]{\text{e}}^{-{\beta }_{0}t}$$ (6)

Given the biological properties of HIV infection, we can impose the condition that both β and α be positive, analytic, and asymptotically constant functions, and, in addition, that α(a) be null both at 0 and at infinity. We can then extend the above derivation of I(g, t) for general death and birth rates by noting that a bounded death rate function β(a) can always be approximated with a step function (a function that is constant on a given partition), and f̃ in Eq. (4) can be calculated for a generic birth rate from Eq. (3) using the Taylor expansion of α.

Finally, we use a simulation based on equations (4) and (5) to generate I(g, t) for different choices of piecewise linear death rate functions and a piecewise linear birth rate function as defined above. For these choices of birth and death rate functions, we generate the full population of infected cells, out of which we randomly sample N₀ sequences at each day since the start of infection. At any given time t, we assume that each infected cell in I(g, t) carries one proviral strain that has undergone exactly g infection cycles from the MRCA. Therefore, for each one of the N₀ sequences, knowing how many infection cycles it has undergone, we randomly draw from a Poisson distribution the number of mutations it has accumulated from the MRCA. We then calculate the mean intersequence HD assuming a star phylogeny, in other words, for any two given sequences s₁ and s₂ in the sample, HD[s₁, s₂] = HD₀[s₀, s₁] + HD₀[s₀, s₁], where s₀ is the MRCA, and HD₀ is the Hamming distance from the MRCA. Finally, we calculate the mean HD over all pairs and average over 10,000 runs. In Figure 1 we show the results when both death and birth rates are linear functions of age. Different choices of birth and death rates do not change the linearity in growth of the mean HD, but only affect the rate at which the mean HD grows (results not shown). This result confirms what we have previously shown in Lee et al. (2009) using a discrete generation model, namely that the mean HD is proportional to 2εgN_B.

Figure 1.

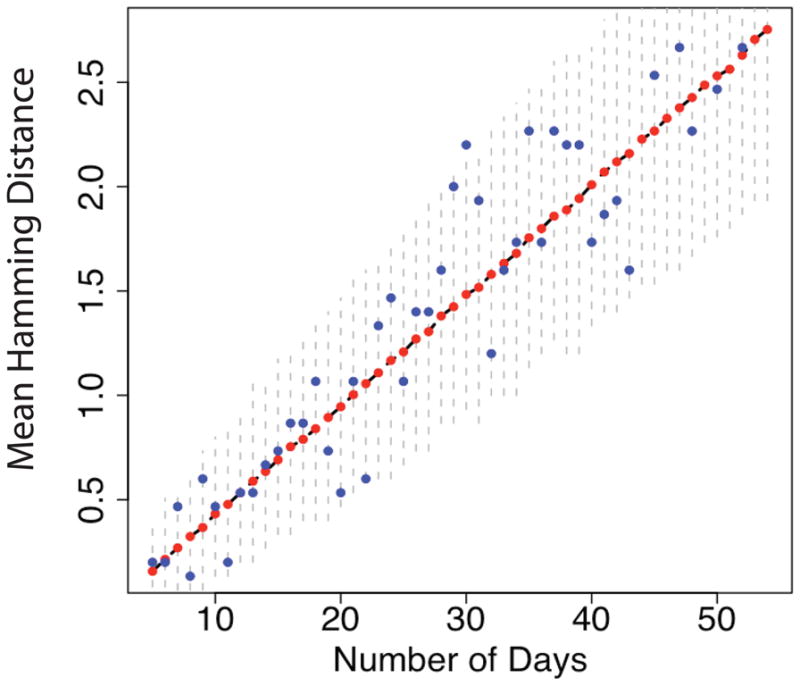
We generated I(g, t) using the continuous, age-dependent model described in Section 1. Here N_B = 2, 600 base pairs, α(a) = α₀(a − Λ) for a > Λ, and β(a) = β₀a. At each day we sampled N₀ = 30 sequences, calculated the mean HD and then averaged over 10,000 runs. The blue dots shot the mean HD for one particular run, the red dots the average over all runs, and the black dashed line underneath shows the mean HD calculated from the theoretical framework. The vertical dashed lines are the 95% confidence intervals.

2.3. Recombination

We now discuss the effect of recombination on the growth of the mean HD. We start with the same scenario described in Lee et al. (2009): a single infecting strain establishes infection, no selection, exponentially growing viral population, and a negligible probability of observing doubly mutated sites (we show in Lee et al. (2009) that the probability of back mutations is $\le O\left(\frac{g^2{\epsilon }^2}{N_B}\right)$, which is negligible in our scenario of early infections). This is an apt description of early, heterosexually transmitted, HIV infections (Keele et al., 2008), and, under this scenario, prior to the onset of selection, the HD frequency counts follow a Poisson distribution. However, while in a Poisson model the mean HD of a sample of N sequences should approximately equal the HD variance times $\frac{N}{N-1}$, the HD variance was 4.7% lower than expected when averaging across all homogeneous subjects described in Keele et al. (2008). This difference fell within the 95% CI and was not statistically significant. Nonetheless, given the current advances in sequencing technology and the availability of larger sample sizes (i.e. 454 sequencing (Margulies, 2005)) it’s interesting to investigate whether this difference is due to recombination, which we neglected in our original model.

We now show that in the presence of recombination the HD frequency counts no longer follow a Poisson distribution, thus explaining possible divergences between the variance and the mean. As discussed in the previous section, in the absence of recombination, our simulation results show that both the continuous and stochastic models yield the same basic results as the previous simplified discrete generation model, namely that the mean HD is proportional to 2εgN_B.

Preliminary phylogenetic analyses conducted on viral samples attained at serial time points from early, homogeneous infections suggest that the mutation rate ε may vary greatly across patients (Wallstrom et al., 2010). Therefore, in all that follows, we revert to our simplified, synchronous infection model and assume that changes in the mean HD growth rate caused by possible divergences from such a simplified model are folded into the parameter ε, which needs to be measured in each patient individually.

To allow for the possibility of multiple strains infecting the same cell and possibly giving rise to a recombinant strain, we introduce a recombination rate 0 < ρ < 1. As a simplification, at each generation we let each viral strain either undergo a mutation event or a recombination (not both) with probabilities ρ and (1 − ρ)ε respectively. The more general case can easily be solved using the same methods. We assume ρ is constant in time and, for simplicity, we also assume that the parental strains recombine at a single position θ, which is a uniformly distributed random variable between 0 and the length N_B of the genome. Given the MRCA s₀, let HD₀(s, t) be the Hamming distance of sequence s from s₀, where s was sampled at time t. For sufficiently small sample sizes, early homogeneous infections follow a star-like phylogeny and both the HD₀ and the intersequence HD follow a Poisson distribution (Lee et al., 2009; Keele et al., 2008). In particular, the expectations are related, i.e. E[HD] = 2E[HD₀]. Under these assumptions, the HD₀ probability distribution at time t + dt is given by

$$\stackrel{\sim }{P}({HD}_0=d;t+dt)=(1-\rho )P_{\epsilon }({HD}_0=d;t+dt)+\rho P_{\rho }({HD}_0=d;t+dt)$$ (7)

where P_ε and P_ρ are the probability of a genome being at distance d from s₀ after a mutation or a recombination event, respectively. Suppose that P_ρ has mean μ_ρ and variance ${\sigma }_{\rho }^2$. Similarly, we denote by μ_ε and ${\sigma }_{\epsilon }^2$ the mean and variance of P_ε. Then

$$\stackrel{\sim }{\mu }(t)=E({HD}_0\mid t)=(1-\rho ){\mu }_{\epsilon }(t)+\rho {\mu }_{\rho }(t)$$ (8)

and

$${\stackrel{\sim }{\sigma }}^2=\mathit{Var}({HD}_0)={\sigma }_{\epsilon }^2+2\rho {\mu }_{\epsilon }({\mu }_{\epsilon }-{\mu }_{\rho })+\rho ({\mu }_{2,\rho }-{\mu }_{2,\epsilon })-{\rho }^2{({\mu }_{\epsilon }-{\mu }_{\rho })}^2$$ (9)

where μ_2,ε and μ_2,ρ indicate the second moments of P_ε and P_ρ, respectively. When ρ = 0, we get ${\stackrel{\sim }{\sigma }}^2={\sigma }_{\epsilon }^2$ and when ρ = 1, ${\stackrel{\sim }{\sigma }}^2={\sigma }_{\rho }^2$. Notice also that when μ_ε = μ_ρ one has

$${\stackrel{\sim }{\sigma }}^2(t)={\sigma }_{\epsilon }^2(t)+\rho ({\mu }_{2,\rho }(t)-{\mu }_{2,\epsilon }(t))$$ (10)

In what follows, we suppress the variable t when it is clear from the context. When viral genomes undergo mutation

$$P_{\epsilon }({HD}_0=d;t+dt)=\sum _{k=0}^d\stackrel{\sim }{P}(d-k;t)P_m(k;dt)$$ (11)

where P_m(k; dt) is the probability of having k mutations appear in a time interval dt. Assuming the independence of P̃ and P_m, we can use the fact that cumulants add under convolution. Let dλ be the mean of the distribution P_m in the time interval dt (for example, in a discrete, synchronous model, it would be the mutation rate times the sequence length). Then, omitting O(dλ²) terms,

$$\begin{array}{ccc}{\mu }_{\epsilon }(t+dt)& =& \stackrel{\sim }{\mu }(t)+d\lambda \\ {\sigma }_{\epsilon }^2(t+dt)& =& {\stackrel{\sim }{\sigma }}^2(t)+d\lambda \\ {\mu }_{2,\epsilon }(t+dt)& =& {\stackrel{\sim }{\mu }}_2(t)+(1+2\stackrel{\sim }{\mu }(t))d\lambda \end{array}$$ (12)

2.4. Recombination alone

In order to compute P_ρ, it is useful to first envision a scenario in which an initial, genetically diverse population of I₀ sequences is allowed to grow exponentially with no accumulation of mutations. In other words, we set ε = 0 and ρ = 1. Suppose the HD₀ distribution of the I₀ sequences has initial mean μ₀ and variance ${\sigma }_0^2$. At each generation a recombination position θ is drawn randomly from a uniform distribution, with θ = 0, …, N_B, where the two parental strings split and recombine. If θ = 0, then the recombinant is exactly the first sequence, whereas if θ = N_B, the recombinant is the second sequence. Under this scenario it is easy to see that the mean Hamming distance of a population of sequences will remain unchanged from the initial μ₀, whereas the total variance in the population will decline. As we show in Appendix C, at any generation g, the expectation values of the mean HD₀, μ(g), and the estimator of the variance s²(g) are given by

$$\mu (g)={\mu }_0$$ (13)

and

$$s^2(g)=\frac{N_B-1}{N_B}{\mu }_0+\frac{1}{N_B}{\sigma }_0^2+2\frac{{\sigma }_0^2-{\mu }_0}{g+2}\left[{\left(\frac{N_B}{N_B+1}\right)}^{g-1}+O(N_B^{-1})\right]{\prod }_{j=0}^{g-1}\frac{N_j-1}{N_j}$$ (14)

where μ₀ and ${\sigma }_0^2$ are the mean and variance HD₀ of the initial population of I₀ sequences, N_j is the size of the population at generation j, and N_B is the total sequence length.

In order to test the formulae in (14), we devised a simulation based on the previously described synchronous infection model (Lee et al., 2009) where no site is mutated more than once (infinite site assumption). We start at generation g = 0 with I₀ sequences, each with an initial HD₀ drawn from a probability distribution with mean and variance μ₀ and ${\sigma }_0^2$ respectively (in the simulations shown in the figures we used ${\mu }_0={\sigma }_0^2=10$). At each later generation we resample $I_0{R}_0^g$ sequences from the previous population of size $I_0{R}_0^{g-1}$, and introduce recombination and mutation events as described below.

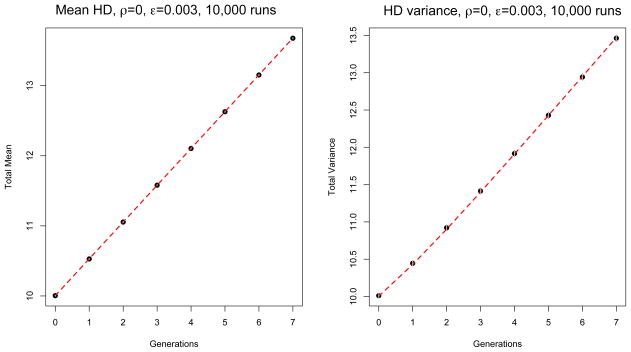
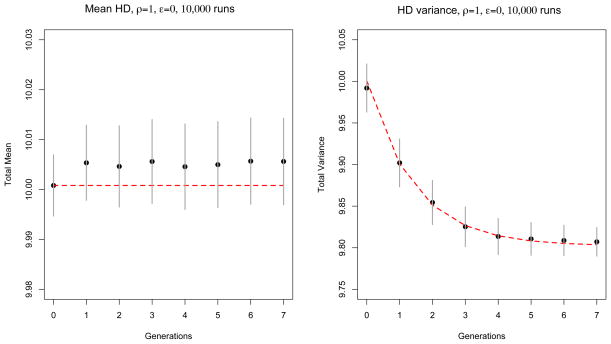
We first tested the scenario where ρ = 0 and ε = 0.003 (we used a much larger value than the estimated 10⁻⁵ HIV-1 mutation rate in order to make mutations accumulate faster since by the time we reach a population size of 2¹⁰ or larger the simulation becomes computationally intensive). In the mutation only scenario, we randomly draw the number of positions to mutate from a Poisson distribution with mean εN_B, where N_B is the length of the sequences. If HD₀(s, g − 1) is the HD₀ of a sequence s at generation g − 1, and d is randomly drawn from Pois(λ = εN_B), then HD₀(s, g) = HD₀(s, g − 1)+d, and the d positions where these mutations take place are drawn randomly from a uniform distribution. Conversely, in the recombination only scenario, i.e., when ρ = 1 and ε = 0, at every generation g, for every sequence s in the sample, we draw the two parents from the previous generation and a recombination position θ uniformly and form s as the recombinant child.

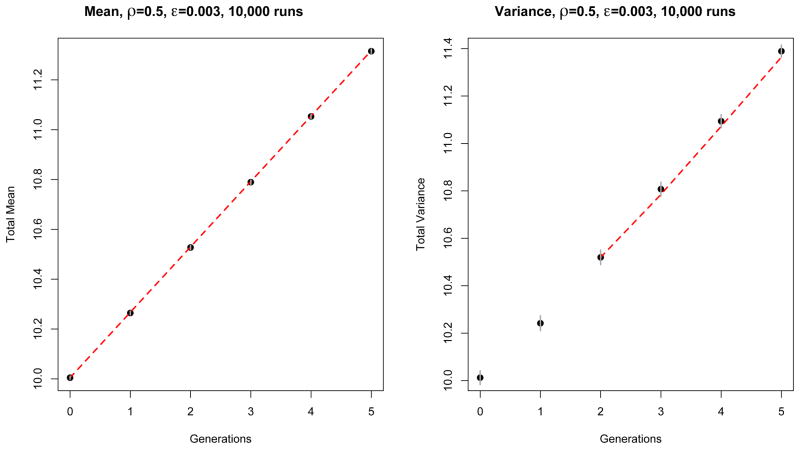
In Figures 2 and 3 we show the mean HD₀ and variance HD₀ for the two scenarios respectively, averaged over 10,000 runs. The simulation is represented by the black dots, and the theoretical results are shown in the red dashed line. 95% confidence intervals are shown in gray, though in Figure 2 they are barely visible. In both scenarios the simulation results fall within the 95% confidence intervals from the theoretical expectations. Note that in Figure 3, since the fluctuations at different times are positively correlated, all points remain above the mean, following a large fluctuation in the first generation.

Figure 2.

Comparison between theory (red dashed line) and simulation (black dots) for an exponentially growing population with ρ = 0 (no recombination) and ε = 0.003. Mean and variance of the HDs are averaged over 10,000 runs. At generation g = 0 the initial population is made of 100 sequences with HD mean and variance λ₀ = 10. Confidence intervals (±1.96 times the standard deviation over runs) are represented by vertical gray segments, which are smaller than the size of the symbols in the figure and hence are not visible.

Figure 3.

Comparison between theory (red dashed line) and simulation (black dots) for an exponentially growing population with ρ = 1 and ε = 0 (recombination only). Mean and variance of HD are averaged over 10,000 runs. At generation g = 0 the initial population is made of 100 sequences with HD mean and variance λ₀ = 10. Confidence intervals (±1.96 times the standard deviation over runs) are represented by vertical gray segments. Errors at different time points are positively correlated.

2.5. Mutations and Recombination

In Appendix C we generalize the methods used to derive Eq. (14) and find recursive formulae for the general case when both ρ and ε are non-zero. For the mean HD₀ we obtain

$$\mu (g)=N_B\epsilon (1-\rho )g+{\mu }_0.$$ (15)

This shows that even in the presence of recombination, the mean HD₀ grows linearly like in the mutation only scenario. The slope of the linear growth here is diminished by a factor 1 − ρ, which reflects the fact that in our model a recombining sequence does not mutate.

Let ξ = (1 − ρ)ε, and let x and y be any given positions in the genome. In Appendix D we derive the following expressions for the HD₀ mean μ_x at position x, the HD₀ variance estimator $s_x^2$ at position x, and the HD₀ covariance estimator s_xy between any two positions x and y:

$${\mu }_x(g+1)={\mu }_x(g)+\xi$$ (16)

$$s_x^2(g+1)=\frac{N_g-1}{N_g}{s}_x^2(g)+\xi (1-\xi )$$ (17)

$$s_{xy}(g+1)=\left(1-\rho \frac{y-x}{N_B+1}\right)\frac{N_g-1}{N_g}{s}_{xy}(g)-\frac{N_{g+1}}{N_{g+1}-1}{\xi }^2+\xi \left(\epsilon -\frac{1}{N_{g+1}}\right)-2\epsilon {\xi }^2\frac{1-\epsilon }{N_{g+1}}$$ (18)

By summing Eqs. (16), (17), and (18) across all positions x and y we get the mean HD₀ and the variance estimator s²(g) in the general case when both mutation and recombination are present. Again, we verified these theoretical derivations against numerous simulation runs. The simulation was designed as follows.

For a fixed recombination rate ρ and mutation rate ε, we first draw the number of recombination events from a binomial distribution with probability ρ. Subsequently, for each sequence s in the new generation, if s is a recombinant, we uniformly draw the two parents and a recombination position θ, and form s as the recombinant child. Else, we randomly draw a number of mutated positions from a Poisson distribution with mean εN_B, where N_B is the length of the sequences. If HD₀(s, g − 1) is the HD₀ of a sequence s at generation g − 1, and d is randomly drawn from a Poisson distribution with mean εN_B, then HD₀(s, g) = HD₀(s, g − 1) + d, and the d positions where these mutations take place are drawn randomly from a uniform distribution.

Because of computational limitations, we limited the number of generations to 6–8 and simulated 10,000 sets, then averaged the HD₀ means and variances and compared the results to the theoretical results discussed in the previous sections. Instead of simulating from the very beginning of the infection, we started at generation g = 0 with I₀ = 100 sequences, each proviral sequence with an HD₀ from the founder strain randomly drawn from a Poisson distribution with mean λ = 10. The code was written in R (R Development Core Team, 2010).

In Figures 4, 5, and 6 we compare the simulation results with the theoretical derivations. The simulation results are denoted with the black dots and the theoretical derivations with the red dashed lines. Notice that because Eq. (D.3) and Eq. (D.4) were obtained up to terms of the order N⁻², where N is the sample size, when we carry the summation over all positions to obtain the general expression for s²(g), the fluctuations become of the order N⁻¹. In Figure 6 we omit the comparison with the theoretical derivation for the first two generations. In fact, for these, the sample size is small enough that fluctuations are sizable. However, starting from g = 3, theory and simulation overlap almost perfectly.

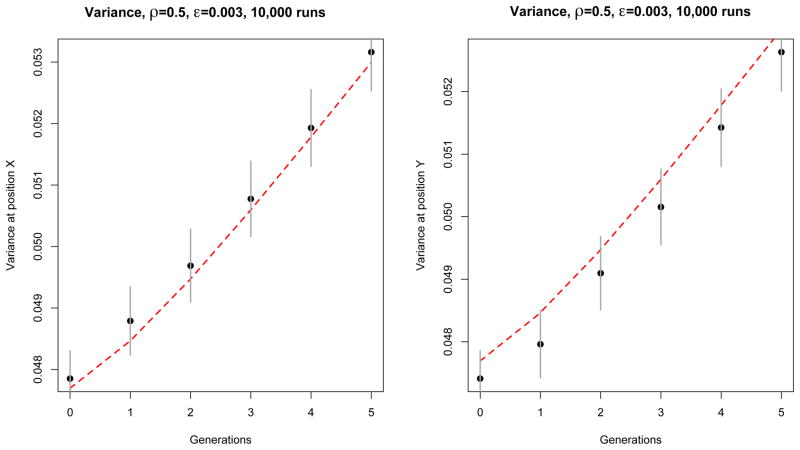
Figure 4.

Comparison between theory (red dashed line) and simulation (black dots) of the contribution of each position (denoted x and y, located at one third and two thirds of the genome) to the variance of HD₀ for an exponentially growing population. Here ρ = 0.5 and ε = 0.003. These results were obtained from 10,000 independent simulation runs with the same initial conditions, as described in the main text. The simulation is represented by the black dots, and the theory by the dashed red line. Confidence intervals (±1.96 times the standard deviation over runs) are represented by vertical gray segments. Notice that the errors are positively correlated.

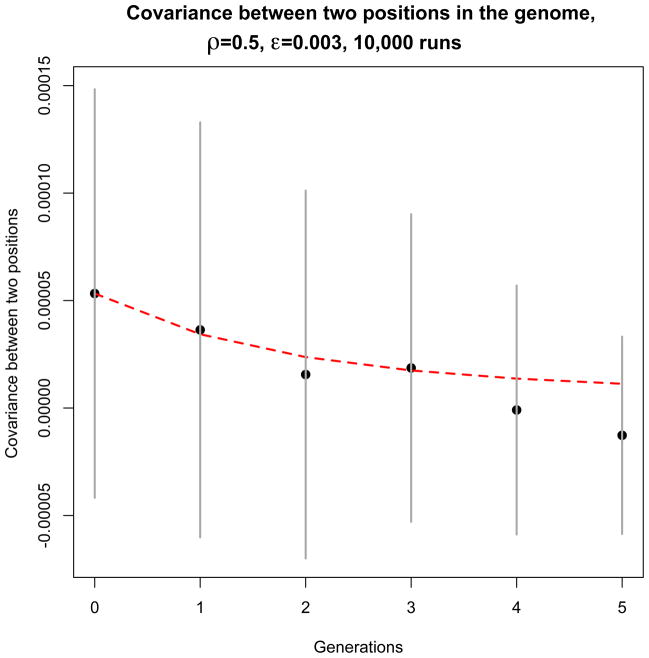
Figure 5.

Comparison between theory (red dashed line) and simulation (black dots) of the contribution of each position pair (denoted x and y, which here we took to be one third and two thirds of the genome) to the variance of HD₀ for an exponentially growing population. Here ρ = 0.5 and ε = 0.003. These results were obtained from 10,000 independent simulation runs with the same initial conditions, as described in the main text. The simulation is represented by the black dots, and the theory by the dashed red line. Confidence intervals (±1.96 times the standard deviation over runs) are represented by vertical gray segments.

Figure 6.

Comparison between theory (red dashed line) and simulation (black dots) of the mean and variance HD₀ for an exponentially growing population with ρ = 0.5 and ε = 0.003. The left panel represents the mean, and the right panel the variance, both averaged over 10,000 runs. Like before, at generation g = 0 the initial population is made of 100 sequences with HD mean and variance λ₀ = 10. The simulation is represented by the black dots, and the theory by the dashed red line. Confidence intervals (±1.96 times the standard deviation over runs) are represented by vertical gray segments. In the right panel, the first few generations are omitted. The theory we developed neglects early stochastic events, which are of the order $\frac{1}{N_g}$, where N_g is the population size at generation g. Hence, we find that only when the population size is large enough, do theory and simulation overlap.

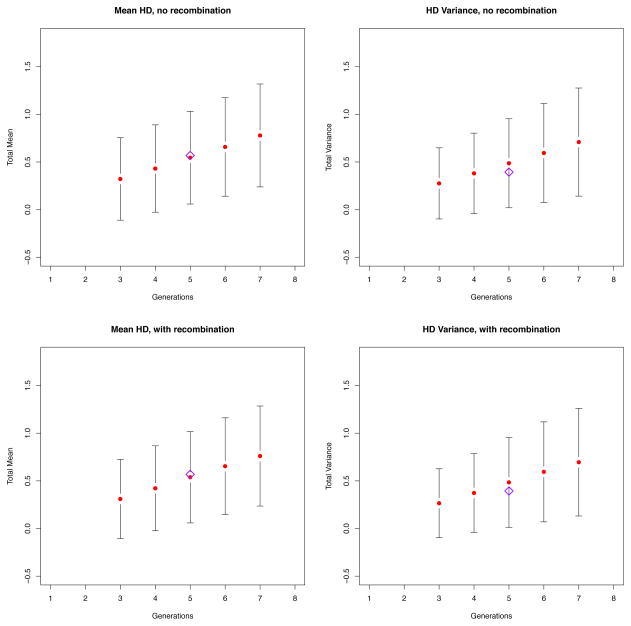
We performed a simulation with parameters taken from the early homogeneous sample SUMA, previously described in Keele et al. (2008) and Lee et al. (2009) (Figure 7). This time the initial population consisted of a single infecting strain and, at each generation, we sampled N = 35 sequences, which was the sample size of the original alignment. Under this particular scenario, on average, the HD variance was lower than the mean HD. This was consistent with what observed across all homogeneous patients in Keele et al. (2008), for whom the HD variance was, on average, 4.7% lower than what expected from a Poisson model. According to our original Poisson model, SUMA was estimated to be 5 generations into the infection, which was consistent with a Fiebig stage II. In Figure 7 we show that adding recombination to the model does indeed cause the HD frequency counts to no longer follow a Poisson distribution, but the effect is so small that the estimate attained through our original model still remains valid.

Figure 7.

Simulation runs based on the patient SUMA (Keele et al., 2008). Assuming a single strain initiated the infection, at every generation we sampled N = 35 sequences, calculated the HD mean and HD variance, and then repeated 10,000 times. The top panels represent the simulation run in the absence of recombination, the bottom panels represent the simulation when recombination was present (ρ = 2 × 10⁻⁵, as estimated in Neher et al. (2010)). The red dots represent the HD mean (left) and HD variance (right) averaged over 10,000 runs. The black vertical bars represent the 95 % CIs. Finally, the purple diamond denotes SUMA’s HD mean (left) and HD variance (right). As one can see, the effect of recombination is so small that both models fit the data well, thus validating our previous approach.

3. Conclusions

We developed a model to study the rates of evolution and genetic diversification in acute HIV-1 infection. We used the model to examine the effects of recombination in acute HIV infection sampled prior to the onset of selection and during the exponential growth of the viral population. Previously, we neglected recombination and used a simplified model of infection where all infected cells produced virions and died synchronously (Lee et al., 2009). Using this model we showed that the mean intersequence HD grows linearly with time as E(HD) ∝ 2εN_Bg, where ε is the mutation rate, N_B is the length of the sequences, and g is the generation number. We applied this model to homogeneously infected subjects (Keele et al., 2008; Wood et al., 2009) and, using the linearity in time of the mean HD, for each homogeneously infected subject, were able to estimate the time since the most recent common ancestor.

In this paper, we explored a more complex model of HIV replication. This was motivated by the fact that in general, our estimates in Keele et al. (2008) were well correlated with the time since the infection obtained from clinical data. However, in a Poisson model, we expect the mean HD₀ to be equal to the variance of the HD₀ times $\frac{N-1}{N}$, where N is the sample size. Even though not statistically divergent from a Poisson distribution, all homogeneous subjects presented in Keele et al. (2008) had a variance HD that was on average 4.7% lower than the expected theoretical value had the distribution been a Poisson. Here we showed that even in an age-dependent continuous model of infection, the mean HD₀ still grows linearly with time, and this continues to hold in a fully stochastic model. While recombination did not affect the linearity of the mean HD₀ growth, in the presence of recombination the HD₀ distribution is no longer Poisson. In this paper we modeled the new dependency of the variance HD₀ with time, as it no longer equals that of the mean HD₀. We also showed how this new framework helps explain some of the divergence between mean and variance HD in homogeneous samples previously described in Keele et al. (2008). Furthermore, because the effect is small, our work validates our previous methods that estimate the time of infection based on a Poisson model.

This work suggests that our previous, simplified model (Lee et al., 2009) provides reasonable estimates of the time and number of generations since a founder strain initiates the infection even in the presence of in vivo recombination. It is also robust against instances of in vitro recombination (Salazar-Gonzales et al., 2008), which becomes a relevant issue particularly when using 454 deep sequencing (Fischer et al., 2010). For 454 samples in particular, where sample sizes can reach the tens of thousands, our method provides a robust alternative to computationally intense methods such as those employed in the software package BEAST (Drummond et al., 2007).

Finally, we notice that the mathematical framework developed here can be used in cell division models where it is relevant to keep track of the number of divisions cells undergo (generations) (Zilman et al., 2010; Bernard et al., 2003).

Highlights.

• We describe a continuous time, age-dependent model of early HIV infection.

• We show that the new model yields the same results as a simplified model we published in 2009.

• We introduce recombination in the model.

• We show how recombination affects the results compared to our previous model.

Appendix A. Stochastic model

We present a stochastic formulation of the continuous model presented in Section 2.1. In all that follow we use the same mathematical framework developed for birth and death stochastic processes, with the added parameter g for generation. To keep the discussion more general, we will use the word “births” instead of “new infections.” Clearly, when applied to the infection model described in this paper, new births are newly infected cells.

Denote U = ℝ₊ × ℤ₊ the space of all pairs u = (a, g), as defined in Section 2. We define a state of the system as a function I: U → ℤ₊ that associates to every u ∈ U a positive integer I(u) = I(a, g), the number of infected cells of age a and generation g.

Let be the space of all functions I: ℝ₊ × ℤ₊ → ℤ₊. At any given time t ∈ ℝ₊, and for any given state I ∈ , let P (I; t) be the probability of the system being described by the state I at time t. Even though P: × ℝ₊ →[0, 1], for simplicity we omit the dependency in time and consider P as an element in S( ), where S( ) = { → [0, 1]}, the space of all operators from into [0, 1].

To better illustrate the derivation, we first show how to obtain the master equation discretized in time increments Δt. Define Δ: ℝ₊ × → as follows. Given τ ∈ ℝ₊, I ∈ , and (a, g) ∈ U, then Δ_τ I(a, g) = I(a + τ, g) − I(a, g). From the above notice that for every I ∈ and every (a, g) ∈ U, (I + Δ_τ I)(a, g) = I(a + τ, g). Δ_τ I represents the difference between state I at time t + τ and state I at time t when cells age only (e.g. no deaths nor births). It follows that, given I_t+τ, the state at time t is I_t+τ − Δ_τ I.

We also define the Kroenecker Delta operator as δ: U → as follows. Given u₀ ∈ U, δ_u0∈ is defined so that for every u ∈ U such that u ≠ u₀, δ_u0 (u) = 0 and δ_u0(u₀) = 1.

Suppose now that at a given time t, the system is completely described by the state I. We wish to compute the probability P(I, t + Δt). In other words, we want to see how the system evolves after an increment in time of Δt. There are three possible contributions to the term P(I, t + Δt). In what follows we assume that for every age a and generation g, out of all infected cells I(a, g) only one can die or be born at the time. Hence, the contributions are:

1. No deaths, no births, cells can only survive. The contribution in this case is

   $$\begin{array}{c}P(I-{\mathrm{\Delta }}_{\mathrm{\Delta }t}I;t){\prod }_{u\in U}{(1-\beta (u)\mathrm{\Delta }t)}^{(I-{\mathrm{\Delta }}_{\mathrm{\Delta }t}I)(u)}\\ {\prod }_{u\in U}{(1-\alpha (u)\mathrm{\Delta }t)}^{(I-{\mathrm{\Delta }}_{\mathrm{\Delta }t}I)(u)}\end{array}$$ (A.1)
2. One cellu₀ dies. The contribution (summed over all possible u₀ ∈ U ) is

   $$\sum _{u_0\in U}P(I+{\delta }_{u_0};t)\left(\prod _{u\ne u_0}{(1-\beta (u)\mathrm{\Delta }t)}^{I(u)}\right)\beta (u_0)\mathrm{\Delta }t(I(u_0)+1)$$ (A.2)
3. One cellu₀ is born. The contribution (summed over all possible u₀ ∈ U ) is

   $$\begin{array}{c}{\sum }_{u\in U}P(I-{\delta }_{u_0=(0,g+1)};t)\left({\prod }_u{(1-\beta (u)\mathrm{\Delta }t)}^{I(u)}\right)\\ \alpha (u)\mathrm{\Delta }t\left(I(u)-{\delta }_{u_0=(0,g+1)}\right)\end{array}$$ (A.3)

We expand each of the above terms in Δt and neglect terms in O(Δt²) to obtain, for each piece respectively:

1. $$P(I-{\mathrm{\Delta }}_{\mathrm{\Delta }t}I;t)\left(1-\sum _{u\in U}(I-{\mathrm{\Delta }}_{\mathrm{\Delta }t}I)(u)[\beta (u)+\alpha (u)]\mathrm{\Delta }t\right)$$ (A.4)
2. $$\sum _{u\in U}P(I+{\delta }_u;t)(I(u)+1)\beta (u)\mathrm{\Delta }t$$ (A.5)
3. $$\sum _{u\in U}P(I-{\delta }_{u_0=(0,g+1)};t)(I(u)-{\delta }_{u_0=(0,g+1)})\alpha (u)\mathrm{\Delta }t$$ (A.6)

The first order master equation of the process, discretized in time, is therefore

$$\begin{array}{c}\frac{P(I;t+\mathrm{\Delta }t)-P(I-{\mathrm{\Delta }}_{\mathrm{\Delta }t}I;t)}{\mathrm{\Delta }t}=\\ =-P(I-{\mathrm{\Delta }}_{\mathrm{\Delta }t}I;t)({\sum }_{u\in U}(I-{\mathrm{\Delta }}_{\mathrm{\Delta }t}I)(u)[\beta (u)+\alpha (u)])+\\ +{\sum }_{u\in U}P(I+{\delta }_u;t)(I(u)+1)\beta (u)+\\ +{\sum }_{u\in U}P(I-{\delta }_{(0,g+1)};t)\left(I(u)-{\delta }_{u_0=(0,g+1)}\right)\alpha (u)\end{array}$$ (A.7)

To obtain the continuous master equation we have to take the limit for Δt → 0 on both sides of Eq. (A.7). In order to do so, we use an approximation that is a direct consequence of the definition of functional derivative (Gelfand et al., 1963): given x, y ∈ and f ∈ S( ), the following holds

$$f(x+y)\simeq f(x)+{\int }_{U}y(u)\frac{\partial f}{\partial x(u)}du$$ (A.8)

Using the above, the left-hand side of Eq. (A.7) becomes

$$\frac{\partial P}{\partial t}-{\int }_U\frac{\partial I}{\partial a}(u)\frac{\partial P}{\partial I(u)}du$$ (A.9)

Notice that in the absence of births and deaths (i.e. α = β = 0), the above reduces to

$$\frac{\partial P}{\partial t}(I;t)-{\int }_U\frac{\partial I}{\partial a}(u)\frac{\partial P}{\partial I(u)}(I;t)du=0$$ (A.10)

which describes the survival of all cells present at time t = 0.

In order to expand the right-hand side (RHS) of Eq. (A.7), we collect the terms in β together, and similarly for the terms in α. We approximate to the first order in Δt and let Δt → 0.

$$\text{RHS}(\beta )=P(I;t)({\sum }_{u}I(u)\beta (u)+{\sum }_u\beta (u)-{\sum }_{u}I(u)\beta (u))+{\sum }_u\left(\frac{\partial P}{\partial I(u)}(I)\right)I(u)\beta (u)+o(\mathrm{\Delta }t)$$ (A.11)

In the limit the above becomes

$$P(I;t){\int }_U\beta (u)du+{\int }_U\beta (u)\frac{\partial P}{\partial I(u)}I(u)du$$ (A.12)

By expanding RHS(α) in a similar way, one obtains the continuous master equation

$$\begin{array}{c}\frac{\partial P}{\partial t}(I;t)={\int }_U\frac{\partial I}{\partial a}(u)\frac{\partial P}{\partial I(u)}(I;t)du=\\ ={\int }_U\mu (u)\left[P(I;t)+\frac{\partial P}{\partial I(u)}(I;t)I(u)\right]du+\\ -{\int }_{\partial U}\alpha (u)\left[P(I;t)-\frac{\partial P}{\partial I(u)}(I;t)I(u)\right]du+\\ -{\int }_U\frac{\partial P}{\partial I(0,g+1)}(I;t)I(u)\alpha (u)du\end{array}$$ (A.13)

where ∂U = {u = (a, g) ∈ U|a = 0, g > 0}. In all that follows we assume that newborn cells cannot give birth, which implies that α_|∂U = 0. As a consequence, the second term on the RHS is null. We now use the following two claims to re-write the above equation.

Claim Appendix A.1

Let u ∈ U. We define a map S( ) → S( ) that to every P ∈ S( ) associates a P̃_u ∈ S( ) so defined: P̃_u(I) = I(u)P (I). Then

$$\frac{\partial {\stackrel{\sim }{P}}_u(I)}{\partial I(u)}=P(I)+I(u)\frac{\partial P(I)}{\partial I(u)}$$ (A.14)

Proof

Given ε > 0 and u₀ ∈ U, define δ_u0,ε ∈ as the following Kroencker delta: δ_u0,ε(u) = ε δ(u − u₀). Then

$${\stackrel{\sim }{P}}_u(I+{\delta }_{u,\epsilon })-{\stackrel{\sim }{P}}_u(I)=(I+{\delta }_{u,\epsilon })(u)P(I+{\delta }_{u_0,\epsilon })-I(u)P(I)={\delta }_{u,\epsilon }(u)P(I+{\delta }_{u_0,\epsilon })+I(u)[P(I+{\delta }_{u,\epsilon })-P(I)]$$ (A.15)

By dividing by ε and letting ε → 0 we get the assert.

Claim Appendix A.2

Given u₀ ≠ u, we have

$$\frac{\partial {\stackrel{\sim }{P}}_u(I)}{\partial I(u_0)}=I(u)\frac{\partial P(I)}{\partial I(u_0)}$$ (A.16)

As a consequence, we can rewrite the master equation as follows

$$\begin{array}{c}\frac{\partial P}{\partial t}(I;t)-{\int }_U\frac{\partial I}{\partial a}(u)\frac{\partial P}{\partial I(u)}(I;t)du\\ ={\int }_U\frac{\partial }{\partial I(u)}[I(u)P(I;t)]\mu (u)du\\ -{\int }_U\frac{\partial }{\partial I(u_0)}[I(u)P(I;t)]\alpha (u)du\end{array}$$ (A.17)

where u₀ = (0, g + 1).

Eq. (A.17) reduces to well known results when the birth and death rates are both constant, in which case, if we integrate both sides over the domain = {I ∈ |∫_U I = N_t}, where N_t is the total number of cells at time t, and N₀ is the initial number of cells. we obtain

$$\frac{\partial P}{\partial t}(N_t;t)=\beta [(N_t+1)P(N_t+1;t)-N_{t}P(N_t;t)]+\alpha [(N_t-1)P(N_t-1;t)-N_{t}P(N_t;t)]$$ (A.18)

which is the master equation of the classic linear birth and death process. This is fully discussed in Reichl (1998), where a solution is given in terms of the generating function F(z; t) = Σ_NtP (N_t; t) z^N_t by

$$F(z;t)={\left[\frac{\beta (z-1){\text{e}}^{(\alpha -\beta )t}-\alpha z+\beta }{\alpha (z-1){\text{e}}^{(\alpha -\beta )t}-\alpha z+\beta }\right]}^{N_0}.$$ (A.19)

Here N₀ is the initial number of infected cells.

Appendix B. Continuous model, closed form solution

We now develop the closed form solution to Eq. (1). One can verify that, given a smooth function ε(g, x) such that ε(g, x) = 0 when x < 0, then

$$I(a,g,t)=\varphi (g,t-a){\text{e}}^{-{\int }_0^a\beta (s)ds}$$ (B.1)

satisfies the first equation in (1). Substituting into the renewal condition, one gets that ε should also satisfy

$$\varphi (g+1,t)={\int }_{\mathrm{\Lambda }}^{\infty }\alpha (a){\text{e}}^{-{\int }_0^a\beta (s)ds}\varphi (g,t-a)da.$$ (B.2)

Given the initial population of I₀ cells, at any given time t, the only cells at g = 0 are the survivors from the initial population. In other words:

$$I(a,0,t)=\{\begin{array}{cc}{I}_0{\text{e}}^{-{\int }_0^a\beta (s)ds}& \text{if}a=t\\ 0& \text{otherwise}.\end{array}$$ (B.3)

It follows that for g = 0, ε is completely determined by ε(0, t − a) = δ(t − a)I₀, where δ(t − a) is the singular density. When g = 1

$$I_0{\int }_0^{\infty }f(a)\delta (a-t)da=I_{0}f(t)=\varphi (1,t)$$ (B.4)

and therefore one can show recursively that for g ≥ 1

$$\varphi (g,t)=I_0{\int }_0^{\infty }\cdots {\int }_0^{\infty }\left(\prod _{i=1}^{g}f(a_i){da}_i\right)\delta ({\sum }_{i=1}^g{a}_i-t).$$ (B.5)

By reordering the above and substituting f with its Fourier transform f̃ one obtains

$$\begin{array}{c}\varphi (g,t)=I_0{\int }_0^{\infty }\cdots {\int }_0^{\infty }{\int }_{-\infty }^{\infty }{\text{e}}^{ik(\sum a_i-t)}\frac{dk}{2\pi }({\prod }_{i=1}^{g}f(a_i){da}_i)=\\ =\frac{I_0}{2\pi }{\int }_{-\infty }^{\infty }{\text{e}}^{-\mathit{ikt}}({\prod }_{i=1}^g{\int }_0^{\infty }f(a_i){\text{e}}^{{\mathit{ika}}_i}{da}_i)dk=\\ =\frac{I_0}{2\pi }{\int }_{-\infty }^{\infty }{\text{e}}^{-\mathit{ikt}}\stackrel{\sim }{f}{(k)}^{g}dk\end{array}$$ (B.6)

Substituting Eq. (B.6) in Eq. (B.1), one gets Eq. (4):

$$I(g,t)=\frac{I_0}{2\pi }{\int }_0^t{\text{e}}^{-{\int }_0^a\beta (s)ds}{\int }_{-\infty }^{\infty }\stackrel{\sim }{f}{(k)}^g{\text{e}}^{-ik(t-a)}dkda$$ (B.7)

which reduces the problem to a quadrature.

Appendix C. HD variance for an exponentially growing population in the presence of recombination alone

We now illustrate how to obtain expressions for the mean HD₀ and the expected value of the variance of HD₀ as functions of generation g in the case where the population grows exponentially, the mutation rate is ε = 0, and the recombination rate is ρ = 1.

For every position x between 1 and N_B, we compute both the mean HD₀ and the HD₀ variance at that position across all sequences, and for every pair of positions x and y, we will compute the covariance across all sequences, and finally we will obtain the total mean HD₀ and HD₀ variance by summing across all positions.

Since there are no new mutations, at any generation g, the mean HD at d position x is given by ${\overline{HD}}_x(g)=\frac{d}{N_B}$, and hence

$$\mu (g)=\sum _{x=1}^{N_B}{\overline{HD}}_x(g)=d.$$ (C.1)

An unbiased estimator of the variance at position x is given by

$$s_x^2(g)=\frac{N_g}{N_g-1}\left(\overline{H{D}_x^2}-{\overline{HD}}_x^2\right),$$ (C.2)

Here, for simplicity of notation, we have omitted the dependency in g. So, if $s_x^2(g+1)$ is the expected variance at generation g + 1, summing over all sequences s we obtain

$$s^2(g+1)=\frac{1}{N_g}\left(\sum _s{\left({HD}_x-\frac{1}{N_g}\sum _{s^{\prime }}{HD}_x\right)}^2\right)=\frac{N_g-1}{N_g}{s}^2(g).$$ (C.3)

This is not quite the total variance as we still need to add in the contribution from the covariance between every pair of positions x and y.

To understand how the expected covariance s_x,y between any two sites x and y changes with generation g, we make the following observation: if the split position θ falls between the two positions, then x and y will be inherited independently to the next generation. If, on the other hand, θ does not split the two positions, then the new covariance will be a random variate with expectation the second cumulant of the covariance at the previous distribution. In order to use this observation, we split the set of sequences in two groups: the ones derived from two parent sequences which recombined somewhere between x and y, and those derived instead from a recombination split outside x and y.

Let N₁ be the number of sequences in the first group, and N₂ the number of sequences in the second group, so that N₁ + N₂ = N_g (when clear from the context, we omit the dependency in g for simplicity of notation). We define $w_i=E\left(\frac{N_i}{N_g}\right)$ and ${\kappa }_{1x}^i$ and ${\kappa }_{11}^i$ the cumulants of the HD in the i-th group at a fixed generation g. An unbiased estimator of the covariance is given by

$$s_{xy}(g)=\frac{1}{N_g-1}\sum _{s\in N_g}({HD}_x-{\overline{HD}}_x)({HD}_y-{\overline{HD}}_y)$$ (C.4)

where N_g is the total number of sequences at generation g, HD_x and HD_y are the Hamming distances at positions x and y respectively, and ${\overline{HD}}_x$ and ${\overline{HD}}_y$ their means. By splitting the summation over sequences in N₁ and sequences in N₂, one gets

$$s_{xy}(g)=\sum _{i=1,2}\frac{N_i-1}{N_g-1}{s}_i+\sum _{i=1,2}\frac{N_i}{N_g-1}({\overline{HD}}_{x,i}-{\overline{HD}}_x)({\overline{HD}}_{y,i}-{\overline{HD}}_y)$$ (C.5)

where s_i is the variance over subset N_i, and ${\overline{HD}}_{x,i}$ and ${\overline{HD}}_{y,i}$ are the means at positions x and y respectively within group N_i. Taking expectations on both sides of the above equation, one obtains

$$E(s_{xy}){\mid }_{g+1}={\sum }_{i=1,2}{w}_i{\kappa }_{11}^i+\frac{N_{g+1}}{N_{g+1}-1}\left[{\sum }_{i=1,2}{w}_i{\kappa }_{1x}^i{\kappa }_{1y}^i-\left({\sum }_{i=1,2}{w}_i{\kappa }_{1x}^i\right)\left({\sum }_{j=1,2}{w}_j{\kappa }_{1y}^j\right)\right].$$ (C.6)

Notice that the first term on the right hand side is the weighted average of the ${\kappa }_{11}^i$’s, and the second one is the weighted covariance between ${\kappa }_{1x}^i$ and ${\kappa }_{1y}^i$.

The first cumulants are the mean of the corresponding distribution, hence ${\kappa }_{1x}^i={\kappa }_{1y}^i=d$ at all times, whereas with the above definitions of N₁ and N₂, we get ${\kappa }_{11}^1=0$ (the split position separates x and y and hence the number of mutations at each site become independent variables), and ${\kappa }_{11}^2=\frac{N_g-1}{N_g}E(s_{xy})$. Furthermore, $w_2=\left(1-\frac{y-x}{N_B+1}\right)$. Therefore, substituting all of the above into Equation (C.6), we obtain

$$E(s_{xy})(g+1)=\left(1-\frac{y-x}{N_B+1}\right)\frac{N_g-1}{N_g}E(s_{xy})(g)$$ (C.7)

By adding across all positions we get

$$\begin{array}{c}{s}^2(g)={\sum }_{x=1}^{N_B}{s}_x^2(g)+2{\sum }_{x<y}{s}_{xy}(g)=\\ ={\prod }_{j=0}^{g-1}\frac{N_j-1}{N_j}\left[{\sum }_{x=1}^{N_B}{s}_x^2(0)+2{\sum }_{x<y}{\left(1-\frac{y-x}{N_B+1}\right)}^g{s}_{x,y}(0)\right]\end{array}$$ (C.8)

With these recursive relations, we have reduced the problem to computing the initial quantities $s_x^2(0)$ and s_x,y(0). Consider the initial population to be made of I₀ sequences such that the HD₀ of any given sequence s from the founder strain s₀ is a random variable from a probability distribution P with mean and variance μ₀ and σ₀ respectively. Then the moment generating function M of the HD₀ distribution is given by

$$M(u_1,\dots ,u_{N_B-1})={\left[\frac{1}{N_B}\left(1+\sum _{i=1}^{N_B-1}{\text{e}}^{u_i}\right)\right]}^{{\mu }_0{N}_B^{-1}}.$$ (C.9)

Here N_B is the length of the genomes, and u₁, … u_NB−1 are independent variables representing the positions in the genome (there’s a total of N_B positions, but only N_B − 1 are independent due to the constraint that the initial mean is μ₀). Taking the first and second derivatives, we find

$$s_x^2(0)=\frac{N_B-1}{N_B^2}{\mu }_0+\frac{1}{N_B^2}{\sigma }_0^2$$ (C.10)

and

$$s_{xy}(0)=\frac{1}{N_B^2}({\sigma }_0^2-{\mu }_0)$$ (C.11)

It’s easy to verify that summing the above two equations over all positions, one gets the initial variance ${\sigma }_0^2$.

Combining equations (C.8), (C.10), and (C.11), we get the expression for the total HD variance at generation g > 0:

$$\begin{array}{c}{\sigma }_{\rho }^2(g)=d\left(1-\frac{1}{N_B}\right)-2\frac{d}{N_B^2}{\sum }_{x<y\le N_B}{\left(1-\frac{y-x}{N_B+1}\right)}^g{\prod }_{j=0}^{g-1}\frac{N_j-1}{N_j}=\\ =d\left(1-\frac{1}{N_B}\right)-2\frac{d}{g+2}\left[{\left(\frac{N_B}{N_B+1}\right)}^{g-1}+O(N_B^{-1})\right]{\prod }_{j=0}^{g-1}\frac{N_j-1}{N_j}\end{array}$$ (C.12)

where we have used the following relationship:

$$2{\sum }_{x=1}^{N_B-1}{\sum }_{y=x+1}^{N_B}{\left(1-\frac{y-x}{N_B+1}\right)}^g=\frac{2}{{(N_B+1)}^g}{\sum }_{k=1}^{N_B-1}k{(k+1)}^g=\frac{N_B^{g+1}}{(g+2){(N_B+1)}^{g-1}}+O(N_B).$$ (C.13)

Appendix D. HD variance for an exponentially growing population when both recombination and mutation rate are non-null

We now extend the methods used to derive Eq. (14) and find recursive formulae for the general case when both ρ and ε are non-null. Eq. (C.6) can be generalized to an indefinite number of partitions N_i such that Σ_i N_i = N_g, the total number of sequences at generation g. We use this to find analogous recursive formulae for the cumulants of the mean HD₀ distribution when both recombination and mutation events are present.

Fix positions x and y and choose N₁ to be the number of sequences derived from a recombination event that split positions x and y; N₂ the number of sequences derived from either a recombination event that did not split positions x and y, or from a division with no mutation; and, finally, denote N_k, with k = 3, 4 or 5 the number of sequences such that only the x position has mutated, only the y position, or both, respectively. Like before, let $w_i=E\left(\frac{N_i}{N_g}\right)$. Assume that mutations happen with a rate ε (per site, per generation), and recombination events happen with a rate ρ. Given this set-up, we notice that

$$E(w_j)=\{\begin{array}{ccc}\frac{y-x}{N_B+1}\rho & \text{if}& \text{j}=1\\ \left(1-\frac{y-x}{N_B+1}\right)\rho +(1-\rho )(1-\epsilon )& \text{if}& \text{j}=2\\ \epsilon (1-\rho )(1-\epsilon )& \text{if}& \text{j}=3\text{or}4\\ (1-\rho ){\epsilon }^2& \text{otherwise}.& \end{array}$$ (D.1)

Let ξ = ε(1 − ρ). Carrying out similar computations as sketched in the previous section, one notices that, for every positions x and y

$${\mu }_x(g+1)={\mu }_x(g)+\xi$$ (D.2)

$$s_x^2(g+1)=\frac{N_g-1}{N_g}{s}_x^2(g)+\xi (1-\xi )$$ (D.3)

$$s_{xy}(g+1)=\left(1-\rho \frac{y-x}{N_B+1}\right)\frac{N_g-1}{N_g}{s}_{xy}(g)-\frac{N_{g+1}}{N_{g+1}-1}{\xi }^2+\xi \left(\epsilon -\frac{1}{N_{g+1}}\right)-2\epsilon {\xi }^2\frac{1-\epsilon }{N_{g+1}}$$ (D.4)

By summing Eq. (D.2) over all positions x one obtains Eq. (15). Similarly, by summing Eq. (D.3) and Eq. (D.4) across all positions, and noticing that we can still use the same initial values we used in Appendix C, one obtains the general expression for s²(g).