Condition Number Regularized Covariance Estimation

Abstract

Estimation of high-dimensional covariance matrices is known to be a difficult problem, has many applications, and is of current interest to the larger statistics community. In many applications including so-called the “large p small n” setting, the estimate of the covariance matrix is required to be not only invertible, but also well-conditioned. Although many regularization schemes attempt to do this, none of them address the ill-conditioning problem directly. In this paper, we propose a maximum likelihood approach, with the direct goal of obtaining a well-conditioned estimator. No sparsity assumption on either the covariance matrix or its inverse are are imposed, thus making our procedure more widely applicable. We demonstrate that the proposed regularization scheme is computationally efficient, yields a type of Steinian shrinkage estimator, and has a natural Bayesian interpretation. We investigate the theoretical properties of the regularized covariance estimator comprehensively, including its regularization path, and proceed to develop an approach that adaptively determines the level of regularization that is required. Finally, we demonstrate the performance of the regularized estimator in decision-theoretic comparisons and in the financial portfolio optimization setting. The proposed approach has desirable properties, and can serve as a competitive procedure, especially when the sample size is small and when a well-conditioned estimator is required.

1 Introduction

We consider the problem of regularized covariance estimation in the Gaussian setting. It is well known that, given n independent samples x₁, …, x_n ∈ ℝ^p from a zero-mean p-variate Gaussian distribution, the sample covariance matrix

$$S=\frac{1}{n}\sum _{i=1}^n{x}_i{x}_i^T,$$

maximizes the log-likelihood as given by

$$\begin{array}{l}l(\mathrm{\sum })=log\prod _{i=1}^n\frac{1}{{(2\pi )}^p{(det\mathrm{\sum })}^{\frac{1}{2}}}exp\left(-\frac{1}{2}{x}_i^T{\mathrm{\sum }}^{-1}{x}_i\right)\\ =-(np/2)log(2\pi )-(n/2)(\mathbf{tr}({\mathrm{\sum }}^{-1}S)-logdet{\mathrm{\sum }}^{-1}),\end{array}$$ (1)

where det A and tr(A) denote the determinant and trace of a square matrix A respectively. In recent years, the availability of high-throughput data from various applications has pushed this problem to an extreme where in many situations, the number of samples, n, is often much smaller than the dimension of the estimand, p. When n < p the sample covariance matrix S is singular, not positive definite, and hence cannot be inverted to compute the precision matrix (the inverse of the covariance matrix), which is also needed in many applications. Even when n > p, the eigenstructure tends to be systematically distorted unless p/n is extremely small, resulting in numerically ill-conditioned estimators for Σ; see Dempster (1972) and Stein (1975). For example, in mean-variance portfolio optimization (Markowitz, 1952), an ill-conditioned covariance matrix may amplify estimation error because the optimal portfolio involves matrix inversion (Ledoit and Wolf, 2003; Michaud, 1989). A common approach to mitigate the problem of numerical stability is regularization.

In this paper, we propose regularizing the sample covariance matrix by explicitly imposing a constraint on the condition number.¹ Instead of using the standard estimator S, we propose to solve the following constrained maximum likelihood (ML) estimation problem

$$\begin{array}{ll}\text{maximize}\hfill & l(\mathrm{\sum })\hfill \\ \text{subject}\text{to}\hfill & \text{cond}(\mathrm{\sum })\le {\kappa }_{max},\hfill \end{array}$$ (2)

where cond(M) stands for the condition number, a measure of numerical stability, of a matrix M (see Section 1.1 for details). The matrix M is invertible if cond(M) is finite, ill-conditioned if cond(M) is finite but high (say, greater than 10³ as a rule of thumb), and well-conditioned if cond(M) is moderate. By bounding the condition number of the estimate by a regularization parameter κ_max, we directly address the problem of invertibility or ill-conditioning. This direct control is appealing because the true covariance matrix is in most situations unlikely to be ill-conditioned whereas its sample counterpart is often ill-conditioned. It turns out that the resulting regularized matrix falls into a broad family of Steinian-type shrinkage estimators that shrink the eigenvalues of the sample covariance matrix towards a given structure (James and Stein, 1961; Stein, 1956). Moreover, the regularization parameter κ_max is adaptively selected from the data using cross validation.

Numerous authors have explored alternative estimators for Σ (or Σ⁻¹) that perform better than the sample covariance matrix S from a decision-theoretic point of view. Many of these estimators give substantial risk reductions compared to S in small sample sizes, and often involve modifying the spectrum of the sample covariance matrix. A simple example is the family of linear shrinkage estimators which take a convex combination of the sample covariance matrix and a suitably chosen target or regularization matrix. Notable in the area is the seminal work of Ledoit and Wolf (2004) who study a linear shrinkage estimator toward a specified target covariance matrix, and choose the optimal shrinkage to minimize the Frobenius risk. Bayesian approaches often directly yield estimators which shrink toward a structure associated with a pre-specified prior. Standard Bayesian covariance estimators yield a posterior mean Σ that is a linear combination of S and the prior mean. It is easy to show that the eigenvalues of such estimators are also linear shrinkage estimators of Σ; see, e.g., Haff (1991). Other nonlinear Steinian-type estimators have also been proposed in the literature. James and Stein (1961) study a constant risk minimax estimator and its modification in a class of orthogonally invariant estimators. Dey and Srinivasan (1985) provide another minimax estimator which dominates the James-Stein estimator. Yang and Berger (1994) and Daniels and Kass (2001) consider a reference prior and hierarchical priors, that respectively yield posterior shrinkage.

Likelihood-based approaches using multivariate Gaussian models have provided different perspectives on the regularization problem. Warton (2008) derives a novel family of linear shrinkage estimators from a penalized maximum likelihood framework. This formulation enables cross-validation of the regularization parameter, which we discuss in Section 3 for the proposed method. Related work in the area include Sheena and Gupta (2003), Pourahmadi et al. (2007), and Ledoit and Wolf (2012). An extensive literature review is not undertaken here, but we note that the approaches mentioned above (and the one proposed in this paper) fall in the class of covariance estimation and related problems which do not assume or impose sparsity, on either the covariance matrix, or its inverse (for such approaches either in the frequentist, Bayesian, or testing frameworks, the reader is referred to Banerjee et al. (2008); Friedman et al. (2008); Hero and Rajaratnam (2011, 2012); Khare and Rajaratnam (2011); Letac and Massam (2007); Peng et al. (2009); Rajaratnam et al. (2008)).

1.1 Regularization by shrinking sample eigenvalues

We briefly review Steinian-type eigenvalue shrinkage estimators in this subsection. Dempster (1972) and Stein (1975) noted that the eigenstructure of the sample covariance matrix S tends to be systematically distorted unless p/n is extremely small. They observed that the larger eigenvalues of S are overestimated whereas the smaller ones are underestimated. This observation led to estimators which directly modify the spectrum of the sample covariance matrix and are designed to “shrink” the eigenvalues together. Let l_i, i = 1, …, p, denote the eigenvalues of the sample covariance matrix (sample eigenvalues) in nonincreasing order (l₁ ≥ … ≥ l_p ≥ 0). The spectral decomposition of the sample covariance matrix is given by

$$S=Q\text{diag}(l_1,\dots ,l_p)Q^T,$$ (3)

where diag(l₁, …, l_p) is the diagonal matrix with diagonal entries l_i and Q ∈ ℝ^p×p is the orthogonal matrix whose i-th column is the eigenvector that corresponds to the eigenvalue l_i. As discussed above, a large number of covariance estimators regularizes S by modifying its eigenvalues with the explicit goal of better estimating the eigenspectrum. In this light Stein (1975) proposed the class of orthogonally invariant estimators of the following form:

$$\widehat{\mathrm{\sum }}=Q\text{diag}({\widehat{\lambda }}_1,\dots ,{\widehat{\lambda }}_p)Q^T.$$ (4)

Typically, these estimators shrink the sample eigenvalues so that the modified eigenspectrum is less spread than that of the sample covariance matrix. In many estimators, the shrunk eigenvalues are required to maintain the original order as those of S: λ̂₁ ≥ ··· ≥ λ̂_p.

One well-known example of Steinian-type shrinkage estimators is the linear shrinkage estimator as given by

$${\widehat{\mathrm{\sum }}}_{\text{LS}}=(1-\delta )S+\delta F,0\le \delta \le 1$$ (5)

where the target matrix F = cI for some c > 0 (Ledoit and Wolf, 2004; Warton, 2008). For the linear estimator the relationship between the sample eigenvalues l_i and the modified eigenvalues λ̂_i is affine:

$${\widehat{\lambda }}_i=(1-\delta )l_i+\delta c$$

Another example, Stein’s estimator (Stein, 1975, 1986), denoted by Σ̂_Stein, is given by λ̂_i = l_i/d_i, i = 1, …, p, with d_i = (n − p + 1 + 2l_i Σ_j≠i(l_i − l_j)⁻¹)/n. The original order in the estimator is preserved by applying isotonic regression (Lin and Perlman, 1985).

1.2 Regularization by imposing a condition number constraint

Now we proceed to introduce the condition number-regularized covariance estimator proposed in this paper. Recall that the condition number of a positive definite matrix Σ is defined as

$$\text{cond}(\mathrm{\sum })={\lambda }_{max}(\mathrm{\sum })/{\lambda }_{min}(\mathrm{\sum })$$

where λ_max(Σ) and λ_min(Σ) are the maximum and the minimum eigenvalues of Σ, respectively. (Understand that cond(Σ) = ∞ if λ_min(Σ) = 0.) The condition number-regularized covariance estimation problem (2) can therefore be formulated as

$$\begin{array}{ll}\text{maximize}\hfill & l(\mathrm{\sum })\hfill \\ \text{subject}\text{to}\hfill & {\lambda }_{max}(\mathrm{\sum })/{\lambda }_{min}(\mathrm{\sum })\le {\kappa }_{max}.\hfill \end{array}$$ (6)

An implicit condition is that Σ be symmetric and positive definite².

The estimation problem (6) can be reformulated as a convex optimization problem in the matrix variable Σ⁻¹ (see Section 2). Standard methods such as interior-point methods can solve the convex problem when the number of variables (i.e., entries in the matrix) is modest, say, under 1000. Since the number of variables is about p(p + 1)/2, the limit is around p = 45. Such a naive approach is not adequate for moderate to high dimensional problems. One of the main contributions of this paper is a significant improvement on the solution method for (6) so that it scales well to much larger sizes. In particular, we show that (6) reduces to an unconstrained univariate optimization problem. Furthermore, the solution to (6), denoted by Σ̂_cond, has a Steinian-type shrinkage of the form as in (4) with eigenvalues given by

$${\widehat{\lambda }}_i=min(max({\tau }^{★},l_i),{\kappa }_{max}{\tau }^{★})=\{\begin{array}{ll}{\tau }^{★},\hfill & l_i\le {\tau }^{★}\hfill \\ l_i,\hfill & {\tau }^{★}<l_i<{\kappa }_{max}{\tau }^{★}\hfill \\ {\kappa }_{max}{\tau }^{★},\hfill & l_i\ge {\kappa }_{max}{\tau }^{★},\hfill \end{array}$$ (7)

for some τ^★ > 0. Note that the modified eigenvalues are nonlinear functions of the sample eigenvalues, meet the order constraint of Section 1.1, and even when n < p, the nonlinear shrinkage estimator Σ̂_cond is well-conditioned. The quantity τ^★ is determined adaptively from the data and the choice of the regularization parameter κ_max. This solution method was first considered by two of the authors of this paper in a previous conference proceeding (Won and Kim, 2006). In this paper, we give a formal proof of the assertion that the matrix optimization problem (6) reduces to an equivalent unconstrained univariate minimization problem. We further elaborate on the proposed method by showing rigorously that τ^★ can be found exactly and easily with computational effort of order O(p) (Section 2.1).

The nonlinear shrinkage in (7) has a simple interpretation: the eigenvalues of the estimator Σ̂_cond are obtained by truncating the sample eigenvalues larger than κ_maxτ^★ to κ_maxτ^★ and those smaller than τ^★ to τ^★. Figure 1 illustrates the functional form of (7) in comparison with that of the linear shrinkage estimator. This novel shrinkage form is rather surprising, because the original motivation of the regularization in (6) is to numerically stabilize the covariance estimate. Note that this type of shrinkage better preserves the eccentricity of the sample estimate than the linear shrinkage which shrinks it toward a spherical covariance matrix.

Figure 1.

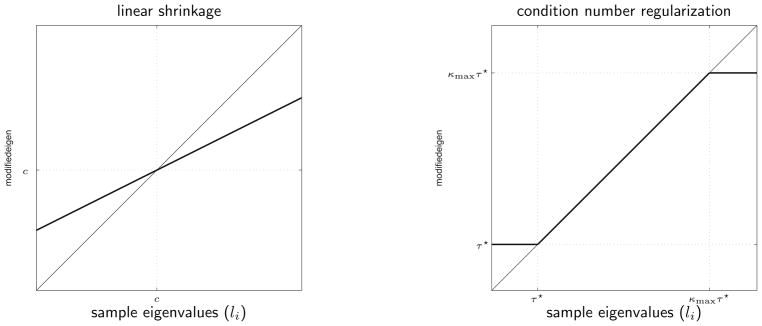
Comparison of eigenvalue shrinkage of the linear shrinkage estimator (left) and the condition number-constrained estimator (right).

Other major contributions of the paper include a detailed analysis of the regularization path of the shrinkage enabled by a geometric perspective of the condition number-regularized estimator (Section 2.2), and an adaptive selection procedure for choosing the regularization parameter κ_max under the maximum predictive likelihood criterion (Section 3) and properties thereof.

We also undertake a Bayesian analysis of the condition number constrained estimator (Section 4). A detailed application of the methodology to real data, which demonstrates the usefulness of the method in a practical setting, is also provided (Section 6). In particular, Section 6 studies the use of the proposed estimator in the mean-variance portfolio optimization setting. Section 5 undertakes a simulation study in order to compare the risk of the condition number-regularized estimator to those of others. Risk comparisons in higher dimensional settings (as compared to those given in the preliminary conference paper) are provided in this Section. Asymptotic properties of the estimator are also investigated in Section 5.

2 Condition number-regularized covariance estimation

2.1 Derivation and characterization of solution

This section gives the derivation of the solution (7) of the condition number-regularized covariance estimation problem as given in (6) and shows how to compute τ^★ given κ_max. Note that it suffices to consider the case κ_max < l₁/l_p = cond(S), since otherwise, the condition number constraint is already satisfied and the solution to (6) simply reduces to the sample covariance matrix S.

It is well known that the log-likelihood (1) of a multivariate Gaussian covariance matrix is a convex function of Ω = Σ⁻¹. Note that Ω is the canonical parameter for the (Wishart) natural exponential family associated with the likelihood in (1). Since cond(Σ) = cond(Ω), it can be shown that the condition number constraint on Ω is equivalent to the existence of u > 0 such that uI ⪯ Ω ⪯ κ_maxuI, where A ⪯ B denotes that B − A is positive semidefinite (Boyd and Vandenberghe, 2004, Chap. 7). Therefore the covariance estimation problem (6) is equivalent to

$$\begin{array}{ll}\text{minimize}\hfill & \mathbf{tr}(\mathrm{\Omega }S)-logdet\mathrm{\Omega }\hfill \\ \text{subject}\text{to}\hfill & uI\prec \mathrm{\Omega }\prec {\kappa }_{max}uI,\hfill \end{array}$$ (8)

where the variables are a symmetric positive definite p×p matrix Ω and a scalar u > 0. The above problem in (8) is a convex optimization problem with p(p + 1)/2 + 1 variables, i.e., O(p²).

The following lemma shows that by exploiting structure of the problem it can be reduced to a univariate convex problem, i.e., the dimension of the system is only of O(1) as compared to O(p²).

Lemma 1

The optimization problem (8) is equivalent to the unconstrained univariate convex optimization problem

$$\mathit{minimize}\sum _{i=1}^p{J}_{{\kappa }_{max}}^{(i)}(u),$$ (9)

where

$$J_{{\kappa }_{max}}^{(i)}(u)=l_i{\mu }_i^{★}(u)-log{\mu }_i^{★}(u)=\{\begin{array}{ll}{l}_i({\kappa }_{max}u)-log({\kappa }_{max}u),\hfill & u<1/({\kappa }_{max}{l}_i)\hfill \\ 1+log{l}_i,\hfill & 1/({\kappa }_{max}{l}_i)\le u\le 1/l_i\hfill \\ l_{i}u-logu,\hfill & u>1/l_i,\hfill \end{array}$$

and

$${\mu }_i^{★}(u)=min\{max\{u,1/l_i\},{\kappa }_{max}u\},$$ (10)

in the sense that the solution to (8) is a function of the solution u^★ to (9), as follows.

$${\mathrm{\Omega }}^{★}=Q\text{diag}({\mu }_1^{★}(u^{★}),\dots ,{\mu }_p^{★}(u^{★}))Q^T,$$

with Q defined as in (3).

Proof

The proof is given in the Appendix.

Characterization of the solution to (9) is given by the following theorem.

Theorem 1

Given κ_max ≤ cond(S), the optimization problem (9) has a unique solution given by

$$u^{★}=\frac{{\alpha }^{★}+p-{\beta }^{★}+1}{{\sum }_{i=1}^{{\alpha }^{★}}{l}_i+{\sum }_{i={\beta }^{★}}^p{\kappa }_{max}{l}_i},$$ (11)

where α^★ ∈ {1, …, p} is the largest index such that 1/l_α★ < u^★ and β^★ ∈ {1, …, p} is the smallest index such that 1/l_β★ > κ_maxu^★. The quantities α^★ and β^★ are not determined a priori but can be found in O(p) operations on the sample eigenvalues l₁ ≥ … ≥ l_p. If κ_max > cond(S), the maximizer u^★ is not unique but Σ̂_cond = S for all the maximizing values of u.

Proof

The proof is given in the Appendix.

Comparing (10) to (7), it is immediately seen that

$${\tau }^{★}=1/({\kappa }_{max}{u}^{★})=\frac{{\sum }_{i=1}^{{\alpha }^{★}}{l}_i/{\kappa }_{max}+{\sum }_{i={\beta }^{★}}^p{l}_i}{{\alpha }^{★}+p-{\beta }^{★}+1}.$$ (12)

Note that the lower cutoff level τ^★ is an average of the (scaled and) truncated eigenvalues, in which the eigenvalues above the upper cutoff level κ_maxτ^★ are shrunk by a factor of 1/κ_max.

We highlight the fact that a reformulation of the original minimization into a univariate optimization problem makes the proposed methodology very attractive in high dimensional settings. The method is only limited by the complexity of spectral decomposition of the sample covariance matrix (or the singular value decomposition of the data matrix). The approach proposed here is therefore much faster than using interior point methods. We also note that the condition number-regularized covariance estimator is orthogonally invariant: if Σ̂_cond is the estimator of the true covariance matrix Σ, then UΣ̂_condU^T is the estimator of the true covariance matrix UΣU^T, for U orthogonal.

2.2 A geometric perspective on the regularization path

In this section, we shall show that a simple relaxation of the optimization problem (8) provides an intuitive geometric perspective on the condition number-regularized estimator. Consider the function

$$J(u,v)=\underset{uI\prec \mathrm{\Omega }\prec vI}{min}(\mathbf{tr}(\mathrm{\Omega }S)-logdet\mathrm{\Omega })$$ (13)

defined as the minimum of the objective of (8) over a range uI ⪯Ω ⪯ vI, where 0 < u ≤ v. Note that the relaxation in (13) above differs from the original problem in the sense that the optimization is no longer with respect to the variable u. In particular, u and v are fixed in (13). By fixing u, the problem has now been significantly simplified. Paralleling Lemma 1, it is easily shown that

$$J(u,v)=\sum _{i=1}^p\underset{u\le {\mu }_i\le v}{min}(l_i{\mu }_i-log{\mu }_i).$$

Recall that the truncation range of the sample eigenvalues is therefore given by (1/v, 1/u). Now for given u, let α ∈ {1, …, p} be the largest index such that l_α > 1/u and β ∈ {1,…, p} be the smallest index such that l_β < 1/v, i.e., the set of indexes where truncation at either end of the spectrum first starts to become a binding constraint. With this convention it is easily shown that J(u, v) can now be expressed in simpler form:

$$J(u,v)=\sum _{i=1}^p(l_i{\mu }_i^{★}(u,v)-log{\mu }_i^{★}(u,v))$$ (14)

$$=\sum _{i=1}^{\alpha }(l_{i}u-logu)+\sum _{i=\alpha +1}^{\beta -1}(1+log{l}_i)+\sum _{i=\beta }^p(l_{i}v-logv),$$ (15)

where

$${\mu }_i^{★}(u,v)=min\{max\{u,1/l_i\},v\}=\{\begin{array}{ll}u,\hfill & 1\le i\le \alpha \hfill \\ 1/l_i,\hfill & \alpha <i<\beta \hfill \\ v,\hfill & \beta \le i\le p.\hfill \end{array}$$ (16)

Comparing (16) to (10), we observe that (Ω^*)⁻¹, the covariance estimate whose inverse achieves the minimum in (13), is obtained by truncating the eigenvalues of S greater than 1/u to 1/u, and less than 1/v to 1/v.

Furthermore, note that the function J(u, v) has the following properties:

1. J does not increase as u decreases and v increases simultaneously. This follows from noting that simultaneously decreasing u and increasing v expands the domain of the minimization in (13).

2. J(u, v) = J(1/l₁, l/l_p) for u ≤ 1/l₁ and v ≥ 1/l_p. Hence J(u, v) is constant on this part of the domain. For these values of u and v, (Ω^★)⁻¹ = S.

3. J(u, v) is almost everywhere differentiable in the interior of the domain {(u, v) : 0 < u ≤ v}, except for on the lines u = 1/l₁,…, 1/l_p and v = 1/l₁,…, 1/l_p. This follows from noting the the indexes α and β changes their values only on these lines. Hence the contribution to the three summands in (14) changes at these values.

We can now see the following obvious relation between the function J(u, v) and the original problem (8): the solution to (8) as given by u^★ is the minimizer of J(u, v) on the line v = κ_maxu, i.e., the original univariate optimization problem (9) is equivalent to minimizing J(u, κ_maxu). We denote this minimizer by u^★(κ_max) and investigate how u^★(κ_max) behaves as κ_max varies. The following proposition proves that u^★(κ_max) is monotone in κ_max. This result sheds light on the regularization path, i.e., the solution path of u^★ as κ_max varies.

Proposition 1

u^★(κ_max) is nonincreasing in κ_max and v^★(κ_max), ≜ κ_maxu^★(κ_max) is nondecreasing, both almost surely.

Proof

The proof is given in the Appendix.

Remark

The above proposition has a very natural and intuitive interpretation: when the constraint on the condition number is relaxed to allow higher value of κ_max, the gap between u^★ and v^★ widens so that the ratio of v^★ to u^★ remains at κ_max. This implies that as κ_max is increased, the lower truncation value u^★ decreases and the higher truncation value v^★ increases. Proposition 1 can be equivalently interpreted by noting that the optimal truncation range τ^★(κ_max), κ_maxτ^★(κ_max) of the sample eigenvalues is nested.

In light of the solution to the condition number-regularized covariance estimation problems in (7), Proposition 1 also implies that once an eigenvalue l_i is truncated for κ_max = ν₀, then it remains truncated for all κ_max < ν₀. Hence the regularized eigenvalue estimates are not only continuous, but they are also monotonic in the sense that they approach either end of the truncation spectrum as the regularization parameter κ_max is decreased to 1. This monotonicity of the condition number-regularized estimates gives a desirable property that is not always enjoyed by other regularized estimators, such as the lasso for instance (Personal communications: Jerome Friedman, Department of Statistics, Stanford University).

With the above theoretical knowledge on the regularization path of the sample eigenvalues, we now provide an illustration of the regularization path; see Figure 2. More specifically, consider the plot of the path of the optimal point (u^★(κ_max), v^★(κ_max)) on the u–v plane from (u^★(1), u^★(1)) to (1/l₁, 1/l_p) when varying κ_max from 1 to cond(S). The left panel shows the path of (u^★(κ_max), v^★(κ_max)) on the u–v plane for the case where the sample eigenvalues are (21, 7, 5.25, 3.5, 3). Here a point on the path represents the minimizer of J(u, v) on a line v = κ_maxu (hollow circle). The path starts from a point on the solid line v = u (κ_max = 1, square) and ends at (1/l₁, 1/l_p), where the dashed line v = cond(S) · u passes (κ_max = cond(S), solid circle). Note that the starting point (κ_max = 1) corresponds to Σ̂_cond = γI for some data-dependent γ > 0 and the end point (κ_max = cond(S)) to Σ̂_cond = S. When κ_max > cond(S), multiple values of u^★ are achieved in the shaded region above the dashed line, yielding nevertheless the same estimator S. The right panel of Figure 2 shows how the eigenvalues of the estimated covariance vary as a function of κ_max. Here we see that as the constraint is made stricter the eigenvalue estimates decrease monotonically. Furthermore, the truncation range of the eigenvalues simultaneously decreases and remains nested.

Figure 2.

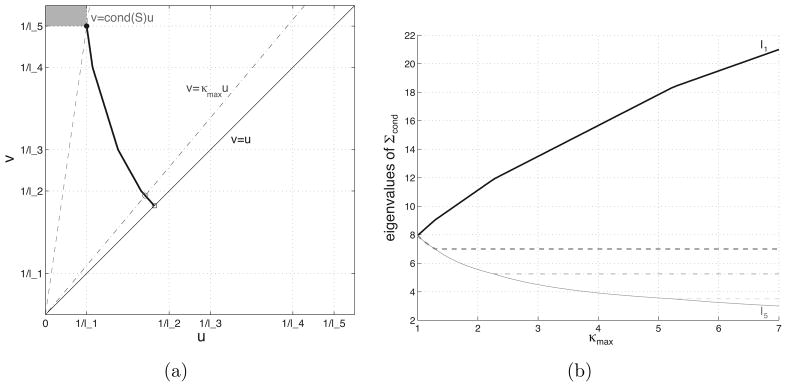
Regularization path of the condition number constrained estimator. (a) Path of (u^★(κ_max), v^★(κ_max)) on the u-v plane, for sample eigenvalues (21, 7, 5.25, 3.5, 3) (thick curve). (b) Regularization path of the same sample eigenvalues as a function of κ_max. Note that the estimates decreases monotonically as the condition number constraint κ_max decreases to 1.

3 Selection of regularization parameter κ_max

Sections 2.1 and 2.2 have already discussed how the optimal truncation range (τ^★, κ_maxτ^★) is determined for a given regularization parameter κ_max, and how it varies with the value of κ_max. This section proposes a data-driven (or adaptive) criterion for selecting the optimal κ_max and undertakes an analysis of this approach.

3.1 Predictive risk selection procedure

A natural approach is to select κ_max that minimizes the predictive risk, or the expected negative predictive likelihood as given by

$$\text{PR}(\nu )=\mathbf{E}\left[{\mathbf{E}}_{\stackrel{\sim }{X}}\left\{\mathbf{tr}({\mathrm{\sum }}_{\nu }^{-1}\stackrel{\sim }{X}{\stackrel{\sim }{X}}^T)-logdet{\widehat{\mathrm{\sum }}}_{\nu }^{-1}\mid {\text{x}}_1,\dots ,{\text{x}}_n\right\}\right],$$ (17)

where Σ̂_ν is the estimated condition number-regularized covariance matrix from independent samples x₁, ···, x_n, with the value of the regularization parameter κ_max set to ν, and X̃ ∈ ℝ^p is a random vector, independent of the given samples, from the same distribution. We approximate the predictive risk using K-fold cross validation. The K-fold cross validation approach divides the data matrix $\mathbf{X}=(x_1^T,\cdots ,x_n^T)$ into K groups so that ${\mathbf{X}}^T=(X_1^T,\dots ,X_K^T)$ with n_k observations in the k-th group, k = 1, …, K. For the k-th iteration, each observation in the k-th group X_k plays the role of X̃ in (17), and the remaining K − 1 groups are used together to estimate the covariance matrix, denoted by ${\widehat{\mathrm{\sum }}}_{\nu }^{[-k]}$. The approximation of the predictive risk using the k-th group reduces to the predictive log-likelihood

$$l_k({\widehat{\mathrm{\sum }}}_{\nu }^{[-k]},X_k)=-(n_k/2)\left[\mathbf{tr}\{{({\widehat{\mathrm{\sum }}}_{\nu }^{[-k]})}^{-1}{X}_k{X}_k^T/n_k\}-logdet{({\widehat{\mathrm{\sum }}}_{\nu }^{[-k]})}^{-1}\right].$$

The estimate of the predictive risk is then defined as

$$\widehat{\text{PR}}(\nu )=-\frac{1}{n}\sum _{k=1}^K{l}_k({\widehat{\mathrm{\sum }}}_{\nu }^{[-k]},X_k).$$ (18)

The optimal value for the regularization parameter κ_max is selected as ν that minimizes (18), i.e.,

$${\widehat{\kappa }}_{max}=inf(arg\underset{\nu \ge 1}{inf}\widehat{\text{PR}}(\nu )).$$

Note that the outer infimum is taken since $l_k({\widehat{\mathrm{\sum }}}_{\nu }^{[-k]},X_k)$ is constant for ν ≥ cond(S^[−k]), where S^[−k] is the k-th fold sample covariance matrix based on the remaining K − 1 groups.

3.2 Properties of the optimal regularization parameter

We proceed to investigate the behavior of the selected regularization parameter κ̂_max, both theoretically and in simulations. We first note that κ̂_max is a consistent estimator for the true condition number κ. This fact is expressed below as one of the several properties of κ̂_max:

• (P1)For a fixed p, as n increases, κ̂_max approaches κ in probability, where κ is the condition number of the true covariance matrix Σ.

This statement is stated formally below:

Theorem 2

For a given p,

$$\underset{n\to \infty }{lim}\mathbf{pr}\left({\widehat{\kappa }}_{max}=\kappa \right)=1.$$

Proof

The proof is given in Supplemental Section A.

We further investigate the behavior of κ_max in simulations. To this end, consider iid samples from a zero-mean p-variate Gaussian distribution with the following covariance matrices:

1. Identity matrix in ℝ^p.

2. diag(1, r, r², …, r^p), with condition number 1/r^p = 5.

3. diag(1, r, r², …, r^p), with condition number 1/r^p = 400.

4. Toeplitz matrix whose (i, j)th element is 0.3^|i−j| for i, j = 1, …, p.

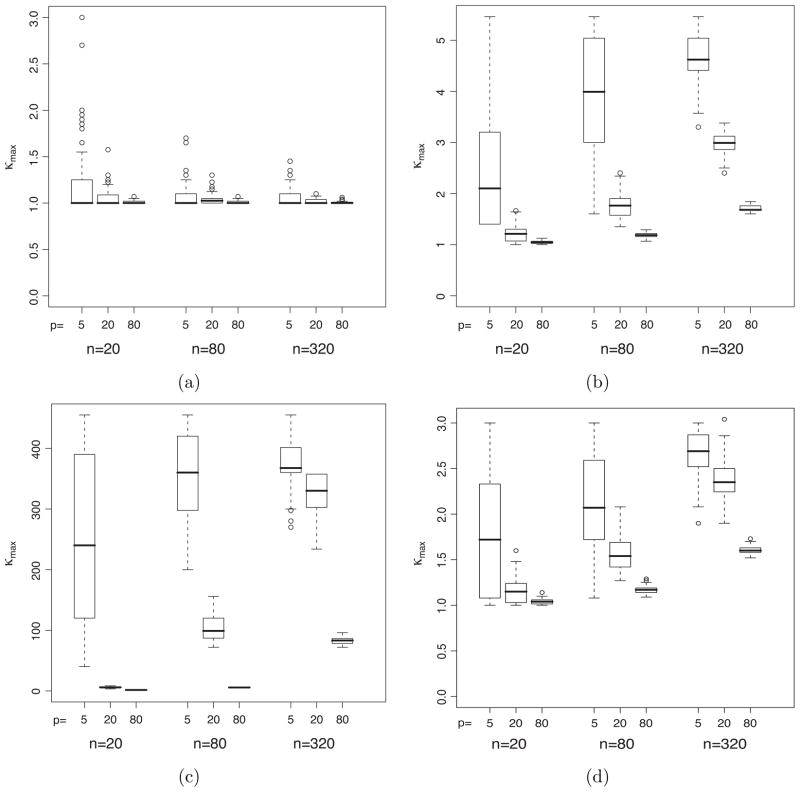
We consider different combinations of sample sizes and dimensions of the problem as given by n = 20, 80, 320 and p = 5, 20, 80. For each of these cases 100 replicates are generated and κ̂_max computed with 5-fold cross validation. The behavior of κ̂_max is plotted in Figure 3 and leads to insightful observations. A summary of the properties of the κ̂_max is given in (P2)–(P4) below:

Figure 3.

Box plots summarizing the distribution of κ̂_max for dimensions p = 5, 20, 80 and for sample sizes n = 20, 80, 320 for the following covariance matrices (a) identity (b) diagonal exponentially decreasing, condition number 5, (c) diagonal exponentially decreasing, condition number 400, (d) Toeplitz matrix whose (i, j)th element is 0.3^|i−j| for i, j = 1, 2,…, p.

• (P2)If the condition number of the true covariance matrix remains finite as p increases, then for a fixed n, κ̂_max decreases.
• (P3)If the condition number of the true covariance matrix remains finite as p increases, then for a fixed n, κ̂_max converges to 1.
• (P4)The variance of κ̂_max decreases as either n or p increases.

These properties are analogous to those of the optimal regularization parameter δ̂ for the linear shrinkage estimator (5), found using a similar predictive risk criterion (Warton, 2008).

4 Bayesian interpretation

In the same spirit as the Bayesian posterior mode interpretation of the LASSO (Tibshirani, 1996), we can draw parallels for the condition number regularized covariance estimator. The condition number constraint given by λ₁(Σ)/λ_p(Σ) ≤ κ_max is similar to adding a penalty term g_max(λ₁(Σ)/λ_p(Σ)) to the likelihood equation for the eigenvalues:

$$\begin{array}{ll}\text{maximize}\hfill & exp\left(-(n/2){\sum }_{i=1}^p{l}_i/{\lambda }_i\right){\left({\prod }_{i=1}^p{\lambda }_i\right)}^{-n/2}exp(-g_{max}{\lambda }_1/{\lambda }_p)\hfill \\ \text{subject}\text{to}\hfill & {\lambda }_1\ge \cdots \ge {\lambda }_p>0\hfill \end{array}$$

The above expression allows us to qualitatively interpret the condition number-regularized estimator as the Bayes posterior mode under the following prior

$$\pi ({\lambda }_1,\dots ,{\lambda }_p)=exp(-g_{max}{\lambda }_1/{\lambda }_p),{\lambda }_1\ge \cdots \ge {\lambda }_p>0$$ (19)

for the eigenvalues, and an independent Haar measure on the Stiefel manifold, as the prior for the eigenvectors. The aforementioned prior on the eigenvalues has useful interesting properties which help to explain the type of eigenvalue truncation described in previous sections. We note that the prior is improper but the posterior is always proper.

Proposition 2

The prior on the eigenvalues in (19) is improper, whereas the posterior yields a proper distribution. More formally,

$${\int }_C\pi (\underset{\_}{\lambda })d\underset{\_}{\lambda }={\int }_{C}exp(-g_{max}{\lambda }_1/{\lambda }_p)d\underset{\_}{\lambda }=\infty ,$$

and

$${\int }_C\pi (\underset{\_}{\lambda })f(\underset{\_}{\lambda },\underset{\_}{l})d\underset{\_}{\lambda }\propto {\int }_{C}exp(-(n/2)\sum _{i=1}^p{l}_i/{\lambda }_i){(\prod _{i=1}^p{\lambda }_i)}^{-n/2}exp(-g_{max}{\lambda }_1/{\lambda }_p)d\underset{\_}{\lambda }<\infty ,$$

where λ = (λ₁,…, λ_p) and C = {λ : λ₁ ≥ ··· ≥ λ_p > 0}.

Proof

The proof is given in Supplemental Section A.

The prior above puts the greatest mass around the region {λ ∈ ℝ^p : λ₁ = ··· = λ_p} which consequently encourages “shrinking” or “pulling” the eigenvalues closer together. Note that the support of both the prior and the posterior is the entire space of ordered eigenvalues. Hence the prior simply by itself does not immediately yield a hard constraint on the condition number. Evaluating the posterior mode yields an estimator that satisfies the condition number constraint.

A clear picture of the regularization achieved by the prior above and its potential for “eigenvalue shrinkage” emerges when compared to the other types of priors suggested in the literature and the corresponding Bayes estimators. The standard MLE implies of course a completely flat prior on the constrained space C. A commonly used inverse Wishart conjugate prior Σ⁻¹ ~ Wishart(m, cI) yields a posterior mode which is a linear shrinkage estimator (5) with δ = m/(n + m). Note however that the coefficients of the combination do not depend of the data X, and are a function only of the sample size n and the degrees of freedom or shape parameter from the prior, m. A useful prior for covariance matrices that yields a data-dependent posterior mode is the reference prior proposed by Yang and Berger (1994). For this prior, the eigenvalues are inversely proportional to the determinant of the the covariance matrix, as given by ${\prod }_{i=1}^p{\lambda }_i$, and also encourages shrinkage of the eigenvalues. The posterior mode using this reference prior can be formulated similarly to that of condition number regularization:

$$arg{max}_{{\lambda }_1\ge \dots \ge {\lambda }_p>0}exp(-(n/2)\sum _{i=1}^p{l}_i/{\lambda }_i){(\prod _{i=1}^p{\lambda }_i)}^{-n/2}{(\prod _{i=1}^p{\lambda }_i)}^{-1}=arg{min}_{{\lambda }_1\ge \dots \ge {\lambda }_p>0}(n/2)\sum _{i=1}^p{l}_i/{\lambda }_i+((n+2)/2)\sum _{i=1}^{p}log{\lambda }_i.$$

An examination of the penalty implied by the reference prior suggests that there is no direct penalty on the condition number. In Supplemental Section B we illustrate the density of the priors discussed above in the two-dimensional case. In particular, the density of the condition number regularization prior places more emphasis on the line λ₁ = λ₂ thus “squeezing” the eigenvalues together. This is in direct contrast with the inverse Wishart or reference priors where this shrinkage effect is not as pronounced.

5 Decision-theoretic risk properties

5.1 Asymptotic properties

We now show that the condition number-regularized estimator Σ̂_cond has asymptotically lower risk than the sample covariance matrix S with respect to entropy loss. Recall that the entropy loss, also known as Stein’s loss, is defined as follows:

$${\mathcal{L}}_{\text{ent}}(\widehat{\mathrm{\sum }},\mathrm{\sum })=\mathbf{tr}({\mathrm{\sum }}^{-1}\widehat{\mathrm{\sum }})-logdet({\mathrm{\sum }}^{-1}\widehat{\mathrm{\sum }})-p.$$ (20)

Let λ₁, …, λ_p, with λ₁ ≥ ··· ≥ λ_p, denote the eigenvalues of the true covariance matrix Σ and Λ = diag(λ₁, …, λ_p). Define λ = (λ₁, …, λ_p), ${\underset{\_}{\lambda }}^{-1}=({\lambda }_1^{-1},\dots ,{\lambda }_p^{-1})$, and κ = λ₁/λ_p.

First consider the trivial case when p > n. In this case, the sample covariance matrix S is singular regardless of the singularity of Σ, and 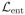(S, Σ) = ∞, whereas the loss and therefore the risk of Σ̂_cond are always finite. Thus, Σ̂_cond has smaller entropy risk than S.

For p ≤ n, if the true covariance matrix has a finite condition number, it can be shown that for a properly chosen κ_max, the condition number-regularized estimator asymptotically dominates the sample covariance matrix. This assertion is formalized below.

Theorem 3

Consider a class of covariance matrices 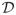(κ, ω), whose condition numbers are bounded above by κ and with minimum eigenvalue bounded below by ω > 0, i.e.,

$$\mathcal{D}(\kappa ,\omega )=\{\mathrm{\sum }=R\mathrm{\Lambda }{R}^T:R\mathit{orthogonal},\mathrm{\Lambda }=\text{diag}({\lambda }_1,\dots ,{\lambda }_p),\omega \le {\lambda }_p\le \dots \le {\lambda }_1\le \kappa \omega \}.$$

Then, the following results hold.

1. Consider the quantity Σ̃(κ_max, ω) = Qdiag(λ̃₁, …, λ̃_p)Q^T, where

   $${\widehat{\lambda }}_i=\{\begin{array}{ll}\omega ,\hfill & if{l}_i\le \omega \hfill \\ l_i,\hfill & if\omega \le l_i<{\kappa }_{max}\omega \hfill \\ {\kappa }_{max}\omega ,\hfill & if{l}_i\ge {\kappa }_{max}\omega ,\hfill \end{array}$$

   and the sample covariance matrix given as S = Qdiag(l₁, …, l_p)Q^T, Q orthogonal, l₁ ≥ … ≥ l_p. If the true covariance matrix Σ ∈ 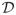(κ_max, ω), then ∀ n, Σ̂(κ_max, ω) has a smaller entropy risk than S.

2. Consider a true covariance matrix Σ whose condition number is bounded above by κ, i.e., Σ ∈ ∪_ω>0 (κ, ω). If ${\kappa }_{max}\ge \kappa {(1-\sqrt{\gamma })}^{-2}$, then as p/n → γ ∈ (0, 1),

   $$\mathbf{pr}\left(\left\{\mathrm{\sum }\in \mathcal{D}({\kappa }_{max},{\tau }^{★})\right\}\mathit{eventually}\right)=1,$$

   where τ^★ = τ^★(κ_max) is given in (12).

Proof

The proof is given in Supplemental Section A.

Combining the two results above, we conclude that the estimator Σ̂_cond = Σ̂(κ_max, τ^★(κ_max)) asymptotically has a lower entropy risk than the sample covariance matrix.

5.2 Finite sample performance

This section undertakes a simulation study in order to compare the finite-sample risks of the condition number-regularized estimator Σ̂_cond with those of the sample covariance matrix (S) and the linear shrinkage estimator (Σ̂_LS) in the “large p, small n” setting. The regularization parameter δ for Σ̂_LS is chosen as prescribed in Warton (2008). The optimal Σ̂_cond is calculated using the adaptive parameter selection method outlined in Section 3. Since Σ̂_cond and Σ̂_LS both select the regularization parameters similarly, i.e., by minimizing the empirical predictive risk (18), a meaningful comparison between two estimators can be made. We consider two loss functions traditionally used in covariance estimation risk comparisons: (a) entropy loss as given in (20) and (b) quadratic loss ${\mathcal{L}}_{\text{Q}}(\widehat{\mathrm{\sum }},\mathrm{\sum })={\Vert \widehat{\mathrm{\sum }}{\mathrm{\sum }}^{-1}-I\Vert }_{\text{F}}^2$.

Condition number regularization applies shrinkage to both ends of the sample eigenvalue spectrum and does not affect the middle part, whereas linear shrinkage does this to the entire spectrum uniformly. Therefore, it is expected that Σ̂_cond works well when a small proportion of eigenvalues are found at the extremes. Such situations rise very naturally when only a few eigenvalues explain most of the variation in data. To understand the performance of the estimators in this context the following scenarios were investigated. We consider diagonal matrices of dimensions p = 120, 250, 500 as true covariance matrices. The eigenvalues (diagonal elements) are dichotomous, where the “high” values are (1 − ρ)+ ρp and the “low” values are 1 − ρ. For each p, we vary the composition of the diagonal elements such that the high values take only one (singleton), 10%, 20%, 30%, and 40% of the total number of p eigenvalues. The sample size n is chosen so that γ = p/n is approximately 1.25, 2, or 4. Note that for a given p, the condition number of the true covariance matrices is held fixed at 1 + pρ/(1 − ρ) regardless of the composition of eigenvalues. For each of the simulation scenarios, we generate 1000 data sets and compute 1000 estimates of the true covariance matrix. The risks are calculated by averaging the losses over these 1000 estimates.

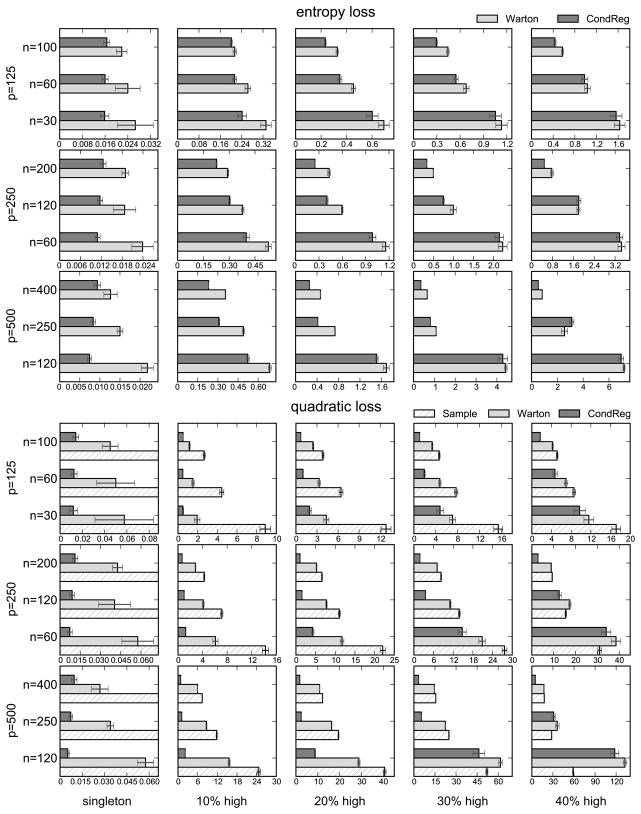
Figure 4 presents the results for ρ = 0.1, and represents a large condition number. It is observed that in general Σ̂_cond has less risk than Σ̂_LS, which in turn has less risk than the sample covariance matrix (entropy loss is not defined for the sample covariance matrix). This phenomenon is most clear when the eigenvalue spectrum has a singleton in the extreme. In this case, Σ̂_cond gives a risk reduction between 27 % and 67 % for entropy loss, and between 67 % and 91 % for quadratic loss. The risk reduction tends to be more pronounced in high dimensional scenarios, i.e., for p large and n small. The performance of Σ̂_cond over Σ̂_LS is maintained until the “high” eigenvalues compose up to 30 % of the eigenvalue spectrum. Comparing the two loss functions, risk reduction of Σ̂_cond is more distinct in quadratic loss. We note that for quadratic loss with large p and large proportion of “high” eigenvalues, there are cases that the sample covariance matrix can perform well.

Figure 4.

Average risks (with error bars) over 1000 runs with respect to two loss functions when ρ= 0.1. sample=sample covariance matrix, Warton=linear shrinkage (Warton, 2008), CondReg=condition number regularization. Risks are normalized by the dimension (p).

As an example of a moderate condition number, results for the ρ = 0.5 case is given in Supplemental Section C. General trends are the same as with the ρ = 0.1 case.

In summary, the risk comparison study provides a numerical evidence that condition number regularization has merit when the true covariance matrix has a bimodal eigenvalue distribution and/or the true condition number is large.

6 Application to portfolio selection

This section illustrates the merits of the condition number regularization in the context of financial portfolio optimization, where a well-conditioned covariance estimator is necessary. A portfolio refers to a collection of risky assets held by an institution or an individual. Over the holding period, the return on the portfolio is the weighted average of the returns on the individual assets that constitutes the portfolio, in which the weight associated with each asset corresponds to its proportion in monetary terms. The objective of portfolio optimization is to determine the weights that maximize the return on the portfolio. Since the asset returns are stochastic, a portfolio always carries a risk of loss. Hence the objective is to maximize the overall return subject to a given level of risk, or equivalently to minimize risk for a given level of return. Mean-variance portfolio (MVP) theory (Markowitz, 1952) uses the standard deviation of portfolio returns to quantify the risk. Estimation of the covariance matrix of asset returns thus becomes critical in the MVP setting. An important and difficult component of MVP theory is to estimate the expected return on the portfolio (Luenberger, 1998; Merton, 1980). Since the focus of this paper lies in estimating covariance matrices and not expected returns, we shall focus on determining the minimum variance portfolio which only requires an estimate of the covariance matrix; see, e.g., Chan et al. (1999). For this we shall use the condition number regularization, linear shrinkage and the sample covariance matrix, in constructing a minimum variance portfolio. We compare their respective performance over a period of more than 14 years.

6.1 Minimum variance portfolio rebalancing

We begin with a formal description of the minimum variance portfolio selection problem. The universe of assets consists of p risky assets, denoted 1,…, p. We use r_i to denote the return of asset i over one period; that is, its change in price over one time period divided by its price at the beginning of the period. Let Σ denote the covariance matrix of r = (r₁,…, r_p). We employ w_i to denote the weight of asset i in the portfolio held throughout the period. A long position in asset i corresponds to w_i > 0, and a short position corresponds to w_i < 0. The portfolio is therefore unambiguously represented by the vector of weights w = (w₁,…, w_p). Without loss of generality, the budget constraint can be written as 1^Tw = 1, where 1 is the vector of all ones. The risk of a portfolio is measured by the standard deviation (w^TΣw)^1/2 of its return.

Now the minimum variance portfolio selection problem can be formulated as

$$\begin{array}{ll}\text{minimize}\hfill & w^T\mathrm{\sum }w\hfill \\ \text{subject}\text{to}\hfill & {\mathbf{1}}^{T}w=1.\hfill \end{array}$$ (21)

This is a simple quadratic program that has an analytic solution w^★ = (1^TΣ⁻¹1)⁻¹Σ⁻¹1. In practice, the parameter Σ has to be estimated.

The standard portfolio selection problem described above assumes that the returns are stationary, which is of course not realistic. As a way of dealing with the nonstationarity of returns, we employ a minimum variance portfolio rebalancing (MVR) strategy as follows. Let $r^{(t)}=(r_1^{(t)},\dots ,r_p^{(t)})\in {\mathbb{R}}^p$, t = 1, …, N_tot, denote the realized returns of assets at time t (the time unit under consideration can be a day, a week, or a month). The periodic minimum variance rebalancing strategy is implemented by updating the portfolio weights every L time units, i.e., the entire trading horizon is subdivided into blocks each consisting of L time units. At the start of each block, we determine the minimum variance portfolio weights based on the past N_estim observations of returns. We shall refer to N_estim as the estimation horizon size. The portfolio weights are then held constant for L time units during these “holding” periods, i.e., during each of these blocks, and subsequently updated at the beginning of the following one. For simplicity, we shall assume the entire trading horizon consists of N_tot = N_estim + KL time units, for some positive integer K, i.e., there will be K updates. (The last rebalancing is done at the end of the entire period, and so the out-of-sample performance of the rebalanced portfolio for this holding period is not taken into account.) We therefore have a series of portfolios w^(j) = (1^T(Σ̂^(j))⁻¹1)⁻¹(Σ̂^(j))⁻¹1 over the holding periods of [N_estim +1+(j − 1)L, N_estim + jL], j = 1,…, K. Here Σ̂^(j) is the covariance matrix of the asset returns estimated from those over the jth holding period.

6.2 Empirical out-of-sample performance

In this empirical study, we use the 30 stocks that constituted the Dow Jones Industrial Average as of July 2008 (Supplemental Section D.1 lists these 30 stocks). We used the closing prices adjusted daily for all applicable splits and dividend distributions downloaded from Yahoo! Finance (http://finance.yahoo.com/). The whole period considered in our numerical study is from the trading date of December 14, 1992 to June 6, 2008 (this period consists of 4100 trading days). We consider weekly returns: the time unit is 5 consecutive trading days. We take

$$\begin{array}{lll}{N}_{\text{tot}}=820,\hfill & L=15,\hfill & N_{\text{estim}}=15,30,45,60.\hfill \end{array}$$

To estimate the covariance matrices, we use the last N_estim weekly returns of the constituents of the Dow Jones Industrial Average.³ The entire trading horizon corresponds to K = 48 holding periods, which span the dates from February 18, 1994 to June 6, 2008. In what follows, we compare the MVR strategy where the covariance matrices are estimated using the condition number regularization with those that use either the sample covariance matrix or linear shrinkage. We employ two linear shrinkage schemes: that of Warton (2008) of Section 5.2 and that of Ledoit and Wolf (2004). The latter is widely accepted as a well-conditioned estimator in the financial literature.

Performance metrics

We use the following quantities in assessing the performance of the MVR strategies. For precise formulae of these metrics, refer to Supplemental Section D.3.

• Realized return. The realized return of the portfolio over the trading period.

• Realized risk. The realized risk (return standard deviation) of the portfolio over the trading period.

• Realized Sharpe ratio. The realized excess return, with respect to the risk-free rate, per unit risk of the portfolio.

• Turnover. Amount of new portfolio assets purchased or sold over the trading period.

• Normalized wealth growth. Accumulated wealth yielded by the portfolio over the trading period when the initial budget is normalized to one, taking the transaction cost into account.

• Size of the short side. The proportion of the short side (negative) weights to the sum of the absolute weights of the portfolio.

We assume that the transaction costs are the same for the 30 stocks and set them to 30 basis points. The risk-free rate is set at 5% per annum.

Comparison results

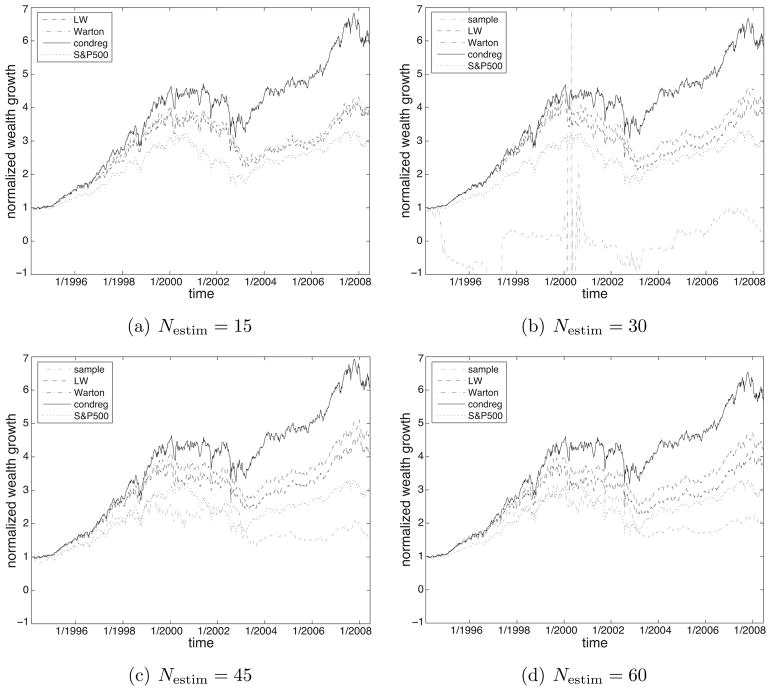
Figure 5 shows the normalized wealth growth over the trading horizon for four different values of N_estim. The sample covariance matrix failed in solving (21) for N_estim = 15 because of its singularity and hence is omitted in this figure. The MVR strategy using the condition number-regularized covariance matrix delivers higher growth as compared to using the sample covariance matrix, linear shrinkage or index tracking in this performance metric. The higher growth is realized consistently across the 14 year trading period and is regardless of the estimation horizon. A trading strategy based on the condition number-regularized covariance matrix consistently performs better than the S&P 500 index and can lead to profits as much as 175% more than its closest competitor.

Figure 5.

Normalized wealth growth results of the minimum variance rebalancing strategy for various estimation horizon sizes over the trading period from February 18, 1994 through June 6, 2008. sample=sample covariance matrix, LW=linear shrinkage (Ledoit and Wolf, 2004), Warton=linear shrinkage (Warton, 2008), condreg=condition number regularization. For comparison, the S&P 500 index for the same period (i.e., index tracking), with the initial price normalized to 1, is also plotted.

A useful result appears after further analysis. There is no significant difference between the condition number regularization approach and the two linear shrinkage schemes in terms of the realized return, risk, and Sharpe ratio. Supplemental Section D.4 summarizes these metrics for each estimator respectively averaged over the trading period. For all values of N_estim, the average differences of the metrics between the two regularization schemes are within two standard errors of those. Hence the condition number regularized estimator delivers better normalized wealth growth than the other estimators but without compromising on other measures such as volatility.

The turnover of the portfolio seems to be one of the major driving factors of the difference in wealth growth. In particular, the MVR strategy using the condition number-regularized covariance matrix gives far lower turnover and thus more stable weights than when using the linear shrinkage estimator or the sample covariance matrix. (See Supplemental Section D.5 for plots.) A lower turnover also implies less transaction costs, thereby also partially contributing to the higher wealth growth. Note that there is no explicit limit on turnover. The stability of the MVR portfolio using the condition number regularization appears to be related to its small size of the short side (reported in Supplemental Section D.6). Because stock borrowing is expensive, the condition number regularization based strategy can be advantageous in practice.

Appendix

Proof of Lemma 1

Recall the spectral decomposition of the sample covariance matrix S = QLQ^T, with L = diag(l₁,…, l_p) and l₁ ≥ … ≥ l_p ≥ 0. From the objective function in (8), suppose the variable Ω has the spectral decomposition RMR^T, with R orthogonal and M = diag(μ₁,…, μ_p), μ₁ ≤ … ≤ μ_p. Then the objective function in (8) can be written as

$$\begin{array}{l}\mathbf{tr}(\mathrm{\Omega }S)-logdet(\mathrm{\Omega })=\mathbf{tr}({\mathit{RMR}}^T{\mathit{QLQ}}^T)-logdet({\mathit{RMR}}^T)\\ =l(R,M)\\ \ge \mathbf{tr}(ML)-logdet\mathit{M}=l(Q,M),\end{array}$$

with equality in the last line when R = Q (Farrell, 1985, Ch. 14). Hence (8) amounts to

$$\begin{array}{ll}\text{minimize}\hfill & {\sum }_{i=1}^p(l_i{\mu }_i-log{\mu }_i)\hfill \\ \text{subject}\text{to}\hfill & u\le {\mu }_1\le \cdots \le {\mu }_p\le {\kappa }_{max}u,i=1,\dots ,p,\hfill \end{array}$$ (22)

with the optimization variables μ₁, …, μ_p and u.

For the moment we shall ignore the order constraints among the eigenvalues. Then problem (22) becomes separable in μ₁,…, μ_p. Call this related problem (22*). For a fixed u, the minimizer of each summand of the objective function in (22) without the order constraints is given as

$${\mu }_i^{★}(u)=\underset{u\le {\mu }_i\le {\kappa }_{max}u}{\text{argmin}}(l_i{\mu }_i-log{\mu }_i)=min\{max\{u,1/l_i\},{\kappa }_{max}u\}.$$ (23)

Note that (23) however satisfies the order constraints. In other words, ${\mu }_1^{★}(u)\le \dots \le {\mu }_p^{★}(u)$ for all u. Therefore (22*) is equivalent to (22). Plugging (23) in (22) removes the constraints and the objective function reduces to a univariate one:

$$J_{{\kappa }_{max}}(u)\triangleq \sum _{i=1}^p{J}_{{\kappa }_{max}}^{(i)}(u),$$ (24)

where

$$J_{{\kappa }_{max}}^{(i)}(u)=l_i{\mu }_i^{★}(u)-log{\mu }_i^{★}(u)=\{\begin{array}{ll}{l}_i({\kappa }_{max}u)-log({\kappa }_{max}u),\hfill & u<1/({\kappa }_{max}{l}_i)\hfill \\ 1+log{l}_i,\hfill & 1/({\kappa }_{max}{l}_i)\le u\le 1/l_i\hfill \\ l_{i}u-logu,\hfill & u>1/l_i.\hfill \end{array}$$

The function (24) is convex, since each $J_{{\kappa }_{max}}^{(i)}$ is convex in u.

Proof of Theorem 1

The function $J_{{\kappa }_{max}}^{(i)}(u)$ is convex and is constant on the interval [1/(κ_maxl_i), 1/l_i]. Thus, the function $J_{{\kappa }_{max}}(u)\triangleq {\sum }_{i=1}^p{J}_{{\kappa }_{max}}^{(i)}(u)$ has a region on which it is a constant if and only if

$$\left[1/({\kappa }_{max}{l}_1),1/l_1\right]\cap \left[1/({\kappa }_{max}{l}_p),1/l_p\right]\ne \varnothing ,$$

or equivalently, κ_max > cond(S). Therefore, provided that κ_max ≤ cond(S), the convex function J_κmax (u) does not have a region on which it is constant. Since J_κmax (u) is strictly decreasing for 0 < u < 1/(κ_maxl₁) and strictly increasing for u > 1/l_p, it has a unique minimizer u^★. If κ_max > cond(S), the maximizer u^★ may not be unique because J_κmax (u) has a plateau. However, since the condition number constraint becomes inactive, Σ̂_cond = S for all the maximizers.

Now assume that κ_max ≤ cond(S). For α ∈ {1,…, p − 1} and β ∈ {2, …, p}, define the following two quantities.

$$u_{\alpha ,\beta }=\frac{\alpha +p-\beta +1}{{\sum }_{i=1}^{\alpha }{l}_i+{\sum }_{i=\beta }^p{\kappa }_{max}{l}_i}\text{and}{v}_{\alpha ,\beta }={\kappa }_{max}{u}_{\alpha ,\beta }.$$

By construction, u_α,β coincides with u^★ if and only if

$$1/l_{\alpha }<u_{\alpha ,\beta }\le 1/l_{\alpha +1}\text{and}1/l_{\beta -1}\le {\kappa }_{max}{u}_{\alpha ,\beta }<1/l_{\beta }.$$ (25)

Consider a set of rectangles {R_α,β} in the uv-plane such that

$$R_{\alpha ,\beta }=\{(u,v):1/l_{\alpha }<u\le 1/l_{\alpha +1}\text{and}1/l_{\beta -1}\le v<1/l_{\beta }\}.$$

Then condition (25) is equivalent to

$$(u_{\alpha ,\beta },v_{\alpha ,\beta })\in R_{\alpha ,\beta }$$ (26)

in the uv-plane. Since {R_α,β} partitions {(u, v) : 1/l₁ < u ≤ 1/l_p and 1/l₁ ≤ v < 1/l_p} and (u_α,β, v_α,β) is on the line v = κ_maxu, an obvious algorithm to find the pair (α, β) that satisfies the condition (26) is to keep track of the rectangles R_α,β that intersect this line. To understand that algorithm takes O(p) operations, start from the origin of the uv-plane, increase u and v along the line v = κ_maxu. Since κ_max > 1, if the line intersects R_α,β, then the next intersection occurs in one of the three rectangles: R_α+1,β, R_α,β+1, and R_α+1,β+1. Therefore after finding the first intersection (which is on the line u = 1/l₁), the search requires at most 2p tests to satisfy condition (26). Finding the first intersection takes at most p tests.

Proof of Proposition 1

Recall that, for κ_max = ν₀,

$$u^{★}({\nu }_0)=\frac{\alpha +p-\beta +1}{{\sum }_{i=1}^{\alpha }{l}_i+{\nu }_0{\sum }_{i=\beta }^p{l}_i}$$

and

$$v^{★}({\nu }_0)={\nu }_0{u}^{★}({\nu }_0)=\frac{\alpha +p-\beta +1}{\frac{1}{{\nu }_0}{\sum }_{i=1}^{\alpha }{l}_i+{\sum }_{i=\beta }^p{l}_i},$$

where α = α(ν₀) ∈ {1,…, p} is the largest index such that 1/l_α < u^★(ν₀) and β = β(ν₀) ∈ {1,…, p} is the smallest index such that 1/l_β > ν₀u^★(ν₀). Then

$$1/l_{\alpha }<u^{★}({\nu }_0)\le 1/l_{\alpha +1}$$

and

$$1/l_{\beta -1}\le v^{★}({\nu }_0)<1/l_{\beta }.$$

The lower and upper bounds u^★(ν₀) and v^★(ν₀) of the reciprocal sample eigenvalues can be divided into four cases:

1. 1/l_α < u^★(ν₀) < 1/l_α+1 and 1/l_β−1 < v^★(ν₀) < 1/l_β.

   We can find ν > ν₀ such that

   $$1/l_{\alpha }<u^{★}(\nu )\le 1/l_{\alpha +1}$$
   and

   $$1/l_{\beta -1}\le v^{★}(\nu )<1/l_{\beta }.$$
   Therefore,

   $$u^{★}(\nu )=\frac{\alpha +p-\beta +1}{{\sum }_{i=1}^{\alpha }{l}_i+\nu {\sum }_{i=\beta }^p{l}_i}<\frac{\alpha +p-\beta +1}{{\sum }_{i=1}^{\alpha }{l}_i+{\nu }_0{\sum }_{i=\beta }^p{l}_i}=u^{★}({\nu }_0)$$
   and

   $$v^{★}(\nu )=\frac{\alpha +p-\beta +1}{\frac{1}{{\nu }_0}{\sum }_{i=1}^{\alpha }{l}_i+{\sum }_{i=\beta }^p{l}_i}>\frac{\alpha +p-\beta +1}{\frac{1}{\nu }{\sum }_{i=1}^{\alpha }{l}_i+{\sum }_{i=\beta }^p{l}_i}=v^{★}({\nu }_0).$$

2. u^★(ν₀) = 1/l_α+1 and 1/l_β−1 < v^★(ν₀) < 1/l_β.

   Suppose u^★(ν) > u^★(ν₀). Then we can find ν > ν₀ such that α(ν) = α(ν₀) + 1 = α + 1 and β(ν) = β(ν₀) = β. Then,

   $$u^{★}(\nu )=\frac{\alpha +1+p-\beta +1}{{\sum }_{i=1}^{\alpha +1}{l}_i+\nu {\sum }_{i=\beta }^p{l}_i}.$$
   Therefore,

   $$\begin{array}{l}\frac{1}{u^{★}({\nu }_0)}-\frac{1}{u^{★}(\nu )}=1/l_{\alpha +1}-\frac{{\sum }_{i=1}^{\alpha +1}{l}_i+\nu {\sum }_{i=\beta }^p{l}_i}{\alpha +1+p-\beta +1}\\ =\frac{(\alpha +p-\beta +1)l_{\alpha +1}-({\sum }_{i=1}^{\alpha +1}{l}_i+\nu {\sum }_{i=\beta }^p{l}_i)}{\alpha +1+p-\beta +1}>0,\end{array}$$
   or

   $$l_{\alpha +1}>\frac{{\sum }_{i=1}^{\alpha +1}{l}_i+\nu {\sum }_{i=\beta }^p{l}_i}{\alpha +p-\beta +1}>\frac{{\sum }_{i=1}^{\alpha +1}{l}_i+{\nu }_0{\sum }_{i=\beta }^p{l}_i}{\alpha +p-\beta +1}=l_{\alpha +1},$$

   which is a contradiction. Therefore, u^★(ν) ≤ u^★(ν₀).

   Now, we can find ν > ν₀ such that α(ν) = α(ν₀) = α and β(ν) = β(ν₀) = β. This reduces to case 1.

3. 1/l_α < u^★(ν₀) < 1/l_α+1 and v^★(ν₀) = 1/l_β−1.

   Suppose v^★(ν) < v^★(ν₀). Then we can find ν > ν₀ such that α(ν) = α(ν₀) = α and β(ν) = β(ν₀) − 1 = β − 1. Then,

   $$v^{★}(\nu )=\frac{\alpha +p-\beta +2}{\frac{1}{\nu }{\sum }_{i=1}^{\alpha }{l}_i+{\sum }_{i=\beta -1}^p{l}_i}.$$
   Therefore,

   $$\begin{array}{l}\frac{1}{v^{★}({\nu }_0)}-\frac{1}{v^{★}(\nu )}=1/l_{\beta -1}-\frac{{\sum }_{i=1}^{\alpha }{l}_i+\nu {\sum }_{i=\beta -1}^p{l}_i}{\alpha +p-\beta +2}\\ =\frac{(\alpha +p-\beta +1)l_{\beta -1}-({\sum }_{i=1}^{\alpha }{l}_i+\nu {\sum }_{i=\beta }^p{l}_i)}{\alpha +p-\beta +2}<0,\end{array}$$
   or

   $$l_{\beta -1}<\frac{{\sum }_{i=1}^{\alpha }\frac{1}{\nu }{l}_i+{\sum }_{i=\beta -1}^p{l}_i}{\alpha +p-\beta +1}<\frac{{\sum }_{i=1}^{\alpha +1}\frac{1}{{\nu }_0}{l}_i+{\sum }_{i=\beta }^p{l}_i}{\alpha +p-\beta +1}=l_{\beta -1},$$

   which is a contradiction. Therefore, v^★(ν) ≥ v^★(ν₀).

   Now, we can find ν > ν₀ such that α(ν) = α(ν₀) = α and β(ν) = β(ν₀) = β. This reduces to case 1.

4. u^★(ν₀) = 1/l_α+1 and v^★(ν₀) = 1/l_β−1. 1/l_α+1 = u^★(ν₀) = v^★(ν₀)/ν₀ = 1/(ν₀l_β−1). This is a measure zero event and does not affect the conclusion.