Summary
Ecological momentary assessment (EMA) is a method for collecting real-time data in subjects’ environments. It often uses electronic devices to obtain information on psychological state through administration of questionnaires at times selected from a probability-based sampling design. This information can be used to model the impact of momentary variation in psychological state on the lifetimes to events such as smoking lapse. Motivated by this, a probability-sampling framework is proposed for estimating the impact of time-varying covariates on the lifetimes to events. Presented as an alternative to joint modeling of the covariate process as well as event lifetimes, this framework calls for sampling covariates at the event lifetimes and at times selected according to a probability-based sampling design. A design-unbiased estimator for the cumulative hazard is substituted into the log likelihood, and the resulting objective function is maximized to obtain the proposed estimator. This estimator has two quantifiable sources of variation, that due to the survival model and that due to sampling the covariates. Data from a nicotine patch trial are used to illustrate the proposed approach.
Keywords: Ecological momentary assessment, Estimating equations, Parametric hazard, Smoking
1. Introduction
The impact of time-varying covariates on the lifetimes to events may be investigated using Ecological Momentary Assessment (EMA), a collection of research methods focused on collection of subjects’ current psychological states in their every-day environments (Stone and Shiffman, 1994; Stone et al., 2007; Shiffman et al., 2008). Observations are typically obtained using modern electronic devices such as Personal Digital Assistants (PDAs) or smart phones programed for data collection. The use of EMA methods is growing rapidly with examples ranging from alcohol abuse (Collins et al., 1998) to pain (Raselli and Broderick, 2007), eating disorders (Pieters et al., 2006), and asthma (Smyth et al., 2001). EMA has also been used to assess outcome of randomized clinical trials, and to analyze putative processes that may mediate effects of treatment (Shiffman, 2009). EMA is particularly well suited for patient-reported outcomes related to subjective symptoms, discrete behavioral events, and quality of life (Hufford and Shiffman, 2003). In a nicotine patch trial, for example, Shiffman et al. (2006) and Ferguson et al. (2006) instruct participants to record each cigarette on an electronic diary (here, a PDA) both before and after treatment began on a designated quit date. Covariate information was obtained from electronically administered questionnaires regarding current mood and environment at the times of randomly selected cigarettes before the quit date, all cigarettes following the quit date, and at randomly selected times during each day of the investigation. Since questions focus on current psychological states, EMA avoids recall biases inherent in retrospective reports, and EMA avoids effects introduced in an artificial laboratory environment increasing the ecological validity of the data (Shiffman and Stone, 1998). Shiffman et al. (2002) and Rathbun et al. (2007) investigated ad-lib (that is, ongoing, unrestricted) smoking behavior before the quit time, finding that the momentary risk of smoking a cigarette is an increasing function of the smokers’ restlessness. In the current paper, we consider the impact of time-varying covariates on the lifetime to smoking lapse (i.e., first cigarette) after the designated quit date.
Maximum partial likelihood estimation (Cox, 1975) of survival-model parameters requires not only the values of the covariates at the lifetimes of each subject, but also their values in the risk sets comprised of all remaining individuals at risk at the lifetimes of each subject. For fully parametric models, maximum likelihood estimation requires that the covariates be known functions of time. In either case, this covariate information is not available in the smoking cessation study. A joint modeling approach may be applied (DeGruttola and Tu, 1994; Wulfsohn and Tsiatis, 1997; Xu and Zeger, 2001; Ratcliffe et al., 2004), under which the joint distribution of the lifetimes to the events and the time-varying covariates is used to impute the covariates in the risk sets. The joint-modeling approach has been extended to recurrent event modeling by Zhang et al. (2008) and Liu and Huang (2009). Conditional score (Tsiatis and Davidian, 2001; Song et al., 2002) and corrected score (Wang 2006) estimators relax assumptions regarding the distribution of random effects, and are based on estimating equations that are easier to compute. Bayesian inference has been considered, for example, by Faucett and Thomas (1996), Wang and Taylor (2001), Brown et al. (2005), and more recently by Hansen et al. (2011) and Huang et al. (2011). The above approaches all assume that the covariates are specified, usually continuous functions of time, and departure from the specified model is treated as measurement error (Tsiatis and Davidian 2004). The estimators are consistent under correctly specified models, are robust against violations of assumptions regarding the distribution of random effects (Hsieh et al., 2006), but may be biased if the covariate model is misspecified.
Smoking lapse may be a function of mood (Shiffman et al., 1996), which may vary in response to multiple stimuli occurring at arbitrary intervals and at frequencies greater than the frequency at which mood is sampled. No model is likely to adequately capture this variation in mood, so a joint modeling approach may yield biased estimates of survival model parameters. We propose a probability-sampling framework for estimating the impact of time-varying covariates on lifetimes to events as an alternative to the joint modeling approach. Originally proposed in the context of Poisson point process modeling (Rathbun et al., 2007), application of the proposed framework to survival analysis calls for construction of a design-unbiased estimator for the cumulative hazard from probability samples of the covariates. Taken from survey sampling (Cassel et al., 1977), an estimator is said to be design-unbiased for a parameter if its expectation is equal to that parameter under the probability distribution induced by the sampling design. The estimated cumulative hazard is substituted into the full likelihood equations, which are then solved to obtain the proposed estimator for survival-model parameters. Inference is conditional on the realized pattern of temporal variation in the covariates, so no model assumptions are required regarding the covariates. Our approach requires parametric models for baseline hazard, a requirement frequently shared by Bayesian survival analysis (e.g., Faucett and Thomas, 1996; Wang and Taylor, 2001; Brown et al. 2005). The probability-sampling framework is well suited for the analysis of EMA data, where probability-base designs are routinely used to sample time-varying covariates.
Our results extend those of Rathbun et al. (2007), who considered the log-linear model for Poisson point process intensity. Although our primary focus is on the lifetime to a single event, our results may also be applied to conditional-intensity models for recurrent events. Moreover, we no longer require that the intensity or hazard be a log-linear function of the time-varying covariates.
The application of the proposed probability-sampling framework to survival analysis is outlined in Section 2 and the large-sample properties of the resulting estimator are proved in the appendix. In Section 3, the relative merits of the joint-modeling approach and proposed probability-sampling framework are explored in a simulation study. The proposed probability-sampling framework is illustrated using data from an EMA of smoking in Section 4. In Section 5, we discuss the strengths and limitations of the proposed method.
2. Probability-Sampling Framework for Survival Analysis
Suppose that n subjects are independently sampled with lifetimes Si and censoring times Ci for each subject i = 1, ···, n. Define Ti = min(Si, Ci), and let Δi = I (Si ≤ Ci) denote the censoring indicator. Assume that the censoring time is independent of the survival time given the covariates. For each subject i, let xi(t) denote a vector of time-dependent covariates. The lifetimes of the subjects are assumed to depend on the covariates through a fully parametric hazard function
where θ is a parameter vector. In the above, the hazard at each time t may depend on past values of the covariates, but in the following we will make the modelling assumption that the hazard only depends on the current values of the covariates. Under the multiplicative hazards model, for example, the hazard takes the form hi(t; θ) = h0 (t; γ) exp {βTxi(t)} where h0 (t; γ) is the baseline hazard and θ = (γ, β). One limitation of our approach is that only fully parametric hazard models may be fit to the data. However, proportional hazards may be considered, for example, by fitting spline models to the log baseline hazard. For simplicity of presentation, the following also focuses on the case where each subject experiences only a single event, but as detailed in the Appendix, our approach can readily accommodate recurrent events data.
The full log likelihood for the hazard model is
| (1) |
where
| (2) |
is the cumulative hazard. The maximum likelihood estimator θ̂ may be obtained by solving the score equations Un(θ) = 0, where
| (3) |
and and are the derivatives of hi (Ti; θ) and Hi(Ti; θ) with respect to θ. Unless the covariates are known functions of time, it is not generally feasible to evaluate Hi(Ti; θ). However, for each value of θ, Hi(Ti; θ) may be regarded as the population total for hi(t; θ), where the population is taken to be the collection of all points t ∈ [0, Ti].
A point-process sampling design may be used to obtain design-unbiased estimates of the cumulative hazards for each subject. For each subject, ui1, ui2, ···, are sampled from point processes, independent of the event times and covariates, with known conditional intensity
where
denotes the number of covariate sample times in the interval [t, t + δ), and the history
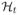 is the σ-algebra generated by
for r < t. Here,
is the σ-algebra generated by
for r < t. Here,
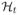 contains all of the information about the sampling times before time t. The covariate sample times might be generated from an inhomogeneous Poisson process. The self-correcting point process of Isham and Westcott (1970) yields more regularly spaced covariate-sampling times than the Poisson process, reducing burden on study subjects. It has conditional intensity
, where β, ρ > 0. This point process is self-correcting in the sense that if
strays too far from the target t/ρ, then the intensity of the process compensates to force this difference back towards zero. Our investigations of the asymptotic inference for the proposed estimator requires that the intensity πi (t) be bounded below by a positive constant, a requirement not satisfied by the self-correcting point process. To fix this, covariate samples may be generated from the superposition of a self-correcting point process and a homogeneous Poisson process with some arbitrarily small intensity.
contains all of the information about the sampling times before time t. The covariate sample times might be generated from an inhomogeneous Poisson process. The self-correcting point process of Isham and Westcott (1970) yields more regularly spaced covariate-sampling times than the Poisson process, reducing burden on study subjects. It has conditional intensity
, where β, ρ > 0. This point process is self-correcting in the sense that if
strays too far from the target t/ρ, then the intensity of the process compensates to force this difference back towards zero. Our investigations of the asymptotic inference for the proposed estimator requires that the intensity πi (t) be bounded below by a positive constant, a requirement not satisfied by the self-correcting point process. To fix this, covariate samples may be generated from the superposition of a self-correcting point process and a homogeneous Poisson process with some arbitrarily small intensity.
The covariate sampling intensity πi (t) is specified during study design, and algorithms generating samples from a point process with a given conditional intensity can be programmed into the electronic devices used to implement EMA. Optimal choice of πi(t) is beyond the scope of the current paper, but is the subject of current research which suggests that it should be set proportional to the hazard function hi (t; θ).
Given that covariates are sampled at times generated from conditional intensity πi (t) bounded below by a positive constant, a design-unbiased estimator
| (4) |
may be constructed for Hi (Ti; θ), where denotes the number of sample times generated in the interval [0, Ti] for subjects i = 1, ···, n. Only the values of the covariates in the probability sample and not at the events enter in the computation of (4). The proposed estimator for the parameter vector θ is obtained by finding θ̃ that maximizes the objective function
| (5) |
obtained by replacing the cumulative hazard in the log likelihood (1) by its estimator (4). In practice, θ̃ may be obtained by solving the approximate score equations
| (6) |
through an application of the Newton-Raphson algorithm. For the multiplicative hazards model, the estimating function is well-behaved, so convergence is generally achieved within 5–10 iterations.
The large-sample properties of θ̃ may be investigated under the regularity condition A–E of Andersen et al. (1993; pp. 420–421) on the hazard function hi (t; θ) and conditions outlined in the Appendix on the sampling intensity πi(t). Define
| (7) |
and
| (8) |
where Yi(t) is the at-risk process, taking the value one when subject i is at risk, and zero when otherwise. Existence of Vn (θ) is ensured if πi (t) is bounded below. The aforementioned conditions include the assumption that n−1Jn(θ0) → Σ(θ0) and n−1Vn (θ0) → Γ(θ0) in probability as n → ∞, where θ0 is the true value of θ. When study subjects are independently sampled,
where
as demonstrated in the Appendix. Here, the variability of θ̃ is partitioned into two sources, that which is inherent to the survival model as quantified by (Σ (θ0))−1, and that due to random sampling of the covariate as quantified by (Σ(θ0))−1Γ(θ0)(Σ(θ0))−1. Note that the first component is equal to the asymptotic variance of the maximum likelihood estimator. Therefore, the loss of efficiency due to sampling the covariates may be quantified by comparing Ξ(θ0) with (Σ(θ0))−1.
The following plug-in estimator may be used to estimate the variance-covariance matrix of θ̃n:
We may estimate Jn(θ) using the observed Fisher information
and Vn(θ) using
For the multiplicative hazard function with unit baseline hazard, Ĵn(θ) = XTX, where the rows of X are comprised of the covariate vectors at the event times.
3. Simulations
Two simulation studies were carried out to explore the finite-population properties of the proposed estimator. The aim of the first study was to compare the proposed estimator to the joint modeling estimator of Wulfoshn and Tsiatis (1997) and the conditional score estimator (Tsiatis and Davidian 2001; Song et al., 2002) under a misspecified model for the time-varying covariates. Simulations in the latter papers demonstrate that the conditional score performs better than the naive methods (last value carried forward, naive regression) and regression calibration. Moreover, the conditional score performs better than the corrected score for classical models assuming normally-distributed measurement errors (Song and Huang, 2005). The second study was designed to explore the properties of the proposed estimator in a setting comparable to that of the EMA smoking data.
For Study 1, the time-varying covariates are quadratic functions of time: x(t) = α0 + α1t + α2t2. For each subject, the coefficients α0, α1, and α2 are independently sampled from normal distributions with respective means of 0.0, 5.0, and −1.25 and respective standard deviations of 1.0, 1.0, and 0.25. Under the mean values of the coefficients, the covariate function increases to a peak of x (t) = 5.0 at t = 2.0 years, the time at which the data are censored. The hazard function is taken to be h(t) = exp{β0 + β1x(t)}, where β0 = −3 and β1 = 1. Covariate sample intensities of 4, 8, and 16 per year were considered, with respective means of 5.3, 9.6, and 18.1 covariate samples per subject. Censoring at 2.0 years resulted in a censor rate of 13.7%. Samples of n = 100 and 300 were considered, and for each subject, covariates were sampled at times generated according to an independent homogeneous Poisson process with constant intensity π (Ripley, 1987, pp. 100–101). To explore the effects of covariate-model missepecification, the joint-modeling and conditional score estimators were estimated under the false assumption that the time-varying covariates are linear as opposed to quadratic functions of time. All estimators were based on a correctly specified model for the hazard. An observation at time zero was included to ensure a minimum of two covariate observations for fitting the linear covariate model under the joint modelling approach. When fewer than two covariate observations were available, the joint modeling approach often failed to converge. This time-zero observation was ignored in implementations of the proposed approach since its observation time was not randomly generated as required under the probability-sampling framework.
The joint modeling and conditional score estimators of β1 had much higher biases than those of the proposed estimator (Table 1). This indicates that misspecification of the covariate function model can lead to serious bias in survival model parameters. The proposed approach does not assume a model for the covariate function, and so bias in survival model parameters is small. The bias of the joint modeling estimator was not sensitive to the covariate sampling intensity, but the bias in the conditional score and proposed estimators does increase with decreasing sampling intensity. Standard deviations of the proposed estimator were similar to those of the joint modeling and conditional score estimators, but owing to the high bias, coverage rates of 95% confidence intervals were poor for the joint modeling and conditional score estimators. Coverage rates of the proposed estimator were good except for smaller samples with low covariate sampling intensities. Similar results were obtained for the intercept β0. The proposed estimator was much more computationally efficient than the joint modeling likelihood approach. When n = 300 and π = 16.0, for example, the joint modeling likelihood approach took 4 days to complete the parameter estimation for the 1000 simulation runs, whereas the proposed method was completed within 20 seconds. The joint modeling approach was implemented using code written in C++ while the proposed method was implemented using code written in FORTRAN. All simulations were run on computers with Intel Xeon CPUs and clock speeds of 3.2 GHz.
Table 1.
Simulation results for Study 1; bias, standard deviation of estimates (SD), and percent coverage of nominal 95% confidence intervals (CR).
| n | π | Method | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Proposed | Joint Modeling | Conditional Score | ||||||||
| Bias | SD | CR | Bias | SD | CR | Bias | SD | CR | ||
| 300 | 16 | 0.009 | 0.062 | 95.5 | 0.092 | 0.065 | 71.4 | −0.031 | 0.067 | 90.3 |
| 8 | 0.011 | 0.068 | 95.3 | 0.099 | 0.067 | 68.9 | −0.085 | 0.066 | 72.0 | |
| 4 | 0.011 | 0.078 | 94.4 | 0.102 | 0.068 | 71.0 | −0.204 | 0.066 | 15.5 | |
| 100 | 16 | 0.024 | 0.110 | 93.7 | 0.104 | 0.117 | 89.0 | −0.021 | 0.117 | 93.9 |
| 8 | 0.033 | 0.119 | 94.3 | 0.112 | 0.119 | 88.2 | −0.071 | 0.119 | 86.5 | |
| 4 | 0.033 | 0.134 | 91.1 | 0.109 | 0.122 | 89.7 | −0.189 | 0.123 | 59.6 | |
In Study 2, 12 5-point Likert-scale variables were generated from a multivariate version of an ordered probit model (Fu et al. 2000). The first three of these variables were held constant among subjects so as to represent the baseline hazard, while the remaining elements vary among subjects. With respect to the former, a vector ε0 (t) of 3 independent zero-mean, unit-variance Gaussian processes with exponential correlation functions ρ(r) = exp{−r/α} and with α set to 15, 9, and 9 days respectively, were generated by sampling from the spectrum (Mejia and Rodriguez-Iturbe 1974). Then three interdependent latent processes were generated according to a linear model of coregionalization (Wackernagel 1995) by taking z0 (t) = Bε0 (t), where B is a 3 × 3 symmetric banded Toeplitz matrix with unit diagonal elements, and first sub- and supra-diagonal elements set to 0.5, and the remaining elements set to zero. A vector y0 (t) of 3 5-point Likert scale variables were then constructed by setting y0 (t) equal to the quintile (coded 1–5) of the standard normal distribution to which the corresponding element z0 (t) belongs. For each subject, vectors yi (t) of 9 5-point Likert-scale covariates were independently generated as described in the above, but with range of temporal correlation α to set 1 day. Lifetimes were then generated according to a multiplicative hazard function λi (t) = exp{βTxi (t), where xi (t) = (1, y0 (t), yi (t)) and β is given in Table 2.
Table 2.
Simulation results for Study 2; bias, standard deviation of estimates (SD), and percent coverage of nominal 95% confidence intervals (CR) of regression coefficients are compared for cumulative hazard functions estimated using the conditional intensity with those estimated using empircal rates, with and without missing data.
| Parameter | True Value | Conditional (complete data) | Empirical (complete data) | Empirical (missing data) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias | SD | Coverage | Bias | SD | Coverage | Bias | SD | Coverage | ||
| β0 | −10.0 | −0.128 | 0.662 | 96.7 | −0.090 | 0.658 | 96.6 | −0.090 | 0.659 | 96.3 |
| β1 | 0.5 | −0.003 | 0.096 | 95.1 | 0.012 | 0.095 | 95.2 | 0.011 | 0.095 | 95.2 |
| β2 | 0.5 | 0.016 | 0.150 | 95.4 | −0.050 | 0.149 | 92.2 | −0.050 | 0.149 | 92.1 |
| β3 | 0.5 | 0.005 | 0.099 | 98.6 | 0.044 | 0.099 | 95.8 | 0.044 | 0.099 | 95.8 |
| β4 | 0.1 | 0.003 | 0.092 | 97.2 | 0.003 | 0.091 | 96.8 | 0.003 | 0.091 | 96.7 |
| β5 | 0.1 | −0.003 | 0.116 | 95.7 | −0.002 | 0.115 | 96.8 | −0.002 | 0.115 | 96.5 |
| β6 | 0.0 | 0.002 | 0.109 | 96.3 | 0.001 | 0.108 | 96.9 | 0.001 | 0.108 | 96.8 |
| β7 | 0.0 | −0.014 | 0.104 | 94.8 | −0.013 | 0.103 | 95.5 | −0.013 | 0.103 | 95.6 |
| β8 | 0.0 | −0.011 | 0.100 | 94.8 | −0.010 | 0.099 | 96.0 | −0.010 | 0.099 | 95.7 |
| β9 | 0.1 | 0.021 | 0.104 | 96.6 | 0.020 | 0.103 | 97.0 | 0.020 | 0.103 | 96.7 |
| β10 | 0.0 | −0.001 | 0.110 | 99.1 | 0.000 | 0.109 | 98.6 | 0.000 | 0.109 | 98.7 |
| β11 | 0.0 | 0.010 | 0.115 | 97.2 | 0.010 | 0.114 | 97.5 | 0.010 | 0.114 | 97.5 |
| β12 | 0.1 | −0.008 | 0.091 | 98.9 | −0.007 | 0.090 | 99.5 | −0.007 | 0.090 | 99.6 |
In the application, covariate samples were stratified by day. Each day, inter-arrival times of covariate samples were regenerated from a uniform distribution over a two-hour period, initiated at the wake-up times of the subjects. Subjects did not always respond to prompts from the electronic diary at times of random assessments. Prompts became increasingly shrill until the subject either responds or two minutes have elapsed, so about 9% of observations were missing. Covariate-sampling intensities were not recorded for the EMA smoking data, and owing to missing covariate assessments, they could not be reconstructed for all covariate samples. Therefore, covariate samples were treated as simple random samples, with sampling rate set to the empirical rate π(t) = m/|A|, where m is the number of covariate samples taken on a given day, and |A| is the length of time over which the subject was observed that day. For each simulation run, data were generated for a sample of 300 subjects, censored at 16 days yielding a mean censoring rate of 50% and mean 16,225 covariate samples per simulation run. Three estimators were compared: The first used the true intensities π(t) = 1/(0.4 − (t − t*)) to estimate cumulative hazards, where t* is the time of the last covariate sample, while the second and third estimators were based on empirical covariate sampling rates. The first two estimators were based on complete data, while to study the impact of missing data, 9% of the covariate samples were independently removed before computing the third estimator. A total of 1000 independent simulations were completed.
The results were similar to those of Study 1; the use of all three estimators for the cumulative hazards yielded small biases, comparable student errors, and excellent coverage rates for 95% confidence intervals (Table 2). Except for the baseline hazard parameters β1 to β3, use of the empirical estimator did not result in increased bias, but did result in slightly smaller standard deviations and confidence-interval coverage rates that exceeded their nominal 95% levels. Missing data had negligible effects on the results as is expected when data are missing completely at random. Note that with an average of over 100 covariate samples per observed lifetime, the variance component due to sampling the covariates (not shown) is an order of magnitude smaller relative to the variance component due to the model. So it is not surprising that the estimators of regression coefficients based on estimating cumulative hazards using empirical sampling rates yield standard errors and coverage rates similar to those based on using conditional intensities to estimate cumulative hazards.
4. Ecological Momentary Assessment of Smoking
The proposed approach is illustrated using data on a nicotine-patch trial designed to investigate psychological processes that may mediate the effects of treatment on smoking lapse. A total of 412 volunteer smokers were recruited into the study. Upon enrollment and training with the electronic diary, smokers were asked to continue smoking as per their usual habits for two weeks prior to a target quit date. During that period of ad-lib smoking, 88 participants withdrew. On the target quit date, participants were randomized to receive either an active high-dose (35 mg) nicotine patch (n = 188) or matched placebo patch (n = 136). Nicotine patches are well known to reduce the risk of smoking (e.g., Shiffman et al., 2006). Covariate information was obtained from electronically administered assessments of mood restlessness, and craving on an 11-point scale (coded 0 – 10) at the time of lapse (assessed at the end of the lapse event) and at times selected from a stratified random sampling design, stratified by day. Factor analysis on ten items (happy, content, calm, frustrated, irritable, miserable, sad, worried, spacey and hard to concentrate) yielded two orthogonal factors negative affect and positive affect, a result consistent with the so-called circumplex model of affect (Russell 1980). Negative affect refers to negatively-toned emotions such as anxiety or anger, while positive affect refers to positively-toned emotions such as happy or content. Although intuition suggests that negative and positive emotions should be negatively correlated, a substantial body of empirical analyses suggests that they are orthogonal (e.g., Watson and Telegan 1985). The items “spacey” and “hard to concentrate” were averaged to compute attention disturbance. Additional details regarding the study design may be found in Shiffman et al. (2006).
The following considers the lifetimes to smoking lapse, the point at which smokers first smoked after establishing abstinence for at least 24 hours. It is known that once abstinent smokers engage in any smoking, they have a very high probability of relapsing completely (Kenford et al., 1994). The lifetimes of events are modeled according to the parametric hazard model hi (t) = h0 (t; γ)exp{βTxi (t), where xi (t) is a vector of time-varying covariates specified in Table 3. The baseline hazard is modeled as a step function on the partition (0, 1, 2, 5, 10, 15, 20, 54) over the 54-day study interval. The partition of the study interval described above reflects the observed frequency distribution of lifetimes to smoking lapse. The plurality of lapses occurred within the first few days of attempting to quit, and few lapses were observed after 20 days. Quadratic and cubic B-spline models for the log baseline hazard were also considered. Choice of baseline hazard model had very little impact on estimates of β and their corresponding standard errors. In either case, the log baseline function may be written as log h0 (t; γ) = γTx̃(t), where x̃(t) contains either a vector of indicator functions defined with respect to the above partition or the spline basis functions. So, taking zi (t) = (xi (t), x̃ (t)) and θ = (β, γ), then the hazard takes the multiplicative form hi (t) = exp{θT zi (t)}.
Table 3.
Parameter estimators for the fitted hazards model predicting smoking hazard from treatment and time-varying covariates. Ranges of each variable are given in parentheses. The variance components are multiplied by 105
| Covariates | Variance Components (×105) | z | p-value | |||
|---|---|---|---|---|---|---|
| Estimate | Model | Sampling | SE | |||
| Treatment (0,1) | 0.2129 | 2701.4 | 208.7 | 0.1706 | 1.25 | 0.2120 |
| Craving (1–11) | 0.4234 | 72.1 | 2.4 | 0.0273 | 15.51 | <0.0001 |
| Negative Affect (−2.31, 5.85) | 0.4941 | 453.1 | 56.3 | 0.0714 | 6.92 | <0.0001 |
| Restlessness (1–11) | 0.0631 | 76.0 | 5.1 | 0.0285 | 2.21 | 0.0268 |
| Attention Disturbance (1–11) | −0.0573 | 144.1 | 22.4 | 0.0410 | 1.40 | 0.1602 |
| Positive Affect (−3.43, 2.84) | 0.0856 | 663.0 | 98.2 | 0.0872 | 0.98 | 0.3266 |
Covariates were sampled at the times of smoking lapse, and at times selected from a stratified random sampling design, stratified by subject and day. On each day, inter-arrival times of covariate samples were generated from a uniform distribution over a two-hour period, initiated at the wakeup times of the subjects. Unfortunately, covariate sampling intensities πi (t) were not recorded, and owing to missing data could not be reconstructed for all covariate. Therefore, we set the sampling intensities to the empirical rates πi (t) = mij/|Aij| for t ∈ Aij, where mij is the number of times covariates were sampled on day j for smoker i, and Aij is the set of times smoker i was awake on day j. The results of the second simulation study in Section 3 suggest that the use of empirical rates in place of the true sampling intensities did not add significant bias or lead to poor coverage rates of 95% confidence intervals. The parameter vector θ may be estimated by finding θ̂ that solves the estimating equation Ûn(θ) = 0, where
Here uijk is the covariate-sampling time for sample k on day j for smoker i, and di is the number of days the smoker was followed. The large-sample variance-covariance matrix was estimated using
where Sij (θ̃) is the sample variance-covariance matrix of
for k = 1, ···, mij.
Table 3 shows the effects of the time-covariates craving, negative affect, restlessness, attention disturbance and positive affect on smoking hazard; estimates of baseline parameters are not presented in the interest of saving space. Starting with θ = 0, convergence was achieved to the sixth decimal place within 10 iterations. In general, the variance components for the model were an order of magnitude higher than the variance components for sampling the covariates. This suggests that little efficiency is lost compared to the maximum likelihood estimator, which would have asymptotic variance equal to the model variation. This minimal loss of efficiency may be attributed to the observation of 181 smoking lapses, compared to 22,107 covariate sample times. The results suggest that smoking hazard is an increasing function of craving, negative affect, and restlessness.
Adjusted and unadjusted hazard ratios together with corresponding 95% confidence intervals are compared in Table 4. When no time-varying covariates were included in the model, nicotine replacement therapy (NRT) was estimated to reduce the hazard of lapsing by 40% (HR = 0.60, 95% confidence interval, 0.44, 0.82), confirming the finding reported by Shiffman et al. (2006). After adjusting for the impact of the time-varying covariates, however, treatment did not have a significant impact on the risk of smoking lapse (HR = 1.24; 95% confidence interval, 0.89, 1.73). This suggests that the above reduction in lapse risk may be attributed to the action of NRT on the time-varying covariates, consistent with the conclusions of Ferguson et al. (2006) and with the notion that the “effect of treatment should manifest through the marker” (Tsiatis and Davidian 2004). In general, adjusted hazard ratios are closer to one than the unadjusted hazard ratios. Table 4 also compares hazard ratios for smoking lapse to adjusted hazard ratios for ad lib smoking from the two weeks leading up to the designated quit date, computed using the methods of Rathbun et al. (2007). Hazard ratios for craving, negative affect, and restlessness were larger for smoking lapse than they were for ad lib smoking. These results are consistent with findings from cruder methods of analysis, which have also concluded that negative affect is not associated with ad lib smoking, but is strongly associated with smoking lapse (Shiffman et al., 2002; Shiffman, 2005). Interpretation of this contrast is limited since mood ratings for lapse events were obtained retrospectively after the lapse, which could introduce bias. However, prospective data have also supported the role of negative affect in lapses (Shiffman, 2005; Shiffman and Waters, 2004). When smokers are experiencing negative affect, this may both increase motivation to smoke to relieve distress and undermine smokers’ ability to cope with the temptation because experiencing emotional distress makes it difficult to call up coping resources. The finding that lapses are associated with heightened restlessness, even after accounting for negative affect is also confirmed in other analyses (Shiffman and Waters, 2004). Aside from its relationship to affective distress, subjectively-experienced restlessness may reflect the activation of motivational systems that drive towards smoking (Shiffman and Waters, 2004). In any case, the findings derived from the new methods are consistent with and extend theoretically-coherent findings from other analytic methods.
Table 4.
Unadjusted and adjusted hazard ratios for Cox proportional hazards model for smoking lapse, and adjusted hazard ratios for Poisson point process model for ad lib smoking; 95% confidence intervals are given in parentheses.
| Covariates | Smoking Lapse | Ad-Lib Smoking | |
|---|---|---|---|
| Unadjusted | Adjusted | ||
| Treatment | 0.601 (0.440, 0.821) | 1.237 (0.886, 1.729) | — |
| Craving | 1.684 (1.599, 1.773) | 1.527 (1.448, 1.611) | 1.283 (1.269, 1.297) |
| Negative Affect | 2.521 (2.272, 2.798) | 1.639 (1.425, 1.885) | 0.957 (0.931, 0.983) |
| Restlessness | 1.466 (1.405, 1.530) | 1.065 (1.007, 1.126) | 1.020 (1.010, 1.030) |
| Attention Disturbance | 1.282 (1.201, 1.369) | 0.944 (0.871, 1.023) | 0.976 (0.963, 0.989) |
| Positive Affect | 0.917 (0.785, 1.072) | 1.089 (0.918, 1.293) | 0.967 (0.946, 0.988) |
5. Discussion
The probability-sampling framework is offered as an alternative to the joint modeling approach for analyzing the impact of time-varying covariates on lifetimes to events. Since no covariate model is required, it may be readily implemented by investigators familiar with survival analysis but not longitudinal data analysis. It is particularly well suited to settings such as considered here where the trajectory of the covariate is subject to frequent extrinsic perturbations, and thus cannot be readily modeled parametrically. Since no covariate model is required, parameter estimation is computationally efficient; convergence is generally achieved within ten iterations. Although we require a fully parametric hazard function, the log baseline hazard can be modeled using spline or other suitably flexible basis functions lending flexibility to our approach.
The joint modeling approach can be sensitive to violations of covariate model assumptions. Our simulation results show that the proposed estimator competes well with maximum likelihood and partial likelihood estimators when the covariates are known functions of time. However, when model assumptions are not satisfied, joint modeling approaches can yield biased estimates of model parameters. However, with careful diagnostics, joint modeling can lead to insight regarding the processes that may lead to failure. A wide variety of models are available for time varying covariates under the joint modeling approach including polynomial, spline and stochastic process models (Tsiatis and Davidian 2004) adding considerable flexibility to the approach. Through the careful application of appropriate diagnostic procedures, a careful statistician should arrive at a correctly specified model provided that the data are sufficient to capture the temporal variation in the covariates. Since the proposed estimator is robust against covariate modeling assumptions, it may be considered to be an additional diagnostic tool. If a joint-modeling estimator is not close to the proposed estimator, this would suggest that covariate model assumptions may be violated.
In some respects our results resemble those regarding statistical inference for Cox’s proportional hazards model from complex survey data. To obtain design-based inferences in a finite population setting, Binder (1992) defined the parameter of interest θ0 to be the partial likelihood estimator for a population of N subjects. Lin (2000) extended this to a superpopulation model under which the data for the population are generated according to a Cox proportional hazards model with parameter θ0. Whereas Lin (2000) generates the population from the survival model before obtaining a probability sample of subjects, we generate the sample directly from the survival model. Both Binder (1992) and Lin (2000) accommodate time-varying covariates, but assume that covariates are known functions of time. We relax this assumption, and take independent probability samples within each subject to obtain the covariate information. Like Lin (2000), we obtain an asymptotic variance that can be partitioned into two terms, the first of which describes the variation due to the survival model. While Lin’s (2000) second term describes variation due to sampling the subjects, our second term describes variation due to sampling the covariates within subjects.
The above methods assume that the covariates are measured without error. If the covariates are measured with error, however, the estimating function Ûn(θ) is biased in the sense that it has non-zero expectation under θ = θ0. Consequently, the proposed estimator is not consistent under measurement error. However, bias-corrected estimating equations can be constructed to obtain consistent estimators for θ. In particular, suppose that instead of observing realizations of xi (t), we observe realizations of Xi (t) = xi (t)+εi (t); i = 1, ··· n, where the errors εi (t) are independently sampled from a zero-mean normal distribution with known variance-covariance matrix Ω. Then, for the multiplicative hazard function, the bias-corrected estimating function is
Covariates are not considered to be measured with error in the current application, so investigation of the properties of the solution to Û(θ) = 0 falls beyond the scope of the current paper. Our probability-sampling framework requires that the time-varying covariates be sampled using a known probability-based sampling design over the lifetimes of the study subjects to ensure that the observed values of the covariates are representative of the values occurring during the lifetimes of the subjects. Implementation with convenience samples can lead to biased estimates of survival model parameters when a representative sample is not obtained. The proposed methods are particularly well suited to data collected using EMA, where the use of probability-based designs for sampling time-varying covariates is routine (Stone et al., 2007; Shiffman, 2007). While only fully parametric models may be considered for baseline hazards, the log baseline hazard can be modeled using spline, any other suitably flexible basis functions, or as a step function as was done here.
Acknowledgments
We would like to thank Richard Chandler, the Associate Editor and a Referee for their constructive comments, which improved the quality of this paper. This work was supported by NSF grant SES-0720195, and by NIH National Institute on Drug Abuse grants DA006084 and DA02074. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation and the National Institutes of Health.
Appendix
The theory of counting processes (Andersen et al. 1993) provides the framework for demonstrating the large-sample properties of θ̃n. For a sample of n independently sampled subjects, define the counting processes and where counts the number of events and counts the number probability samples for the covariate in the interval [0, t] for each subject i = 1, ···, n. When each subject experiences only a single event, we have one-jump counting processes , jumping at the lifetimes of the individual subjects i = 1, ···, n. Although the focus of the current paper is on the investigation of lifetimes to a single event for each subject, our results can be applied more generally to the point pattern of recurrent events. Without loss of generality, assume the censored lifetimes fall in an interval [0, τ] with probability one where τ < ∞. Corresponding the two counting processes, we may define the locally finite martingale
| (9) |
for the event process, and the locally finite martingale
| (10) |
for the probability sample of the covariates, where is taken to be censored at Ti. Here, Yi (t) is the at-risk process taking the value one at times when subjects are at risk, and zero otherwise. The martingales and are mutually orthogonal for all i, j = 1, ···, n provided that their compensators (second terms in both expressions) are continuous (see Andersen et al. 1993; p. 74). Theorems VI.1.1 and VI.1.2 of Andersen et al. (1993) prove the consistency and asymptotic normality of the maximum likelihood estimator under regularity conditions A–E on the hazard function; see pp. 420–421. To demonstrate the consistency and asymptotic normality of the proposed estimator θ̃n, we require additional assumptions regarding the probability-sampling design used to sample the covariates. Assume that for each subject i = 1, 2, ···, the covariates are sampled at times generated from a point process with conditional intensity πi (t) satisfying the following conditions:
For all t > 0, the intensity πi (t) satisfies 0 < dl ≤ πi (t) ≤ du < ∞.
-
There exists a nonnegative definite matrix Γ(θ0) such that
as n → ∞.
-
For each j and every ε > 0.
converges to zero in probability for all j = 1, ···, p, as n → ∞.
-
For all j, k,
converges in probability to a finite quantity as n → ∞.
Proof of consistency closely parallels the proof of Theorem VI.1.1 in Andersen et al., where they demonstrate the consistency of the maximum likelihood estimator. Our proof requires the demonstration that our estimating function Ûn(θ, τ) converges uniformly to the score function Un(θ, τ) for all θ in the neighborhood of θ0 as n → ∞. The consistency of the proposed estimator is proved in Theorem 1:
Theorem 1
Under assumptions A,B, D and E of Andersen et al., (a), (b) and (d) above, the estimator θ̃n converges in probability to θ0 as n → ∞.
Proof
As pointed out by Andersen et al. (1993) in their proof of their Theorem VI.1.1, it suffices to demonstrate that
| (11) |
and
| (12) |
as n → ∞, and that there exists a finite upper bound M, not depending on θ, such that
| (13) |
To prove (11), we partition
In their proof of Theorem VI.1.1, Andersen et al. demonstrate that as n → ∞. The second term in the expression above may be written as
Lenglart’s inequality may then be used to show that as n → ∞ under conditions (a) and (b), proving (11). The same methods can be used to prove (12) under conditions (a), and (d). To prove (13), note that
| (14) |
where Hin (t) and Gin (t) are defined under condition E of Andersen et al., who demonstrate that the first term in the expression above converges in probability to a finite quantity. The second term is the optional variation of the local square integrable martingale . This martingale has predictable variation process . Since the optional and predictable variation processes have the same limits in probability, conditions E of Andersen et al. (1993) and (a) imply that the second term on the right hand side of expression (14) also converges to a finite quantity as n → ∞, proving (13), and completing the proof.
Theorem 2 proves that the proposed estimator is asymptotic normally distributed.
Theorem 2
Suppose that assumptions A–E of Andersen et al. and (a)–(d) are satisfied. Then
as n → ∞, where Ξ(θ0) = (Σ(θ0))−1 + (Σ(θ0))−1Γ(θ0)(Σ(θ0))−1.
Proof
Rearrangement of the terms in the Taylor series expansion of Ûn(θ̃n, τ) yields
where θ* lies between θ̃n and θ0. Arguments in Theorem 1 may be used to demonstrate that
as n → ∞ under assumptions A,B, D and E of Andersen et al. and assumptions (a), (b) and (d) above. Now Ûn(θ0) = Un(θ0) + {Ûn(θ0) − Un(θ0}, where
and
| (15) |
are orthogonal square integrable martingales with quadratic variation given by expressions (7) and (8), respectively. In their proof of Theorem VI.1.2, Andersen et al. (1993) use Robolledo’s martingale central limit theorem demonstrate that n−1/2Un (θ0) converges in distribution to a multivariate normal random vector with mean zero and variance-covariance matrix Σ(θ0) under conditions B–D. Using the same arguments, we can also demonstrate that n−1/2{Ûn(θ0) − Un(θ0}converges in distribution to a multivariate normal random vector with mean zero and variance-covariance matrix Γ(θ0) under conditions (b) and (c), completing the proof of the theorem.
References
- Andersen PK, Borgan Ø, Gill RD, Keiding N. Statistical Models Based on Counting Processes. New York: Springer-Verlag; 1993. [Google Scholar]
- Binder DA. Fitting Cox’s proportional hazards models from survey data. Biometrika. 1992;79:139–147. [Google Scholar]
- Brown ER, Ibrahim JG, DeGruttola V. A flexible B-spline model for multiple longitudinal biomarkers and survival. Biometrics. 2005;61:64–73. doi: 10.1111/j.0006-341X.2005.030929.x. [DOI] [PubMed] [Google Scholar]
- Cassel C-M, Särndal C-E, Wretman JH. Foundations of inference in survey sampling. New York: Wiley; 1977. [Google Scholar]
- Collins RL, Morsheimer ET, Shiffman S, Paty JA, Gnys M, Papandonatos GD. Ecological momentary assessment in a behavioral drinking moderation training program. Experimental and Clinical Psychopharmacology. 1998;6:306–315. doi: 10.1037//1064-1297.6.3.306. [DOI] [PubMed] [Google Scholar]
- Cox DR. Partial likelihood. Biometrika. 1975;62:269–276. [Google Scholar]
- DeGruttola V, Tu XM. Modelling progression of CD4-lymphocyte count and its relationship to survival time. Biometrics. 1994;50:1003–1014. [PubMed] [Google Scholar]
- Faucett CL, Thomas DC. Simultaneously modelling censored survival data and repeatedly measured covariates: A Gibbs sampling approach. Statistics in Medicine. 1996;15:1663–1685. doi: 10.1002/(SICI)1097-0258(19960815)15:15<1663::AID-SIM294>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
- Ferguson SG, Shiffman S, Gwaltney CJ. Does reducing withdrawal severity mediate nicotine patch efficacy? A randomized clinical trial. Journal of Consulting and Clinical Psychology. 2006;74:1153–1161. doi: 10.1037/0022-006X.74.6.1153. [DOI] [PubMed] [Google Scholar]
- Fu TT, Li LA, Lin YM, Kan K. A limited information estimator for the multivariate ordinal probit model. Applied Economics. 2000;32:1841–1851. [Google Scholar]
- Hanson TE, Branscum AJ, Johnson WO. Predictive comparison of joint longitudinal-survival modeling: a case study illustrating competing approaches. Lifetime Data Analysis. 2011;17:3–28. doi: 10.1007/s10985-010-9162-0. [DOI] [PubMed] [Google Scholar]
- Hsieh F, Tseng YK, Wang JL. Joint modeling of survival and longitudinal data: Likelihood approach revisited. Biometrics. 2006;62:1037–1043. doi: 10.1111/j.1541-0420.2006.00570.x. [DOI] [PubMed] [Google Scholar]
- Huang X, Li G, Elashoff RM, Pan J. A general joint model for longitudinal measurements and competing risks survival data with heterogeneous random effects. Lifetime Data Analysis. 2011;17:80–100. doi: 10.1007/s10985-010-9169-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hufford MR, Shiffman S. Assessment methods for patient-reported outcomes. Disease Management and Health Outcomes. 2003;11:77–86. [Google Scholar]
- Isham V, Westcott M. A self-correcting point process. Stochastic Processes and their Applications. 1970;8:335–347. [Google Scholar]
- Kenford SL, Fiore MC, Jorenby DE, Smith SS, Wetter D, Baker TB. Predicting smoking cessation - Who will quit with and without the Nicotine Patch. Journal of the American Medical Association. 1994;271:589–594. doi: 10.1001/jama.271.8.589. [DOI] [PubMed] [Google Scholar]
- Lin DY. On fitting Cox’s proportional hazards models to survey data. Biometrika. 2000;87:37–47. [Google Scholar]
- Liu L, Huang XL. Joint analysis of correlated repeated measures and recurrent events processes in the presence of death with applications to a study of acquired immune difficiency syndrome. Applied Statistics. 2009;58:65–81. [Google Scholar]
- Mejia JM, Rodriguez-Iturbe I. On the synthesis of random field sampling from the spectrum: An application to the generation of hydrologic spatial processes. Water Resources Research. 1974;10:705–711. [Google Scholar]
- Pieters G, Vansteelandt K, Claes L, Probst M, Van Mechelen I, Vandereycken W. The usefulness of experience sampling in understanding the urge to move in anorexia nervosa. Acta Neuropsychiatrica. 2006;18:30–37. doi: 10.1111/j.0924-2708.2006.00121.x. [DOI] [PubMed] [Google Scholar]
- Raselli C, Broderick JE. The association of depression and neuroticism with pain reports: A comparison of momentary and recalled pain assessment. Journal of Psychosomatic Research. 2007;62:313–320. doi: 10.1016/j.jpsychores.2006.10.001. [DOI] [PubMed] [Google Scholar]
- Ratcliffe SJ, Guo W, Have TRT. Joint modeling of longitudinal and survival data via a common frailty. Biometrics. 2004;60:892–899. doi: 10.1111/j.0006-341X.2004.00244.x. [DOI] [PubMed] [Google Scholar]
- Rathbun SL, Shiffman S, Gwaltney C. Modeling the effects of partially observed covariates on Poisson process intensity. Biometrika. 2007;94:153–165. [Google Scholar]
- Ripley BD. Stochastic Simulation. New York: John Wiley & Sons; 1987. [Google Scholar]
- Shiffman S. Dynamic influences on smoking relapse process. Journal of Personality. 2005;73:1715–1748. doi: 10.1111/j.0022-3506.2005.00364.x. [DOI] [PubMed] [Google Scholar]
- Shiffman S. Designing protocols for ecological momentary assessment. In: Stone AA, Shiffman S, Atienza A, Nebeling L, editors. The Science of Real-Time Data Capture: Self-Reports in Health Research. New York: Oxford University Press; 2007. pp. 27–53. [Google Scholar]
- Shiffman S. Ecological momentary assessment (EMA) in studies of substance use. Psychological Assessment. 2009;21:486–497. doi: 10.1037/a0017074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shiffman S, Stone AA. Ecological momentary assessment: a new tool for behavioral medicine research. In: Kratz DS, Baum A, editors. Technology and Methods in Behavioral Medicine. Philadelphia: Lawrence Erlbaum Associates; 1998. pp. 117–132. [Google Scholar]
- Shiffman S, Waters AJ. Negative affect and smoking lapses: A prospective analysis. Journal of Consulting and Clinical Psychology. 2004;72:192–201. doi: 10.1037/0022-006X.72.2.192. [DOI] [PubMed] [Google Scholar]
- Shiffman S, Paty JA, Gnys M, Kassel JD, Hickcox M. First lapses to smoking: Within-subjects analyses of real-time reports. Journal of Consulting and Clinical Psychology. 1996;64:366–379. doi: 10.1037//0022-006x.64.2.366. [DOI] [PubMed] [Google Scholar]
- Shiffman S, Gwaltney CJ, Balabanis M, Liu KS, Paty JA, Kassel JD, Hickcox M, Gnys M. Immediate antecedents of cigarette smoking: An analysis from ecological momentary assessment. Journal of Abnormal Psychology. 2002;111:531–545. doi: 10.1037//0021-843x.111.4.531. [DOI] [PubMed] [Google Scholar]
- Shiffman S, Scharf DM, Shadel WG, Gwaltney CJ, Dang Q, Paton SM, Clark DB. Analyzing milestones in smoking cessation: illustration in a nicotine patch trial in adult smokers. Journal of Consulting and Clinical Psychology. 2006;74:276–285. doi: 10.1037/0022-006X.74.2.276. [DOI] [PubMed] [Google Scholar]
- Shiffman S, Stone AA, Hufford M. Ecological momentary assessment. Annual Review of Clinical Psychology. 2008;4:1–32. doi: 10.1146/annurev.clinpsy.3.022806.091415. [DOI] [PubMed] [Google Scholar]
- Smyth J, Litcher L, Hurewitz A, Stone A. Relaxation training and cortisol secretion in adult asthmatics. Journal of Health Psychology. 2001;6:217–227. doi: 10.1177/135910530100600202. [DOI] [PubMed] [Google Scholar]
- Song X, Huang Y. On corrected score approach for proportional hazards model with covariate measurement error. Biometrics. 2005;61:702–714. doi: 10.1111/j.1541-0420.2005.00349.x. [DOI] [PubMed] [Google Scholar]
- Song X, Davidian M, Tsiatis AA. An estimator for the proportional hazards model with multiple longitudinal covariates measured with error. Biostatistics. 2002;3:511–28. doi: 10.1093/biostatistics/3.4.511. [DOI] [PubMed] [Google Scholar]
- Stone AA, Shiffman S. Ecological momentary assessment (EMA) in behavioral medicine. Annals of Behavioral Medicine. 1994;16:199–202. [Google Scholar]
- Stone AA, Shiffman S, Atienza AA, Nebeling L. Self-Reports in Public Health. New York: Oxford University Press; 2007. The Science of Real-Time Data Capture. [Google Scholar]
- Tsiatis AA, Davidian M. A semiparametric estimator for the proportional hazards model with longitudinal covariates measured with error. Biometrika. 2001;88:447–458. doi: 10.1093/biostatistics/3.4.511. [DOI] [PubMed] [Google Scholar]
- Tsiatis AA, Davidian M. Joint modeling of longitudinal and time-to-event data: an overview. Statistica Sinica. 2004;14:809–834. [Google Scholar]
- Yao F. Functional principal component analysis for longitudinal and survival data. Statistica Sinica. 2007;17:965–983. [Google Scholar]
- Wackernagel H. Multivariate Geostatistics. Berlin: Springer; 1995. [Google Scholar]
- Wang CY. Corrected score estimator for joint modeling of longitudinal and failure time data. Statistica Sinica. 2006;16:235–253. [Google Scholar]
- Wang Y, Taylor JMG. Jointly modeling longitudinal and event time data with application to acquired immunodeficiency syndrome. Journal of the American Statistical Association. 2001;96:895–905. [Google Scholar]
- Watson D, Tellegen A. Toward a consenual structure of mood. Psychological Bulletin. 1985;98:219–235. doi: 10.1037//0033-2909.98.2.219. [DOI] [PubMed] [Google Scholar]
- Wulfsohn MS, Tsiatis AA. A joint model for survival and longitudinal data measured with error. Biometrics. 1997;53:330–339. [PubMed] [Google Scholar]
- Xu J, Zeger SL. Joint analysis of longitudinal data comprising repeated measures and times to events. Applied Statistics. 2001;50:375–387. [Google Scholar]
- Zhang HP, Ye YQ, Diggle P, Shi J. Joint modeling of time series measures and recurrent events and analysis of the effects of air quality on respiratory systems. Journal of the American Statistical Association. 2008;103:48–60. [Google Scholar]


