Responses to Light Intensity in a Genome-Scale Model of Rice Metabolism^,,,

Analysis of a genome-scale metabolic of rice shows numerous coordinated changes between chloroplast and mitochondrial reactions in response to alteration in available light.

Abstract

We describe the construction and analysis of a genome-scale metabolic model representing a developing leaf cell of rice (Oryza sativa) primarily derived from the annotations in the RiceCyc database. We used flux balance analysis to determine that the model represents a network capable of producing biomass precursors (amino acids, nucleotides, lipid, starch, cellulose, and lignin) in experimentally reported proportions, using carbon dioxide as the sole carbon source. We then repeated the analysis over a range of photon flux values to examine responses in the solutions. The resulting flux distributions show that (1) redox shuttles between the chloroplast, cytosol, and mitochondrion may play a significant role at low light levels, (2) photorespiration can act to dissipate excess energy at high light levels, and (3) the role of mitochondrial metabolism is likely to vary considerably according to the balance between energy demand and availability. It is notable that these organelle interactions, consistent with many experimental observations, arise solely as a result of the need for mass and energy balancing without any explicit assumptions concerning kinetic or other regulatory mechanisms.

Rice (Oryza sativa) makes up nearly 20% of the total caloric intake for the human population as a whole; the income of more than 100 million households in developing countries depends on rice cultivation. Although rice yield has increased, though gradually more slowly, during the last four decades, the world population continues to grow, while the land and water resources for cultivation are declining, leading to a need for high-yielding, stress-tolerant, nutrient-rich rice cultivars (Nguyen and Ferrero, 2006).

Researchers are trying to meet the challenges of improving production in different ways. Some of the efforts include (1) identifying the stress-tolerant rice varieties and stress-responsive genes (Xiang et al., 2007), (2) producing a “Green Super Rice” combining, in a single plant, many different favorable characteristics from the large number of available strains and cultivars, guided by molecular marker-based selection (Zhang, 2007), (3) introducing the genes of C₄ plant to change the leaf anatomy of rice and hence improving the photosynthesis (Kajala et al., 2011), and (4) producing vitamin A-enriched golden rice (Al-Babili and Beyer, 2005). In addition, current research on the genetic basis of signaling between nitrogen-fixing soil bacteria and legumes (Xie et al., 2012) has the potential to allow the engineering of nodule formation in cereal crops such as rice and wheat (Triticum aestivum).

Here, we present a genome-scale model of rice metabolism and examine its responses to changing light availability. Because rice is also a model organism for other cereal crops, such as wheat, this effort should help researchers to understand the biochemistry of a photosynthetic crop plant as well as to compare it with other plants. In addition, the metabolic model of rice, which is the second metabolic model of a crop plant, can be used as a template for comparing the metabolism of different varieties of rice that are pathogen tolerant, drought tolerant, lower or higher yield, etc., and thus, it may also help in identifying characteristics of individual varieties that may assist rice biotechnologists to breed the desired rice crop.

MODELING METABOLISM

Modeling Approaches

There are two broad classes of metabolic models: those that depend upon knowledge of enzyme kinetics (kinetic models) and those that do not (structural models; Schuster and Fell, 2007). Another distinction can be made between small metabolic models constructed manually to represent a small section of metabolism and large models that seek to represent the entire metabolic capabilities of an organism and that are built from data extracted from databases and termed genome-scale metabolic models (GSMs). The difficulty of obtaining kinetic equations and parameters for all of the enzymes and transporters involved in a GSM, in spite of the development of robots for performing large numbers of enzyme measurements (Gibon et al., 2004), means that all such models investigated to date are structural.

A further advantage of structural modeling over kinetic modeling is that the structure of the network is completely defined by the set of reactions involved and their stoichiometric chemical equations. For example, the number of independent fluxes in a metabolic network, and the relationships between them at steady state, can be determined from the null space of the stoichiometry matrix (Reder, 1988; Schuster and Schuster, 1989), and those metabolite concentrations constrained by mass conservation can be determined from the left null space of the stoichiometry matrix (Reder, 1988; Schuster and Höfer, 1991).

One early development was the use of linear programming to examine the constraints on metabolic function and product yields set by reaction stoichiometry and network structure (Fell and Small, 1986; Varma and Palsson, 1994), the methodology eventually becoming known by the term flux balance analysis (FBA) coined by the Palsson group (Varma and Palsson, 1994). This type of computational analysis is a more efficient and thorough replacement for older conventional approaches, which consisted of manual accounting of the stoichiometry of metabolic conversions along defined pathways. Later, the development of elementary modes analysis (Schuster et al., 1999, 2000) showed that even small subsets of cellular metabolic networks could have many more paths and functions than are described as pathways in textbooks. Edwards and Palsson (2000) pioneered the construction and analysis of metabolic networks consisting of the reactions catalyzed by the enzymes contained in the annotations of whole genomes, beginning with Escherichia coli. Though the linear programming/FBA methodology, and certain other techniques such as null space analysis, scale easily to cope with the few thousand reactions of a GSM, elementary modes analysis undergoes a combinatorial explosion of enumerable pathways, and interpretation of the output becomes challenging, though not impossible (Carlson, 2009).

Though other methods have been proposed for finding feasible routes through metabolic networks, unless they explicitly take into account the conservation of mass throughout the network, represented by the stoichiometric constraints, as do elementary modes analysis and FBA, then the routes will not be functional on a sustained basis (de Figueiredo et al., 2009). With the appropriate methods, it is possible to find the maximum yield of metabolic products from nutrients for a given metabolic network and how this might be altered by knocking out certain enzyme reactions or introducing novel enzymes into the network (Trinh et al., 2008). Combined with some experimentally derived constraints, such as the maximum uptake rate of a nutrient, the rate of growth, and the composition of the organism’s biomass, FBA can predict an optimal set of internal fluxes within the network, and these predictions have been shown to be close to measurements made by metabolic flux analysis (Schuetz et al., 2007; Lee et al., 2008; Williams et al., 2010).

GSMs and Their Analysis

Currently, there are approximately 100 published GSMs of varying completeness and quality, plus several hundred existing as automatically generated draft reconstructions (Henry et al., 2010). The major assumption in their analysis, as mentioned above, is that the production and consumption of all internal metabolites is stoichiometrically balanced, so their concentrations are constant and the system is at a steady state. Additional constraints are placed on the models, such as specifying maximum production rates of biomass components and/or nutrient uptake that are consistent with experimental observations. A common requirement in their analysis is the setting of an objective function that is optimized by the linear programming to produce a prediction of the fluxes in the network as nutrients are converted into excretory products and biomass. Most commonly, the objective function is to maximize the biomass yield from the nutrients used (Schuster et al., 2008), which has been shown to be appropriate for E. coli growing in a chemostat (Fong et al., 2003; Lewis et al., 2010), but which does not always reflect the use of fermentative catabolism unless additional constraints are set (Teusink et al., 2009). Another possible objective function is the minimization of total flux in the system (Holzhütter, 2004; Poolman et al., 2009), which represents economy in the enzymic machinery.

A major application of GSMs is investigating and generating hypotheses about the operating characteristics of metabolic networks, represented by the differences between flux patterns in the network if control mechanisms operate to implement the different objectives mentioned above. GSMs also have the potential to be used as a framework for integrating and interpreting other types of high-throughput data, such as gene expression and proteomics measurements (Shlomi et al., 2007; Oberhardt et al., 2009), if the data can be incorporated into either the constraints or the objective function.

Eukaryotic GSMs

The majority of GSMs to date are of prokaryotes. The first eukaryotic GSM was that of Saccharomyces cerevisiae (Förster et al., 2003), which has gone through several iterations (Heavner et al., 2012) and has been followed by models of several other yeasts. The metabolic networks of human (Mo et al., 2007) and mouse (Selvarasu et al., 2010) exist as reconstructions, that is, as a compendium of reactions with gene associations en route to becoming a computable model. Photosynthetic organisms are represented at the microalgal level by Chlamydomonas reinhardtii (Boyle and Morgan, 2009; Chang et al., 2011) and Ostreococcus spp. (Krumholz et al., 2012). For plants, there are now several models of Arabidopsis (Arabidopsis thaliana; Poolman et al., 2009; de Oliveira Dal’Molin et al., 2010; Mintz-Oron et al., 2012), and these are currently undergoing a process of collaborative reconciliation. The model of C₄ metabolism for maize (Zea mays), sorghum (Sorghum bicolor), and sugar cane (Saccharum officinarum; Dal’Molin et al., 2010) was in fact derived from the Arabidopsis model rather than from the maize genome, but a model based on the maize genome was published shortly after (Saha et al., 2011). Hence, to date, there is only one GSM of a true crop plant (maize).

All the eukaryotic models vary in the extent to which cellular compartmentation is explicitly represented, and this remains a difficult problem owing to the incomplete and contradictory information about the localization of the enzymes and the specificity of intracellular transporters. This is most marked in plants, which have specialized metabolic roles for cytosol, mitochondria, chloroplasts, and peroxisomes (Seaver et al., 2012). Furthermore, whereas microbial metabolism can be analyzed on the assumption that it is directed toward efficient growth (Schuster et al., 2008), other imperatives shape the metabolism of multicellular organisms, such as the need for mutual support of different tissues that implement different subsets of the genomically encoded metabolic network by tissue-specific gene expression (Seaver et al., 2012).

A GSM for Rice

In this paper, we describe a GSM for rice derived from the RiceCyc database (Youens-Clark et al., 2011), representing a network capable of the photoautotrophic production of all major biomass precursors (carbohydrate, amino acids, nucleotide bases, etc.) in experimentally observed proportion.

We analyze the model to identify feasible changes in reaction flux distribution in response to changes in photon flux, with the goal of identifying coordinated response across the whole system. It is clear that there must be some positive minimum value of photon flux below which precursor synthesis is not possible at the rate specified and another higher value beyond which the additional energy cannot be put to any use and must therefore be dissipated by the system. Our interest is to investigate how the metabolic network and its energy transduction mechanisms, and in particular those of the mitochondrion, respond as photon flux varies from minimal sustainable to hyperabundance. Shastri and Morgan (2005) have previously examined dependence of photosynthetic metabolism on light energy, but in the prokaryote Synechocystis spp. The investigation of the C. reinhardtii GSM (Chang et al., 2011) was somewhat different, as a more detailed model of the light reactions was used to model the dependence of growth rate on light quality.

A very similar approach (identifying response to changes in energy demand in heterotrophic plant cells) has been validated experimentally (Williams et al., 2010) using ¹³C metabolic flux analysis.

In our analysis, we additionally consider the consequences of saturation of the Calvin cycle, here represented by an imposition of an upper limit on the sum of fluxes in the Rubisco carboxylation and oxygenation reactions, which also captures the effect of competition between CO₂ and oxygen (O₂). This modeling assumption remains valid even if, in reality, other Calvin cycle reactions effectively limit the rate of assimilation.

The exact choice of the value for this upper limit is arbitrary, but was chosen such that its effects are only discernible at a photon flux above that where the metabolic state had stabilized, and allows us to explore responses at much higher light intensities where the chloroplast could become overenergized.

RESULTS

General Model Properties

The initial reconstruction from RiceCyc generated a model with 1,484 metabolites in 1,736 reactions, of which 1,029 could carry flux from nutrients to the specified biomass components and at least 790 reactions had gene associations. (The gene-reaction associations are underestimated, because we have not included counts for the manually added reactions, such as the lumped light reactions and the compartmented mitochondrial and chloroplast metabolism.) When optimal flux distributions were obtained over the range of light fluxes tested, 309 reactions were used in at least some part of the range.

General Responses to Varying Light Levels

We repeatedly solved the linear program described by Equation 1, incrementing the constraint representing the incident photon flux for each solution. In this way, we accumulated a set of solutions allowing us to plot the fluxes associated with individual reactions as a function of photon flux.

The minimum photon flux for which a solution to Equation 1 (see “Materials and Methods”) could be found was 0.321 light flux units, corresponding to a maximally efficient quantum demand of 13.4 photons per carbon fixed. The assimilation quotient (AQ; CO₂ fixed per O₂ released, the reciprocal of the photosynthetic quotient) at this point is 0.98, corresponding to 13.1 photons per O₂ released. As the light levels increase, the AQ falls in stages to a minimum of 0.87 and then remains constant at this value.

The number of reactions being utilized at any particular photon flux across the range varied between 270 and 277. Of these, 142 responded to changing light flux, all but 10 of which carried flux over the entire range of light flux values. The remaining 167 remained constant, reflecting the constant ratios of biomass components.

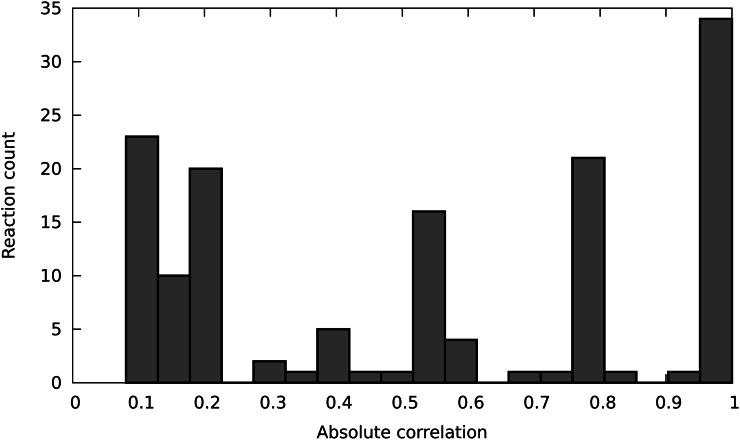
Above the threshold of minimal light flux, the objective value increases, for all intents and purposes, linearly (data not shown). However, the responses of individual reactions are far more varied. Figure 1 shows the distribution of correlations of reaction fluxes with photon flux. The strong responders are obviously highly coupled to the light reactions and involve transmission of reductant to the rest of the cell. The weak and moderate responders represent buffering between the strong responders and the constant biomass production. An examination of the reactions showing changes reveals that this is associated with shifting patterns of interaction between chloroplast and mitochondrial metabolism, as described below.

Figure 1.

Reaction flux correlation with photon flux. These are calculated as the absolute values (i.e. ignoring the distinction between correlated increases and decreases) of the pairwise (Pearson’s) correlation coefficients of each of the 142 variable fluxes with the photon flux across the range of light values. The reactions that show no flux changes are excluded.

Specific Responses to Varying Light

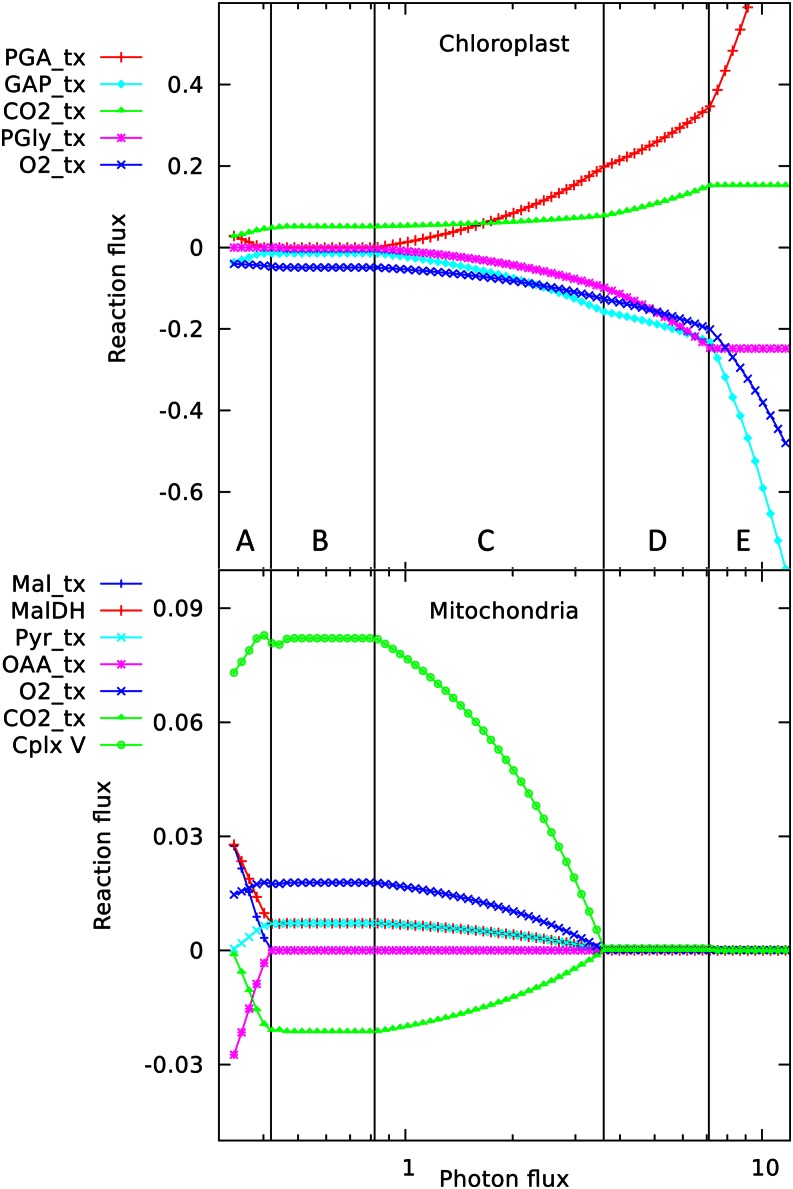
The changing interactions between chloroplast and mitochondrial metabolism are shown in Figures 2 and 3. Across the range of photon fluxes scanned, five major metabolic patterns can be seen (Fig. 3, A–E), with transitions between them occurring at the points where the set of reactions in the optimal solution changes, as indicated by the vertical boundaries between the regions. In regions A and B (Fig. 3), ATP is generated by the mitochondria (shown by the flux in complex 5, the ATP synthase), falling away in region C (Fig. 3). The ATP synthesis is driven by carbon and reductant exported from the chloroplast; hence, there are corresponding changes in the chloroplast transport reactions. A corollary is that some of the photosynthetic O₂ is utilized by mitochondrial respiration, and conversely, the CO₂ evolved by respiration is refixed in the chloroplast. The small fluctuations in reaction rates near the A and B border (Fig. 3) are associated with shifts in in nitrogen metabolism, as described later.

Figure 2.

Responses of solutions in the chloroplast and mitochondrion to varying photon fluxes. Suffix _tx indicates transport of the named metabolite, positive values represent import to the compartment, and negative values represent export. The abscissa is plotted as a logarithmic scale to enable the full set of responses to be easily seen; this causes the reaction responses to appear as curves, whereas they vary linearly with light intensity, showing abrupt changes in slope where the pattern of fluxes changes. The four major flux rearrangements are indicated by vertical lines dividing the flux patterns into five major regions labeled A to E. The transition between regions A and B is shown at higher magnification in Figure 3. PGA, phosphoglycerate; GAP, glyceraldehyde 3-P; PGly, phosphoglycolate; Mal, malate; MalDH, malate dehydrogenase; Pyr, pyruvate; OAA, oxaloacetate Cplx V, complex v.

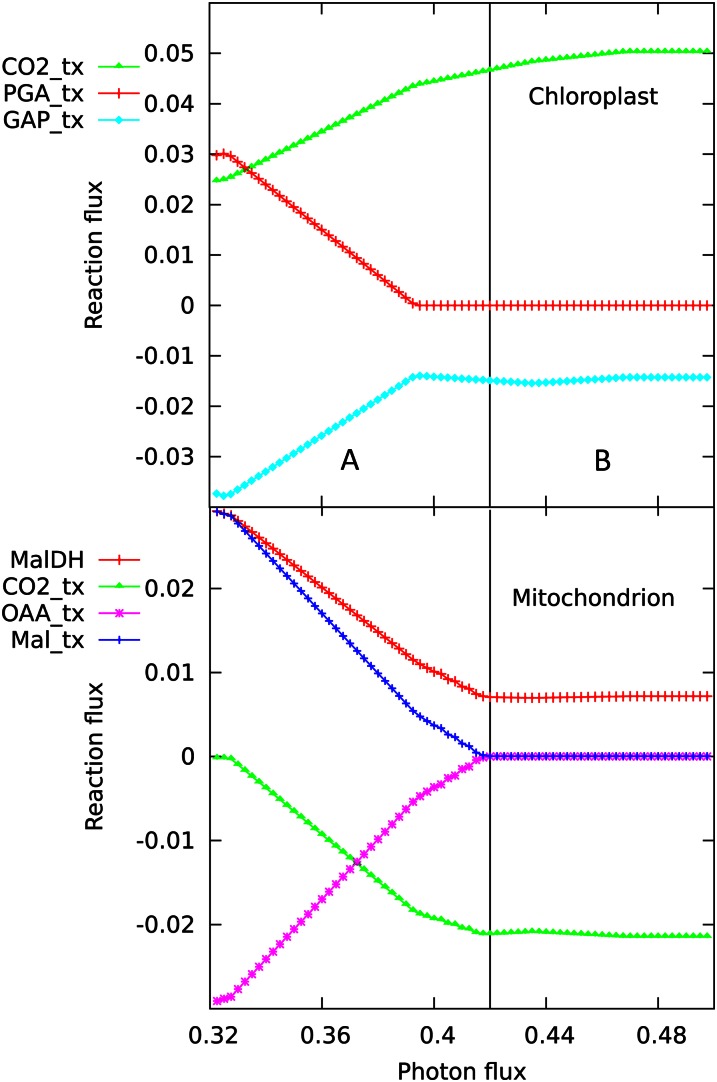
Figure 3.

Chloroplast and mitochondrial transport responses at low light levels. This shows a magnified view of the transition between the states A and B shown in Figure 2. At lowest light levels, there is a maximum import of 3-phosphoglycerate (3-PGA) into the chloroplast, corresponding with the maximum export of glyceraldehyde 3-P (GAP), acting as a shuttle to export reductant and ATP. At the same point, the mitochondrial malate-oxaloacetate (Mal-OAA) shuttle is maximally active, as demonstrated by the import of Mal, the activity of malate dehydrogenase (MalDH), and the export of OAA. Thus, in this region, there is a net transfer of reductant from the chloroplast to the cytosol. The two curves for CO₂ transport demonstrate the recycling from mitochondria to chloroplast.

Mitochondrial Response

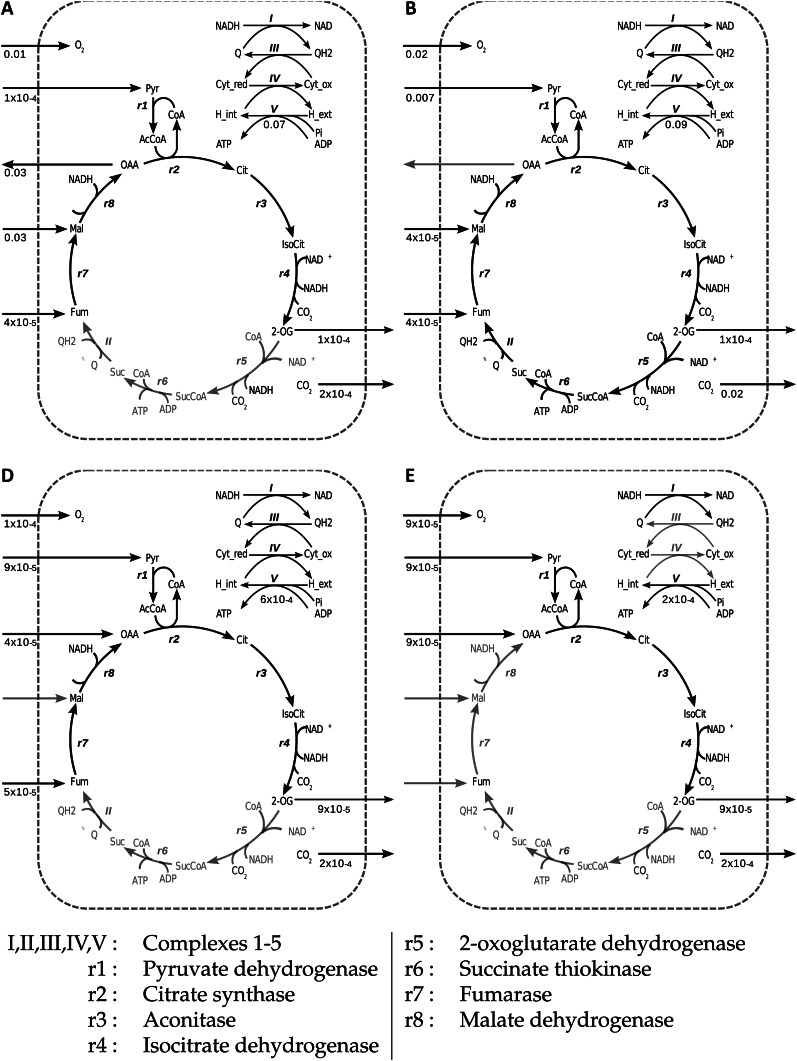
The changing flux distributions shown in Figures 2 and 3 correspond to various modes of operation of the mitochondrial metabolism presented in Figure 4.

Figure 4.

Flux distributions in the mitochondrial module at various photon fluxes. Results are shown for specific flux values in the labeled regions as follows: A, 0.3; B, 0.8; D, 4.0; and E, 8.0. State C (not shown) is intermediate between B and D. Flux figures are rounded to 1 significant figure for clarity. Reactions that are grayed out carry zero flux. In state B, all reactions are active, and this then describes the structure of the mitochondrial module. I, Complex 1; II, complex 2; III, complex 3; IV, complex 4; V, complex 5; r1, pyruvate dehydrogenase; r2, citrate synthase; r3, aconitase; r4, isocitrate dehydrogenase; r5, oxoglutarate dehydrogenase; r6, succinate thiokinase; r7, fumarase; r8, malate dehydrogenase; Cyt_red, cytochrome reduced; Cyt_ox, cytochrome oxidized; Q, ubiquinol; QH2, ubiquinone; OAA, oxaloacetate; Mal, malate; Fum, fumarate; Suc, succinate; SucCoA, succinyl CoA; IsoCit, isocitrate; Cit, citrate; H_int, internal proton; H_ext, external proton; AcAoA, acetyl-coA.

In region A (Fig. 4), most flux is accounted for by generation of ATP through the operation of the electron transport chain (ETC), with reductant supplied primarily from the operation of a mitochondrial malate-oxaloacetate shunt, with only a small contribution from the partial oxidation of pyruvate. Overlaid on this is a much smaller flux generating 2-oxoglutarate (2-OG) from fumarate and pyruvate, and the tricarboxylic acid (TCA) cycle between 2-OG fumarate, including complex 2 (succinate dehydrogenase), is inactive. As region A is traversed, the flux patterns seen in region B gradually emerge (Fig. 4).

Throughout region B (Fig. 4), pyruvate is completely oxidized, and most flux is accounted for by the conventional operation of the citric acid cycle and the ETC, including complex 2, leading to an increased synthesis of ATP at a near-constant rate throughout and the maximum reoxidation of photosynthetic assimilate to CO₂. In addition to this, there is a small uptake of fumarate and malate, which now accounts for the export of 2-OG at the same rate as in region A (Fig. 4). The malate-oxaloacetate shunt is inactive.

Region D (C is a transition between B and D; Fig. 4) represents an unchanging state in which most of the cell’s energetic requirements are met externally to the mitochondria. The ETC again operates, but without complex 2 and with much lower flux than previously; ATP production is reduced to less than 1% of that in regions A and B (Fig. 4), and oxygen consumption is minimal. Reductant is generated by the reactions of the TCA cycle from fumarase to isocitrate dehydrogenase oxidizing fumarate, oxaloacetate, and pyruvate to generate 2-OG.

Region E (Fig. 4) represents minimum activity of the mitochondrion (also corresponding to the saturation of both the carboxylase and oxygenase reactions of Rubisco). Here, oxaloacetate and pyruvate are still being incompletely oxidized to generate 2-OG, with the resulting NADH being reoxidized via the operation of an incomplete ETC comprising complexes 1 and 5 with the addition of the operation of the alternative oxidase reaction. It is only in this region that the alternative oxidase reaction is active, and this leads to a further fall in mitochondrial ATP production.

Chloroplast Response

In region A (Fig. 4), there is a glyceraldehyde 3-P exchange with 3-phosphoglycerate across the chloroplast membrane, resulting in the transfer of reducing power from the chloroplast to the cytosol, where oxaloacetate is reduced to malate that is taken up by the mitochondria. It is interesting to note that, although the chloroplast module contains a functioning malate-oxaloacetate transporter, this redox shuttle mechanism was not utilized in any of the solutions described here. Although the model represented by Equation 1 remains soluble if a flux is explicitly set in these reactions, all subsequent solutions are then suboptimal. As the light intensity increases toward region B (Fig. 4), the import of 3-phosphoglycerate declines, as it is converted in the cytosol to the pyruvate that is taken up by the mitochondria. Also, the gross CO₂ fixation rate increases as more is recycled from rising mitochondrial oxidation of pyruvate.

Throughout region B, the chloroplast metabolism, like that of the mitochondria, remains largely constant, until the transition to region C, where mitochondrial ATP production starts to decline in the face of the increasing production of ATP by the light reactions, evidenced by an increase in oxygen evolution from the light reactions (Fig. 4). The ATP is exported from the chloroplast to the cytosol by the restarting of the 3-phosphoglycerate/glyceraldehyde 3-P shuttle, generating ATP at the phosphoglycerate kinase reaction. The associated extra cytosolic-reducing potential is accounted for by reactions associated with photorespiration, which becomes active at this point with an increasing export of phosphoglycolate throughout region C (Fig. 4). The gross rate of CO₂ fixation increases, as that released by photorespiration more than replaces the declining mitochondrial production. Net evolution of O₂ from the chloroplast increases in spite of its utilization in the Rubisco oxygenase reaction, but this is balanced by increased consumption in the rest of the cell, as phosphoglycolate is recycled.

Across region D (Fig. 4), photorespiration continues to increase, accompanied by increasing exchange in the 3-phosphoglycerate/glyceraldehyde 3-P shuttle. The light reactions generate more O₂, which is used in the photorespiration pathway. There is also an increased return of CO₂ to the chloroplast from photorespiration, with a further increase in the gross rate of assimilation.

In region E (Fig. 4), Rubisco has become saturated for both carboxylation and the oxygenase reaction. Continued increases in the light reactions result in a further increase in export of O₂ from the chloroplast to the cytosol, where it causes oxidation of ascorbate, and reductant is exported from the chloroplast to rereduce the dehydroascorbate. Substrate cycling by the simultaneous polymerization and hydrolysis of starch is one of the ways the excess chloroplastic ATP is dissipated.

Nitrogen Uptake Response

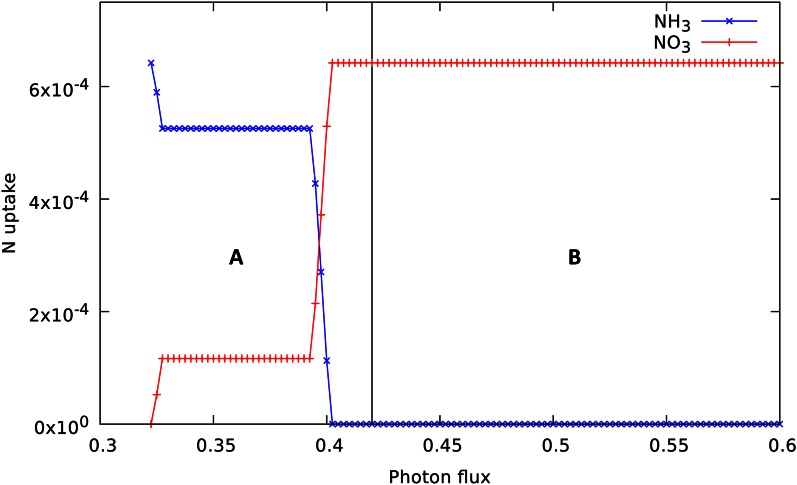
In our model, we consider that the rice leaf metabolism can take both NH₃ and NO₃ as nitrogen sources. Figure 5 shows that there is a transition between NH₃ and NO₃ utilization that takes place within region A of Figure 2. At the very low intensity of light, the model favors NH₃ over NO₃, but utilizes both, then the utilization of NH₃ decreases and the NO₃ increases, and finally, at photon flux values above 0.4, only NO₃ is consumed. Because the use of NH₃ can save energy compared with NO₃, plant leaves may favor the utilization of NH₃ at low light intensities to optimize the energy available for biosynthesis. The shift to NO₃ utilization is accompanied by a fall in AQ from 0.98 to 0.87, and at this point, the quantum demand is 16.6 photons per fixed carbon. This certainly reflects the generation of the additional reductant needed for the assimilation of NO₃.

Figure 5.

Variation in nitrogen source utilization with varying photon flux. Regions A and B are as shown in Figure 2. Note, however, the different photon flux range of this figure. [See online article for color version of this figure.]

DISCUSSION

General Model Properties

Reaction Utilization

An effect of minimizing total flux in the network is to tend to also minimize the total number of reactions used, because if there are two alternative routes to convert metabolite A into metabolite C (A → C and A → B → C), the first option will always minimize total flux. This is not to say that the number of reactions found by this approach is the absolute minimum, but it does serve to place an upper limit upon that minimum.

The fact that only 309 of the 1,029 available reactions were utilized in the solutions found here is therefore unsurprising and comparable with our previous study of heterotrophic metabolism in Arabidopsis (Poolman et al., 2009), in which 232 out of 1,406 available reactions were used. In addition, the solutions refer to only one physiological state of the cell, and a different set of reactions would be used during nighttime metabolism. The number of reactions used here can be associated with a total of 568 unique genes, although this figure is certainly an underestimate, as mitochondrial and chloroplast reactions were not represented with BioCyc identifications.

Comparison with Other Models

Our analysis is not readily comparable with that of previous plant GSMs (Poolman et al., 2009; de Oliveira Dal’Molin et al., 2010; Dal’Molin et al., 2010; Saha et al., 2011; Mintz-Oron et al., 2012), as they have not considered a detailed biochemical analysis of the responses to light intensity. For example, Saha et al. (2011) considered two fixed photosynthetic states of maize, dependent solely on noncyclic photophosphorylation and concentrated on intercellular interactions of C₄ metabolism and the properties of mutants in biosynthetic pathways. Conceptually, our approach is closer to that of Shastri and Morgan (2005), but as their subject was the cyanobacterium Synechocystis spp., the lack of intracellular compartmentation and the different mode of life limit the meaningfulness of detailed comparison.

Boyle and Morgan (2009) reported results for three states of their C. reinhardtii model (autotrophic, heterotrophic, and mixotrophic) and carried out a light intensity scan for mixotrophic growth with acetate, but this differs in many details from plant metabolism. Chang et al. (2011) studied the response of C. reinhardtii to light in great detail, but in the biotechnological context of predicting the growth rate expected given the spectral characteristics of the light source.

In effect, the diversity of the studies to date indicates the wide range of potential applications for genome-scale metabolic modeling and hints at the scope for further development.

Utility of LP Constraint Scanning

The results presented here support our original contention that scanning constraints, as described in “Materials and Methods,” does reveal potential correlated responses in a network, and such observations can be used to generate further hypotheses concerning the in vivo behavior of the system. This continues an approach adopted in the early studies of E. coli metabolism by FBA (Varma et al., 1993; Varma and Palsson, 1993) before the model was genome derived, where a series of different metabolic phases were identified by scanning the oxygen supply rate. Here, we have restricted ourselves to one dimension by fixing the biomass production rate, so that we essentially consider the ratio of light intensity to growth rate, which still gives us a challenging and rich behavior to analyze. In the future, we need to consider different phases in the space defined by variation in light, growth rate, starch deposition, and Suc accumulation.

It is particularly interesting that simply scanning the light intensity results in the Rubisco oxygenase reaction becoming active at superoptimal photon fluxes. This is, of course, a well-known phenomenon, but there are no explicit or implicit features in the model or its analysis that make this a forgone conclusion. The observation thus lends further credence to this approach for the analysis of genome-scale models.

Comparison of Specific Responses to Light with Experimental Observations

Photorespiration

The fact that photorespiration is spontaneously activated at supraoptimal photon flux suggests that the inhibition of this pathway might not be wholly beneficial to the plant. Plants are always likely to be exposed to supraoptimal light and have to be able to dissipate excess energy to prevent damage and overreduction of the chloroplast. There are several mechanisms that contribute to this, and our results support the view that photorespiration is among these (Padmasree et al., 2002). It increases the net supply of CO₂ to the chloroplast and absorbs the extra O₂, as the changes in their fluxes (Fig. 2, C and D) occur with no net impact on the CO₂ and O₂ fluxes for the whole cell, as is further discussed in the next subsection. The substantial export of glyceraldehyde 3-P and the import of 3-phosphoglycerate in regions C, D, and E (Fig. 2) show how reductant and ATP are moved out of the overenergized chloroplast. The importance of mitochondrial metabolism in the light for maximization of photosynthetic performance has been noted by a number of authors (Padmasree et al., 2002) and is apparent in our model as described further below, but we have underrepresented its contribution to photorespiration, because this version of the model is not fully compartmented and does not assign Gly oxidation to the mitochondrion.

Quantum Demand and Photosynthetic Yield

The relationships between light absorbed, CO₂ fixed, and O₂ evolved are at the center of agronomic and ecological assessments of the roles of photosynthetic organisms, but they are difficult to measure experimentally, and the theoretical limiting values are likewise hard to calculate from first principles. Both approaches share some common problems: photosynthesis is potentially simultaneously supporting export and storage of assimilate, growth, and cell maintenance. At the same time, photorespiration and mitochondrial respiration can be taking place with their own stoichiometries for CO₂ and O₂. Furthermore, the instantaneous and long-term, and leaf and whole plant values are of interest. While metabolic modeling does not resolve the issue of the relative mix of the different processes, it does allow rapid calculation for different well-controlled scenarios, such as different proportions of biomass and exported assimilate. Our calculations are for an average cell in an expanding leaf that is not yet a major exporter of assimilate, so have more in common with algal cultures than mature leaf or whole plant measurements.

Previous calculations of the minimum quantum demand for photosynthetic assimilation (Raven, 1982; Pirt, 1986) have used older stoichiometries for cyclic and noncyclic photophosphorylation and have accounted for fixing CO₂ and nitrate or ammonia to biomass on the basis of pathway-based calculations of the corresponding ATP and NADPH demands for making the basic constituents. From the lowest light level at which biomass can be produced in Figure 2, where ammonia is being used as the nitrogen source and photorespiration is not active, we compute a quantum demand of 13.4 mol mol^–1 (of absorbed photons) with our assumed maintenance requirement. The point at which nitrate becomes the nitrogen source for biomass in Figure 5 corresponds to a higher quantum demand of 16.6 mol mol^–1. Raven (1982)’s pathway-based calculations of algal quantum demand led to an estimate of 14.1, after correction by Pirt (1986), excluding maintenance and polymerization costs, while Pirt (1986) computed a lower value of 7.6 on NO₃, or 6.4 on NH₃. Pirt (1986) reviewed measurements on algae and concluded that the minimal quantum demand (corrected for maintenance) was likely less than 8.0. Hence, our network-based calculations are essentially similar. The quantum demand reported for the GSM of the cyanobacterium Synechocystis spp. was 13.9 to 14.7 using nitrate as the nitrogen source (Nogales et al., 2012). Experimental measurements on mature (i.e. nongrowing) leaves of C₃ plants reviewed by Skillman (2008) gave an average value of 19.2 mol mol^–1, presumably with maintenance included, under ambient atmospheric conditions. In measurements where photorespiration was suppressed, the median measurement fell to 10.4, but with a wide variation depending on the methodology.

The simplistic view of photosynthesis is that the AQ is 1, i.e. one CO₂ fixed per O₂ released, and this figure is often assumed in calculations of photosynthetic performance. As pointed out by several authors over many decades (Raven, 1982), this is naive and oversimplified, because the elemental composition of the majority of biomass components requires that more O₂ must be released than CO₂ fixed to balance the stoichiometric equations for their formation. For example, Raven (1982) computed an AQ of 0.71 for algal growth with NO₃ as nitrogen source and 0.89 with NH₃. Our corresponding values for rice leaf biomass are 0.87 and 0.98, respectively, reflecting the substantial proportion of cellulose. It is often assumed that mitochondrial respiration and photorespiration will have significant effects on the value of AQ (Skillman, 2008), but though it may seem surprising, even at the highest light levels in our model, neither changes in mitochondrial respiration nor photorespiration have any effect on AQ. We are conducting a more detailed examination of the reasons for this.

A number of experimental studies (Searles and Bloom, 2003; Cousins and Bloom, 2004; Rachmilevitch et al., 2004) showed that the AQ was about 0.1 higher for growth on NH₃ compared with NO₃ in ambient atmospheric conditions for wheat, maize, tomato (Solanum lycopersicum), and Arabidopsis, in agreement with our calculation for rice. However, the lower AQ for NO₃ was not seen under conditions where photorespiration was suppressed, such as elevated CO₂ or reduced O₂, and NO₃ assimilation was reduced. This led to the suggestion (Rachmilevitch et al., 2004) that NO₃ assimilation depended on photorespiration. This is not supported by our model, which exhibits unchanged nitrogen uptake characteristics from those shown in Figure 5 when the Rubisco oxygenase reaction is blocked. This implies that such experimental observations do not reflect a stoichiometric coupling but a kinetic or regulatory interaction.

Mitochondria and Chloroplasts

The involvement of mitochondrial reactions in the solutions across the photon flux range (Fig. 2, A–E) is support for the accumulated evidence that mitochondrial respiration has a role in optimizing photosynthetic performance (Padmasree et al., 2002). A number of the aspects of plant mitochondrial metabolism in the light described in their paper are evident in our results:

(1) Oxidation of pyruvate and malate during photosynthesis (Fig. 4), prevention of overreduction of the chloroplast, and support of maximal photosynthesis. At lower light levels (Fig. 4, A–C), the oxidation of pyruvate and malate is associated with the generation of ATP to support cytosolic metabolism. For an electron pair moved between water and NADPH, mitochondria can generate more ATP and are therefore more effective at rebalancing reductant and ATP requirements than chloroplasts. The mitochondrial ETC is active at all light levels, and the reductant being used is derived from the chloroplast light reactions. At high light levels, the model shows a shift to use of the alternative oxidase. (The flux in complex 4 in region E goes to zero [Fig. 4], so that disposal of reductant is not linked to generation of ATP, which is now provided in excess by the chloroplast.) This is consistent with the experimental evidence that the alternative oxidase is necessary to protect against the harmful effects of excess light (Bartoli et al., 2005)

(2) Export of 2-OG derived from pyruvate and C₄ precursors to support nitrogen metabolism and amino acid synthesis. This activity continues at all light levels in our scan, though this invariance is because we have modeled a constant biomass production. There is some experimental evidence for export of citrate and its conversion to 2-OG by the parallel cytosolic reactions (Plaxton and Podestá, 2006), which we do not see in our solutions.

(3) Operation of an incomplete TCA cycle. Succinate dehydrogenase (complex 2), and hence the complete TCA cycle, is only active at the lower light levels in Figure 2, A to C, becoming active through region A and reaching its maximum level in region B before declining in C, whereas the other electron transport complexes and ATP synthesis continue at a low level in regions D and E. As a result, the responses to light intensity of the three neighboring enzymes succinate dehydrogenase, fumarase, and malate dehydrogenase are all different, as emphasized in Figure 4. This ability of the TCA cycle reactions in plants to reconfigure to fulfill different needs has also been pointed out by other authors (Sweetlove et al., 2010), and some of the flux patterns shown in that paper can be seen in Figure 4. Also, the phenotypes of transgenic plants with reduced activities of succinate dehydrogenase and fumarase are different; tomato plants with fumarase reduced sufficiently to inhibit mitochondrial respiration have a reduced rate of photosynthesis and growth (Nunes-Nesi et al., 2007), while the opposite is the case for tomato and Arabidopsis with reduced succinate dehydrogenase (Araújo et al., 2011; Fuentes et al., 2011). In both cases, the primary mechanism of the effect is reported to be through effects on stomatal conductance, possibly caused by metabolite signaling to the guard cells, rather than an effect on photosynthetic capacity. However, even if signaling is the dominant mechanism, the usefulness of fumarate and malate levels as signals could well be related to the reconfiguration of fluxes in this part of the TCA cycle at different light levels. Though succinate dehydrogenase is active in our optimal solutions obtained in light level regions A to C (Fig. 2), it is not essential for biomass generation by photosynthesis, because solutions, albeit suboptimal, are obtained when its activity is deleted from the model.

(4) Light inhibition of pyruvate dehydrogenase. Although this enzyme is present in solutions throughout the light range, its activity is at its maximum at the lower light levels of region B (Fig. 2) and then falls away to the much lower level needed for synthesis of 2-OG. It carries the same flux as the pyruvate transporter Pyr_tx.

It is, perhaps, surprising that the model can capture such a range of realistic behavior of plant metabolism without having included any explicit regulatory mechanisms or enzyme kinetics. Pyruvate dehydrogenase offers an interesting illustration, as it is known to be inactivated by light (Padmasree et al., 2002). The assumption that metabolism will be optimal, combined with the stoichiometric constraints, leads to the conclusion that its activity should fall at high light levels, which implies the existence of a mechanism to achieve this without its having been specified in the model.

The results also show that the metabolic interactions between the plant organelles in the light are not fixed but shift according to the conditions. For this reason, we cannot expect to capture all the behavior shown by a C₃ plant in experiments, as we have so far only considered a leaf growing at a fixed rate with an adequate supply of CO₂ and not yet exporting nutrients to the rest of the plant. Because a mature leaf can produce variable proportions of starch, Suc, and amino acids and operate at different levels of CO₂ and light, we expect the model to reveal more potential for plasticity as we interrogate it in more detail.

There are aspects where we do not yet replicate some experimental observations reviewed in Padmasree et al. (2002). One comes from the representation of photorespiration. The model does not yet fully represent the compartmentation of the reactions involved nor that the NADH generated by Gly decarboxylase is preferentially oxidized by mitochondrial pathways that do not generate ATP (Igamberdiev et al., 1997). Hence, we do not show the total O₂ consumption and CO₂ production of the mitochondria at high light levels nor the associated interchange of amino groups between mitochondria and chloroplasts.

Nitrogen Assimilation

The model showed a transition between the use of NH₃ and NO₃ as light intensity increased from the lowest level able to support biomass formation. For our simulation, we assumed a fixed biomass generation rate and varied the light flux; hence, the result more generally shows the tradeoffs between nitrogen source, growth rate, and photosynthetic rate. Because the photon demand is smaller for growth on NH₃, wherever light intensity is limiting, faster growth will be possible using NH₃ than NO₃. At higher light intensities, the use of NO₃ provides a sink for reductant generated by the excess photons. This illustrates the utility to the plant of having access to both nitrogen sources.

CONCLUSION

Overall, having added very few kinetic constraints to our stoichiometric model (saturation of Rubisco, or the dark reactions of the Calvin cycle, and the limitation that cyclic photophosphorylation rate cannot exceed the noncyclic rate), we find that realistic physiological behavior emerges. This suggests that important aspects of plant photosynthetic metabolism are determined by stoichiometric imperatives and that the specific kinetic and regulatory features are a way to satisfy these constraints and achieve a steady state. In turn, this implies that metabolism can only be fully understood at the whole network level, not as a mosaic of separate pathways.

MATERIALS AND METHODS

Model Construction and Curation

Construction: General

The model was built using the same approach as for our previous model of Arabidopsis (Arabidopsis thaliana; Poolman et al., 2009). An initial reaction set was generated from a publically available database. This set was curated and combined with a set of smaller submodels (modules) defining various functionality not present in the set obtained from the database (described below).

The initial reaction set was extracted from the RiceCyc database (http://www.gramene.org/pathway/ricecyc.html; Youens-Clark et al., 2011) derived from International Rice Genome Sequencing Project’s annotation of the rice (Oryza sativa japonica ‘Nipponbare’) genome sequence. This database is available as part of the BioCyc collection (Karp et al., 2005).

The BioCyc format is particularly useful for metabolic reconstructions, as it clearly defines the hierarchical relationships between genes ↔ proteins ↔ enzymes ↔ reactions ↔ metabolites and, where the database is under active curation by domain experts, these relationships get updated rather than being frozen as ancillary data in the metabolic model.

The ScrumPy software package used here allows models to be defined in a modular manner such that logically separate groups of reactions are placed in separate files. This greatly facilitates data management and curation in situations where reactions defined in a database are combined with those from other sources.

In addition to the module defined by the reactions obtained from RiceCyc, two important extra modules were those defining the chloroplast and mitochondrial compartments. Other modules were included for convenience and are more completely described in Supplemental Data S1.

The Chloroplast Module

The chloroplast module comprises the light reactions, Calvin cycle, the Rubisco oxygenase reaction (other reactions of photorespiration were treated as cytosolic, as there is no explicit peroxisome compartment in this version of the model), starch metabolism, and reactions (that in the cytosol would be described as glycolytic) from phosphoglycerate to pyruvate and malate dehydrogenase. Full details are given in Supplemental Data S1 and S2.

The light reactions were represented as two lumped reactions, one for cyclic and one for noncyclic photophosphorylation. The stoichiometries were determined from the elementary modes analysis of a detailed model of the light reactions constructed on the basis of stoichiometries of the underlying molecular processes (Allen, 2003). The equations used for cyclic and noncyclic photophosphorylation were, respectively,

and

In steady-state photosynthesis, noncyclic and cyclic photophosphorylation are the major contributors in rice leaves (Makino et al., 2002). Though the water-water cycle (also known as the Mehler peroxidase reaction) can supply extra ATP needed in plant leaf metabolism, its maximum contribution is reported to be less than 5% of the linear electron flow in C₃ leaves (Ruuska et al., 2000; Kramer and Evans, 2011). In addition, it is mainly functional during photosynthetic induction of rice leaves and not steady state, so these reactions were not included.

Consideration was also given to the potential impact of a plastid terminal oxidase reaction (Carol et al., 1999; Josse et al., 2000; Sun and Wen, 2011), which acts to oxidize plastoquinol to plastoquinone and has thus been proposed to act as a safety valve under stress conditions.

When incorporated in the light reaction model, one new elementary mode was found, but the net stoichiometry was identical to that of the cyclic photophosphorylation mode above. Therefore, under the conditions investigated here, although plastid terminal oxidase reaction may carry flux, this will not impact the behavior of the rest of the model.

The model used to generate these elementary modes is provided in Supplemental Data S4.

The Mitochondrial Module

The mitochondrial module was that used and described by Poolman et al. (2009) and comprises the TCA cycle, ETC, and oxidative phosphorylation (see also Supplemental Data S3 and Fig. 4B).

Curation

For the results generated by a model to be of use, it is essential that a number of criteria are met; failure so to do would generate results implying violation of mass and/or energy conservation.

The first step in ensuring mass conservation is simply to determine the atomic balance of individual reactions. This check is readily achieved, as BioCyc databases contain the empirical formulae of most metabolites. Attention must then be turned to those for which no empirical formula is available. The most common of these are polymers, and reactions involved with these must be treated with some caution if serious errors are to be avoided (Poolman et al., 2006). The problem arises when different reactions utilize different numbers of monomeric subunits; for example, starch synthase catalyzes the addition of a single Glc subunit to starch, but amylase removes two. The two reactions together would thus allow the generation of two Glc molecules from one. The issue can be easily resolved by defining the smallest monomeric subunit and rescaling stoichiometric coefficients to reflect this. Thus, the problem in the previous example may be resolved by considering Glc as the smallest monomeric subunit of starch and defining the amylase reaction to produce one-half molecule of maltose.

Energy and redox conservation may be readily checked using the linear program described in Equation 1 below. All inputs and outputs are set to zero and a demand for energy imposed in the form of flux in, for example, a generic ATPase reaction. If a solution exists, then it will contain at least one reaction with incorrectly defined direction or reversibility. Happily, it is our experience that such solutions contain only a small number of reactions that may be conveniently checked against online databases or other sources.

Another potential problem related to reaction irreversibility is that of inconsistent subsets. In brief, an enzyme (or reaction) subset is a set of (possibly not contiguous) reactions that carry steady-state flux in a fixed ratio, a simple linear pathway being a trivial example (Pfeiffer et al., 1999). If two or more reactions in a subset have been defined as irreversible in opposing directions, then no steady-state flux is possible in the reactions comprising the subset. Subsets are identified from analysis of the null space of the system, a subject beyond the scope of this paper, but see Fell et al. (2010) for further details. When inconsistent subsets are identified, a judgment must be made as to the correct directionality of the irreversibility of the reactions within it.

A final check was to verify the stoichiometric consistency of the network with respect to carbon, nitrogen, phosphorus, and sulfur, as described by Gevorgyan et al. (2008).

Biomass Composition

The model described here corresponds to a mesophyll cell in an expanding leaf, i.e. one that is producing cell components for a growing leaf, but not yet exporting material via the phloem to the rest of the plant. The relative proportions of the leaf components were taken from data by Juliano (1986), except for the nucleic acid content and composition, which were estimated from the results of Kwon and Soh (1985). The other biomass components were amino acids for protein plus β-Ala; nucleoside and deoxynucleoside monophosphates for DNA and RNA; polymerized Glc for starch and cellulose; coniferyl, coumaryl, and sinapyl alcohols for lignin; linoleic acid for lipid and Glc; and Suc for soluble metabolites.

Biomass components were assigned an individual transporter, whose flux can be set independently, providing a more convenient mechanism to investigate variations in biomass composition than defining a single biomass reaction consuming all components, which has the disadvantage of making compositional variables into parameters as stoichiometric coefficients. The rates are represented as moles per arbitrary time unit and are given in the model files in Supplemental Data S1.

An ATP hydrolysis reaction was included to represent the energy costs of polymerization, turnover, and cellular maintenance. In our previous application of genome-scale modeling to Arabidopsis root cells in culture (Poolman et al., 2009), we determined a value of 7.1 mmol g^–1 dry weight^–1 h^–1, which is in the range of experimental values reported for both bacteria and algae. This corresponded to approximately one-half the substrate input being used to meet this energy requirement, though this is probably higher than for a plant cell in its natural surroundings. Accordingly, we set the generic ATPase reaction at 0.1 light flux units, which implies a photon demand of 0.1 to 0.2 light flux units depending on the routes used to generate the ATP.

Model Analysis

Apart from the determination of inconsistent subsets and stoichiometric consistency, a linear programming approach was taken for the major part of the analysis. This was defined as:

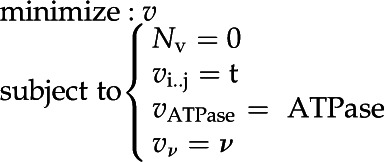(1)

Thus, we minimize total flux, subject to a number of constraints: N_v = 0 defines steady state, v_i..j = t defines the constraints imposed by the requirement for individual biomass components (inputs of CO₂ and inorganic nutrients along with the O₂ output flux were left unconstrained), v_ATPase = ATPase defines the energy demand for polymerization and cell maintenance, and v_v = ν is the photon flux into the system.

A number of variants of this were used in the curation phase; for example, setting v_i..j and ν to zero while setting ATPase to an arbitrary positive value was used to check energetic consistency as described above.

Light Scanning

As light intensity varies more rapidly (diurnal and transient) and over a much greater magnitude than the availability of CO₂ or mineral nutrients, this is the natural place in which to start our response analysis. Hence, for this study, we have analyzed the responses of the solution of Equation 1 to variation in ν. The range investigated was from zero (where obviously no solution is found) up to the point beyond which all flux responses remain linear. The minimum flux below which no solution is possible was identified from a simple bisection search.

Two additional constraints were imposed for this aspect of the study: cyclic photophosphorylation could not exceed noncyclic and an arbitrary limit set on the sum of the Rubisco carboxylase and oxygenase reactions to implement the limit on Calvin cycle flux as mentioned previously. To check the effect of the limitation on cyclic photophosphorylation, we repeated the light scans at different settings, and this only affected the photon flux values at which the various transitions described in “Results” occur, specifically the region B to C transition. The key features of the flux distributions in the mitochondria and chloroplast remain.

Software

All computation was achieved using the software package ScrumPy (Poolman, 2006). This includes facilities for performing linear programming (using the Gnu Linear Programming Kit, http://www.gnu.org/software/glpk/) and interrogating BioCyc flat-file databases.

The package and further information can be obtained from http://mudshark.brookes.ac.uk/ScrumPy or by contacting Mark Poolman.

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Data S1. The “Model” sub-directory contains the model in ScrumPy (.spy) and SBML format.

• Supplemental Data S2. The file “Chloroplast.pdf” contains a structural diagram of the chloroplast module (Model/Chloroplast.spy).

• Supplemental Data S3. The file Model/Mito.spy describes the mitochondrial module.

• Supplemental Data S4. The file LightReacs.spy contains a detailed structural model of the light reactions. The elementary modes of this model define the stoichiometries of the lumped light reactions used in the chloroplast module.

Glossary

GSM

genome-scale metabolic model

FBA

flux balance analysis

AQ

assimilation quotient

TCA

tricarboxylic acid

2-OG

2-oxoglutarate

ETC

electron transport chain