Quantification of Extracellular Carbonic Anhydrase Activity in Two Marine Diatoms and Investigation of Its Role^,,

eCA enhances CO₂ supply for photosynthesis in two marine diatoms.

Abstract

Many microalgae induce an extracellular carbonic anhydrase (eCA), associated with the cell surface, at low carbon dioxide (CO₂) concentrations. This enzyme is thought to aid inorganic carbon uptake by generating CO₂ at the cell surface, but alternative roles have been proposed. We developed a new approach to quantify eCA activity in which a reaction-diffusion model is fit to data on ¹⁸O removal from inorganic carbon. In contrast to previous methods, eCA activity is treated as a surface process, allowing the effects of eCA on cell boundary-layer chemistry to be assessed. Using this approach, we measured eCA activity in two marine diatoms (Thalassiosira pseudonana and Thalassiosira weissflogii), characterized the kinetics of this enzyme, and studied its regulation as a function of culture pH and CO₂ concentration. In support of a role for eCA in CO₂ supply, eCA activity specifically responded to low CO₂ rather than to changes in pH or HCO₃⁻, and the rates of eCA activity are nearly optimal for maintaining cell surface CO₂ concentrations near those in the bulk solution. Although the CO₂ gradients abolished by eCA are small (less than 0.5 μm concentration difference between bulk and cell surface), CO₂ uptake in these diatoms is a passive process driven by small concentration gradients. Analysis of the effects of short-term and long-term eCA inhibition on photosynthesis and growth indicates that eCA provides a small energetic benefit by reducing the surface-to-bulk CO₂ gradient. Alternative roles for eCA in CO₂ recovery as HCO₃⁻ and surface pH regulation were investigated, but eCA was found to have minimal effects on these processes.

To overcome the inefficiencies of Rubisco, many phytoplankton operate a CO₂-concentrating mechanism (CCM) that increases Rubisco’s rate of carbon fixation and reduces oxygen fixation by increasing the concentration of CO₂ around the enzyme. CCMs typically consist of inorganic carbon (C_i) pumps, carbonic anhydrases (CAs) to equilibrate HCO₃⁻ and CO₂, and a compartment to confine Rubisco, such as the pyrenoid or carboxysome, minimizing the volume in which CO₂ is elevated (Badger et al., 1998; Kaplan and Reinhold, 1999; Giordano et al., 2005). Intracellular carbonic anhydrases (iCAs) play multiple roles in CCMs, including the conversion of accumulated HCO₃⁻ to CO₂ around Rubisco and the prevention of CO₂ leakage (Badger, 2003). Some organisms also have an extracellular carbonic anhydrase (eCA) associated with the cell wall, plasma membrane, or periplasmic space. The role of eCA has been enigmatic, although it is clearly related to the CCM. In Chlamydomonas reinhardtii, where eCA has been most thoroughly studied, the major eCA (Cah1) is up-regulated at low CO₂, and its regulatory network includes a transcription factor that induces the expression of other CCM genes as well (Yoshioka et al., 2004; Ohnishi et al., 2010). In other organisms, eCA activity generally increases, in some cases dramatically, at low CO₂, supporting its association with the CCM, but the genetic details of regulation are not known (Nimer et al., 1997; Rost et al., 2003).

When first discovered in microalgae, eCA was thought to facilitate CO₂ influx by keeping surface CO₂ at bulk solution concentrations (Moroney et al., 1985). Many microalgae take up CO₂ to support photosynthesis, but because of the low concentration of CO₂ in most natural waters and the slow rate of HCO₃⁻ dehydration, this uptake can lead to some depletion of CO₂ in the diffusive boundary layer surrounding the cell. eCA accelerates the dehydration of HCO₃⁻ to CO₂ within the boundary layer, increasing the surface CO₂ concentration. Support for this role has come from experiments showing that inhibition of eCA reduces photosynthetic rates and C_i accumulation in disparate microalgae, including the green alga C. reinhardtii, the dinoflagellate Prorocentrum micans, the prymnesiophyte Phaeocystis globosa, and the diatom Thalassiosira weissflogii (Moroney et al., 1985; Nimer et al., 1999; Elzenga et al., 2000; Burkhardt et al., 2001).

Although there is strong support for the role of eCA in CO₂ supply, some observations suggest that it may have additional or alternative roles. In some organisms, blocking eCA does not inhibit photosynthesis, and in C. reinhardtii, knocking out the major eCA had only minor effects on photosynthesis (Van and Spalding, 1999; Moroney et al., 2011). In C. reinhardtii, these results may be explained by the fact that only a small fraction of the total eCA activity is apparently required to support photosynthetic CO₂ uptake, so that if inhibition is not fully effective, CO₂ could still be kept high at the cell surface (Moroney et al., 1985; Palmqvist et al., 1990; Moroney et al., 2011). Such excess may point to other roles for eCA. On the basis of a correlation between HCO₃⁻ uptake and eCA activity, Trimborn et al. (2009) suggested that eCA in diatoms may be used to recover leaked CO₂, converting it to HCO₃⁻ to enhance uptake. eCA may also have a role in pH homeostasis, which is a common role for CA in heterotrophic organisms (Boron, 2004; Swietach et al., 2010).

We sought to better understand the role of eCA in two diatoms by making quantitative measurements of eCA rates and modeling the effect of eCA on boundary-layer chemistry. Our approach to quantify eCA activity is an adaptation of a common method to measure CA activity based on the enzyme’s acceleration of ¹⁸O removal from labeled C_i. This technique has been used to measure the kinetics of isolated CA enzymes (Silverman, 1982), iCA activity (Tu et al., 1978), and eCA activity (Palmqvist et al., 1994; Delacruz et al., 2010). The advance presented here is to extract a quantitative, intrinsic measure of surface eCA activity by applying a simple box model of ¹⁸O-exchange kinetics to the data that accounts for the localization of the enzyme. In contrast, previous methods to measure eCA activity have effectively treated the activity as dispersed throughout the solution and, in some cases, are semiquantitative (Palmqvist et al., 1994; Elzenga et al., 2000; Delacruz et al., 2010). Previous approaches based on ¹⁸O exchange use the long-term rate of ¹⁸O removal as a quantitative but empirical measure of eCA activity (Palmqvist et al., 1994; Delacruz et al., 2010). Another technique uses the rate of equilibration of ¹⁴C between CO₂ and HCO₃⁻, quantifying eCA activity as an increase in the rate of CO₂ hydration in the bulk solution (Elzenga et al., 2000; Martin and Tortell, 2006). A key advantage of our approach is that eCA catalysis is treated as a surface phenomenon, allowing the measured activities to be used in modeling the effects of eCA on boundary-layer chemistry. Using the eCA rates measured in the diatoms, we assessed the potential role of eCA in CO₂ supply, CO₂ recovery, and pH homeostasis.

RESULTS

To determine eCA activity on the cell surface, paired measurements of ¹⁸O-labeled C_i exchange were made in the presence and absence of an eCA inhibitor. When an eCA inhibitor is present, the ¹⁸O-CO₂ data were used to determine iCA activity and CO₂ and HCO₃⁻ fluxes into the cell (Tu et al., 1978). Subsequently, surface eCA activity was quantified by comparing simulations using a model that describes the temporal evolution of the isotopologs of C_i in and around a cell (Fig. 1; see “Materials and Methods”), with ¹⁸O removal rates measured in the absence of an eCA inhibitor.

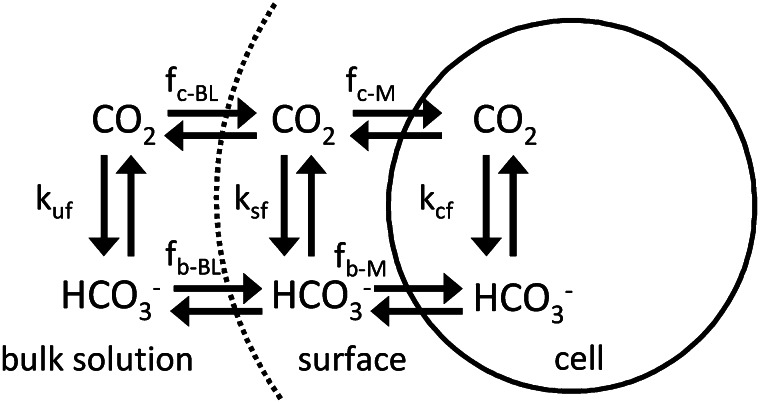
Figure 1.

Diagram of the compartments and fluxes in the box model used to determine eCA activity (Eqs. 1–6; Table III). Fluxes between the compartments are described using mass transfer coefficients, and the reactions are treated using first-order rate constants.

iCA Kinetics and Mass Transfer Coefficients

Our method for the determination of eCA activity requires that iCA activity and mass transfer coefficients for passive CO₂ and HCO₃⁻ fluxes be known. These terms were determined from ¹⁸O-removal kinetics when eCA activity was inhibited using the CA inhibitor acetazolamide (AZ) or dextran-bound acetazolamide (DBAZ; Tu et al., 1978; Hopkinson et al., 2011). iCA activities depended on culture conditions, ranging between 80 and 200 s⁻¹ for Thalassiosira pseudonana and between 20 and 150 s⁻¹ for T. weissflogii. Mass transfer coefficients for CO₂ (f_c) were 1.3 ± 0.4 × 10⁻⁸ cm³ s⁻¹ for T. pseudonana and 2.9 ± 0.9 × 10⁻⁸ cm³ s⁻¹ for T. weissflogii, while HCO₃⁻ mass transfer coefficients were less than 1 × 10⁻¹² cm³ s⁻¹ for T. pseudonana and 1.9 ± 1.6 × 10⁻¹⁰ cm³ s⁻¹ for T. weissflogii, similar to previously reported values (Hopkinson et al., 2011).

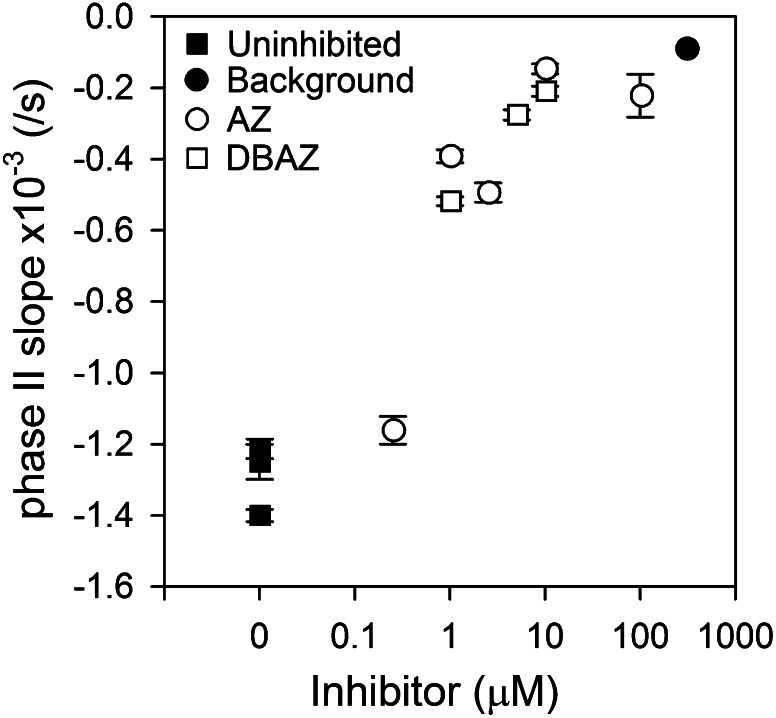
Accurate determination of iCA activity and CO₂ and HCO₃⁻ mass transfer coefficients requires that eCA be fully inhibited. ¹⁸O removal follows a biphasic pattern in which there is an initial, rapid removal of ¹⁸O as CO₂ enters CA-containing cells followed by a slower, long-term loss of ¹⁸O due to the depletion of ¹⁸O from HCO₃⁻ (Silverman et al., 1976; Fig. 2). We used the long-term rate of ¹⁸O removal or “phase II slope” (calculated as the slope of a linear fit through natural log-transformed ¹⁸O atom fraction data) as an empirical measure of eCA activity to establish that eCA effectively inhibited the CA inhibitors (Fig. 3; Delacruz et al., 2010). Application of increasing concentrations of AZ or DBAZ to cells expressing eCA reduces the phase II slope to near background, uncatalyzed exchange rates, verifying that eCA activity was effectively eliminated. The presence of iCA accelerates long-term ¹⁸O removal slightly above the background rate. We verified that neither AZ nor DBAZ had a detectable effect on iCA activity of low-pH-grown cells (where eCA is absent; see below) and so did not pass through the plasma membrane to any significant extent (data not shown).

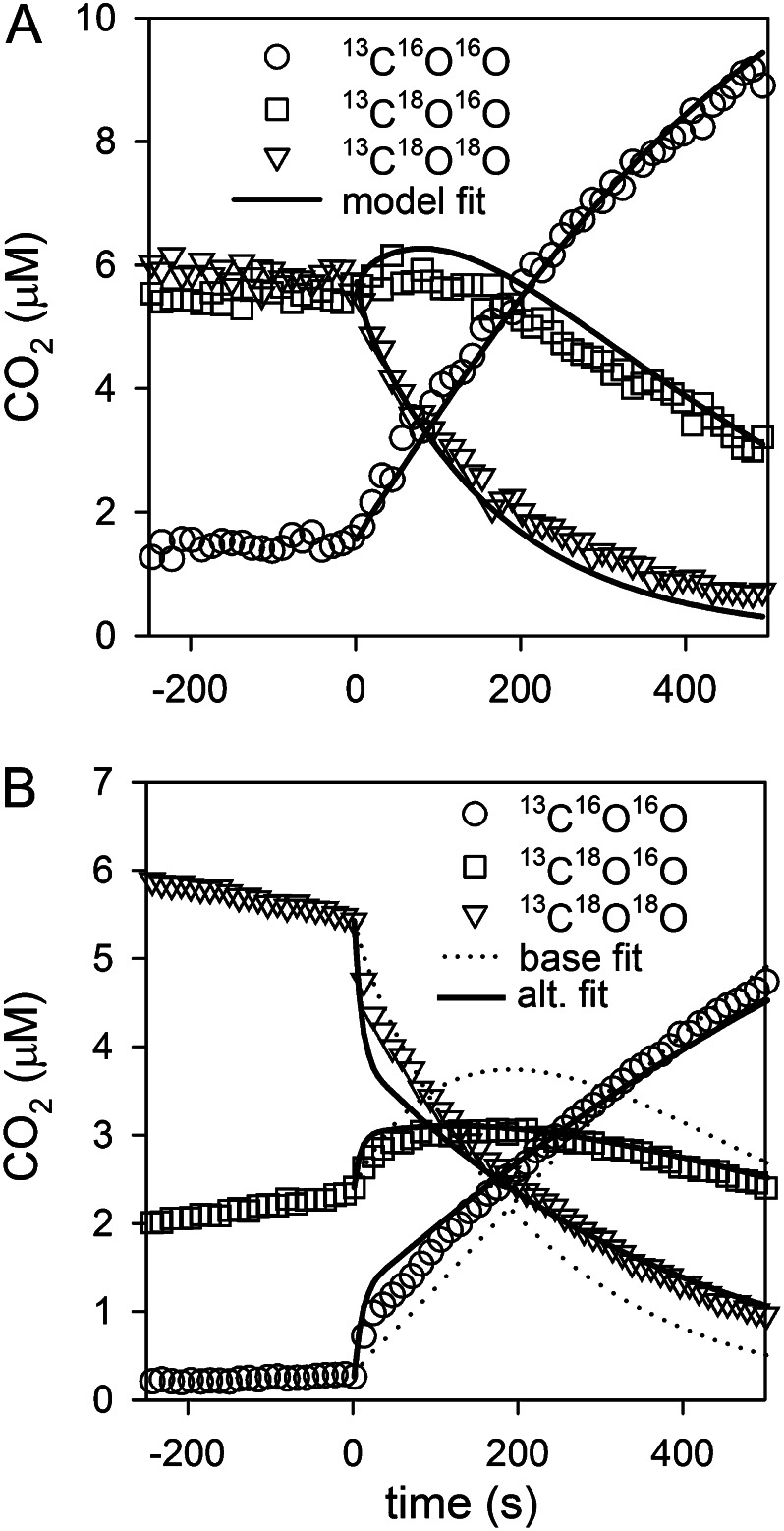
Figure 2.

Sample model fits to ¹⁸O-CO₂ data for the determination of eCA activity. Cells expressing eCA were added to the assay solution at time 0, accelerating ¹⁸O removal. A shows a good fit to the data. B shows an example where a better fit can be achieved by reducing f_b-BL 10-fold, but the eCA activities are similar in both fits (base, k_sf = 1.7 × 10⁻⁶; reduced, f_b-BL k_sf = 1.5 × 10⁻⁶). For clarity, only every other ¹⁸O-CO₂ data point is shown.

Figure 3.

Long-term rate of ¹⁸O removal (phase II slope) as a function of eCA inhibitor concentration. The background rate, prior to cell addition, is also plotted.

Determination of eCA Rate Constants

After determining the rate constants for iCA and CO₂ and HCO₃⁻ mass transfer coefficients, eCA activity in T. pseudonana and T. weissflogii was quantified by fitting the box model of isotope exchange to the observations (see Eqs. 1–6 in “Materials and Methods”). k_sf, the first-order rate constant for eCA-catalyzed CO₂ hydration, is used as a measure for eCA activity, since it can be directly compared with the boundary-layer mass transfer coefficient for CO₂ (f_c-BL) to assess the effectiveness of eCA (see “Materials and Methods”). The model gave good fits to the ¹⁸O-CO₂ data in most cases, and the eCA activities were consistent in replicate runs (Fig. 2A). eCA activities (k_sf) varied with culture and assay conditions, ranging between 0 and 3.5 × 10⁻⁷ cm³ s⁻¹ for T. pseudonana and between 0 and 40 × 10⁻⁷ cm³ s⁻¹ for T. weissflogii.

In some runs, the model fits could not account for a depletion of the ¹³C¹⁸O¹⁶O intermediate species later in the assay (Fig. 2B). This signature suggests reduced exchange between the surface layer and the bulk solution (Silverman et al., 1981), and the fit can be improved by reducing the diffusive HCO₃⁻ flux to the cell surface (e.g. due to the presence of an extracellular matrix that reduces the diffusivity of charged ions; Stewart, 2003). However, this improvement of the fit alters the estimated eCA activity by less than 20% (Fig. 2B). Similarly, eCA activity is not sensitive to the choice of the size of the surface boundary-layer volume (Table I). The effect of potential residual eCA activity when determining iCA rate constants and cross-membrane fluxes was also assessed using the eCA box model. eCA activity and HCO₃⁻ permeability have similar effects on ¹⁸O-CO₂ behavior, because both expose the extracellular HCO₃⁻ pool to CA and so accelerate the long-term rate of ¹⁸O removal. If eCA was not fully inhibited during the determination of iCA activity and mass transfer coefficients, the activity would be treated as increased HCO₃⁻ transfer through the cell membrane (greater f_b-M). To determine the maximal residual eCA activity, we fit ¹⁸O-CO₂ data from runs in which eCA should have been completely inhibited (50 μm or greater AZ or DBAZ) to the eCA box model (Eqs. 1–6), setting HCO₃⁻ membrane permeability to zero (f_b-M = 0) and treating iCA activity (k_cf), CO₂ permeability (f_c-M), and eCA activity (k_sf) as unknowns. The potential residual eCA activities (T. pseudonana, 5.2 ± 7.1 × 10⁻⁹ cm³ s⁻¹; T. weissflogii, 5.4 ± 4.6 × 10⁻⁸ cm³ s⁻¹) were low relative to measured eCA activities. Thus, both the empirical analysis (Fig. 3) and the modeling approach show that the eCA inhibitors were highly effective.

Table I. Effect of model surface volume on derived eCA activity.

Surface Volume	eCA Activity
cm3	cm3 s−1
2.0 × 10−12	7.29 × 10−8
8.2 × 10−12	7.34 × 10−8
4.8 × 10−11	7.31 × 10−8
1.1 × 10−10	7.32 × 10−8

eCA Kinetics: Effect of pH and C_i

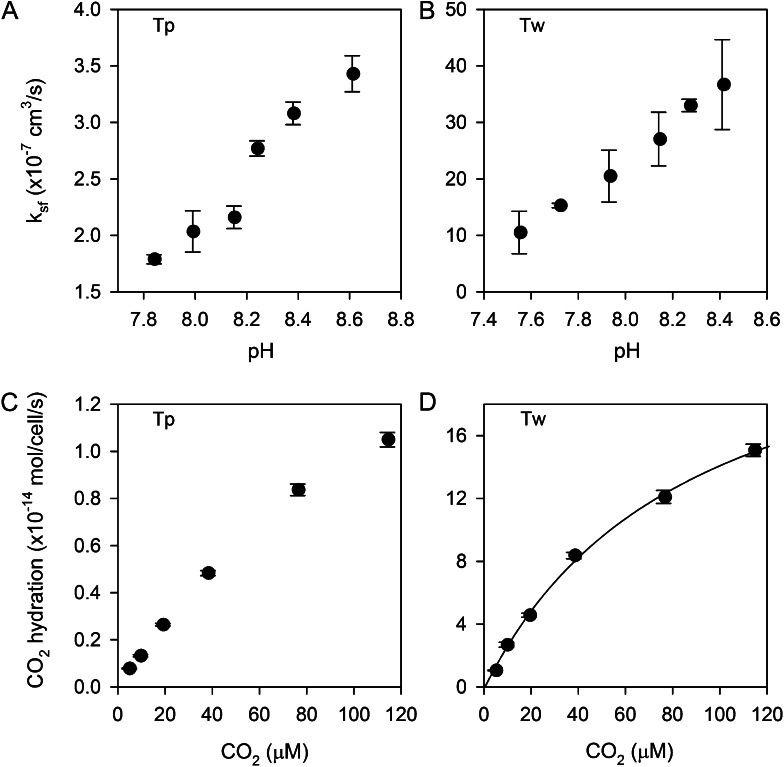
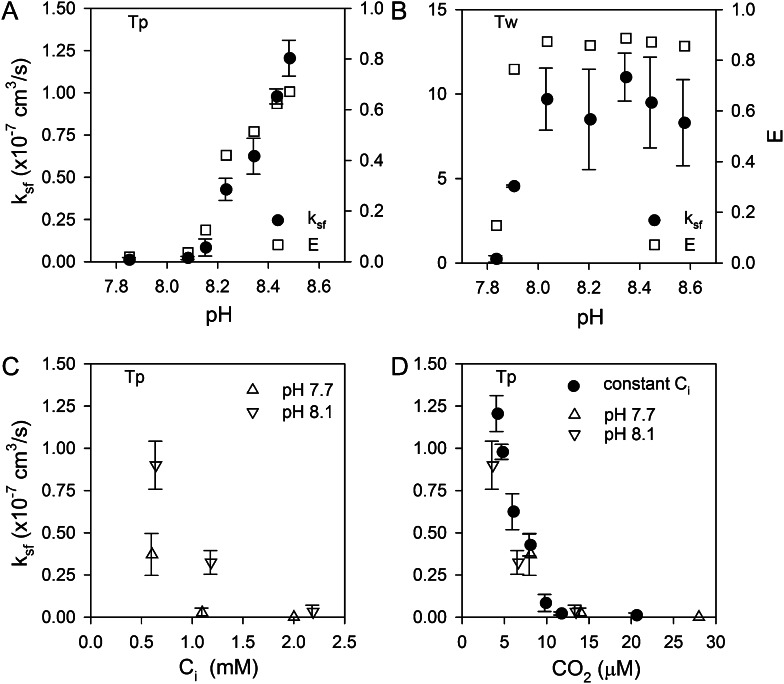
To characterize eCA enzyme kinetics, strong eCA activity was induced by growing cultures to high density without pH or CO₂ control (final culture pH of 8.6–8.8). The cells were then concentrated and immediately assayed for eCA activity at a range of pHs and C_i concentrations. Enzyme activity (k_sf) increased linearly with pH in T. pseudonana (7.8–8.6) and in T. weissflogii (7.5–8.4; Fig. 4, A and B) over a pH range typical of marine environments. CA activity typically shows a logarithmic increase with pH as water at the active site is deprotonated (Silverman and Lindskog, 1988). Our observations indicate a linear response, which may reflect the small pH range tested or result from differences between solution and cell surface pH.

Figure 4.

eCA kinetics. A and B, Effects of assay pH on eCA activity in T. pseudonana (Tp; A) and T. weissflogii (Tw; B). C and D, Reaction rates (CO₂ hydration rate) as a function of substrate concentration (CO₂) in T. pseudonana (C) and T. weissflogii (D). A Michaelis-Menten fit to the T. weissflogii data, which shows some saturation, gives a CO₂ half-saturation constant of 87 ± 10 μm and a maximal reaction rate of 26 ± 2 × 10⁻¹⁴ mol cell⁻¹ s⁻¹.

We assessed the effect of C_i concentration on eCA reaction rates. eCA activity was measured at pH 7.9 and varying C_i from 0.5 to 12 mm, with corresponding CO₂ concentrations ranging from 5 to 115 μm (Fig. 4, C and D). In T. pseudonana, nonlinearity in the reaction rate (CO₂ hydration rate) versus substrate concentration (CO₂) was observed only at the very highest CO₂ concentration. In T. weissflogii, there is more significant nonlinearity, allowing a Michaelis-Menten function to be fit to the data. From this fit, the half-saturation constant of eCA for CO₂ is 87 ± 10 μm. These results show that CO₂ hydration and HCO₃⁻ dehydration are effectively first order with respect to substrate concentration in the environmentally relevant range (approximately 2 mm C_i, CO₂ of 5–20 μm), validating our use of a first-order rate constant as a measure of eCA activity.

eCA Expression: Effect of CO₂ and pH

T. pseudonana and T. weissflogii were grown for several generations at different pHs (7.7–8.6) maintained by a pH buffer 4-(2-Hydroxyethyl)piperazine-1-propanesulfonic acid (EPPS) at constant C_i (2 mm), concentrated, and assayed for eCA activity at constant pH (8.0) and C_i (2 mm) to determine the effect of growth conditions on eCA expression. Under these culture conditions, pH and CO₂ covary with CO₂, ranging between 24 μm at pH 7.8 and 3 μm at pH 8.6. In T. pseudonana, eCA activity was undetectable from pH 7.8 to 8.1 but then increased dramatically above this pH (Fig. 5A). eCA activity in T. weissflogii was undetectable only in cells grown at the lowest pH (7.8) and then increased quickly to a high, constant value from pH 8.0 to 8.6 (Fig. 5B). iCA activity (k_cf) also increased substantially from low to high culture pH in both species (T. pseudonana, 80–200 s⁻¹; T. weissflogii, 20–150 s⁻¹). Complementary experiments in which the culture pH was held constant but C_i was varied also showed that low CO₂ induced eCA expression in T. pseudonana (Fig. 5C). The T. pseudonana eCA activity data from the constant C_i and constant pH experiments converge, following a single trend, when plotted as a function of CO₂ concentration in the growth medium, showing that eCA expression was primarily controlled by CO₂ (Fig. 5D).

Figure 5.

Expression of eCA as a function of culture pH and C_i. A and B, When grown at a constant total C_i (2 mm) but varying pH, both diatoms induce eCA at high pH/low CO₂ (A, T. pseudonana [Tp]; B, T. weissflogii [Tw]). The level of activity is sufficient to reduce surface-to-bulk CO₂ gradients, as shown by the effectiveness index (E; Eq. 13). C, When T. pseudonana was grown at constant pH (7.7 or 8.1) but varying C_i, eCA was induced at low C_i. D, All the T. pseudonana data converge when plotted as a function of CO₂, showing that it is the major control on eCA expression.

Effect of eCA Inhibition on Photosynthesis

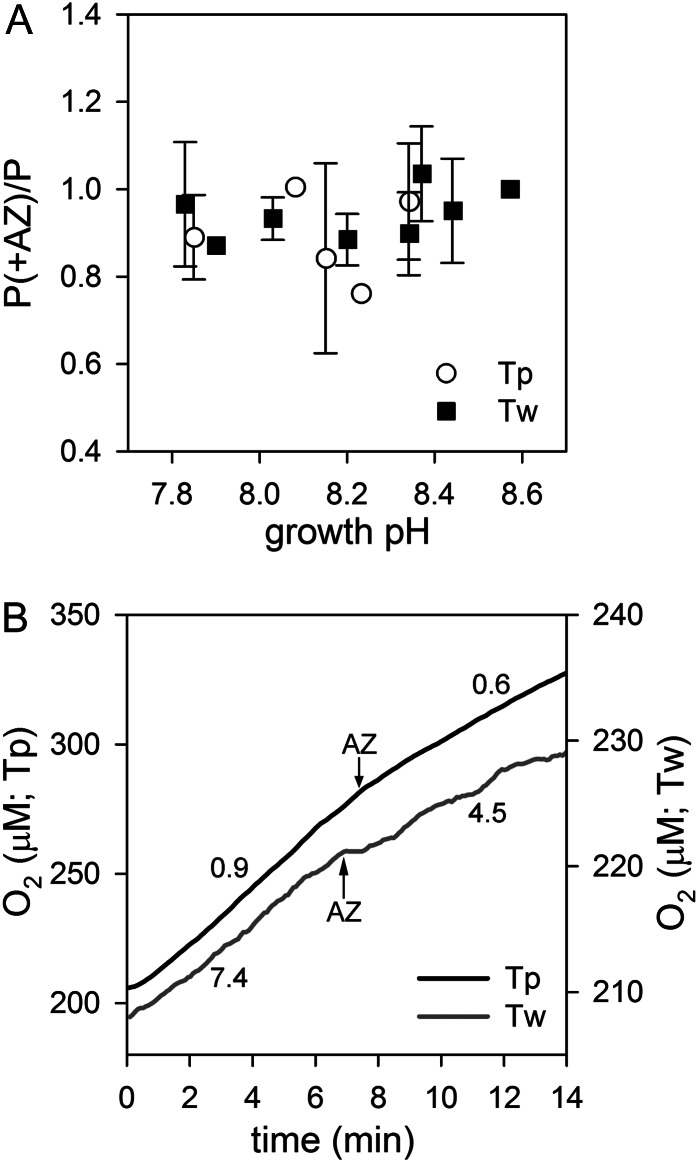
We tested the effects of short-term eCA inhibition on photosynthesis. At a concentration of AZ sufficient to inhibit all detectable eCA activity (50 μm), there was no consistent effect of short-term eCA inhibition on photosynthesis under environmentally relevant conditions of C_i availability (C_i, 2 mm; pH 7.8–8.6; Fig. 6A). We assessed the effects of AZ ranging from 1 to 500 μm on photosynthesis in T. pseudonana and T. weissflogii grown without pH control to pH 8.7 and assayed at the same pH, but we found no significant inhibition of photosynthesis even at the highest AZ concentrations (data not shown). Only at very low CO₂ concentrations (1 μm; pH 8.7; C_i, 1 mm) did short-term eCA inhibition consistently reduce photosynthesis, inhibiting oxygen production by 42% ± 5% in T. weissflogii and by 25% ± 8% in T. pseudonana (Fig. 6B).

Figure 6.

Effect of the eCA inhibitor AZ on photosynthesis. A, Effect of short-term inhibition of eCA on photosynthesis shown as the ratio of the photosynthetic rate in the presence of the inhibitor (P+AZ) to the rate without the inhibitor (P). The diatoms (T. pseudonana [Tp] and T. weissflogii [Tw]) were grown and assayed at a range of pHs with constant C_i (2 mm). B, Oxygen traces showing inhibition of photosynthesis at 1 μm CO₂ after the addition of AZ. The numbers next to the traces indicate the rate of oxygen production (×10⁻¹⁷ mol cell⁻¹ s⁻¹) before and after AZ addition.

Effect of eCA Inhibition on Growth

To test the long-term effects of eCA inhibition, growth rates of the two diatoms were measured in the presence and absence of DBAZ (Table II). The cultures were grown for 4 to 6 d under the same environmental conditions as other cultures (20°C, 16/8-h photoperiod at 125–150 μmol photons m⁻² s⁻¹) with 20 μm DBAZ added initially and 5 μm additional DBAZ added in the morning of day 3. In T. weissflogii, DBAZ reduced growth by approximately 10% at pH 8.4 (5 μm CO₂) but had no effect on growth at pH 7.8 (24 μm CO₂), demonstrating that the inhibitor did not have any nonspecific effects on metabolism. DBAZ had no significant effect on growth of T. pseudonana at pH 8.4.

Table II. Effect of DBAZ on growth rate.

The asterisk indicates that the DBAZ treatment was significantly different (P < 0.05; n = 4) from the control based on Student’s t test.

Diatom	Culture pH	Growth Rate
		Control	DBAZ
		d−1 ± sd
T. pseudonana	8.4	1.15 ± 0.01	1.14 ± 0.02
T. weissflogii	8.4	0.55 ± 0.01	0.51 ± 0.03*
T. weissflogii	7.8	0.94 ± 0.02	0.94 ± 0.02

Model Assessment of eCA on Surface Boundary-Layer Chemistry

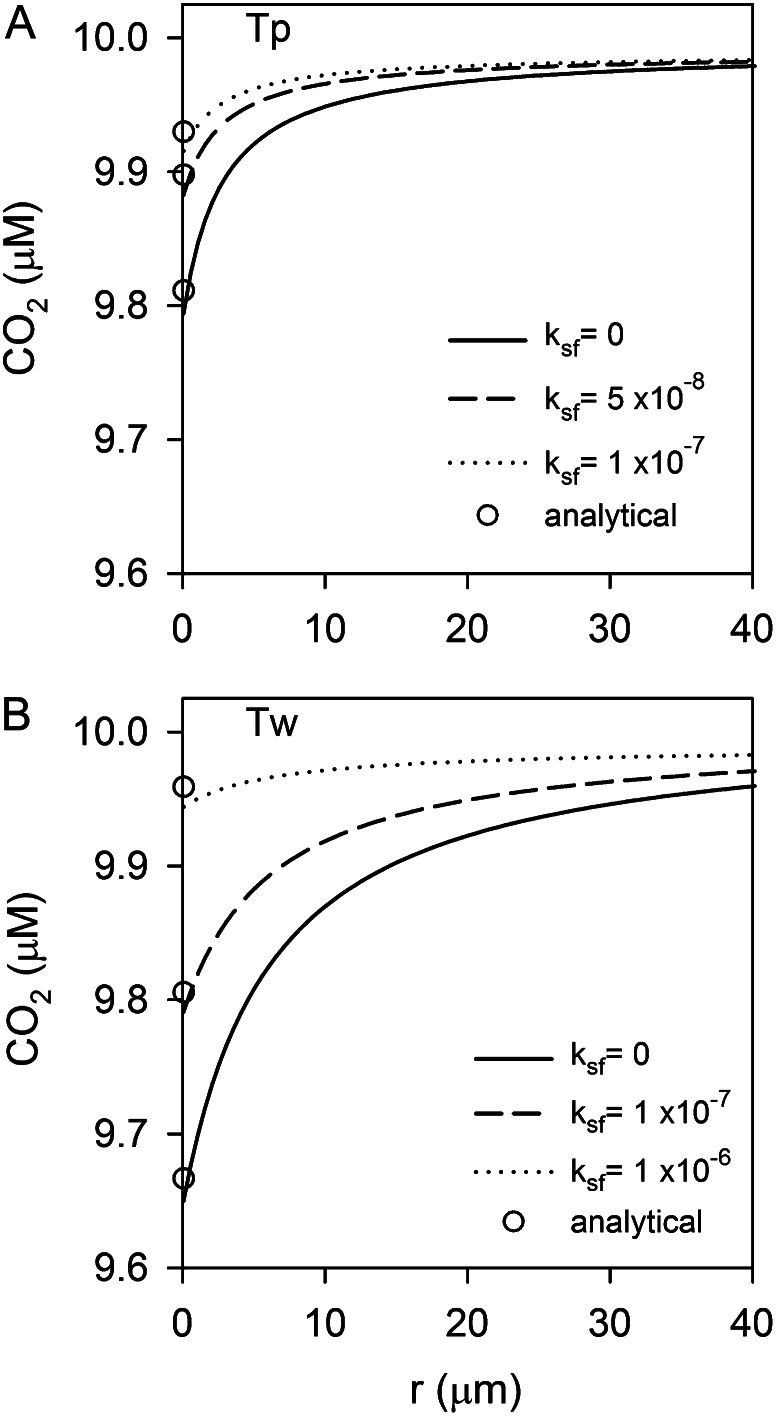
We used a spatially resolved reaction-diffusion model of the diffusive boundary layer to quantify the effect of eCA on boundary-layer chemistry (for details, see “Materials and Methods”). The primary role of eCA is thought to be the maintenance of bulk solution CO₂ concentrations at the cell surface during photosynthesis. To assess this role, a model simulation was run in which a diatom takes up CO₂ at two-thirds its photosynthetic rate, which is typical of cultured marine diatoms (Burkhardt et al., 2001; Rost et al., 2003; Hopkinson et al., 2011). Average photosynthetic rates measured in this study were used in the simulation (T. pseudonana, 1.7 × 10⁻¹⁷ mol cell⁻¹ s⁻¹; T. weissflogii, 7 × 10⁻¹⁷ mol cell⁻¹ s⁻¹). The analysis shows that the measured eCA activities are sufficient to maintain cell surface CO₂ near bulk concentrations despite photosynthetic carbon uptake in both species (Fig. 7). In all cases, however, the absolute size of the CO₂ gradient is relatively small. In the absence of eCA, the concentration difference between the bulk solution and the cell surface is only 0.2 μm for T. pseudonana and 0.35 μm for T. weissflogii.

Figure 7.

Model simulations of the effect of eCA on surface boundary-layer chemistry during CO₂ uptake. (A, T. pseudonana [Tp]; B, T. weissflogii [Tw]). The effect of eCA on the CO₂ profiles is shown at two eCA activities, the lower at a magnitude similar to f_c-BL and the higher approximating maximal expression levels. k_sf values used in the simulations are indicated. Analytical approximations for surface CO₂ concentrations obtained using Equation 12 are indicated with white circles, agreeing well with the numerical solution.

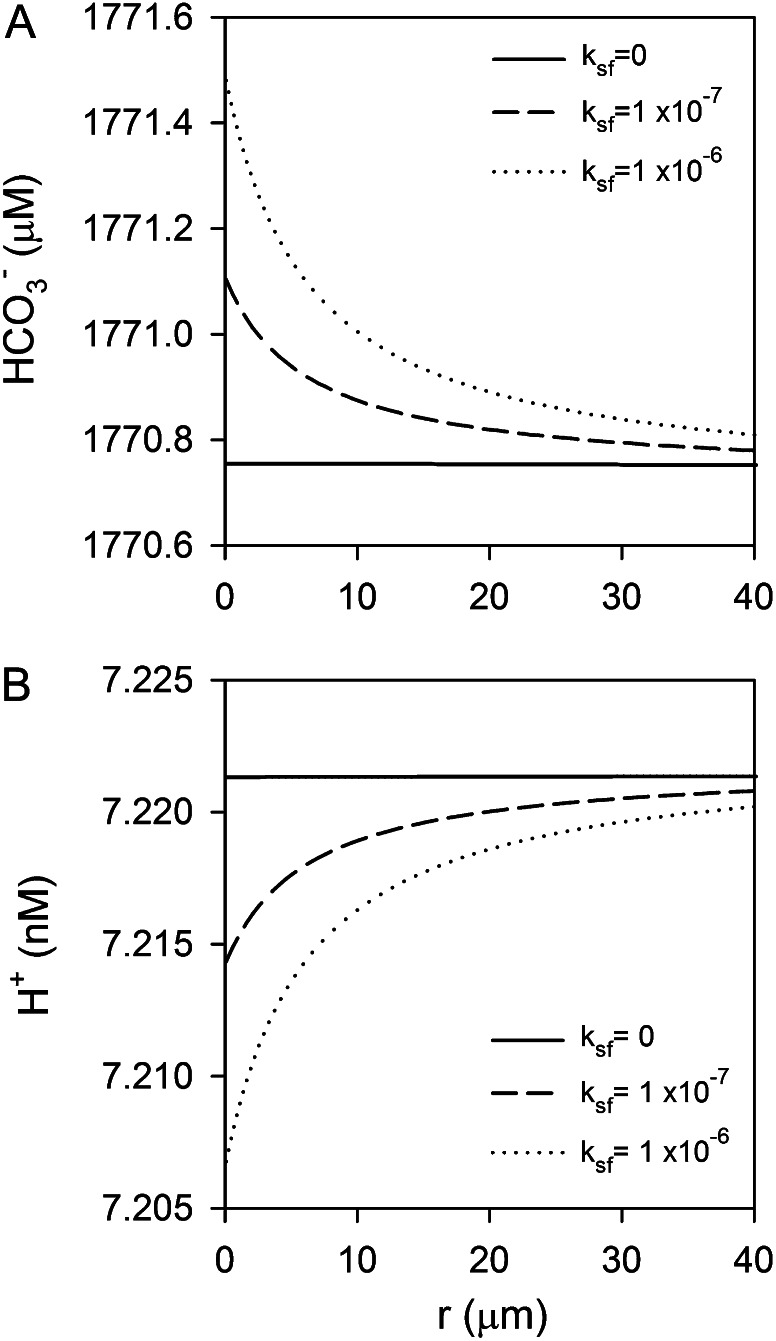
An alternative role for eCA in the recovery of leaked CO₂ as HCO₃⁻ for subsequent uptake has also been suggested (Trimborn et al., 2008). As CO₂ leakage is just the inverse of CO₂ uptake, the modeled effects of eCA on CO₂ gradients are very similar. In both diatoms, fully induced eCA activity is able to convert nearly all the leaked CO₂ to HCO₃⁻. However, even when eCA is effective, the changes in surface HCO₃⁻ concentrations are minuscule. The largest increase in HCO₃⁻ concentration is 0.7 μm, which is only a 0.04% increase (Fig. 8A).

Figure 8.

Model simulations showing that the effects of eCA on surface boundary-layer HCO₃⁻ and H⁺ concentrations are small. A, If CO₂ leaks from the cell, eCA can convert this leaked CO₂ to HCO₃⁻, but the surface HCO₃⁻ concentration increases by less than 1 μm. B, eCA has only a minor effect on the H⁺ concentration during CO₂ uptake. Both panels show results from simulations with T. weissflogii, since the effects of eCA, although still small, are more significant for this species.

Finally, eCA could also be involved in the control of surface pH, since the C_i system dominates pH buffering in seawater. One scenario, discussed below, involves H⁺ uptake equimolar to HCO₃⁻ uptake to compensate for intracellular H⁺ consumption required to convert HCO₃⁻ to CO₂ for photosynthesis. This scenario was simulated with rates of H⁺ and HCO₃⁻ uptake at the cell surface equal to photosynthetic rates, but we found that eCA activity had no effect on the surface H⁺ perturbation induced by this uptake, because of rapid acid/base equilibration among buffer species (data not shown). CO₂ uptake creates a pH disequilibrium in the boundary layer that can be reestablished by eCA (Fig. 8B), but the effect on the H⁺ concentration is very small.

DISCUSSION

Although there is strong evidence that eCA is linked to the CCM, its exact role has been controversial (Van and Spalding, 1999; Trimborn et al., 2008; Moroney et al., 2011). Enhancement of CO₂ availability for photosynthesis is the most logical role for eCA, since CO₂ concentrations are low in most natural waters and can become depleted in cell boundary layers. But alternative roles in the recovery of leaked CO₂ and pH homeostasis have also been suggested, based in part on observations that the elimination of eCA does not always reduce photosynthesis. The lack of a quantitative, intrinsic measure of eCA activity has hindered the evaluation of its role. Here, we have developed an approach to quantify eCA activity, applied it to two marine diatoms, and evaluated the potential role of eCA in these organisms through an analysis of the effect of eCA activity on surface boundary-layer chemistry.

Enhancement of CO₂ Supply

eCA is commonly thought to facilitate CO₂ influx by dehydrating HCO₃⁻ at the cell surface. Many microalgae take up CO₂ for photosynthesis (Badger et al., 1994; Burkhardt et al., 2001), which is most likely driven by a diffusive gradient (Kaplan and Reinhold, 1999; Hopkinson et al., 2011), despite the fact that HCO₃⁻ is much more abundant than CO₂ in the ocean. Net CO₂ uptake into the cell can be supported either by diffusion of CO₂ from the bulk solution or generation of CO₂ from HCO₃⁻ within the boundary layer, which for microalgae would need to be catalyzed by eCA because uncatalyzed HCO₃⁻ dehydration is slow (Wolf-Gladrow and Riebesell, 1997).

Consistent with a role for eCA in CO₂ supply, we find that eCA is up-regulated at low CO₂ concentrations and that induction occurs at a higher CO₂ concentration in the larger diatom T. weissflogii, which is more prone to diffusive limitation (Fig. 5; Pasciak and Gavis, 1974; Riebesell et al., 1993). Typically, the effect of CO₂ on eCA expression is assessed by varying pH at a constant C_i concentration or by bubbling cultures with air containing varying levels of CO₂ (Nimer et al., 1997; Rost et al., 2003). In both approaches, CO₂ and pH are closely coupled, with CO₂ decreasing as pH increases, but it is generally assumed that CO₂ is the key variable regulating eCA activity. Both T. pseudonana and T. weissflogii expressed eCA at low CO₂/high pH (Fig. 5, A and B) in such an experiment, as is commonly observed. But by additionally culturing T. pseudonana at constant pH but variable C_i (Fig. 5C), we were able to clearly show that eCA activity responds to low CO₂ concentrations, rather than changes pH or HCO₃⁻, consistent with a role for eCA in CO₂ uptake (Fig. 5D).

A key finding, made possible by the quantitative nature of the eCA measurements, is that the amount of eCA expressed by both diatoms is appropriate to support CO₂ uptake, but not excessive. As shown in Equations 11 to 13 (see “Materials and Methods”), the relative magnitude of the boundary-layer mass transfer coefficient (f_c-BL) and eCA activity (k_sf) controls the sources of CO₂ (diffusion or dehydration) for net uptake and describes the extent to which eCA is able to mitigate CO₂ drawdown in the boundary layer. eCA activity at low CO₂ in T. pseudonana and T. weissflogii is two to 10 times greater than the boundary-layer mass transfer coefficient (f_c-BL; T. pseudonana, 5.9 × 10⁻⁸ cm³ s⁻¹; T. weissflogii, 1.4 × 10⁻⁷ cm³ s⁻¹), such that eCA activity is nearly optimal for the abolishment of bulk solution to surface CO₂ gradients (Fig. 5). A spatially resolved model confirms that the eCA activities are able to maintain surface CO₂ concentrations at near bulk concentrations (Fig. 7; for model description, see “Materials and Methods”). The lack of excess eCA for CO₂ supply in these diatoms contrasts with C. reinhardtii, where there is apparently excess eCA for CO₂ supply (Moroney et al., 1985), which could be taken to imply that it has other roles.

While the magnitude of the CO₂ drawdown at the cell surface is relatively small (0.2–0.35 μm; Fig. 7), it is similar in size to the CO₂ gradient across the cytoplasmic membrane that drives CO₂ influx. For example, given the permeability of the T. weissflogii membrane to CO₂ (Hopkinson et al., 2011), a 0.4 μm CO₂ gradient across the plasma membrane would be needed to support CO₂ uptake at the rate estimated for our culture conditions. The high permeability of membranes to CO₂ means that this influx occurs passively, which is potentially more energy efficient than active uptake of HCO₃⁻, but requires the cell to generate a CO₂ gradient across the cytoplasmic membrane. In the absence of eCA, intracellular CO₂ would need to be drawn down further to maintain CO₂ uptake, which diatoms are capable of doing, as shown by their ability to take up CO₂ over a wide range of extracellular CO₂ concentrations (Burkhardt et al., 2001), but at the cost of increased energetic expenditure.

Short-term inhibition of eCA at CO₂ concentrations greater than 1 μm did not reduce photosynthesis, presumably because cytoplasmic CO₂ concentrations could be lowered to maintain CO₂ influx (Fig. 6A). Photosynthesis was only reduced when extracellular CO₂ concentrations decreased to 1 μm (Fig. 6B), at which point the cytoplasmic CO₂ concentration was 0.4 μm in T. pseudonana and 0.2 μm in T. weissflogii, as estimated using boundary-layer mass transfer coefficients and the cytoplasmic membrane permeability for each species. The cells apparently could not lower their intracellular CO₂ concentrations further, and for T. weissflogii, the intracellular CO₂ concentration was so low that greater reduction would not significantly increase CO₂ influx. Long-term inhibition of eCA reduced the growth of T. weissflogii at low CO₂ (Table II), consistent with an increased energetic cost of C_i acquisition without eCA, although inhibition of eCA had no detectable effect on the growth of T. pseudonana, perhaps because its smaller size minimizes the magnitude of the bulk-to-surface CO₂ gradient and the energetic costs associated with compensating for this gradient. However, even a small energetic savings that allows minor increases in growth rate can have major consequences for the ecological success of plankton in the ocean (Tilman, 1977).

Alternative Roles for eCA

Alternative roles for eCA in the recovery of leaked CO₂ and the regulation of cell surface pH have been suggested (Trimborn et al., 2008). The CCM is not perfectly efficient, in large part because of the high permeability of membranes to CO₂, leading to CO₂ leakage out of the chloroplast or plasma membranes. While eCA could effectively convert leaked CO₂ to HCO₃⁻, the increase in HCO₃⁻ concentration achieved by CO₂ recovery would be very small compared with the approximately 1.8 mm HCO₃⁻ concentration in seawater (Fig. 8A). Assuming that diatom HCO₃⁻ transporters follow Michaelis-Menten kinetics, in which the greatest sensitivity of uptake rate to substrate is a linear increase at low substrate concentrations, the increased cell surface HCO₃⁻ concentration would allow at most a 0.04% increase in uptake rate. Additionally, diatoms exhibit a net CO₂ influx rather than a net CO₂ efflux under normal conditions (Burkhardt et al., 2001; Hopkinson et al., 2011), so there is no CO₂ leaking from the cell to be recovered.

CAs are commonly involved in pH regulation (Boron, 2004), so it is conceivable that eCA may be involved in pH maintenance, since the C_i system is the main pH buffer in seawater. The best example of the role of eCA in pH maintenance comes from human cancer cells, where high rates of respiration lead to a high acid load (in the form of CO₂). By converting CO₂ to HCO₃⁻ and H⁺ outside the cell, eCA helps to maintain an alkaline internal environment at the expense of a more acidic extracellular environment (Swietach et al., 2010). Photosynthetic organisms such as diatoms, on the other hand, import CO₂ and HCO₃⁻ for carbon fixation. Since CO₂ is ultimately the species fixed by Rubisco, the import and subsequent consumption of CO₂ has no net effect on intracellular acid/base balance. However, imported HCO₃⁻ must be converted to CO₂ for fixation, consuming a proton in the process. Organisms that transport HCO₃⁻ then need to import a proton (or export OH⁻) for each molecule of HCO₃⁻. eCA could help supply H⁺ to the cell surface to balance HCO₃⁻ uptake, potentially accounting for the observed correlation between eCA and HCO₃⁻ uptake in several marine phytoplankton (Trimborn et al., 2008). Simulation of the effect of eCA on boundary-layer pH for diatoms importing HCO₃⁻ and H⁺ revealed that the boundary-layer pH changes induced by uptake are very small because of rapid reactions among the buffer species HCO₃⁻/CO₃²⁻ and B(OH)₄⁻/B(OH)₃. Furthermore, eCA does not alter the small pH changes, because the slow CO₂/HCO₃⁻ equilibrium is not significantly involved in boundary-layer pH buffering in this case. Alternatively, eCA could help establish pH equilibrium during CO₂ uptake. We simulated the effect of eCA on boundary-layer pH, assuming that the diatoms obtain all their carbon for photosynthesis from CO₂. eCA does have an effect on boundary-layer pH in this case, and the highest rates are effective at reestablishing pH equilibrium, but the absolute effect of eCA on H⁺ concentration is very small (Fig. 8B).

CONCLUSION

Using a newly developed approach to quantify eCA-catalyzed CO₂ hydration rates, eCA activity was measured in two diatoms, T. pseudonana and T. weissflogii, and its potential roles in CO₂ supply, CO₂ recovery, and pH regulation were investigated. In support of the role of eCA in photosynthetic CO₂ supply, its activity increased at low CO₂ concentrations, was appropriate to abolish bulk-to-surface CO₂ gradients, and was greater in the larger diatom (T. weissflogii), which is more prone to diffusive limitation. The differences in CO₂ concentration between the bulk solution and the cell surface that are eliminated by eCA are small (less than 0.5 μm), but small gradients drive significant passive CO₂ influxes in these diatoms (Hopkinson et al., 2011). The consequences of short-term inhibition of eCA can be overcome by decreasing the cytoplasmic CO₂ concentration to maintain CO₂ influx rates. However, this requires increased energetic expenditure, which may explain the decreased growth rate of T. weissflogii when eCA was inhibited. We investigated alternative roles for eCA in the recovery of leaked CO₂ for HCO₃⁻ uptake and pH regulation but found that eCA activity would not have a significant effect on boundary-layer HCO₃⁻ and H⁺ concentrations. Taken together, these results support a role for eCA in CO₂ supply.

MATERIALS AND METHODS

Culturing

The diatoms Thalassiosira pseudonana (CCMP1335) and Thalassiosira weissflogii (CCMP1336) were obtained from the National Center for Marine Algae and Microbiota and maintained in Aquil medium (Price et al., 1988). For most experimental work, the algae were grown in Aquil made from a natural seawater base with 5 mm 4-(2-Hydroxyethyl)piperazine-1-propanesulfonic acid (EPPS) buffer to maintain constant pH and C_i conditions. To assess the pH and C_i dependence of enzyme kinetics, cultures were grown in Aquil to high density without pH or CO₂ control (final culture pH of 8.6–8.8) to induce strong eCA activity. For experiments in which C_i concentrations were varied, North East Pacific Culture Collection Enriched Seawater, Artificial Seawater (NEPCC ESAW) medium was used with 5 mm EPPS buffer added (Harrison et al., 1980). This medium uses an artificial seawater base, and C_i was left out in the initial medium preparation, being added later at the desired concentration. All cultures were grown in an incubator at 20°C under fluorescent lights (125–150 μmol photons m⁻² s⁻¹) on a light/dark cycle (16 h on, 8 h off). Cell numbers were counted daily with a Coulter Counter, and cells were harvested during exponential growth.

The initial pH of the culture medium was adjusted with HCl or NaOH (stored in sealed serum vials to avoid CO₂ absorption) and measured on the total hydrogen ion scale using thymol blue (Zhang and Byrne, 1996). The C_i concentration was measured at the beginning and end of the experiments using membrane inlet mass spectrometry (MIMS; Beckmann et al., 2009; Hopkinson et al., 2011). Additional carbon system parameters (CO₂, HCO₃⁻, and CO₃²⁻ concentrations) were calculated from pH and C_i (Dickson and Goyet, 1994; Lueker et al., 2000).

¹⁸O-Exchange Experiments

The rate of ¹⁸O removal from labeled C_i was used to determine iCA and eCA activities. ¹⁸O-labeled ¹³C-C_i (2 mm, unless otherwise noted) was added to assay buffer (C_i-free artificial seawater, 20 mm Tris at pH 8.0, unless otherwise noted) in a MIMS chamber. Temperature in the chamber was maintained at 20°C using a water jacket. ¹⁸O-CO₂ species were monitored by MIMS for approximately 10 min to determine the background rate of CO₂ hydration/HCO₃⁻ dehydration, after which cells were added to the chamber from a concentrated suspension. ¹⁸O removal catalyzed by cellular CA was then monitored in the dark for 15 to 20 min. To determine iCA activity, an inhibitor of eCA was added prior to the addition of cells. In most cases, 50 μm AZ was used, but 50 μm DBAZ (Ramidus) was used in select experiments to confirm that diatom membranes were not permeable to AZ.

Photosynthetic Rates

The effect of eCA inhibitors on photosynthesis was assessed from measurements of oxygen production made using MIMS. Assay buffer with 2 mm C_i, unless otherwise noted, was added to the MIMS chamber, and cells were added from a concentrated suspension. Light was provided from a tungsten lamp at 200 μmol photons m⁻² s⁻¹. Oxygen production was monitored for approximately 10 min, at which point AZ or DBAZ was added and oxygen production was monitored for a further approximately 10 min. Measurements were made at the same pH as the cultures were grown and at pH 8.0.

eCA Model Development

The eCA box model considers ¹⁸O-CO₂ and ¹⁸O-HCO₃⁻ isotopologs in three compartments: the bulk solution, the boundary layer at the cell surface, and the intracellular space (Fig. 1; Table III). Fluxes between the compartments are described by mass transfer coefficients, and the uncatalyzed and catalyzed CO₂ hydration/HCO₃⁻ dehydration reactions, responsible for ¹⁸O removal, are treated as first-order reactions, since the enzyme is undersaturated for C_i (Fig. 4). The model is described by the following system of differential equations:

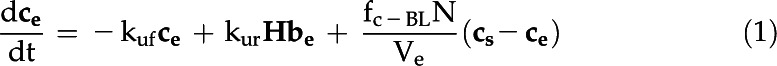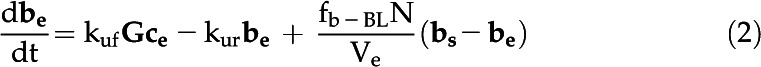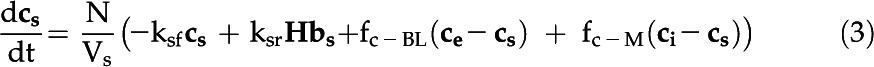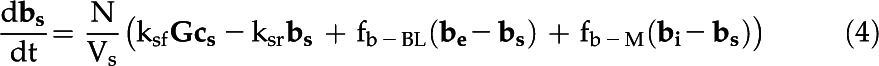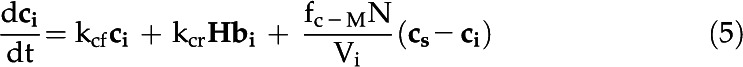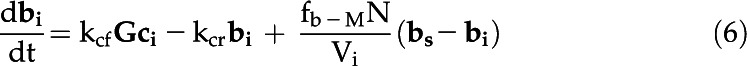with variables and parameters as described in Table III.

Table III. Model notation.

Boldface symbols denote concentration vectors: c = [C¹⁶O₂; C¹⁶O¹⁸O; C¹⁸O₂]; b = [HC¹⁶O₃⁻; HC¹⁶O₂¹⁸O⁻; HC¹⁶O¹⁸O₂⁻; HC¹⁸O₃⁻].

Symbol	Definition	Units	Source/Method Reference
ce	Concentration of 18O-CO2 species in the bulk solution	mol cm−3	MIMS measurement
cs	Concentration of 18O-CO2 species in the surface boundary layer	mol cm−3	Modeled
ci	Concentration of 18O-CO2 species inside the cell	mol cm−3	Modeled
be	Concentration of 18O-HCO3− species in the bulk solution	mol cm−3	Modeled
bs	Concentration of 18O-HCO3− species in the surface boundary layer	mol cm−3	Modeled
bi	Concentration of 18O-HCO3− species inside the cell	mol cm−3	Modeled
kuf	Uncatalyzed CO2 hydration rate constant	s−1	Background 18O removal rate
kur	Uncatalyzed HCO3− dehydration rate constant	s−1	Background 18O removal rate
ksf	eCA-catalyzed CO2 hydration rate constant	cm3 s−1	eCA assay (this study)
ksr	eCA-catalyzed HCO3− dehydration rate constant	cm3 s−1	eCA assay (this study)
kcf	iCA-catalyzed CO2 hydration rate constant	s−1	iCA assay (Tu et al., 1978)
kcr	iCA-catalyzed HCO3− dehydration rate constant	s−1	iCA assay (Tu et al., 1978)
fc-BL	Boundary-layer mass transfer coefficient for CO2	cm3 s−1	iCA assay (Tu et al., 1978)
fb-BL	Boundary-layer mass transfer coefficient for HCO3−	cm3 s−1	iCA assay (Tu et al., 1978)
fc-M	Membrane mass transfer coefficient for CO2	cm3 s−1	iCA assay (Hopkinson et al., 2011)
fb-M	Membrane mass transfer coefficient for HCO3−	cm3 s−1	iCA assay (Hopkinson et al., 2011)
N	Number of cells in the assay chamber	–	Coulter Counter measurement
Ve	Bulk solution volume	cm3	Measured
Vs	Surface layer volume	cm3	Imposed, 8 × 10−12 cm3
Vi	Intracellular volume	cm3	Coulter Counter measurement
G	Stoichiometric matrix describing the hydration of CO2 species to HCO3−	–	Hopkinson et al. (2011)
H	Stoichiometric matrix describing the dehydration of HCO3− species to CO2	–	Hopkinson et al. (2011)

The solution volume (V_e) was measured directly, and the intracellular volume was determined using a Coulter Counter. The volume of the boundary layer compartment (V_s) was set to 8 × 10⁻¹² cm³, reflecting a surface layer thickness on the order of 0.1 μm. The uncatalyzed CO₂ hydration/HCO₃⁻ dehydration rates in the bulk solution (k_uf, k_ur) were determined from ¹⁸O removal rates prior to the addition of cells, and the observed values agree well with published rates (Johnson, 1982). The mass transfer coefficients for diffusive flux between the bulk solution and the boundary layer (f_c-BL, f_b-BL) were calculated assuming the cells are spherical, with radii determined from Coulter Counter measurements (T. pseudonana, 2.5 μm; T. weissflogii, 6 μm):

where R is the cell radius and D is the diffusivity of CO₂ (1.65 × 10⁻⁵ cm² s⁻¹ at 20°C) or HCO₃⁻ (1.05 × 10⁻⁵ cm² s⁻¹ at 20°C; Pasciak and Gavis, 1974). The parameters for iCA activity (k_cf, k_cr) and the mass transfer coefficients for membrane passage (f_c-M, f_b-M) were determined from analysis of ¹⁸O-exchange rates in the presence of an eCA inhibitor (Tu et al., 1978; Hopkinson et al., 2011). eCA-catalyzed hydration/dehydration rate constants (k_sf, k_sr) are related to each other via the CO₂/HCO₃⁻ equilibrium constant, assuming microscopic reversibility. k_sf, the first-order rate constant for eCA-catalyzed CO₂ hydration, was determined by optimizing the model fit to the ¹⁸O-CO₂ data (Supplemental Data S1).

Models of Surface Boundary-Layer Chemistry

To assess the effects of eCA on boundary-layer chemistry, we developed a simple analytical approximation and a one-dimensional numerical reaction diffusion model. The analytical model treats the case in which there is a net CO₂ influx (photosynthetic uptake) to, or efflux (leakage) from, the cell. A net CO₂ influx (an efflux is similar except for a change of sign) is supported by diffusion of CO₂ from the bulk solution and, when eCA is present, the net generation of CO₂ from eCA-catalyzed HCO₃⁻ dehydration. Diffusion through the boundary layer is dependent on the CO₂ gradient between the bulk solution and the cell surface. For a spherical cell, the net diffusive CO₂ flux (NC_D) is:

The net generation of CO₂ from HCO₃⁻ dehydration at the cell surface is:

In the marine environment, which our assay and culture conditions replicate, HCO₃⁻ concentrations are high, approximately 1.8 mm, and so are not significantly depleted at the cell surface. Taking the HCO₃⁻ concentration at the surface to be equal to the bulk solution, and using the fact that at equilibrium the forward and backward reaction rates will be equal (k_sf[CO₂] = k_sr[HCO₃⁻]), Equation 9 can be rewritten as:

In effect, the net CO₂ supply from eCA depends on the same CO₂ gradient as the diffusive supply, although the physicochemical processes underlying these net CO₂ sources are very different. The diffusive flux is driven by the actual spatial CO₂ gradient, whereas net CO₂ production by eCA is the result of disequilibrium between CO₂ and HCO₃⁻ at the cell surface. The total net CO₂ influx is the sum of the diffusive and reactive supply:

This equation shows that the importance of diffusion or eCA activity for net CO₂ supply depends on the relative sizes of f_c-BL and k_sf, justifying k_sf as a measure of eCA activity.

Rearranging Equation 11, we can find an expression for the surface CO₂ concentration:

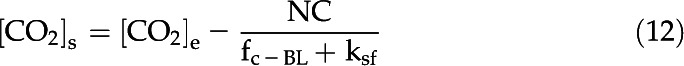which shows that as eCA activity (k_sf) increases, the surface CO₂ concentration approaches that of the bulk solution. To measure the impact of eCA on CO₂ exchange between the cell and the bulk solution, we define the effectiveness of eCA (E) as:

which varies between 0 (no impact of eCA) and 1 (eCA dominates over diffusive exchange). E is both the fraction of net CO₂ supply supported by eCA and the fraction of the maximum potential CO₂ gradient abolished by eCA activity.

For a more detailed evaluation of the effect of eCA on boundary-layer carbon chemistry and pH, a spherical reaction-diffusion model was developed. The model domain extends from the cell surface 100 μm out to the bulk solution. Chemical concentrations are held constant in the bulk solution but are allowed to vary at the cell surface due to imposed uptake and export fluxes and reaction-diffusion within the boundary layer. Dissolved C_i species (CO₂, HCO₃⁻, and CO₃²⁻) and other important components determining seawater pH [H⁺, OH⁻, B(OH)₃, and B(OH)₄⁻] are included in the model. Bulk solution pH, C_i, and total boron were set at typical oceanic values (pH 8.14; C_i, 2 mm; total boron, 415 μm). All reactions are treated kinetically using rate constants from Zeebe and Wolf-Gladrow (2001) and diffusion coefficients from Boudreau (1997). The model was solved in Matlab.

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Data S1. Description of scripts used to process isotope exchange data and implement the eCA box model.

Glossary

CCM

CO₂-concentrating mechanism

C_i

inorganic carbon

CA

carbonic anhydrase

iCA

intracellular carbonic anhydrase

eCA

extracellular carbonic anhydrase

AZ

acetazolamide

DBAZ

dextran-bound acetazolamide

MIMS

membrane inlet mass spectrometry