Differences between Perception and Eye Movements during Complex Motions

Abstract

During passive whole-body motion in the dark, the motion perceived by subjects may or may not be veridical. Either way, reflexive eye movements are typically compensatory for the perceived motion. However, studies are discovering that for certain motions, the perceived motion and eye movements are incompatible. The incompatibility has not been explained by basic differences in gain or time constants of decay. This paper uses three-dimensional modeling to investigate gondola centrifugation (with a tilting carriage) and off-vertical axis rotation. The first goal was to determine whether known differences between perceived motions and eye movements are true differences when all three-dimensional combinations of angular and linear components are considered. The second goal was to identify the likely areas of processing in which perceived motions match or differ from eye movements, whether in angular components, linear components and/or dynamics. The results were that perceived motions are more compatible with eye movements in three dimensions than the one-dimensional components indicate, and that they differ more in their linear than their angular components. In addition, while eye movements are consistent with linear filtering processes, perceived motion has dynamics that cannot be explained by basic differences in time constants, filtering, or standard GIF-resolution processes.

1. Introduction

In the absence of vision, humans perceive whole-body self-motion by means of sensed angular and linear accelerations, or equivalently, forces. However, spatial disorientation and misperception of motion can occur, particularly during unusual combinations of angular and linear accelerations. At the same time, eye movements arise from both the angular and linear accelerations, with the eye movements being roughly compensatory for the perceived motion, at least during relatively simple motions. Because these eye movements can be measured in an objectively quantitative manner, eye movements have sometimes been used as a proxy for perceived motion, and research on “self-motion perception” has often been facilitated by analyzing eye movements.

However, substantial differences have been discovered between perception and eye movements, making it clear that self-motion perception is more sophisticated than indicated by existing understanding of eye movements as demonstrated by eye-movement models. Two complex motions for which perception and eye movements have been found to differ are gondola centrifugation (in which a tangentially-facing subject is tilted in roll to prevent net interaural acceleration as centripetal acceleration builds up), and off-vertical axis rotation (OVAR). During gondola centrifugation, subjects report much greater changes in pitch during deceleration than during acceleration, but vertical eye movements are of similar amplitude during acceleration and deceleration [19]. During OVAR with subjects tilted diagonally and rotated about their own longitudinal axis, most subjects at rotation speeds such as 45°/s perceive motion progressing around a cone with pivot somewhere below the head or body, but horizontal eye movements are completely out of phase with the perceived translation around the cone [50]. In addition, simpler motions have mismatches between perception and eye movements, for example during vertical linear oscillation [32] and during sinusoidal roll tilt [34, 35]. One set of studies that has taken the next step, demonstrating and testing our understanding of perception versus eye movements through the use of modeling, showed that during sinusoidal roll tilt, the interaural translation component of perception followed an internal model of verticality, while horizontal eye movements did not [34, 35].

In the process of embarking upon further investigation of perception as compared to eye movements, the question arises whether certain perceived motions are really, in fact, incompatible with the eye movements, especially for three-dimensional motions such as gondola centrifugation and OVAR. After all, the same eye movements can be compensatory for either rotational or translational motion, so perceptions and eye movements that at first seem mismatched may actually correspond to the same motion. A hypothetical example: While pitch motion is normally associated with vertical eye movements, changes in pitch can logically be accompanied by lack of vertical eye movements. One example (Fig. 1) is rightward yaw toward nose-down from an orientation of rightward roll. The seemingly mismatched nonzero pitch change with zero vertical eye movements become clearly matched upon considering the full three-dimensional motion.

Figure 1.

Hypothetical perceived motion for which one-dimensional perception and eye movements would appear to be incompatible—in perceived pitch versus vertical eye movements—but are actually compatible during the three dimensional motion: backward curve with rightward yaw velocity, starting in a rightward roll orientation. The motion is shown in freeze-frame format by displaying a head at 0.5 s intervals through an arc that lasts 2 s. The perceived motion has nonzero rate of change of forward pitch, but compensatory eye movements would have zero vertical component.

Much work remains to determine where the true mismatches lie and then to what extent, for which components, and in what manner self-motion perception differs from eye movements. A challenge arises especially for complex motions such as gondola centrifugation and OVAR, for which three-dimensional modeling is necessary in order to perform full analyses.

1.1. Known Properties of Perception

For simple motions, at least, self-motion perception follows known patterns. Most importantly, perception “understands” basic physics. Angular acceleration, for example, is interpreted to indicate a change in angular velocity. If the axis of rotation is not aligned with the perceived Earth-vertical, then the perceived rotation is appropriately interpreted to mean a change in orientation with respect to vertical. However, unlike in the laws of physics, perceived rotation decays in the absence of angular acceleration [7].

This decay may indicate a tendency of perceived motion toward a familiar motion, stationarity, and is often formalized by means of a differential equation or feedback loop with a time constant giving the rate of decay. Eye movements also decay with a similar pattern, though with a shorter time constant than for perception [12].

Linear acceleration is more complicated because of the presence of gravity, but it also involves a natural perceptual understanding of physics. Humans sense the total gravito-inertial acceleration (GIA), which is the sum of actual linear acceleration and “pseudo-acceleration” upward due to the presence of gravity; acceleration/force sensors cannot detect actual linear acceleration separately from gravity. Cleverly, perception appears to distinguish the actual linear acceleration as the portion of the GIA not matching the perceptually-expected upward vector due to gravity. This perceptual ability is called GIF-resolution (GIF = gravito-inertial force) and depends upon having a perception of “upward”; the storage of information about upward has been termed an “internal model” and has been demonstrated experimentally also for eye movements [33, 36, 37] and neuron responses [1]. However, one set of studies indicated that GIF-resolution may not occur for eye movements during sinusoidal roll tilt [34, 35].

Linear acceleration affects two aspects of perceived motion: linear velocity and tilt. Perceived linear velocity arises from linear acceleration, and decays. The time constant of decay for perceived linear velocity, in contrast to that for eye movements, has been found to depend on nondirectional cues such as noise and vibration [44, 52]. Simultaneously, perceived tilt changes in such a way that the perceived Earth-vertical direction moves toward alignment with the GIA [8, 15], and a constant GIA will eventually be interpreted as indicating upward. This is another property of perception that could be phrased as a tendency toward the familiar, because gravity gives a familiar constant GIA.

These known properties form the core of existing three-dimensional models of human self-motion perception [e.g. 3, 4, 6, 10, 14, 21, 24, 30, 33, 38, 39, 41, 53]. The angular, linear and tilt properties are often implemented in different manners, but the models give the same tendencies as the known properties, regardless of whether implemented by leaky integration, velocity storage, feedback, optimal filtering, priors in Bayesian modeling, or time constants in transfer functions or differential equations.

1.2. Perception of Complex Motions

Recent research has shown that perception of complex motion has properties not captured by the above “standard” model, for gondola centrifugation [25] and OVAR [28]. For gondola centrifugation, the standard model could not explain acceleration-deceleration pitch asymmetries or paradoxical tumble [19], nor could it explain roll-tilt differences between forward- and backward-facing accelerations [45]. For OVAR, the standard model could not predict the typical perception of motion around a cone with pivot below the head or body [9, 17, 48, 50], and instead predicted motion around a cone with pivot above the head no matter what parameter values were used [28]. These studies focused on perception alone, and did not include eye movements.

The present paper investigates whether, or how, perception is compatible with eye movements during complex motions. For gondola centrifugation, three-dimensional perception is compared to vertical and horizontal eye movements. For OVAR, three-dimensional perception is compared to horizontal and torsional eye movements. Two questions are addressed:

1. Are the perceived motions truly incompatible with the eye movements, once interactions between three-dimensional rotation and translation are taken into account?

2. In what ways does perception differ from, and agree with, eye movements, particularly for

   1. angular motion components,
   2. linear motion components, and
   3. dynamics, e.g. short-term versus long-term?

One hypothesis for the linear acceleration components is that eye movements use simple filtering, while perception uses GIF-resolution [34, 35], so the testing includes two different three-dimensional models.

2. Methods

2.1. Coordinate System

The standard coordinate system was used for subject motion [22]: For translation, the positive x direction is noseward, the positive y direction is leftward, and the positive z direction is head-upward. Rotation used the right-hand rule about the same axes: Positive x is rightward roll, positive y is forward pitch, and positive z is leftward yaw.

Specification of eye movements used the rotational rule. Positive x indicates torsional slow phase rotating the top of the eye rightward; this compensates for negative x rotation (leftward roll). Positive y indicates vertical slow phase head-downward; this compensates for negative y rotation (backward pitch) as well as head-upward translation. Positive z indicated horizontal slow phase leftward; this compensates for negative z rotation (rightward yaw) as well as rightward translation.

2.2. Experimental Data

Published, peer-reviewed data were used as the basis for the investigation of gondola centrifugation and OVAR.

Gondola centrifugation was phrased here as counterclockwise, with the subject seated upright facing tangentially in a large-radius (6+ meters) centrifuge and for which the subject was continuously tilted in roll—phrased here as leftward—to keep the body axis aligned in roll with the GIA. Perception was reported in pitch [19, 31], roll [45, 46], and vertical linear translation [19], while eye movement data was reported for vertical and horizontal eye movements [31] (Table 1). The apparent mismatch between data on perception and eye movements appeared in the pitch/vertical direction. Pitch perception in a 6.1 m radius centrifuge accelerating to 122°/s in 19 s (6.4°/s², 70.5° actual roll, 3 g maximum z-directed GIA) was summarized as follows:

‘During acceleration, the reported pitch position change was small relative to the deceleration perception and was not accompanied by unusual pitch angular changes. During deceleration, large pitch changes were accompanied by strong pitch plane velocities that provoked paradoxical perceptions, for example, “I'm pitched forward 90 degrees and still tumbling.”’ [31, p. 334]

Table 1.

Experimental results on perception and eye movements

GONDOLA CENTRIFUGATION 1			OVAR 2
	Acceleration	Deceleration		Amplitude	Phase
PERCEPTION			PERCEPTION
Pitch orientation[19,31]	back 10°	forward 90°	Tilt[9,49,50]	<15° to >30°	-30° to >0°
Pitch angular velocity[19,31]	none	forward	Translation[50]	0.9m	-30° to >0°
Roll orientation[45,46]	gain 0.4	~0°
Vertical linear velocity[19]	“increased weight”	upward
EYE MOVEMENTS			EYE MOVEMENTS
Vertical SPV peak[31]	25-30°/s down	25-30°/s up	Torsion[50]	3°	-25°
Horizontal SPV peak[31]	15-20°/s right	15°/s left	Horizontal SPV[50]	5°/s	+60° to +100°

¹For gondola centrifugation, measures given in absolute units are for 6.1 m radius, 6.4°/s² for 19 s.

²For OVAR, measures are for 20° tilt and 45°/s rotation.

Vertical eye movements, in contrast, peaked at similar magnitudes of 25-30°/s during acceleration and deceleration [31, Fig. 2,7] (Table 1, Fig. 4B,D). Horizontal eye movements were also recorded [31, Fig. 2,7] (Table 1, Fig. 4A,C). For perception, ascent was reported during deceleration, while increased weight was reported during or after acceleration [19]. In other large-radius centrifuges, perception of roll was reported at approximately 0.4 times the actual roll during acceleration, but was absent during deceleration. Specifically, in a 7.25 m radius centrifuge accelerating at 15°/s² to 1.1 g, 1.7 g, 2.5 g, or 4.5 g maximum z-directed GIA (with corresponding roll tilt of 25°, 54°, 66°, or 77°), the subjective visual horizontal at the end of the acceleration showed gains of 0.65, 0.45, 0.41, and 0.40, respectively, relative to the actual roll tilt [46]. In a 9.1 m radius centrifuge accelerating at 7.8°/s² to 2 g maximum z-directed GIA (with corresponding roll tilt of 60°), the mean angle of the subjective visual horizontal at the end of the acceleration was 21° [45].

Figure 2.

The models, representing well-known properties of perception and eye movements in three dimensions. Input of linear and angular acceleration is at left, and output is at right. Eye movement computations are shown by the thinner lines, with output of horizontal, vertical and torsional vestibulo-ocular reflex (VOR). Perception uses the same core, with additional portions shown by thicker lines to produce separate output of angular (ω) and linear (v) velocity, as well as position (r) in the Earth-fixed reference frame, and orientation as given by three vectors in head-based coordinates: an Earth-upward vector (g) of magnitude g, and two heading vectors (i, j) representing fixed orthogonal directions in the Earth horizontal plane. Computations of ω, v, r, g, i, and j are based upon standard physical relationships between the vectors modified by the nervous system's tendency toward angular and linear stationarity, and vertical alignment with the GIA, according to time constants τ_a, τ_l and τ_t, respectively. The only exception occurs in the dashed box, which shows the two different versions of the model, the GIF-Resolution Model and the Filter Model. The GIF-Resolution Model mirrors physics in three dimensions, while the Filter Model disregards the tilt in processing linear acceleration. For eye movements, VOR output is computed as that compensatory for the computed three-dimensional combination of velocities, scaled by gains. To handle possible mismatch between angular tilt velocity and change in tilt orientation, the model allows VOR to arise from angular velocity and/or from change in orientation relative to vertical by using the “MAX”imum calculation after applying a fractional weight, w, to the change in orientation.

Figure 4.

Simulations of eye movements in a gondola centrifuge as compared with the pattern of data, for the two different versions of the model: Filter Model and GIF-Resolution Model. The actual pattern of data (x's) is as shown in McGrath et al. [31]. Details of the models’ parameter values are given in the text. For the Filter Model, the two different values of τ_l gave graphs that were barely distinguishable, so the value τ_l = 0.25 s is used for this display. (A) Centrifuge acceleration, horizontal slow phase velocity (SPV) of eye movements. (B) Centrifuge acceleration, vertical SPV. (C) Centrifuge deceleration, horizontal SPV. (D) Centrifuge deceleration, vertical SPV.

OVAR was phrased here as clockwise, which typically produces perceived motion counterclockwise around a cone with pivot below the feet or at least below the head, and for concreteness focused on 20° tilt and 45°/s rotation speed, which produces the conical perception and for which both horizontal and torsional eye movements are nonzero. Data on OVAR at 180°/s, for which only horizontal eye movements differ statistically from zero, were also used as needed to check appropriate frequency dependence of the models. During 45°/s OVAR, the horizontal and torsional eye movements are out of phase [50], in contrast to perceived translation and tilt,. For the present research, phases are stated relative to a cone whose pitch-back orientation coincides with the actual pitch-back orientation:

1. perceived tilt phase = 0° if the perceived backward pitch orientation coincides with the actual backward pitch orientation, and is positive if it occurs before (leads) the actual backward pitch orientation,

2. perceived translation phase = 0° if the maximum rightward linear velocity coincides with the actual backward pitch orientation (or the right- and leftmost turnaround points coincide with the actual right- and leftmost roll orientations), and is positive if it occurs before (leads) the actual pitch back orientation (or the turnaround points occur before the actual maximum roll orientation).

Reports of phase (Table 1) appeared to depend upon the method of reporting, with phase lag reported with a continuous joystick method [50] and phase lead with a push-button method [9, 50], although it is interesting to note that even in the light, a phase lead was reported for perceived velocity with a push-button method [9], indicating that pushbutton reports may include an inherent anticipatory lead. Perceived amplitude of tilt also varied (Table 1), with reported tilt angle usually less than the actual tilt, around 15° or less for OVAR with 20° tilt and 45°/s rotation when using joystick or visual methods [49, 50] and often as much as twice the actual tilt with verbal reports [9, 50]. Perceived translation was typically reported in phase with tilt [50] consistent with a conical shape. Perceived amplitudes (center-to-peak) were around 0.4 m for OVAR with 30° tilt and 30°/s rotation [48], and around 0.9 m for OVAR with 20° tilt and 45°/s rotation [50]. Eye movement data (Table 1) showed torsional peak amplitude 3° and phase -25° [50, Fig. 4], meaning that leftmost torsional position lagged the rightmost actual roll orientation. Data on horizontal eye movements showed horizontal SPV amplitude 5°/s and phase in the range +60° to +100° as given by the standard error of the mean, averaging around +85° [50, Fig. 4], meaning that peak leftward SPV led the actual backward pitch orientation. For comparison, fast OVAR at 180°/s showed insignificant torsional eye movements and a wider range of phase for horizontal eye movements: Horizontal SPV amplitude was in the range 11°/s to 17°/s and phase was in the range -10° to +50° [50].

2.3. Motions that Match Both Perception and Eye Movements

The first question was whether perceived motions and eye movements are truly mismatched, as suggested by a quick look at the data, for gondola centrifugation and OVAR. Because the same eye movements could be compensatory for many different three-dimensional motions, the goal was to determine whether any of these motions are compatible with the reports of perceived motion. Geometry relates perceived motion to eye movements. If perceived motion and target distance are given by

• (v_x, v_y, v_z) = linear velocity, in m/s,

• (ω_x, ω_y, ω_z) = angular velocity, in rad/s, and

• d = target distance, in m,

using the conventions described in 2.1. Coordinate System above, then compensatory nystagmus,

• (s_x, s_y, s_z) = slow phase velocity vector, in rad/s,

representing the torsional, vertical and horizontal components, respectively, as described in 2.1. Coordinate System, is given by

$$(s_x,s_y,s_z)=(-k_x{\omega }_x,k_y(-{\omega }_y+v_z∕d),k_z(-{\omega }_z-v_y∕d))$$ (Equation 1)

where gains k_x = k_y = k_z = 1 would give perfect compensation. However, healthy eye movements in the dark often have a gain less than one, depending on the conditions [reviewed in 42]. Therefore, a motion was considered to match both perception and eye movements even if the eye-movement gain was less than one, as long as the relative magnitude of eye movements was appropriate for the motions involved. To guarantee that all three-dimensional motions were considered, the investigation proceeded systematically:

First, the most prominent aspects of perceived motion were specified by variables. For example, a reported leftward translation would be entered as v_x in the equations.

Second, eye movement data were used to deduce additional motion parameters. For example, horizontal eye movement value s_z could be used in conjunction with translation v_x in the s_z equation to deduce yaw angular velocity ω_z. The values were understood to be approximate because of the nature of perception and the non-unity gain of eye movements, yet were clear enough to ultimately determine the shape of the three-dimensional motion.

Third, three-dimensional motions were determined from the components, once the components had been constrained as described above by the prominent aspects of perception and data on eye movements. These three-dimensional motions were presented as tentative candidates to demonstrate compatibility between perception and eye movements in three dimensions.

Finally, the deduced three-dimensional motions were compared to any additional features of reported perception, to determine whether the deduced motions could realistically have been the perceived motions. If so, then the result of the investigation was that perceived motion and eye movements may actually be compatible in three dimensions, despite the superficial “one-dimensional” componentwise mismatch. On the other hand, if the additional features of reported perception did not match the deduced three-dimensional motions, then the result of the investigation was that perceived motions really do differ from those predicted by eye movements.

2.4. Differences between Perception and Eye Movements

The second question addressed the ways in which perception agreed with and/or differed from eye movements. One goal was to identify commonalities across different types of three-dimensional motion. Because of the complexity and interactions between components, three-dimensional modeling was used for both perception and eye movements.

Eye movements were modeled in a standard manner, described below. Although numerous eye movement models have been developed to explain subtleties under different conditions for various types of motion, the focus here was to appropriately model the eye movements under investigation with a single model that captured all of the features that were relevant for comparison to perception.

Two versions of the eye-movement model were tested, the Filter Model with simple filtering for linear stimuli, and the GIF-Resolution Model with GIF-resolution (Fig. 2). The underlying model for both was based upon the standard foundation of existing three-dimensional models, with angular velocity and its decay, linear velocity and its decay, and tilt (which is associated with torsion, for example, if the tilt is in roll), as explained in the Introduction. A “MAX”imum operation was included to allow both angular velocity and tilt-from-GIA to cause eye movements, consistent with the eye-movement data. It is worth noting that some three-dimensional eye-movement models have additional special features to capture additional subtleties in eye movement data, but such fine-tuning was not found necessary or appropriate for the general comparison with perception.

For this investigation, the first stage was to use eye movement data for OVAR, because numerical values were available for these data, to tune the models’ parameters of time constants and gain. Then the resulting tuned models were used to simulate eye movements during acceleration and deceleration in a gondola centrifuge. The results were compared with centrifuge eye movement data in order to determine which model best fit the data.

Next, to directly compare three-dimensional perception to eye movements, predicted perceived motion was generated using the best eye-movement model. To generate perceived motion, the model was extended to include the perceptually-relevant output of position and orientation including heading (Fig. 2), and was adjusted to have a greater angular time constant, a standard basic adjustment between eye movements and perception [18, 47]. In addition, the other type of model was run with those same parameters, so that both Filter Model and GIF-Resolution Model versions of predicted perceived motion were produced. Differences between perception and eye movements were then identified by differences between actual subject reports of perceived motion and the output of the models.

The remaining stage of research lay in identifying commonalities across different components and types of motion, based upon the results. Addressed was whether perception consistently agreed with, or differed from, eye movement for each of (a) angular motion, (b) linear motion, and (c) dynamics.

2.5. Hardware and Software

The models were implemented in Matlab (The MathWorks, Natick, Massachusetts) with custom-written scripts on Mac Pro and MacBook Pro computers with Intel processors. Output was generated and analyzed in several ways: numerically, graphically for each component, and with three-dimensional graphics for perception.

3. Results

3.1. Motions that Match Perception and Eye Movements for Gondola Centrifugation

Motions consistent with perceptual reports in a counterclockwise-rotating gondola centrifuge had to have an orientation of slight backward pitch and leftward roll tilt during acceleration, but large forward pitch and/or tumbling with no roll tilt during deceleration. Simultaneously, vertical eye movements associated with the motions had to be relatively symmetric, reaching magnitude approximately 25°/s during both acceleration and deceleration (Table 1).

For the acceleration stage, the key was that angular velocity ω about an Earth-vertical axis (producing yaw ω_z = ω cos 30° cos 10° and pitch ω_y = – ω sin 30° cos 10° when oriented 30° leftward roll and 10° backward pitch, Table 1) had to be combined with linear velocities v_x, v_y and v_z so that s_y = 25°/s and s_z = –15°/s (Table 1) in Equation 1. The exact values of gain and target distance were found to not affect the overall shape of motion, so k_x = k_y = 0.5 and d = 2 m were used to calculate and display the results. The remaining three variables in two equations gave one additional degree of freedom, so interaural motion was assumed to occur only to the small extent that was a side-effect of being in a tilted orientation during forward motion, which was set to 4 m/s, about 1/3 the actual velocity at the end of the acceleration. This gave v_x = 3.9 m/s and constrained the system so that values could be calculated:

• ω = 23°/s, v_y = 0.35 m/s, v_z = 1.3 m/s.

A three-dimensional simulation of the result gave a motion that spirals upward (Fig. 3A). During the actual acceleration the values of the perceptual variables may change over time, but simulations with different values gave a similar shape. Notable was that Earth-upward velocity appeared in all three-dimensional motions that matched data on both perception and eye movements for centrifuge acceleration, a point that is further discussed below.

Figure 3.

Three-dimensional motions that are consistent with data on eye movements, and are also as compatible as possible with published reports of perceived motion. Numerical values of motion parameters are given in the text. (A) Potentially perceived motion during acceleration in a gondola centrifuge, shown with a head at 1 s intervals, at ten times normal size for viewability. The subject spirals counterclockwise, forward and upward, while in an orientation tilted slightly leftward in roll and backward in pitch. (B) Potentially perceived motion during deceleration in a gondola centrifuge. The motion begins upward, transitioning into forward pitch velocity with simultaneous rightward yaw velocity. Shown is the first 6 s of motion; further simulation, which would display a blob of indiscernible heads at the top position, indicates that the yaw velocity later produces a slight wobble in the forward tumble. This version has no sideways slippage, while a version with balanced interaural and yaw motion has slow rightward motion mostly after the tumbling begins (not shown). (C) Potentially perceived motion during OVAR. The motion is circular and tilted outward 15° (seen upon close inspection), i.e. a cone, and with slight oscillations in yaw.

For the deceleration stage, two degrees of freedom were found in Equation 1 after fixing gain k_x = k_y = 0.5 and target distance d = 2 m. One degree of freedom lay in combining pitch velocity ω_y with vertical linear velocity v_z in order for s_y = –25°/s (Table 1), while the other lay in combining yaw velocity ω_z and interaural velocity v_y in order for s_z = 10°/s simultaneous with s_y = –25°/s at around the 15 s mark in Fig. 4C,D. The value of s_z was actually less during much of the deceleration (Fig. 4C), but 10°/s was chosen as the greatest during the broad s_y peak, and therefore the most challenging region to fit. Given these requirements and degrees of freedom, two examples of constraints on the s_z equation were chosen:

1. “No sideways slippage”:

   • ω_z = –20°/s, v_y = 0 m/s.
2. “Balanced interaural linear and yaw angular motion”:

   • ω_z = –10°/s, v_y = –0.35 m/s.

For both examples, the s_y equation was constrained by starting with v_z to match initial downward eye movements (Fig. 4D) and perception of ascent, then phasing in ω_y in order to match increasing upward eye movements over 10 s (Fig. 4D) while phasing out v_z by the time the head reached 90° forward pitch in order to avoid descent, which was not the typically reported direction of motion. Pitch angular and z-directed linear motion were thus given as functions of time t:

• ω_y = 5t °/s for t = 0 to 10 s, then leveling off at 50°/s,

• v_z = 0.35(1 – t/6) m/s, for t = 0 to 6 s, then remaining zero.

Although other combinations were technically possible, this was the simplest combination compatible with the data. Because the s_z eye movement peak was later than the s_y peak (Fig. 4C,D), the values for ω_z and v_y in (1) and (2) above were phased in over 15 s. Other subtleties in the eye movement traces did not affect the overall shape of the resulting motion. Putting together all of these resulting vertical and horizontal variables gave three-dimensional motion (Fig. 3B) generally consistent with the data on both perception and eye movements. The most notable exception in comparison with subject reports was that the pitch orientation did not level out at 90°, but continued to tumble. Further analysis showed that the pitch could be made to level out at 90° by using the vertical degree of freedom in the equations, but the resulting motion fell toward the Earth while moving “backward” toward the feet unrealistically fast.

In conclusion, the resulting three-dimensional motions that are potentially perceived during acceleration and deceleration in a gondola centrifuge show that perception and eye movements are more compatible than originally apparent from the componentwise data.

At the same time, the three-dimensional analysis demonstrated aspects where discrepancies exist between perception and data on eye movements. For acceleration, Earth-vertical motion was necessary (Fig. 3A), but was not listed as being reported by subjects, who instead reported “increasing weight” [19]. For deceleration, the three-dimensional motion (Fig. 3B) could not contain paradoxical tumble while in a fixed pitch forward orientation, as reported by subjects [19].

3.2. Motions that Match Perception and Eye Movements for OVAR

Motions consistent with perceptual reports during 45°/s OVAR at 20° tilt must progress around a cone in phase with or lagging the actual GIA rotation (Table 1). Phase –25° was used here for the construction because it is most consistent with torsional eye movements (Table 1). For concreteness, calculations used tilt amplitude 15° and translation amplitude of 0.9 m (Table 1 and Methods) which corresponds to 0.71 m/s velocity. Therefore,

• v_x = 0.71 sin((π/4)t – 25π/180) and

• v_y = –0.71 cos((π/4)t – 25π/180),

• and tilt angular velocity components

• ω_x = 0.21 cos((π/4)t – 25π/180) and

• ω_y = 0.21 sin((π/4)t – 25π/180).

Next, data on eye movements were used to determine the remaining components. Horizontal eye movements had amplitude 5°/s (0.087 rad/s) and showed a significant phase lead (Table 1), averaging around +85°, so

• s_z = 0.087 cos((π/4)t + 85π/180).

Using gain k_z = 0.5 and trigonometric identities, a preliminary equation was thereby produced from Equation 1 for ω_z, giving a sinusoid. However, this oscillatory yaw affected the implicit assumption that the subject's heading remained constant for the v_x and v_y equations above. Therefore, modified v_x and v_y equations were derived and a least-squares fit was performed, resulting in

• ω_z = 0.22 sin((π/4)t + 45π/180).

This is a periodic z-axis rotation of amplitude 16°. Torsional eye movements have phase –25°, consistent with perception, and amplitude 3° (Table 1) as compared to amplitude 15° of perceived tilt, which implies gain k_x = 0.2 in Equation 1 because gain during sinusoidal motion is the same for velocity as for position. The only remaining component is vertical linear velocity, which in the absence of published reports of consistent perceived vertical motion was set to

• v_z = 0.

The result is a three-dimensional conical motion with sinusoidal z-axis rotation (Fig. 3C). This motion is consistent with both perceived motion around a cone and data on eye movements. The remaining question is whether subjects perceive this oscillatory yaw rotation during motion around the cone. According to published reports, subjects do not typically report this periodic yaw rotation. Instead, subjects typically report a constant heading [9, 48] after perception of unidirectional z-axis rotation decays [48]. However, more complicated perceptions do exist [9], so it is possible that the slight yaw rotation (Fig. 3C) may be perceived by some subjects.

3.3. Differences between Perception and Eye Movements

In the first step toward finding differences between perception and eye movements, both models—the Filter Model and the GIF-Resolution Model (Fig. 2)—were found capable of accurately modeling horizontal and torsional eye movement data for OVAR (Table 1). For 45°/s OVAR, the models produced torsional eye movements of amplitude 3° and phase –25°, along with horizontal eye movements of amplitude 5°/s and phase +80° and +85°, respectively, for the Filter Model and GIF-Resolution Model. The Filter Model used time constants τ_l = 0.25 s, τ_t = 0.6 s, and target distance 7 m. The GIF-Resolution Model used time constants τ_l = 4 s, τ_t = 0.6 s, and target distance 14 m. Both had gain 0.7 for the VOR, with weight w = 0.25 for the change in orientation. In both cases, the value of τ_a made negligible difference, so was set to 6 s, a lower bound for experimentally-determined values [47]. This choice was made because τ_a = 6 s was subsequently found to best fit eye movement data for the centrifuge, where the angular acceleration axis moves significantly out of alignment with a GIA vector that has magnitude substantially greater than 1 g.

The models were then tested for appropriate frequency dependence by performing simulations for 180°/s OVAR. Indeed, for the GIF-Resolution Model the horizontal eye movements’ phase lead decreased to +34°, well within the range –10° to +50° obtained experimentally, and for the Filter Model the phase lead decreased to +52°. Because +52° was at the edge of the range, further testing was performed on the Filter Model, revealing τ_l = 0.5 s as a value that more closely fit the 180°/s data, with +32° phase, while still fitting the 45°/s data, with +70° phase. Ensuing results on the Filter Model were obtained and reported throughout the paper for both values, τ_l = 0.25 s and τ_l = 0.5 s. Amplitude also showed appropriate frequency dependence, but in a manner linear with respect to acceleration rather than velocity, perhaps related to the fact that the otoliths are considered to transduce acceleration rather than velocity. Specifically, a velocity-to-acceleration conversion through multiplication by the ratio of the two frequencies gave 15°/s and 11°/s amplitude horizontal SPV by the Filter Model with τ_l = 0.25 s and τ_l = 0.5 s, respectively, in agreement with the range 11°/s to 17°/s obtained experimentally, and gave 8°/s by the GIF-Resolution Model. In all cases, the amplitude increased with increasing frequency, as seen in the experimental data.

With the above parameters that fit the OVAR data, both models were used to simulate eye movements during acceleration and deceleration of the gondola centrifuge. The results from the Filter Model were consistent with data for both horizontal and vertical eye movements during both acceleration and deceleration (Fig. 4). However, the results from the GIF-Resolution Model were inconsistent with the data (Fig. 4). In summary, the Filter Model was found consistent with eye movement data across both OVAR and gondola centrifugation, while the GIF-Resolution Model was not.

In the second stage of this investigation, the model that was successfully consistent with eye movements was run again to simulate the associated three-dimensional perceived motion. In addition, the GIF-Resolution Model was run with the same “successful” parameters, in order to produce a GIF-resolution version of perception. For the perception runs of the models, the angular time constant was changed from τ_a = 6 s to τ_a = 10 s in order to capture the fact that the perception time constant is 1-2 times that for eye movements [18, 47].

Data on perception (Table 1) were compared with the results (Fig. 5) in order to identify differences between perception and what would be predicted by eye movements, i.e. by the successful eye-movement model extended to perception (Fig. 5). While the Filter Model was the successful model for eye movements, the GIF-Resolution Model was also included in order to test the hypothesis that the difference between perception and eye movements consisted solely of a difference between GIF-resolution and simple filtering. The first observation about the results (Fig. 5) is that the two models make the same predictions for angular components of motion, because their difference is in the treatment of the linear components, with filtering versus GIF-resolution. In general, three aspects of motion were considered: angular, linear and dynamics.

Figure 5.

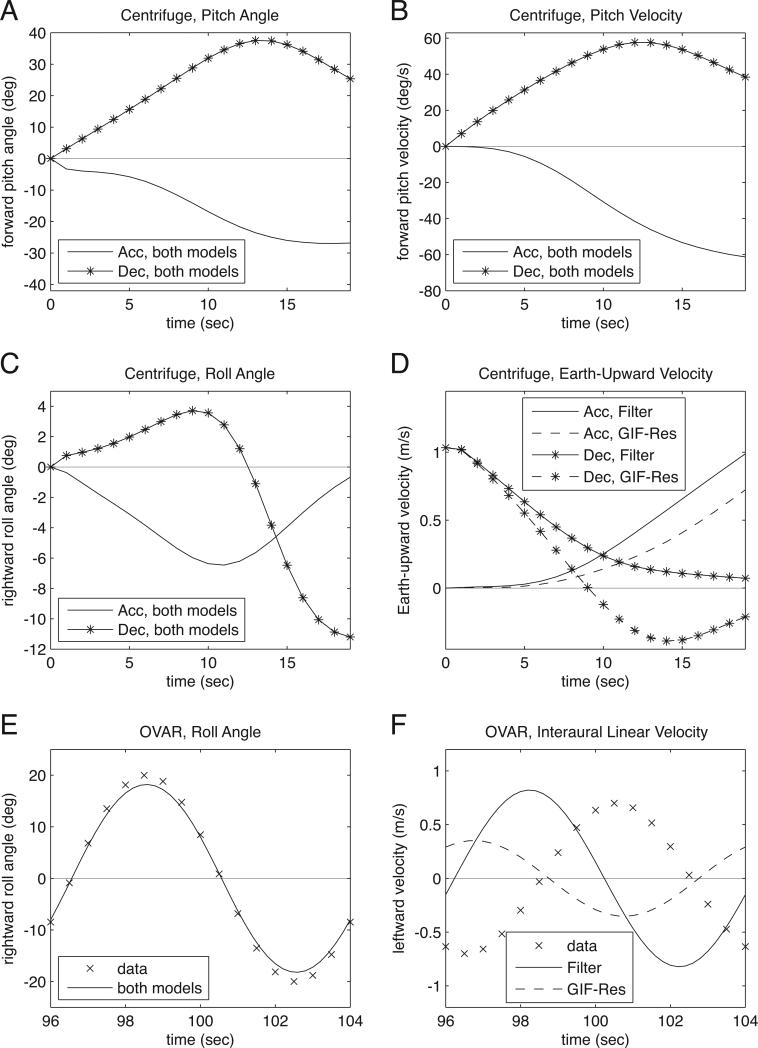
The perceptions that would be associated with recorded eye movements. The Filter Model (“Filter” in the legends) associates perception directly with eye movements, while the GIF-Resolution Model (“GIF-Res” in the legends) gives an alternative, that perception and eye movements differ only in their processing of linear acceleration. Both models give the same results for angular components. Details of the models’ parameter values are given in the text, with the Filter Model using τ_l = 0.25 s for these graphs; τ_l = 0.5 s produced the same results except for translation as described in parts D and F. (A) Centrifuge acceleration (Acc) and deceleration (Dec), pitch angle. (B) Centrifuge acceleration and deceleration, pitch velocity. (C) Centrifuge acceleration and deceleration, roll angle. (D) Centrifuge acceleration and deceleration, velocity Earth-upward. For the Filter Model with τ_l = 0.5 s, the results were essentially identical in shape to these, but with double the amplitude. (E) OVAR, roll angle. The x's show perception data by means of a sinusoid with amplitude 20° and phase –25°, typical values within the range of amplitude and phase given by subject reports of perceived tilt angle (Table 1). (F) OVAR, interaural linear velocity. The x's show perception data by means of a sinusoid with amplitude 0.7 m/s = 0.9(π/4) m/s and phase –25° (Table 1). For the Filter Model with τ_l = 0.5 s, the resulting sine waves were slightly shifted, approximately 0.25 s to the right (phase shift around 10°), and with double the amplitude. For all graphs, the comparison with perception data (Table 1) is discussed in the text.

For angular motion, five types of data were available: the centrifuge data included pitch angle, pitch velocity and roll angle, while the OVAR data included tilt phase and tilt amplitude. For the centrifuge, the asymmetry in perceived pitch angle between acceleration and deceleration (Table 1) was consistent with both models—and therefore with eye movements—because both models predicted greater perceived pitch during deceleration (Fig. 5A). The asymmetry in perceived pitch velocity (Table 1) was consistent with both models, at least for the first half (~10 s) of the motion (Fig. 5B). The asymmetry in perceived roll orientation (Table 1) was consistent with both models, at least for the first half (~10 s) of the motion (Fig. 5C). For OVAR, both the phase and amplitude of perceived roll (Table 1) were consistent with both models (Fig. 5E). In summary, the angular aspects of perception matched eye movements, at least for the first half (~10 s) of the motion. The dynamics are discussed further below.

For linear motion, three types of data were available for testing: The centrifuge data included Earth-up velocity, while the OVAR data included translation phase and amplitude. For the centrifuge, the asymmetry in perceived Earth-upward motion (Table 1) was consistent with both models—and therefore with eye movements—at the beginning (~7 s) of the motion (Fig. 5D). For OVAR, the perceived phase (Table 1) was not consistent with either model (Fig. 5F). Striking is that the two models predicted two different phases, and yet neither matched the data. Both models, except when the Filter Model used τ_l = 0.5 s and produced double the amplitude, predicted amplitude consistent with the data. However, in the context of a mismatched phase, this “success” in amplitude is misleading and does not indicate a real match. In summary, the linear aspects of perception did not consistently match eye movements.

To further test linear motion for gondola centrifugation, x- and y-directed linear velocity were modeled. The Filter Model predicted perception of forward motion during acceleration and backward motion during deceleration, with little sideways motion, as might be expected. However, the GIF-Resolution Model predicted perception of backward motion during acceleration and forward motion during deceleration, arguing against the GIF-Resolution Model for perception.

For dynamics, six types of data were available: The centrifuge data included pitch angle, pitch velocity, roll angle and Earth-up velocity, while the OVAR data included phase of tilt and phase of translation. For the centrifuge, a theme across all four components was that the acceleration-deceleration asymmetries in perception (Table 1) were consistent with both models at the beginning of the motion (Fig. 5A-D). The angular asymmetries were consistent for at least 10 s (Fig. 5A-C), while the linear asymmetry was consistent for less than 10 s (Fig. 5D). For OVAR, the dynamics of perceived tilt (Table 1) matched that of the models (Fig. 5E), but the dynamics of perceived translation (Table 1) did not (Fig. 5F). It is possible that the perceived translation during OVAR began deviating from the model near the start of the motion, as it did in the centrifuge, though data were not available for the beginning of the motion. In summary, perception and eye movements have substantially different dynamics in the long term when tested with the same models, though they are consistent with each other at the beginning of the motion.

Overall, the angular components of perception are generally consistent with eye movements, the linear components are consistent for a shorter amount of time or may not match at all, and the dynamics are different from those of eye movements. In particular, perception is compatible with eye movements at the beginning of motion, but not later in the motion. This difference cannot be explained by basic time constants or standard GIF-resolution.

4. Discussion

Certain three-dimensional motions have been deduced to be simultaneously compatible with both perception and eye movements during gondola centrifugation and OVAR (Fig. 3), but this compatibility does not follow known patterns of response to angular and linear acceleration, as shown by three-dimensional modeling that can resolve the influences of angular and linear motion. When eye movements are shown to a fit classic model, the simultaneous perceived motion is shown to fit that same model—and thus the eye movements—only in certain respects. The most compatible aspects of perception and eye movements were found to be the angular components, such as rotation and tilt, especially at the beginning of the motion. The least compatible aspects were the linear components and the later portion of motion. The differences between perception and eye movements turned out to be more complicated than just a difference between GIF-resolution and linear filtering, which had been a difference identified for sinusoidal roll rotation [34, 35].

That perception deviated fundamentally from eye movements after the first several seconds indicates that more is involved in perception than standard linear-angular interaction and time constants for decay of components. The beginning of the motion may be the key, as it was a crucial factor noted previously for perception, “Principle C4. The initial perceived motion profoundly affects the ensuing perception during complex motion.” [26]. A closer look at the results for gondola centrifugation indicates that long-term perception generally matched the predicted short-term perception, rather than following the curve predicted by standard processing (Table 1, Fig. 5A-D). The question arises why perceived motion would remain similar to that predicted by the initial stimulus, rather than continuously changing with the changing stimulus.

One possible answer lies in the hypothesis that perception tends toward more familiar and/or understandable three-dimensional motions. Further analysis and simulation of the models’ results for gondola centrifugation show that the long-term perceived motions predicted by the changing stimuli become complicated in three dimensions, with Earth-vertical motion accompanied by both roll and pitch velocities. Instead, reported perceived motions during both acceleration and deceleration had a relatively compatible—perhaps more familiar and/or understandable—combination of roll and pitch, and appeared to choose those components that were strongest at the beginning of the motion. For acceleration, nonzero roll and pitch angles were perceived as predicted, but a pitch velocity predicted by the later stimulus did not develop. For deceleration, nonzero pitch angle and velocity were perceived, but a lesser roll tilt predicted by the stimulus did not develop. It is possible that some subjects experienced the additional components, but these components were not reported as significant across subjects.

That perception is influenced by “familiarity of the whole” is a well-known concept in psychology [5], and may also help to explain why perceived linear components of motion do not match eye movements. Further analysis and simulation of both models’ results for gondola centrifugation and OVAR show unusual trajectories in three dimensions when using the linear motion that matches eye movements. The predicted perceived motions for centrifuge acceleration spiral upward and outward, and for deceleration twist around while tumbling. For OVAR, the predicted perceived motions spiral with tilt and translation out of phase; in fact, it has been shown that no combination of parameters of the GIF-Resolution Model will put tilt and translation into phase with each other to produce a cone during OVAR [28]. Nevertheless, actual perception produces a cone, with the more familiar combination of in-phase tilt and translation as occurs during everyday tilts, causing perceived translation to be out of phase with eye movements [50].

It is interesting that perceived linear motion, more than perceived angular motion, differs from that expected from analysis of eye movements. Perhaps perception of linear motion is more malleable toward compatibility, in the sense of everyday experience, with other sensory input. This hypothesis would be consistent with experiments showing that perceived linear motion is greatly influenced by other sensory cues such as noise and vibration [44, 52]. In addition, perceived linear motion has been shown to be reversed by visual scene motion during vertical linear oscillation, with subjects reporting perceived motion matching the phase of the visual scene rather than the phase of the actual linear acceleration [51].

4.1. Relationship to Earlier Work

Perception and eye movements have been compared through modeling for sinusoidal roll tilt and interaural translation [34, 35]. The findings were that eye movement data could be matched by a model with simple filtering but not by a model with GIF-resolution, while the perception data was the opposite, with amplitude of perceived translation matching the GIF-resolution model and not the simple filter model. Those results are compatible with the present results, showing that perception differs from eye movements in a fundamental way. The present work has continued this line of research, showing that as motion gets even more complex, specifically for gondola centrifugation and OVAR, perception deviates even more from eye movements. While eye movements continue to mirror the predictions of simple filtering, as they did for tilt and translation [34, 35], perception no longer mirrors the predictions of GIF-resolution, nor does it follow the predictions of simple filtering. Instead, more global principles about dynamics and about linear versus angular motion may be coming into play, governing the shape of perceived motion as a whole in three dimensions.

For OVAR, this research extends earlier work that had different goals. OVAR has previously been modeled, both for eye movements [3, 11, 20, 21, 29, 33, 40, 43] and for specific components of perception [10, 28, 30, 48]. However, the perceived phase of translation has rarely been modeled accurately [10, 28], and has not previously been modeled in comparison with eye movements. Recent experimental work [50] has made the direct comparison possible.

For gondola centrifuges, as well, perception and eye movements have not previously been compared through modeling. Nevertheless, eye movements have been modeled by an approximation that considered the angular stimulus alone [31], and perception has been simulated to predict roll tilt [13], three-dimensional consequences of the stimulus itself [23], output of the GIF-Resolution Model [25], and has been modeled in diagram form with an explicit filter for tilt [2]. Most relevant to the present work is the finding that, besides being substantially influenced by the start of the motion, perception did not follow the GIF-Resolution Model because of differences in perceived roll tilt during forward-facing versus backward-facing runs [25]. This finding further supports the current hypothesis that perception differs from eye movements by more than GIF-resolution.

4.2. Questions Raised

If perception is performing neither GIF-resolution nor simple filtering during complex motions, then what is it doing? Possible answers for individual motions include phase-linking of translation to tilt during OVAR [28], and modified GIF-resolution during fixed-carriage [27] and tilting-carriage [25] centrifugation, all of which consider the familiarity of motion as a whole in three dimensions. A more universal model will be necessary in order to fully predict spatial disorientation in novel environments. At present, a complete answer to the question about perception would be premature, but the current results provide evidence toward the potential relevance of the initial perception and about differential treatment of linear versus angular components. The obvious question for experimental work is whether these patterns are sustained for other types of complex motion. In other words, for other complex motions, does perception match eye movements at the beginning and then deviate from eye movements? Does the perception of translation differ from eye movements’ predictions more than does the perception of angular motion and tilt? The current results demonstrate the value of future data on these specific questions.

Differences between perception and eye movements are also relevant for understanding neural processing. While perception and eye movements share sensors and primary afferents, much work is still in progress on the neural pathways governing the vestibular control of eye movements versus perception [reviewed in 16]. A driving question is, Which pathways are shared, and where do the pathways diverge? Clues appear in similarities and differences between perception and eye movements, and the results here form one piece of a larger puzzle.

4.3. Conclusion

Complex motion produces perceptions that deviate from eye movements. This idiosyncrasy of perception has not yet been fully characterized, but may be governed by a tendency toward familiar combinations of components, and familiar types of motion as a whole in three dimensions. This whole-motion tendency would mirror the componentwise tendency toward the most common values of individual components—angular velocity tends toward zero, linear velocity tends toward zero, and tilt tends toward alignment with the GIA—as has often been modeled by time constants, error signals, optimal filtering, etc., and more recently through Bayesian priors. Evidence is beginning to point in the direction of a more encompassing principle of whole-motion familiarity, with perception choosing three-dimensional motions that share properties with everyday motions.