Abstract
According to theory, drift load in randomly mating populations is determined by past population size, because enhanced genetic drift in small populations causes accumulation and fixation of recessive deleterious mutations of small effect. In contrast, segregating load due to mutations of low frequency should decline in smaller populations, at least when mutations are highly recessive and strongly deleterious. Strong local selection generally reduces both types of load. We tested these predictions in 13 isolated, outcrossing populations of Arabidopsis lyrata that varied in population size and plant density. Long-term size was estimated by expected heterozygosity at 20 microsatellite loci. Segregating load was assessed by comparing performance of offspring from selfings versus within-population crosses. Drift load was the heterosis effect created by interpopulation outbreeding. Results showed that segregating load was unrelated to long-term size. However, drift load was significantly higher in populations of small effective size and low density. Drift load was mostly expressed late in development, but started as early as germination and accumulated thereafter. The study largely confirms predictions of theory and illustrates that mutation accumulation can be a threat to natural populations.
Keywords: conservation genetics, inbreeding depression, genetic drift, genetic load, mutation accumulation, population size
Introduction
Evolutionary biologists are interested in mutation load—fitness decline due to deleterious mutations—because of its importance in the evolution of sex and outbreeding, and its link with population size dynamics (Maynard Smith, 1989; Byers and Waller, 1999). Mutation load is also relevant in conservation biology (Frankham et al., 2003; Leberg and Firmin, 2008), the genetic preservation of domestic species (Kristensen and Sørensen, 2005) and in human genetics (Crow, 2000; Keightley, 2012). The magnitude of the mutation load that is fixed (or segregating at high frequency in the population) should be linked to long-term population size and changes in size. When a population declines in size, it may initially undergo inbreeding and express segregating recessive deleterious mutations (Frankham, 1995; Keller and Waller, 2002). If small size combined with population isolation persists, a fraction of that segregating load will become fixed due to genetic drift. It will then be expressed throughout the population as drift load (Lynch et al., 1995a), potentially leading to dwindling population size, which feeds back to enhance drift load, causing eventual extinction (Lynch et al., 1995a, 1995b). Theory also states that stronger local selection reduces drift load and segregating load (Glémin, 2003). In this paper, we tested predictions about the effect of demography and competition on segregating and drift load in outcrossing populations of Arabidopsis lyrata.
Deleterious mutations that are dominant rarely persist in populations, so most mutation load is due to recessive alleles. Mutation load can be split into a fraction due to recessive alleles occurring at low frequency and another fraction due to recessive alleles that are fixed, occur at high frequency, or are not entirely recessive. The former load is expressed under inbreeding and called here the segregating load. The latter load is expressed even if individuals are mating randomly; we call it drift load (or fixed load, in cases where the allele frequency is 1). Drift load in an outcrossing population is similar to a commonly used definition of mutation load: the population-mean fitness reduction due to deleterious alleles compared to when such alleles are absent (Crow, 1970; Kirkpatrick and Jarne, 2000). This definition also includes expression of segregating load in an outcrossing population, which will be relatively rare.
The magnitudes of segregating and drift load are predicted to depend on the size of the population and its history of exposure to natural selection. Population size is important because it affects the importance of drift and the likelihood that deleterious alleles appear in the homozygous state. In the following, we review briefly theoretical predictions for segregating and drift load for the case of a stable large population, a population that goes through an intense bottleneck (for example, a reduction to N=5) with rapid recovery of size, and a population that remains small for a long time. Selection is important because it can purge load.
In a large population, rare recessive deleterious mutations can occur at low frequency because they are sheltered in the heterozygous state. This produces segregating load (Kimura, 1980; Assaf and Mobilia, 2011). The sheltering effect disappears when a population declines in size during a severe bottleneck: recessive deleterious alleles occur more often in the homozygous state and segregating load decreases somewhat due to purging (Kirkpatrick and Jarne, 2000). When population size remains small for some time, the segregating load may decrease because of weak purging, confined to alleles that are highly recessive and strongly deleterious (Glémin, 2003), and the fixation of mildly deleterious mutations (Bataillon and Kirkpatrick, 2000).
The other type of load—drift load—is predicted to be very low in large, stable populations (Kimura et al., 1963; Bataillon and Kirkpatrick, 2000; Glémin, 2003). Bottlenecks should lead to an increase in drift load, however, particularly due to highly recessive alleles with strong deleterious effect, because of the stochastic increase in frequency of some such alleles and their resulting homozygous expression (Kirkpatrick and Jarne, 2000). However, drift load due to (sub-)lethals will decline again rapidly after size recovery (Kirkpatrick and Jarne, 2000). Long-term small population size also leads to high drift load, but here it is due to the fixation of both pre-existing and new deleterious alleles of weak negative effect and a wider recessiveness range (Kimura et al., 1963; Lynch et al., 1995a; Bataillon and Kirkpatrick, 2000; Glémin, 2003).
Segregating and drift load are usually not distinguished explicitly in empirical studies. In conservation biology, for example, fitness declines linked to small population size or reduced genetic marker diversity are often attributed to inbreeding depression (Frankham, 1995; Keller and Waller, 2002). Of course, small populations suffer from both kinds of load: they may indeed exhibit inbreeding and express segregating load (which is inbreeding depression, by definition), but they also accumulate mutations under genetic drift because of long-term small size (which is drift load, constitutively expressed). Because segregating and drift load are predicted to react differently to population size dynamics, it is important to use methods that separate the two. So far, few empirical studies on experimental or natural populations have done that (van Treuren et al., 1993; Paland and Schmid, 2003; Willi et al., 2005; Escobar et al., 2008; Coutellec and Caquet, 2011). The two types of load can be distinguished in some study designs. A common approach to assessing segregating load is to compare fitness between inbred and within-population outbred individuals, using pedigree information (Gibbs and Grant, 1989), relatedness based on genetic markers (Willi et al., 2005) or experimental crosses with various degrees of inbreeding (Paland and Schmid, 2003; Willi, 2012). Drift load can be estimated from heterosis in between-population crosses relative to within-population crosses, either by tracking offspring of immigrants or, again, by performing experimental crosses (Ebert et al., 2002; Saccheri and Brakefield, 2002; Willi and Fischer, 2005; Coutellec and Caquet, 2011). These studies assume that heterosis is caused by masking high-frequency, recessive deleterious alleles (Crow, 1987): the drift load.
Variation in natural selection can impact genetic load, although most empirical studies of load assume that replicates have experienced similar selection. As selection becomes stronger, its importance relative to drift increases (Wright, 1931), such that part of the load is effectively purged (Glémin, 2003). Intraspecific competition is an important agent of soft selection in plants (sensu Wallace, 1975). For example, in a field study following cohorts of cassava plants, Pujol and McKey (2006) found that individuals in denser clusters had higher mortality, that the advantage of large size was larger in such clusters, and that the advantage of higher multilocus heterozygosity was also larger. This leads to the expectation that both kinds of genetic load should be lower in populations with high densities of competing individuals.
The goal of our study was to test the following hypotheses: (1) segregating load should be somewhat lower in small than in large populations, (2) drift load should be higher in small than in large populations and (3) both types of load should be reduced under high levels of intraspecific competition. Segregating load was estimated as inbreeding depression under selfing, and drift load as heterosis under between-population outcrossing. We tested these hypotheses on 13 outcrossing populations of the plant A. lyrata ssp. lyrata in the Great Lakes region of North America. Previous molecular investigations and progeny array analysis showed that these populations are predominantly outcrossing (outcrossing rate >0.8) and exhibit little ongoing inter-population gene flow, even over relatively small spatial scales of several kilometers (Willi and Määttänen, 2010). Therefore, they can be treated as distinct replicates in population comparisons. The 13 populations vary in expected heterozygosity (HE) at microsatellite loci (Willi and Määttänen, 2011). Heterozygosity is a valid surrogate of population size in this system because gene flow among populations is low, and HE is known to reflect long-term effective population size under population isolation (Kimura and Crow, 1964; Crow and Kimura, 1970; Ohta and Kimura, 1973). In our system, HE is correlated with current population census size (Willi and Määttänen, 2011). Populations also varied in intraspecific density, which may reflect the importance of intraspecific competition.
Materials and methods
Plant material
In summer 2007, we collected seed material from 13 outcrossing populations of A. lyrata in the Great Lakes region of North America. At each site, tissue and ripe fruits (siliques) were collected from 30 plants at 5-m intervals along three parallel transects separated by 5 m (grid area 10 × 45 m2). If no plant with ripe fruits was within 2.5 m of a grid point, a replacement was found along a 5-m extension of a transect. Transect sampling could not be done in three smaller populations on rocky outcrops, because plants grew in patches. There, we sampled plants such that distances within patches of occurrence were maximized and the combined surface area of the patches sampled was about 450 m2. The outcrossing mode of reproduction was revealed by progeny array analysis (Willi and Määttänen, 2010, 2011). The density of all bolted A. lyrata within a surface area of 0.25 m2 at each of the 30 grid points was taken as a measure of intraspecific competition.
Crossing experiment
One plant per field-collected silique was raised in a greenhouse. Twelve individuals per population were chosen at random as target plants for use in three types of crosses: self-pollination (self), outcrossing with a haphazardly chosen plant from the same population (within-population cross: WPC) and outcrossing with a haphazardly chosen plant from a randomly chosen different population (between-population cross: BPC). We performed hand-pollinations at the bud stage, when self-incompatibility is not yet (fully) expressed and can therefore be overcome. Pollen donors for BPC included plants of four selfing populations and one mixed-mating population, which were grown at the same time in the context of another study, as well as the 13 outcrossing populations. Pollen donors of selfing and mixed-mating populations accounted for 27% of BPC. Immature anthers were first removed, and then anthers with pollen from another flower/plant were rubbed over the stigma. Contamination was avoided by holding the forceps over a flame and dipping them into alcohol after each pollination. We verified the absence of contamination by comparing the multilocus microsatellite genotypes of 100 offspring from 73 selfed and within-population crosses with those of their parents.
Inference about past demography
We used 20 microsatellite loci to estimate long-term population size and evidence for recent bottlenecks. Expected heterozygosity based on allele frequencies (HE) was used as a proxy for long-term population size, given previous evidence that populations were isolated (Kimura and Crow, 1964; Crow and Kimura, 1970; Ohta and Kimura, 1973).
DNA was extracted from field-collected plant tissue. Data from 10 of the loci were previously published in Willi and Määttänen (2010, 2011). The 10 new loci were designed using the A. lyrata genome (Hu et al., 2011) and amplified using the Universal Primer multiplex method of Blacket et al. (2012) (Supplementary Appendix S1). Fragments were sequenced using an ABI 3500 capillary sequencer (Applied Biosystems, Zug, Switzerland) and genotyping was performed in GeneMapper v. 4.0 (Applied Biosystems). We checked loci for overall pairwise linkage with the program GENEPOP v4.0.10 (Raymond and Rousset, 1995) and for null alleles using INEst (Chybicki and Burczyk, 2009). Out of 190 pairwise tests for genotypic linkage disequilibrium across all populations, none was significant at a Bonferroni-adjusted α of 0.0003 (Markov chain parameters: dememorization: 10 000; batches: 100; iterations per batch: 5000). From a total of 226 polymorphic population-locus combinations, null allele frequency was significantly different from 0 in 30 cases. When these population-locus combinations were excluded, the assumption of HWE (Hardy–Weinberg equilibrium) was upheld in all populations except one (Helderberg, NY, P=0.0017) (using GENEPOP v4.0.10; Bonferroni-adjusted α=0.05/13=0.0038). We suspect that Helderberg deviated from HWE due to null alleles at a frequency too low to be detected by the INEst analysis. Expected heterozygosity adjusted for sample size was calculated according to Nei (1978), and values were jackknifed over loci (Miller, 1968); for population-locus combinations with significant null allele frequency, we adjusted allele frequencies under the assumption that all allelic dropout arose from a single null. A comparison between HE and expected heterozygosity based on allele numbers was used to detect evidence for recent bottlenecks (Bottleneck v1.2.02; Cornuet and Luikart, 1996). We excluded loci that had significant null allele frequency or that were monomorphic (or with a second allele only occurring once) and assumed a two-phase mutation model with 70% stepwise mutations and a variance of 30 (10 000 iterations).
Common-garden experiment
Performance of offspring from the three kinds of crosses was assessed over 4 years in an outdoor-garden experiment. When siliques were mature, we haphazardly chose three seeds from each seed family for measurement of seed length under a dissecting scope, and then transferred the seeds to a dark room at 3 °C for 7 days. Four seeds per cross were germinated in each of two tubs (7 × 7 × 8 cm3 filled with 1:1 volume of peat and sand), split into two blocks in separate air-conditioned greenhouse cabinets (16:8 light:dark at 100 μE m−2s−1; temperature 18 °C:16 °C; RH >50%). We recorded whether each seed germinated.
On 27–29 April 2009, 3 weeks after sowing, we removed all except one randomly chosen seedling per tub and transferred the tubs to a garden. Seedlings that germinated later were also removed unless there was no earlier seedling. The two tubs per cross were distributed over two garden beds, with positions within beds assigned at random. During the first summer, the beds were covered with 50% shade cloth, watered daily, and provided with slug repellent and occasional insecticides. In July, some plants were infected by the white rust pathogen, Albugo candida, and thereafter excluded from analyses of later life stages, except for multiplicative performance II (defined below).
Male and female contributions to fitness were estimated for every plant. We scored the onset of flowering during the first and second reproductive seasons (unit: days since germination/start of the year). Male reproductive output was estimated from pollen counts conducted on two of the earliest, freshly opened flowers in the first year (2009). The inner part of the flower was freed from sepals and petals and dried at 60 °C for 40 h. The flower was then combined with 12 ml of an isotonic solution and shaken in an ultrasound bath for 3 min. Pollen grains were counted with a CASY TTC Cell Counter (Schärfe System GmbH, Reutlingen, Germany), set to record three serial aliquots of 400 μl. We considered particles within the size range of 14–27 μm to be pollen. We recorded total flower production (based on the number of flower pedicels) and total fruit production at the end of the reproductive seasons of 2009, 2010, 2011 and 2012.
Analysis
The main dependent variable was multiplicative performance, calculated for each plant as the proportion of seeds germinating in its tub times the sum of flowers (multiplicative performance I) or fruits (multiplicative performance II; including plants that were diseased in 2009) produced in all 4 years. Thus, multiplicative performance integrated the respective measure of fecundity with survival throughout the study.
Multiplicative performance and its individual components were first analyzed with hierarchical mixed models using restricted maximum likelihood, with tub (for germination) or plant nested within cross identity, maternal plant and maternal population at the first level, then cross identity nested within maternal plant and population at the second level, maternal plant nested within population at the third level and population at the fourth level (MIXED procedure in SAS; Singer, 1998; SAS Institute, 2002). For germination, pollen number and pollen size, the replicate within tub represented a further level in the random part of the model. Germination, pathogen infection, and 2009 flower and fruit production were binary dependent variables, and cumulative flower and fruit number and multiplicative performance were analyzed assuming a Poisson distribution (GLIMMIX procedure in SAS). Seed size, fruit production and multiplicative performance II were ln-transformed. Cross type was a fixed effect on the level of the cross identity. The random interaction involving cross type was included at levels higher than cross identity, and we assumed a ‘banded main diagonal' variance–covariance matrix (SAS Institute, 2002). Block, where applicable, was a fixed effect.
Next, segregating load was estimated for each population by (WWP−Wself)/WWP, where WWP is the mean performance of within-population crosses, and Wself is the mean performance of selfed crosses. Drift load was calculated as the extent to which heterosis led to an increase in performance due to between-population outcrossing (WBP), (WBP−WWP)/WWP. For pathogen infection and timing of flowering, higher values correspond to weaker performance, so infection was given the value of 0 for lack of resistance, and timing of flowering was expressed as the number of days to the population-cross type combination that flowered last. Loads for multiplicative performance II and cumulative fruit production were based on ln-transformed data. Estimates of population-level segregating load and heterosis were tested in a general linear model with expected heterozygosity and ln-transformed A. lyrata plant density in the field as continuous variables, both centered. Estimates of load from cross type means calculated at the level of the population were compared with those at the level of the maternal plant (results can deviate; Johnston and Schoen, 1994). The load of a maternal plant was set to 0 when both cross type means used in the calculation were 0 (three and five cases for multiplicative performance I and II, respectively). When the mean of within-population crosses was 0 but the mean of selfed crosses or between-population crosses was higher, then segregating load of a maternal plant was set to −1 and heterosis was set to 1, respectively (11 and 25 cases for multiplicative performance I and II, respectively).
Results
Expected heterozygosity reflecting long-term demography varied among populations from 0.260±0.059 to 0.548±0.056 (jackknifed means and standard errors). No population showed significant evidence of having experienced a recent bottleneck (all P>0.07 under two-tailed testing), and therefore the effect of recent bottlenecks on genetic load was not considered further. Average density of A. lyrata plants growing in the field varied over two orders of magnitude among populations, from 0.4 to 35.5 bolted plants per m2, and was not correlated with expected heterozygosity (N=13, P=0.28, based on log-transformed density). Mixed model analysis of the two multiplicative performance measures revealed significant effects of cross type and population (Table 1). Cross type was significant for the components of fruit production in 2009, pollen number and size, flowering time in 2010 and cumulative production of both flowers and fruit up to the second and fourth year. In each case, performance components improved from selfing to WPC to BPC; pollen size declined in the same order, and pollen number was highest under WPC (Supplementary Appendix S2). Populations differed significantly in seed size, flowering time in both years of assessment, cumulative flower and fruit production up to the second and fourth year, and in pollen number and size. Cross-type-by-population interactions were significant only for flowering time in the second year and flower production up to the second and fourth year. Variation among cross types and populations validated our approach of comparing segregating and drift load based on population-level cross type means.
Table 1. Summary of hierarchical mixed-effects linear models testing for differences in fitness components among cross types (CT), populations and their interaction in Arabidopsis lyrata.
| Dependent variable | N |
Effects |
||
|---|---|---|---|---|
| Cross type | Population | CT × Pop. | ||
| Summary performance measures | ||||
| Multipl. perform. I | 813 | 13.00*** | 7.96** | 2.66 |
| ln Multipl. perform. II | 928 | 17.71*** | 8.15** | 0.83 |
| Life stage components | ||||
| ln Seed size | 1320 | 0.17 | 49.40*** | 5.90 |
| Germination | 3176 | 2.99 | −46.11 | 0.00 |
| Pathogen infection | 918 | 0.71 | −56.98 | 0.00 |
| Flowering time 2009 | 590 | 1.25 | 6.70** | 2.30 |
| Flowers 2009 | 796 | 3.29 | −22.40 | 0.00 |
| Fruits 2009 | 796 | 4.18* | −19.38 | 0.16 |
| Pollen number | 1106 | 3.87* | 10.20** | 1.00 |
| Pollen size | 1106 | 15.24*** | 11.70*** | 3.30 |
| Flowering time 2010 | 689 | 5.22* | 7.40** | 8.40* |
| Flowers up to 2010 | 796 | 8.30** | 4.19* | 9.76* |
| ln Fruits up to 2010 | 796 | 10.36*** | 4.36* | −3.66 |
| Flowers up to 2012 | 796 | 9.21** | 6.48* | 10.08* |
| ln Fruits up to 2012 | 796 | 13.29*** | 7.85** | −0.84 |
F-values for the fixed effect of CT (df=2,24), and likelihood ratio statistics for the random effects of population (df=1) and CT-by-population (df=3). Block was included in the models but not shown here. Other random effects not shown were maternal genotype within population, the maternal genotype-by-cross type interaction, cross identity within maternal genotype and population, and, where applicable, tub/plant within cross identity, maternal genotype and population. Significance is indicated: *P<0.05, **P<0.01, ***P<0.001.
Segregating load in multiplicative performance was on average significantly larger than 0, but was unrelated to expected heterozygosity or A. lyrata density in the field (Table 2). The table also reports the range of loads estimated from the model based on the lowest and highest observed population-level values of HE and A. lyrata density. Life stage components with significant segregating load were flower production in the first year, flower and fruit production up to the second and fourth year, pollen number per flower, and timing of flowering in the second year. Flowering time in the second year showed declining segregating load with increasing expected heterozygosity.
Table 2. Summary of general linear models of the relationships between segregating load and drift load with expected heterozygosity (H E), reflecting long-term population size and (ln-transformed) average density of A. lyrata, reflecting intraspecific competition.
| Dependent variable |
Segregating load (δ) |
Drift load/heterosis (H) |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Intercept |
HE |
Density |
Intercept |
HE |
Density |
|||||||
| Estimate | t | Range | F | Range | F | Estimate | t | Range | F | Range | F | |
| Summary performance measures | ||||||||||||
| Multipl. perform. I | 0.19 | 3.21** | 0.15/0.21 | 0.09 | 0.15/0.22 | 0.11 | 0.49 | 3.20** | 2.01/−0.39 | 20.16** | 1.39/−0.46 | 9.89* |
| ln Multipl. perform. II | 0.18 | 3.83** | 0.13/0.21 | 0.23 | 0.11/0.24 | 0.55 | 0.36 | 1.99(*) | 1.75/−0.44 | 11.89** | 1.21/−0.52 | 6.16* |
| Life stage components | ||||||||||||
| ln Seed size | −0.01 | −0.50 | −0.01/−0.01 | 0.00 | −0.01/−0.01 | 0.00 | 0.01 | 0.61 | 0.05/−0.02 | 2.26 | 0.01/0.00 | 0.02 |
| Germination | 0.01 | 0.68 | 0.03/0.00 | 0.35 | −0.02/0.04 | 0.86 | 0.03 | 2.81* | 0.05/0.02 | 0.50 | 0.08/−0.02 | 6.46* |
| Pathogen resistance | −0.03 | −1.24 | −0.09/0.00 | 1.17 | −0.04/−0.02 | 0.07 | 0.06 | 1.60 | 0.26/−0.06 | 7.04* | 0.17/−0.06 | 3.01 |
| Flowering time 2009 | −0.20 | −1.00 | −0.20/−0.20 | 0.00 | −0.13/−0.27 | 0.03 | 0.02 | 0.12 | 0.34/−0.17 | 1.04 | 0.15/−0.12 | 0.23 |
| Flowers 2009 | 0.14 | 3.41** | 0.27/0.07 | 2.06 | 0.17/0.11 | 0.14 | 0.06 | 0.84 | 0.41/−0.14 | 5.13* | 0.15/−0.04 | 0.49 |
| Fruits 2009 | 0.15 | 1.94(*) | 0.26/0.08 | 0.43 | 0.26/0.03 | 0.60 | 0.16 | 2.34* | 0.40/0.02 | 2.53 | 0.11/0.21 | 0.17 |
| Pollen number | 0.09 | 2.79* | 0.14/0.07 | 0.41 | 0.07/0.12 | 0.15 | −0.06 | −1.76 | −0.01/−0.09 | 0.51 | −0.03/−0.09 | 0.21 |
| Pollen size | −0.01 | −2.14(*) | −0.02/−0.01 | 0.34 | −0.01/−0.01 | 0.08 | −0.01 | −1.79 | −0.01/−0.01 | 0.05 | −0.01/−0.01 | 0.02 |
| Flowering time 2010 | 0.18 | 4.15** | 0.47/0.01 | 9.58* | 0.29/0.05 | 2.24 | 0.71 | 1.50 | 4.40/−1.41 | 12.34** | 2.74/−1.42 | 5.24* |
| Flowers up to 2010 | 0.15 | 2.59* | 0.19/0.13 | 0.07 | 0.20/0.10 | 0.17 | 0.39 | 2.48* | 1.42/−0.21 | 9.10* | 1.00/−0.26 | 4.51(*) |
| ln Fruits up to 2010 | 0.18 | 3.46** | 0.18/0.19 | 0.00 | 0.19/0.17 | 0.01 | 0.23 | 1.95(*) | 0.87/−0.14 | 6.03* | 0.61/−0.17 | 2.96 |
| Flowers up to 2012 | 0.16 | 2.46* | 0.19/0.15 | 0.02 | 0.18/0.14 | 0.03 | 0.42 | 2.99* | 1.66/−0.30 | 16.13** | 1.11/−0.31 | 7.16* |
| ln Fruits up to 2012 | 0.17 | 3.42** | 0.15/0.18 | 0.03 | 0.17/0.17 | 0.00 | 0.23 | 2.09(*) | 0.92/−0.16 | 7.65* | 0.62/−0.17 | 3.40(*) |
Segregating load (δ=inbreeding depression due to one generation of selfing) and heterosis (H) were calculated as described in Materials and methods, and their relation with expected heterozygosity and A. lyrata density in nature was tested with a general linear model on population estimates (N=13). Test statistics are t-value for the intercept and F-value for the two centered covariates. The range of segregating and drift loads corresponds to model-estimated loads based on the largest and smallest observed population-level values of expected heterozygosity and A. lyrata density. Significance is indicated in bold: (*)P<0.1, *P<0.05, **P<0.01, ***P<0.001.
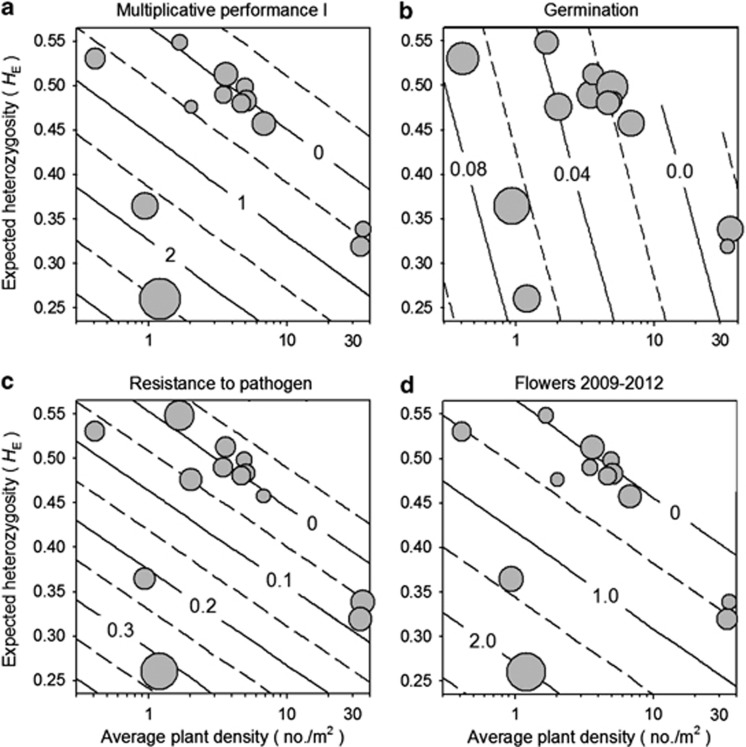
Drift load estimated from heterosis declined with increasing expected heterozygosity and increasing A. lyrata density for both multiplicative performance measures (Table 2; Figure 1a). Only multiplicative performance I had heterosis higher than 0 for the average population (significant intercept). Decreasing heterosis with increasing expected heterozygosity was observed for the following life stages: pathogen resistance in the first year (Figure 1c), flower production in the first year, timing of flowering in the second year, and cumulative flower and fruit production up to the second and fourth year (Figure 1d). Significantly declining heterosis with increasing A. lyrata density occurred for germination (Figure 1b), timing of flowering in the second year, and in flower production up to the fourth year (Figure 1d).
Figure 1.
Relationships between drift load estimated via heterosis in outcrossing populations of A. lyrata and expected heterozygosity, HE, and local A. lyrata density. Drift load was revealed by experimental crosses and assessment of multiplicative performance I over 4 years (a), germination (b), pathogen resistance (c) and flower production during all 4 years (d). Contour plots illustrate the models fitted in Table 2; the contour interval is the model-estimated value of drift load, as defined in Materials and methods. Symbols represent populations, with the diameter of the bubble proportional to ln(drift load+constant).
When segregating load and heterosis were calculated on the level of the maternal genotype and averaged across populations, the pattern was similar to that based on population means. Segregating load was significantly greater than zero (multiplicative performance I estimate±s.e.: 0.19±0.08; multiplicative performance II: 0.19±0.05) but was not related to expected heterozygosity or A. lyrata density for either performance measure (all P>0.5). Heterosis in multiplicative performance I decreased with increasing expected heterozygosity (F=6.70, P=0.027; predicted range: 0.98/0.00), but not with increasing density (P=0.16). Heterosis in multiplicative performance II decreased with increasing expected heterozygosity (F=15.82, P=0.003; 0.59/−0.08) and with increasing density (F=8.35, P=0.016; 0.42/−0.11). For both performance measures, the intercept of the model differed from zero (multiplicative performance I estimate±s.e.: 0.36±0.11; multiplicative performance II: 0.16±0.05), indicating that the average population suffered from drift load.
Discussion
Our key finding is that drift load was present at heightened levels in populations of small size (that is, low HE) and with low levels of intraspecific competition, whereas segregating load was not associated with either population size or local plant density. It is not clear whether this implies a demographic meltdown (sensu Lynch et al., 1995a) in small, sparse populations. However, if the reduction in performance due to drift load decreases population growth rate, then this would only reinforce the small population size and low local densities that exacerbated drift load in the first place. Given that the 13 populations assessed here were selected without prior knowledge of long-term population size or intraspecific competition, we suggest that many A. lyrata ssp. lyrata populations in nature harbor substantial genetic loads.
The average segregating load of around 0.2 was low relative to values observed in other outcrossing plant populations (⩾0.5; Winn et al., 2011). Our study populations, or the ancestral populations that gave rise to them, may have purged part of the segregating load at the end of the last glacial maximum as they underwent multiple founder events during range expansion. It could also be argued that segregating load was low because of benign conditions in the experimental common-garden environment (Armbruster and Reed, 2005). But stressful conditions seem to increase load only moderately, and interspecific competition—a potential source of stress in nature for this species—does not generally interact with segregating load to enhance it (Willi et al., 2007a). Also, the high levels of drift load present in some populations indicate that common-garden conditions were not so benign as to prevent the expression of load.
Our results are in line with theoretical predictions that segregating load should not strongly decrease in populations of long-term small size (Glémin, 2003). Other empirical studies confirm this. Comparisons of naturally large and small populations of plants and snails find that segregating load can be substantial, but is unrelated to population size (van Treuren et al., 1993; Willi et al., 2005; Escobar et al., 2008). One study of a self-compatible gentian reported reduced segregating load in smaller populations (Paland and Schmid, 2003), possibly because these populations have declined only in the last 50 years and purging via non-random mating may have occurred.
Drift load in A. lyrata was substantial, particularly in long-term small populations and those with low plant density. Our estimates may even be low if heterosis was reduced by a certain level of outbreeding depression (Lynch, 1991). Other studies that compare a reasonable number of replicate populations (>5) also report that drift load is high and sometimes related to population size. The plant and snail studies mentioned earlier found that drift load was significantly greater in small populations in some cases (Willi and Fischer, 2005; Willi et al., 2007b; Escobar et al., 2008) but not others (van Treuren et al., 1993). The experimental study of snails revealed significant heterosis for the smallest bottleneck size class compared with any of the three larger classes (Coutellec and Caquet, 2011). Here again, Paland and Schmid's (2003) gentian study was an exception, with generally low drift load uncorrelated with population size. On balance, drift load seems to be important in populations that are small or have gone through a recent bottleneck, but further studies that include an adequate number of replicate populations would be valuable.
Drift load declined with increasing intraspecific density. When plants from low-density populations were out-crossed, their seeds were more likely to germinate than those from within-population crosses (Figure 1b). This suggests that there was drift load for germination. In later life stages, drift load declined with density for flowering time in the second year and for cumulative flower production up to the fourth year of plants that had successfully germinated and established in the first year without being diseased (Figure 1d). These results confirm those of Pujol and McKey (2006), who observed that individuals with higher multilocus heterozygosity were favored in denser plant clusters, because purging of deleterious mutations appears to be more likely under conditions of high intraspecific competition.
Both types of genetic load were generally expressed late in life. Segregating load was absent for seed size, germination, seedling establishment and early pathogen infection, but it strengthened after the onset of reproduction for both male and female performance components. Drift load affected earlier life history components as well as reproductive output. There was significant drift load in germination, and drift load for pathogen resistance was negatively correlated with long-term population size (Figure 1c). Load expression patterns found here agree with those observed in selfing species, for which there is very low segregating load for seed production, germination, and survival to reproduction, but substantial load in growth and reproduction (Husband and Schemske, 1996). Husband and Schemske concluded that most early-acting load must be due to recessive lethals and is purged through inbreeding, whereas much of the late-acting load is due to weakly deleterious mutations and is difficult to purge. If early-acting recessive lethals in our outcrossing A. lyrata were purged during postglacial recolonization, then population sizes must have remained low since then to prevent the recovery of segregating load (Kirkpatrick and Jarne, 2000). In contrast, purging of late-acting and presumably weakly deleterious mutations in our system seems hampered by long-term small size and low competition. This has led to relatively high drift load in small, sparse populations.
Why is it important to distinguish segregating load and drift load? One reason is that the two kinds of load have different influences on important evolutionary transitions. For example, the evolution of selfing from outcrossing is expected only if segregating load is smaller than a certain threshold value (Lande and Schemske, 1985); the level of drift load is not directly relevant to this transition. Similarly, the evolution of asexuality from sexuality (and the long-term persistence of asexuality) is more likely under low segregating and particularly under low drift load, because the load in asexual lines can only increase (Muller, 1964; reviewed in Hartfield and Keightley, 2012). The two types of load also have different implications in applied fields such as conservation biology. Fitness decline caused by load that is fixed within relatively isolated populations is unlikely to be reversed without migration, whether natural or assisted. While segregating load remains mostly unaffected by long-term small population size, fixed drift load requires tens to hundreds of generations of large size to be overcome without genetic restoration. For example, Caenorhabditis elegans kept for 240 generations as single-individual bottlenecked lines accumulated substantial drift load, and required up to 80 generations of culture at large population size under highly competitive conditions to experience fitness recovery (Estes and Lynch, 2003). In natural systems with lower levels of competition, recovery may take a few hundred generations.
Our results highlight an important point about neutral evolution and mutation accumulation that contradicts general wisdom in evolutionary biology and conservation. Many specialist species are poor dispersers and occur in habitats with patchy distribution. Small populations of such species undergo neutral evolution that is not actually neutral with respect to fitness, because mutation accumulation lowers mean fitness. Conservation biologists believe that mutation accumulation in small and isolated populations is a less important threat than inbreeding depression and the loss of genetic diversity (Frankham, 2005). The reasoning is that inbreeding depression acts immediately, and a loss of genetic variation is important whenever the environment changes, whereas it takes many generations for mutation accumulation and fixation to appreciably lower mean fitness. This makes good sense for species of conservation concern that have declined in population size recently; not enough generations have passed for drift load to accumulate. However, many species have persisted in small and isolated populations for a long time, and under these conditions mutation accumulation can take its toll. This is exemplified by some populations of A. lyrata.
More generally, this study questions the adaptationist perception that populations usually exist on or near local fitness optima. A well-known challenge to this perspective comes from studies of the genetic, developmental and selective constraints that bias the production of variation and response to selection in certain traits (Maynard Smith et al., 1985). But high levels of genetic load represent a more general challenge to adaptation because they cause a reduction in population mean fitness that limits adaptation in all traits at once (Lynch and Lande, 1993; Willi et al., 2006; Willi and Hoffmann, 2009). Species that have naturally fragmented distributions, for which drift load is especially important, may be badly positioned for long-term persistence. This is true even under ordinary conditions, but when the environment changes quickly drift load combines with low genetic diversity to sharply limit persistence time of small populations (Hoffmann and Willi, 2008; Willi and Hoffmann, 2009). Although bottlenecks and founder events might occasionally produce adaptive novelty (Carson, 1975; Templeton, 1980; Wright, 1982), the more typical fate of such populations is extinction. Many species exist in populations that are small or that have experienced repeated bottlenecks, and in this case neither genetic innovation nor healthy growth rate for long-term persistence can be expected.
Data archiving
Data deposited in the Dryad repository: doi:10.5061/dryad.q329b.
Acknowledgments
We thank the many people who helped with crossing and assessing plants: Janine Brunner, Robert Duenner, Anna von Ins, Daniela Lang, Marie Vance, Edith Willi, Jasmin Winkler and Claudia Winteler. Markus Willi helped extracting pollen data. Collection permits were granted by the Palisades Interstate Park Commission, the Nature Conservancy of eastern New York, the New York State Office of Parks, the Commonwealth of Pennsylvania, the US National Park Service, the Illinois Department of Natural Resources, the Michigan Department of Natural Resources and John Haataja. We were supported by the Swiss National Science Foundation (31003A-116270, PP00P3-123396/1), the Institute of Evolutionary Biology and Environmental Studies of the University of Zürich, the Botanical Garden of the University of Neuchâtel, and the Fondation Pierre Mercier pour la Science, Lausanne.
The authors declare no conflict of interest.
Footnotes
Supplementary Information accompanies the paper on Heredity website (http://www.nature.com/hdy)
Supplementary Material
References
- Armbruster WS, Reed DH. Inbreeding depression in benign and stressful environments. Heredity. 2005;95:235–242. doi: 10.1038/sj.hdy.6800721. [DOI] [PubMed] [Google Scholar]
- Assaf M, Mobilia M. Fixation of a deleterious allele under mutation pressure and finite selection intensity. J Theor Biol. 2011;275:93–103. doi: 10.1016/j.jtbi.2011.01.025. [DOI] [PubMed] [Google Scholar]
- Bataillon T, Kirkpatrick M. Inbreeding depression due to mildly deleterious mutations in finite populations: size does matter. Genet Res. 2000;75:75–81. doi: 10.1017/s0016672399004048. [DOI] [PubMed] [Google Scholar]
- Blacket MJ, Robin C, Good RT, Lee SF, Miller AD. Universal primers for fluorescent labelling of PCR fragments-an efficient and cost-effective approach to genotyping by fluorescence. Mol Ecol Res. 2012;12:456–463. doi: 10.1111/j.1755-0998.2011.03104.x. [DOI] [PubMed] [Google Scholar]
- Byers DL, Waller DM. Do plant populations purge their genetic load? Effects of population size and mating history on inbreeding depression. Ann Rev Ecol Syst. 1999;30:479–513. [Google Scholar]
- Carson HL. The genetics of speciation at the diploid level. Am Nat. 1975;109:83–92. [Google Scholar]
- Chybicki IJ, Burczyk J. Simultaneous estimation of null alleles and inbreeding coefficients. J Hered. 2009;100:106–113. doi: 10.1093/jhered/esn088. [DOI] [PubMed] [Google Scholar]
- Cornuet JM, Luikart G. Description and power analysis of two tests for detecting recent population bottlenecks from allele frequency data. Genetics. 1996;144:2001–2014. doi: 10.1093/genetics/144.4.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coutellec MA, Caquet T. Heterosis and inbreeding depression in bottlenecked populations: a test in the hermaphroditic freshwater snail Lymnaea stagnalis. J Evol Biol. 2011;24:2248–2257. doi: 10.1111/j.1420-9101.2011.02355.x. [DOI] [PubMed] [Google Scholar]
- Crow JF.1970Genetic loads and the cost of natural selectionIn: Kojima K, (ed.).Mathematical Topics in Population Genetics Springer: Berlin; 128–177. [Google Scholar]
- Crow JF. Muller, Dobzhansky, and overdominance. J Hist Biol. 1987;20:351–380. [Google Scholar]
- Crow JF. The origins, patterns and implications of human spontaneous mutation. Nat Rev Genet. 2000;1:40–47. doi: 10.1038/35049558. [DOI] [PubMed] [Google Scholar]
- Crow JF, Kimura M. An Introduction to Population Genetics Theory. Burgess: Minneapolis, MN, USA; 1970. [Google Scholar]
- Ebert D, Haag C, Kirkpatrick M, Riek M, Hottinger JW, Pajunan VI, et al. A selective advantage to immigrant genes in a Daphnia metapopulation. Science. 2002;295:485–488. doi: 10.1126/science.1067485. [DOI] [PubMed] [Google Scholar]
- Escobar JS, Nicot A, David P. The different sources of variation in inbreeding depression, heterosis and outbreeding depression in a metapopulation of Physa acuta. Genetics. 2008;180:1593–1608. doi: 10.1534/genetics.108.092718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Estes S, Lynch M. Rapid fitness recovery in mutationally degraded lines of Caenorhabditis elegans. Evolution. 2003;57:1022–1030. doi: 10.1111/j.0014-3820.2003.tb00313.x. [DOI] [PubMed] [Google Scholar]
- Frankham R. Conservation genetics. Ann Rev Genet. 1995;29:305–327. doi: 10.1146/annurev.ge.29.120195.001513. [DOI] [PubMed] [Google Scholar]
- Frankham R. Genetics and extinction. Biol Conserv. 2005;126:131–140. [Google Scholar]
- Frankham R, Ballou JD, Briscoe DA. Introduction to Conservation Genetics. Cambridge University Press: Cambridge, UK; 2003. [Google Scholar]
- Gibbs HL, Grant PR. Inbreeding in Darwin's Medium Ground Finches (Geospiza fortis) Evolution. 1989;43:1273–1284. doi: 10.1111/j.1558-5646.1989.tb02574.x. [DOI] [PubMed] [Google Scholar]
- Glémin S. How are deleterious mutations purged? Drift versus nonrandom mating. Evolution. 2003;57:2678–2687. doi: 10.1111/j.0014-3820.2003.tb01512.x. [DOI] [PubMed] [Google Scholar]
- Hartfield M, Keightley PD. Current hypotheses for the evolution of sex and recombination. Integ Zool. 2012;7:192–209. doi: 10.1111/j.1749-4877.2012.00284.x. [DOI] [PubMed] [Google Scholar]
- Hoffmann AA, Willi Y. Detecting genetic responses to environmental change. Nat Rev Genet. 2008;9:421–432. doi: 10.1038/nrg2339. [DOI] [PubMed] [Google Scholar]
- Hu TT, Pattyn P, Bakker EG, Cao J, Cheng JF, Clark RM, et al. The Arabidopsis lyrata genome sequence and the basis of rapid genome size change. Nat Genet. 2011;43:476–481. doi: 10.1038/ng.807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Husband BC, Schemske DW. Evolution of the magnitude and timing of inbreeding depression in plants. Evolution. 1996;50:54–70. doi: 10.1111/j.1558-5646.1996.tb04472.x. [DOI] [PubMed] [Google Scholar]
- Johnston MO, Schoen DJ. On the measurement of inbreeding depression. Evolution. 1994;48:1735–1741. doi: 10.1111/j.1558-5646.1994.tb02209.x. [DOI] [PubMed] [Google Scholar]
- Keightley PD. Rates and fitness consequences of new mutations in humans. Genetics. 2012;190:295–304. doi: 10.1534/genetics.111.134668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller LF, Waller DM. Inbreeding effects in wild populations. Trends Ecol Evol. 2002;17:230–241. [Google Scholar]
- Kimura M. Average time until fixation of a mutant allele in a finite population under continued mutation pressure: studies by analytical, numberical, and pseudo-sampling methods. Proc Natl Acad Sci USA. 1980;77:522–526. doi: 10.1073/pnas.77.1.522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M, Crow JF. The number of alleles that can be maintained in a finite population. Genetics. 1964;49:725–738. doi: 10.1093/genetics/49.4.725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M, Maruyama T, Crow JF. Mutation load in small populations. Genetics. 1963;48:1303–1312. doi: 10.1093/genetics/48.10.1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick M, Jarne P. The effects of a bottleneck on inbreeding depression and the genetic load. Am Nat. 2000;155:154–167. doi: 10.1086/303312. [DOI] [PubMed] [Google Scholar]
- Kristensen TN, Sørensen AC. Inbreeding—lessons from animal breeding, evolutionary biology and conservation genetics. Anim Sci. 2005;80:121–133. [Google Scholar]
- Lande R, Schemske DW. The evolution of self-fertilization and inbreeding depression in plants. I. Genetic models. Evolution. 1985;39:24–40. doi: 10.1111/j.1558-5646.1985.tb04077.x. [DOI] [PubMed] [Google Scholar]
- Leberg PL, Firmin BD. Role of inbreeding depression and purging in captive breeding and restoration programmes. Mol Ecol. 2008;17:334–343. doi: 10.1111/j.1365-294X.2007.03433.x. [DOI] [PubMed] [Google Scholar]
- Lynch M. The genetic interpretation of inbreeding depression and outbreeding depression. Evolution. 1991;45:622–629. doi: 10.1111/j.1558-5646.1991.tb04333.x. [DOI] [PubMed] [Google Scholar]
- Lynch M, Conery J, Bürger R. Mutation accumulation and the extinction of small populations. Am Nat. 1995a;146:489–518. [Google Scholar]
- Lynch M, Conery J, Bürger R. Mutational meltdowns in sexual populations. Evolution. 1995b;49:1067–1080. doi: 10.1111/j.1558-5646.1995.tb04434.x. [DOI] [PubMed] [Google Scholar]
- Lynch M, Lande R.1993Evolution and extinction in response to environmental changeIn: Kareiva PM, Kingsolver JG, Huey RB, edsBiotic Interactions and Global Change Sinauer Associates: Sunderland, MA; 234–250. [Google Scholar]
- Maynard Smith J, Burian R, Kauffman S, Alberch P, Campbell J, Goodwin B, et al. Development constraints and evolution. Quart Rev Biol. 1985;60:265–287. [Google Scholar]
- Maynard Smith J. Evolutionary Genetics. Oxford University Press: New York, NY; 1989. [Google Scholar]
- Miller RG. Jackknifing variances. Ann Math Stat. 1968;39:567–582. [Google Scholar]
- Muller HJ. The relation of recombination to mutational advance. Mutat Res. 1964;1:2–9. doi: 10.1016/0027-5107(64)90047-8. [DOI] [PubMed] [Google Scholar]
- Nei M. Estimation of average heterozygosity and genetic distance from a small number of individuals. Genetics. 1978;89:583–590. doi: 10.1093/genetics/89.3.583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohta T, Kimura M. A model of mutation appropriate to estimate the number of electrophoretically detectable alleles in a finite population. Genet Res. 1973;22:201–204. doi: 10.1017/s0016672300012994. [DOI] [PubMed] [Google Scholar]
- Paland S, Schmid B. Population size and the nature of genetic load in Gentianella germanica. Evolution. 2003;57:2242–2251. doi: 10.1111/j.0014-3820.2003.tb00236.x. [DOI] [PubMed] [Google Scholar]
- Pujol B, McKey D. Size asymmetry in intraspecific competition and the density-dependence of inbreeding depression in a natural plant population: a case study in cassava (Manihot esculenta Crantz, Euphorbiaceae) J Evol Biol. 2006;19:85–96. doi: 10.1111/j.1420-9101.2005.00990.x. [DOI] [PubMed] [Google Scholar]
- Raymond M, Rousset F. GENEPOP version 1.2.: population genetics software for exact tests and ecumenicism. J Hered. 1995;86:248–249. [Google Scholar]
- Saccheri IJ, Brakefield PM. Rapid spread of immigrant genomes into inbred populations. Proc Roy Soc Lond Ser B. 2002;269:1073–1078. doi: 10.1098/rspb.2002.1963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SAS Institute SAS OnlineDoc®. SAS Institute: Cary, NC; Version. 2002;9:1. [Google Scholar]
- Singer JD. Using SAS PROC MIXED to fit multilevel models, hierarchical models, and individual growth models. J Edu Behav Stat. 1998;24:323–355. [Google Scholar]
- Templeton AR. The theory of speciation via the founder principle. Genetics. 1980;94:1011–1038. doi: 10.1093/genetics/94.4.1011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Treuren R, Bijlsma R, Ouborg NJ, van Delden W. The significance of genetic erosion in the process of extinction. IV. Inbreeding depression and heterosis effects caused by selfing and outcrossing in Scabiosa columbaria. Evolution. 1993;47:1669–1680. doi: 10.1111/j.1558-5646.1993.tb01259.x. [DOI] [PubMed] [Google Scholar]
- Wallace B. Hard and soft selection revisited. Evolution. 1975;29:465–473. doi: 10.1111/j.1558-5646.1975.tb00836.x. [DOI] [PubMed] [Google Scholar]
- Willi Y.2012Mutational meltdown in selfing Arabidopsis lyrata Evolutionin press. [DOI] [PubMed]
- Willi Y, Dietrich S, van Kleunen M, Fischer M. Inter-specific competitive stress does not affect the magnitude of inbreeding depression. Evol Ecol Res. 2007a;9:959–974. [Google Scholar]
- Willi Y, Fischer M. Genetic rescue in interconnected populations of small and large size of the self-incompatible Ranunculus reptans. Heredity. 2005;95:437–443. doi: 10.1038/sj.hdy.6800732. [DOI] [PubMed] [Google Scholar]
- Willi Y, Hoffmann AA. Demographic factors and genetic variation influence population persistence under environmental change. J Evol Biol. 2009;22:124–133. doi: 10.1111/j.1420-9101.2008.01631.x. [DOI] [PubMed] [Google Scholar]
- Willi Y, Määttänen K. Evolutionary dynamics of mating system shifts in Arabidopsis lyrata. J Evol Biol. 2010;23:2123–2131. doi: 10.1111/j.1420-9101.2010.02073.x. [DOI] [PubMed] [Google Scholar]
- Willi Y, Määttänen K. The relative importance of factors determining genetic drift: mating system, spatial genetic structure, habitat and census size in Arabidopsis lyrata. New Phyt. 2011;189:1200–1209. doi: 10.1111/j.1469-8137.2010.03569.x. [DOI] [PubMed] [Google Scholar]
- Willi Y, Van Buskirk J, Fischer M. A threefold genetic Allee effect: population size affects cross-compatibility, inbreeding depression and drift load in the self-incompatible Ranunculus reptans. Genetics. 2005;169:2255–2265. doi: 10.1534/genetics.104.034553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willi Y, Van Buskirk J, Hoffmann AA. Limits to the adaptive potential of small populations. Ann Rev Ecol Evol Syst. 2006;37:433–458. [Google Scholar]
- Willi Y, van Kleunen M, Dietrich S, Fischer M. Genetic rescue persists beyond first-generation outbreeding in small populations of a rare plant. Proc R Soc B. 2007b;274:2357–2364. doi: 10.1098/rspb.2007.0768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winn AA, Elle E, Kalisz S, Cheptou PO, Eckert CG, Goodwillie C, et al. Analysis of inbreeding depression in mixed mating plants provides evidence for selective interference and stable mixed mating. Evolution. 2011;65:3339–3359. doi: 10.1111/j.1558-5646.2011.01462.x. [DOI] [PubMed] [Google Scholar]
- Wright S. Evolution in Mendelian populations. Genetics. 1931;16:97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. The shifting balance theory and macroevolution. Ann Rev Genet. 1982;16:1–19. doi: 10.1146/annurev.ge.16.120182.000245. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.