Parallel multiscale simulations of a brain aneurysm

Abstract

Cardiovascular pathologies, such as a brain aneurysm, are affected by the global blood circulation as well as by the local microrheology. Hence, developing computational models for such cases requires the coupling of disparate spatial and temporal scales often governed by diverse mathematical descriptions, e.g., by partial differential equations (continuum) and ordinary differential equations for discrete particles (atomistic). However, interfacing atomistic-based with continuum-based domain discretizations is a challenging problem that requires both mathematical and computational advances. We present here a hybrid methodology that enabled us to perform the first multi-scale simulations of platelet depositions on the wall of a brain aneurysm. The large scale flow features in the intracranial network are accurately resolved by using the high-order spectral element Navier-Stokes solver εκ αr. The blood rheology inside the aneurysm is modeled using a coarse-grained stochastic molecular dynamics approach (the dissipative particle dynamics method) implemented in the parallel code LAMMPS. The continuum and atomistic domains overlap with interface conditions provided by effective forces computed adaptively to ensure continuity of states across the interface boundary. A two-way interaction is allowed with the time-evolving boundary of the (deposited) platelet clusters tracked by an immersed boundary method. The corresponding heterogeneous solvers ( εκ αr and LAMMPS) are linked together by a computational multilevel message passing interface that facilitates modularity and high parallel efficiency. Results of multiscale simulations of clot formation inside the aneurysm in a patient-specific arterial tree are presented. We also discuss the computational challenges involved and present scalability results of our coupled solver on up to 300K computer processors. Validation of such coupled atomistic-continuum models is a main open issue that has to be addressed in future work.

1. Introduction

Cerebral aneurysms occur in up to 5% of the general population, with a relatively high potential for rupture leading to strokes in about 30,000 Americans each year [1]. There are no quantitative tools to predict the rupture of aneurysms and no consensus exists among medical doctors when exactly to operate on patients with cerebral aneurysms.

The biological processes preceding the aneurysm rupture are not well understood. There are several theories relating the wall shear stress patterns and pressure distribution within aneurysm and pathological changes at cellular level occurring at the arterial wall layers. Realistic simulation of such processes must be based on resolving concurrently the macro- (centimeter) as well as the micro- (sub-micron) scale flow features, and also the interaction of blood cells with the endothelial cells forming the inner layer of the arterial wall. Such complex processes are clearly multiscale in nature necessitating the use of different mathematical models to resolve each scale.

In the current work, we consider the initial formation of a platelet clot in brain aneurysm as a representative example. Clots form not only in brain aneurysms but also in aortic aneuryms [2], coronary arteries [3], veins [4], etc. The main focus of this paper is the general framework we propose for multi-scale modeling of arterial blood flow, including modeling of the initial thrombus formation. This multiscale methodology is developed based on atomistic and continuum descriptions, and can be used to simulate, for instance, clot formation and growth in aortic aneurysms or in carotid arteries. Some algorithmic and computational aspects of the coupled atomistic-continuum model can also be used in other research areas, e.g. in materials modeling and solid mechanics. In the following we review (a) physiological aspects related to cerebral aneurysms, and (b) recent advances and open issues in multiscale modeling.

1.1. Cerebral aneurysm: overview

Cerebral aneurysms are pathological, blood-filled permanent dilations of intracranial blood vessels usually located near bifurcations in the Circle of Willis (CoW) [5, 6, 7, 8], see figure 1. Currently, prospective rupture rates are culled from various studies, but these rates do not take into account patient-specific anatomic and physiologic factors which may affect rupture risk. These limitations are more magnified when considering one paradox that prevails when analyzing rupture rates from the literature: The prospective rate of rupture of anterior circulation aneurysms less than 7mm in size is extremely low [7], but the majority of ruptured aneurysms in most series are anterior circulation aneurysms less than 7mm in size [10]. Analysis of patient-specific anatomic and physiologic data may be used to identify specific patients who might be at higher risk for rupture.

Figure 1.

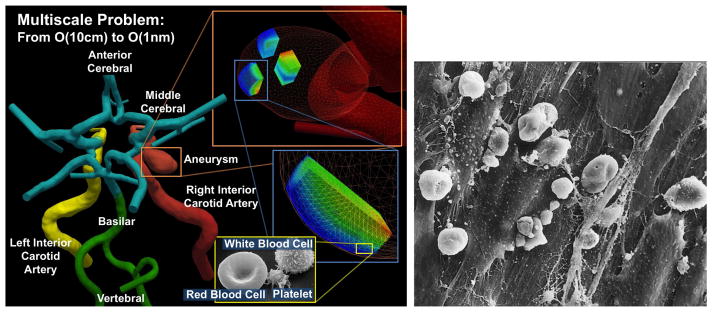
Blood flow in the brain is a multiscale problem. Left: the macrodomain where the large-scale flow dynamics is modeled by the Navier-Stokes equations; different colors correspond to different computational patches (Courtesy of Prof. J.R. Madsen, Harvard Medical School). Shown in the inset are the microdomains where dissipative particle dynamics is applied to model the micro-scale features. Right: Scanning electron microscope image of the inside layer of a ruptured MCA aneurysm showing the disrupted pattern of endothelial cells and blood cells adhered to the inter-endothelial cell gaps [9].

The processes of initiation, growth and rupture of CAs are not well understood, and several – often contrasting - hypotheses on the modified hemodynamics have emerged in recent years, e.g. see the recent reviews in [5, 6, 8, 11] and references therein. While one would expect that aneurysm rupture be associated with high pressure or high wall shear stress (WSS) magnitude, this is not the case with CAs as no elevated peak pressure and typically low WSS values are observed within the aneurysm.

Histological observations have revealed a degeneration of endothelial cells (EC) and degradation of the intracellular matrix of the arterial walls due to decreasing density of smooth muscle cells (SMCs) [12, 13]. WSS is related to the endothelial gene expression, and in laminar flow produces a quiescent phenotype protecting from inflammation or cell apoptosis. However, flow instabilities and oscillatory WSS can trigger certain genetic traits that affect the elastic properties of the arterial wall [14, 15]. For example, recent studies reported that low WSS levels in oscillatory flow can cause irregular EC patterns, potentially switching from an atheroprotective to an atherogenic phenotype [5, 15, 16, 17]. On the other hand, low WSS can also be protective as it leads to thickening of arterial walls, which then becomes more tolerant to mechanical loads. Hence, by simply examining the magnitude of WSS we cannot arrive at a consistent theory of aneurysm growth or rupture. To this end, experimental studies with ECs subjected to impinging flow in [15, 18] have shown the importance of WSS gradients (WSSG) (rather than the magnitude) on the migration of ECs downstream of the stagnation region.

Perhaps the most dramatic evidence on the role of ECs and their interaction with blood cells has been documented in a Japanese clinical study comparing ruptured and unruptured aneurysms [9]. Ruptured aneurysms exhibited significant endothelial damage and inflammatory cell invasion compared with unruptured aneurysms; see figure 1(right) for a typical image. We observe that the EC layer is drastically altered and covered with blood cells and a fibrin network. Similarly, it was reported in [9] that leukocytes (White Cells, WCs) in the wall could be associated with subarachnoid hemorrhage (SAH), and endothelial erosion enhances leukocyte invasion of the wall before rupture.

Damaged EC typically initiates a thrombus (blood clot) formation process. One of the most important building blocks in the clot is a 2 − 3μm in size blood cell called platelet. The role of platelets has not been fully explored in experimental work, but clinical tests have documented the existence of spontaneous thrombosis in giant aneurysms [19, 20, 21] due to platelet deposition. Thrombus formation within the aneurysm is non-uniform due to the complex flow patterns and the interaction of platelets with the damaged EC layer [22]. Similarly, it was found in endovascular studies that creation of spontaneous thrombosis occurs after stent placement [23]. In other studies, enhanced platelet aggregability has been observed in cerebral vasospasm following aneurysmal SAH [24]. B. Furie and B. C. Furie reviewed two independent pathways to thrombus formation [25]. Platelets activation may start due to exposure of blood cells to either subendothelial collagen or thrombin generated by tissue factor derived from the vessel wall. The authors also emphasized that large scale flow features such as shear and turbulence affect the thrombus formation process.

A key question regarding the process of aneurysm progression is how to correlate the blood cell dynamics and interactions to the complex flow patterns observed within the aneurysms [26]. To this end, there are currently two schools of thought: high-flow effects and low-flow effects [5]. The former suggests that localized elevated WSS cause endothelial injury that causes an overexpression of NO production, which in turn can lead to apoptosis of SMCs and subsequent wall weakening. The latter points to the stagnation type flow in the dome of the aneurysm, which also causes irregular production of NO. This dysfunction of flow-induced NO leads to the aggregation of red blood cells and the accumulation and adhesion of platelets and leukocytes along the intimal surface (the first layer of the arterial wall). This, in turn, may damage the intima, allowing for infiltration of white blood cells (WBC) and fibrin [27]. We should also note that the response of damaged aneurysm endothelium to stimuli such as WSS maybe different from the response of healthy endothelial tissue. To this end, to advance our understanding, we need to investigate scenarios beyond the pure mechanical point of view. In particular, we need to understand the role of endothelial cells and their interactions with the blood cells, i.e., platelets, RBCs and WBCs.

1.2. Multi-scale modeling of blood flow

Modeling the blood flow as a multiscale phenomenon, using coupled continuum-atomistic models is essential to better understand the thrombus formation process. Seamless integration of heterogeneous computer codes based on continuum models with codes that implement atomistic-level descriptions is key to the successful realization of parallel multiscale modeling of realistic physical and biological systems.

Multiscale hybrid approaches [28, 29, 30, 31, 32, 33, 34, 35] can potentially provide an elegant solution for non-feasible micro-scale simulations performed in very large computational domains. The main challenge in developing efficient hybrid methods [36] is formulating robust interface conditions coupling multiple descriptions (e.g., continuum, atomistic, mesoscopic) such that the main physical quantities (mass, momentum, and energy) and their fluxes are conserved at the domain interface. In general, most existing hybrid methods can be classified into two main categories of coupling approaches [36]: (i) the state-exchange method [28, 32, 33, 34, 37, 35] and (ii) the flux-exchange method [29, 30, 31] or their combination.

The state-exchange method relies on the state information (e.g., boundary velocity) which is transferred between various descriptions across the interfaces of (in most cases) overlapping domains. In the overlapping region all participating descriptions must be valid and the constrained dynamics is often imposed via a dynamic relaxation technique [34]. The state-exchange method is closely related to the alternating Schwarz method [38], where the integration in continuum and atomistic domains is performed in a sequential or simultaneous fashion with a consecutive coupling strategy between different domains. The main drawback of the state-exchange method is that the information propagation (e.g., flow development) through the interface may be unphysical, resulting in a slow convergence to steady-state for steady-flow problems or in significant restrictions of the method’s applicability to fast unsteady flows. In general, the state-exchange method can properly handle unsteady flows which can be considered as quasi-steady.

The flux-exchange method is based on the exchange of relevant fluxes (e.g., mass flux, momentum flux) between different descriptions. Even though the flux-exchange method naturally follows the conservation laws, it does not guarantee the continuity of state variables, which may require an additional treatment [39]. Moreover, the flux-exchange method appears to be more restrictive with respect to an efficient time decoupling [36] than the state-exchange method, which is absolutely necessary for a large disparity of timescales in atomistic and continuum representations. The choice of a particular hybrid method or of their combination is dictated by the flow problem, i.e., considering the main flow characteristics, the disparity of length and time scales, and the efficiency of the chosen algorithm.

Imposing interface conditions at artificial boundaries of atomistic and continuum domains creates an additional challenge in coupled simulations. Even though boundary conditions (BC) in continuum approaches can often be properly imposed, the extraction of required state information from atomistic particle-based solution is a difficult task. The extraction of the mean field properties (ensemble averages) typically requires spatio-temporal sampling of characteristics computed by atomistic solver. Hadjiconstantinou et. al. [40] obtained an a priori estimate for the number of samples required to measure the average of flow properties in a cell of a selected volume for a fixed error. The number of samples depends on the significance of deterministic flow properties with respect to the thermal fluctuations amplitude and can be very large if thermal fluctuations overwhelm deterministic flow characteristics. There are also approaches which attempt to minimize the drawback of the presence of thermal fluctuations [39] or to filter them out as we will present in this paper. Non-periodic BCs in particle methods are associated with particle insertions/deletions [41] and the application of effective boundary forces [33, 35, 42]. The existing BC algorithms for Newtonian fluids in particle methods work quite well; however, the corresponding algorithms for complex fluids (e.g., polymeric and biological suspensions) are still under active development. Insertion of bonded particles (e.g. polymers, red blood cells, etc.) demands more sophisticated methods than insertion of non-bonded particles (e.g., representing blood plasma). The main challenge here is to minimize non-physical disturbances in local density and velocity fluctuations.

In summary, for multiscale modeling of blood flow we need to address all the aforementioned challenges. The first challenge is in deriving mathematical models accurately predicting physiological processes. The second challenge is designing robust interface conditions required to integrate the continuum and atomistic simulations. The third challenge is in processing non-stationary data from atomistic simulations. Due to relatively frequent data exchange between the stochastic and deterministic solvers, statistical averaging should be performed on data calculated within short time intervals. The fourth challenge is a computational one. In particular, billions of degrees of freedom are required to accurately resolve the micro-scales and also the interaction between the blood cells and endothelial cells in a volume as small as 1mm³. Simulating effects of small scales on the larger scales requires increased local resolution in the discretization of computational domain with the continuum description. For example, clot formation starts from aggregation of individual blood cells and the clot must grow to a certain size before affecting the large scale flow dynamics. However, to accurately capture the clot geometry and its shading off segments, very high local resolution is required. Moreover, to follow the detached clot segment an adaptive local hp-type mesh refinement must be used.

In this paper we address some of the aforementioned difficulties. In section 2 we describe the numerical methods applied to simulate blood flow and clot formation process at various scales with sufficiently high resolution. In the same section we describe our approach for coupling the atomistic and continuum solvers. Specifically, we review the interface conditions and ways to increase the computational efficiency. In section 3 we present results of coupled simulations of a blood flow and clot formation in a simplified domain of an artery and also in a patient-specific brain vasculature with an aneurysm. In section 4 we summarize our study, discuss the current limitations of our methods, and provide an outlook for future development.

2. Methods

In this section we describe the numerical methods used to simulate blood flow at both continuum and atomistic levels. First, a numerical method for solving the Navier-Stokes equations using a continuum description is reviewed. Specifically, we focus on spatio-temporal discretization and on the smoothed profile method (SPM) [43, 44] implemented in our research code εκ αr. Second, we describe a numerical approach for coarse-grained atomistic simulation using the dissipative particle dynamics (DPD) method [45, 46] and a projection method of atomistic data to continuum field. Finally, coupling of the continuum solver εκ αr with the atomistic solver DPD-LAMMPS (based on the open source LAMMPS code [47]) is described.

2.1. Continuum-based modeling: spectral element method

The large-scale flow dynamics is modeled by the Navier-Stokes equations:

$$\frac{\partial \mathbf{u}}{\partial t}+\mathbf{u}·\nabla \mathbf{u}=-\nabla p+\nu {\nabla }^2\mathbf{u}+\mathbf{f},\nabla ·\mathbf{u}=0,$$ (1)

where u is the velocity vector, p is the pressure, ν is the kinematic viscosity, t is the time, and f is a force term, which we will discuss in more detail further below. The flow problem is defined in a rigid domain Ω_C of arterial networks. To model large-scale flow dynamics, we assume blood to be an incompressible Newtonian fluid with constant density and viscosity.

The three-dimensional (3D) Navier-Stokes equations are solved using the open-source parallel code εκ αr developed at Brown University. εκ αr employs the spectral/hp element spatial discretization (SEM/hp) [48], which provides high spatial resolution and is suitable for solving unsteady flow problems in geometrically complex domains. The computational domain is decomposed into polymorphic elements. Within each element the solution of equation (1) is approximated by hierarchical, mixed order, semi-orthogonal Jacobi polynomial expansions [48]. Figure 2 shows an illustration of the domain decomposition and the polynomial basis used in εκ αr. For time integration εκ αr employs a high-order semi-implicit time-stepping scheme [49].

Figure 2.

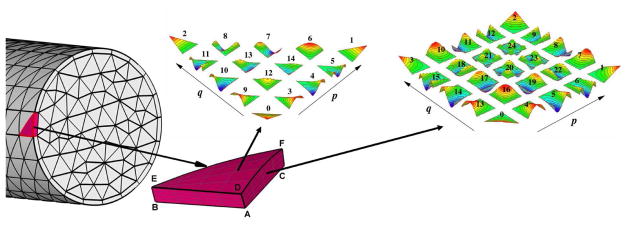
A schematic of the unstructured surface grid and the polynomial basis employed in 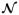εκ αr. The computational domain is decomposed into non-overlapping elements. Within each element the solution is approximated by mixed order, semi-orthogonal Jacobi polynomial expansions. The shape functions associated with the vertex, edge and face modes for a fourth-order polynomial expansion defined on triangular and quadrilateral elements are shown in color.

To simulate moving objects or time-evolving structures within a fixed computational domain we use the smoothed profile method [43, 44]. SPM belongs to the family of immersed boundary methods, and hence it has no requirements on the mesh to be conformal with the boundaries of moving objects or structures. The forcing term f in equation (1) is computed using SPM such that no-slip boundary conditions (BCs) are weakly imposed at any (virtual) surface Γ_v(t, x) ∈ Ω_C.

The equations (1) are solved in several steps using the numerical scheme outlined below. In the following equations the index n in the scheme corresponds to the time step tⁿ = nΔt, where Δt is the size of a time step; γ₀ and α_k are coefficients for the backward differentiation, β_k are extrapolation coefficients, and Je is the time discretization order.

The first step in solving equation (1) includes explicit computing of the provisional velocity field u*:

$$\frac{{\mathbf{u}}^{\ast }-{\sum }_{k=0}^{Je-1}({\alpha }_k{\mathbf{u}}^{n-k})}{\mathrm{\Delta }t}=-\sum _{k=0}^{Je-1}({\beta }_k{\mathbf{u}}^{n-k}·\nabla {\mathbf{u}}^{n-k}).$$ (2)

In the second step we solve implicitly the Helmholtz equation for each velocity vector component:

$$\frac{{\gamma }_0\stackrel{\sim }{\mathbf{u}}-{\mathbf{u}}^{\ast }}{\mathrm{\Delta }t}=\nabla p+\nu {\nabla }^2\stackrel{\sim }{\mathbf{u}},$$ (3)

where the pressure field p is computed from the Poisson equation:

$${\nabla }^{2}p={(\mathrm{\Delta }t)}^{-1}\nabla ·{\mathbf{u}}^{\ast }.$$ (4)

The Poisson equation for p is derived by applying the divergence operator to equation (3) and using the condition ∇ · u ≡ 0. In the case of zero force term, the second step completes the numerical integration of equation (1) and the solution vector at time step t + Δt is defined to be uⁿ⁺¹ = ũ. With a non-zero force term, an additional step is required to obtain solution at time step t + Δt.

At the third step, the velocity field ũ obtained in the second step is corrected in order to impose no-slip BCs at moving boundaries Γ_v(t, x):

$${\gamma }_0\frac{{\mathbf{u}}^{n+1}-\stackrel{\sim }{\mathbf{u}}}{\mathrm{\Delta }t}={\phi }^{n+1}\frac{{\mathbf{u}}_p-\stackrel{\sim }{\mathbf{u}}}{\mathrm{\Delta }t}-\nabla \stackrel{\sim }{p},$$ (5)

where the pressure field p̃ is calculated from:

$${\nabla }^2\stackrel{\sim }{p}={(\mathrm{\Delta }t)}^{-1}\nabla ·[{\phi }^{n+1}({\mathbf{u}}_p-\stackrel{\sim }{\mathbf{u}})+{\mathbf{u}}^{\ast }].$$ (6)

The Poisson equation for p̃ is derived by applying the divergence operator to equation (5) and assuming that ∇ · uⁿ⁺¹ ≡ 0.

The scalar field φ(t, x) in equation (6) is the so-called indicator function. This function is zero outside the region(s) bounded by Γ_v(t, x), while inside this region(s) φ(t, x) = 1. Note that φ(t, x) is not a step function such that it smoothly varies from zero to one around Γ_v(t, x) with φ(t, Γ_v) = 0.5. The vector u_p(t, x) specifies required flow velocity with its values being important only for φ(t, x) > 0. The smoothness of fields φ and u_p is very important, since high-order accuracy can only be achieved for smooth fields. In section 2.3 we will further extend the discussion of Γ_v, φ, and u_p, and show the relation of these fields to data provided by the atomistic solver.

The patient-specific arterial network considered in our study is very large. Moreover, to accurately represent the wall shear stresses (an important characteristic in biological flows) high spatial resolution is required. This leads to an extremely large size of computational problem (in terms of degrees of freedom (DOF)) with O(10⁹) DOF. To efficiently solve such large problem we employed a multi-patch domain decomposition method [50]. This method decomposes the full tightly-coupled problem into a number of small tightly-coupled problems defined in subdomains (patches), where the global continuity (coupling) is enforced by providing proper interface conditions. Thus, the multi-patch method significantly improves computational efficiency and essentially removes the limits imposed due to large problem size. The multi-patch approach is well suited with the functional decomposition strategy we employ in multiscale simulations such that in each patch a different numerical model for the flow problem can be applied. For example, the computational domain of brain arteries shown in figure 1 is decomposed into four patches, but only one patch has an interface with the atomistic solver, where the SPM method is employed. The solution of equation (1) with a non-zero force term implies that one more Poisson equation and three additional projection problems must be solved, which practically doubles the computational effort. Using the flow solver with the SPM in a single patch leads to a better management of computational resources.

2.2. Atomistic based modeling: dissipative particle dynamics method

To model blood flow dynamics at atomistic/mesoscopic scale we employ a coarse-grained stochastic molecular dynamics approach [51] using the dissipative particle dynamics (DPD) method [45, 46]. DPD is a mesoscopic particle method with each particle representing a molecular cluster rather than an individual molecule. The DPD can be seamlessly applied to simulate bonded structures (e.g., polymers, blood cells) and non-bonded particles (e.g., blood plasma). The DPD system consists of N point particles interacting through conservative, dissipative, and random forces given respectively by

$${\mathbf{F}}_{ij}^C=a_{ij}\left(1-\frac{r_{ij}}{r_c}\right){\widehat{\mathbf{r}}}_{ij},{\mathbf{F}}_{ij}^D=-\gamma {\omega }^D(r_{ij})({\mathbf{v}}_{ij}·{\widehat{\mathbf{r}}}_{ij}){\widehat{\mathbf{r}}}_{ij},{\mathbf{F}}_{ij}^R=\sigma {\omega }^R(r_{ij})\frac{{\xi }_{ij}}{\sqrt{\mathrm{\Delta }t}}{\widehat{\mathbf{r}}}_{ij},$$ (7)

where r̂_ij = r_ij/r_ij, v_ij = v_i − v_j, Δ_t is the time step, and r_c is the cutoff radius beyond which all forces vanish. The coefficients a_ij, γ, and σ define the strength of conservative, dissipative, and random forces, respectively. ω^D and ${\omega }^R(r_{ij})={\left(1-\frac{r_{ij}}{r_c}\right)}^k$ with the exponent k are weight functions, and ξ_ij = ξ_ji is a normally distributed random variable. The random and dissipative forces form a thermostat and must satisfy the fluctuation-dissipation theorem [46] leading to the two conditions: ω^D(r_ij) = [ω^R(r_ij)]² and σ² = 2γk_BT with T being the equilibrium temperature. The motion of DPD particles is governed by Newton’s law:

$$\frac{{d\mathbf{r}}_i}{dt}={\mathbf{v}}_i{m}_i\frac{{d\mathbf{v}}_i}{dt}={\mathbf{f}}_i{\mathbf{f}}_i=\sum _{j,i\ne j}({\mathbf{F}}_{ij}^C+{\mathbf{F}}_{ij}^D+{\mathbf{F}}_{ij}^R).$$ (8)

The atomistic problem is defined in a fixed non-periodic domain Ω_A, where the fluid is represented by a collection of solvent particles with a number of suspended platelets. The domain boundaries Γ_A are discretized into triangular elements , where local BC velocities are imposed. In general, we impose effective boundary forces F_eff on the particles near boundaries that represent solid walls and inflow/outflow BCs. Such forces impose no-slip BCs at solid walls and control the flow velocities at inflow/outflow [42]. In addition, at inflow/outflow we insert/delete particles according to local particle flux [42]. Figure 3 presents a typical discretization of Γ_A. In coupled atomistic-continuum simulations the BCs prescribed at Γ_A are based on data received from the continuum solver, which will be described in the next section.

Figure 3.

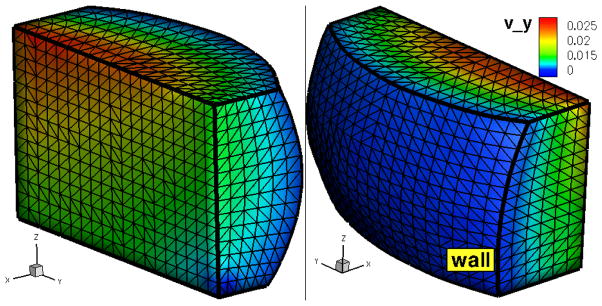
(in color) Atomistic domain Ω_A with a triangulation of the domain boundaries Γ_A. Colors represent the y–component of the velocity imposed at Γ_A.

Coupling of atomistic and continuum solvers requires the calculation of averaged properties in Γ_A such as velocity and density. Accurate computing of the averaged fields through processing of atomistic data presents several challenges including geometrical complexity of the atomistic domains, thermal fluctuations, and flow unsteadiness. To compute average properties we adopt a spatio-temporal binning strategy. The computational domain Ω_A is discretized into tetrahedral elements (bins) Ω_b. The time-space average velocity and density are computed by sampling data over predefined time intervals Δt_s within each bin:

$${\overline{\mathbf{u}}}_b=\frac{1}{N_p}\sum _{n=n_1}^{n_1+N_{ts}}\sum _i{\mathbf{u}}_i^n,$$ (9)

where ū_b denotes the average velocity in bin b, N_p is the number of particles n passing through Ω_b over the time interval Δt_s = N_tsΔt, and ${\mathbf{u}}_i^n$ is the velocity of a particle i at time step n.

The averaging of atom properties over bin’s volume leads to cell centered data, which is discontinuous at the bin interfaces. As we mentioned above, the spectral convergence in the spectral element method can be achieved only for smooth fields. To map the cell centered data to a vertex centered C⁰ continuous field we apply a projection operator P_cc2vc:

$${\overline{\mathbf{u}}}_v=P_{cc2vc}({\overline{\mathbf{u}}}_b)=\sum _{b=1}^{N_b}({\omega }_{vb}{\overline{\mathbf{u}}}_b),$$ (10)

where v represents a vertex of Ω_b, N_b is the number of bins sharing the vertex v, and ω_vb are the normalized integration weights: ∀v Σ_b ω_vb = 1. The weights are inversely proportional to the distance between the vertex v and the center of bin b. An alternative method to compute vertex centered flow properties is to sample the atomistic data within a spherical volume centered at the vertices of elements Ω_b. Both methods produce similar results, while the main difference is in computational complexity. In general, it is computationally more efficient to determine if a particle is located inside a spherical bin in comparison to that inside a polymorphic element. Moreover, the number of vertices is typically a fraction of the number of elements. However, possible overlap between the volumes centered at each vertex requires that the location of each particle is tested in a number of spherical bins, which significantly increases the computational burden. In case of hexahedral bins, where bin faces are properly aligned with the coordinate system, calculation of cell centered data and their projection on the vertex centered configuration is the most efficient. However, such hexahedral bins cannot be used in arbitrary complex geometries.

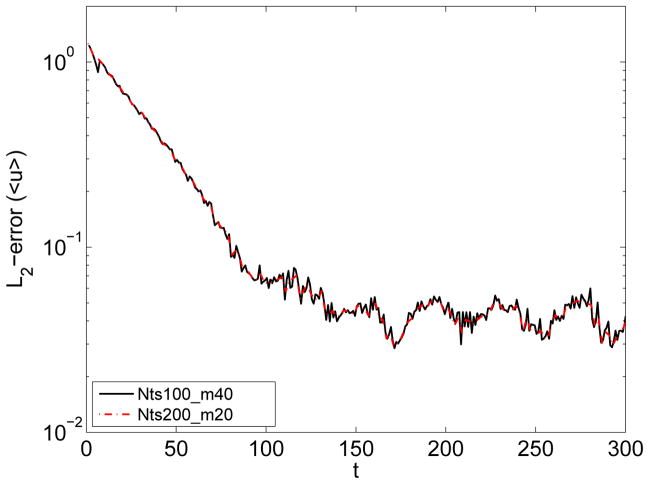
The accuracy in computing of average properties is controlled by the size of a bin and the time interval Δt_s. In steady flows Δt_s can be chosen very large to minimize the effect of thermal fluctuations and accurately capture the deterministic component. In non-stationary flows, for instance blood flow considered in our study, the averaged properties are time dependent, and it is not always clear how to define the time interval Δt_s. Thus, data averaged over a short Δt_s may be very noisy due to thermal fluctuations, while averaging over a long Δt_s will inadequately approximate the time variation of the deterministic component within the atomistic fields. In order to overcome this difficulty we employ the window proper orthogonal decomposition (WPOD) [52, 53]. WPOD is a spectral analysis tool used to transform a field into M orthogonal temporal and spatial modes. The low-order POD modes contain most of the energy and correspond to the ensemble average field, while the high-order POD modes reflect thermal fluctuation components. To construct the POD modes we apply the method of snapshots [54], where each snapshot contains a spatio-temporal average of atomistic data computed over a relatively short Δt_s. Figure 4 illustrates the application of WPOD method for processing of atomistic data. The plots clearly show that WPOD substantially improves the accuracy in the reconstruction of the time dependent average flow field and also its derivatives. For this problem, the averaged solution obtained with the WPOD technique was approximately one order of magnitude more accurate (in L₂-norm) than the solution obtained using standard averaging. Our simulation tests indicate that in order to achieve a certain accuracy, the WPOD approach allows us to balance the number of POD modes and the length of time interval Δt_s for averaging of a single snapshot. Figure 5 shows that for MΔt_s = const identical accuracy in reconstruction of the deterministic component of an unsteady flow can be achieved in practice.

Figure 4.

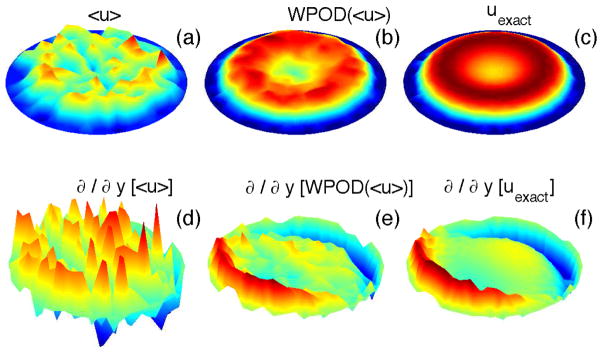
(in color) Processing of data from the DPD simulation of unsteady flow in a pipe: (a) - averaged solution (streamwise velocity component, aligned with the x axis) computed with a standard averaging with N_ts = 50; (b) - averaged solution processed with the WPOD; here the data is reconstructed using the first two POD modes. (c) -exact solution. (d–f) - gradients of the streamwise component of the velocity filed.

Figure 5.

(in color) Processing of data from the DPD simulation of unsteady flow in a pipe: accuracy. The streamwise velocity is computed from atomistic data using the WPOD method. The time window over which the data is processed is kept constant. Black solid curve - each snapshot is computed over 100 time steps, number of POD modes is 40. Red dot-dash curve - each snapshot is computed over 200 time steps, number of POD modes is 20.

2.3. Coupled atomistic-continuum solver

To construct a solver for multiscale simulations we couple the continuum solver εκ αr with the atomistic solver DPD-LAMMPS. A schematic representation of functional decomposition implemented in our coupled solver is presented in figure 6 and an example of a coupled problem is provided in figure 1. Each solver fully preserves its original capabilities, in particular the multi-patch domain decomposition in εκ αr and multiple replicas to compute the statistical properties more accurately in DPD-LAMMPS. Independent tightly-coupled problems are solved within each continuum or atomistic domain using non-overlapping groups of processors. Additional sub-groups of processors are derived to handle tasks required to impose BCs at inlets/outlets and also at inter-domain interfaces.

Figure 6.

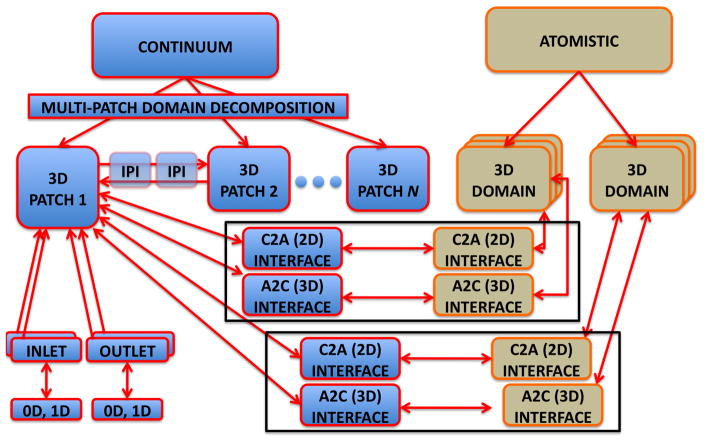
A schematic representation of task parallelism in our coupled solver. The continuum domain is partitioned into N overlapping patches Ω_Ci, and the patches exchange data via inter-patch communicators. Each Ω_Ci has multiple inlets and outlets, and each patch may be connected to 0D or 1D arterial network model in order to model BCs for inlets/outlets. Two atomistic domains Ω_Ai are placed inside Ω_C1. Each Ω_Ai can be replicated several times to reduce statistical error. Each Ω_Ai is linked to a Ω_C1via two interfaces: A 2D interface which considers the boundaries of Ω_Ai and uses data computed in Ω_Ci as BCs. A 3D interface, which is tailored to the immersed boundary method; Ω_C1 uses an external force field computed in Ω_Ai.

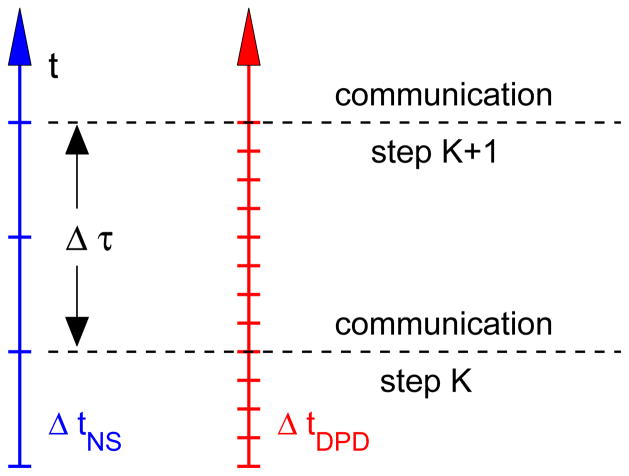
Coupling of the atomistic and continuum solvers follows the framework described in [35], where the continuum solver for Navier-Stokes equations is coupled to DPD and also to molecular dynamics (MD). The flow domain is decomposed into a number of overlapping regions, which may employ different descriptions such as MD, DPD, or continuum. Each sub-domain is integrated independently. The coupling between overlapping sub-domains is performed by exchanging state variables every Δτ in time progression as shown in figure 7. The time Δτ may correspond to a different number of time steps for distinct descriptions. In this paper we also extend the method of [35] and apply it to unsteady flow in a complex geometry.

Figure 7.

A schematic representation of the time progression in different sub-domains. The time step ratio employed in our study is Δt_NS/Δt_DPD = 20, and Δτ = 10Δt_NS = 0.0344s.

To set up a multiscale problem with heterogeneous descriptions we have to define length and time scales. In principle, the choice of spatio-temporal scales may be flexible, but it is limited by various factors such as method applicability (e.g., stability, flow regime) and problem constraints (e.g., temporal resolution, microscale phenomena). For example, a unit of length (LC) in Ω_C corresponds to 1 mm, while a unit of length (L_A) in Ω_A is about 1 μm. In addition, fluid properties (e.g., viscosity) in different descriptions may not necessarily be in the same units in various methods. To properly couple different domains we are required to consistently non-dimensionalize the time and length scales and to match non-dimensional numbers which characterize the flow. For example, to match the Reynolds number (Re) in different domains the velocity in Ω_A is scaled as:

$${\mathbf{u}}_A={\mathbf{u}}_C\frac{L_C}{L_A}\frac{{\nu }_A}{{\nu }_C},$$ (11)

where ν_C and ν_A are the kinematic fluid viscosities in the Ω_C and Ω_A. The time scale in each sub-domain is defined as t ~ L²/ν and is governed by the choice of fluid viscosity. In our simulations a single time step in the continuum solver (Δt_NS) corresponds to 20 time steps in the atomistic solver (Δt_DPD). The data exchange between the two solvers occurs every Δτ = 10Δt_NS = 200Δt_DPD ~ 0.0344 s.

Figure 8 illustrates the setup for coupled atomistic-continuum simulation of platelet aggregation. First, the continuum domain Ω_C is created. Second, the atomistic domain Ω_A is placed in the area of interest, such that Ω_A ∈ Ω_C. Third, an additional sub-domain Ω_S for sampling of atomistic data is inserted into Ω_A such that Ω_S ∈ Ω_A. The boundaries of Ω_A are discretized using 2D elements (triangles), while the volume of Ω_S is discretized using 3D elements (bins).

Figure 8.

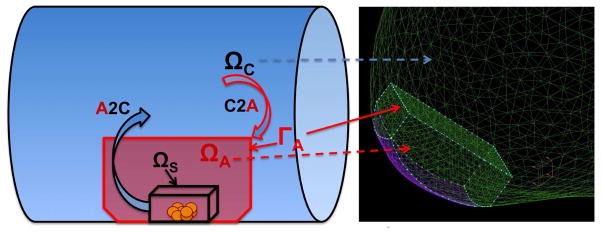
(in color) A coupled atomistic-continuum simulation: illustration of computational domains and inter-domain data exchange. An atomistic domain Ω_A fully embedded into the continuum domain Ω_C in the region where platelet (yellow dots) deposition is simulated. Interface velocity conditions are imposed at the boundaries Γ_A of Ω_A. Virtual boundary conditions for velocity are imposed inside Ω_C using the smoothed profile method, which requires the indicator function Φ(t, x) and the particle velocity u_p(t, x).The fields Φ(t, x) and u_p(t, x) are sampled within the sub-domain Ω_S placed inside Ω_A. Right – computational domain of an aneurysm Ω_A ∈ Ω_C is placed at the wall of Ω_C, where the contact surface is colored in purple.

The interface conditions used for atomistic-continuum coupling are based on the requirements for each solver. The atomistic solver requires a local velocity flux to be imposed at each element 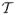of Γ_A. The coordinates of 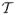centers are provided by the atomistic solver to the continuum solver at the preprocessing stage, and interpolation operators projecting the velocity from the continuum filed onto the centers of 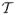are constructed. During time integration data computed by the continuum solver is interpolated and transferred to the atomistic solver. The continuum solver also requires the indicator function φ and the velocity u_p. The main objective of the simulation shown in figure 8 is to study the formation of blood clot. The clot is formed by aggregation of the DPD particles (platelets) on the arterial wall, i.e., the blood clot is simulated by the atomistic solver. The interaction between the micro and macro scales strongly depends on the effects of the clot growth on the flow. Specifically, the clot forms an obstacle attached to the wall, and also some parts of the clot may break up and advect downstream. Since the clot is formed by an evolving cluster of DPD particles which represent platelets, the local density of these particles increases in comparison to that in bulk blood flow. To mimic this obstacle (aggregate) we construct the indicator function φ in such a way that it has a value of one in the region with high-density of active (sticky) platelets and zero in the region with normal platelets density as in bulk flow. To this end, the indicator function is defined as:

$$\phi (t,\mathbf{x})=0.5\left[tanh\left(\frac{{\rho }_p(t,\mathbf{x})-{\rho }_0}{{\text{L}}_{\rho }}\right)+1\right],$$ (12)

where ρ_p(t, x) is the concentration of active platelets, ρ₀ is the predefined threshold (in our simulations ρ₀ is two to three times greater than the bulk platelet density), and Ł_ρ is the scaling factor which controls the steepness of the indicator function. The values of the indicator function are computed by the atomistic solver within Ω_S at the coordinates which correspond to the locations of grid points in Ω_C. Due to a high-spatial resolution in the continuum domain the number of grid points can be very large. To compute the indicator function efficiently the density ρ_p(t, x) is first computed at the bin centers by spatio-temporal averaging over time interval Δτ. Then, the projection operator P_cc2vc is applied to compute the vertex-centered data. The projection from cell-centered to vertex-centered data is followed by the interpolation of ρ_p(t, x) at bin vertices to the grid points of Ω_C using local linear interpolation within each bin. The indicator function is then calculated from the interpolated density values.

Monitoring the size of the blood clot over time may be a very difficult task. The major challenge is to define the clot and its boundaries in terms of the active platelets and their velocity. The description of the blood volume occupied by active platelets by an indicator function provides a convenient method to measure the volume occupied by the clot. For example, we may simply integrate the indicator function φ(t, x) over Ω_A or Ω_C instead of counting individual active platelets. However, such method will also include the regions occupied by moving objects composed of aggregated platelets, which are not a part of the static blood clot near the wall. Thus, to make the estimation of the clot growth more reliable, it might be necessary to introduce weights for the indicator function which assume a value of one in the region of very slow flow and decay exponentially fast as the flow velocity increases.

2.4. Platelet aggregation model

Platelets are modeled by single DPD particles with a larger effective radius [55] than that of plasma particles and are coupled to the plasma through the DPD dissipative interactions. The model of platelet aggregation is adopted from [56], where platelets can be in three different states: passive, triggered, and activated. In the passive state, platelets are non-adhesive and interact with each other through the repulsive DPD forces, which provide their excluded volume interactions. Passive platelets may be triggered if they are in close vicinity of an activated platelet or injured wall. When a platelet is triggered, it still remains non-adhesive during the so-called activation delay time, which is chosen randomly from a specified time range. After the selected activation delay time, a triggered platelet becomes activated and adhesive. Activated platelets interact with other activated particles and adhesive sites, which are placed at the wall representing an injured wall section, through the Morse potential as follows

$$U_M(r)=D_e[e^{2\beta (r_0-r)}-2e^{\beta (r_0-r)}],$$ (13)

where r is the separation distance, r₀ is the zero force distance, D_e is the well depth of the potential, and β characterizes the interaction range. The Morse potential interactions are implemented between every activated platelet or adhesive site if they are within a defined potential cutoff radius r_d. The Morse interactions consist of a short-range repulsive force when r < r₀ and of a long-range attractive force for r > r₀ such that r₀ corresponds approximately to the effective radius of a platelet. Finally, activated platelets may become passive again, if they did not interact with any activated platelet or adhesive site during a finite recovery time.

2.5. Accuracy considerations

Validation of the mathematical models used for complex biological systems is extremely difficult. Ultimately, it would require the possibility to perform experiments on the onset and subsequent growth of the clot formation in the brain, which is currently not feasible. The accuracy of the coupled atomistic-continuum solver depends on modeling and discretization errors. Specifically, modeling errors in the continuum approach can be related to the assumption of rigid vessel walls, while real vessel walls are deformable, and to uncertainties in the inflow/outflow boundary conditions as well as in material properties. At the atomistic level, the platelet aggregation model may also lead to modeling errors. We used the platelet aggregation method presented in [56], which produced platelet aggregation rates comparable with experimentally observed ones in in-vitro experiments [57]. However, the clot formation process may be very different in the brain, and its biomechanical details have not been quantified yet. In addition, interactions between red blood cells, white blood cells, and fibrinogen have to be included, and such interactions are particularly important for simulating advanced stages of clot formation. Moreover, modeling clot formation at the initial and intermediate stages may require the use of time-dependent models such that aggregation interactions are time dependent, for example, to treat the depth of the Morse potential (D_e) as a time-varying parameter.

The discretization errors are attributed to the usual time-space discretization parameters, i.e., Δ_t, h and p mesh refinement, errors in the DPD solver due to thermal noise, to coupling errors between continuum and atomistic descriptions, but also to the statistical errors in computing ensemble averages. The numerical accuracy of different components in our coupled solver has been verified by performing time and space- discretization refinement in the continuum solver. We have also performed atomistic simulations using three different resolutions, with L_A/L_C ratio equal to 100, 200 and 400. Comparable results have been obtained with L_A/L_C = 200 and L_A/L_C = 400, while the finest resolution has been used in the simulations presented below. Errors in coupling the continuum and atomistic descriptions for simulating stationary flows have been explored in [35], where it was shown that convergence of solution in the continuum and atomistic domains can be achieved. Here, we consider a non-stationary flow and a different approach for coupling the Ω_A to Ω_C, while a similar approach for coupling Ω_C to Ω_A. Eventhough, we do observe that the main large scale features of the flow computed in Ω_A, i.e., generated secondary flows due to the obstacle, are present in Ω_C, the coupling approach may require additional verification steps that need to be carefully designed in future studies. Numerical errors in sampling atomistic data using WPOD have been addressed in section 2.2, and also in [53]. The errors in the SPM method implemented in our solver have been explored in [44]; in general, the SPM errors are sensitive to the h discretization and to the steepness of the indicator function. Verification of accuracy of the SPM method has been performed in separate studies using exact solutions, e.g. creeping flow (Wannier flow problem) and also simulations of fast spinning marine propeller at Reynolds number up to 320K. In these simulations the numerical errors could be kept quite low (1-5%) with a proper choice of the steepness of the indicator function.

3. Results

In this section we present results of two multiscale simulations using the two-way coupling approach and show the scalability of our coupled solver. The first test models thrombus formation in an idealized cylindrical vessel with steady flow conditions at the inlet. The second test corresponds to modeling thrombus development in an aneurysm using a patient-specific domain of brain vasculature with unsteady flow conditions imposed at the domain’s four inlets. In both cases the thrombus is formed next to a small wall section, where we randomly place a number of adhesive sites, which mimic an injured wall. An atomistic domain encloses the flow volume around the injured wall section such that five planar surfaces of the domain are interfaced with the global continuum domain, while the sixth boundary surface overlaps with the wall, see figures 9 and 10. The size of the atomistic domain in both tests is chosen to be large enough to properly resolve and capture the dynamics of thrombus formation (e.g., a unit length in the atomistic domain corresponds to approximately 1 μm). The velocities in Ω_A are scaled according to equation (11) in order to keep the same Re number in both continuum and atomistic domains, since Re is the main governing parameter for this flow. DPD particles representing blood plasma and passive (inactive) platelets are inserted at Γ_A with a constant and uniform density according to local velocity flux at the boundaries.

Figure 9.

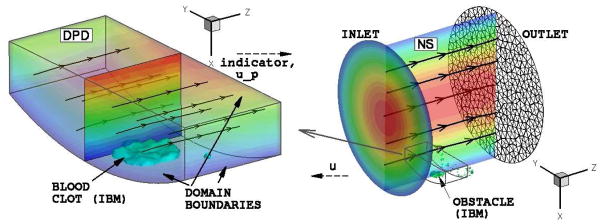
Pipe flow: coupled continuum-atomistic simulation with Re = 350. A clot is formed by platelet aggregation at the wall of a pipe. Left - atomistic modeling. Streamlines show the flow direction; colors show the stream-wise velocity component magnitude; iso-surface corresponds to the active platelet density 1.75 times larger than the bulk normal density. Right - continuum modeling. Streamlines show the flow direction; colors show the stream-wise velocity component magnitude; obstacle is shown by plotting an iso-surface of indicator function φ = 0.5.

Figure 10.

Brain vasculature: coupled continuum-atomistic simulation. Continuity in the velocity fields computed by the continuum and atomistic solvers. Streamlines and vectors depict instantaneous flow direction.

The code scalability study was performed using the patient-specific domain of brain vasculature. A perfect strong scaling of our solver has been observed on up to 72 Racks (about 300K cores) of BlueGene/P computer at the Jülich Supercomputing Centre and on up to 190K cores of CRAY XT5 at the National Institute for Computational Sciences and Oak Ridge National Laboratory.

3.1. Coupled simulations of platelet aggregation

Platelet deposition simulation in idealized vessel geometry was performed using a continuum domain of a pipe with radius of 235 μm, where a Poiseuille flow (Re = 350) was imposed at the inlet and zero pressure conditions at the outlet. An atomistic sub-domain of size 100 × 200 × 100 μm³ was placed close to the pipe wall around the injured wall section as shown in figure 9. The injured wall section was modeled by placing randomly a number of adhesive sites within a circular region of the wall with radius of 22 μm and the particle density 5/μm². Platelet interactions were modeled with the Morse potential, see equation (13). The strength of platelet adhesion De = [1000 2000] k_BT was set to be sufficiently large to ensure firm platelet adhesion. The other parameters were chosen to be β = 0.5 μm⁻¹ and r₀ = 0.75 μm. The maximum activation delay time of triggered platelets was set to be 200Δt_DPD corresponding to approximately 0.0344 s. The platelet recovery time was equal to 20000Δt_DPD ≈ 3.44 s. The platelet time constants affect the dynamics of clot formation, however they have an insignificant effect on the final thrombus structure. Note that our time constants are smaller than those used in [56], which allows us to accelerate thrombus formation for the modeling and code testing purpose. The bulk concentration of passive platelets in blood flow was equal to 0.25 per μm³, which is larger than the normal platelet concentration in blood and was used to accelerate the clot formation dynamics. The DPD fluid (blood plasma) parameters are given in table 1. With these parameters, we obtain the DPD fluid’s dynamic viscosity η = 2.952. The time step in simulations was set to Δt_DPD = 0.007.

Table 1.

DPD fluid parameters used in simulations. n is the plasma number density.

a	γ	kBT	k	rc	n
75.0	15.0	1.0	0.1	1.0	3.0

Figure 9 presents the velocity field in the streamwise direction (z axis) computed by the continuum and atomistic solvers. The clot size is shown by an iso-surface which corresponds to the density level of active platelets 1.75 times larger than the bulk platelet density in the atomistic domain (left plot). The obstacle shown by an iso-surface in figure 9 (right) corresponds to the indicator function level of φ = 0.5 in the continuum domain. The velocity field near the platelet deposition gets distorted, since the thrombus serves as an obstacle to the flow. The platelet aggregate grows dynamically to a certain size. Then, its growth stops due to fluid flow stresses and thrombus instability as it becomes large. At this point we observe the detachment of some parts of the clot and consequent minor re-growth. It is clear that the attractive interactions with a finite strength between activated platelets and adhesive sites can only sustain a finite shear stress, which increases with the thrombus growth. The stability of a realistic blood clot is enforced by fibrinogen proteins, which form a cross-linked network within the clot in order to maintain the integrity of a thrombus even at high blood flow shear-stresses. Our model of platelet aggregation is not taking into account the presence of such a protein network, and therefore the thrombus becomes unstable above a certain size. As a conclusion, our platelet aggregation model is able to capture only the initial clot growth, where fibrinogen does not play a significant role. To capture thrombus formation beyond the initial growth, the current model has to include fibrinogen network interactions within a thrombus, which we will pursue in the future.

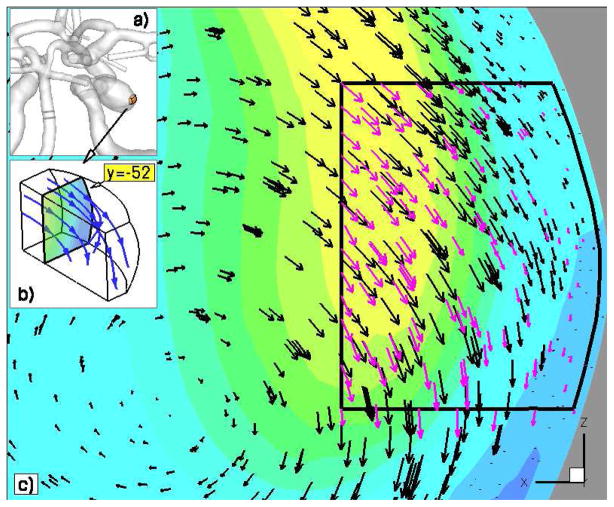
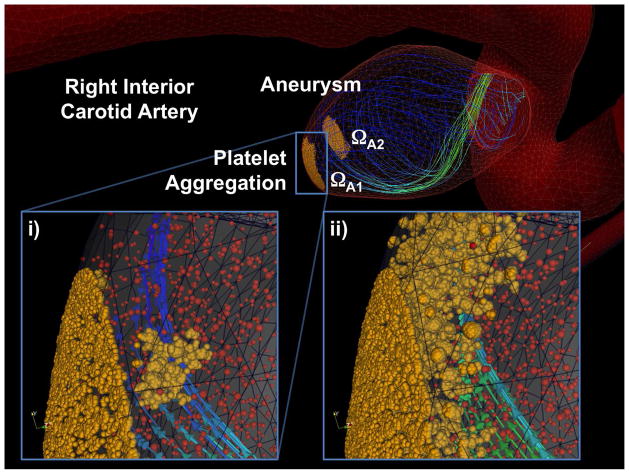
Platelet deposition simulation in patient-specific brain vasculature with an aneurysm was performed using the domain of Circle of Willis and its branches reconstructed from MRI images, see figures 1 and 10a. Patient-specific flow BCs at the four inlets and RC [58] BCs for the pressure at all outlets of Ω_C were imposed. The unsteady blood flow is characterized by two non-dimensional flow parameters: Reynolds number Re = 394 and Womersley number Ws = 3.7.

Three atomistic sub-domains with the volume of about 4 mm³ each were placed inside the aneurysm as depicted in figure 1. The clot formation is modeled in the two sub-domains Ω_A1 and Ω_A2 attached to the wall. The approximate size of each sub-domain was 1.25×1.25×2.5 mm³. The injured wall section in the two sub-domains attached to the aneurysm wall was modeled by a circular region of approximately 0.5 mm radius with the density 5/μm² of adhesive sites. The platelet interaction parameters, bulk density, and the characteristic activation/deactivation times were set the same as those used for the platelet deposition simulation in a pipe flow described above. The DPD fluid parameters are given in table 1. The atomistic domain boundaries Γ_A are discretized with more than 2000 triangular elements, at which fluid particles and platelets either leave Ω_Ai or are inserted according to the local velocity flux.

Figure 10 shows the velocity fields computed in Ω_A1 and Ω_C, where we find the solution to be continuous across the continuum-atomistic interface. The atomistic data has been co-processed using the WPOD which adaptively selects the number of POD modes for reconstructing the ensemble average solution [53]. In this simulation between one and three POD modes were required. The plot also illustrates that the coupled solver properly captures blood flow profile within the atomistic sub-domains. Figure 11 presents the deposition of active platelets at the injured wall section and illustrates shedding and advection of active platelet clusters along the flow. In the left plot one can see the onset of thrombus formation, where yellow particles depict activated platelets or adhesive sites at the aneurysm wall, while red particles correspond to passive platelets in bulk flow. The right plot of figure 11 shows a snapshot later in time, where we observe platelet deposition and shedding of platelet clusters. Significant advection of platelet aggregates along the flow appears to be due to relatively fast platelet aggregation dynamics, which we assumed in order to accelerate the clot formation, and due to a high bulk density of platelets. To further illustrate the initial clot development within the aneurysm, figure 12 shows the clot size at two time instances. Similarly to the first test of platelet deposition in pipe flow we observe a thrombus instability as it grows beyond a certain size. One can also see that its development appears to be non-steady and spatially non-uniform with a non-smooth structure. Several effects may contribute to the irregular clot development including unsteady flow and varying local shear rates and stresses both in time and space. In addition, our simulation times are rather short O(1s), while realistic clot formation occurs on the timescale of at least several minutes.

Figure 11.

Brain vasculature: coupled continuum-atomistic simulation of platelet aggregation at the wall of an aneurysm with Re = 394 and Ws = 3.75. Yellow dots correspond to active platelets and red dots to inactive platelets. Streamlines depict instantaneous velocity field. (i) Onset of clot formation; (ii) Clot formation as it progresses in time and space, and detachment of small platelet clusters due to shear-flow.

Figure 12.

Brain vasculature: coupled continuum-atomistic simulation of platelet deposition at the wall of an aneurysm with Re = 394 and Ws = 3.75. Left - side view; right - bottom view. Yellow dots - active platelets; streamlines with arrows depict the flow direction; colors correspond to the velocity magnitude. (a) - onset and (b) advanced stage of clot growth.

3.2. Parallel performance of coupled solver

Table 2 presents results for strong scaling of our coupled solver in simulations of platelet aggregation in patient-specific brain vasculature with an aneurysm. The number of DPD particles employed is 823,079,981 which corresponds to more than 8 billion molecules assuming a coarse-graining factor 10 : 1 in the DPD method. We note that we also employ non-periodic BCs and have to update the particle neighbor lists (function neigh_modify in LAMMPS) every time step. The atomistic solver obtains data from the Navier-Stokes solver every 200 steps, while the continuum solver obtains data from the atomistic solver every 20 time steps. The CPU-time presented in table 2 also includes the time required to save on the disk averaged velocity and density fields by DPD-LAMMPS every 500 timesteps. In the coupled multiscale simulations we observe a super-linear scaling, which can be attributed to two factors: i) a better utilization of cache memory; and ii) a reduction in computational load per single CPU required to impose interface conditions by the atomistic solver. In general, the computational cost in DPD-LAMMPS is linear, i.e. ∝ C N, where C can be considered to be nearly constant for a fixed simulation system, since it depends on the number of particle neighbors, the choice of inter-particle interactions, and on the number of triangular elements in boundary discretization, while N is the number of particles in each partition. However, the dependence of C on BCs and specifically on the number of faces for each partition might be significant. Thus, for normal scaling, i.e. without BCs, N decreases as the number of cores increases, while C remains constant. The use of non-periodic BCs, however, causes C to also decrease resulting in the super-linear scaling.

Table 2.

Coupled εκ αr-DPD-LAMMPS solver: strong scaling in coupled blood flow simulation in the domain of figure 1. N_core is the number of cores and CPU-time is the time required for 4,000 DPD-LAMMPS timesteps. The total number of DPD particles is 823,079,981. Efficiency is computed as a gain in CPU-time divided by the expected gain due to increase in N_core with respect to a simulation with lower core-count. Simulations were performed on IBM Blue-Gene/P computer at Jülich Supercomputing Centre in Forschungszentrum Jülich (FZJ) and on CRAY XT5 computer at the National Institute for Computational Sciences and Oak Ridge National Laboratory.

Ncore	CPU-time [s]	efficiency
Blue Gene/P (4 cores/node)
32,768	3580.34	–
131,072	861.11	1.04
262,144	403.92	1.07
294,912	389.85	0.92
Cray XT5 (12 cores/node)
21,396	2194	–
30,036	1177	1.24
38,676	806	1.10
97,428	280	1.07
190,740	206	.68

4. Summary and Outlook

In this paper we have presented some advances towards the development of a new methodology for multiscale simulations of blood flow with focus on brain aneurysms. Specifically, we have applied this methodology to simulate platelet deposition in a patient-specific domain of cerebro-vasculature with an aneurysm. The simulations have been performed using a hybrid continuum-atomistic solver which couples the high-order spectral element code εκ αr with the atomistic code DPD-LAMMPS. A two-way coupling between the atomistic and continuum fields has been implemented. The continuum solver feeds the atomistic solver with data at the boundaries of the atomistic domain (interface conditions). The atomistic solver provides to the continuum solver volume data required to prescribe the location and the speed of an obstacle (clot) within the continuum description by means of an immersed boundary method. The hierarchical task decomposition and multilevel communicating interface designed to couple heterogeneous solvers and to perform an efficient data exchange are key features to scaling on hundreds of thousands computer cores.

While the coupled solver incorporates several numerical techniques, additional modeling and algorithmic issues should be addressed. The future modeling issues include:

• developing a model for interaction of blood cells and endothelial cells to simulate more advanced stages of clot growth.

• modeling of fibrinogen in clot formation.

• modeling the stability of the clot and, specifically, simulation of thrombus break up and its advection through the vascular network.

• model validation by comparing simulation results to experiments - a rather difficult task.

The algorithmic issues include:

• capturing the interface with plasma more accurately by adaptive hp-refinement, where the clot is formed.

• simulating clot disaggregation and its advection through the arterial network beyond the area bounded by the atomistic sub-domain. To this end, we will need to develop an atomistic domain moving with the clot, or, otherwise, simulating the detached part of the thrombus using a continuum approach through fluid-structure interaction.

• simulation of moving clot will also need to integrate the solution of a contact problem in order to model the interaction between the blood flow, vessel walls and the thrombus.

• modeling blood vessel wall deformations, which presents a substantial challenge on its own and will add additional complexity.

The aforementioned issues refer to the hemodynamic aspects of the problem. However, addressing the issue of rupture of the aneurysm, as discussed in the Introduction, will require coupling of our solvers to an advanced solid mechanics code that will account for the anisotropic structure of the formed thrombus and its interaction with the tissue [59]. This complex multiscale/multiphysics problem remains untackled so far.