Abstract
Decision-making often requires taking into consideration immediate gains as well as delayed rewards. Studies of behavior have established that anticipated rewards are discounted according to a decreasing hyperbolic function. Although mathematical explanations for reward delay discounting have been offered, little has been proposed in terms of neural network mechanisms underlying discounting. There has been much recent interest in the potential role of the hippocampus. Here we demonstrate that a previously-established neural network model of hippocampal region CA3 contains a mechanism that could explain discounting in downstream reward-prediction systems (e.g., basal ganglia). As part of its normal function, the model forms codes for stimuli that are similar to future, predicted stimuli. This similarity provides a means for reward predictions associated with future stimuli to influence current decision-making. Simulations show that this “predictive similarity” decreases as the stimuli are separated in time, at a rate that is consistent with hyperbolic discounting.
Keywords: hippocampus, reward discounting, neural network, prediction
Introduction
A hallmark of intelligent decision-making is the ability to adequately balance short-term gains against long-term rewards. For example, is $20 now better than $100 in a week? It seems like a better deal to wait a week for the $100. However, the answer to the question may become less clear if the question is about $20 now versus $100 in a month. Studies have now shown that decisions about reward made by pigeons, rats, and humans, can be described in terms of decreasing discounting functions that are well fit by hyperbolic curves (Kacelnik, 1997; Mazur, 1987; Mazur & Biondi, 2009). Measuring such functions empirically involves determining the point at which organisms chose between two options, e.g., an immediate small reward and a delayed large rewards, with equal probability. A typical study with pigeons involves observing as they learn to press either a red button or a blue button, each of which leads to a different fixed amount of grain (e.g., red = grain for 2 seconds versus blue = grain for 6 seconds). By adjusting the delay to the larger reward, experimenters can determine the delay for which the pigeons choose the red and blue buttons with equal probability, that is, the point when the immediate small reward and delayed large reward are treated as equivalent.
Going back to the $20 versus $100 example for illustrative purposes, suppose we have an imaginary participant whose discounting behavior is described by the hyperbolic function V(t) = α/(1 + 0.29t). In this equation, α is the offered reward, t is the time that will elapse before obtaining the reward (here, in days), and V(t) is the discounted value. Then for our participant, $100 in a week is worth $33 which is greater than the $20 now, and our participant would choose to wait, as discussed above. However, using the same equation, $100 in 31 days would be worth only $10.01 – approximately half of the $20 – so the imaginary participant would be more willing to take the $20 now. Indeed, for participants with steep discounting functions, like children (Green et al., 1999), the $20 now would be selected far more often in both situations. Discounting curves can thus be experimentally measured for individuals and groups and used to predict decision-making behavior. Computational theories like Reinforcement Learning successfully incorporate this aspect of decision making using a parameter called the “discount factor,” typically approximated using an exponentially decreasing function (Sutton & Barto, 1998).
Although reward delay discounting is well established in the behavioral literature, proposals as to how neural networks in the brain give rise to the discounting function or its characteristic shape are lacking. Neuroscientists have, however, begun to implicate the involvement of particular brain regions in reward discounting. For example, one idea is that discounting emerges from interactions within the prefrontal-posterior and parietal-basal ganglia system (Kable & Glimcher, 2007, 2010), or between ventromedial prefrontal cortex and lateral prefrontal cortex (Figner et al., 2010; Hare et al., 2009). Another proposal is that discounting reflects a tradeoff between the prefrontal cortex and limbic regions, with prefrontal regions involved in procuring delayed rewards whereas limbic regions are involved in immediate rewards (McClure et al., 2007, 2004).
Of particular interest is a third proposal based on findings that hippocampal lesions increase the preference for immediate rewards, i.e., increased discounting (Cheung & Cardinal, 2005; Gupta et al., 2009; Mariano et al., 2009; Rawlins et al., 1985). Here, the suggestion is that discounting may be mediated by an interaction, rather than a trade-off, between prefrontal and hippocampal regions. A possible pathway for this interaction is a projection from hippocampus to the ventral striatum (Kelley & Domesick, 1982), and in vivo work suggests strong functional connectivity between these regions (Lansink et al., 2009; Pennartz et al., 2004).
The case for hippocampal contributions to reward delay discounting is bolstered by a recent neuroimaging study (Peters & Büchel, 2010). In participants with intact brains, “episodic future thinking” reduced reward discounting such that future rewards were valued more highly. In the study, episodic future thinking refers to an experimental manipulation which arguably directs attention to the hippocampal formation, which is thought to be involved in episodic cognitive representations. The decrease in reward discounting was accompanied by increased functional connectivity between the prefrontal cortex and the temporal lobe, where hippocampus resides. Taken together, these data suggest that increases in hippocampal activity can result in an increase in the value of future (delayed) reward predictions.
Despite all of these findings, the question remains: how precisely might the hippocampus contribute to reward delay discounting? There have not been proposals to explain how hippocampal neural network mechanisms would generate a decreasing reward-prediction function. Although not specified in terms of neural network mechanisms, the main possibility discussed in the existing literature is one called future “mental simulation.” The mental simulation idea is based on findings that the hippocampus appears to be required for the imagination of future events (Addis et al., 2011; Gamboz et al., 2010; Hassabis et al., 2007; Schacter & Addis, 2009). These “mental simulations” putatively allow an organism to evaluate the value of future events (Johnson et al., 2007; Johnson & Redish, 2007). Although it is straightforward to see how mental simulation could be used to decide between two options with eventual outcomes of differing value, it is less obvious whether mental simulation allows an organism to discount delayed rewards and thereby make decisions that take intervening time into consideration.
Here we propose an account of hippocampal involvement in reward delay discounting based on a previously formulated model of hippocampal region CA3 established by Levy and colleagues (Levy, 1989, 1996; Levy et al., 2005). The model is centered on region CA3 of the hippocampus and the theory that this region re-encodes representations of stimuli or events to become more similar to the events that they predict. This re-encoding leads to representations in the present that partially activate representations for those future events, and is a basis for sequence prediction. However, the similarity of encoding with respect to a fixed early portion of a sequence (i.e., the time when a decision might be made) has not been evaluated in the context of reward prediction and decision making. Here, we posit that these partial reactivations could cause activity in downstream reward-predictive regions, namely in the striatum, resulting in the generation of discounted reward predictions. An analysis shows that this “predictive similarity” decreases in time in a manner that approximates hyperbolic discounting. Finally, we operationalize the mental simulation account of reward delay discounting within the model in an attempt to evaluate its compatibility with the model.
Methods
Reward-Prediction Component
The first component of the model is a two-layer network that generates “bottom-up” reward predictions for a sensory stimulus. When an activity pattern x (e.g., a visual stimulus) is presented on the input layer of this network, its output layer represents the amount of reward the organism expects to subsequently receive, V(x). This component is inspired by the idea that reward predictions may be learned through the strengthening of projections from neocortex to the striatum by phasic dopamine activity in the presence of unexpected reward (Bamford et al., 2004; Reynolds & Wickens, 2002). This manner of modeling the storage of value using putative cortico-striatal projections is common in actor-critic reinforcement learning architectures (Joel et al., 2002; Suri & Schultz, 1998). After learning is completed, stimuli that have become associated with reward evoke reward prediction responses in the striatum (Hollerman et al., 1998; Schultz et al., 1997).
To generate its reward predictions, the network computes a weighted sum of each element of the x vector multiplied by its corresponding element in a weight vector w and then optionally applies a monotonic activity function f. Thus the resulting output is the model’s predicted reward for the stimulus, V(x) = f(w · x), here assumed to be a some linear scaling function.
Importantly, in the present model, we do not assume lateral interactions within the putative striatal network. This means that reward predictions due to one input will not interact with reward predictions for another simultaneous input. In particular, the presence of an additional input corresponding to a future anticipated stimulus will not be affected by other reward-associated stimuli. Reward predictions generated by multiple stimuli at the same time are assumed be simply additive, such that V(a + b) = V(a) + V(b). With this assumption in hand, we focus on the inputs to the reward-predicting network. Specifically, we will study the extent to which inputs from the simulated hippocampus to the simulated striatum at decision time are similar to the sensory inputs when the anticipated stimulus was previously presented (and associated with reward).
Discounting Component
The second component of the model is the source of the representations that lead to discounted reward predictions, and comprises a recurrent network and a decoder network. This component is based on a minimalist biologically-inspired neural network model of the hippocampus (Levy, 1989, 1996; Levy et al., 2005). The model’s architecture and usage are inspired by a range of anatomical, functional, and neurophysiological findings in hippocampus. The model and its accompanying theory have been previously used to develop mechanistic explanations for putatively hippocampally-dependent phenomena in the brain like orthogonalization of similar episodic experiences, the generation of sparse representations, and the temporal compression of replayed sequences during sleep (see Levy, 1996, for a review). Although there exist many hippocampal models with family resemblance in terms of the phenomena they explain, the present model was selected specifically because of its focus on sequence learning and prediction.
The core part of the model is the putative CA3 recurrent network consisting of a large number of randomly, sparsely connected, neuron-like units organized in an activity-controlled recurrent network. The neuron-like units are McCulloch-Pitts (binary or “on-off”) units, but more realistic spiking units can also be used (e.g., integrate-and-fire units, August & Levy, 1999). During each simulated time-step, the units integrate inputs on their dendrites and then emit a spike if the weighted sum is sufficiently large according to a dynamic threshold. The excitation y of each unit j on time-step t is modeled as a weighted sum of the binary output of all of its afferent input units on the previous time-step,
| (1) |
Unit j spikes (Zj = 1) if the excitation for that unit exceeds a network-wide dynamic threshold θt, or if the unit is directly stimulated (i.e., clamped) by an external input xj(t):
| (2) |
The threshold being set on each time-step allows for a k-winners-take-all (or “competitive”) activity control. Such activity control is intended to capture the effects of the extensive network of inhibitory interneurons in CA3 that keeps the network-wide activity to an approximately constant level.
The strength of the synaptic connections between the neurons, or weights, wij, ranges from 0 to 1. Because the network is sparsely connected, the majority of those weights are fixed 0 to indicate that neurons share no connections.
Learning in the network occurs according to a temporally-asymmetric Hebbian-like learning rule inspired by spike-timing dependent plasticity or STDP, which has been observed in the form of temporal contiguity requirements for long-term potentiation (Bi & Poo, 1998; Levy & Steward, 1983; Markram et al., 1997). Each weight from neuron i to neuron j is updated only on time-steps when the post-synaptic neuron j is active (i.e., Zj = 1). The update depends on the difference between the current weight wij and a running average of afferent presynaptic activity,
| (3) |
where the running average saturates when the presynaptic neuron fires, and decreases exponentially otherwise, i.e.,
| (4) |
The constant μ is a network-wide synaptic weight modification rate constant (i.e., “learning rate”). The use of a running average of afferent presynaptic activity for weight modification is intended to mimic a saturate-and-decay model of the NMDA receptor. Equation 4 indicates that the running average of spiking activity is updated on every time-step for each neuron i. The quantity α is a time-constant of the decay (i.e., of the modeled NMDA receptors). Although real time and simulated time can be equated through careful tuning of the α parameter as per Mitman et al. (2003), the present modeling work does not make use of time in the absolute sense, only in the relative sense. That is, no attempt is made to model real time.
Synaptic plasticity mechanisms between the units cause neurons that initially fire for a given stimulus to gradually, through learning, begin spiking for stimuli that anticipate the later stimuli (Abbott & Blum, 1996; Levy et al., 2005; Mitman et al., 2003). An analog of this “earlier-shifting” has been observed to occur in recordings of rat hippocampus (e.g., Mehta et al., 1997, 2000). This shifting is proposed, according to the present “predictive similarity” account, to be a mechanism mediating reward discounting.
The parameters used in the reported simulations were based on previous reports from the Levy laboratory allowing for robust learning of sequences (e.g., Mitman et al., 2003; Polyn et al., 2000). Each network consisted of 4,096 neurons with a random connection probability of 8% (self-connections were not allowed) and activity level was regulated to be 7.5% on each time-step through a winners-take-all competitive mechanism as per Equation 2. More specifically, on each time-step the 7.5% of the units with the highest summed weighted input were set to be active on the subsequent time-step. Each network was trained for 120 trials on a sequence of 20 orthogonal (non-overlapping) stimuli each activating 100 neurons for 5 time-steps. On each time-step of stimulation input, random noise was applied so that 30% of the input was randomly deactivated. This random noise is beneficial to learning sequences of orthogonal patterns sustained over multiple time-steps because it helps prevent the development of stable attractors that are detrimental to sequence learning. Prior to each trial, baseline activity provided to the network with a new random input initialization vector such that a random 7.5% of the neurons were active. In general, these multiple sources of noise have been shown to be beneficial to learning in this network (Shon et al., 2002; Sullivan & Levy, 2004). The synaptic weights wij were all initialized to 0.4 prior to learning, and the synaptic weight modification rate μ was 0.01 per time-step. The parameter α was set to 0.8 (Mitman et al., 2003). Each simulation took approximately 28 minutes to train on a 2.66 GHz Intel Xeon as implemented in single-threaded Java code. (Source code is available from http://github.com/plaurent/mcpstdp/).
Assessing predictive similarity
To quantify how much discounting will occur for an anticipated reward-associated stimulus in this model, it is necessary to measure the similarity between the pattern output by the CA3 model at the time of reward association and the pattern output at the time of the decision. According to our hypothesis, the similarity will decrease with increased delay between the decision time and the time at which the rewarded stimulus is predicted to occur. This comparison can be quantified by treating network activity as a vector and using cosine similarity (i.e., the normalized dot product) between pairs of network state (i.e., neuronal spiking) vectors,
| (5) |
which returns a similarity value ranging from zero (i.e., orthogonal vectors) to 1 (i.e., identical vectors).
The similarity of the current pattern to the discounted future pattern will, through connections to the ventral striatum via CA1 (Kelley & Domesick, 1982), partially re-activate ensembles and reward predictions for the future stimuli (Lansink et al., 2009; Pennartz et al., 2004).
Results
Our hypothesis is that reward delay discounting occurs because at the time of decision-making, the organism makes a comparison between (1) reward predictions associated with the immediate stimulus and (2) reward predictions associated with a discounted representation of the future stimulus. Thus, the amount of discounting is hypothesized to depend on the extent to which the hippocampal representation of the present is similar to the hippocampal representation of the future, anticipated stimulus when it is activated (and when reward was delivered). To test this hypothesis, we quantified the degree to which the representation for the present code resembled the representation when the future stimulus was present – i.e., its predictive similarity.
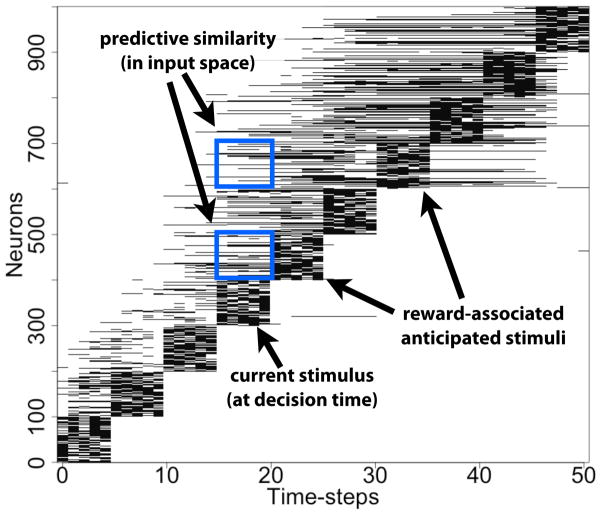
Figure 1 shows the spiking over time of the simulated neurons that were used as input neurons during the last trial of training (these neurons were clamped as part of the stimulation). By examining this figure, one obtains a visual sense of predictive similarity: for example, the activity within the dotted box shows that neurons that were normally clamped for the fifth and seventh patterns in the sequence have started spiking during the fourth pattern. Thus, if a decision is being made at the time of the fourth pattern, anticipatory activity would be present in the hippocampus for the upcoming patterns. The figure only shows the clamped neurons, although below we quantify these results for both the clamped and the non-clamped neurons separately.
Figure 1. Illustrating ‘predictive similarity’ among the clamped neurons.
This figure shows a uniform sampling of the first 1000 neurons during the last trial of training. Although predictive similarity develops throughout the network, it is most easily illustrated in the input space of the network where the neurons are clamped during training. Each horizontal dash represents a spike during a time step, and long horizontal lines indicate sustained spiking for multiple time-steps. The two outlined boxes highlight predictive similarity with respect to the fourth stimulus pattern (i.e., pattern 4, labeled “decision time”). The spiking in those boxes are of neurons associated with two of the anticipated stimuli (i.e., patterns 5 and 7, labeled “reward-associated stimuli”). As can be seen, some set of the neurons in the boxes have come to be fire at the time of the earlier stimulus. Note that the effect in the input space is constrained compared to other neurons in the recurrent portion of the network, because these clamped neurons become depotenti-ated from afferent activity at other times and effectively “anchored” at their place in the sequence.
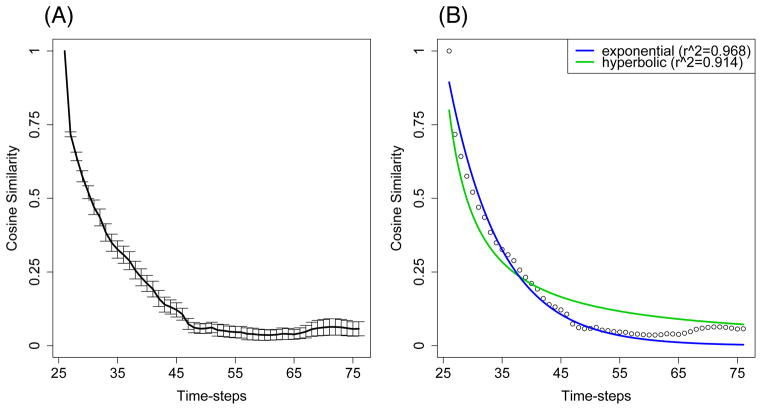
To quantify predictive similarity numerically, the cosine similarity between the spiking pattern one quarter of the way into the sequence and each subsequent pattern in the sequence was computed. (The initial and final quarters of the sequences were excluded from the analysis to ensure that measures reflected on-line function, and to avoid biases that might occur due to end effects.) The result for 50 simulated networks is shown graphically in Figure 2A. Standard error bars report the uncertainty around the mean which is due to the variance in the sample population. This variance comes from three sources: (1) the random connectivity matrix when each model is created, (2) the randomness present in the input patterns on each trial of training, and (3) the random initial firing vector at the beginning of each trial. As can be seen in that figure, the similarity between the hippocampal representations decreases in similarity over time, in a manner that approximates exponential or hyperbolic discounting. In Figure 2B, it can be seen that both exponential and hyperbolic functions provide a good fit to predictive similarity ( and , respectively). The fitted functions are, respectively, Vexp(t) = 1/e0.112 and Vhyp(t) = 1/(1+0.252t). To ensure that the results were not specific to the similarity metric, we also used Minkowski r-distance (which we inverted and normalized to obtain a similarity metric). The results were qualitatively similar, suggesting the results are robust to the selected metric, with the R2 values of 0.901 and 0.886 for exponential and hyperbolic fits, respectively. Taken together, these results suggest that hippocampal predictive similarity is suitable as a mechanism for understanding how reward delay discounting might manifest in downstream reward prediction systems.
Figure 2. Reward discounting from hippocampally-mediated predictive similarity.
(A) Emergent similarity of hippocampal CA3 representations for orthogonal stimuli decreases as the stimuli are increasingly separated in time. The plot on the left illustrates this by taking a time-point one-quarter of the way into the sequence, and comparing the activity pattern on that time-step to each subsequent time-step of activity (average of N =50 simulations, all 4,096 neurons in the network used; error bars are standard error of the mean). (B) The plot on the right shows exponential and hyperbolic functions fitted to the data comparison (see Results). It is proposed that this phenomenon is a basis for how hippocampal neural networks contribute to reward delay discounting. As in Figure 1, data are from the last trial of training.
In this network the non-clamped neurons play a formative role in the learning of the sequence by providing local context (Wallenstein & Hasselmo, 1997; Wu et al., 1996). It is interesting to consider what aspects of the predictive similarity are contributed by the 2,000 clamped and 2,096 non-clamped neurons, respectively. The predictive similarity curve was generally similar for both populations of neurons and remained well fit by both exponential and hyperbolic functions. Restricting analysis to the clamped neurons only biased the curve to be slightly less exponential (clamped only: ) whereas restricting analysis to the non-clamped only biased the curve to be more exponential and less hyperbolic ( ). This suggests that the relative strength of the input patterns (e.g., their salience) compared to recurrent excitation may be a factor in determining the precise shape and functional form of the reward delay discounting curve.
We confirmed that the number of training trials (i.e., 120) did not play a particularly influential role in the obtained results by training networks for 50 trials and for 150 trials. In both cases, the results were comparable to the present results. With 50 trials each, the predictive similarity curve was slightly more exponential, whereas with 150 trials each, the curve was slightly more hyperbolic. There is likely some interplay between number of training trials, noise levels in the externally clamped units, and overall activity levels in the network. Further research may provide constraints on these parameters.
As mentioned in the introduction, the most common account of hippocampal contributions to decision-making is the “mental simulation” account according to which future reward payoffs are evaluated by imagining future events. Studies show that when rats deliberate in a T-maze, neurons in their hippocampus fire as though they were exploring the two options in the maze (Johnson et al., 2007; Johnson & Redish, 2007). A simulation study of T-maze decision making using the present hippocampal model has demonstrated activity in both paths in the model (Monaco & Levy, 2003). Although it is clear that this delayed activation could be used to select actions based on eventual outcomes, it is not immediately obvious whether or how this mechanism might lead to discounting of those delayed rewards.
One way to operationalize reward discounting in this model according to the “mental simulation” account is to hypothesize a decreasing robustness of recalled activity (i.e., decreasing similarity to the original activity generated by the stimuli) as the “mental simulation” episode proceeds. Indeed, we can test this hypothesis within the current model: the present model can be run in “mental simulation” mode by providing it with just the input pattern at the beginning of the sequence, and then allowing it to activate subsequent representations without any further input (August & Levy, 1999). Evaluating the mental simulation account within the context of this model then involves quantifying the degree to which the recalled representations resemble the original input activations and thereby activate the associated reward predictions.
In this model, “preplay” in the absence of further external inputs (i.e., free recall) typically occurs faster than the original sequence was presented during training (August & Levy, 1999). Figure 3A shows a similarity matrix for a single trained network during such a simulation episode, after the first input pattern of the sequence was presented. The network traverses the sequence in 55 time-steps, which is a speed up by a factor of approximately 2. We measured the maximum similarity of the recalled activity compared to the activity during the last trial of training and plotted this in Figure 3B. Counter to the predictions of the mental simulation account, the maximal similarity between recall and training patterns did not decrease over the course of the simulation episode, but rather increased slightly for the 50 simulated networks (excluding the first 5 time-steps, the mean slope of 0.0009 was greater than 0, t(49) > 3.82, p < 0.0004). The relationship still holds even if the measurement is extended to time-step 100 (mean slope 0.0002, t(49) > 2.83, p < 0.007) although this later activation is usually due to the sequence repeating itself. Thus, the robustness of the recalled patterns does not decrease as a sequence simulated, indicating that the present model makes predictions that are not compatible with the mental simulation account.
Figure 3. Evaluating the mental similarity account.
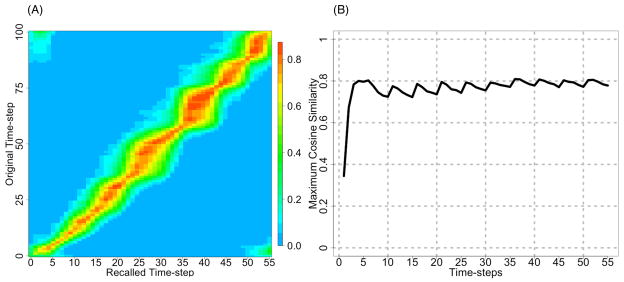
According to one operationalization of the mental simulation account, reward discounting occurs because stimuli predicted farther in the future decrease in similarity compared to their original representations as a function of lag. That is, the robustness of recall should decrease as a function of the delay to future predicted stimuli, resulting in weaker activity in downstream reward prediction systems. However, that hypothesis is not supported here: (A) Similarity in a typical example network between each “simulated” (recalled) pattern (x-axis) and the original training pattern as represented in the CA3 model (y-axis). (B) The average maximum similarity for 50 networks on each time-step is approximately constant throughout the simulated sequence. That is, each mentally-simulated stimulus is activated equally robustly as simulation episode proceeds. Because the fidelity of the simulated experience did not decrease, these results suggest that the present theory is not compatible with the mental simulation account. Note that unlike Figures 1 and 2, these plots are after training has been completed. The network was stimulated with the first pattern in the sequence only, and then played the rest of the sequence without any further external input.
Discussion
We took an existing computational model of hippocampal function and used it develop a novel, mechanistic explanation for reward discounting. This explanation suggests how projected activity from hippocampus to the striatum might serve a networked system that explains observed patterns in decision-making behavior about rewards (see Figure 4). An analysis of simulation results showed that, in the model, reward delay discounting arises when a recurrent network re-encodes input stimuli so that their similarity to future stimuli is increased. At decision time, the magnitude of this “predictive similarity” approximates a hyperbolic or exponential decreasing function. That is, the similarity of hippocampal output to future patterns decays with increasing temporal delay to the rewarded stimulus. Because the hippocampus has a strong functional projection to the ventral striatum, it follows that activity generated in the reward system for anticipated stimuli might also reflect this decay. This suggests that predictive similarity recoding could be an explanation of reward discounting and its particular functional form.
Figure 4. Systems-level view of the predictive similarity theory of reward discounting.
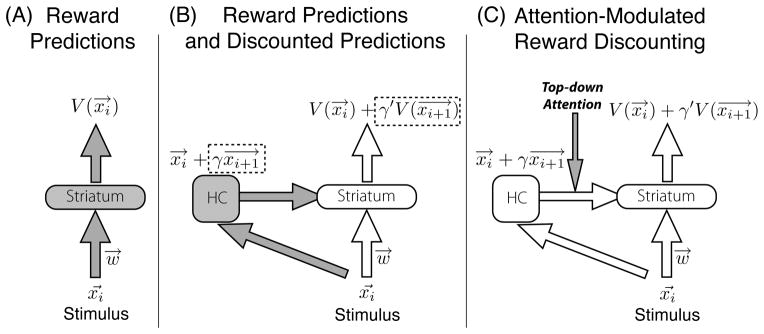
From left to right, the panels show the construction of the complete theory described in the text. (A) In typical reward-prediction network implementations of Reinforcement Learning using function approximators, a state representation x (e.g., visual stimulus) is presented to a neural network and is processed through a set of putatively cortico-striatal weights, generating a learned reward prediction V(x). This value can be used for optimal decision making or action selection. (B) The hippocampus (HC) forms a representation based on the stimulus at decision time that has predictive similarity to anticipated stimuli. Hippocampal input to the striatum partially activates previously learned reward predictions for future stimuli, augmenting the reward prediction to include discounted future reward. (C) The hippocampus’ contribution may be modulated by top-down attention, either increasing the gain of the hippocampo-striatal projection or modulating the relative salience of the sensory input to hippocampus. Both are hypothesized to increase the contribution of predictive similarity to the final reward prediction output.
Although we cannot make any strong claims against the mental simulation account playing a role in reward delay discounting, our analysis does suggest that the present theory is incompatible with that account. To briefly review, the mental simulation account proposes that future rewards influence decisions because at the time of a decision, the hippocampus simulates paths to reward-associated stimuli. We offer two proposals for operationalizing reward discounting based on mental simulation within the context of neural networks. The first possibility is that in the course of simulating the paths to a reward-associated stimulus, the strength of the representation degrades later in the sequence, thereby resulting in weaker hippocampo-striatal drive for delayed reward-associated stimuli. However, we found that when the CA3 network was allowed to perform sequence recall, patterns were recalled with equal robustness throughout the sequence. Thus, although it is clear that mental simulation occurs and may be useful for cognition, the present simulation results argue against a role for mental simulation in reward discounting per se. Future experimental and modeling work would be helpful to provide insight into understanding the possible joint contributions of the mental simulation and predictive similarity mechanisms. The equally-robust recall throughout the sequence likely occurred because this network forms transient attractors during learning, as do others with time-spanning associative learning rules (Liljenström & Wu, 1995; Sompolinsky & Kanter, 1986; Wu & Liljenstrom, 1994). Because the input patterns were orthogonal and all received the same number of training trials, the transient attractors during the sequence all had a similar shape.
The second possible way to operationalize mental simulation as a mechanism for reward discounting is to consider the possibility that some internal mental chronometer measures the elapsed simulated time until the reward-associated stimulus prediction is reached. According to this account, decisions about rewards that are delayed should take proportionally longer than decisions about more immediate rewards. However, this is not the case according to the data in Peters and Büchel. They examined reaction time by condition and by (undiscounted) value, and found that reaction time was independent of condition (see their Figure 2C).
Some of the other results of Peters and Büchel (2010) might be explained by future work with this theory, possibly through extensions of the present model. As mentioned above, Peters and Büchel (2010) found that participants imagining future events exhibited a decrease in reward discounting, and that this appeared to be mediated by increased functional connectivity between the prefrontal cortex and hippocampus. This increase in functional connectivity may influence the effective salience of intervening stimuli. Such a manipulation is likely to have an effect on the rate passing by the transient attractors, and might lead to an increase in similarity for successive patterns and a reduction of reward discounting – providing an explanation for the result found by Peters and Büchel (2010).
The attentional results might also be explained mechanistically by an increase in the gain of the hippocampal influence on activity in the striatal reward-predicting network (e.g., Figure 4C). Such a modulated projection could allow attention to enhance the stability and retrieval of both spatial and non-spatial representations in the hippocampus that are associated with reward (Muzzio et al., 2009). Thus there are at least two mechanisms that should be explored both theoretically and experimentally to better understand the modulatory effects of attention on reward delay discounting.
The hippocampal model used in this investigation (i.e., the model developed by Levy and colleagues) was chosen specifically because it emphasizes the generations of predictions in a temporal sequence. This afforded the examination of similarity across successive stimulus predictions. There exist many other hippocampal models, which all share family resemblance. However, the results here are only claimed to be general for the class of recurrent attractor models that are capable of learning sequences.
This article focused on the hippocampus as a source of discounted similarity influencing reward predictions in downstream regions like the striatum. However it is also possible that recurrent networks in other brain regions (e.g., the prefrontal cortex) could influence reward predictions and similarly promote reward discounting. Because reward delay discounting appears to affect decisions on many different timescales ranging from months and days down to the level of milliseconds (e.g., in the case of saccadic eye movements, Shadmehr et al., 2010), it is likely that diverse brain mechanisms underlie reward delay discounting.
Acknowledgments
I thank Chip Levy, Joe Monaco, Sean Polyn, Steve Yantis, Kechen Zhang, and the anonymous reviewers for helpful discussions and comments on an earlier version of this manuscript. This work was supported by NIH grant R01-DA013165 to Steve Yantis.
References
- Abbott LF, Blum KI. Functional significance of long-term potentiation for sequence learning and prediction. Cereb Cortex. 1996;6:406–16. doi: 10.1093/cercor/6.3.406. [DOI] [PubMed] [Google Scholar]
- Addis DR, Cheng T, Roberts RP, Schacter DL. Hippocampal contributions to the episodic simulation of specific and general future events. Hippocampus. 2011;21:1045–52. doi: 10.1002/hipo.20870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- August DA, Levy WB. Temporal sequence compression by an integrate-and-fire model of hippocampal area CA3. J Comput Neurosci. 1999;6:71–90. doi: 10.1023/a:1008861001091. [DOI] [PubMed] [Google Scholar]
- Bamford NS, Zhang H, Schmitz Y, Wu NP, Cepeda C, Levine MS, Schmauss C, Zakharenko SS, Zablow L, Sulzer D. Heterosynaptic dopamine neurotransmission selects sets of corticostriatal terminals. Neuron. 2004;42:653–63. doi: 10.1016/s0896-6273(04)00265-x. [DOI] [PubMed] [Google Scholar]
- Bi GQ, Poo MM. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J Neurosci. 1998;18:10464–72. doi: 10.1523/JNEUROSCI.18-24-10464.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung THC, Cardinal RN. Hippocampal lesions facilitate instrumental learning with delayed reinforcement but induce impulsive choice in rats. BMC Neurosci. 2005;6:36. doi: 10.1186/1471-2202-6-36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Figner B, Knoch D, Johnson EJ, Krosch AR, Lisanby SH, Fehr E, Weber EU. Lateral prefrontal cortex and self-control in intertemporal choice. Nat Neurosci. 2010;13:538–9. doi: 10.1038/nn.2516. [DOI] [PubMed] [Google Scholar]
- Gamboz N, Brandimonte MA, De Vito S. The role of past in the simulation of autobiographical future episodes. Exp Psychol. 2010;57:419–28. doi: 10.1027/1618-3169/a000052. [DOI] [PubMed] [Google Scholar]
- Green L, Myerson J, Ostaszewski P. Discounting of delayed rewards across the life span: Age differences in individual discounting functions. Behavioural Processes. 1999;46:89–96. doi: 10.1016/S0376-6357(99)00021-2. [DOI] [PubMed] [Google Scholar]
- Gupta R, Duff M, Denburg N, Cohen N, Bechara A, Tranel D. Declarative memory is critical for sustained advantageous complex decision-making. Neuropsychologia. 2009;47:1686–1693. doi: 10.1016/j.neuropsychologia.2009.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hare TA, Camerer CF, Rangel A. Self-control in decision-making involves modulation of the vmpfc valuation system. Science. 2009;324:646–8. doi: 10.1126/science.1168450. [DOI] [PubMed] [Google Scholar]
- Hassabis D, Kumaran D, Vann SD, Maguire EA. Patients with hippocampal amnesia cannot imagine new experiences. Proc Natl Acad Sci U S A. 2007;104:1726–31. doi: 10.1073/pnas.0610561104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollerman JR, Tremblay L, Schultz W. Influence of reward expectation on behavior-related neuronal activity in primate striatum. J Neurophysiol. 1998;80:947–63. doi: 10.1152/jn.1998.80.2.947. [DOI] [PubMed] [Google Scholar]
- Joel D, Niv Y, Ruppin E. Actor-critic models of the basal ganglia: new anatomical and computational perspectives. Neural Netw. 2002;15:535–47. doi: 10.1016/s0893-6080(02)00047-3. [DOI] [PubMed] [Google Scholar]
- Johnson A, van der Meer MAA, Redish AD. Integrating hippocampus and striatum in decision-making. Curr Opin Neurobiol. 2007;17:692–7. doi: 10.1016/j.conb.2008.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson A, Redish AD. Neural ensembles in CA3 transiently encode paths forward of the animal at a decision point. J Neurosci. 2007;27:12176–89. doi: 10.1523/JNEUROSCI.3761-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kable JW, Glimcher PW. The neural correlates of subjective value during intertemporal choice. Nat Neurosci. 2007;10:1625–33. doi: 10.1038/nn2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kable JW, Glimcher PW. An “as soon as possible” effect in human intertemporal decision making: behavioral evidence and neural mechanisms. J Neurophysiol. 2010;103:2513–31. doi: 10.1152/jn.00177.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kacelnik A. Normative and descriptive models of decision making: time discounting and risk sensitivity. Ciba Found Symp. 1997;208:51–67. doi: 10.1002/9780470515372.ch5. discussion 67–70. [DOI] [PubMed] [Google Scholar]
- Kelley A, Domesick V. The distribution of the projection from the hippocampal formation to the nucleus accumbens in the rat: An anterograde and retrograde-horseradish peroxidase study. Neuroscience. 1982;7:2321–2335. doi: 10.1016/0306-4522(82)90198-1. [DOI] [PubMed] [Google Scholar]
- Lansink CS, Goltstein PM, Lankelma JV, McNaughton BL, Pennartz CMA. Hippocampus leads ventral striatum in replay of place-reward information. PLoS Biol. 2009;7:e1000173. doi: 10.1371/journal.pbio.1000173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy W. A computational approach to hippocampal function. Computational models of learning in simple neural systems. 1989;23:243–305. [Google Scholar]
- Levy WB. A sequence predicting CA3 is a flexible associator that learns and uses context to solve hippocampal-like tasks. Hippocampus. 1996;6:579–90. doi: 10.1002/(SICI)1098-1063(1996)6:6<579::AID-HIPO3>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- Levy WB, Sanyal A, Rodriguez P, Sullivan DW, Wu XB. The formation of neural codes in the hippocampus: trace conditioning as a prototypical paradigm for studying the random recoding hypothesis. Biol Cybern. 2005;92:409–26. doi: 10.1007/s00422-005-0568-9. [DOI] [PubMed] [Google Scholar]
- Levy WB, Steward O. Temporal contiguity requirements for long-term associative potentiation/depression in the hippocampus. Neuroscience. 1983;8:791–7. doi: 10.1016/0306-4522(83)90010-6. [DOI] [PubMed] [Google Scholar]
- Liljenström H, Wu XB. Noise-enhanced performance in a cortical associative memory model. Int J Neural Syst. 1995;6:19–29. doi: 10.1142/s0129065795000032. [DOI] [PubMed] [Google Scholar]
- Mariano TY, Bannerman DM, McHugh SB, Preston TJ, Rude-beck PH, Rudebeck SR, Rawlins JNP, Walton ME, Rushworth MFS, Baxter MG, Campbell TG. Impulsive choice in hippocampal but not orbitofrontal cortex-lesioned rats on a nonspatial decision-making maze task. Eur J Neurosci. 2009;30:472–84. doi: 10.1111/j.1460-9568.2009.06837.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H, Lübke J, Frotscher M, Sakmann B. Regulation of synaptic efficacy by coincidence of postsynaptic aps and epsps. Science. 1997;275:213–5. doi: 10.1126/science.275.5297.213. [DOI] [PubMed] [Google Scholar]
- Mazur J. An adjusting procedure for studying delayed reinforcement. Quantitative Analyses of Behavior: The Effects of Delay and of Intervening Events on Reinforcement Value. 1987;5:55. [Google Scholar]
- Mazur JE, Biondi DR. Delay-amount tradeoffs in choices by pigeons and rats: hyperbolic versus exponential discounting. J Exp Anal Behav. 2009;91:197–211. doi: 10.1901/jeab.2009.91-197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClure SM, Ericson KM, Laibson DI, Loewenstein G, Cohen JD. Time discounting for primary rewards. J Neurosci. 2007;27:5796–804. doi: 10.1523/JNEUROSCI.4246-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClure SM, Laibson DI, Loewenstein G, Cohen JD. Separate neural systems value immediate and delayed monetary rewards. Science. 2004;306:503–7. doi: 10.1126/science.1100907. [DOI] [PubMed] [Google Scholar]
- Mehta M, Barnes C, McNaughton B. Experience-dependent, asymmetric expansion of hippocampal place fields. Proceedings of the National Academy of Sciences of the United States of America. 1997;94:8918. doi: 10.1073/pnas.94.16.8918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehta M, Quirk M, Wilson M. Experience-dependent asymmetric shape of hippocampal receptive fields. Neuron. 2000;25:707–715. doi: 10.1016/s0896-6273(00)81072-7. [DOI] [PubMed] [Google Scholar]
- Mitman K, Laurent P, Levy W. Defining time in a minimal hippocampal CA3 model by matching time-span of associative synaptic modification and input pattern duration. Neural Networks, 2003. Proceedings of the International Joint Conference on; 2003. pp. 1631–1636. [Google Scholar]
- Monaco J, Levy W. T-maze training of a recurrent CA3 model reveals the necessity of novelty-based modulation of LTP in hippocampal region CA3. Neural Networks, 2003. Proceedings of the International Joint Conference on; 2003. pp. 1655–1660. [Google Scholar]
- Muzzio IA, Levita L, Kulkarni J, Monaco J, Kentros C, Stead M, Abbott LF, Kandel ER. Attention enhances the retrieval and stability of visuospatial and olfactory representations in the dorsal hippocampus. PLoS Biol. 2009;7:e1000140. doi: 10.1371/journal.pbio.1000140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pennartz CMA, Lee E, Verheul J, Lipa P, Barnes CA, Mc-Naughton BL. The ventral striatum in off-line processing: ensemble reactivation during sleep and modulation by hippocampal ripples. J Neurosci. 2004;24:6446–56. doi: 10.1523/JNEUROSCI.0575-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters J, Büchel C. Episodic future thinking reduces reward delay discounting through an enhancement of prefrontal-mediotemporal interactions. Neuron. 2010;66:138–48. doi: 10.1016/j.neuron.2010.03.026. [DOI] [PubMed] [Google Scholar]
- Polyn S, Wu X, Levy W. Entorhinal/dentate excitation of CA3: A critical variable in hippocampal models. Neurocomputing. 2000;32:493–499. [Google Scholar]
- Rawlins JN, Feldon J, Butt S. The effects of delaying reward on choice preference in rats with hippocampal or selective septal lesions. Behav Brain Res. 1985;15:191–203. doi: 10.1016/0166-4328(85)90174-3. [DOI] [PubMed] [Google Scholar]
- Reynolds JNJ, Wickens JR. Dopamine-dependent plasticity of corticostriatal synapses. Neural Netw. 2002;15:507–21. doi: 10.1016/s0893-6080(02)00045-x. [DOI] [PubMed] [Google Scholar]
- Schacter DL, Addis DR. On the nature of medial temporal lobe contributions to the constructive simulation of future events. Philos Trans R Soc Lond B Biol Sci. 2009;364:1245–53. doi: 10.1098/rstb.2008.0308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997;275:1593–9. doi: 10.1126/science.275.5306.1593. [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Orban de Xivry JJ, Xu-Wilson M, Shih TY. Temporal discounting of reward and the cost of time in motor control. J Neurosci. 2010;30:10507–16. doi: 10.1523/JNEUROSCI.1343-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shon AP, Wu XB, Sullivan DW, Levy WB. Initial state randomness improves sequence learning in a model hippocampal network. Phys Rev E Stat Nonlin Soft Matter Phys. 2002;65:031914. doi: 10.1103/PhysRevE.65.031914. [DOI] [PubMed] [Google Scholar]
- Sompolinsky &, Kanter I. Temporal association in asymmetric neural networks. Phys Rev Lett. 1986;57:2861–2864. doi: 10.1103/PhysRevLett.57.2861. [DOI] [PubMed] [Google Scholar]
- Sullivan DW, Levy WB. Quantal synaptic failures enhance performance in a minimal hippocampal model. Network. 2004;15:45–67. [PubMed] [Google Scholar]
- Suri RE, Schultz W. Learning of sequential movements by neural network model with dopamine-like reinforcement signal. Exp Brain Res. 1998;121:350–4. doi: 10.1007/s002210050467. [DOI] [PubMed] [Google Scholar]
- Sutton RS, Barto AG. Reinforcement learning: an introduction. IEEE Trans Neural Netw. 1998;9:1054. [Google Scholar]
- Wallenstein GV, Hasselmo ME. Gabaergic modulation of hippocampal population activity: sequence learning, place field development, and the phase precession effect. J Neurophysiol. 1997;78:393–408. doi: 10.1152/jn.1997.78.1.393. [DOI] [PubMed] [Google Scholar]
- Wu X, Baxter RA, Levy WB. Context codes and the effect of noisy learning on a simplified hippocampal CA3 model. Biol Cybern. 1996;74:159–65. doi: 10.1007/BF00204204. [DOI] [PubMed] [Google Scholar]
- Wu X, Liljenstrom H. Regulating the nonlinear dynamics of olfactory cortex. Network: Computation in Neural Systems. 1994;5:47–60. [Google Scholar]