Abstract
The non-Newtonian properties of blood are of great importance since they are closely related with incident cardiovascular diseases. A good understanding of the hemodynamics through the main vessels of the human circulatory system is thus fundamental in the detection and especially in the treatment of these diseases. Very often such studies take place in vitro for convenience and better flow control and these generally require blood analogue solutions that not only adequately mimic the viscoelastic properties of blood but also minimize undesirable optical distortions arising from vessel curvature that could interfere in flow visualizations or particle image velocimetry measurements. In this work, we present the viscoelastic moduli of whole human blood obtained by means of passive microrheology experiments. These results and existing shear and extensional rheological data for whole human blood in the literature enabled us to develop solutions with rheological behavior analogous to real whole blood and with a refractive index suited for PDMS (polydymethylsiloxane) micro- and milli-channels. In addition, these blood analogues can be modified in order to obtain a larger range of refractive indices from 1.38 to 1.43 to match the refractive index of several materials other than PDMS.
INTRODUCTION
Human blood is a dense suspension of elements, such as platelets, leucocytes, and mainly erythrocytes in an aqueous polymer solution, the plasma.1, 2 Blood rheology is essentially determined by the behavior of the erythrocytes, which aggregate/disaggregate depending on the local flow conditions, and have the capacity to deform if needed.3 The deformation of erythrocytes and its aggregates under shear and periodic forcing, leads to cyclic storage and release of elastic energy in addition to a shear-thinning viscosity and normal stress effects. These non-Newtonian properties of blood have long been recognized, measured, and modelled.4, 5, 6, 7
The non-Newtonian behavior of blood, which affects its flow in both large, but mostly in small vessels characteristic of the microcirculation, is closely related to incident cardiovascular events like ischaemic heart disease and stroke.8, 9, 10 Therefore, a fundamental understanding of the detailed fluid dynamics of blood flow and of the distribution of the wall shear stress in small vessels is essential to help detect cardiovascular diseases and to develop preventive measures and design suitable treatments.11 Moreover, recent developments in blood sample loading and blood/tumor cell sorting devices12, 13, 14 warrant the study of the viscoelastic properties of blood in microfluidic devices.
The manipulation of real whole blood and the study of its flow dynamics in vitro are difficult because of the cost, safety, and ethics issues involved. Furthermore, the erythrocytes in vitro could be damaged in the absence of oxygen and nutrients leading to a change of its properties. This fact limits the use of real blood in long term experiments. Additionally, the rheological properties of blood at room temperature are different from those at body temperature15 leading to an additional complication in setting up experiments.16 For these reasons, the development of reliable blood analogues and the study of their flow characteristics are of great importance.
Most proposed analogues in the literature are either Newtonian, using glycerol and water/glycerol mixtures or non-Newtonian aqueous solutions based on xanthan gum and PAA (polyacrylamide),17, 18, 19, 20, 21 some of which have been used in micro-channels with simple planar geometries.22, 23 Sousa et al.22 used two blood analogue fluids to show that despite their similar steady shear rheology, the flow behavior in micro scale devices is markedly different, thus demonstrating that the elastic character also needs to be considered in the development of reliable blood analogues. Additionally, in geometries with solid-liquid interfaces with curvature (e.g., of circular cross-section), typical of the cardiovascular system, the blood analogue fluids to be used should have the same refractive index of the material of the microchannel in order to reduce undesirable optical distortions, hidden regions and reflections that preclude accurate measurements when using optical flow diagnostic tools, as in flow visualizations and in particle image velocimetry.17
There is a wide range of transparent liquids with refractive indices from 1.28 to 1.75,24 but matching the refractive index and the fluid rheology simultaneously considerably narrows the range of options. In fact, to choose an adequate fluid for a particular application one has to consider, in addition to the refractive index and the fluid rheology, optical transparency, density, material compatibility, chemical stability, safety, and price.25, 26 In microfluidics, polydimethylsiloxane (PDMS) is one of the most widely used polymers to manufacture channels because of its transparency at optically visible wavelengths, biocompatibility, low autofluorescence, low cost, deformability and ability to mold easily among other advantages, which make this polymer a good candidate for manufacturing model vessels to study the dynamics of vascular diseases.27, 28, 29
In this work, we develop transparent non-Newtonian blood analogues that exhibit rheological behavior under shear and extension very similar to real whole blood. To this end, we first measured the linear viscoelastic properties of real whole blood, the storage (G′) and loss (G″) moduli, using passive microrheology. These viscoelastic properties were combined with the viscosity curves in Thurston4 and Valant et al.30 to develop the blood analogues and subsequently checked also in terms of the relaxation time measured in extension by Brust et al.31 In addition, the blood analogues have a refractive index between 1.38 and 1.43, which makes them suitable to be studied in micro- and milli-PDMS model vessels, whose refractive index is 1.41.
The manuscript is organized as follows: in Sec. 2, the materials and experimental methods used are explained. In Sec. 3, we present the results of the rheology of whole human blood and their analogues in terms of the viscosity curves, relaxation time in extension and viscoelastic moduli, followed by the analysis of the refractive index and its influence on the flow studies in micro- and milli-channels. Finally, the main conclusions are summarized in Sec. 4.
EXPERIMENTAL TECHNIQUES
Whole blood samples and blood analogues
The real whole blood samples were obtained from a healthy male donor. Approximately 4 ml of blood was drawn to which 7.2 mg of ethylenediaminetetraacetic acid (EDTA) were added in order to avoid coagulation. This anticoagulant offers one of the best performances in terms of blood cell preservation32 and additionally, it is easily accessible and regularly used in the scientific community.30, 33, 34 The blood samples were kept at 4 °C for a maximum of three days during which all experiments were carried out. The blood analogue polymer solutions were mixed using magnetic stirrers at low speeds to prevent mechanical degradation of the polymers chains and their refractive indices were measured using ABBE Refractometer (Model 315RS Digital, Zuzi).
Fluid rheology and passive microrheology
The steady shear rheology experiments were performed on a stress-controlled shear rheometer (T.A. Instruments, model AR-G2), with a cone-plate of 60 mm diameter and 1° of angle, and with a plate-plate geometry of 60 mm diameter and a gap of 100 μm. Steady shear flow curves were obtained in the range of shear rates, , and were carried out at 20.0 °C. For the rheological extensional flow experiments, a Haake CaBER-1 capillary break-up extensional rheometer (Thermo Haake GmbH) was used, equipped with circular plates 4 mm in diameter and a laser micrometer to follow the time evolution of the filament diameter. In the present study, the initial and the final gap between plates were set to 2.0 and 6.56 mm, respectively. Fluid samples were carefully loaded between the plates using a syringe to ensure the absence of trapped air within the sample. As the fluids to be characterized are only very weakly elastic, the oscillatory tests could not be performed using shear rheometers due to their limited sensitivity. Instead, one-point passive microrheology was used to determine the viscoelastic storage and loss moduli, G′ and G″, respectively, for all fluids (including real blood samples and blood analogues).35, 36 Microrheology is also preferred when the material is available only in very small quantities (). Note that two-point passive microrheology could not be performed due to aggregation of tracer particles at higher concentrations, resulting in poor statistics.37
Passive microrheology is based on the diffusivity of tracer particles dispersed in a solution. For a spherical particle with a radius a diffusing in a Newtonian liquid of viscosity η, the particle's mean square displacement (MSD) is the averaged squared distance that the tracer particle travels in a given time interval, referred to as lag time (τ)
| (1) |
where x is the tracer position in one dimension, t is time and ⟨ ⟩ refers to the time and ensemble average of all the tracer particles.37, 38
The MSD is then related to the diffusivity D via ⟨Δx2 (τ)⟩ = 2D where
| (2) |
This equation is known as the Stokes-Einstein relation and it asserts that the measurement of the diffusivity of a thermally excited particle can be used to extract the viscosity of the fluid, relating the dynamics of an embedded tracer particle with the rheology of the medium. For a viscoelastic material, this equation has been modified to obtain the Generalized Stokes-Einstein relation which provides the viscoelastic properties of the medium35, 36, 39
| (3) |
where G*(ω) is the complex modulus as a function of frequency, ω and ⟨Δr(ω2)⟩ is the Fourier transform of the MSD. The real G′(ω) and imaginary G″(ω) parts of the complex shear modulus are called the storage and loss moduli, respectively, and represent the solid-like and liquid-like behavior of the material.
The passive microrheology experiments were performed on an inverted microscope (Olympus CKX41), equipped with a 40× objective with numerical aperture NA = 0.55. The sample chamber consisted of a 200 μm high precision cell made of quartz (Quartz Suprasil®, Hellma Analytics). As tracer particles we used monodisperse 2.8 μm diameter beads (Dynabeads® M-270 Carboxylic Acid); the particle size was chosen according to the maximum viscosity of the system and lag time of tracer particles movement.40 The tracer particles were dried beforehand and redispersed in the blood (or blood analogue samples) to avoid possible changes in the rheology due to the presence of water. Image stacks were recorded by video microscopy leading to movies of 45 s at 90 fps. The particle trajectories were then obtained using tracking routines similar to those reported in Crocker and Grier.38 Around 60 particles are tracked in each image, which with our field of view corresponds to a particle volume fraction of around .41
Imaging of blood analogue flow in PDMS micro- and milli-channels
To evaluate the effect of the refractive index of the blood analogues on their imaging in PDMS model vessels, we tested the image quality during flow in PDMS channels using standard brightfield optical microscopy. We used two different PDMS channels with simplified geometries at the micro- and milli-scale, representative of blood vessels of different diameters. The micro-channel was fabricated in PDMS using standard soft-lithography techniques from an SU-8 photo-resist mold,42 which confers the geometry a planar configuration with a constant depth throughout. In contrast, the milli-channel exhibits a circular cross-section, which provides a more realistic approach to real human vessels. It was fabricated using the lost-sucrose casting technique,43 allowing the assessment of wall curvature effects on the imaging of the flow field. During the imaging, we focused at the middle plane of the channels using a 4× objective for the milli-channels with circular cross-section and a 20× objective for the micro-channels with a rectangular cross-section. To visualise the flow and assess the distortion effects, a small amount of carboxylated polystyrene spheres of 15.48 μm diameter (Microparticles Gmbh) were added to the blood analogues.
RESULTS AND DISCUSSION
Viscoelastic properties of blood
Whole blood is well characterized in the literature in terms of steady shear rheology and several flow curves have been published.4, 8, 44, 45 However, given the viscoelastic nature of blood, viscosity measurements in steady shear flow are not enough to fully characterize the fluid rheology and tests under oscillatory shear are essential. These allow the evaluation of the relative contributions of viscous and elastic responses. However, reliable data obtained under these conditions are still lacking. Valant et al.30 have reported the viscosity curves obtained for three female and three male healthy donors at 37 °C with different hematocrit (Hct) values. For all donors, the viscosity was markedly shear-thinning confirming the early measurements of Chien et al.46, 47 and Thurston4 and providing evidence of contributions of both viscosity and elasticity in the rheology of whole blood (which will be separately evaluated as G′ and G″ afterwards). At low shear rates, the red blood cells tend to aggregate leading to a solid-like behavior, but as the shear rate is increased the red blood cells disaggregate and align with the flow imparting a liquid-like behavior to blood, with a reduced ability to store elastic energy. The differences among the six viscosity curves obtained by Valant et al.30 correspond to the differences in the Hct values, showing stronger shear-thinning as the concentration of red blood cells increases.30, 48, 49
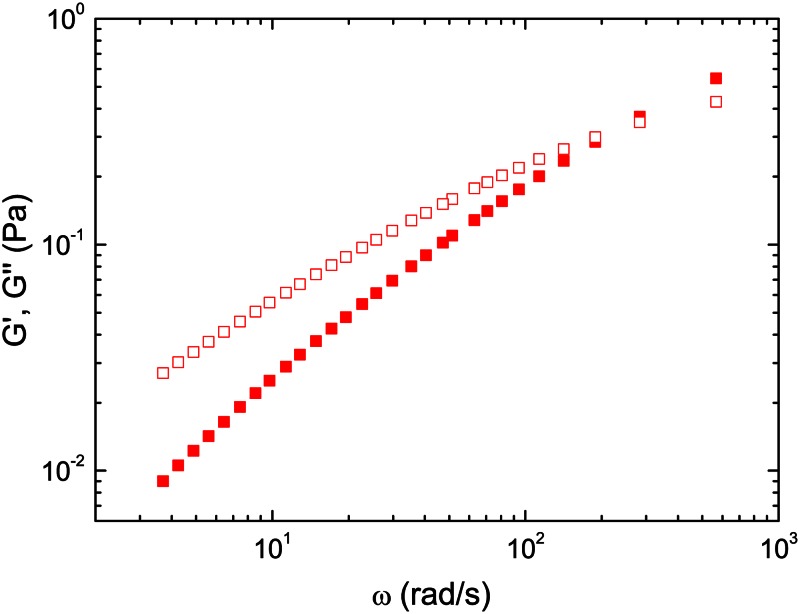
In order to quantify the relative magnitude of elastic and viscous behavior of blood, passive microrheology experiments were carried out with real whole blood. In Figure 1, the viscoelastic moduli of the human blood sample with Hct = 44% at 27 °C determined using microrheology are plotted. It is clear that G″ (loss modulus) is larger than G′ (storage modulus) indicating a liquid like behavior in the whole range of frequencies studied. Both storage and loss moduli increase as frequency is increased, albeit this increase is higher for the elastic component. These curves confirm that there is a non-negligible elastic contribution to the bulk rheology of whole human blood.
Figure 1.
Storage (red filled squares) and loss (red empty squares) moduli of whole human blood with Hct = 44% determined by passive microrheology at T = 27 °C, within the viscoelastic linear range.
To obtain the viscoelastic moduli of real blood at the characteristic temperature of the human circulatory system (37 °C), we rescaled the data using the time-temperature superposition principle. According to the steady shear data measured by Langstroth15 at temperatures ranging from 5 to 37 °C, it is possible to obtain the temperature shift factor (aT), which is given by
| (4) |
where η(T) and ρ are the shear viscosity and fluid density at temperature T; η(Tref) and refer to the same properties at a reference temperature Tref. For the small range of temperatures used in their measurements, the fluid density is approximately constant and the scaled curve can be determined after reducing the viscosity and shear rate according to Eqs. 5, 6, respectively
| (5) |
| (6) |
yielding aT = 1.96 from the data of Langstroth.15
According to Bird, Armstrong, and Hassager50 the master curves for the viscoelastic moduli can be rescaled as
| (7) |
| (8) |
while the angular frequency scales similarly as the shear rate
| (9) |
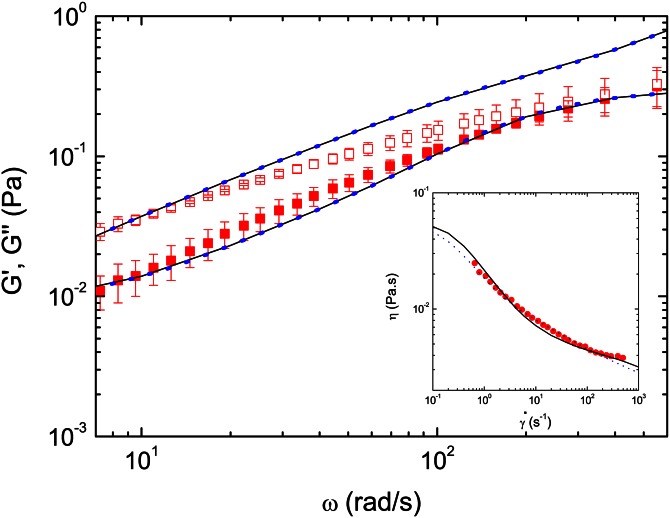
The rescaled viscoelastic moduli for real whole blood at (37 °C) are shown in Figure 2 as symbols. Previous works dealing with the rheological behavior of blood with increasing temperature15 have shown that the temperature has a strong influence in the shear viscosity. This relationship is slightly non-linear at the high and low end of temperatures; however, in this work the viscoelastic moduli were shifted linearly as it is a common practice for the small range of temperatures used. Some works dealing with the blood flow and red blood cells flow in micro channels51, 52 mimicking the blood behavior through the circulatory system have been performed at room temperature, since the proper normalization of data makes the results valid at body temperature.
Figure 2.
Storage (red filled squares) and loss (red empty squares) moduli of blood from Figure 1 rescaled to 37 °C using time-temperature superposition, and the fits to multi-mode Giesekus (solid line) and sPTT (blue dots) models. Figure inset shows comparison between the steady shear viscosity curve of whole real blood (red circles) obtained experimentally by Valant et al.30 and the model fits.
It is often advantageous for reference and numerical calculations to have a constitutive equation for blood rheology. Usually, the purely viscous Generalized Newtonian fluid model is used with the viscosity described by equations like the Casson, Carreau, Quemada and power law models, amongst others.53, 54, 55, 56 These models can describe the shear-thinning behavior of blood but are not able to account for its viscoelasticity. Although scarcer, viscoelastic models are necessary for more complete descriptions of blood rheology, and often some of its parameters are dependent on the evolution of structures formed by the erythrocytes.2, 5, 6, 7, 57
Here, the viscoelastic moduli and the steady viscosity data were fitted using two viscoelastic multi-mode differential constitutive equations: the simplified Phan-Thien-Tanner (sPTT) and Giesekus models58, 59 with a Newtonian solvent contribution of viscosity , but without the use of structure-dependent parameters. These two multi-mode models can be compactly written as
| (10) |
| (11) |
| (12) |
with
| (13) |
where ∇ is the upper-convected derivative and
| (14) |
The deformation tensor is given by
| (15) |
Each model for has four modes (N = 4) and three coefficients in each mode: the relaxation time (), the viscosity contribution to the zero shear viscosity () and the extensibility coefficient (ϵ) or the mobility factor (α). For the sPTT model and ϵ should lie in the range although it is more often in the range . For the Giesekus model and the mobility factor should lie in the range . The best fits for each model give the parameters shown in Table TABLE I. and are plotted in Figure 2 as lines, where the models are compared to the experimental data of real blood at 37 °C. Although the Giesekus model shows a better fit, the nonlinear term introduces a nonzero second normal stress difference, which so far has not been reported for blood. Hence, the sPTT model should preferably be used and the Giesekus model should only be used when there is the certainty that blood flow presents this second normal stress difference.
TABLE I.
Parameters of the multi-mode Giesekus and sPTT model fits for whole human blood.
| Giesekus (ϵ = 0) | sPTT (α = 0) | |||||
|---|---|---|---|---|---|---|
| Mode (i) | (Pa s) | (s) | (-) | (Pa s) | (s) | (-) |
| 1 | 0.05 | 7 | 0.06 | 0.05 | 7 | 0.2 |
| 2 | 0.001 | 0.4 | 0.001 | 0.001 | 0.4 | 0.5 |
| 3 | 0.001 | 0.04 | 0.001 | 0.001 | 0.04 | 0.5 |
| 4 | 0.0016 | 0.006 | 0.001 | 0.0016 | 0.006 | 0.5 |
| 5 (solvent) | 0.0012 | 0 | 0 | 0.0012 | 0 | 0 |
Blood analogue characterization
Based on our data for the viscoelastic moduli of blood and the viscosity curves from Thurston,4 we developed four different polymer solutions as blood analogues and subsequently checked them in terms of relaxation time in extensional flow. The composition of the different solutions are presented in Table TABLE II. (polyacrylamide (PAA) with Mw = 18 × 106 g/mol, from Polysciences, xanthan gum (XG) and hyaluronic acid (HA) from Sigma Aldrich and sucrose from AnalaR Normapur). The refractive indices of the solutions are 1.39 for the solutions with sucrose and water as a solvent, and 1.41 for the solutions with DMSO and water as a solvent. The shear viscosity curves for the four blood analogue solutions are shown in Figure 3 and were measured using a cone-plate (appropriate for measurements at the low end of shear rates) and a plate-plate (appropriate for measurements at high shear rates) geometries in order to obtain reliable viscosity measurements in a wide range of shear rates.
TABLE II.
Composition of blood analogues and refractive index. The concentration of DMSO and sucrose is given in wt.% in distilled water. a
| Acronym | PAA | XG | DMSO | HA | Sucrose | Refractive index | |
|---|---|---|---|---|---|---|---|
| DP | PAA + HA + DMSO | 60 ppm | — | 50% | 25 ppm | — | 1.41 |
| DX | XG + DMSO | — | 100 ppm | 52% | — | — | 1.41 |
| SP | PAA + HA + sucrose | 34 ppm | — | — | 17 ppm | 35% | 1.39 |
| SX | XG + sucrose | — | 100 ppm | — | — | 35% | 1.39 |
PAA = polyacrylamide, XG = xanthan gum, DMSO = dimethylsulfoxide, HA = hyaluronic acid.
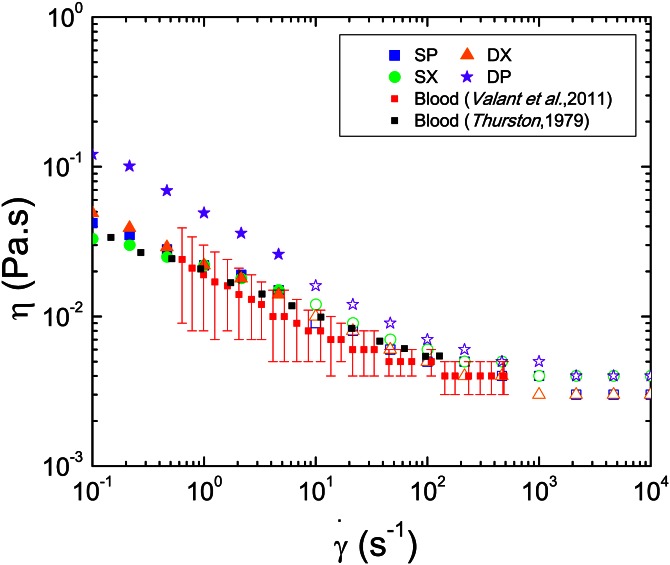
Figure 3.
Viscosity curves for the four analogue solutions in comparison with the viscosity curves of whole human blood of Valant et al.30 (average between F1 and M3 samples and error bars representing the standard deviation of their averaged values) and Thurston's data.4 For the analogue solutions open and closed symbols denote measurements with parallel plates and cone-plate, respectively.
The shear-thinning behavior observed for the blood analogues is broadly in good agreement with the non-Newtonian characteristics found in steady shear experiments with whole real blood carried out by Thurston4 and by Valant et al.30 taking into account the variation associated with the different Hct values in the samples considered in the latter case. Both xanthan gum solutions in DMSO and in sucrose show shear-thinning behavior which is in agreement with the viscosity curve for whole real blood, as shown in Figure 3. The solution of PAA, HA, and DMSO exhibits higher values of the shear viscosity than the other analogues, though above 200 s–1 the shear viscosity behavior is close to that of blood, resulting in a valid analogue alternative at high shear rates.
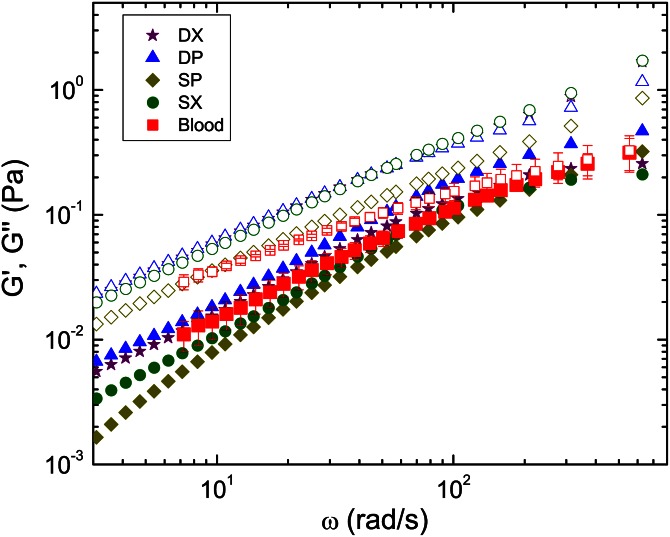
In Figure 4, the storage (G′) and loss (G″) moduli obtained by passive microrheology are presented for the four viscoelastic solutions over a wide range of frequencies and compared to those of blood. In all cases, the behavior is clearly liquid-like since G″ is larger than G′ in the whole frequency range studied. Solutions with sucrose as a solvent show slightly lower G′ values than solutions based on DMSO, though all four solutions present viscoelastic behavior similar to whole human blood. At large frequencies, blood undergoes a progressively lower variation of G″ with frequency, whereas the corresponding variation for the blood analogues is more linear, yielding a higher deviation from the whole blood data at high frequencies. Nevertheless, the good overall agreement between the analogues and blood, as obtained from both the flow curves and single-particle microrheology, confirms the applicability of the proposed solutions as blood analogues.
Figure 4.
Storage (G′, closed symbols) and loss (G″, open symbols) moduli measured by passive microrheology. Comparison between data for the blood analogue solutions at 20 °C and data for real blood (Hct = 44%) shifted to 37 °C. For real blood the results shown are the average of three measurements. The error bars correspond to differences at P < 0.05 (Student's t-test).
It has been shown that developing blood analogue solutions taking into account only the rheological behavior under shear flow is not enough to ensure an accurate representation of blood22 and for that reason a complete rheological characterization based also on the extensional properties has also been done. Very recently, Brust et al.31 measured the relaxation time of whole human blood in extensional flow, obtaining an approximated value of 2 ms. Table TABLE III. shows the characteristic relaxation times of the four blood analogue solutions measured in the capillary breakup extensional rheometer. It is clear that even though the viscosity curves and viscoelastic moduli of the four solutions are very similar, the relaxation time of the samples prepared with XG is one order of magnitude smaller than those prepared with PAA and HA. For that reason, and in comparison with the findings of Brust et al.,31 we can state that samples DX and SX constitute more complete blood analogues, as they present relaxation times very similar to whole human blood (≈2 ms).
TABLE III.
Relaxation times (λ) obtained from CaBER for the four analogues solutions at room temperature.
| Blood analogue | λ (ms) |
|---|---|
| DP | 13.4 ± 0.9 |
| DX | 1.6 ± 0.2 |
| SP | 12.5 ± 0.3 |
| SX | 1.5 ± 0.6 |
Refractive index matching
Importantly, all the blood analogues can be modified in order to obtain a wider range of refractive indices from 1.38 to 1.43 to match the refractive index of materials typically used for the fabrication of model vessels. In the case of the analogues with DMSO and distilled water as solvent, the refractive index decreases from 1.41 to 1.38 and the viscosity increases to ≈4 mPa s if we decrease the concentration of DMSO to 35 wt. %.60 Nevertheless, the viscosity still compares well to that of real blood and the shape of the shear-thinning is maintained. Upon increasing the fraction of DMSO to 65%, the refractive index increases from 1.41 to 1.43 and the viscosity decreases from 3.5 mPa s to 3 mPa s approximately,60 respectively, while the shear thinning behavior is retained. In the case of the analogues with sucrose and water as a solvent, the behavior is similar taking into account that 1% of sucrose in water will increase the refractive index by around 0.135. However, care must be taken because sucrose addition has a larger impact on the viscosity of the solvent than DMSO addition, limiting the concentration of sucrose to be used and hence the refractive index is kept within the range 1.38-1.40 approximately.
The effect of the different refractive indices of the blood analogues on the imaging of their flow through the PDMS micro- and milli-channels is shown in Figure 5. It is clearly observed that flowing a blood analogue solution with a refractive index of 1.33, which is much lower than that of PDMS (1.41), through the circular cross-section milli-channels, leads to a wide black region close to the walls. This hinders the detection of particle positions, which would make flow visualizations or μPIV experiments rather limited in scope. However if we increase the refractive index to 1.39, this image distortion diminishes and completely disappears when the refractive index of the solutions is the same as that of the PDMS. In the latter case, a clear image across the channel is obtained, as in the case of the analogue using DMSO as a solvent.
Figure 5.
Microscope images in the middle plane of a PDMS milli-channel with circular cross-section (top) and micro-channel of rectangular cross-section (bottom) filled with solutions with different refractive index: 1.33 (left), 1.39 (middle), and 1.41 (right) containing 15.47 μm spherical particles (refractive index of PDMS was 1.41).
On the other hand, in the case of the micro channels, these optical distortion effects due to the refractive index mismatch are less significant as a result of their rectangular cross-section (Figure 5). Nevertheless, the solutions with refractive indices of 1.33 and 1.39 still show a slightly darker region close to the walls. Therefore, even though any of the four blood analogues are suitable for use in rectangular PDMS channels, a blood analogue solution with a matching refractive index of 1.41 is still preferential.
CONCLUSIONS
We have successfully used passive microrheology to measure the shear response of human blood preserved with EDTA. The results confirm the elastic nature of blood and allowed us to quantify its relative viscous and elastic contributions. Moreover, multi-mode Giesekus and sPTT models have been fitted to the experimental data, providing a useful tool for future use in computational rheology. In addition, four different polymer solutions with different refractive indices (1.39 and 1.41) were proposed as viscoelastic blood analogues capable of mimicking the shear and extensional rheology of human blood. The rheological behavior of the analogues obtained from steady shear and passive microrheology experiments is in good agreement with the rheological properties of whole human blood preserved with EDTA, and in the case of samples SX and DX resulted in complete blood analogues as they matched also the relaxation time of the whole human blood measured in extensional flow. It has also been shown that these analogues are suitable for use in PDMS in vitro models of the circulatory system due to their matching refractive index. In particular, the DX and DP solutions with a refractive index matching that of PDMS (1.41) are the most suitable for use in channels with non-planar cross-section, while all the proposed blood analogues are well suited for use in planar micro-channels, since refractive index matching is not crucial in this case.
ACKNOWLEDGMENTS
The authors acknowledge funding from Fundação para a Ciencia e a Tecnologia (FCT), COMPETE, and FEDER through projects PTDC/EME-MFE/99109/2008, PTDC/EME-MFE/114322/2009, PTDC/EQU-FTT/118718/2010, REEQ/928/EME/2005, and REEQ/298/ EME/2005 and scholarship SFRH/BPD/69664/2010. R.P.A.D. and D.G.A.L.A. thank EPSRC for funding. L.C.D. wants to thank Dr. Andrew Thompson, safety officer from the University of Oxford, and Dr. F. J. Galindo-Rosales for their valuable inputs, João Carneiro for his technical help, and Dr. Chris Blackwell, safety officer from the chemistry department of the University of Oxford, for arranging all safety and ethics protocols that made the measurements with blood possible to perform. L.C.D. also thanks Professor Eric Weeks for the fruitful discussions.
References
- Kim S., Cho Y., Jeon A. H., Hogenauer B., and Kensey K. R., J. Non-Newtonian Fluid Mech. 94, 47 (2000). 10.1016/S0377-0257(00)00127-0 [DOI] [Google Scholar]
- Owens R. G., J. Non-Newtonian Fluid Mech. 140, 57 (2006). 10.1016/j.jnnfm.2006.01.015 [DOI] [Google Scholar]
- Kim S., Cho Y., Hogenauer B., and Kensey K. R., J. Non-Newtonian Fluid Mech. 103, 205 (2002). 10.1016/S0377-0257(02)00004-6 [DOI] [Google Scholar]
- Thurston G. B., Biorheology 16, 149 (1979). [DOI] [PubMed] [Google Scholar]
- Moyers-Gonzalez M., Owens R. G., and Fang J., J. Fluid Mech. 617, 327 (2008). 10.1017/S002211200800428X [DOI] [Google Scholar]
- Moyers-Gonzalez M. and Owens R. G., J. Non-Newtonian Fluid Mech. 155, 146 (2008). 10.1016/j.jnnfm.2008.06.009 [DOI] [Google Scholar]
- Moyers-Gonzalez M., Owens R. G., and Fang J., J. Non-Newtonian Fluid Mech. 155, 161 (2008). 10.1016/j.jnnfm.2008.04.001 [DOI] [Google Scholar]
- Dintenfass L., Nature 199, 813 (1963). 10.1038/199813a0 [DOI] [PubMed] [Google Scholar]
- Woodward M., Rumley A., Tunstall-Pedoe H., and Lowe G. D. O., Br. J. Haematol. 104, 246 (1999). 10.1046/j.1365-2141.1999.01158.x [DOI] [PubMed] [Google Scholar]
- Zeng H. and Zhao Y., Sens. Actuators, A 166, 207 (2011). 10.1016/j.sna.2010.01.031 [DOI] [Google Scholar]
- Johnston B. M., Johnston P. R., Corney S., and Kilpatrick D., J. Biomech. 37, 709 (2004). 10.1016/j.jbiomech.2003.09.016 [DOI] [PubMed] [Google Scholar]
- Karimi A., Yazdi S., and Ardekani A. M., Biomicrofluidics 7, 021501 (2013). 10.1063/1.4799787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cima I., Yee C. W., Iliescu F. S., Phyo W. M., and Lim K. H., Biomicrofluidics 7, 011810 (2013). 10.1063/1.4780062 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvankarian J., Bahadorimehr A., and Majlis B. Y., Biomicrofluidics 7, 014102 (2013). 10.1063/1.4774068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langstroth L., J. Exp. Med. 30, 597 (1919). 10.1084/jem.30.6.597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oates C. P., Phys. Med. Biol. 36, 1433 (1991). 10.1088/0031-9155/36/11/003 [DOI] [PubMed] [Google Scholar]
- Nguyen T. T., Biadillah Y., Mongrain R., Brunette J., Tardif J. C., and Bertrand O. F., J. Biomech. Eng. 126, 529 (2004). 10.1115/1.1785812 [DOI] [PubMed] [Google Scholar]
- Gray J. D., Owen I., and Escudier M. P., Exp. Fluids 43, 535 (2007). 10.1007/s00348-007-0317-z [DOI] [Google Scholar]
- van den Broek C. N., Pullens R. A. A., Frobert O., Rutten M. C. M., Hartog W. F., and van de Vosse F. N., Biorheology 45, 651 (2008). 10.3233/BIR-2008-0513 [DOI] [PubMed] [Google Scholar]
- Wickramasinghe S. R., Kahr C. M., and Han B., Biotechnol. Prog. 18, 867 (2002). 10.1021/bp010192h [DOI] [PubMed] [Google Scholar]
- Gijsen F. J. H., van de Vosse F. N., and Janssen J. D., J. Biomech. 32, 601 (1999). 10.1016/S0021-9290(99)00015-9 [DOI] [PubMed] [Google Scholar]
- Sousa P. C., Pinho F. T., Oliveira M. S. N., and Alves M. A., Biomicrofluidics 5, 014108 (2011). 10.1063/1.3567888 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anastasiou A. D., Spyrogianni A. S., Koskinas K. C., Giannoglou G. D., and Paras S. V., Med. Eng. Phys. 34, 211 (2012). 10.1016/j.medengphy.2011.07.012 [DOI] [PubMed] [Google Scholar]
- Tang S. K. Y. and Whitesides G. M., “Optical components based on dynamic liquid-liquid interfaces,” in Optofluidics: Fundamentals, Devices, and Applications (McGraw-Hill Professional, 2010), Chap. 3. [Google Scholar]
- Budwing R., Exp. Fluids 17, 350 (1994). 10.1007/BF01874416 [DOI] [Google Scholar]
- Malsch D., Gleichmann N., Kielpinski M., Mayer G., Henkel T., Mueller D., van Steijn V., Kleijn C. R., and Kreutzer M. T., Microfluid. Nanofluid. 8, 497 (2010). 10.1007/s10404-009-0479-5 [DOI] [Google Scholar]
- Unger M. A., Chou H.- P., Thorsen T., Scherer A., and Quake S. R., Science 288, 113 (2000). 10.1126/science.288.5463.113 [DOI] [PubMed] [Google Scholar]
- Xia Y. N. and Whitesides G. M., Annu. Rev. Mater. Sci. 28, 153 (1998). 10.1146/annurev.matsci.28.1.153 [DOI] [Google Scholar]
- Hardy B. S., Uechi K., Zhen J., and Kavehpour H. P., Lab Chip 9, 935 (2009). 10.1039/b813061b [DOI] [PubMed] [Google Scholar]
- Valant A. Z., Ziberna L., Papaharilaou Y., Anayiotos A., and Georgiou G. C., Rheol. Acta 50, 389 (2011). 10.1007/s00397-010-0518-x [DOI] [Google Scholar]
- Brust M., Schaefer C., Doerr R., Pan L., Garcia M., Arratia P. E., and Wagner C., Phys. Rev. Lett. 110, 078305 (2013). 10.1103/PhysRevLett.110.078305 [DOI] [PubMed] [Google Scholar]
- Reinhart W. H., Haeberli A., Stark J., and Straub P. W., J. Lab. Clin. Med. 115, 98 (1990). [PubMed] [Google Scholar]
- Rainer C., Kawanishi D. T., Chandraratna P. A. N., Bauersachs R. M., Reid C. L., Rahimtoola S. H., and Meisekman H. J., Circulation 76, 15 (1987). 10.1161/01.CIR.76.1.15 [DOI] [PubMed] [Google Scholar]
- Eugster M., Hausler K., and Reinhart W. H., Clin. Hemorheol. Microcirc. 36, 195 (2007). [PubMed] [Google Scholar]
- Mason T. G., Rheol. Acta 39, 371 (2000). 10.1007/s003970000094 [DOI] [Google Scholar]
- Waigh T. A., Rep. Prog. Phys. 68, 685 (2005). 10.1088/0034-4885/68/3/R04 [DOI] [Google Scholar]
- Crocker J. C. and Hoffman B. D., Methods Cell Biol. 83, 141 (2007). 10.1016/S0091-679X(07)83007-X [DOI] [PubMed] [Google Scholar]
- Crocker J. C. and Grier D. G., J. Colloid Interface Sci. 179, 298 (1996). 10.1006/jcis.1996.0217 [DOI] [Google Scholar]
- Squires T. M. and Mason T. G., Annu. Rev. Fluid Mech. 42, 413 (2010). 10.1146/annurev-fluid-121108-145608 [DOI] [Google Scholar]
- Breedveld V. and Pine D. J., J. Mater. Sci. 38, 4461 (2003). 10.1023/A:1027321232318 [DOI] [Google Scholar]
- Schultz K. M. and Furst E. M., Soft Matter 8, 6198 (2012). 10.1039/c2sm25187f [DOI] [Google Scholar]
- McDonald J. C., Duffy D. C., and Anderson J. R., Electrophoresis 21, 27 (2000). [DOI] [PubMed] [Google Scholar]
- Costa E. D., Carneiro J., Oliveira M. S. N., Campos J. B. L. M., and Miranda J. M., in Proceedings of the 15th International Conference Experimental Mechanics, Porto, Portugal, 2012.
- Merrill E. W., Physiol. Rev. 49, 863 (1969). [DOI] [PubMed] [Google Scholar]
- Fåhræus R., Acta Med. Scand. 161, 151 (1958). 10.1111/j.0954-6820.1958.tb15531.x [DOI] [PubMed] [Google Scholar]
- Chien S., Usami S., Dellenback R. J., and Gregersen M. I., Science 157, 827 (1967). 10.1126/science.157.3790.827 [DOI] [PubMed] [Google Scholar]
- Chien S., Usami S., Dellenback R. J., Gregersen M. I., Nanninga L. B., and Guest M. M., Science 157, 829 (1967). 10.1126/science.157.3790.829 [DOI] [PubMed] [Google Scholar]
- Picart C., Piau J. M., Galliard H., and Carpentier P., J. Rheol. 42, 1 (1998). 10.1122/1.550883 [DOI] [PubMed] [Google Scholar]
- Yeow Y. L., Wickramasinghe S. R., Leong Y. K., and Han B., Biotechnol. Prog. 18, 1068 (2002). 10.1021/bp025558k [DOI] [PubMed] [Google Scholar]
- Bird R. B., Armstrong R. C., and Hassager O., Dynamics of Polymeric Liquids, Volume 1, Fluid Mechanics, 2nd ed. (John Wiley & Sons, Inc., 1987). [Google Scholar]
- Lima R., Wada S., Tanaka S., Takeda M., Tsubota K., Ishikawa T., and Yamaguchi T., in World Congress on Medical Physics and Biomedical Engineering (2007), Vol. 14, p. 283.
- Trafton A., MIT Tech Talk, March 14, 2007, p. 5.
- Sousa P. C., Coelho P. M., Oliveira M. S. N., and Alves M. A., J. Non-Newtonian Fluid Mech. 160, 122 (2009). 10.1016/j.jnnfm.2009.03.009 [DOI] [Google Scholar]
- Casson N., “Flow equations for pigment-oil suspensions of the printing ink type,” in Rheology of Dispersed Systems, edited by Mills C. C. (Pergamon, New York, 1959), Chap. 5. [Google Scholar]
- Quemada D., Biorheology 18, 501 (1981). [DOI] [PubMed] [Google Scholar]
- Barnes H. A., A Handbook of Elementary Rheology (Institute of Non-Newtonian Fluid Mechanics, University of Wales, Aberystwyth, Wales, 2000). [Google Scholar]
- Baaijens J. P. W., Vansteenhoven A. A., and Janssen J. D., Biorheology 30, 63 (1993). [PubMed] [Google Scholar]
- Giesekus H., J. Non-Newtonian Fluid Mech. 11, 69 (1982). 10.1016/0377-0257(82)85016-7 [DOI] [Google Scholar]
- Phan-Thien N. and Tanner R. I., J. Non-Newtonian Fluid Mech. 2, 353 (1977). 10.1016/0377-0257(77)80021-9 [DOI] [Google Scholar]
- Omota L. G., Iulian O., Ciocirlan O., and Nita I., Rev. Roum. Chim. 53, 977 (2008). [Google Scholar]