Improved Bloch-Siegert Based B₁ Mapping by Reducing Off-Resonance Shift

Abstract

Recently, an MRI method based on the Bloch-Siegert (BS) shift phenomenon has been proposed as a fast and precise way to map the radio-frequency (RF) transmit field (B₁⁺ field). For MRI at high field, the mapping sensitivity of this approach is limited by tissue heating associated with the BS irradiation pulse. To mitigate this, we investigated the possibility of lowering the off-resonance frequency of this pulse, as theoretical analysis indicated that the sensitivity of Bloch-Siegert based B₁⁺ mapping can be substantially improved when irradiating closer to resonance. Using optimized irradiation pulse shape and gradient crushers to minimize direct excitation effects, in vivo experiments on human brain at 7T confirmed the improved sensitivity available with this approach. This improved sensitivity translated into an 80% reduction in B₁⁺ estimation errors, without increasing tissue heating.

INTRODUCTION

In MRI, spatial variations in the RF transmit field (the B₁⁺ field, shortened to B₁ in the following) can result in imprecise volume selection, and can affect contrast and sensitivity (1). B₁ mapping techniques provide a way to quantify this inhomogeneity and take it into account or manipulate it using applications such as transmit calibration (2), RF shimming (1), and parallel transmission (3,4). Because of the continuing increase in the number of available transmit channels and the sophistication of their use for RF excitation, there is an ongoing need for B₁ mapping methods with improved speed and accuracy. Especially, a recently proposed phase-based method by Sacolick, et al. (5), which is based on the Bloch-Siegert (BS) frequency shift (6), has been shown to provide robust performance over a range of experimental conditions. Because of their robustness and rapid mapping capability, BS based methods are finding increased use in various applications (7-12). Unfortunately, the speed and sensitivity of the BS methods are often limited by the amount of RF power deposited in the tissue, which may exceed the safety limits for allowable tissue heating (indicated by specific absorption rate - SAR) (13). For this reason, several BS variants (14-20) have been proposed to reduce SAR by changing the imaging approach and image readout scheme, by optimizing the BS irradiation pulse parameters, and by introducing gradient spoiling schemes to eliminate spurious signal excited by the BS pulse. These variants have improved mapping sensitivity, accuracy, and speed (14,18-21). Here, we attempt to further improve B₁ mapping performance.

BS methods have traditionally used large frequency offsets for the BS irradiation pulse (relative to both the variation in resonance frequency γB₀ over the object and the pulse amplitude γB₁) for two reasons: to minimize sensitivity to off-resonance, and to minimize direct excitation of magnetization by this pulse (5). In addition, the use of large frequency offsets facilitates B₁ calculation since it allows approximating the relationship between the square of B₁ amplitude and the BS frequency shift by a linear function. However, it may be possible to improve on B₁ mapping performance by reducing this frequency offset and correcting for the negative side effects mentioned above. To investigate this, we performed theoretical analysis of the BS mapping technique without restricting the irradiation offset. Based on this, we demonstrate that with some sequence modifications, the BS-based sequence can be applied far beyond the regime of offsets originally defined by (5) to achieve lower RF power deposition and better Signal-to-Noise Ratio (SNR) efficiency. Finally, for a gradient-echo (GRE) based BS mapping sequence, the effect of sequence parameters on SNR at a given SAR level is studied. The theoretical findings were then confirmed with studies of human brain at 7T.

METHODS

Basic Equations for BS Shift

BS B₁ mapping generally involves subtraction of phase shifts induced by BS pulses at positive and negative off-resonance frequencies ω_RF (5). These phase shifts arise from changes in the apparent precession frequency occurring during a BS pulse. As shown in the Appendix I, the frequency difference induced by two BS pulses (ω_2BS) at off-resonance frequencies +/-ω_RF (ω_RF=2πΔf_RF>0) in the presence of local static main field (B₀) inhomogeneity Δω_Bo=2πΔf_Bo is given by:

$${\omega }_{2BS}=(\Delta {\omega }_{Bo}+{\omega }_{RF})\left(\sqrt{1+{\left(\frac{\gamma B_1}{\Delta {\omega }_{Bo}+{\omega }_{RF}}\right)}^2}-1\right)-(\Delta {\omega }_{Bo}-{\omega }_{RF})\left(\sqrt{1+{\left(\frac{\gamma B_1}{\Delta {\omega }_{Bo}-{\omega }_{RF}}\right)}^2}-1\right).$$ (1)

Under the assumption |ω_RF|>|Δω_Bo| (Assumption 1, see Appendix I), the BS induced phase shift difference is:

$${\varphi }_{2BS}={\int }_0^T{\omega }_{2BS}dt={\int }_0^T{\omega }_{RF}\left(\sqrt{{\left(1+\frac{\Delta {\omega }_{Bo}}{{\omega }_{RF}}\right)}^2+{\left(\frac{\gamma B_1\left(t\right)}{{\omega }_{RF}}\right)}^2}+\sqrt{{\left(1-\frac{\Delta {\omega }_{Bo}}{{\omega }_{RF}}\right)}^2+{\left(\frac{\gamma B_1\left(t\right)}{{\omega }_{RF}}\right)}^2}-2\right)dt,$$ (2)

for any arbitrary pulse shape B₁(t)=B_1,peakB_1,normalized(t)=B_1pB_1n(t). In analogy to (5), when |γB_1p|<<ω_RF , this can be approximated to first order by:

$${\varphi }_{2BS}=B_{1p}^2{\int }_0^T\frac{{\omega }_{RF}}{{{\omega }_{RF}}^2-\Delta {{\omega }_{Bo}}^2}{\left(\gamma B_{1n}\left(t\right)\right)}^{2}dt,$$ (3)

which is equivalent to Eq.6 in (5) for Δω_Bo=0.

SAR Consideration for Constant-Frequency BS Pulse

Because a typical BS pulse is a large flip-angle pulse (18) (generally several 2π rotations), it is usually the dominant contributor to SAR by far, especially for GRE-based sequences. Thus, reducing the energy of the BS pulse is an effective way to reduce the SAR of the B₁ mapping sequence. For an arbitrarily shaped BS pulse, we have:

$$SA{R}_{BS}\propto {\int }_0^T{\left(V\left(t\right)\right)}^{2}dt\propto {\int }_0^T{\left(B_1\left(t\right)\right)}^{2}dt,$$ (4)

where V(t) is the voltage applied at the RF amplifier on the system to generate the pulse.

Assuming ω_RF is kept constant over the duration of the pulse T, as is generally done in practical applications, and Assumption 1 holds (|ω_RF|>|Δω_Bo|), Eq.3 can be further simplified to:

$${\varphi }_{2BS}={\gamma }^2\frac{{\omega }_{RF}}{{{\omega }_{RF}}^2-\Delta {{\omega }_{Bo}}^2}{\int }_0^T{\left(B_1\left(t\right)\right)}^{2}dt,$$ (5)

leading to:

$$SA{R}_{BS}\propto {\int }_0^T{\left(B_1\left(t\right)\right)}^{2}dt=\frac{1}{{\gamma }^2}{\varphi }_{2BS}{\omega }_{RF}\left(1-{\left(\frac{\Delta {\omega }_{Bo}}{{\omega }_{RF}}\right)}^2\right).$$ (6)

This suggests that the only way to reduce SAR without affecting the SNR in B₁ map (see Appendix I) is to reduce ω_RF. A drawback however is that at low ω_RF, the linear approximation may no longer be valid, and this needs to be accounted for in order to avoid systematic B₁ estimation errors. Another important observation from Eq.6 is that under the linear approximation, the energy efficiency of the BS pulse (generated shift per unit SAR) (18) is independent of pulse shape, given:

$${\varphi }_{2BS}∕SA{R}_{BS}\propto {\varphi }_{2BS}∕{\int }_0^T{\left(B_1\left(t\right)\right)}^{2}dt={\gamma }^2∕\left({\omega }_{RF}\left(1-{\left(\frac{\Delta {\omega }_{Bo}}{{\omega }_{RF}}\right)}^2\right)\right).$$ (7)

i.e. under linear approximation, the energy efficiency of the BS pulse only depends on the frequency offsets and is independent of the pulse shape.

In practice, potential problems with reducing ω_RF are

• an increased sensitivity to B₀ inhomogeneity (reflected in Δω_Bo);

• the generation of artifacts originating from magnetization directly excited by the BS pulse;

• a reduction in the range of B₁ values that satisfies the linear approximation assumption (Eq. 3).

Although each of these may reduce mapping accuracy (5,18,20), this can be avoided by proper adjustments.

Specifically, to counteract the increased sensitivity to B₀ inhomogeneity, the distribution of Δω_Bo can be measured either simultaneously with an integrated sequence (e.g. (20) and Figure 1b) or with a separate sequence. Based on this, the effect of off-resonance can be accounted for through the use of Eq.2 or via pre-computed lookup tables (18).

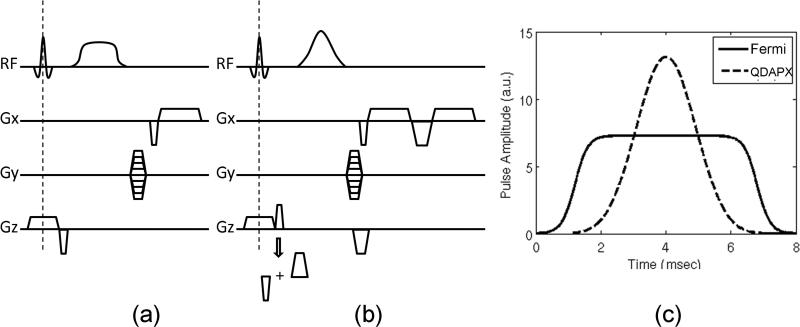
Figure 1.

Pulse sequence modification proposed to suppress direct excitation effects of the BS pulse. (a) Original GRE-based BS B₁ mapping sequence diagram; (b) a modified version with bipolar crushers around the BS pulse and integrated B₀ measurement through dual echo acquisitions; (c) pulse shapes of the original Fermi pulse (solid line) and the modified Bloch-Siegert pulse (“QDAPX”, dashed line) with the same RF energy deposition.

Artifacts related to the direct excitation effect may be suppressed by crusher gradients (14,16,19-21). As it turns out, the crushers in BS sequences also help to reduce some of the non-linear effect associated with low frequency offsets due to averaging across magnetization phases. As shown in Appendix II, crushers of sufficient gradient moment reduce the dependency of the BS shift on the imaging flip angle, and this is particularly important when operating under the non-linear regime. As large gradient moments require long crusher durations, which lead to T₂*-induced signal loss, crusher moment optimization needs to be performed.

Finally, the effects of operating the BS sequence outside the linear regime can potentially be accounted once the effects of the irradiation pulse have been accurately determined. This can be done through simulations, as will be shown in the following section.

Bloch-Siegert Shift Close to Resonance

When trying to increase mapping efficiency by reducing ω_RF, fairly soon one starts violating the condition |γB_1p|<<ω_RF under which the linear approximation (5) holds, and the relationship between B_1p and ϕ_BS becomes more complicated than Eq.3, even when ignoring the increased direct excitation effects. As illustration, if Δf_RF=500 Hz is used, for any B_1p>12μT, we have γB_1p>ω_RF, and our linearity condition is violated. In the following, we will refer to this situation as “overdriven” Bloch Siegert mapping, or OBS mapping. The situation where the linear condition still holds will be referred to as the “regular” condition.

As shown in Eq. A2.5, even with sufficient crushers, the recovered BS phase shifts (Eq.2) from image phase difference will have a B₁ dependency (shown in θ) for large B₁. Thus in general, Eq.2 is no longer applicable under the overdriven condition. As a result, derivation of analytical equations becomes very hard, and if at all possible, these equations will be pulse shape dependent.

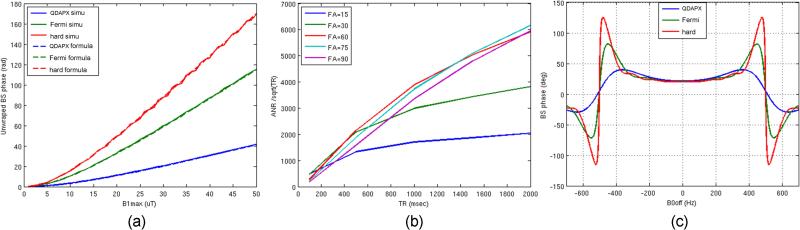
In the following, the signal evolution during OBS mapping was studied by simulations of the Bloch equations. For this purpose, a previously developed GRE-based sequence (20) (Figure 1b) was used, in which Δf_RF was set to 500Hz for demonstration purpose, given that this value, under practical conditions, can easily satisfy both Assumption 1 and the overdriven condition. Figure 2a shows how ϕ_2BS changes as a function of B_1p for the hard pulse, Fermi pulse (5), and our pulse (“QDAPX” as shown in Figure 1c, which was previously optimized for stop-band performance at Δf_RF=2kHz) (20). Solid lines represent the results from the Bloch simulation, whereas the dashed lines represent corresponding values calculated from Eq.2. The figure shows that over a large range of B_1p levels, ϕ_2BS continues to follow the general trend defined by Eq.2 quite well, although at high B_1p values, depending on the pulse shape, different degrees of oscillation can be observed. The smoothness of this curve directly relates to the robustness in B₁ estimation in the presence of noise in ϕ_2BS, since a ϕ_2BS-B₁ curve with large oscillations has regions where small changes in ϕ_2BS correspond to large changes in B₁. In addition, the QDAPX pulse is the least sensitive to noise in B₀ offsets (Figure 2c). Based on these to facts, the QDAPX pulse was chosen for further optimizations of the OBS sequence.

Figure 2.

Bloch-simulation results for Δf_RF=500Hz: (a) Bloch-Siegert phase shift v.s. the peak B₁ value calculated from simulation (solid lines) and from Eq.2 (dashed lines), for the hard pulse (red), Fermi pulse (green), and our pulse (“QDAPX”, blue). At large B₁, simulated BS phase shift start oscillating around corresponding analytical curves; (b) ANR efficiency versus TR at a constant SAR level calibrated from a volunteer study at a range of imaging flip angles; (c) Bloch-Siegert phase shift v.s. Δf_Bo at a low constant SAR level.

To optimize the sequence parameters (such as imaging flip angle and repetition time TR) at a constant SAR level, both the SNR and the SAR level acquired in a previous volunteer study (20) were used to calibrate the simulation parameters. In addition, for each simulation, the steady state magnetization level was computed by simulating the imaging sequence repeatedly for durations longer than five times T₁ value (T₁ was assumed to be 1.5 seconds). Angle-to-Noise Ratio (ANR) efficiency, i.e. mapping sensitivity, was determined from the calculated BS phase shift angle, divided by the thermal noise level and the square root of the scan time. Simulation results for various imaging flip angles at a given SAR level (100%) (Figure 2b) show that for a specific SAR level, optimal ANR is achieved at long TR; furthermore, at a specific TR value, ANR is optimal when using imaging flip angles close to the Ernst angle, (e.g. 30° for TR=200ms and 60° for TR=1000ms for T₁=1.5s).

MRI Experimental Setup

The performance of the OBS sequence was demonstrated on three volunteers (approved by Institutional Review Board). All experiments were performed on a Siemens Magnetom 7T (Erlangen, Germany) whole-body scanner based on an Agilent 7T-830-AS (Oxford, UK) shielded magnet design, with a 32-channel receive with a volume-transmit head coil (Nova Medical Inc., Wilmington, MA, USA). Common imaging parameters were: field-of-view=256mm, image matrix size=64×64, slice thickness=5mm, and BS pulse duration T=8ms.

The following single slice experiments were performed on two volunteers:

1. A reference B₁ map based on the original GRE sequence (Figure 1a) was used, with Δf_RF=8kHz Fermi pulse shape, nominal ϕ_2BS=70°, γB_1p/ω_RF=0.068, TR=844ms, TE=11ms, 90° imaging flip angle, 10 averages (to increase SNR). SAR level was at 100% of maximal allowable value;

2. B₁ mapping with the modified sequence (Figure 1b) using QDAPX pulse at Δf_RF=500Hz: OBS B₁ mapping with γB_1p/ω_RF=1.54 and sufficient crusher moments, and regular Bloch-Siegert B₁ mapping at γB_1p/ω_RF=0.37 with and without crusher. TR=500ms, TE=[15,16]ms, 45° imaging flip angle, single repetition;

3. ANR study with modified sequence on the second volunteer: TR was varied from 74ms to 1000ms (corresponding γB_1p/ω_RF ranged from 0.42 to 1.54, respectively via increasing B_1p), SAR = 55% of maximum, imaging flip angles using Ernst angle calculated from each TR , with QDAPX pulse at Δf_RF=500Hz, with 10 averages to derive the ANR map, which was determined by dividing the mean of the averages by their standard deviation. For comparison, the original sequence using Δf_RF=8kHz Fermi pulse at TR=1000ms was also acquired with 10 averages at 98% maximum SAR. All TE values were kept the same (TE=[14.88ms, 15.88ms]).

In addition, the crusher moment was optimized on one of the volunteers by setting imaging flip angle to 0° and monitoring the signal amplitude while stepping through various crusher moment values, until the direct excitation equaled the noise floor. This ensured that artifacts from direct excitation by the BS pulse were minimized.

To investigate multi-slice BS mapping, which is more challenging than the single slice experiment due to a potential detrimental effect of a BS pulse for a specific slice affecting the magnetization of other slices, the following in vivo data were acquired as well:

1. Acquisition of a 16-slice B₀ map covering the entire brain using double-echo GRE sequence (TE =[3.33, 4.33]ms) with 5mm slice thickness and 5mm gap, TR=500ms, 45° imaging flip angle, single repetition;

2. Acquisition of a reference B₁ map with the original GRE sequence (Figure 1a), with Δf_RF=8kHz Fermi pulse shape, nominal ϕ_2BS=33.6°, γB_1p/ω_RF=0.047, TR=2081ms, 75° imaging flip angle, 10 averages (to increase SNR and derive ANR). SAR level was at 98% of maximal allowable value. Due to the long scan time (4 minutes 26 seconds per repetition) for this experiment, only four 5mm slices were acquired, with 15mm gap between slices. Minimum TE values ([10.33ms 11.33ms]) were used for optimal SNR;

3. The modified sequence (Figure 1b) using the QDAPX pulse at Δf_RF=500Hz and γB_1p/ω_RF=1.37 with imaging parameters identical to previous experiment. Minimum TE values ([14.88ms 15.88ms]) were used for optimal SNR.

All B₁ maps based on the overdriven condition were reconstructed using simulated ϕ_2BS-B₁ curves similar to Figure 2a, while including Δf_Bo, which was derived from a simultaneously acquired B₀ map. After this, the B₁ maps were rescaled with respect to the nominal B₁ value to generate a relative B₁ map. Then the relative B₁ estimation errors were computed by taking the difference between measured and the reference B₁ maps, and dividing by the reference B₁ map. The Root-Mean-Squared Error (RMSE) within brain was then computed for each B₁ map to derive a quantitative metric for accuracy.

RESULTS

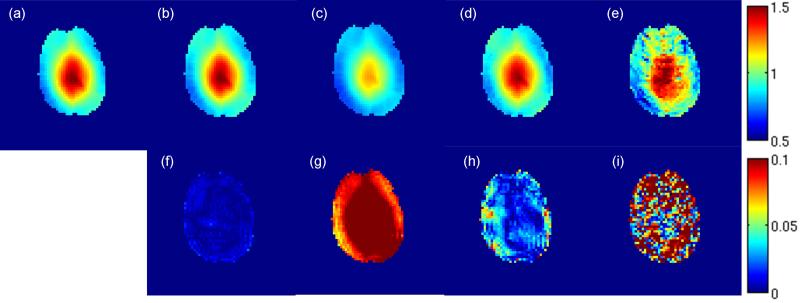
The advantage of OBS in terms of accuracy in B₁ map is demonstrated in Figure 3 and Table 1. Under the overdriven condition with γB_1p/ω_RF=1.54 and sufficient crusher, the B₁ map computed from the ϕ_2BS-B₁ curve has an RMSE of 0.57%. In fact, for most of the brain region within the slice, the relative B₁ errors are below 1%. In contrast, the B₁ map computed based on linear assumption under this condition underestimated the actual B₁, and has an RMSE of 11.47%. When operating under regular condition (γB_1p/ω_RF=0.37), the B₁ map acquired with crushers and computed based on linear assumption has a RMSE of 3.01%, which is comparable to that achieved in recent studies (e.g. (18,20)), but about 5-fold larger than the RMSE acquired under the overdriven condition. Without crushers, large errors (RMSE=12.57%) can be observed in the B₁ map even when operating under regular condition, as a result of direct excitation from the BS pulse. This suggests that the use of a crusher is necessary when the frequency offset of the BS pulse is brought closer to the Lamor frequency (e.g. 500Hz in this case). For the results presented in the following crusher moments fifteen times larger than that of the slice rephasing gradient were used, amounting to 98.9 mT/m*ms.

Figure 3.

Single slice in vivo BS mapping: (a) reference B₁ map acquired by 8kHz Fermi pulse with 10 averages; relative B₁ map (b-e) acquired with 500Hz QDAPX pulse (scaled from 50% to 150%) and corresponding relative error map in B₁ (f-i) (scaled from 0% to 10%). (b,f) acquired with γB_1p/ω_RF=1.54 and optimized crusher, with B₁ calculated using ϕ_2BS-B₁ curve; (c,g) acquired with γB_1p/ω_RF=1.54 and sufficient crusher, with B₁ calculated using original equation proposed in (5); (d,h) acquired with γB_1p/ω_RF=0.37 and sufficient crusher, with B₁ calculated using original equation proposed in (5); (e,i) acquired with γB_1p/ω_RF=0.37 without any crusher (as in (5)), with B₁ calculated using original equation proposed in (5).

Table 1.

Root-Mean-Squared Errors (RMSE) from B₁ maps shown in Figure 3 acquired by our pulse with Δf_Rf=500Hz under various condition.

γB1P/ωRF	1.54	1.54	0.37	0.37
Crusher	Yes	Yes	Yes	No
B1 calculation	ϕ2BS-B1 curve	linear model (Eq.3)	linear model (Eq.3)	linear model (Eq.3)
RMSE (%)	0.57	11.47	3.01	12.57

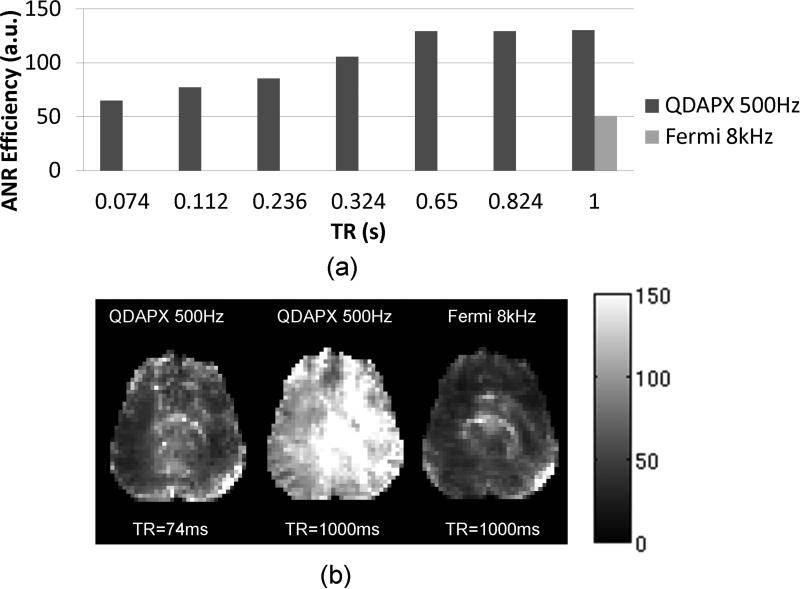
The ANR advantage of OBS is illustrated by the results presented in Figure 4. As predicted by the simulations, the mapping efficiency increases with increasing TR. This increase results from fact that at a constant level of RF power deposition (i.e. SAR), increased TR allows an increase in BS pulse amplitude. The associated (approximately linear) increase in ϕ_2BS with increase in TR translates into an efficiency gain of roughly sqrt(TR), due to reduced averaging per unit scan time associated with longer TR. Thus long TR sequences are preferred in terms of ANR efficiency at a given SAR level. Unlike predicted by simulation (Figure 2b), with the imaging flip angle properly adjusted with TR, this increase starts to saturate at longer TR, due to uncounted system instability. Nevertheless, comparison of an OBS sequence with a traditional BS sequence used at identical TR, TE, and imaging flip angle (Figure 4b) shows ANR efficiencies of 130.39 and 50.84 respectively (OBS: Δf_RF=500Hz, QDAPX pulse, 55% maximum SAR level, BS: Δf_RF=8kHz, Fermi pulse, 98% maximum SAR level). The OBS sequence achieved at least 2.5 times improvement in ANR with 44% lower RF energy deposition than the BS mapping under conventional conditions.

Figure 4.

Effect of TR and BS pulse angle on ANR efficiency: (a) average ANR efficiency at constant SAR level; (b) ANR efficiency maps (scaled from 0 to 150). Left: QDAPX pulse, Δf_RF=500Hz, SAR= 55% of maximum, TR=74ms, imaging flip angle 25°, middle: QDAPX pulse, Δf_RF=500Hz, SAR= 55% of maximum, TR=1000ms, imaging flip angle 59°, and right: the reference scan, i.e. Fermi pulse, Δf_RF=8kHz, SAR= 98% of maximum TR=1000ms, imaging flip angle 59°.

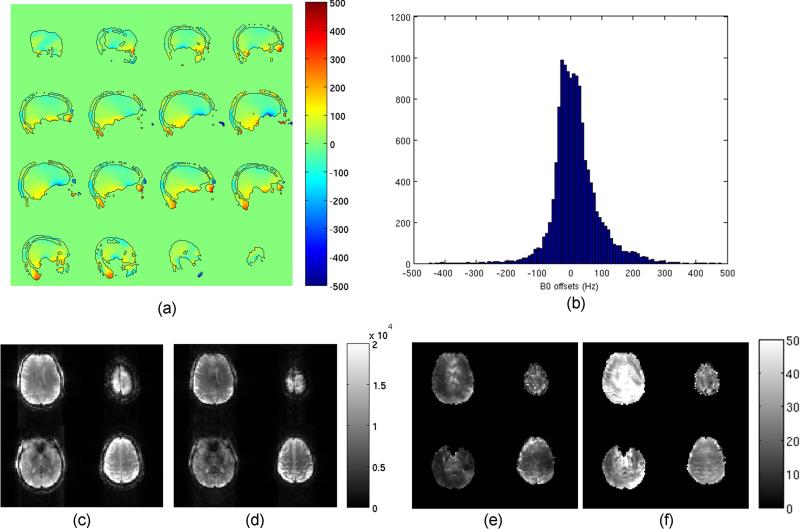
Figure 5 summarizes the results on multi-slice acquisition. Figure 5a and b show sagittal B₀ maps and corresponding histogram covering the entire brain, indicating that the B₀ offset is within the range from -500Hz to 500Hz. This suggests that the Assumption 1 is satisfied. The ANR advantage of OBS during multi-slice acquisition is demonstrated by Figure 5c-f. In fact, when comparing OBS with BS, the root-mean-squared ratio in ANR between these two sequences is 2.97, despite of a roughly 25% loss in imaging signal under the overdriven condition. The latter is attributed to the increase in TE necessitated by the crushers and a potential signal saturation associated with irradiating close to resonance.

Figure 5.

Multi-slice OBS mapping: (a) multi-slice B₀ offset map (scaled from -500Hz to 500Hz), with the boundaries of the mask delineated by black lines; (b) corresponding histogram of B₀ offset; (c,d) magnitude images (in arbitrary units) after 10 averages acquired by the B₁ sequences using (c) Fermi pulse (Δf_RF=8kHz) and (d) QDAPX pulse (Δf_RF=500Hz) at the same SAR level (98% of maximum) and minimum TE, scaling from 0 to 20,000; (e,f) corresponding ANR images for (e) Fermi pulse and (f) QDAPX pulse respectively, scaling from 0 to 50.

DISCUSSION

In this study, it is shown that the BS-based B₁ mapping sequences can be performed with γB_1p/ω_RF ratios far higher than those used previously, and well outside the regime for which the linear approximation holds. As predicted by the theoretical findings regarding the relationship between SAR and ω_RF, significant gains in B₁ mapping sensitivity can be achieved while maintaining or reducing the SAR level without sacrificing B₁ estimation accuracy. In addition, the analytical equations for the BS shift in the presence of off-resonance irradiation were derived and simplified assuming upper limits for B₀ inhomogeneity. These equations provide alternative formulae with better theoretical accuracy than the original linear approximation under both traditional and overdriven cases. Although Eq.2 is derived under a sufficient off-resonance assumption proposed by Ramsey (22), the actual BS phase shift under overdriven condition will oscillate around the value calculated by Eq.2 when a sufficiently large crusher pair is used. The amplitude of the oscillation is pulse-shape dependent. In general, Eq.2 provides a rough estimate of the BS shift without the need of actual Bloch simulations. In addition, since Eq.2 was derived without Taylor-series approximation, it could be used as a more accurate alternative to the linear approximation (5) even when |γB_1p|<ω_RF.

The introduction of crusher gradients into the BS sequences was found to have benefit additional to the reducing direct excitation artifacts suggested in previous reports (14,16,19-21). In fact, a sufficiently strong crusher pair removes the dependency on imaging flip angle and reduces the sensitivity to actual slice profiles and steady state effects. Thus, the flip angle of the imaging pulse can be simply set to the Ernst angle to further improve SNR. Crusher gradients stabilize the ϕ_2BS at high B₁ values (i.e. overdriven states), which makes the B₁ estimation from ϕ_2BS more robust to the noise. The benefits of crusher gradients are not limited to conditions specific to OBS, but apply to traditional BS mapping conditions as well. Therefore, crusher gradients are expected to improve the performance of the BS mapping in general. A drawback of using strong crushers is the associated increase in TE, which leads to some signal (and efficiency) loss. This suggests that the actual crusher moments should be optimized rather than using an arbitrarily large value.

It is found both in theory and in experiment that for GRE-based BS sequences, long TR is preferred for better ANR efficiency. It also suggested that the optimal imaging flip angle should be close to the Ernst angle. In this context, EPI-readout (19) is preferable over single line readout (as used here) to speed up the acquisition without sacrificing SNR.

The in vivo results suggest that the TR can be increased to improve ANR efficiency. However in practice, there is an upper limit on TR when no additional gain is achievable in ANR efficiency. Theoretically, when Δω_Bo<<ω_RF, the asymptotes for Eq.2. are

$${\varphi }_{2BS}={\int }_0^T\frac{{\left(\gamma B_1\right)}^2}{{\omega }_{RF}}dt,$$ (7)

for |γB_1p|<<ω_RF and:

$${\varphi }_{2BS}={\int }_0^{T}2(\mid \gamma B_1\mid -{\omega }_{RF})dt,$$ (8)

for |γB_1p|>>ω_RF. In the region when Eq.8 applies, ϕ_2BS only increases linearly with B_1p, thus the ANR efficiency starts to level off. A practical limit to TR may be dictated by system instabilities (such as B₀ drifting or phase instability), which will eventually become dominant and reduce the ANR efficiency, as demonstrated by Figure 4a. The actual upper limit in practice depends on system stability and the level of physiologic noise and motion of the subject.

Both analytical equations and simulation show that the pulse shape has little effect on how ϕ_2BS changes with pulse energy when the linear approximation applies (|γB_1p|<<ω_RF). In this regime, the energy efficiency only depends on ϕ_RF. However, under the overdriven condition, the relationship between ϕ_2BS and pulse energy or B₁ does become dependent on pulse shape. An extreme example is when |γB_1p|>>ω_RF, based on Eq. 8, the most energy efficient pulse will be the block pulse. As shown with the simulation, different pulse shapes have different smoothness of the ϕ_2BS-B₁ curve and different deviations from Eq.2. This translates into varying robustness to noise in the estimation of B₁ from ϕ_2BS. In addition, although not explored here, different pulses will also have different sensitivity to _ΔωBo. In this paper, for demonstration purpose, a previously designed pulse (20) was chosen for its robustness to noise in the phase image and in the B₀ map. It is possible to formulate a pulse optimization problem based on the findings of this paper to further improve the pulse, although the result will be system- and subject-dependent.

The range of the Δω_Bo through the imaging volume determines lower limits of ω_RF that can be used through Assumption 1. In the experiments presented above, 500Hz frequency offset was chosen for demonstration purpose, with |ω_RF|>|Δω_Bo| verified by B₀ mapping in vivo. For other applications where Δω_Bo could be potentially larger than 500Hz, BS pulse with higher frequency offset has to be used to satisfy Assumption 1. However, this does not prevent overdriving BS sequences to achieve better SNR efficiency. In addition, further reduction in ω_RF in our experiments is limited by regions with large Δω_Bo located at the boundary of large susceptibility changes, e.g. near the nasal cavity and other air-tissue interfaces. In GRE data, these regions generally also suffer from signal loss due to intra-voxel dephasing. Both these issues may be further improved by more advanced B₀ shimming methods. In addition, SNR in B₀ map also has some effects on the final B₁ map. Although it has no effects on either the ANR or the mapping efficiency, it does affect the SNR in the final B₁ map if a B₀ correction is used. This is not only affecting B₁ mapping under overdriven condition, but also applicable generally to any Bloch-Siegert based B₁ mapping whenever B₀ information is used. The question of how to minimize the effect of the B₀ correction on the B₁ map is beyond the scope of this paper, but generally speaking for Bloch-Siegert sequences, it depends on the echo spacing, the frequency offset of the Bloch-Siegert pulse, and the Δω_Bo sensitivity for a particular pulse shape. In practice, the robustness to noise in the B₀ map can be increased by optimizing the pulse shape as shown above, using a high SNR B₀ map, or increasing ω_RF which in turn reduces the ANR and thus the SNR in the B₁ map as well. Since dual frequency acquisition is used in most of the Bloch-Siegert sequences, B₀ dependency is in first order compensated for and therefore at a reasonable SNR level, the lower limit of ω_RF shouldn't be affected much by the SNR in the B₀ map.

One interesting thing to consider is the potentially adverse effect of the crushers on the imaging signal magnitude. Since the Bloch-Siegert pulse is a non-selective pulse, in theory there could be the chance that during multi-slice acquisition, some magnetization outside the current imaging slice is saturated by the Bloch-Siegert pulse and thus results in signal loss when that location is excited soon after. This, again, depends on the actual pulse shape, the subject, and the system. In addition, the use of crushers also prolongs the minimum TE that can be used, which will result in additional signal losses. In our study, after the optimization, a crusher moment about 99 mT/s*ms was used. However, as demonstrated by our experiments (Figure 5c-f), these two adverse effects on SNR are more than compensated for by the large sensitivity gain brought by operating BS sequences under overdriven condition. In addition, although not investigated by this study, SNR losses caused by these two aforementioned effects can be further suppressed by further minimizing the direct excitation effects of the pulse for low-frequency offset purpose, e.g. via similar methods used in (23,24).

It should also be mentioned that B₁ mapping is an active area of research and that some of the novel approaches under development may prove to be preferable over BS methods. For example, methods like the one proposed recently by Bornert et al (25,26), may be more straightforward and less limited by SAR concerns. Such methods would obviate the need for the various optimization steps required for BS methods, and therefore be more desirable in practice.

CONCLUSION

Reducing the off-resonance frequency of the irradiation pulse in BS-based B₁ mapping allows improved mapping efficiency and speed. Potential detrimental effects of this approach on B₁ mapping accuracy can be mitigated by modifications to the acquisition technique and to the theoretical model used for the B₁ calculation. As a result, improved B₁ accuracy can be achieved for given scan time and SAR, as was demonstrated in human studies.

ABBREVIATION LIST

RF

Radio-frequency

SAR

Specific Absorption

GRE

Gradient Echo

BS

Bloch-Siegert

OBS

Overdriven Bloch-Siegert

ANR

Angle-to-Noise Ratio

RMSE

Root-Mean-Squared Error

SNR

Signal-to-Noise Ratio

APPENDIX I

Basic Equations for BS Shift

While equations for the linear approximation for the BS shift were given in (5), here we further examine the BS effect as well as some important details that were not emphasized in (5). We first start with the equation for the Bloch-Siegert frequency shift derived by Ramsey (22) (Note equation (3) in Ramsey's paper has a sufficient off-resonant assumption). In a static main magnetic field with strength B₀ without application of RF, the magnetic resonance frequency will equal the Lamor frequency ω₀=γB₀. If, after excitation, an RF pulse with frequency ω₂ is applied, and ω_off=ω₀-ω₂, the resonance frequency ω during this pulse is given by:

$$\omega =({\omega }_0-{\omega }_2)\sqrt{1+{\left(\frac{{\omega }_1}{{\omega }_0-{\omega }_2}\right)}^2}+{\omega }_2={\omega }_{off}\sqrt{1+{\left(\frac{{\omega }_1}{{\omega }_{off}}\right)}^2}+{\omega }_0-{\omega }_{off},$$ (A1.1)

where ω₁=γB₁. This will introduce an additional frequency shift (i.e. the BS frequency shift ω_BS) given as a function of ω_off:

$${\omega }_{BS}\left({\omega }_{off}\right)=\omega -{\omega }_0={\omega }_{off}\left(\sqrt{1+{\left(\frac{{\omega }_1}{{\omega }_{off}}\right)}^2}-1\right).$$ (A1.2)

As pointed out in (5), in practice, to remove undesired phase effects in the image, the phase difference between images acquired with both positive and negative frequency shifts is used in calculating the final B₁ map. For convenience, let us define ω_RF=2πΔf_RF>0, and BS pulses with frequence offsets +ω_RF and -ω_RF symmetrically placed around ω₀ are used. For completeness, we assume there is a local B₀ inhomogeneity resulting in off-resonance precession at frequency ω₀+Δω_Bo rather than at ω₀, with Δω_Bo=2πΔf_Bo. In this case, the measurement with the BS pulse at +ω_RF will have ω_off=Δω_Bo+ω_RF, whereas the measurement with the BS pulse at -ω_RF will have ω_off=Δω_Bo-ω_RF. In this case the resulting BS frequency difference will be:

$${\omega }_{2BS}={\omega }_{BS}(\Delta {\omega }_{Bo}+{\omega }_{RF})-{\omega }_{BS}(\Delta {\omega }_{Bo}+{\omega }_{RF}),$$ (A1.3)

which yields Eq.1.

To facilitate further derivation, here we introduce the first practical assumption.

Assumption 1: The local B₀ inhomogeneity is not larger than the frequency offset of the BS pulse, i.e. Δω_Bo < ω_RF. At a given level of inhomogeneity, this condition can be met by using sufficiently large frequency offsets for the BS pulses.

Under this assumption, Eq.1 can be rearranged as:

$${\omega }_{2BS}={\omega }_{RF}\left(\sqrt{{\left(1+\frac{\Delta {\omega }_{Bo}}{{\omega }_{RF}}\right)}^2+{\left(\frac{{\omega }_1}{{\omega }_{RF}}\right)}^2}+\sqrt{{\left(1-\frac{\Delta {\omega }_{Bo}}{{\omega }_{RF}}\right)}^2+{\left(\frac{{\omega }_1}{{\omega }_{RF}}\right)}^2}-2\right).$$ (A1.4)

Since equation (A1.4) is symmetric regarding ±Δω_Bo, for convenience, we can further assume Δω_Bo≥0. In this context, the corresponding equation for the general BS phase shift, i.e. Eq.2, can be derived with the integration over the entire pulse duration. Since pulse parameters (frequency offset ω_RF, normalized shape B_1n(t), and pulse duration T) in Eq.2 can be determined before the experiment, and the local B₀ inhomogeneity can be measured as well, Eq.2 forms a mapping from the local peak B₁ (B_1p) to the resulting BS phase shift, which generally can be solved numerically for any predefined pulse in mapping the local B₁ from the BS phase shift.

Taylor Expansion of the BS Shift

For this purpose, we introduce an additional assumption.

Assumption 2: The pulse sequence operates in a low-SAR regime, so that |γB_1p|≤ω_RF. At given B_1p, this condition can be met in practice by using BS pulses with sufficiently large frequency offsets. Under this assumption, based on the Taylor expansion, we have:

$${\varphi }_{2BS}={\int }_0^T{\omega }_{RF}\left(\frac{1}{{{\omega }_{RF}}^2-\Delta {{\omega }_{Bo}}^2}{\left(\gamma B_1\left(t\right)\right)}^2-\frac{{{\omega }_{RF}}^2+3\Delta {{\omega }_{Bo}}^2}{4{({{\omega }_{RF}}^2-\Delta {{\omega }_{Bo}}^2)}^3}{\left(\gamma B_1\left(t\right)\right)}^4+O\left({\left(\frac{\gamma B_1\left(t\right)}{{\omega }_{RF}}\right)}^6\right)\right)dt.$$ (A1.5)

Note that the equations above also apply to conditions where ω_RF and Δω_Bo are time dependent.

When Δω_Bo=0, and only first order Taylor approximation is used, we have:

$${\varphi }_{2BS}={\int }_0^T\frac{{\left(\gamma B_1\left(t\right)\right)}^2}{{\omega }_{RF}}dt=B_{1p}^2{\int }_0^T\frac{{\left(\gamma B_{1n}\left(t\right)\right)}^2}{{\omega }_{RF}}dt.$$ (A1.6)

Or:

$$B_{1p}=\sqrt{\frac{{\varphi }_{2BS}}{{\int }_0^T\frac{{\left(\gamma B_{1n}\left(t\right)\right)}^2}{{\omega }_{RF}}}dt}.$$ (A1.7)

Based on the theory of error propagation, it can show that SNR_B1∝ SNR_imageγ²SAR/ω_RF, which suggests for a constant image SNR (e.g. fixed TE and TR), the SNR in B₁ map is proportional to SAR/ω_RF.

APPENDIX II

In general, with ignoring relaxation effects, the rotation of a magnetization vector under the effect of some pulse with B₁ (ω₁=γB₁), duration t, and frequency offset ω_off=2πΔf_off is given by:

$${\mathbf{M}}_2=\mathbf{Rotx}(-\theta )\mathbf{Rotz}\left(\phi \right)\mathbf{Rotx}\left(\theta \right){\mathbf{M}}_1,$$ (A2.1)

with M₁ and M₂ are the magnetization vector before and after the application of the pulse, respectively; θ=tan^-1(ω₁/ω_off), $\phi =\mathrm{sqrt}({\omega }_1^2+{\omega }_{off}^2)t$; and rotation matrices are:

$$\mathbf{Rotx}\left(\alpha \right)=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cos \left(\alpha \right)\hfill & \hfill -\sin \left(\alpha \right)\hfill \\ \hfill 0\hfill & \hfill \sin \left(\alpha \right)\hfill & \hfill \cos \left(\alpha \right)\hfill \end{array}\right],\mathbf{Rotz}\left(\alpha \right)=\left[\begin{array}{ccc}\hfill \cos \left(\alpha \right)\hfill & \hfill -\sin \left(\alpha \right)\hfill & \hfill 0\hfill \\ \hfill \sin \left(\alpha \right)\hfill & \hfill \cos \left(\alpha \right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right].$$ (A2.2)

When sufficient bipolar crusher pair is applied around the pulse, Eq.A2.1 becomes:

$${\mathbf{M}}_2=\frac{\oint \mathbf{Rotz}(-\beta )\mathbf{Rotx}(-\theta )\mathbf{Rotz}\left(\phi \right)\mathbf{Rotx}\left(\theta \right)\mathbf{Rotz}\left(\beta \right){\mathbf{M}}_{1}d\beta }{\oint d\beta }.$$ (A2.3)

In case of the BS-based sequence presented in this paper, let's further assume the flip angle of the imaging pulse is FA, and the normalized initial magnetization is M₁ =[0,0,1]^T. The integrand in (A2.3) becomes:

$$\left[\begin{array}{c}\hfill \cos \left(\phi \right){\cos }^2\left(\beta \right)\sin \left(FA\right)+\sin \left(\phi \right)\sin \left(\theta \right)\cos \left(\beta \right)\cos \left(FA\right)\\ \hfill +\cos \left(\phi \right){\cos }^2\left(\theta \right){\sin }^2\left(\beta \right)\sin \left(FA\right)-\cos \left(\phi \right)\sin \left(\theta \right)\cos \left(\theta \right)\sin \left(\beta \right)\cos \left(FA\right)\\ \hfill +{\sin }^2\left(\theta \right){\sin }^2\left(\beta \right)\sin \left(FA\right)+\sin \left(\theta \right)\cos \left(\theta \right)\sin \left(\beta \right)\cos \left(FA\right)\\ \hfill ,-\cos \left(\phi \right)\sin \left(\beta \right)\cos \left(\beta \right)\sin \left(FA\right)+2\sin \left(\phi \right)\cos \left(\theta \right){\sin }^2\left(\beta \right)\sin \left(FA\right)\\ \hfill -\sin \left(\phi \right)\sin \left(\theta \right)\sin \left(\beta \right)\cos \left(FA\right)+\cos \left(\phi \right){\cos }^2\left(\theta \right)\sin \left(\beta \right)\cos \left(\beta \right)\sin \left(FA\right)\\ \hfill -\cos \left(\phi \right)\sin \left(\theta \right)\cos \left(\theta \right)\cos \left(\beta \right)\cos \left(FA\right)+{\sin }^2\left(\theta \right)\sin \left(\beta \right)\cos \left(\beta \right)\sin \left(FA\right)\\ \hfill +\sin \left(\theta \right)\cos \left(\theta \right)\cos \left(\beta \right)\cos \left(FA\right)\\ \hfill ,-\sin \left(\phi \right)\sin \left(\theta \right)\cos \left(\beta \right)\sin \left(FA\right)-\cos \left(\phi \right)\sin \left(\theta \right)\cos \left(\theta \right)\sin \left(\beta \right)\sin \left(FA\right)\\ \hfill +\cos \left(\phi \right){\sin }^2\left(\theta \right)\cos \left(FA\right)+\sin \left(\theta \right)\cos \left(\theta \right)\sin \left(\beta \right)\sin \left(FA\right)\\ \hfill +{\cos }^2\left(\theta \right)\cos \left(FA\right)\end{array}\right].$$ (A2.4)

The final magnetization vector becomes:

$${\mathbf{M}}_2=\left[\begin{array}{c}\hfill \frac{1}{2}(\cos \left(\phi \right)(1+{\cos }^2\left(\theta \right))+{\sin }^2\left(\theta \right))\sin \left(FA\right)\hfill \\ \hfill \sin \left(\phi \right)\cos \left(\theta \right)\sin \left(FA\right)\hfill \\ \hfill (\cos \left(\phi \right){\sin }^2\left(\theta \right)+{\cos }^2\left(\theta \right))\cos \left(FA\right)\hfill \end{array}\right],$$ (A2.5)

with a significant reduction in complexity due to the periodicity of sinusoid functions. Since the ratio between x and y components determines the phase shift in the x-y plane, i.e. the phase shift in the signal, it is obvious that with the presence of sufficient bipolar crusher, the Bloch-Siegert phase shift (derived from φ) does not depend on the imaging flip angle FA, so long as FA>0. Another important point is that although Eq.A2.1 implicitly assumes a constant B₁ (i.e. hard pulse), for an arbitrary pulse with time-varying B₁ values, at any instance, the current magnetization has some equivalent flip angle, thus the conclusion from Eq.A2.5 does not change, i.e. the Bloch-Siegert phase shift does not depend on imaging flip angle for any pulse when a sufficient surrounding bipolar crusher pair presents. Nevertheless, since sin(FA) contributes the total magnitude of the transverse magnetization vector in the x-y plane, it does affect the SNR in the phase angle calculation when noise is present.