EMPHYSEMA QUANTIFICATION IN A MULTI-SCANNER HRCT COHORT USING LOCAL INTENSITY DISTRIBUTIONS

Abstract

This article investigates the suitability of local intensity distributions to analyze six emphysema classes in 342 CT scans obtained from 16 sites hosting scanners by 3 vendors and a total of 9 specific models in subjects with Chronic Obstructive Pulmonary Disease (COPD). We propose using kernel density estimation to deal with the inherent sparsity of local intensity histograms obtained from scarcely populated regions of interest. We validate our approach by leave-one-subject-out classification experiments and full-lung analyses. We compare our results with recently published LBP texture-based methodology. We demonstrate the efficacy of using intensity information alone in multi-scanner cohorts, which is a simpler, more intuitive approach.

1. INTRODUCTION

Chronic obstructive pulmonary disease (COPD) is a major cause of chronic morbidity and mortality throughout the world. Beyond spirometric pulmonary function tests (PFTs), computed tomography (CT) has been postulated adequate for assessing the severity and extension of emphysema in vivo, allowing for monitoring its progression and evaluating its response to therapy [1]. A standard technique employed is called densitometric analysis [2]. This technique consists of choosing a Hounsfield unit threshold in the lung mask to discriminate emphysema from non emphysematous tissue. Although densitometry is very sensitive to noise and acquisition parameters [3], it represents the method of choice for most clinical studies [4].

Much of the work developed in the field of emphysema quantification in CT has attempted to enrich thresholding approaches by incorporating the spatial structure of density values, or texture [5-8]. Most of these approaches introduce several disadvantages: low performance, poor understanding of the consequences of inter-scanner variability, and obscurity of physical meaning.

Prototypic radiologic patterns of emphysematous involvement of the secondary pulmonary lobule corresponding to centrilobular, paraseptal and panlobular disease have been described [9]. This view eventually leads to six distinct emphysema patterns: normal tissue (NT), paraseptal (PS), panlobular (PL) and mild/moderate/severe centrilobular emphysema (CL1/2/3). In Fig. 1 we provide examples of these patterns, which illustrate their radiographic expression.

Fig. 1.

Examples of emphysema regions of size 24.18 × 24.18 mm² in the window [−1000, −500] HU. (a) NT. (b) CL1. (c) CL2. (d) CL3. (e) PL. (f) PS.

We postulate that the discrimination problem is primarily based on variations in local intensity rather than on spatial regularity (spatial statistics of order greater than one), especially as datasets from several scanners are introduced in the classification problem. One approach to emphysema quantification in which texture and intensity are accounted for in an orthogonal manner resides in the work by Sørensen et. al. [10], based on Local Binary Patterns (LBPs) [11].

Although [10] finds that coupling locally-computed LBPs and intensity produces good classification, we will show that as scanner-dependent intensity-range variations come into place, the LBP component becomes irrelevant, and properly modeled local intensity performs better and more simply.

2. METHODS

2.1. ROI Size

The proposed methodology is based in proper labeling of two-dimensional regions of interest. The physical extent of such regions is critical to the classification, since an ROI that is too small will not contain a whole secondary lobe, and an ROI that is too big will dim the boundaries between regions with different pattern classes. Therefore we work with physically normalized image units, across the different scanner resolutions.

2.2. High Order Spatial Statistics: Local Binary Patterns

Local Binary Patterns (LBPs) were originally proposed by Ojala et. al. [11] as a compact encoding of the grey values around a pixel location. When LBP values have been computed for every voxel in the ROI, LBP histograms can be constructed. Such representation captures the frequency of certain micro-structures like corners, edges and constant regions. Figure 2 shows LBP histograms averaged for all available samples of the six classes under study.

Fig. 2.

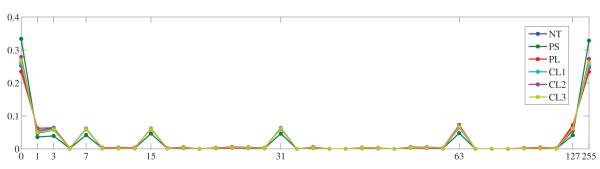
Average LBP code histograms for the six emphysema classes under study

In their work Sørensen et. al. [10] proposed a methodology based on the coupling of LBPs and adaptively binned intensity histograms (LBPINT), obtaining remarkable classification success. It is our goal to investigate which part of that success is due to the intensity part of the description, and which part can be genuinely attributed to textural information.

2.3. First Order Spatial Statistics: Local Intensity

The intensity probability function of a given tissue class is a complete description of its first-order spatial statistics. In parametric approaches, the underlying probability function for a given tissue class can be established in terms of a model distribution and a number of parameters estimated from training data. This is partially exploited in some texture approaches like Haralick descriptors [12]. As opposed to this, non-parametric approaches do not assume any model distributions, and do not require parameter estimation.

2.3.1. Kernel Density Estimation

Intensity probability distribution functions (PDFs) can be estimated using the classic method known as kernel density estimation (KDE). Given an independent and identically distributed sample set (x₁, x₂, …, x_n), drawn from some distribution with an unknown density f, we are interested in estimating the shape of this function f. Its kernel density estimator is known to be

$${\widehat{f}}_h\left(x\right)=\frac{1}{n}\sum _{i=1}^n{K}_h(x-x_i)=\frac{1}{nh}\sum _{i=1}^{n}K\left(\frac{x-x_i}{h}\right),$$ (1)

where K(·) is usually a Gaussian kernel and h > 0 is a smoothing parameter called the bandwidth. In all our results we use the methodology described in state-of-the-art work by Botev et al. [13], to determine the value of the bandwidth parameter (independently for each sample). See Fig. 3 for a plot of the density estimates averaged for all available samples of the six classes under study.

Fig. 3.

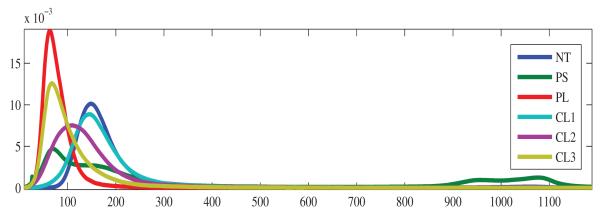
Average kernel density estimates for all samples for the six emphysema classes under study

2.4. Classifier

All previously described histograms (LBP, INT, LBPINT, KDE) are taken as representation of a given ROI. In order to classify unseen ROIs we make use of the kNN classifier using the Minkowski L1 distance as metric. This distance is computed from a test sample to every training sample and then we classify it using the most frequent class label among the k closest samples in the training set, or the closest sample label if two or more labels are equally the most frequent among them.

3. EXPERIMENTAL RESULTS

342 CT scans were randomly selected from the COPDGene cohort with 50 scans each from smokers with different severity levels defined by Global Initiative on Obstructive Lung Disease severity level (GOLD) 0 to 4 and GOLD U plus 42 non-smoking controls. The 342 CT scans were acquired at 16 sites hosting scanners by 3 vendors and a total of 9 specific models. On a subset of 267 CT scans, samples from the six classes under study were selected by an experienced pulmonologist by clicking on locations surrounded by the desired type of tissue, providing a total of 1525 samples.

Methodological parameters have been tuned according to previous findings. ROI size (24.18 × 24.18 mm²), LBP parameters (R = 1, P = 8) and size of adaptive histograms (N = 10) have been chosen according to [10]. The value of k for the kNN classifier was determined empirically to be optimal in terms of classification success for k = 5 when chosen among k ∈ {1, 3, 5, 7, 9}.

3.1. Leave-One-Subject-Out Sample Classification

We evaluate the performance of the proposed descriptions by leave-one-subject-out classification success estimation using the manually selected samples. See Table 1 for a comparison of Sørensen’s LBPs, adaptively binned intensity histograms (INT), joint LBP-intensity histograms (LBPINT), and PDFs reconstructed via KDE. In each leave-out trial, all ROIs from one subject are held out and designated for testing, and subsequently, the ROIs in the test set are classified using all the remaining ROIs as prototypes in the classifier.

Table 1.

Classification success for reference methods (LBP, INT and LBPINT) and proposed method (KDE)

Method	Classification Success
	NT	PS	PL	CL1	CL2	CL3	mean(std)
LBP	0.474	0.557	0.115	0.157	0.411	0.107	0.303 (±0.2004)
LBPINT	0.882	0.821	0.750	0.401	0.589	0.455	0.650 (±0.1984)
INT	0.880	0.874	0.790	0.350	0.557	0.472	0.654 (±0.2248)
KDE	0.904	0.854	0.770	0.373	0.634	0.449	0.664 (±0.2175)

3.2. Full-lung analysis

For further validation we proceed by full-lung classification of 342 of the CT scans from the aforementioned workshop. Regularly sampling and classifying the lung field results in an approximation of the percentage of every tissue class for a given scan. The classification was performed at a fixed sampling grid with spacing 10 × 10 × 20 pixels. We perform classification of the grid locations according to our bench-mark methodology [10] and to the developed methodology. In Fig. 4 we represent, for every tissue class, the percentage of ROIs that have been classified as belonging to that class for every CT scan. This is done for both methodologies in a two-dimensional plot. Regression lines are computed for every tissue class. The proximity of the obtained regressions to the identity function suggests that our technique and the reference technique based on a texture descriptor are similar suggesting that the extra complexity brought by the LBP descriptor might not be needed for this problem.

Fig. 4.

Scatter plot that shows the percentage labeled ROIs obtained using the LBPINT and KDE for the 342 analyzed subjects. (a) NT. (b) PS. (c) PL. (d) CL1. (e) CL2. (f) CL3. For reference, the identity line is shown. Notice the good agreement between both methods for each tissue class.

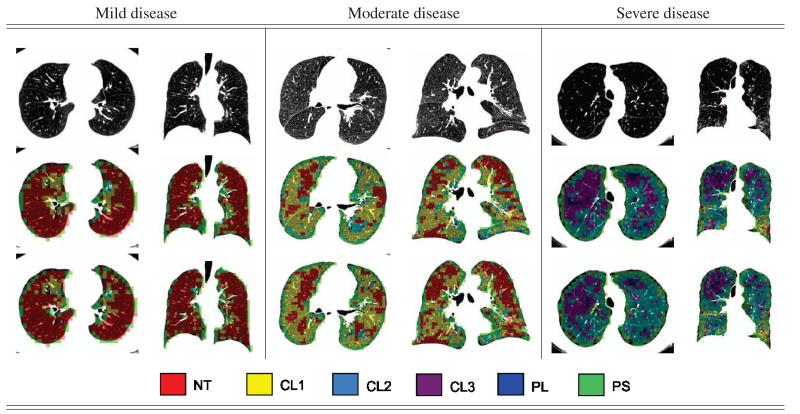
In Fig. 5 we show the labelings obtained using both the benchmark methodology (LBPINT) and the propose method (KDE), over-imposed on the concerned CT slice.

Fig. 5.

Classification results for three stages of disease severity using the methodologies under study. (Top row) axial and coronal slices for the original CTs. (Middle row) Classification results for KDE. (Bottom row) Classification results using LBPINT.

4. DISCUSSION

We show that emphysema discrimination in multi-scanner cohorts using intesity and texture fails in favor of more simple descriptions based on intensity only. We also demonstrate that as we model intensity probability distribution non-parametrically using kernels, the classification is even better. High correlates of emphysema class percentages for reference and proposed methodologies suggests that texture-based techniques based on LBP do not incorparte additional knowledge with respect to the local density.