AUTOMATIC AIRWAY ANALYSIS FOR GENOME-WIDE ASSOCIATION STUDIES IN COPD

Abstract

We present an image pipeline for airway phenotype extraction suitable for large-scale genetic and epidemiological studies including genome-wide association studies (GWAS) in Chronic Obstructive Pulmonary Disease (COPD). We use scale-space particles to densely sample intraparenchymal airway locations in a large cohort of high-resolution CT scans. The particle methodology is based on a constrained energy minimization problem that results in a set of candidate airway points situated in both physical space and scale. Those points are further clustered using connected components filtering to increase their specificity. Finally, we use the particle locations to perform airway wall detection using an edge detector based on the zero-crossing of the second order derivative. Given the airway wall locations, we compute three phenotypes for airway disease: wall thickening (Pi10,WA%) and luminal remodeling (P%). We validate the airway extraction technique and present results in 2,500 scans for the association of the extracted phenotypes with clinical outcomes that will be deployed as part of the COPDGene study GWAS analysis.

1. INTRODUCTION

The Human Genome Project opened the door for the exploration of genetic factors associated with diseases by means of genome wide association studies (GWAS). GWAS consists of testing genetic variants in a large cohort of individuals by means of phenotypes that can be extracted from those individuals. In particular, image-based phenotypes have become attractive sources of data for the gene discovery process.

COPD is a condition defined as airflow limitation that is not fully reversible due to tobacco smoke. The disease has two main components: emphysema and airway disease. COPD is strongly associated with smoking, but only a minority of smokers will develop COPD, suggesting that there may be genetic differences between people leading to greater susceptibility to the effects of cigarette smoke. Therefore, there is a need to develop new phenotypes that can better inform the GWAS process. Fully automatic image analysis approaches that can process data in a robust fashion despite abnormalities due to inherent disease conditions are critical to generate those phenotypes.

Airway analysis has been typically divided into two steps: airway localization (segmentation and centerline sampling) and bronchial wall detection. Airway segmentation algorithms have been described elsewhere [2-4] and are mostly based on variations of region growing approaches. Unlike these techniques, the method presented in this paper is unique in that it directly samples airway centerlines within the whole lung parenchyma – without front evolution – using scale-space particles based on the Hessian. The main advantages of this approach are that it (1) is less sensitive to the discretization errors introduced by the binarization that become critical for smaller structure, (2) has the capability to overcome gaps in the data due to mucus plugs or disease progression, (3) has a low computational cost and (4) is fully automatic. We validate the airway centerline sampling and demonstrate the efficacy of three airway phenotypes with clinical correlates that will be part of the COPDGene GWAS analysis [1].

2. METHODS

2.1. Airway centerline sampling by scale-space particles

Scale-space particles have been previously used for the sampling of features described by the Hessian [5]. Here we present a similar approach, focusing on the specifics for airway centerline sampling that maximizes measurements of feature strength along scale. The airway lumen can be seen as ridge lines of the CT densities and can therefore be described by the Hessian matrix at a given scale. In the following discussion, f_CT (x) denotes the CT dataset, σ represents the scale dimension, and f(x, σ) = G(x, σ) ∗ f_CT is the linear scale-space decomposition of f_CT, where G(x, σ) is a Gaussian kernel at scale σ. We denote the eigenvectors of the Hessian, Hf(x, σ), at sampling location x and scale σ as v₁(x, σ), v₂(x, σ), and v₃(x, σ). The eigenvalues are denoted λ₁(x, σ), λ₂(x, σ) and λ₃(x, σ).

The scale-space particles algorithm performs constrained numerical minimization of the following energy functional

$$\underset{\left\{\right({\mathbf{x}}_i,\sigma )\mid i=1,\dots ,N\}}{\mathrm{argmin}}(1-\alpha )\sum _{i=1}^N{E}_i+\alpha \sum _{i,j=1}^N{E}_{ij}$$ (1)

subjected to ${\mathbf{x}}_i=\underset{{\mathbf{x}}_i}{\mathrm{argmin}}f(\mathbf{x},\sigma ):{\mathbf{x}}_i\in \Pi \left({\sigma }_i\right)$ where {(x_i, σ)|i = 1, …, N} is the set of N particles, E_i is the image-particle energy term, E_ij is the inter-particle energy, α is a blending factor, and Π(σ_i) is the plane spanned by the eigenvectors v₁(x_i, σ_i) and v₂(x_i, σ_i). Upon convergence of the minimization, the system achieves a dense and uniform feature sampling across both scale and physical space. The image-particle term for airway centerline extraction is defined as E_i = −γλ₂(x_i, σ_i) where γ is a scaling factor. λ₂ has to be large at the airway centerline locations [6]. The inter-particle energy term is given by E_ij = Φ (r, s_n) where $r=\frac{\mid \mid {\mathbf{x}}_i-{\mathbf{x}}_j\mid \mid }{{\sigma }_r}$ and $s_n=\frac{\mid {\sigma }_i-{\sigma }_j\mid }{{\sigma }_s}$. We have used two energy functions for this study: Φ₁ and Φ₂. Φ₁ is designed to repel particles in both scale and space

$${\Phi }_1(r,s_n)={\Phi }_q\left(\sqrt{r^2+s_n^2}\right)$$ (2)

where ${\Phi }_q\left(x\right)=1+\frac{12w}{1-4w}x+\left(3+\frac{9}{4w-1}\right)x^2+\frac{8+4w}{1-4w}{x}^3+\frac{3}{4w-1}{x}^4$ is a quartic polynomial with a potential well at distance x = w to create some attraction and generate a compact packing of the particles. The second energy term, Φ₂, that we have employed attracts in scale while repelling in space

$${\Phi }_2(r,s_n)=(1-\beta ){\Phi }_q\left(r\right)\mathcal{W}\left(s\right)+\beta {\Phi }_s\left(s_n\right)\mathcal{W}\left(r\right)$$ (3)

where ${\Phi }_s\left(s_n\right)=\mathcal{W}\left(s_n\right)s_n^2$ and $\mathcal{W}\left(x\right)=\frac{1}{1+{\left(\frac{x}{b_{cut}}\right)}^{2n}}$ is a Butterworth filter-like function of order n = 10 and cut-off b_cut = 0.7 to localize the energy response in scale-space.

2.2. Implementation

Before the application of the particles sampling, the lung is segmented according to the method described in [7]. The left and right CT subvolumes are then cropped and deconvolved with a B-spline kernel. The subvolumes are then blurred using a discrete Gaussian kernel with five scales uniformly distributed in the range σ = [0, 6] pixels. This range captures the common sizes of the airways that are found in the lung parenchyma.

Next, the particles system is initialized with a set of points, {x_i}, that are placed within an approximate airway mask. The initialization step is critical to minimize the number of false positives and the computation time. The approximate airway mask is generated by taking advantage of the fact that the pulmonary vasculature runs parallel to the main bronchial tree. A vessel mask is initially defined using threshold of −500 HU. The vessel mask is dilated (three iterations) using a circular structuring element with an eight voxel radius. The final approximate airway mask is obtained by keeping the voxels within the dilated vessel mask below −800 HU. For every location x_i, particles are placed at every discrete scale in the selected range.

Throughout the optimization procedure, the Hessian is computed by convolving the image with the analytical derivatives of a fifth-degree, C³ continous, polynomial approximation filter. The three stages of the optimization procedure and the parameter values used are summarized below.

Step 1. An initial scale-space particle system is run to sample the airways across their scale extent while applying the image-particle energy term to capture strong airway features. The scale-space parameters employed in this stage are: E_ij = Φ₁, w = 0.7, α = 1 and β = 0.7. The system is run for 80 iterations.

Step 2. The resulting particles are used to initialize a second particle system that pulls the particles to the scale of maximal strength. The parameters for this stage are: α = 0 and β = 0.5. The system is run for 10 iterations.

Step 3. The final stage redistributes particles to allow for a good feature sampling. The parameters are: E_ij = Φ₂, w = 0.7,α = 0.5 and β = 0.5. 50 iterations are used. At the end of this stage the gradient and the Hessian are sampled at the particle location and are stored as attributes for that point.

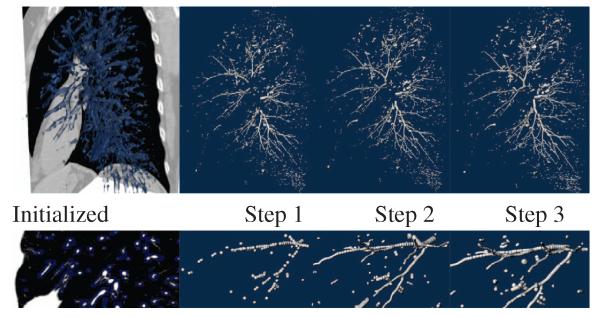
These parameters have been selected based on a qualitative assessment of the results in a subset of 20 cases. Fig. 1 illustrates the particles process for the left lung of one of the cases used for validation. It is worth noting how the approximate airway includes the main airway points within the parenchyma. In some sections airway segments are not sufficiently near a vessel, and so those airway regions are not initialized. However, the repulsion forces that particles exert on each other can generally recover those gaps during optimization. Because the initialization is done over the entire lung region, our method is able to recover airways with high stenosis that are not necessarily topologically connected.

Fig. 1.

Airway extraction using scale-space particles. Top row depicts (from left to right) the mask used for initialization, and the particle points after step 1, step 2 and step 3, respectively. Bottom row shows a detailed view from the images on the top row. The detailed views show the improvement in the final result by each phase.

Particles Post-Processing

The particles system tends to be quite sensitive but not specific. To improve specificity, we pass the particles through a connected components filter, where connectivity is defined by proximity in both scale and space, and direction similarity. The connected components filter proceeds in two stages. In the first stage, particles are grouped according to how linearly aligned they are. Two particles are considered connected provided they are spatially close (within 1.7mm) and if the vector connecting their spatial locations is sufficiently parallel to each of the particles’ minor eigenvectors, v₃(x_i, σ_i). These pairwise tests are performed recursively to produce a set of labeled, linear components. All components consisting of seven (experimentally determined) or less particles are then removed.

For the second stage of the filter, the components from the first stage are tested for linkages. Here the proximity requirement is relaxed in order to link components that may be farther from each other but that nonetheless form part of the airway tree. Also, an additional “junction” linkage is attempted to accommodate bifurcations. The resulting set of particles forms the final set used for further analysis.

Bronchial wall extraction

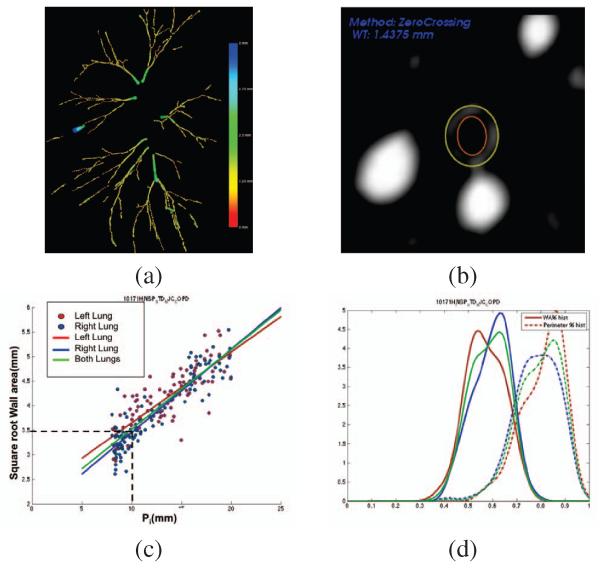
After the airway particles have been filtered, we proceed to the detection of the bronchial wall. The airway wall is defined by fitting an elliptical model to the points obtained from an edge detector based on the zero crossing of the second order derivative. For each particle, thirty rays are uniformly cast from the particle center x_i in the plane spanned by v₁(σ_i) and v₂(σ_i), and the zero crossings are computed using the Newton-Raphson method. Finally, the least squares ellipse fitting is done for the inner and outer boundary. Fig. 2b shows the extracted wall for a particle.

Fig. 2.

(a) Particle filtering result for the case shown in Fig. 1. (b) Bronchial wall extraction using a elliptical model. (c) $\sqrt{WA}$ vs P_i for the subject shown in Fig. 1. (d) Histograms for WA% (solid) and P% (dash).

Airway phenotypes

The final step of our analysis pipeline is the definition of airway phenotypes that can be used in GWAS. The challenge of this step is to reduce this wealth of information into phenotypic data that has clinical significance. Phenotypes that demonstrate such clinical importance are more valuable for subsequent genetic investigation. From our data, we have computed three airway phenotypes. The first phenotype, known as P_i10, defines bronchial wall thickening by computing the regression line between the square root of bronchial wall area and the inner perimeter and extrapolating the wall thickness corresponding to a nominal airway of inner perimeter, P_i = 10mm. Fig. 2c shows the computation of the quantity from the particle measurements in one subject. The other two quantities that have been computed are the histograms of wall area percentage, $WA\%=\frac{A_o-A_i}{A_o}$, and perimeter percentage, $P\%=1-\frac{P_o-P_i}{P_o{P}_i}$ as shown in Fig. 2d. These quantities tracked the remodeling process. We have chosen the WA% 75th percentile (WAPperc75) and the P% 25th percentile (P%perc25) as phenotypes.

3. RESULTS

Detection validation

In order to quantify the detection accuracy of the particles system, we performed a thorough analysis on a set of seven cases with varying levels of disease. (It should be emphasized that our methodology was more broadly applied to a set of 2, 500 cases and the efficacy of the approach is born out with correlation to clinical phenotypes). Our goal for the detection study was to determine measures of sensitivity and specificity. One pulmonologist and one radiologist manually selected points in all visually discernible airway segments in airway generations 3 – 7 in a dual reader strategy (one point per airway generation). To compare the particles data to the manual ground-truth, we considered any manually selected generation point within 4mm to a particle point as detected. We also created an interactive tool that enables users to visualize the particles data and overlaid CT slice planes. The tool allows users to identify and eliminate non-airway particle groups (false positives).

Table 1 shows the results of the quantitative detection study. True positives are above 80% for up to 6th generation showing the capturing range of our method. As expected, the percent of detected airway generations tends to fall off with increasing generation number. For the most part, the percent of false positives is quite low. However, the percentage of false positives for cases 6 and 7 is significantly higher than for the other cases. The main reason for this is the advanced state of emphysema for these two cases. The particles system tends to detect these locally tube-like, emphysematous regions, and the post-processing filter has difficulty discriminating them as they satisfy the connected components criteria.

Table 1.

Results for the airway detection study. For each of seven cases, the percentage of detected airways (from third to seventh generation) is given. Additionally, the percentage of false positives is given in the last column. Note that our method produces a FP percentage lower than 3% up to the fifth generation, result that is comparable to those reported in the 2009 MICCIA airway challenge (EXACT ’09).

	True Pos. (TP)					False Pos. (FP)
	3rd G.	4th G.	5th G.	6th G.	7th G.
Case 1	100%	100%	98.7%	80.4%	49.5%	0.6%
Case 2	100%	100%	100%	91.8%	86.0%	2.2%
Case 3	94.4%	100%	97.2%	81.8%	62.1%	3.6%
Case 4	100%	100%	93.9%	82.4%	48.6%	7.1%
Case 5	100%	100%	94.1%	79.3%	73.2%	3.7%
Case 6	100%	97.1%	74.2%	50.7%	41.9%	15.7%
Case 7	94.4%	100%	95.8%	94.3%	70.4%	14.0%

Phenotypes validation

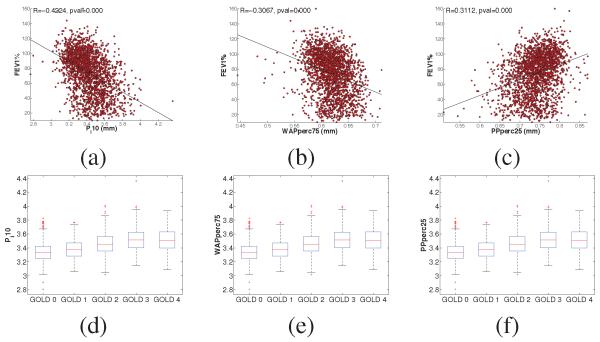
2,500 subjects from the COPDGene study [1] have been processed by our pipeline in a fully unsupervised fashion. The average processing time for each subject was approx. 35 min on an Intel Xeon E7440 at 2.4GHz. We have assessed the validity of our phenotypes by establishing correlations with a metric of lung function typically used in the clinic (FEV1%). Results are shown in Fig. 3(a-c). It can be seen that the three phenotypes capture part of the variability seen by the clinical variable (correlation coefficients between 0.3 and 0.4 (p < 0.001)). Those correlations are similar to other studies. COPD subjects are divided in 5 categories, known as GOLD stages, with GOLD 0 representing normal lung function and GOLD 1-4 representing progressively more severe COPD. We have assessed the distribution of our phenotype for each category (Fig. 3(d-f)). Based on one-way ANOVA, all phenotypes yield differences between groups (p < 0.001) except for GOLD stage 3 and GOLD stage 4 suggesting that severe disease may lead to a much weaker definition of an airway disease phenotype as we can seen in our validation experiments.

Fig. 3.

Correlation of P_i10, WA% and P% with Forced Expiratory Volume in the first second % predicted (FEV1%) (a-c) and phenotype distributions across GOLD stage (d-f).

4. DISCUSSION AND CONCLUSIONS

In this paper we presented a fully automatic airway analysis algorithm suitable for large-scale GWAS studies that is being used in COPDGene. The ability of this particles-based approach to detect multiple airway generations was shown. Our tool focuses on small airways beyond third generation in the parenchyma because these are the locations contributing to airflow obstruction.

Our approach to the airway analysis problem is novel in that we immediately generate a sampling of the airway centerline instead of first passing through an airway segmentation algorithm. This has the advantage that the method is not confounded by issues like stenotic points that normally affect region-growing based methods. The post-processing stage has significant influence over the quality of the final result. While the implementation discussed in this paper has proven effective, we believe it is possible to further improve results. Additional knowledge of airway tree geometry could be incorporated for this purpose.