Test–retest and between‐site reliability in a multicenter fMRI study

Abstract

In the present report, estimates of test–retest and between‐site reliability of fMRI assessments were produced in the context of a multicenter fMRI reliability study (FBIRN Phase 1, http://www.nbirn.net). Five subjects were scanned on 10 MRI scanners on two occasions. The fMRI task was a simple block design sensorimotor task. The impulse response functions to the stimulation block were derived using an FIR‐deconvolution analysis with FMRISTAT. Six functionally‐derived ROIs covering the visual, auditory and motor cortices, created from a prior analysis, were used. Two dependent variables were compared: percent signal change and contrast‐to‐noise‐ratio. Reliability was assessed with intraclass correlation coefficients derived from a variance components analysis. Test–retest reliability was high, but initially, between‐site reliability was low, indicating a strong contribution from site and site‐by‐subject variance. However, a number of factors that can markedly improve between‐site reliability were uncovered, including increasing the size of the ROIs, adjusting for smoothness differences, and inclusion of additional runs. By employing multiple steps, between‐site reliability for 3T scanners was increased by 123%. Dropping one site at a time and assessing reliability can be a useful method of assessing the sensitivity of the results to particular sites. These findings should provide guidance toothers on the best practices for future multicenter studies. Hum Brain Mapp, 2008. © 2007 Wiley‐Liss, Inc.

INTRODUCTION

Multicenter fMRI studies have a number of advantages, as outlined by Friedman et al. [2006] and Friedman and Glover [2006]. They also pose serious challenges. One common goal of most such studies is to literally merge the data from several scanners to increase the sample size applied to a substantive question of interest, for example, the relationship between certain imaging phenotypes and genetic information. Literally merging such data requires data from different scanners to be interchangeable and is only reasonable if scanner differences in fMRI results can be minimized, i.e., the assessments from one scanner to another are reliable.1 One approach to assessing measurement reliability is to perform a reliability study prior to a scientifically substantive study. If the between‐site reliability is low, sources of unreliability might be identified and corrected.

Classically, reliability of this form of data is assessed with an intraclass correlation coefficient, which can be estimated directly from an appropriate analysis of variance table or from variance components [ICC; Cronbach et al., 1972; Shrout and Fleiss, 1979]. The ICC is a number that ranges from 0.0 to 1.0. Cicchetti and Sparrow [1981] [Cicchetti, 2001] presented guidelines for interpretation of ICCs as follows: poor (below 0.40), fair (0.41–0.59), good (0.60–0.74), and excellent (above 0.75). The ICC is a commonly used metric to assess test–retest reliability in fMRI [Aron et al., 2006; Kong et al., 2007; Manoach et al., 2001; Specht et al., 2003; Wei et al., 2004], although other metrics have been employed [Genovese et al., 1997; Le and Hu 1997; Liou et al., 2006; Maitra et al., 2002; Zou et al., 2005].

There are several types of ICC [Shrout and Fleiss, 1979] but if the goal is to literally merge data from sites, then the choice is narrowed to ICC (type 2, 1) in the nomenclature of Shrout and Fleiss [1979] (see below). This ICC measures the degree of absolute agreement of each rater (scanner) with each other rater. If this is sufficiently large, then one has a good basis for merging data.

We present the results of variance components analyses and associated ICCs for a multisite study performed by the Function Biomedical Informatics Research Network (fBIRN). The fBIRN group published a previous article on these data showing the impact of scanner site, task run, and test occasion on functional magnetic resonance imaging results [Zou et al., 2005]. However, this initial study was not aimed at measuring the magnitude of the various sources of unwanted variance in multisite fMRI data. In this article, we use variance components analysis to measure the magnitude of the variance components associated with scanner site, task run, and testing occasion on the amplitude of the fMRI signal [Dunn, 2004].

The present study tests the following hypotheses:

Hypothesis 1. The results of fMRI studies can be expressed in several ways, for example, percent signal change (PSC), t‐value, P‐value, regression β‐weight, Pearson correlation coefficient, location of activation, number of activated voxels, etc. In the present study, we hypothesized that noise would be unreliable across sites and that therefore measures, which have an estimate of noise in the denominator (CNR‐type measures), would have lower reliability than measures of signal magnitude only (PSC). This hypothesis was stimulated partly by the report of Cohen and DuBois [1999], who noted that PSC provided more reliable estimates than number of activated voxels.

Hypothesis 2. Measures that are based on the median value from an ROI will be more reliable than measures that are based on the maximum value from an ROI. This was based on the notion that the maximum value could be some sort of outlier or unusual value, perhaps highly influenced by local venous architecture (especially at 1.5T) [Ugurbil et al., 1999].

Hypothesis 3. In a previous report [Friedman et al., 2006], we found that image smoothness (measured as a FWHM) was related to task effect size.2 In that report, we found that a major cause of site differences in image smoothness was the presence and type of apodization (k‐space) filter employed during image reconstruction. We hypothesize that adjusting for smoothness differences between scanners will increase reliability estimates for CNR type measures.

Hypothesis 4. The size of an ROI could well have an impact on the reliability of the measures taken from it. If an ROI is too small, it may not capture the primary activation from various sites, especially when the same ROI is used across field strength. It is known that geometric distortion of functional images is greater at 3.0T than at 1.5T—such differences could lead to somewhat different results if the same ROI is used for both. On the other hand, an ROI that is too large will have low anatomic specificity.

In the present study, four runs of a sensorimotor task were collected in each visit. This allowed us to compare the reliability of the average of two, three, and four runs to a single run. Theoretically, as is clear from our formulae (see below), reliability will increase with more runs. This is analogous to results from classical test theory, in which increasing the number of test items will increase reliability of the test (Spearman‐Brown Prophecy formula [Lord and Novick, 1968]). However, factors such as increasing fatigue and inattention over time may reduce the reliability of later runs. Therefore, it was of interest to see how well empirical results match the theoretical expectation that averaging runs increases reliability.

The present report is based on the FBIRN Phase I traveling subject study [Friedman and Glover, 2006; Friedman et al., 2006; Zou et al., 2005]. In this study, five subjects were scanned on 10 different scanners on two occasions. This provided an excellent dataset with which to assess test–retest and between‐site reliability and to test our hypotheses.

MATERIALS AND METHODS

Subjects

Five healthy, English‐speaking males (mean age: 25.2, range = 20.2–29) participated in this study. All were right‐handed, had no history of psychiatric or neurological illnesses and had normal hearing in both ears. Each subject traveled to nine sites (10 scanners) (Table I), where they were scanned on two consecutive days for a total of 20 scans per participant. There were no missing subject visits (scan sessions), i.e., all 100 visits (5 subjects × 2 visits × 10 scanners) were available for analysis. However, one scan session (1%) was unusable for technical reasons. All subjects were instructed to avoid alcohol the night before the study, caffeine 2 h prior to the study and to get a normal night's sleep the night before a scan session. This study was conducted in compliance with the Code of Ethics of the World Medical Association (Declaration of Helsinki) and the Standards established by the Institutional Review Board of each participating institution. After a full explanation of the procedures employed, informed consent was obtained from every subject before participation in this study and before every scan session.

Table I.

Description of hardware and sequences of the nine sites (10 scanners) participating in this study, five 1.5T scanners, four 3T scanners, and one 4T scanner

Site code	Abbreviation	Field strength (T)	Manufacturer	RF coil type	Functional sequence
1	SITE 1	1.5	GE Nvi LX	TR quadrature head	Spiral
2	SITE 2	1.5	GE Signa CV/i	TR quadrature head	EPI
3	SITE 3	1.5	Siemens Sonata	RO quadrature head	EPI
4	SITE 4	1.5	Philips/Picker	RO quadrature head	EPI
5	SITE 5	1.5	Siemens Symphony	TR quadrature head	EPI
6	SITE 6	3.0	GE	GE TR research coil	EPI
7	SITE 7	3.0	Siemens Trio	TR quadrature head	EPI ‐Dual Echo
8	SITE 8	3.0	Siemens Trio	TR quadrature head	EPI
9	SITE 9	3.0	GE CV/NVi	Elliptical quadrature head	Spiral in/out
10	SITE 10	4.0	GE Nvi LX	TR quadrature head	Spiral

Image Acquisition

A bite bar was used to stabilize each subject's head and was placed in the subject's mouth at the beginning of each scan session. An initial T2‐weighted, anatomical volume for functional overlay was acquired for each subject (fast spin‐echo, turbo factor = 12 or 13, orientation: parallel to the AC‐PC line, number of slices = 35, slice thickness = 4 mm, no gap, TR = 4,000 ms, TE = ∼68, FOV = 22 cm, matrix = 256 × 192, voxel dimensions = 0.86 mm × 0.86 mm × 4 mm). The parameters for this T2 overlay scan were allowed to vary slightly from scanner to scanner according to field strength or other local technical factors. The anatomical scan was followed either by a working memory task (total of 14.7 min) or an attention task (total of 16 min). Three subjects always performed the working memory task and two subjects always performed the attention task. Over the next hour or so, subjects performed four runs of a sensorimotor task (described below, 4.25 min per run, total of 17 min), two runs of a breath‐hold task (4.25 min), and two resting state scans (fixation on a crosshairs, 4.25 min). These eight scans were performed in a counterbalanced order. The entire scan session was repeated the following day. In the present report, only data from the four sensorimotor runs is presented.

The functional data were collected using echo‐planar (EPI) trajectories (seven scanners) or spiral trajectories (three scanners) (Table I) (orientation: parallel to the AC‐PC line, number of slices = 35, slice thickness = 4 mm, no gap, TR = 3.0 sec, TE = 30 ms on the 3T and 4T scanners, 40 ms on the 1.5T scanners, FOV = 22 cm, matrix = 64 × 64, voxel dimensions = 3.4375 mm × 3.4375 mm × 4 mm). SITE 7 employed a double echo EPI sequence and SITE 9 employed a spiral in/spiral out sequence. All the spiral acquisitions were collected on General Electric (GE) scanners. The sensorimotor task produced four runs of 85 volumes each (85 TRs). The RF coils used varied with each scanner (Table I).

Sensorimotor Task

The sensorimotor (SM) task was designed initially for calibration purposes and employed a block design, with each block taking 10 TRs (30 sec) beginning with five TRs (15 s) of rest (subject instructed to stare at fixation cross) and five TRs (15 s) of sensorimotor activity (see below). There were eight full cycles of this followed by a five TR rest period at the end for a total of 85 TRs (4.25 min). During the active phase, subjects were instructed to tap their fingers bilaterally in synchrony with binaural tones, while watching an alternating contrast checkerboard. The checkerboard flash and tone presentation were simultaneous. The subjects were instructed to tap their fingers in an alternating finger tapping pattern (index, middle, ring, little, little, ring, middle, index, index…) in synchrony with the tones and checkerboard flashes. The thumb was not used in this study. Each tone was 166 ms long with 167 ms of silence. The tone sequence utilized a dissonant series generated by a synthesizer (Midi notes 60, 64, 68, 72, 76, 80, 84, 88, 86, 82, 78, 74, 70, 66, 62, 58). The subjects' responses were recorded and monitored with the PST Serial Response Box (Psychology Software Tools, Pittsburgh, PA).

fMRI Data Analysis

Preprocessing

The first step of image processing was accomplished using Analysis of Functional NeuroImage (AFNI) software [Cox, 1996]. The first two volumes were discarded to allow for T1‐saturation effects to stabilize. All large spikes in the data were removed from each sensorimotor run, and each run was motion‐corrected (i.e., spatially registered to the middle volume of the run, TR = 42). The data were then slice‐time‐corrected. A mean functional (T2*) image was created. The mean T2* image for each run was spatially normalized to an EPI canonical image in MNI space using tools available in SPM5 (http://www.fil.ion.ucl.ac.uk/spm/). This included affine transformations and three nonlinear iterations. We limited the nonlinear iterations to three to control the amount of deformation. The spatial transformations were applied to the time series data as well, and the time series was resampled at a 4 × 4 × 4 mm³ voxel size.

Measuring PSC and CNR

The impulse response functions (IRF) for each voxel were estimated using Keith Worsley's package, FMRISTAT [Worsley et al., 2002] (http://www.math.mcgill.ca/keith/fmristat/), according to the FIR‐Deconvolution method outlined at the FMRISTAT web page. The IRFs were 30 s long (10 time points, 3 s apart), covering the duration of the on and off block periods. Temporal drift was removed by adding a linear and a quadratic component to the model. The PSC IRFs were calculated by dividing the estimates (βs) by the model intercept (mean baseline level) and multiplying by 100. The CNR IRFs were the t‐values for each time point in the FIR model.

Image data transfer between programs (AFNI, SPM5, and FMRISTAT) was greatly facilitated by the application of the new NifTi standard (http://nifti.nimh.nih.gov/nifti-1/).

ROIs

The ROIs are displayed in Figure 1. The ROIs include only voxels that were activated at all 10 scanners with an uncorrected P value <0.00001 and in all five subjects with an uncorrected P value <0.00001. There were six ROIs identified: left and right motor cortex (LM and RM), left and right auditory cortex (LA and RA), bilateral visual cortex (BV), and the bilateral supplementary motor area (SM).

Figure 1.

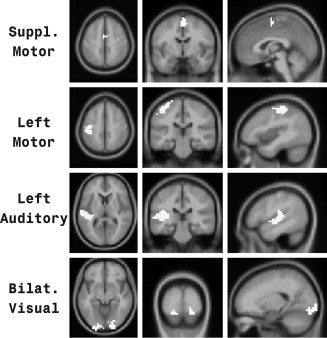
ROIs. Four of six ROIs employed in this study. ROIs are shown in white. For each ROI, an axial, coronal, and sagittal view is presented. The remaining two ROIs (right motor and right auditory) were comparable to the contralateral ROIs shown in this figure.

Extracting Scalar Values from Each ROI

Four IRFs were extracted from each ROI: (1) median IRF in percent change units, (2) maximum IRF in percent change units, (3) median IRF in CNR units, and (4) maximum IRF in CNR units. To arrive at a scalar value from each IRF (for each run of the SM task) the peak value of each IRF from 6 s postblock onset to 18 s postblock onset was obtained.

Statistical Analysis

Data were available for five subjects at 10 scanners. Each subject was scanned on two visits, and there were four SM runs per visit.

Testing field‐strength effects

To test for field‐strength effects, a mixed‐model ANOVA was carried out for median PSC and median CNR. The random factors noted below were included as random factors for this analysis, and fixed‐effects included field‐strength, ROI, and the field‐strength by ROI interaction. The fixed‐effects were tested using planned contrasts between field strength for all ROIs together and each ROI separately. Planned contrasts included a test of 3T > 1.5T. (The 4T > 3T test was not performed since there was only one site at 4T.) Since these contrasts were obvious directionally specific hypotheses, the P‐values provided are one‐tailed. The multiple ROI contrasts were controlled for the false discovery rate (FDR) [Benjamini and Hochberg, 1995] using SAS PROC MULTTEST. Cohen's D values are also provided to compare effect sizes. Effect sizes for the field‐strength effect from PSC and CNR were compared using a paired t‐test.

Measuring reliability

Variance components were estimated for each scalar using SAS PROC Varcomp (SAS, Cary, NC), which employed the restricted maximum likelihood (REML) method. The variance components are estimated according to the following model:

with Y_ijkl denoting the dependent measure for subject i, site j, visit k, and run l. Each factor was treated as a random effect. (The site factor is often thought of as a fixed effect, but in the context of a multicenter study it is desirable to think about a population of potential sites.) In this formulation, visits are treated as nested within site‐subject combinations and the residual term is an estimate of the variance for runs nested within subject‐by‐site‐by‐visit. This formulation models visits and the runs that occur on these visits as distinct measurement occasions. The model also allows for possible day‐to day variation in magnet performance. As discussed below, alternative models are possible and do not appreciably change the reliability results.3

Tables II and III presents results from the variance components analysis of PSC (Table II) and CNR (Table III). Analyses are carried out for each of six brain regions, separately for 1.5T and 3.0T imaging sites. Two different measures of reliability are developed and presented in Tables II and III. To describe these measures, we first introduce a “total visit variance” term, which is the sum of all of the variance components associated with the above model:

where VD stands for “variance due to.” We divide VD_unexplained by 4 to get the “total visit variance” (average over four runs) rather than “total variance for a single run.” A measure of between‐site reliability (for a visit consisting of four runs) is the correlation of two measures (based on the mean of four runs) for the same subject but at different sites. In terms of the variance components estimated as above (and presented in Tables II and III) this is:

Note that the between‐site reliability coefficient provides an estimate of the reliability of an imaging parameter averaged across four runs for a randomly selected subject studied at a single randomly selected site on one randomly selected occasion.

Table II.

Variance components and reliability estimates for PSC

ROI extraction method	Field	Region	Site	Subject	Site × Subject	Visit	Unexplained	ICC_BETa	ICC_T‐Rb
Median	1.5	BV	0.003	0.036	0.001	0.007	0.010	0.72	0.80
	1.5	LA	0.009	0.001	0.002	0.001	0.004	0.08	0.85
	1.5	LM	0.005	0.002	0.002	0.001	0.006	0.16	0.77
	1.5	RA	0.012	0.001	0.002	0.002	0.005	0.07	0.83
	1.5	RM	0.008	0.000	0.002	0.003	0.004	0.02	0.74
	1.5	SM	0.007	0.006	0.002	0.002	0.011	0.29	0.75
	3	BV	0.027	0.060	0.011	0.011	0.024	0.52	0.85
	3	LA	0.001	0.004	0.003	0.007	0.007	0.22	0.47
	3	LM	0.002	0.009	0.006	0.006	0.010	0.37	0.66
	3	RA	0.004	0.006	0.008	0.001	0.010	0.29	0.83
	3	RM	0.001	0.002	0.007	0.004	0.010	0.14	0.62
	3	SM	0.000	0.008	0.016	0.007	0.020	0.22	0.68
Maximum	1.5	BV	0.193	3.731	0.000	3.941	2.195	0.44	0.47
	1.5	LA	0.307	0.151	0.068	0.171	0.209	0.20	0.70
	1.5	LM	0.019	0.014	0.030	0.137	0.173	0.06	0.26
	1.5	RA	0.359	0.386	0.063	0.628	0.366	0.25	0.53
	1.5	RM	0.027	0.000	0.054	0.102	0.148	0.00	0.37
	1.5	SM	0.008	0.033	0.021	0.014	0.078	0.34	0.65
	3	BV	1.971	3.001	0.000	1.726	1.187	0.43	0.71
	3	LA	0.000	0.193	0.215	0.186	0.296	0.29	0.61
	3	LM	0.000	0.282	0.338	0.460	0.537	0.23	0.51
	3	RA	0.074	0.846	0.137	0.217	0.604	0.59	0.74
	3	RM	0.000	0.000	0.149	0.468	0.425	0.00	0.21
	3	SM	0.008	0.119	0.083	0.082	0.110	0.37	0.66

^aICC_BET = between‐site ICC.

^bICC_T‐R = test–retest ICC.

Table III.

Variance components and reliability estimates for CNR

ROI extraction method	Field (T)	Region	Site	Subject	Site × Subject	Visit	Unexplained	ICC_BETa	ICC_T‐Rb
Median	1.5	BV	0.082	0.141	0.025	0.056	0.080	0.44	0.77
	1.5	LA	0.050	0.018	0.017	0.019	0.053	0.15	0.72
	1.5	LM	0.071	0.015	0.006	0.024	0.055	0.12	0.71
	1.5	RA	0.084	0.026	0.015	0.015	0.044	0.17	0.83
	1.5	RM	0.037	0.006	0.011	0.031	0.055	0.07	0.55
	1.5	SM	0.050	0.072	0.014	0.029	0.108	0.37	0.71
	3	BV	0.490	0.360	0.023	0.111	0.278	0.34	0.83
	3	LA	0.095	0.127	0.075	0.120	0.132	0.28	0.66
	3	LM	0.084	0.201	0.029	0.081	0.249	0.44	0.69
	3	RA	0.299	0.180	0.165	0.121	0.160	0.22	0.80
	3	RM	0.287	0.087	0.029	0.053	0.251	0.17	0.78
	3	SM	0.228	0.251	0.187	0.073	0.317	0.31	0.81
Maximum	1.5	BV	0.124	0.632	0.110	0.446	0.820	0.42	0.57
	1.5	LA	0.352	0.364	0.106	0.278	0.731	0.28	0.64
	1.5	LM	0.125	0.013	0.074	0.065	0.492	0.03	0.53
	1.5	RA	0.307	0.884	0.317	0.178	0.767	0.47	0.80
	1.5	RM	0.047	0.000	0.202	0.088	0.589	0.00	0.51
	1.5	SM	0.050	0.125	0.062	0.057	0.326	0.33	0.63
	3	BV	3.965	2.740	0.824	0.837	2.101	0.31	0.85
	3	LA	0.428	2.695	0.144	0.709	1.658	0.61	0.74
	3	LM	0.069	0.444	0.091	0.325	1.140	0.37	0.50
	3	RA	1.032	2.054	0.691	0.303	1.572	0.46	0.84
	3	RM	0.543	0.328	0.033	0.251	1.395	0.22	0.60
	3	SM	0.290	0.782	0.308	0.054	0.933	0.47	0.83

^aICC_BET = between‐site ICC.

^bICC_T‐R = test‐retest ICC.

A measure for test–retest reliability asks about the reliability (or correlation) of two visits for the same subject at the same site but on different days. This reliability is calculated as

The between‐site reliability estimates are analogous to ICC (type 2, 1) and the test–retest reliability estimates are analogous to ICC (type 1, 1) from Shrout and Fleiss [1979] but have been adapted to the more complex design.

RESULTS

Field‐Strength Effects (Fig. 2, Table IV)

Figure 2.

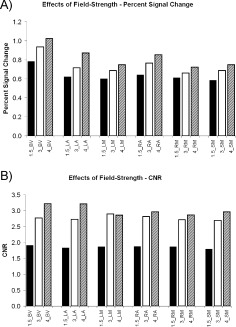
Field strength effects. (A) Mean PSC estimates (based on median ROI extraction) for 1.5T, 3T, and the 4T scanner across six ROIs (BV= bilateral visual cortex, LA = left auditory cortex, LM = left motor cortex, RA = right auditory cortex, RM = right motor cortex and SM = supplementary motor cortex). (B) Mean CNR estimates (based on median ROI extraction) for 1.5T, 3T, and the 4T scanner across six ROIs.

Table IV.

Field‐strength effects

	Contrast	Region	Estimate	T	df	One‐tailed P‐value	FDR P‐value	Cohen's D
Percent signal change	3 T > 1.5 T	ALL	0.10	2.28	7	0.028		1.72
	3 T > 1.5 T	BV	0.15	3.25	8.57	0.005	0.030	2.22
	3 T > 1.5 T	LA	0.09	2.04	8.57	0.037	0.056	1.39
	3 T > 1.5 T	LM	0.09	1.87	8.57	0.048	0.058	1.28
	3 T > 1.5 T	RA	0.12	2.67	8.57	0.013	0.039	1.82
	3 T > 1.5 T	RM	0.05	1.02	8.57	0.168	0.168	0.70
	3 T > 1.5 T	SM	0.10	2.16	8.57	0.030	0.056	1.48
Contrast‐to‐noise ratio	3 T > 1.5 T	ALL	0.91	3.68	7	0.004		2.78
	3 T > 1.5 T	BV	0.85	3.39	7.56	0.005	0.005	2.47
	3 T > 1.5 T	LA	0.90	3.56	7.56	0.004	0.005	2.59
	3 T > 1.5 T	LM	1.03	4.08	7.56	0.002	0.005	2.97
	3 T > 1.5 T	RA	0.94	3.72	7.56	0.003	0.005	2.71
	3 T > 1.5 T	RM	0.85	3.36	7.56	0.005	0.005	2.44
	3 T > 1.5 T	SM	0.90	3.57	7.56	0.004	0.005	2.60

Median PSC and CNR both increase with field‐strength (Fig. 2). The 3T scanners had higher median PSC than the 1.5T scanners (Fig. 2A, Table IV). The all‐region test was statistically significant as were five of six ROI‐specific tests. Controlling for an FDR of 0.05, two of the ROI‐specific tests were statistically significant. The Cohen's D effect sizes were very large. The 3T scanners had higher median CNR than the 1.5T scanners (Fig. 2B, Table IV). The all‐region test was statistically significant as were all of the ROI‐specific tests. Controlling for an FDR of 0.05, all of the ROI‐specific tests were statistically significant. The Cohen's D effect sizes were also very large. However, the effect sizes for median CNR were statistically significantly higher than the effect sizes for median PSC (P = 0.001, two‐tailed, paired t‐test). The presence of consistent mean elevations for the 4T scanner compared to the 3T scanners (11 of 12 measures), indicates that including the 4T scanner with the 3T scanners will lower reliability. For this reason, we chose not to lump the 4T in with the high field group.

Test–Retest Reliability (Fig. 3A, Tables II and III)

Figure 3.

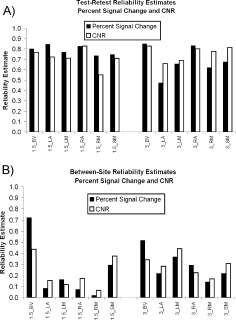
Reliability. (A) Test–retest reliability estimates for PSC and CNR for 1.5T and 3T scanners at six ROIs. See Figure 2 for ROI definitions. (B) Between‐site reliability estimates for PSC and CNR for 1.5T and 3T scanners at six ROIs.

Test–retest reliability was generally high (Fig. 3A). For the median PSC measure, the median test–retest reliability was 0.76 (25th percentile = 0.67, 75th percentile = 0.83). For the median CNR measure, the median test–retest reliability was 0.74 (25th percentile = 0.70, 75th percentile = 0.80). Thus, the central tendency of test‐retest reliability is at the border between good and excellent reliability.

Between‐Site Reliability (Fig. 3B, Tables II and III)

Between‐site reliability was much lower than test–retest reliability (Fig. 3B versus Fig. 3A). For the median PSC measure, the median between‐site reliability was 0.22 (25th percentile = 0.13, 75th percentile = 0.31). For the median CNR measure, the median between‐site reliability was 0.25 (25th percentile = 0.16, 75th percentile = 0.35). Both ICCs can be described as poor.

Comparing Median‐based Measures to Maximum‐based Measures on Between‐Site Reliability (Fig. 4, Table V)

Figure 4.

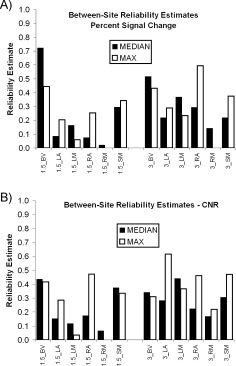
Comparing the median and the maximum. (A) Between‐site reliability estimates for PSC based on either median ROI extraction or maximum ROI extraction for 1.5T and 3T scanners at six ROIs. See Figure 2 for ROI definitions. (B) Between‐site reliability estimates for CNR based on either median ROI extraction or maximum ROI extraction for 1.5T and 3T scanners at six ROIs.

Table V.

Between‐site reliability estimates for median‐based and maximum‐based measures

Measure	ROI extraction method	25th percentile	Median	75th percentile
Percent signal change	Median	0.13	0.22	0.31
Percent signal change	Maximum	0.17	0.27	0.39
CNR	Median	0.16	0.25	0.35
CNR	Maximum	0.27	0.35	0.46

Between‐site reliability estimates for median and maximum PSC (Fig. 4A) and CNR (Fig. 4B) measures are summarized in Table V. There is no obvious winner in these comparisons, and Wilcoxon Paired Tests reveal no statistically significant differences. The maximum measures do have higher median reliability (Table V) but the pattern is not consistent across regions and measures. Moreover, for PSC for the 1.5T_BV measure, where reliability is greatest, there is a marked drop in reliability estimate in going from median to maximum measure.

The Effect of Smoothness Adjustment on Between‐Site Reliability (Fig. 5, Table VI)

Figure 5.

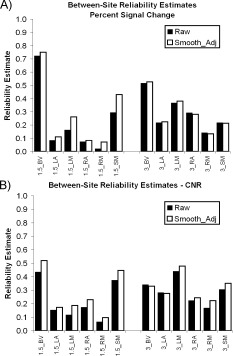
Effects of controlling for smoothness. (A) The effect of prior adjustment for smoothness on between‐site reliability of median PSC at 1.5T and 3T for six ROIs. See Figure 2 for ROI definitions. (B) The effect of prior adjustment for smoothness on between‐site reliability of median CNR at 1.5T and 3T for six ROIs.

Table VI.

Slope estimates for the relationship between image smoothness and PSC or CNR

Field	Region	PSC_Slope	PSC P‐value	CNR_Slope	CNR_P‐value
1.5	BV	−0.036	0.14	0.378	0.00000
1.5	LA	−0.052	0.00007	0.201	0.00000
1.5	LM	−0.071	0.00000	0.316	0.00000
1.5	RA	−0.039	0.00890	0.237	0.00000
1.5	RM	−0.101	0.00000	0.243	0.00000
1.5	SM	−0.096	0.00000	0.247	0.00000
3	BV	−0.028	0.55	0.466	0.00082
3	LA	−0.011	0.58	0.477	0.00000
3	LM	−0.013	0.58	0.541	0.00000
3	RA	0.056	0.01136	0.803	0.00000
3	RM	0.012	0.55	0.789	0.00000
3	SM	0.026	0.39	0.738	0.00000

In a previous report [Friedman et al., 2006; see also Lowe and Sorenson, 1997], we found that image smoothness had a strong effect on activation effect size, i.e., the multiple R ². This is most similar to the CNR measure used herein, although it would be better related to contrast‐to‐total‐temporal‐variance‐ratio. Having in our possession smoothness estimates from that paper and median PSC and CNR estimates here, it was of interest to determine if prior adjustment for smoothness differences would have a beneficial effect on between‐site reliability.

Median PSC and CNR measures were regressed against average smoothness estimates (FWHM units) (Table VI). Generally, there was a negative slope for the relationship between smoothness and median PSC. Although the effect is small, with a median slope of −0.032, the relationship was statistically significant for six measures. With this slope, each increase by 1 mm in smoothness (FWHM) is associated with a 0.03 decline in median PSC. With PSC estimates in the range of 0.6–1.0, this amounts to between 3 and 5% of PSC estimates. For median PSC (Fig. 5A) smoothness adjustment improves reliability for 9 of 12 measures (Wilcoxon Test, P = 0.041, two‐tailed). For median CNR (Fig. 5B) smoothness adjustment improves reliability for 10 of 12 measures (Wilcoxon Test, P = 0.005, two‐tailed).

The Effect of ROI Size on Between‐Site Reliability (Fig. 6)

Figure 6.

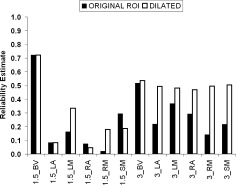
Effect of dilating ROIs. Between‐site ICCs for median PSC with and without ROI dilation. Note the improved reliability with dilated ROIs especially at 3T.

One concern was that our ROIs were too small, even though they were defined to include activations from all sites (see above). All the original ROIs were dilated in the x, y, and z direction by three voxels. The dilated ROIs produced statistically significant increases in between‐site ICC for PSC (Wilcoxon Test, P = 0.034), especially at 3T (improvement at 1.5T = 47%, improvement at 3T = 93%) (Fig. 6).

The Effect of Dropping One Site on Between‐Site Reliability (Table VII)

Table VII.

The effect of dropping one site at a time on variance components and between‐site reliability

Site that was dropped	Measure	ROI extraction method	Field	Site	Subject	Site × subject	Visit	Residual	Between‐site ICC
ALL_IN	CNR	Median	1.5						0.44
SITE 1	CNR	Median	1.5	0.09635	0.13354	0.02948	0.06330	0.08511	0.39
SITE 2	CNR	Median	1.5	0.03733	0.14157	0.02467	0.04876	0.06907	0.53
SITE 3	CNR	Median	1.5	0.08097	0.15893	0.01838	0.06547	0.08711	0.46
SITE 4	CNR	Median	1.5	0.09754	0.10948	0.02281	0.03093	0.07174	0.39
SITE 5	CNR	Median	1.5	0.09937	0.16168	0.02832	0.06957	0.08726	0.42
ALL_IN	PSC	Median	1.5						0.72
SITE 1	PSC	Median	1.5	0.00358	0.03336	0.00261	0.00601	0.00894	0.70
SITE 2	PSC	Median	1.5	0.00456	0.03558	0.00000	0.00704	0.00946	0.72
SITE 3	PSC	Median	1.5	0.00330	0.03821	0.00043	0.00844	0.00950	0.72
SITE 4	PSC	Median	1.5	0.00000	0.03619	0.00103	0.00504	0.01013	0.81
SITE 5	PSC	Median	1.5	0.00394	0.03598	0.00138	0.00929	0.01073	0.68
ALL_IN	CNR	Median	3						0.34
SITE 6	CNR	Median	3	0.01004	0.40512	0.01930	0.15419	0.30249	0.61
SITE 7	CNR	Median	3	0.67092	0.28861	0.00000	0.09184	0.27842	0.26
SITE 8	CNR	Median	3	0.72608	0.35661	0.02849	0.14302	0.27573	0.27
SITE 9	CNR	Median	3	0.54591	0.37612	0.10214	0.01753	0.25724	0.34
ALL_IN	PSC	Median	3						0.52
SITE 6	PSC	Median	3	0.00347	0.05069	0.01885	0.01305	0.02654	0.55
SITE 7	PSC	Median	3	0.03281	0.05497	0.00649	0.01502	0.02200	0.48
SITE 8	PSC	Median	3	0.02891	0.05924	0.01550	0.00924	0.02194	0.50
SITE 9	PSC	Median	3	0.04419	0.07350	0.00355	0.00743	0.02535	0.54

The notion of dropping one site to increase between‐site reliability is obviously a drastic step, but in some cases may be warranted. At the least, an analysis of reliability with and without a site can be a powerful diagnostic tool. In Table VII, the effect of dropping one site at a time from the variance components and between‐site reliability calculations is compared to the case where all sites are included. For this analysis, all the data come from the BV ROI exclusively. Dropping SITE 2 from the analysis increased the reliability of median PSC for 1.5T scanners from 0.44 to 0.53. Dropping SITE 4 from the analysis of median CNR for 1.5T scanners increased the reliability from 0.72 to 0.81. For both measures at 3T, SITE 6 site was bringing down the reliability. For CNR, the change was quite marked (0.34–0.61), whereas for PSC the change was modest (0.52–0.55).

The Effect of Number of Runs on Test–Retest and Between‐Site Reliability (Fig. 7)

Figure 7.

Effect of increasing number of runs. Relationship between number of runs contributing to the average estimate (abscissa) and test–retest ICC for 24 measures [two measurement PSC vs. CNR), six ROIs, and two field strengths). In the most panel, the predicted means and standard errors are plotted from a repeated measures polynomial contrast model. The curves are spread across six panels to enhance visibility of curve. The source of the data in each curve is not identified the figure.

The better the estimate of the PSC measure or CNR measure, the higher the reliability should be. One way to improve the estimates is to base them on averages across runs. Such an analysis is presented in Figure 7, for test–retest reliability. There are six ROIs, two field strengths, and two measurement types (PSC and CNR) or 24 total analyses, all of which are plotted in Figure 7. The six panels were used to spread the curves out for visibility, and the source data for individual curves are not identified for the present purpose. The points represent either data from run 1, the average of runs 1 and 2, the average of runs 1, 2, and 3 or the average of all four runs. The mean curve on the left plots predicted values and standard errors from a polynomial regression (F = 25.6, df = 1.7, 40, P = 0.0001). As predicted, test–retest reliability increases with averaging, but not in every single case. Reliability for the average of four runs is higher than reliability for a single run (t = 5.76, df = 23, P = 0.000004, paired t‐test, one‐tailed). The average of four runs demonstrates higher reliability than the average of three runs in 18 of 24 cases (t= 2.55, df = 23, P = 0.009, paired t‐test, one‐tailed). Clearly one way to enhance test–retest reliability is to increase the number of runs, and it seems likely that reliability will continue to increase beyond four runs. The pattern of increasing reliability with increasing the number of runs included in the average was not consistently apparent for between‐site reliability estimates.

Concatenating “Reliability Enhancing Steps” (Fig. 8)

Figure 8.

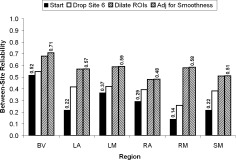
Concatenating steps to improve reliability. Effect of a series of steps, described in the text, on between‐site reliability for median PSC from 3T scanners.

To illustrate the effects of accumulating the benefits of several steps to improve between‐site reliability, we began with the original data for median PSC for 3T scanners (Fig. 8). In the first step, SITE 6 site was dropped and this led to a substantial increase in between‐site reliability. In the second step, we dilated the all of the ROIs as described above. This further increased between‐site reliability. In the final step, we adjusted for smoothness differences between sites. This latter effect was almost unnoticeable except for the BV ROI. The median initial reliability was 0.26 and the median final reliability was 0.58, a statistically significant (Wilcoxon, P = 0.014, one‐tailed) improvement of 123%.

DISCUSSION

A key goal of this report was to assess test–retest reliability and between‐site reliability for a multicenter fMRI study involving 10 sites and a robust sensorimotor activation task. Measures of reliability are obtained from a variance components analysis of the fMRI activations for the study in which five subjects visited each of 10 sites for two visits (on consecutive days). In general, test–retest reliability was high, but initially, between‐site reliability was low. Several methods were evaluated for improving between‐site reliability. By employing multiple methods, marked increases in between‐site reliability were noted.

Test–Retest Reliability

We report high test–retest reliability for a 1 day interval for activations from a robust sensorimotor task in several ROIs. This indicates that fMRI tasks can be reliable when retested on subsequent days within a site, but this reliability level will likely depend highly on the robustness of the task and the number of runs studied. The present report is similar in several respects to the recent report of Aron et al. [2006]. These authors compared test–retest reliability on a learning task (without practice effects) with a test–retest interval of 1 year. The dependent measure used for ICC calculation in Aron et al. [2006] was a measure of signal change (rather than CNR), and signal changes were mean estimates from ROIs. All of the ROI‐based test–retest ICCs Aron et al. [2006] reported were in the excellent range. Kong et al. [2007] reported test–retest ICCs for a unilateral finger tapping task, which included primary motor and supplementary motor areas. They employed a measure of signal magnitude and obtained an ICC for the left motor area of 0.68—quite similar to the ICCs for the LM and RM ROIs reported herein (Fig. 3). The test–retest reliability for the supplementary motor area in the Kong et al. [2007] study was 0.51—somewhat lower than we report herein.

As expected, an increase in the number of runs used in an average estimate was associated with increase in the test–retest reliability. The effect of increasing numbers of runs on the estimate of test–retest reliability was greatest for the difference between a single run and two runs, and less for the addition of each addition run, but was still statistically significant for the difference between three runs and four runs. Since we ran only four runs of the sensorimotor task, we could not empirically estimate the effect of more runs. However, the improvement in reliability with increasing runs should increase as a function of 1/N _runs. Thus, it seems unlikely that significant improvement in reliability with increasing numbers of runs will continue beyond ∼6–8 runs. On the other hand, fatigue is accumulating through the scanning session, and it seems likely that attention and motivation will wane as more and more runs are tested. Thus, we predict that the empirical relationship between number of runs and reliability will peak at some point and then either plateau or actually decline. Therefore, we recommend that in preliminary studies prior to a major multicenter study, the fMRI task be tested on many runs at one or more sites, to determine the optimal number of runs to enhance reliability.

Previous fMRI reliability studies have reported increased reliability when more data are collected. For example, Genovese et al. [1997] reported increased test–retest reliability within a scanning session as a function of increasing the run duration (number of volumes collected). In a PET rCBF study, Grabowski and Damasio [1996] reported that the replication rate for activations increased markedly when the analysis was based on two PET runs rather than a single run. Of particular interest is the report by Maitra et al., [2002], in which the estimates of reliability were based on 2–12 replications (1 run per visit, 12 visits) of a finger‐tapping task. They report that the gain in reliability “… is most pronounced when we move from 2 to 3 replications, and tapers off substantially at around 5 or 6 replications.”

Between Site Reliability

It was hypothesized that a measure of percent signal change (PSC) would produce higher between‐site reliability than a measure of contrast‐to‐noise‐ratio (CNR). This hypothesis was based on the notion that noise would likely be highly variable across sites and this would lower the reliability of the CNR measure but not the PSC measure. This was apparently not the case, since the comparison of between‐site reliability based on PSC versus CNR did not show a marked advantage for either measure, and actually showed a slight advantage to CNR measures. This statement only applies to the methods of assessment of PSC and CNR tested herein. There are numerous methods for computing PSC and CNR that may produce different results. For example, instead of PSC and CNR measures from an FIR‐deconvolution, one could have used PSC and CNR measures from the regression of a predetermined temporal model [events convolved with a canonical hemodynamic response function (HRF)]. Future research will be required for a comprehensive comparison of different measures of PSC and CNR. Cohen and Dubois [1999] compared the stability of regression β‐weights (a signal magnitude measure) to the stability of “number of activated voxels” and found the former to be much more stable than the latter. However, high ICC values have been reported for t‐values (a CNR measure) [Specht et al., 2003]. These authors employed an event‐related visual activation paradigm on two visits and computed within‐site ICC estimates for each voxel based on t‐values. In their “attend” condition, there was very high reliability for t‐values in the primary visual cortex (ICCs > 8). We also hypothesized that the extraction of a median IRF from each ROI would lead to more reliable results than the extraction of the maximum IRF. In many cases, data based on the maximum IRF was more reliable than data based on the median IRF, and no clear winner was obvious.

We also hypothesized that controlling for site differences in the native smoothness of the images [Friedman et al., 2006] would improve between‐site reliability. This was based on the notion that CNR measures would be related to image smoothness, and that scanners that produced smoother images would show higher CNR. This turned out to be the case, since adjusting for smoothness differences in CNR prior to between‐site reliability estimation produced a statistically significant increase in reliability. Furthermore, adjusting for smoothness differences in PSC also produces a statistically significant increase in between‐site reliability. The slope of the relationship between image smoothness and PSC was negative, indicating that the smoother the data, the lower the PSC estimate. This could be the result of spatial smoothness tending to round off the peaks and troughs of the raw image data and thus leading to a reduced PSC.

Our hypothesis that increasing the ROI size would increase between‐site reliability was borne out, particularly at 3T. Perhaps this is simply due to the fact that our original ROIs were too small, even though they were defined to include activations from all sites. The marked beneficial effect of ROI dilation at 3T could be due to the established fact that spatial image distortions are increased at 3T compared with 1.5T. In the present study, no B0‐distortion correction procedures were applied for the EPI acquisitions. Such correction procedures should reduce variance in the activation sites, especially at 3T. Furthermore, different spatial normalization techniques may have differential effects on reliability. Future FBIRN data acquisitions employ B0‐correction procedures, so this source of unwanted variance should be minimized somewhat going forward.

The ROIs we studied reflected common activation across all scanners. Our study examined sources of variation in signal magnitude for voxels where the P‐value was consistently above a statistical threshold across sites. We chose this definition of an ROI because conjunction methods of deriving ROIs are commonly used in fMRI studies [Friston et al., 1999; Quintana et al., 2003]. This ROI definition, based on multisite consistency, should produce an elevated between‐site reliability compared to ROI definitions that are not based on multisite consistency. However, employment of this ROI without other “reliability enhancing procedures” produced low reliability estimates (1.5T median: 0.22, 3T median: 0.25). Employment of ROIs that are not defined in reference to multisite activation consistency (e.g., atlas‐based ROIs) are likely to produce reliability estimates even closer to 0.0. The present study emphasizes the critical importance of ROI definition on reliability. Clearly, follow‐up studies which compare different methods of ROI definition are warranted.

We also examined the notion that increasing the number of runs of a task would increase the between‐site reliability. Although such an effect was unequivocally demonstrated for test–retest reliability, the effect of increasing the number of runs on between‐site reliability was not consistently observed. Between‐site reliabilities were generally poor initially, and the lack of effect of increasing the number of runs may simply reflect the notion that unreliable entities are not made more reliable by repeated sampling.

The notion of combining runs to increase accuracy only makes sense if there are no practice effects for the task under consideration. A number of fMRI studies have now documented practice effects for some tasks [for review, see Kelly and Garavan, 2005]. If one is to gain the reliability increase associated with averaging runs of a task, one should establish that practice effects are not an important characteristic of the task.

The notion of dropping a site to improve between‐site reliability is a drastic step. Nonetheless, the marked improvement in between‐site reliability for PSC at 3T after dropping the SITE 6 site suggests that in the present case, this might be warranted. Regardless of whether one chooses to actually drop a site, the “drop‐one‐site” analysis is a useful tool to highlight sites that are particularly influential in increasing or decreasing between‐site reliability. In the case of SITE 6, we have shown in previous publications [Friedman and Glover, 2006; Friedman et al., 2006] that this site had the weakest activations of any of the high‐field scanners. Since we are employing a reliability estimate that assesses absolute agreement, any site difference in PSC or CNR will lower reliability. We have recently been informed that this site has been severely impacted by environmental noise from a nearby subway train for years. Dropping SITE 2 from the 1.5T scanners was also associated with a substantial increase in between‐site reliability. As we have pointed out in an earlier report [Friedman et al., 2006], SITE 2 site employed a rather severe k‐space (apodization) filter and therefore produced unusually smooth images. This marked increase in smoothness would be expected to produce markedly elevated CNR estimates. Removal of this site would homogenize CNR across sites and lead to greater between‐site reliability. Removal of SITE 4 was associated with increased reliability for PSC at 1.5T. Further examination revealed that SITE 4 had the lowest PSC estimates of any 1.5T site for four of five ROIs. This was an older Picker 1.5T scanner that has since been decommissioned and replaced. This analysis emphasizes the importance of fully evaluating the performance of each scanner prior to inclusion in multicenter studies. A single unusual scanner can markedly affect between‐site reliability estimates.

Another goal of this report was to illustrate the usefulness of using within‐site ICC estimates as a benchmark for between‐site ICC estimates. In the multicenter context, between‐site reliability has only subject variance in the numerator, whereas test–retest reliability has subject, site, and subject‐by‐site variance in the numerator. So, by definition, test–retest reliability will always be higher than between‐site reliability. However, test–retest reliability can be assessed in one or several unicenter studies. If one accepts the goal that between‐site reliability should be in the good (0.60–0.74) or excellent range (above 0.75), it is probably wise to assess test–retest reliability at one or several sites prior to initiation of a multicenter study. If test–retest reliability is not in the excellent range, it seems unlikely that between‐site reliability will be in the good range, due to the additional variance due to site and the subject‐by‐site interaction. It seems likely that there will always be some degradation of reliability due to changes in hardware and setting.

A concern for the present study and for future studies of within‐site or between‐site reliability is the sample size of the reliability study. Several approaches to prospectively estimating sample sizes for reliability studies have been proposed [Charter, 1999; Giraudeau and Mary, 2001; Walter et al., 1998]. These approaches relate sample sizes to the widths of the confidence intervals around ICC estimates. Obviously, the more subjects in a study, the narrower the confidence limits. Confidence limits also narrow as reliability estimates increase. In the present study, with a sample size of five subjects, the confidence limits would be quite large. Although five subjects is a very small sample for such a study by any criteria, sending five subjects to 10 scanners around the USA for two scanning sessions was a very difficult and expensive procedure, and few research teams are likely to have the resources for such a study, much less a much larger study.

Another key point is that the variance of subjects in a reliability study should approximate the variance likely to be included in the substantive study. For example, the subjects in the reliability study should have roughly the same age‐range and gender mix as the proposed follow‐on substantive study.

In the present study, a simple and robust sensorimotor paradigm was employed for the assessment of within‐site and between‐site reliability. One question which naturally arises is: Would similar reliability been obtained if we had used a cognitive task? ICCs are available in the literature from several cognitive tasks [Aron et al., 2006; Manoach et al., 2001; Wei et al., 2004]. The results are varied. What is needed is a head to head comparison of the test‐retest reliability of a simple sensorimotor paradigm and several cognitive paradigms.

CONCLUSION

In conclusion, between‐site reliability in multicenter studies can be improved by choosing a robust task with high test–retest reliability, adjusting for smoothness differences between scanners [Friedman et al., 2006], increasing the number of runs, and optimizing the size of the ROIs. The method of “dropping one site” can provide useful diagnostic information as to which sites are most important in lowering reliability. In extreme cases, when dropping one site leads to marked increases in between‐site reliability, the approach may be justified. Prior to initiation of large multicenter fMRI trials, it is probably wise to perform test–retest reliability studies at one or more centers. This will allow the determination of the test‐retest reliability of the task and the optimal number of runs to collect.