A connectivity model for the locomotor network of Caenorhabditis elegans

Abstract

Recently, we described a new method for representing and analyzing the connectivity of a motoneuronal network. We used it to deduce a connectivity model for the neuromuscular network that generates locomotion in the nematode Caenorhabditis elegans. The network regulates muscle contraction and for this reason we used the location or function of body wall muscles to map every element (neuron or muscle cell) in a new framework, namely the peri-motor space. The previously published connectivity data for C. elegans locomotion network are incomplete; in particular, the connectivity of motoneurons in the posterior half of the animal is missing or partial. When we analyzed the connectivity data for motoneurons in the anterior half, we detected repeating patterns which we named iterativity. We analyzed the iterativity of each class of motoneuron and statistically validated that it is higher than expected by chance. We could then extrapolate the iteration into the posterior half. Here we will explain the new terms and elaborate on the process of analysis and the features of the new connectivity model.

The Locomotor Network

Throughout it lifetime, C. elegans moves almost continuously forward and backward by generating a dorsoventral undulatory wave. Locomotion acts as the common output pathway for the majority of the behaviors studied in C. elegans, including foraging, escape, entry and emergence from quiescence, aspects of mating and thermo- chemo- and klino-taxis. In recent years, the use of genetically encoded calcium indicators has led to new knowledge about the activity of the motoneurons responsible for locomotor behavior^1-3 and optogenetic tools enable locomotor circuits to be directly manipulated.^4,5 However, these efforts are constrained by our limited knowledge of the connectivity among the locomotor motoneurons. This is true even though the wiring diagram and connectivity data set of the C. elegans nervous system⁶ is the only existing nervous system described in detail. However, the data set is complete for the head and the tail regions and includes only the anterior half of the ventral nerve cord,^6-9 leaving 21 of 75 motoneurons with partial or no connectivity data. Furthermore, some of the data for the posterior portion of the ventral nerve cord originated from a male nematode and were omitted from our study (a total of 28 motoneurons without data). Over the 25 years since the publication of the original data set, it has been widely used by experimental and computational neuroscientists and mathematicians. Most publications ignore its incompleteness and those that acknowledge it, do so only briefly. Two studies^7,8 have improved the consistency, annotated the data set and added connections but did not resolve the gap in the data.

Peri-Motor

In our publication,¹⁰ we presented the known connections as a graph in a new space we named “Peri-motor.” Neuronal networks are often represented as graphs in which each neuron or group of neurons is represented as a vertex or node and their connections with other nodes (structural such as chemical synapses and gap junctions or functional such as deduced from MRI or electrophysiology) are represented as edges. The shape and interpretability of such graphs depends heavily on the choice of coordinate system and the location of the nodes in that space. Depending on the aim of the representation, commonly used coordinates are generated from the connectivity itself (for example, force-directed algorithms that position nodes apart by assigning repulsive and attractive forces or spectral layouts that uses eigenvectors of the adjacency matrix as a coordinate system). In our work, we mapped every muscle cell and motoneuron in the locomotor network to a position along the rostrocaudal axis associated with their function during locomotor behavior. In an undulating or swimming animal, body wall muscles contract to bend the body wall at their location along the rostrocaudal axis. We mapped each motoneuron to the average location of the muscle cells they innervate (Fig. 1A), weighted by the anatomical value of the neuromuscular junction (data from Chen et al.⁷) to provide a “functionally” meaningful location. The chemical synapses and gap junctions among the motoneurons were than mapped in perimotor space by connecting the mapped motoneurons (Fig. 1A). We accepted the assumption made by Chen et al.⁷ that muscle arms are perpendicular to the ventral cord and used the location of muscle cells from WormAtlas.⁹

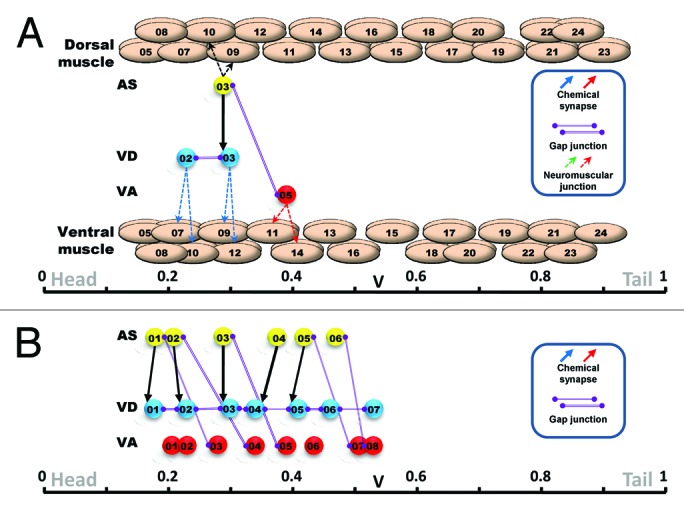
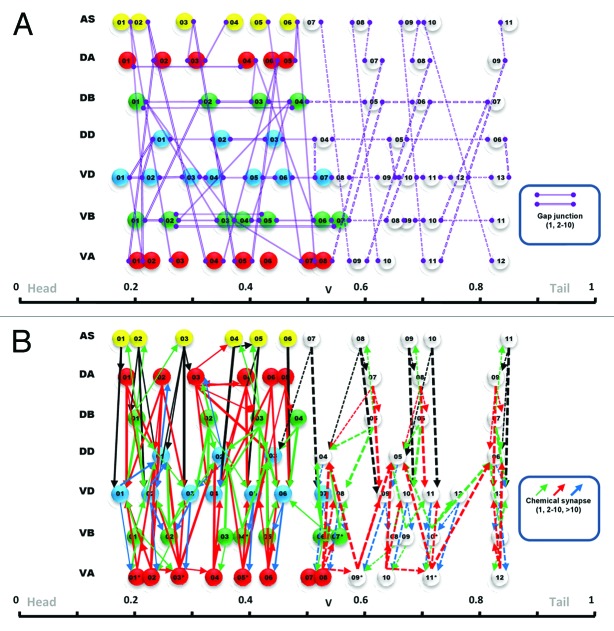
Figure 1. Peri-motor mapping and iterative connections. (A) In the peri-motor representation, muscle cells are positioned along the peri-motor axis at their corresponding locations along the rostrocaudal axis of the worm. Motoneurons are mapped at the average location of the muscle they innervate, weighted by the anatomical size of the neuromuscular junction (dotted line arrow). All 75 muscle cells are shown with only four motoneurons: AS03, VD02, VD03 and VA05. Chemical synapses (solid line arrow) and gap junctions (solid purple line) connect the motoneurons. (B) Connections that are parallel lines in this representation are iterative because they connect to motoneurons at similar relative positions. Shown are three examples of such iterativity of the connections in a AS-VD (chemical synapse), AS-VA (gap junction) and VD-VD (gap junction).

Iterativity

Once the motoneurons were mapped into their perimotor locations and all the chemical synapses and gap junctions from the connectivity database were mapped onto them, a repeating pattern emerged that we termed “iterativity.” We defined a connection as iterating if the source motoneurons were of the same class, the target motoneurons were of the same class and the source and target were the same peri-motor distance from each other two or more times. In the perimotor representation, iterative connections are parallel and easily identified (Fig. 1B). The Matlab code that we used to quantify the iterativity is available at MatlabCentral.com and includes a graphical user interface (GUI) that allows specific parameters to be adjusted (Fig. 2A and B). Although we found that a large fraction (90%) of connections in the locomotor network are iterating, it was unclear what level of iterativity would be expected by chance in a network of this size and connection density. To explore this question, we generated 500 randomly shuffled networks by keeping the neurons and the number of connections they make but shuffling the targets of those connections (this feature is also available through the GUI). We than analyzed the shuffled networks and compared the range of iterativity of each motoneuron to that of the real motoneuron of the data set. The differences between the iterativity of the actual and shuffled networks were statistically significant for all motoneurons.¹⁰

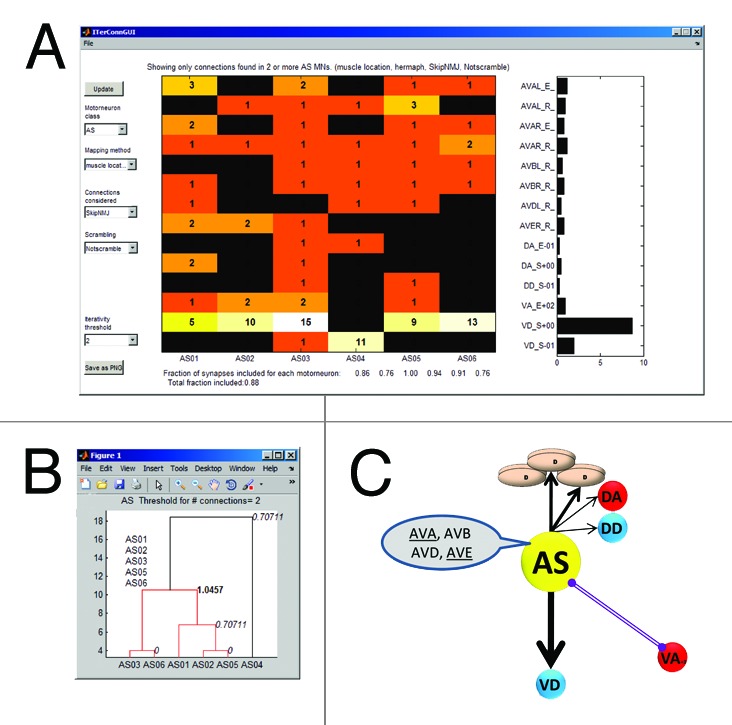
Figure 2. Peri-motor analysis GUI in Matlab and diagram. Example windows of the analysis program we used in Matlab. The GUI (A) allows the user to choose parameters for the analysis (here: motoneuron class AS, mapping method is muscle location with an iteration threshold of 2 and illustrates the iterative connections as a color map and a histogram. Iterativity indices for each motoneuron are indicated below the color map. A dendrogram (B) showing hierarchical clustering of the motoneurons in the class. An alternative presentation (C) of the iterative connections of a stereotypical AS motoneuron is a summary of the histogram in (A). (C) is reprinted from part of Figure 5A in reference 10.

Because iterated connections repeat along the rostrocaudal axis of the worm, it was necessary to establish an appropriate rostrocaudal window to perform the analysis. If the window was too narrow, too few connections were present for the analysis. By contrast, if it was too wide it might encompass several smaller iterating units. We used the minimal bin-width that captured the majority of iterated connections that turned out to be 1.5 times the average length of a muscle cell (0.06 of total body length).

The New Connectivity Model

Once iterativity of the connections has been identified, we suggested two ways it might be used to construct a connectivity model that spans the length of the animal. The first, which we described but did not fully implement, was to keep the 75 muscle cells and 75 motoneurons mapped in their peri-motor locations and keep the connectivity data for the anterior part. Then, we repeated each iterating connection to extrapolate into the posterior region where data are missing or partial (Fig. 3). The second method, which we described in more detail, involves constructing a single repeating unit, composed of 6 muscle pairs and 12 motoneurons and repeating that unit six times to complete the connectivity model (Fig. 4). The three anterior segments replace the database connectivity and the three posterior segments extrapolate into the posterior region. It is important to note that some of the connections described in the model (Haspel et al.,¹⁰ Table 2) do not apply to all the motoneurons of a specific class along the whole nerve cord but are limited to a portion of it. For example, the paired interneurons AVE only spans the anterior half of the nerve cord and does not innervate AS08-AS11, DA07-DA09 and VA09-VA12. Similarly, the head motoneurons SABD and SABVL innervate only the most anterior VA and DA motoneurons.

Figure 3. Interconnectivity of nerve cord motoneurons presented in peri-motor space. Illustrating all the gap junctions (A) and chemical synapses (B) among motoneurons from the original data set (solid lines and arrows) in peri-motor space. Note that iterative connections are easily identified because they form parallel lines in peri-motor space. The iterative connections are then extrapolated into the posterior portion (dotted lines and arrows) to produce a complete model of the interconnectivity.

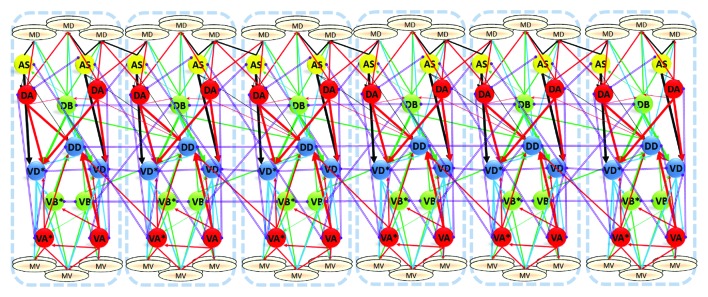
Figure 4. The segmented connectivity model. Six repeating units, each composed of 12 muscle cells innervated by 12 motoneurons are interconnected to produce the complete motor network for the nematode. Figure reprinted from Figure 8A in reference 10.

Implications and Other Motor Networks

The connectivity formulation we have described provides a concrete infrastructure for computational models of the locomotor network and an interpretation framework for experimental data. In addition, the model predicts the connectivity of the posterior portion of the ventral cord that will be confirmed or refuted by future connectivity data.

In our work, we have used the peri-motor representation and the analysis of iterative connectivity in the C. elegans locomotor network. However, either or both of these concepts can be applied to other motor systems. In the case of the nematode network, development of these methods was facilitated for two reasons: (1) in an undulating animal, the muscles can be mapped in peri-motor space according to their anatomical location; (2) the number of motoneurons is small and very few interneurons are involved. Although we have used the location of body wall muscles to map the synaptic connections of motoneurons, other parameters could be used in systems in which the functional actions of a muscle are complex and act across multiple joints. Furthermore, it may be possible to extend the utility of this approach by mapping neuronal connections into more than a single dimension. Moreover, the mapping parameter need not be spatial. For example the timing of muscle activity within a step or a swim cycle might be used as the mapping parameter. The connections of motoneurons and interneurons could then be mapped along this axis. The success of the method in revealing and displaying patterns of connections arises because the remapping generates a highly regular network in which it is much easier to detect repeated connections than in the irregular anatomical map from which it was generated. Thus repeating connections appear as parallel lines distributed along the map. If the method is applied to more complex networks, it may allow network motifs to be identified based on geometric patterns in the map.

Haspel G, O'Donovan MJ. A peri-motor framework reveals functional segmentation in the motoneuronal network controlling locomotion in Caenorhabditis elegans. J Neurosci. 2011;31:14611–23. doi: 10.1523/JNEUROSCI.2186-11.2011.