Bayesian latent structure models with space-time-dependent covariates

Abstract

Spatial-temporal data requires flexible regression models which can model the dependence of responses on space- and time-dependent covariates. In this paper, we describe a semiparametric space-time model from a Bayesian perspective. Nonlinear time dependence of covariates and the interactions among the covariates are constructed by local linear and piecewise linear models, allowing for more flexible orientation and position of the covariate plane by using time-varying basis functions. Space-varying covariate linkage coefficients are also incorporated to allow for the variation of space structures across the geographical location. The formulation accommodates uncertainty in the number and locations of the piecewise basis functions to characterize the global effects, spatially structured and unstructured random effects in relation to covariates. The proposed approach relies on variable selection-type mixture priors for uncertainty in the number and locations of basis functions and in the space-varying linkage coefficients. A simulation example is presented to evaluate the performance of the proposed approach with the competing models. A real data example is used for illustration.

1 Introduction

There is an increasing attention in the analysis of spatially and temporally referenced data in both methodological and applied research. Such data are of substantial interest in a variety of disciplines such as epidemiology, ecology, political sciences and economics. For example, one might be interested in geographical patterns and trends of a certain disease in a particular region over time. We start with describing a general space-time model.

Suppose that the dependent variable y_it is observed in the ith spatial unit (e.g., region or individual) and the tth time point with i = 1, …, n and t = 1, …, T. A general space-time model can be expressed as

$$y_{it}~f(y_{it}\mid \cdot ),$$ (1.1)

where f (y_it|·) denotes a conditional distribution of y_it given observed covariates, latent variables and measurement errors, with mean μ_it, μ_it = E(y_it), which is typically related to a linear predictor η_it through a suitable link function g(·), where η_it = g(μ_it). The response variable could be observed as a continuous (e.g., disease rate), categorical (e.g., indicates of disease or health status) and count (e.g., disease or death number) outcome. The predictor η_it is usually expressed as

$${\eta }_{it}={\text{x}}_{it}^{\prime }\beta +u_i+v_i+{\delta }_t,$$ (1.2)

where x_it = (1, x_it2, …, x_itp)′ denotes a p × 1 vector of covariates associated with unit i and time t, β = (β₁, …, β_p)′ denotes ap × 1 vector of population parameters, u_i and v_i denote random effects measuring spatial similarity and excess heterogeneity, respectively, and δ_t denotes a structured temporal random component. Conventionally, the fixed effects β can be modelled to follow a multivariate normal prior. The parameters u_i and v_i are assumed to be independent. The parameter v_i captures the heterogeneity among the units which is chosen to follow an exchangeable normally distributed prior, while u_i captures the clustering property of spatial data which is assumed to follow a conditional autoregressive (CAR) distribution (a special case of the general class of Markov random field) (Besag, 1974), $u_i\mid u_{-i}~\text{N}({\stackrel{‒}{u}}_i,{\left(\tau m_i\right)}^{-1})$, where u_−i = (u₁, …, u_i−1, u_i+1, …, u_n)′, ${\stackrel{‒}{u}}_i=m_i^{-1}{\sum }_{j\in {\partial }_i}{u}_j$ with ∂_i denoting the neighbour set of unit i, m_i denotes the number of neighbours of unit i and τ denotes the precision parameter. The constraint ${\sum }_{i=1}^n{u}_i=0$ is defined for the purpose of identifiability of the overall intercept. The temporal parameter δ_t is assumed to follow AR(1) prior.

When responses are count data, model (1) becomes a typical spatio-temporal model based on which some hierarchical models were developed (Waller et al., 1997; Knorr-Held and Besag, 1998; Lagazio et al., 2003; among others). More complex issues occur when the space-time interaction effect, θ_it, is included in the predictor (2). Knorr-Held (2000) incorporated a space-time interaction for inseparable space-time variation in disease risk where four types of space-time interaction were described. Richardson et al. (2006) proposed a joint spatio-temporal modelling of two diseases with shared space-time interaction. Lagazio et al. (2001) focussed on the birth cohort model to assess latent effects associated with temporal trends. Ugarte et al. (2009) evaluated the performance of various spatio-temporal Bayesian models. Hossain and Lawson (2010) also evaluated ST (spatial-temporal) small area models but with an emphasis on cluster recovery/detection. When the effect of covariates on the response is the main focus, some space-time models with space-dependent coefficients (e.g., Assunçao, 2003; Gamerman et al., 2003) or time-dependent coefficients (Dreassi et al., 2005) were developed. In practice, the space-time-dependent effect of a specific space-time covariate on responses is also of substantial interest (e.g., effects of poverty rates on low birth weight may vary across different regions and time points). Although some work has been done (Gelfand et al., 2005; Paez et al., 2008), there is still lack of development for such models. Typically, one may consider a space-time model based on linear combinations of covariates such as ${\eta }_{it}={\text{x}}_{it}^{\prime }{\beta }_{it}+u_i+{\nu }_i+{\delta }_t$. This expression can be treated as a general case including the model with a space-time interaction term, the model with space-dependent covariates (Assunção, 2003) and the model with time-dependent covariates (Dreassi et al., 2005). However, linear models prove too rigid when large quantities of data are considered and there exists nonlinearity (Hastie and Tibshirani, 1990).

Outside the context of the space-time data analysis, there exists a fairly rich literature of nonlinear regression modelling in both the frequentist and Bayesian framework. For example, Friedman (1991) proposed multivariate adaptive regression splines by using flexible tensor product splines. Holmes and Mallick (2001, 2003) described a Bayesian approach of piecewise linear model with covariate surface constructed by basis functions. Bigelow and Dunson (2007) extended the method to allow the spline coefficients to be subject specific. Pintore et al. (2006) derived a spatially adaptive smoothing splines based on a reproducing kernel Hilbert space representation. Numerous references can be found in Denison et al. (2002) and Ruppert et al. (2003), and therein.

Within the context of spatial and temporal modelling, Schmid and Held (2004) investigated space-time trends by incorporating intercept terms of covariates of interest with additional spatial component into the model. Banerjee and Johnson (2006) proposed to model single and multi resolution spatially varying growth curves as Gaussian processes that capture associations at single and multiple resolutions. Kneib and Fahrmeir (2006) described a general class of structured additive regression models for categorical responses, allowing for a semiparametric predictor. Zhao et al. (2006) developed general design generalized linear mixed models in which random effects with spatial correlation structure are included. Among the methods developed, however, none of them simultaneously consider, space- and time-specific effects of space-time covariates on responses.

In this paper, we focus on developing a general space-time model with main interest in the effect of space- and time-dependent covariates on the response. We extend the generalized multivariate regression splines (Holmes and Mallick, 2001) to flexibly accommodate the space- and time-specific covariates, allowing for flexible orientation and position of the covariate plane by using time-varying basis functions. Space-varying covariate linkage coefficients are incorporated for variation of space structures across geographical locations. Such multivariate regression models allow for effects of covariates on responses not only across space but also over time (i.e., interactions) in a flexible manner. We develop an approach which relies on variable selection-type mixture priors for uncertainty in the number and locations of the piecewise linear basis functions and in the space-varying linkage coefficients.

The remainder of the paper is organized as follows. Section 2 describes the space-time latent structure model with multivariate linear splines for a covariate linkage. Prior specification and posterior implementation are described. Section 3 discusses the model evaluation and comparison. Section 4 evaluates the performance of the approach based on a simulated example. Section 5 illustrates the approach via a real spatial-temporal data. Finally, Section 6 summarizes and discusses the results.

2 Space-time models with latent structure

2.1 The model and prior specification

We consider to model the unknown linear predictor as

$${\eta }_{it}=\sum _{k=1}^K{\beta }_{ik}{\left({\text{x}}_{it}^{\prime }{u}_{tk}\right)}_{+},$$ (2.1)

where β_i = (β_i1, …, β_iK)′ denotes a K × 1 vector of candidate space-specific linkage parameters for the underlying latent effects, u_tk denotes a p × 1 vector of time-varying basis parameters and (x_itu_tk)₊ denotes a basis function which is an inner product of x_it and u_tk truncated below by 0. To allow each model to include an intercept term, we define (x_itu_t1)₊ to be one for all i and t. When β_i are typically subject-specific coefficients, this formula is a generalization of the formulae by Holmes and Mallick (2001) and Bigelow and Dunson (2007). In model (3), the linkage coefficients β_i have spatially structured effects on covariates. To avoid identifiability problem, we constrain ${\sum }_{i=1}^n{\beta }_{ik}=C_k$, where C_k is some constant (Assunção et al., 2002). One may typically decompose β_ik as α_k + ζ_ik, where α_k denotes the global effect and ζ_ik denotes the spatially structured effect with ${\sum }_{i=1}^n{\xi }_{ik}=0$ to identify the overall effect due to the location invariance of the CAR prior. An attractive property of the structure of equation (2.1) is that the basis functions are time dependent which provide flexible orientation and position of the covariate plane and important trends in the impact of covariates over time. It is clear that each of the (K – 1) non-intercept basis functions contains linear effect for at least one covariate. When a basis contains multiple covariate effects, the proposed model allows for the effects of interactions (i.e., dependence) of space-time covariates on the response. The proposed model can be thought of as a more general spatio-temporal model. For example, if the observations are only spatially dependent, then basis functions are time irrelevant. In this case, the model reduces to the space-varying regression model (Assunção, Gamerman et al., 2003) with time-dependent covariates, i.e., ${\eta }_{it}={\text{x}}_{it}^{\prime }{\theta }_i$.

The proposed approach allows for a flexible number of unknown basis functions and the linkage coefficients. Since the number of basis functions related to covariates is unknown a priori, one may consider the reversible jump MCMC (Markov chain Monte Carlo) (Green, 1995) for such models (e.g., Holmes and Mallick, 2001; Bigelow and Dunson, 2007). However, it involves complicated marginal likelihood calculation or approximation. To avoid this complexity, we adopt variable selection-type mixture priors for uncertainty of the number and locations of piecewise basis functions. To allow the kth basis to be effectively excluded from the model, we choose a mixture prior including a point mass at zero and a CAR distribution for the linkage coefficient β_ik given the indicator γ_k:

$${\beta }_{ik}\mid {\gamma }_k~{\gamma }_k{\delta }_0\left({\beta }_{ik}\right)+(1-{\gamma }_k)\text{N}({\stackrel{‒}{\beta }}_{{\partial }_i,k},{\left({\tau }_k{m}_i\right)}^{-1}),$$ (2.2)

where γ_k is an indicator variable which is 1 for exclusionor 0 for inclusion of the kth basis function, δ₀(·) denotes a point mass at zero, ${\stackrel{‒}{\beta }}_{{\partial }_i,k}=m_i^{-1}{\sum }_{j\in {\partial }_i}{\beta }_{jk}$ with ∂_i denoting the neighbour set of unit i, m_i denotes the number of neighbours of unit i and τ_k denotes the precision parameter. We refer to prior (4) as a zero-inflated CAR prior, ZI-CAR(γ_k, τ_k). The prior probability of the kth basis out of the K candidate bases related to covariates being excluded is p_1,k0 = Pr(H_1,k0: β_ik = 0). The prior for γ_k is then chosen as a Bernoulli distribution, Bern(p_1,k0). The prior for τ_k is chosen as Gamma(a_τ, b_τ), where Gamma(a, b) is a gamma distribution with mean a/b and variance a/b².

To reflect time-dependent measurements in each region, we use multivariate dynamic normal priors for u_tk,−1 which can be written as

$${\text{u}}_{tk,-1}~N_{p-1}({\rho }_k{\text{u}}_{t-1,k,-1},\nu ),t=1,\dots ,T,$$

where ρ_k denotes the variation of the temporal autocorrelation in the risk, u_0k,−1 denotes the starting vector of u_tk−1 and ν denotes a diagonal covariance matrix, diag(ν₂, …, ν_p). Due to lack of unique solutions of β_ik and u_tk to the same model for each k, following Holmes and Mallick (2001), we normalize each component of u_tk,−1 = u_tk/u_tk,1 = (u_tk,2, …, u_tk,p)′, i.e., ||u_tk,−1|| = 1 for t = 1, …, T and k = 1, …, K, so that u_tk/u_tk,1 can be used for orientation of the plane in (p –1)-dimension covariate space and u_tk,1 for the position of the plane. To flexibly select the components from p – 1 covariates at each time point, we first choose u_0k,−1 to be zero. We then choose a variable selection-type mixture prior with a point mass at zero for variance ν_l, for l = 2, …, p,

$${\nu }_l~{\kappa }_l{\delta }_0\left({\nu }_l\right)+(1-{\kappa }_l)\text{IG}({\nu }_l;a_{\nu },b_{\nu }),$$ (2.3)

where κ_l is an indicator variable which is 1 for exclusionor 0 for inclusion of the lth covariate and IG(·) denotes an inverse gamma distribution. We refer to prior (5) as ZI-IG(κ_l, a_ν, b_ν). The prior for κ_l is chosen as Bern(p_2,l0), where p_2,l0 denotes the probability of the lth covariate being excluded. The first element of u_tk can be defined as $u_{tk1}=-{\text{x}}_{i^{\prime }t,-1}^{\prime }{\text{u}}_{tk,-1}$, where x_i′t,−1 is randomly selected with i′ ∈ {1, …, n}. With probability of p_2,l0, all u_tkl are zeroes, for t = 1, …, T and k = 1, …, K, indicating that the lth covariate is excluded from the model. The mixture prior allows for the locations of the splines to vary over time by effectively excluding the elements from each basis function. The overall prior probability of excluding all covariates (except intercept) from the model at time t is ${\Pi }_{l=2}^p{p}_{2,l0}$.

To allow for flexibility of the prior probability, p_1,k0, we consider choosing a hyper-prior beta distribution for the prior exclusion probability, p_1,k0 ~ Beta(c₁, d₁). Given the assumption that all prior probabilities are equal (say, p₀), the full conditional for p_1,k0 can be easily calculated (see details in Appendix). Similarly, the prior of p_2,l0 is chosen as a beta distribution, Beta(c₂, d₂), allowing for more flexibility in adapting the desired model. For the choice of c_i and d_i (i = 1, 2), following the suggestion by Geisser (1984), we choose c_i = d_i = 1 which yields the uniform hyperprior. Scott and Berger (2006) discuss the choice of priors for the prior probability. They conclude that the objective prior (i.e., the uniform prior) for the prior probability can easily be implemented computationally while incorporation of subjective prior information can be beneficial when available. In our case, we have no subjective information about the prior probability of inclusion of the covariates, resulting in choosing a uniform prior. For more details, please refer to Geisser (1984), Scott and Berger (2006, 2008) and Cui and George (2008), among others.

2.2 Posterior computation

The joint posterior distribution for the parameters is

$$\pi (\beta ,\text{u},\tau ,\nu ,\gamma ,\kappa \mid \text{y},\text{x})\propto \underset{i=1}{\overset{n}{\Pi }}\underset{k=1}{\overset{T}{\Pi }}f\left\{\sum _{k=1}^K{\beta }_{ik}{\left({\text{x}}_{it}^{\prime }{\text{u}}_{tk}\right)}^{+}\right\}\pi (\beta \mid \gamma )\pi \left(\gamma \right)\pi (\text{u}\mid \nu ,\kappa )\pi (\nu \mid \kappa )\pi \left(\tau \right),$$

where β = (β₁, …, β_n)′, u = (u₁, …, u_T)′ and f(·) can be normal linear, Poisson and logistic regression models for the continuous, count and binary outcomes, respectively, described as

$$\begin{array}{cc}\hfill f(y_{it}\mid {\eta }_{it})& =\sqrt{\frac{\tau }{2\pi }}\text{exp}\left\{-\frac{\tau }{2}{\left(y_{it}-{\eta }_{it}\right)}^2\right\}(\text{normal}\text{linear}\text{with}{\eta }_{it}={\mu }_{it})\hfill \\ \hfill & =\frac{1}{y_{it}!}\text{exp}\{y_{it}{\eta }_{it}-\text{exp}\left({\eta }_{it}\right)\}(\text{Poisson}\text{with}{\eta }_{it}=\log {\mu }_{it})\hfill \\ \hfill & =\frac{\text{exp}\left(y_{it}{\eta }_{it}\right)}{1+\text{exp}\left({\eta }_{it}\right)}\left(\text{logistic}\text{with}{\eta }_{it}=\log \frac{{\mu }_{it}}{1-{\mu }_{it}}\right).\hfill \end{array}$$

We choose priors for the parameters as described in Section 2.1. The posterior computation relies on a stochastic search variable selection Gibbs sampling algorithm (George and McCulloch, 1993), in which we iteratively sample from the full conditional distributions of each of the parameters. For each element of β_i and ν, the posterior has a mixture structure with a point mass at zero and a conjugate (for normal linear) or non-conjugate (for Poisson and logistic) distribution. To sample from the non-conjugate distribution, we use adaptive rejection Metropolis sampling (Gilks et al., 1995). Under the linear normal case, reparameterization allows the model to have conditionally linear structure for each parameter which facilitates the use of conjugate priors. For the purpose of generality, we instead provide a general full conditional posterior distribution for sampling.

The posterior computation relies on the Gibbs sampler and Metropolis-Hastings algorithms. After initializing values for the parameters, the proposed MCMC algorithm proceeds which is detailed in Appendix. Samples from the joint posterior distribution of the parameters are generated by repeating these steps for a large number of iterations after apparent convergence. Obviously, for identity link, the parameters can be sampled from the conjugate full conditional distributions.

As to guidance of how to specify the initial number for truncated planes for a particular analysis, from the simulation experiments that we conducted, we found that a large initial number of truncated planes, K, may provide sufficient space for change of dimension. However, after a minimum necessary number reaches, any further increase only marginally affects the fit while the computation time increases dramatically. Too low values of K, however, result in an inflexible modelling of the unknown linear predictor. Thus, we recommend to start with at least 10 number of truncated planes for small sample sizes and for large sample sizes of n > 20, referring to the heuristic rule of thumb given by Ruppert (2002) in the context of penalized splines of K = min(40, n/4).

3 Model comparison

The deviance information criterion (DIC)(Spiegelhalter et al., 2002) is widely used as a model comparison tool. DIC is shown to be an approximation to a penalized loss function based on the deviance with a penalty derived from a cross-validation argument. However, the implicit approximation is valid only when the effective number of parameters is much smaller than the number of independent observations (Plummer, 2008). Plummer (2008) pointed out that in disease mapping, this assumption does not hold, resulting in that DIC under-penalizes the complex models. Plummer (2008) proposed penalized loss functions instead of p_D, the effective number of parameter, to assess model adequacy. However, as Plummer (2008) noticed, this method requires MCMC runs with each observation left out in turn. Such calculation is not feasible in general, especially for large datasets. In this paper, we consider the comparison method based on the conditional predictive ordinate (CPO) (Gelfand et al., 1992; Geisser, 1993; Dey et al., 1997; Sinha and Dey, 1997). The CPO for the ith observation at time t is defined as the cross-validated marginal posterior predictive density

$$\begin{array}{cc}\hfill {\text{CPO}}_{it}& =f(y_{it}\mid {\text{y}}_{\left(it\right)})\hfill \\ \hfill & =\int f(y_{it}\mid \theta )f(\theta \mid {\text{y}}_{\left(it\right)},{\text{x}}_{\left(it\right)})\text{d}\theta \hfill \\ \hfill & ={\left(\int \frac{1}{f(y_{it}\mid \theta ,{\text{x}}_i)}f(\theta \mid \text{y},\text{x})\text{d}\theta \right)}^{-1},\hfill \end{array}$$

where y_(it) denotes the vector of observations with the ith observation at time t deleted and θ is the vector of model parameters. The cross-validation likelihood can be estimated by

$$L_{CV}=\underset{i=1}{\overset{n}{\Pi }}\underset{t=1}{\overset{T}{\Pi }}{\text{CPO}}_{it}.$$

Since the quantity of the cross-validation likelihood is typically close to zero, the negative cross-validatory predictive log-likelihood (Spiegelhalter et al., 1996; Draper and Krnjajić, 2006) can be used

$$NLL{K}_{CV}=-\sum _{i=1}^n\sum _{t=1}^T\log {\text{CPO}}_{it}.$$

Since a closed form of CPO_it is usually unavailable, a Monte Carlo estimate of CPO_it can be obtained straightforwardly through MCMC samples ${\left\{{\theta }^{\left(s\right)}\right\}}_{s=1}^N$ from the postrior distribution f(θ|y,x)

$${\widehat{\text{CPO}}}_{it}={\left(\frac{1}{N}\sum _{s=1}^N\frac{1}{f(y_{it}\mid {\theta }^{\left(s\right)},{\text{x}}_i)}\right)}^{-1},$$

where N is the number of iterations after a burn-in period. The estimate of the negative cross-validatory predictive log-likelihood can be calculated accordingly. Since a large CPO indicates agreement between the observation and the model, a model with a smaller NLLK_CV for all observations implies a better fit.

4 A simulated example

The motivation of this simulation was to evaluate the performance of the proposed approach, including the accuracy of the estimates, the sensitivity to different choices of hyperparameters and comparison of the proposed model with other space-time models. Without loss of generality and for illustration purpose, we created the data based on Belgium map available from GeoBUGS in WinBUGS (Lunn et al., 2000) containing 43 districts. We considered the case of count responses. The data were generated for each of n = 43 districts over an observation period of T = 10 based on the model y_it ~ Poisson(E_it exp(η_it)), where the log-relative risk ${\eta }_{it}={\text{x}}_{it}^{\prime }\alpha +{\tilde{x}}_{it}^{\prime }{\xi }_i+{\nu }_i+{\delta }_t$, where ${\text{x}}_{it}={\tilde{x}}_{it}={(1,x_{it2},x_{it3},x_{it4},x_{it5})}^{\prime }$. E_it is an expected number of events obtained by Rn_it, where n_it is the population count in district i at time t and $R={\sum }_{it}{y}_{it}∕{\sum }_{it}{n}_{it}$. This model is similar to the one by Assunção (2003), where space-dependent covariates are included. The fixed effect α was chosen as (1, 1, 1, 0, 0)′, implying that the last two covariates are irrelevant. We generated ζi from a multivariate CAR, MVCAR(τ), where τ⁻¹ is a 3 × 3 covariance matrix with components along the row as {0.5, 0.2, 0.2, 0.2, 0.4, 0.2, 0.2, 0.2, 0.8}, v_i ~ N(0, 1) and and δ_t ~ N(δ_t−1, 2) for t = 2, …, T with δ₁ ~ N(0, 2). We generated x_itl ~ U(0, 1) for l = 2, …, 5. For practical reason, the expected count E_it was sampled from U(1, 5).

We specified the priors for the parameters of the proposed model as follows. We used Gamma(0.05, 0.05) as the prior for τ_k. The prior for the spatially structured random effects β_ik was chosen as the prior in (4) with $N({\stackrel{‒}{\beta }}_{{\partial }_{ik}},{\left({\tau }_k{m}_{ik}\right)}^{-1})$. For the time-varying bases u_tk,−1, the prior was chosen as N(u_t−1,k,−1, ν), where ν_l ZI-IG(κ_l, 0.05, 0.05) for l = 2, …, 5. The starting vector of u_tk,−1, u_0k,−1 was chosen as 0 ρ_k as 1. For a flexible hyperprior beta distribution of p_1,k0 and p_2,l0, we chose c = d = 1 which yields the uniform hyperprior. Following Holmes and Mallick (2001), we chose the initial number of truncated planes as K = 30. We also tried several larger initial numbers of truncated planes which yielded essentially identical results.

We implemented the analysis using the Gibbs sampling algorithm described in Section 2. We generated 50 000 iterations after a burn-in of 10 000 iterations. Convergence was assessed by using a variety of diagnostics described by Cowles and Carlin (1995) and implemented using CODA (Plummer et al., 2006) in R. The diagnostic tests showed rapid convergence and efficient mixing. The parameters were estimated by thinning the chain by factor of 5 to obtain a sample of size 10 000. Sensitivity test of the results to the prior specification was assessed by repeating the analysis with different hyperparameters, which showed very similar results.

We compared the proposed model (Model 5) with the four competing spatio-temporal models. The log-relative risks of these models are listed as follows:

$$\text{Model}1:{\eta }_{it}={\text{x}}_{it}^{\prime }\alpha +{\xi }_i+{\delta }_t,$$

$$\text{Model}2:{\eta }_{it}={\text{x}}_{it}^{\prime }\alpha +{\xi }_i+v_i+{\delta }_t,$$

$$\text{Model}3:{\eta }_{it}={\text{x}}_{it}^{\prime }\alpha +{\xi }_i+v_i+{\delta }_t+b_{it}\text{and}$$

$$\text{Model}4:{\eta }_{it}={\text{x}}_{it}^{\prime }\alpha +{\text{x}}_{it}^{\prime }{\xi }_i+v_i+{\delta }_t$$

In the first three models, we followed conventional settings by specifying the prior of α as ${\mathrm{N}}_p(0,{\sum }_{\alpha })$ with ${\sum }_{\alpha }~\text{IWishart}(p,{\sum }_0^{-1})$ and Σ₀ = {0.1, 0.005, 0.005, 0.005, 0.1, 0.005, 0.005, 0.005, 0.1}. The prior of ζ_i was chosen as $\mathrm{N}({\stackrel{‒}{\xi }}_i,{\left({\tau }_1{m}_i\right)}^{-1})$ with ${\stackrel{‒}{\xi }}_i=m_i^{-1}{\sum }_{j\in \partial i}{\xi }_j$ and τ₁ ~ Gamma(0.005, 0.005). The prior of v_i was taken as $\mathrm{N}(0,{\tau }_2^{-1})$ with τ₂ ~ Gamma(0.005, 0.005). The prior of δ_t was chosen as $\mathrm{N}({\delta }_{t-1},{\tau }_3^{-1})$ with ${\delta }_0~\mathrm{N}(0,{\tau }_3^{-1})$ and τ₃ ~ Gamma(0.005, 0.005). We chose the prior of b_it to be $\mathrm{N}(0,{\tau }_4^{-1})$ with τ₄ ~ Gamma(0.005, 0.005). For Model 4, the prior of ζ_i was chosen as $N({\stackrel{‒}{\xi }}_{{\partial }_i},{\left({\sum }_{\xi }{m}_i\right)}^{-1})$ with ${\stackrel{‒}{\xi }}_{{\partial }_i}=m_i^{-1}{\sum }_{j\in {\partial }_i}{\xi }_j$ and ${\sum }_{\xi }~\text{Wishart}(p,{\sum }_0)$. We implemented Models 1-4 using WinBUGS (Lunn et al., 2000). Although Model 5 can also be implemented by WinBUGS, it is computationally intensive. A C program was instead written to carry out the proposed algorithm.

The second column in Table 1 presents the comparison of the estimated negative cross-validatory predictive log-likelihoods for the five models. We can see that Model 1 and Model 2 are basically the same. This is due to the fact that the unstructured random effects vary moderately across regions which is consistent with the setting. It is evident that Models 3-5 appear much better than the first two models with Model 5 being the best. Since Model 4 is the model where the data are generated, its performance is very close to Model 5.

Table 1.

Model comparison based on the negative cross-validatory log-likelihood for the simulated example and the application to the low birth weight data in South Carolin

Model	NLLKCV, sim	NLLKCV,app
Model 1	1160.967	1820.849
Model 2	1161.409	1802.395
Model 3	767.532	1746.393
Model 4	637.534	1763.222
Model 5	634.297	1738.383

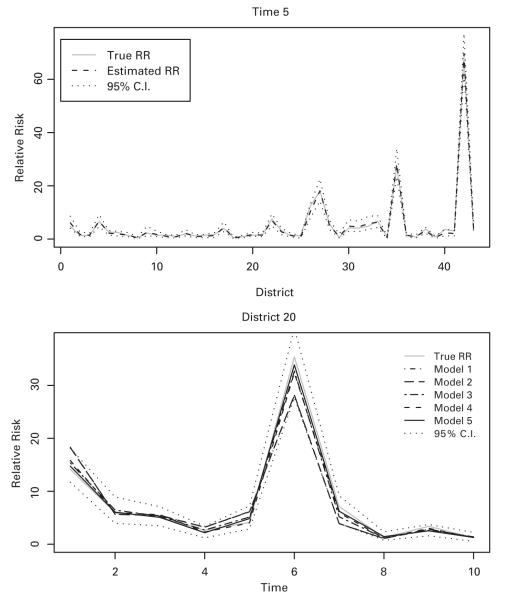
In Figure 1, the upper plot represents true and pointwise estimated relative risks with 95% credible intervals from the proposed approach (Model 5) across all districts at time 5. The lower plot shows true and estimated relative risks for district 20 over time based on the five models along with 95% credible intervals from Model 5. It is clear that the proposed model provides closer estimates than the others.

Figure 1.

Results from the simulated example. Top panel: true and estimated relative risks with 95% pointwise credible intervals from the proposed approach (Model 5) across all districts at time 5. Bottom panel: true and estimated relative risks with 95% pointwise credible intervals from the proposed approach across time points for district 20, along with posterior estimates from Models 1-4

Figure 2 shows posterior densities of variance parameters ν₄ and ν₅ and boxplots of the posterior means for the time-varying basis components u₄ and u₅ at each time point in the simulated example. We can see that the two variances ν₄ and ν₅ corresponding to the time-varying coefficients, u_tk4 and u_tk5, are close to zero, implying that x_it4 and x_it5 are not involved. This is consistent with the simulation design.

Figure 2.

Left panel: posterior densities of the parameters ν₄ and ν₅ in the simulated example. Right panel: boxplots of the posterior means for the time-varying basis components u₄ and u₅ at each time point in the simulation. The horizontal line denotes the true value

Sensitivity of the results to the prior specification was assessed by repeating the analysis with different hyperparameters. Figure 3 shows the histograms of the posterior number of truncated planes and the probabilities of inclusion of covariates in the basis functions. We noticed that the average number of components varies insubstantially with various choices of the hyperparameters. It is evident that the last two covariates are basically excluded from the model, which is consistent with the design of the covariates.

Figure 3.

(a) Histogram of the posterior number of truncated planes and (b) the probabilities of inclusion of covariates in the basis functions for the simulated data

5 Application

As an illustration, we applied the approach to the data of county-specific low birth weights (i.e., birth weight is less than 2500 gram) across 46 counties in the state of South Carolina during the period 1997-2007. A number of county-level low birth weights were obtained from South Carolina Department of Health and Environmental Control. The population density, the proportion of African American population, the household income and the poverty rate were acquired from the U.S. census. The unemployment rates were attained from the U.S. Bureau of Labor Statistics.

In the data, y_it denotes the number of low birth weights in county i during year t and x_it = (1, x_it1, x_it2, x_it3, x_it4, x_it5)′ with x_it1 indicating the county-level population density, x_it2 the proportion of black people, x_it3 the median household income, x_it4 the poverty rate and x_it5 the unemployment rate in county i for year t, for i = 1, …, 46 and t = 1, …, 11. The population density is defined as population divided by the total land area in square miles. The expected low birth weight counts for county i in year t, E_it, is calculated by n_it R, where n_it is the total number of births for county i in year t and R is the overall statewide low birth weight rate which can be calculated by the total low birth weight counts divided by the total number of births over the entire counties and time periods.

We completed the specification of the proposed model by choosing prior Gamma(0.05, 0.05) for τ_k and ZI-IG(0.05, 0.05) for ν_l. The prior probability of a point mass at zero for the variance components of β_i and u_tk,−1 is chosen to follow Beta(1, 1). Since five covariates were initially included in the model, the initial number of truncated planes was chosen as 30. We collected 10 000 samples by thinning 50 000 samples by factor of 5 after a burn-in of 10 000 iterations.

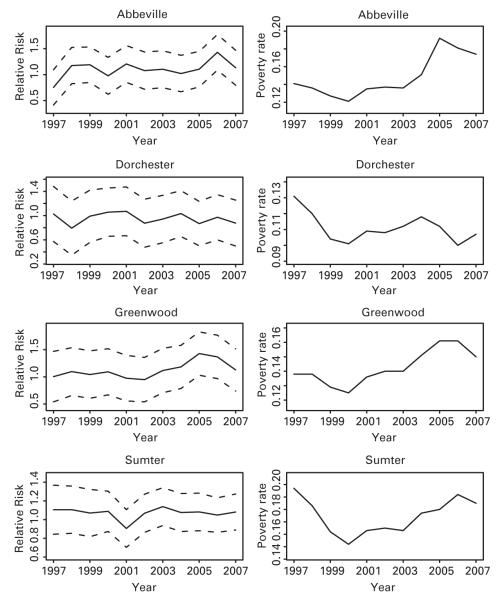
Figure 4 displays spatial maps of the posterior means and the standard deviations of relative risk in years 1997, 2002 and 2007. Figure 5 shows the posterior means and the 95% pointwise credible intervals for relative risk of low birth weight in four representative counties (randomly selected) along with their corresponding poverty rates over years 1997-2007. We can see that the estimated relative risk of low birth weight in County Dorchester with decreasing poverty rates slightly decreases over the 11-year time period. Counties Abbeville and Greenwood with increasing poverty rates basically have ascending trends over time. County Sumter roughly has a ‘V’ shape of poverty rate over time and the estimated relative risks, and interestingly the estimated relative risk has a similar curve. We also investigated the sensitivity of the number of truncated planes for β_i to various choices of the hyperparameters, which varies slightly. The posterior mean of the number of truncated planes is 12.4 with 95% credible interval (9.6, 16.5). We note that proportion of black people, the median household income, the poverty rate and the unemployment rate are included in the model with posterior probability of inclusion over 97% for each covariate while the population density has over 98% posterior probability of exclusion, implying that the population density can be excluded from the model at 5% significant level.

Figure 4.

Spatial maps of (a) posterior mean and (b) posterior standard deviation (STD) of relative risks in years 1997, 2002 and 2007 for the low birth weight data in South Carolina. Left panel: posterior means of relative risk. Right panel: posterior STD of relative risk

Figure 5.

Posterior means and 95% pointwise credible intervals of relative risks of low birth weight for the four counties along with the corresponding poverty rates in SC through 11-year time period. Left panel: solid lines denote posterior means of relative risks and dashed lines denote 95% pointwise credible intervals. Right panel: poverty rate over time

The third column in Table 1 shows the estimated negative cross-validatory predictive log-likelihoods for the proposed model along with the four competing models. We can see that the estimated NLLK_CV,app values for Model 1 and 2 are close while the other three models have much lower NLLK_CV,app values. The proposed model (Model 5) has the smallest NLLK_CV,app value, evincing that it is the best among all the models. The priors of the parameters and the settings for the hyperparameters used were similar to those in the models of the simulated example.

6 Discussion

We proposed a Bayesian regression model with multivariate linear splines for the analysis of space-time data. The proposed approach extends generalized multivariate regression splines (Holmes and Mallick, 2001) to flexibly accommodate the space- and time-specific covariates, allowing for flexible orientation and position of the covariate plane by incorporating time-varying basis functions.

One of the major advantages of a semiparametric modelling specification is the ability to flexibly model variation within a localized areas of a study region. In the proposed model, we allow geographically localized definition of the dependence of covariates and provide a flexible method of incorporation of variates via zero-inflation mixture priors. Although in the examples the covariate profiles show some impact on the overall county rates, it is evident that the estimated negative cross-validatory predictive log-likelihoods supports the proposed model over conventional space-time random effect models. This suggests that even with the degree of para-meterization, there is an overall benefit in the use of such semiparametric models, especially when covariates are to be flexibly accommodated. Computational intensity is noticed in the proposed approach, though it is reasonably efficient when it is coded in C language. Future work will focus on developing space-time models with nonparametric modelling and clustering on spatial effects coefficients, and on developing a more efficient sampling method.

Appendix

Full conditional distributions in Section 2.2.

Step 1: Update β_ik, for k = 1, …, K, from its full conditional posterior distribution,

$$\underset{i=1}{\overset{n}{\Pi }}\underset{t=1}{\overset{T}{\Pi }}f\left\{\sum _{k=1}^K{\beta }_{ik}{\left({\text{x}}_{it}^{\prime }{\text{u}}_{tk}\right)}_{+}\right\}\text{exp}\left\{-\frac{{\tau }_k}{2}\sum _{i=1}^n\sum _{i~j}{({\beta }_{ik}-{\beta }_{jk})}^2\right\}$$

with the conditional posterior probability

$$1-{\widehat{p}}_{1,k}=Pr({\gamma }_k=0\mid \beta ,{\gamma }_{-k})=\frac{1}{1+C_k},$$

where C_k = p_1,k0/(1 – p_1,k0) × L(β_k = 0, β_−k, u, τ, ν, γ)/L(β_k = β_k, β_−k, u, τ, ν, γ) with $L({\beta }_k,{\beta }_{-k},\text{u},\tau ,\nu ,\gamma )={\Pi }_{i=1}^n{\Pi }_{t=1}^{T}f\left\{{\sum }_{k=1}^K{\beta }_{ik}{\left({\text{x}}_{it}^{\prime }{\text{u}}_{tk}\right)}_{+}\right\}$ and β_k = (β_1k, …, β_nk)′. Otherwise, β_ik is assigned to be zero. Simultaneously, γ_k (k = 1, …, K) can be sampled from its full conditional posterior distribution, $\left({\widehat{p}}_{1,k}\right)$.

Step 2: Update p_1,k0 from its full conditional distribution,

$$p_{1,k_0}\mid \gamma ~\text{Beta}(c_1+n_{\gamma },d_1+K-n_{\gamma }),$$

where γ corresponds to a model from the model space M containing 2^K models, and n_γ denotes the number of excluded predictors in the model, i.e., ${\sum }_{k=1}^K{\gamma }_k$.

Step 3: Update τ_k, for k = 1, …, K, from its full conditional posterior distribution,

$$\text{Gamma}\left(a_{\tau }+\frac{n}{2},b_{\tau }+\frac{1}{2}\sum _{t=1}^n\sum _{i~j}{({\beta }_{ik}-{\beta }_{jk})}^2\right).$$

Step 4: Update ν_l, for l = 2, …, p, from its full conditional distribution with a point mass at zero

$${\kappa }_l{\delta }_0\left({\nu }_l\right)+(1-{\kappa }_l)\text{IG}\left\{a_{\nu }+\frac{KT}{2},b_{\nu }+\frac{1}{2}\sum _{t=1}^T\sum _{k=1}^K{(u_{tkl}-{\rho }_k{u}_{t-1,kl})}^2\right\},$$

where ${\kappa }_l~\text{Bern}\left({\widehat{p}}_{2,l}\right)$ with ${\widehat{p}}_{2,l}=\left(p_{2,l0}L(\beta ,{\text{u}}_l=0,\tau ,\nu ,\gamma )\right)∕(p_{2,l0}L(\beta ,{\text{u}}_l=0,\tau ,\nu ,\gamma )+(1-p_{2,l0})L(\beta ,{\text{u}}_l=u_l,{\text{u}}_{-l},\tau ,\nu ,\gamma ))$ and u_l = {u_tkl}_t,k.

Step 5: Update u_tk from its full conditional distribution, for t = 1}, …, T and k = 1, …, K,

$$\underset{i=1}{\overset{n}{\Pi }}\underset{t=1}{\overset{T}{\Pi }}f\left\{\sum _{k=1}^K{\beta }_{ik}{\left({\text{x}}_{it}^{\prime }{\text{u}}_{tk}\right)}_{+}\right\}\text{exp}\left\{-\frac{1}{2}{(u_{tk}-{\rho }_k{\text{u}}_{t-1},k)}^{\prime }{\nu }^{-1}({\text{u}}_{tk}-{\rho }_k{\text{u}}_{t-1,k})\right\},$$

For each t and k, we standardize the components of u_tk,−1 and u_tk1 = x_it,−1

Step 6: Update p_2,l0 from its full conditional distribution,

$$p_{2,l0}\mid \kappa ~\text{Beta}(c_2+n_{\kappa },d_2+p-1-n_k),$$

where n_κ denotes the number of excluded predictors in the model, i.e., ${\sum }_{l=2}^p{\kappa }_l$.

Step 7: When link function is identity, update τ from its full conditional distribution

$$\text{Gamma}\left\{c_{\tau }+\frac{nT}{2},d_{\tau }+\frac{1}{2}\sum _{i=1}^n\sum _{t=1}^T{(y_{it}-{\eta }_{it})}^2\right\},$$

where π(τ) ~ Gamma(c_τ, d_τ).